State Estimation of Memristor Neural Networks with Model Uncertainties

Abstract

This paper is concerned with the problem of state estimation of memristor neural networks with model uncertainties. Considering the model uncertainties are composed of time-varying delays, floating parameters and unknown functions, an improved method based on long short term memory neural networks (LSTMs) is used to deal with the model uncertainties. It is proved that the improved LSTMs can approximate any nonlinear model with any error. On this basis, adaptive updating laws of the weights of improved LSTMs are proposed by using Lyapunov method. Furthermore, for the problem of state estimation of memristor neural networks, a new full-order state observer is proposed to achieve the reconstruction of states based on the measurement output of the system. The error of state estimation is proved to be asymptotically stable by using Lyapunov method and linear matrix inequalities. Finally, two numerical examples are given, and simulation results demonstrate the effectiveness of the scheme, especially when the memristor neural networks with model uncertainties.

1. Introduction

Since the prototype of memristor was born in 1971 by Chua [1], memristor have been widely used in all walks of life. The vector–matrix multiplication is realized by the crossbar array structure of memristor, and a neural network can be realized by the corresponding coding scheme based on it. Various neural networks based on memristor hardware have been developed rapidly. Because of an incomparable advantage that memristor neural networks can reflect the memorized information, the memristor neural networks are particularly suitable for self-adaptability, nonlinear systems, self-learning, and associative storage, so memristor neural networks are widely used in brain simulation, pattern recognition, neural morphologic computation, knowledge acquisition, and various hardware applications involving neural networks [2,3,4,5,6,7,8,9,10,11,12,13,14,15]. To list a few, the experimental implementation of transistor-free metal-oxide memristor crossbars, with device variability sufficiently low to allow operation of integrated neural networks, in a simple network: a single-layer perceptron (an algorithm for linear classification) was shown in [16]. In [17], a structure suppressing the overshoot current was investigated to approach the conditions required as an ideal synapse of a neuromorphic system. In [18], fully memristive artificial neural networks were built by using diffusive memristors based on silver nanoparticles in a dielectric film. The electrical properties and conduction mechanism of the fabricated IGZO-based memristor device in a 10 × 10 crossbar array were analyzed in [19]. Operation of one-hidden layer perceptron classifier entirely in the mixed-signal integrated hardware was demonstrated in [20]. Therefore, the research on memristor neural networks is very necessary and meaningful. Although many papers have extended the memristor neural networks and solved some problems, there are still problems in the memristor neural networks. Therefore, memristor neural networks including their various kinds of deformation have broad market prospects. Especially, the research on memristor neural networks with model uncertainties has become a hot topic.

In recent decades, scholars have carried out a great amount of research and analysis on memristor neural networks. The results can be broadly divided into four categories: (1) Stability analysis of memristor neural networks [21,22,23,24,25]; (2) State estimation of memristor neural networks [26,27,28,29]; (3) Synchronization problem of memristor neural networks [30,31,32]; (4) Control problem of memristor neural networks [33,34,35]. In practice, time-varying delays must exist in the hardware implementation of memristor neural networks. Due to the existence of time-varying delays, the future states of the system are affected by the previous states, which leads to instability of the system and poor control performance. Consequently, state estimation of memristor neural networks is of great research value and a large part of the research has focused on state estimation of memristor neural networks. Note that the above results are generally based on the known structures and parameters of memristor neural networks without model uncertainties. In practice, the hardware implementation of memristor neural networks usually fails to attain the ideal design values, and there are design deviations. In particular, model uncertainties often exist in the hardware implementation of memristor neural networks. Therefore, model uncertainties and model errors are common in hardware memristor neural networks. Similarly, affected by model uncertainties, state estimation of memristor neural networks is also a challenging problem. Considering the above analysis, it is needed to study state estimation of memristor neural networks with model uncertainties.

A great amount of valuable research on state estimation of memristor neural networks with model uncertainties can be found in [26,27,28,29,36,37,38]. In [26], it used passivity theory to deal with the state estimation problem of memristor-based recurrent neural networks with time-varying delays. By using Lyapunov–Krasovskii function (LKF), convex combination technique and reciprocal convexity technique, a delay-dependent state estimation matrix was established, and the expected estimator gain matrix was obtained by solving linear matrix inequalities (LMIs). It is a pity that the model of the system must be determined and the functions in the system must be known. In [27], for memristor neural networks with randomness, the random system was transformed into an interval parameter system by Filippov, and the H∞ state observer was designed on this basis. One of the problems in the paper is that it is a random interference that affects the system rather than model uncertainty. The random interference is regular and limited. In [28], for memristor-based bidirectional associative memory neural networks with additive time-varying delays, a state estimation matrix was constructed by selecting an appropriate LKF and using the Cauchy-Schwartz-based summation inequality, and the gain matrix was obtained by the LMIs. The paper also has the problems mentioned above. In [29], for a class of memristor neural networks with different types of inductance functions and uncertain time-varying delays, a state estimation matrix was constructed by selecting a suitable LKF, and the gain matrix was solved by using the LMIs and Wirtinger-type inequality. Model uncertainty is involved in the paper, but it is only for the uncertainty of the time-varying delays. In [36], an extended dissipative state observer was proposed by using nonsmooth analysis and a new LKF. In [37], based on the basic properties of quaternion-valued, a state observer was designed for quaternion-valued memristor neural networks, and algebraic conditions were given to ensure global dissipation. The methods proposed in [36,37] are not suitable for memristor neural networks with model uncertainties. In [38], for memristor neural networks with random sampling, the randomness was represented by two different sampling periods, which satisfied a Bernoulli distribution. The random sampling system was transformed into a system with random parameters by using an input delay method. On this basis, a state observer was designed based on the LMIs and a LKF. Through the above discussion, it is not difficult to find that a similar method is used to estimate the states of memristor neural networks. By selecting an appropriate LKF, the state observation matrix is constructed based on the structure of the system, and the gain matrix is solved by utilizing the LMIs. It can be seen from the above analysis that most studies on state estimation of memristor neural networks have the same problem, which requires that the system cannot contain the model uncertainties. Some studies include model uncertainties, which are only for time-varying delays. Other studies also include model uncertainties, which are only about the fluctuation of parameters. There are few studies on the state estimation of memristor neural networks whose model uncertainties include time-varying delays, floating parameters and unknown functions. It has a huge research potential to tap.

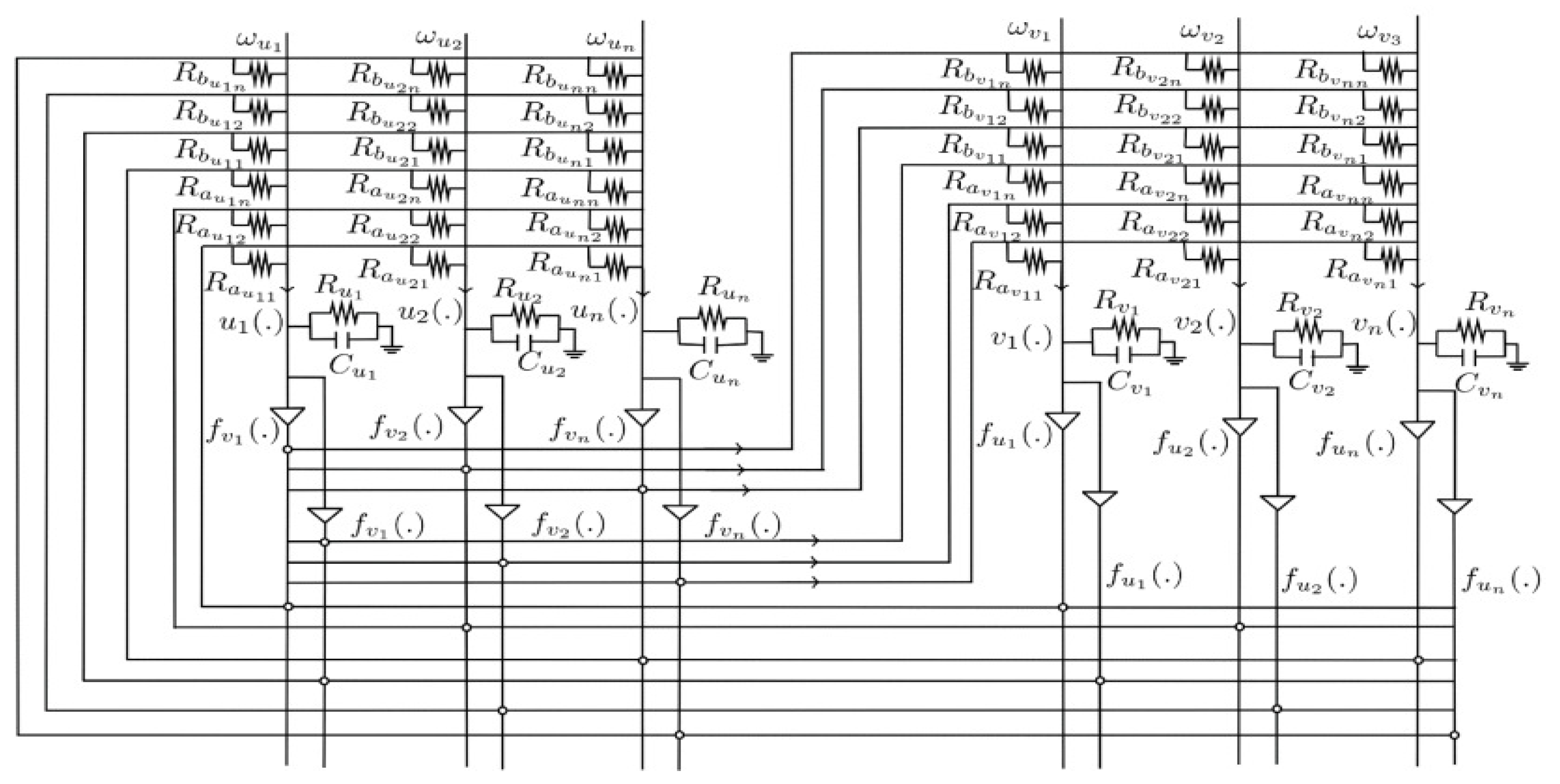
When the memristor neural networks are designed and translated into hardware by the designer, the model uncertainties of the system only include the time-varying delays and floating parameters. In practice, the situation is not unique. Sometimes it is necessary to analyze the memristor neural networks designed by other designers. At this time, the model uncertainties of memristor neural networks include time-varying delays, floating parameters and unknown functions. The model of the memristor neural networks can be designed as in Figure 1 [28]. Motivated by the above discussion, the main concern of this paper is to design a state observer for memristor neural networks with model uncertainties, which include time-varying delays, floating parameters and unknown functions. Model uncertainties are composed of current states, past states and unknown functions. In order to approach the model uncertainties that contain memory information, improved long short term memory neural networks (LSTMs) are proposed. It is theoretically proved that the improved LSTMs can approach the model uncertainties with arbitrary error. Memristor neural networks with model uncertainties can be transformed into a new system with an improved LSTMs. On this basis, a full-order state observer is designed according to the output of the system. An error matrix of the states is constructed by a designed LKF, and the gain matrix is solved by the LMIs. In order to make the new system more accurate, a new error matrix of the states is constructed by using Young’s inequality based on a LKF. On this basis, adaptive updating laws of the weights of improved LSTMs are designed to reduce the errors of the states. The main contributions of this paper are as follows.

• Improved LSTMs are proposed for memristor neural networks with model uncertainties. It is proved that the improved LSTMs can well approach the model uncertainties in memristor neural networks. Model uncertainties include time-varying delays, floating parameters and unknown functions. It has not been seen in other studies.
• By utilizing the LMIs and a LKF, a full-order observer based on the output of the system is presented to obtain state information and solve the problem of state estimation.
• By using Young’s inequality and a designed LKF, adaptive updating laws of the weights of improved LSTMs are given to obtain the new system with improved LSTMs precisely.

This paper is organized as follows. In Section 2, the problem is formulated, and several essential assumptions and lemmas are listed. Section 3 presents the primary theorems, including improved LSTMs, observer design for memristor neural networks with model uncertainties, and adaptive updating laws of the weights of improved LSTMs. In Section 4, the effectiveness of the proposed scheme is demonstrated through numerical examples. Finally, the conclusions are drawn in Section 5.

Notation: ${\mathcal{R}}^n$ denotes the n dimensional Euclidean space. For a given matrix $\mathbf{A}$ or vector $\mathbf{B}$, ${\mathbf{A}}^{\mathrm{T}}$ and ${\mathbf{B}}^{\mathrm{T}}$ denote their transpose, and $tr\left\{\mathbf{A}\right\}$ denotes its trace. $\mathbf{A}<0$ indicate a negative definite matrix.

2. Preliminaries

Considering the memristor neural networks as follows, the same model can be found in [26,27,28,36,37],

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \left\{\begin{array}{c}{\dot{x}}_1\left(t\right)=-a_1{x}_1\left(t\right)+{\displaystyle \sum _{j=1}^n}{b}_{1j}\left(x_1\left(t\right)\right)f_j\left(x_j\left(t\right)\right)+{\displaystyle \sum _{j=1}^n}{c}_{1j}\left(x_1\left(t\right)\right)g_j\left(x_j(t-{\tau }_j\left(t\right))\right)+U_1\hfill \\ {\dot{x}}_2\left(t\right)=-a_2{x}_2\left(t\right)+{\displaystyle \sum _{j=1}^n}{b}_{2j}\left(x_2\left(t\right)\right)f_j\left(x_j\left(t\right)\right)+{\displaystyle \sum _{j=1}^n}{c}_{2j}\left(x_2\left(t\right)\right)g_j\left(x_j(t-{\tau }_j\left(t\right))\right)+U_2\hfill \\ ⋮\hfill \\ {\dot{x}}_n\left(t\right)=-a_n{x}_n\left(t\right)+{\displaystyle \sum _{j=1}^n}{b}_{nj}\left(x_n\left(t\right)\right)f_j\left(x_j\left(t\right)\right)+{\displaystyle \sum _{j=1}^n}{c}_{nj}\left(x_n\left(t\right)\right)g_j\left(x_j(t-{\tau }_j\left(t\right))\right)+U_n\hfill \\ y_1\left(t\right)={\displaystyle \sum _{j=1}^n}{h}_{1j}{x}_j\left(t\right)\hfill \\ y_2\left(t\right)={\displaystyle \sum _{j=1}^n}{h}_{2j}{x}_j\left(t\right)\hfill \\ ⋮\hfill \\ y_m\left(t\right)={\displaystyle \sum _{j=1}^n}{h}_{nj}{x}_j\left(t\right)\hfill \end{array}\right.,\end{array}\end{array}$$

(1)

where $x_i\left(t\right)(i=1,\cdots ,n)$ represents the state variable of the memristor neural networks, and n is the system dimension; $a_i(i=1,\cdots ,n)$ is the self-feedback coefficient, which satisfies $a_i>0$; $f_j\left(x_j\left(t\right)\right)$ and $g_j\left(x_j(t-{\tau }_j\left(t\right))\right)$$(j=1,\cdots ,n)$ represent the activation functions of states $x_j\left(t\right)$ and $x_j(t-{\tau }_j\left(t\right)$ respectively; $b_{ij}\left(x_i\left(t\right)\right)$ represents the memristive synaptic connection weight between states $x_i\left(t\right)$ and $x_j\left(t\right)$, and $c_{ij}\left(x_i\left(t\right)\right)$ represents the memristive synaptic connection weight between states $x_i\left(t\right)$ and $x_j(t-{\tau }_j\left(t\right))$; ${\tau }_j(j=1,\cdots ,n)$ denotes the time-varying delay which satisfies $0⩽{\tau }_j⩽{\tau }_{max}$, and ${\tau }_{max}$ is the upper bound constant; $U_i(i=1,\cdots ,n)$ denotes the input of the system, and $y_i\left(t\right)(i=1,\cdots ,m)$ represents the measurement output of the system; $h_{ij}(i=1,\cdots ,m;j=1,\cdots ,n)$ is the measurement constant from state $x_j\left(t\right)$ to output $y_i\left(t\right)$, and m is the output dimension.

The system (1) can be represented in vector form,

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \left\{\begin{array}{c}\dot{\mathbf{x}}\left(t\right)=-\mathbf{A}\mathbf{x}\left(t\right)+\mathbf{B}\mathbf{f}\left(\mathbf{x}\left(t\right)\right)+\mathbf{C}\mathbf{g}\left(\mathbf{x}(t-\tau \left(t\right))\right)+\mathbf{U}\hfill \\ \mathbf{y}\left(t\right)=\mathbf{H}\mathbf{x}\left(t\right)\hfill \end{array}\right.,\end{array}\end{array}$$

(2)

where $\mathbf{A}=\left[\begin{array}{cccc}{a}_1& 0& \cdots & 0\\ 0& a_2& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & a_n\end{array}\right]$, $\mathbf{B}=\left[\begin{array}{cccc}{b}_{11}& b_{12}& \cdots & b_{1n}\\ b_{21}& b_{22}& \cdots & b_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ b_{n1}& b_{n2}& \cdots & b_{nn}\end{array}\right]$, $\mathbf{U}=\left[\begin{array}{c}{U}_1\\ U_2\\ ⋮\\ U_n\end{array}\right]$, $\mathbf{f}\left(\mathbf{x}\left(t\right)\right)=\left[\begin{array}{c}{f}_1\left(x_1\left(t\right)\right)\\ f_2\left(x_2\left(t\right)\right)\\ ⋮\\ f_n\left(x_n\left(t\right)\right)\end{array}\right]$, $\mathbf{g}\left(\mathbf{x}(t-\tau \left(t\right))\right)=\left[\begin{array}{c}{g}_1\left(x_1(t-{\tau }_1\left(t\right))\right)\\ g_2\left(x_2(t-{\tau }_2\left(t\right))\right)\\ ⋮\\ g_n\left(x_n(t-{\tau }_n\left(t\right))\right)\end{array}\right]$, $\mathbf{y}\left(t\right)=\left[\begin{array}{c}{y}_1\left(t\right)\\ y_2\left(t\right)\\ ⋮\\ y_m\left(t\right)\end{array}\right]$, $\mathbf{C}=\left[\begin{array}{cccc}{c}_{11}& c_{12}& \cdots & c_{1n}\\ c_{21}& c_{22}& \cdots & c_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ c_{n1}& c_{n2}& \cdots & c_{nn}\end{array}\right]$, $\mathbf{H}=\left[\begin{array}{cccc}{h}_{11}& h_{12}& \cdots & h_{1n}\\ h_{21}& h_{22}& \cdots & h_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ h_{m1}& c_{m2}& \cdots & h_{mn}\end{array}\right]$, $\mathbf{x}\left(t\right)=\left[\begin{array}{c}{x}_1\left(t\right)\\ x_2\left(t\right)\\ ⋮\\ x_n\left(t\right)\end{array}\right]$.

As mentioned in the introduction, most studies involve model uncertainties that only include floating parameters. In the process of neural network hardware implementation as memristor neural networks, the memristive synaptic connection weights $b_{ij}$ and $c_{ij}$ will produce deviations [28]. The fluctuation of parameters $b_{ij}$ and $c_{ij}$ is regarded as model uncertainty. This is the starting point of much research on state estimation of memristor neural networks, such as [26,27,28,36,37,38]. Some studies regard time-varying delay ${\tau }_j\left(t\right)$ as model uncertainty and study state estimation of memristor neural networks based on it, for example [29]. It should be noted that model uncertainties in all the above studies do not include $f_i\left(x_i\left(t\right)\right)$ and $g_i\left(x_i(t-{\tau }_i)\right)$. Both $f_i\left(x_i\left(t\right)\right)$ and $g_i\left(x_i(t-{\tau }_i)\right)$ must be known, and $b_{ij}$ and $c_{ij}$ float within the ideal range. If $f_i\left(x_i\left(t\right)\right)$ and $g_i\left(x_i(t-{\tau }_i)\right)$ are unknown, and the ideal values of $b_{ij}$ and $c_{ij}$ are unknown, the model uncertainties include floating parameters $b_{ij}$ and $c_{ij}$, time-varying delay ${\tau }_j\left(t\right)$ and unknown functions $f_i\left(x_i\left(t\right)\right)$ and $g_i\left(x_i(t-{\tau }_i)\right)$, and all the above studies are not applicable. The state estimation of memristor neural networks with model uncertainties including floating parameters, time-varying delays and unknown functions is the main concern in this paper.

Remark 1.

In other studies, model uncertainties only include floating parameters $b_{ij}$ and $c_{ij}$ or time-varying delay ${\tau }_j\left(t\right)$. Functions $f_i\left(x_i\left(t\right)\right)$ and $g_i\left(x_i(t-{\tau }_i)\right)$ must be known. In this paper, model uncertainties include floating parameters $b_{ij}$ and $c_{ij}$, time-varying delay ${\tau }_j\left(t\right)$ and unknown functions $f_i\left(x_i\left(t\right)\right)$ and $g_i\left(x_i(t-{\tau }_i)\right)$.

As shown in system (2), the model uncertainties contain memory information $x_i(t-{\tau }_i)$. The LSTMs are the most suitable to deal with the model uncertainties. LSTMs are networks of basic LSTMs cells, and the architecture of a conventional LSTMs cell is illustrated in Figure 2. A memory cell, an input gate, an output gate and a forgetting gate make up a LSTMs cell. The forgetting gate, input gate, and output gate respectively determine whether historical information, input information, and output information are retained [39]. The specific computation is shown in Equation (3).

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \left(\begin{array}{c}{\mathbf{f}}_t\\ {\mathbf{i}}_t\\ {\mathbf{o}}_t\\ {\mathbf{g}}_t\end{array}\right)& =\left(\begin{array}{c}\sigma \left({\mathbf{W}}_f\left[{\mathbf{x}}_t,{\mathbf{h}}_{t-1}\right]+{\mathbf{b}}_f\right)\\ \sigma \left({\mathbf{W}}_i\left[{\mathbf{x}}_t,{\mathbf{h}}_{t-1}\right]+{\mathbf{b}}_i\right)\\ \sigma \left({\mathbf{W}}_o\left[{\mathbf{x}}_t,{\mathbf{h}}_{t-1}\right]+{\mathbf{b}}_o\right)\\ tanh\left({\mathbf{W}}_g\left[{\mathbf{x}}_t,{\mathbf{h}}_{t-1}\right]+{\mathbf{b}}_g\right)\end{array}\right)\hfill \\ \hfill {\mathbf{c}}_t& ={\mathbf{f}}_t\otimes {\mathbf{c}}_{t-1}\oplus {\mathbf{i}}_t\otimes {\mathbf{g}}_t\hfill \\ \hfill {\mathbf{h}}_t& ={\mathbf{o}}_t\otimes tanh\left({\mathbf{c}}_t\right),\hfill \end{array}\end{array}$$

(3)

where ${\mathbf{f}}_t$ denotes the forgetting gate; ${\mathbf{i}}_t$ and ${\mathbf{o}}_t$ represent input gate and output gate, respectively; ${\mathbf{g}}_t$ is the updating vector of the LSTM cell; ${\mathbf{h}}_t$ is the hidden state vector; ${\mathbf{h}}_{t-1}$ is the hidden state vector at step $t-1$; ${\mathbf{x}}_t$ is the input vector of the LSTM cell; ${\mathbf{c}}_t$ is the state vector of the cell; ${\mathbf{c}}_{t-1}$ is the state vector of the cell at step $t-1$; $\mathbf{W}$ is the weight matrix and $\mathbf{b}$ refers to the bias vector; $\sigma$ and $tanh(·)$ are the sigmoid and tanh activation functions, respectively; ⊗ and ⊕ represent elementwise multiplication and addition, respectively.

Remark 2.

LSTMs cell is not completely suitable for estimating the states of memristor neural networks with model uncertainties. LSTMs cell needs to be improved to save computation and be more suitable for state estimation.

Moreover, in order to improve the LSTMs, design the state observer of memristor neural networks with model uncertainties, and derive the updating laws of the weights of the improved LSTMs, some assumptions and lemmas need to be introduced for the following proof.

Assumption 1.

The functions $f_j(·)$ and $g_j(·)$ satisfy local Lipschitz conditions. For all $k,p\in \mathcal{R}$, have $\left|f_j\left(k\right)-f_j\left(p\right)\right|⩽K_f\left|k-p\right|$ and $\left|g_j\left(k\right)-g_j\left(p\right)\right|⩽K_g\left|k-p\right|$, where $K_f$ and $K_g$ are Lipschitz constants, and satisfy $f_j\left(0\right)=g_j\left(0\right)=0$.

$f_j(·)$ and $g_j(·)$ are the activation functions of memristor neural networks, so Assumption 1 is generally tenable.

Lemma 1

([40]). $k(·)$ is a continuous function defined on a set Ω. Multilayer neural networks can be defined as,

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \overline{k}={\mathbf{W}}^{\mathrm{T}}S\left(\mathbf{VI}\right),\end{array}\end{array}$$

where $\mathbf{W}$ and $\mathbf{V}$ are the second weight matrix and the first weight vector of the Multilayer neural networks, respectively; $\mathbf{I}$ is the input vector of Multilayer neural networks, and $S(·)$ is the activation function of Multilayer neural networks.

Then, for a given desired level of accuracy $\epsilon >0$, there exist the ideal weights $\overline{\mathbf{W}}$ and $\overline{\mathbf{V}}$ to satisfy the following inequality,

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \underset{\mathbf{I}\in \Omega }{sup}\parallel k(·)-\overline{k}\parallel ⩽\epsilon .\end{array}\end{array}$$

Lemma 2.

(Young’s inequality) For all $x,y\in \mathcal{R}$, the following inequality holds,

$$\begin{array}{c}\hfill \begin{array}{c}\hfill xy⩽\frac{{\epsilon }^p}{p}{\parallel x\parallel }^p+\frac{1}{q{\epsilon }^p}{\parallel y\parallel }^q,\end{array}\end{array}$$

where $\epsilon >0$, $p>1$, $q>1$, and $(p-1)(q-1)=1$.

3. Main Result

In this part, improved LSTMs, state observer design for memristor neural networks with model uncertainties, and adaptive updating laws of the weights of improved LSTMs will be discussed.

To begin with, the system (2) can be redefined as follows,

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \left\{\begin{array}{c}\dot{\mathbf{x}}\left(t\right)=-\mathbf{A}\mathbf{x}\left(t\right)+\mathbf{K}\left(\mathbf{x}\left(t\right),\mathbf{x}(t-\tau (t\left)\right))\right)+\mathbf{U}\hfill \\ \mathbf{y}\left(t\right)=\mathbf{H}\mathbf{x}\left(t\right)\hfill \end{array}\right.,\end{array}\end{array}$$

(4)

where $\mathbf{K}(·)$ is a vector of functions, which can be defined as $\left[K_1(\mathbf{x}\left(t\right),\mathbf{x}(t-\tau \left(t\right)))\right)$, $K_2(\mathbf{x}\left(t\right),\mathbf{x}(t-\tau \left(t\right)))),\cdots ,K_n(\mathbf{x}\left(t\right),\mathbf{x}(t-\tau \left(t\right))){\left)\right]}^{\mathrm{T}}$.

As mentioned in Remark 1, $\mathbf{K}(·)$ is the function vector of model uncertainties formed by floating parameters $b_{ij}$ and $c_{ij}$, time-varying delay ${\tau }_j\left(t\right)$ and unknown functions $f_i\left(x_i\left(t\right)\right)$ and $g_i\left(x_i(t-{\tau }_i)\right)$. In order to approximate the unknown function vector $\mathbf{K}\left(\mathbf{x}\left(t\right),\mathbf{x}(t-\tau (t\left)\right))\right)$, improved LSTMs are proposed, and an improved LSTMs cell is shown in Figure 3.

Comparing Figure 2 and Figure 3, it can be seen that the input gate ${\mathbf{i}}_t$ and the hidden state vector ${\mathbf{h}}_{t-1}$ at step $t-1$ have been removed. Since $\mathbf{x}\left(t\right)$ is part of $\mathbf{K}(·)$ in the form of a function vector, the input gate can be removed. $\mathbf{x}\left(t\right)$ should be part of LSTMs cell in the form of tanh function. The reason why ${\mathbf{h}}_{t-1}$ is removed is that $\mathbf{K}(·)$ contains $\mathbf{x}(t-\tau (t\left)\right)$, so the functions of ${\mathbf{h}}_{t-1}$ can be combined into ${\mathbf{c}}_{t-1}$ to save computation. Remove the output gate ${\mathbf{o}}_t$ and use ${\mathbf{h}}_t$ as the output of LSTMs cell to simplify the structure of LSTMs cell. Therefore, the improved LSTMs cell is made up of the following parts: (1) The state vector $\mathbf{x}\left(t\right)$ of the system at time t and the state vector with weights ${\mathbf{c}}_{t-1}$ of the system at time $t-1$ constitute the input of the improved LSTMs cell; (2) ${\mathbf{c}}_t$ is the vector that holds the state of the improved LSTMs cell at time t; (3) ${\mathbf{h}}_t$ is the output vector of the improved LSTMs cell at time t; (4) $\sigma \left(\mathbf{x}\right(t\left)\right)$ is the forgetting function at time t, which is used to control whether the memory information stored by the improved LSTMs cell at time $t-1$ is added to the improved LSTMs cell calculation at time t. The specific computation of a simplified and improved LSTMs cell can be expressed as follows,

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \begin{array}{c}{\mathbf{c}}_t={\mathbf{W}}_{t,i}{\mathbf{x}}_t\oplus {\mathbf{c}}_{t-1}\otimes \sigma \left({\mathbf{x}}_t\right)\hfill \\ {\mathbf{h}}_t=tanh\left({\mathbf{W}}_{t,i}{\mathbf{x}}_t\oplus {\mathbf{c}}_{t-1}\otimes \sigma \left({\mathbf{x}}_t\right)\oplus b_{t,i}\right),\hfill \end{array}\end{array}\end{array}$$

(5)

where ${\mathbf{W}}_{t,i}=\left[W_{t,i,1},W_{t,i,2},\cdots ,W_{t,i,n}\right]$ denotes the weight vector of the ith cell and $b_{t,i}$ is a bias constant of the ith cell; ${\mathbf{x}}_t={\left[x_1\left(t\right),x_2\left(t\right),\cdots ,x_n\left(t\right)\right]}^{\mathrm{T}}$ represents the state vector at time t.

Based on the simplified and improved LSTMs cell, the improved LSTMs are illustrated in Figure 4. In Figure 4, each column represents a neural network composed of p improved LSTMs cells at time j. The outputs of the p improved LSTMs cells pass through the weight matrix ${\mathbf{V}}_j$ to obtain the output vector of the neural network at time j, which is used to approximate $\mathbf{K}(·)$. The neural network at each time can be connected through ${\mathbf{c}}_j$ and ${\mathbf{c}}_{j-1}$ to form neural networks at all times. $x_j$ represents the state vector at time j, and $j\in [1,t]$. $c_j^i$ denotes the output of the hidden states of the ith$(i\in [1,p\left]\right)$ LSTMs cell at time j, and p is the number of LSTMs cells. ${\mathbf{W}}_{j,i}$ represents the weight vector of the ith LSTMs cell at time j. $b_{j,i}$ is the bias of the ith LSTMs cell at time j. $h_j^i$ denotes the output of the states of the ith LSTMs cell at time j. $V_{j,i,l}$ represents the weight coefficient from the output of the ith LSTMs cell to the lth system output at time j, and $l\in [1,m]$. $y_{j,l}$ denotes the lth system output at time j. The improved LSTMs can approximate any nonlinear function by the following theorem.

Theorem 1.

$k(·)$ is a continuous nonlinear function defined on a set Ω. Improved LSTMs are shown in Figure 3. $\overline{k}$ is an approximate function of $k(·)$ based on the improved LSTMs. Then, for a given desired level of accuracy $\epsilon >0$, there exist the ideal weights ${\overline{\mathbf{W}}}_{j,i}(j\in [1,t],i\in [1,p])$ and ${\overline{V}}_{j,i,l}(j\in [1,t],i\in [1,p],l\in [1,m])$ to satisfy the following inequality,

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \underset{{\mathbf{x}}_j\in \Omega }{sup}\parallel k(·)-\overline{k}\parallel ⩽\epsilon .\end{array}\end{array}$$

(6)

The proof of Theorem 1 can be found in Appendix A.

Based on Theorem 1, the estimation system for the system (4) can be defined as the following formula,

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \left\{\begin{array}{c}\dot{\widehat{\mathbf{x}}}\left(t\right)=-\mathbf{A}\widehat{\mathbf{x}}\left(t\right)+\overline{\mathbf{K}}+\mathbf{L}·\left[\mathbf{y}\left(t\right)-\mathbf{H}·\widehat{\mathbf{x}}\left(t\right)\right]+\mathbf{U}\hfill \\ \widehat{\mathbf{y}}\left(t\right)=\mathbf{H}\widehat{\mathbf{x}}\left(t\right)\hfill \end{array}\right.,\end{array}\end{array}$$

(7)

where $\mathbf{L}\in {\mathcal{R}}^{n\times m}$ denotes the observer gain matrix; $\overline{\mathbf{K}}\in {\mathcal{R}}^n$ is an estimated function vector of $\mathbf{K}\left(\mathbf{x}\left(t\right),\mathbf{x}(t-\tau (t\left)\right))\right)$ based on the improved LSTMs, which satisfies Theorem 1. $\overline{\mathbf{K}}$ is given in Equation (8),

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \overline{\mathbf{K}}={\overline{\mathbf{V}}}_t^{\mathrm{T}}·tanh\left\{{\overline{\mathbf{W}}}_t{\mathbf{x}}_t+{\displaystyle \sum _{i=1}^{t-1}}\left[{\overline{\mathbf{W}}}_i{\mathbf{x}}_i·{\displaystyle \prod _{j=i+1}^t}\sigma \left({\mathbf{x}}_j\right)\right]+{\overline{\mathbf{b}}}_t\right\},\end{array}\end{array}$$

(8)

where ${\overline{\mathbf{V}}}_t\in {\mathcal{R}}^{p\times n}$ and ${\overline{\mathbf{W}}}_i\in {\mathcal{R}}^{p\times n}$ denote the ideal weight matrices, and ${\overline{\mathbf{b}}}_t\in {\mathcal{R}}^p$ is the ideal bias vector.

The function $\sigma \left({\mathbf{x}}_j\right)$ is determined by the time-varying delay ${\tau }_j\left(t\right)$ which satisfies $0⩽{\tau }_j\left(t\right)⩽{\tau }_{max}$. $\sigma \left({\mathbf{x}}_j\right)$ is 1 in the range of $\left[t-{\tau }_{max},t\right]$, and $\sigma \left({\mathbf{x}}_j\right)$ is 0 in the rest of the range. This ensures that all the data in the interval $t-{\tau }_{max}$ to t will be included in the calculation. Considering the system (4) and the estimation system (7), the error system can be obtained as follows

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \mathbf{e}\left(t\right)& =\widehat{\mathbf{x}}\left(t\right)-\mathbf{x}\left(t\right),\hfill \\ \hfill \dot{\mathbf{e}}\left(t\right)& =\dot{\widehat{\mathbf{x}}}\left(t\right)-\dot{\mathbf{x}}\left(t\right)\hfill \\ & =\left[-\mathbf{A}\widehat{\mathbf{x}}\left(t\right)+\overline{\mathbf{K}}+\mathbf{L}·\left[\mathbf{y}\left(t\right)-\mathbf{H}·\widehat{\mathbf{x}}\left(t\right)\right]+\mathbf{U}\right]\hfill \\ & -\left[-\mathbf{A}\mathbf{x}\left(t\right)+\mathbf{K}\left(\mathbf{x}\left(t\right),\mathbf{x}(t-\tau (t\left)\right))\right)+\mathbf{U}\right]\hfill \\ & =-\left(\mathbf{A}+\mathbf{LH}\right)\mathbf{e}\left(t\right)+\left[\overline{\mathbf{K}}-\mathbf{K}\left(\mathbf{x}\left(t\right),\mathbf{x}(t-\tau (t\left)\right)\right)\right].\hfill \end{array}\end{array}$$

(9)

Assumption 2.

For the unknown function $K_i\left(\mathbf{x}\left(t\right),\mathbf{x}(t-\tau (t\left)\right))\right)$ and the estimated function ${\overline{K}}_i$$(i=1,2,\cdots ,n)$, there exist Lipschitz constant vectors ${\mathbf{K}}_{L1}$ and ${\mathbf{K}}_{L2}$, which satisfy the following inequality,

$$\begin{array}{c}\hfill \begin{array}{cc}& \left|K_i\left(\mathbf{x}\left(t\right),\mathbf{x}(t-\tau (t\left)\right))\right)-{\overline{K}}_i\right|⩽{\mathbf{K}}_{L1}^{\mathrm{T}}|\mathbf{x}\left(t\right)-\widehat{\mathbf{x}}\left(t\right)|+{\mathbf{K}}_{L2}^{\mathrm{T}}|\mathbf{x}(t-\tau \left(t\right))-\widehat{\mathbf{x}}(t-\tau \left(t\right))|.\hfill \end{array}\end{array}$$

(10)

Considering Theorem 1, ${\overline{K}}_i$ is an estimated function of the finite error of $K_i\left(\mathbf{x}\left(t\right),\mathbf{x}(t-\tau (t\left)\right)\right)$. Similarly, ${\overline{K}}_i$ is a function of $\widehat{\mathbf{x}}\left(t\right)$ and $\widehat{\mathbf{x}}(t-\tau \left(t\right))$. On this basis, considering Assumption 1, Assumption 2 is tenable.

Theorem 2.

Suppose that Assumption 2 holds for the system (4) and the estimation system (7), if there exist symmetric positive definite matrices $\mathbf{P}$, $\mathbf{Q}$, $\mathbf{M}$, a diagonal matrix $\mathbf{F}$, a matrix $\mathbf{G}\in {\mathcal{R}}^{n\times p}$ and a real constant $\delta >0$ such that inequality (11) holds,

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \left[\begin{array}{cccc}{\mathbf{\Omega }}_1& \mathbf{P}& \mathbf{M}& \mathbf{M}\\ \mathbf{P}& -\mathbf{F}& 0& 0\\ \mathbf{M}& 0& {\mathbf{\Omega }}_2& -2\mathbf{M}\\ \mathbf{M}& 0& -2\mathbf{M}& -2\mathbf{M}\end{array}\right]<0,\end{array}\end{array}$$

(11)

where ${\mathbf{\Omega }}_1=-{\mathbf{A}}^{\mathrm{T}}\mathbf{P}-{\mathbf{H}}^{\mathrm{T}}{\mathbf{G}}^{\mathrm{T}}-\mathbf{P}\mathbf{A}-\mathbf{GH}+\mathbf{Q}+2{\mathbf{K}}_{L1}tr\left\{\mathbf{F}\right\}{\mathbf{K}}_{L1}^{\mathrm{T}}$, and ${\mathbf{\Omega }}_2=2{\mathbf{K}}_{L2}tr\left\{\mathbf{F}\right\}{\mathbf{K}}_{L2}^{\mathrm{T}}-(1-\delta )\mathbf{Q}-2\mathbf{M}$.

Then, the error system (9) is asymptotically stable with observer gain matrix calculated by $\mathbf{L}={\mathbf{P}}^{-1}\mathbf{G}$. The proof of Theorem 2 can be found in Appendix B.

Based on Theorem 2, the observer gain matrix $\mathbf{L}$ can be obtained. Considering the function vector $\overline{\mathbf{K}}$ in system (7), the weight matrices ${\overline{\mathbf{W}}}_i$ and ${\overline{\mathbf{V}}}_i$ are ideal. In fact, the ideal weights are hard to select, and the estimated weights need to be adjusted by adaptive laws to be close to the ideal weights. With reference to the system (7), the estimated system can be redefined as follows

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \left\{\begin{array}{c}\dot{\widehat{\mathbf{x}}}\left(t\right)=-\mathbf{A}\widehat{\mathbf{x}}\left(t\right)+\widehat{\mathbf{K}}+\mathbf{L}·\left[\mathbf{y}\left(t\right)-\mathbf{H}·\widehat{\mathbf{x}}\left(t\right)\right]+\mathbf{U}\hfill \\ \widehat{\mathbf{y}}\left(t\right)=\mathbf{H}\widehat{\mathbf{x}}\left(t\right)\hfill \end{array}\right.,\end{array}\end{array}$$

(12)

where $\widehat{\mathbf{K}}$ is an estimated function vector of $\overline{\mathbf{K}}$.

$\widehat{\mathbf{K}}$ is given in Equation (13),

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \widehat{\mathbf{K}}={\widehat{\mathbf{V}}}_t^{\mathrm{T}}·tanh\left\{{\widehat{\mathbf{W}}}_t{\mathbf{x}}_t+{\displaystyle \sum _{i=1}^{t-1}}\left[{\widehat{\mathbf{W}}}_i{\mathbf{x}}_i·{\displaystyle \prod _{j=i+1}^t}\sigma \left({\mathbf{x}}_j\right)\right]+{\widehat{\mathbf{b}}}_t\right\},\end{array}\end{array}$$

(13)

where ${\widehat{\mathbf{V}}}_t$ and ${\widehat{\mathbf{W}}}_i$ are estimated weight matrices; ${\widehat{\mathbf{b}}}_t$ is a estimated bias vector.

With reference to the error system (9), the error system can be obtained as follows by using the Equation (6)

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \dot{\mathbf{e}}\left(t\right)=-\left(\mathbf{A}+\mathbf{LH}\right)\mathbf{e}\left(t\right)+\left(\widehat{\mathbf{K}}-\overline{\mathbf{K}}-{ϵ}_1\right),\end{array}\end{array}$$

(14)

where ${ϵ}_1$ is an error vector.

For error weight matrices ${\tilde{\mathbf{V}}}_t$ and ${\tilde{\mathbf{W}}}_i$ and a error weight vector ${\tilde{\mathbf{b}}}_t$, we have

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\tilde{\mathbf{V}}}_t& ={\widehat{\mathbf{V}}}_t-{\overline{\mathbf{V}}}_t\hfill \\ \hfill {\tilde{\mathbf{W}}}_i& ={\widehat{\mathbf{W}}}_i-{\overline{\mathbf{W}}}_i\hfill \\ \hfill {\tilde{\mathbf{b}}}_t& ={\widehat{\mathbf{b}}}_t-{\overline{\mathbf{b}}}_t.\hfill \end{array}\end{array}$$

(15)

Theorem 3.

For the error system (14), the design parameters ${\mathbf{N}}_{w\text{\_}i}\in {\mathcal{R}}^p$, ${\mathbf{N}}_{v\text{\_}t}\in {\mathcal{R}}^p$ and ${\mathbf{N}}_{b\text{\_}t}\in {\mathcal{R}}^{p\times n}$ satisfy following inequality

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \left[\begin{array}{ccc}{\mathbf{\Omega }}_3& -\mathbf{P}& \frac{1}{2}{\mathbf{\Omega }}_{wvb}^{\mathrm{T}}\\ -\mathbf{P}& \mathbf{0}& \mathbf{0}\\ \frac{1}{2}{\mathbf{\Omega }}_{wvb}& \mathbf{0}& \mathbf{0}\end{array}\right]⩽0,\end{array}\end{array}$$

where ${\mathbf{\Omega }}_3=-{\left(\mathbf{A}+\mathbf{LH}\right)}^{\mathrm{T}}\mathbf{P}-\mathbf{P}\left(\mathbf{A}+\mathbf{LH}\right)$,

${\mathbf{\Omega }}_{wvb}=\left[\begin{array}{c}{\mathbf{\Omega }}_{w\text{\_}t}\\ {\mathbf{\Omega }}_{w\text{\_}t-1}·\sigma \left({\mathbf{x}}_t\right)\\ ⋮\\ {\mathbf{\Omega }}_{w\text{\_}1}·{\prod }_{j=2}^t\sigma \left({\mathbf{x}}_j\right)\\ {\mathbf{\Omega }}_{v\text{\_}t}\\ {\mathbf{N}}_{b\text{\_}t}\end{array}\right]$, ${\mathbf{\Omega }}_{w\text{\_}i}=\left[\begin{array}{cccc}{\mathbf{N}}_{w\text{\_}i}& \mathbf{0}& \cdots & \mathbf{0}\\ \mathbf{0}& {\mathbf{N}}_{w\text{\_}i}& \cdots & \mathbf{0}\\ ⋮& ⋮& \ddots & ⋮\\ \mathbf{0}& \mathbf{0}& \cdots & {\mathbf{N}}_{w\text{\_}i}\end{array}\right]$,

${\mathbf{\Omega }}_{v\text{\_}t}=\left(\left[\begin{array}{cccc}{\mathbf{N}}_{v\text{\_}t}& \mathbf{0}& \cdots & \mathbf{0}\\ \mathbf{0}& {\mathbf{N}}_{v\text{\_}t}& \cdots & \mathbf{0}\\ ⋮& ⋮& \ddots & ⋮\\ \mathbf{0}& \mathbf{0}& \cdots & {\mathbf{N}}_{v\text{\_}t}\end{array}\right]-2\left[\begin{array}{c}{ϵ}_2·{\mathbf{P}}_{1•}\\ {ϵ}_2·{\mathbf{P}}_{2•}\\ ⋮\\ {ϵ}_2·{\mathbf{P}}_{n•}\end{array}\right]\right)$.

The adaptive updating laws of the weights can be given as follows

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\dot{\widehat{\mathbf{W}}}}_i& ={\mathbf{N}}_{w\text{\_}i}·{\mathbf{e}}^{\mathrm{T}}\left(t\right)-4{\widehat{\mathbf{V}}}_t\mathbf{P}\mathbf{e}\left(t\right){\mathbf{x}}_i^{\mathrm{T}}(i=1,2,\cdots ,t)\hfill \\ \hfill {\dot{\widehat{\mathbf{V}}}}_t& ={\mathbf{N}}_{v\text{\_}t}·{\mathbf{e}}^{\mathrm{T}}\left(t\right)-2{\widehat{\mathbf{S}}}_t{\mathbf{e}}^{\mathrm{T}}\left(t\right)\mathbf{P}\hfill \\ \hfill {\dot{\widehat{\mathbf{b}}}}_t& ={\mathbf{N}}_{b\text{\_}t}·\mathbf{e}\left(t\right)-4{\widehat{\mathbf{V}}}_t\mathbf{P}\mathbf{e}\left(t\right),\hfill \end{array}\end{array}$$

(16)

then the error system (14) is asymptotically stable. The proof of Theorem 3 can be found in Appendix C.

Considering (16), the adaptive updating laws of the weights are determined by $\mathbf{e}\left(t\right)$. Hence, it requires that $\mathbf{e}\left(t\right)$ is a n-dimensional vector. According to (12), we have

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \widehat{\mathbf{y}}\left(t\right)-\mathbf{y}\left(t\right)=\mathbf{H}·\left(\widehat{\mathbf{x}}\left(t\right)-\mathbf{x}\left(t\right)\right)=\mathbf{H}·\mathbf{e}\left(t\right).\end{array}\end{array}$$

(17)

If there exists ${\mathbf{H}}^{-1}$, the $\mathbf{e}\left(t\right)$ can be obtained as follows by using (17)

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \mathbf{e}\left(t\right)={\mathbf{H}}^{-1}·\left(\widehat{\mathbf{y}}\left(t\right)-\mathbf{y}\left(t\right)\right).\end{array}\end{array}$$

(18)

In general, m is not equal to n, and ${\mathbf{H}}^{-1}$ does not exist. Hence, (18) does not hold. To solve this problem, the following assumption is given.

Assumption 3.

$\widehat{\mathbf{y}}\left(t\right)$ and $\mathbf{y}\left(t\right)$ are continuously differentiable functions and the first derivative of $\widehat{\mathbf{y}}\left(t\right)$ and $\mathbf{y}\left(t\right)$ are bounded and measurable.

Theorem 4.

Based on Assumption 3, if the given matrix $\mathbf{G}$ is left invertible, the $\mathbf{e}\left(t\right)$ can be obtained as follows

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \mathbf{e}\left(t\right)={\mathbf{G}}^{-1}·\mathbf{Y},\end{array}\end{array}$$

(19)

where $\mathbf{G}=\left[\begin{array}{c}\mathbf{H}\\ -\mathbf{H}\left(\mathbf{A}+\mathbf{LH}\right)\end{array}\right]$ and $\mathbf{Y}=\left[\begin{array}{c}\widehat{\mathbf{y}}\left(t\right)-\mathbf{y}\left(t\right)\\ \dot{\widehat{\mathbf{y}}}\left(t\right)-\dot{\mathbf{y}}\left(t\right)\end{array}\right]$. The proof of Theorem 4 can be found in Appendix D.

Remark 3.

Based on Theorem 1, the estimated system (12) can be given. By using Theorem 2, the observer gain matrix $\mathbf{L}$ can be obtained. By using Theorems 3 and 4, the adaptive updating laws of the weights can be obtained.

4. Simulation Analysis

In this section, two numerical cases are presented to verify the rationality of the above results.

4.1. Examples

Example 1. 2-dimensional memristor neural networks are considered, and the parameters of the system (2) are given as follows,

$$\begin{array}{c}\hfill \begin{array}{cc}& \mathbf{A}=\left[\begin{array}{cc}2.3& 0\\ 0& 2\end{array}\right],\mathbf{B}=\left[\begin{array}{cc}0.31& 0.38\\ 0.49& 0.32\end{array}\right],\mathbf{C}=\left[\begin{array}{cc}0.32& 0.19\\ 0.39& 0.25\end{array}\right],\mathbf{U}=\left[\begin{array}{c}0.2\\ 0.3\end{array}\right],\hfill \\ & \mathbf{H}=\left[\begin{array}{cc}1& 0.5\end{array}\right],\mathbf{f}\left(\mathbf{x}\left(t\right)\right)=\left[\begin{array}{c}\frac{|x_1+1|-|x_1-1|}{2}\\ \frac{|x_2+1|-|x_2-1|}{2}\end{array}\right],\mathbf{g}\left(\mathbf{x}(t-\tau \left(t\right))\right)=\left[\begin{array}{c}{x}_1(t-{\tau }_1\left(t\right))\\ x_2(t-{\tau }_2\left(t\right))\end{array}\right],\hfill \\ & {\tau }_1\left(t\right)={\tau }_2\left(t\right)=\frac{0.05t}{1+t},\mathbf{x}\left(0\right)=\left[\begin{array}{c}1\\ 1\end{array}\right].\hfill \end{array}\end{array}$$

Based on the system (2), the estimated system (17) can be designed as follows,

$\begin{array}{c}\hfill \begin{array}{cc}& \widehat{\mathbf{x}}\left(0\right)=\left[\begin{array}{c}0.2\\ 0.3\end{array}\right],{\mathbf{K}}_{L1}={\mathbf{K}}_{L2}=\left[\begin{array}{c}1\\ 1\end{array}\right],\delta =0.1.\hfill \end{array}\end{array}$

By using Theorem 2 and LMIs tools, the parameters of the estimated system (17) can be obtained,

$\begin{array}{c}\hfill \begin{array}{cc}& \mathbf{P}=\left[\begin{array}{cc}0.03553& -0.00345\\ -0.00345& 0.03629\end{array}\right],\mathbf{Q}=\left[\begin{array}{cc}0.03545& -0.01504\\ -0.01504& 0.04070\end{array}\right],\mathbf{F}=\left[\begin{array}{cc}0.00363& 0\\ 0& 0.00379\end{array}\right],\hfill \\ & \mathbf{M}=\left[\begin{array}{cc}0.00494& -68.44222\\ 68.44222& 0.00505\end{array}\right],\mathbf{L}=\left[\begin{array}{c}-0.88667\\ -0.75623\end{array}\right].\hfill \end{array}\end{array}$

Set sampling time $T=30s$ and sampling period $▵T=0.001s$. Considering (18), set ${\mathbf{x}}_i={\widehat{\mathbf{x}}}_{i·▵T}(i=1,2,\cdots ,t/▵T)$ and $\sigma \left({\mathbf{x}}_i\right)=0(i<t/▵T-30)$. Based on Theorem 3 and Theorem 4, set ${\mathbf{N}}_{w\text{\_}i}$ and ${\mathbf{N}}_{v\text{\_}t}$ and ${\mathbf{N}}_{b\text{\_}t}$ are negative unit vectors and matrix.

The state trajectories of the state $\mathbf{x}\left(t\right)$ and the state observer $\widehat{\mathbf{x}}\left(\mathbf{t}\right)$ are drawn in Figure 5. Figure 6 is drawn for the estimated error between the state $\mathbf{x}\left(t\right)$ and the state observer $\widehat{\mathbf{x}}\left(\mathbf{t}\right)$. In Figure 7, the trajectories of the derivative of the state $\dot{\mathbf{x}}\left(t\right)$ and the derivative of the state observer $\dot{\widehat{\mathbf{x}}}\left(t\right)$ are depicted. The trajectories of the error between $\dot{\mathbf{x}}\left(t\right)$ and $\dot{\widehat{\mathbf{x}}}\left(t\right)$ are given in Figure 8. In Figure 9, the output curve $y\left(t\right)$ and the estimated output curve $\widehat{y}\left(t\right)$ are given. Figure 10 shows the estimated error curve between $y\left(t\right)$ and $\widehat{y}\left(t\right)$.

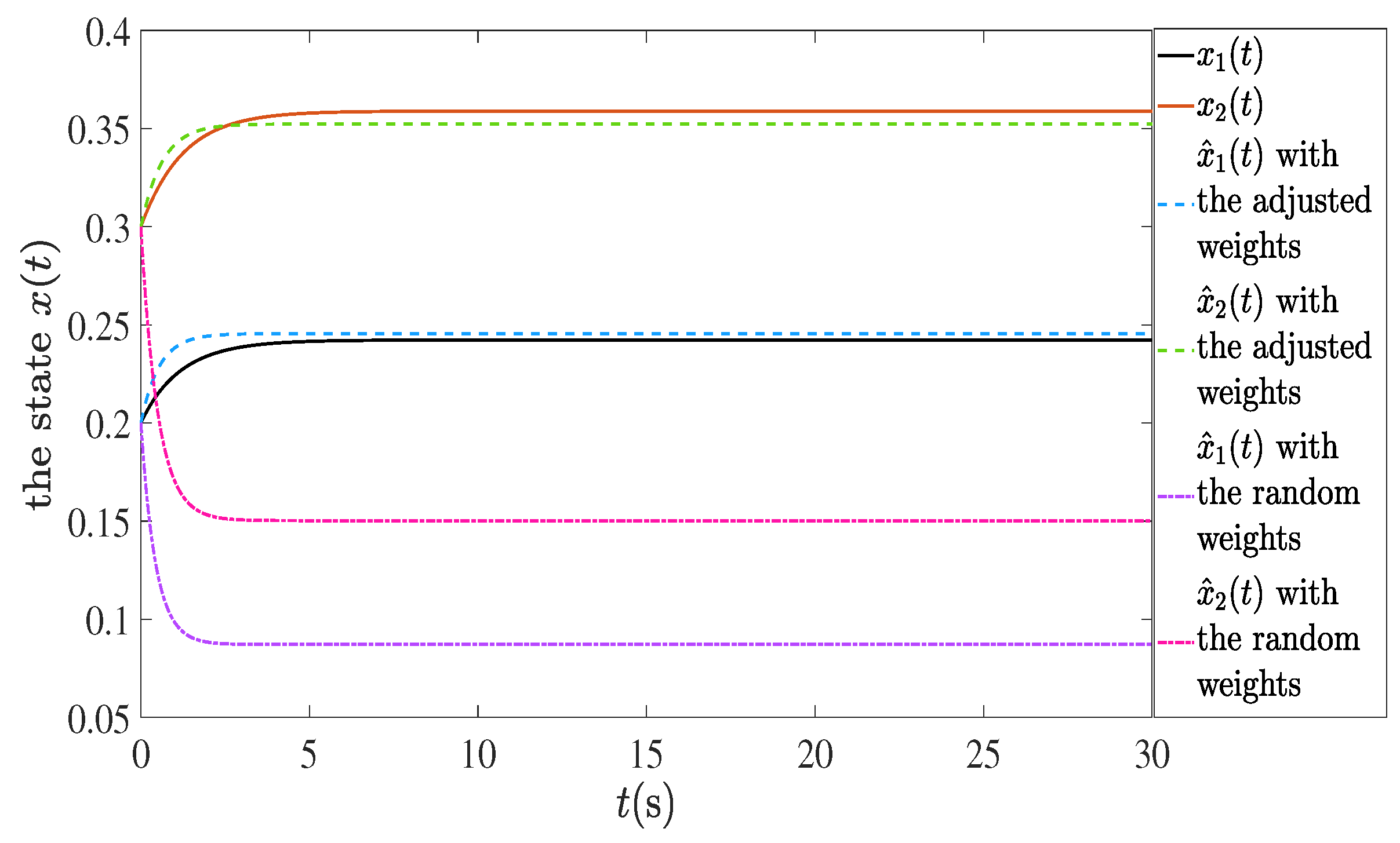
In order to verify the accuracy of the estimated structure, a test system is designed based on the gain observation matrix $\mathbf{L}$. Under the same simulation conditions as above, the effects of the adjusted weights and the random weights on the system are compared. In Figure 11, the state trajectories of the real system and the estimated system with the adjusted weights and the system with the random weights are given. Figure 12 shows the real output curve and the estimated output with the adjusted weights and the output curve with the random weights.

Example 2. 3-dimensional memristor neural networks are considered, and the parameters of the system (2) are given as follows,

$\begin{array}{c}\hfill \begin{array}{cc}& \mathbf{A}=\left[\begin{array}{ccc}2.5& 0& 0\\ 0& 2.5& 0\\ 0& 0& 3.3\end{array}\right],\mathbf{B}=\left[\begin{array}{ccc}0.2& 0.15& 0.35\\ 0.15& 0.35& 0.08\\ 0.1& 0.15& 0.3\end{array}\right],\mathbf{C}=\left[\begin{array}{ccc}0.125& 0.15& 0.136\\ 0.35& 0.18& 0.3\\ 0.2& 0.04& 0.05\end{array}\right],\hfill \\ & \mathbf{H}=\left[\begin{array}{ccc}1& 1& 1\\ 1& 0& 1\end{array}\right],\mathbf{f}\left(\mathbf{x}\left(t\right)\right)=\left[\begin{array}{c}\frac{|x_1+1|-|x_1-1|}{2}\\ \frac{|x_2+1|-|x_2-1|}{2}\\ \frac{|x_3+1|-|x_3-1|}{2}\end{array}\right],\mathbf{g}\left(\mathbf{x}(t-\tau \left(t\right))\right)=\left[\begin{array}{c}{x}_1(t-{\tau }_1\left(t\right))\\ x_2(t-{\tau }_2\left(t\right))\\ x_3(t-{\tau }_3\left(t\right))\end{array}\right],\hfill \\ & \mathbf{U}=\left[\begin{array}{c}0.2\\ 0.3\\ 0.1\end{array}\right],\mathbf{x}\left(0\right)=\left[\begin{array}{c}1\\ 1\\ 1\end{array}\right],{\tau }_1\left(t\right)={\tau }_2\left(t\right)={\tau }_3\left(t\right)=\frac{0.05t}{1+t}.\hfill \end{array}\end{array}$

Based on the system (2), the estimated system (17) can be designed as follows,

$\begin{array}{c}\hfill \begin{array}{cc}& \widehat{\mathbf{x}}\left(0\right)=\left[\begin{array}{c}0.4\\ 0.5\\ 0.6\end{array}\right],{\mathbf{K}}_{L1}={\mathbf{K}}_{L2}=\left[\begin{array}{c}1\\ 1\\ 1\end{array}\right],\delta =0.1.\hfill \end{array}\end{array}$

By using Theorem 2 and LMIs tools, the parameters of the estimated system (17) can be obtained,

$\begin{array}{c}\hfill \begin{array}{cc}& \mathbf{P}=\left[\begin{array}{ccc}0.51349& 0.03364& 0.10199\\ 0.03364& 0.71344& -0.02472\\ 0.10199& -0.02472& 0.39999\end{array}\right],\mathbf{Q}=\left[\begin{array}{ccc}-0.30425& -0.32097& -0.34837\\ -0.32097& -0.51236& -0.19432\\ -0.34837& -0.19432& 0.00547\end{array}\right],\hfill \\ & \mathbf{F}=\left[\begin{array}{ccc}0.10879& 0& 0\\ 0& 0.17792& 0\\ 0& 0& 0.20825\end{array}\right],\mathbf{M}=\left[\begin{array}{ccc}0.05344& -47.67758& -16.83918\\ 47.67685& 0.04188& -39.81878\\ 16.83445& 39.83217& 0.07044\end{array}\right],\hfill \\ & \mathbf{L}=\left[\begin{array}{cc}-0.29468& -0.06180\\ -0.99352& 0.98883\\ 0.32407& -0.98883\end{array}\right].\hfill \end{array}\end{array}$

Set sampling time $T=30s$ and sampling period $▵T=0.001s$. Considering (18), set ${\mathbf{x}}_i={\widehat{\mathbf{x}}}_{i·▵T}(i=1,2,\cdots ,t/▵T)$ and $\sigma \left({\mathbf{x}}_i\right)=0(i<t/▵T-30)$. Based on Theorems 3 and 4, set ${\mathbf{N}}_{w\text{\_}i}$ and ${\mathbf{N}}_{v\text{\_}t}$ and ${\mathbf{N}}_{b\text{\_}t}$ are negative unit vectors and matrix.

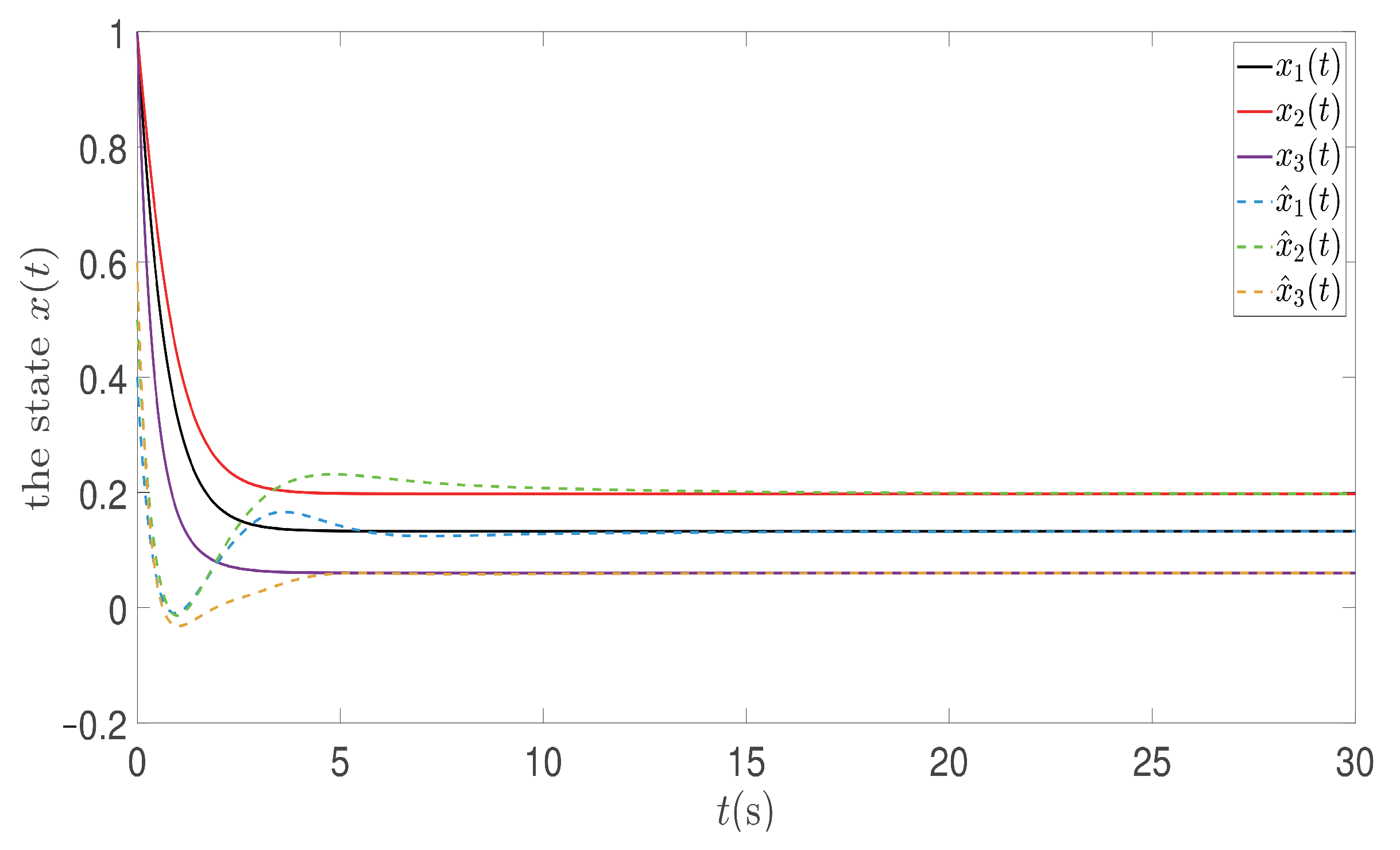
The state trajectories of the state $\mathbf{x}\left(t\right)$ and the state observer $\widehat{\mathbf{x}}\left(\mathbf{t}\right)$ are drawn in Figure 13. Figure 14 is drawn for the estimated error between the state $\mathbf{x}\left(t\right)$ and the state observer $\widehat{\mathbf{x}}\left(\mathbf{t}\right)$. In Figure 15, the trajectories of the derivative of the state $\dot{\mathbf{x}}\left(t\right)$ and the derivative of the state observer $\dot{\widehat{\mathbf{x}}}\left(t\right)$ are depicted. The trajectories of the error between $\dot{\mathbf{x}}\left(t\right)$ and $\dot{\widehat{\mathbf{x}}}\left(t\right)$ are given in Figure 16. In Figure 17, the output curve $y\left(t\right)$ and the estimated output curve $\widehat{y}\left(t\right)$ are given. Figure 18 shows the estimated error curve between $y\left(t\right)$ and $\widehat{y}\left(t\right)$.

In order to verify the accuracy of the estimated structure, a test system is designed based on the gain observation matrix $\mathbf{L}$. Under the same simulation conditions as above, the effects of the adjusted weights and the random weights on the system are compared. In Figure 19, the state trajectories of the real system and the estimated system with the adjusted weights and the system with the random weights are given. Figure 20 shows the real output curve and the estimated output with the adjusted weights and the output curve with the random weights.

4.2. Description of Simulation Results

Figure 5 and Figure 13 show that the estimated state vector is a good approximation of the real state vector. On the other hand, Figure 6 and Figure 14 verify that the estimation error vector of states is going to zero. Figure 7 and Figure 15 show that the derivative vector of estimated states is a good approximation of the derivative vector of real states. On the other hand, Figure 8 and Figure 16 verify that the estimation error vector of derivative of states is going to zero. Figure 9 and Figure 17 show that the estimated output vector is a good approximation of the real output vector. On the other hand, Figure 10 and Figure 18 verify that the estimation error vector of outputs is going to zero. Figure 11 and Figure 19 show that the estimated state vector with adaptive weights is better than that with random weights. Figure 12 and Figure 20 show that the output vector with adaptive weights is better than that with random weights. Simulation results indicate that the state observer proposed in this paper has stronger adaptability and more accurate estimation results for memristor neural networks with model uncertainties.

5. Conclusions

The state estimation of memristor neural networks with model uncertainties is discussed in this paper. In particular, model uncertainties include time-varying delays, floating parameters and unknown functions. An improved approach based on LSTMs is proposed to deal with model uncertainties. This paper proves that the improved neural networks can approximate any nonlinear function with any error. On this basis, a full-order state observer is proposed to achieve the reconstruction of states based on the measurement output of the system. The adaptive updating laws of the weights of improved neural networks are proposed based on a LKF. By using LKF and LMIs tools, this paper obtains the asymptotic stability conditions for the error systems. The simulation results show that by using the full-order state observer and the adaptive updating laws of the weights, an accurate estimate of the solution can be obtained. The test results show that the model uncertainties can be approximated accurately. As mentioned in the introduction, the improved LSTMs designed in this paper can also be realized by crossbar array of memristor, which will be our next work.