Deep Subdomain Transfer Learning with Spatial Attention ConvLSTM Network for Fault Diagnosis of Wheelset Bearing in High-Speed Trains
Abstract
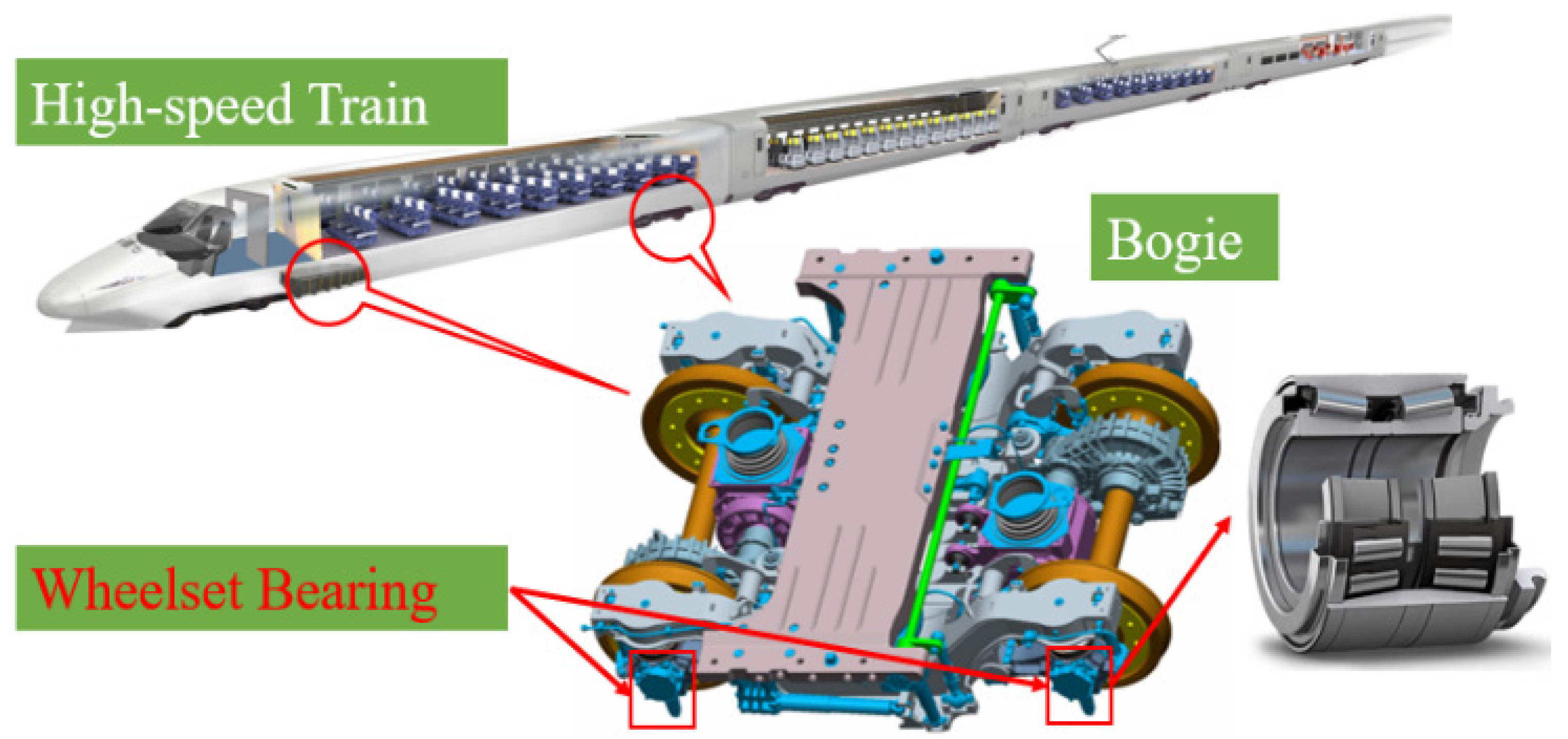
1. Introduction
- (1)
- The subdomain adaptation principle is applied to the intelligent fault detection of wheelset bearings, and the effectiveness of this principle is demonstrated using a deep learning model implementation.
- (2)
- A deep network model based on SA-ConvLSTM and CNNs is proposed, which uses distribution discrepancy metrics of the relevant subdomain and adversarial transfer method to achieve subdomain transfer learning for bearing fault diagnosis.
- (3)
- The performance of the proposed model is evaluated using several metrics on a dataset for wheelset bearings, and a visualization technique is used to understand the subdomain transfer learning feature learning process.
2. Subdomain Transfer Learning Problem
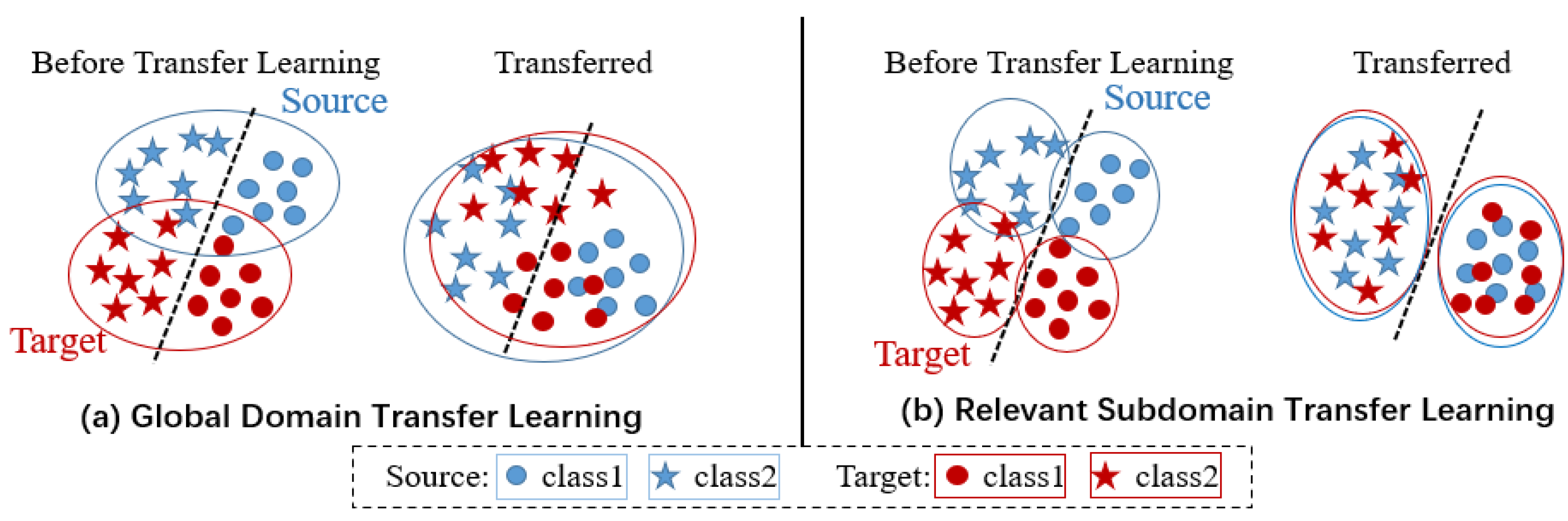
2.1. Unsupervised Subdomain Transfer Learning
2.2. Local Maximum Mean Discrepancy (Distribution Discrepancy Metrics of Relevant Subdomain)
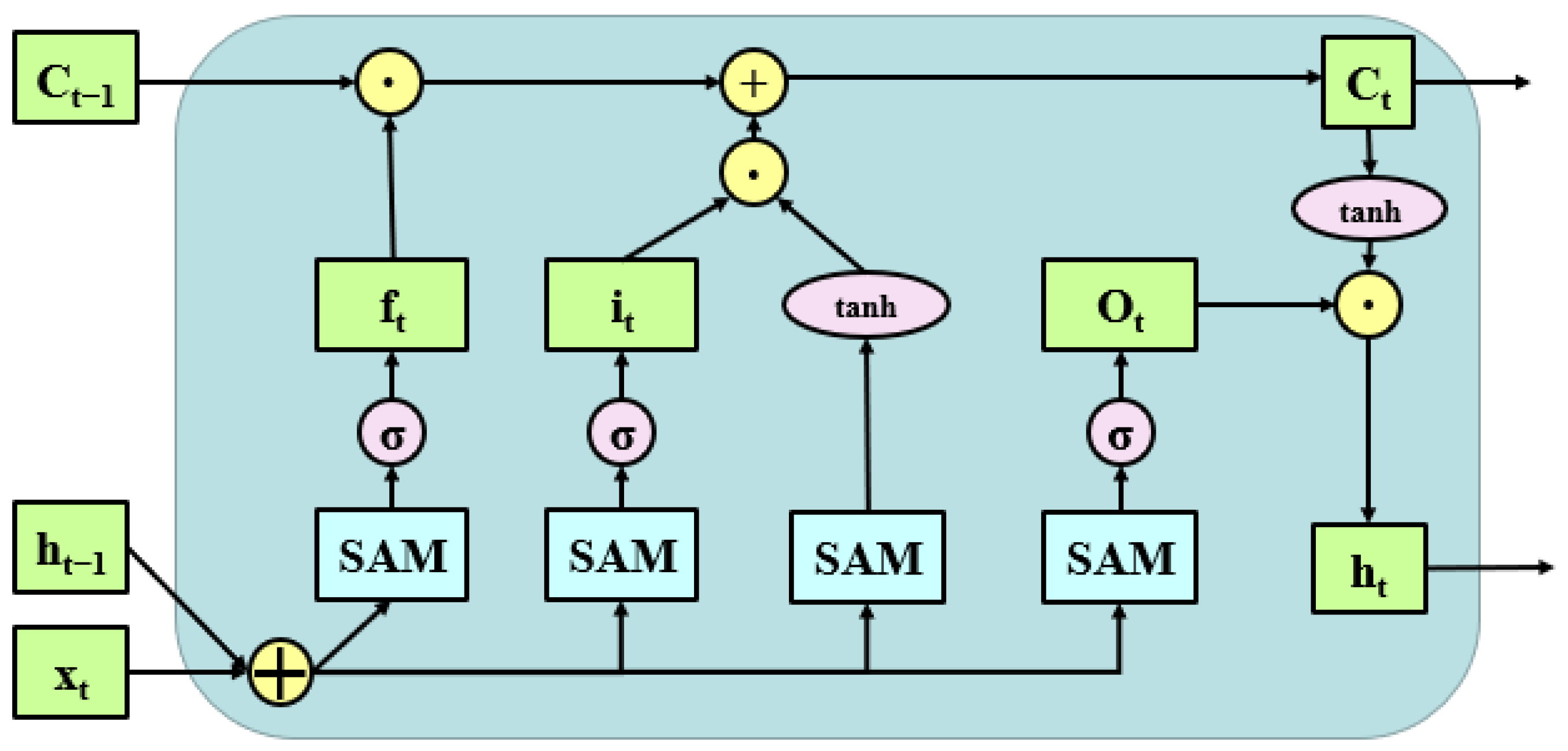
3. Spatial Attention ConvLSTM
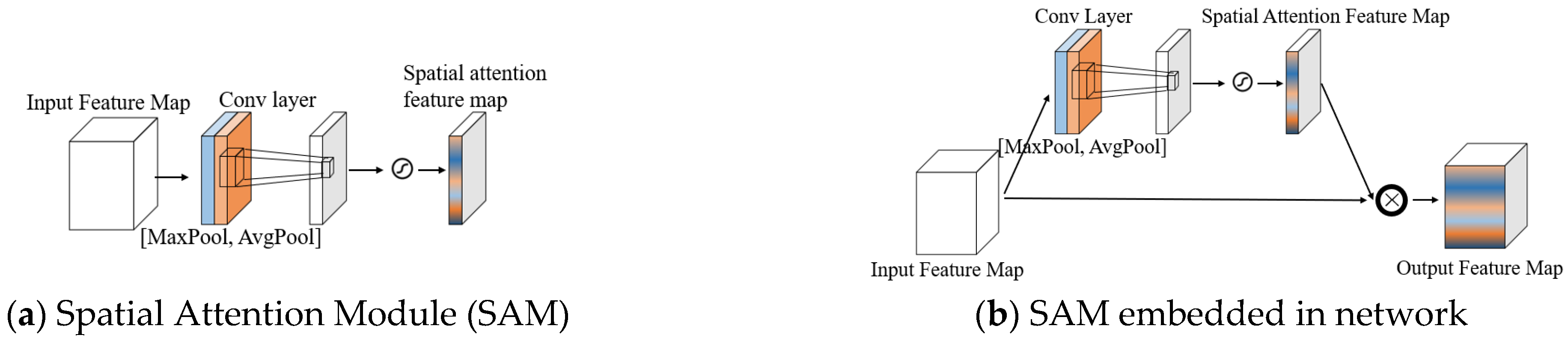
3.1. Spatial Attention Module
3.2. Spatial Attention ConvLSTM
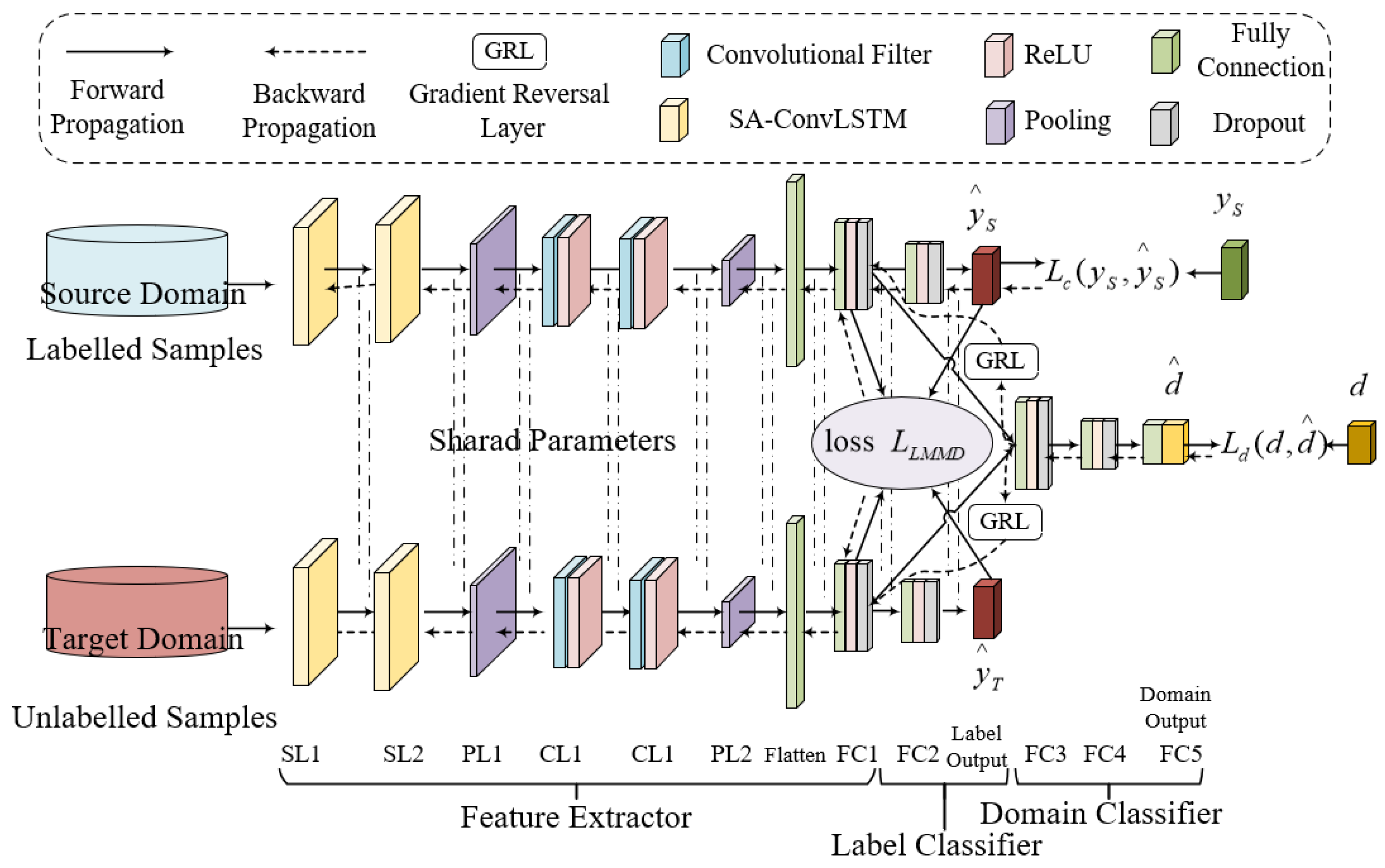
4. Proposed Method
4.1. Deep Subdomain Transfer Learning Network (DSTLN)
- (1)
- Feature extractor module
- (2)
- Label classification module
- (3)
- Domain adaptation module
4.2. Optimization Objective
- (1)
- Object 1: Health status classification error term. The DSTLN aims to learn an invariant feature representation directly on the source domain dataset through the feature extractor module. As a result, the critical optimization objective of DSTLN is to minimize the health status classification error on data from the source domain. To achieve this, a typical softmax regression loss can be used as the expected objective function for a dataset with N categories of health status, as expressed below:where J(·) is the cross entropy function; is the predicted distribution of the ith sample across N fault categories and is its real label.
- (2)
- Object 2: Adversarial domain classification error term. The adversarial domain classification error term serves a unique purpose in the DSTLN. The feature extractor is trained to deceive the domain classifier by maximizing this loss. In contrast, the adversarial domain classifier is educated to distinguish between the source domains by minimizing its loss. This ensures low classification errors in the source domain, all while minimizing the loss of the label classifier.
- (3)
- Object 3: LMMD distribution discrepancy metrics term. The output Y of the label classifier module is used as the pseudo label of the target domain sample, and then the distribution difference of the subdomains is computed. By minimizing this function, aligning the distributions of relevant subdomains within the same category of the source and target domains is realized.where denotes the kernel function; and denote the weight of and belonging to category C of the ith sample, respectively.
4.3. Network Training Strategy
| Algorithm 1. DSTLN Training Strategy. |
| Input: source domain datasets with labels and target domain datasets without labels |
| Output: predict the fault class of the unlabeled target domain |
| Start |
| Step1: preprocessing of source domain and target domain datasets |
| Step2: creation of the neural network and initialization of the parameters randomly |
| Step3: input the preprocessed data to compute the Lc, Ld, and LLMMD, and compute the total Loss with the variable λ and μ according to current epoch |
| Step4: update network parameters by Adam optimizer, and Steps 3 and 4 should be repeated until the desired epoch is attained |
| Step5: save the trained model parameters to a file |
| Step6: utilizing the trained model, analyze the unlabeled target domain data |
| Step7: predict the fault category of the target domain for the input |
| End |
5. Experiment Results and Comparisons
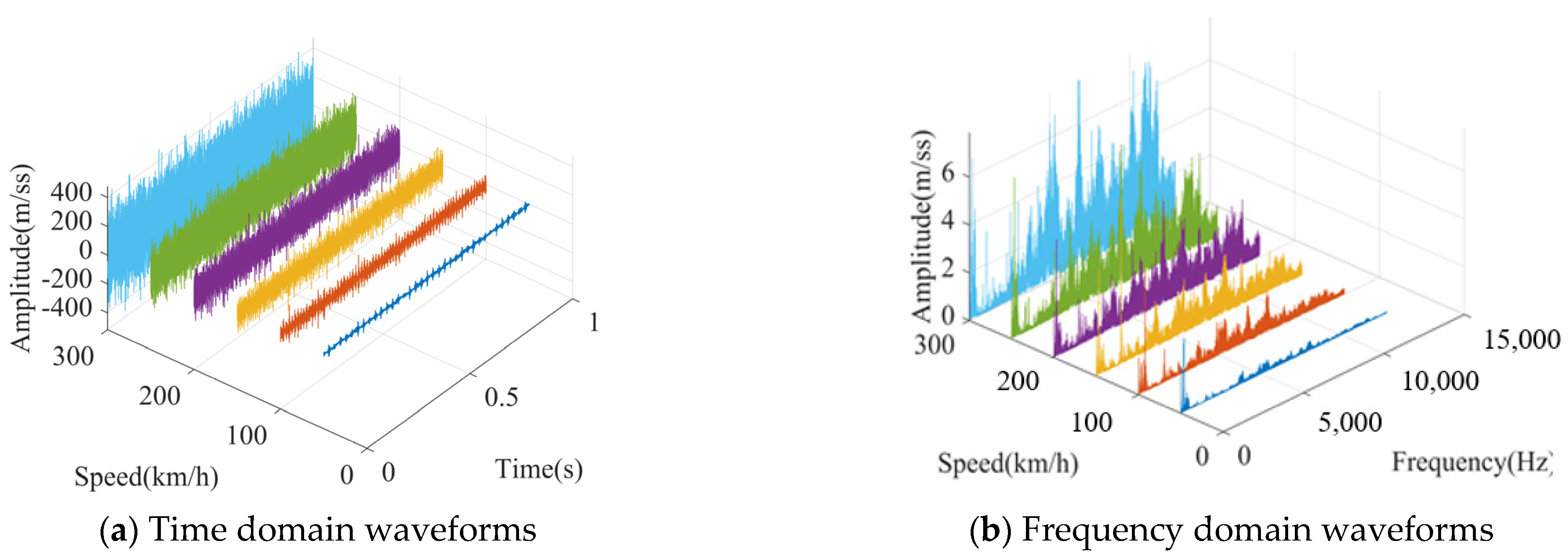
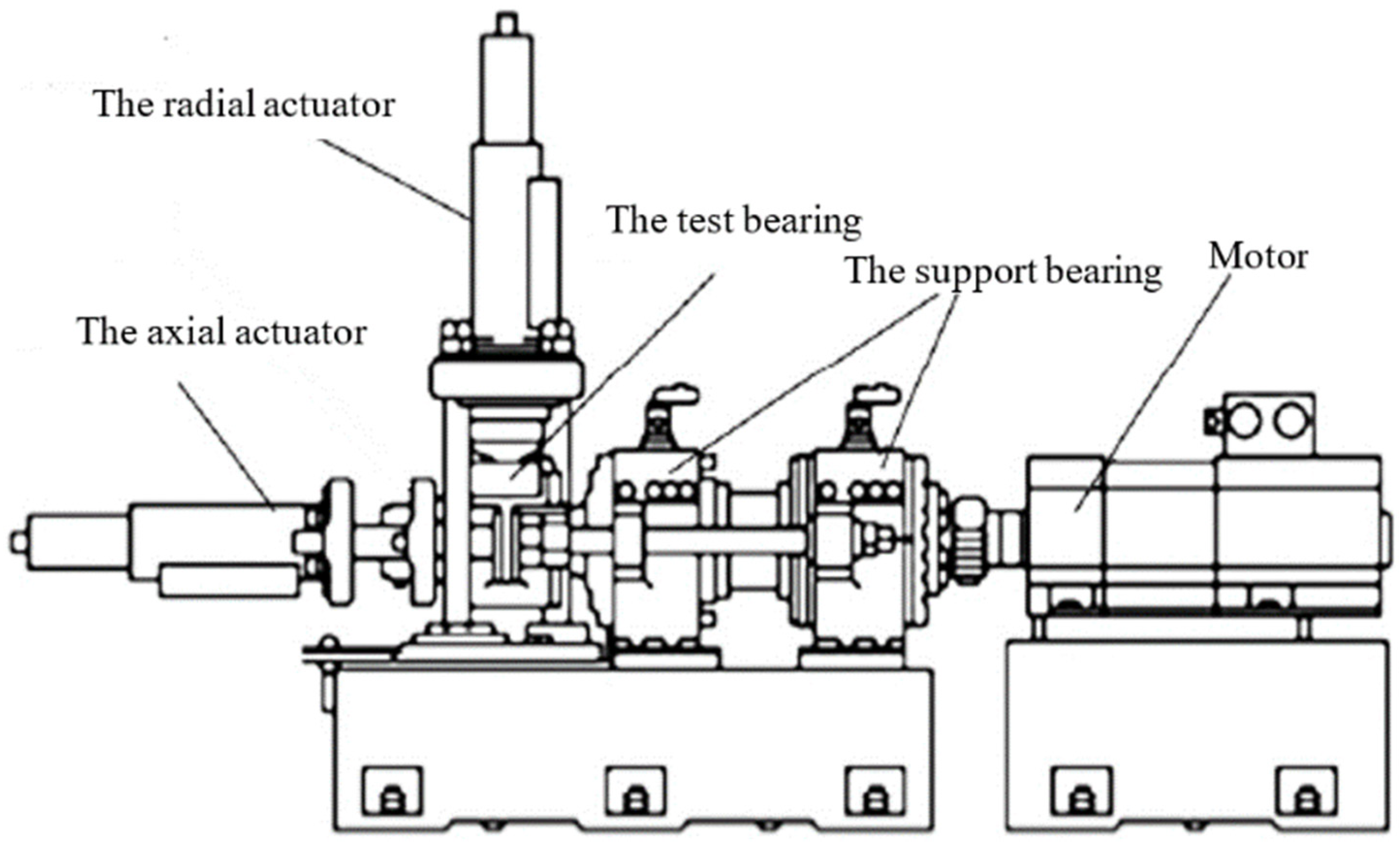
5.1. Experiment and Dataset
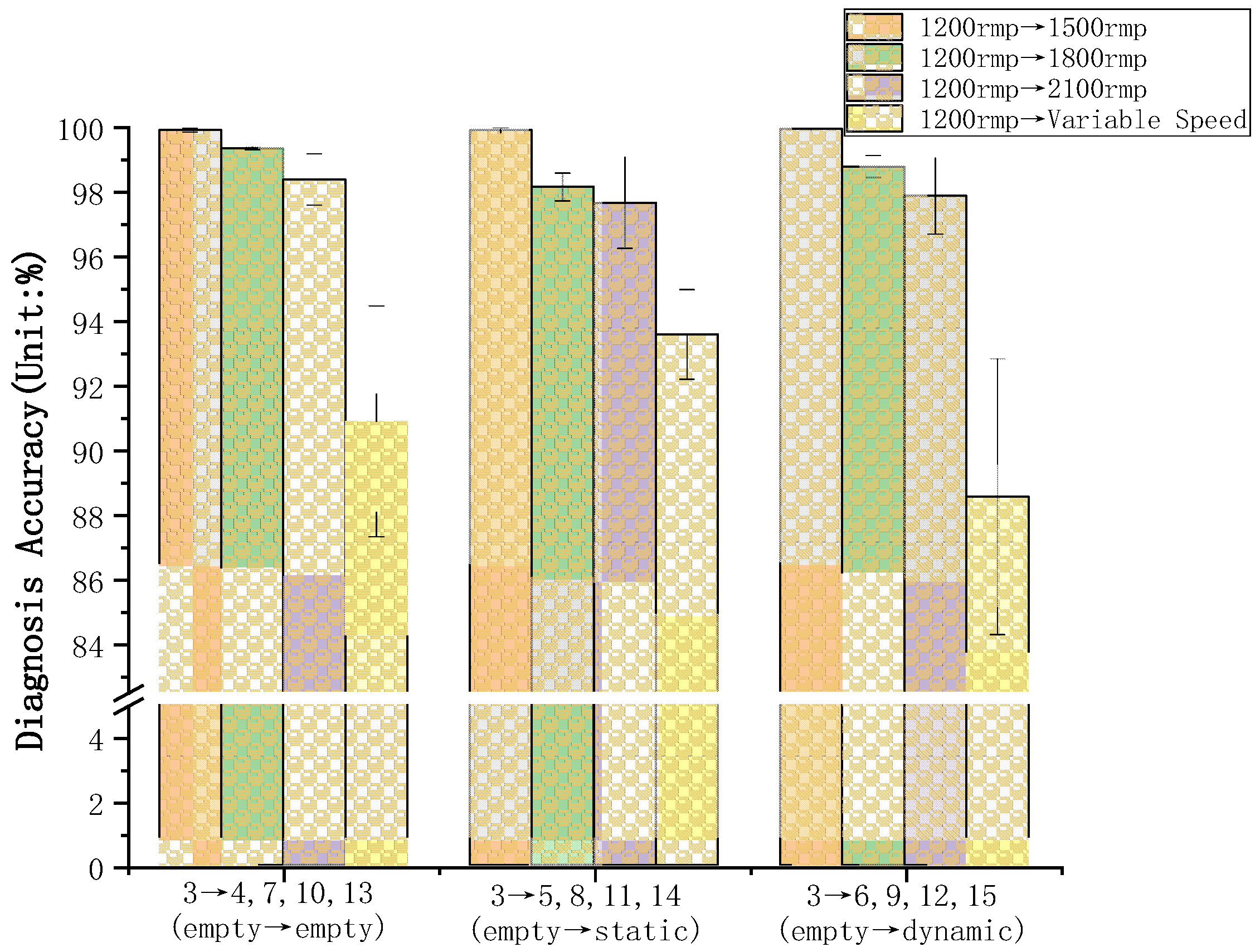
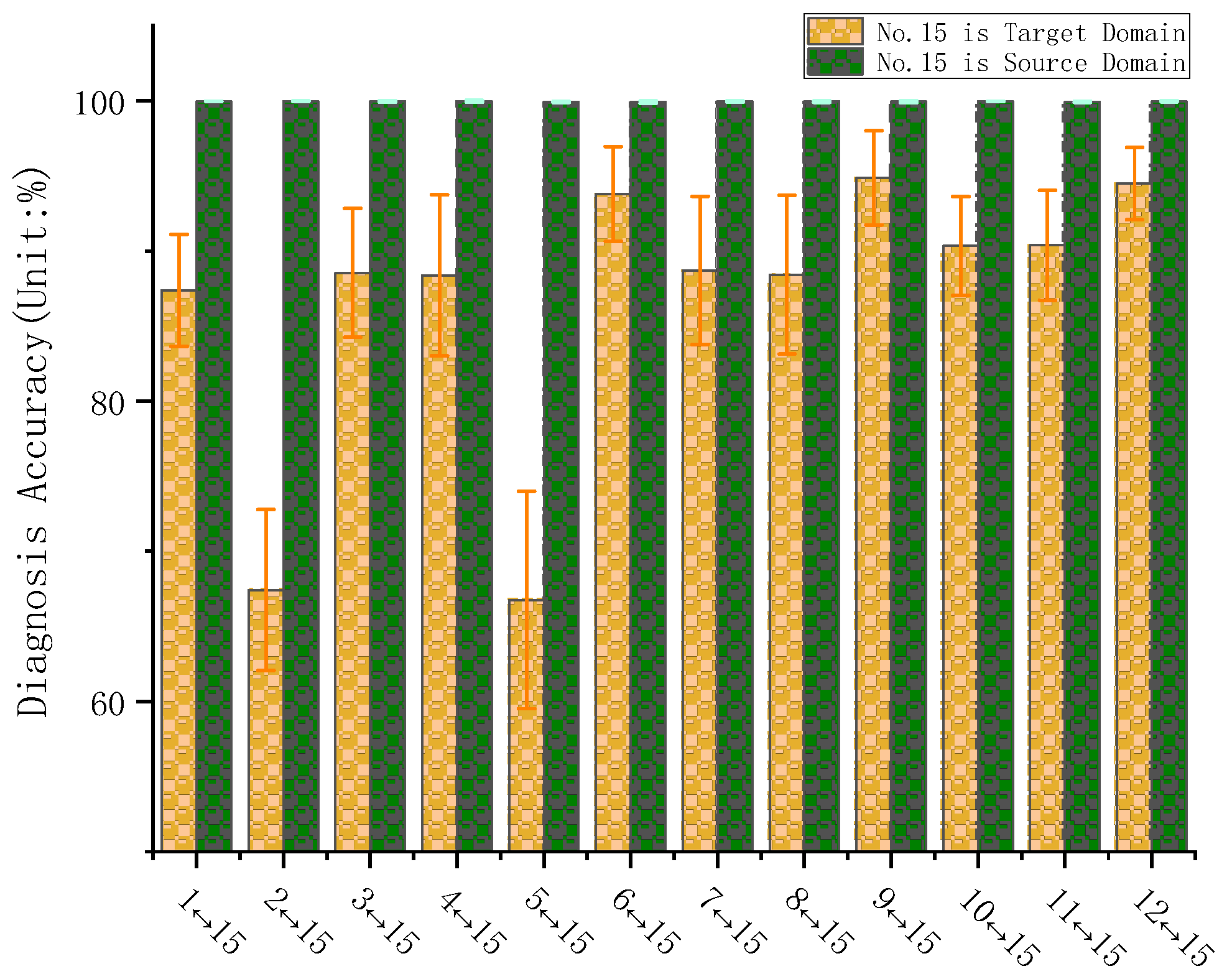
5.2. Transfer Fault Diagnosis of the DSTLN
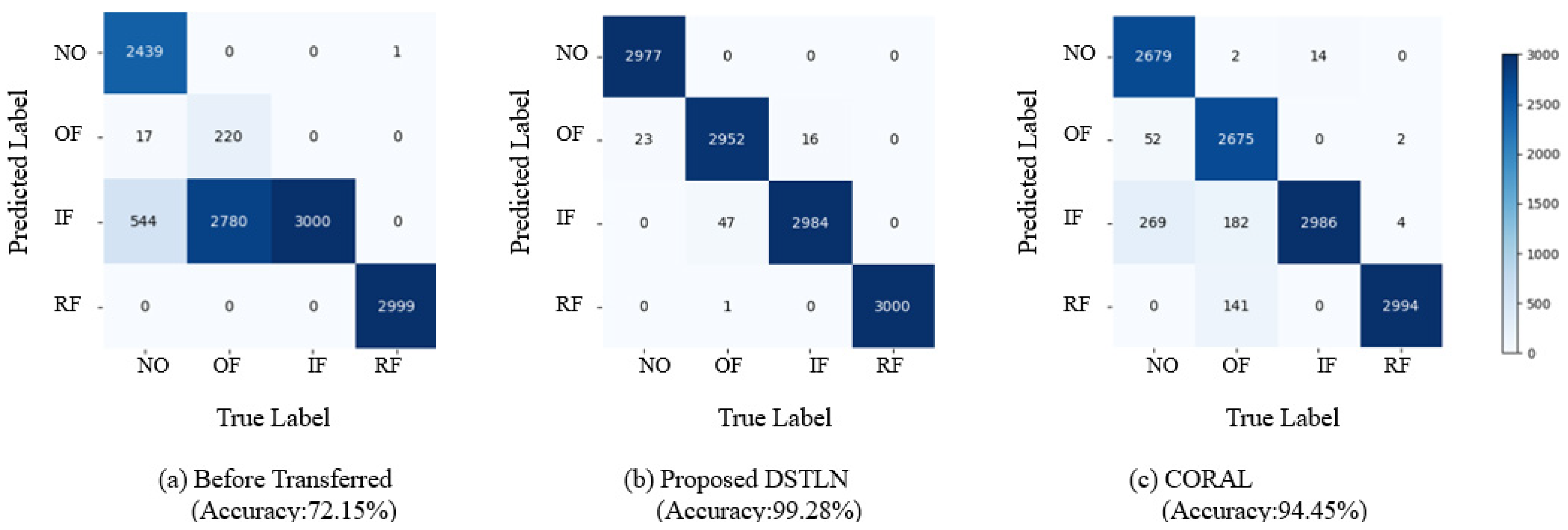
5.3. Comparison Results
- (1)
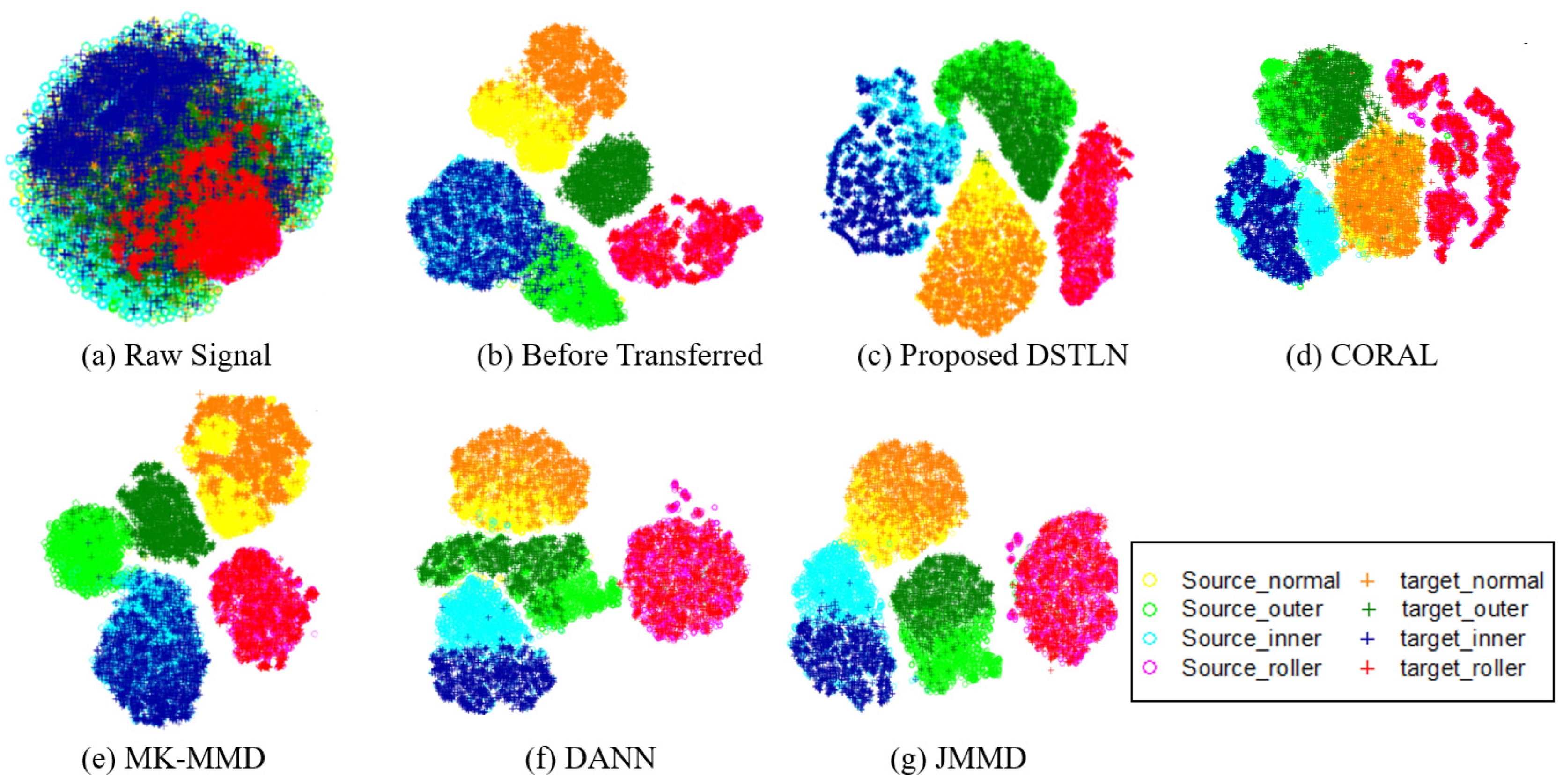
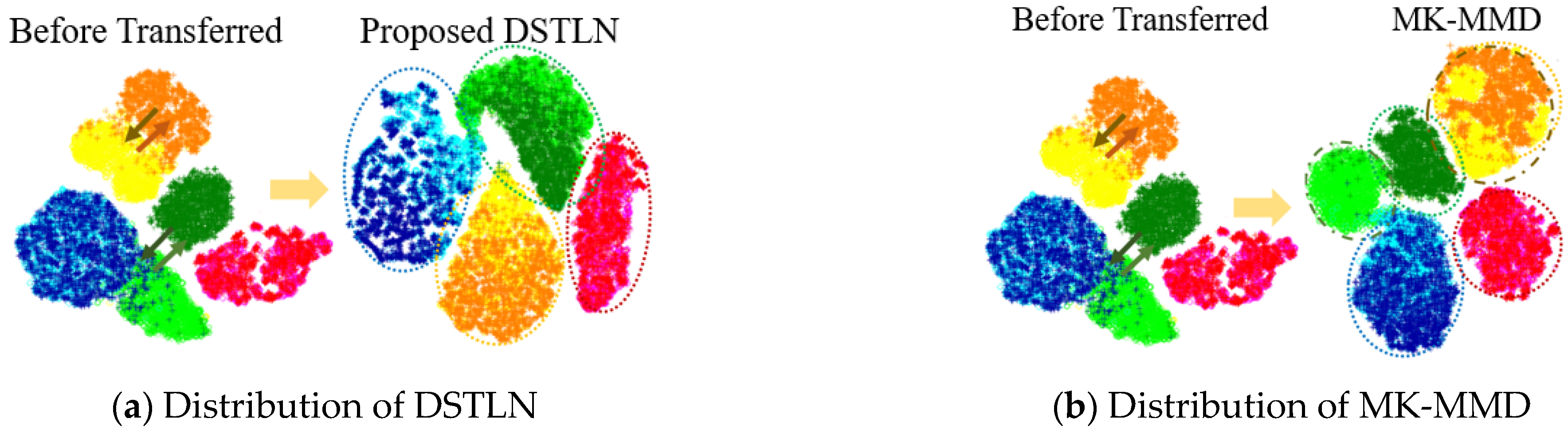
- When analyzing the visualization result prior to transfer learning shown in Figure 14b, it becomes evident that the extracted features from the source domain are separated; however, the extracted features from the target domain differ from the source domain, and without transfer learning, the target domain’s distribution cannot be matched to the correct classifier, resulting in poor diagnosis accuracy. This indicates that without transfer learning, applying intelligent fault diagnosis of bearings with unlabeled data of varying working conditions may be challenging.
- (2)
- Compared to the result before the transfer, the transfer learning methods can align the identical class distributions in the source and target domains, as shown in Figure 14c–g. The transfer learning methods shift the target domain’s feature distribution to align with the source domain’s distribution. This suggests that the transfer learning methods effectively handle unlabeled data of varying working conditions.
- (3)
- As demonstrated in Figure 14d–g, other compared transfer learning techniques shift the feature distribution of the target domain to align with the source domain; however, they ignore the relationships between the subdomains with the same class in both domains. As a result, some data from the source and target domains are misclassified, and the distributions of the extracted features from different classes are mixed up, as depicted in Figure 15b. In contrast, the proposed DSTLN method aligns the distributions of relevant subdomains within the same class in both source and target domains, as shown in Figure 15a, resulting in improved diagnostic accuracy performance.
6. Conclusions
6.1. Conclusions of Results
- (1)
- Transfer learning-based intelligent fault diagnosis methods deliver higher diagnostic accuracy than deep learning methods without transfer learning processing, especially for bearing data with variable working conditions and no labels in the target domain.
- (2)
- The dataset under variable operating conditions comprises a more comprehensive set of characteristic information. A higher diagnostic accuracy can be achieved when it is set as the source domain dataset. This result can guide us to conduct further experiments under more variable speed and load force conditions. It can help us obtain a more comprehensive dataset for high-speed train wheelset bearings in the future.
- (3)
- The proposed DSTLN method captures fine-grained information. It aligns the distributions of relevant subdomains within the same source and target domain category, resulting in better diagnostic accuracy performance than other global domain transfer learning methods.
6.2. Discussions of Future Work
- (1)
- Limitation of the wheelset bearing data. Although we conducted experiments on four healthy bearings under 15 different working conditions, it is still insufficient to cover all possible scenarios of real running high-speed trains. Our current testing rig cannot simulate rail–wheel excitement, which significantly impacts the vibration signals. In the future, we aim to conduct more experiments using our new roller test rig based on a real high-speed train bogie to acquire more accurate vibration data.
- (2)
- Metric measuring the transferability between different datasets for transfer learning. In our study, we used t-SNE visualization to understand the distribution of source and target datasets. However, we still need a quantitative measure of transferability between datasets. In the future, we plan to develop a quantitative measure to help us organize a complete dataset and avoid negative transfer learning.
- (3)
- Development of an embedded diagnostic system. Our proposed diagnostic method was implemented on a personal computer, which is both expensive and energy intensive. In the future, we aim to design and develop a more cost-effective and energy-efficient diagnostic model that can be deployed on an embedded system.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, H.; Shi, L.; Zhou, S.; Yue, Y.; An, N. A Multi-Source Consistency Domain Adaptation Neural Network MCDANN for Fault Diagnosis. Appl. Sci. 2022, 12, 10113. [Google Scholar] [CrossRef]
- Rezazadeh, N.; De Luca, A.; Lamanna, G.; Caputo, F. Diagnosing and Balancing Approaches of Bowed Rotating Systems: A Review. Appl. Sci. 2022, 12, 9157. [Google Scholar] [CrossRef]
- Wu, G.; Yan, T.; Yang, G.; Chai, H.; Cao, C. A Review on Rolling Bearing Fault Signal Detection Methods Based on Different Sensors. Sensors 2022, 22, 8330. [Google Scholar] [CrossRef] [PubMed]
- Jiang, X.; Wang, J.; Shi, J.; Shen, C.; Huang, W.; Zhu, Z. A coarse-to-fine decomposing strategy of VMD for extraction of weak repetitive transients in fault diagnosis of rotating machines. Mech. Syst. Signal Process. 2019, 116, 668–692. [Google Scholar] [CrossRef]
- Peng, H.; Zhang, H.; Fan, Y.; Shangguan, L.; Yang, Y. A Review of Research on Wind Turbine Bearings’ Failure Analysis and Fault Diagnosis. Lubricants 2023, 11, 14. [Google Scholar] [CrossRef]
- Manjurul Islam, M.M.; Kim, J.-M. Reliable multiple combined fault diagnosis of bearings using heterogeneous feature models and multiclass support vector Machines. Reliab. Eng. Syst. Saf. 2019, 184, 55–66. [Google Scholar] [CrossRef]
- Peng, B.; Bi, Y.; Xue, B.; Zhang, M.; Wan, S. A Survey on Fault Diagnosis of Rolling Bearings. Algorithms 2022, 15, 347. [Google Scholar] [CrossRef]
- Kuncan, M.; Kaplan, K.; Minaz, M.R.; Kaya, Y.; Ertunç, H.M. A novel feature extraction method for bearing fault classification with one dimensional ternary patterns. ISA Trans. 2020, 100, 346–357. [Google Scholar] [CrossRef]
- Jiao, Y.; Zhang, Y.; Ma, S.; Sang, D.; Zhang, Y.; Zhao, J.; Liu, Y.; Yang, S. Role of secondary phase particles in fatigue behavior of high-speed railway gearbox material. Int. J. Fatigue 2020, 131, 105336. [Google Scholar] [CrossRef]
- Liu, Z.; Yang, S.; Liu, Y.; Lin, J.; Gu, X. Adaptive correlated Kurtogram and its applications in wheelset-bearing system fault diagnosis. Mech. Syst. Signal Process. 2021, 154, 107511. [Google Scholar] [CrossRef]
- Liu, J.; Wang, W.; Golnaraghi, F. An Extended Wavelet Spectrum for Bearing Fault Diagnostics. IEEE Trans. Instrum. Meas. 2008, 57, 2801–2812. [Google Scholar] [CrossRef]
- Liu, D.; Cheng, W.; Wen, W. Rolling bearing fault diagnosis via STFT and improved instantaneous frequency estimation method. Procedia Manuf. 2020, 49, 166–172. [Google Scholar] [CrossRef]
- Mejia-Barron, A.; Valtierra-Rodriguez, M.; Granados-Lieberman, D.; Olivares-Galvan, J.C.; Escarela-Perez, R. The application of EMD-based methods for diagnosis of winding faults in a transformer using transient and steady state currents. Measurement 2018, 117, 371–379. [Google Scholar] [CrossRef]
- Liu, W.; Yang, S.; Li, Q.; Liu, Y.; Hao, R.; Gu, X. The Mkurtogram: A Novel Method to Select the Optimal Frequency Band in the AC Domain for Railway Wheelset Bearings Fault Diagnosis. Appl. Sci. 2021, 11, 9. [Google Scholar] [CrossRef]
- Gu, X.H.; Yang, S.P.; Liu, Y.Q.; Hao, R.J. A novel Pareto-based Bayesian approach on extension of the infogram for extracting repetitive transients. Mech. Syst. Signal Process. 2018, 106, 119–139. [Google Scholar] [CrossRef]
- Gu, X.; Yang, S.; Liu, Y.; Hao, R.; Liu, Z. Multi-objective Informative Frequency Band Selection Based on Negentropy-induced Grey Wolf Optimizer for Fault Diagnosis of Rolling Element Bearings. Sensors 2020, 20, 1845. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.; Gu, X.; Liu, Y.; Hao, R.; Li, S. A general multi-objective optimized wavelet filter and its applications in fault diagnosis of wheelset bearings. Mech. Syst. Signal Process. 2020, 145, 106914. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, S.; Wang, B.; Habetler, T.G. Deep Learning Algorithms for Bearing Fault Diagnostics—A Comprehensive Review. IEEE Access 2020, 8, 29857–29881. [Google Scholar] [CrossRef]
- You, K.; Qiu, G.; Gu, Y. Rolling Bearing Fault Diagnosis Using Hybrid Neural Network with Principal Component Analysis. Sensors 2022, 22, 8906. [Google Scholar] [CrossRef]
- Lei, Y.; Jia, F.; Lin, J.; Xing, S.; Ding, S.X. An Intelligent Fault Diagnosis Method Using Unsupervised Feature Learning Towards Mechanical Big Data. IEEE Trans. Ind. Electron. 2016, 63, 3137–3147. [Google Scholar] [CrossRef]
- Ling, L.; Wu, Q.; Huang, K.; Wang, Y.; Wang, C. A Lightweight Bearing Fault Diagnosis Method Based on Multi-Channel Depthwise Separable Convolutional Neural Network. Electronics 2022, 11, 4110. [Google Scholar] [CrossRef]
- Peng, D.; Liu, Z.; Wang, H.; Qin, Y.; Jia, L. A Novel Deeper One-Dimensional CNN With Residual Learning for Fault Diagnosis of Wheelset Bearings in High-Speed Trains. IEEE Access 2019, 7, 10278–10293. [Google Scholar] [CrossRef]
- Ban, H.; Wang, D.; Wang, S.; Liu, Z. Multilocation and Multiscale Learning Framework with Skip Connection for Fault Diagnosis of Bearing under Complex Working Conditions. Sensors 2021, 21, 3226. [Google Scholar] [CrossRef]
- Liu, P.; Yang, S.; Liu, Y.; Gu, X.; Liu, Z.; Liu, H. An excitation test and dynamic simulation of wheel polygon wear based on a rolling test rig of single wheelset. Zhendong Chongji/J. Vib. Shock 2022, 41, 102–109. [Google Scholar] [CrossRef]
- He, Z.Y.; Shao, H.D.; Zhong, X.; Zhao, X.Z. Ensemble transfer CNNs driven by multi-channel signals for fault diagnosis of rotating machinery cross working conditions. Knowl. -Based Syst. 2020, 207, 106396. [Google Scholar] [CrossRef]
- Guo, L.; Lei, Y.; Xing, S.; Yan, T.; Li, N. Deep Convolutional Transfer Learning Network: A New Method for Intelligent Fault Diagnosis of Machines With Unlabeled Data. IEEE Trans. Ind. Electron. 2019, 66, 7316–7325. [Google Scholar] [CrossRef]
- He, Y.; Hu, M.; Feng, K.; Jiang, Z. An Intelligent Fault Diagnosis Scheme Using Transferred Samples for Intershaft Bearings Under Variable Working Conditions. IEEE Access 2020, 8, 203058–203069. [Google Scholar] [CrossRef]
- Li, X.; Jiang, H.; Zhao, K.; Wang, R. A Deep Transfer Nonnegativity-Constraint Sparse Autoencoder for Rolling Bearing Fault Diagnosis With Few Labeled Data. IEEE Access 2019, 7, 91216–91224. [Google Scholar] [CrossRef]
- Li, J.; Huang, R.; He, G.; Wang, S.; Li, G.; Li, W. A Deep Adversarial Transfer Learning Network for Machinery Emerging Fault Detection. IEEE Sens. J. 2020, 20, 8413–8422. [Google Scholar] [CrossRef]
- He, W.; Chen, J.; Zhou, Y.; Liu, X.; Chen, B.; Guo, B. An Intelligent Machinery Fault Diagnosis Method Based on GAN and Transfer Learning under Variable Working Conditions. Sensors 2022, 22, 9175. [Google Scholar] [CrossRef]
- Zhang, R.; Gu, Y. A Transfer Learning Framework with a One-Dimensional Deep Subdomain Adaptation Network for Bearing Fault Diagnosis under Different Working Conditions. Sensors 2022, 22, 1624. [Google Scholar] [CrossRef]
- Gretton, A.; Borgwardt, K.M.; Rasch, M.J.; Scholkopf, B.; Smola, A. A Kernel Two-Sample Test. J. Mach. Learn. Res. 2012, 13, 723–773. [Google Scholar]
- Gretton, A.; Sriperumbudur, B.; Sejdinovic, D.; Strathmann, H.; Balakrishnan, S.; Pontil, M.; Fukumizu, K. Optimal kernel choice for large-scale two-sample tests. In Proceedings of the 25th International Conference on Neural Information Processing Systems, Lake Tahoe, NV, USA, 3–6 December 2012; Volume 1, pp. 1205–1213. [Google Scholar]
- Long, M.; Zhu, H.; Wang, J.; Jordan, M.I. Deep transfer learning with joint adaptation networks. In Proceedings of the Proceedings of the 34th International Conference on Machine Learning, Sydney, NSW, Australia, 6–11 August 2017; Volume 70, pp. 2208–2217. [Google Scholar]
- Zhu, Y.; Zhuang, F.; Wang, J.; Ke, G.; Chen, J.; Bian, J.; Xiong, H.; He, Q. Deep Subdomain Adaptation Network for Image Classification. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 1713–1722. [Google Scholar] [CrossRef] [PubMed]
- Woo, S.; Park, J.; Lee, J.-Y.; Kweon, I.S. CBAM: Convolutional Block Attention Module. arXiv 2018, arXiv:1807.06521. [Google Scholar]
- Shi, X.; Chen, Z.; Wang, H.; Yeung, D.Y.; Wong, W.K.; Woo, W.C. Convolutional LSTM Network: A Machine Learning Approach for Precipitation Nowcasting. Adv. Neural Inf. Process. Syst. 2015, 28, 802–810. [Google Scholar]
- Zhang, W.; Peng, G.; Li, C.; Chen, Y.; Zhang, Z. A New Deep Learning Model for Fault Diagnosis with Good Anti-Noise and Domain Adaptation Ability on Raw Vibration Signals. Sensors 2017, 17, 425. [Google Scholar] [CrossRef] [PubMed]
- Meng, Z.; Guo, X.; Pan, Z.; Sun, D.; Liu, S. Data Segmentation and Augmentation Methods Based on Raw Data Using Deep Neural Networks Approach for Rotating Machinery Fault Diagnosis. IEEE Access 2019, 7, 79510–79522. [Google Scholar] [CrossRef]
- Yang, B.; Li, Q.; Chen, L.; Shen, C. Bearing Fault Diagnosis Based on Multilayer Domain Adaptation. Shock Vib. 2020, 2020, 8873960. [Google Scholar] [CrossRef]
- Jj, A.; Ming, Z.A.; Jing, L.B.; Kl, A. Residual joint adaptation adversarial network for intelligent transfer fault diagnosis. Mech. Syst. Signal Process. 2020, 145, 106962. [Google Scholar]
- An, J.; Ai, P. Deep Domain Adaptation Model for Bearing Fault Diagnosis with Riemann Metric Correlation Alignment. Math. Probl. Eng. 2020, 2020, 1–12. [Google Scholar] [CrossRef]
- Zhao, Z.; Zhang, Q.; Yu, X.; Sun, C.; Wang, S.; Yan, R.; Chen, X. Unsupervised Deep Transfer Learning for Intelligent Fault Diagnosis: An Open Source and Comparative Study. arXiv 2019, arXiv:1912.12528. [Google Scholar]
- Wan, L.; Li, Y.; Chen, K.; Gong, K.; Li, C. A novel deep convolution multi-adversarial domain adaptation model for rolling bearing fault diagnosis. Measurement 2022, 191, 110752. [Google Scholar] [CrossRef]



| Modules | Layers | Tied Parameters | Activation Function |
|---|---|---|---|
| Feature Extractor | SL1 | SA-ConvLSTM1d 20@32 | - |
| SL2 | SA-ConvLSTM1d 20@3 | - | |
| PL1 | Max Polling: kernel = 2, stride = 2 | - | |
| CL1 | Conv1d 64@3 | ReLU | |
| CL2 | Conv1d 128@3 | ReLU | |
| PL2 | Max Pooling: kernel = 4, stride = 4 | - | |
| FC1 | Output 256 features | ReLU | |
| Label Classifier | FC2 | Output 256 features; Dropout 0.5 | Softmax |
| Domain Classifier | FC3 | Output 1024 features; Dropout 0.5 | ReLU |
| FC4 | Output 512 features; Dropout 0.5 | ReLU | |
| FC5 | Output 2 features | Sigmoid |
| Name | Roller Diameter | Pitch Diameter | Contact Angle | Roller Number |
|---|---|---|---|---|
| FAG F-80781109 | 26.5 mm | 185 mm | 10 deg | 17 |
| Condition Number | Speed (km/h) | |||||
|---|---|---|---|---|---|---|
| 200 | 250 | 300 | 350 | 0 → 350 → 0 | ||
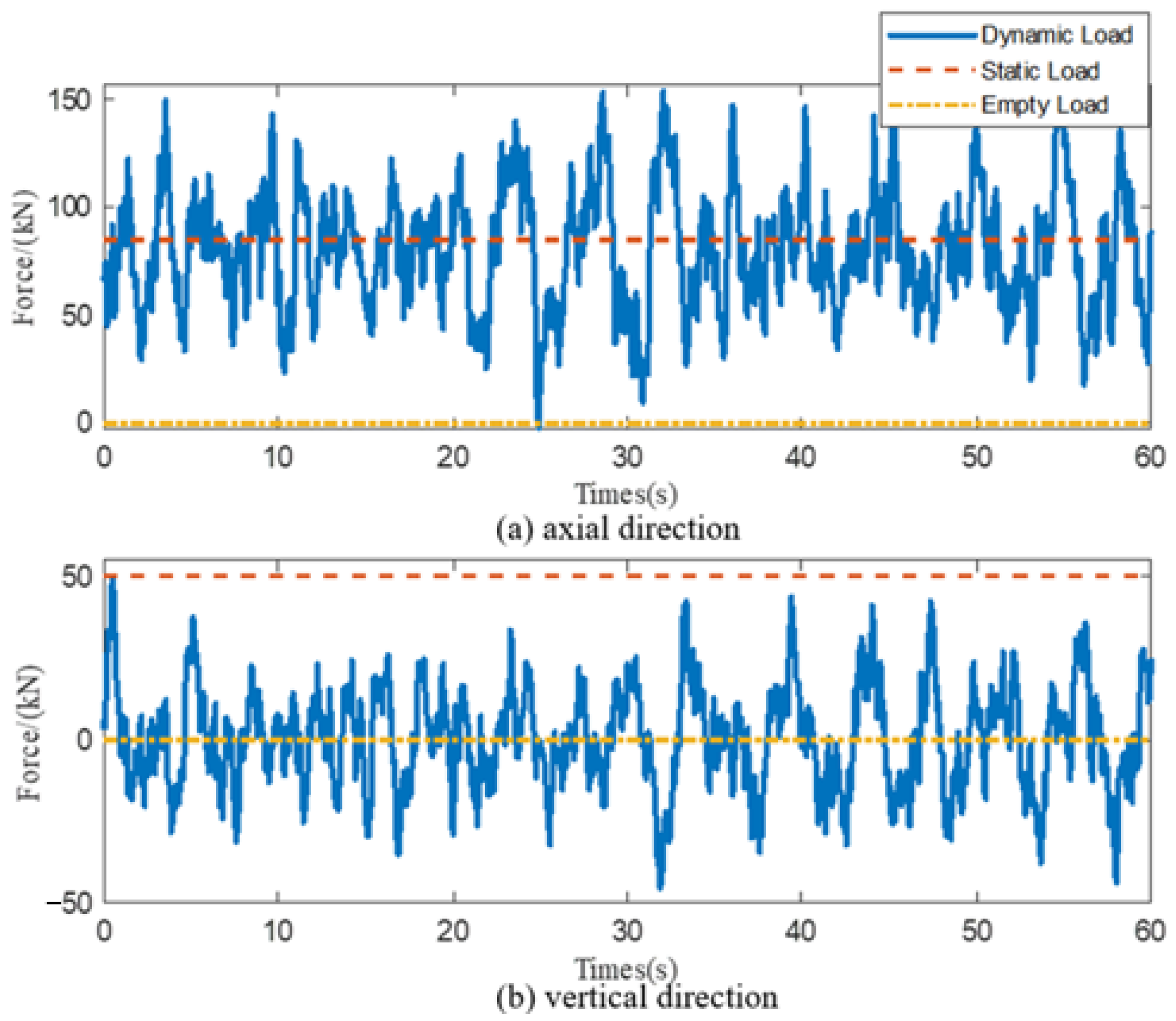
| Load | Empty load | 1 | 4 | 7 | 10 | 13 |
| Static load (Vertical 85 kN; axial 50 kN) | 2 | 5 | 8 | 11 | 14 | |
| Dynamic load (Vertical 80 kN with 0.2–20 Hz; axial 40 kN with 0.2–20 Hz) | 3 | 6 | 9 | 12 | 15 | |
| Target Domain | 1200 rpm | 1500 rpm | 1800 rpm | 2100 rpm | Variable Speed 0 →2100 → 0 rpm | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Source Domain | Empty Load | Static Load | Dynamic Load | Empty Load | Static Load | Dynamic Load | Empty Load | Static Load | Dynamic Load | Empty Load | Static Load | Dynamic Load | Empty Load | Static Load | Dynamic Load | ||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |||
| 1200 rpm | Empty Load | 1 | - | 99.55% ±0.40 | 99.17% ±0.28 | 99.83% ±0.14 | 98.28% ±1.31 | 98.55% ±0.41 | 98.82% ±0.44 | 97.66% ±0.24 | 98.29% ±0.34 | 99.76% ±0.24 | 98.38% ±0.44 | 98.39% ±0.28 | 91.79% ±1.84 | 86.67% ±2.42 | 87.38% ±3.73 |
| Static Load | 2 | 99.83% ±0.13 | - | 99.78% ±0.12 | 99.5% ±0.38 | 99.92% ±0.04 | 99.67% ±0.26 | 99.32% ±0.54 | 98.42% ±0.25 | 98.13% ±0.76 | 98.73% ±0.36 | 98.83% ±0.15 | 97.29% ±0.45 | 92.33% ±2.39 | 92.38% ±3.65 | 67.42% ±5.36 | |
| Dynamic Load | 3 | 99.88% ±0.14 | 99.38% ±0.82 | - | 99.92% ±0.06 | 99.92% ±0.08 | 99.96% ±0.04 | 99.36% ±0.86 | 98.16% ±0.43 | 98.79% ±0.34 | 98.39% ±0.80 | 97.67% ±1.42 | 97.88% ±1.18 | 90.88% ±3.58 | 93.58% ±1.39 | 88.54% ±4.28 | |
| 1500 rpm | Empty Load | 4 | 98.38% ±0.82 | 99.71% ±0.26 | 99.88% ±0.10 | - | 99.38% ±0.82 | 99.96% ±0.02 | 99.48% ±0.72 | 98.25% ±0.26 | 98.25% ±0.36 | 98.96% ±0.42 | 97.63% ±0.92 | 97.58% ±0.84 | 91.71% ±3.82 | 86.38% ±4.27 | 88.38% ±5.36 |
| Static Load | 5 | 98.96% ±0.06 | 99.43% ±0.42 | 99.68% ±0.21 | 99.38% ±0.82 | - | 99.88% ±0.08 | 99.83 ±0.14 | 99.63% ±0. | 99.75% ±0.26 | 99.96% ±0.02 | 99.71% ±0.28 | 99.54% ±0.36 | 91.63% ±2.24 | 94.83% ±2.18 | 66.75% ±7.24 | |
| Dynamic Load | 6 | 98.29% ±0.15 | 98.45% ±0.68 | 98.38% ±0.28 | 99.38% ±0.82 | 99.56% ±0.22 | - | 99.38% ±0.22 | 99.82% ±0.08 | 99.79% ±0.14 | 99.52% ±0.32 | 99.96% ±0.03 | 99.75% ±0.23 | 93.38% ±3.06 | 87.83% ±4.52 | 93.79% ±3.16 | |
| 1800 rpm | Empty Load | 7 | 98.96% ±0.02 | 99.31% ±0.56 | 98.79% ±0.64 | 99.02 ±0.32 | 99.22% ±0.56 | 99.92% ±0.06 | - | 99.79% ±0.19 | 99.25% ±0.38 | 99.38% ±0.27 | 99.5% ±0.42 | 98.83% ±0.12 | 91.17% ±4.18 | 85.83% ±5.17 | 88.71% ±4.92 |
| Static Load | 8 | 97.96% ±0.03 | 99.83% ±0.14 | 99.54% ±0.36 | 98.84 ±0.59 | 99.83% ±0.09 | 99.74% ±0.26 | 99.38% ±0.82 | - | 98.92% ±0.94 | 99.83% ±0.06 | 99.71% ±0.26 | 99.54% ±0.32 | 91.29% ±2.02 | 88.83% ±3.28 | 88.42% ±5.28 | |
| Dynamic Load | 9 | 98.38% ±0.44 | 98.18% ±0.38 | 98.23% ±0.62 | 98.91% ±0.39 | 98.87% ±0.92 | 99.21% ±0.48 | 99.48% ±0.36 | 99.54% ±0.21 | - | 99.82% ±0.10 | 99.96% ±0.03 | 99.92% ±0.04 | 94.83% ±2.14 | 90.83% ±2.18 | 94.88% ±3.14 | |
| 2100 rpm | Empty Load | 10 | 98.56% ±0.29 | 99.12% ±0.35 | 98.89% ±0.22 | 99.12% ±0.71 | 99.67% ±0.26 | 99.96% ±0.02 | 99.96% ±0.04 | 99.79% ±0.18 | 99.38% ±0.36 | - | 99.75% ±0.16 | 99.04% ±0.72 | 91.42% ±3.29 | 87.88% ±3.48 | 90.33% ±3.28 |
| Static Load | 11 | 98.88% ±0.30 | 99.02% ±0.58 | 99.22% ±0.49 | 98.87 ±0.72 | 98.62 ±0.38 | 99.88% ±0.10 | 99.83% ±0.12 | 99.54% ±0.34 | 99.54% ±0.38 | 99.92% ±0.26 | - | 99.71% ±0.26 | 89.63% ±3.16 | 92.54% ±2.39 | 90.38% ±3.66 | |
| Dynamic Load | 12 | 98.32% ±0.35 | 98.43% ±0.58 | 98.38% ±0.69 | 99.25% ±0.52 | 98.89% ±0.42 | 98.82% ±0.68 | 98.94% ±0.59 | 99.10% ±0.38 | 99.34% ±0.25 | 99.72% ±0.28 | 99.88% ±0.06 | - | 95.25% ±3.48 | 95.25% ±1.36 | 94.5% ±2.40 | |
| Variable Speed 0→2100→0 rpm | Empty Load | 13 | 99.64% ±0.24 | 99.45% ±0.25 | 99.68% ±0.36 | 99.24% ±0.52 | 99.79% ±0.16 | 99.88% ±0.07 | 99.13% ±0.69 | 99.88% ±0.09 | 100% ±0 | 100% ±0 | 99.33% ±0.35 | 99.75% ±0.16 | - | 95.25% ±3.48 | 94.88% ±2.06 |
| Static Load | 14 | 99.88% ±0.13 | 99.25% ±0.36 | 99.38% ±0.29 | 99.12% ±0.46 | 99.27% ±0.38 | 99.24% ±0.32 | 99.92% ±0.04 | 99.28% ±0.52 | 99.96% ±0.08 | 99.35% ±0.26 | 99.92% ±0.06 | 99.88% ±0.10 | 97.88% ±1.36 | - | 94.79% ±2.42 | |
| Dynamic Load | 15 | 99.96% ±0.02 | 99.97% ±0.03 | 99.96% ±0.05 | 99.98% ±0.06 | 99.92% ±0.04 | 99.91% ±0.08 | 99.96% ±0.04 | 99.95% ±0.05 | 99.94% ±0.07 | 99.96% ±0.02 | 99.93% ±0.05 | 99.96% ±0.03 | 98.79% ±0.53 | 97.5% ±1.16 | - | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Yang, S.; Liu, Y.; Wen, G. Deep Subdomain Transfer Learning with Spatial Attention ConvLSTM Network for Fault Diagnosis of Wheelset Bearing in High-Speed Trains. Machines 2023, 11, 304. https://doi.org/10.3390/machines11020304
Wang J, Yang S, Liu Y, Wen G. Deep Subdomain Transfer Learning with Spatial Attention ConvLSTM Network for Fault Diagnosis of Wheelset Bearing in High-Speed Trains. Machines. 2023; 11(2):304. https://doi.org/10.3390/machines11020304
Chicago/Turabian StyleWang, Jiujian, Shaopu Yang, Yongqiang Liu, and Guilin Wen. 2023. "Deep Subdomain Transfer Learning with Spatial Attention ConvLSTM Network for Fault Diagnosis of Wheelset Bearing in High-Speed Trains" Machines 11, no. 2: 304. https://doi.org/10.3390/machines11020304
APA StyleWang, J., Yang, S., Liu, Y., & Wen, G. (2023). Deep Subdomain Transfer Learning with Spatial Attention ConvLSTM Network for Fault Diagnosis of Wheelset Bearing in High-Speed Trains. Machines, 11(2), 304. https://doi.org/10.3390/machines11020304







