Indirect Estimation of Tire Pressure on Several Road Pavements via Interacting Multiple Model Approach
Abstract
1. Introduction
2. Vehicle Dynamics and Road Profile Synthesis Modelling
2.1. Road Surface Profile Synthesis
3. Interacting Multiple Model Filter
- 1.
- Mode Probability Prediction:
- 2.
- Mixing of the previous estimates:
- 3.
- Mode dependent UKFs, whose equations can be found in [34].
- 4.
- Mode Probability Correction:
- 5.
- IMMUF’s corrected estimates:
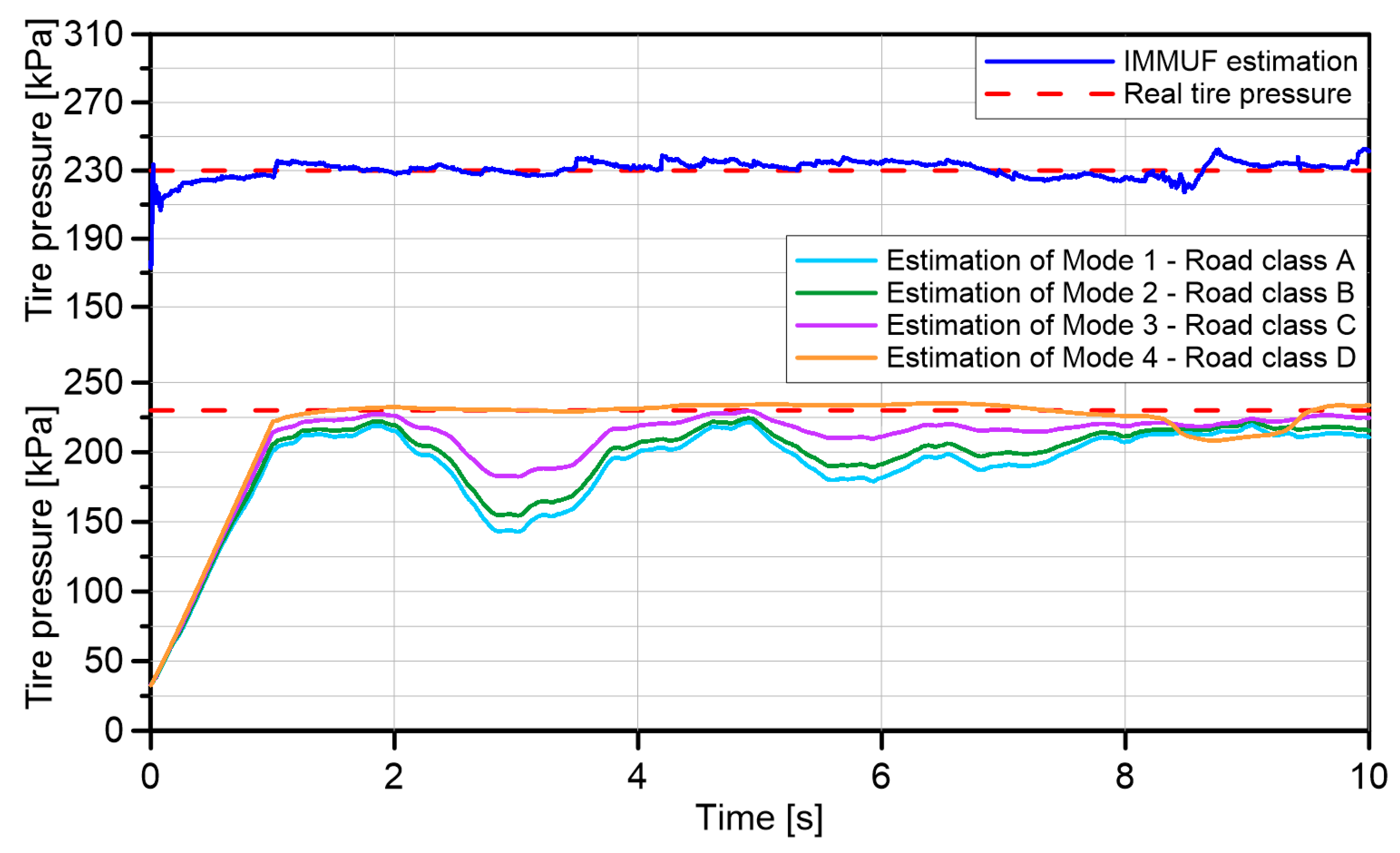
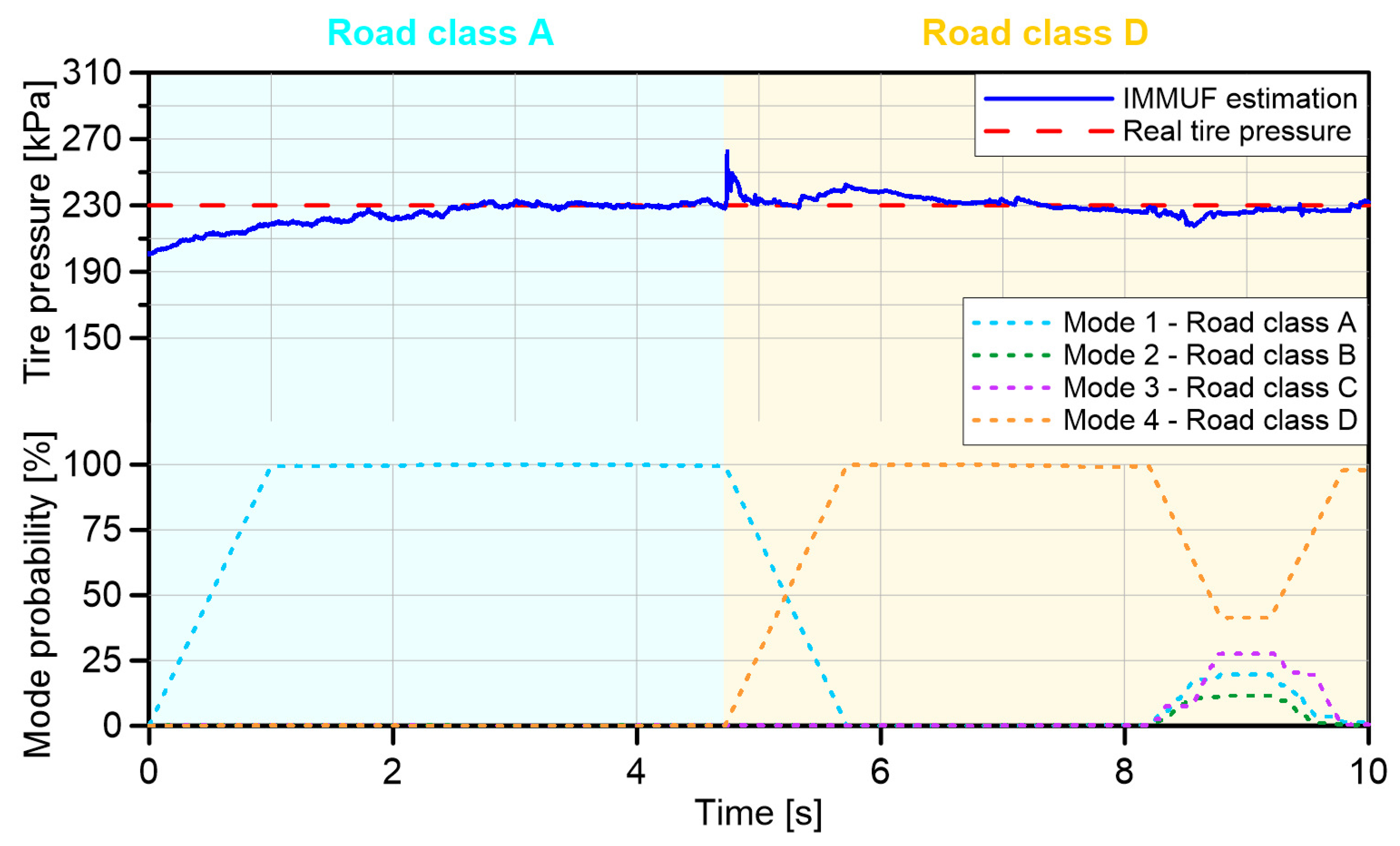
4. Tire Inflation Pressure Estimation
5. Algorithm Validation
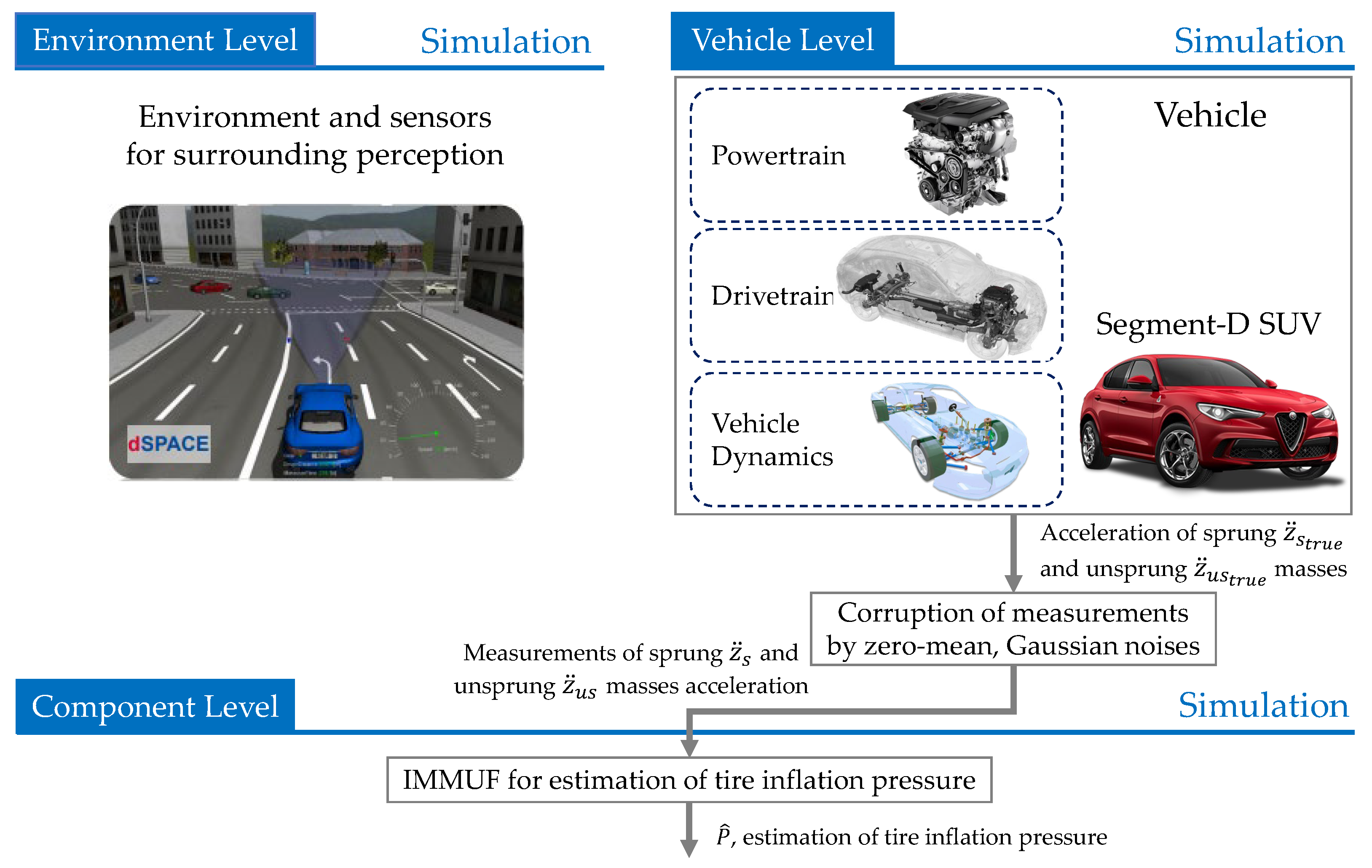
5.1. Simulation Platform
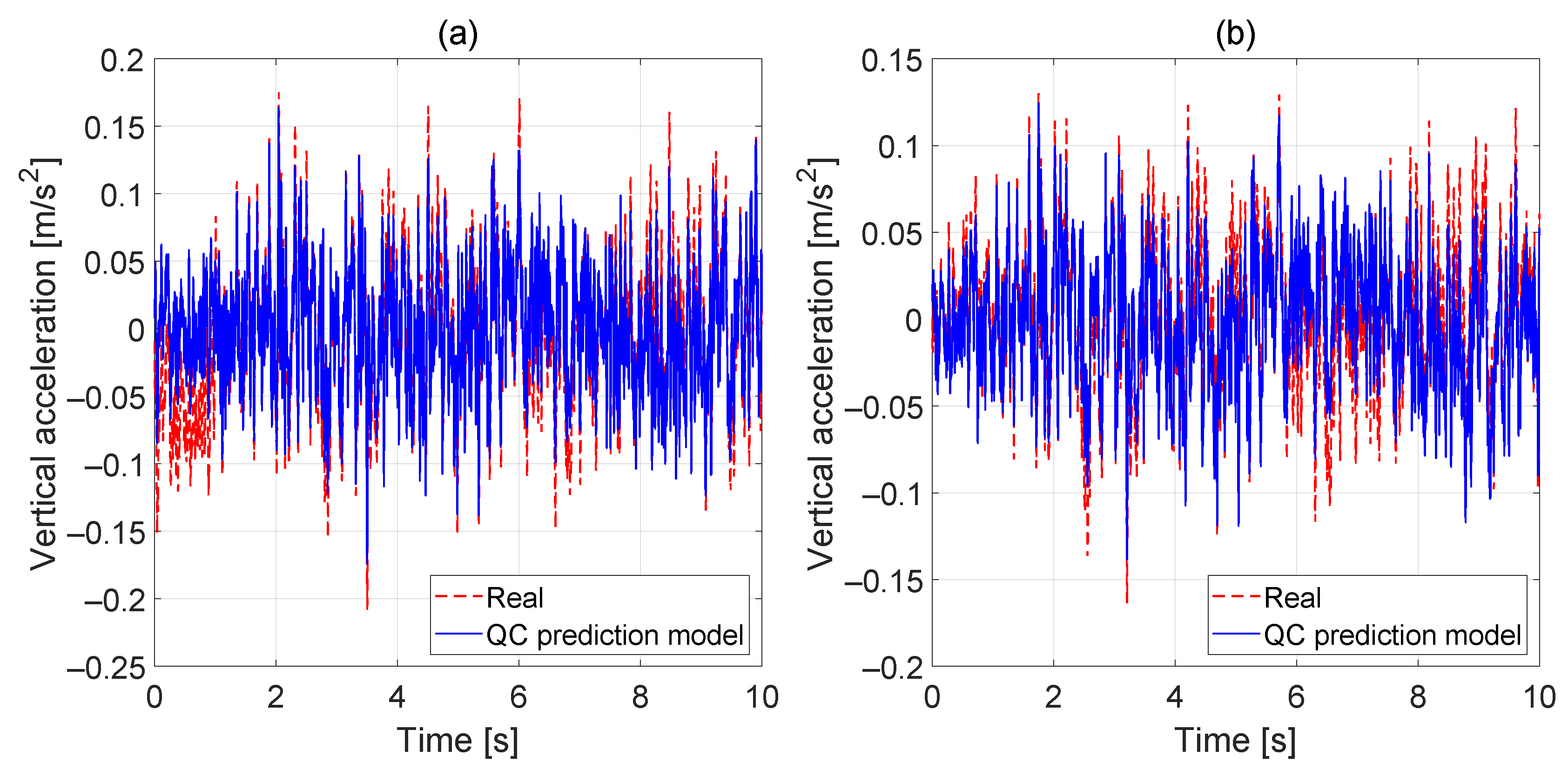
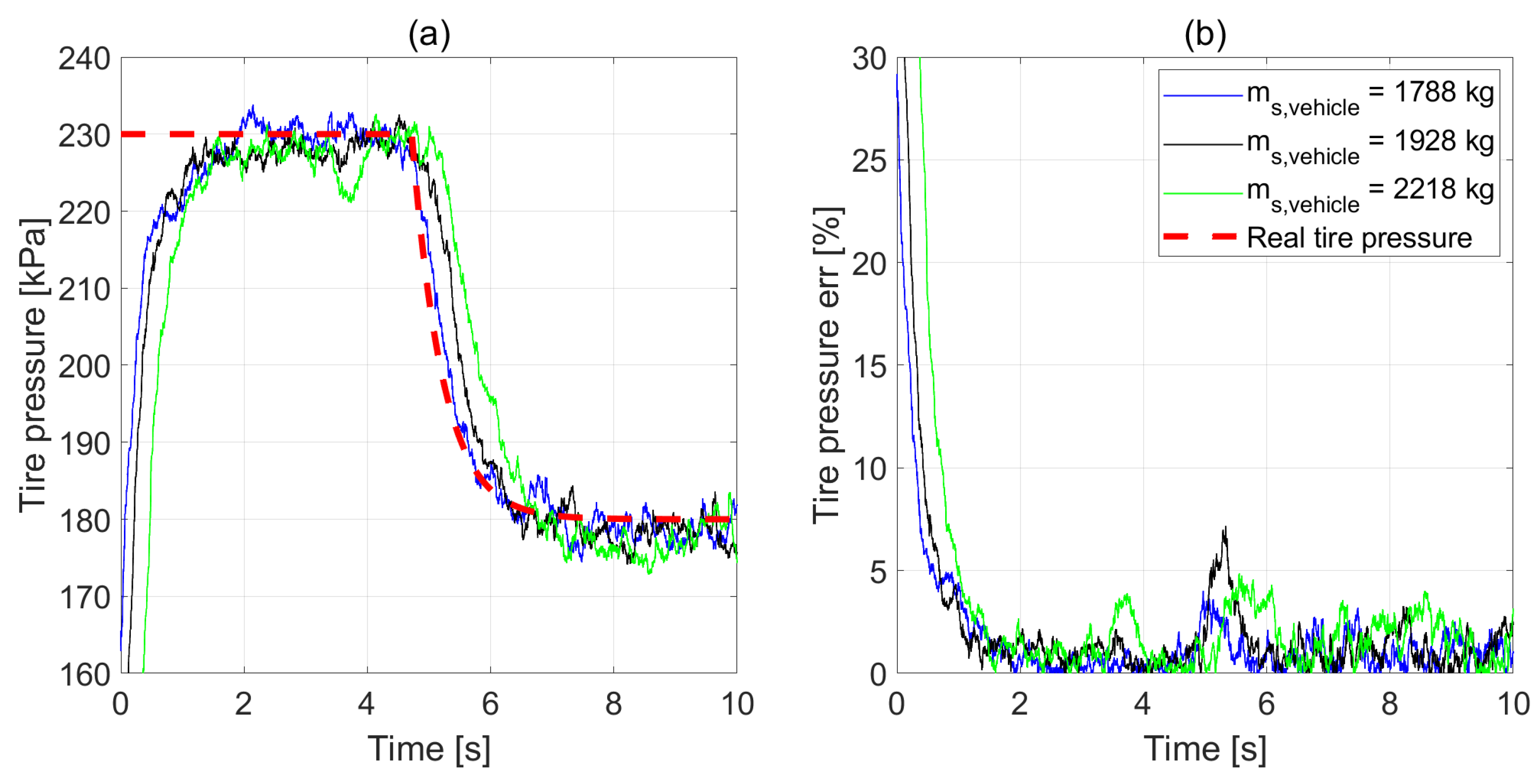
5.2. 2DOF QC Parameters Identification
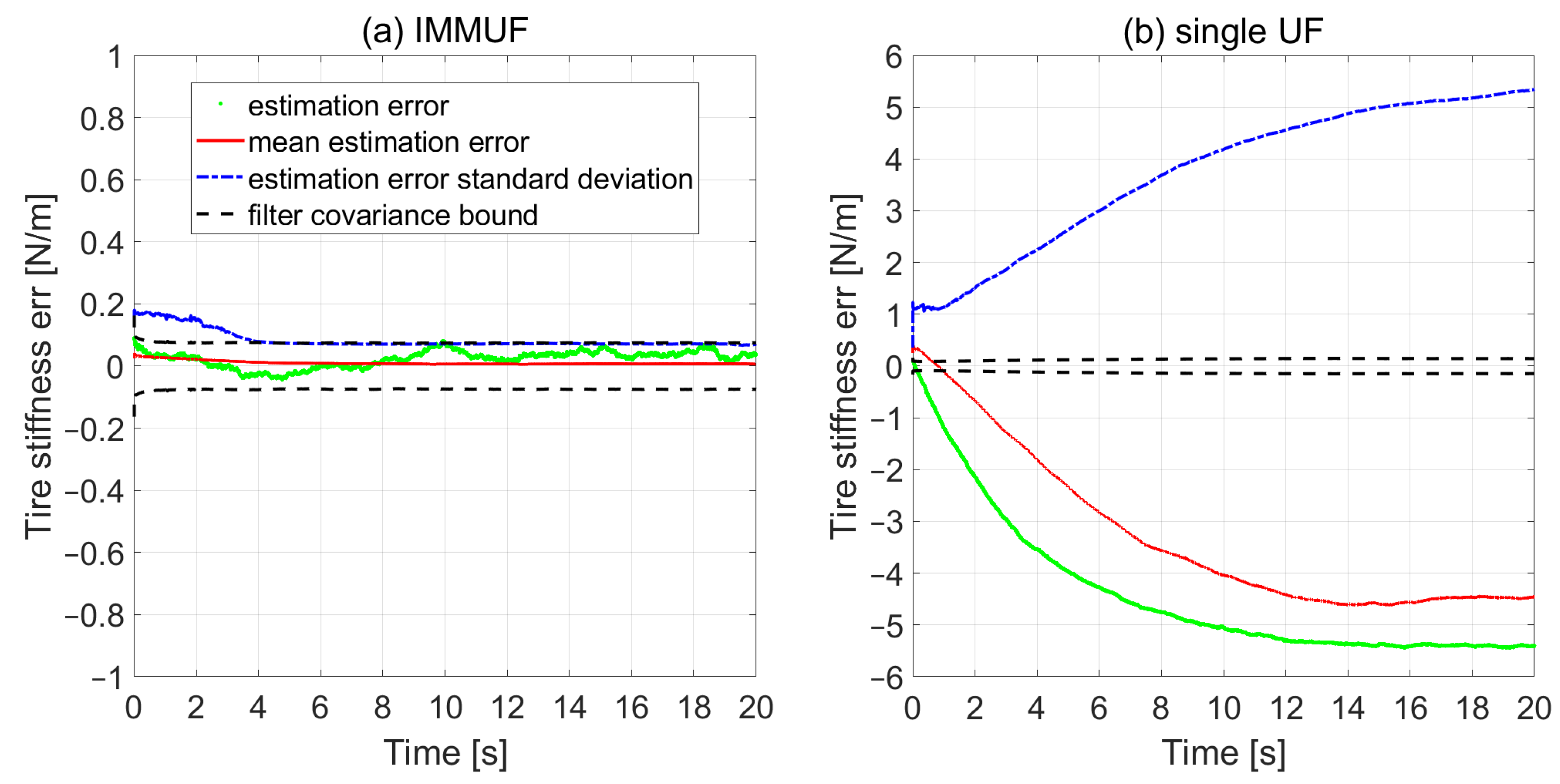
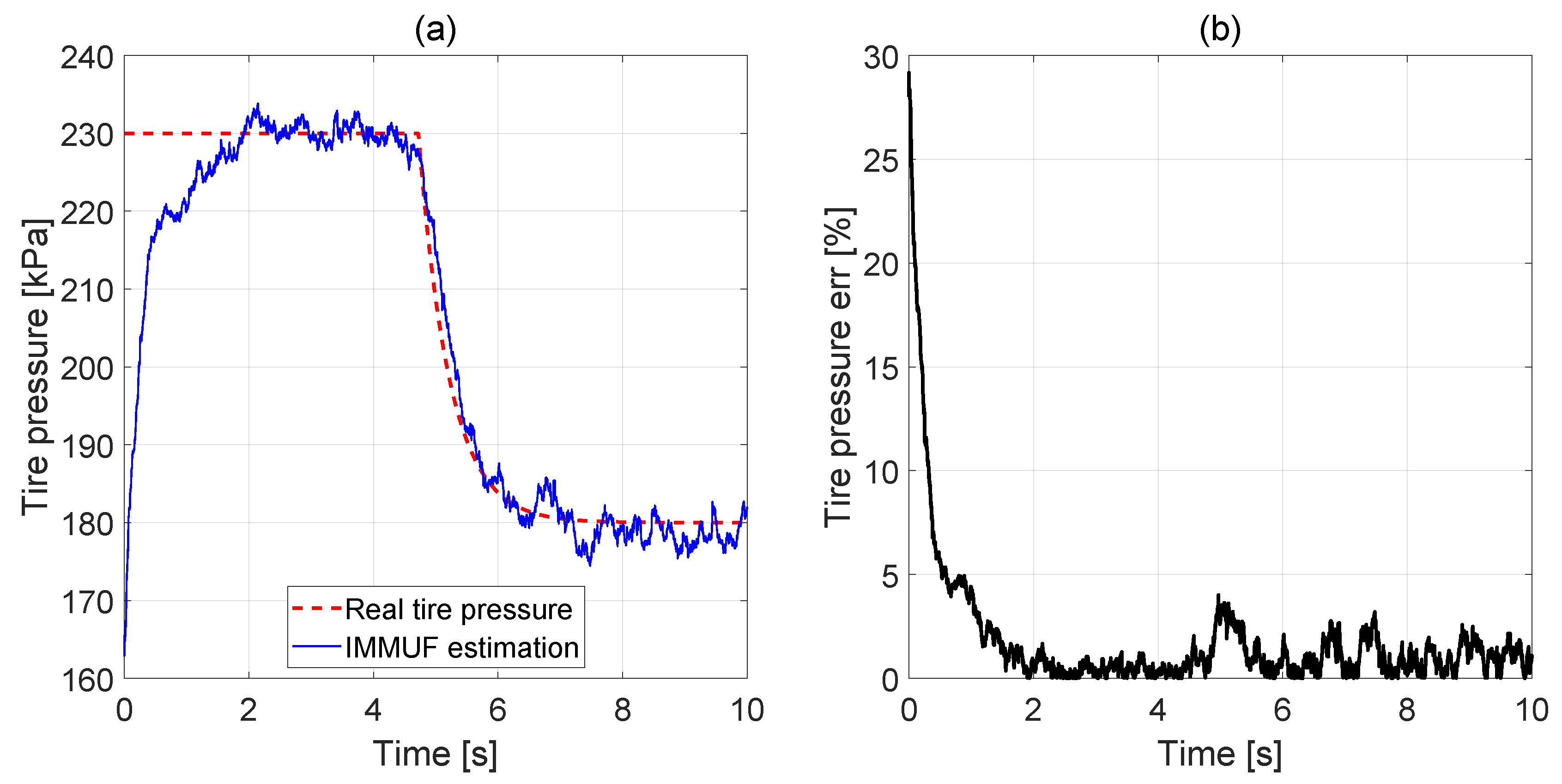
5.3. Monte Carlo Simulation
- Mean estimation error from all the Monte Carlo samples (the red line in Figure 6). For each -th time step, the mean estimation error is calculated as
- Standard deviation of the estimation errors (the dashed blue line in Figure 6). For each -th time step, the standard deviation of the errors is calculated as
- Covariance bound computed by the filter (the dashed black line in Figure 6). For each -th time step, the -bounds is calculated by the square root of the diagonal elements of the covariance matrix P, as
- Comparison of sample estimation error (the green line in Figure 6) with the -bounds.
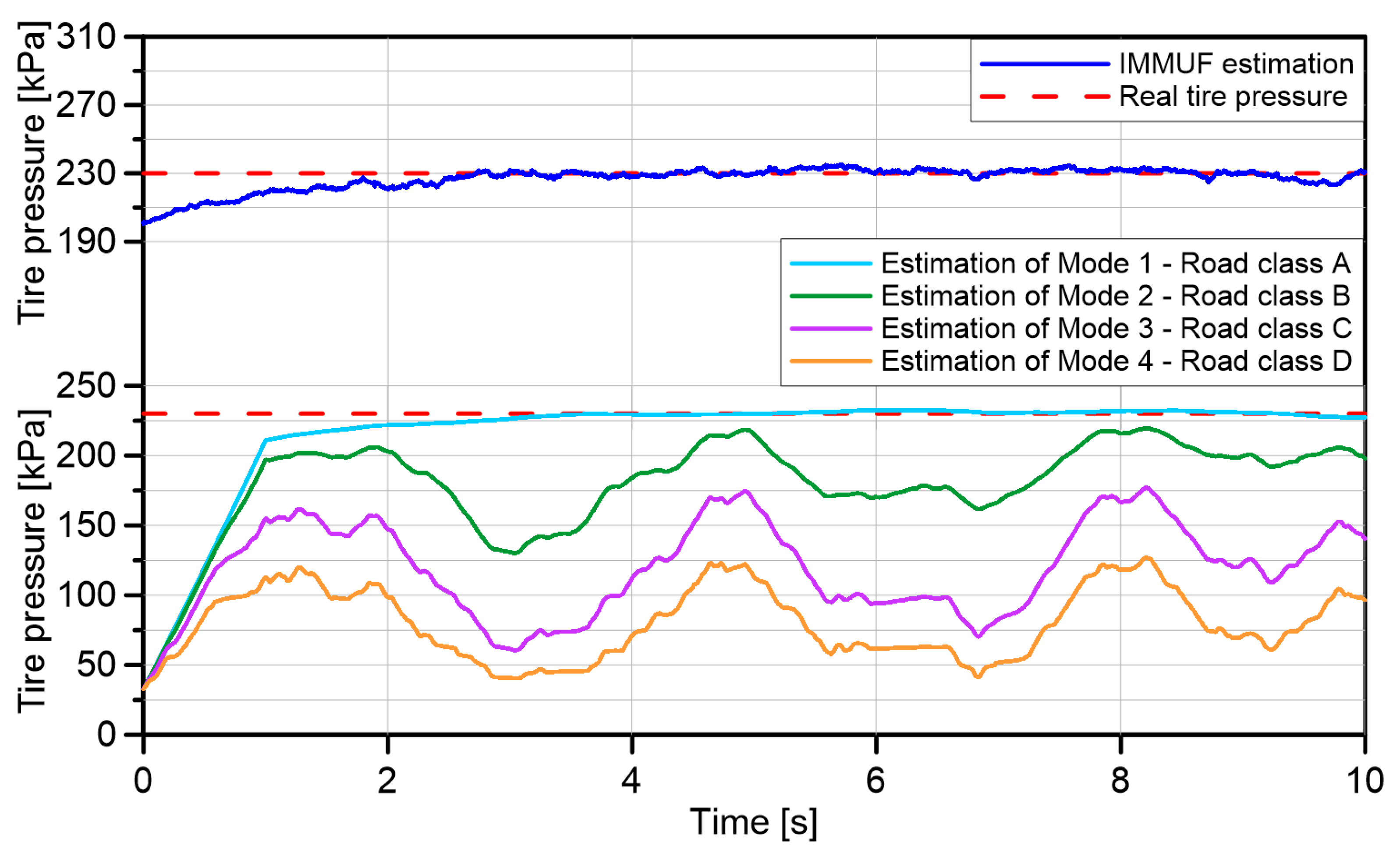
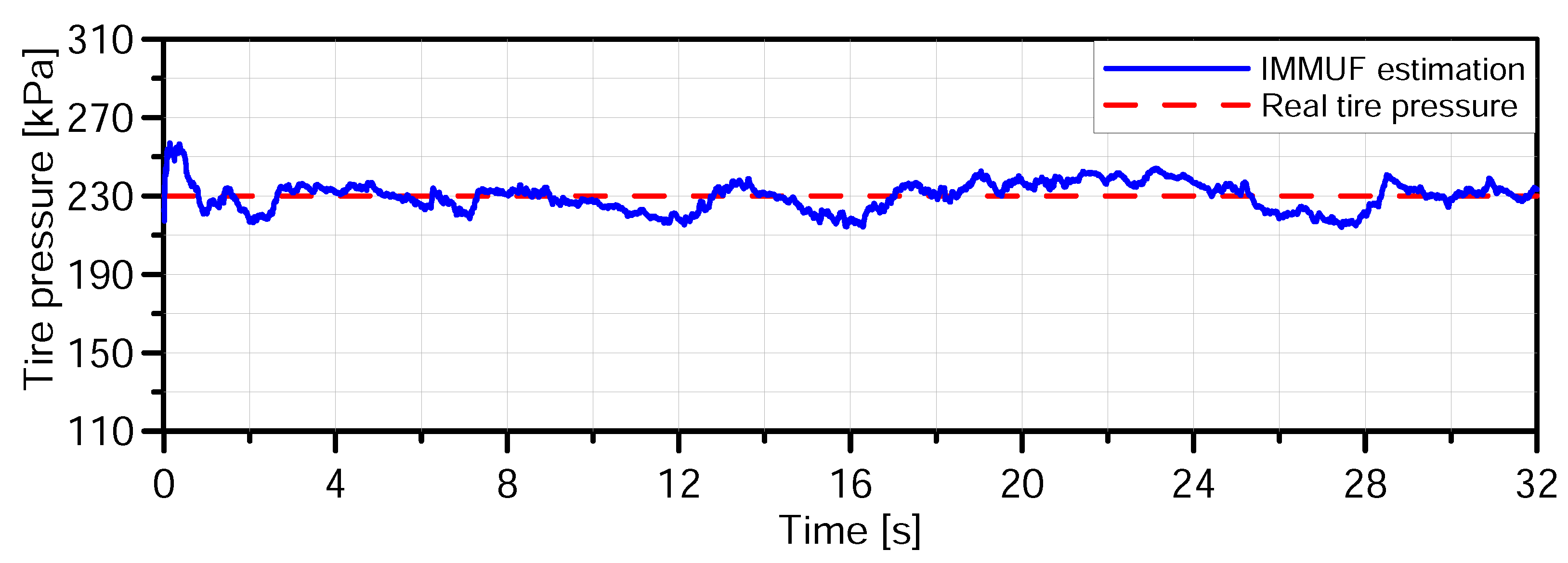
5.4. Tire Inflation Pressure Estimation
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| NHTSA | National Highway Traffic Safety Administration |
| TPMS | Tire Pressure Monitoring System |
| dTPMS | direct Tire Pressure Monitoring System |
| iTPMS | indirect Tire Pressure Monitoring System |
| KF | Kalman Filter |
| EKF | Extended Kalman Filter |
| UKF | Unscented Kalman Filter |
| MM | Multiple Model |
| IMM | Interactive Multiple Model |
| IMMUF | Interacting Multiple Model Unscented Filter |
| 2DOF | Two Degree Of Freedom |
| QC | Quarter Car |
| PSD | Power Spectral Density |
| MTM | Markov Transition Matrix |
| RMSE | root Mean Square Error |
| ASM | Automotive Simulation Model |
Nomenclature
| Symbol | Description | Symbol | Description |
| Sprung mass | Unsprung mass | ||
| vehicle chassis mass | loading mass | ||
| total sprung mass of the vehicle | l | wheelbase | |
| rear semiwheel base | inflation pressure increment | ||
| Linear damping coefficient | Non-linear square damping coefficient | ||
| Linear spring stiffness coefficient | Non-linear cube spring stiffness coefficient | ||
| Tire stiffness coefficient | vertical stiffness at the nominal inflation pressure | ||
| sprung mass vertical displacement | unsprung mass vertical displacement | ||
| Symbol | Description | Symbol | Description |
| road profile | nominal pressure | ||
| effective pressure | pressure effect on vertical stiffness | ||
| angular frequency | PSD | ||
| road roughness variance | v | vehicle longitudinal velocity | |
| linear shape filter parameter | probability vector | ||
| reference spacial frequency | lower spatial frequency | ||
| upper spatial frequency | Probability transition matrix | ||
| Q | process noise covariance matrix | state vector | |
| measurement vector | process function | ||
| measurement function | P | covariance matrix | |
| noise covariance matrix | sprung mass acceleration variance | ||
| time step | noise |
References
- Elfasakhany, A. Tire Pressure Checking Framework: A Review Study. Reliab. Eng. Resil. 2019, 1, 12–28. [Google Scholar]
- Mayer, A.; Emig, G.; Gmehling, B.; Popovska, N.; Hölemann, K.; Buck, A. Passive regeneration of catalyst coated Knitted fiber Diesel particulate traps. SAE Trans. 1996, 105, 36–44. [Google Scholar]
- Isermann, R. Automotive Control: Modeling and Control of Vehicles; Springer: Berlin/Heidelberg, Germany, 2022. [Google Scholar]
- Persson, N.; Gustafsson, F.; Drevö, M. Indirect tire pressure monitoring using sensor fusion. SAE Trans. 2002, 111, 1657–1662. [Google Scholar]
- Weispfenning, T. Fault detection and diagnosis of components of the vehicle vertical dynamics. Meccanica 1997, 32, 459–472. [Google Scholar] [CrossRef]
- Isermann, R.; Wesemeier, D. Indirect vehicle tire pressure monitoring with wheel and suspension sensors. IFAC Proc. Vol. 2009, 42, 917–922. [Google Scholar] [CrossRef]
- Solmaz, S. A Novel Method for Indirect Estimation of Tire Pressure. J. Dyn. Syst. Meas. Control 2016, 138, 054501. [Google Scholar] [CrossRef]
- Reina, G.; Gentile, A.; Messina, A. Tyre pressure monitoring using a dynamical model-based estimator. Veh. Syst. Dyn. 2015, 53, 568–586. [Google Scholar] [CrossRef]
- Kang, S.W.; Kim, J.S.; Kim, G.W. Road roughness estimation based on discrete Kalman filter with unknown input. Veh. Syst. Dyn. 2019, 57, 1530–1544. [Google Scholar] [CrossRef]
- Lee, D.H.; Yoon, D.S.; Kim, G.W. New indirect tire pressure monitoring system enabled by adaptive extended Kalman filtering of vehicle suspension systems. Electronics 2021, 10, 1359. [Google Scholar] [CrossRef]
- Tsunashima, H.; Murakami, M.; Miyataa, J. Vehicle and road state estimation using interacting multiple model approach. Veh. Syst. Dyn. 2006, 44, 750–758. [Google Scholar] [CrossRef]
- Battistini, S.; Brancati, R.; Lui, D.G.; Tufano, F. Enhancing ADS and ADAS Under Critical Road Conditions Through Vehicle Sideslip Angle Estimation via Unscented Kalman Filter-Based Interacting Multiple Model Approach. In Proceedings of the Advances in Italian Mechanism Science; Springer International Publishing: Cham, Switzerland, 2022; pp. 450–460. [Google Scholar]
- Ping, X.; Cheng, S.; Yue, W.; Du, Y.; Wang, X.; Li, L. Adaptive estimations of tyre–road friction coefficient and body’s sideslip angle based on strong tracking and interactive multiple model theories. Proc. Inst. Mech. Eng. Part D J. Autom. Eng. 2020, 234, 3224–3238. [Google Scholar] [CrossRef]
- Musa, A.; Pipicelli, M.; Spano, M.; Tufano, F.; De Nola, F.; Di Blasio, G.; Gimelli, A.; Misul, D.A.; Toscano, G. A review of model predictive controls applied to advanced driver-assistance systems. Energies 2021, 14, 7974. [Google Scholar] [CrossRef]
- Mohite, A.G.; Mitra, A.C. Development of linear and non-linear vehicle suspension model. Mater. Today Proc. 2018, 5, 4317–4326. [Google Scholar] [CrossRef]
- Sayers, M.W. The Little Book of Profiling: Basic Information about Measuring and Interpreting Road Profiles; Technical Report; University of Michigan, Transportation Research Institute: Ann Arbor, MI, USA, 1998. [Google Scholar]
- Hurel, J.; Mandow, A.; García-Cerezo, A. Kinematic and dynamic analysis of the McPherson suspension with a planar quarter-car model. Veh. Syst. Dyn. 2013, 51, 1422–1437. [Google Scholar] [CrossRef]
- McGee, C.G.; Haroon, M.; Adams, D.E.; Luk, Y.W. A frequency domain technique for characterizing nonlinearities in a tire-vehicle suspension system. J. Vib. Acoust. 2005, 127, 61–76. [Google Scholar] [CrossRef]
- Nagarkar, M.P.; Patil, G.J.V.; Patil, R.N.Z. Optimization of nonlinear quarter car suspension–seat–driver model. J. Adv. Res. 2016, 7, 991–1007. [Google Scholar] [CrossRef]
- Lemaitre, J. Handbook of Materials Behavior Models, Three-Volume Set: Nonlinear Models and Properties; Elsevier: Amsterdam, The Netherlands, 2001. [Google Scholar]
- Guiggiani, M. The Science of Vehicle Dynamics; Springer: Pisa, Italy, 2014; p. 15. [Google Scholar]
- Maher, D.; Young, P. An insight into linear quarter car model accuracy. Veh. Syst. Dyn. 2011, 49, 463–480. [Google Scholar] [CrossRef]
- Wong, J.Y. Theory of Ground Vehicles; John Wiley & Sons: Hoboken, NJ, USA, 2022. [Google Scholar]
- Taylor, R.; Bashford, L.; Schrock, M. Methods for measuring vertical tire stiffness. Trans. ASAE 2000, 43, 1415–1419. [Google Scholar] [CrossRef]
- Besselink, I.; Schmeitz, A.; Pacejka, H. An improved Magic Formula/Swift tyre model that can handle inflation pressure changes. Veh. Syst. Dyn. 2010, 48, 337–352. [Google Scholar] [CrossRef]
- ISO (International Organization for Standardization) 8608:2016; Mechanical Vibration—Road Surface PROFILES—Reporting of Measured Data. Available online: https://www.iso.org/standard/71202.html (accessed on 18 October 2022).
- Ulsoy, A.G.; Peng, H.; Çakmakci, M. Automotive Control Systems; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Tyan, F.; Hong, Y.F.; Tu, S.H.; Jeng, W.S. Generation of random road profiles. J. Adv. Eng. 2009, 4, 1373–1378. [Google Scholar]
- Dharankar, C.S.; Hada, M.K.; Chandel, S. Numerical generation of road profile through spectral description for simulation of vehicle suspension. J. Braz. Soc. Mech. Sci. Eng. 2017, 39, 1957–1967. [Google Scholar] [CrossRef]
- Schiehlen, W. White noise excitation of road vehicle structures. Sadhana 2006, 31, 487–503. [Google Scholar] [CrossRef]
- Goenaga, B.; Fuentes, L.; Mora, O. Evaluation of the methodologies used to generate random pavement profiles based on the power spectral density: An approach based on the International Roughness Index. Ing. E Investig. 2017, 37, 49–57. [Google Scholar] [CrossRef]
- Shannon, C.E. Communication in the presence of noise. Proc. IRE 1949, 37, 10–21. [Google Scholar] [CrossRef]
- Lenkutis, T.; Čerškus, A.; Šešok, N.; Dzedzickis, A.; Bučinskas, V. Road surface profile synthesis: Assessment of suitability for simulation. Symmetry 2020, 13, 68. [Google Scholar] [CrossRef]
- Battistini, S.; Menegaz, H.M. Interacting multiple model unscented filter for tracking a ballistic missile during its boost phase. In Proceedings of the 2017 IEEE Aerospace Conference, Big Sky, MT, USA, 4–11 March 2017; pp. 1–8. [Google Scholar]
- Varshney, D.; Bhushan, M.; Patwardhan, S.C. State and parameter estimation using extended Kitanidis Kalman filter. J. Process Control 2019, 76, 98–111. [Google Scholar] [CrossRef]
- Stellantis. Segment-D SUV Vehicle Specifications’ Documents. 2022. Available online: https://stellantis-na-product-media.info/alfa-romeo/stelvio (accessed on 29 November 2022).
- Maino, C.; Misul, D.; Musa, A.; Spessa, E. Optimal mesh discretization of the dynamic programming for hybrid electric vehicles. Appl. Energy 2021, 292, 116920. [Google Scholar] [CrossRef]
- Gimelli, A.; Luongo, A.; Muccillo, M. Efficiency and cost optimization of a regenerative Organic Rankine Cycle power plant through the multi-objective approach. Appl. Therm. Eng. 2017, 114, 601–610. [Google Scholar] [CrossRef]
- Brancati, R.; Muccillo, M.; Tufano, F. Crank mechanism friction modeling for control-oriented applications. In Proceedings of the The International Conference of IFToMM ITALY; Springer: Cham, Switzerland, 2020; pp. 729–737. [Google Scholar]
- Petrillo, A.; Prati, M.V.; Santini, S.; Tufano, F. Improving the NOx reduction performance of an Euro VI d SCR System in real-world condition via nonlinear model predictive control. Int. J. Engine Res. 2021. [CrossRef]
- Papadopoulos, C.E.; Yeung, H. Uncertainty estimation and Monte Carlo simulation method. Flow Meas. Instrum. 2001, 12, 291–298. [Google Scholar] [CrossRef]
- De Nola, F.; Giardiello, G.; Noviello, B.; Tufano, F. A control-oriented and physics-based model of the engine crank mechanism friction for the base calibration: Parametric analysis. In Proceedings of the AIP Conference Proceedings; AIP Publishing LLC: College Park, MD, USA, 2019; Volume 2191, p. 020060. [Google Scholar]
- Harding, B.; Tremblay, C.; Cousineau, D. Standard errors: A review and evaluation of standard error estimators using Monte Carlo simulations. Quant. Methods Psychol. 2014, 10, 107–123. [Google Scholar] [CrossRef]
- Harrison, R.L. Introduction to monte carlo simulation. In Proceedings of the AIP Conference Proceedings; American Institute of Physics: College Park, MD, USA, 2010; Volume 1204, pp. 17–21. [Google Scholar]
- Ge, Q.; Shao, T.; Duan, Z.; Wen, C. Performance analysis of the Kalman filter with mismatched noise covariances. IEEE Trans. Autom. Control 2016, 61, 4014–4019. [Google Scholar] [CrossRef]
- Šroubek, F.; Šorel, M.; Žák, J. Precise international roughness index calculation. Int. J. Pavement Res. Technol. 2022, 15, 1413–1419. [Google Scholar] [CrossRef]



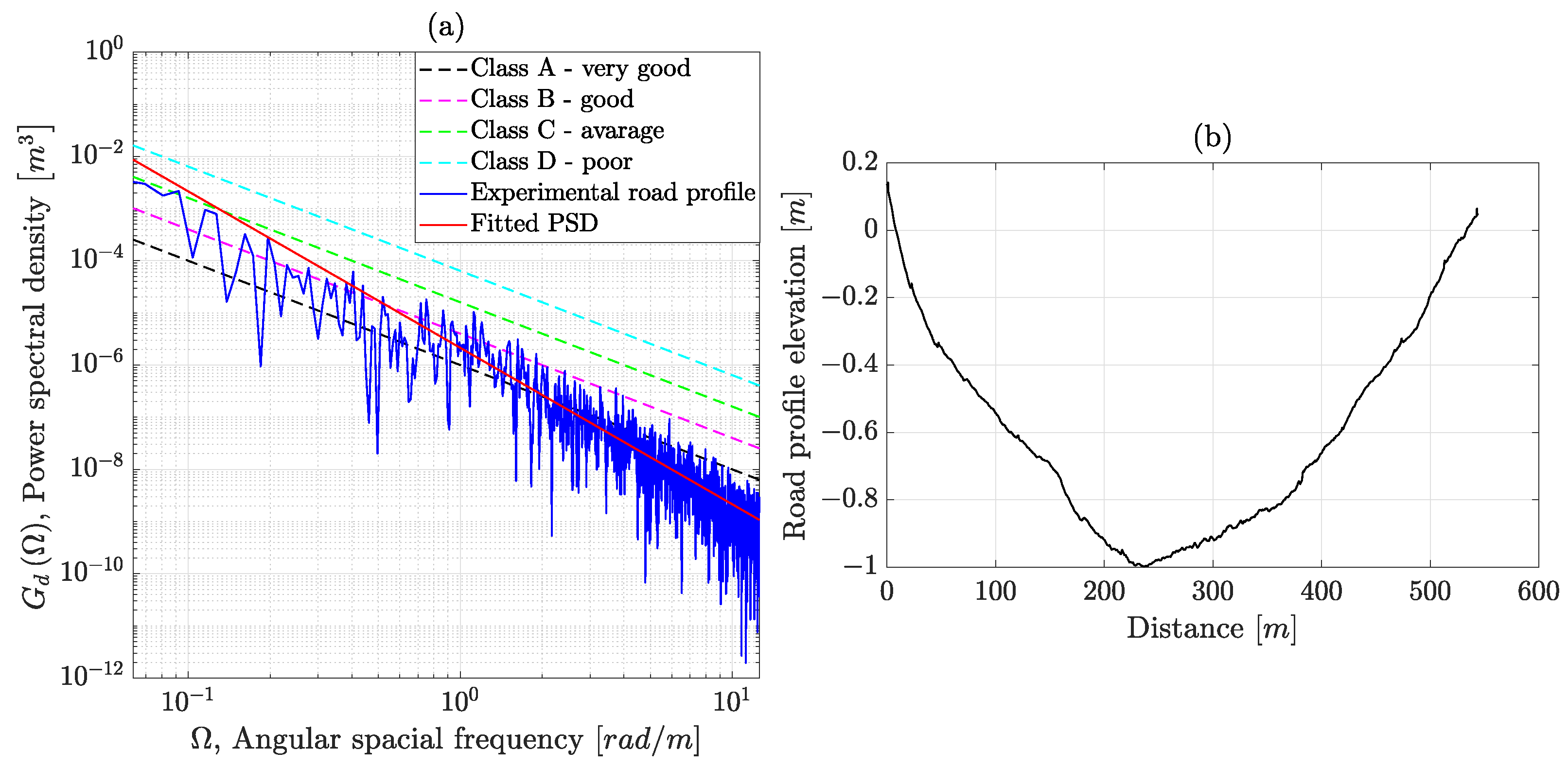
| Quantity | Value | Quantity | Value |
|---|---|---|---|
| Mass of vehicle chassis (vehicle body) | 1788 kg | Height of the center of mass | 0.6 m |
| Front semi-wheelbase | 1.347 m | Rear semi-wheelbase | 1.471 m |
| Front track width | 1.606 m | Rear track width | 1.6364 m |
| Yaw moment of inertia | 3230 kg m2 | Frontal area | 2.75 m2 |
| Front wheel mass | 61.14 kg | Rear wheel mass | 52.75 kg |
| Nominal pressure of inflated tire | 250 kPa | vertical stiffness at | 264,700 N/m |
| Parameter | Description |
|---|---|
| Linear damping coefficient | |
| Non-linear square damping coefficient | |
| Linear spring stiffness coefficient | |
| Non-linear cube spring stiffness coefficient |
| Parameter | Road Class A | Road Class B | Road Class C | Road Class D |
|---|---|---|---|---|
| [Ns/m] | 6576 | 4585 | 14,819 | 14,708 |
| [Ns/m2] | 4319 | 6016 | 5839 | 4555 |
| [N/m] | 113,086 | 173,415 | 94,544 | 118,114 |
| [N/m3] | 130,098 | 151,886 | 62,836 | 121,723 |
| Parameter | Range |
|---|---|
| (130–230) [kPa] | |
| v | 40–80 [km/h] |
| a | 0–3 [-] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brancati, R.; Tufano, F. Indirect Estimation of Tire Pressure on Several Road Pavements via Interacting Multiple Model Approach. Machines 2022, 10, 1221. https://doi.org/10.3390/machines10121221
Brancati R, Tufano F. Indirect Estimation of Tire Pressure on Several Road Pavements via Interacting Multiple Model Approach. Machines. 2022; 10(12):1221. https://doi.org/10.3390/machines10121221
Chicago/Turabian StyleBrancati, Renato, and Francesco Tufano. 2022. "Indirect Estimation of Tire Pressure on Several Road Pavements via Interacting Multiple Model Approach" Machines 10, no. 12: 1221. https://doi.org/10.3390/machines10121221
APA StyleBrancati, R., & Tufano, F. (2022). Indirect Estimation of Tire Pressure on Several Road Pavements via Interacting Multiple Model Approach. Machines, 10(12), 1221. https://doi.org/10.3390/machines10121221






