Minimizing Misalignment and Frame Protrusion of Shoulder Exoskeleton via Optimization for Reducing Interaction Force and Minimizing Volume

Abstract

Although industrial shoulder exoskeletons have undergone rapid advancement, their acceptance by industrial workers is limited owing to the misalignment and interference between the exoskeletal frame and the wearer’s body and bulkiness of the frames. Several joint mechanisms have been developed to offset misalignments; however, none of the existing systems can simultaneously alleviate the interference and bulkiness problems. Furthermore, the reduction in the misalignments in terms of forces generated at the human–robot interface has not been experimentally verified. Therefore, in this study, design optimization was performed to address the various factors that limit the use of the existing industrial shoulder exoskeletons. Upper body motions were captured and converted into a target trajectory for the exoskeleton to follow. The optimal prismatic–revolute–revolute joint configuration was derived and used to manufacture a skeletal mock-up, which was used to perform experiments. The misalignments of the optimized configuration in the considered motions were 67% lower than those for the conventional joint configuration. Furthermore, the interaction forces were negligible (1.35 N), with a maximum reduction of 61.8% compared to those of conventional configurations.

1. Introduction

Workers at various occupational sites perform repeated lifting and carrying motions that may lead to severe musculoskeletal disorders related to the lumbar [1] and shoulder [2]. Several types of robots have been developed to prevent these injuries. Wearable robots, aimed at assisting workers, have been noted to be particularly effective [3]. Kim et al. [4] and Liu et al. [5] showed that the use of exoskeletons can prevent work-related injuries by reducing the muscle activity and fatigue of the shoulder.

Shoulder exoskeletons that adopt passive elements (such as springs) for generating an assistive force have drawn considerable attention in the industrial domain owing to their lightweight structure. However, several limitations must be overcome to promote their acceptance among industrial workers. The first problem pertains to the interaction forces generated by the misalignment between the exoskeletal frame and the wearer’s body. Specifically, the wearer is often subjected to undesirable forces when the rigid frames of the exoskeleton, which are connected to the wearer’s upper arm, are misaligned [6]. Notably, industrial exoskeletons have a limited number of joints to promote wearability, which makes it challenging to align the exoskeletal frame with the human flexible joint movements [7,8,9]. Such misalignment is frequently encountered in the case of passive shoulder exoskeletons, given that the shoulder has one of the most complex joint structures in the human body [6,8]. Repeated misalignment and interaction forces may lead to musculoskeletal injuries and deteriorate the performance of the exoskeletons by hindering the accurate transmission of the assistance force. Therefore, misalignments must be offset in passive shoulder exoskeletons.

Second, the exoskeletal frames may interfere with certain working motions of the workers. At construction sites, workers often carry items such as pipes and boxes on their shoulders. In most commercialized industrial shoulder exoskeletons, the joint mechanisms operate above the shoulder [10,11,12,13], which may disrupt the working motions of the workers. Additionally, the exoskeletal frames are located next to the wearer’s head and thus pose a risk of collision. Therefore, the joint mechanisms located above the shoulder limit the wearability of the shoulder exoskeleton.

Finally, wearable devices must be low weight and compact to ensure the comfort of the wearer. To satisfy these requirements, exoskeletons with one revolute joint have been developed, which have highly simplified joint mechanisms [10,11,13]. However, the resulting lack of degree of freedom (DOF) makes it challenging for these mechanisms to follow the upper arm movement, resulting in positional and orientation errors between the wearer’s body and exoskeletal frame. Such non-optimized reduction in the weight and volume of the exoskeletons tends to aggravate the misalignment and interference.

To address these problems, researchers have developed innovative joint mechanisms for shoulder exoskeletons. For example, redundant DOFs were introduced in the joint [6,14,15,16,17,18] to eliminate misalignment. However, these exoskeletons were aimed at rehabilitation, and the massive joint mechanisms were not appropriate for mobile industrial exoskeletons. Focusing on mobile industrial exoskeletons, Hyun et al. developed lightweight multi-linkage structures to reduce misalignment without any kinematic redundancy [19]. However, the mechanism was located above the shoulder and could realize only a certain elliptical trajectory determined by the length of the four bars. Therefore, this framework could not compensate for the misalignment induced by variable arm movements.

Park et al. [20] and Christensen and Bai [21] developed an under-shoulder joint mechanism consisting of redundant joints to compensate for the misalignment. However, these mechanisms were bulky and heavy. Castro et al. developed a compact scissors linkage mechanism located under the shoulder [22], which was lightweight and could alleviate misalignment. However, no experimental evidence was provided regarding the efficacy of misalignment reduction in terms of the force applied at the human–robot interaction point. This experimental validation was also not carried out for other joint mechanisms of industrial shoulder exoskeletons [19,20]. In this context, it is necessary to experimentally evaluate the human–machine mechanism to validate its effect of reducing the undesired forces that may cause discomfort and injury [6,23].

To address the abovementioned limitations and satisfy the fundamental criteria of passive shoulder exoskeletons, in this study, a kinematic optimization framework of the joint configuration of industrial shoulder exoskeletons was established. Specifically, to reduce the misalignment and eliminate the interference between the wearer and exoskeletal frame, motion capture techniques were used to determine the target trajectories and orientation to be followed by the joint mechanism of the exoskeleton. To ensure that the exoskeleton was compact, we attempted to reduce the misalignment caused only by horizontal arm movements, as described in [8,20]. In other words, the target trajectories were limited to two-dimensional (2-D) components in the transverse plane. In general, because the exoskeletons assist arm lifting in the direction opposite to that of gravity, the assistance torque must be applied in the direction in which the upper arm is raised. Therefore, the target orientation was limited to the component on the transverse plane. To define the arm orientation in 2-D and minimize the influence of human soft tissues, a flexible square marker cluster was attached on the shoulder instead of using discrete markers [6]. The motion capture data, i.e., the extracted human body data and target trajectories and orientation, were used to determine the mathematical design constraints and scoring standards for optimization.

The optimization results were verified by manufacturing skeletal mock-ups with different joint mechanisms. The physical interaction at the exoskeleton cuff was measured using a six-axis force/torque (F/T) sensor to validate the misalignment reduction of the optimized configuration. Consequently, this study proposes the design method of a human–machine friendly mechanism for industrial shoulder exoskeleton and the validation method of the optimization framework.

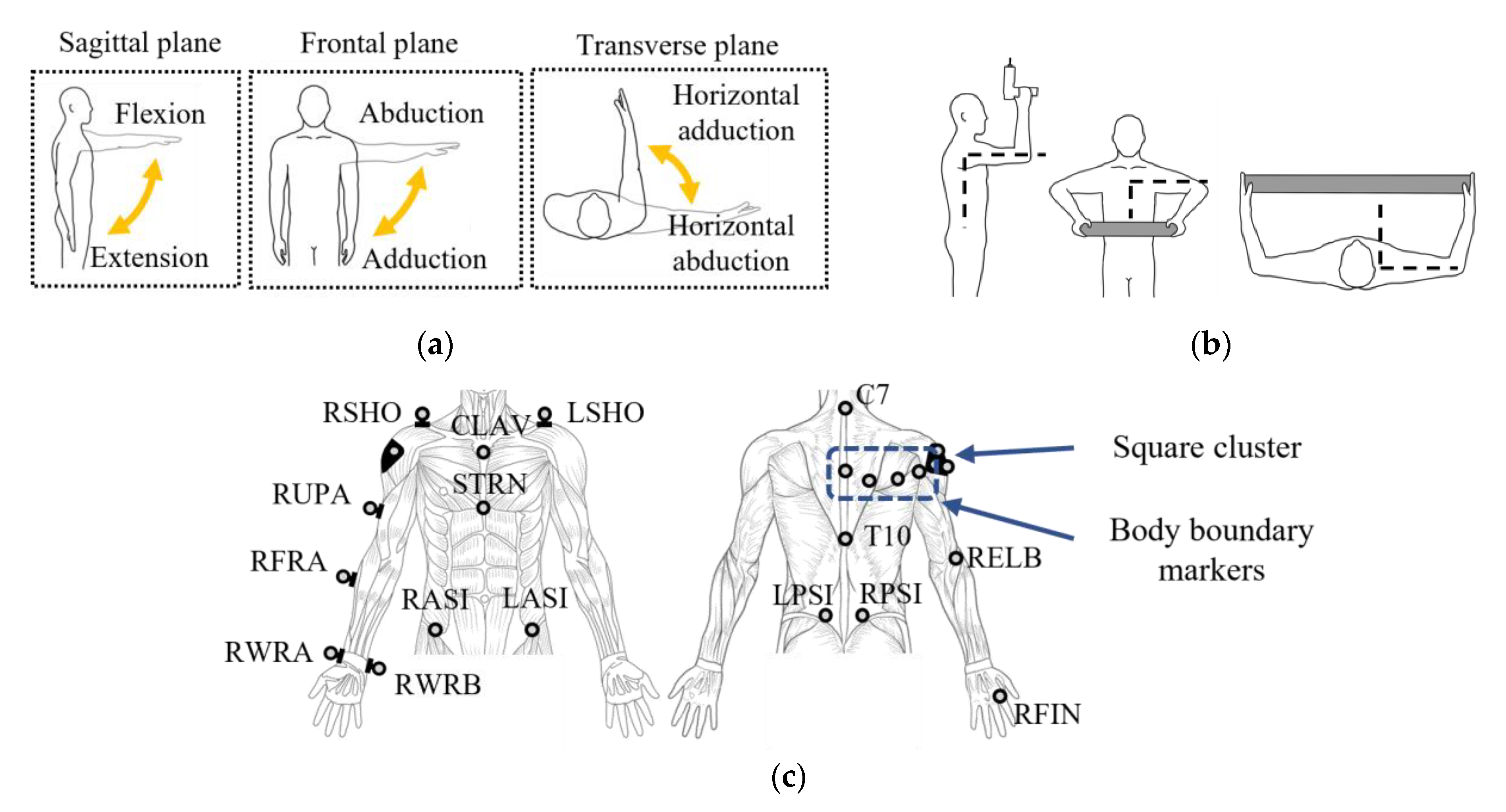
2. Motion Capture to Extract the Target Exoskeleton Trajectory and Orientation

2.1. Experimental Setup

To design compact joint mechanisms for exoskeletons that reduce misalignment and eliminate interference with the movement of the wearers, human motion data were acquired using motion capture technologies. Using eight cameras (VICON, two Vantage 5, and six T-Series) were used to capture motion data from three basic 1-DOF movements of the shoulder during flexion/extension in the sagittal plane, abduction/adduction in the frontal plane, and horizontal abduction/adduction in the transverse plane (Figure 1a). A healthy participant (height and weight of 1.75 m and 75 kg, respectively) with the average Korean body size according to SIZEKOREA (1.74 $\pm$ 0.056 m, and 74.2 $\pm$ 10.9 kg) performed motions in the range of 0° to 90° at a constant speed using a metronome. This range was selected considering the range of motions (ROM) of the upper arms in general work-related motions such as drilling and box lifting (Figure 1b). Each motion was performed for 10 cycles. The data for the first five cycles were not used in the optimization analysis as they corresponded to the participant adapting to the metronome speed.

As shown in Figure 1c, the markers were attached to the upper body of the participant according to the plug-in gait marker set. The operating range of the joint configuration to be optimized lay under the shoulder of the user. Consequently, the mechanism did not generate interference with the user’s head, and the motion of the head was not captured. More details regarding the type of joint configuration are presented in Section 3. Markers were attached to the right arm, and the motions of both arms were assumed to be symmetrical. Four additional markers and a square marker cluster were attached to the right part of the back of the thorax and lateral side of the right shoulder, respectively. These four additional markers formed 2-D boundary lines of the thorax in the transverse plane and thus indicated the interferences of the joint configuration with the wearer. Additionally, a marker was placed at the medial point of the back as the origin for extracting the trajectories of the markers. A square marker cluster made of a flexible material was attached at the target location on the skin. The cluster position and orientation were used to calculate the target position and orientation of the gravity compensation module (GCM), which is the core element of the target exoskeleton that generates an assistance torque based on the elastic restoring force according to the shaft rotation [24].

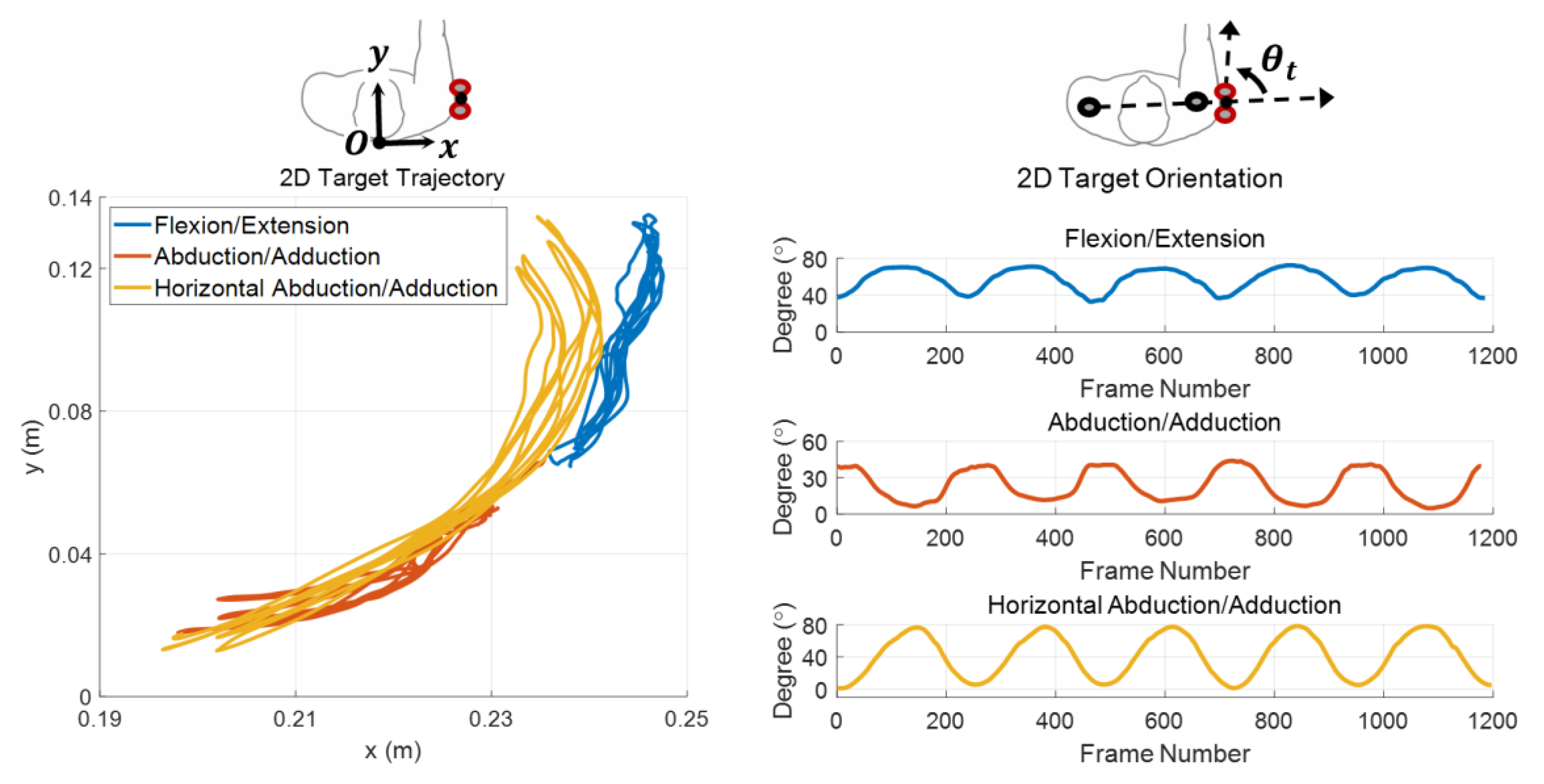
2.2. Required Trajectory and Orientation Information of the Exoskeleton in 2-D

The GCM interacts with the wearer’s arm through a rigid link and cuff. Therefore, to reduce the misalignment and interaction forces at the cuff and transmit the exact assistance forces to the upper arm, the GCM must be appropriately located and aligned. The target trajectory and orientation that the exoskeletal joint mechanism must follow were defined as the appropriate location and orientation of the GCM. In particular, the target trajectory and orientation of the GCM were limited to 2-D components in the transverse plane for minimizing the bulkiness and complexity of the configuration.

To ensure that the exoskeleton was compact, we attempted to reduce only the misalignment due to horizontal arm movements. In general, elevation and depression movements of the shoulder joint caused by the scapulohumeral rhythm are expected to lead to misalignment of the shoulder exoskeletons [8,21]. To compensate for this misalignment, a design that facilitates the elevation and depression movements of the joint mechanism of the exoskeleton depending on the arm elevation angle must be used. The exoskeletons proposed in [12,20] adopt a flexible beam mechanism located above the shoulder with bulky and heavy pulley-driven systems, respectively. These additional mechanisms for tracking the elevation movements of the shoulder are not conducive for realizing an under-shoulder joint mechanism that is compact. Therefore, as mentioned previously, the objective of this study was to reduce only horizontal misalignment, and the target trajectory was limited to 2-D components, i.e., the x and y coordinates in the transverse plane.

Furthermore, the target orientation was limited to a transverse plane component considering the characteristics of industrial shoulder exoskeletons, in which the shaft of the GCM was used as a revolute joint to enable arm elevation and depression movement and generate assistance torque in the upper arm. Because the exoskeleton was aimed at generating assistance torque in the direction in which the arm is raised, the shaft of the GCM was required to be parallel to the transverse plane. If the orientation of the GCM has other three-dimensional components, the assistance forces applied in the undesired direction will not counter gravity and tend to disrupt the wearer’s motions. Consequently, the target data, i.e., the x and y coordinates of the trajectory and orientation in the transverse plane, were extracted using the cluster.

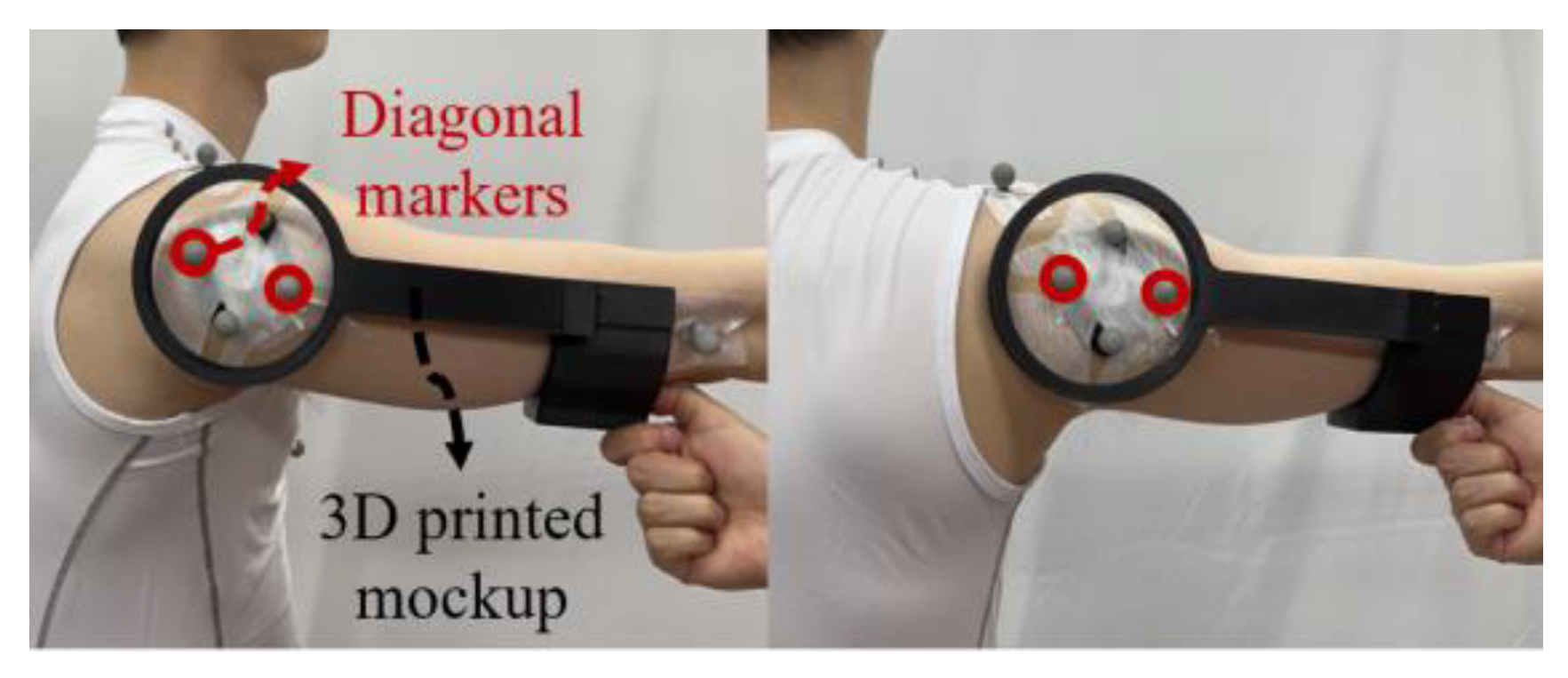
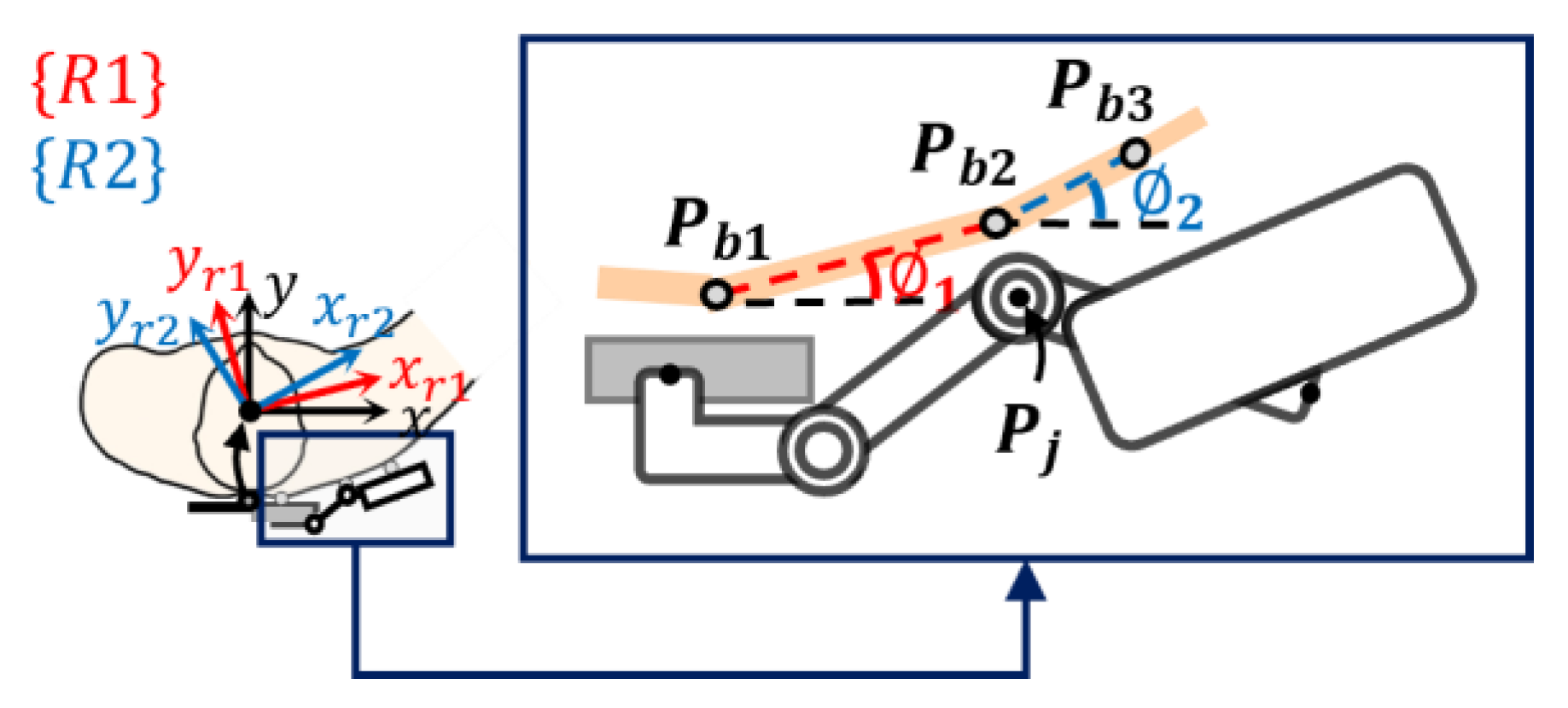
2.3. Acquisition of the Target Trajectory and Orientation Using a Cluster

In general, no theoretical reference is available for the attachment of discrete markers to determine the target position and orientation for the GCM. In this study, to define the target trajectory and orientation in 2-D and reduce the influence of human soft tissues, a flexible square marker cluster and a 3D printed mock-up were used [6]. As shown in Figure 2, a square cluster was attached to the lateral skin of the right shoulder using a 3D printed mock-up that mimicked the GCM and arm link. Specifically, two markers on the diagonal of a square cluster were aligned parallel to the upper arm when the shoulder elevation angle was approximately 90°.

The cluster was used to obtain a unique orientation. Figure 3 schematically illustrates the target orientation (${\theta }_t$) when the upper arm angles are 0° and 90° during each motion, respectively. ${\theta }_t$, which is the angle between two vectors ($\overrightarrow{v_{sj}}$ and $\overrightarrow{v_c}$) including two shoulder joint center points and two projected markers points of the square cluster located diagonally, can be expressed as

$${\theta }_t={\cos }^{-1}(\frac{\overrightarrow{v_{sj}}·\overrightarrow{v_c}}{\left|\overrightarrow{v_{sj}}\right|·\left|\overrightarrow{v_c}\right|})$$

(1)

To analyze the captured motion data of the participant, a body model was developed using Visual 3D (2020, C-Motion, Inc., Germantown, MD, USA). The data of all the attached markers and generated data of the human internal joint were processed using a low-pass filter with a cut-off frequency of 6 Hz. The target data were subsequently transformed into a local coordinate system of the thorax and extracted. In particular, because the passive shoulder exoskeleton was fixed on the thorax, the coordinate system of the exoskeleton could be intuitively described based on the thorax. Therefore, to use the motion data acquired on the global coordinate from the motion capture system, the data were transformed to the local coordinates of the thorax. Figure 4 shows the extracted target trajectory and orientation during the last five cycles of each motion. The origin of the trajectory plot was the position of the marker attached at the medial point of the back.

3. Kinematic Optimization of 3-DOF Joint Configuration

Based on the human motion data and target data, the joint configuration was optimized to eliminate the conditions in which exoskeleton use must be avoided. A 3-DOF prismatic–revolute–revolute (PRR) joint type was selected for optimization to achieve a low weight and compact industrial shoulder exoskeleton. In general, to track all target components in 2-D space, at least 3-DOF joints must be used. A larger number of passive joints means higher weight and dynamics of the joint configuration, which are not conducive for achieving the objectives of a light and compact design. Additionally, compared with the other 3-DOF joint combinations, the 3-DOF PRR joint type has been noted to be effective for realizing misalignment compensation and compact design [25]. Therefore, the optimization objective was a 3-DOF PRR configuration in which a prismatic joint was stably placed on the back plate of the exoskeleton, and two revolute joints were connected sequentially.

3.1. Kinematic Model and Design Variables

Figure 5 shows the kinematic model of the optimization and five design variables of the joint configuration. The human body model was built using the marker data extracted as described in Section 2. The design variables were the vertical offset from the surface of the back plate ($l$), lengths of three bar links ($L_1$, $L_2$, $L_3$), and bonding angle between the joint mechanism and GCM ($\alpha$). Additionally, the model involved the kinematic parameters ($d$, ${\theta }_1$, ${\theta }_2$) of each joint and diameter and thickness of the GCM. The GCM was cylindrical with a diameter of 120 mm and thickness of 45 mm [24]. The optimization objective was to determine the position of the two revolute joints and bonding angle of the GCM for which the target data in the cluster could be best tracked without any interferences, and the protrusion of the joint configuration was minimized.

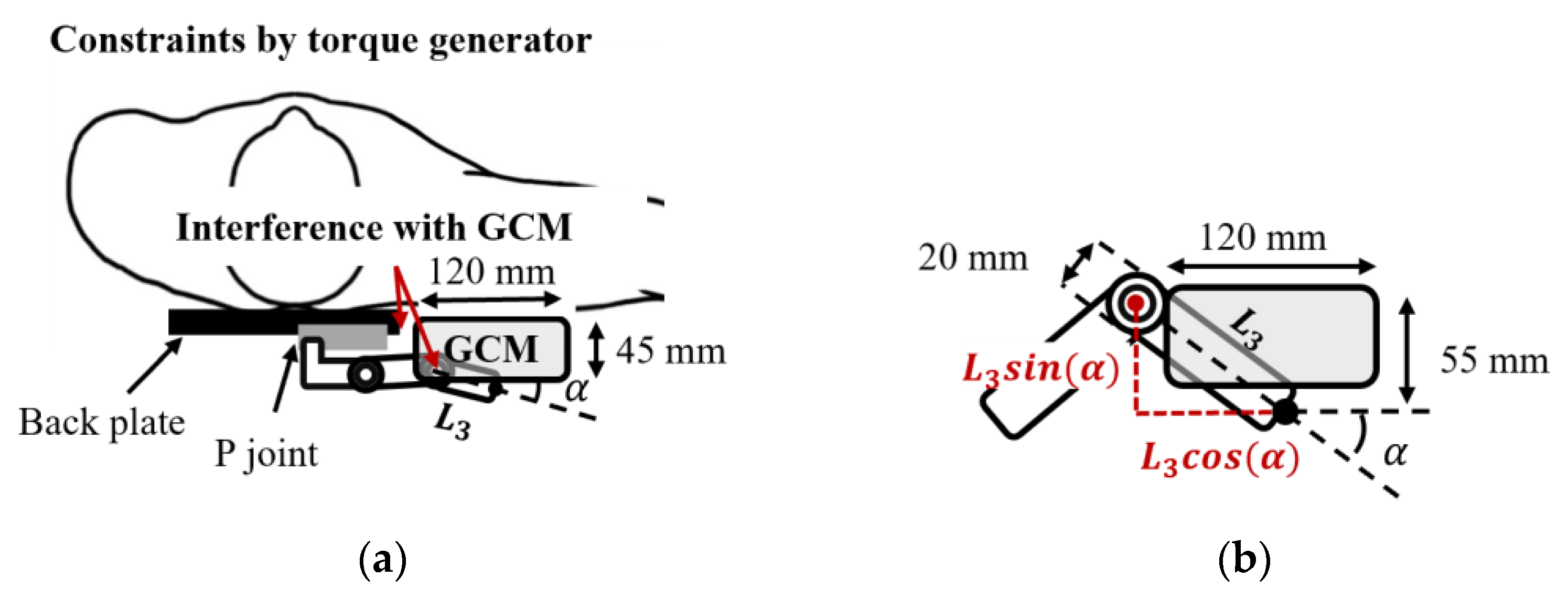
3.2. Design Constraints

3.2.1. Interference with Human Body

The constraints of 3-DOF PRR joint configurations can be defined in terms of the interference with the human body and GCM. The interference between the wearer and the exoskeleton is limited during the optimization process. The presence of this interference can be formulated using the 2-D boundary lines of the thorax, as shown in Figure 5. The occurrence of any interference between the joint configuration and wearer signifies that the second revolute joint crosses the boundary lines of the thorax. This interference can be formulated using the parameters represented in Figure 6.

The angle of each boundary line can be derived using the coordinate data of the body boundary markers extracted as described in Section 2:

$${\varnothing }_1={\tan }^{-1}(\frac{y_{b2}-y_{b1}}{y_{b2}-y_{b1}})$$

(2)

$${\varnothing }_2={\tan }^{-1}(\frac{y_{b3}-y_{b2}}{y_{b3}-y_{b2}})$$

(3)

From the frame rotation matrices, expressed as in Equations (4) and (5), the coordinates of each boundary marker for frames {$R1$} and {$R2$} can be transformed as indicated in Equations (6) and (7), respectively.

$$R_{\left\{R1\right\}}=\left[\begin{array}{cc}\cos \left({\varnothing }_1\right)& \sin \left({\varnothing }_1\right)\\ -\sin \left({\varnothing }_1\right)& \cos \left({\varnothing }_1\right)\end{array}\right]$$

(4)

$$R_{\left\{R2\right\}}=\left[\begin{array}{cc}\cos \left({\varnothing }_2\right)& \sin \left({\varnothing }_2\right)\\ -\sin \left({\varnothing }_2\right)& \cos \left({\varnothing }_2\right)\end{array}\right]$$

(5)

$$P_{b1·r1}=R_{\left\{R1\right\}}·P_{b1}$$

(6)

$$P_{b2·r2}=R_{\left\{R2\right\}}·P_{b2}$$

(7)

Similarly, the coordinates of the second joint position can be transformed for frames {$R1$} and {$R2$} can be transformed as indicated in Equations (8) and (9), respectively.

$$P_{j·r1}=R_{\left\{R1\right\}}·P_j$$

(8)

$$P_{j·r2}=R_{\left\{R1\right\}}·P_j$$

(9)

If the y coordinate of the framework in Equation (8) exceeds that in Equation (6), and simultaneously, the y coordinate of the framework in Equation (9) exceeds that in Equation (7), the second revolute joint can be considered to cross the body boundary line. Therefore, the occurrence of interference between the wearer and joint configuration can be formulated as in Equation (10)

$$g=\left(y_{j·r1}+\xi \ge y_{b1·r1}\right)\cap \left(y_{j·r2}+\xi \ge y_{b2·r2}\right),$$

(10)

where a$\cap$b is 1 if both a and b are true, and 0 otherwise. $\xi$ denotes the offset based on the link thickness and workwear volume ($\xi$ = 20 mm in this study). If $g$ is 1 at least once while tracking the target trajectory, the optimization algorithm concludes that the given joint configuration interferes with the wearer.

3.2.2. Interference with GCM

The interferences caused by the GCM incorporated at the end of the joint configuration limit the width of the exoskeleton base back plate. If the width of the back plate exceeds a certain value, interference occurs between the GCM and plate when the joint configuration traces the medial trajectories during horizontal abduction, as shown in Figure 7a. Consequently, the length of the P joint attached to the back plate is limited, which influences the kinematics of the joint configuration. In this study, a 110-mm-long LM guide (SSEBL-MX13-110, MISUMI Group Inc., Tokyo, Japan) was used as a P joint, and the maximum stroke was 77 mm, according to the width standard of the block.

Additionally, a rectangular space constraint exists in the transverse plane because of the GCM volume. Although the geometries of the bar links can be easily transformed (for example, to form a curved link) to avoid interference with GCM, the revolute joint of the exoskeleton must be located outside this area. The design variables $L_3$ and $\alpha$ determine the position of the second revolute joint, as shown in Figure 7b. Considering the width and thickness of the GCM, bar link, and revolute joint, the position constraint of the second revolute joint can be expressed as

$$h=(\alpha >0)\cap (L_3·\cos \left(\alpha \right)<65\mathrm{mm})\cap (L_3·\cos \left(\alpha \right)<65\mathrm{mm}),$$

(11)

where a$\cap$b$\cap$c is 1 if all a, b, and c are true, and 0 otherwise. If $h$ is 1, the optimization algorithm concludes that the given joint configuration generates interference with the GCM.

3.3. Objective Functions

3.3.1. Reducing Misalignment by Tracking Target Data

To satisfy the multiple objectives of shoulder exoskeletons, the optimization objective involved two parts: reducing misalignment by tracking the appropriate trajectory and orientation of the GCM, and minimizing the frame protrusion of exoskeletons.

To minimize the misalignment of exoskeletons, the joint mechanism must track each target datum, including the appropriate location and orientation of the GCM. As shown in Figure 8a, the instantaneous target coordinate of the cluster obtained by motion capture was translated to $P_{offset}$, which is the actual point that the end of the joint configuration must track considering the offset $\xi$ and thickness values of the GCM and link. The translation matrix and translated coordinate $P_{offset}$ were defined as in Equations (12) and (13), respectively

$$T=\left[\begin{array}{ccc}1& 0& \left(\xi +55\right)·\sin \left({\theta }_t\right)\\ 0& 1& -\left(\xi +55\right)·\cos \left({\theta }_t\right)\\ 0& 0& 1\end{array}\right]$$

(12)

$$P_{offset}=T·P_c$$

(13)

where ${\theta }_t$ is the target orientation using the cluster extracted as described in Section 2. $P_c$ is the instantaneous coordinate of the cluster represented in Figure 8a.

In the optimized state, the end of the joint configuration could track $P_{offset}$ and ${\theta }_t$ of the entire motion to reduce the misalignment. However, accurately tracking all three components of the target data was challenging given the constraints of interferences with the wearer’s body and the objective of realizing a compact 3-DOF design. Therefore, it was necessary to obtain a configuration that best tracked the three components of target data in the entire motion. Among the three components, we prioritized the tracking performance of the target orientation. Because of the characteristics of the exoskeletal rigid frame that interacts with the upper arm, when the orientations of the upper arm and exoskeletal frame are misaligned, the wearer experiences the largest amount of undesirable interaction forces. Therefore, the optimization objective was designed to ensure that the joint configuration preferentially tracked the target orientation ${\theta }_t$ to minimize the error between the trajectory of $P_{offset}$ and that of the end point of the joint configuration ($P_{end}$). In other words, the objective function of reducing misalignment was defined as in Equation (14), in terms of the root mean square error (RMSE) of $P_{offset}$ and $P_{end}$, with the orientation of the joint configuration being identical to the target orientation in the ideal state:

$$f_1=\sqrt{\frac{1}{n}{{\displaystyle \sum }}_{i=1}^n{\left(P_{offset}\left(i\right)-P_{end}\left(i\right)\right)}^2},$$

(14)

where $n$ is the number of points in the target trajectory.

3.3.2. Minimizing Frame Protrusion

In the considered 3-DOF PRR joint configuration, the joint kinematics can be defined in two cases depending on the joint protrusion, as shown in Figure 8b. For each case, a different value of $\gamma$, which represents the maximal distance from the surface of the back plate to the protruded frame, is defined. If no frame protrusion exists, $\gamma$ is defined as $l$, which is a design variable and indicates the vertical distance of the joint configuration from the surface of the back plate. Because the minimum value of $l$ is 0.04, the minimum value of $\gamma$ is also 0.04. In contrast, when the frame protrudes, $\gamma$ is defined as the vertical distance of the protruding joint from the surface of the back plate obtained by adding the maximum protruding distance ($u_{max}$) to $l$. The objective function $f_2$ is defined as the product of $\gamma$ and a base gain value:

$$f_2=25·\gamma$$

(15)

This gain value of 25 was chosen based on the minimum value of $l$ so that the minimum value of $f_2$ becomes 1. This was to ensure that $f_2$ is normalized to the same scale as $f_1$. Because each objective function has a different magnitude and extent of changes, this calibration can help set the weights to adjust the relative importance of each objective function.

Consequently, the complete objective function of the optimization is formulated as in Equation (16). $w_1$ and $w_2$ are the weights for adjusting the effect of each function arbitrarily. In this study, the value of $w_2$/$w_1$ was set as 2.67 based on the preference for each objective function, which was quantified based on the feedback from the workers on construction sites. The optimization was performed and tested several times by changing the weight. The tested weight sets corresponded to notable changes in each objective function. The weight set that helped achieve high performances for both objective functions was selected.

$$\phi =w_1·f_1+w_2·f_2$$

(16)

3.4. Optimization Process

In the optimization process, each design variable exhibited a wide range, and various geometries were generated. Because the configuration featured multiple local optima, a genetic algorithm incorporated in MATLAB (R2021a, MathWorks, Natick, MA, USA) was used to determine the global optimal design variables. Figure 9 illustrates the process flow of calculating an objective function.

First, five design variables are updated through the optimization algorithm. As shown in Figure 5, the updated variables determine the geometry of the 3-DOF PRR configuration. Next, the occurrence of interferences between the GCM and determined geometry is verified using Equation (11). If there is no interference with the GCM, the human body and target data acquired as described Section 2.3 are updated, and the kinematics of the joint configuration are calculated. In the movable range of the P joint stroke ($d$) and two R joints (${\theta }_1$, ${\theta }_2$), the coordinate of the end point of the 3-DOF PRR configuration ($P_{end}$) can be calculated through the forward kinematics.

The x and y coordinates of $P_{end}$, $P_{end.x}$ and $P_{end.y}$ can be expressed as in Equations (17) and (18), respectively

$$P_{end.x}=d+L_1+L_2·\cos \left({\theta }_1\right)+L_3·\cos \left({\theta }_1+{\theta }_2\right)$$

(17)

$$P_{end.y}=-l+L_2·\sin \left({\theta }_1\right)+L_3·\sin \left({\theta }_1+{\theta }_2\right)$$

(18)

where $L_1$, $L_2$, and $L_3$ are the lengths of the bar links that are design variables, as shown in Figure 5. $d$, ${\theta }_1$, and ${\theta }_2$ are the kinematic parameters of each joint.

Subsequently, the values of $d$, ${\theta }_1$, and ${\theta }_2$ that minimize the error between $P_{offset}$ and $P_{end}$ are calculated over the entire motion. The error can be determined using Equation (19), which is formulated using Equations (13), (17) and (18)

$$\epsilon \left(i\right)=\sqrt{{\left(P_{offset.x}\left(i\right)-P_{end.x}\left(d\left(i\right),{\theta }_1\left(i\right),{\theta }_2\left(i\right)\right)\right)}^2+{\left(P_{offset.y}\left(i\right)-P_{end.y}\left(d\left(i\right),{\theta }_1\left(i\right),{\theta }_2\left(i\right)\right)\right)}^2}, (i=1,2,\cdots ,n)$$

(19)

where $n$ is the number of points in the target trajectory.

Additionally, as mentioned, the target orientation ${\theta }_t$ and orientation of the GCM are prioritized to be identical in the trajectories. Therefore, the relation between ${\theta }_1$ and ${\theta }_2$ can be expressed as in Equation (20)

$${\theta }_1+{\theta }_2+\alpha ={\theta }_t,$$

(20)

where $\alpha$ (a design variable) is the bonding angle between the joint mechanism and GCM.

Equation (19) can be simplified as Equation (21) using Equation (20), and the values of $d$, ${\theta }_1$, and ${\theta }_2$ that minimize Equation (21) can be derived by the forward kinematics of the mathematical model expressed in Equation (22). The upper and lower limits of d can be determined by the standard of the LM guide mentioned in Section 3.2.2 and those of ${\theta }_1$ are determined based on our experience to avoid the occurrence of any singularity when tracking the target data.

$$\epsilon \left(i\right)=\sqrt{{\left(P_{offset.x}\left(i\right)-P_{end.x}\left(d\left(i\right),{\theta }_1\left(i\right)\right)\right)}^2+{\left(P_{offset.y}\left(i\right)-P_{end.y}\left(d\left(i\right),{\theta }_1\left(i\right)\right)\right)}^2}, (i=1,2,\cdots ,n)$$

(21)

$$\mathrm{Minimize} \epsilon \left(i\right)=\left\{d\left(i\right),{\theta }_1\left(i\right)\right\}, \mathrm{s}.\mathrm{t}:\left\{\begin{array}{c}0\le d\left(i\right)\le 77 \mathrm{mm}\\ {\theta }_t-\alpha -170°\le {\theta }_1\left(i\right)\le 100°\end{array}\right.$$

(22)

During the computation of Equation (22) in the complete trajectories, Equation (10) and $u\left(i\right)$ are calculated at each point of the trajectory to verify the occurrence of interference with the wearer and protrusion of frame. In the event of no interference with the wearer in the complete trajectories, the objective function presented in Equation (16) is defined as the score for a given PRR joint configuration. Subsequently, the design variables are updated, and the processes are repeated until the parameters are optimized using the genetic algorithm. The complete optimization problem can be described as in Equation (23)

$$\phi \left(r\right)=\left\{f_1\left(r\right),f_2\left(r\right)\right\}, \mathrm{s}.\mathrm{t}:\left\{\begin{array}{c}{\displaystyle \sum }_{i=1}^{n}g\left(i\right)=0\\ h=0\\ r^L<r<r^U\end{array}\right.$$

(23)

where $\phi$ is defined as in Equation (16). $g$ and $h$ are the constraint functions of interferences with the wearer and GCM, expressed as in Equations (10) and (11), respectively. $r$ is the vector of the design variables, $r^L$ and $r^U$ are the lower and upper limits of the parameters, respectively.

3.5. Optimization Result

The population size of the genetic algorithm was set as 500, and optimization was performed with parallel computation using 18 cores of an Intel^® Core™ i9-10980XE (Intel Corporation, Santa Clara, CA, USA). The total number of iterations was 123, and the total iteration time was approximately 36 h. The optimal design variables are presented in

Table 1. Optimized design variables.

Optimized Variables
$l$(m)	0.040
$L_1$(m)	0.080
$L_2$ (m)	0.0679
$L_3$ (m)	0.1678
$\alpha (°)$	5

. The RMSE of the optimized configuration ($f_1$) was 3.1584 mm, and the protruding ratio ($f_2$) was 2.6718. The final value of the objective function ($\phi$) was 10.2972, which was 47% lower than that of the first generation.

To evaluate the reductions in both the misalignment and interaction forces of the optimized configuration, we conducted an experiment with worn skeletal mock-ups based on the optimized PRR joint configuration and one revolute joint configuration, as described in Section 4.

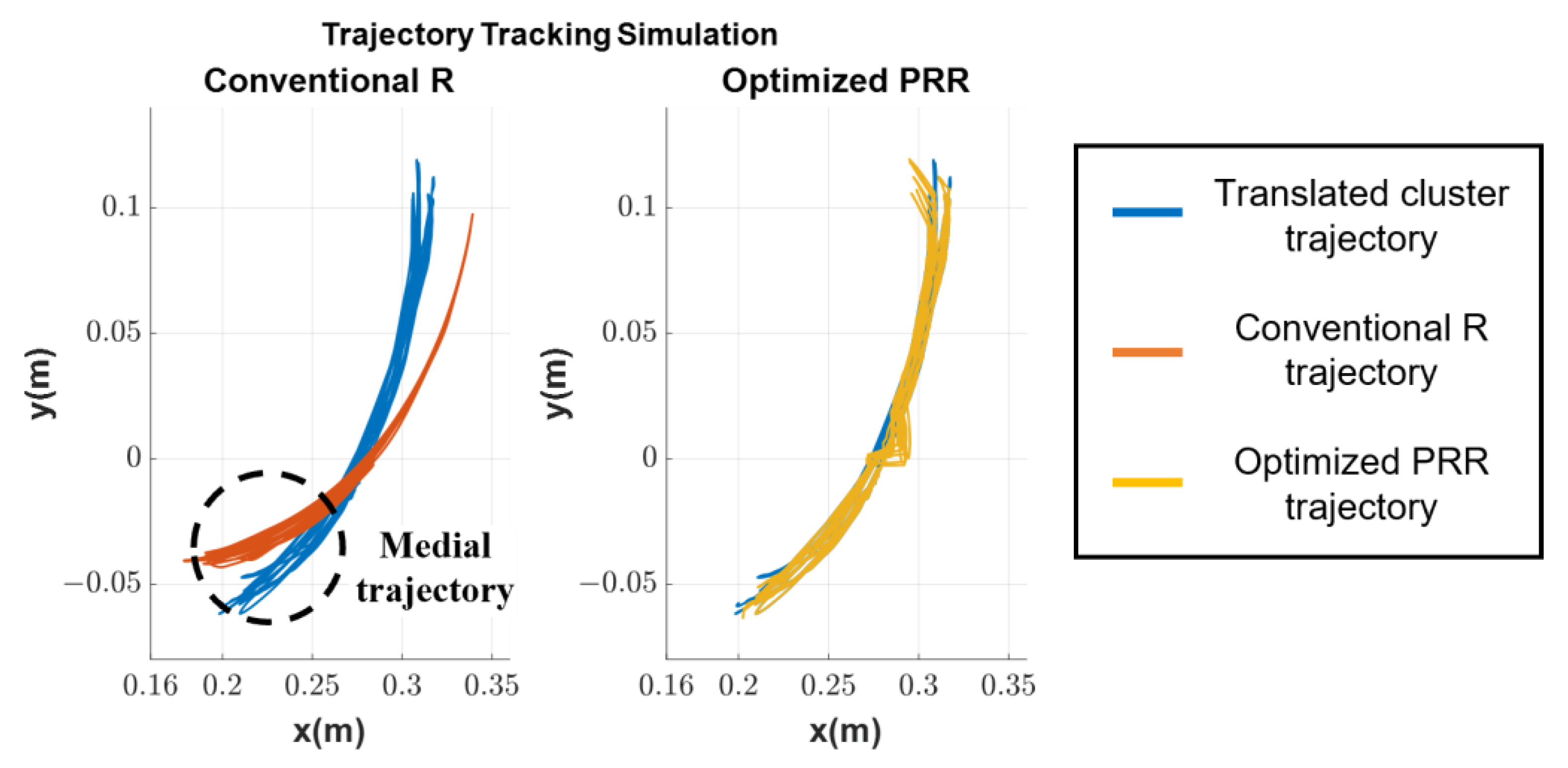
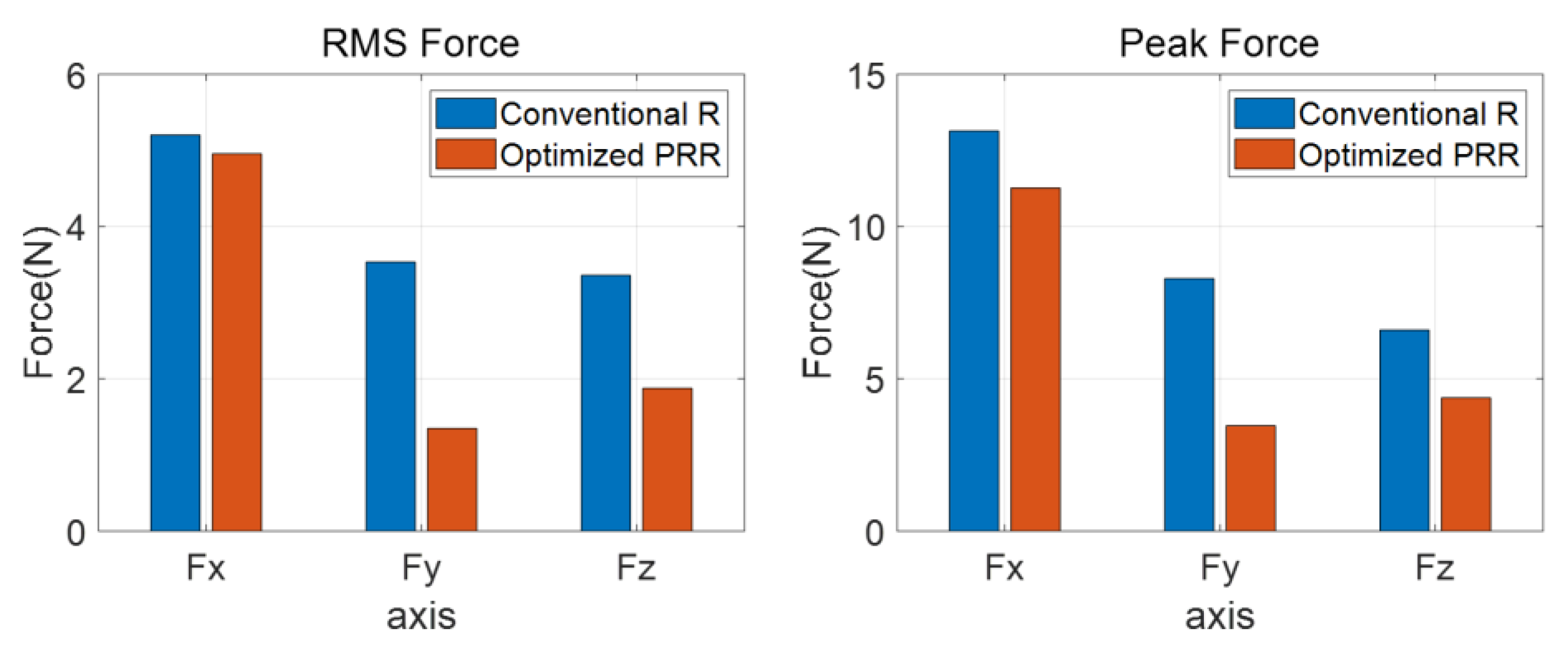
4. Simulation and Experiment Based Verification

An experiment was conducted to verify the effectiveness of the optimized PRR joint configuration in an actual environment, and the results were compared with those of a simulation. The performance of the proposed configuration was validated in comparison with that of the conventional R joint configuration with one revolute joint above the shoulder, which has been adopted in many previous studies [10,11,13]. Notably, the conventional R configuration is a simple and light mechanism that is employed in several commercialized shoulder exoskeletons that do not have any mechanisms for misalignment compensation. This configuration was selected because of its ease of design without knowing the exact dimensions of the exoskeletal frame. The simulation results for the two different joint configurations are presented in Section 4.1.

4.1. Simulation Result

The simulation results for the joint configuration are summarized in

Table 2. Optimal objective function values.

	Conventional R	Optimized PRR
Mechanism	Over shoulder	Under shoulder
$f_1$ (mm)	21.9039	3.1584
$f_2$	1	2.6718

and Figure 10. As mentioned, $f_1$ is the RMSE of the translated target trajectory and the trajectory of the mechanism when each orientation is identical, and $f_2$ is the protrusion rate for the most compact design. The conventional R joint configuration is composed of only one revolute joint that does not result in frame protrusion. Therefore, $f_2$ is 1 for the most compact design. However, the RMSE is considerably higher than that of the PRR joint configuration because misalignment frequently occurs. In contrast, the RMSE of the optimized PRR joint configuration is 85.6% lower than that of the conventional R configuration. However, to compensate for the misalignment, $f_2$ increases to 2.6718. Although $f_2$ of the optimized PRR joint configuration is higher than that for the most compact design, this increase can be compensated via the positive effect of minimizing $f_1$. In other words, the tracking performance can be enhanced while eliminating interferences and maintaining a relatively compact design.

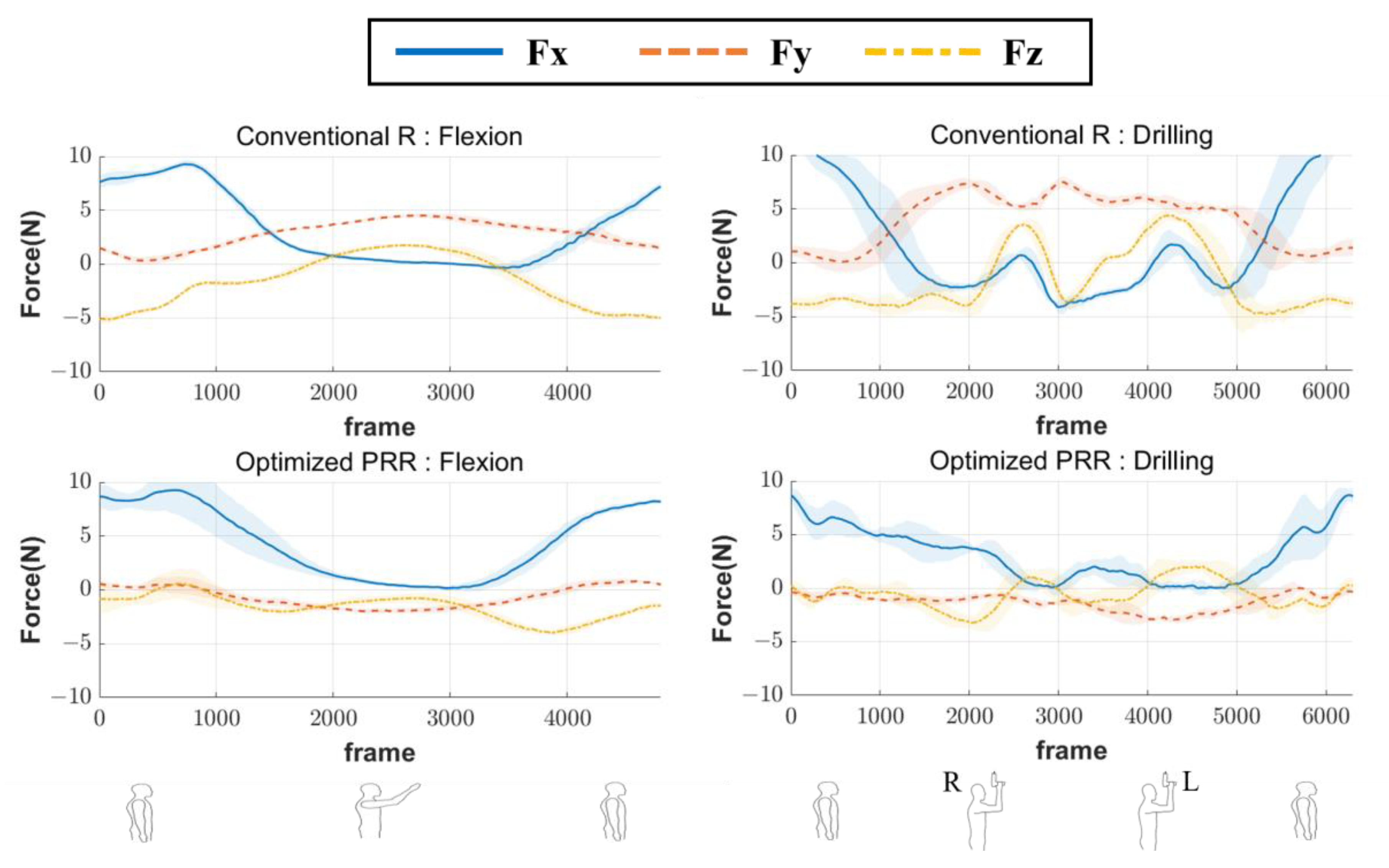
4.2. Experiment Setup and Protocol

Each skeletal mock-up was developed in the form of a vest for the experiment. To minimize any differences between each mock-up, both vests were fabricated with the same materials and patterns by the same designer. The link length of the conventional R joint configuration; that is, the radius of the trajectory, was determined by referring to the exoskeleton in [10] to track the entire trajectory appropriately without any significant interference with the human body at the medial trajectory, as shown in Figure 10. The optimized configuration was designed using the optimal variables listed in Table 1. Figure 11a shows the worn skeletal mock-ups with different configurations.

The motion capture experiment was repeated under the conditions of not wearing the skeletal mock-ups and wearing the skeletal mock-ups with different configurations. In this experiment, the body boundary and additional markers covered by the harness were removed. In addition, several simple motions mimicking industrial tasks were incorporated in addition to the three ROM motions used in the optimization to verify the versatility of each configuration. The motions selected were box lifting from the waist level to the head level and overhead drilling. These motions were selected with reference to the existing research on exoskeletons because they corresponded to the general motions that typically lead to shoulder muscle injuries in the industrial field [4,11,13,19,26]. Each motion was maintained for 3 s at the height of the head and then returned to the original position. Additionally, because the industrial boxes have various sizes, and the wearer’s arm posture and kinematics of the joint configuration change with these sizes, the lifting task involved two tasks with different box sizes. Consequently, each joint configuration was evaluated for six motions. Each motion was performed for 10 cycles at a constant speed using a metronome, and only the last five cycles were used in the analysis, as described in Section 2.

The GCM, box and shelf used in the experiment were arranged in the form of skeletal mock-ups to prevent marker masking. Figure 11b shows the skeletal mock-ups designed for the experiment and a representation of the motions of lifting a small box from the waist level to the head level. The actual tracking ability of the joint configuration was evaluated using the cluster and markers attached to the mock-up module. Additionally, the undesired forces generated by the misalignment of each joint configuration at the human–robot interaction point were measured using a F/T sensor inserted in the arm brace of the skeletal mock-up during the experiment. The validity of the optimized configuration was proven through the correlation between the measured tracking ability and interaction forces.

4.3. Experiment Result

The actual trajectories of each joint configuration, RMSE, and peak error (PE) of the trajectory and orientation are presented in Figure 12 and

Table 3. Actual trajectory and orientation error during optimized motions.

	Conventional R	Optimized PRR
RMSE of trajectory (mm)	42.9561	16.3124
PE of trajectory (mm)	76.2605	33.8092
$\mathrm{RMSE} \mathrm{of} \mathrm{orientation} (°)$	18.9	12.2
$\mathrm{PE} \mathrm{of} \mathrm{orientation} (°)$	50.0	25.7

. The origin of the plot is the position of the center of the thorax, created using Visual 3D. Because of friction, deflection of the skin and flexibility of harness, which could not be considered in the theoretical simulation, the actual results were slightly different than the simulation results. Nevertheless, the tracking performance of the optimized PRR joint configuration (for example, the RMSE of the trajectory) was significantly improved by up to 62% compared with that of the conventional R joint configuration, and the tendency of the actual trajectory of each configuration was the same as that of the simulation trajectory. In addition, the optimized PRR joint configuration was noted to be effective for work-related motions not considered in the optimization process, as shown in

Table 4. Actual trajectory and orientation error during additional work-related motions.

	Conventional R	Optimized PRR
RMSE of trajectory (mm)	60.8039	19.1988
PE of trajectory (mm)	82.5807	31.2178
$\mathrm{RMSE} \mathrm{of} \mathrm{orientation} (°)$	25.0	13.6
$\mathrm{PE} \mathrm{of} \mathrm{orientation} (°)$	35.9	28.2

. The RMSE of the trajectory was reduced by 68.4%.

The triaxial forces measured at the human–robot interaction point by the F/T sensor are shown in Figure 13 and Figure 14. Figure 13 shows the root mean square (RMS) value and peak magnitude of each axis force for six motions. Notably, the coordinate system of the F/T sensor was a moving system based on the wearer’s arm movement. The x- and y-axes (blue and green arrows represented in Figure 11a,d) were set to be parallel and vertical to the upper arm, respectively, and the z-axis (red circle in Figure 11a,d) was in the normal direction. All the measured triaxial forces of the optimized PRR joint configuration were lower than those of the conventional R joint configuration, owing to the improved tracking performance, as shown in Figure 12. Because the optimized configuration could track the appropriate trajectory and orientation of the GCM, which could not be realized by the conventional R configuration, the offset between the wearer and GCM was reduced, and the interaction forces also decreased.

Figure 14 shows the variation in the interaction force during the entire cycle of flexion/extension and drilling as a representative of the performed motions. The y- and z-axis forces of the optimized PRR configuration were negligible in the entire cycle of each motion. The corresponding forces for the conventional R configuration were higher when the joint configuration could not track the target data during the motions, as shown in Figure 12. The x-axis forces of both joint configurations were negligible during the motions. However, higher interaction forces were observed for both configurations when the participant was in natural standing posture. The variations in the triaxial interaction forces for other motions were measured and evaluated in a similar manner.

5. Discussion and Conclusions

This paper proposes a framework for kinematic optimization to facilitate a human–machine friendly design of an industrial shoulder exoskeleton. To address multiple limitations such as the misalignment, interaction force, interference with a human body, and protrusion of the exoskeletal frame without any additional mechanism, we designed a motion-data-based kinematic optimization framework and used it to establish an innovative harness architecture of the passive shoulder exoskeleton, in which the operation range of the mechanism is limited to under the user’s shoulders. To validate the optimization results, an experiment was performed with the designed skeletal mock-up worn. An F/T sensor was attached to the skeletal mock-up to measure the interaction force. The optimized PRR joint configuration could effectively reduce the misalignment and interaction forces. The reduction rates of the RMSE of trajectory and orientation for all experimented motions were approximately 67.1% and 43.1%, respectively, and those of the y- and z-axes force were approximately 61.8% and 44.1%, respectively. Notably, the results were affected by small differences in the weight, comfort, and other characteristics of the vests. However, these effects are expected to be insignificant because the vests are designed to be securely attached to the wearer’s body. Furthermore, although the human–machine interaction force and misalignment were strongly correlated, the correlation was not perfectly linear. This phenomenon occurred because other related factors must be considered. These factors must be identified and considered in further studies.

In the exoskeleton experiment, the misalignment caused in the medial region of the target trajectory led to the highest interaction forces and least user comfort, potentially because the medial region is related to the wearer’s natural motions, and misalignment during the natural motion of wearers may lead to wearer discomfort. Therefore, medial trajectory tracking must be prioritized when designing the shoulder exoskeleton with human motion data. In addition, the misalignment and protrusion of the frame exhibited an inverse relationship, at least in the 3 DOF PRR configuration. Therefore, to alleviate the two limitations, the weights must be appropriately selected based on the user’s preferences. In the optimization performed in this study, compactness was prioritized over misalignment reduction. Nevertheless, the y- and z-axis RMS forces generated in the optimized PRR configuration at the human–robot interaction point were low (approximately 1.35 N and 1.88 N, respectively). Considering the forces measured based on the mass corresponding to the mechanisms during dynamic motions, the measured interaction forces in the y- and z-axis directions can be considered negligible. According to the user’s preference, these forces may be further reduced. In contrast, the x-axis force exhibited a relatively large value for both joint mechanisms, which could be attributable to the design of the arm cuff mock-up used in the experiment. To follow arm movements suitably and transmit the interaction force to the sensor precisely, the cuff was designed to cover most of the upper arm. Owing to the wide contact area of the plastic arm cuff, friction was generated near the armpit in the participant’s natural standing posture, which resulted in interaction forces in the positive x direction of the F/T sensor. In our actual exoskeleton version that does not include a mock-up, the cuff is designed using flexible materials such as fabric and strap, and the width of the cuff is decreased. In future research based on this cuff design, the x-axis force is expected to be decreased.

Although the results of one participant may not be adequately representative, this research has a notable contribution in terms of a framework for kinematic optimization as a guiding study for the human–machine friendly design of an exoskeleton without any additional mechanisms. Even if the number of joints or type of exoskeleton are changed, the optimal configuration can be promptly obtained by extending the proposed optimization framework. Therefore, the proposed approach can be used in a facile manner to design exoskeletons for the waist and lower limbs as well as active configurations. In this study, we selected the optimization weights considering our preference of each objective function, i.e., by prioritizing compactness by minimizing frame protrusion based on the feedback from workers in construction sites. Because the optimization required considerable computational time (36 h), only four weight sets could be tested. However, the tested sets showed clear changes in each objective function, and the selected weight set yielded a satisfactory performance. In further research, we plan to reduce the optimization time by improving the algorithm structure and selecting a more suitable optimization methodology. In addition, setting appropriate saturation levels considering the fabrication errors can further reduce the computation time. After reducing the optimization time, the optimal weight set can be identified through additional experiments. Specifically, according to the user’s preference, the optimization weights can be modified, and the misalignment and interaction force could be further reduced. Future research can also be aimed at acquiring multiple motion data from various participants and grouping the motion data based on the participants’ body sizes (e.g., medium or large). These grouped data can be used to derive the representative frame structure according to body size. Furthermore, the improved exoskeleton must be validated under conditions that include the full range of motion in the shoulder. Specifically, after archiving the motions performed in various industries, an interaction force experiment and muscle activity experiment can be conducted to evaluate the performance of the proposed exoskeleton. The proposed human–machine friendly design framework of exoskeletons can promote the introduction of passive exoskeletons in various occupational fields and prevent worker injuries.