Hierarchical Reinforcement Learning for Multi-Objective Real-Time Flexible Scheduling in a Smart Shop Floor

Abstract

With the development of intelligent manufacturing, machine tools are considered the “mothership” of the equipment manufacturing industry, and the associated processing workshops are becoming more high-end, flexible, intelligent, and green. As the core of manufacturing management in a smart shop floor, research into the multi-objective dynamic flexible job shop scheduling problem (MODFJSP) focuses on optimizing scheduling decisions in real time according to changes in the production environment. In this paper, hierarchical reinforcement learning (HRL) is proposed to solve the MODFJSP considering random job arrival, with a focus on achieving the two practical goals of minimizing penalties for earliness and tardiness and reducing total machine load. A two-layer hierarchical architecture is proposed, namely the combination of a double deep $Q$-network (DDQN) and a dueling DDQN (DDDQN), and state features, actions, and external and internal rewards are designed. Meanwhile, a personal computer-based interaction feature is designed to integrate subjective decision information into the real-time optimization of HRL to obtain a satisfactory compromise. In addition, the proposed HRL framework is applied to multi-objective real-time flexible scheduling in a smart gear production workshop, and the experimental results show that the proposed HRL algorithm outperforms other reinforcement learning (RL) algorithms, metaheuristics, and heuristics in terms of solution quality and generalization and has the added benefit of real-time characteristics.

1. Introduction

Intelligent manufacturing is the core of the new scientific revolution, which is achieved through the use of information technology to achieve the rapid development of productivity and solve social problems such as energy consumption. The future outlook and direction in terms of the development of digitalized, networked, and intellectualized manufacturing is intelligent manufacturing, which is essentially the achievement of “smart workshops” that are based on cyber-physical production systems (CPPS) [1]. Machine tools [2] are the “mothership” of the equipment manufacturing industry, and it is impossible to achieve intelligent manufacturing without the intelligence of machine tools.

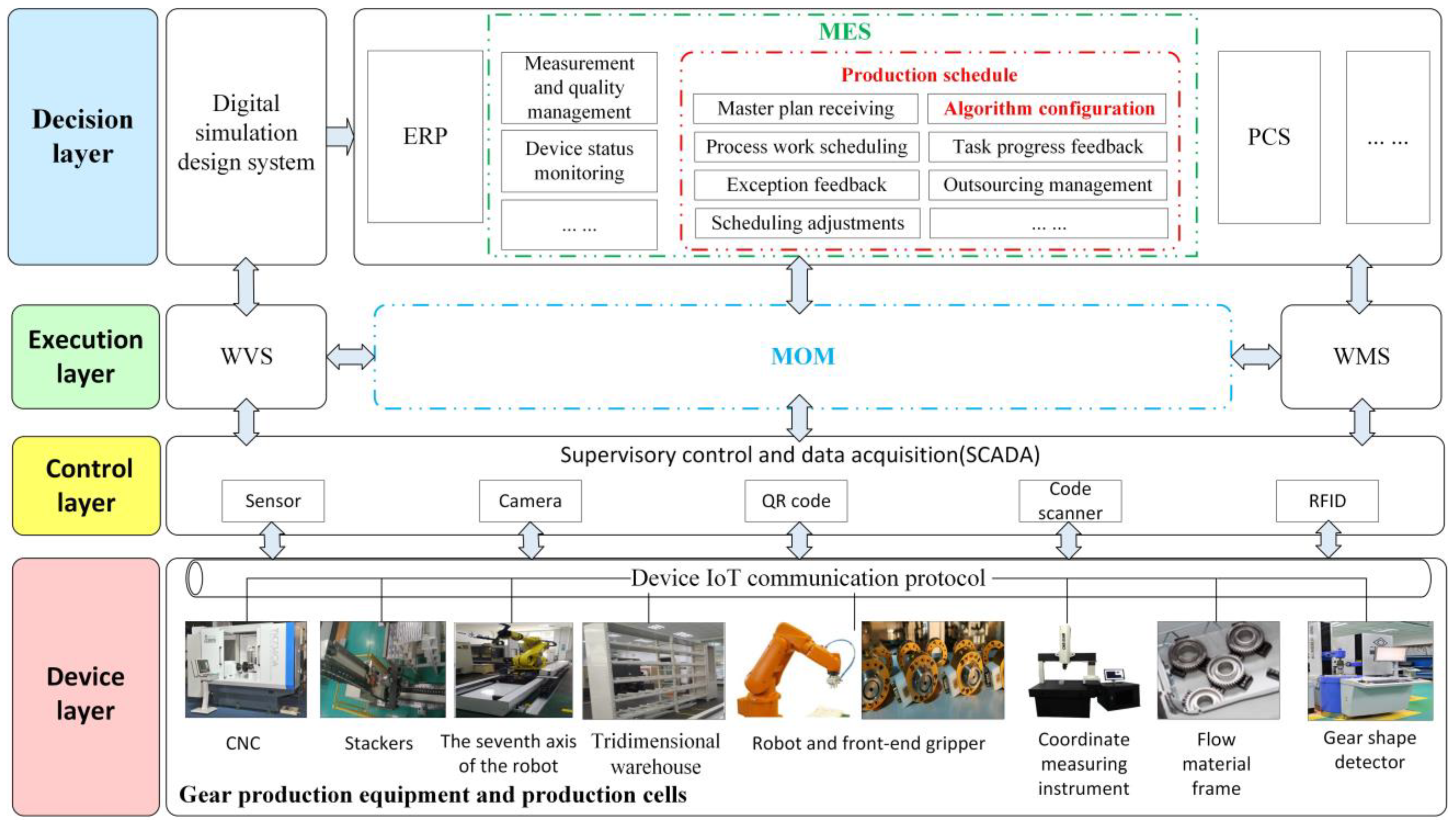
In line with the ANSI/ISA-95.00.02-2018 standard [3], modern factories have become closely integrated with actual workshop production scenarios based on the structure of enterprise resource planning (ERP), manufacturing execution systems (MESs), and process control systems (PCSs) as prototypes and manufacturing operations management (MOM) consisting of production, maintenance, quality, inventory, etc. Machine tool workshops are becoming more flexible and intelligent alongside the development of cloud computing, the Internet of Things [4], big data [5], machine learning, and other advanced technologies. Because of the wide combination and deep penetration of automation hardware, such as robots, CNC machine tools, stackers, and sensors with intelligent MOM, visualization system (WVS), and logistics management system (WMS) software, a manufacturing shop has the capabilities of autonomous perception, analysis, decision making, and processing. Referring to the GB/T 37393-2019 standard [6], which mentions the digital workshop system structure, an intelligent workshop system integrating the physical production–data acquisition–recipe control–execution flow has been built, such as in the example of a smart gear workshop structure in Figure 1 [7].

Due to the dynamic configuration of production methods required to achieve flexible production in the workshop, the core of intelligent manufacturing, MES, is the focal point of intellectualization transformation upon which other functional requirements can be extended. Based on the classic decision-making activity of the flexible job shop scheduling problem (FJSP) in MES, this paper analyzes the current challenges of scheduling algorithms (the key technology of intelligent manufacturing) and provides theoretical and practical solutions to intelligently match the dispersed resources (manpower, materials, processing equipment, etc.) of the workshop in real time to meet the needs of diversification, customization, and small-batch production.

Compared to the classical job shop scheduling problem (JSP) [8], the FJSP breaks through the uniqueness restriction of production resources and has been proven to be a strong NP-hard problem [9] whose real-time optimization improves production efficiency while reducing costs. From Figure 1, with real-time monitoring, data collection, machine tool machining, and the rapidly changing production state of the smart workshop, the FJSP presents the following characteristics. Firstly, production dynamics: various uncertain events occur, such as random job arrival, machine failures, and delivery date changes, all of which require rescheduling to adapt to dynamic changes in the production environment. Secondly, human–machine interaction constraints: when solving production scheduling, a decision maker has a preference for order arrangement and production targets. Without holographic modeling, the handling of unexpected events still requires the subjective opinion and judgment of decision makers.

At present, the traditional methods of solving the dynamic FJSP (DFJSP) are mainly heuristic and metaheuristic algorithms. Heuristic methods, such as first in first out (FIFO) and first in last out (FILO), etc., are simple and efficient, but they have poor universality and uneven solution quality due to different scheduling rules applicable to different types of scheduling problems and production objectives. Metaheuristic methods, such as the genetic algorithm (GA) [10] and particle swarm algorithm [11], improve solution quality through parallel searching and iterative searching, but their time complexity is poor and they do not have the required characteristic of real-time scheduling optimization in a smart workshop.

With the advance in artificial intelligence and machine learning, Zhang et al. [12] solved the JSP in 1995 using a temporal difference algorithm, which was the first time reinforcement learning (RL) was applied in the scheduling field. The core idea of using RL in solving the scheduling problem is to transform the dynamic scheduling process into a Markov decision process (MDP) [13]. When an operation is finished or random events occur, a scheduling rule is determined according to the production state. Because different production objectives correspond to different reward functions and scheduling rules, traditional RL cannot simultaneously optimize all objectives to solve the multi-objective DFJSP (MODFJSP) [14]. Hierarchical reinforcement learning (HRL) [15,16,17] has long held the promise of learning such complex tasks, in which a hierarchy of policies is trained to perform decision making and control at different levels of spatiotemporal abstraction. A scheduling agent is trained using the two-layer policy, in which a higher-level controller learns a goal policy over a longer time scale and a lower-level actuator applies atomic actions to the production environment to satisfy the temporary objective. Therefore, HRL maximizes external cumulative return in the long run while achieving a satisfactory compromise considering multiple production objectives.

In the actual production environment of machine tool processing, the swift completion of products results in higher inventory pressure, whereas delays in completing the job result in financial damage [18]. The total machine load not only affects financial costs but also involves energy saving and emission reduction. For the real-time optimization and decision-making of multi-objective flexible scheduling in a smart shop floor, an HRL method is proposed in this study to solve the MODFJSP considering random job arrival so as to minimize penalties for earliness and tardiness as well as total machine load. The four contributions of this research are as follows:

(1)

To the best of our knowledge, this is the first attempt to solve the MODFJSP with random job arrival and minimize the total penalties for earliness and tardiness, as well as total machine load, using HRL. The work can thus fill a research gap regarding solving the MODFJSP using HRL.

(2)

A key problem in multi-objective optimization is solved by one human–machine interaction feature, i.e., the scheduling expert or management decision maker assigns the relative importance of the two objectives, which are combined with subjective decision information in the algorithmic optimization process to obtain a compromise solution.

(3)

The HRL-based scheduling agent consists of a single-stream double deep $Q$-network (DDQN) as a high-level controller and a two-stream dueling DDQN (DDDQN) as a low-level actuator. This ensures the effectiveness and generalization of the proposed method under the premise of the agent’s learning speed.

(4)

To balance and optimize the two production scheduling targets in real time, four state indicators are designed for the high-level goal, and each state indicator corresponds to an external reward function to maximize the cumulative return during training.

The overall structure of the study takes the form of six sections, including this introductory section. Section 2 introduces a brief review of RL-based dynamic scheduling methods. The mathematical model for the MODFJSP with random job arrival in a smart machine tool processing workshop is established in Section 3. Section 4 presents the background of DDQNs and DDDQNs, and the implementation details are provided. Section 5 provides a case study of the proposed HRL algorithm in the flexible production scheduling of gears and presents the results of numerical experiments. Conclusions and future research directions are summarized in Section 6.

2. Related Works

To intelligently match the dispersed production resources of the smart workshop in real time, more and more researchers and practitioners have been paying attention to RL algorithms, software, and frameworks to solve production scheduling problems.

Fonseca et al. [19] applied Q-learning to study the flow job shop scheduling problem (FSP) for minimum completion time. He et al. [20] solved the dynamic FSP (DFSP) for minimum cost and energy consumption, in the context of the textile industry, using multiple deep Q-network (DQN) agents. Shahrabi et al. [21] solved the dynamic JSP (DJSP) to minimize average flow time via Q-learning, dynamically adjusting the parameters of a variable neighborhood search algorithm. Kuhnle et al. [22] proposed a framework for design, implementation, and evaluation of on-policy RL to solve the JSP with order dynamic arrival in order to maximize machine utilization while minimizing order delivery time. Wang et al. [23] solved an assembly JSP with random assembly times for minimum total weighted earliness penalty and completion time using dual Q-learning agents, where the top-level agent focused on the scheduling policy and the bottom-level agent optimized global targets. Bouazza et al. [24] used intelligent software products to solve the partially FJSP with new job insertions to minimize makespan through the use of a Q-learning algorithm. Luo et al. [14] proposed a two-layer deep reinforcement learning model where the high-level DDQN determines the optimization objective and the low-level DDQN selects the scheduling rule to solve the FJSP with minimum total delay and maximum average machine utilization. Johnson et al. [25] proposed a multi-agent system and applied multiple independent DDQN agents to solve the FJSP in a robotic assembly production cell with random job arrival to minimize makespan.

Table 1. Existing RL methods for dynamic production scheduling problems.

Work	Type	Objective	Algorithm	Agent	State	Action Space	Interaction
Fonseca et al. [19]	FSP	Makespan	Q-learning	Single agent	Discrete	1	No
He et al. [20]	FSP	Cost, energy consumption	DQN	Multiple agents	Continuous	3	No
Shahrabi et al. [21]	JSP	Mean flow time	Q-learning	Single agent	Discrete	8	No
Kuhnle et al. [22]	JSP	Machine utilization, lead time of orders	Trust region policy optimization	Single agent	Continuous	4	No
Wang et al. [23]	JSP	Total earliness penalty, completion time cost	Dual Q-learning	Multiple agents	Discrete	4	No
Bouazza et al. [24]	FJSP	Total weighted completion time	Q-learning	Multiple agents	Discrete	4	No
Luo et al. [14]	FJSP	Total tardiness, machine utilization rate	HRL	Single agent	Continuous	6	No
Johnson et al. [25]	FJSP	Makespan	DDQN	Multiple agents	Continuous	12	No
Our work	FJSP	Penalties for earliness and tardiness, total machine load	HRL	Single agent	Continuous	10	Yes

summarizes the differences between the aforementioned studies and our work.

From the above literature review, research has mainly focused on using RL to solve single-objective DFSPs, DJSPs, and DFJSPs. Use of RL to solve multi-objective DFJSPs has not been deeply explored in research. Additionally, there is currently no RL method that considers the dynamic preference of decision makers toward production targets via human–computer interaction.

Studies in the literature [19,21,23,24] have used RL with linear value function approximation, which forces state discretization when dealing with continuous-state problems. Refined perception of the environment leads to an explosion in the number of discrete states [26], with vast increases in the computational requirements of the model (e.g., state–action pair Q-tables) and reduced agent learning speed. Therefore, to reduce computational complexity, simple discretization discards some critical information about the state of the domain structure, which ultimately affects the quality of the agent’s decision making.

In the work of Luo et al. [14], an HRL-based agent was utilized to solve the MODFJSP, as opposed to a DDQN which learns slowly with the increased number of actions [27]. Because there is not a single heuristic rule that performs well in all production scheduling problems, this study expands the action space by increasing the number of scheduling rules and applies a combination of DDQN and DDDQN hierarchical reinforcement learning to solve the MODFJSP so as to improve the learning efficiency and generalization of the algorithm.

3. Problem Formulation

3.1. Problem Description

There are several production lines in a smart machine tool processing workshop, and each production line includes multiple production units due to the division of labor. Each production unit is regarded as an independent processing machine. We describe the DFJSP with random job arrival in a smart machine tool processing workshop using symbols defined as follows: There are $m$ independent processing machines $M=\left\{M_1,M_2,\cdots ,M_m\right\}$, which can machine $n$ independent jobs $J=\left\{J_1,J_2,\cdots ,J_n\right\}$ with successive arrival time $A=\left\{A_1,A_2,\cdots ,A_n\right\}$ and due date $D=\left\{D_1,D_2,\cdots ,D_n\right\}$. Each job $J_i$ consists of $h_i$ predetermined operations. The jth operation of job $J_i$ is denoted as $O_{ij}$, which can be machined on a compatible set of machines $M_{ij}\left(M_{ij}\subseteq M\right)$. $t_{ijk}$ is the processing time of $O_{ij}$ on independent machine $M_k$. In this study, the assumptions and constraints were as follows:

(1)

Each operation can be processed by only one independent machine at a time without interruption.

(2)

There are precedence constraints among the operations of one job, and the order of precedence of operations belonging to different jobs is not being followed.

(3)

There is no priority assigned to any job.

(4)

The setup time of the machine tool, the time for the robot to grasp the workpiece and move it to the fixture, the time the stacker takes to transfer job frames, the scanning time of the two-dimensional code on the job, and the breakdown time of the machine tool are negligible.

(5)

It is assumed that three-dimensional warehouses and loading stations are unlimited.

3.2. Mathematical Model

A mathematical model of the MODFJSP with random job arrival in a smart machine tool processing workshop was established. All notations used to describe the problem are summarized in

Table 2. Related mathematical notations and their definitions.

	Symbol	Definition	Symbol	Definition
Indices	$k$	Index of machine tools, $k=1,2,\cdots ,m$	$j$,$t$	Index of operations belonging to $J_i$ and $J_r$, $j=1, 2,\cdots ,h_i; t=1,2,\cdots ,h_r$
	$i$,$r$	Index of jobs, $i,r=1,2,\cdots ,n$
Constants	$m$	The number of independent processing machines	$n$	The number of independent jobs
	$t_{ijk}$	The processing time of $O_{ij}$ on $M_k$	$h_i$	The operation number of job $J_i$
	$M_{ij}$	The suitable machine set for $O_{ij}$	$f_i$	The delivery relaxation factor of $J_i$
	$w_i^e$	Unit (per day) earliness cost of $J_i$	$w_i^t$	Unit (per day) tardiness cost of $J_i$
	$A_i$	The arrival time of $J_i$	$D_i$	The due date of $J_i$
	$t_{ij}$	The average processing time of $O_{ij}$ on $M_{ij}$	$n_{ini}$	The number of initial jobs
	$n_{add}$	The number of newly added jobs	$E_{ave}$	Average value of exponential distribution between two successive job arrivals
Sets	$M$	Set of processing machines, $M=\left\{{\mathrm{M}}_1,M_2,\cdots ,M_m\right\}$	$J$	Set of jobs, $J=\left\{J_1,J_2,\cdots ,J_n\right\}$
	$M_{ij}$	Set of compatible machines for $O_{ij}$, where $M_{ij}\subseteq M$
Variables	$x_{ijk}$	If $O_{ij}$ is assigned to $M_k$, $x_{ijk}=1$, else $x_{ijk}=0$	$y_{ijrtk}$	If $O_{ij}$ is processed on $M_k$ before $O_{rt}$, $y_{ijrtk}=1$, else $y_{ijrtk}=0$
	$s_{ij}$	The starting time of $O_{ij}$	$c_{ij}$	The completion time of $O_{ij}$
	$C_i$	The completion time of $J_i$	$C{T}_k\left(t\right)$	The completion time of the last operation on machine $M_k$ at timestep $t$
	$O{P}_i\left(t\right)$	The current number of completed operations of $J_i$ at timestep $t$	$Machine\text{\_}T\left(t\right)\left[k\right]$	The processing time of each operation processed by machine $M_k$ at timestep $t$
	$MT\left[k\right]$	The load of machine $M_k$ at timestep $t$	$Loa{d}_r$	The current estimated remaining processing time at timestep $t$
	$U{C}_{job}\left(t\right)$	The uncompleted job set at timestep $t$
Production situation observation	${\overline{U}}_m\left(t\right)$	The average utilization rate of the machines at timestep $t$	$F_e\left(t\right)$	Estimated total machine load at timestep $t$
	$E{T}_e\left(t\right)$	Estimated earliness and tardiness rate at timestep $t$	$P_e\left(t\right)$	Estimated earliness and tardiness penalty at timestep $t$
	$Imp\left(t\right)$	The relative importance of objectives at timestep $t$

in line with the literature [18]. For each job $J_i$, its due date $D_i$ can be calculated as $D_i=A_i+f_i\times {{\displaystyle \sum }}_{j=1}^{h_i}{t}_{ij}$, where $t_{ij}=mea{n}_{k\in M_{ij}}{t}_{ijk}$ represents the average processing time of $O_{ij}$ on its compatible machine set $M_{ij}$ [14].

In this study, the production objective was to obtain a real-time flexible schedule with the lowest total weighted penalties for earliness and tardiness ($TWET$) and the lowest total machine load ($Fuhe$). Based on the notations of parameters and decision variables above, the objective functions are given by Equation (1), and some constraints are given in Equations (2)–(5).

Objective:

$$\min \left\{\begin{array}{c}TWET={{\displaystyle \sum }}_{i=1}^n\left(w_i^e\times \max \left\{D_i-C_i,0\right\}+w_i^t\times \max \left\{C_i-D_i,0\right\})\right)\\ Fuhe={{\displaystyle \sum }}_{i=1}^n{{\displaystyle \sum }}_{j=1}^{h_i}{{\displaystyle \sum }}_{k=1}^m{t}_{ijk}\times x_{ijk}\end{array}\right.$$

(1)

Subject to

$$s_{ij}\ge 0, (s_{i1}-A_i)\times x_{i1k}\ge 0 \forall i,j,k$$

(2)

$$s_{ij}+t_{ijk}\times x_{ijk}\le s_{i\left(j+1\right)} \forall i,j,k$$

(3)

$$s_{ij}+t_{ijk}\le s_{rt}+Z\times \left(1-y_{ijrtk}\right) \forall i,r,j,t,k$$

(4)

$${{\displaystyle \sum }}_{k=1}^{\left|M_{ij}\right|}{x}_{ijk}=1 \forall i,j$$

(5)

Equation (2) ensures that each job cannot be machined until it arrives. Equation (3) ensures that the precedence constraints between the operations of the same job must be satisfied. Equations (4) and (5) indicate that a job can only be processed by one machine tool at a time without interruption and at the same time, respectively, where $Z$ is a large enough positive number.

4. Proposed HRL

4.1. Background of DDQNs and DDDQNs

Since DQNs [28] first combined RL with nonlinear value functions in 2013, representing a milestone, RL has been rapidly developed and become widely applicable. In RL, an agent interacts with environment $E$ at each $t$ of a sequence of discrete time steps, perceives state $s_t$, $s_t\in S$ (set of all states), and selects action $a_t$ from possible action set $A$ under its policy $\pi$, where $\pi$ is mapping probability $p$ from $s_t$ to $a_t$. Responding to $a_t$, the environment $E$ presents new state $s_{t+1}$ and assigns scalar reward $r_t$ to the agent. They interact until the agent reaches a terminal state. The agent obtains the total accumulated return $R_t={{\displaystyle \sum }}_{k=1}^{\infty }{\gamma }^k\times r_{t+k}$, $0<\gamma \le 1$, where discount rate $\gamma$ trades off immediate and delayed rewards. Solving an RL task means finding an optimal policy, ${\pi }^{\ast }$, to maximize the expected accumulated return from each state, $s_t$, over the long run. The recursive expression of the state–action value function $Q\left(s_t,a_t\right)$ is shown in Equation (6), which turns Bellman equations into updated rules for improving approximations of the desired value functions and obtaining the dynamic programming algorithm.

$$\begin{gathered} Q^{{\pi }^{\ast }}\left(s_t,a_t\right)\stackrel{\mathrm{def}}{=}{\max }_{\pi }{Q}^{\pi }\left(s_t,a_t\right) \\ =E\left[r_t+\gamma \times {\max }_{a^{\prime }}{Q}^{{\pi }^{\ast }}\left(s_{t+1},a^{\prime }\right)\right] \\ ={\displaystyle \sum }_{s_{t+1},r_t}p\left(s_{t+1},r_t|s_t,a_t\right)\times \left[r_t+\gamma \times {\max }_{a^{\prime }}{Q}^{{\pi }^{\ast }}\left(s_{t+1},a^{\prime }\right)\right] \end{gathered}$$

(6)

On-policy RL is attractive in continuous control, but off-policy RL provides more generalized, stable, and efficient learning methods in discrete control [15]. In the DQN, the parameters, ${\theta }_t$, of the neural network are adjusted by randomly sampling state–action–reward transition tuples ($s_t$, $a_t$, $r_t$, $s_{t+1}$) at each time step $t$. The iterative updating formulas of ${\theta }_t$ and the target $y_t{}^{DQN}$ are shown in Equations (7) and (8), respectively, where $\eta$ is the learning rate used by the gradient descent algorithm. It is clear that the state–action values from the same neural network are used in selecting and evaluating an action. Therefore, the predicted value of $Q$ is substantially overestimated, which may reduce the learning quality of an agent.

$${\theta }_{t+1}={\theta }_t+\eta \times \left(y_t-Q\left(s_t,a_t;{\theta }_t\right)\right)\times {\nabla }_{{\theta }_t}Q\left(s_t,a_t;{\theta }_t\right)$$

(7)

$$y_t^{DQN}=r_t+\gamma \times {\mathrm{argmax}}_{a^{\prime }}Q\left(s_{t+1},a^{\prime };{\theta }_t\right)$$

(8)

In order to decouple the selection from the evaluation, a DDQN was designed by Hasselt et al. [29], where the online network $Q$ value and the target network $\widehat{Q}$ value are used to select an action and evaluate the action, respectively. The iterative formula of target $y_t{}^{DDQN}$ is shown in Equation (9).

$$y_t^{DDQN}=r_t+\gamma \times \widehat{Q}\left(s_{t+1},{\mathrm{argmax}}_{a^{\prime }}Q\left(s_{t+1},a^{\prime };{\theta }_t\right);\widehat{{\theta }_t}\right)$$

(9)

According to Equations (11) and (12), only one state–action value $Q\left(s_t,a_t\right)$ is updated at each time step, and all other action values of $s_t$ remain untouched. When the number of actions increases, an agent needs increasingly more action value updates for learning. In addition, the differences among action values for $s_t$ are often very small relative to the magnitude of $Q$. For example, after training with the DDQN in [18], the average gap between the $Q$ values of the best and the second-best action across visited states is roughly 0.06, whereas the average action value across those states is about 17. Action values are frequently reordered, and actions chosen by behavior strategies are correspondingly changed, which brings small amounts of noise in the updates.

Based on the above two reasons, Wang et al. designed a DDDQN [27] with two streams to separately estimate state value, $V\left(s_t,{\theta }_t,{\alpha }_t\right),$ and the advantages, $adv\left(s_t,a,{\theta }_t,{\beta }_t\right)$, for each action. Here, ${\theta }_t$ represents the parameters of the sharing layers, while ${\alpha }_t$ and ${\beta }_t$ denote the parameters of each of the two streams. The state–action $Q$ value is calculated using Equation (10), where $A\left(s_t,a,{\theta }_t,{\beta }_t\right)$ is an $\left|A\right|$-dimensional vector.

$$\begin{gathered} Q\left(s_t,a,{\theta }_t,{\alpha }_t,{\beta }_t\right)=V\left(s_t,{\theta }_t,{\alpha }_t\right)+adv\left(s_t,a,{\theta }_t,{\beta }_t\right) \\ =V\left(s_t,{\theta }_t,{\alpha }_t\right)+[A\left(s_t,a,{\theta }_t,{\beta }_t\right)-\frac{{{\displaystyle \sum }}_{i=1}^{\left|A\right|}A\left(s_t,a_i,{\theta }_t,{\beta }_t\right)}{\left|A\right|}] \end{gathered}$$

(10)

4.2. Model Architecture

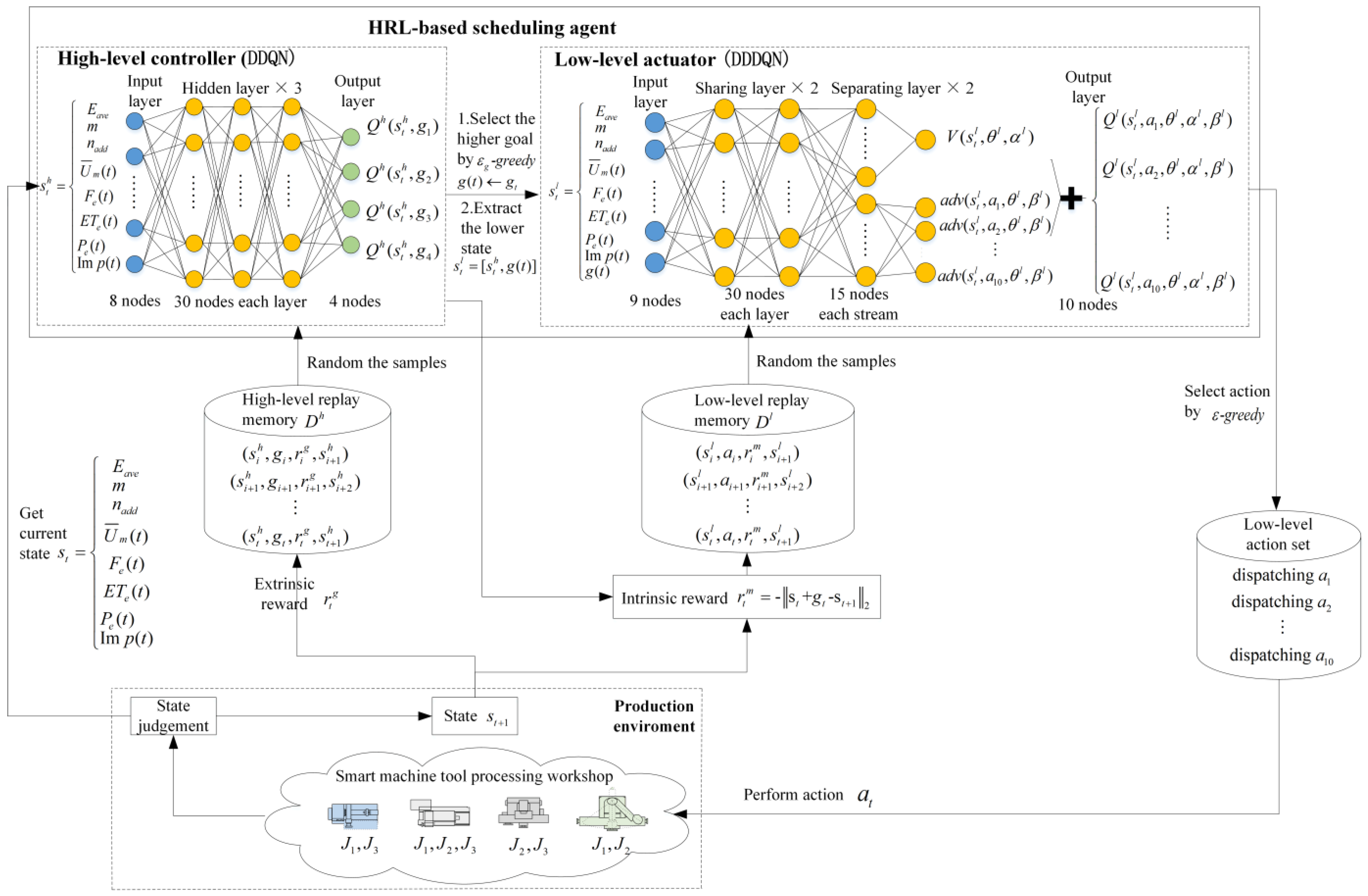
In this paper, an HRL framework is used to solve the MODFJSP. The algorithm model is shown in Figure 2, including the manufacturing environment of a smart machine tool workshop, the hierarchical agent, and the reinforcement learning process. The instances are generated from the scheduling type, constraint conditions, and dynamic attributes defined by the production environment of a smart workshop. The production instance is expressed as a semi-Markov decision process (semi-MDP) [30] through definitions of different levels of temporal abstraction, states, actions, and rewards. The agent constantly interacts with the semi-MDP to obtain the training data sample set and performs training expression and policy learning through the HRL algorithm.

The hierarchical agent consists of a high-level controller, ${\pi }^h$, and a low-level actuator, ${\pi }^l$. According to the current production state of the workshop, the high-level controller determines the temporary production goal, which is directly related to the desired observation value. The low-level actuator chooses the scheduling action rule according to the current state and the production goal and directly applies the action to the shop floor environment.

The DDQN algorithm is utilized for the high-level controller, consisting of five fully connected layers with three hidden layers. The number of nodes in the input and output layers is eight (the number of production state features) and four (the number of state indicators of goals), respectively. The activation function is a rectified linear unit (ReLU) and the parameter optimization function is Adam.

The low-level actuator adopts the DDDQN learning algorithm consisting of six fully connected layers with four hidden layers. The hidden layers contain two sharing layers and two separating layers. The number of nodes in the input is nine (corresponding to one higher goal) and the number of nodes in the output is ten (the number of scheduling rules). The activation function and optimization function are consistent with the high-level controller. The learning process is as follows:

(1)

The high-level controller obtains the current state, $s_t$, of the flexible production environment of a smart machine tool machining workshop;

(2)

The high-level controller determines a temporary optimization objective, $g_t~{\pi }^h$, according to the online network’s $Q^h$ value and the behavior policy ${\epsilon }_g-greedy$;

(3)

The low-level actuator obtains $s_t$ and $g_t$;

(4)

According to the online network’s $Q^l$ value and the behavior policy $\epsilon -greedy$, the low-level actuator determines scheduling rule $a_t$, and operation $O_{ij}$ and a feasible machine, $M_k$, are selected;

(5)

The smart machine tool machining workshop performs $a_t$, and $s_t$ is transferred to the next production state, $s_{t+1}$;

(6)

The high-level controller obtains the extrinsic reward, $r_t^g$, and the experience tuple ($s_t$, $g_t$, $r_t^g$, $s_{t+1}$) is stored in the high-level experience replay, $D^h$;

(7)

The low-level actuator obtains the intrinsic reward, $r_t^m$, from the high-level controller, and the experience tuple ($s_t$, $g_t$, $r_t^m$, $a_t$, $s_{t+1}$, $g_{t+1}$) is stored in the low-level experience replay, $D^l$;

(8)

Randomizations of the samples are both performed in $D^h$ and $D^l$ to respectively update the online network parameters ${\theta }_t^h$ and ${\theta }_t^l$.

4.3. State Features

To comprehensively represent the complex production situation of a smart machine tool machining shop at the rescheduling point, eight generic state features are extracted, including three task-specific features, four environment-specific features, and one human–computer interaction feature. The specific details of these features are as follows:

(1)

Average job arrival number per unit time $E_{ave}$;

(2)

Number of machines $m$;

(3)

Number of newly added jobs $n_{add}$;

(4)

Average utilization rate ${\overline{U}}_m\left(t\right)$;

The average utilization rate of the machines is denoted by ${\overline{U}}_m\left(t\right)$, which is calculated using Equation (11) [14,18]. At rescheduling point $t$, the completion time of the last operation on machine $M_k$ and the current number of completed operations of job $J_i$ are denoted by $C{T}_k\left(t\right)$ and $O{P}_i\left(t\right)$, respectively.

$${\overline{U}}_m\left(t\right)=\frac{{{\displaystyle \sum }}_{k=1}^m\left(\frac{{{\displaystyle \sum }}_{i=1}^n{{\displaystyle \sum }}_{j=1}^{O{P}_i\left(t\right)}{t}_{ijk}\times x_{ijk}}{C{T}_k\left(t\right)}\right)}{m}$$

(11)

(5)

Estimated total machine load $F_e\left(t\right)$;

$Machine\text{\_}T\left(t\right)\left[k\right]$ represents the processing time of each operation processed by machine $M_k$ with $Machine\text{\_}T\left(t\right)\left[k\right]. length$ operations having been processed at the current time $t$. $MT\left[k\right]$ represents the load of machine $M_k$, and the machine load at the rescheduling point $t$ is ${{\displaystyle \sum }}_{k=1}^{m}MT\left[k\right]$. $Loa{d}_r$ represents the current estimated remaining processing time, so $F_e\left(t\right)$ is equal to ${{\displaystyle \sum }}_{k=1}^{m}MT\left[k\right]$ plus $Loa{d}_r$. The calculating method for $F_e\left(t\right)$ is given in Algorithm 1.

Algorithm 1 Procedure of calculating the estimated total machine load $F_e\left(t\right)$

1: Input:

2: $Machine\text{\_}T\left(t\right)$, $O{P}_i\left(t\right)$, $h_i$, $m$, $n$

3: Output:

4: $F_e\left(t\right)$

5: Procedure

6: $MT\left[m\right]$ ← 0, $Loa{d}_r$ ← 0

7: for ($k=1$; $k\le m$; $k++$) do

8: $MT\left[k\right]$ ← ${{\displaystyle \sum }}_{i=1}^{Machine\text{\_}T\left(t\right)\left[k\right].length}Machine\text{\_}T\left(t\right)\left[k\right]\left[i\right]$

9: end for

10: for ($i=1$; $i\le n$; $i++$) do

11: if $O{P}_i\left(t\right)$ < $h_i$ then

12:  $T_{left}$ ← 0

13:  for ($j=O{P}_i\left(t\right)+1$; $j\le$ $h_i$; $j++$) do

14:   $t_{ij}\leftarrow mea{n}_{k\in M_{ij}}{t}_{ijk}$

15:   $T_{left}$ ← $T_{left}$ + $t_{ij}$

16:  end for

17:  $Loa{d}_r$ ← $Loa{d}_r$ + $T_{left}$

18: end if

19: end for

20: $F_e\left(t\right)$ ← ${{\displaystyle \sum }}_{k=1}^{m}MT\left[k\right]$ + $Loa{d}_r$

21: Return $F_e\left(t\right)$

(6)

Estimated earliness and tardiness rate $E{T}_e\left(t\right)$ and estimated earliness and tardiness penalty $P_e\left(t\right)$;

The methods for calculation of $E{T}_e\left(t\right)$ and $P_e\left(t\right)$ are the same as those for the actual earliness and tardiness rate, $E{T}_a\left(t\right)$, and the actual earliness and tardiness penalty, $P_a\left(t\right)$, in [18], respectively.

(7)

Degree of relative importance $Imp\left(t\right)$.

Since managers, scheduling decision makers, and experienced experts have preferences in terms of scheduling objectives, their subjective opinions and judgments are still needed to deal with emergencies under the premise of nonholographic modeling. The degree of relative importance $Imp\left(t\right)$ between 1 and 9 is obtained through human–computer interaction, indicating the relative importance of $TWET$ to $Fuhe$. Thereafter, the production target is affected by many complex factors, so $Imp\left(t\right)$ is randomly generated in this study.

4.4. Action Set

According to [31,32], the ten scheduling rules were designed to complete operation sequencing and machine selection of the FJSP. The set of unfinished jobs at current time $t$ is denoted by $U{C}_{job}\left(t\right)$. The ten scheduling rules are as follows:

(1)

Dispatching Rule 1: According to Equation (12), the job, $J_i$, is selected from the uncompleted job set, $U{C}_{job}\left(t\right)$, and the minimum redundancy time of its remaining operations is the selection principle. The operation, $O_{i\left(O{P}_i\left(t\right)+1\right)}$, is selected, and the machine with the minimum completion time is allocated for $O_{i\left(O{P}_i\left(t\right)+1\right)}$. Moreover, the machine is selected according to Equation (13) in dispatching rules (1)–(8).

$$\underset{iϵU{C}_{job}\left(t\right)}{\min }\{(D_i-\frac{{{\displaystyle \sum }}_{k=1}^{m}C{T}_k\left(t\right)}{m})/\left(h_i-O{P}_i\left(t\right)\right)\}$$

(12)

$$\underset{k\in M_{i\left(O{P}_i\left(t\right)+1\right)}}{\min }\left\{\max \{C{T}_k\left(t\right),c_{iO{P}_i\left(t\right)},A_i\right\}+t_{i(O{P}_i\left(t\right)+1)k}\}$$

(13)

(2)

Dispatching Rule 2: According to Equation (14), the job, $J_i$, with the largest estimated remaining processing time is selected from the uncompleted job set, $U{C}_{job}\left(t\right)$, and its operation, $O_{i\left(O{P}_i\left(t\right)+1\right)}$, is selected.

$$\underset{iϵU{C}_{job}\left(t\right)}{\max }\{{{\displaystyle \sum }}_{j=O{P}_{i}t+1}^{h_i}{t}_{ij}\}$$

(14)

(3)

Dispatching Rule 3: According to Equation (15), the job, $J_i$, with the smallest estimated remaining processing time is selected from the uncompleted job set, $U{C}_{job}\left(t\right)$, and its operation, $O_{i\left(O{P}_i\left(t\right)+1\right)}$, is selected.

$$\underset{iϵU{C}_{job}\left(t\right)}{\min }\{{{\displaystyle \sum }}_{j=O{P}_{i}t+1}^{h_i}{t}_{ij}\}$$

(15)

(4)

Dispatching Rule 4: According to Equation (16), the job, $J_i$, with the smallest sum of the processing time of the current process and the average processing time of the subsequent process is selected from the uncompleted job set, $U{C}_{job}\left(t\right)$, and its operation, $O_{i\left(O{P}_i\left(t\right)+1\right)}$, is selected.

$$\underset{iϵU{C}_{job}\left(t\right)}{\min }\left\{\left(c_{iO{P}_i\left(t\right)}-s_{iO{P}_i\left(t\right)}\right)+t_{i(O{P}_{i}t+1)}\right\}$$

(16)

(5)

Dispatching Rule 5: According to Equation (17), the job, $J_i$, with the largest ratio of the processing time of the subsequent process to the estimated remaining processing time is selected from the uncompleted jobs, $U{C}_{job}\left(t\right)$, and its operation, $O_{i\left(O{P}_i\left(t\right)+1\right)}$, is selected.

$$\underset{iϵU{C}_{job}\left(t\right)}{\max }\{t_{i(O{P}_{i}t+1)}/{{\displaystyle \sum }}_{j=O{P}_{i}t+1}^{h_i}{t}_{ij}\}$$

(17)

(6)

Dispatching Rule 6: According to Equation (18), the job, $J_i$, with the smallest value for the subsequent processing time multiplied by the estimated remaining processing time is selected from the uncompleted jobs, and its operation, $O_{i\left(O{P}_i\left(t\right)+1\right)}$, is selected.

$$\underset{iϵU{C}_{job}\left(t\right)}{\min }\{t_{i(O{P}_{i}t+1)}\times {{\displaystyle \sum }}_{j=O{P}_{i}t+1}^{h_i}{t}_{ij}\}$$

(18)

(7)

Dispatching Rule 7: According to Equation (19), the job, $J_i$, with the largest ratio of the processing time of the subsequent process to the estimated total processing time is selected from the uncompleted jobs, and its operation, $O_{i\left(O{P}_i\left(t\right)+1\right)}$, is selected.

$$\underset{iϵU{C}_{job}\left(t\right)}{\max }\{t_{i(O{P}_{i}t+1)}/{{\displaystyle \sum }}_{j=1}^{h_i}{t}_{ij}\}$$

(19)

(8)

Dispatching Rule 8: According to Equation (20), the job, $J_i$, with the smallest value for the subsequent processing time multiplied by the estimated total processing time is selected from the uncompleted job set, $U{C}_{job}\left(t\right)$, and its operation, $O_{i\left(O{P}_i\left(t\right)+1\right)}$, is selected.

$$\underset{iϵU{C}_{job}\left(t\right)}{\min }\{t_{i(O{P}_{i}t+1)}\times {{\displaystyle \sum }}_{j=1}^{h_i}{t}_{ij}\}$$

(20)

(9)

Dispatching Rule 9: According to Equation (21), the job, $J_i$, with the earliest delivery date is selected from the uncompleted job set, $U{C}_{job}\left(t\right)$, and its operation, $O_{i\left(O{P}_i\left(t\right)+1\right)}$, is selected. From the suitable machine set of $O_{i\left(O{P}_i\left(t\right)+1\right)}$, the machine tool with the smallest load is then selected according to Equation (22).

$$\underset{iϵU{C}_{job}\left(t\right)}{\min }\left\{D_i\right\}$$

(21)

$$\underset{kϵM_{i\left(O{P}_i\left(t\right)+1\right)}}{\min }\{{{\displaystyle \sum }}_{i=1}^n{{\displaystyle \sum }}_{j=1}^{O{P}_i\left(t\right)}{t}_{ijk}\times x_{ijk}\}$$

(22)

(10)

Dispatching Rule 10: According to Equation (23), the job, $J_i$, with the smallest critical ratio (CR) of the minimum redundancy time to the estimated remaining processing time is selected from $U{C}_{job}\left(t\right)$, and its operation, $O_{i\left(O{P}_i\left(t\right)+1\right)}$, is selected. The machine is selected according to Equation (25).

$$\underset{iϵU{C}_{job}\left(t\right)}{\min }\{(D_i-\frac{{{\displaystyle \sum }}_{k=1}^{m}C{T}_k\left(t\right)}{m})/{{\displaystyle \sum }}_{j=O{P}_{i}t+1}^{h_i}{t}_{ij}\}$$

(23)

4.5. Reward Mechanism

In the traditional RL framework, the learned policy corresponds to a maximization of the expected return for a single reward function [33]. In the HRL framework, a range of reward functions, $r_t^g$, which are indexed or parametrized by a current goal, $g$, are considered to accomplish complex control tasks.

Each goal, $g$, corresponding to a set of states, $S^g\subset S$, is considered to be achieved when the hierarchical agent is in any state, $s_t\in S^g$ [33]. The high-level controller produces the action, $g_t$, which is a state feature of the lower-level actuator when performing actions that yield an observation close to $s_t+g_t$, and the lower-level policy, ${\pi }^l$, gets an intrinsic reward, $r_t^m=r\left(s_t,a_t,s_{t+1},g_t\right)$.

4.5.1. High-Level Goals

Some state features are more natural goal subspaces because of the high-level goal, $g_t$, indicating desired relative changes in observations [15]. The two scheduling objectives of this paper optimize four status indicators of estimated earliness and tardiness penalty, $P_e$, estimated earliness and tardiness rate, $E{T}_e$, estimated total machine load, $F_e$, and average utilization rate of the machines, ${\overline{U}}_m$. Therefore, the value set of high-level goal $g$ is $\left\{1,2,3,4\right\}$.

4.5.2. Extrinsic Reward $r_t^g$

To keep the increasing direction of the cumulative return consistent with the direction of optimizing the objectives and avoiding sparse rewards [16], the extrinsic reward function $r_t^g$ corresponds to the high-level goal and four status indicators at times $t$ and $t+1$. Since the state indicator features $P_e\left(t\right)$ and $F_e\left(t\right)$ are closely related to the production objectives, their corresponding rewards and punishments fluctuate wildly to improve the learning efficiency of the agent.

If the high-level goal $g_t=g_1=1$ at rescheduling point $t$, $P_e\left(t\right)$ and $P_e\left(t+1\right)$ are selected as the feature indicators, and $r_t^g$ is calculated using Equation (24).

$$r_t^g=\left\{\begin{array}{c}2 P_e\left(t\right)>P_e\left(t+1\right)\\ 0 P_e\left(t\right)=P_e\left(t+1\right)\\ -2 P_e\left(t\right)<P_e\left(t+1\right)\end{array}\right.$$

(24)

If the high-level goal $g_t=g_2=2$, $E{T}_e\left(t\right)$ and $E{T}_e\left(t+1\right)$ are selected as the feature indicators, and $r_t^g$ is calculated using Equation (25).

$$r_t^g=\left\{\begin{array}{c}1 E{T}_e\left(t\right)>E{T}_e\left(t+1\right)\\ 0 E{T}_e\left(t\right)=E{T}_e\left(t+1\right)\\ -1 E{T}_e\left(t\right)<E{T}_e\left(t+1\right)\end{array}\right.$$

(25)

If the high-level goal $g_t=g_3=3$, $F_e\left(t\right)$ and $F_e\left(t+1\right)$ are selected as the feature indicators, and $r_t^g$ is calculated using Equation (26).

$$r_t^g=\left\{\begin{array}{c}2 F_e\left(t\right)>F_e\left(t+1\right)\\ 0 F_e\left(t\right)=F_e\left(t+1\right)\\ -2 F_e\left(t\right)<F_e\left(t+1\right)\end{array}\right.$$

(26)

If the high-level goal $g_t=g_4=4$, ${\overline{U}}_m\left(t\right)$ and ${\overline{U}}_m\left(t+1\right)$ are selected as the feature indicators, and $r_t^g$ is calculated using Equation (27).

$$r_t^g=\left\{\begin{array}{c}1 {\overline{U}}_m\left(t\right)<{\overline{U}}_m\left(t+1\right)\\ 0 {\overline{U}}_m\left(t\right)={\overline{U}}_m\left(t+1\right)\\ -1 {\overline{U}}_m\left(t\right)>{\overline{U}}_m\left(t+1\right)\end{array}\right.$$

(27)

4.5.3. Intrinsic Reward $r_t^m$

Intrinsic motivation [33], which is closely related to the intelligence level of an agent, involves learning with an intrinsically specified objective.

At decision point $t$, after receiving the goal, $g_t$, from the high-level controller, the low-level actuator selects a scheduling rule, which is applied to the smart workshop environment. The higher-level controller provides the low-level policy with an intrinsic reward, $r_t^m$. In [15], the intrinsic reward, $r_t^m$, is parameterized based on the distance between the current state, $s_{t+1}$, and the goal state, $s_t+g_t$. It is calculated using Equation (28).

$$r_t^m=-\Vert s_t+g_t-s_{t+1}{\Vert }_2$$

(28)

4.6. Action Selection Strategy

The production scheduling objective is dynamically controlled in a cooperative human–machine way, and the degree of relative importance, $Imp\left(t\right)$, is added to the behavior selection strategy of the high-level controller. In this study, a ${\epsilon }_g-greedy$ behavior strategy was designed, which is calculated using Equation (29) where $r_{0–1}$ is a random number between 0 and 1. If the value of $Imp\left(t\right)$ is larger, it means that decision makers make a decision: objective $TWET$ is more important than objective $Fuhe$, and optimizing $TWET$ is a priority at current time $t$. Furthermore, the indication characteristic, $P_e$, of the high-level goal, $g_1$, is closely related to $TWET$. Therefore, if $Imp\left(t\right)\ge 5$, the high-level controller selects $g_1$ with the current production target $TWET$; otherwise, the annealed linearly $\epsilon -greedy$ strategy is used.

$${\epsilon }_g=\left\{\begin{array}{c}{g}_1 if Imp\left(t\right)\ge 5\\ g_{random} if Imp\left(t\right)<5 and \epsilon <r_{0-1} \\ {\mathrm{argmax}}_g{Q}^h\left(s_t^h,g\right) if Imp\left(t\right)<5 and \epsilon \ge r_{0-1} \end{array}\right.$$

(29)

4.7. Procedure of the HRL Algorithm

By defining five key elements (state, dispatching rule, goal, reward, and behavior strategy), the MODFJSP is formulated and transformed into an HRL problem. Algorithm 2 is the training method of the hierarchical scheduling agent, where $EP$ is the number of epochs to train the neural network, $L$ is the training time in an epoch, $in{t}_{1–9}$ is the random integer between 1 and 9, $t$ represents the rescheduling time, $T$ is the sum of the operations of all current jobs at the current time $t$, and $C$ is the update step of the target network.

Algorithm 2 The HRL training method

1: Initialize replay memory $D^h$ to capacity $N^h$ and memory $D^l$ to capacity $N^l$

2: Initialize high-level online network action-value $Q^h$ with random weights ${\theta }^h$

3: Initialize high-level target network action-value ${\widehat{Q}}^h$ with weights ${\widehat{\theta }}^h={\theta }^h$

4: Initialize low-level online network action-value $Q^l$ with random weights ${\theta }^l$

5: Initialize low-level target network action-value ${\widehat{Q}}^l$ with weights ${\widehat{\theta }}^l={\theta }^l$

6: for epoch = 1: $EP$ do

7:  for episode = 1: $L$ do

8:   Initialize a new production instance with $E_{ave}$, $m$ and $n_{add}$

9:   Initialize state $s_1=\left\{E_{ave}, m,n_{add},Imp\left(1\right),{\overline{U}}_m\left(1\right),F_e\left(1\right),E{T}_e\left(1\right),P_e\left(1\right)\right\}=\left\{E_{ave}, m,n_{add},in{t}_{1-9},0,0,0,0\right\}$

10:  Initialize the high-level feature $s_1^h=s_1$

11:  Select high goal $g\left(1\right)$ according to $Q^h$ and ${\epsilon }_g-greedy$

12:  Initialize the low-level feature $s_1^l=\left[s_1^h, g\left(1\right)\right]$

13:  for t = 1: $T$ do

14:   Select an action $a_t$ according to $Q^l$ and $\epsilon -greedy$

15:   Execute action $a_t$, calculate the immediate reward $r_t^g$ using Equations (24)–(27) and $r_t^m$ using Equation (28) and observe the next workshop state $s_{t+1}$

16:   Set the high-level feature $s_{t+1}^h=s_{t+1}$

17:   Select high goal $g\left(t+1\right)$ according to $Q^h$ and ${\epsilon }_g-greedy$

18:   Set the low-level feature $s_{t+1}^l=\left[s_{t+1}^h, g_{t+1}\right]$

19:   Store transition: $D^h\leftarrow \left(s_t^h,g_t,r_t^g,s_{t+1}^h\right)$ $D^l\leftarrow \left(s_t^l,a_t,r_t^m,s_{t+1}^l\right)$

20:   Sample a random minibatch of $k_1$ transitions $\left(s_j^h,g_j,r_j^g,s_{j+1}^h\right)$ from $D^h$

21:   Set $$\begin{gathered} y_j^h= \\ \left\{\begin{array}{cc}\hfill r_j^g, & if episode terminates at step j+1\\ r_j^g+\gamma {\widehat{Q}}^h\left(s_{j+1}^h,{\mathrm{argmax}}_{g^{\prime }}{Q}^h\left(s_{j+1}^h,g^{\prime };{\theta }^h\right);{\widehat{\theta }}^h\right), & otherwise\end{array}\right. \end{gathered}$$

22:   Calculate the loss function ${\left(y_j^h-Q^h\left(s_j^h,g_j;{\theta }^h\right)\right)}^2$ and perform Adam with respect to the parameters ${\theta }^h$ of online network $Q^h$

23:   Sample a random minibatch of $k_2$ transitions $\left(s_j^l,a_j,r_j^m,s_{j+1}^l\right)$ from $D^l$

24:   Set $$\begin{gathered} y_j^l= \\ \left\{\begin{array}{c} r_j^m, if episode terminates at step j+1\\ r_j^m+\gamma \times {\widehat{Q}}^l\left(s_{j+1}^l,{\mathrm{argmax}}_{a^{\prime }}{Q}^l\left(s_{j+1}^l,a^{\prime };{\theta }^l\right);{\widehat{\theta }}^l\right), otherwise\end{array}\right. \end{gathered}$$

25:   Calculate the loss function ${\left(y_j^l-Q^l\left(s_j^l,a_j;{\theta }^l\right)\right)}^2$ and perform Adam with respect to the parameters ${\theta }^l$ of online network $Q^l$

26:   Every $C$ steps, reset ${\widehat{\theta }}^h={\theta }^h$ and ${\widehat{\theta }}^l={\theta }^l$

27:  end for

28: end for

29: end for

5. Numerical Experiments

As a mechanical component that transmits movement and power, gears are an important basic component of mechanical equipment. Due to its wide range of applications, improvements in green gear production efficiency contribute to the construction of advanced equipment manufacturing systems. Gears are rich in variety and have different processes, such as pre-hot and post-hot processing of planetary gears and post-hot processing of disk gears and shaft gears. The gear production line involves a turning and milling unit, tooth shaping unit, internal grinding and flat grinding unit, external grinding unit, and gear grinding unit. The problem instances were generated by actual gear production data from a factory, and the HRL-based agent was trained to solve the MODFJSP with random gear arrival.

In this section, the process of training the scheduling agent, the settings of hyperparameters, and three performance metrics in terms of multi-objective optimization are provided, followed by a comparison of learning rates between the DDDQN and DDQN and performance comparisons of the proposed HRL algorithm with each action scheduling rule. To show the effectiveness, generality, and efficiency of the HRL algorithm, we compared it with other RL algorithms, metaheuristics, and heuristics with different production configurations. To further verify the generalization of the proposed method, the trained scheduling agent was tested on a new set of extended instances with larger production configurations. The training and test results and two videos demonstrating the MODFJSP being solved using the proposed HRL algorithm are available in the Supplementary Materials.

5.1. Parameter Settings

5.1.1. Parameter Settings of Problem Instances

At the very beginning, there are several jobs in a flexible gear production workshop. The arrival of subsequent new gears obeys a Poisson distribution [18], whereas the arrival interval follows an exponential distribution with an average rate, $E_{ave}$ [21]. $UF$ represents a real interval uniform distribution, and $UI$ is an integer interval uniform distribution. The parameter settings are shown in

Table 3. Configuration of production example parameters.

Parameter	Value
Number of machines ($m$)	{10,30,50}
Number of initial jobs ($n_{ini}$)	$UI$[1,10]
Number of newly added jobs ($n_{add})$	{10,50,100}
Average value of exponential distribution between two successive job arrivals ($E_{ave}$)	{30,50,100}
Delivery relaxation factor ($f_i$)	$UF$[0.5,2]
Unit (per day) of earliness cost ($w_i^e$)	$UF$[1,1.5]
Unit (per day) of tardiness cost ($w_i^t$)	$UF$[1,2]
Number of operations in a job ($h_i$)	$UI$[1,20]
Processing time of an operation on a machine ($t_{ijk}$)	$UF$[0,50]

.

5.1.2. Hyperparameter Settings

In line with the literature [34], MODFJSPs are divided into $3\times 3\times 3=27$ classes using different parameter settings of $E_{ave}$, $m$, and $n_{add}$. The configuration of $E_{ave}$, $m$, and $n_{add}$ in Table 2 is repeated two times, generating $27\times 2=54$ different production instances. To more effectively evaluate the performance of the HRL algorithm, we randomly divided the 54 instances into 38 training instances (occupying 70% of all instances) and 16 validation instances (occupying 30% of all instances). In the process of training the agent, the 200 epochs are set. There are 38 episodes in an epoch for one episode generated on each instance, so the agent is trained on a total number of $200\times 38=7600$ instances.

The low-level policy is updated under the control of the high-level policy. The high-level goal $g$, which corresponded to action $a$ in the past transfer experience sample, corresponds to action $a^{\prime }$ ($a\ne a^{\prime }$) in the current low-level policy. Moreover, the action of the low-level policy affects the state distribution of the high-level policy, resulting in unstable learning in the high-level controller. To address this nonstationary problem, this study adopts the method in [14]: the high-level replay memory size $N^h$ is equal to minibatch size $k$. The hyperparameter settings and their values are shown in

Table 4. List of hyperparameters and their values.

Hyperparameter	Value
Number of training epochs $EP$	200
Number of episodes per epoch $L$	54
High-level replay memory size $N^h$	32
Low-level replay memory size $N^l$	2000
Minibatch size $k$	32
Greedy exploration $\epsilon$	Decreasing linearly from 1 to 0.1
Discount factor $\gamma$	0.95
Learning rate $\eta$	0.00025
Update step of the target network $C$	1000
Replay start size	>32

.

The proposed HRL algorithm and the smart shop floor environment for machine tools processing of gears were coded in Python 3.8.3. The training and test experiments were performed on a PC with an Intel(R) Core (TM) i7-6700 @ 3.40 GHz CPU and 16 GB of RAM.

5.2. Performance Metrics

The main aim of solving the MODFJSP is to find a set of uniformly distributed nondominated solutions. To fully evaluate the quality of the Pareto-optimal front $A$, three metrics are utilized to analyze performance in terms of convergence, distribution, and comprehensiveness. Because the real Pareto-optimal front $P$ is unknown in advance, the solutions obtained by all compared algorithms in the paper are merged, and those that are nondominated are taken as $P$.

In general, a set of solutions with smaller values in generational distance (GD) [14,35], spread (Δ) [14,36], and inverted generational distance (IGD) [14,37] is preferred. A smaller GD value means that the Pareto-optimal front $A$ is closer to the real Pareto-optimal front $P$, indicating higher convergence between the Pareto-optimal solutions. The smaller the Δ value, the more evenly distributed in the target space the Pareto solutions in $A$. The smaller the IGD value, the higher the convergence and distributivity of the synthetically obtained solutions.

5.3. Comparison of Learning Rates between the DDQN and DDDQN

To demonstrate the learning effectiveness of the low-level actuator, the DDDQN and the DDQN were trained with a single target: $\min \left\{0.5\times TWET+0.5\times Fuhe\right\}$. In addition, the reward function is shown in Equation (30), where $f\left(t\right)=0.5\times P_e\left(t\right)+0.5\times F_e\left(t\right)$.

$$r_t=\left\{\begin{array}{c}1 f\left(t\right)>f\left(t+1\right)\\ 0 f\left(t\right)=f\left(t+1\right)\\ -1 f\left(t\right)<f\left(t+1\right)\end{array}\right.$$

(30)

The single target value of the first 200 epochs calculated by both algorithms is shown in Figure 3, where the target value of one epoch is equal to the average of 38 different production instances. It is easy to see from the two curves that the average goal value drops smoothly and that volatility decreases gradually as the training steps increase. Furthermore, the DDDQN converges faster than the DDQN. It is further demonstrated that the DDDQN with dual streams improves the learning efficiency of the agent when solving DFJSPs with a large action space.

5.4. Comparisons of the HRL Algorithm with the Proposed Composite Dispatching Rules

To verify the effectiveness and generalization of the proposed HRL algorithm, 27 different instances were generated for each type of MODFJSP. Moreover, the policy RA, randomly selecting the high-level goal and the low-level scheduling rule, was designed to demonstrate the learning ability of the HRL agent. In each instance, the HRL algorithm and the composite rules were independently repeated 20 times. The GD, Δ, and IGD values of the Pareto-optimal front obtained by each method are available in the Supplementary Materials.

From the experimental results, the proposed HRL algorithm outperforms other comparative methods in terms of convergence, diversity, and comprehensiveness of Pareto solutions for most production instances. Firstly, compared with RA, the HRL algorithm obtained better results in all test instances, demonstrating its ability to learn difficult hierarchical policies when solving the MODFJSP. Secondly, compared with scheduling rules, HRL obtained the best results for most instances in terms of the convergence of GD, further indicating that there is no single scheduling rule that performs optimally in all MODFJSPs. It also obtained the best results for all test instances in terms of the diversity of Δ and the comprehensiveness of IGD.

The high-level goal $g_t$ is highly correlated with the scheduling objectives. The high-level DDQN controller determines a feasible goal, $g_t$, based on the current state at each rescheduling point. The low-level DDDQN actuator selects a scheduling rule based on the production state and $g_t$. Through the long-term training process, the agent effectively trades off between the two production objectives. Accordingly, the proposed HRL algorithm outperforms the single scheduling rule in terms of effectiveness and generalization. The Pareto fronts obtained by HRL and 10 scheduling rules for some representative instances are shown in Figure 4.

5.5. Comparison of HRL to Other Methods

To further verify the effectiveness and generalization of the proposed HRL algorithm, the trained agent was compared to three other RL algorithms (HRL with a DDQN as the low-level actuator (DDHRL), DDDQN and SARSA), a famous metaheuristic algorithm (GA) and two of the most commonly used heuristics rules (FIFO and shortest subsequent operation (SSO)). An instance was generated for each type of MODFJSP, and the HRL and the other algorithms were independently repeated 20 times in each instance. The GD, Δ, and IGD values of the Pareto-optimal fronts obtained using comparative methods are as available in the Supplementary Materials.

In this study, the only difference between the DDHRL method and the proposed HRL algorithm was the network structure of the low-level actuator. The DDDQN without $g_t$ was the same as the low-level actuator of the proposed HRL algorithm. In SARSA, nine discrete states are designed using a neural network with a self-organizing mapping layer (SOM) from [18,38]. A $Q$-table with 9 × 10 $Q$-values was maintained. The immediate reward function of the single agent, DDDQN and SARSA, was calculated using Equation (30).

In the GA [33], the method in [39,40] was used for fast nondominated ordering. The fitness calculation, the selection, crossover, mutation operations, and the hyperparameter settings were from [18].

FIFO chose the next job operation with the earliest arriving time, and SSO chose the next job operation with the shortest subsequent processing time from the unfinished jobs. The selection of processing machine for both was determined using Equation (14).

5.5.1. Effectiveness Analysis

To show the effectiveness of the proposed HRL algorithm, the average values of the three metrics for all the algorithms compared in all test instances were calculated, as shown in Figure 5. As can be seen in Figure 5, the proposed HRL algorithm outperformed the competing methods. It can also be seen that RL (HRL, DDHRL, DDDQN, and SARSA) outperformed the heuristic methods (FIFO and SSO) in almost all instances, indicating the effectiveness of the proposed scheduling rules in terms of the two investigated objectives, whereas hierarchical reinforcement learning (HRL and DDHRL) outperformed traditional RL (DDDQN and SARSA) and the metaheuristic method (GA), which confirms the necessity and effectiveness of using a single agent with a two-layer hierarchical policy. Additionally, the proposed HRL algorithm was superior to DDHRL, which demonstrates the superiority of the dueling architecture in low-level policy.

5.5.2. Generalization Analysis

To verify the generalizability of HRL, the winning rate was defined in terms of each metric, which was calculated in line with [18], as shown in Figure 6. For the convergence metric GD, HRL had the best results in 24 kinds of instances, and the winning rate was about 89%. For the diversity metric Δ, HRL had the smallest value for 20 scheduling problems, and the winning rate was about 74%. For the comprehensive metric IGD, HRL had the minimum value for 20 instances, with a winning rate of about 74%. The proposed HRL algorithm had the highest winning rate of the three metrics and generally performed at a level that was superior to the compared algorithms.

5.5.3. Efficiency Analysis

To show the efficiency of HRL, the average CPU times of all the algorithms that were used for comparison in all test instances were calculated and are available in the Supplementary Materials. Because of the number of jobs greatly expanding the size of the scheduling solution space, average CPU times were grouped by the number of newly added jobs, as shown in

Table 5. CPU times (s) for comparative methods and their average values.

${\mathit{n}}_{\mathit{a}\mathit{d}\mathit{d}}$	HRL	DDHRL	DDDQN	SARSA	GA	FIFO	SSO
10	7.26 × 100	7.72 × 100	5.09 × 100	4.88 × 100	2.01 × 102	3.92 × 10−2	4.65 × 10−2
50	2.89 × 101	3.21 × 101	1.84 × 101	1.75 × 101	1.09 × 103	2.70 × 10−1	3.53 × 10−1
100	6.11 × 101	6.38 × 101	3.34 × 101	3.25 × 101	2.58 × 103	4.82 × 10−1	8.33 × 10−1
Ave	3.24 × 101	3.45× 101	1.90 × 101	1.83 × 101	1.29 × 103	2.64 × 10−1	4.11 × 10−1

.

As can be seen in Table 5, FIFO and SSO are highly efficient, but they have poor solution quality and generalization, as shown above. GA also does not exhibit real-time characteristics. In addition, the time complexity of hierarchical reinforcement learning (HRL and DDHRL) and traditional RL (DDDQN and SARSA) is roughly the same, but the proposed HRL algorithm outperforms traditional RL significantly in terms of effectiveness and generalization.

Furthermore, considering the number of jobs in the test instances [34], the average scheduling time of HRL is 0.66 s on a PC with low specifications, which could reach the millisecond level or even less with the support of greater computing power. Therefore, HRL demonstrates the ability to optimize scheduling in real time in smart workshops.

It can be seen that, on the whole, the HRL algorithm proposed in this study clearly outperformed the other six methods in terms of effectiveness and generalization and has real-time characteristics. HRL solves the multi-objective scheduling problem as a semi-MDP, where the high-level policy determines the temporary objective according to the production state and the low-level policy determines the ongoing action based on the state and temporary objective. Therefore, hierarchical deep neural networks trained by HRL have multi-objective learning and decision-making capabilities at the rescheduling point and are more effective, robust, generalized, and efficient.

5.6. Extended Application of HRL

To further verify the effectiveness and generalization of HRL, the trained agent was applied to scheduling instances related to gear production with larger production configurations: new planetary gear, disk gear, and shaft gear arrivals of 135, 330, and 500, respectively; $E_{ave}$ set to 10, 30, and 50, respectively; 11 flexible machining machines; and the rest of the parameters the same as in training. Each comparison method in Section 5.5 was independently repeated 20 times on each extended instance. The metric values of the Pareto front obtained by each compared method are shown in

Table 6. Metric values for the Pareto-optimal fronts obtained by comparative methods, with the best results in bold.

Metric	${\mathit{n}}_{\mathit{a}\mathit{d}\mathit{d}}$	HRL	DDHRL	DDDQN	SARSA	GA	FIFO	SSO
GD	135	0.00 × 100	9.81 × 101	3.23 × 102	4.38 × 102	3.31 × 102	6.82 × 104	2.71 × 104
	330	0.00 × 100	8.72 × 102	1.58 × 103	2.41 × 103	2.27 × 103	4.17 × 105	1.73 × 105
	500	2.32 × 102	1.66 × 103	3.42 × 103	4.08 × 103	2.13 × 103	9.25 × 105	4.36 × 105
Spread	135	1.97 × 10−1	2.46 × 10−1	4.28 × 10−1	4.51 × 10−1	5.65 × 10−1	1.00 × 100	1.00 × 100
	330	1.87 × 10−1	2.75 × 10−1	3.08 × 10−1	2.99 × 10−1	3.32 × 10−1	1.00 × 100	1.00 × 100
	500	9.80 × 10−2	1.04 × 10−1	4.38 × 10−1	7.41 × 10−1	3.24 × 10−1	1.00 × 100	1.00 × 100
IGD	135	0.00 × 100	4.27 × 102	7.08 × 102	8.20 × 102	5.28 × 102	1.56 × 105	6.37 × 104
	330	1.01 × 103	1.24 × 103	3.07 × 103	3.10 × 103	2.03 × 103	9.49 × 105	4.02 × 105
	500	2.07 × 103	2.66 × 103	4.00 × 103	6.33 × 103	2.75 × 103	1.94 × 106	9.26 × 105

. The Pareto fronts of the HRL algorithm and other algorithms for the three real instances are given in Figure 7, where the yellow line in the enlarged figure represents the real Pareto optimal front $P$.

As can be seen in Table 6, HRL had the best results for all three metrics in the three extended instances. Figure 7 shows that the set of nondominated solutions ($A$) provided by the HRL algorithm was equal to the true Pareto front $P$ for the instance with 135 new planetary gear arrivals, close to the $n_{add}$ maximum (100) in the training set. One Pareto solution was not found by the HRL algorithm in the instance with 330 new disk gear arrivals, whereas two Pareto solutions were not found and one nondominated solution from the proposed method was not in $P$ for the instance with 500 shaft gear arrivals.

It can be seen that, on the whole, the greater the difference between the extended instances and the original instances, the greater the degradation in HRL performance. However, the overall performance of HRL did not significantly deteriorate, and it outperformed the six other methods in terms of effectiveness and generalization in extended large instances.

6. Conclusions

This study introduced an HRL method for solving the multi-objective dynamic FJSP with random job arrival in a smart machine tool processing workshop to satisfy the dual objectives of minimizing penalties for earliness and tardiness and total machine load. On the basis of establishing a mathematical model, a combined DDQN and DDDQN two-hierarchy architecture for the MODFJSP was constructed, and the continuous-state features, scheduling rules with large action spaces, and external and internal rewards were accordingly designed. Moreover, the decision-maker’s preference for production targets was integrated into the HRL algorithm as a state feature by human–computer interaction. Thus, by adaptively learning the feasible goal and efficiently exploring the dispatching rule space, the HRL-based agent not only conducts the scheduling in real time but also achieves a satisfactory compromise considering different objectives in the long term.

Numerical experiments were conducted on a large set of production instances to verify the effectiveness and generalization of the proposed HRL algorithm in practical applications of gear production. We showed that our approach with the proposed HRL algorithm produced state-of-the-art results in 24 (on convergence) and 20 (on both diversity and comprehensiveness) of the 27 test instances compared to DDHRL, DDDQNs, SARSAs, GAs, FIFO, and SSO, with no adjustment to the architecture or hyperparameters.

Real-time optimization of multi-objective DFJSPs through HRL intelligently matches the dispersed resources of the smart machine tool processing workshop and contributes to the implementation of an adaptive and flexible scheduling system, which meets the intellectualization and green needs of intelligent manufacturing. This work fills a research gap regarding solutions to MODFJSPs with random job arrival that minimize total penalties for earliness and tardiness as well as total machine load by using HRL. Moreover, the human–machine interaction feature integrates subjective decision information into the algorithmic optimization process to achieve a satisfactory compromise considering multiple objectives, which solves a key problem in multi-objective optimization.

In future work, the significance to production of real-time scheduling for flexible machining of machine tools in a smart workshop can be further improved through investigation of additional dynamic events and production objectives. Meanwhile, the number of actions (equal to the rule number of selecting an operation multiplied by the rule number of selecting a machine) should be increased for a more general agent. Such large action spaces are difficult to efficiently explore and, thus, successfully training DQN-like networks in this context is likely intractable [26]. Consequently, we will apply state-of-the-art off-policy methods, such as use of a deep deterministic policy gradient (DDPG) [26,41] and proximal on-policy optimization [42,43], for solving MODFJSPs.