Modeling and Characteristic Analysis of a Cylinder Block/Valve Plate Interface Oil Film Model for 35 MPa Aviation Piston Pumps
Abstract
1. Introduction
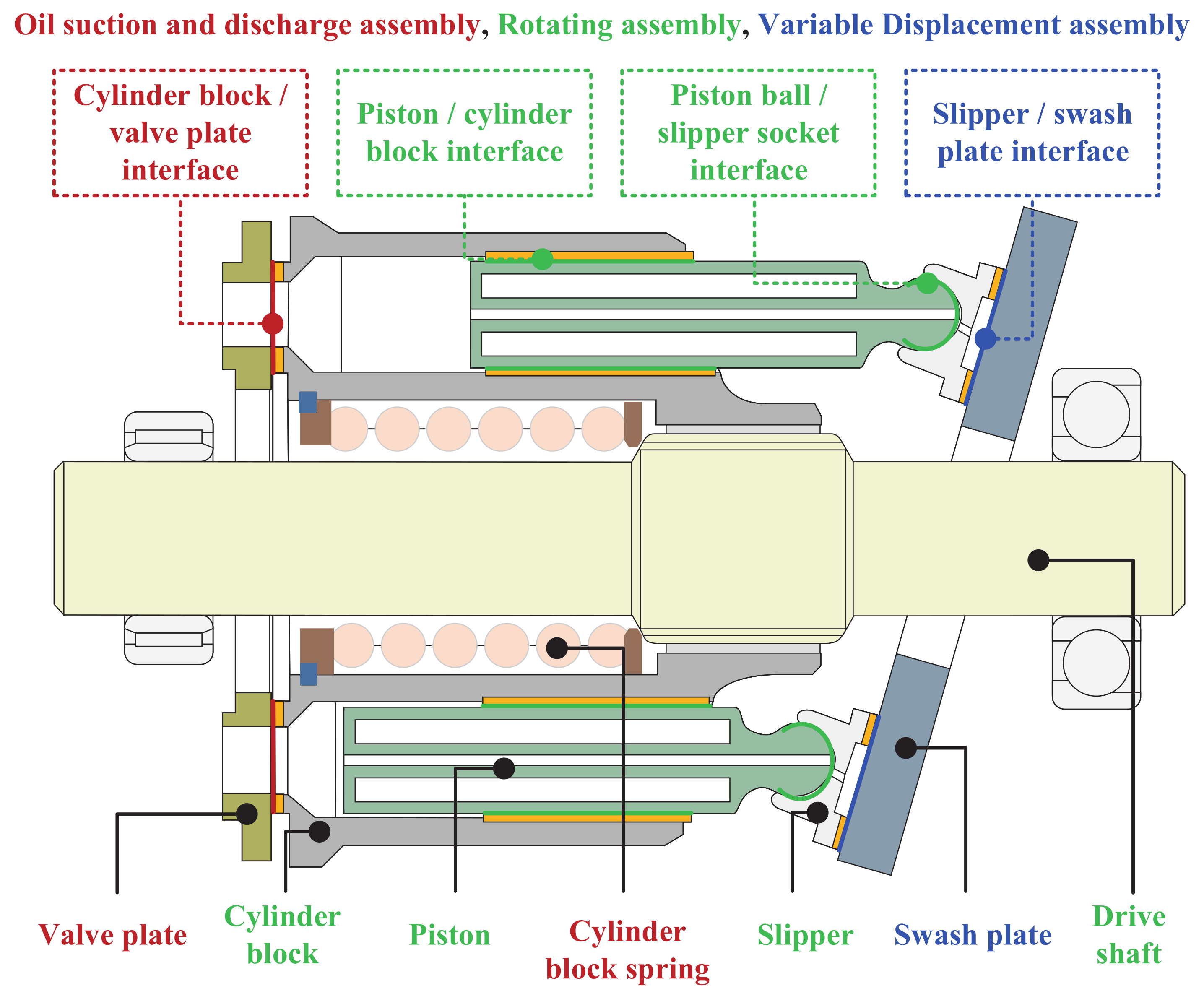
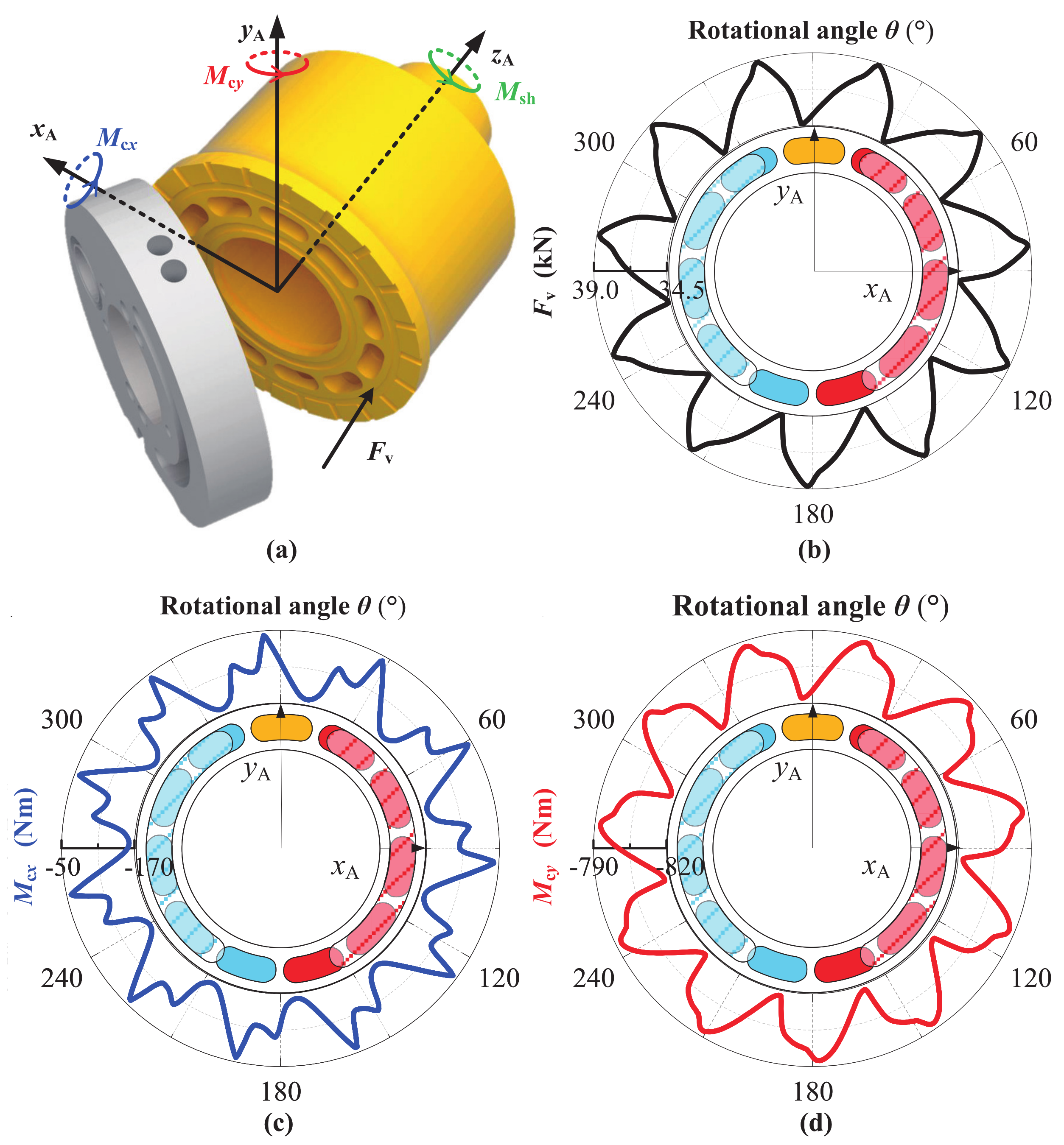
2. Problem Formulation
3. Oil Film Modeling
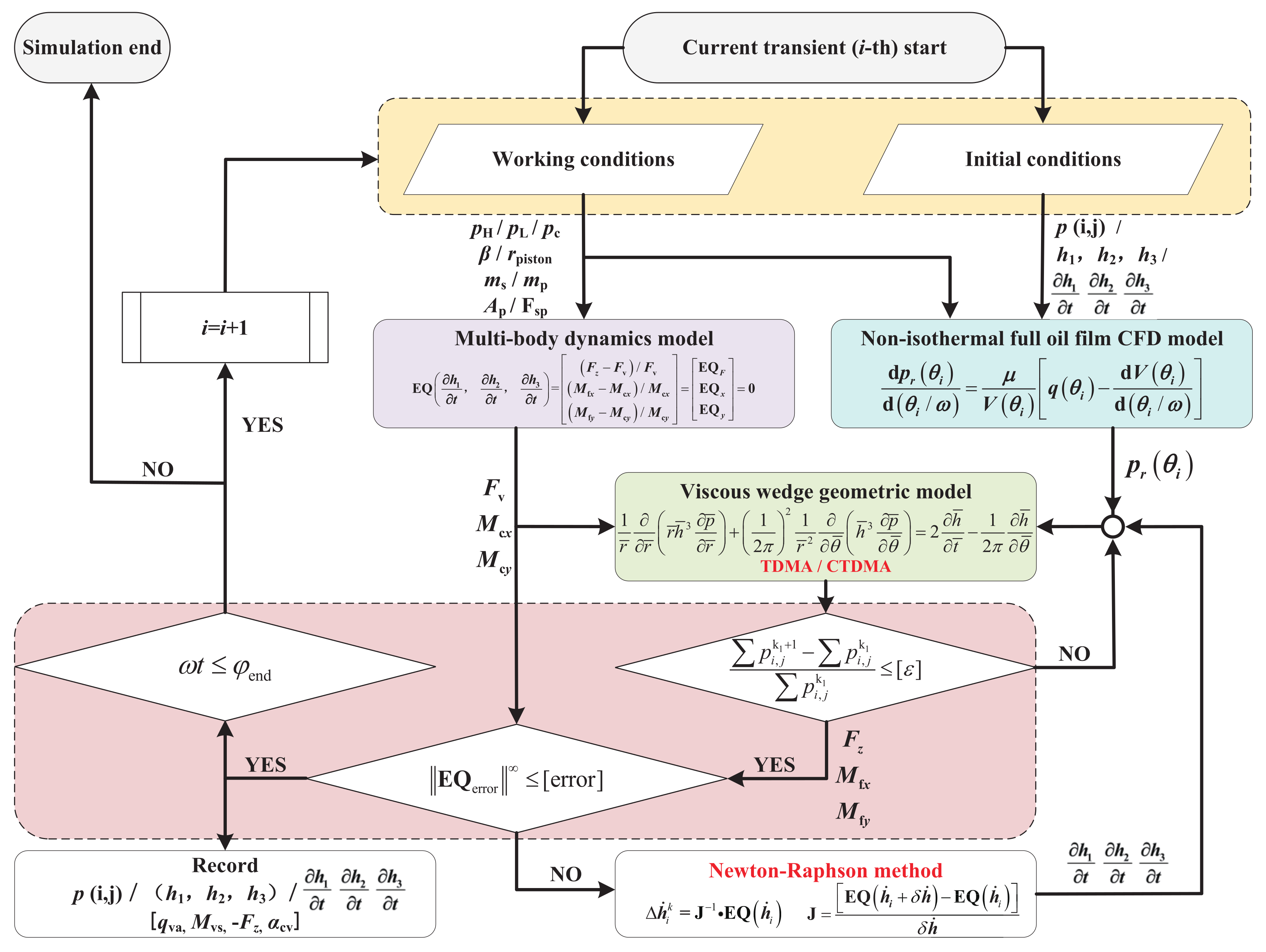
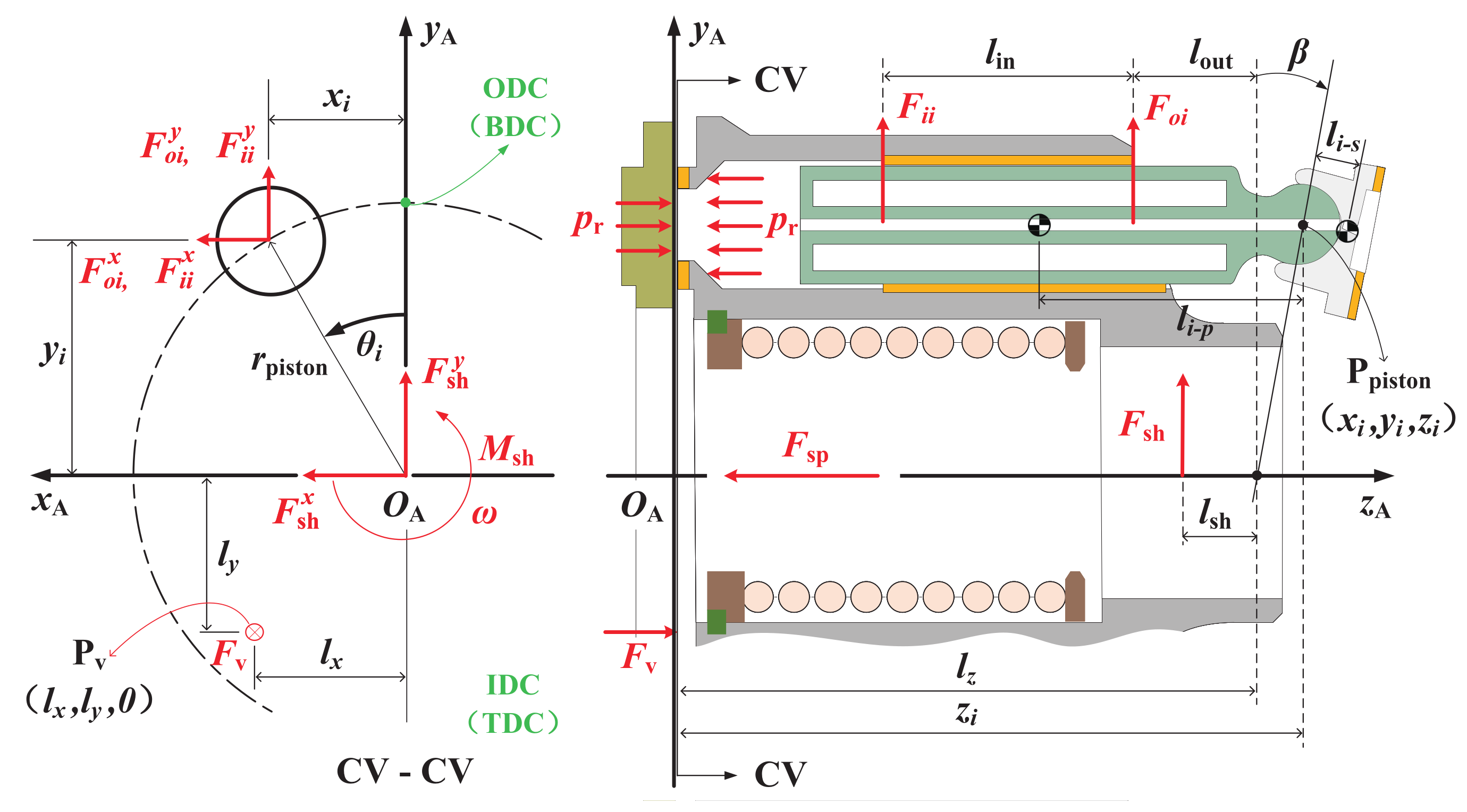
3.1. Model Overview
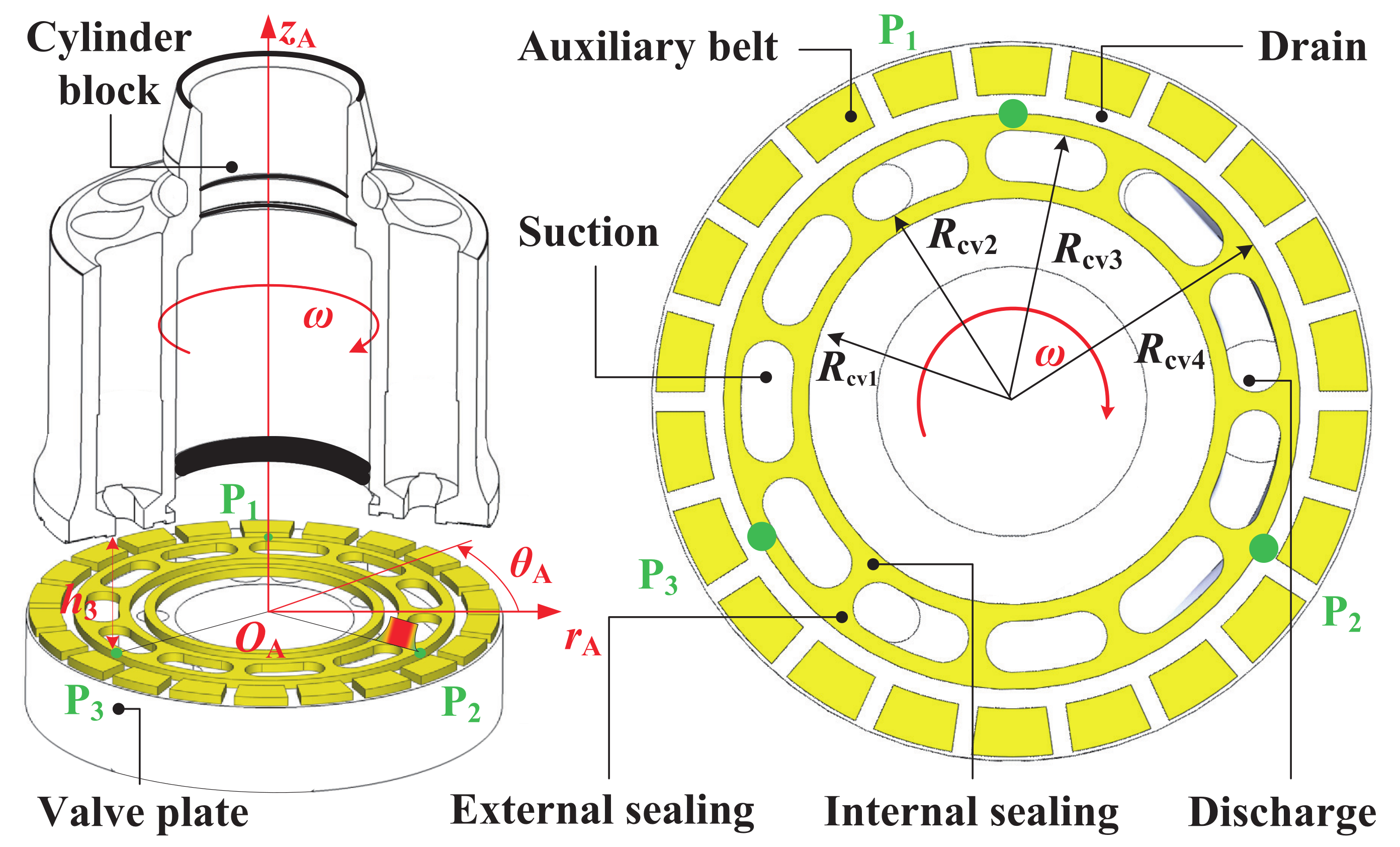
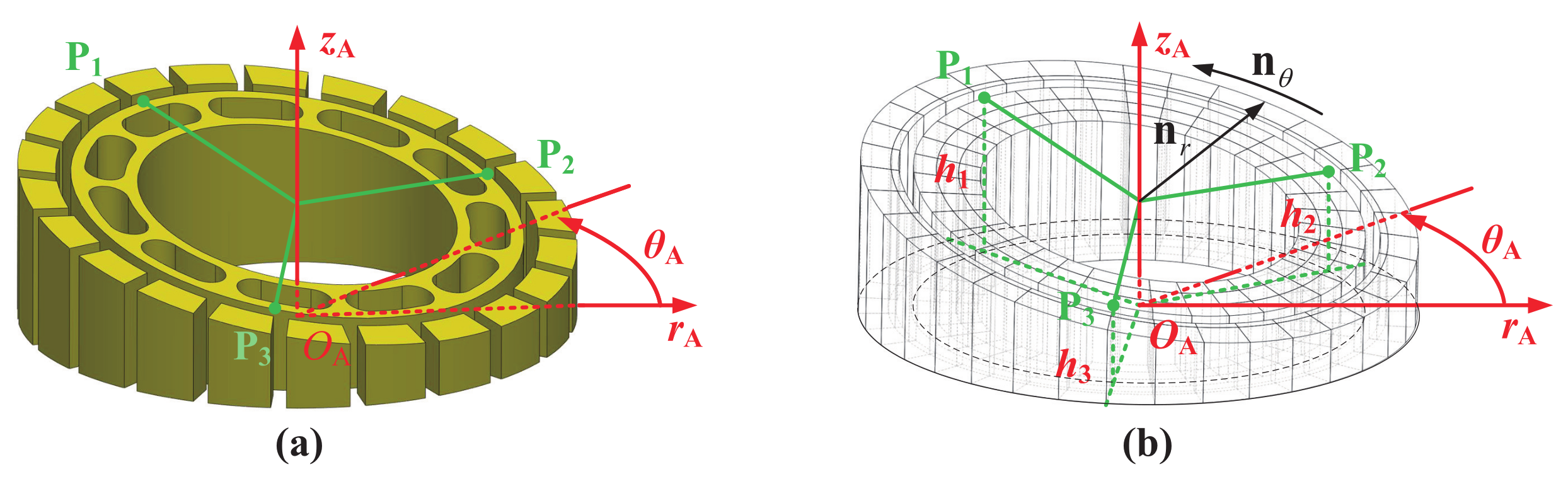
3.2. Viscous Wedge Geometric Model
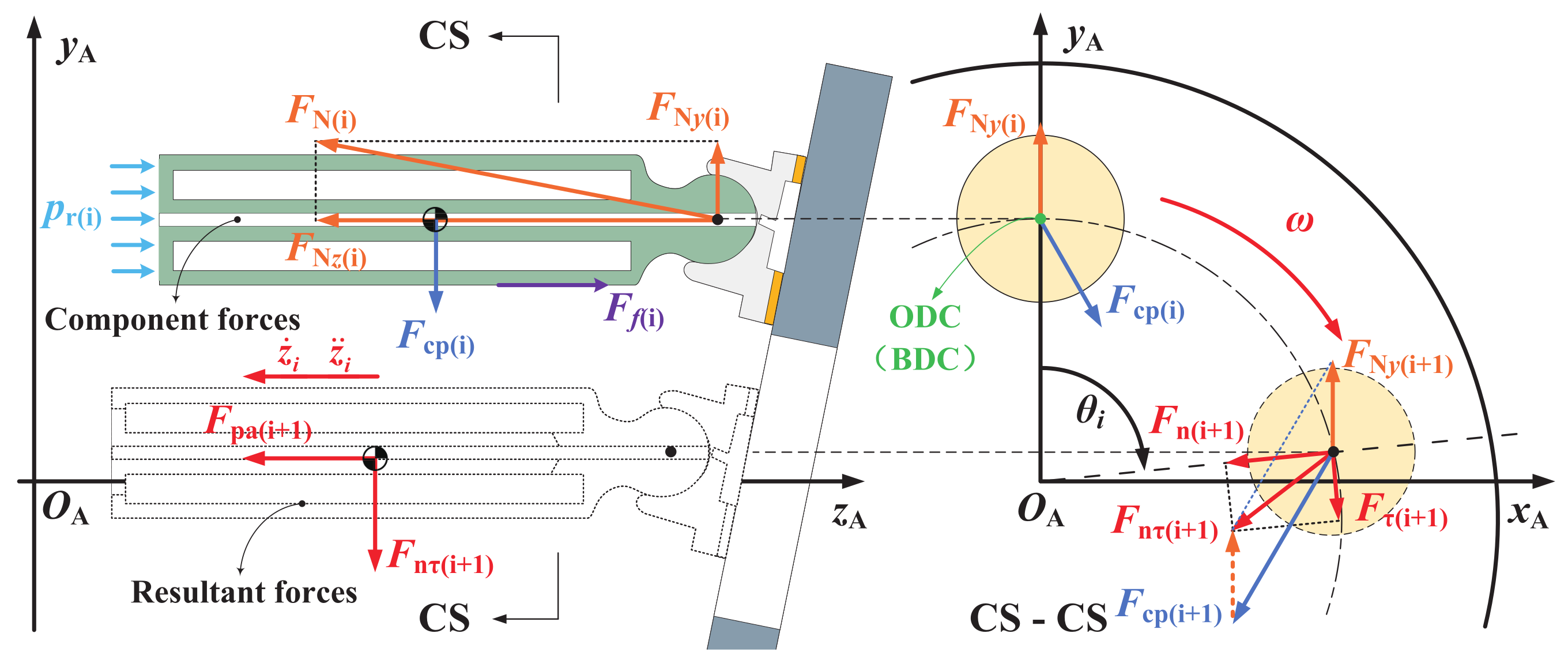
3.3. Multi-Body Dynamics Model
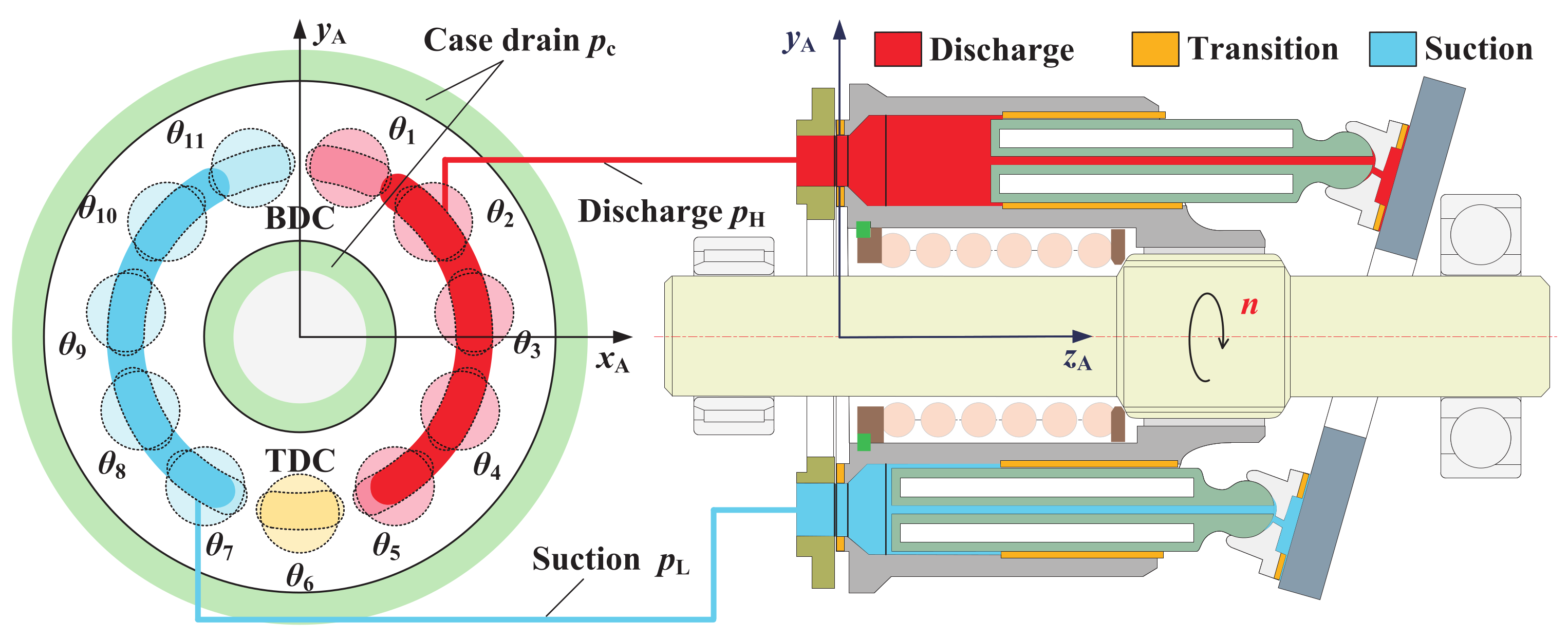
3.4. Non-Isothermal Full Oil Film Fluid Model
4. Simulation Results and Analysis
4.1. Simulation Setup
4.1.1. Mesh Independence Test
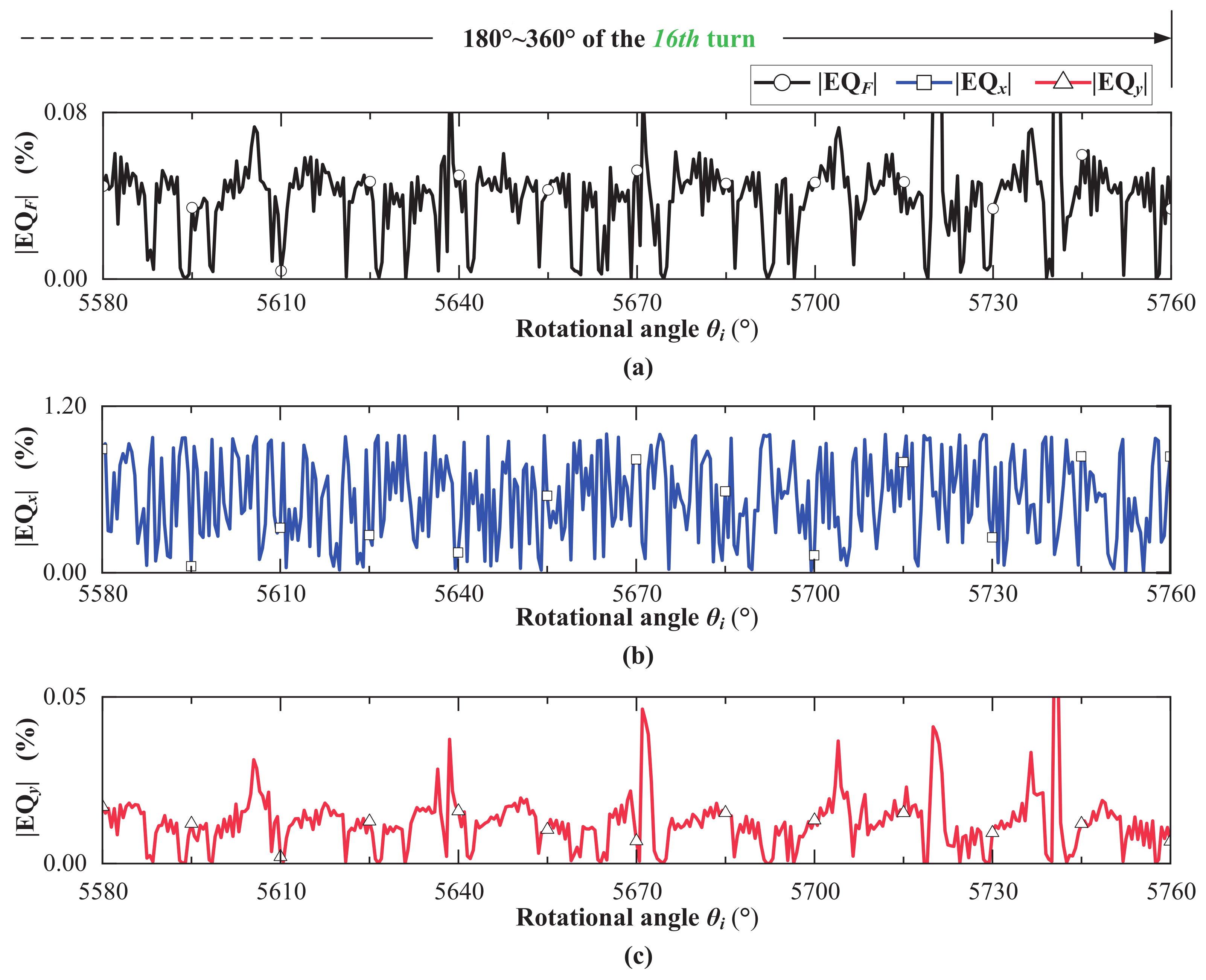
4.1.2. Oil Film Force Balance Error Analysis
4.2. Simulation Design
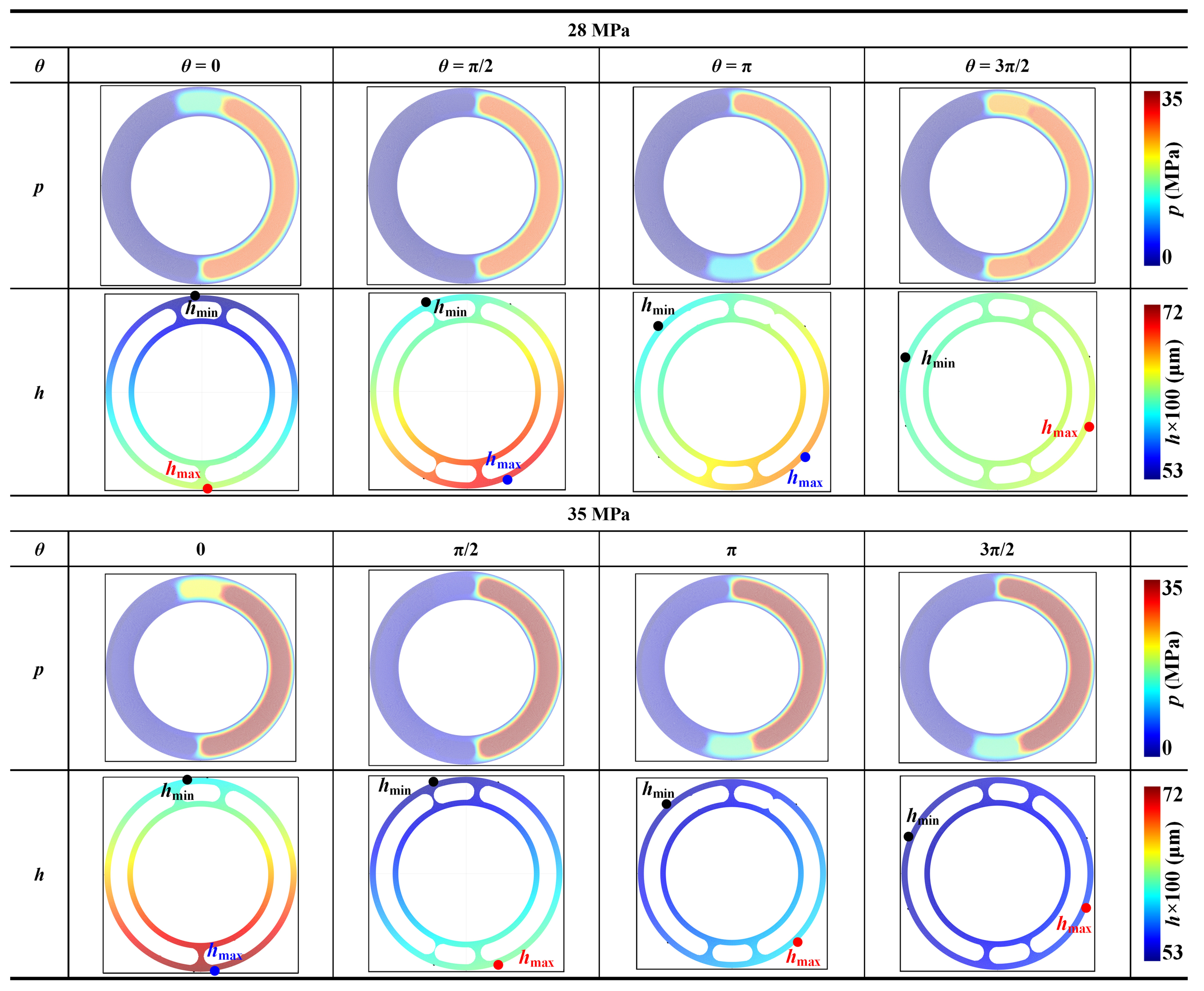
4.3. Oil Film Pressure and Thickness
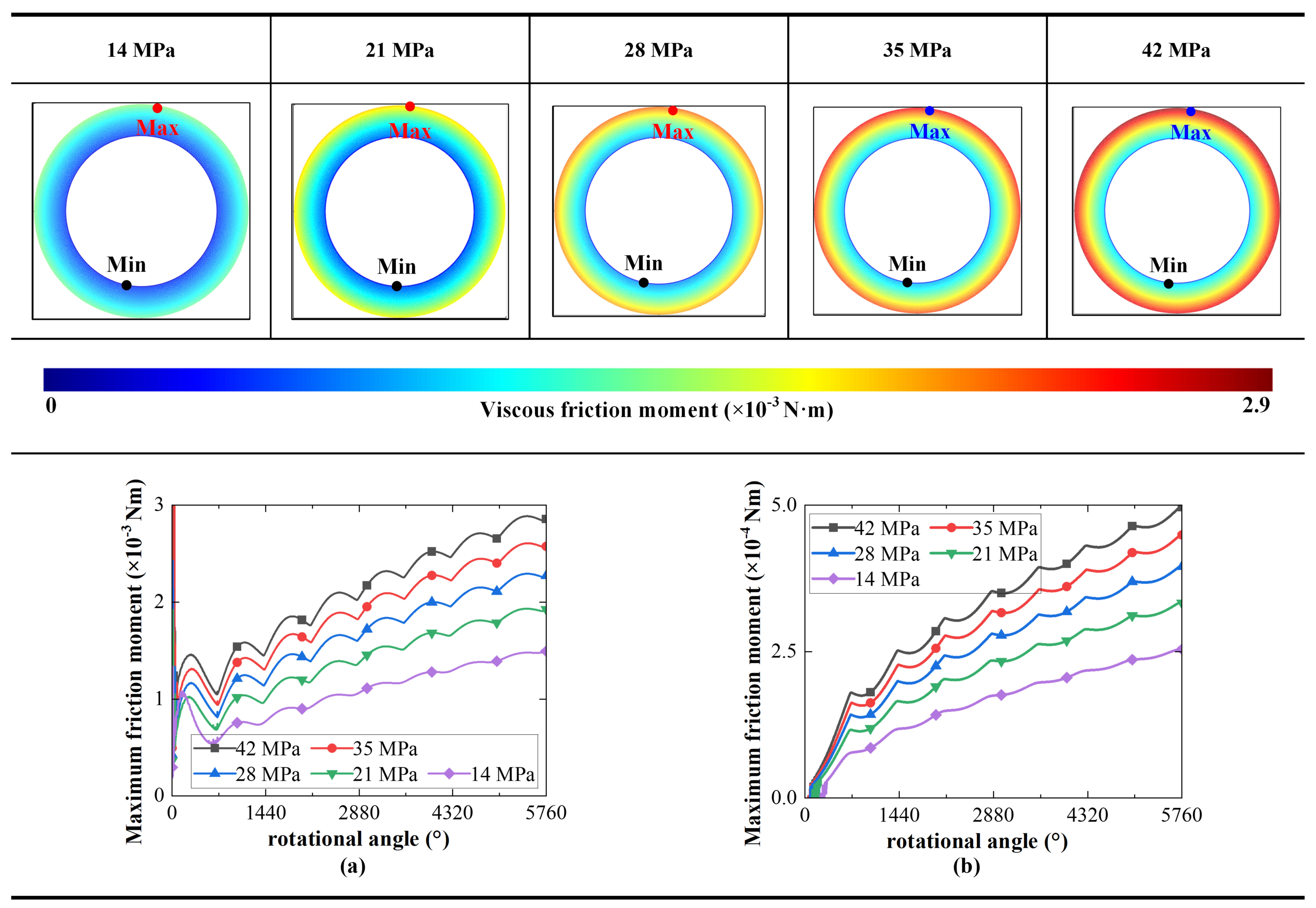
4.4. Lubricating Characteristics
4.5. Sealing Characteristics
4.6. Load-Bearing Characteristics
4.7. Overturning Characteristics
4.8. Discussions
- (1)
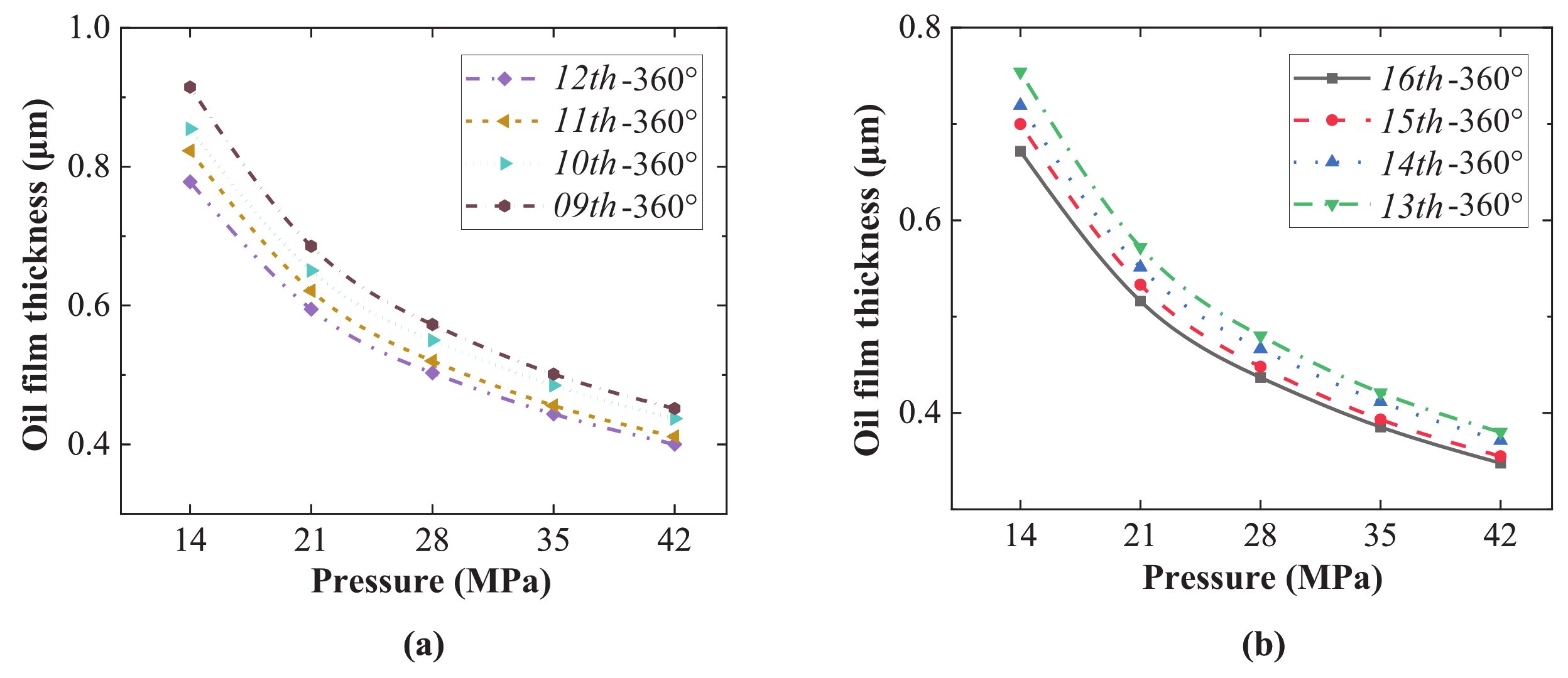
- Figure 16 and Figure 17 show that at 35 MPa, the viscous friction moment of the outer sealing belt increases significantly and the lubricating characteristic decreases. The reason is that increased pressure increases the viscosity and cylinder block overturning force while reducing the oil film thickness and load-bearing area. In terms of structure, this paper proposes to increase the load-bearing area of the oil film by adding auxiliary support belts. In terms of operating conditions, this paper proposes to reduce the cylinder block overturning force by reducing the rotational speed and the viscosity by increasing the temperature. The above suggestions can optimize the lubrication state of the cylinder block/valve plate interface, reduce its viscous friction moment, and ease its wear. After adopting these suggestions, the edge wear of the valve plate will be significantly reduced at 35 MPa.
- (2)
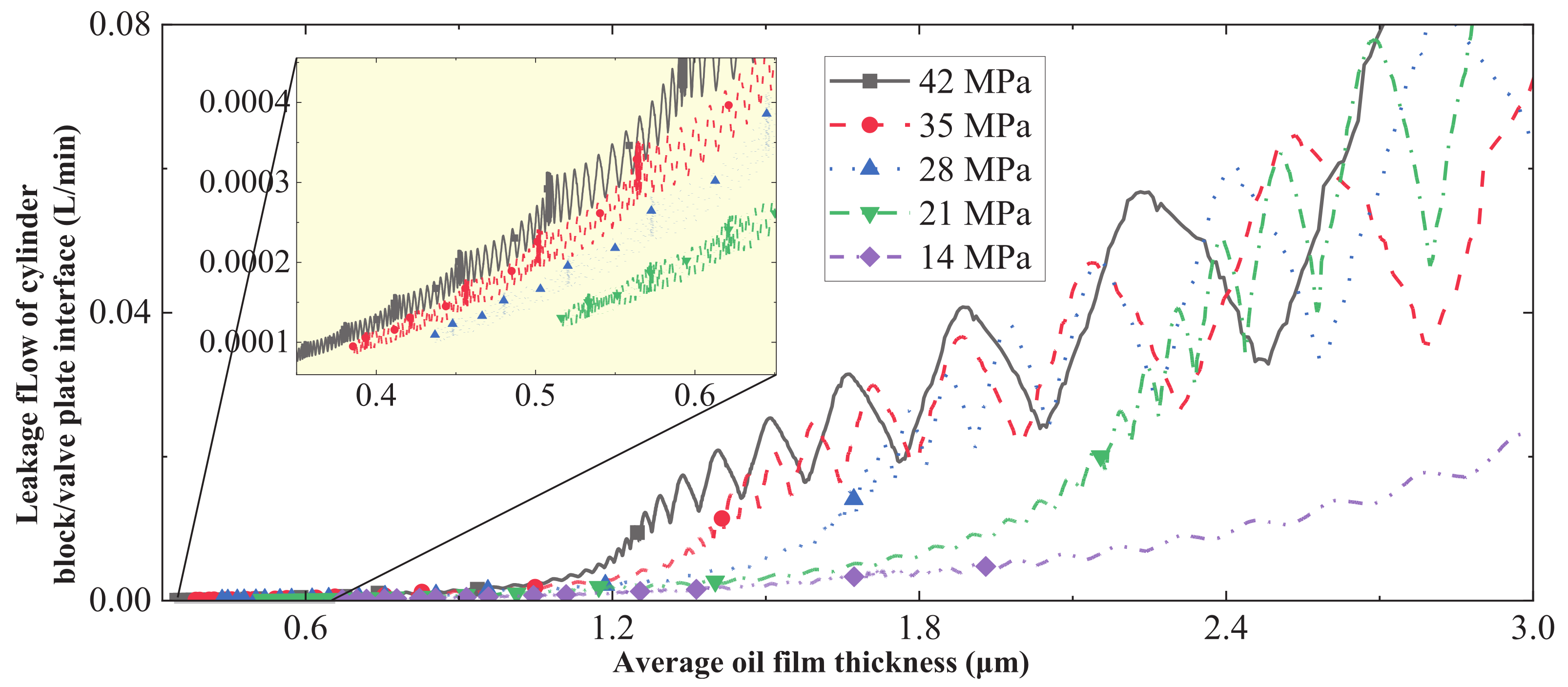
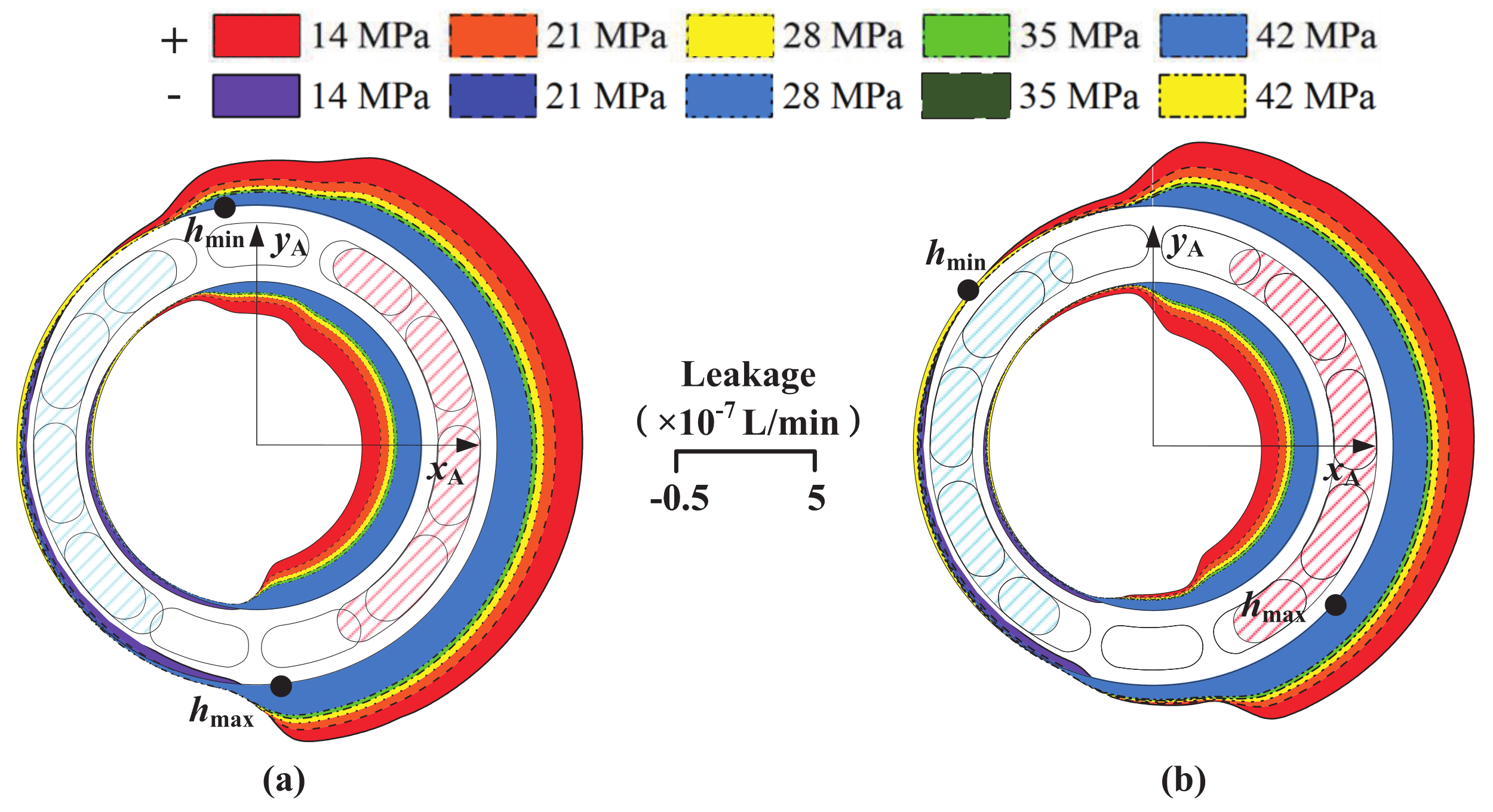
- Figure 18, Figure 19 and Figure 20 show that at 35 MPa, the leakage of the cylinder block/valve plate interface increases significantly and the sealing characteristic decreases. The reason is that an increase in pressure increases the pressure difference between the oil-suction and -discharge kidney grooves and the case. In terms of structure, this paper proposes to appropriately increase the pre-compression length and stiffness of the cylinder block spring to increase the residual compression coefficient of the cylinder block/valve plate interface, thereby reducing the oil film thickness and leakage. After adopting these suggestions, the leakage of the cylinder block/valve plate interface will be reduced at 35 MPa.
- (3)
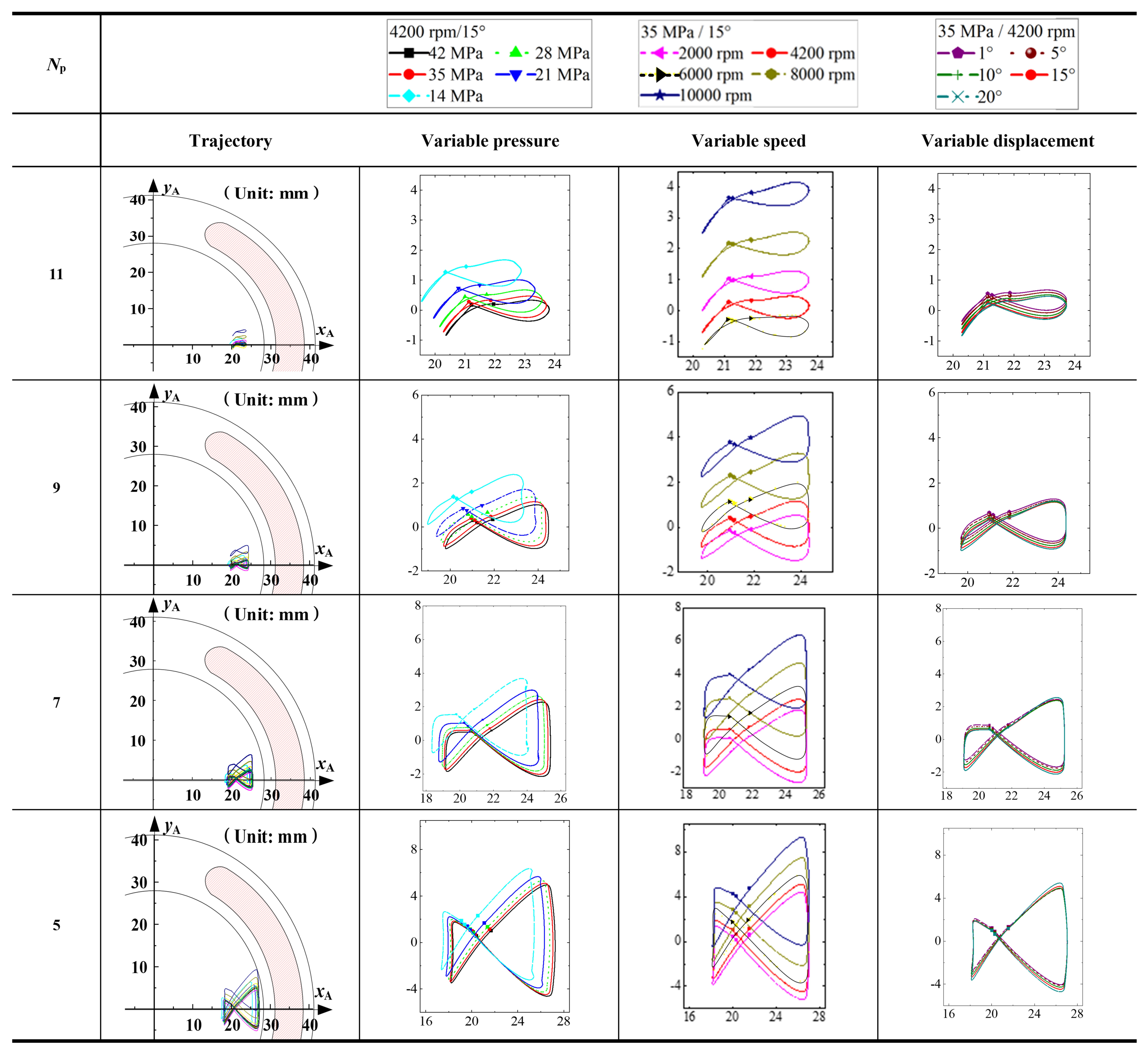
- Figure 22 shows that at 35 MPa, the oil film thickness of the cylinder block/valve plate interface is significantly reduced, the anti-overturning force action point trajectory moves outward, and the load-bearing characteristic is greatly reduced. The reason is that the pressure increase will weaken the oil film hydrodynamic effect and increase the cylinder block overturning force. In terms of structure, an 11-piston layout is proposed in this paper to reduce the overturning force trajectory envelope of the cylinder block. In terms of operating conditions, this paper proposes to reduce the rotational speed and the swash plate inclination angle at zero displacement, which can enhance the hydrodynamic effect and load-bearing characteristic of the oil film while reducing the overturning force of the cylinder block. After adopting these suggestions, the anti-overturning force and load-bearing capacity of the cylinder block/valve plate interface will be increased at 35 MPa.
- (4)
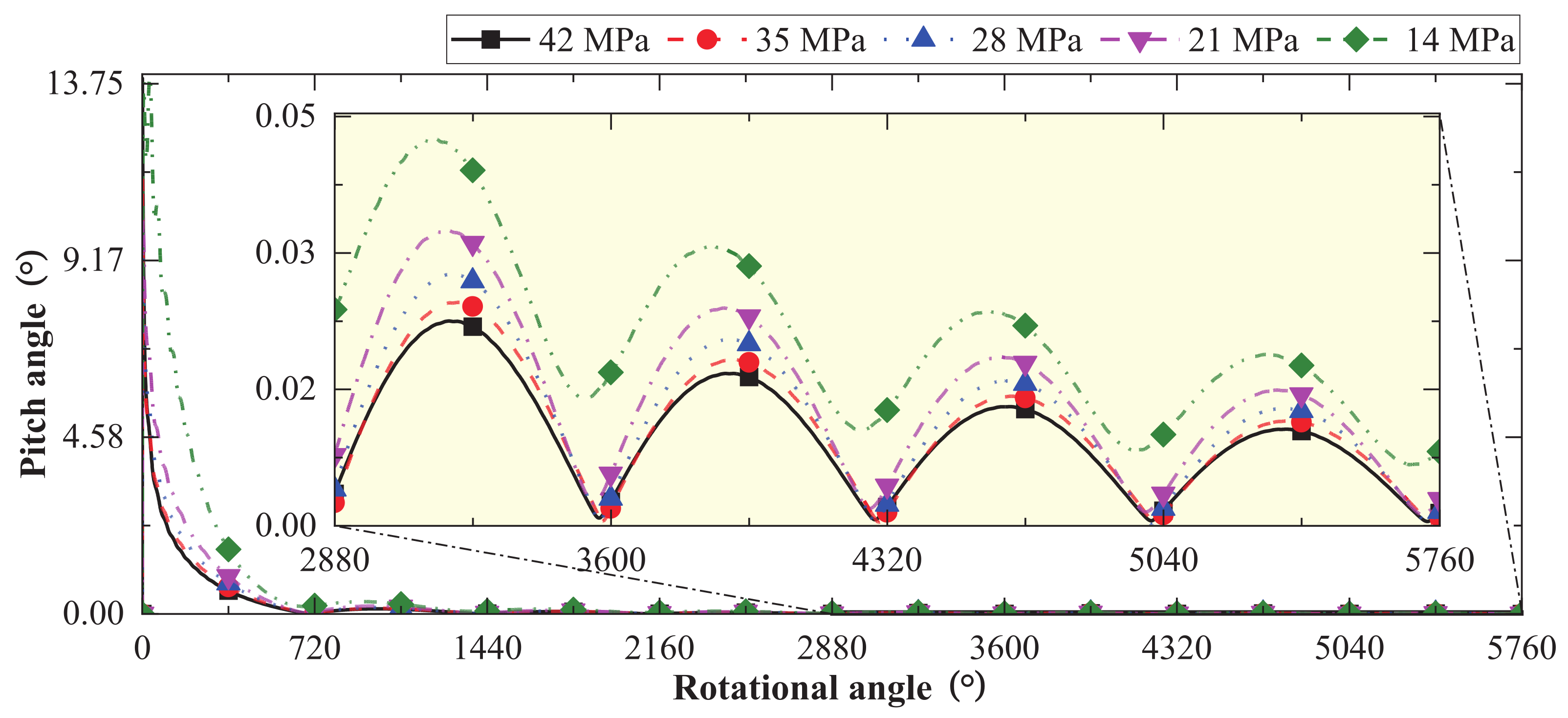
- Figure 23 and Figure 24 show that at 35 MPa, the pitch angle and azimuth angle of the cylinder block both show severe periodic changes, resulting in easy edge collision and wear with the valve plate. The reason is that the pressure increase will aggravate the overturning behavior of the cylinder block in the axial and circumferential directions. In terms of structure, this paper proposes to adopt an external support cylinder configuration (that is, to add an extra bearing between the cylinder block and the case) to fix the cylinder circumferentially and optimize the force-bearing form of the drive shaft. This method can fundamentally eliminate the risk of collision between the cylinder block and the valve plate. After adopting these suggestions, the cylinder block will not overturn at 35 MPa.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| APP | Aviation Piston Pump |
| CFD | Computational Fluid Dynamics |
| MTBF | Mean Time Between Failure |
| CTDMA | Cyclic Tridiagonal Matrix Algorithm |
| TDMA | Tridiagonal Matrix Algorithm |
| ODC | Outer Dead Center |
| BDC | Bottom Dead Center |
| IDC | Inner Dead Center |
| TDC | Top Dead Center |
| Nomenclature | |
| Effective action area of a single piston (m) | |
| Axial force error of the oil film (N) | |
| Moment error in the direction of the axis (N·m) | |
| Moment error in the direction of the axis (N·m) | |
| Resultant vector composed of errors in all directions (-) | |
| Allowable error of the oil film force and moment solutions (-) | |
| Allowable error of the oil film pressure solution (-) | |
| , | Distances from the anti-overturning force equivalent to the action point to / axes (m) |
| f | Friction coefficient (-) |
| Reaction force of the cylinder block to the piston (N) | |
| , | Reaction forces of the cylinder block to the piston in the directions of the / axes (N) |
| Friction force of the piston reciprocating motion (N) | |
| , | Inner/outer forces of the piston on the copper bushing of the piston bore (N) |
| Reaction force of the swash plate to the slipper (N) | |
| Resultant force of the circumferential and radial resultant forces on the piston-slipper assembly (N) | |
| , | Outer forces of the piston on the copper bushing of the piston bore in the directions of the / axes (N) |
| , , and | Axial/circumferential/radial resultant forces on the piston-slipper assembly (N) |
| , | Force/moment of the drive shaft on the cylinder block (N)/(N·m) |
| , | Forces of the drive shaft on the cylinder block in the directions of the / axes (N) |
| Preload force of the cylinder block spring (N) | |
| Overturning force on the cylinder block (N) | |
| Anti-overturning force (N) | |
| h | Thickness of the oil film mesh (m) |
| , | Minimum/maximum oil film thicknesses (m) |
| Oil film thickness at the valve plate center (m) | |
| , , and | Oil film thicknesses at points , , and (m) |
| k | Number of iterations (-) |
| , | Effective lengths of the piston inside/outside the piston bore (m) |
| Position of the spline (m) | |
| , | Distances from the overturning force equivalent action point to the / axes (m) |
| Position of the swash plate (m) | |
| , | Overturning moments on the cylinder block in the directions of the / axes (N·m) |
| , | Anti-overturning moments in the direction of / (N·m) |
| Mass of the piston (kg) | |
| Mass of the slipper (kg) | |
| n | Rotational speed (rev/min) |
| Number of pistons (-) | |
| , | Number of meshes in the circumferential/radial directions of the oil film (-) |
| p | Pressure of the oil film mesh (Pa) |
| , , | Discharge/suction/drain pressure (Pa) |
| Transient pressure in the piston chamber (Pa) | |
| , | Leakages of inner/outer sealing belt (L/min) |
| r | Radius of the oil film mesh (m) |
| Radius of the piston (m) | |
| Piston pitch radius (m) | |
| , | Inner/outer radii of the inner sealing belt (m) |
| , | Inner/outer radii of the outer sealing belt (m) |
| , | Inner/outer radii of the auxiliary support belt (m) |
| t | Time (s) |
| V | Piston chamber volume (m) |
| , | Radial/circumferential linear velocities (m/s) |
| , , and | Center point displacements of the piston ball hinge in the direction of // (m) |
| z | Coordinate of the oil film in the direction of the axis (m) |
| , | Piston velocity/acceleration in the direction of the axis (m/s)/(m/s) |
| Pitch angle (rad) | |
| Maximum angle of the swash plate () | |
| Circumferential azimuth of the oil film mesh (rad) | |
| Angular velocity (rad/s) | |
| Dynamic viscosity of the oil (Pa·s) | |
| Fluid density (kg/m) | |
| Azimuth angle (rad) | |
| , | Radial length/circumferential radian of the oil film mesh (m) |
| Phase angle of the ith piston (rad) | |
| Number of meshes in the oil film region (-) |
References
- Moir, I.; Seabridge, A. Aircraft Systems: Mechanical, Electrical, and Avionics Subsystems Integration, 3rd ed.; Wiley: Chichester, UK, 2008. [Google Scholar]
- Li, L.; Lee, K.; Ouyang, X.; Yang, H. Analytical harmonic method for modeling high-frequency oscillation with applications to aircraft piston pump vibration analysis. IEEE/ASME Trans. Mechatron. 2021, 26, 918–929. [Google Scholar] [CrossRef]
- Chao, Q.; Zhang, J.; Xu, B.; Huang, H.; Pan, M. A review of high-speed electro-hydrostatic actuator pumps in aerospace applications: Challenges and solutions. J. Mech. Des. 2019, 141, 050801. [Google Scholar] [CrossRef]
- Guo, S.; Chen, J.; Lu, Y.; Wang, Y.; Dong, H. Hydraulic piston pump in civil aircraft: Current status, future directions and critical technologies. Chin. J. Aeronaut. 2020, 33, 16–30. [Google Scholar] [CrossRef]
- Collin, P.; Malec, D.; Lefevre, Y. A general method to compute the electric flux lines between two magnet wires in close contact and its application for the evaluation of partial discharge risks in the slots of electric machines embedded in future transportation systems. Adv. Aerosp. Sci. Technol. 2021, 6, 24–42. [Google Scholar] [CrossRef]
- Zhao, J.; Fu, Y.; Ma, J.; Fu, J.; Chao, Q.; Wang, Y. Review of cylinder block/valve plate interface in axial piston pumps: Theoretical models, experimental investigations, and optimal design. Chin. J. Aeronaut. 2021, 34, 111–134. [Google Scholar] [CrossRef]
- Chao, Q. Derivation of the Reynolds equation in cylindrical coordinates applicable to the slipper/swash plate interface in axial piston pumps. Proc. Inst. Mech. Eng. Part J.-J. Eng. Tribol. 2021, 235, 798–807. [Google Scholar] [CrossRef]
- Zhao, J.; Fu, Y.; Wang, M.; Fu, J.; Chao, Q.; Wang, S.; Deng, M. Experimental research on tribological characteristics of TiAlN coated valve plate in electro-hydrostatic actuator pumps. Tribol. Int. 2021, 155, 106782. [Google Scholar] [CrossRef]
- Zhang, J.; Lyu, F.; Xu, B.; Huang, W.; Wu, W.; Guo, Z.; Xu, H.; Huang, X. Simulation and experimental investigation on low wear rate surface contour of piston/cylinder pair in an axial piston pump. Tribol. Int. 2021, 162, 107127. [Google Scholar] [CrossRef]
- Fagg, A. Fluid film lubrication of parallel thrust surfaces. Proc. Inst. Mech. Eng. 1946, 155, 49–67. [Google Scholar] [CrossRef]
- Mckeown, J.; Milner, D.; Shute, N.; Turnbull, D. Hydrodynamic factors affecting the design of valve plates and thrust bearings. Proc. Inst. Mech. Eng. 1966, 181, 653–666. [Google Scholar] [CrossRef]
- Manring, N. Tipping the cylinder block of an axial-piston swash-plate type hydrostatic machine. J. Dyn. Sys., Meas. Control 2000, 122, 216–221. [Google Scholar] [CrossRef]
- Yamaguchi, A. Formation of a fluid film between a valve plate and a cylinder block of piston pumps and motors: 1st report, a valve plate with hydrodynamic pads. Bull. JSME 1986, 29, 1494–1498. [Google Scholar] [CrossRef]
- Yamaguchi, A.; Sekine, H. Formation of a fluid film between a valve plate and a cylinder block of piston pumps and motors: 3rd report, fluid film sluctuation and loss power. Trans. Jpn. Soc. Mech. Eng. Part B 1989, 55, 427–433. [Google Scholar] [CrossRef]
- Bergada, J.; Watton, J.; Kumar, S. Pressure, flow, force, and torque between the barrel and port plate in an axial piston pump. J. Dyn. Syst. Meas. Control 2008, 130, 011011. [Google Scholar] [CrossRef]
- Wieczorek, U.; Ivantysynova, M. Computer aided optimization of bearing and sealing gaps in hydrostatic machines—The simulation tool CASPAR. Int. J. Fluid Power 2002, 3, 7–20. [Google Scholar] [CrossRef]
- Wang, Z.; Hu, S.; Ji, H.; Wang, Z.; Liu, X. Analysis of lubricating characteristics of valve plate pair of a piston pump. Tribol. Int. 2018, 126, 49–64. [Google Scholar] [CrossRef]
- Jiang, J.; Yan, W.; Li, G. Analysis on micro-motion of cylinder block based on elasto-hydrodynamic lubrication. Ind. Lubr. Tribol. 2019, 72, 645–650. [Google Scholar] [CrossRef]
- Ivantysynova, M.; Huang, C. Investigation of the gap flow in displacement machines considering elastohydrodynamic effect. Proc. JFPS Int. Symp. Fluid Power 2002, 2002, 219–229. [Google Scholar] [CrossRef]
- Ivantysynova, M.; Baker, J. Power Losses in the Lubricating Gap Between Cylinder Block and Valve Plate of Swash Plate Type Axial Piston Machines. Int. J. Fluid Power 2009, 10, 29–43. [Google Scholar] [CrossRef]
- Huang, C.; Ivantysynova, M. A new approach to predict the load carrying ability of the gap between valve plate and cylinder block. In Proceedings of the Bath Workshop of Power Transmission and Motion Control, Bath, UK, 24 September 2003. [Google Scholar]
- Lv, Q.; Wang, D.; E, S.; Chen, H.; Hu, B. Study on the effects of the textured surface to improve the performance of cylinder block/valve plate interfaces. AIP Adv. 2019, 9, 45128. [Google Scholar] [CrossRef]
- Wang, Z.; Hu, S.; Zhang, H.; Ji, H.; Yang, J.; Liang, W. Effect of surface texturing parameters on the lubrication characteristics of an axial piston pump valve plate. Lubricants 2018, 6, 49. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, J.; Xu, B.; Chao, Q.; Liu, G. Multi-objective optimization of micron-scale surface textures for the cylinder/valve plate interface in axial piston pumps. Tribol. Int. 2019, 138, 316–329. [Google Scholar] [CrossRef]
- Li, Y.; Ji, Z.; Yang, L.; Zhang, P.; Xu, B.; Zhang, J. Thermal-fluid-structure coupling analysis for valve plate friction pair of axial piston pump in electro-hydrostatic actuator(EHA) of aircraft. Appl. Math. Model. 2017, 47, 839–858. [Google Scholar] [CrossRef]
- Ivantysyn, R.; Shorbagy, A.; Weber, J. Analysis of the Run-in Behavior of Axial Piston Pumps. In Proceedings of the Global Fluid Power Society PhD Symposium, Samara, Russia, 18–20 July 2018. [Google Scholar]
- Chacon, R.; Ivantysynova, M. Thermal effects on the fluid film in the cylinder block/valve plate interface due to compression and expansion of the fluid. JFPS Int. J. Fluid Power Syst. 2019, 11, 136–142. [Google Scholar] [CrossRef]
- Wang, S.; Tomovic, M.; Liu, H. Commercial Aircraft Hydraulic Systems: Shanghai Jiao Tong University Press Aerospace Series, 1st ed.; Elsevier: Waltham, MA, USA, 2015. [Google Scholar]
- Sharoni, A.; Etsion, I. Performance of end-face seals with diametral tilt and coning-hydrodynamic effects. ASLE Trans. 1981, 24, 61–70. [Google Scholar] [CrossRef]
- Kelkar, K.; Choudhury, D.; Minkowycz, W. Numerical method for the computation of flow in irregular domains that exhibit geometric periodicity using nonstaggered grids. Numer. Heat Transf. Part B 1997, 31, 1–21. [Google Scholar] [CrossRef]
- Aziz, K.; Settari, A. Petroleum Reservoir Simulation, 1st ed.; Applied Science Publishers: London, UK, 1979. [Google Scholar]
- Zecchi, M. A Novel Fluid Structure Interaction and Thermal Model to Predict the Cylinder Block/Valve Plate Interface Performance in Swash Plate Type Axial Piston Machines. Ph.D. Thesis, Purdue University, West Lafayette, IN, USA, November 2013. [Google Scholar]
- Richardson, D. Hydrodynamic Lubrication of Floating Valve Plate in An Axial Piston Pump. Ph.D. Thesis, Purdue University, West Lafayette, IN, USA, May 2019. [Google Scholar]
- Zhao, J.; Fu, J.; Li, Y.; Qi, H.; Wang, Y.; Fu, Y. Flow characteristics of integrated motor-pump assembly with phosphate ester medium for aerospace electro-hydrostatic actuators. Chin. J. Aeronaut 2022, in press. [Google Scholar] [CrossRef]
- Huang, X.; Xu, B.; Huang, W.; Xu, H.; Lyu, F.; Su, Q. Active pressure ripple reduction of a self-supplied variable displacement pump with notch least mean square filter. Micromachines 2021, 12, 932. [Google Scholar] [CrossRef]
- Dong, H.; He, Y.; Wang, Y.; Kou, G. Numerical investigation of effect of a centrifugal boost impeller on suction performance of an aircraft hydraulic pump. Chin. J. Aeronaut. 2022, 35, 236–248. [Google Scholar] [CrossRef]
- Zhang, B.; Zhao, C.; Hong, H.; Cheng, G.; Yang, H.; Feng, S.; Zhai, J.; Xiao, W. Optimization of the outlet unloading structure to prevent gaseous cavitation in a high-pressure axial piston pump. Proc. Inst. Mech. Eng. Part C J. Eng. Mech. Eng. Sci. 2022, 236, 3459–3473. [Google Scholar] [CrossRef]
- Xia, S.; Xia, Y.; Xiang, J.; Kou, G. Modeling and fault detection for specific cavitation damage based on the discharge pressure of axial piston pumps. Mathematics 2022, 10, 2461. [Google Scholar] [CrossRef]
- Chao, Q.; Wei, X.; Lei, J.; Tao, J.; Liu, C. Improving accuracy of cavitation severity recognition in axial piston pumps by denoising time–frequency images. Meas. Sci. Technol. 2022, 33, 055116. [Google Scholar] [CrossRef]
- Chao, Q.; Xu, Z.; Tao, J.; Liu, C. Capped piston: A promising design to reduce compressibility effects, pressure ripple and cavitation for high-speed and high-pressure axial piston pumps. Alex. Eng. J. 2023, 62, 509–521. [Google Scholar] [CrossRef]
- A Descriptive Summary of Vickers Inline Pumps and Their Applications. Available online: https://1library.net/document/zlvdm5oy-descriptive-summary-vickers-inline-pumps-applications.html (accessed on 4 December 2022).







| Parameters | Symbols | Values |
|---|---|---|
| Discharge pressure (MPa) | 28/35 | |
| Drain pressure (MPa) | 0.7 | |
| Suction pressure (MPa) | 0.35 | |
| Maximum angle of swash plate () | 15 | |
| Rotational speed (rpm) | n | 4200 |
| Dynamic viscosity of the oil (Pa·s) | 0.0116 | |
| Fluid density (kg/m) | 840 | |
| Piston number (-) | 11 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, T.; Fang, J.; Liu, H.; Chen, L.; Ouyang, X.; Guo, S.; Zhao, X.; Lu, Y. Modeling and Characteristic Analysis of a Cylinder Block/Valve Plate Interface Oil Film Model for 35 MPa Aviation Piston Pumps. Machines 2022, 10, 1196. https://doi.org/10.3390/machines10121196
Wang T, Fang J, Liu H, Chen L, Ouyang X, Guo S, Zhao X, Lu Y. Modeling and Characteristic Analysis of a Cylinder Block/Valve Plate Interface Oil Film Model for 35 MPa Aviation Piston Pumps. Machines. 2022; 10(12):1196. https://doi.org/10.3390/machines10121196
Chicago/Turabian StyleWang, Tianzhao, Jingjing Fang, Hao Liu, Lijun Chen, Xiaoping Ouyang, Shengrong Guo, Xiaojun Zhao, and Yijie Lu. 2022. "Modeling and Characteristic Analysis of a Cylinder Block/Valve Plate Interface Oil Film Model for 35 MPa Aviation Piston Pumps" Machines 10, no. 12: 1196. https://doi.org/10.3390/machines10121196
APA StyleWang, T., Fang, J., Liu, H., Chen, L., Ouyang, X., Guo, S., Zhao, X., & Lu, Y. (2022). Modeling and Characteristic Analysis of a Cylinder Block/Valve Plate Interface Oil Film Model for 35 MPa Aviation Piston Pumps. Machines, 10(12), 1196. https://doi.org/10.3390/machines10121196







