A New Manufacturing Methodology under Limited Machining Capabilities and Application to High-Performance Hemispherical Resonator

Abstract

High-performance component production requires nearly homogeneous materials, ultra-precise machining and a high surface integrity. However, conventional design and manufacturing methodologies, which continuously increase the geometric tolerance to meet the performance requirements, lead to cost increases that even exceed the existing machining capabilities. This paper presents a general manufacturing methodology for high-performance components under realistic conditions, such as the current capability for material forming and machining. In order to achieve an excellent component performance, this methodology includes parameter extraction, sensitivity analysis, and trimming processes that consider the effect of material removal resolution and processing uncertainties. Simulations performed on the hemispherical resonator demonstrate how the proposed methodology is applied to fabricate extremely high-performance resonators. An efficient modal tuning strategy is proposed based on a sensitivity analysis of the tuning process parameters subject to material removal resolution and uncertainties. The tuning results prove the feasibility of this new methodology for high-performance components manufacturing. The elimination of the frequency split can finally be achieved with surface tuning iteratively. The proposed methodology provides an effective solution to achieve high-performance components under limited machining capabilities.

1. Introduction

Modern life is inseparable from manufacturing. Nowadays, critical components are manufactured at a high level of precision [1]. With increasingly stricter dimensional tolerances on high-performance components, these precision techniques have become increasingly popular in attaining the expected performance of production [2,3]. The product performance should be satisfactory after its careful assembly if the geometric dimensions, tolerances, and surface roughness specified in the drawings are correctly satisfied during the manufacturing processes. In addition, most of the finished components require no additional or trimming processes [4]. In brief, the geometric constraints of the components determined during the design process accurately ensure the expected performance of the products through this geometric-oriented manufacturing.

As manufacturing improves, more and more industries are placing higher demands on product performance. These demands, in turn, have led to higher standards for the critical components of such products. For example, the hemispherical resonator gyroscope (HRG) is one of the most precise gyroscopes that is available today. Hemispherical resonators, the core component of HRG, should be uniform in mass, elasticity, and damping and have a perfect surface shape to reduce the drift error [5]. However, a perfect hemispherical shell cannot be machined. The actual vibration performance is inevitably different from the expected performance. To address this problem, many researchers introduced trimming processes to tune the resonators [6,7,8]. However, the yield is not effectively guaranteed. The reason is that trace materials in a specific area must be removed during the tuning process, but there are uncontrollable errors in all of the processing removal methods. A gyroscope with an extremely high performance is sensitive to the manufacturing tolerance. Thus, a near-perfect hemispherical shell requires an increasing level of processing accuracy, but this causes an extensive loss of time and economic costs that limit the use of these products.

Dongming Guo, a co-author of this paper, proposed a basic methodology of high-performance components a decade ago and successfully implemented it in manufacturing processes [9,10,11,12]. This methodology has three stages: (1) the conceptual design and optimization of the expected performance without considering manufacturing process constraints; (2) the component design considering the material and machining processes capabilities; (3) the performance-oriented manufacturing considering the uncertainties using the mechanical trimming process. The first stage is relatively straightforward. However, in the second component design stage, the design of the previous step must be appropriately adapted to the available machine tools. Therefore, the expected performance of the component must also be adjusted accordingly. At the same time, the manufacturing tolerances of the component must be carefully designed and assigned in this step. Klocke et al. gave a weighted form of tolerance assignment based on the product performance [13]. This method is essential for high-performance component manufacture because high-performance products are more sensitive to the manufacturing tolerances. Therefore, many researchers have developed processing models such as metal cutting (machining) processes [14] and surface modification [15,16] to ensure that the final performance of the components is accurately achieved. However, processing modeling is time-consuming and has the problem of not being accurate, which limits its mass production and application [17,18]. Consequently, performance-oriented manufacturing is essential for products with high-performance requirements.

In order to achieve accurate performance, the uncertainty of the process parameters and the trimming process need to be taken into consideration. In exploring the processing uncertainties, Morse et al. revisited the uncertainty management methodology from the conceptual design to the final product for controlling the component tolerances to ensure the products’ functionality [19]. The uncertainty and geometric specification are described in a mathematical model. However, there is no correlation between the product performance and the processing uncertainties. The product performance is dependent on processing uncertainty, and it is difficult to control precisely, which means that it remains unresolved. Particularly for the components that fulfill their function but do not perform as well as they should, the trimming process can provide the necessary enhancement.

This paper establishes a mathematical model for manufacturing high-performance components using available machine tools. This methodology introduces the sensitivity analysis of the process parameters which considers the processing uncertainties and is implemented on the modal tuning of hemispherical resonators. It will be possible to achieve the expected performance of the components using the parameter extraction, sensitivity analysis and trimming processes that consider the material removal resolution and the processing uncertainties innovatively. The proposed methodology resolves the contradiction between a limited manufacturing capability and stringent requirements for controlling the performance deviations.

2. Manufacturing Methodology of High-Performance Components

Engineers have been exploring the manufacturing of high-performance parts under limited machining capabilities. When it comes to mechanical watches, the hairspring is the core part of its accuracy performance. Due to limited machining precision, each hairspring and the regulator to which it is attached must be manually adjusted. By testing the rate performance of the watches and empirically adjusting the regulator to change the bending stiffness of the hairspring alternately, the watches finally achieve a reasonable drift error ± 2~60 s per day [20]. These are iterative processes to eventually reach the expected performance through performance testing and trimming processes. The dynamic balance of the shaft systems also uses a similar method since it is extremely costly to manufacture the shaft systems with uniform materials and high machining and assembly accuracy in order to meet the requirements of the shaft systems. Guo [12] refined the above manufacturing methods into a systematic methodology for manufacturing high-performance components.

The performance of such components is affected in complex ways by their geometric dimensions, material properties and machining processes. In order to meet high-performance requirements, these factors must be considered holistically. Mathematically, the actual performance of a component can be described as follows:

$${\Phi }_i=g\left(G,M\right)$$

(1)

where Φ_i is the i-th performance indicator of the specific component, and it is dependent on the geometric dimensions G and the material properties M. The function g is a vector-valued function.

It is noted that the mechanical process changes the geometric dimensions, and the geometric dimensions G in Equation (1) have two parts:

$$G=G_0+G_{\mathrm{d}}\left(P\right)$$

(2)

where G₀ is the expected geometric dimensions during the component design. G_d is the geometric error related to mechanical manufacturing, including the microtopography of the machined surface, so G_d is dependent on the mechanical process parameters P.

Similar to Equation (2), the material property M in Equation (1) can also be described as:

$$M=M_0+M_{\mathrm{d}}\left(P\right)=M_{0\mathrm{C}}+M_{0\mathrm{F}}+M_{\mathrm{d}}\left(P\right)$$

(3)

where M_0C is the expected material properties determined by the component design, independent of manufacturing processes. M_0F is the material property error produced in the material preparation processes, but not in the mechanical manufacturing processes discussed in this paper. M_d is the material property errors induced by mechanical manufacturing, such as surface microstructure, residual stress, and microscopic defects. In general, material forming precedes the mechanical processes. Neither M_0C nor M_0F will change during the mechanical processes. In summary, the G and M are all vectors and vector-valued functions of the mechanical process parameters P in Equation (3). The component performance Φ_i in Equation (4) is dependent on the mechanical process parameters P, and it can be written as:

$${\Phi }_i=g\left(G\left(P\right),M\left(P\right)\right)$$

(4)

On the other hand, the expected performance of the component, <Φ_i>, can be expressed as a function of the expected vector of the geometry dimensions and the material properties:

$$\langle {\Phi }_i\rangle =g\left(G_0,M_{0\mathrm{C}}\right)$$

(5)

During the component design stage, the performance is optimized using Equation (5). However, the actual geometry dimensions G and material properties M inevitably differ from the expected value G₀ and M_0C due to mechanical manufacturing uncertainties. Therefore, the actual performance Φ_i must differ from the expected performance <Φ_i>. The performance deviation ΔΦ_i is dependent on the mechanical process parameters P:

$$\mathsf{\Delta }{\Phi }_i\left(P\right)={\Phi }_i-\langle {\Phi }_i\rangle$$

(6)

If we suppose that the effect of the deviation of the geometry dimensions and the material properties on the component performance is negligible or controllable, this results in a slight deviation in the final performance. In this case, the performance is easy to achieve. However, high-performance component performance is sensitive to the deviation of the mechanical process parameters. If the standard deviation σ_X represents the uncertainty or deviation of any physical quantity X, the performance uncertainty of the component σ_Φi is related to the geometric and material uncertainty induced by mechanical manufacturing:

$${\sigma }_{{\Phi }_i}^2=\mathrm{Var}\left[{\Phi }_i\left(P\right)\right]\approx {\left[{\frac{\mathrm{d}{\Phi }_i\left(P\right)}{\mathrm{d}P}|}_{P={\mathsf{\mu }}_P}\right]}^{\mathrm{T}}\Sigma \left(P\right)\left[{\frac{\mathrm{d}{\Phi }_i\left(P\right)}{\mathrm{d}P}|}_{P={\mathsf{\mu }}_P}\right]$$

(7)

where

$$\frac{\mathrm{d}{\Phi }_i\left(P\right)}{\mathrm{d}P}=\frac{\partial {\Phi }_i\left(P\right)}{\partial M}\frac{\mathrm{d}M}{\mathrm{d}P}+\frac{\partial {\Phi }_i\left(P\right)}{\partial G}\frac{\mathrm{d}G}{\mathrm{d}P}\equiv S_i\left(P\right)$$

(8)

is the sensitivity vector. μ_P is the expected vector of mechanical process parameters P. Σ is the covariance matrix of the mechanical process parameters P whose (m, n) element is Cov (P_m, P_n).

Component performance is usually sensitive to processing uncertainties in precision and ultra-precision machining. It is also likely that the component performance will not meet the requirements if the performance deviation is of the same order of magnitude as the processing uncertainties. The ratio of the performance deviations to the expected value can quantify how much the processing uncertainties affect the component’s performance:

$$C{V}_i=\frac{{\sigma }_{{\Phi }_i}}{\langle {\Phi }_i\rangle }$$

(9)

It should have an upper bound of CV_{i max}:

$$C{V}_i<C{V}_i{}_{\hspace{0.17em}\max }$$

(10)

Therefore, in the production of high-performance components, it is necessary to evaluate the performance deviation and confirm the appropriate process parameters that are to be adjusted. By minimizing the performance deviation ΔΦ_i in Equation (6), the corrected vectors in the trimming process ΔG and ΔM of the geometric dimensions G and the material properties M are found. 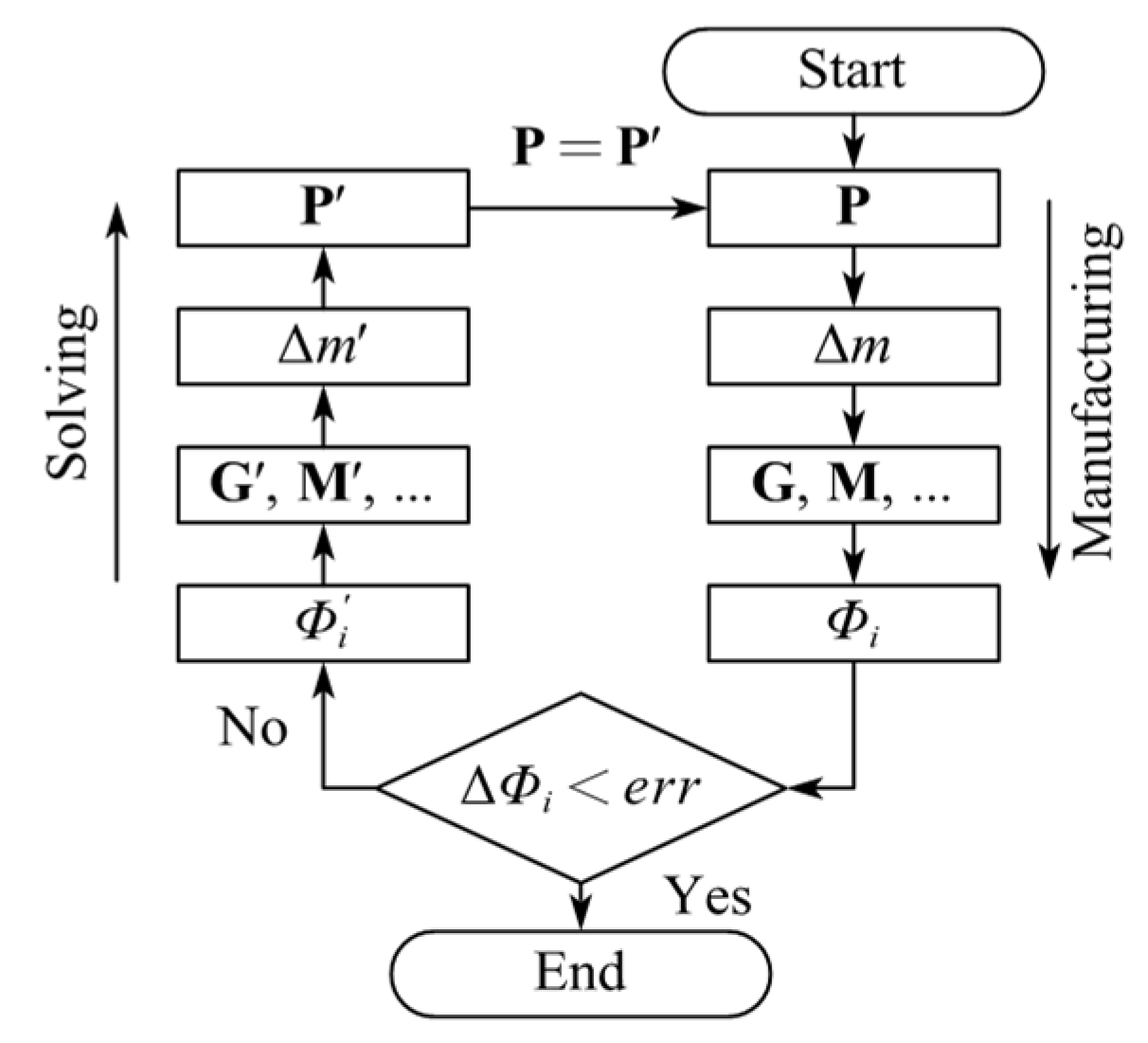After determining the trimming techniques, the trimming process is performed using the process parameters P′ determined by ΔG and ΔM. This procedure is shown in Figure 1.

In general, analyzing the component’s performance based on information about the geometry, material, and manufacturing is a positive problem, and most of these problems are well posed. However, finding the trimming process parameter P’ according to the performance deviation is an inverse problem involving the multi-parameter composite function. Most of the inverse problems are ill posed because too little information is known. The ill-posed problems often have multiple solutions, or the solutions are unstable and easily affected by perturbation. Fortunately, the sensitivity analysis and optimization method is an alternative method that is used to solve this inverse problem. It is also a necessary method to reveal the influence of the processing uncertainties on the performance of the components. The sensitivity S_i of component performance Φ_i to the parameters P of a specific process technique can be expressed as Equation (8).

Two conditions generally constrain the process parameters. One of them is the need to correct the performance deviation quickly. The sensitivity should not be too small in this case. The other is the limitation of the machine tools’ capabilities. Under this condition, the sensitivity should not be too high or exceed the capabilities of the machine tools. Moreover, according to Equations (7), (9) and (10), a high sensitivity will cause drastic changes in the final performance, and these will even deviate from the expected performance with the same processing uncertainty. Therefore, the sensitivity must have the upper and lower bounds of each process parameter P_k.

$$S_i{\left(P_k\right)}_{\min }\le S_i\left(P_k\right)\le S_i{\left(P_k\right)}_{\max }$$

(11)

Finally, the optimization model for the trimming of high-performance components can be expressed in the following form:

$$\begin{array}{l}\min \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\Vert \mathsf{\Delta }{\Phi }_{\mathrm{i}}\left(P\right)\Vert }_2={\left({\Phi }_{\mathrm{i}}-\langle {\Phi }_{\mathrm{i}}\rangle \right)}^2\\ \mathrm{s}.\mathrm{t}.\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\{\begin{array}{l}{S}_i{\left(P_k\right)}_{\min }\le S_i\left(P_k\right)\le S_i{\left(P_k\right)}_{\max }\hfill \\ P_i{}_{\min }\le P_i\le P_i{}_{\max }\hfill \\ C{V}_i<C{V}_{i\max }\hfill \end{array}\end{array}$$

(12)

Since most of the components have multiple performance indicators, finding the optimal process parameters is often a multi-objective optimization problem. Moreover, Equation (5) cannot be written explicitly for many components, so numerical models are commonly used to obtain an accurate performance through multiple iterations.

3. Application to Hemispherical Resonator Modal Tuning

The high-performance hemispherical resonator is one of the most complex high-performance components to be machined. The precession angle of the n = 2 standing wave is used to sensitize the rotation angle of the base. There are no frequency splits in the balanced hemispherical resonators, and the n = 2 flexing mode is double degenerate. The location of this n = 2 standing wave does not change if no angular velocity is inputted. An unbalanced mass on the hemispherical resonators results in symmetric breaking, which leads to the frequency split between two basic flexing modes. 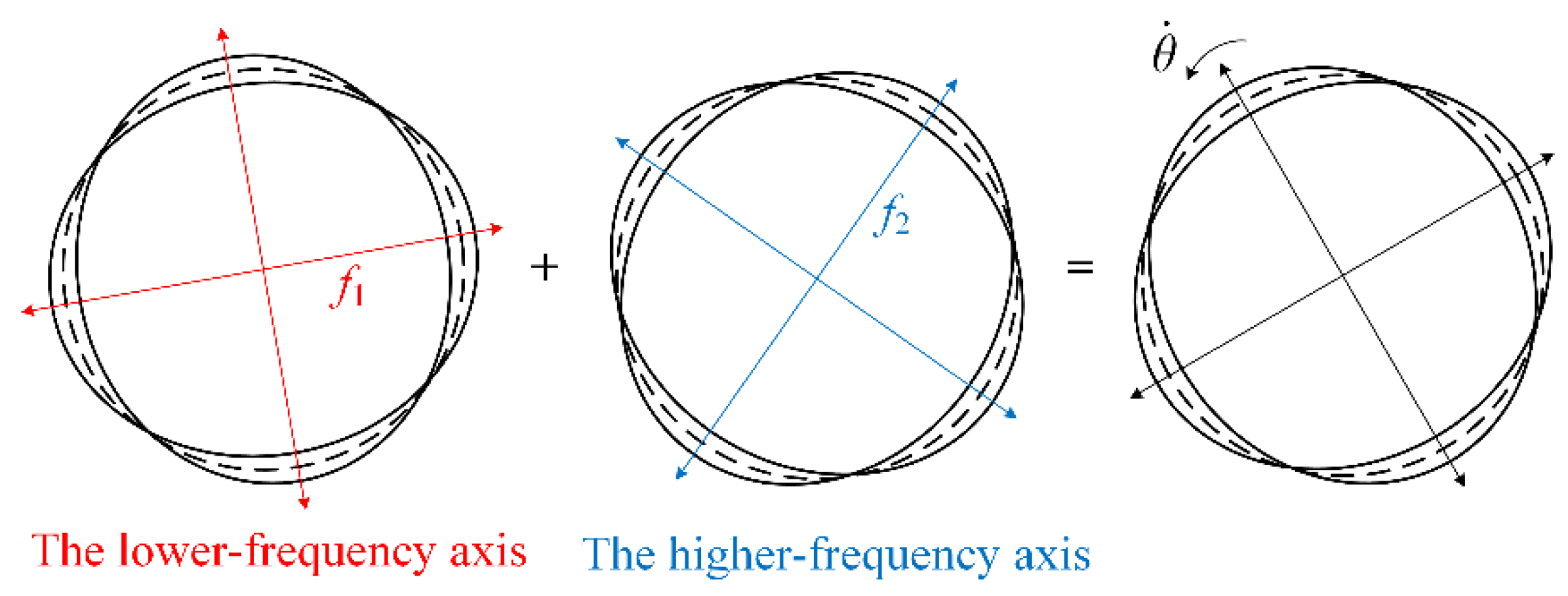The ideal n = 2 flexing mode will split into two basic modes, and these have two principle axes with two different natural frequencies, f₁ and f₂, as shown in Figure 2. The resonator vibrates as a superposition of these two basic modes. Finally, the frequency split Δf results in a drift error $\dot{\theta }$ of a gyroscope linearly, and it gravely determines the gyroscope’s performance. For the inertial navigation level HRGs, the drift error must be less than 0.01°/h [21]. If we suppose that the hemispherical resonators induce the drift error solely, the frequency split has a linear relationship with the drift error:

$$\mathsf{\Delta }f\approx k\dot{\theta }$$

(13)

where k is a linear coefficient. Equation (13) reveals the mechanism of the performance deviation induced by unbalanced mass. The resonators with a zero-drift rate or a frequency split are therefore expected.

However, the mechanical processing inevitably induces defects on hemispherical fused silica resonators. After etching and polishing, the resonator generally has a frequency split of about 0.05 Hz, which is still far from the requirements of the inertial navigation-level HRG. The coaxiality between the shell and the rib has reached the limitation of the machine tools. Blindly tightening tolerances at this time is not feasible due to the high cost of performing them. Therefore, a conventional manufacturing methodology, which focuses on geometric accuracy, is not an appropriate solution to producing high-performance hemispherical resonators. The tuning technique is essential to correcting the frequency split precisely. Clarifying the relationship between the resonator frequency split and the tuning process parameters is key to producing high-performance HRGs at the inertial navigation level.

According to the previous research, the frequency split of a hemispherical resonator during the tuning process can be expressed as follows:

$$\mathsf{\Delta }f=f\left(G\left(p_i\right)\right),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{p}_i=p\left({\theta }_i,{\phi }_i\right)$$

(14)

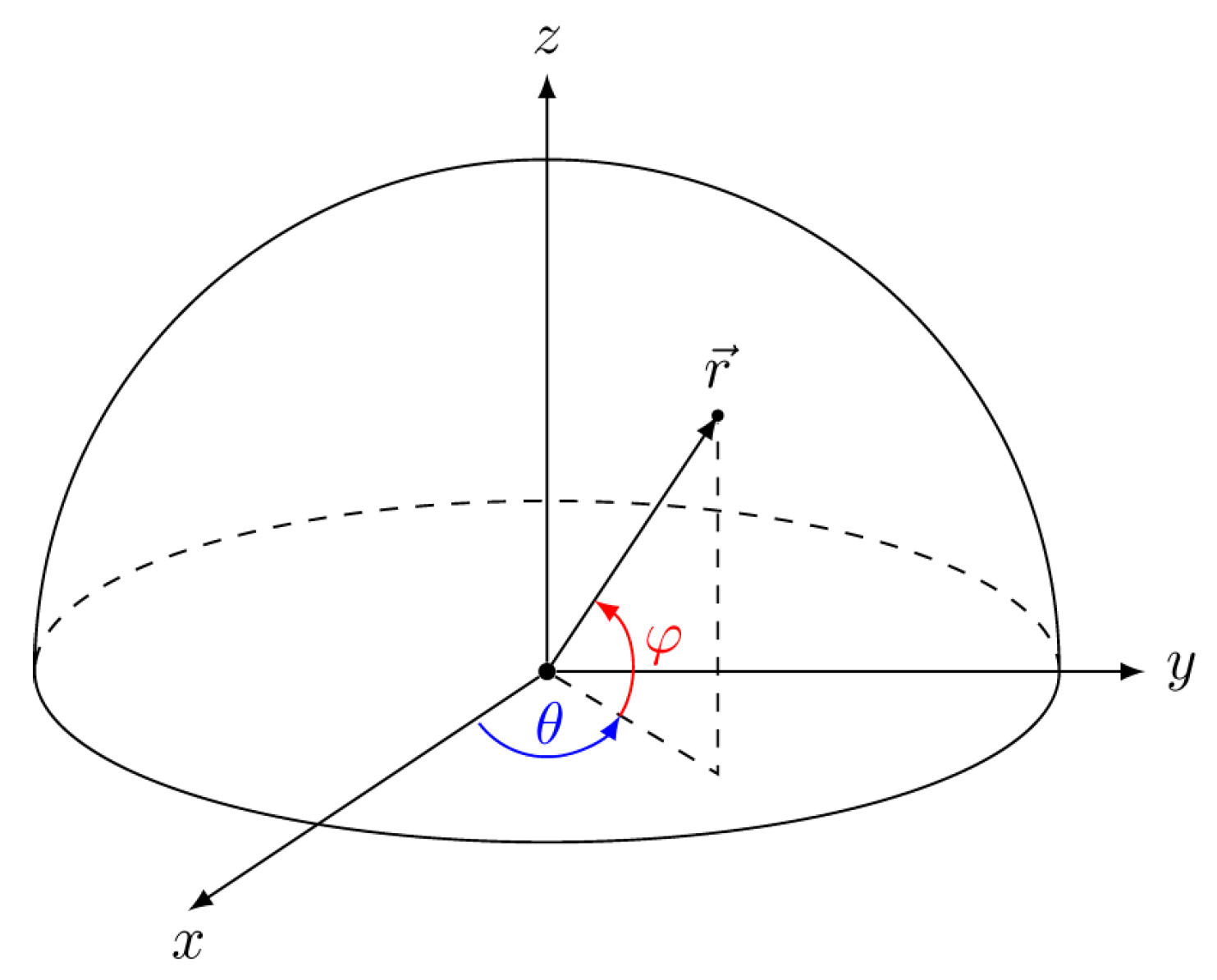
where Δf is the frequency split of the resonator, which is related to the geometric dimensions of the resonator, and the tuning process does not affect the material property M. p_i is the material removal amount of the i-th tuning. Equation (14) is function of the longitude angle θ_i and the latitude angle φ_i in the spherical coordinate system, as shown in Figure 3. The frequency split should be as close as possible to the design value 0. So the objective function is:

$$\min \hspace{0.17em}\mathsf{\Delta }{f}^2$$

(15)

3.1. Numerical Modeling

Finite element models of hemispherical resonators are established for numerical tuning, one of them is shown in Figure 4. The second-order hexahedral elements are generated by the sweep method to ensure the uniformity of the mass distribution and minimize the initial frequency split. The rib of the resonator is fixed. When the defect element is not specified, the frequency split of the n = 2 mode shape is in the order of 10⁻⁸ Hz, which meets the needs of the following calculations. 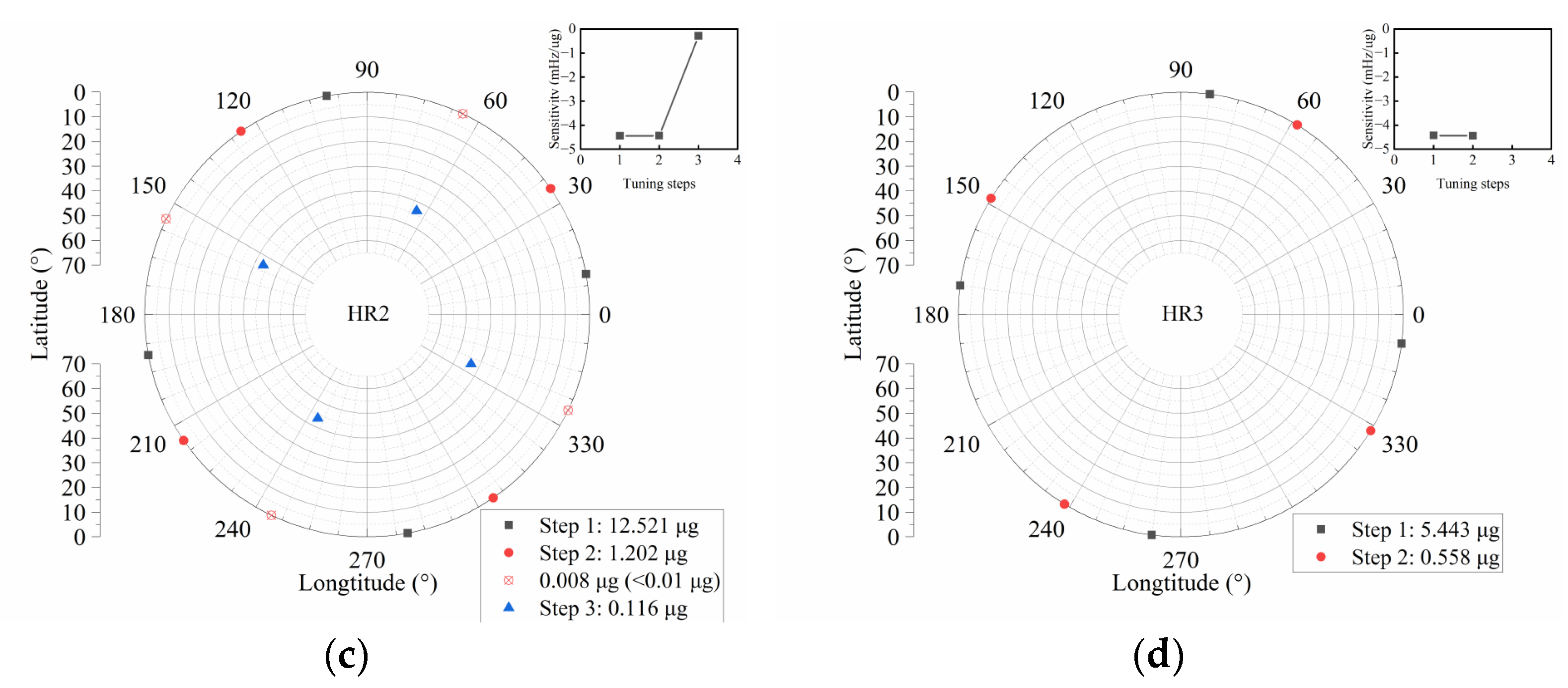Then, based on this model, two groups of defects with 10 points each were artificially generated, as shown in Figure 4 (purple elements (Type 1) and red elements (Type 2)), and the material parameters are listed in

Table 1. Material parameters of three HRs.

Density (kg/m3)	HR 1	HR 2	HR 3
Fused Silica	2210	2210	2210
Type 1 defects (purple)	2250	2600	2500
Type 2 defects (red)	2240	2400	2700
Initial frequency split (mHz)	71	221	96

. The initial frequency splits of these three hemispherical resonators (HRs) are measured, and they are close to the residual frequency split of the resonator after etching and polishing.

3.2. The Mathematical Model for Resonator Tuning

The frequency split after one tuning step is affected by the material removal amount Δm_i and the tuning position (longitude angle θ_i; latitude angle φ_i), namely:

$$\mathsf{\Delta }{f}_i=g\left(\mathsf{\Delta }{m}_i,\hspace{0.17em}{\theta }_i,\hspace{0.17em}{\phi }_i\right)$$

(16)

The subscript i represents the i-th tuning step. i = 0 represents the initial state of the resonator. Although there is no explicit expression for Equation (16), the local behavior of this function can be analyzed by performing a sensitivity analysis. The sensitivity of the i-th tuning process S_mi (mHz/μg) is defined as the ratio of current frequency split to the amount of material that is to be removed from a specific location (θ_i, φ_i):

$$S_{mi}\left({\theta }_i,{\phi }_i\right)=\frac{\partial \mathsf{\Delta }{f}_{i-1}}{\partial \mathsf{\Delta }{m}_i}$$

(17)

For the numerical calculation, Δm_i is determined by the machining capability, i.e., the minimum material removal amount. In this paper, the tuning capability is Δm_min = 10 ng, and the uncertainty of the tuning process is σ = 5 ng. A negative sensitivity indicates a smaller frequency split after tuning. Otherwise, the frequency split increases after tuning. In addition, the frequency split deviation caused by the ±1σ (2CV) processing uncertainty must also be kept within a reasonable range, such as 50%. In summary, all of the constraints can be written as:

$$\{\begin{array}{l}{S}_{mi}\left({\theta }_i,{\phi }_i\right)<0\hfill \\ \mathsf{\Delta }{m}_i\ge \mathsf{\Delta }{m}_{\min }\hfill \\ 2CV<50\%\hfill \end{array}$$

(18)

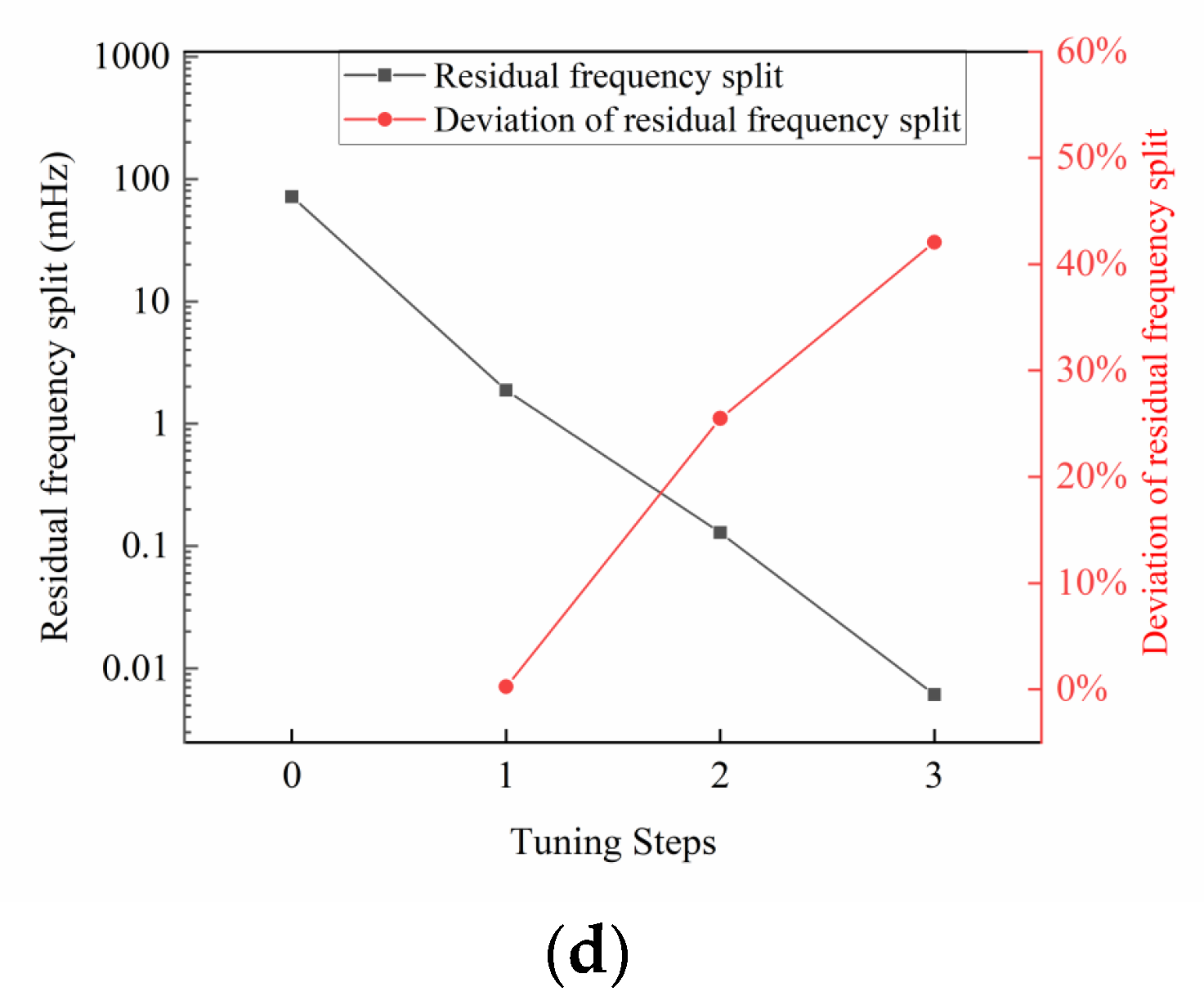
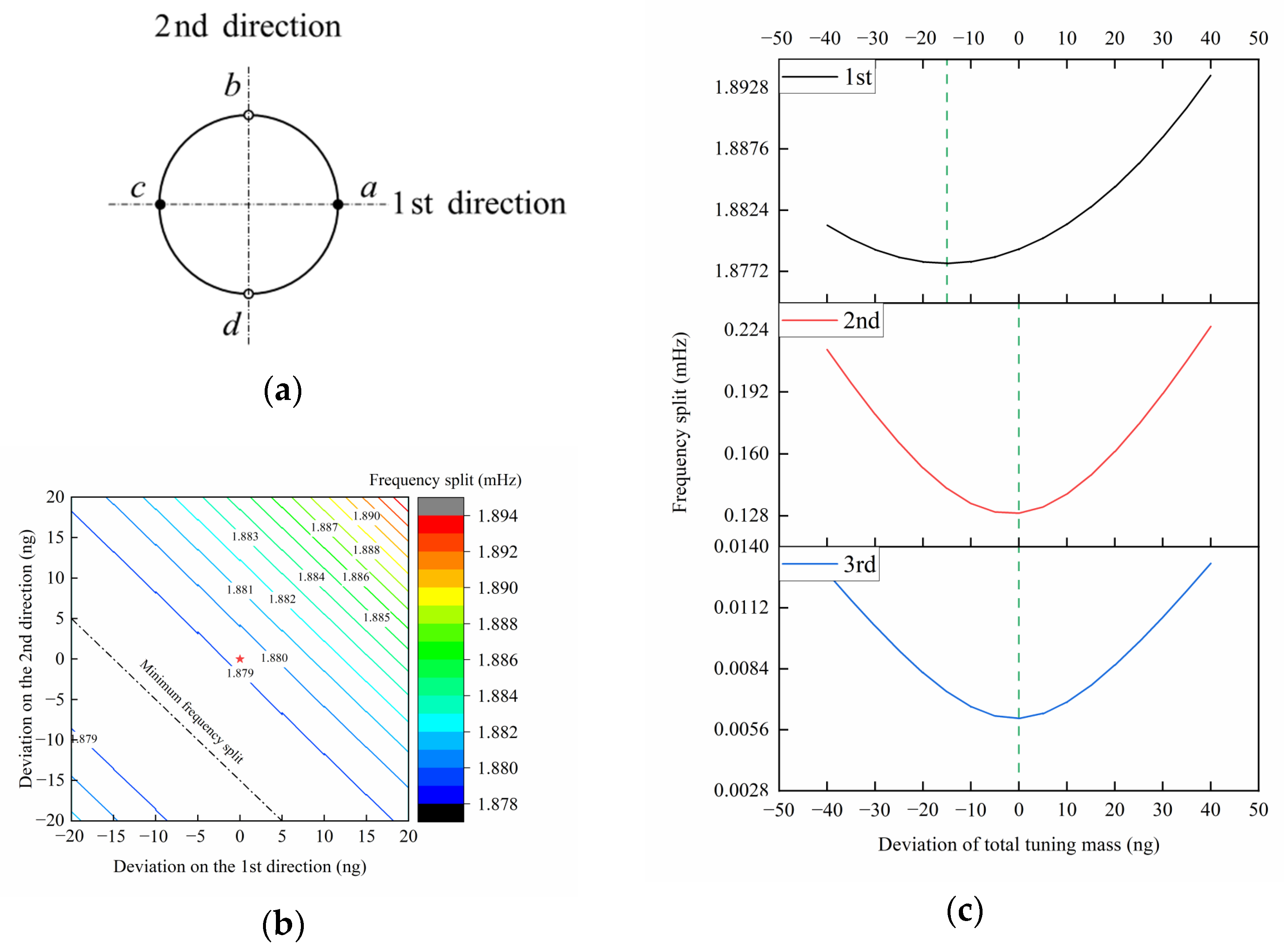
To eliminate the frequency split quickly, tiny amounts of material are removed at four orthogonal positions of the lower frequency axis and its orthogonal axis [6,8,22]. However, exceeding the machining capability is more likely to occur when the frequency split is extremely low. It is necessary to analyze the sensitivity of the residual frequency split to the tuning amount on the surface rather than on the lip. Therefore, tuning at an insensitive position is an alternative method. By selecting the appropriate positions, the amount that should be removed by four-position orthogonal tuning can be evaluated:

$$\mathsf{\Delta }{m}_i=\frac{\mathsf{\Delta }{f}_{i-1}}{4S_{mi}}$$

(19)

According to Equations (14)–(19), the mathematical model of high-performance hemispherical resonator tuning is:

$$\begin{array}{l}\min \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathsf{\Delta }{f}^2\\ \mathrm{s}.\mathrm{t}.\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\{\begin{array}{l}-\frac{\mathsf{\Delta }{f}_{i-1}}{4\mathsf{\Delta }{m}_{\min }}\le S_{mi}\left({\theta }_i,{\phi }_i\right)<0\hfill \\ 0\le {\theta }_i<\frac{\mathsf{\pi }}{2},\hspace{0.17em}\hspace{0.17em}0\le {\phi }_i<\frac{\pi }{2}\hfill \\ 2CV<50\%\hfill \end{array}\end{array}$$

(20)

4. Results and Discussion

Firstly, the sensitivity analysis results of the numerical model are discussed, and a new tuning strategy is given. Then, a tuning experiment is conducted on the numerical models to prove the feasibility of manufacturing a high-performance resonator. Finally, the influence of the tuning uncertainty on the performance is analyzed and discussed theoretically.

4.1. Sensitivity of Modal Tuning on the Surface

The tuning sensitivity on the hemispherical surface is calculated using Equation (19), and the results are demonstrated in Figure 5a. The sensitivity has a cyclic distribution on the surface. Further, it has a fourth-order harmonic distribution on the lip, as it is shown clearly in Figure 5b. It can be seen that the position with the highest negative sensitivity is to be sought precisely during conventional tuning. There are four orthogonal positions on the lip, each with an interval of 90°. This position is the lower frequency axis. The acute angle usually is used to represent its azimuth. For this resonator, θ = 22.5°. Depending on the positive and negative values, the results are divided into two regions: the tuning region and the non-tuning region (gray region). It can be seen that the range of ±22.5° near the lower frequency axis is the tuning region. A high level of sensitivity can be found near the azimuth of the lower frequency axis, as well as the highest degree of tuning efficiency. The other regions (gray region) have no tuning effects, and the frequency split will increase. In addition, the tiny defects of the hemispherical shell do not significantly affect the cyclic symmetry of the sensitivity on the lip.

In order to analyze the feasibility of surface tuning of a hemispherical resonator, the tuning sensitivity on different meridians is calculated according to Figure 5a, and the results are shown in Figure 5c–e. It can be seen that the tuning sensitivity on different meridians decreases with an increasing latitude from a larger value on the equator to nearly zero at the high latitudes. Additionally, the tuning sensitivity consistently decreases when the meridian of the tuning region is selected (the white region in Figure 5b). Otherwise, the residual frequency split will increase. In addition, the frequency split of the resonator is insensitive to the amount of tuning mass at the root, as shown in Figure 5c–e. The tuning sensitivity near the equator is at its highest, and it is more sensitive to process instabilities, but the frequency split can be largely eliminated by removing a small amount of mass to improve the tuning efficiency. If the tuning process cannot be implemented on the lip due to a limited tuning capability, it is still possible to tune a small amount of the frequency split in the high latitude region precisely due to insensitivity and stability. Therefore, the high latitude regions on the meridian of the tuning region should be selected for high resolution tuning.

4.2. Modal Tuning Strategy and Its Implementation

Based on the sensitivity analysis in the previous section, the following tuning strategy can be implemented:

• Tune on the lip of the lower frequency axis in order to rapidly eliminate the frequency split until the tuning capability (Δm_min = 10 ng).
• Choose a suitable latitude line and turn on the lower frequency axis to eliminate frequency split more precisely and stably.

Guided by the manufacturing methodology proposed in this paper, Figure 6 illustrates how the high-performance hemispherical resonator (Δf < 0.1 mHz) is tuned. Using this methodology, tuning efficiency is assured, and high precision is guaranteed.

A numerical tuning experiment at four orthogonal positions is conducted on the resonator mentioned above. The tuning results are shown in Figure 7a. HR1 and HR2 can theoretically be tuned to approximately 0.1 mHz by conducting two rounds of tuning, while HR3 is already below 0.1 mHz. These results show that it is impossible to remove all of the frequency splits at once using the existing manufacturing method for hemispherical resonances. The performance of the hemispherical resonators must be iteratively tested and tuned to achieve the expected performance. To implement the tuning strategy in Figure 6, the optimization model (20) is required.

A sensitivity analysis is performed to determine how much mass should be removed during tuning. The 3rd tuning step calculation using Equation (19) shows that about 7 ng is required for tuning on the lip for HR1 and HR2, which exceeds the tuning capability. However, it is possible to tune in the high latitude region to ensure that the amount of material removal is not beyond the tuning capability, as shown in Figure 7b–d. After performing three step tunings for all of the HRs, it is theoretically possible to have a negligible frequency split with 6 μHz. This result indicates that the frequency split can be almost eliminated iteratively under the guidance of this methodology. In addition, the minimum tuning sensitivity on the lip did not change significantly after tuning, indicating that small mass distribution changes do not change tuning sensitivity significantly.

4.3. Uncertainty Analysis of Tuning Process

HR1 has finally achieved the highest level of modal tuning at a frequency split that is close to the μHz level. However, process uncertainty makes it difficult to achieve a very low level of frequency split for the high-performance hemispherical resonators. The tuning uncertainty analysis involves evaluating how the processing instabilities affect the performance. With the deviation (σ) of each tuning step 5 ng, the instabilities in the residual frequency split of the resonator are analyzed. The results of HR1 are demonstrated in Figure 8. Specifically, Figure 8b–d shows the effects of the deviation of the material removal amount on the residual frequency split in the two tuning directions (1st, 2nd) illustrated in Figure 8a. A positive deviation means that more material is removed than the expected value. The percentage of the frequency split deviation (±1σ) during each tuning step is marked in the respective figures.

It can be seen that the three result graphs show obvious checkerboard patterns, indicating that the influence of the process instability on the residual frequency split is regular. Theoretically, if the expected removal amount of the machining process at position k (k = a, b, c, d) is μ_k and the standard deviation is σ_k, the adjusted mass removal function ρ₁(φ) for four-position orthogonal tuning is expressed as follows according to the Fourier series theory [5]:

$${\rho }_1\left(\phi \right)={\displaystyle \sum _k\left\{\frac{{\mu }_k}{2\pi }+\frac{{\mu }_k}{\pi }{\displaystyle \sum _{n=1}^{\infty }\cos n\left(\phi -\frac{k\pi }{2}\right)}\right\}}+{\displaystyle \sum _k\left\{\frac{{\sigma }_k}{2\pi }+\frac{{\sigma }_k}{\pi }{\displaystyle \sum _{n=1}^{\infty }\cos n\left(\phi -\frac{k\pi }{2}\right)}\right\}}$$

(21)

The frequency split is proportional to the amplitude of the fourth harmonic V₄, so the frequency split deviation is proportional to the V₄ deviation:

$$V_4={\displaystyle \sum _k\frac{{\sigma }_k}{\pi }\cos 4\left(\phi -\frac{k\pi }{2}\right)}=\frac{\left({\sigma }_a+{\sigma }_b\right)-\left({\sigma }_c+{\sigma }_d\right)}{\pi }\cos 4\phi$$

(22)

Equations (21) and (22) show that the same material removal amount at two positions in one of two directions, the dotted, dashed line as shown in Figure 8a, has an opposite effect on the frequency split. The same tuning deviation of two positions in one of two directions leads to the opposite tuning effect. For example, if we suppose that the tuning deviations of the two positions a and c are all + 5 ng, the frequency split will decrease when tuning it on position a, and it will increase when tuning it on position c. As a result, there are several ways to eliminate the residual frequency difference so that many possible tuning solutions mix into one. In short, there are several ways to tune the resonator. It can be seen clearly from Figure 8b that there are contour lines Δm_x + Δm_y = C. It is possible to achieve the same residual frequency split using these solutions on the same contour line. The tuning problem can theoretically have a unique solution if four-position orthogonal tuning is implemented. This tuning method induces a new constraint Δm_x = Δm_y, which is a 45° line in the counter (not drawn on the graphs). These results reveal that the residual frequency split is dependent on total tuning mass uncertainty, as detailed in Figure 8c. In addition, Figure 8b shows that the first tuning step is not the optimal solution, but the solution is near the contour x + y = –15, as shown clearly in Figure 8c. Both of the last two rounds have a relative minimum residual frequency split under stable tuning. However, four-position orthogonal tuning cannot achieve a relative minimum, but it can be performed iteratively. These results also reveal that the initial resonator has a significant imbalance. The solutions for the following two tuning rounds are all optimal, confirming the convergence of the four-position orthogonal tuning.

The fluctuations of the residual frequency split (2σ/μ = 2CV) are calculated at each tuning step. It can be observed that the residual frequency split decreases gradually during the tuning processes. The amount of material removed increases in the last step by tuning on the resonator surface rather than on the lip, but the influence of tuning instability is increasing compared with the previous two steps, as shown clearly in Figure 8c. Due to the inevitable instability in the tuning process, the precise control of the tuning process is required. Moreover, the first tuning step does not entirely eliminate the frequency split according to the optimal solution. Only tuning on the lip will result in an endless demand for an improved machining capability. Therefore, the elimination of the frequency split can finally be achieved with surface tuning as a supplement. Additionally, Figure 8d shows the tuning effect and its uncertainty. It can be seen that the performance uncertainty increases with an increasing number of tuning rounds. The frequency split decreases linearly on a logarithmic scale, which means that it decays rapidly in an exponential function form.

5. Conclusions

This paper proposes a manufacturing methodology for high-performance components that considers the existing material properties and processing capacities to maximize the processing efficiency. A tuning process of a hemispherical resonator is taken as an example, and the implementation of this methodology is demonstrated by performing a numerical simulation. The following conclusions are drawn in this study:

• A mathematical model for the manufacturing methodology of high-performance components is established. By considering the effect of the material removal resolution and the processing uncertainties, the component performance deviation can be controlled within a reasonable range under limited machining capabilities.
• The mathematical model of the resonator tuning is established using the proposed methodology. The tuning position and amount are determined by performing a sensitivity analysis. The results demonstrate that the position of maximum sensitivity coincides with the low-frequency axis, which is also the position of four-point tuning, orthogonally.
• A highly efficient tuning strategy for a hemispherical resonator is given by a sensitivity analysis. The frequency split elimination can finally be achieved near 6 μHz with surface tuning as a supplement.
• The uncertainty analysis indicates that there are infinitely many solutions to tune a resonator and achieve the same residual frequency split. If four-position orthogonal tuning is implemented, this new constraint is induced mathematically, and the tuning problem will have a unique solution.