DC-Link Electrolytic Capacitors Monitoring Techniques Based on Advanced Learning Intelligence Techniques for Three-Phase Inverters

Abstract

The reliability of the electronic converter is a vital concern in an industrialized area. Capacitors are critical in electronic converters and are more likely to fail than other electronic gears. Due to aging, the capacitor progressively loses its original quality and capacitance, and the equivalent series resistance escalates. Hence, condition monitoring is a fundamental procedure for evaluating capacitor health that affords prognostic repairs to guarantee stability in power networks. The ESR and capacitance of the capacitor are commonly employed to estimate the condition grade. This study proposes an estimation scheme that utilizes the source current to assess the health condition of an aluminum capacitor. Several advanced intelligence techniques are adopted to estimate the parameters of an AEC in a three-phase inverter system. First, different signals used as inputs, such as input power, capacitor current, voltage, and power, output current, voltage, and power, are analyzed using fast Fourier transform and discrete wavelet transform analysis. Then, various indexes of the analyzed signals, such as RMS, average, median, and variance, are used as the inputs in learning models to monitor the AEC’s parameters. In addition, various input signals are combined to obtain the best combinations for capacitor monitoring. The estimated results prove that utilizing the source current combined with selected indexes improves the monitoring accuracy of the AEC’s health status.

1. Introduction

Capacitors are an essential component of most power electronic converters, which suppress voltage fluctuation, absorb ripples, and steady the immediate power fluctuation of the source and load in networks [1]. They also afford energy for abnormal conditions in practical systems [2]. Nevertheless, capacitors suffer from various problems, such as thermal and electrical issues, and their core weaknesses are a limited life cycle and high degradation catastrophe rate [3]. Research has found that capacitors cause about 30% of the faults in converters due to aging degradation, making them the most vulnerable part of electronic networks [4]. With the rising spread of converters for transmission in networks, prolonging the stability of converters to certify system operation safety is vital.

The aluminum electrolytic capacitor (AEC) is the most general category used in power systems because its advantages are its high volumetric productivity and low cost. It is available in enormous capacities and sizes [5]. Furthermore, AECs must be linked in sequences and necessitate safety resistors to preserve the requisite high voltage in power networks, which results in a more complicated network and might be the reason for extra destruction when they crash [6]. AEC damage is due to numerous thermal and electrical issues. Its electrolyte vaporizes and leads to the degradation of the oxide layer, resulting in a considerable reduction in capacitance (C) and an escalation in equivalent series resistance (ESR) rates [7].

Nonetheless, the effective lifespan of the AEC is much less than that of converters and it must be replaced once or twice within the converter’s lifespan. Condition monitoring approaches are centered on the estimated valuations of the capacitance (C) or the ESR, which indicates the degraded condition of the capacitor. According to the datasheet for capacitors, the lifespan of AECs terminates if the C value decreases by 20% of its original rate or the ESR increases to twice its initial rate [8]. Several investigative techniques have been suggested to examine the state of AECs employed in converters [9,10,11]. The techniques in [8,9,10] require the presence of a current sensor connected in series with the capacitor for monitoring. Using an additional current sensor might increase the stray inductance, distorting the capacitor voltage, as previously reported [10]. Several techniques have been suggested [12,13] to avoid using a current sensor in the DC link. In these methods, the capacitor current is obtained based on the circuit relationship to monitor the health of the AEC. All the mentioned techniques require additional hardware or complex algorithms.

With the advancement of information technology, artificial intelligence (AI) methods have become popular and offer potential strategies for fault diagnosis, such as arc fault detection [14,15,16,17,18,19]. Several innovative algorithms, such as the artificial neural network and adaptive neuro-fuzzy inference system (ANFIS) algorithms, have been employed to evaluate the health grade of AECs [20,21,22,23]. The ANFIS distinguishes the aging burdens of AECs in the converter based on the aged connections between the valued parameters and actual capacitor factors using curve fitting methods. The innovative techniques can observe the capacitor condition using feedback data generated during the usual and aging error conditions of the capacitor. However, research on capacitor estimation-based AI algorithms is still in the initial stages, and a thorough estimation process has not been formed.

Conventional estimation schemes demand extra hardware, a complex system, and strict requirements (signal injections, sampling time). Utilizing advanced learning techniques can eliminate all the above difficulties and ensure the estimated performance. Additionally, conventional approaches commonly obtain the capacitor current directly from the sensor or indirectly from the circuit relationship and switching states. This drawback increases the complexity and cost of the estimation scheme. This paper proposes an estimation scheme for the health condition of AECs utilizing the source current instead of the capacitor current or voltage. Utilizing the source current avoids the need for additional hardware and reduces the cost. Various advanced learning algorithms combined with indexes were adopted to estimate the capacitor parameters to compare the effectiveness of the proposed scheme. Different input signals, such as capacitor current and voltage, load current and voltage, were analyzed using DWT. The fast Fourier transform (FFT) usually analyzes the sampling signals in conventional approaches. However, capacitance and ESR dominate in different frequency spectrums. Therefore, filters are required to extract the specific signals for capacitance or ESR estimation. On the other hand, DWT is a powerful analyzing technique in the frequency domain, and it needs no filter to extract the signals. The analyzed signals were used as inputs in AI models to estimate the parameters of AECs. Four indexes—root mean square (RMS), average, median, and variance values—were employed to compare the different inputs’ performance. Additionally, this research investigates the finest appropriate input that yields the highest accuracy for the capacitor parameters without extra hardware or any increase in the complexity of the estimation scheme. The estimated results prove that utilizing source current combined with DWT and the indexes mentioned could estimate the capacitor parameters with an accuracy of 99.9%. This study is organized as follows: Part 2 describes the characteristics of capacitors. Part 3 describes the AI techniques and combination inputs for capacitor parameter estimations. Part 4 evaluates the estimated parameters of the eight AI techniques using different combinations of inputs. Finally, in Part 5, recommendations for capacitor estimation and future work are discussed.

2. Properties of Aluminum Electrolytic Capacitors

The curvatures of capacitor dreadful conditions are presented in Figure 1. The end-of-life of AECs is recognized at a decline of 20% capacitance or a rise of twice the ESR value. Figure 2 presents an equivalent circuit of an electrolytic capacitor and a diagram of the dominant impedances according to their spectra in the frequency domain. The capacitor impedance is measured by the C, ESR, and the equivalent series inductance (ESL) in Regions I, II, and III, respectively. An individual capacitor or a group of capacitors in a power system is regularly operated for power decoupling, bypassing, filtering, and energy buffering. Hence, if a capacitor crashes, the network might suffer. The impedance of the capacitor regarding the equivalent circuit in Figure 2a is stated as follows:

$$Z_{cap}=\sqrt{ES{R}^2+{\left(ESL·\omega -1/C\omega \right)}^2}$$

(1)

where $\omega =2\pi f$ is the angular frequency. Because the converters usually work in low and middle frequencies, the ESL is neglected; then Equation (1) becomes

$$Z_{cap}=\sqrt{ES{R}^2+{\left(1/C\omega \right)}^2}.$$

(2)

The C is valued using the capacitor voltage $v_{C\_I}$ and current $i_{C\_I}$ in region I, as follows:

$$C=\frac{\int i_{C\_I}dt}{\mathsf{\Delta }{v}_{C\_I}}$$

(3)

where $\mathsf{\Delta }{v}_C$ denotes the difference in capacitor voltage in the estimated period. The impedance of the capacitor is measured using the ESR if $f$ is placed in Region II. The ESR of a capacitor is obtained using the proportion between the capacitor’s voltage and the current for a definite range of frequency in Region II, as follows:

$$ESR=\frac{V_{C\_II}}{i_{C\_II}}$$

(4)

where $i_{C\_II}$ and $V_{C\_II}$ represent the capacitor current and voltage in Region II.

Figure 3 shows the circuit diagram of the three-phase inverter used in this study. Three-phase inverters are commonly used in numerous practical applications. Thus, this converter type was selected to investigate and provide a more practical insight when implementing the estimation scheme in practical systems. In addition, $i_s \mathrm{and} i_L$ are the source and load currents, and $v_L$ is the load voltage. The three-phase converter is controlled by a space vector modulation technique using a digital signal processor (TMS320F28335) with a switching frequency of 5 kHz. The switching device in the three-phase inverter is a silicon-insulated gate bipolar transistor (IXA371F1200HJ). The capacitor must be replaced at least twice within the converter’s lifetime [6]. Thus, the capacitance values were selected as five to emulate capacitor replacement within the converter’s life. The capacitance values were varied for five capacitors from 106 to 553 μF and the data were sampled using an oscilloscope (MSO3054) at 250 kHz. The sampling frequency was chosen on the basis of several studies that employed advanced learning algorithms in fault detection and capacitor estimation [16,19,23]. Using a higher sampling frequency oscilloscope can obtain more information for each signal. However, it could increase the computation burden and the demand for powerful processors thus increasing the system’s cost. Therefore, the sampling rate of 250 kHz is high enough to balance the efficiency and cost. First, the space vector modulation technique was used to drive the converter. Then, the signals were sampled by the sensors, which were implemented for control purposes. Finally, the data were saved and transferred to the computer for the estimation process using MATLAB.

The experimental waveforms are presented in Figure 4. $i_C$ is the capacitor current. The signal $v_C$ is the AC coupling signal of capacitor voltage. $i_L$ and $v_L$ are the load current and voltage, respectively.

Table 1. Experiment Specifications.

Parameters	Values
DC source	100 V
Load resistance	10 Ω
Load inductance	10 mH
Switching frequency	5 kHz

presents the specifications of the experimental setup.

Table 2. Capacitor Parameters.

Capacitors	Capacitance (μF)	ESR (mΩ)
Cap 1	106.9167 μF	490.8295 mΩ
Cap 2	219.0449 μF	229.5632 mΩ
Cap 3	330.9029 μF	155.3454 mΩ
Cap 4	442.4869 μF	121.914 mΩ
Cap 5	553.5659 μF	103.6098 mΩ

lists the actual parameters of the capacitors. These actual parameters were measured using an LCR meter (model E4980A).

3. Intelligence Learning Techniques and Signal Processing

3.1. Intelligence Learning Techniques

Figure 5 reveals the theory and structure of several machine learning (ML) and deep learning (DL) models. Ensemble learning regression (ELR) is a procedure that uses a group of algorithms, each achieved by employing an intelligence progression to a specified problem. This group of algorithms was incorporated to acquire the final estimation. In addition, ELR aims to associate numerous algorithms with improving the estimated precision of learning models with a numerical target variable [24]. The Gaussian process model is a probabilistic supervised ML structure commonly employed in classification and regression assignments. A Gaussian process regression (GPR) algorithm could produce predictions integrating the mentioned information [25]. The support vector machine determines the largest perimeter, which is applied to sort the components into categories [26]. Linear regression is a linear methodology for demonstrating the correlation between a scalar response and one or more descriptive variables. The correlations are demonstrated using linear analyst functions whose unidentified parameters are guesstimated from the data [27]. A decision tree configuration represents a tree flow diagram, which explores all potential choices and the consequences of those choices. This configuration demonstrates the estimates subsequent to altered nodes. The root node denotes the beginning, and the configuration is completed with the decision assembled at the “leaves” [28].

Alternatively, DL techniques imitate the ordinary computational capabilities of human beings, for example, studying. A process prototype is implemented to train and categorize components based on numerous data types, such as images, letters, or sounds. These DL techniques can accomplish outstanding precision and beat human quantity functioning in several assignments. A vast information collection is generally applied to train DL techniques. Three DL techniques are employed in this study to estimate the capacitor parameters: deep neural networks (DNNs), gated unit current (GRU), and long short-term memory (LSTM) [17,18]. There are numerous layers in the DL configuration: the input, hidden, and output layers. The hidden layer organization contains numerous layers. The first DNN layer was constructed as follows:

$${\mathit{h}}_1=f_1\left({\mathit{W}}_1^T\mathit{X}+{\mathit{b}}_1\right)$$

(5)

where X denotes the input data, ${\mathit{W}}_1^T$ and ${\mathit{b}}_1$ represent the weight and bias in the first layer, and ${\mathit{h}}_1$ indicates the output.

In LSTM, long-term and short-term memories are controlled separately, where $h_{t-1}$ and $h_t$ denote short-term states at earlier and present moments, respectively, and $C_{t-1}$ and $C_t$ represent long-term memory states at earlier and present moments, respectively. Additionally, $W_0$ and $b_o$ indicate the weight and bias, respectively, and $x_t$ and $y_t$ denote the input and output, respectively. The output is calculated as follows:

$$y_t=\left(\sigma \left(h_{t-1}{x}_t+W_0{h}_{t-1}+C_t{C}_{t-1}+b_o\right)\right)tanh\left(c_t\right),$$

(6)

where σ determines how much the weight and bias vary in one iteration, $h_{t-1}$ and $h_t$ are the states at the earlier and present moments, respectively, $z_t$ and ${\widehat{h}}_t$ represent the update gate vector and candidate activation vector, and $x_t$ denotes the input. The GRU is characterized by combining the long- and short-term memory information. Equation (7) provides the output of the GRU neuron:

$$h_t=z_t{\widehat{h}}_t+\left(1-z_t\right)h_{t-1}$$

(7)

The DNN contains two hidden layers; whereas, GRU and LSTM share a three-hidden layer configuration. The hidden layers of DNN, GRU, and LSTM are fully connected. The trial-and-error technique selects the hidden layouts. The DNN hidden layers have 100 and 50 neurons, respectively. The GRU and LSTM hidden layers each have 36, 18, and 8 neurons. The designated configurations of the DL algorithms provide the highest efficiency across numerous configurations. However, other probable configurations exist that might also be suitable.

Table 3. Comparison of advanced learning algorithms.

Learning Models	Machine Learning					Deep Learning
	ELR	GPR	SVM	DT	LR	LSTM	DNN	GRU
Structure	Simply					Complex
Feature extraction	Required					Optional
Data size	Small or medium					Large
Processor	Medium powerful processor					High powerful processor
Adjustability	Medium					High
Flexibility	Medium					High

presents a comparison of various aspects of advanced learning techniques. For example, DL techniques contain more layers and neurons compared to ML techniques; thus, their structures are more complex and demand a more powerful processor compared to ML techniques. In addition, ML techniques require the extraction of features with a small or medium data size; whereas, DL techniques require a large data size, whether feature extraction is required or not. Owing to the complex structures, which can be modified alternatively, DL techniques could be applied in different fields with several adjustments. On the other hand, ML structures are more straightforward than those of DL so their ability is suitable for simple tasks in specific areas. The learning algorithms in this study are the most popular in numerous fields recently. Therefore, they were chosen to investigate the ability to estimate the parameters of the capacitor.

3.2. Signal Processing

Features can be studied in the time or frequency domains. As shown in Figure 2b, the capacitance and ESR dominate in different ranges of the frequency domain. Thus, this research focuses on signal analysis in the frequency domain. The FFT and DWT techniques were employed to analyze the signals. Then, various indexes of analyzed signals, such as RMS, average, median, and variance values, were used as an indicator to estimate the capacitance and ESR of the capacitor. Figure 6 illustrates the normalization of the analyzed signals using the FFT technique. After FFT, filters were adopted to obtain signals in low- and middle-frequency ranges. Then, four indexes (RMS, average, median, variance) were obtained and normalized. As shown in Figure 6, the normalized index values of source current and power (${\mathit{P}}_{\mathit{i}\mathit{n}}$), capacitor current, voltage, and power (${\mathit{P}}_{\mathit{C}}$), load current, voltage, and power (${\mathit{P}}_{\mathit{L}}$) show the differences regarding various capacitors. The normalized index values of source current and power, capacitor current, voltage, and power change linearly up-trend or down-trend when the capacitance increases or the ESR decreases; whereas, load current, voltage, and power fluctuate continuously. Figure 7 demonstrates the normalized index of different input signals using the DWT analysis. This research used Daubechies wavelet (db5) to decompose the signals. The modal maxima of the wavelet decompositions reveal the sudden alteration point characteristics of the signals and could be used to estimate the capacitor parameters. As shown in Figure 7, the rising or declining trend of normalized DWT indexes, such as source current and power, capacitor current, voltage, and power, are clear and consistent compared with load current, voltage, and power. Generally, the FFT and DWT indexes related to the source and capacitor are promising indicators to estimate the capacitor status compared to the indexes related to the load.

Table 4. Comparison of input signals.

Input Signals	${\mathit{i}}_{\mathit{S}}$	${\mathit{i}}_{\mathit{C}}$	${\mathit{i}}_{\mathit{L}}$	${\mathit{v}}_{\mathit{L}}$	${\mathit{v}}_{\mathit{C}}$	${\mathit{P}}_{\mathit{S}}$	${\mathit{P}}_{\mathit{C}}$	${\mathit{P}}_{\mathit{L}}$
Availability	⩗	X	⩗	⩗	⩗	X	X	X
Related to Capacitor	Medium	High	Low	Low	High	Medium	High	Low
Obtainable method	Direct	Indirect	Direct	Direct	Direct	Indirect	Indirect	Indirect

compares input signals regarding their availability, relationship to the capacitor, and obtainable methods. The source current, capacitor voltage, load current, and voltage are available and directly obtained by sensors, which were already implemented for control purposes. In contrast, other signals are only obtained from the converter’s circuit relationship and switching states. This is an indirect method of collecting these signals. The capacitor current, voltage, and power are highly related to the capacitor whereas other signals are medium or low. Combining the information from Table 4 and Figure 6 and Figure 7, it can be concluded that the source current is balanced among all aspects and could be a promising indicator of capacitor estimation.

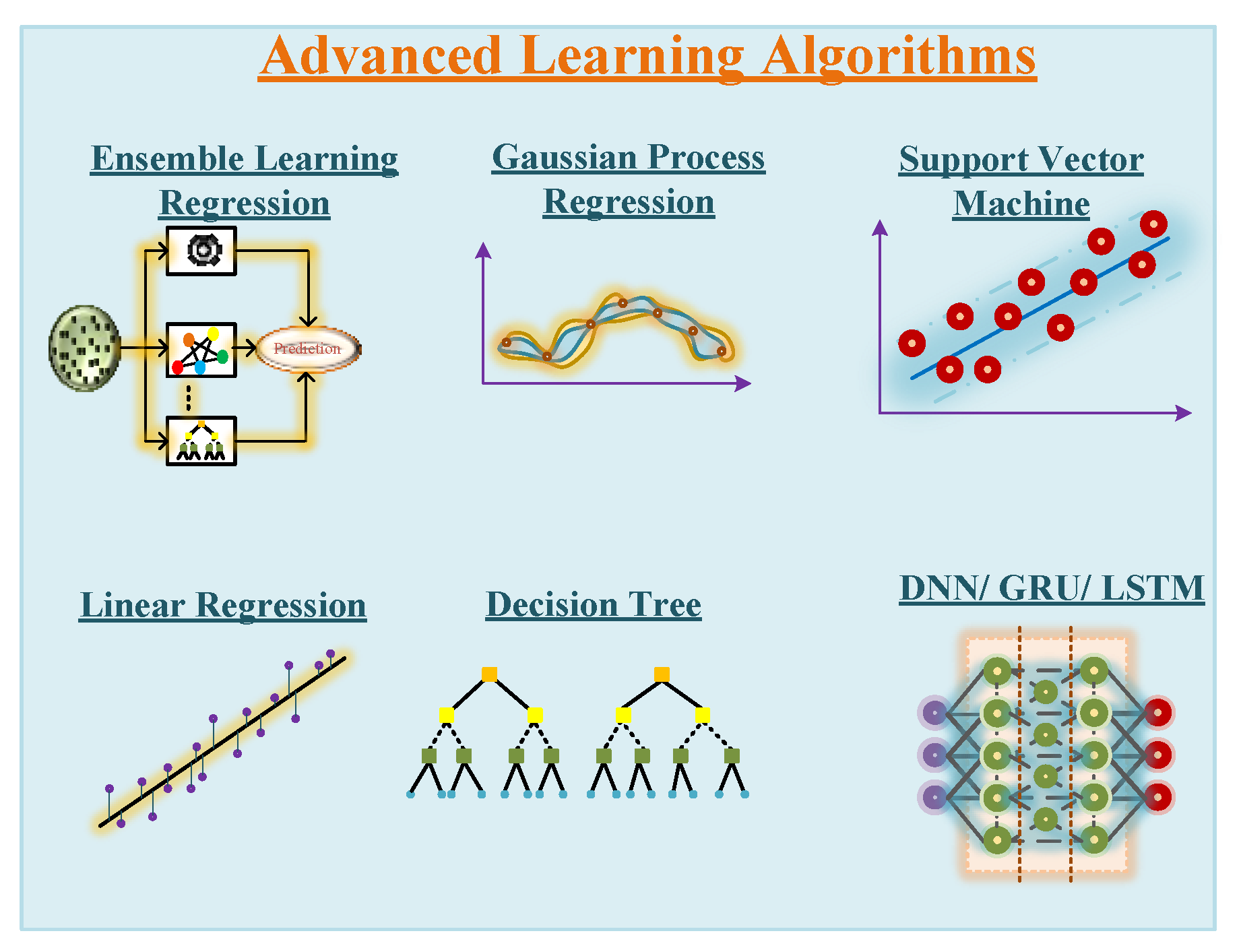
4. Artificial Learning Algorithms in Parameter Estimation of Capacitors

Figure 8 presents the estimation scheme for AECs. First, the capacitor current and voltage, load current, and voltage data were collected, and then the source power, capacitor power, and load power were obtained. These signals were analyzed using FFT and DWT. There are two FFT filters: the low-pass filter (LPF) and the high-pass filter (HPF). Two frequency ranges were employed for each LPF and HPF to investigate the effect of accuracy on various frequency ranges of the filters.

Table 5. Frequency range of the filters.

Filters	Frequency Ranges
Low-pass filters 1 (LPF1)	100–1000 Hz
Low-pass filters 2 (LPF2)	1000–3000 Hz
High-pass filters 1 (HPF1)	10–20 kHz
High-pass filters 2 (HPF2)	20–40 kHz

presents the frequency ranges of the LPF and HPF. In [8], odd harmonic signals were injected into the inverter system to estimate the capacitance. These harmonics are located at hundreds of hertz range; thus, the range of LPF1 was chosen to be from 100 to 1000 Hz. The LPF2 range was chosen to be 1–3 kHz to investigate the effectiveness of LPF1 and the imbalance of the frequency ranges. The frequency range of LPF2 is more extensive than that of LPF1. Thus, the information in LPF2 is much higher than in LPF1, which could improve the accuracy of the estimated capacitance, theoretically. In [7], the range for the dominant ESR was from 10 to 100 kHz, and this paper used a signal of around a three-time switching frequency (15 kHz). Therefore, the range of HPF1 was from 10 to 20 kHz. Similarly, the range of HPF2 was chosen for performance comparison with HPF1.

After signal filtering, four index values (RMS, average, median, and variance) were obtained from the analyzed filtering signals. In total, nine input signals were investigated. They were source current, source power, capacitor current, capacitor voltage, capacitor power, load current, load voltage, load power, and the combination of source and load powers. The general formula determines the powers of the source, capacitor, and load as:

$$P_x\left(t\right)=i_x\left(t\right)·v_x\left(t\right)$$

(8)

where $x$ represents the source, capacitor, or load. The ratio data corresponding to the training and test stages is 1:1. The accuracy is defined as

$$Accuracy=\frac{Estimated value}{Actual value}\times 100\%$$

(9)

If the estimated value is close to the actual value, the accuracy is close to 100%. Otherwise, the accuracy deviates far from 100%. The best technique is the technique with 100% accuracy. The average accuracy is demonstrated because the estimated results are large in size and could confuse the reader. The average accuracy is obtained by:

$$Average accuracy=\frac{Accurac{y}_1+Accurac{y}_2+\dots +Accurac{y}_n}{n}$$

(10)

where $n$ is the number of estimated accuracies.

Figure 9 presents the accuracy of the estimated capacitance using different input signals from the FFT analysis with LPF1. The input related to the source and capacitor provided higher accuracy than the input related to the load for all learning techniques. The GRU technique provided the highest accuracy using the ${\mathit{i}}_{\mathit{s}}$, ${\mathit{i}}_{\mathit{C}}$, ${\mathit{v}}_{\mathit{C}}$, ${\mathit{P}}_{\mathit{s}}$, and ${\mathit{P}}_{\mathit{C}}$ input signals. The DNN, LSTM, and GPR techniques also had high accuracy. The accuracy of the other techniques was poor. The combination of $P_s$ and $P_L$ offered high accuracy for all DL techniques and GPR. The average accuracy of DL techniques was higher than that of ML techniques.

Figure 10 demonstrates the estimated ESR accuracy using various input signals from the FFT analysis and HPF1. Similar to the estimated capacitance in Figure 9, the accuracy for all AI techniques improved when the input signals related to the source and capacitor were employed; whereas, the load input signals performed poorly for all learning models. The GRU accuracy among the three DL techniques was higher than that of the DNN and LSTM. The GPR offered the highest accuracy compared to other ML techniques. The ELR, linear regression, and decision trees performed poorly compared with all the remaining models. The overall accuracy of the DL models was higher than that of the ML models.

Figure 11 illustrates the average accuracy of the estimated capacitance using various input signals from the FFT analysis and LPF2. The source and capacitor input signals provided higher accuracy than the input related to the load for all learning techniques. The GRU technique provided the highest accuracy compared to the other techniques. The overall accuracy of the DL techniques was higher than that of the ML techniques. The accuracy of the other ML techniques was mediocre or poor. The performance of LPF1 was excellent compared to LPF2. In another study [8], odd harmonic signals were used in the inverter system to estimate the capacitance. These harmonics are located in the range of LPF1, which is why the accuracy of LPF1 was higher than that of LPF2, especially for ML models.

Figure 12 demonstrates the estimated ESR accuracy using various input signals from the FFT analysis and HPF2. Similar to the estimated ESR in Figure 10, the accuracy of all AI techniques improved when the input signals related to the source and capacitor were employed. However, the improvement was considerably affected by the HPF2. The overall accuracy for all learning models was higher when using HPF1 rather than HPF2. This is because the magnitudes of high-frequency signals are generally smaller than low-frequency signals. Thus, the differences between low-frequency signals are more visible for classification than high-frequency signals. Hence, the performance of HPF1 was superior to that of HPF2.

Figure 13 presents the average accuracy of the estimated capacitance using various input signals from the DWT analysis. The inputs related to the source and capacitor provided higher accuracy than those related to the load for all learning techniques. Compared with other AI models, the GRU technique provided the highest accuracy when using the source and capacitor input signals. Among the five ML models, GPR showed the best accuracy. The overall accuracy of the DL techniques was higher than that of the ML techniques. The performance of the estimated capacitance using the DWT analysis was similar to the performance of the estimated capacitance using the FFT analysis with LPF1 and was higher than that of LPF2 (Figure 8), especially for ML techniques.

Figure 14 demonstrates the average accuracy of the estimated ESR using various input signals from the DWT analysis. The accuracy of all AI techniques was higher when the input signals related to the source and capacitor were employed. The load input signal caused significant errors for all AI models. The GRU and GPR were the best techniques with the lowest errors; whereas, the ELR and decision trees performed poorly. Other techniques displayed mediocre performances. Compared with HPF1 and HPF2, the DWT offers higher accuracy for ML techniques.

Figure 15 presents the comparison of all input signals. The load signals (load current, voltage, and power) showed poor performances when their average accuracies were far from 100% accuracy. The combination of source and load power demonstrated the redundancy of the load signal; its average accuracy was closer to the source signals than the load signals. Similarly, the combination of all input signals shared the same trend when its average accuracy linked the capacitor and source signals. Comparing the capacitor and source signals, the source current offers a lower deviation than the capacitor current and voltage. The measure of capacitor current can be obtained using direct or indirect methods. The direct method is achieved by inserting an additional current sensor. However, this solution results in extra costs and is difficult to implement when the number of capacitors is increased. The indirect method involves obtaining the capacitor current by using the circuit relationship and switching states. However, this solution should be used for a general converter and fixed switching frequency to improve the obtained capacitor current accuracy. Generally, the deviations are lower when the input signals contain the signals related to the source for capacitor estimation. Figure 16 illustrates the performance of all advanced learning techniques. Among the eight learning techniques, DL techniques showed superior performance compared to ML techniques because the number of layers and neurons in the DL techniques is more than in ML. Thus, the overall accuracies of the DL techniques were higher than those of the ML techniques. Furthermore, DWT analysis does not require filters to extract the essential characteristics. This reduces the complexity and processing time of the estimation scheme.

Table 6. Comparison to other approaches.

Methods	Signal Analysis Techniques	Input Signals	Indexes	Hidden Layers	Learning Technique	Highest Accuracy
Ref. [20]	FFT + filter	Capacitor ripple voltage	X	1	DNN	99.9%
Ref. [21]	X	Source current and capacitor ripple voltage	RMS	1	DNN	99.9%
Proposed scheme	DWT	Source current	RMS, average, median, variance	3	LSTM	99.9%

compares the proposed estimation scheme and other approaches. The proposed scheme utilizes DWT analysis, whereas other techniques use FFT analysis and a filter. The measurement of capacitor ripple voltage requires more effort than the measurement of the source voltage. All monitoring schemes utilize DL techniques and offer high accuracy. This research may be helpful when choosing AI techniques, types of input, and signal processing algorithms; therefore, this study might contribute to assembling reliable and safer systems involving capacitor estimation schemes associated with different primacies, such as reliability, execution time, costs, and robustness.

5. Conclusions

This study has demonstrated the parameter estimation of a capacitor using source current as an input signal and various advanced algorithms. Other signals were also employed to evaluate the performance. Conventional approaches commonly obtain the capacitor current directly from the sensor or indirectly from the circuit relationship. This drawback increases the complexity and cost of the estimation scheme. The measure of capacitor current can be performed using direct or indirect methods. The direct method involves inserting an additional current sensor. However, this solution results in extra costs and is difficult to implement when the number of capacitors is increased. The indirect solution involves obtaining the capacitor current from the circuit relationship and switching states. However, this solution should be used for a general converter and fixed switching frequency to improve the obtained capacitor current accuracy. The load signals (load current, voltage, and power) showed poor performances when their average accuracies were far from 100% accuracy. This is because the load signals are affected by various factors, such as switching noise, nonlinear loads, or the reduction of signal quality in transmission when the system contains numerous transmission stages. Comparing the capacitor and source signals, the source current offers a lower deviation than the capacitor current and voltage. Therefore, using source current instead of capacitor current as input could be an excellent solution. The combination of source and load power demonstrates the redundancy of the load signal; its average accuracy is closer to the source signals than the load signals. Similarly, the combination of all input signals shares the same trend when its average accuracy links the capacitor and source signals. The capacitance and ESR dominate in different ranges in the frequency domain. Thus, this research has analyzed frequency domain signals using FFT and DWT algorithms. Additionally, the DWT analysis does not require filters with different frequency ranges. This reduces the complexity and processing time of the estimation scheme. Among the eight learning techniques, DL techniques showed superior performance compared to ML techniques because the number of layers and neurons in the DL techniques is greater than that in the ML techniques. Thus, the processing ability of DL techniques, especially LSTM, is superior compared to ML techniques and the overall accuracies of DL techniques are higher than ML techniques whether FFT or DWT analysis is adopted. The difficulty of using DL models is the selection of suitable hidden configurations. Nevertheless, there is no way to ensure that the chosen configurations yield the best execution for all circumstances. Furthermore, all AI algorithms’ results vary with the working circumstances (current amplitudes, types of loads, and switching frequency). This indicates that the optimal configurations in one particular situation are not ideal for others. A possible solution is to use a trial-and-error method. However, it will require additional time to determine the finest arrangements. This paper provides an estimation scheme without the need for extra hardware or complex algorithms. The estimated results and comparisons validated the effectiveness of the proposed scheme.