Modeling and Simulation of a Novel Low-Speed High-Torque Permanent Magnet Synchronous Motor with Asymmetric Stator Slots
Abstract
1. Introduction
2. Structure and Analysis Model
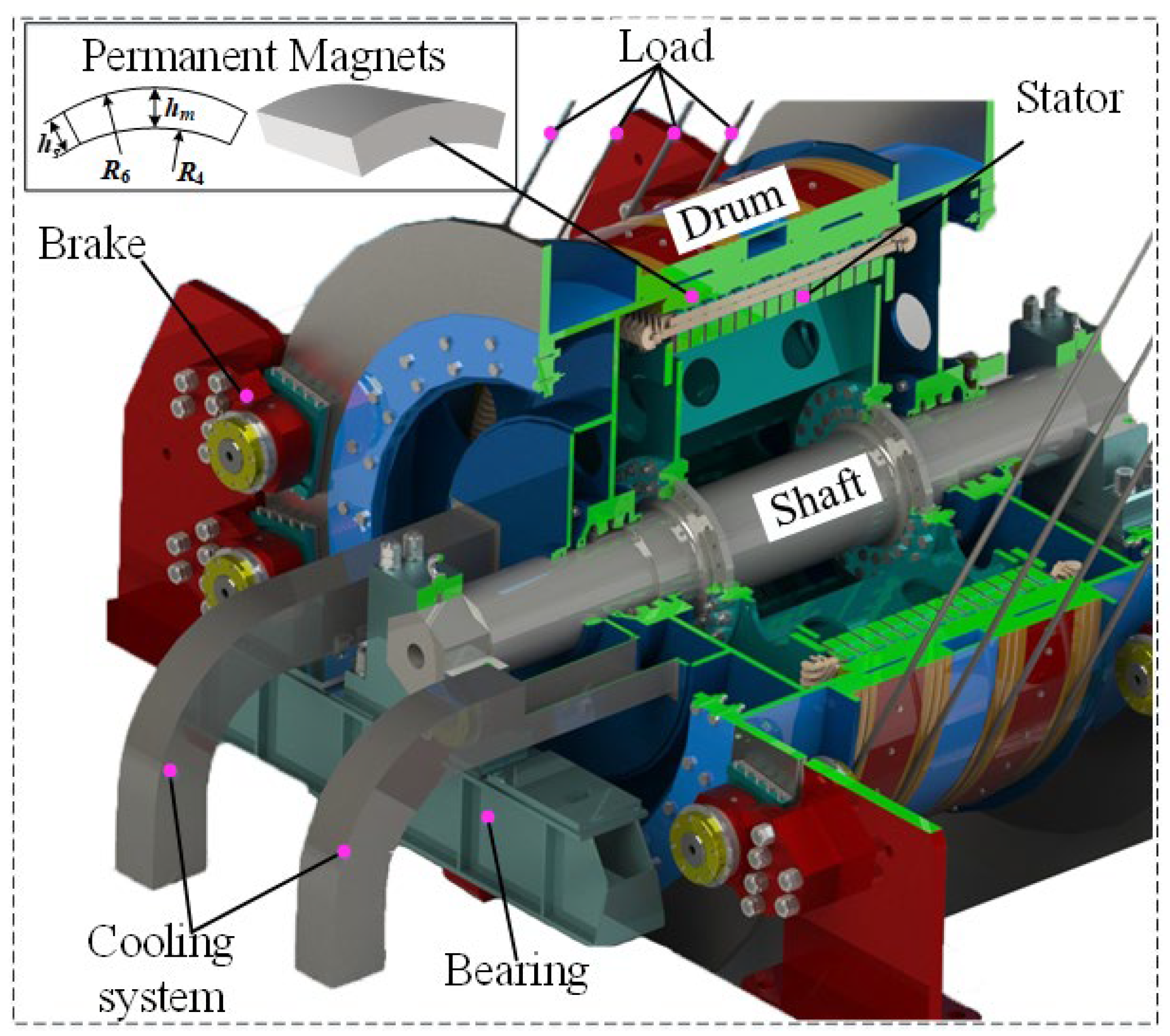
2.1. Structure of LHPMSM
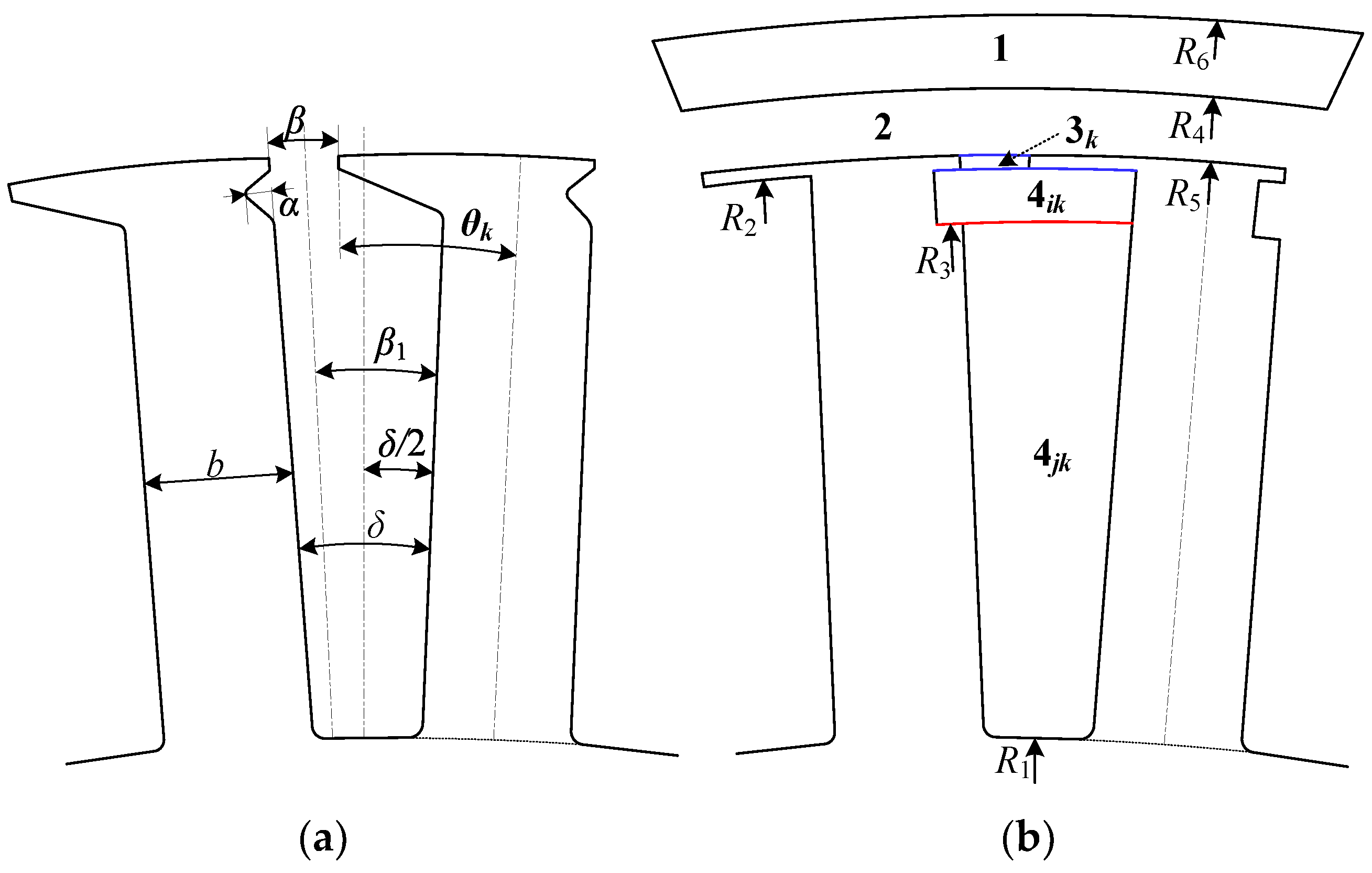
2.2. Analysis Model
- (1)
- The asymmetry of the slot opening: the deviation degree of the center line of slot opening relative to the center line of stator slot, which is defined as λ, as shown in Equation (1). It should be noted that when β1 < δ/2, the slotting effect has a serious impact on the magnetic flux density. Therefore, this situation is ignored during the analysis.
- (2)
- The asymmetry of the inside slot: the deviation degree of the center line of the asymmetric region within the slot relative to the center line of the stator slot, which is defined as
3. Analytical Solution of Magnetic Field
3.1. Field Solutions in Asymmetric Slot Opening
3.2. Field Solutions in Asymmetric Slot Body
3.3. Cogging Torque Calculation
3.4. Field Solutions in the Rest Subdomains
4. Integration Constants
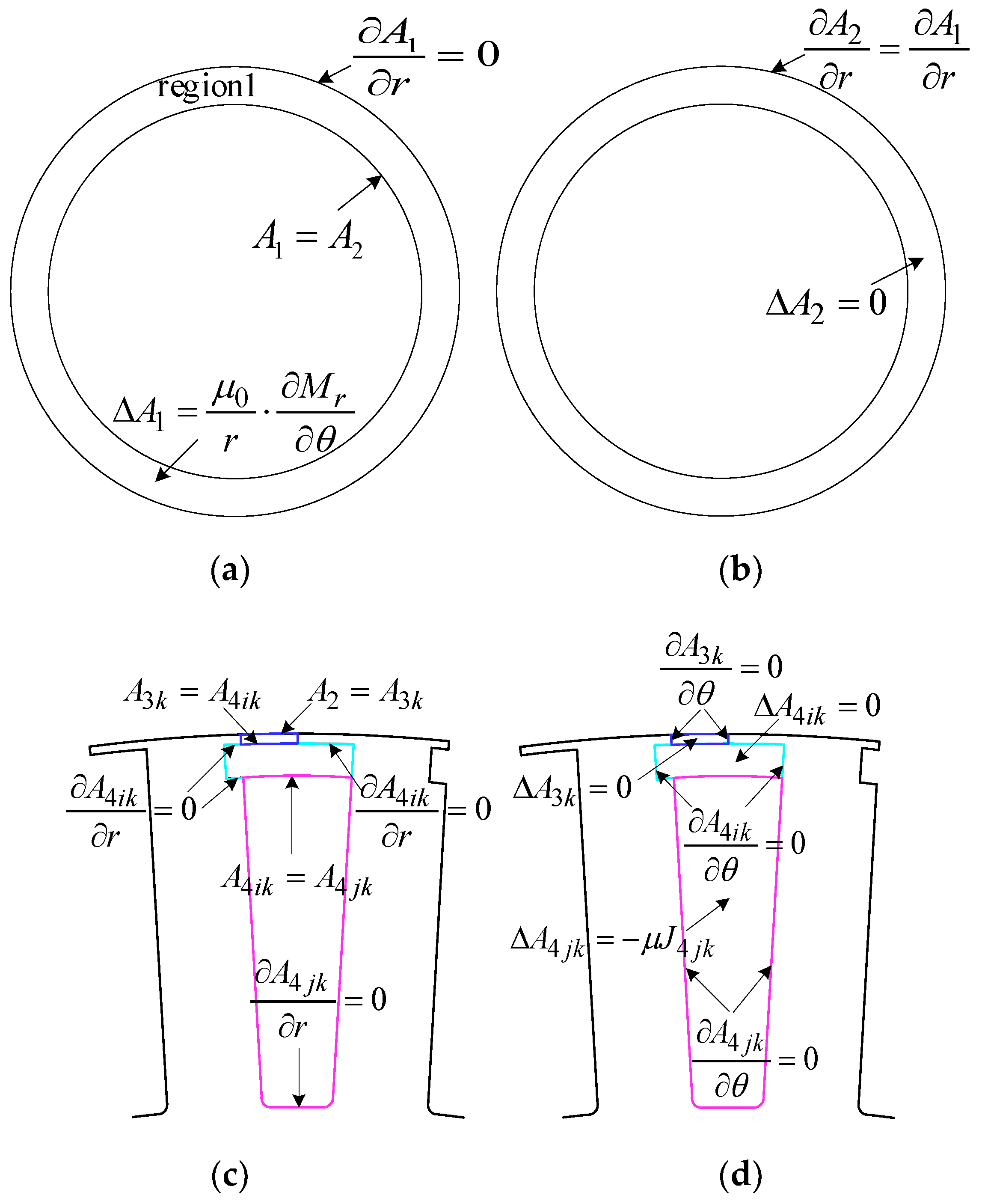
4.1. Interface between Region 1 and Region 2
4.2. Interface between Region 2 and Region 3k
4.3. Interface between Region 3k and Region 4ik
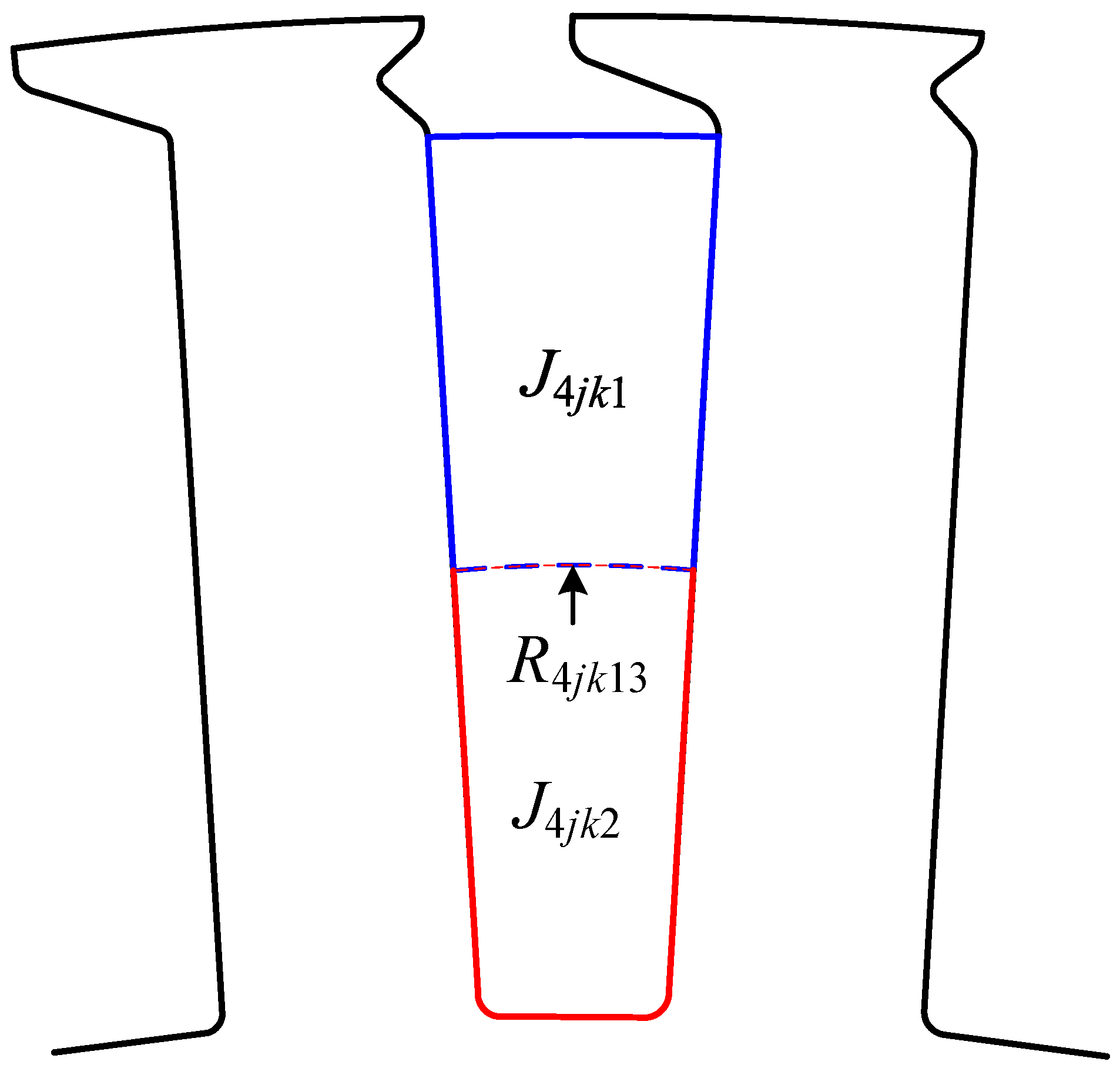
4.4. Interface between Region 4ik and Region 4jk1
4.5. Interface between Region 4jk1 and Region 4jk2
5. FEM Results and Analysis
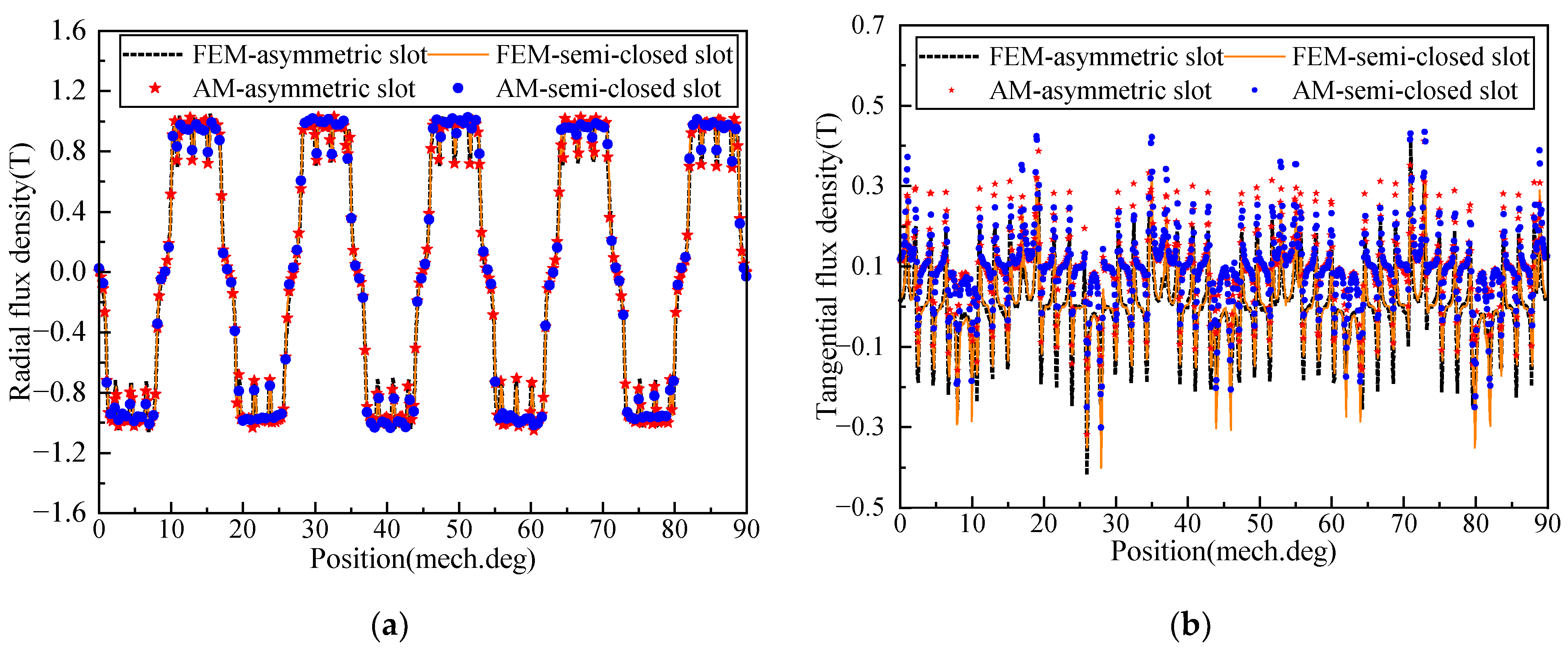
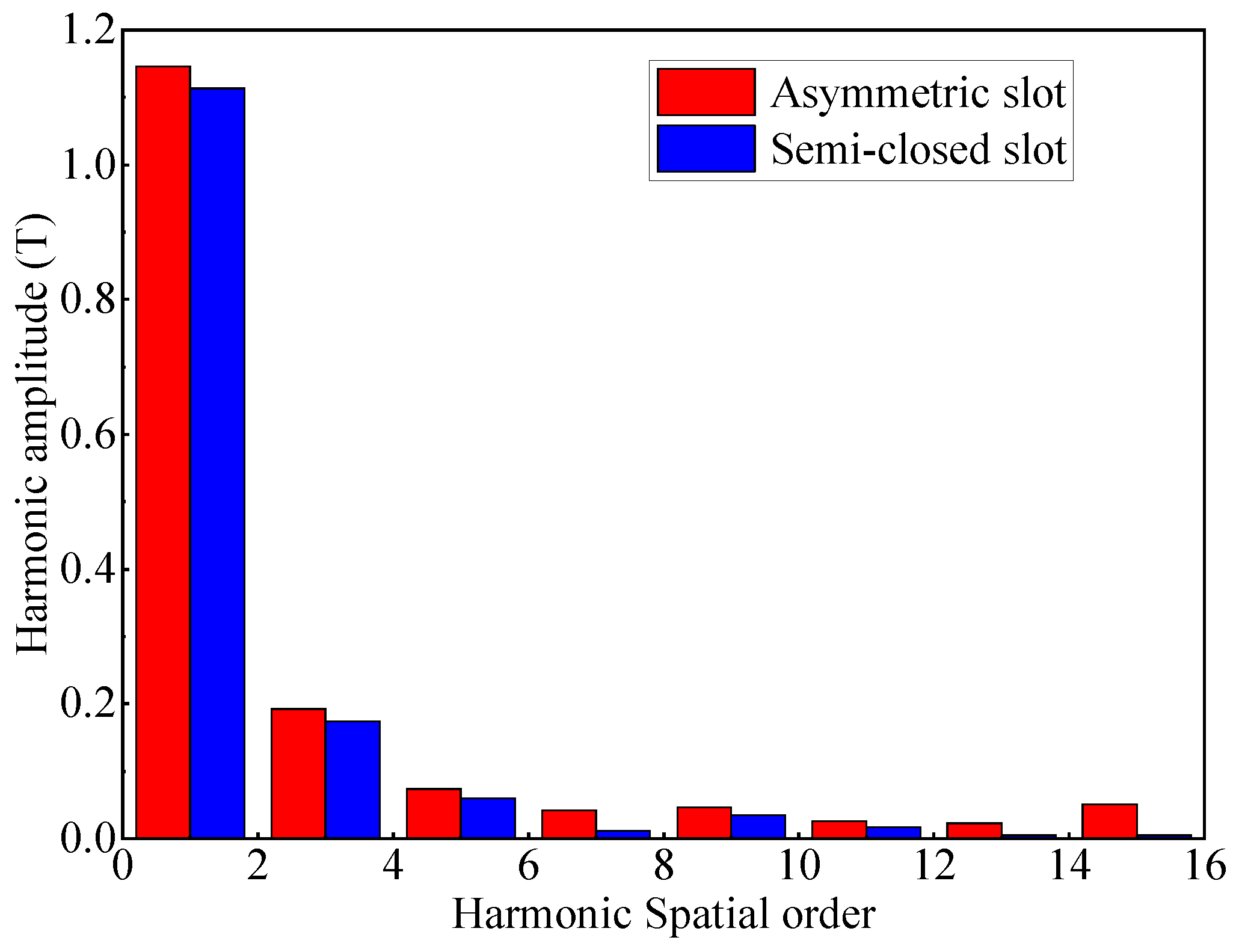
5.1. Air-Gap Magnetic Flux Density
5.2. Electromagnetic Torque and Cogging Torque
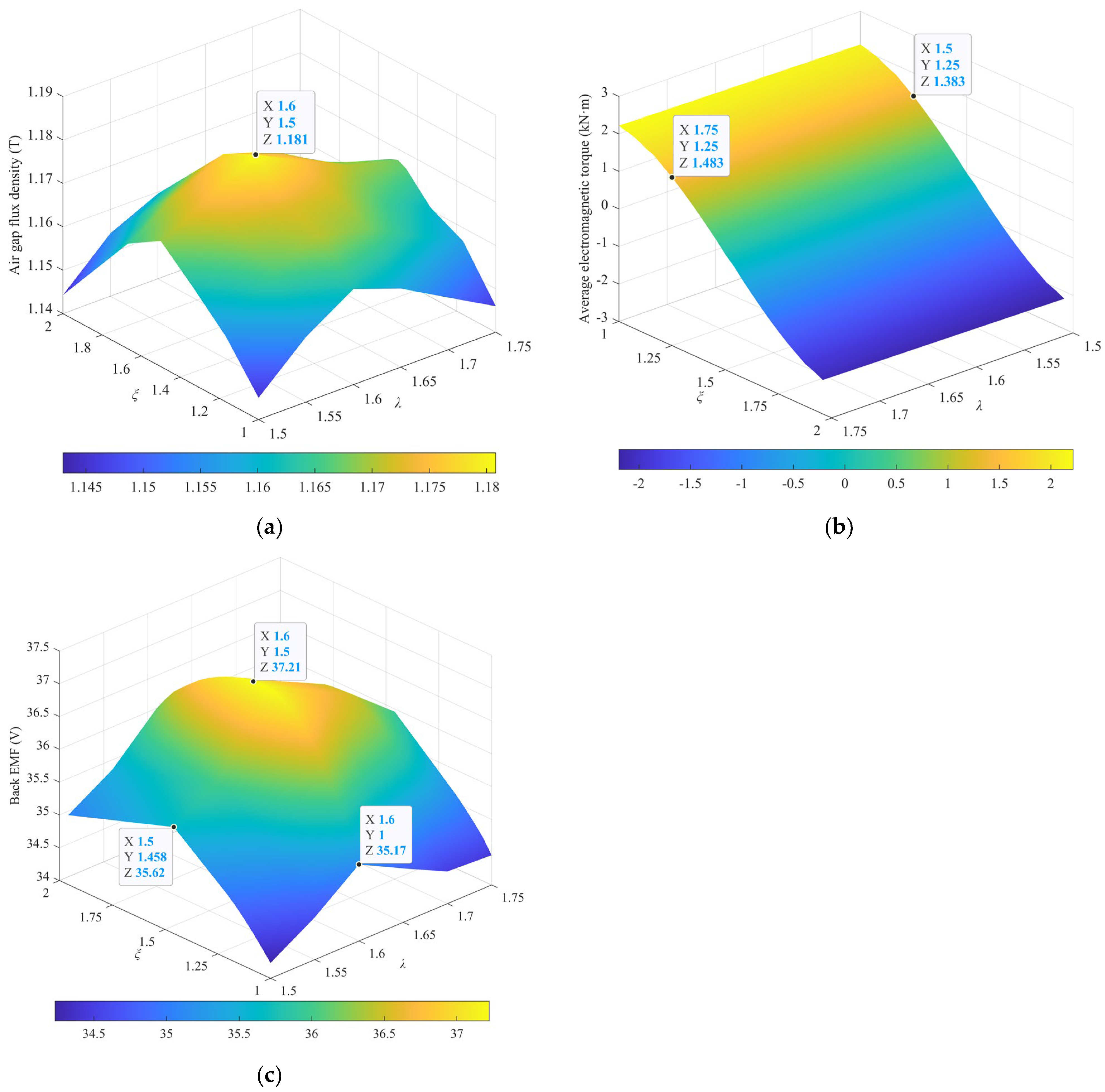
6. Influence of Key Parameters
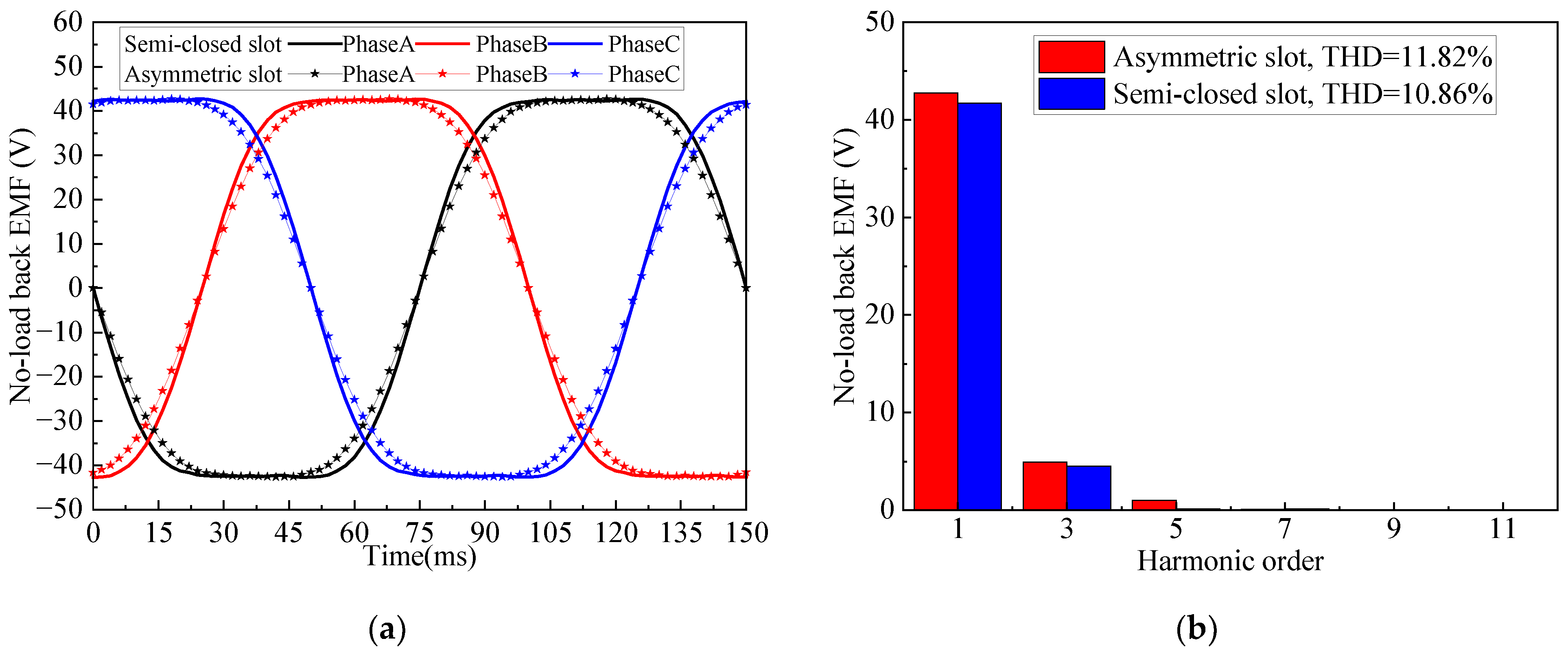
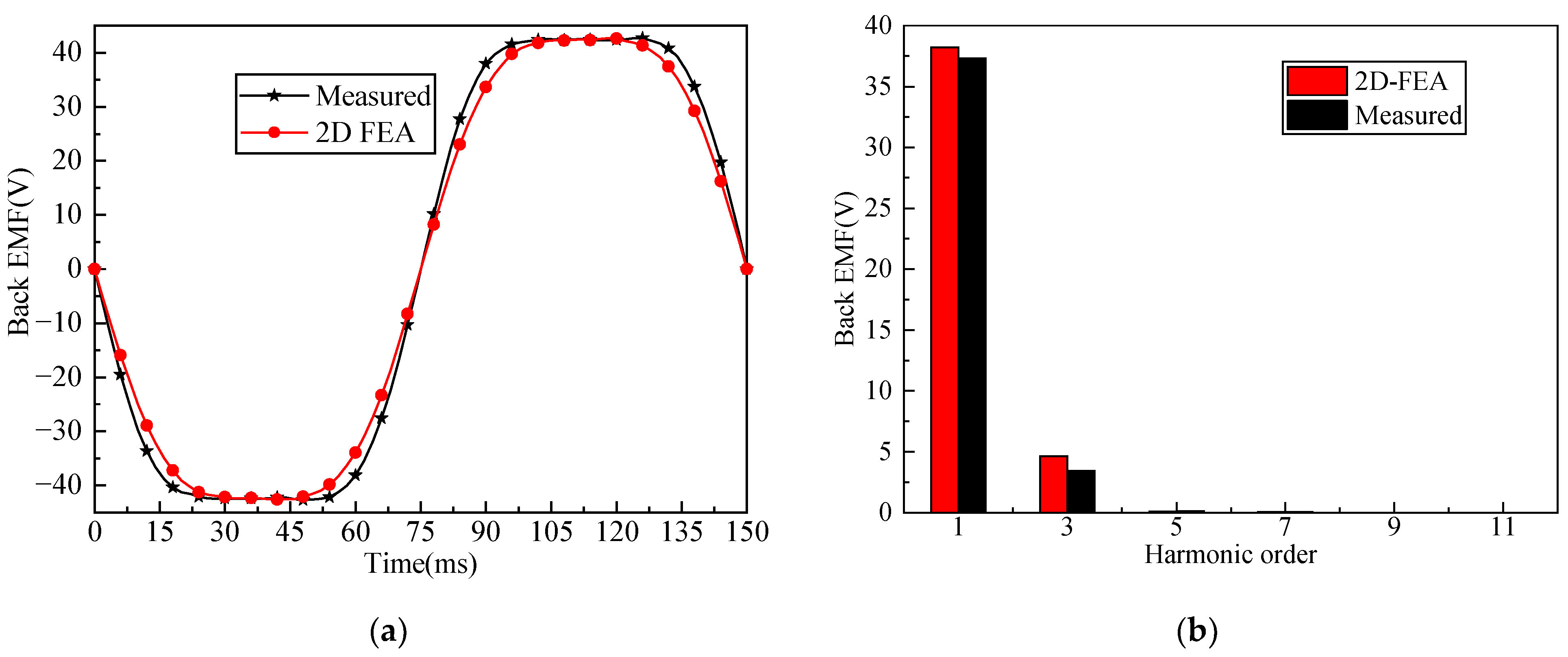
7. Experimental Result
8. Conclusions
- (1)
- For LHPMSM with multiple slots, the effective amplitude of the radial air gap flux density is increased by 2.4%, the harmonic of the air gap flux density is weakened by 8.8%, the average torque of the motor is increased by 2.6%, the torque ripple is weakened by 10.2%, and the cogging torque is weakened by 15.65% compared with the traditional semi-closed stator slot.
- (2)
- The two correction factors, i.e., the asymmetry of the slot opening λ and the asymmetry of the inside slot ξ have significant effects on the electromagnetic characteristic of the motor. Specifically, the 168-slot/40-pole LHPMSM has the best electromagnetic characteristics when λ = 1.6 and ξ = 1.5. The values of λ and ξ are related to the slot pitch angle of the stator. In addition, we found that the electromagnetic torque is slightly affected by ξ. Therefore, it is necessary to properly select the two factors to obtain the optimum electromagnetic characteristic.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lu, E.; Li, W.; Yang, X.F.; Xu, S.Y. Composite Sliding Mode Control of a Permanent Magnet Direct-Driven System For a Mining Scraper Conveyor. IEEE Access 2017, 5, 22399–22408. [Google Scholar] [CrossRef]
- Tlali, P.M.; Wang, R.J.; Gerber, S.; Botha, C.D.; Kamper, M.J. Design and Performance Comparison of Vernier and Conventional PM Synchronous Wind Generators. IEEE Trans. Ind. Appl. 2020, 56, 2570–2579. [Google Scholar] [CrossRef]
- Sheng, L.C.; Li, W.; Wang, Y.Q.; Fan, M.B.; Yang, X.F. Sensorless Control of a Shearer Short-Range Cutting Interior Permanent Magnet Synchronous Motor Based on a New Sliding Mode Observer. IEEE Access 2017, 5, 18439–18450. [Google Scholar] [CrossRef]
- Xie, B.C.; Zhang, Y.; Wang, J.Q.; Liang, B.X.; Zhang, F.G. An efficient multidisciplinary design research for the integrated low speed permanent magnet motor system based on analytical and numerical hybrid analysis. Energy Rep. 2022, 8, 199–208. [Google Scholar] [CrossRef]
- Gan, B.P.; Zhang, B.Y.; Li, Q.S.; Feng, G.H. Investigation into fault tolerant capability of new modular low-speed and high-torque direct-drive permanent magnet motor based on unequal span winding. IET Electr. Power Appl. 2021, 15, 1358–1383. [Google Scholar] [CrossRef]
- Chu, W.Q.; Zhu, Z.Q. Reduction of On-Load Torque Ripples in Permanent Magnet Synchronous Machines by Improved Skewing. IEEE Trans. Magn. 2013, 49, 3822–3825. [Google Scholar] [CrossRef]
- Wang, H.M.; Guan, P.J.; Liu, S.; Wu, S.; Shi, T.N.; Guo, L.Y. Modeling and Analyzing for Magnetic Field of Segmented Surface-Mounted PM Motors with Skewed Poles. J. Electr. Eng. Technol. 2022, 17, 1097–1109. [Google Scholar] [CrossRef]
- Pang, Y.; Zhu, Z.Q.; Feng, Z.J. Cogging Torque in Cost-Effective Surface-Mounted Permanent-Magnet Machines. IEEE Trans. Magn. 2011, 47, 2269–2276. [Google Scholar] [CrossRef]
- Ashabani, M.; Mohamed, Y. Multiobjective Shape Optimization of Segmented Pole Permanent-Magnet Synchronous Machines With Improved Torque Characteristics. IEEE Trans. Magn. 2011, 47, 795–804. [Google Scholar] [CrossRef]
- Zhao, J.; Hu, H.; Li, B. Influence of Edge Permanent-Magnet Shape on Performance of an Arc-Linear Permanent-Magnet Synchronous Machine; IEEE: New York, NY, USA, 2015. [Google Scholar]
- Wang, H.M.; Liu, S.; Wu, S.; Guo, L.Y.; Shi, T.N. Optimal Design of Permanent Magnet Structure to Reduce Unbalanced Magnetic Pull in Surface-Mounted Permanent-Magnet Motors. IEEE Access 2020, 8, 77811–77819. [Google Scholar] [CrossRef]
- Peng, C.; Wang, D.H.; Feng, Z.K.; Wang, B.D. A New Segmented Rotor to Mitigate Torque Ripple and Electromagnetic Vibration of Interior Permanent Magnet Machine. IEEE Trans. Ind. Electron. 2022, 69, 1367–1377. [Google Scholar] [CrossRef]
- Xing, Z.Z.; Wang, X.H.; Zhao, W.L. Cogging torque reduction based on segmented skewing magnetic poles with different combinations of pole-arc coefficients in surface-mounted permanent magnet synchronous motors. IET Electr. Power Appl. 2021, 15, 200–213. [Google Scholar] [CrossRef]
- Peng, C.; Wang, D.H.; Wang, B.D.; Li, J.C.; Xu, C.; Wang, X.H. Torque Ripple and Electromagnetic Vibration Suppression in Permanent Magnet Synchronous Motor Using Segmented Rotor With Different Pole Widths. IEEE Trans. Magn. 2022, 58, 5. [Google Scholar] [CrossRef]
- Wang, K.; Liang, Y.P.; Wang, D.M.; Wang, C.G. Cogging torque reduction by eccentric structure of teeth in external rotor permanent magnet synchronous motors. IET Electr. Power Appl. 2019, 13, 57–63. [Google Scholar] [CrossRef]
- Ahn, J.M.; Son, J.C.; Lim, D.K. Optimal Design of Outer-Rotor Surface Mounted Permanent Magnet Synchronous Motor for Cogging Torque Reduction Using Territory Particle Swarm Optimization. J. Electr. Eng. Technol. 2021, 16, 429–436. [Google Scholar] [CrossRef]
- Qu, H.; Zhu, Z.Q. Analysis of Split-Tooth Stator Slot PM Machine. IEEE Trans. Ind. Electron. 2021, 68, 10580–10591. [Google Scholar] [CrossRef]
- Huang, J.X.; Sui, Y.; Yin, Z.S.; Yuan, Z.H.; Zheng, P. A Novel High Torque Density Dual Three-Phase PMSM With Low Space Harmonic Content. IEEE Trans. Magn. 2022, 58, 7. [Google Scholar] [CrossRef]
- Xing, Z.Z.; Wang, X.H.; Zhao, W.L. Optimization of Stator Slot Parameters for Electromagnetic Vibration Reduction of Permanent Magnet Synchronous Motors. IEEE Trans. Transp. Electrif. 2022, 8, 4337–4347. [Google Scholar] [CrossRef]
- Liu, T.; Huang, S.D.; Gao, J.; Lu, K.Y. Cogging Torque Reduction by Slot-Opening Shift for Permanent Magnet Machines. IEEE Trans. Magn. 2013, 49, 4028–4031. [Google Scholar] [CrossRef]
- Petrov, I.; Ponomarev, P.; Alexandrova, Y.; Pyrhonen, J. Unequal Teeth Widths for Torque Ripple Reduction in Permanent Magnet Synchronous Machines With Fractional-Slot Non-Overlapping Windings. IEEE Trans. Magn. 2015, 51, 9. [Google Scholar] [CrossRef]
- Tang, X.; Wang, X.; Sun, S.; Zhao, J. Analytical analysis and study of reduction methods of cogging torque in line-start permanent magnet synchronous motors. Proc. CSEE 2016, 36, 1395–1403. [Google Scholar] [CrossRef]
- Tang, X.; Wang, X.; Tian, M.; Meng, X. Study of reduction methods of cogging torque in line-start permanent magnet synchronous motor by changing the parameters of stator teeth and slots. Trans. China Electrotech. Soc. 2016, 31, 1–8. [Google Scholar]
- Zhao, J.; Yan, Y.-S.; Chen, H.; Liu, X.-D. Effect of different rotor configurations on torque characteristics of a 10-pole/12-slot flux switching permanent magnet machine. Electr. Mach. Control 2016, 20, 51–56. [Google Scholar] [CrossRef]
- Hu, H.Z.; Zhao, J.; Liu, X.D.; Guo, Y.G. Magnetic Field and Force Calculation in Linear Permanent-Magnet Synchronous Machines Accounting for Longitudinal End Effect. IEEE Trans. Ind. Electron. 2016, 63, 7632–7643. [Google Scholar] [CrossRef]
- Gao, L.L.; Cai, Z.Q.; Liang, Y.P.; Wang, D.M.; Niu, Q.; Li, J. An Improved Analytical Model of Magnetic Field in Surface-Mounted Permanent Magnet Synchronous Motor With Magnetic Pole Cutting. IEEE Access 2021, 9, 142804–142814. [Google Scholar] [CrossRef]






| Symbol | Quantity | Title 3 | |
|---|---|---|---|
| Semi-Closed Slot | Asymmetric Slot | ||
| p | Pole pairs number | 20 | 20 |
| Q | Slot number | 168 | 168 |
| R1 | Radius of slot bottom | 764 mm | 764 mm |
| R2 | Inner radius of slot opening | 824 mm | 824 mm |
| R3 | Outer radius of slot body | 821 mm | \ |
| R4 | Inner radius of PMs | 828 mm | 828 mm |
| R5 | Outer radius of slot opening | 825 mm | 825 mm |
| R6 | Outer radius of PMs | 840 mm | 840 mm |
| b | Tooth width of stator | 20 mm | 20 mm |
| h0 | Toothed boots height | 1 mm | 1 mm |
| l | The depth of U-shaped groove | 1.29 mm | \ |
| hs1 | The width of U-shaped groove | 3 mm | \ |
| hs2 | Stator tooth height | 57 mm | 57 mm |
| g | Air-gap length | 3 mm | 3 mm |
| αp | Pole-arc coefficient | 0.94 | 0.94 |
| λ | The asymmetry of slot opening | variable | 1 |
| ξ | The asymmetry of inside slot | variable | 1 |
| δ | Slot pitch angle of stator | 2.14° | 2.14° |
| Symbol | Quantity | Value |
|---|---|---|
| UN | Rated voltage | 380 V |
| IN | Rated current | 20 A |
| PN | Rated power | 12 kW |
| nN | Rated rotating speed | 50 rpm |
| RN | Resistance per phase | 1.05 Ω |
| \ | Number of conductors | 28 |
| \ | Number of parallel branches | 8 |
| Comparison | Air-Gap Flux Density (T) | Air-Gap Flux Density THD (%) | Average Value of Electromagnetic Torque Tavg (kN·m) | Torque Ripple (%) | Cogging Torque (N·m) | No-Load Back EMF THD (%) | |
|---|---|---|---|---|---|---|---|
| Br | Bt | ||||||
| semi-closed slot | 1.118 | 0.076 | 26.95% | 2.19 | 2.43% | 12.65 | 10.86% |
| Asymmetric slot | 1.146 | 0.082 | 29.56% | 2.25 | 2.18% | 10.67 | 11.82% |
| change | 2.4%↑ | 7.3% ↑ | 8.8% ↓ | 2.6% ↑ | 10.2% ↓ | 15.65% ↓ | 8.12% ↑ |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kou, S.; Kou, Z.; Wu, J.; Wang, Y. Modeling and Simulation of a Novel Low-Speed High-Torque Permanent Magnet Synchronous Motor with Asymmetric Stator Slots. Machines 2022, 10, 1143. https://doi.org/10.3390/machines10121143
Kou S, Kou Z, Wu J, Wang Y. Modeling and Simulation of a Novel Low-Speed High-Torque Permanent Magnet Synchronous Motor with Asymmetric Stator Slots. Machines. 2022; 10(12):1143. https://doi.org/10.3390/machines10121143
Chicago/Turabian StyleKou, Shaokai, Ziming Kou, Juan Wu, and Yandong Wang. 2022. "Modeling and Simulation of a Novel Low-Speed High-Torque Permanent Magnet Synchronous Motor with Asymmetric Stator Slots" Machines 10, no. 12: 1143. https://doi.org/10.3390/machines10121143
APA StyleKou, S., Kou, Z., Wu, J., & Wang, Y. (2022). Modeling and Simulation of a Novel Low-Speed High-Torque Permanent Magnet Synchronous Motor with Asymmetric Stator Slots. Machines, 10(12), 1143. https://doi.org/10.3390/machines10121143







