Double-Loop Control for Torque Tracking of Dry Clutch
Abstract
:1. Introduction
2. Dynamic Model
2.1. Drive System Modeling
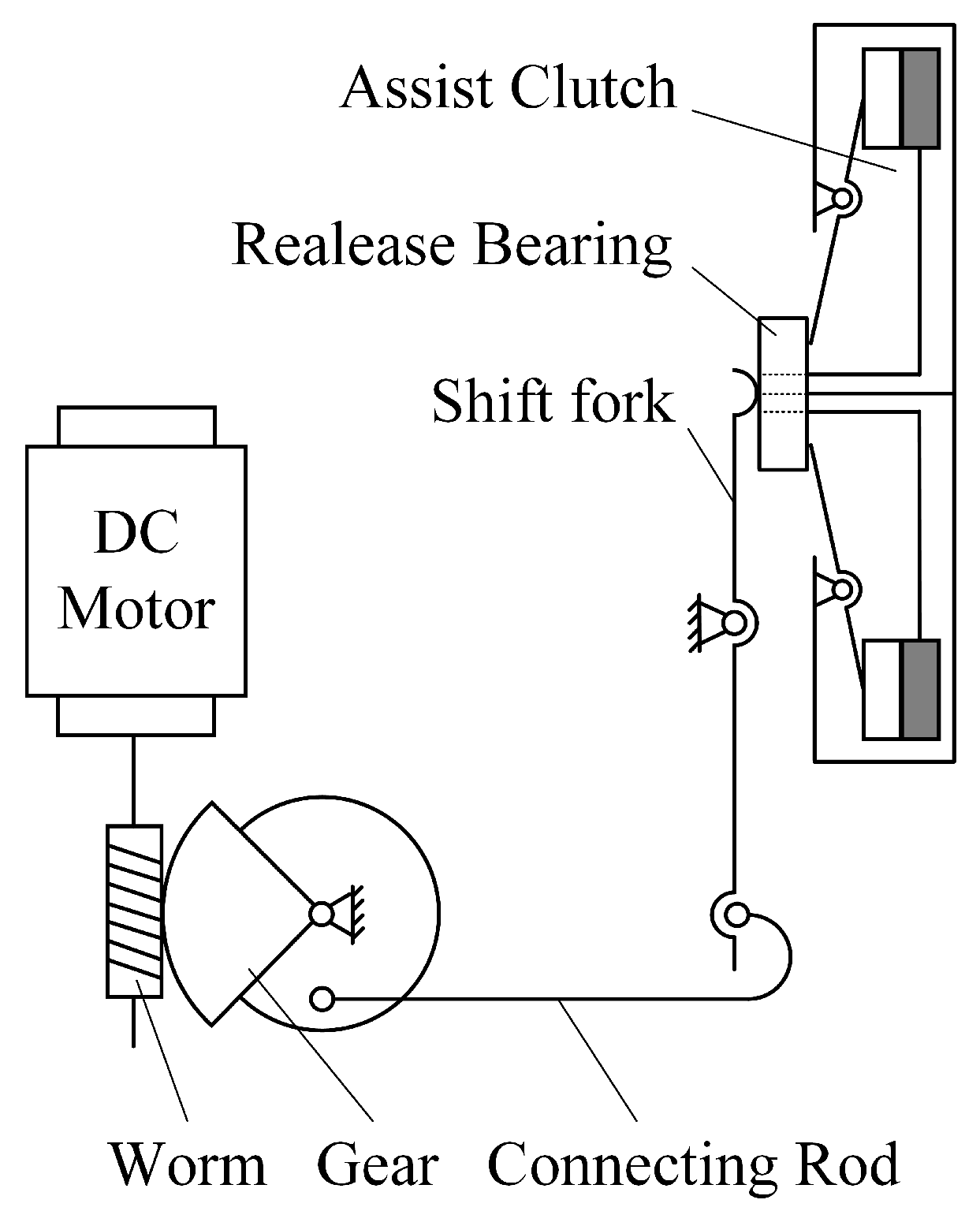
2.2. Clutch Actuator Modeling
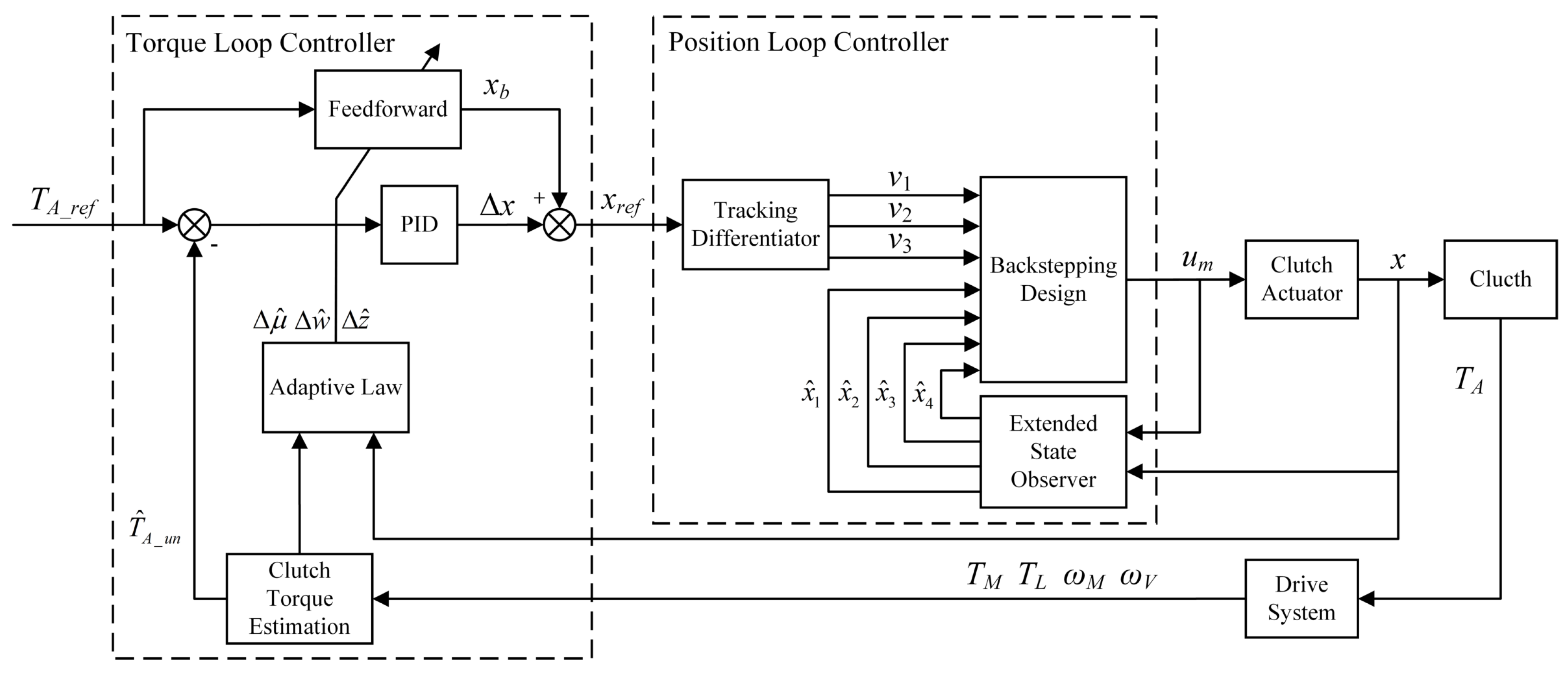
3. Design of Torque Loop Controller
3.1. Feedback Control
3.1.1. Clutch Torque Estimation
3.1.2. PID Control
3.2. Adaptive Feedforward Control
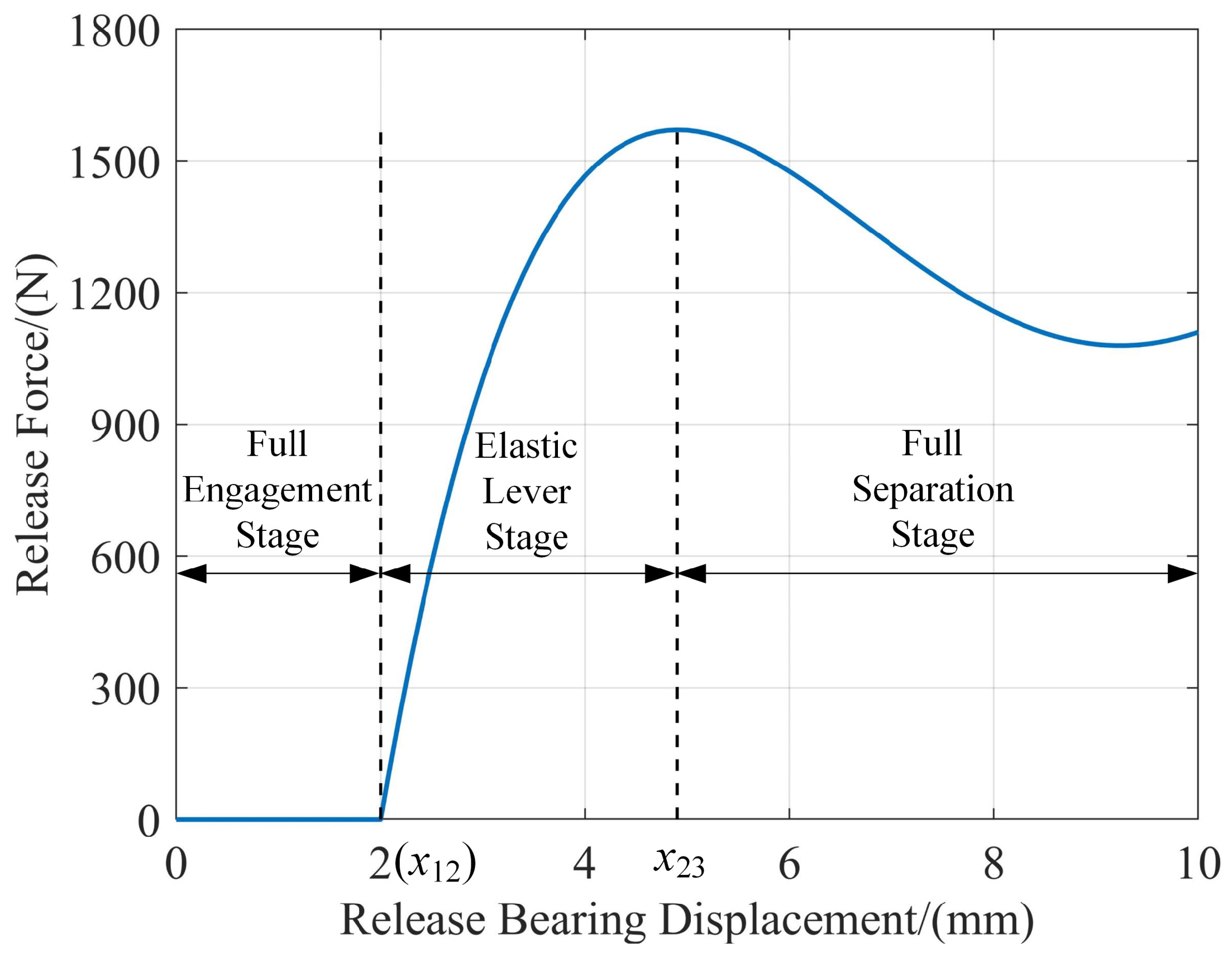
3.2.1. Separation Characteristic Curve and Torque Transmission Characteristics
3.2.2. Adaptive Estimation of Time-Varying Parameters
3.2.3. Stability Analysis
3.2.4. Feedforward Control
4. Design of Position Loop Controller
4.1. Tracking Differentiator
4.2. Extended State Observer
4.3. Backstepping Controller
- (1)
- The displacement tracking error of the release bearing is defined as:where: is the displacement tracking error of the release bearing.
- (2)
- Considering the subsystem (, ):is taken as the virtual control input of the subsystem (, ), and the virtual control error of is defined as:where: is the virtual control error of , is the virtual stabilizing controller.
- (3)
- Considering the entire system, the derivative of is:
5. Double-Loop Controller and Simulation Analysis
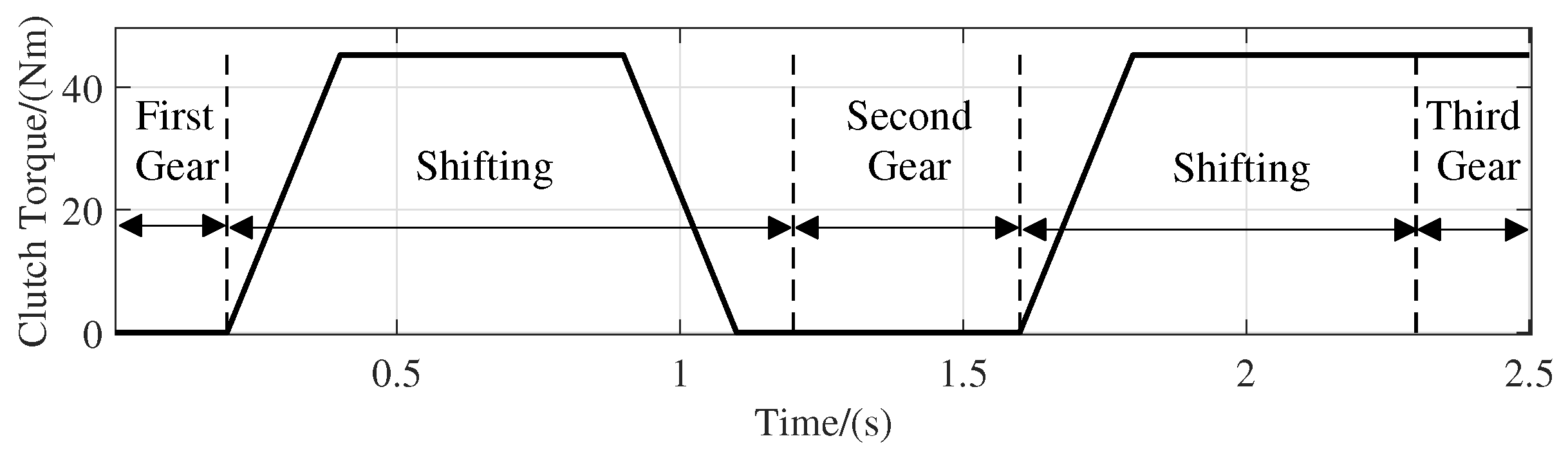
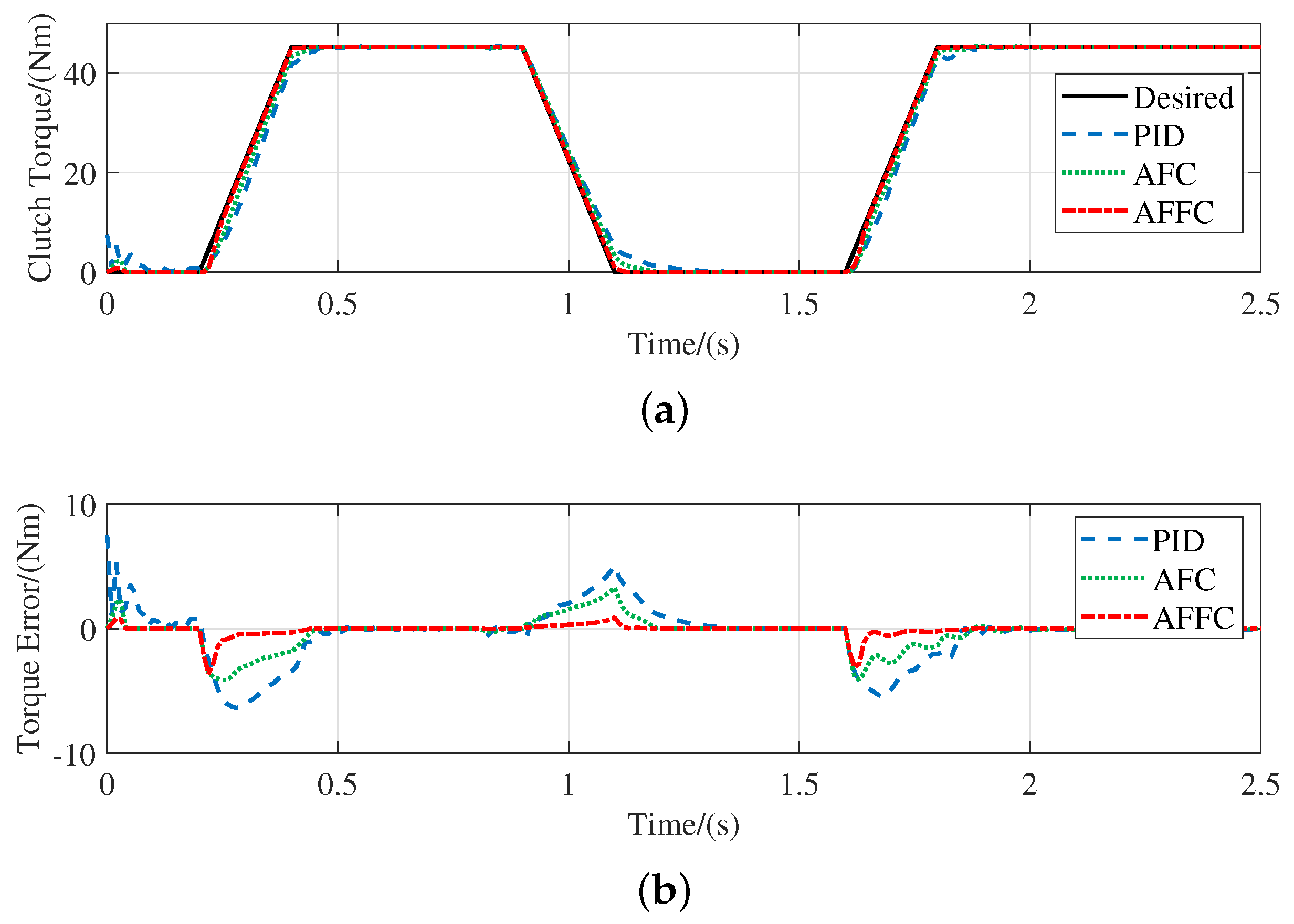
5.1. Simulation of Torque Loop controller
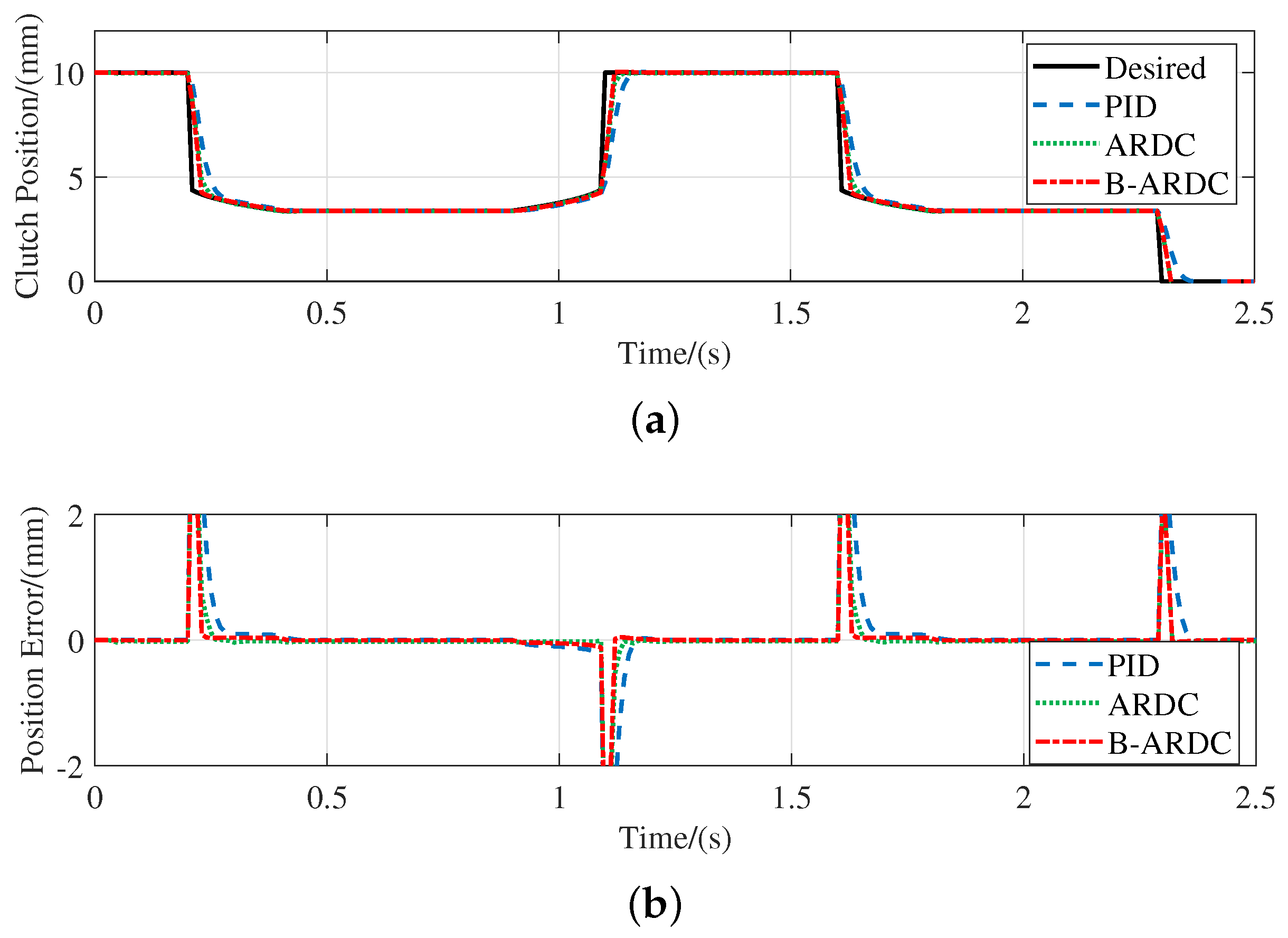
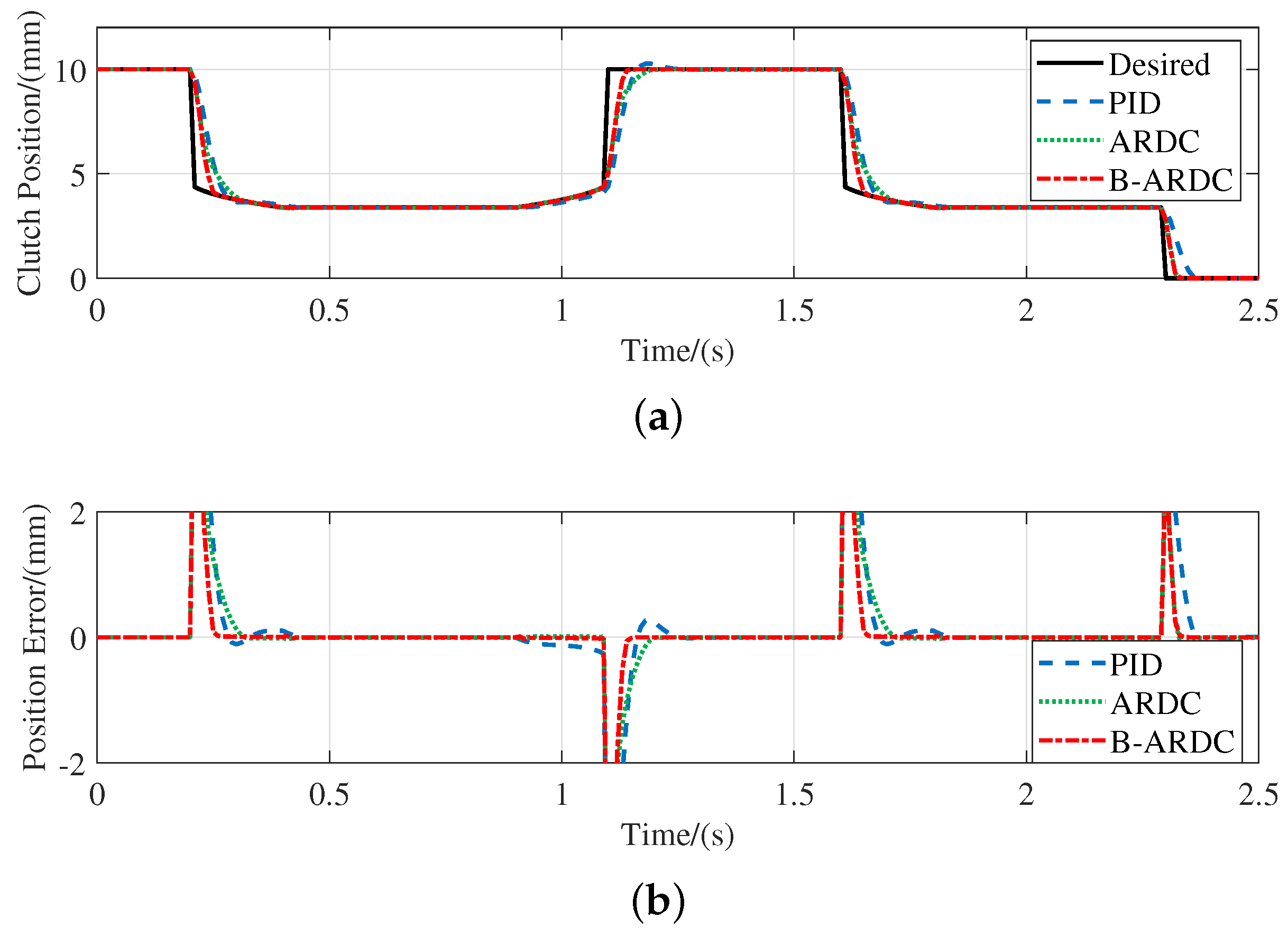
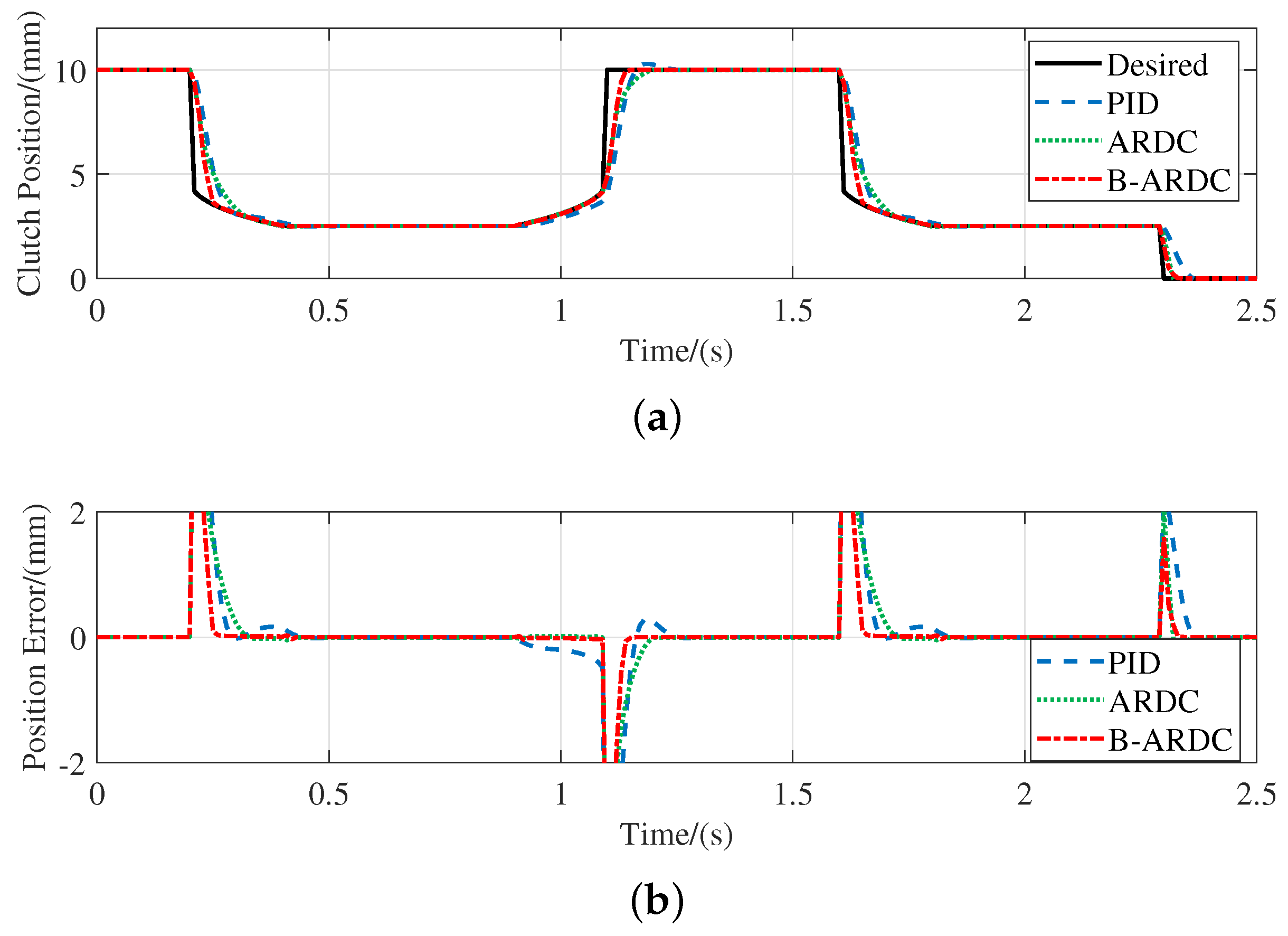
5.2. Simulation of Position Loop Controller
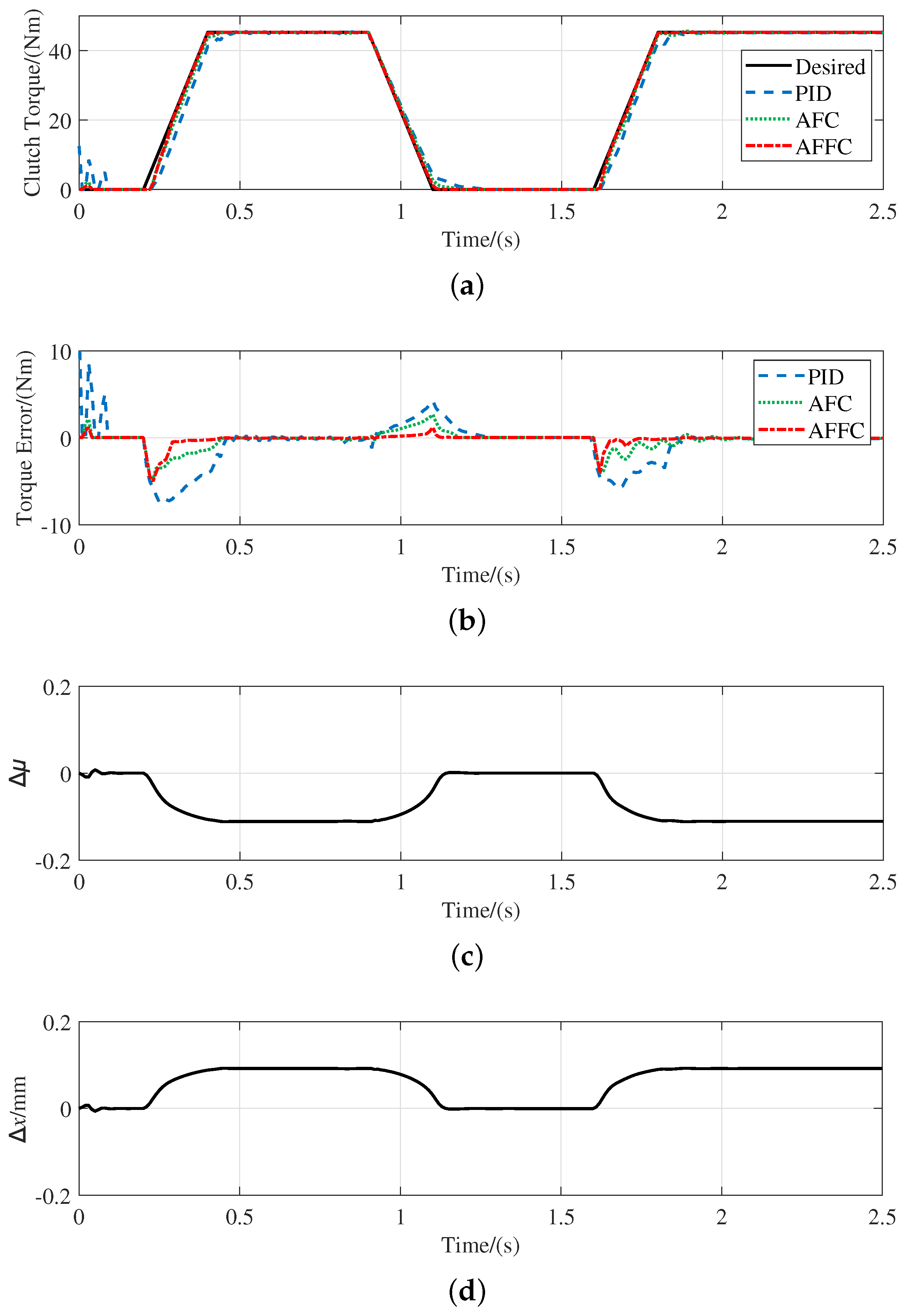
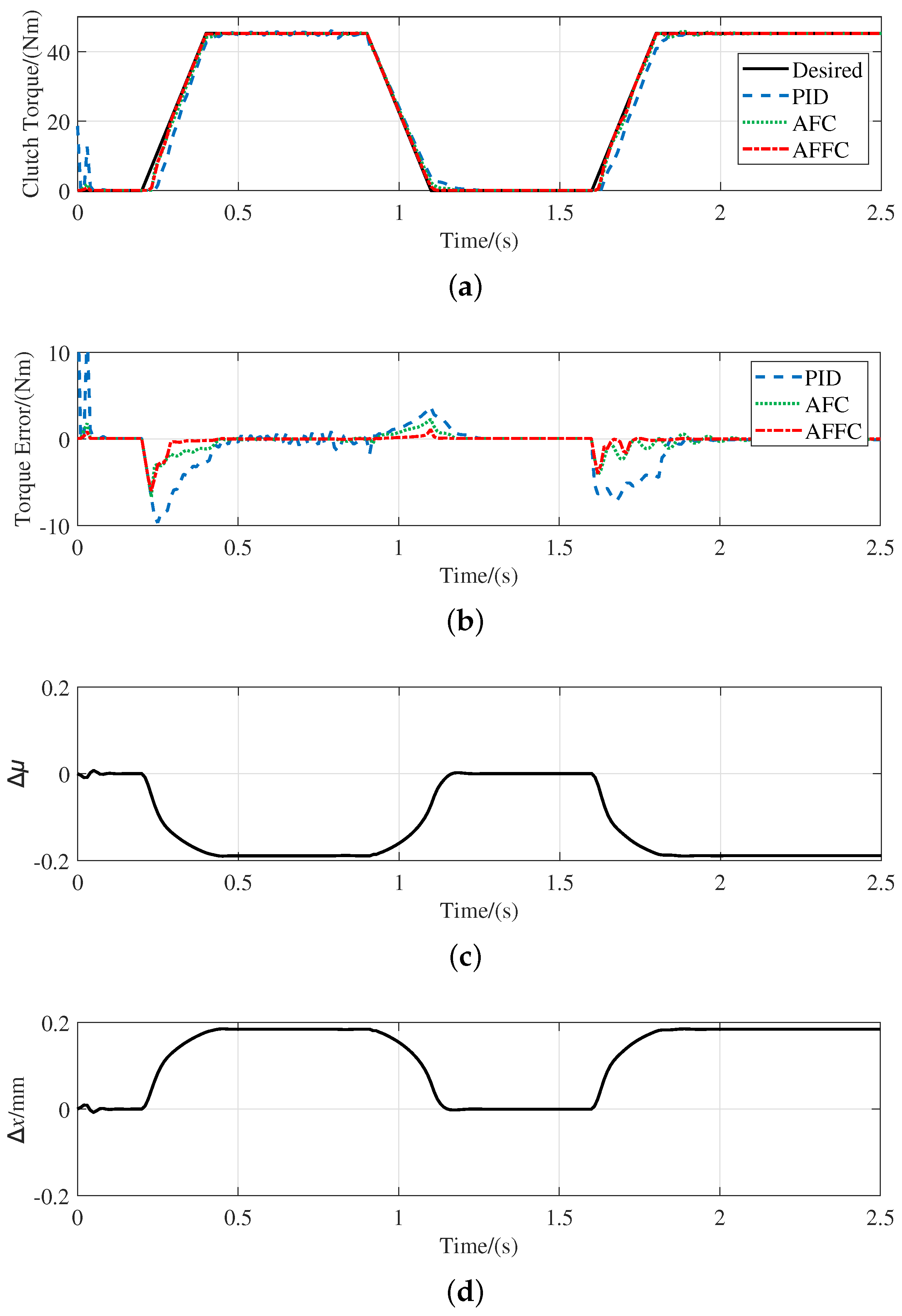
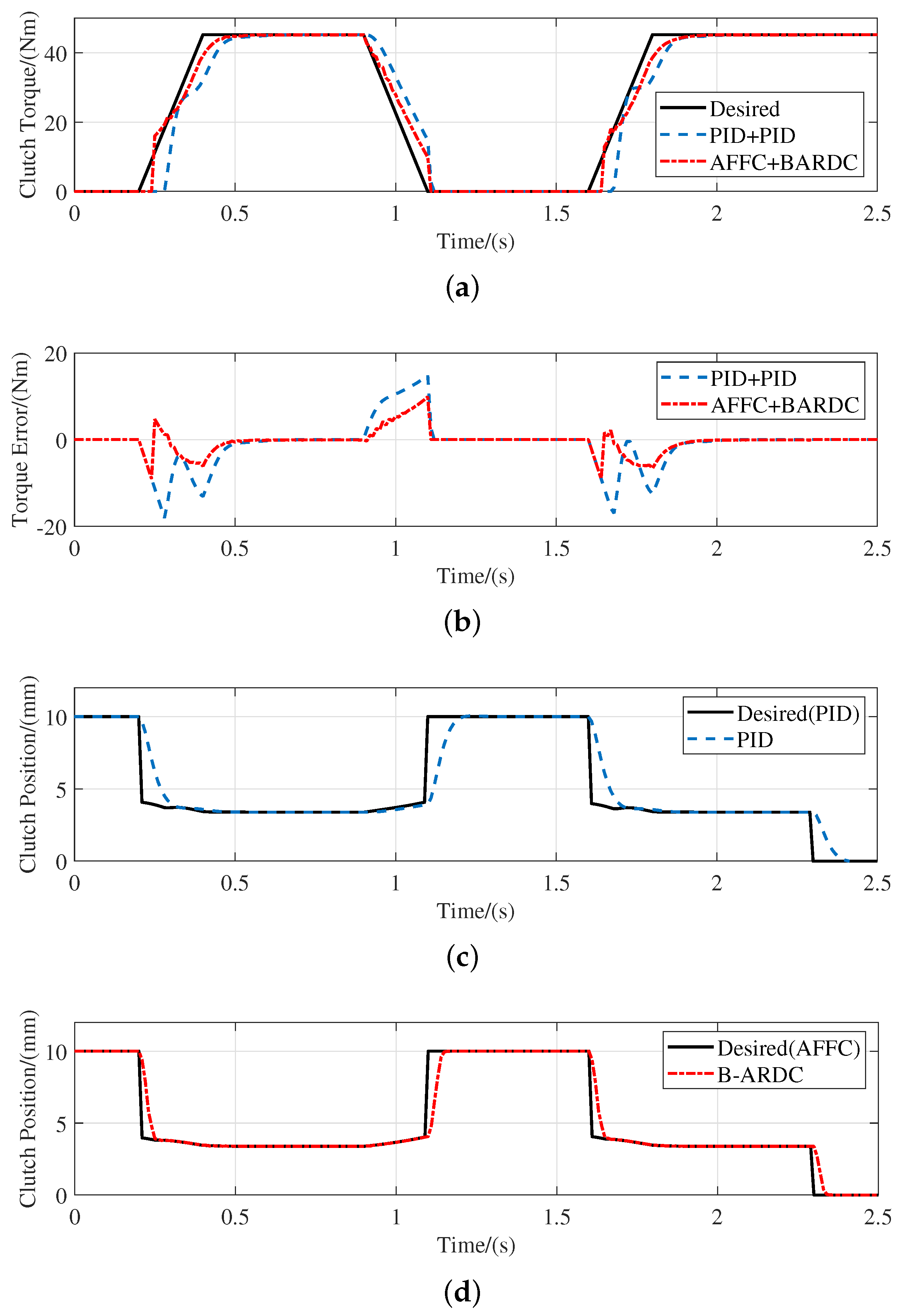
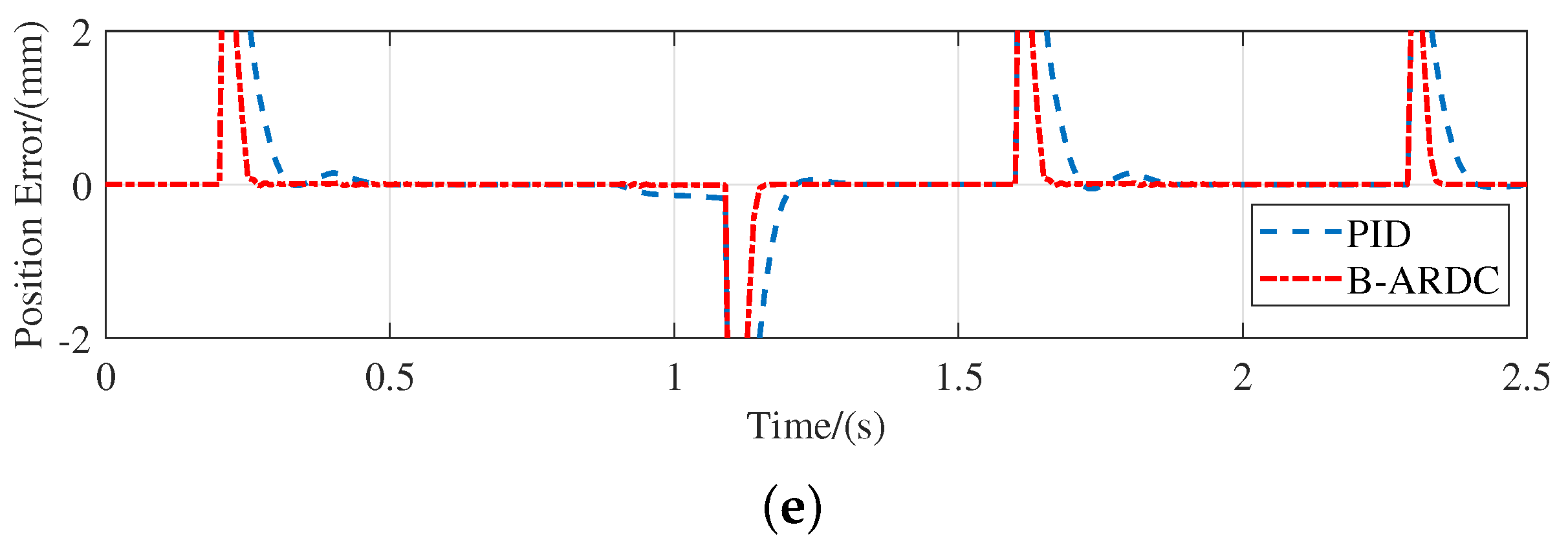
5.3. Simulation of Double-Loop Controller
6. Conclusions
- A double-loop controller with cascade control of torque loop and position loop controller is proposed to achieve torque tracking control of the dry clutch.
- The torque loop controller can adaptively control according to different time-varying parameters of the clutch, integrates the advantages of feedforward and feedback control and has fast response speed, high accuracy and strong robustness.
- The position loop controller can achieve fast and stable position tracking of the release bearing in the presence of load disturbance and unknown disturbance, and has a stronger anti-interference ability.
- Compared with the PID controller, the proposed double-loop controller can achieve better torque tracking performance, which preliminarily verifies the feasibility of the double-loop controller.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AFC | Adaptive feedforward control |
| AFFC | Adaptive feedforward-feedback control |
| AMT | Automatic mechanical transmission |
| ARDC | Active disturbance rejection control |
| B-ARDC | Backstepping based active disturbance rejection control |
| DC | Direct current |
| ESO | Extended state observer |
| PID | Proportional-integral-derivative |
| UIO | Unknown input observer |
References
- Laukenmann, M.A.; Sawodny, O. Model-Based control of a clutch actuator used in hybrid dual-clutch transmissions. Mechatronics 2021, 77, 102585. [Google Scholar] [CrossRef]
- Huang, B.; Wu, S.; Huang, S.; Fu, X.; Yang, Y. Clutch control of a hybrid electrical vehicle based on neuron-adaptive PID algorithm. Clust. Comput. 2019, 22, 12091–12099. [Google Scholar] [CrossRef]
- Sharifzadeh, M.; Pisaturo, M.; Farnam, A.; Senatore, A. Joint structure for the real-time estimation and control of automotive dry clutch engagement. IFAC-PapersOnLine 2018, 51, 1062–1067. [Google Scholar] [CrossRef]
- Meng, F.; Tao, G.; Zhang, T.; Hu, Y.; Geng, P. Optimal shifting control strategy in inertia phase of an automatic transmission for automotive applications. Mech. Syst. Signal Process. 2015, 60, 742–752. [Google Scholar] [CrossRef]
- Ouyang, T.; Lu, Y.; Li, S.; Yang, R.; Xu, P.; Chen, N. An improved smooth shift strategy for clutch mechanism of heavy tractor semi-trailer automatic transmission. Control. Eng. Pract. 2022, 121, 105040. [Google Scholar] [CrossRef]
- Shi, J.; Li, L.; Wang, X.; Liu, C. Robust output feedback controller with high-gain observer for automatic clutch. Mech. Syst. Signal Process. 2019, 132, 806–822. [Google Scholar] [CrossRef]
- Yang, C.; Jiao, X.; Li, L.; Zhang, Y.; Chen, Z. A robust H∞ control-based hierarchical mode transition control system for plug-in hybrid electric vehicle. Mech. Syst. Signal Process. 2018, 99, 326–344. [Google Scholar] [CrossRef]
- Oh, J.J.; Eo, J.S.; Choi, S.B. Torque observer-based control of self-energizing clutch actuator for dual clutch transmission. IEEE Trans. Control Syst. Technol. 2016, 25, 1856–1864. [Google Scholar] [CrossRef]
- Temporelli, R.; Boisvert, M.; Micheau, P. Accurate clutch slip controllers during vehicle steady and acceleration states. IEEE/ASME Trans. Mechatron. 2018, 23, 2078–2089. [Google Scholar] [CrossRef]
- Li, L.; Wang, X.; Qi, X.; Li, X.; Cao, D.; Zhu, Z. Automatic clutch control based on estimation of resistance torque for AMT. IEEE/ASME Trans. Mechatron. 2016, 21, 2682–2693. [Google Scholar] [CrossRef]
- Vasca, F.; Iannelli, L.; Senatore, A.; Reale, G. Torque transmissibility assessment for automotive dry-clutch engagement. IEEE/ASME Trans. Mechatron. 2010, 16, 564–573. [Google Scholar] [CrossRef]
- Gao, B.; Hong, J.; Qu, T.; Yu, S.; Chen, H. An output regulator with rejection of time-varying disturbance: Experimental validation on clutch slip control. IEEE Trans. Control. Syst. Technol. 2019, 28, 1158–1167. [Google Scholar] [CrossRef]
- Kim, J.; Choi, S.B.; Oh, J.J. Adaptive engagement control of a self-energizing clutch actuator system based on robust position tracking. IEEE/ASME Trans. Mechatron. 2018, 23, 800–810. [Google Scholar] [CrossRef]
- Park, J.; Choi, S.; Oh, J.; Eo, J. Adaptive slip engagement control of a wet clutch in vehicle powertrain based on transmitted torque estimation. Mech. Syst. Signal Process. 2022, 171, 108861. [Google Scholar] [CrossRef]
- Kim, S.; Choi, S. Control-oriented modeling and torque estimations for vehicle driveline with dual-clutch transmission. Mech. Mach. Theory 2018, 121, 633–649. [Google Scholar] [CrossRef]
- WU, X.; Zhang, X.; Chen, H.; Yang, M. Torque Tracking PID Control for HEV Automatic Diaphragm Spring Clutch. Trans. Beijing Inst. Technol. 2017, 37, 1072–1076. [Google Scholar]
- Wang, X.; Li, L.; Yang, C. Hierarchical control of dry clutch for engine-start process in a parallel hybrid electric vehicle. IEEE Trans. Transp. Electrif. 2016, 2, 231–243. [Google Scholar] [CrossRef]
- Yonggang, L.; Jingchen, Z.; Yougang, W.; Dongye, S.; Datong, Q. Adaptive shifting control for data driven dual clutch transmission. Automot. Eng. 2021, 43, 891–898+923. [Google Scholar]
- Kurniawan, E.; Harno, H.; Wang, H.; Prakosa, J.; Sirenden, B.; Septanto, H.; Adinanta, H.; Rahmatillah, A. Robust adaptive repetitive control for unknown linear systems with odd-harmonics periodic disturbances. Sci. China Inf. Sci 2022, 1, 1–18. [Google Scholar] [CrossRef]
- Kurniawan, E.; Zhenwei, C.; Zhihong, M. Digital design of adaptive repetitive control of linear systems with time-varying periodic disturbances. IET Control Theory Appl. 2014, 8, 1995–2003. [Google Scholar] [CrossRef]
- Wu, M. Hamilton Jacobi Inequality based sliding mode robust control for optimal torque transmissions of Dry Dual Clutch assembly in torque phase of shift. In Proceedings of the 2017 IEEE International Conference on Mechatronics and Automation (ICMA), Takamatsu, Japan, 6–9 August 2017; pp. 1900–1905. [Google Scholar]
- Mishra, K.D.; Srinivasan, K. Robust control and estimation of clutch-to-clutch shifts. Control Eng. Pract. 2017, 65, 100–114. [Google Scholar] [CrossRef]
- Li, L.; Wang, X.; Hu, X.; Chen, Z. A Modified PFC with Sliding Mode Observer for Automated Dry Clutch Control of Vehicle. J. Dyn. Syst. Meas. Control 2016, 136, 061005. [Google Scholar] [CrossRef]
- Gao, Y.; Liu, Q.; Li, C.; Chen, H. Launch control strategy for AMT vehicles based on ADRC. In Proceedings of the 26th Chinese Control and Decision Conference (2014 CCDC), Changsha, China, 6–9 August 2014; pp. 681–686. [Google Scholar]
- Oh, J.J.; Choi, S.B.; Kim, J. Driveline modeling and estimation of individual clutch torque during gear shifts for dual clutch transmission. Mechatronics 2014, 24, 449–463. [Google Scholar] [CrossRef]
- Sooyoung, K.; Oh, J.J.; Choi, S.B. Driveline Torque Estimations for a Ground Vehicle With Dual-Clutch Transmission. IEEE Trans. Veh. Technol. 2017, 67, 1977–1989. [Google Scholar]
- Zheng, Q.; Gaol, L.Q.; Gao, Z. On stability analysis of active disturbance rejection control for nonlinear time-varying plants with unknown dynamics. In Proceedings of the 2007 46th IEEE Conference on Decision and Control, New Orleans, LA, USA, 12–14 December 2007; pp. 3501–3506. [Google Scholar]
- Gao, B.; Liang, Q.; Xiang, Y.; Guo, L.; Chen, H. Gear ratio optimization and shift control of 2-speed I-AMT in electric vehicle. Mech. Syst. Signal Process. 2015, 50, 615–631. [Google Scholar] [CrossRef]
- Tian, Y.; Ruan, J.; Zhang, N.; Wu, J.; Walker, P. Modelling and control of a novel two-speed transmission for electric vehicles. Mech. Mach. Theory 2018, 127, 13–32. [Google Scholar] [CrossRef]
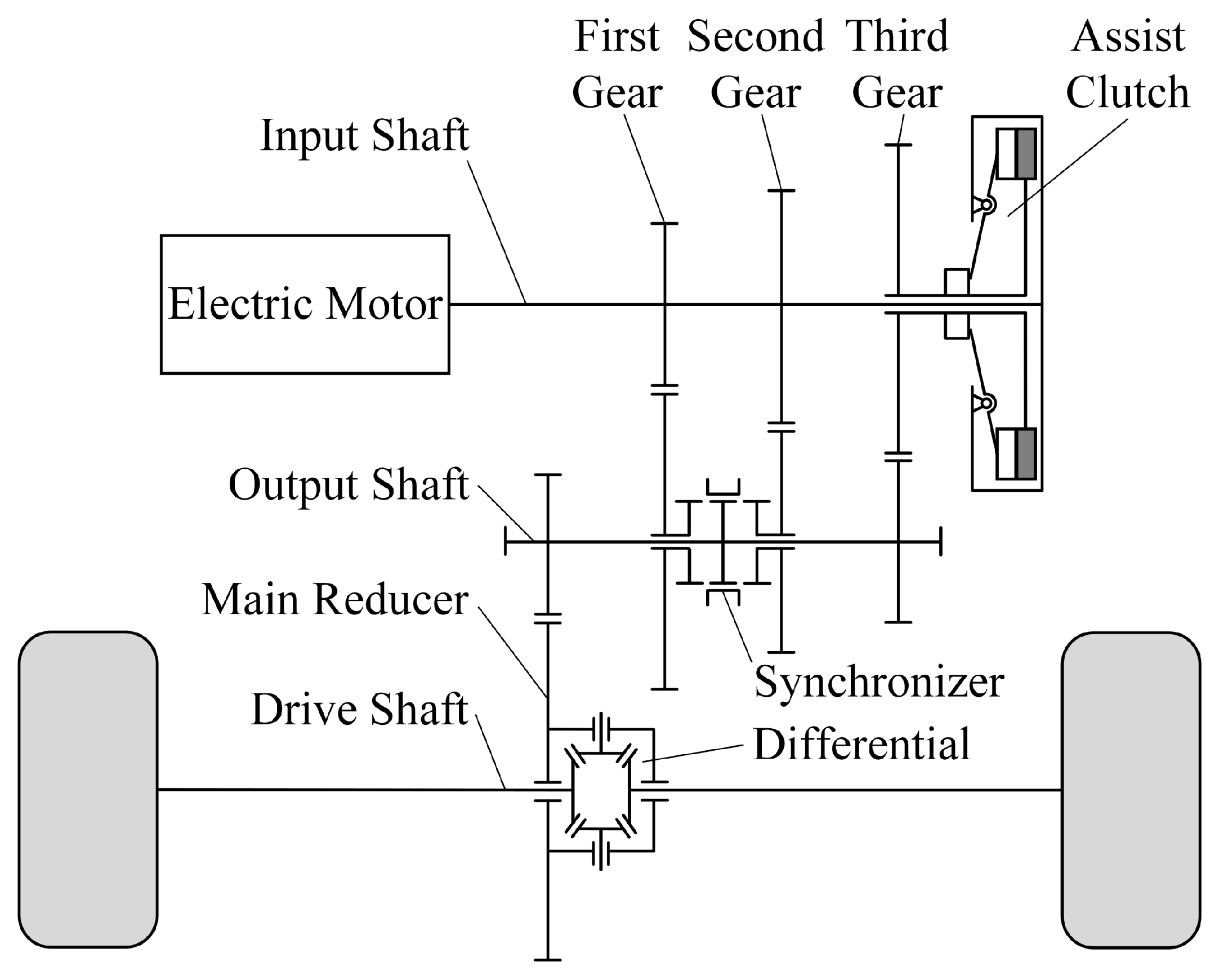
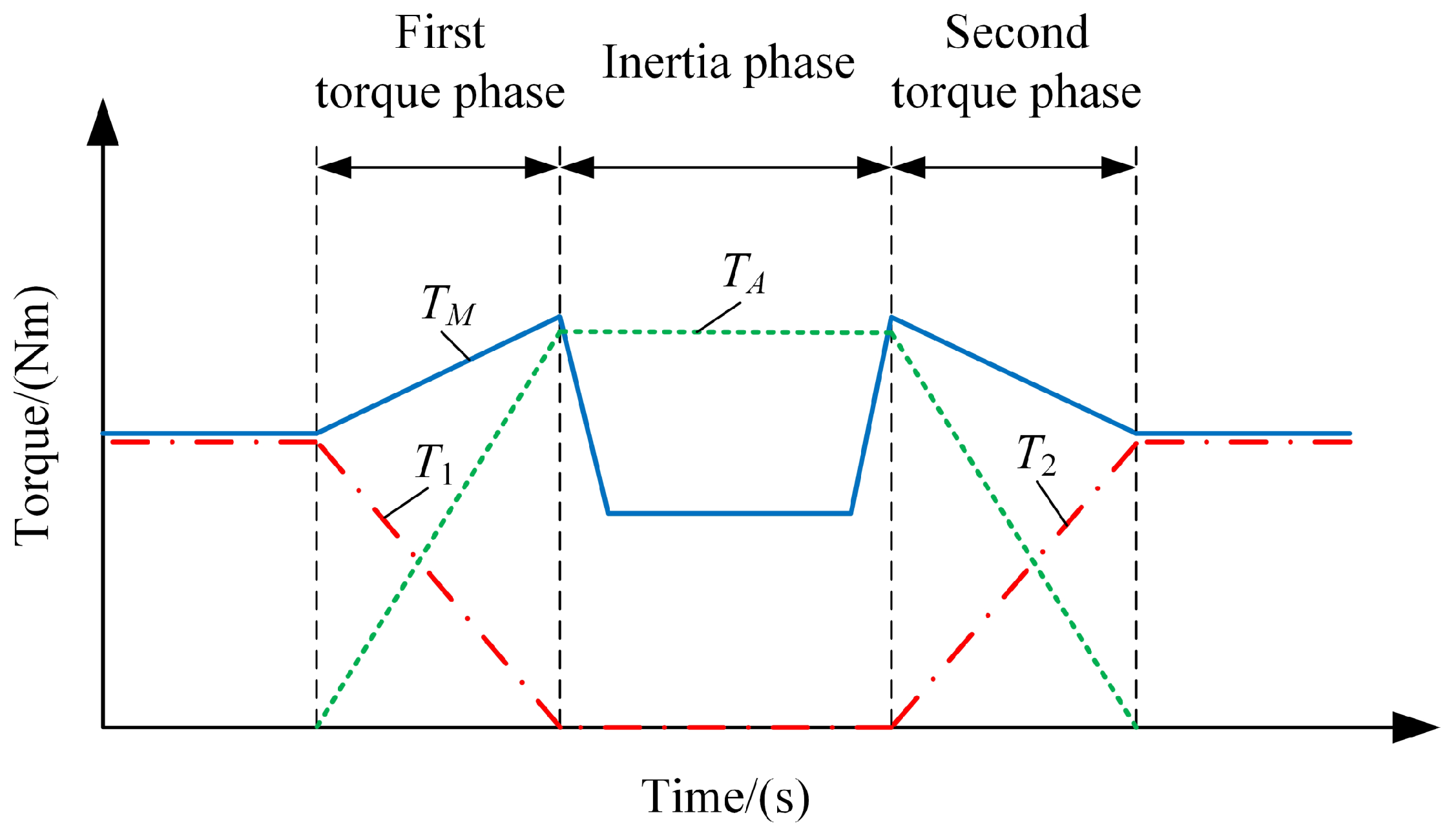
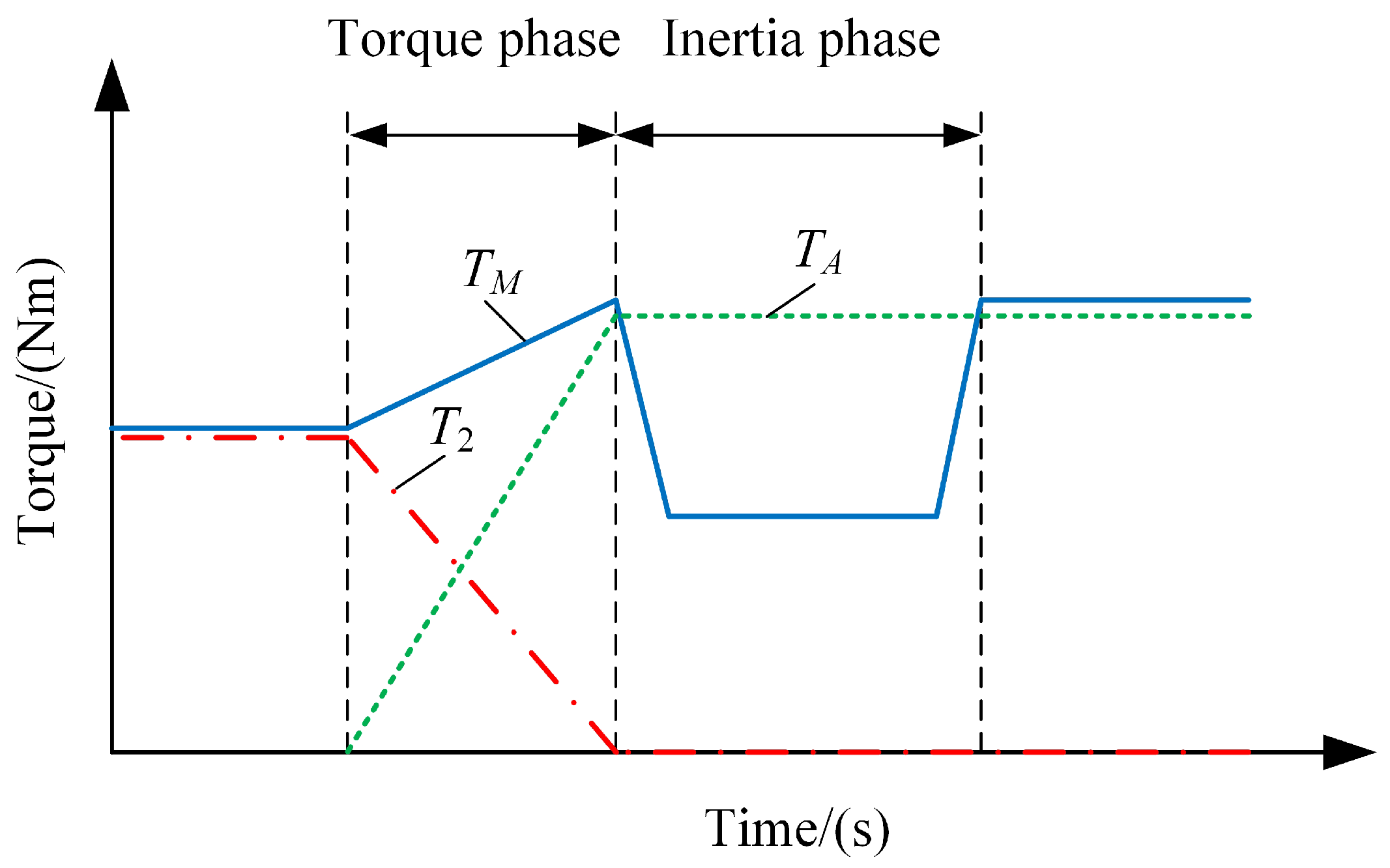
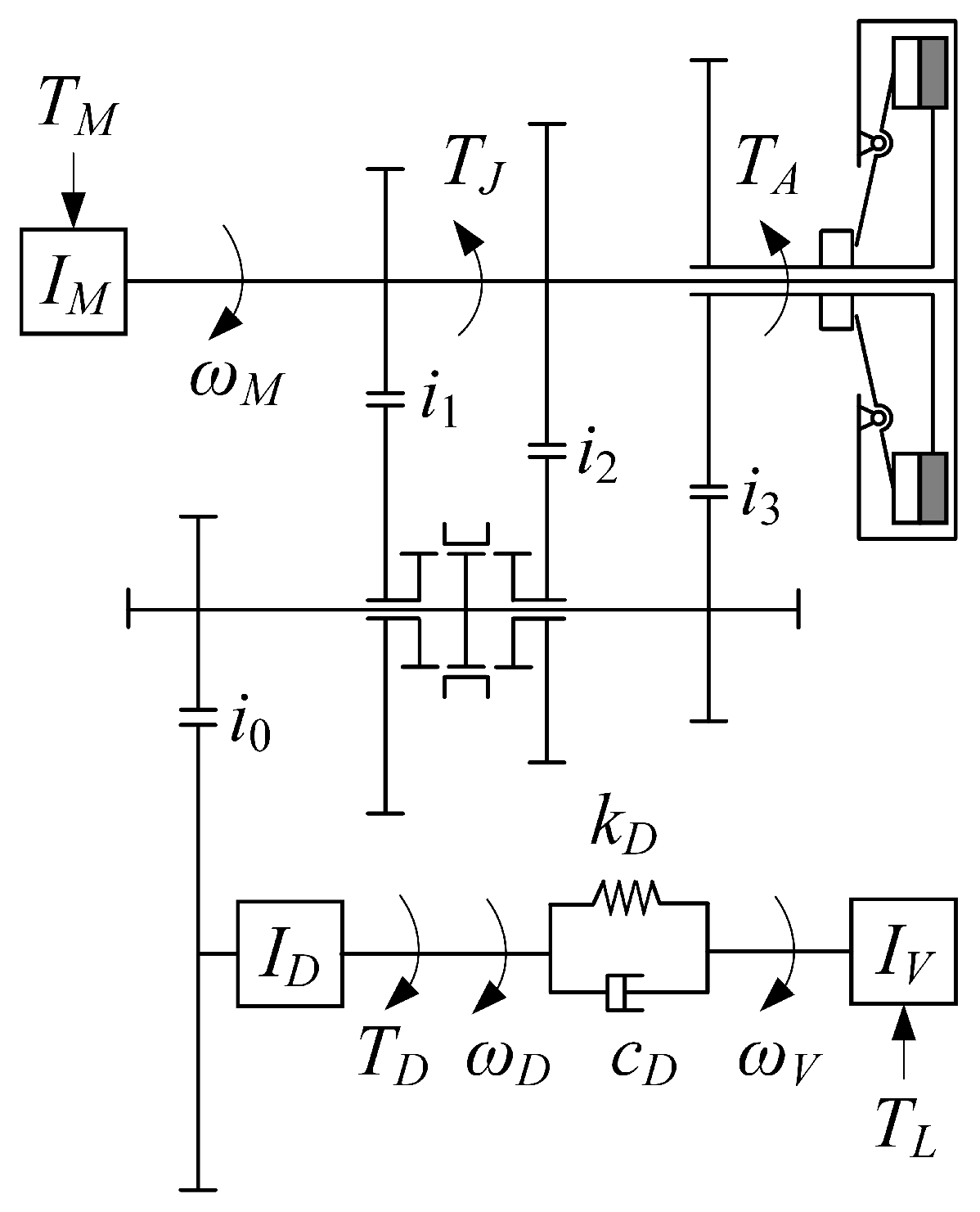


| Category | Parameter | Value |
|---|---|---|
| Drive system | Vehicle mass/(kg) | 1525 |
| Vehicle frontal area/(m) | 2.16 | |
| Air density/(kg/m) | 1.199 | |
| Rolling resistance coefficient | 0.013 | |
| Air resistance coefficient | 0.32 | |
| Wheel radius/(m) | 0.318 | |
| First gear, second gear, third gear and main reducer ratio | 2.83/1.63/1.02/4.06 | |
| Equivalent moment of inertia of the electric motor, input shaft and components on the input shaft/(kg·m) | 0.08 | |
| Equivalent moment of inertia of the output shaft, components on the output shaft, drive shaft and components on the drive shaft/(kg·m) | 2.56 | |
| Equivalent moment of inertia of vehicle/(kg·m) | 120.5 | |
| Drive shaft stiffness coefficient/(Nm/rad) | 3200 | |
| Drive shaft damping coefficient/(Nm·s/rad) | 150 | |
| Clutch actuator | Motor resistance/() | 0.27 |
| Motor inductance/(H) | 0.00216 | |
| Equivalent rotational inertia of the motor and transmission mechanism/(kg·m) | 0.00013 | |
| Motor back electromotive force coefficient/(V·s/rad) | 0.0302 | |
| Motor torque coefficient/(Nm/A) | 0.0305 | |
| Motor rolling damping coefficient/(Nm·s/rad) | 0.0053 | |
| Worm gear ratio | 38 | |
| Distance between the gear center and connecting rod/(m) | 0.02 | |
| Length of the shift fork power arm/(m) | 0.135 | |
| Length of the shift fork resistance arm/(m) | 0.070 | |
| Total transmission efficiency of the transmission mechanism when the motor rotates forward | 0.40 | |
| Total transmission efficiency of the transmission mechanism when the motor reverses | 0.20 |
| Category | Parameter | Value |
|---|---|---|
| Assist Clutch | Preload at full engagement/(N) | 4350 |
| Leverage ratio of the diaphragm spring | 2.8 | |
| Number of friction surfaces | 2 | |
| Equivalent friction radius/(m) | 0.095 | |
| Friction coefficient | 0.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, P.; Qiang, P.; Pan, T.; Zang, H. Double-Loop Control for Torque Tracking of Dry Clutch. Machines 2022, 10, 1142. https://doi.org/10.3390/machines10121142
Wu P, Qiang P, Pan T, Zang H. Double-Loop Control for Torque Tracking of Dry Clutch. Machines. 2022; 10(12):1142. https://doi.org/10.3390/machines10121142
Chicago/Turabian StyleWu, Peng, Penghui Qiang, Tao Pan, and Huaiquan Zang. 2022. "Double-Loop Control for Torque Tracking of Dry Clutch" Machines 10, no. 12: 1142. https://doi.org/10.3390/machines10121142
APA StyleWu, P., Qiang, P., Pan, T., & Zang, H. (2022). Double-Loop Control for Torque Tracking of Dry Clutch. Machines, 10(12), 1142. https://doi.org/10.3390/machines10121142






