Abstract
Collaborative Manufacturing Scheduling (CMS) is not yet a properly explored decision making practice, although its potential for being currently explored, in the digital era, by combining efforts among a set of entities, either persons or machines, to jointly cooperate for solving some more or less complex scheduling problem, namely occurring in job shop manufacturing environments. In this paper, an interoperable scheduling system integrating a proposed scheduling model, along with varying kinds of solving algorithms, are put forward and analyzed through an industrial case study. The case study was decomposed in three application scenarios, for enabling the evaluation of the proposed scheduling model when envisioning the prioritization of internal–makespan-or external–number of tardy jobs-performance measures, along with a third scenario assigning a same importance or weight to both kinds of performance measures. The results obtained enabled us to realize that the weighted application scenario permitted reaching more balanced, thus a potentially more attractive global solution for the scheduling problem considered through the combination of different kinds of scheduling algorithms for the resolution of each underlying sub problem according to the proposed scheduling model. Besides, the decomposition of a global more complex scheduling problem into simpler sub-problems turns them easier to be solved through the different solving algorithms available, while further enabling to obtain a wider range of alternative schedules to be explored and evaluated. Thus, contributing to enriching the scheduling problem-solving process. A future exploration of the application in other types of manufacturing environments, namely occurring in the context of extended, networked, distributed or virtual production systems, integrating an increased and variable set of collaborating entities or factories, is also suggested.
1. Introduction
Collaborative decision-making (CDM) implies an interaction and shared learning process among at least two entities, independent of both sharing the same objective or not [1,2] Although, usually, when the entities fall into a same context or business, they may also have a common goal, which can either occur in the context of traditional or in extended manufacturing environments (EMS) or in agile or virtual enterprises (A/VE), along with cyber physical systems [1,2,3,4,5,6,7,8]. The CDM processes are of the utmost importance nowadays, in the Industry 4.0, once enabling and promoting the interconnection and interoperation among integrated entities, either persons and/or communication and processing devices, along with diver kind of machines, horizontally and/or vertically integrated through the [I]oT ([Industrial] Internet of Things), and supported by appropriate middleware, tools, systems, and platforms [9,10,11,12,13].
In this paper a model is proposed for collaboratively solving a manufacturing scheduling model, which consists of an extension of the well-known Jackson’s model that enables to define the production sequence of a set of jobs to be processed in a classical job shop environment, integrating just two machines or work centers [14]. The proposed scheduling model, besides being applicable to solve classical job shop scheduling problems, with two or more machines, can further be applied for solving scheduling problems occurring in EME or A/VE, integrating two or more factories, for the execution of the jobs, through a distributed manufacturing environment [15].
The proposed scheduling model consists of a novel contribution, as, as far as our knowledge, existing contributions are usually more specific, regarding either its application domain (kind of manufacturing environment) or the approach used for solving the scheduling problem, usually based on some specific or reduced combination of solving algorithms. Instead, through our proposed scheduling model, different approaches or methods/algorithms can be applied or combined to solve a set of underlying sub scheduling problems. Thus, being able to vary from the application of pure mathematical or optimization algorithms, up to the use of varying kind of meta-heuristics or be based on machine learning or agent-based approaches, among others [5,16,17,18].
In order to properly present the contribution put forward in this paper, it is organized as follows. In Section 2, a summarized overview of manufacturing scheduling approaches is presented. In Section 3, the proposed interoperable manufacturing scheduling system is briefly described. In Section 4, the proposed collaborative manufacturing scheduling model is put forward, for being further explored, in Section 5, through an illustrative example of application. A further analysis and discussion of the main results obtained through the application of the proposed scheduling model is also included in Section 5, by using three different application scenarios. Finally, in Section 6, the main conclusions, along with future work suggestions, are provided.
2. Manufacturing Scheduling Evolution
2.1. Scheduling Problems and Solving Approaches
Manufacturing Scheduling (MS) refers to the execution of a set of tasks or operations, usually also referred as jobs, at defined times on specific production resources or machines, also frequently mentioned as processors, workstations or work centers, and which can be locally available at a given shop floor or geographically distributed among factories or companies [19,20,21,22]. The tasks can be sequential and/or occur in parallel, among the production resources [23,24,25,26,27,28,29].
Other definitions of Manufacturing Scheduling are presented in [25,26], who describes, Manufacturing Scheduling as the part of the MPC (Manufacturing Planning and Control) that is responsible for the distribution of the operations by available resources, in order to optimize one or more performance measures. Pinedo & Chao, in 1999 [25] diddefine Manufacturing Scheduling as the process that distributes limited resources across activities, in order to optimize the company’s productive capacity, or any other performance measure. In the meantime, Baker & Trietsche, in 2009 [24], described Manufacturing Scheduling as the decision process that seeks to answer the questions: “What is the best way to distribute resources across operations, to optimize a given performance measure? Besides, “What is the manufacturing sequence and/or production schedule that optimizes a given performance measure?”.
Scheduling problems belong to a much broader class of combinatorial optimization ones that are difficult to solve, being called NP-hard problems. These problems are characterized by having a vast set of possible solutions, which have to be explored in the space of possible solutions for the problems under consideration.
Additionally, to being combinatorial optimization problems, MS problems are also usually dynamic, due to the dynamisms that arises from the real time arrival of new tasks to be scheduled and further to the availability of the production resources, which does also dynamically change over time. These two aspects combined turn industrial scheduling problems quite difficult to solve, which are thus usually solved by using different kind of heuristic methods, for instance, based on constraint programming or a widened set of diverse types of other heuristics or meta-heuristics, such as, Genetic Algorithms, Simulated Annealing or Tabu Search, among other meta-heuristics or approaches, for instance, based on Neural Networks, or Fuzzy Logic, among others [30,31].
Job shops are production systems’ configurations which are arranged in such a way that permits them to take a superior advantage of more or less diversified production and in varied quantities, generally, and currently, in relatively small quantities. These manufacturing systems are usually further arranged according to a functional logic, e.g., grouped according to the functions or processes they perform, enabling different workflows, which provides this kind of production system a popularity or relative advantage when compared to other types of configurations or production systems, more limited or oriented to some kind of products of product families, such as the flow shops.
Although, similar to what happens in other kinds of manufacturing systems, in these kinds of job shop manufacturing environments, things rarely go as expected. This can occur due to several reasons, for instance, due to cancelled scheduled jobs and/or to the arrival of new jobs, namely with a higher priority. Moreover, this usually happens because given resources become unavailable and/or that new resources are considered. Besides, some other disturbances may occur on the shop floor, namely some scheduled tasks that take more or less time than planned, or tasks that arrive earlier or late. Further, other turbulences that may happen can be related, for instance, to machine failures, to operators’ absence or to the unavailability of production tools and/or materials.
Besides, also some given production schedule might become unfeasible because of some unforeseen real time situation occurring on the shop floor. When this happens, a new schedule has to be generated to restore the manufacturing system performance by executing rescheduling, dynamic scheduling or also so-called a real-time scheduling [32,33].
The manufacturing scheduling problems are continuous and dynamic by nature, and a solution will quickly become obsolete. For example, a number of jobs are scheduled, and before all the jobs are processed, new jobs are released on the shop floor, making the solution obsolete before even being executed. Considering that classical, static, scheduling become non-optimal as soon as new manufacturing orders are launched into the shop floor [34,35], it is necessary to find ways to adapt scheduling solutions to the dynamic nature of the problem. Dynamic scheduling can be classified as Reactive, Predictive-Reactive and Proactive Scheduling, depending on how the initial solution is conceived and how it is adapted to changes in the characteristics of the problem [36]. Whenever it is necessary to adapt the solution to the changes in the problem, it is important to determine if an obsolete solution can be adapted to accommodate the changes in the problem, or if it is necessary to devise a completely new solution. Finally, it is necessary to determine when a solution is considered obsolete, that is, if the rescheduling is event-oriented, for example, whenever there is a change in the characteristics of the problem, or if the rescheduling happens periodically.
There are different kinds of approaches that can be used for establishing production schedules, varying from enumerative algorithms to the application of simple priority rules. Moreover, these approaches can be based on pure mathematical programming models or use simulation technique among other approaches [5], for instance, based on multi-agents, among others [18,24,37,38,39].
2.2. The Jackson’s Scheduling Model
Jackson, in 1956 [14] proposed a model for scheduling a set of jobs in a job shop integrating two machines (A and B), by sequencing the jobs according to the following order, on each one:
- Machine A: {A,B} -> {A} -> {B,A}
- Machine B: {B,A} -> {B} -> {A,B}
In which {A} represents the set of jobs that integrate just one operation, and which has to be processed on machine A, {B} represents the set of jobs that integrate also just one operation, and which has to be processed on machine B, {A,B} represents the set of jobs with two operations, in sequence, as in a flow shop, being the first one to be processed on machine A, and the second one on machine B, and {B,A} representing also a set of jobs in a reverse order of processing, e.g., being the first operation to be processed on machine B, and the second one on machine A. These flow shop scheduling sub problems, with two machines, are solved by the traditional Johnson’s rule, and the single machine ones by applying simple sequencing rules, e.g., the Shorted Processing Time (SPT) [14].
2.3. Scheduling Process Complexity
Scheduling processes are complex in nature, particularly the ones occurring in job shop environments [16], as is the case of the classical job shop scheduling problem, where the scheduling problem complexity grows exponentially, with the increase in the number of sets of machines to order, according to the number of machines or work centers available in a job shop. The complexity of a job shop scheduling process can thus be analyzed by using the equation 1, resulting in the number of arrangements of machines to be considered for the jobs to be processed, being m the set size, i.e., the total number of machines in the sample, and p the subset size, i.e., the number of machines to be selected from the sample.
For example, in the simplest case of a job shop with just m = 2 machines (A, and B), as described in the Section 2.2, about the application of the Jackson’s sequencing process of a set of m machines, it will be necessary to sequence or order four sets of machines, as follows: {A}, {B}, {A,B}, and {B,A}, which is calculated through equation 1 by A(2,2) + A(2,1) = 2 + 2 = 4 sets of machines.
This job shop scheduling process complexity grows exponentially, and Figure 1 and Table 1 show this very fast increase in this complexity of the scheduling process, when increasing the number of machines up to 10, reaching 9,864,100 sets of machines to be sequenced. Therefore, it turns out to be of utmost importance to further explore alternative scenarios for carrying out the scheduling process, among a set of collaborating entities or even factories, for instance, in the context of EME or VE that jointly perform a scheduling process.
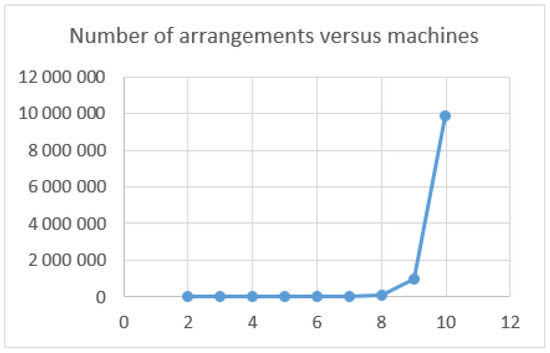
Figure 1.
Relation between the number of machines and the number of sets of arrangements of machines to order.

Table 1.
Problem complexity.
3. Interoperable Manufacturing Scheduling System
3.1. Scheduling System Architecture
In this work, a developed interoperable manufacturing scheduling system (IMSS) was used for solving problems occurring in different kind of more or less complex manufacturing environments, namely in a job shop, by enabling to decompose them into simpler ones through a proposed scheduling model that is an extension of the Jackson’s model for enabling to solve general job shop scheduling problems with three or more work centers, by concatenating the partial solutions or schedules to form a complete solution for the whole original problem carried out by using a central or core scheduling system (CSS). In Figure 2, the architecture of the IMSS is shown, for an application example, occurring in an industrial company, which integrates three work centers (WC1, WC2, and WC3). This IMSS architecture includes thus the CSS, and which is interconnected with the work centers, enabling data sharing with the shop floor’s operational level, and by enabling to automatically acquire data through RFID and store it in a local database, along with further processing through the use of smart objects and additional devices and technology [5,40,41]. Moreover, the CSS is linked to a pre-processing module, which permits the insertion of information arising from the clients’ orders that is also inserted in the corresponding supporting database, and the whole set of information (joint factory and clients data) is subject to a pre-processing function of the IMSS, for data analysis, filtering and other pre-processing procedures, namely for dealing with incomplete data, with the support of historical data sets processed, along with methods for uncertainty treatment, based on dynamic, and fuzzy based approaches [42,43,44] (Figure 3 and Figure 4).
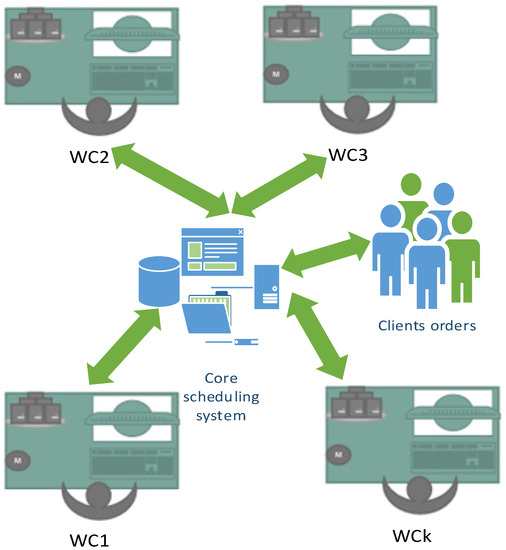
Figure 2.
Interoperable manufacturing scheduling system architecture.
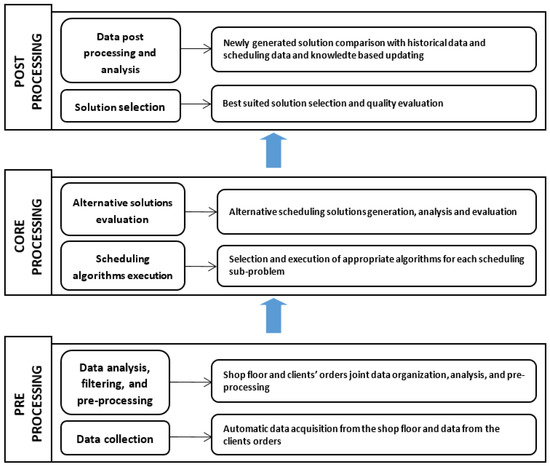
Figure 3.
Scheduling framework.
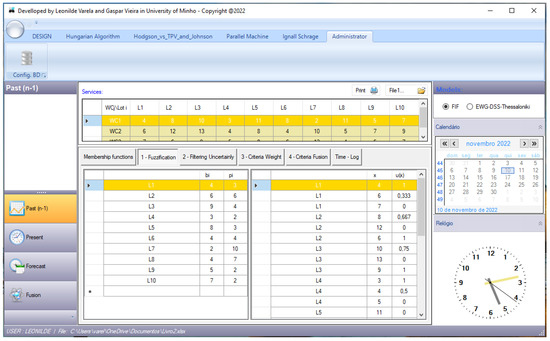
Figure 4.
Scheduling system interface illustration.
The CSS includes a set of scheduling problems solving algorithms, varying from simple heuristics and dispatching rules up to more complex ones, namely based on a diverse kind of heuristics, and meta-heuristics [32,45], along with other AI-based approaches, for instance, based on machine learning [46], and others, namely based on cluster analysis [18].
The IMSS does further include a post-processing module, which permits the selection of a considered best suited solution for a given scheduling problem, based on a comparative analysis of existing alternative solutions, through their quality evaluation, according to the specific companies’ needs and preferences, namely regarding the higher or lower importance or priority assigned to different kind of performance measures, varying between internal and external ones, corresponding to the relative importance that is given, at a given time period, to factories objectives, namely based on production times and/or on client’s oriented objectives, for instance, related to orders due dates, correspondingly. Besides, this post-processing module does further enables us to compare the generated scheduling solutions with historical information, and to dynamically update this repository.
3.2. Ilustrative Scheduling System Interface
The CSS has different kind of processes, through three levels, as expressed in the Figure 3, and by using appropriate interfaces, as illustrated in the Figure 4, which is about a module of the IMSS that enables to access past scheduling data, namely for being compared with some current or new data, and perform specific processes accordingly, namely for dealing with current incomplete or uncertain data about the processing times of some jobs to be scheduled, by applying appropriate data processing models and methods [5,44].
At the first level, the CSS permits automatic data collection and storage arising from the shop floor, along with its integration with information from the clients orders, and its further joint processing, namely for dealing with uncertain or incomplete data, and its further treatment to reach proper data sets for solving a given scheduling problem.
The second level is about the access, selection and execution of diverse kinds of scheduling algorithms put available through the CSS of the IMSS, through the resolution of each sub problem underlying a given scheduling problem, based the proposed scheduling model, which is going to be further described next, in the Section 4.1.
Finally, at the third level the CSS enables further data post processing and analysis, namely for composing a global or complete solution for the scheduling problems considered, also based on the proposed model, and by further enabling other deeper solutions analysis, for instance, based on multivariate data series analysis methods [5,47].
4. Collaborative Scheduling
In this section is briefly described a proposed collaborative manufacturing scheduling (CMS) approach, based on a scheduling model that results from an extension of the Jachson’s job shop scheduling model, in order to permit the resolution of more complex problems, for instance, occurring in varying kind of job shop manufacturing environments.
4.1. Proposed Scheduling Model
The proposed scheduling model for enabling CMS, based on the original approach proposed by Jackson, in 1956 [14], enables to establish the sequencing order of a set of jobs in a classical job shop environment, composed by two or more machines or work centers. Therefore, in this paper, this Jackson’s scheduling approach is extended, in order to schedule jobs in a wider set of machines or work centers or any other kind of production units or factories, which may further be geographically dispersed.
In order to enable to carry out manufacturing scheduling of a set of n jobs in a general job shop manufacturing environment, integrating more than two machines, either in the context of a conventional or classical job shops or occurring in the context of some distributed manufacturing environment, were jobs have to be scheduled to be processed through a set of production units or factories or locally, by a set of machines or work centers, an extension of the Jackson’s model is put forward. This model is represented next, for sequencing jobs in a set of three machines or work centers, defined as A, B, and C, by exploring four possible alternative sequences for processing the jobs in those work centers.
- Work Center A
- Sequence 1:
- {A,B,C}->{A,C,B}->{B,A,C}->{A,B}->{A,C}->{A}->{C,A}->{B,A}->{C,A,B}->{B,C,A}->{C,B,A}
- Sequence 2:
- {A,C,B}->{A,B,C}->{B,A,C}->{A,B}->{A,C}->{A}->{C,A}->{B,A}->{C,A,B}->{C,B,A}->{B,C,A}
- Sequence 3:
- {A,B,C}->{A,C,B}->{B,A,C}->{A,C}->{A,B}->{A}->{B,A}->{C,A}->{C,A,B}->{B,C,A}->{C,B,A}
- Sequence 4:
- {A,C,B}->{A,B,C}->{B,A,C}->{A,C}->{A,B}->{A}->{B,A}->{C,A}->{B,A,C}->{C,B,A}->{B,C,A}
- Work center B
- Sequence 1:
- {B,A,C}->{B,C,A}->{A,B,C}->{B,A}->{B,C}->{B}->{C,B}->{A,B}->{C,B,A}->{A,C,B}->{C,A,B}
- Sequence 2:
- {B,C,A}->{B,A,C}->{A,B,C}->{B,A}->{B,C}->{B}->{C,B}->{A,B}->{C,B,A}->{C,A,B}->{A,C,B}
- Sequence 3:
- {B,A,C}->{B,C,A}->{A,B,C}->{B,C}->{B,A}->{B}->{A,B}->{C,B}->{C,B,A}->{A,C,B}->{C,A,B}
- Sequence 4:
- {B,C,A}->{B,A,C}->{A,B,C}->{B,C}->{B,A}->{B}->{A,B}->{C,B}->{C,B,A}->{C,A,B}->{A,C,B}
- Work center C
- Sequence 1:
- {C,A,B}->{C,B,A}->{B,C,A}->{C,A}->{C,B}->{C}->{B,C}->{A,C}->{A,C,B}->{A,B,C}->{B,A,C}
- Sequence 2:
- {C,B,A}->{C,A,B}->{B,C,A}->{C,A}->{C,B}->{C}->{B,C}->{A,C}->{A,C,B}->{B,A,C}->{A,B,C}
- Sequence 3:
- {C,A,B}->{C,B,A}->{B,C,A}->{C,B}->{C,A}->{C}->{A,C}->{B,C}->{A,C,B}->{A,B,C}->{B,A,C}
- Sequence 4:
- {C,B,A}->{C,A,B}->{B,C,A}->{C,B}->{C,A}->{C}->{A,C}->{B,C}->{A,C,B}->{B,A,C}->{A,B,C}
In this proposed extended model, besides the previous scenarios related to the two machines job shop sub problems, considered in the Jackson’s model, there are further included other job shop scheduling sub problems, with two machines ({A,C},{B,C},{C,A},{C,B}), and job shop sub problems with three machines ({A,B,C},{A,C,B}, {B,A,C},{B,C,A},{C,A,B},{C,B,A}). These can be solved by using the Johnson’s rule for three machines or some other kind of approach, for instance, the Branch-and-Bound (B&B) algorithm by Ignall and Schrage, in 1965 [48], among other approaches, including different kinds of heuristics or meta-heuristics or other AI-based approaches [5,18,45].
As the number of machines/work centers increases, the number of alternative sequences for ordering the sets of jobs for each machine increases too, but fortunately this does not necessarily increase the complexity of the primary scheduling processes, once the number of sets of jobs remains the same, for each alternative sequence to be considered on each machine or work center. Besides, the complexity related to the sequencing problem inherent to ordering the jobs in each corresponding set, requires an extra effort for establishing the alternative sequences for each machine, which turns out to be another additional operation, requiring the examination of the alternative sequences, and the calculation of the performance measure associated to each sequence for the selection of the best one, for each valid or possible complete schedule for each machine/work center. Therefore, the best final sequence of jobs on each machine has to be validated, regarding its feasibility, for each problem instance, while aiming, for instance, at the minimization of the total completion time of the jobs or makespan.
This model can the extended to solve more complex scheduling problems, occurring in job shops with more than three machines or work centers, by using a similar general logic as it was illustrated for the case of a classical job shop with three machines/work centers. Therefore, in these, more complex job shop scheduling environments, the underlying sub-problems to be solved turn out to be increasingly more complex too, with the appearance of more complex underlying flow shop problems, including a higher number of machines/work centers (4, 5, etc.), thus requiring appropriate algorithms, which tend to be more complex too, and this complexity continues to rise when the number of jobs increases, as well as the number of possible alternative sequences for processing the sets of jobs to be further evaluated to reach a final solution for each machine/work center. Thus, with the increase in complexity of the problems it becomes more important to explore different heuristics or meta-heuristics, along with other kinds of approaches, for instance, based on varying kind of AI based ones, to approach corresponding sub-problems [5,18,45].
5. Scheduling Case Study in a Job Shop Environment under Three Different Scenarios
The proposed model for supporting CMS can be implemented through diverse kind of scenarios, considering different priorities attributed to the so-called internal (scenario 1, Sc1) and external (scenario 2, Sc2) performance measures, for evaluating the quality of the solutions obtained, varying from purely or 100% internal or external, to intermediate situations that consider different weights attributed to the internal versus external measures, namely by considering the same importance associated to both kind of measures (scenario 3, Sc3, with 50%–50% for each kind of internal and external performance measure).
In the Table 2 and Table 3 is shown the data from a clothing company about two scheduling problem instances (5 and 27), among a set of thirty analyzed, which include the deadlines (di) and the processing times of the operations of a set of ten jobs (Ji) that belong to a same family of products, and are executed in the corresponding work centers (WCj: WC1, WC2, and WC3), being the operations measured in time units (t.u.).

Table 2.
Scheduling problem (instance 5) data.

Table 3.
Scheduling problem (instance 27) data.
5.1. Internal Performance Oriented Approaches–Scenario 1
In the case of an absolute importance or priority is given to the satisfaction of internal performance measures, such as the typical total or maximum completion time of a set of jobs to be processed in the manufacturing system (makespan) and/or other production time-oriented measures, like the sum or the mean flow time of jobs, through appropriate optimization algorithms selected, available from the whole set of CSS’s scheduling algorithms.
5.2. External Performance Oriented Approaches–Scenario 2
In the case of an absolute importance or priority being given to the satisfaction of external performance measures, typically based on the accomplishment of deadlines or due dates for the jobs, namely measures through the number or tardy jobs (Nt), and/or through other more or less closely related performance measures, such as the maximum tardiness of jobs (Tmax), among others, namely the mean lateness of the jobs, also appropriate optimization methods that have to be selected, from the whole set of scheduling algorithms put available through the CSS of the IMSS to solve them.
5.3. Combined Performance Oriented Approaches–Scenario 3
In the case of the same importance or priority is given to the satisfaction of internal and external performance measures, thus oriented to jobs’ production times and deadlines, by using a 50–50% weighting that has to be attributed to the corresponding solving methods selected from the whole set of scheduling algorithms available through the CSS of the IMSS.
6. Scheduling Model Application Analysis and Discussion
In Figure 5 are expressed the performance measure results obtained for the thirty problem instances that were run under the corresponding application scenarios previously described. These results are thus organized in three groups, from the upper to the lower level, associated to the scenarios 1, 2 and 3 (Sc1, Sc2, and Sc3) about: the maximum completion time of jobs (Cmax), the maximum tardiness of jobs (Tmax), and the number of tardy jobs (Nt), correspondingly.
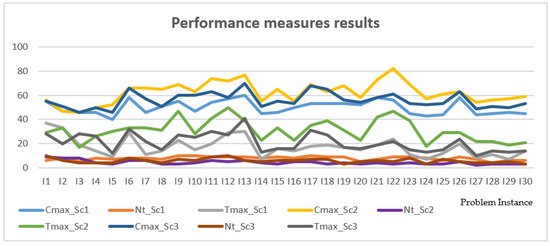
Figure 5.
Performance measures’ values of the thirty scheduling problem instances from scenarios 1, 2 and 3.
The mean values obtained through the execution of the thirty problem instances under the scenarios Sc1, Sc2, and Sc3, for the Cmax, Nt, and Tmax performance measures, correspondingly, are expressed in Figure 6.
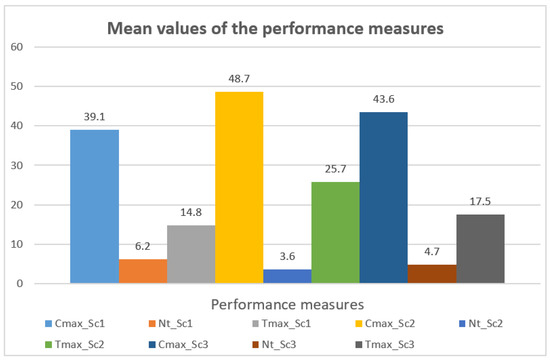
Figure 6.
Mean performance measures’ values of the scheduling solutions from scenarios 1, 2 and 3.
The analysis of this Figure 6 permits to realize that the best mean value of the makespan (Cmax) about the thirty problem instances run was obtained in the scenario Sc1, by applying the Shorted Processing Time (SPT) rule to the sets of jobs with just one operation, along with the Johnsons rule for the sets of jobs with two operations, to be processed in corresponding two work centers flow shops, and the B&B algorithm from Ignall & Schrage, for the sets of jobs integrating three operations, to be processed in three work centers flow shops [5,16].
Regarding the Nt, the best mean value about the thirty problem instances run was obtained in the scenario Sc2, by applying the Earliest Due Date (EDD) rule to the sets of jobs with just one operation, along with a modified version of the Hodgson’s algorithm [5] for solving the sets of jobs with two operations, to be processed in two work centers flow shops, and an adapted version of the Ignall & Schrage’s B&B algorithm to the set of jobs with three operations, to be processed in three WorkCentre flow shops, for minimizing the number of tardy jobs.
In terms of the Tmax the best mean value was reached for the scenario Sc1, by also applying the SPT rule to the sets of jobs with one operation, along with the Johnson’s rule for solving the sets of jobs to be processed in two work centers flow shops, and an adapted version of the Ignall & Schrage’s B&B algorithm to the set of jobs with three operations, to be processed in three work center flow shops, for minimizing the maximum tardiness of the jobs.
In the Figure 7, Figure 8 and Figure 9, are shown the Gantt charts about the best solutions found for the scenarios Sc1, Sc2, and Sc3, correspondingly, after the application of the proposed scheduling model presented in the Section 4.1, for the compilation of the complete sequence of the jobs to be processes in the corresponding work center, and once selected the best one.
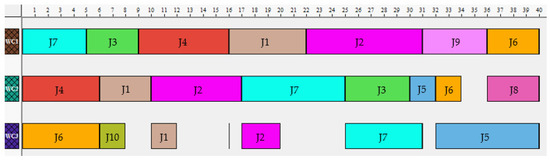
Figure 7.
Gantt chart about the best solution found for scenario 1 (about problem instance 5).
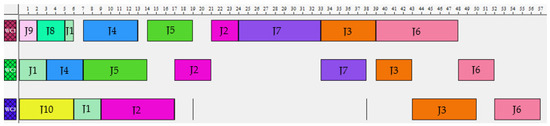
Figure 8.
Gantt chart about the best solution found for scenario 2 (about problem instance 27).
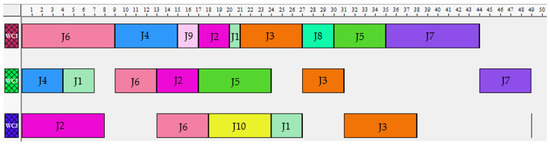
Figure 9.
Gantt chart about the best solution found for scenario 3 (about problem instance 27).
As it can be realized by analyzing the Gantt charts about the best solutions obtained for each application scenario, in the Figure 7 it is visible that a more compact solution was reached, which enables a shorter total completion time of the whole set of jobs to be processed in the corresponding three work centers, thus further enabling its most favorable utilization rate, as just the work centers 2 and 3 (WC2, and WC3) present some relatively reduced idle time, in opposite to what happens to the work centers in the scenarios 2 and 3, on which the three work centers present idle times, being more significant ones.
Although, by further analyzing the summarized results about the performance measures values obtained for the three scenarios about Cmax, Nt, and Tmax for these corresponding best solutions, as expressed in the Table 4, it is possible to perform additional analysis.

Table 4.
Best scheduling problems results.
It is possible to realize that the best solution found about the minimization of the Cmax–maximum completion time of the jobs, did occur in the scenario Sc1 (of 40 t.u.), but the total number of tardy jobs (Nt) does correspond to the worst value among the three best solutions, with 7 late jobs in the whole set of ten jobs to be processes. Contrarily, the best (minimum) value for the Nt was obtained in the scenario Sc2, with 2 late jobs, but this Sc2 did obtain the worst value for the makespan (Cmax = 57 t.u.), and also the worst value for the maximum tardiness of the jobs (Tmax = 25 t.u.), among the three best solutions.
Besides, in terms of the minimization of the Tmax, the best value was also reached in scenario Sc1, of 9-time units, very closely followed by the value obtained in the scenario Sc3 (10 t.u.). Moreover, it can be seen that this scenario Sc3 does further enable to reach a better balance between the values obtained for the three performance measures among the best three solutions reached, with a Cmax of 49-time units, and a Nt of 4 late jobs, besides the Tmax with 10-time units. Therefore, although this balance can, in general, be seen as a good solution to be adopted, once it is always visible a trade-off situation between the quality of the solutions obtained, regarding the corresponding set of internal, external, and a mix of internal and external performance measures considered, through the three application scenarios explored, clearly an indication of priorities or preferences is required, by an experienced manufacturing management decision-maker, while selecting a considered best final solution, regarding each specific manufacturing management conditions verified at a given scheduling moment.
7. Conclusions
In this paper a proposed collaborative scheduling model was presented that consists of an extension of the Jackson’s job shop scheduling model, and its results obtained were analyzed through an industrial example of application, consisting of a set of thirty industrial problem instances from a clothing company. The model was explored under three different application scenarios, about internal, external, and combined performance measures, with the same weight, related to the total completion time of the jobs, the number of late jobs and the tardiness of the jobs being executed in a job shop environment with three work centers. The resolution of the problem instances was carried out through the selection of alternative algorithms put available through a developed interoperable scheduling system, which enables to jointly process scheduling data from a historical repository and information arising from clients, along with incomplete and uncertain data processing. Through the study carried out, it was possible to realize the benefits associated with the use of the presented scheduling system and underlying problem-solving model. One main benefit is related to the possibility of decomposing complex scheduling problems, occurring in job shop manufacturing environment in simpler sub-problems that can be solved individually and then the partial solutions combined to obtain complete alternative solutions for the whole problem to be further analyzed in order to select the one considered best suited in a concrete manufacturing management situation. Moreover, the scheduling algorithms can be selected from a set of varying kind of algorithms put available through the interoperable scheduling system, which range from simple dispatching rules up to more complex ones, for instance, based on branch-and-bound, among other optimization methods and underlying techniques, along with other solving methods, namely a set of heuristics, meta-heuristics, along with other AI-based approaches, including machine learning and clustering algorithms.
The application of different kind of scheduling algorithms was explored, and through the results obtained it was possible to realize that the selection of a certain final solution, will much depend on the priorities or preferences defined by the decision maker, based on each particular conditions underlying a given specific manufacturing and management situation, as each potential possible alternative solution selected will have some drawback and benefit. Although, it was possible to recognize that there are visible general or overall benefits when some weights are attributed to the different kind of performance measures to be considered, namely by using a considered 50-50 performance measures weighting or third scenario, as the alternative solutions tend to present trade-offs, while tending to the optimization of some performance measures, according to the corresponding solving algorithm used, which in this case, were divided in two main subsets, intending the optimization of the so-called internal and external performance measures.
This is a novel contribution, as far as our knowledge, existing contributions do not explore a widened range of alternative methods combinations to solve a given scheduling problem, while decomposing it into simple ones, to further enable different alternatives to concatenate them, in order to permit a wider range of alternative final or complete solutions to be evaluated for reaching a final decision about a considered best suited global solution for a specific problem to be solved. This is considered a relevant contribution for the state of the art in this domain, as it enables a set of entities (decision-makers and/or machines) to collaborate for jointly exploring alternative solutions for solving a given scheduling problem, by running different kind of scheduling algorithms for solving the sub-problems integrating the global one.
As future work, it is planned to further analyze the potential of the proposed extended scheduling model, regarding its potential additional benefits and limitations for carrying out the collaborative manufacturing scheduling in other kind of manufacturing environments, for instance, in the context of distributed manufacturing systems subject to additional constraint, namely about the sets of jobs and their processing units.
Author Contributions
In this paper, the conceptualization and methodology definitions were established by L.R.V.; the main investigation, preparation, writing—original draft was done by L.R.V.; the writing—review and editing, and visualization, was jointly carried out by L.R.V., C.F.V.A., A.S.S., G.G.V., N.L. and G.D.P. The general supervision of this work was performed by L.R.V. and G.D.P.; and the project administration, and funding acquisition, was accomplished by L.R.V. All authors have read and agreed to the published version of the manuscript.
Funding
The project is funded by the FCT—Fundação para a Ciência e Tecnologia through the R&D Units Project Scope: UIDB/00319/2020, and EXPL/EME-SIS/1224/2021.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
This work has been supported by national funds through the FCT—Fundação para a Ciência e Tecnologia through the R&D Units Project Scope: UIDB/00319/2020 and EXPL/EME-SIS/1224/2021.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Putnik, G.D.; Putnik, Z.; Shah, V.; Varela, L.; Ferreira, L.; Castro, H.; Catia, A.; Pinheiro, P. Collaborative Engineering definition: Distinguishing it from Concurrent Engineering through the complexity and semiotics lenses. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1174, 012027. [Google Scholar] [CrossRef]
- Putnik, G.D.; Putnik, Z.; Shah, V.; Varela, L.; Ferreira, L.; Castro, H.; Catia, A.; Pinheiro, P. Collaborative Engineering: A Review of Organisational Forms for Implementation and Operation. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1174, 012028. [Google Scholar] [CrossRef]
- Eijnatten, F.M.; Putnik, G.D. Chaos, Complexity, Learning, and the Learning Organization: Towards a Chaordic Enterprise; Emerald Group Publishing: Bingley, UK, 2004. [Google Scholar]
- Lou, P.; Ong, S.K.; Nee, A.Y.C. Agent-based distributed scheduling for virtual job shops. Int. J. Prod. Res. 2010, 48, 3889–3910. [Google Scholar] [CrossRef]
- Vieira, G.; Varela, M.L.R.; Putnik, G.D. Technologies integration for distributed manufacturing scheduling in a virtual enterprise. In International Conference on Virtual and Networked Organizations, Emergent Technologies, and Tools; Springer: Berlin/Heidelberg, Germany, 2012; pp. 337–347. [Google Scholar]
- Canadas, N.; Machado, J.; Soares, F.; Barros, C.; Varela, L. Simulation of cyber physical systems behaviour using timed plant models. Mechatronics 2018, 54, 175–185. [Google Scholar] [CrossRef]
- Kays, H.M.E.; Karim, A.N.M.; Daud, M.R.C.; Varela, M.L.R.; Putnik, G.D.; Machado, J.M. A collaborative multiplicative Holt-Winters forecasting approach with dynamic fuzzy-level component. Appl. Sci. 2018, 8, 530. [Google Scholar] [CrossRef]
- Putnik, G.D.; Ferreira, L.G.M. Industry 4.0: Models, tools and cyber-physical systems for manufacturing. FME Trans. 2019, 47, 659–662. [Google Scholar] [CrossRef]
- Deloitte, 2012. Retail Globalization. Deloitte Touche Tohmatsu Limited. Available online: https://www.deloitte.com/global/en.html (accessed on 17 October 2022).
- Hankel, M.; Rexroth, B. The reference architectural model industrie 4.0 (rami 4.0). ZVEI 2015, 2, 4–9. [Google Scholar]
- Kagermann, H. Change through digitization—Value creation in the age of Industry 4.0. In Management of Permanent Change; Springer Gabler: Wiesbaden, Germany, 2015; pp. 23–45. [Google Scholar]
- Li, L. China’s manufacturing locus in 2025: With a comparison of “Made-in-China 2025” and “Industry 4.0”. Technol. Forecast. Soc. Chang. 2018, 135, 66–74. [Google Scholar] [CrossRef]
- Sony, M.; Naik, S.S. Ten lessons for managers while implementing Industry 4.0. IEEE Eng. Manag. Rev. 2019, 47, 45–52. [Google Scholar] [CrossRef]
- Jackson, J.R. An extension of Johnson’s results on job lot scheduling. Nav. Res. Logist. Q. 1956, 3, 201–203. [Google Scholar] [CrossRef]
- Arrais-Castro, A.; Varela ML, R.; Putnik, G.D.; Ribeiro, R.A.; Machado, J.; Ferreira, L. Collaborative framework for virtual organisation synthesis based on a dynamic multi-criteria decision model. Int. J. Comput. Integr. Manuf. 2018, 31, 857–868. [Google Scholar] [CrossRef]
- Reddy, M.S.; Ratnam, C.; Agrawal, R.; Varela, M.L.R.; Sharma, I.; Manupati, V.K. Investigation of reconfiguration effect on makespan with social network method for flexible job shop scheduling problem. Comput. Ind. Eng. 2017, 110, 231–241. [Google Scholar] [CrossRef]
- Alves, F.; Varela, M.L.R.; Rocha, A.M.A.; Pereira, A.I.; Leitão, P. A human centered hybrid MAS and meta-heuristics based system for simultaneously supporting scheduling and plant layout adjustment. FME Trans. 2019, 47, 699–710. [Google Scholar] [CrossRef]
- Azevedo, B.F.; Varela, M.L.R.; Pereira, A.I. Production Scheduling Using Multi-objective Optimization and Cluster Approaches. In Proceedings of the International Conference on Innovations in Bio-Inspired Computing and Applications, Online, 16–18 December 2021; pp. 120–129. [Google Scholar]
- Shen, W.; Wang, L.; Hao, Q. Agent-based distributed manufacturing process planning and scheduling: A state-of-the-art survey. IEEE Trans. Syst. Man Cybern. Part C 2006, 36, 563–577. [Google Scholar] [CrossRef]
- Manupati, V.K.; Gokula Krishnan, M.; Varela, M.L.R.; Machado, J. Telefacturing based distributed manufacturing environment for optimal manufacturing service by enhancing the interoperability in the hubs. J. Eng. 2017, 2017, 9305989. [Google Scholar] [CrossRef]
- Fu, Y.; Wang, H.; Huang, M. Integrated scheduling for a distributed manufacturing system: A stochastic multi-objective model. Enterp. Inf. Syst. 2019, 13, 557–573. [Google Scholar] [CrossRef]
- Cheng, Y.; Bi, L.; Tao, F.; Ji, P. Hypernetwork-based manufacturing service scheduling for distributed and collaborative manufacturing operations towards smart manufacturing. J. Intell. Manuf. 2020, 31, 1707–1720. [Google Scholar] [CrossRef]
- Zhou, R.; Chen, G.; Yang, Z.H.; Zhang, J.B. Distributed manufacturing scheduling using a novel cooperative system. In Proceedings of the 2008 IEEE International Conference on Service Operations and Logistics, and Informatics, Beijing, China, 12–15 October 2008; Volume 1, pp. 256–260. [Google Scholar]
- Baker, K.R.; Trietsch, D. Safe scheduling: Setting due dates in single-machine problems. Eur. J. Oper. Res. 2009, 196, 69–77. [Google Scholar] [CrossRef]
- Pinedo, M.; Chao, X. Operations Scheduling with Applications in Manufacturing and Services; McGraw Hill: New York, NY, USA, 1999. [Google Scholar]
- Pinedo, M.L. Scheduling Theory, Algorithms and Systems, 4th ed.; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Mishra, N.; Singh, A.; Kumari, S.; Govindan, K.; Ali, S.I. Cloud-based multi-agent architecture for effective planning and scheduling of distributed manufacturing. Int. J. Prod. Res. 2016, 54, 7115–7128. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, X.; Tang, S.; Królczyk, G.; Li, Z. Solving scheduling problem in a distributed manufacturing system using a discrete fruit fly optimization algorithm. Energies 2019, 12, 3260. [Google Scholar] [CrossRef]
- Mao, X.; Li, J.; Guo, H.; Wu, X. Research on Collaborative Planning and Symmetric Scheduling for Parallel Shipbuilding Projects in the Open Distributed Manufacturing Environment. Symmetry 2020, 12, 161. [Google Scholar] [CrossRef]
- Zijm, W.H.M. The integration of process planning and shop floor scheduling in small batch part manufacturing, Ann. CIRP 1995, 44, 429–432. [Google Scholar] [CrossRef]
- Shen, Y.J.; Wang, M.S. Broadcast scheduling in wireless sensor networks using fuzzy Hopfield neural network. Expert Syst. Appl. 2008, 34, 900–907. [Google Scholar] [CrossRef]
- Madureira, A.; Ramos, R.; Carmo Silva, S. Using Genetic Algorithms for Dynamic Scheduling. In Proceedings of the 14th Annual Production and Operations Management Society Conference (POMS’2003), Savannah, GA, USA, 4–7 April 2003. [Google Scholar]
- Alves, C.; Putnik, G.D.; Varela, M.L.R. How environment dynamics affects production scheduling: Requirements for development of CPPS models. FME Trans. 2021, 49, 827–834. [Google Scholar] [CrossRef]
- Goren, S.; Sabuncuoglu, I. Robustness and Stability Measures for Scheduling: Single Machine Environments. IIE Trans. 2008, 40, 66–83. [Google Scholar] [CrossRef]
- Ouelhadj, D.; Petrovic, S. A Survey of Dynamic Scheduling in Manufacturing Systems. J. Sched. 2009, 12, 417–431. [Google Scholar] [CrossRef]
- Aytug, H.; Lawley, M.A.; McKay, K.; Mohan, S.; Uzsoy, R. Executing production schedules in the face of uncertainties: A review and some future directions. Eur. J. Oper. Res. 2005, 161, 86–110. [Google Scholar] [CrossRef]
- Shen, W. Distributed manufacturing scheduling using intelligent agents. IEEE Intell. Syst. 2002, 17, 88–94. [Google Scholar] [CrossRef]
- Saeidlou, S.; Saadat, M.; Amini Sharifi, E.; Jules, G.D. Agent-based distributed manufacturing scheduling: An ontological approach. Cogent Eng. 2019, 6, 1565630. [Google Scholar] [CrossRef]
- Ramakurthi, V.B.; Manupati, V.K.; Machado, J.; Varela, L. A hybrid multi-objective evolutionary algorithm-based semantic foundation for sustainable distributed manufacturing systems. Appl. Sci. 2021, 11, 6314. [Google Scholar] [CrossRef]
- Guo, Z.; Ngai, E.; Yang, C.; Liang, X. An RFID-based intelligent decision support system architecture for production monitoring and scheduling in a distributed manufacturing environment. Int. J. Prod. Econ. 2015, 159, 16–28. [Google Scholar] [CrossRef]
- Varela, M.L.R.; Putnik, G.D.; Manupati, V.K.; Rajyalakshmi, G.; Trojanowska, J.; Machado, J. Integrated process planning and scheduling in networked manufacturing systems for I4.0: A review and framework proposal. Wirel. Netw. 2021, 27, 1587–1599. [Google Scholar] [CrossRef]
- Chiu, C.; Yih, Y. A learning-based methodology for dynamic scheduling in distributed manufacturing systems. Int. J. Prod. Res. 1995, 33, 3217–3232. [Google Scholar] [CrossRef]
- Varela, M.L.R.; Ribeiro, R.A. Distributed Manufacturing Scheduling Based on a Dynamic Multi-criteria Decision Model. In Recent Developments and New Directions in Soft Computing; Zadeh, L., Abbasov, A., Yager, R., Shahbazova, S., Reformat, M., Eds.; Studies in Fuzziness and Soft Computing; Springer: Cham, Switzerland, 2014; p. 317. [Google Scholar] [CrossRef]
- Vafaei, N.; Ribeiro, R.A.; Camarinha-Matos, L.M.; Varela, L.R. Normalization techniques for collaborative networks. Kybernetes 2019, 49, 1285–1304. [Google Scholar] [CrossRef]
- Santos, A.S.; Madureira, A.M.; Varela, M.L.R. An ordered heuristic for the allocation of resources in unrelated parallel-machines. Int. J. Ind. Eng. Comput. 2015, 6, 145–156. [Google Scholar]
- Putnik, G.D.; Pabba, S.K.; Manupati, V.K.; Varela, M.L.R.; Ferreira, F. Semi-Double-loop machine learning based CPS approach for predictive maintenance in manufacturing system based on machine status indications. CIRP Ann. Manuf. Technol. 2021, 70, 365–368. [Google Scholar] [CrossRef]
- Varela, M.L.R.; Amaral, G.; Pereira, S.; Machado, D.; Falcão, A.; Ribeiro, R.; Sousa, E.; Santos, J.; Pereira, A.F. Interoperable Decision Support System based on Multivariate Time Series for Setup Data Processing and Visualization. In Proceedings of the 19th International on Intelligent Systems Design and Applications (ISDA 2019), Auburn, WA, USA, 3–5 December2019; Advances in Intelligent Systems and Computing. Springer: Cham, Switzerland, 2019; pp. 550–560. [Google Scholar]
- Ignall, E.; Schrage, L. Application of the branch and bound technique to some flow-shop scheduling problems. Oper. Res. 1965, 13, 400–412. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).