Fault-Detection-Based Machine Learning Approach to Multicellular Converters Used in Photovoltaic Systems

Abstract

Today, solar energy systems based on photovoltaic (PV) panels associated with power converters are increasingly used to supply isolated sites. This structure has attracted several studies as a cost-effective, freely available, efficient source of clean and low-cost energy. However, the faults in power converters can affect the stability of the control system by supplying the isolated site with unwanted current and voltage. Therefore, this paper presents a comparative study using a fault-detection-based k-nearest neighbor (KNN) approach, between sliding mode control and exact linearization control applied to an isolated PV-system-based multicellular power converter, in order to assess the robustness and the performance of the two control strategies against the flying capacitor faults. The results obtained for both control methods in different fault cases are analyzed in terms of time series and feature spaces. These results, obtained with MATLAB software, prove the superiority of sliding mode control over exact linearization control in terms of response time, precision, and oscillations of flying capacitor voltages, as well as better separation (classification) between different fault cases in feature space.

1. Introduction

In recent decades, electrical power has played an important role in human life and the growth of the world economy. Most of this energy is produced from non-renewable sources such as fossil fuels, which are harmful to the environment [1]. This situation leads to serious problems related to pollution, which has a significant impact on global climate change. To overcome this issue related to the environment, and to meet the increasing demand for electricity in remote and isolated areas, clean and renewable energy sources such as photovoltaic systems constitute the optimal solution [2,3]. Therefore, the total solar photovoltaic energy that will be installed by 2035 is projected to be over 26 times that of 2010 [4]. Furthermore, according to the International Energy Agency (IEA), the additions in 2021 will be more than 142 GW, while the additions in 2022 will be 149 GW [5].

Due to their outstanding electrical performance as well as their high potential dynamics, multicellular converters are considered to be an excellent solution for renewable energy systems [6]. Indeed, these converters are characterized by a good improvement of the current ripples at their inputs and outputs. Moreover, their multicellular nature offers the capability of obtaining more efficient energy and a very wide range of power by choosing the cells to be used. Again, this is a clear advantage for renewable energy system conversion purposes.

Several studies have been carried out on the different types of power converters used in the exploitation of the electrical energy produced by photovoltaic panels [1,2]. Photovoltaic systems based on a two-level power converter have been used in remote sites for water-pumping systems [7,8]. In [9], a solar photovoltaic system with a standalone configuration was implemented based on a two-level four-leg power converter. Meanwhile, in [10], a solar photovoltaic system based on a two-level power converter was connected to a three-phase grid with power quality enhancement, while a two-level classical topology power converter was used as a distributed generation interfaced converter (DGIC) in [11]. However, in the classical two-level topology of power converters, the increased voltage stress applied to power switches and the high dv/dt ratio can cause damage to the power switches [12,13]. Therefore, power converters with a multilevel topology are used in solar photovoltaic systems to improve their efficiency, as mentioned in [14,15,16]. Among the multilevel topologies, the multicellular power converter has gained interest in recent years due to several advantages, such as increasing the speed by increasing the voltage by controlling the constant voltage/frequency ratio that is used in the control of the synchronous machines with permanent magnets [17]. In addition, due to the low dv/dt stress and low rating of the power-switching devices, multicellular converters can be used in applications with high DC voltage [18] because of the voltage on the DC side being naturally divided in flying capacitors [12,13,19,20,21,22]. Several studies on control methods of power converters have been applied to multicellular converters to enhance their robustness, rapidity, and accuracy. In [12], experimental and simulated results of a multicellular converter with sliding mode control confirmed the robustness and good rapidity of the proposed topology. In addition, a multicellular converter with exact linearization control was proposed in [13] and showed good tracking with acceptable accuracy and rapidity of the capacitor voltages and load current. However, in the event of failure of one or more power switches or flying capacitors, the desired current and voltage would not be obtained, causing uneven distribution of the high DC voltage for all power-switching devices in addition to the high harmonics in the currents and voltages. This deprives us of all the advantages of the multicellular converter topology. In the literature, fault-detection-based machine learning methods have been used. In [23,24], the authors used an early fault diagnosis method to isolate the faults of power switches in wind turbine converters based on an artificial intelligence approach; in [25], a hybrid dynamic classifier was used in order to detect the failure components of a multicellular converter, and in [26] the early detection of simple and multiple power switch faults of multicellular converters was achieved using a self-adaptive learning scheme method.

Remote sites’ electrification requires a sustainable and robust energy source with low maintenance costs. Photovoltaic systems are renewable and sustainable sources [4]; multicellular converters are robust compared with other two-level topologies [12,13], and fault detection using machine learning can reduce maintenance costs by optimizing the displacement schedule of maintenance agents to remote sites. Therefore, the optimal solution at remote sites is to use a photovoltaic system based on a multicellular converter with machine learning fault detection.

RL loads represent the majority of electric loads, including domestic and agricultural equipment. In the present study, a standalone or isolated solar photovoltaic system with an RL load is considered. Then, a failure analysis method using response time, accuracy, and voltage ripple is adopted, in addition to the feature space separation of different operating modes, to determine the most reliable and effective control method between sliding mode and exact linearization control. 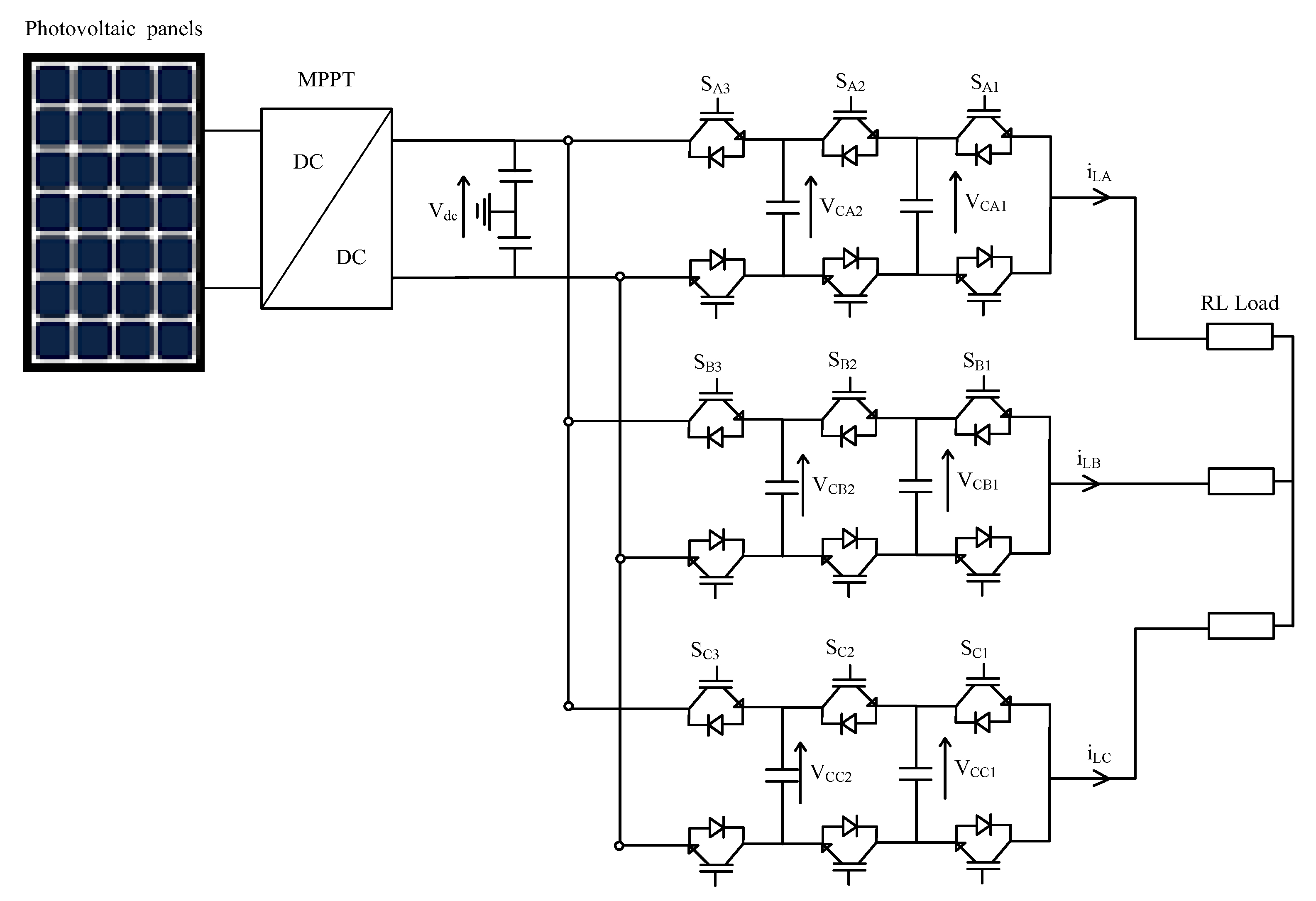Figure 1 shows the proposed photovoltaic system.

To achieve this objective, the modeling of the solar photovoltaic system—including the multicellular converter—is presented in Section 2. After the sliding mode and the exact linearization control methods are discussed in Section 3 and Section 4, respectively, the obtained results and their interpretation are presented in Section 5. Section 6 presents the data processing and feature space analysis, and the KNN algorithm’s implementation is described in Section 7. Finally, Section 8 presents the conclusions of this paper.

2. The Modeling of the Proposed System

The maximum power produced by the photovoltaic module corresponds to the top of the power curve (Figure 2) [27], also called the maximum power point (MPP), which corresponds to the V_MPP and I_MPP coordinates.

The power converter used in this work has a three-cell multicellular topology that includes floating capacitors. The modeling of this type of converter involves the mathematical equations of floating capacitors. In the latter, the instantaneous variations in current and voltage are given by Equations (1) and (2), respectively:

$$i_{Ci}=C_i\frac{d}{\mathit{dt}}{V}_{\mathit{Ci}}$$

(1)

$$\frac{d}{\mathit{dt}}{V}_{\mathit{Ci}}=\frac{1}{C_i}[S_{(i+1)}-S_i]i_L$$

(2)

S_i: Switching functions of the multicellular converter, which takes the two values (0 or 1).

i_Ci: Current of the flying capacitor $C_i$; i = 1,2.

V_Ci: Voltage of the flying capacitor $C_i$.

i_L: Load current.

The application of Kirchhoff’s law from the mid-point of V_dc and a three-phase load gives the following equations:

$$L_L\frac{d{i}_L}{dt}=V_S-R_L{i}_L-\frac{V_{dc}}{2}$$

(3)

$$V_S=S_1\left[V_{C1}\right]+S_2\left[V_{C2}-V_{C1}\right]+S_3\left[V_{dc}-V_{C2}\right]$$

(4)

$$\frac{{\mathit{di}}_L}{\mathit{dt}}=\frac{1}{L_L}\left(S_1\left[V_{C1}\right]+S_2\left[V_{C2}-V_{C1}\right]+S_3\left[V_{dc}-V_{C2}\right]\right)-R_L{i}_L-\frac{V_{dc}}{{2L}_L}$$

(5)

where the switching functions S₁, S₂, and S₃ are the inputs of the multicellular converter.

Flying capacitors C₁ and C₂ are traversed by the currents i_C1 and i_C2, respectively, and the voltages at their terminals are V_C1 and V_C2, respectively.

V_dc: The output voltage of the DC/DC boot converter.

R_L: Load resistor.

L_L: Load inductor.

The nonlinear model of the multicellular converter topology used in the photovoltaic system is given by Equation (6):

$$\left[\begin{array}{c}{\dot{V}}_{C1}\\ {\dot{V}}_{C2}\\ \dot{i_L}\end{array}\right]=\left[\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 0& 0& \frac{-R_L}{L_L}\end{array}\right]\left[\begin{array}{c}{V}_{C1}\\ V_{C2}\\ i_L\end{array}\right]+\left[\begin{array}{ccc}\frac{-i_L}{C_1}& \frac{i_L}{C_1}& 0\\ 0& \frac{-i_L}{C_2}& \frac{i_L}{C_2}\\ \frac{V_{C1}}{L_L}& \frac{V_{C2}-V_{C1}}{L_L}& \frac{V_{dc}-V_{C2}}{L_L}\end{array}\right]\left[\begin{array}{c}{S}_1\\ S_2\\ S_3\end{array}\right]+\left[\begin{array}{c}0\\ 0\\ \frac{-V_{dc}}{2L_L}\end{array}\right]$$

(6)

The state space of the proposed topology can be expressed by the following equation:

$$\dot{x}=f\left(x\right)+g\left(x\right)u+H$$

(7)

where the state vector is expressed by x = [$V_{C1}, V_{C2}, i_L$]^T, and the reference vector is x_ref = [$\frac{V_{dc}}{3}, \frac{2V_{dc}}{3}, i_L$]^T.

$$f(x)=\left[\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 0& 0& \frac{-R_L}{L_L}\end{array}\right], g(x)=\left[\begin{array}{ccc}\frac{-i_L}{C_1}& \frac{i_L}{C_1}& 0\\ 0& \frac{-i_L}{C_2}& \frac{i_L}{C_2}\\ \frac{V_{C1}}{L_L}& \frac{V_{C2}-V_{C1}}{L_L}& \frac{V_{dc}-V_{C2}}{L_L}\end{array}\right], u=[S_1{S}_2{S}_3{]}^T \mathrm{input} \mathrm{vector},$$

$$H=\left[\begin{array}{c}0\\ 0\\ \frac{-V_{dc}}{2L_L}\end{array}\right] \mathrm{is} \mathrm{the} \mathrm{constant} \mathrm{vector}.$$

3. Sliding Mode Control

Sliding mode, also called variable structure control, is used to select the optimal discrete switching function or configuration of the power converter. Its advantages are increased robustness, stability, and rapidity compared to other nonlinear control strategies.

Sliding mode control can be implemented in three steps:

• Determination of sliding surface expression.
• Convergence or stability conditions with Lyapunov functions.
• Control law calculation.

The sliding mode surface (Sr) is given by Equation (8):

$$Sr=x-x_{ref}$$

(8)

The Lyapunov function (V) in Equation (9) is introduced in order to study the stability of the proposed system. The system will be stable if the derivative of the Lyapunov function is negative:

$$V=\frac{1}{2}{\mathit{Sr}}^2(x)$$

(9)

The Lyapunov function’s derivative is given in Equation (10):

$$\dot{V}=\mathit{Sr}(x)\dot{\mathit{Sr}}(x)$$

(10)

where:

$$\dot{\mathit{Sr}}=\dot{x}-{\dot{x}}_{\mathit{ref}}$$

(11)

By substitution of Equation (7), Equation (11) can be rewritten as follows:

$$\dot{\mathit{Sr}}=f\left(x\right)+g\left(x\right)u+H-{\dot{x}}_{\mathit{ref}}$$

(12)

where the input control (u) can be expressed by Equation (13):

$$u=u_{\mathit{eq}}+u_n$$

(13)

To keep the error close to zero and the state variable at the sliding surface, the input control u_n must be equal to the inverse sign function of the sliding surface.

İn ideal sliding mode control, $\mathit{Sr}\left(x\right)= 0$ and $\dot{\mathit{Sr}}\left(x\right)=0$.

$$u_{\mathit{eq}}=-{\left(g\left(x\right)\right)}^{-1}\left(f\left(x\right)+H-{\dot{x}}_{\mathit{ref}}\right)$$

(14)

$$u=-{\left(g\left(x\right)\right)}^{-1}\left(f\left(x\right)+H-{\dot{x}}_{\mathit{ref}}\right)+u_n$$

(15)

Substitution of Equation (15) into Equation (12) gives the derivative of the sliding surface, as shown in Equation (16):

$$\dot{\mathit{Sr}}=g(x)u_n$$

(16)

The derivative of the Lyapunov function can be written as shown in Equation (17):

$$\mathit{Sr}(x)\dot{\mathit{Sr}}(x)=\mathit{Sr}(x)g(x)u_n$$

(17)

where $u_n={\left[\begin{array}{ccc}{u}_{n1}& u_{n2}& u_{n3}\end{array}\right]}^T$ are the sliding surface sign functions of switches 1, 2, and 3, respectively, so Equation (17) can be expressed in Equation (18) as follows:

$$Sr\left(x\right)\dot{Sr}\left(x\right)=Sr\left(x\right){\left[\left(\frac{-i_L}{C_1}+\frac{V_{C1}}{L_L}\right)u_{n1}, \left(\frac{i_L}{C_2}-\frac{i_L}{C_1}+\frac{V_{C2}-V_{C1}}{L_L}\right)u_{n2}, \left(\frac{i_L}{C_2}+\frac{\left(V_{dc}-V_{C2}\right)}{L_L}\right)u_{n3}\right]}^T$$

(18)

According to Lyapunov’s theory of stability, the following condition must be satisfied:

$$\dot{V}(x)<0$$

(19)

-

To ensure $Sr\left(x\right)\left(\frac{-i_L}{C_1}+\frac{V_{C1}}{L_L}\right)u_{n1}<0$, u_n1 must be $u_{n1}=-\mathrm{sign}\left[\mathit{Sr}(x)\left(\frac{-i_L}{C_1}+\frac{V_{C1}}{L_L}\right)\right]$.

-

To ensure $Sr\left(x\right)\left(\frac{i_L}{C_2}-\frac{i_L}{C_1}+\frac{V_{C2}-V_{C1}}{L_L}\right)u_{n2}<0$, u_n2 must be $u_{n2}=-\mathrm{sign}\left[\mathit{Sr}(x)\left(\frac{i_L}{C_2}-\frac{i_L}{C_1}+\frac{V_{C2}-V_{C1}}{L_L}\right)\right]$.

-

To ensure $Sr\left(x\right)\left(\frac{i_L}{C_2}+\frac{\left(V_{dc}-V_{C2}\right)}{L_L}\right)u_{n3}<0$, u_n3 must be $u_{n3}=-\mathrm{sign}\left[\mathit{Sr}(x)\left(\frac{i_L}{C_2}+\frac{\left({\mathrm{V}}_{dc}-V_{C2}\right)}{L_L}\right)\right]$.

From Equations (18) and (19), the switching functions of sliding mode control can be expressed as follows:

$$\left\{\begin{array}{c}{u}_{n1}=-\mathrm{sign}\left[\mathit{Sr}(x)\left(\frac{-i_L}{C_1}+\frac{V_{C1}}{L_L}\right)\right],\\ u_{n2}=-\mathrm{sign}\left[\mathit{Sr}(x)\left(\frac{i_L}{C_2}-\frac{i_L}{C_1}+\frac{V_{C2}-V_{C1}}{L_L}\right)\right],\\ u_{n3}=-\mathrm{sign}\left[\mathit{Sr}(x)\left(\frac{i_L}{C_2}+\frac{\left(V_{dc}-V_{C2}\right)}{L_L}\right)\right],\end{array}\right.$$

(20)

4. Exact Linearization Control

The model of the proposed topology appropriate for the power converter used in the photovoltaic system is given by the system Equations (6) and (7). The exact linearization control aims at finding a direct linear relationship between the output and the input of the system. The idea of this control method consists of deriving the output until the input appears in the derivative of the output.

For this, Equations (6) and (7) can be expressed as follows:

$$\begin{gathered} \dot{x}=f\left(x\right)+g\left(x\right)u+H \\ Y=x \end{gathered}$$

(21)

$$\dot{Y}=f\left(x\right)+g\left(x\right)u+H$$

(22)

A new control input (v) can be introduced as follows:

$$v=\dot{Y}$$

(23)

which can represented as shown in Figure 3.

Therefore, all equations between v and Y can be replaced by an integrator, provided that the matrix g is invertible.

$$v=f\left(x\right)+g\left(x\right)u+H$$

(24)

$$u=g^{-1}\left(x\right)\left[v-H\right]-g^{-1}\left(x\right)f\left(x\right)$$

(25)

A multicellular converter with exact linearization control is presented in Figure 4.

The input control given by Equation (23) for the multicellular converter with exact linearization represented in Figure 4 can be simplified to a closed-loop transfer function with a simple integrator and proportional regulator K_r = (K_r1 K_r1 K_r2), as shown in Figure 5, where:

K_r1: The proportional regulator for flying capacitor voltages V_C1 and V_C2.

K_r2: The proportional regulator for load currents (i_L).

The transfer functions of the flying capacitor voltages represented with a closed loop are equal to $\frac{1}{{\tau }_{1}s+1}$, where the constant time in the voltage loop is ${\tau }_1=\frac{1}{K_{r1}}$, and the closed-loop transfer function of load currents is equal to $\frac{1}{{\tau }_{2}s+1}$, where the constant time in the current loop is ${\tau }_2=\frac{1}{K_{r2}}$.

In first-order systems, the response time is (t_r5% = 3 $\tau$). In the closed-loop flying capacitor voltage, $t_{r1}=30\times {10}^{-3} \mathrm{s}$ to assure good rapidity. Therefore, ${\tau }_1=10\times {10}^{-3}$ s.

In the closed-loop load current, which is faster than the voltage loop, $t_{r2}=3\times {10}^{-4} \mathrm{s}$. Therefore, ${\tau }_1={10}^{-4}$ s.

The regulators are chosen as K_r1 = 100, K_r2 = 15,000 in order to assure the stability of the studied system.

5. Simulation Results

In order to validate the behavior of the multicellular converter with the proposed controls in the case of flying capacitor faults, the system shown in Figure 1 is adopted.

Table 1. System simulation parameters.

Parameter	Value
Photovoltaic system voltage	$V_{\mathit{dc}}=600 \mathrm{V}$
Flying capacitor	$C_1=C_2=400 \mathsf{\mu }\mathrm{F}$
Electric load inductor	$L_L=2 \mathrm{mH}$
Electric load resistor	$R_L=25 \Omega$
Kr1	100
Kr2	1500
fSL	20 KHz

shows the system parameters.

In exact linearization control, the pulse-width modulation (PWM) method is carried out based on a triangular signal (20 kHz) to obtain a binary signal (0,1).

A set of computer simulation runs was conducted using sliding mode control and the exact linearization technique to demonstrate the effectiveness of the proposed control strategies.

The exact linearization and sliding mode controls were tested against load and V_dc variations in [12,18]. Therefore, in this paper, a study of the performance of these control methods was applied to multicellular converters considering all faulty capacitor cases using MATLAB/Simulink software, from healthy mode to faults, in capacitors C₁, C₂, and both simultaneously. A comparison was made to better illustrate the impact of failing capacitors on system behavior and to determine the better controller in this circumstance.

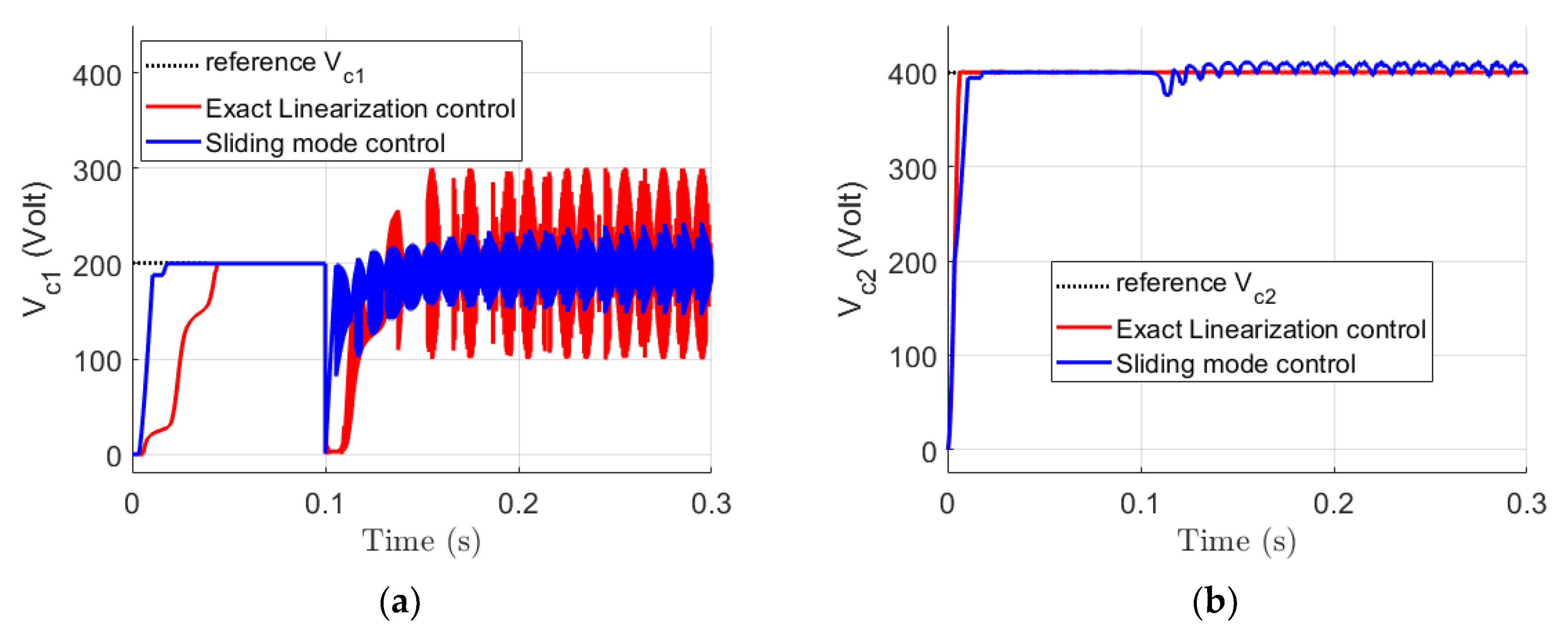
Figure 6 shows the voltage and the corresponding error compared to the reference of flying capacitors V_C1 and V_C2 for both control methods in a healthy operating mode. In sliding mode control, the two voltages track their references in a steady state, with a response time equal to 0.02 s for both V_C1 and V_C2 and a ripple (∆V) of 0.02 V. However, in exact linearization control, the response time for V_C1 and V_C2 is 0.045 s and 0.007 s, respectively, with a ripple of 0.02 V. Hence, the sliding mode control performs better than the exact linearization control in terms of ripple and response time.

The failure of capacitors can be simulated by connecting a high-value resistor (R = 100 ohm) in series with a capacitor [25].

As shown in Figure 7 and Figure 8, in case of the occurrence of a failure in C₁, the ripple magnitude of V_C1 increases in both controls—by 200 V for exact linearization and by 95 V for sliding mode. On the other hand, V_C2 is less affected, and the ripple is less intense, i.e., 15 V for the sliding mode and 1 V for the exact linearization. This implies that the sliding mode control shows better robustness than the exact linearization control.

Figure 9 and Figure 10 illustrate the results for the failure of capacitor C₂. This case shows that the failure in C₂ has less effect on the behavior of the system. This case shows fewer voltage ripples in V_C2 for both controls compared to the ripples generated in V_C1 due to the failure of capacitor C₁.

The associated ripple for V_C2 is 1 V in exact linearization and 60 V in sliding mode, while for V_C1 it is equal to 1 V in the case of exact linearization and 10 V in sliding mode. In addition, the sliding mode control has better accuracy than the exact linearization control—6 V for V_C1 and 10 V for V_C2 in the case of sliding mode control, and 22 V for V_C1 and 33 V for V_C2 in the case of exact linearization.

The impact of the failure of capacitors C₁ and C₂ simultaneously is illustrated in Figure 11 and Figure 12. This case shows that the simultaneous failure of C₁ and C₂ has a significant impact on the system behavior. The flying capacitor voltages follow their references, with strong ripples in sliding mode control of about 90 volts for V_C1 and V_C2. On the other hand, for the exact linearization control, the voltage V_C1 drops to 0 V without ripple, while V_C2 follows the reference with 35 volts of precision. The above findings indicate that the sliding mode control was less affected by this type of fault than the exact linearization control, despite the high ripple generated.

Table 2. Comparison between sliding mode and exact linearization control methods in different operating modes.

Control Mode		Response Time (s)		Precision (V)		∆V (V)
		VC1	VC2	VC1	VC2	VC1	VC2
Sliding mode control	Healthy mode	0.02	0.02	0	0	0.02	0.02
	C1 failure	0.12	0.02	5	5	95	15
	C2 failure	0.01	0.01	6	10	10	60
	C1 and C2 failure	0.01	0.01	5	5	90	90
Exact linearization control	Healthy mode	0.045	0.007	0	0	0.02	1
	C1 failure	0.12	0	0	0	200	1
	C2 failure	0	-	22	33	1	1
	C1 and C2 failure	0	-	200	30	1	1

presents the comparison of the study’s results.

From the above discussion of the simulation results comparing the sliding mode and exact linearization control methods applied to a three-cell multicellular converter used in a photovoltaic system, for different modes (i.e., healthy, C₁ failure, C₂ failure, and simultaneous C₁ and C₂ failure), the slider mode control clearly showed more robustness against all types of faults considered, along with a shorter response time in a transient state, while the exact linearization control showed less voltage ripple. However, the major disadvantage of exact linearization control is that it has zero load current when C₂ is faulty.

The results also indicate that when capacitor C₁ fails, it generates ripples in V_C1—and similarly for capacitor C₂, where it generates ripples in V_C2. It can clearly be seen that the fault of capacitor C₁ causes more severe ripples than the fault relating to C₂. Moreover, the sliding mode control is more robust than exact linearization control in terms of capacitor failure. However, in the healthy case, the exact linearization control shows slightly better performance than the sliding mode control.

In the next section, the changes that occur in feature spaces of the system resulting from faults in capacitors are discussed, along with the impact of capacitor faults on the feature space geometry and/or distribution.

6. Data Processing and Feature Space Analysis

Data processing and analysis is a critical step, for it creates a feature space that distinguishes between different operating conditions, i.e., the feature space differentiates between healthy and faulty operating modes. For this purpose, the chosen features must maximize the separation between the normal operating mode and each of the failure modes in the feature space. In order to define the most sensitive features to distinguish the normal class of each of the failure modes in the multicellular converter, knowledge of the physical dynamics of the latter is needed. The capacitor voltages V_C1 and V_C2 are used for this purpose. Thus, there are a number of features that correspond to the number of capacitors, to which can be added other features such as the load current (i_L) to ensure better separation of the different failure modes. As indicated by Equation (3), the capacitor voltages are regulated to their reference values in the case of a healthy operating mode (normal condition), whereas if a fault occurs in one or two capacitors the corresponding voltages cannot reach their references with the proposed control. This change over time between the real values of the capacitor voltages and their references makes it possible to detect faults through changes in the normal class in the space of the characteristic curves.

Figure 13, Figure 14, Figure 15 and Figure 16 show the characteristics for different operating modes with sliding mode and exact linearization control derived from simulation data. V_C1, V_C2, and i_L were used as the axis for the representation of the space of 2D or 3D entities.

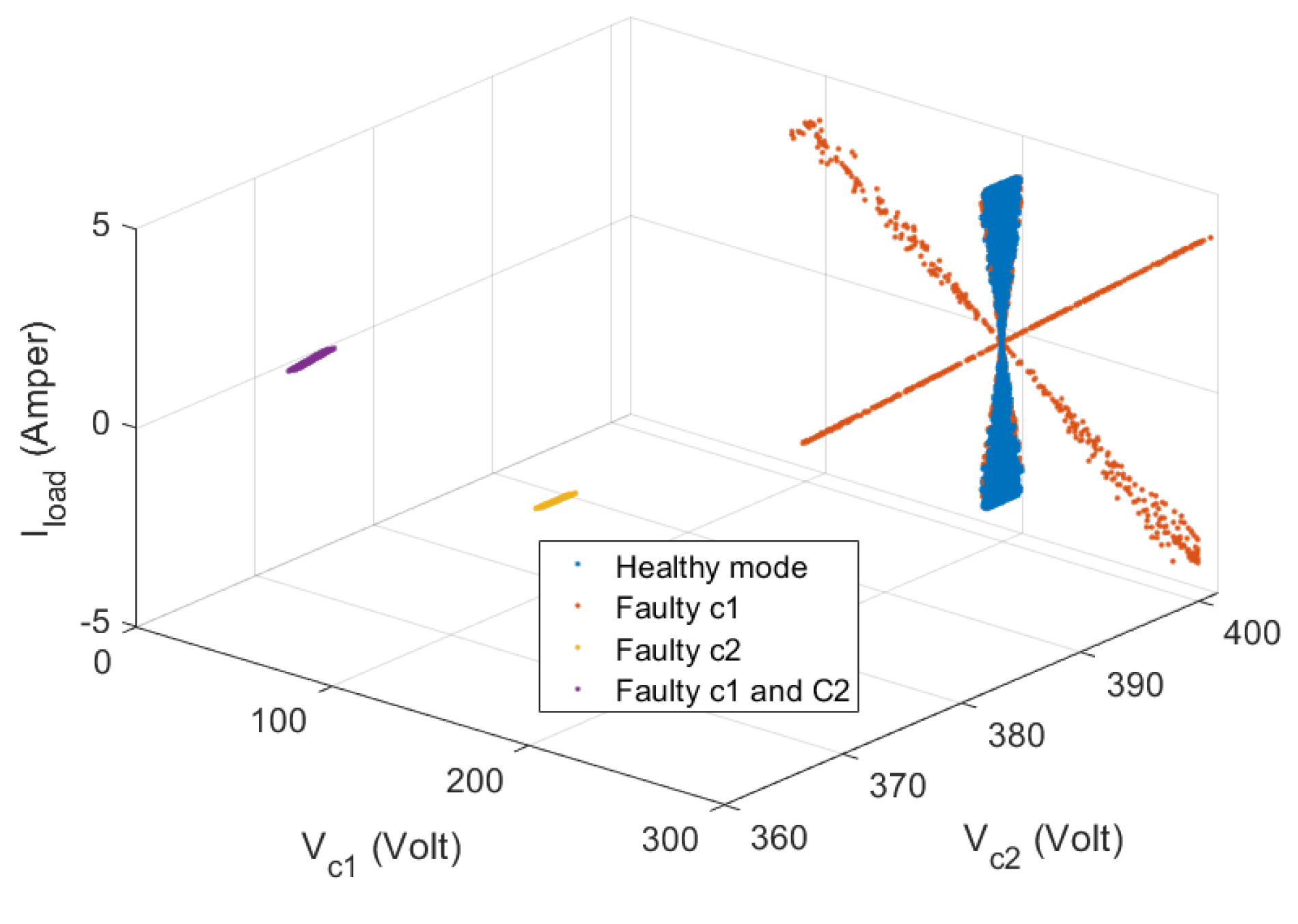
Figure 13 shows the two-axis feature space with sliding mode control for all healthy or faulty modes. It should be noted that healthy feature spaces are very small regimes drowned in the global feature space. The spatial characteristics of the different failure modes are well-separated but with some superposed or interlaced regions. To overcome this situation, the current “i_L” is suggested as the third axis (see Figure 14). This last figure shows that all of the modes are well-separated with no ambiguity. These results show that through these features spaces, it is possible to detect or locate the different faults.

The feature space corresponding to the exact linearization control for all of the modes is shown in Figure 15. It can be seen that the three fault modes in the capacitors C₁, C₂, and C₁/C₂ simultaneously are well-separated. On the other hand, the fault C₁ completely covers the healthy mode; the latter represents a restricted mode compared to the modes with faults. As in the case of sliding mode control, and to overcome this problem of the feature spaces covering one another, the current “i_L” is added as the third axis (see Figure 16). This latest figure shows that all of the modes are better-separated, but always with an ambiguity between the healthy mode and the faulty mode in C₁; however, this ambiguity is not very important. These results show that through these feature spaces, it is possible to detect or locate the various faults with a slight ambiguity in the case of a fault in capacitor C₁.

According to the results obtained from the feature spaces, the sliding mode control presents a better separation between the different modes compared to the exact linearization control. In addition, the sliding mode control shows better robustness compared to the exact linearization control. This can be observed in the zero-load current when C₂ is faulty in the case of exact linearization control.

7. K-Nearest Neighbor (KNN) Implementation

After the data have been collected and the features selected, the available data can be used to apply the machine learning algorithm for classification.

Since the data would be classified into more than two classes, the k-nearest neighbor (KNN) algorithm was chosen because it is multiclass, based on determining the distance between all features. The classification is based on the property of closest distance, which is the feature to which it is similar or identical.

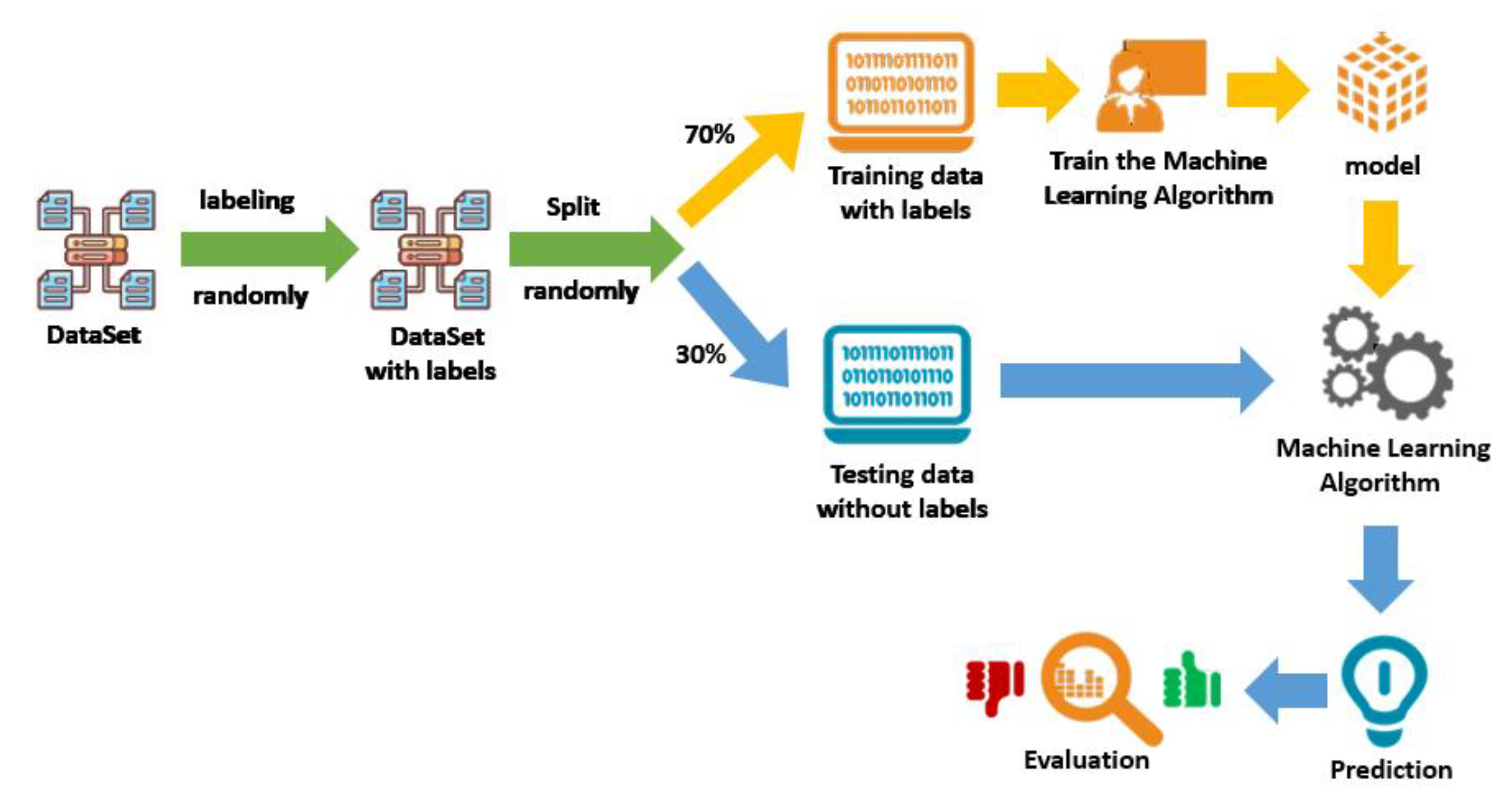
The process entails teaching the algorithm with the available data, i.e., training it to know the characteristics of each case in order to identify and classify them, and this is done by teaching the data and dividing them randomly into 70% training and 30% testing sets, and then submitting the training data to the machine learning algorithm to build a classified model based on them (Figure 17).

In order to compare the sliding mode and exact linearization control methods in terms of processing time and accuracy,

Table 3. Comparison between sliding mode and exact linearization control methods in terms of processing time and accuracy.

	K-Number	1	2	3	4	5
Sliding mode control	Accuracy (%)	99.99	99.98	99.99	99.98	99.99
	Processing time (s)	4.40	4.39	4.39	4.39	4.39
Exact linearization control	Accuracy (%)	91.42	91.91	92.13	92.19	92.25
	Processing time (s)	4.28	3.87	4.29	4.28	4.28

represents the result with variable K values.

The equipment used to implement the machine learning algorithm had the following characteristics:

-

Rating: 4.7 Windows performance index.

-

Processor: Intel (R) Core—i3-3217U @ 1.80 GHZ.

-

RAM: 4.00 GB.

-

System type: 64-bit operating system.

The histogram in the Figure 18 compares the behavior of the proposed fault detection approaches in terms of accuracy. It was observed that the sliding mode classification model was more accurate than the exact linearization model.

8. Conclusions

This paper presents a comparative study between sliding mode and exact linearization control methods applied to a three-cell multicellular converter used in a photovoltaic system under flying capacitor faults. The parameters used to differentiate between the two control methods were the response time, precision, and ripple of flying capacitor voltages in healthy and faulty modes (i.e., C₁ failure, C₂ failure, and simultaneous failure of C₁ and C₂). In the field of time series, sliding mode control showed better performance in terms of robustness and response time compared to exact linearization control in both healthy and faulty modes. It was found that the exact linearization control was smoother (i.e., less ripple) in both healthy and faulty modes.

In order to analyze the behavior of multicellular converters in four operating modes, two-dimensional feature spaces were used with time-domain axes to separate the different operating modes. The use of a KNN algorithm for classification also proved that the sliding mode control presents better class separation compared to the exact linearization control. As a direction for future works, the calculation of remaining useful life (RUL) could be carried out in order to perform a fault prognosis of the considered system.