Analysis of Natural Heat Dissipation Capacity of Hydraulic Tank and Relevant Influencing Factors
Abstract
:1. Introduction
2. Analysis of Heat Dissipation in a Hydraulic Tank
3. Deduction of Mathematical Model for Natural Heat Dissipation in a Hydraulic Tank
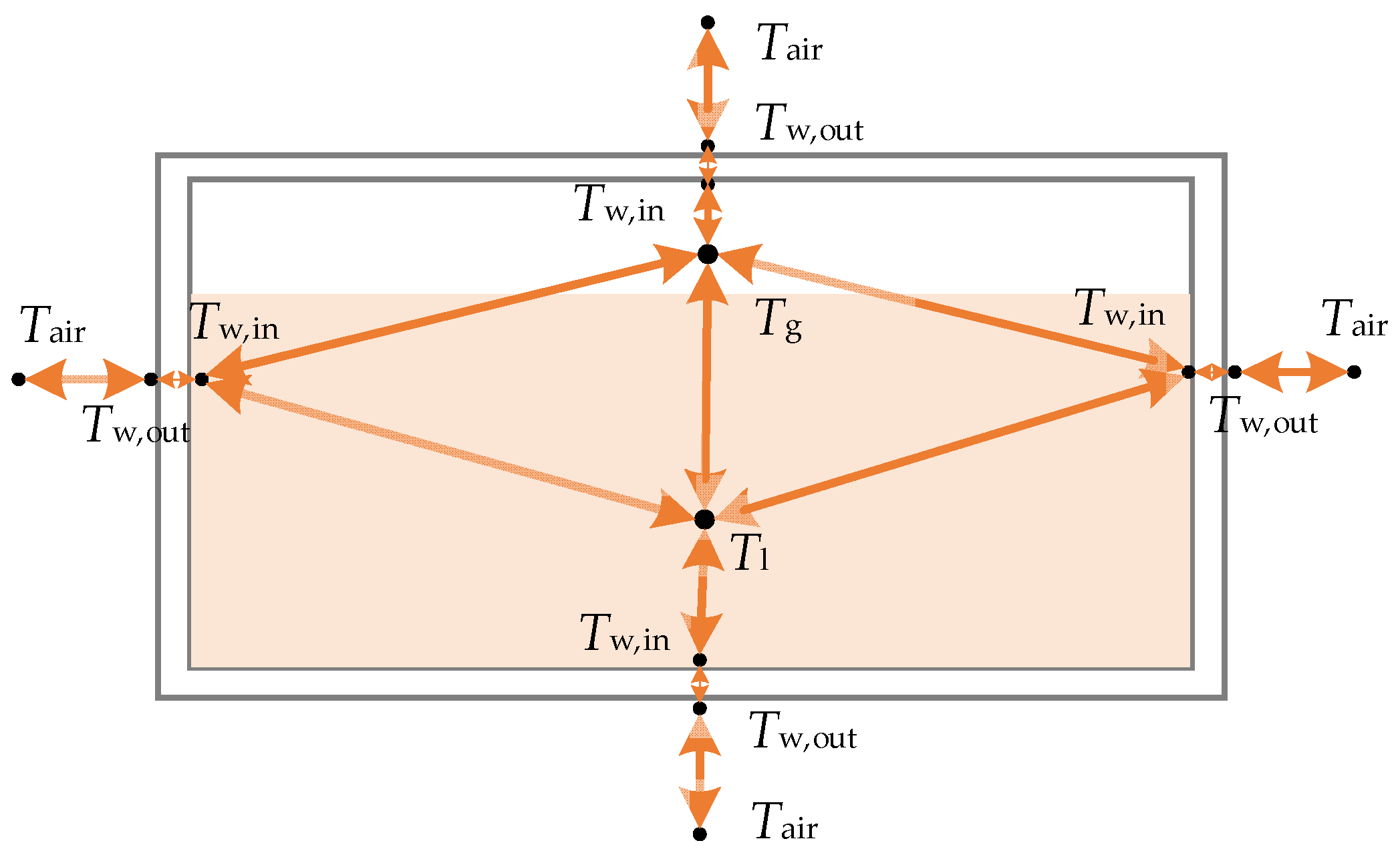
- The temperature of the hydraulic oil, gas, and each wall is a lumped parameter.
- The radiation heat transfer of the hydraulic tank was not considered.
- We only considered the horizontal attitude of the hydraulic tank, regardless of its special conditions.
3.1. Heat Dissipation on the Oil–Tank Wall Contact Area
3.2. Heat Dissipation on the Oil–Air Contact Area
3.3. Natural Heat Dissipation Capacity of Hydraulic Tank
4. Discussion
4.1. Influence of the Oil Height
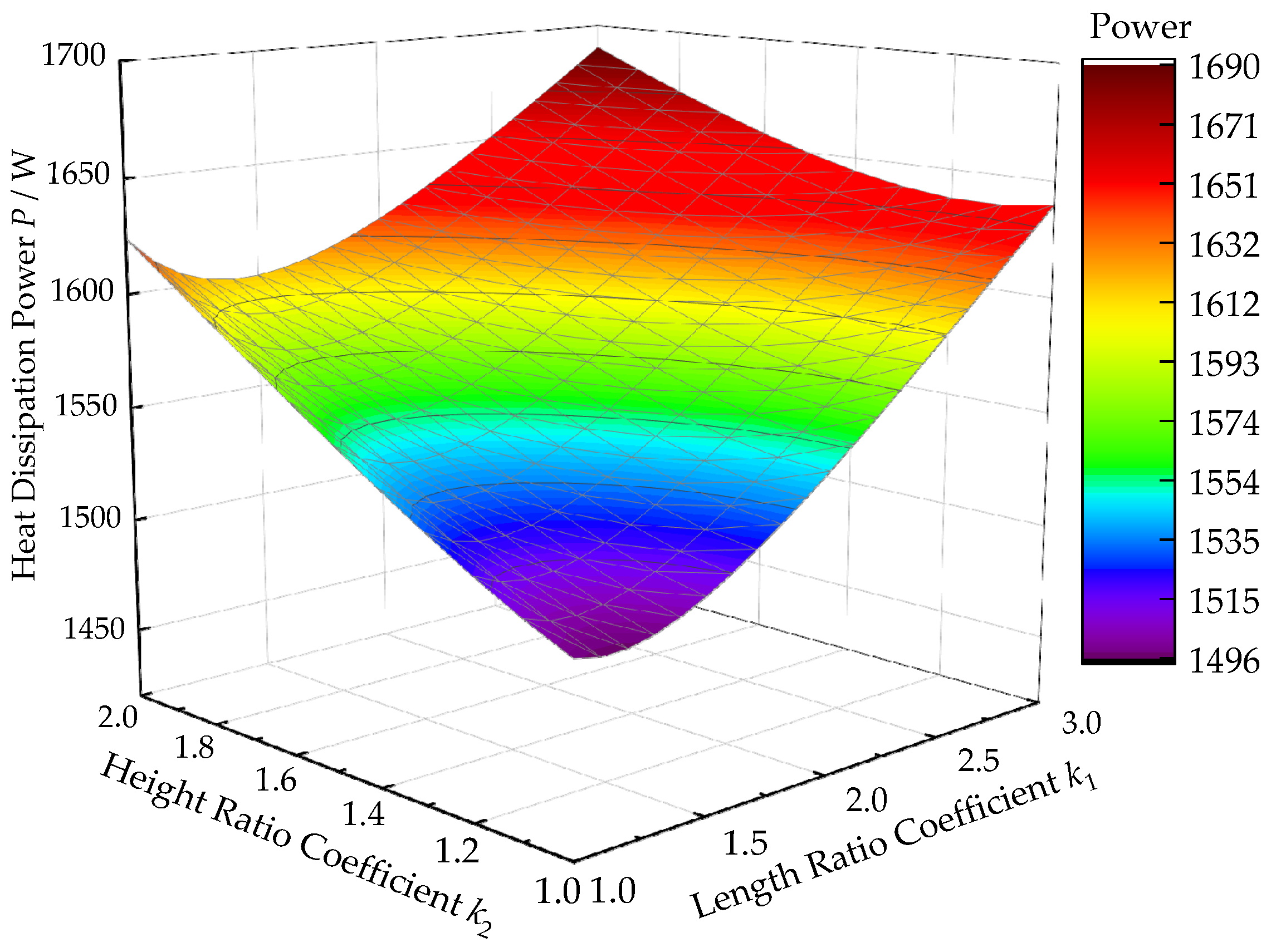
4.2. Influence of the Geometrical Design Proportion
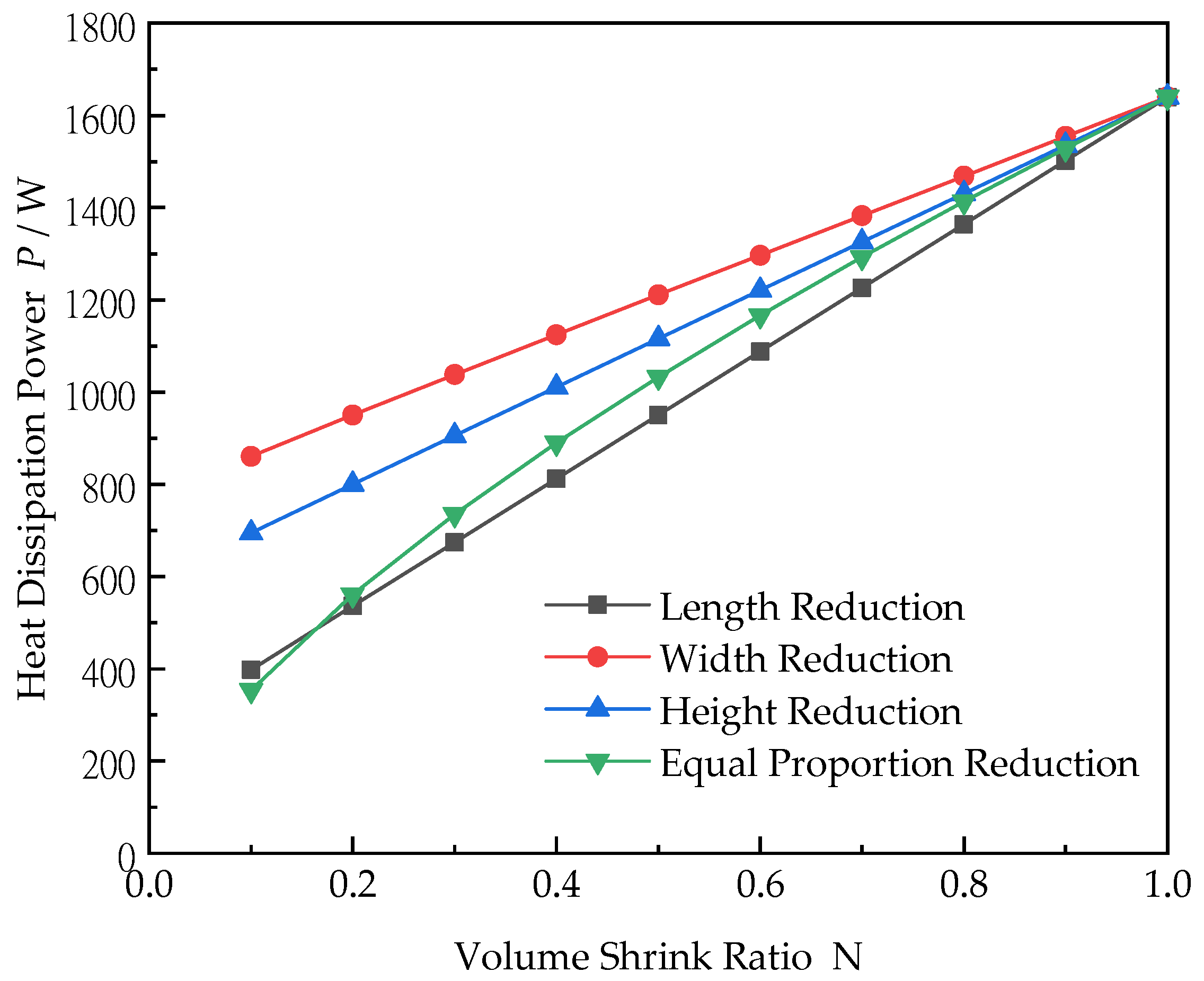
4.3. Influence of Volume Reduction Method of Hydraulic Tank
4.4. Influence of Material and Wall Thickness of Hydraulic Tank
5. Conclusions
- 1.
- The heat dissipation power of the hydraulic tank is proportional to the oil height. That is, the higher the oil height ratio is, the greater the natural heat dissipation power is. This means the capacity of the heat conduction capacity of oil is greater than that of the air.
- 2.
- When the length ratio coefficient k1 is constant, the natural heat dissipation power of the hydraulic tank increases with the height ratio coefficient k2. When k2 is constant, the power decreases first and then increases with the k1. Compared with k2, the length ratio coefficient k1 of the hydraulic tank has a greater impact on the natural heat dissipation capacity.
- 3.
- The order of the effect of the reduction method on the natural heat dissipation power of the hydraulic oil tank is length reduction > equal proportion reduction > height reduction > width reduction.
- 4.
- Moreover, when the thermal conductivity λ of the material is greater than 10 W/(m·K), the material and wall thickness of hydraulic tank have little effect on the heat dissipation capacity of the hydraulic tank. When λ is less than 10 W/(m·K), the effect is great. Therefore, for metal tanks, replacing materials with those with better thermal conductivity cannot effectively improve the heat dissipation capacity of the tank.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tao, L. Design analysis and optimization for the civil aircraft hydraulic supply system based on AMESim. In Proceedings of the 2016 IEEE International Conference on Aircraft Utility Systems (AUS), Beijing, China, 10–12 October 2016; pp. 890–894. [Google Scholar]
- Dong, W.; Han, S.; Jiao, Z.; Wu, S.; Zhao, Y. Compound angle-synchronizing control strategy for dual electro-hydraulic motors in hydraulic flight motion simulator. In Proceedings of the 2014 IEEE Chinese Guidance, Navigation and Control Conference, Yantai, China, 8–10 August 2014; pp. 2219–2224. [Google Scholar]
- Fang, D.L.; Shang, J.Z.; Luo, Z.R.; Feng, Y.; Chen, F. Research on Hydraulic Performance of Downhole Traction Robot in Oil Field. IOP Conf. Ser. Earth Environ. Sci. 2018, 108, 032031. [Google Scholar] [CrossRef]
- Yang, K.; Zhou, L.L.; Rong, X.W.; Li, Y.B. Onboard hydraulic system controller design for quadruped robot driven by gasoline engine. Mechatronics 2018, 52, 36–48. [Google Scholar] [CrossRef]
- Zhou, W. Simulation of Hydraulic System Faults for Marine Machinery Based on AMESim. J. Coast. Res. 2019, 94, 357–361. [Google Scholar] [CrossRef]
- Chen, H.-X.; Ma, Z.; Zhang, W.; Zhu, B.; Zhang, R.; Wei, Q.; Zhang, Z.-C.; Liu, C.; He, J.-W. On the hydrodynamics of hydraulic machinery and flow control. J. hydrodyn. 2017, 29, 782–789. [Google Scholar] [CrossRef]
- Kang, W.L.; Wang, Y. Diagnosis and management of the polluted hydraulic oil. In The First International Workshop on Hydraulic Equipment and Support Systems for Mining; Trans Tech Publications Ltd: Huludao, China, 2013; Volume 619, pp. 447–450. [Google Scholar]
- Wang, C.; Quan, L.; Ou, H. The method of restraining hydraulic impact with active adjusting variable damping. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2019, 233, 3785–3794. [Google Scholar] [CrossRef]
- Chen, K.; Deng, J.; Zhan, C.; Zheng, F. Research on key technology of hydraulic servo cylinder with adaptive variable clearance. In Proceedings of the 2015 Chinese Automation Congress (CAC), Wuhan, China, 27–29 November 2015; pp. 1922–1925. [Google Scholar]
- Kong, X.D.; Zhu, Q.X.; Yao, J.; Shang, Y.X.; Zhu, Y. Basic Theory and Key Technology of “New Method for Lightweight Design and Manufacturing of Hydraulic Components and Systems”. J. Mech. Eng. 2021, 57, 4–12. [Google Scholar]
- Xie, G.; Dong, Y.; Zhou, J.; Sheng, Z. Topology optimization design of hydraulic valve blocks for additive manufacturing. ARCHIVE Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2020, 234, 1899–1912. [Google Scholar] [CrossRef]
- Zhai, F.G.; Li, C.; Ye, Z.; Tan, C.Y.; Chen, Y. Influence of Built-in Filter Boundary on Flow Field in Miniaturized Hydraulic Tank. J. Mech. Eng. 2021, 57, 114–122. [Google Scholar]
- Sliwinski, P.; Patrosz, P. Methods of Determining Pressure Drop in Internal Channels of a Hydraulic Motor. Energies 2021, 14, 5669. [Google Scholar] [CrossRef]
- Załuski, P. Influence of Fluid Compressibility and Movements of the Swash Plate Axis of Rotation on the Volumetric Efficiency of Axial Piston Pumps. Energies 2022, 15, 298. [Google Scholar] [CrossRef]
- Banaszek, A.; Petrovic, R. Problem of non-proportional flow of hydraulic pumps working with constant pressure regulators in big power multipump power pack unit in open system. Teh. Vjesn. 2019, 26, 294–301. [Google Scholar]
- Banaszek, A. Methodology of flow rate assessment of submerged hydraulic ballast pumps on modern product and chemical tankers with use of neural network methods. Procedia Comput. Sci. 2021, 192, 1894–1903. [Google Scholar] [CrossRef]
- Shen, W.; Zhang, J.; Sun, Y.; Zhang, D.-J.; Jiang, J.-H. Effect of cavitation bubble collapse on hydraulic oil temperature. J. Cent. South Univ. 2016, 23, 1657–1668. [Google Scholar] [CrossRef]
- Lou, X.Y. Research on Oil Temperature Control Technology of Mobile Machinery in Closed Hydraulic Transmission System. Adv. Mater. Res. 2014, 1037, 274–277. [Google Scholar] [CrossRef]
- Zhang, S.H.; Zhou, Z.B.; Song, H.L.; Li, Y. The Design of Hydraulic Stripping Attachment’s Oil Tank. Appl. Mech. Mater. 2014, 556–562, 716–719. [Google Scholar] [CrossRef]
- Guo, R.; Zhang, Z.M.; Zhao, J.Y.; Ning, C.; Li, B.L. Research of refrigeration system for a new type of constant temperature hydraulic tank. High Technol. Lett. 2016, 22, 436–444. [Google Scholar]
- Lv, Y.; Zheng, B. Structure Optimization of Hydraulic Exoskeleton Robot Reservoir. Mach. Tool Hydraul. 2019, 47, 56–59. [Google Scholar]
- Liang, J.W.; Feng, Y.B.; Li, S.Z.; Yang, X. Simulation and Improvement on Heat Dissipation of Hydraulic Tank. Mach. Tool Hydraul. 2019, 47, 74–77. [Google Scholar]
- Guan, B.; Feng, Y.B.; Li, S.Z.; Wang, J. Simulation and Research on Heat Dissipation of Fuel Tank Heat Exchanger Plate Based on Phase Change. Mach. Tool Hydraul. 2020, 48, 169–173. [Google Scholar]
- Wu, R.Z.; Ye, Z.Q.; Xue, Z.F.; Shi, J.Z.; He, M.F.; Zhang, J.X. Research on heat balance of large tractor hydraulic steering system. Chin. J. Constr. Mach. 2019, 17, 52–56. [Google Scholar]
- Zhang, X.L.; Wang, X.X.; Tan, L. Research on Modeling and Simulation of Temperature Characteristics of Helicopter Hydraulic System. Mach. Tool Hydraul. 2018, 46, 37–40. [Google Scholar]
- Lan, J.; Zhu, L.; Zhao, J.Q. Modeling and simulation of general fuel tank thermal model. J. Aerosp. Power 2014, 29, 1623–1630. [Google Scholar]
- Wu, W.; Liu, H.; Zhou, J.; Hu, J.; Yuan, S. Energy efficiency of hydraulic regenerative braking for an automobile hydraulic hybrid propulsion method. Int. J. Green Energy 2019, 16, 1046–1053. [Google Scholar] [CrossRef]
- Yao, J.; Liu, X.Y.; LIM, D.; Kong, D.C.; Hu, J.J. Design and Characteristic Analysis of Miniaturized Labyrinth Hydraulic Reservoir. J. Mech. Eng. 2021, 57, 83–92. [Google Scholar]
- Jang, D.H.; Kim, W.J. Warm temperature deformation behavior and processing maps of 5182 and 7075 aluminum alloy sheets with fine grains. Met. Mater. Int. 2018, 24, 455–463. [Google Scholar] [CrossRef]
- Engh, C.A., Jr.; Hopper, R.H., Jr.; Huynh, C.; Ho, H.; Sritulanondha, S.; Engh, C.A., Sr. A prospective, randomized study of cross-linked and non–cross-linked polyethylene for total hip arthroplasty at 10-year follow-up. J. Arthroplast. 2012, 27, 2–7. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.; Yun, Y.S.; Kim, B.; Cho, S.Y.; Jin, H.J. Nylon 610/graphene oxide composites prepared by in-situ interfacial polymerization. J. Nanosci. Nanotechnol. 2014, 14, 5703–5707. [Google Scholar] [CrossRef]

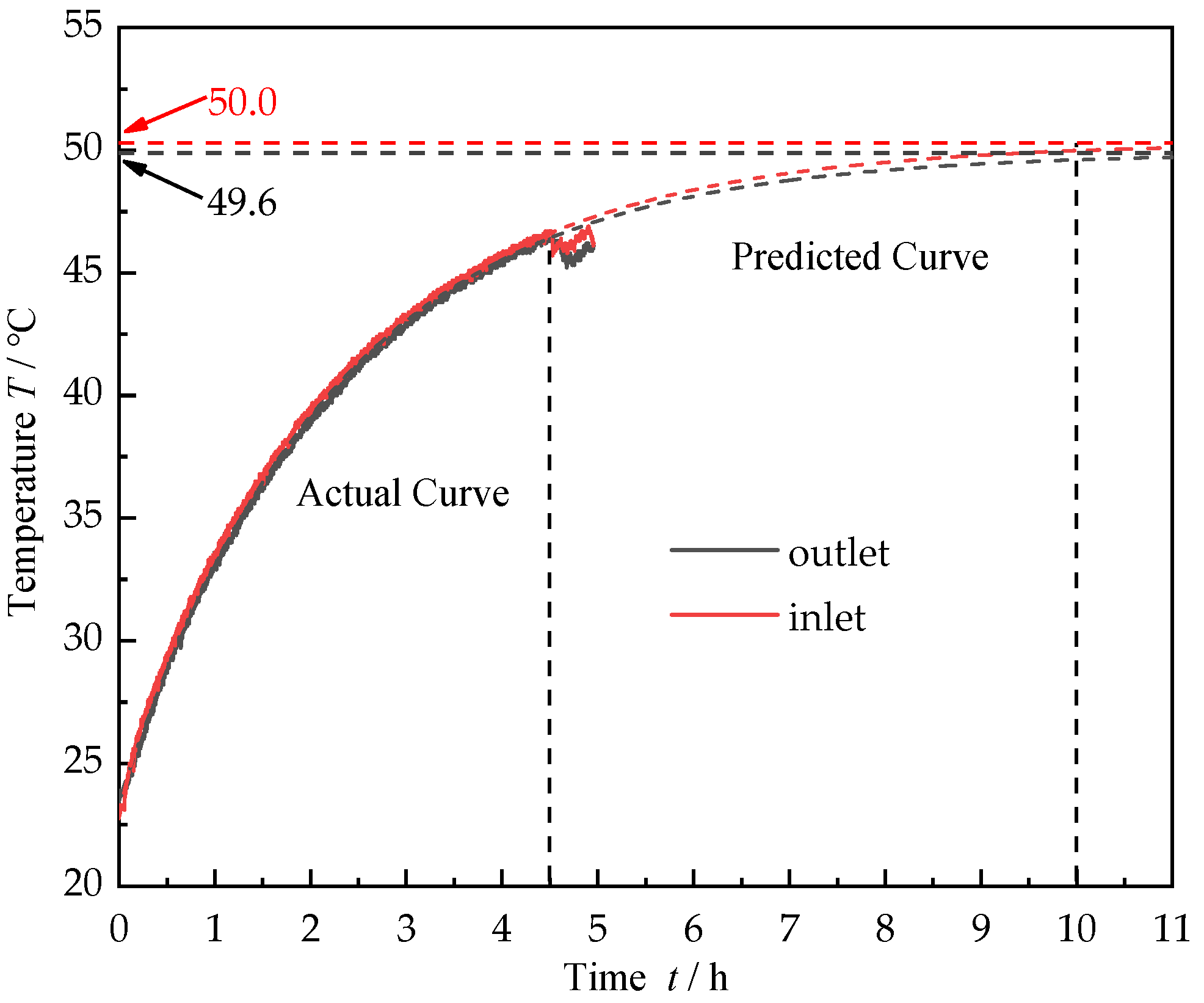

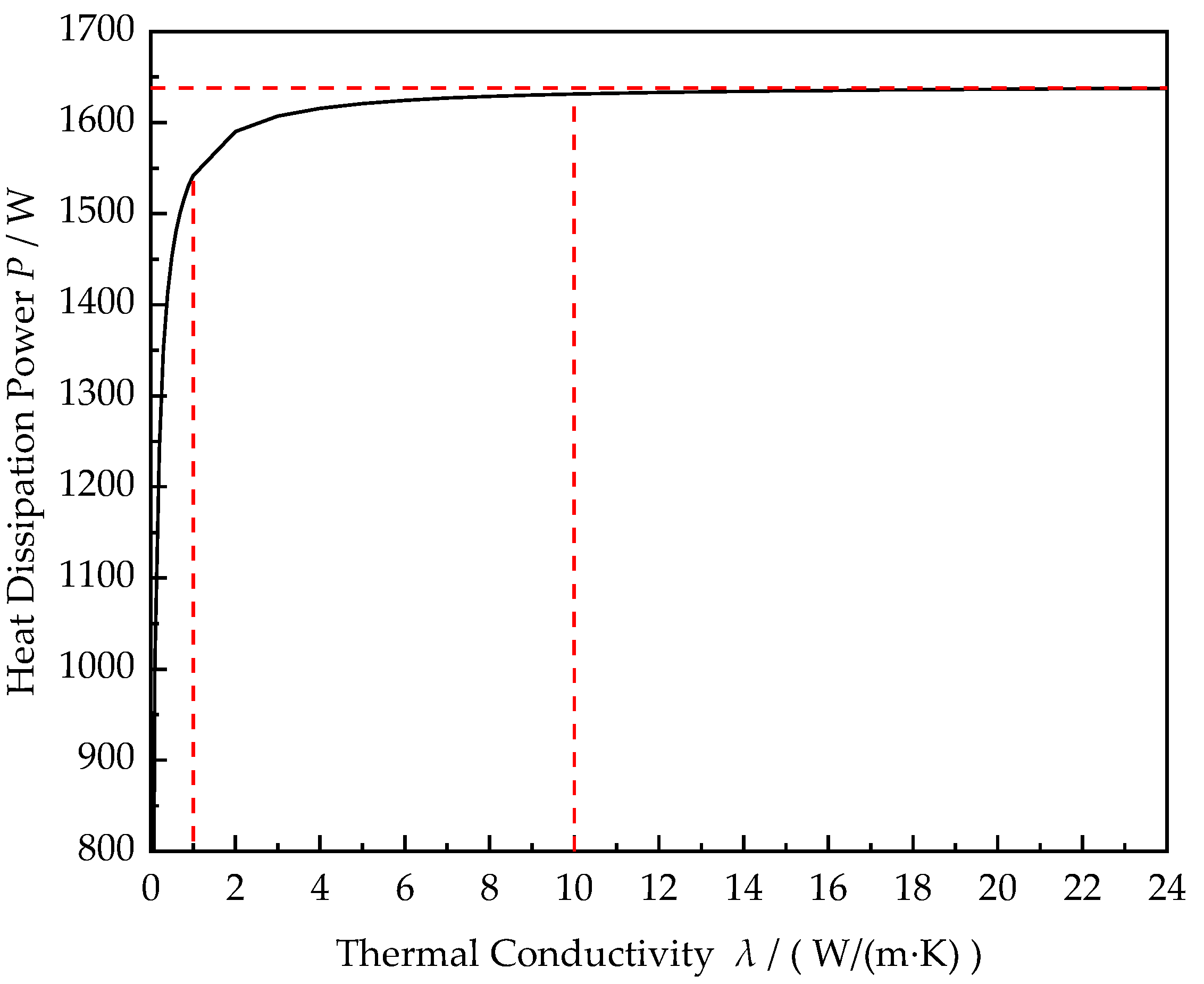
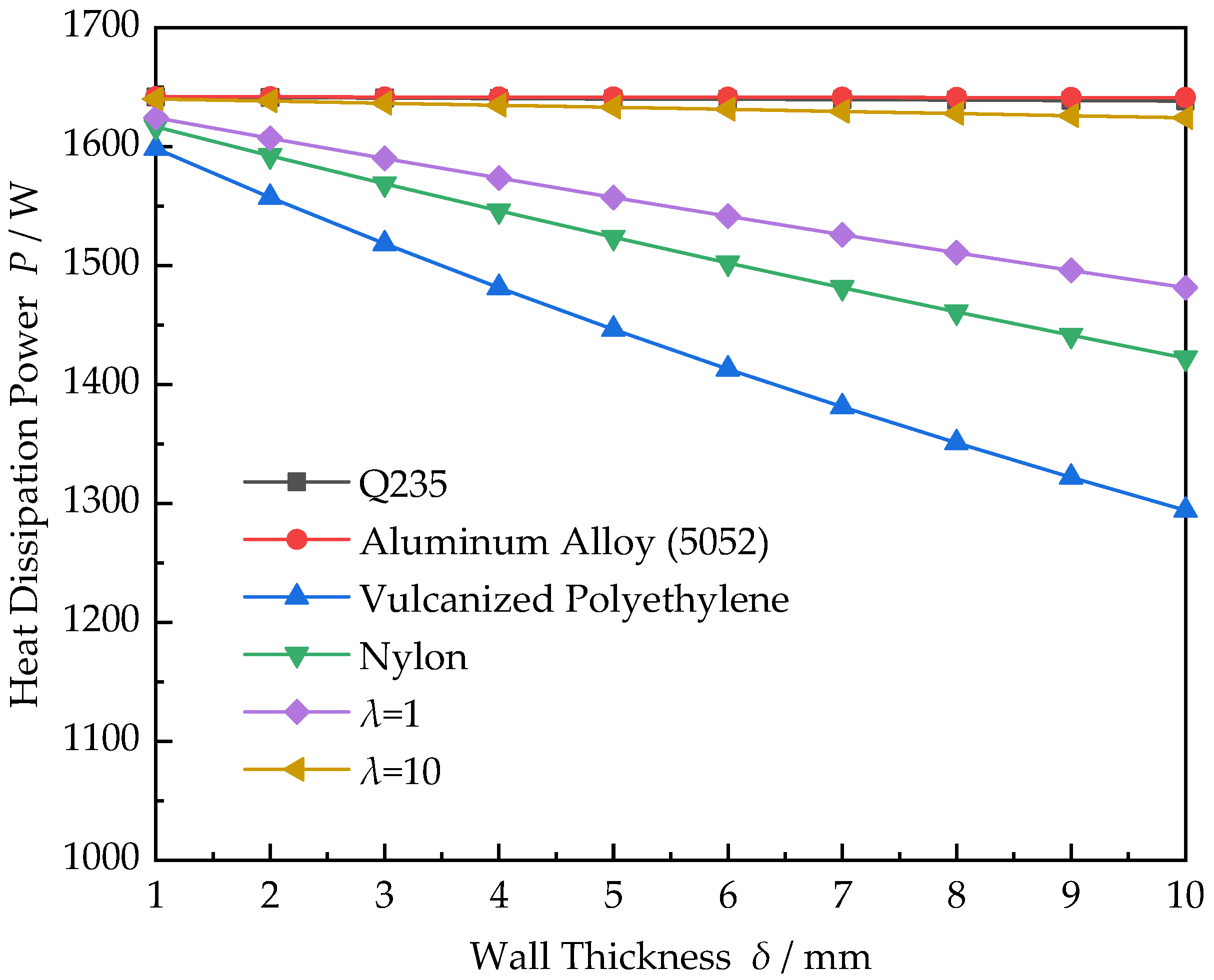
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Tl | 65 °C | K1 | 500 W/(m2·K) |
| Tair | 20 °C | K2 | 12 W/(m2·K) |
| V | 500 L | K3 | 7 W/(m2·K) |
| δ | 6 mm | K4 | 7 W/(m2·K) |
| Design Ratios | 3:1:1 | 3:2:1 | Change |
|---|---|---|---|
| P/W | 1639.9 | 1689.5 | +3.0% |
| a/mm | 1651 | 1310 | −20.7% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhai, F.; Wang, X.; He, Z.; Chen, Y.; Ye, Z.; Yao, J. Analysis of Natural Heat Dissipation Capacity of Hydraulic Tank and Relevant Influencing Factors. Machines 2022, 10, 991. https://doi.org/10.3390/machines10110991
Zhai F, Wang X, He Z, Chen Y, Ye Z, Yao J. Analysis of Natural Heat Dissipation Capacity of Hydraulic Tank and Relevant Influencing Factors. Machines. 2022; 10(11):991. https://doi.org/10.3390/machines10110991
Chicago/Turabian StyleZhai, Fugang, Xiaonan Wang, Zhiqiang He, Yu Chen, Zi Ye, and Jing Yao. 2022. "Analysis of Natural Heat Dissipation Capacity of Hydraulic Tank and Relevant Influencing Factors" Machines 10, no. 11: 991. https://doi.org/10.3390/machines10110991
APA StyleZhai, F., Wang, X., He, Z., Chen, Y., Ye, Z., & Yao, J. (2022). Analysis of Natural Heat Dissipation Capacity of Hydraulic Tank and Relevant Influencing Factors. Machines, 10(11), 991. https://doi.org/10.3390/machines10110991








