Investigating the Combined Effect of Multiple Dent and Bump Faults on the Vibrational Behavior of Ball Bearings
Abstract
1. Introduction
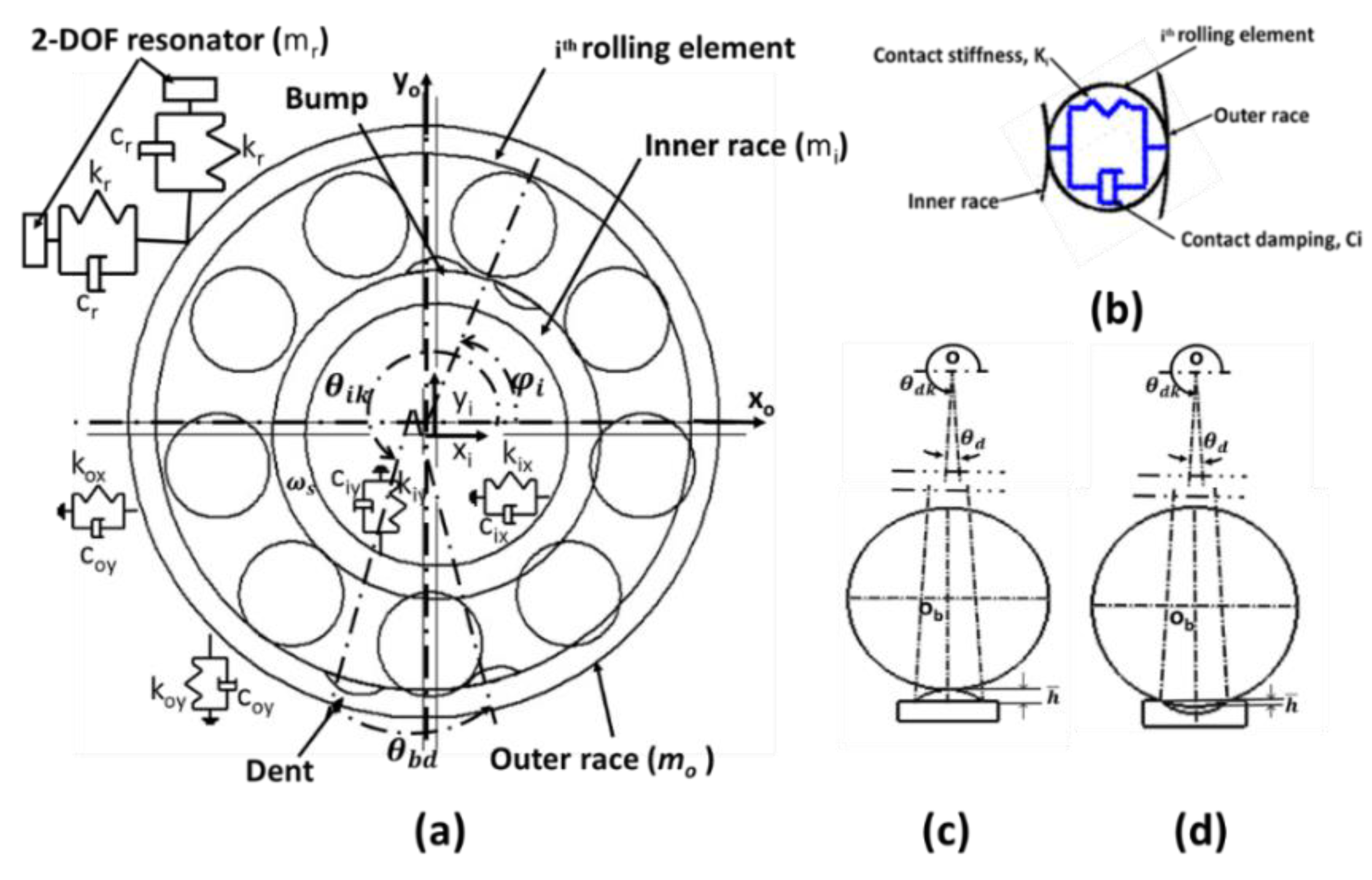
2. Dynamic Modeling of the Ball Bearing
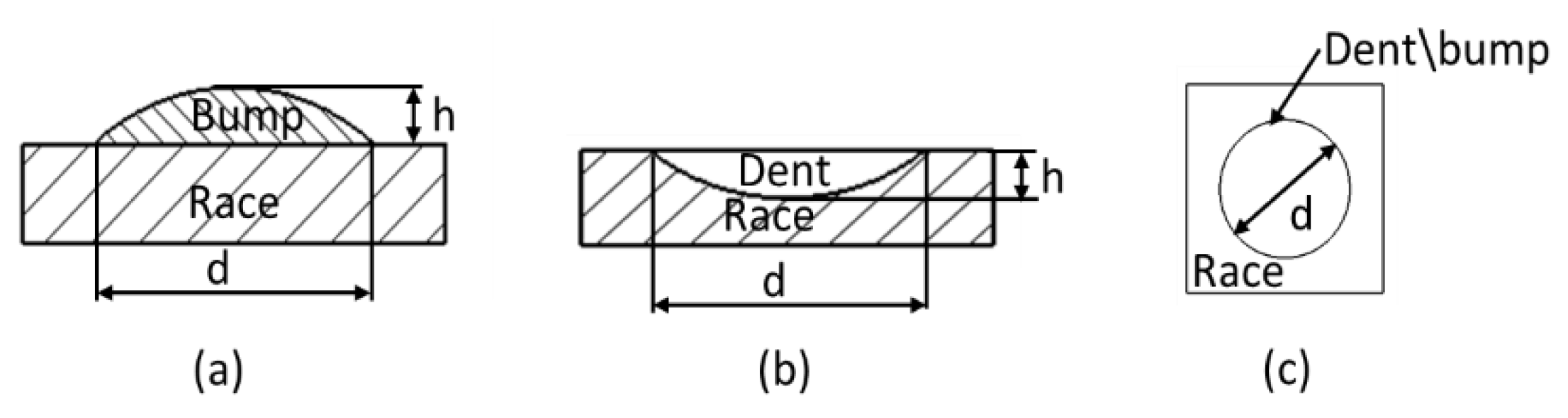
2.1. Defect Shape Modeling
2.2. Time-Varying Contact Force
2.3. Contact Damping force
2.4. Dynamic Equations of Ball Bearing
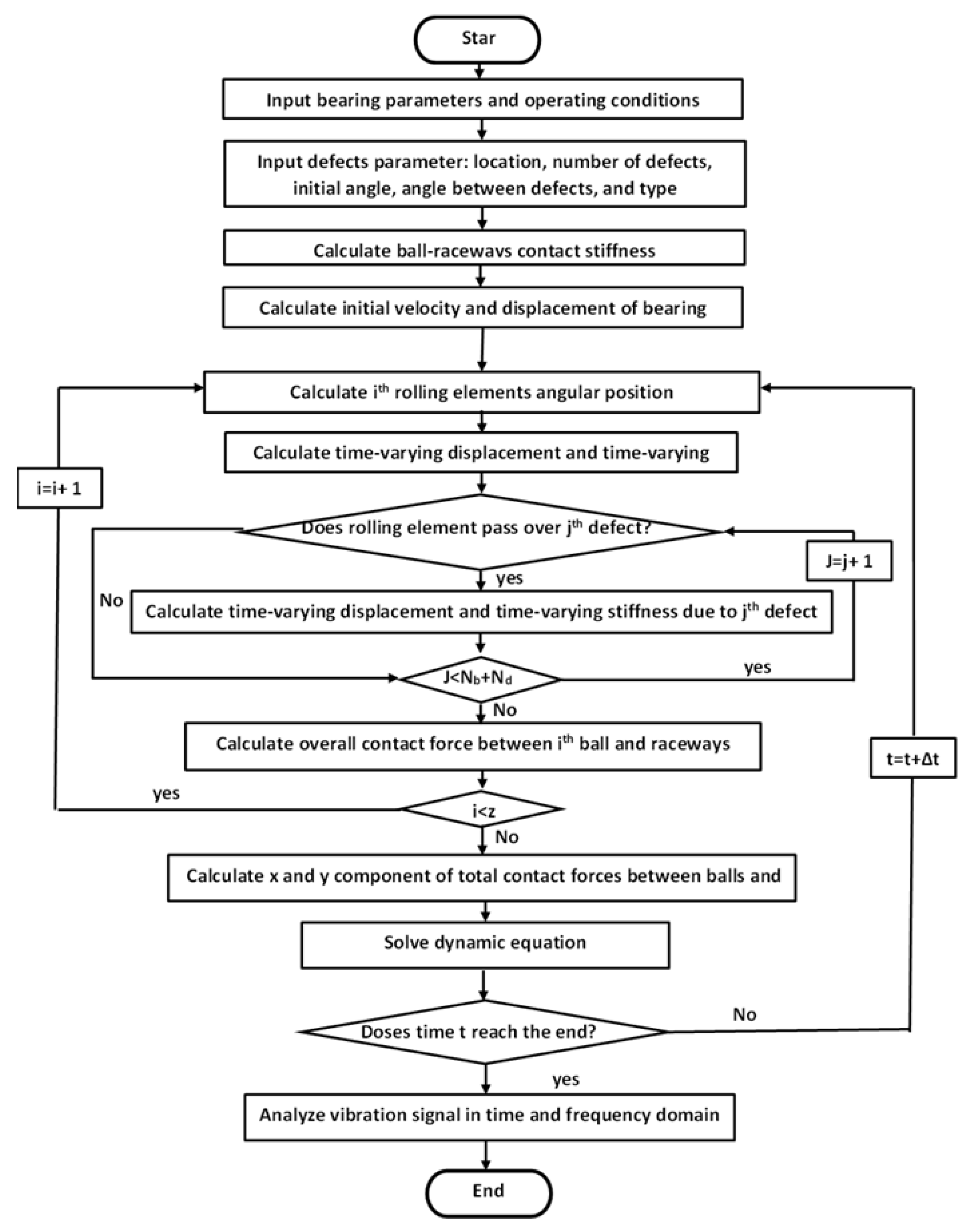
3. Numerical Results
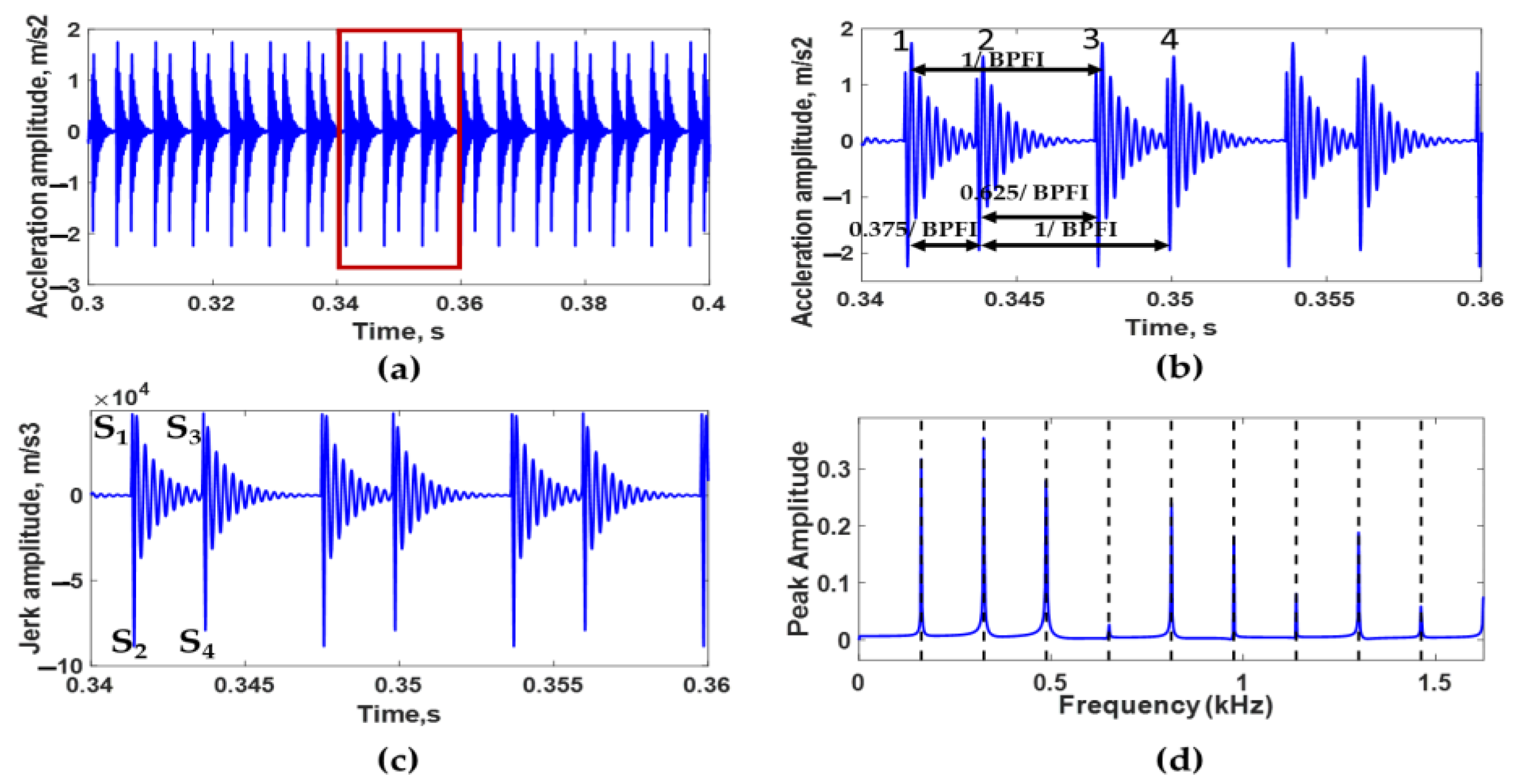
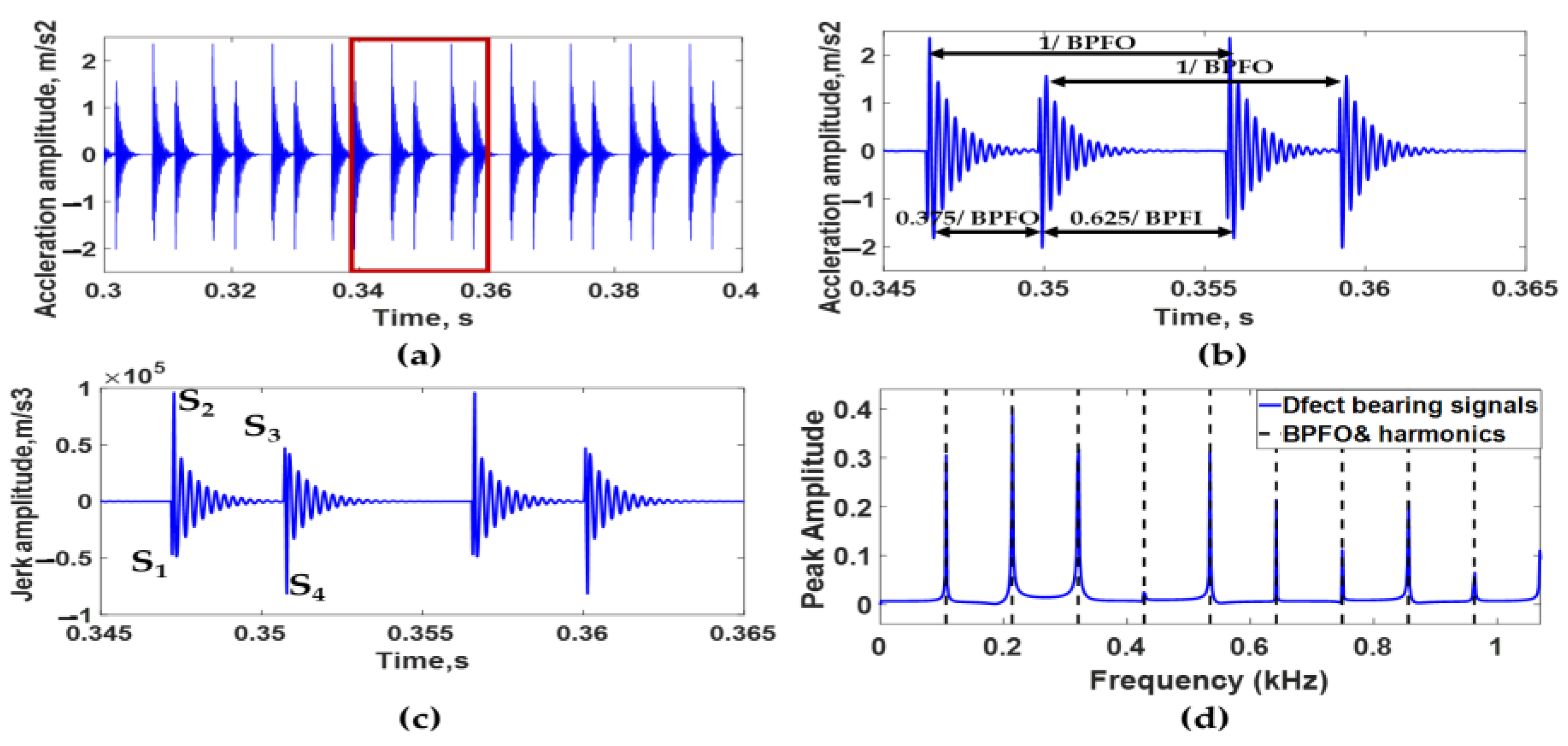
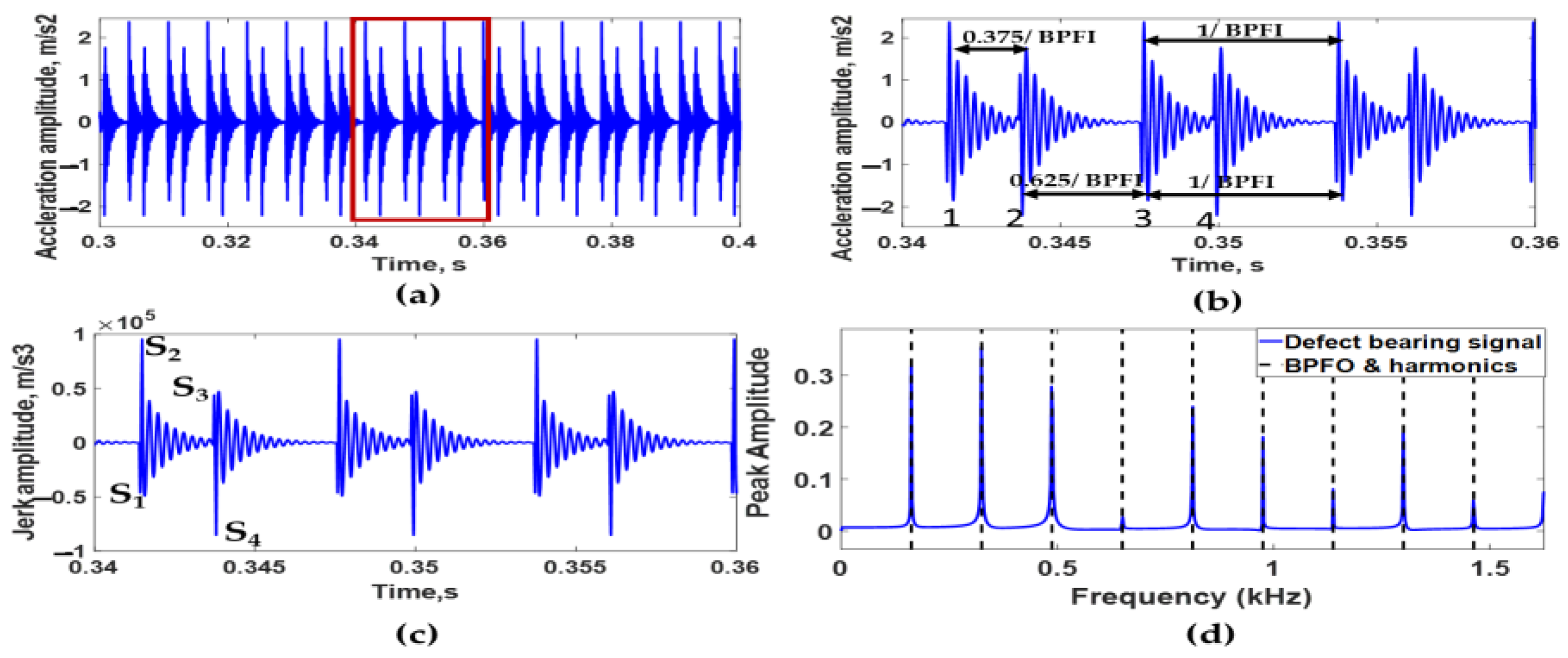
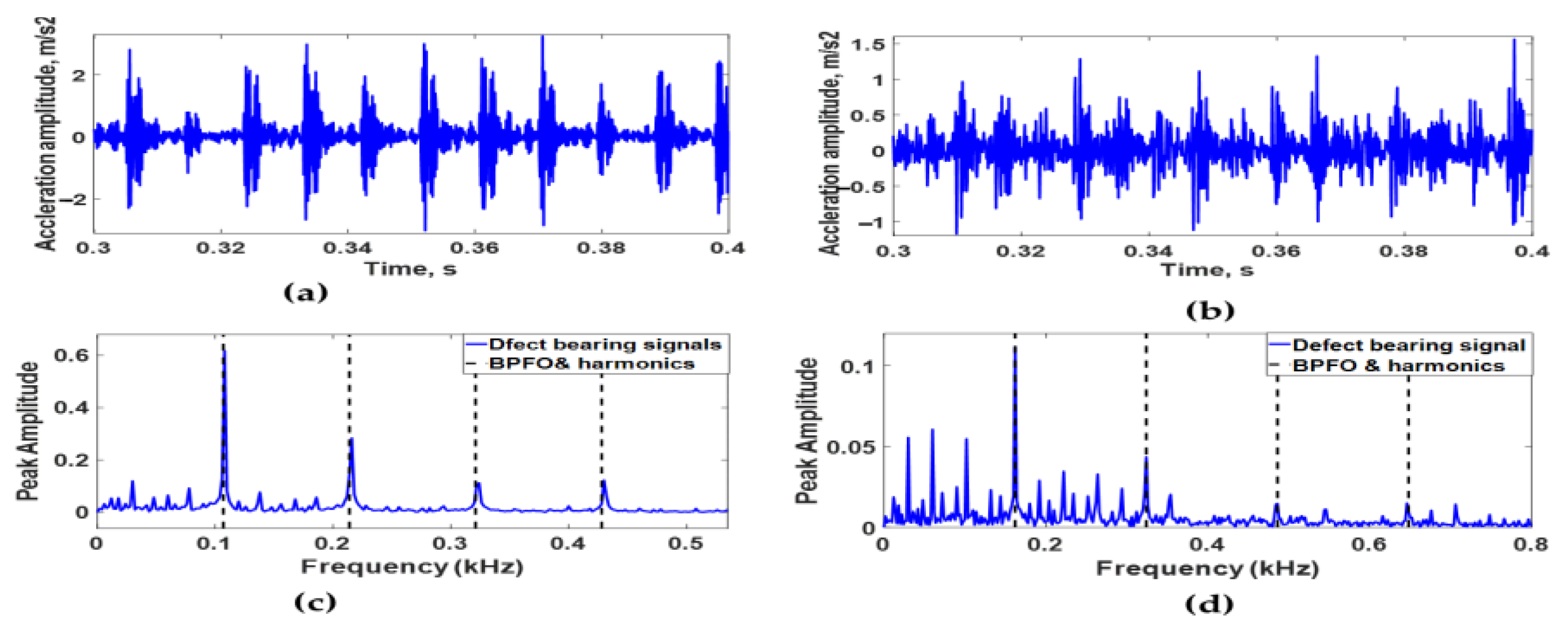
3.1. Simulation Results of Bearing with Double Dents
3.2. Simulation Results of Bearing with a Dent and Bump
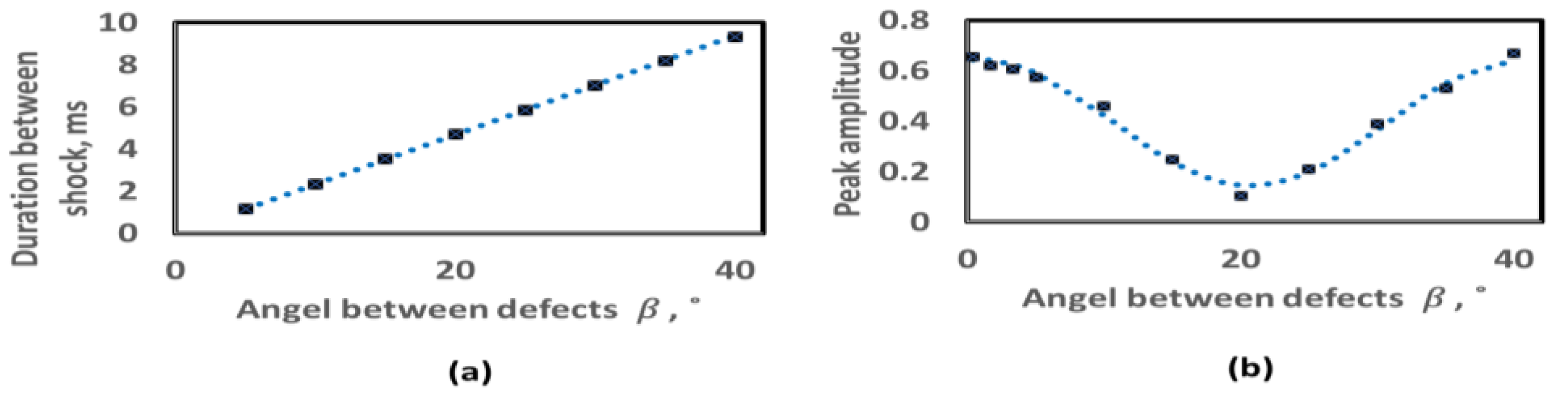
3.3. Effect of Phase Angle between Defects
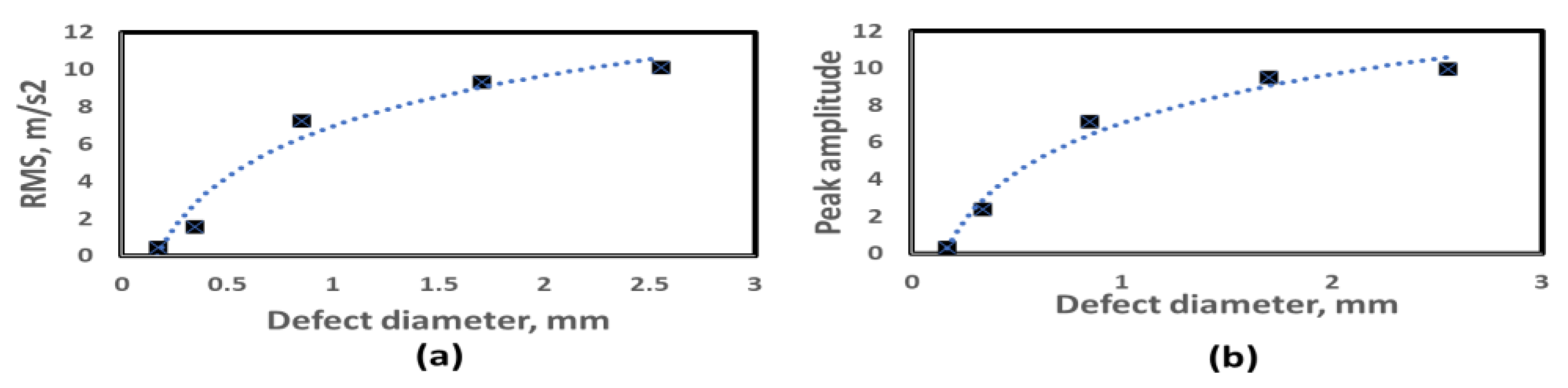
3.4. Effect of Defect Size
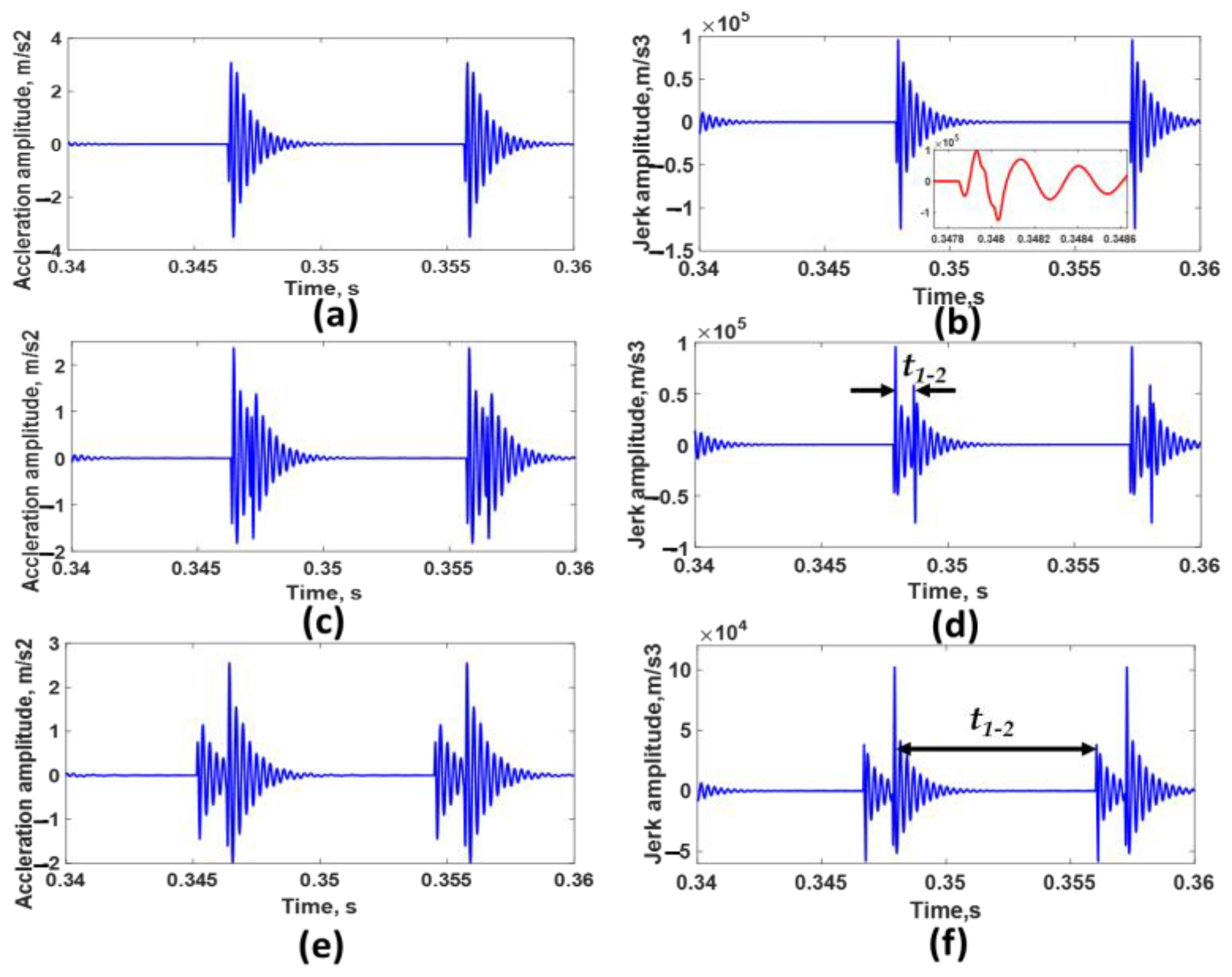
3.5. Effect of Number of Defects
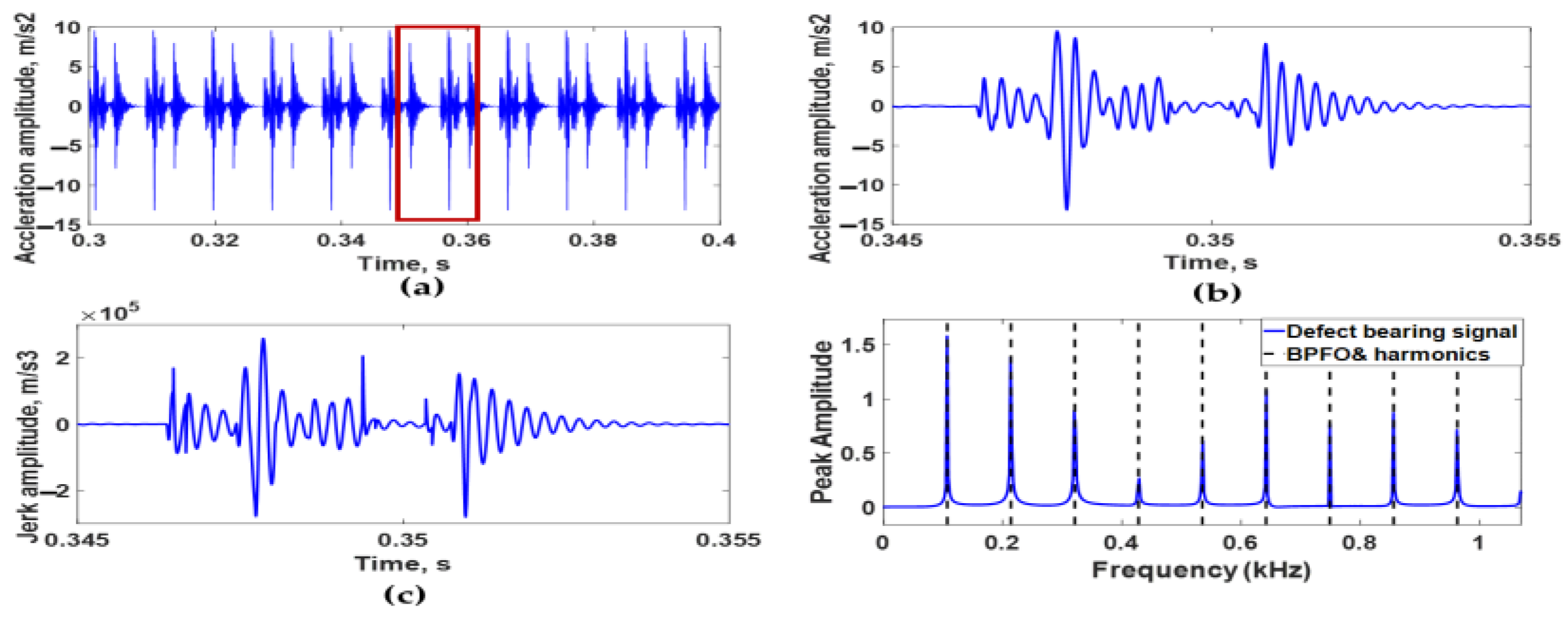
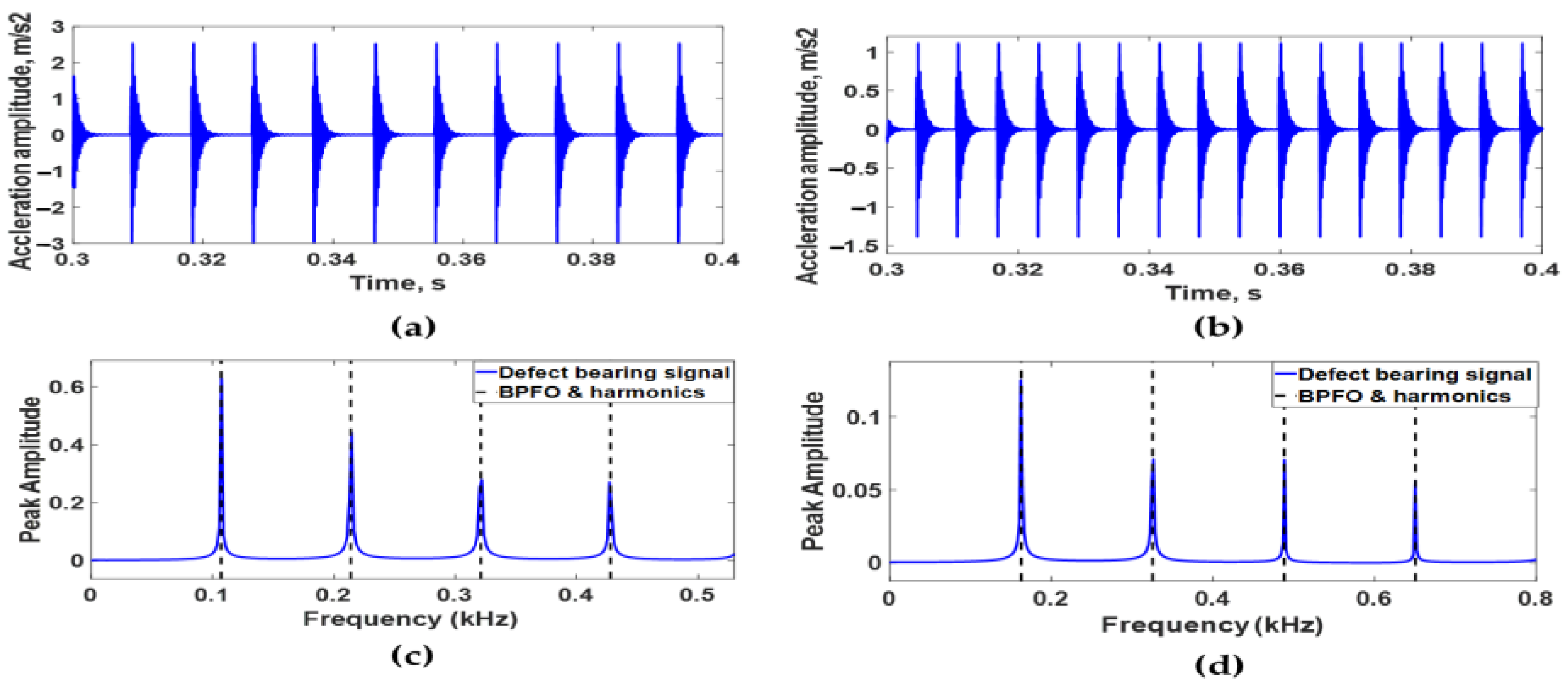
4. Experimental Validation
5. Conclusions
- The vibration pattern of faulty bearings is greatly influenced by the defect type, defect size, and angle between defects.
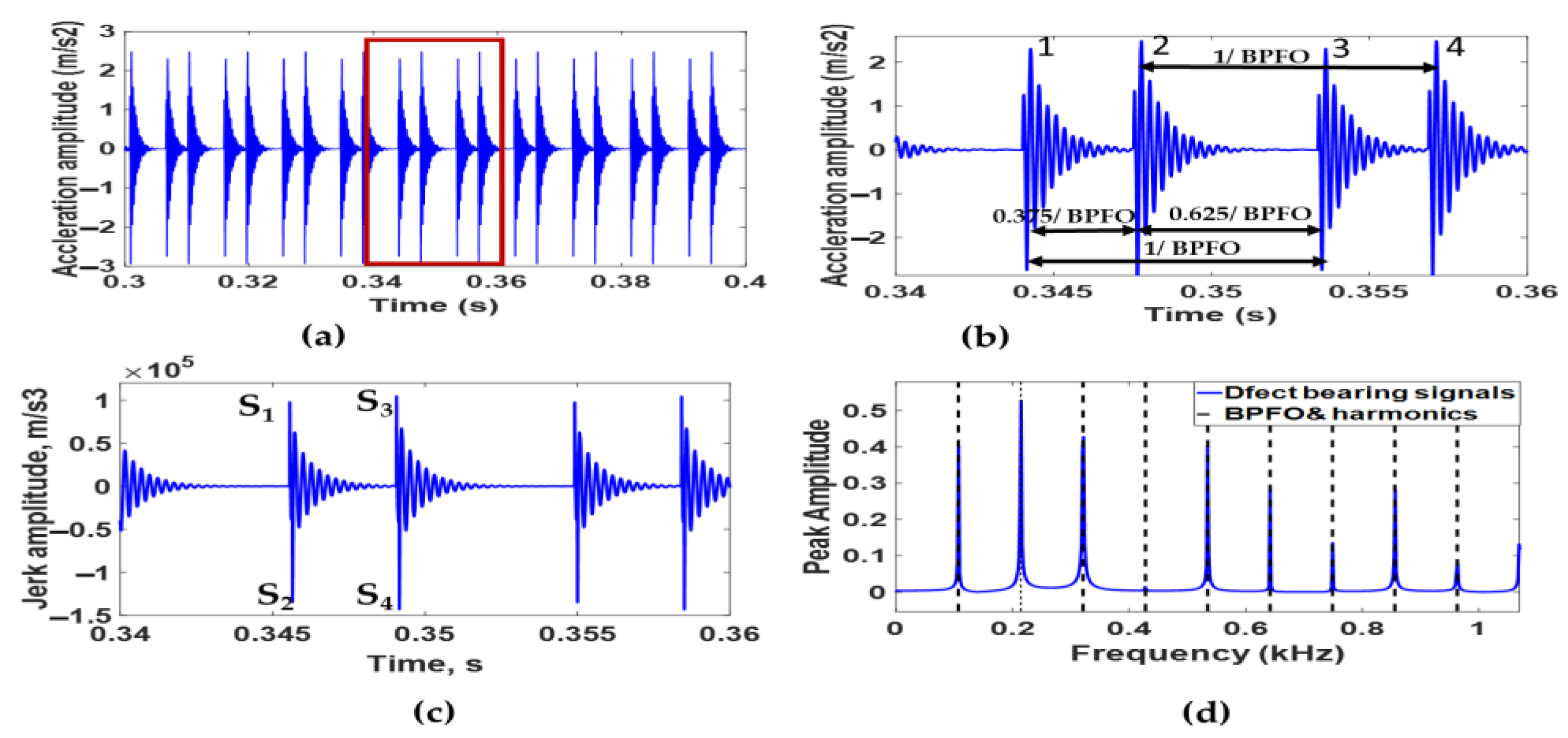
- The envelope spectrum analysis of the vibration acceleration signal showed that the amplitude of BPFO second harmonic peaks decreases as the phase angle between defects is increased until half interval angle between rolling elements, and then the amplitude increases with the increase in angle. Furthermore, the vibration amplitude of the BPFO second harmonics increases with the increase in defect size.
- It is challenging from the analysis of acceleration signals only to predict the number of defects, the angle between each adjacent defect, the size of each defect, and the type of each defect. This difficulty is due to interference of transient impulses produced from sequential defects. To solve this difficulty, it is recommended to use jerk signal analysis.
- The model results for a single defect were verified using bearing test data provided by CWRU in which the EDM process was used to induce localized faults on the raceway with similar spherical geometries and diameters to the modeled faults.
- The developed model did not consider the effect of lubricant film stiffness, internal clearance, slipping of rolling elements, or the combined effect of change of rotating speed and radial load, which has an effect on bearing vibration response.
- Future work will focus on simulation and experimental work on bearing with multiple defects, considering the combined influence of internal radial clearance and oil film lubrication characteristics on the vibration response.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Nassef, M.G.A.; Hussein, T.M.; Mokhiamar, O. An adaptive variational mode decomposition based on sailfish optimization algorithm and Gini index for fault identification in rolling bearings. Measurement 2021, 173, 108514. [Google Scholar] [CrossRef]
- Liu, J.; Xu, Y.; Pan, G. A combined acoustic and dynamic model of a defective ball bearing. J. Sound Vib. 2021, 501, 116029. [Google Scholar] [CrossRef]
- Georgoulas, G.; Loutas, T.; Stylios, C.D.; Kostopoulos, V. Bearing fault detection based on hybrid ensemble detector and empirical mode decomposition. Mech. Syst. Signal Process. 2013, 41, 510–525. [Google Scholar] [CrossRef]
- Moazen-Ahmadi, A.; Howard, C.Q. A defect size estimation method based on operational speed and path of rolling elements in defective bearings. J. Sound Vib. 2016, 385, 138–148. [Google Scholar] [CrossRef]
- Liu, J.; Shao, Y. Overview of dynamic modelling and analysis of rolling element bearings with localized and distributed faults. Nonlinear Dyn. 2018, 93, 1765–1798. [Google Scholar] [CrossRef]
- Ashtekar, A.; Sadeghi, F.; Stacke, L.-E. Surface defects effects on bearing dynamics. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2010, 224, 25–35. [Google Scholar] [CrossRef]
- Sawalhi, N.; Randall, R. Vibration response of spalled rolling element bearings: Observations, simulations and signal processing techniques to track the spall size. Mech. Syst. Signal Process. 2011, 25, 846–870. [Google Scholar] [CrossRef]
- Jiang, Y.; Huang, W.; Luo, J.; Wang, W. An improved dynamic model of defective bearings considering the three-dimensional geometric relationship between the rolling element and defect area. Mech. Syst. Signal Process. 2019, 129, 694–716. [Google Scholar] [CrossRef]
- Kumbhar, S.G.; Sudhagar, E.; Desavale, R. An overview of dynamic modeling of rolling-element bearings. Noise Vib. Worldw. 2021, 52, 3–18. [Google Scholar] [CrossRef]
- Boudiaf, A.; Djebala, A.; Bendjma, H.; Balaska, A.; Dahane, A. A summary of vibration analysis techniques for fault detection and diagnosis in bearing. In Proceedings of the 2016 8th International Conference on Modelling, Identification and Control, ICMIC 2016, Algiers, Algeria, 15–17 November 2016; pp. 37–42. [Google Scholar] [CrossRef]
- El-Thalji, I.; Jantunen, E. A summary of fault modelling and predictive health monitoring of rolling element bearings. Mech. Syst. Signal Process. 2015, 60, 252–272. [Google Scholar] [CrossRef]
- Li, W.; Qiu, M.; Zhu, Z.; Jiang, F.; Zhou, G. Fault diagnosis of rolling element bearings with a spectrum searching method. Meas. Sci. Technol. 2017, 28, 095008. [Google Scholar] [CrossRef]
- Al Bugharbee, H.; Trendafilova, I. A new methodology for fault detection in rolling element bearings using singular spectrum analysis. MATEC Web Conf. 2018, 148, 14002. [Google Scholar] [CrossRef][Green Version]
- Cheng, Y.; Zou, D.; Zhang, W.; Wang, Z. A Hybrid Time-Frequency Analysis Method for Railway Rolling-Element Bearing Fault Diagnosis. J. Sens. 2019, 2019, 8498496. [Google Scholar] [CrossRef]
- Cai, J.; Xiao, Y. Time-frequency analysis method of bearing fault diagnosis based on the generalized S transformation. J. Vibroeng. 2017, 19, 4221–4230. [Google Scholar] [CrossRef]
- Albezzawy, M.N.; Nassef, M.G.A.; Elsayed, E.S.; Elkhatib, A. Early Rolling Bearing Fault Detection Using a Gini Index Guided Adaptive Morlet Wavelet Filter. In Proceedings of the 2019 IEEE 10th International Conference on Mechanical and Aerospace Engineering (ICMAE), Brussels, Belgium, 22–25 July 2019; pp. 314–322. [Google Scholar] [CrossRef]
- Klepka, A. Wavelet based signal demodulation technique for bearing fault detection. Mech. Mech. Eng. 2011, 15, 63–71. [Google Scholar]
- Wang, D.; Sun, S.; Tse, P.W. A general sequential Monte Carlo method based optimal wavelet filter: A Bayesian approach for extracting bearing fault features. Mech. Syst. Signal Process. 2015, 52–53, 293–308. [Google Scholar] [CrossRef]
- Zhou, F.; Chen, J.; He, J.; Bi, G.; Zhang, G.; Li, F. Application of cyclostationary signal processing with wavelet filtering in rolling element bearing fault diagnosis. Zhendong Yu Chongji J. Vib. Shock 2006, 25, 91–93. [Google Scholar]
- Shi, H.; Shang, Y. Initial Fault Diagnosis of Rolling Bearing Based on Second-Order Cyclic Autocorrelation and DCAE Combined with Transfer Learning. IEEE Trans. Instrum. Meas. 2022, 71, 3503818. [Google Scholar] [CrossRef]
- Kumar, S.S.; Mohan, N.; Poornachandran, P.; Soman, K.P. Condition monitoring in roller bearings using cyclostationary features. In Proceedings of the Third International Symposium on Women in Computing and Informatics, Kochi, India, 10–13 August 2015; pp. 690–697. [Google Scholar] [CrossRef]
- Wang, S.; Niu, P.; Guo, Y.; Wang, F.; Li, W.; Shi, H.; Han, S. Early diagnosis of bearing faults using decomposition and reconstruction stochastic resonance system. Measurement 2020, 158, 107709. [Google Scholar] [CrossRef]
- Gong, T.; Yuan, X.; Wang, X.; Yuan, Y.; Zhang, B. Fault diagnosis for rolling element bearing using variational mode decomposition and l1 trend filtering. Proc. Inst. Mech. Eng. Part O J. Risk Reliab. 2020, 234, 116–128. [Google Scholar] [CrossRef]
- Liu, H.; Xiang, J. Kernel regression residual signal-based improved intrinsic time-scale decomposition for mechanical fault detection. Meas. Sci. Technol. 2019, 30, 015107. [Google Scholar] [CrossRef]
- Yakout, M.; Nassef, M.G.A.; Backar, S. Effect of clearances in rolling element bearings on their dynamic performance, quality and operating life. J. Mech. Sci. Technol. 2019, 33, 2037–2042. [Google Scholar] [CrossRef]
- Patil, A.P.; Mishra, B.K.; Harsha, S.P. Vibration based modelling of acoustic emission of rolling element bearings. J. Sound Vib. 2020, 468, 115117. [Google Scholar] [CrossRef]
- Gupta, P.K. Advanced Dynamics of Rolling Elements; Springer: New York, NY, USA, 1984. [Google Scholar] [CrossRef]
- Gupta, P.K. Dynamics of Rolling-Element Bearings Part IV: Ball Bearing Results. J. Tribol. 1979, 101, 319–326. [Google Scholar] [CrossRef]
- Ghaisas, N.; Wassgren, C.R.; Sadeghi, F. Cage Instabilities in Cylindrical Roller Bearings. J. Tribol. 2004, 126, 681–689. [Google Scholar] [CrossRef]
- Jang, G.H.; Jeong, S.W. Analysis of a Ball Bearing with Waviness Considering the Centrifugal Force and Gyroscopic Moment of the Ball. J. Tribol. 2003, 125, 487–498. [Google Scholar] [CrossRef]
- Sopanen, J.; Mikkola, A. Dynamic model of a deep-groove ball bearing including localized and distributed defects. Part 1: Theory. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2003, 217, 201–211. [Google Scholar] [CrossRef]
- Ji, P.; Gao, Y.; Ma, F.; An, Q. Influences of roller diameter error on contact stress for cylindrical roller bearing. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2015, 229, 689–697. [Google Scholar] [CrossRef]
- Liu, J.; Yan, Z.; Shao, Y. An investigation for the friction torque of a needle roller bearing with the roundness error. Mech. Mach. Theory 2018, 121, 259–272. [Google Scholar] [CrossRef]
- Zhenhuan, Y.; Liqin, W. Effects of axial misalignment of rings on the dynamic characteristics of cylindrical roller bearings. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2016, 230, 525–540. [Google Scholar] [CrossRef]
- Xing, Y.; Xu, H.; Pei, S.; Zhang, X.; Chang, W. Mechanical analysis of spherical roller bearings due to misalignments between inner and outer rings. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2017, 231, 3250–3262. [Google Scholar] [CrossRef]
- Patel, V.N.; Tandon, N.; Pandey, R.K. Vibration studies of dynamically loaded deep groove ball bearings in presence of local defects on races. Procedia Eng. 2013, 64, 1582–1591. [Google Scholar] [CrossRef]
- Ghafari, S.H.; Golnaraghi, F.; Ismail, F. Effect of localized faults on chaotic vibration of rolling element bearings. Nonlinear Dyn. 2008, 53, 287–301. [Google Scholar] [CrossRef]
- Mattar, A.H.A.; Sayed, H.; Younes, Y.K.; El-Mongy, H.H. Experimental Verification and Nonlinear Dynamic Response Analysis of a Rolling Element Bearing with Localized Defects. J. Fail. Anal. and Preven. 2022, 22, 1753–1770. [Google Scholar] [CrossRef]
- Nakhaeinejad, M.; Bryant, M.D. Dynamic Modeling of Rolling Element Bearings with Surface Contact Defects Using Bond Graphs. J. Tribol. 2011, 133, 011102. [Google Scholar] [CrossRef]
- Patil, M.S.; Mathew, J.; Rajendrakumar, P.K.; Desai, S. A theoretical model to predict the effect of localized defect on vibrations associated with ball bearing. Int. J. Mech. Sci. 2010, 52, 1193–1201. [Google Scholar] [CrossRef]
- Liu, J.; Shao, Y.; Zhu, W.D. A New Model for the Relationship Between Vibration Characteristics Caused by the Time-Varying Contact Stiffness of a Deep Groove Ball Bearing and Defect Sizes. J. Tribol. 2015, 137, 031101. [Google Scholar] [CrossRef]
- Singh, S.; Köpke, U.G.; Howard, C.Q.; Petersen, D. Analyses of contact forces and vibration response for a defective rolling element bearing using an explicit dynamics finite element model. J. Sound Vib. 2014, 333, 5356–5377. [Google Scholar] [CrossRef]
- Li, D.; Kang, Y.S. Simulation and Experimental Validation of Tapered Roller Bearing Vibration Induced by Geometrical Imperfection on Cup Raceway. In Proceedings of the ASME 2014 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. Volume 8: 26th Conference on Mechanical Vibration and Noise, Buffalo, NY, USA, 17–20 August 2014. [Google Scholar] [CrossRef]
- Liu, J.; Wu, H.; Shao, Y. A theoretical study on vibrations of a ball bearing caused by a dent on the races. Eng. Fail. Anal. 2018, 83, 220–229. [Google Scholar] [CrossRef]
- Shi, Z.; Liu, J.; Chen, Z.; Shao, Y. Vibration Analysis of a Roller Bearing with a Bump Defect. In Proceedings of the ASME 2018 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. Volume 8: 30th Conference on Mechanical Vibration and Noise, Quebec City, QC, Canada, 26–29 August 2018. [Google Scholar] [CrossRef]
- Cerrada, M.; Sánchez, R.-V.; Li, C.; Pacheco, F.; Cabrera, D.; de Oliveira, J.V.; Vásquez, R.E. A review on data-driven fault severity assessment in rolling bearings. Mech. Syst. Signal Process. 2018, 99, 169–196. [Google Scholar] [CrossRef]
- McFadden, P.D.; Smith, J.D. The vibration produced by multiple point defects in a rolling element bearing. J. Sound Vib. 1985, 98, 263–273. [Google Scholar] [CrossRef]
- Zhang, X.; Yan, C.; Liu, Y.; Yan, P.; Wang, Y.; Wu, L. Dynamic Modeling and Analysis of Rolling Bearing with Compound Fault on Raceway and Rolling Element. Shock Vib. 2020, 2020, 8861899. [Google Scholar] [CrossRef]
- Gao, X.; Yan, C.; Liu, Y.; Yan, P.; Yang, J.; Wu, L. A 4-DOF dynamic model for ball bearing with multiple defects on raceways. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2021, 235, 3–18. [Google Scholar] [CrossRef]
- Sawalhi, N.; Randall, R. Simulating gear and bearing interactions in the presence of faults: Part I. The combined gear bearing dynamic model and the simulation of localised bearing faults. Mech. Syst. Signal Process. 2008, 22, 1924–1951. [Google Scholar] [CrossRef]
- Cui, L.; Zhang, Y.; Zhang, F.; Zhang, J.; Lee, S. Vibration response mechanism of faulty outer race rolling element bearings for quantitative analysis. J. Sound Vib. 2016, 364, 67–76. [Google Scholar] [CrossRef]
- Ashtekar, A.; Sadeghi, F.; Stacke, L.-E. A New Approach to Modeling Surface Defects in Bearing Dynamics Simulations. J. Tribol. 2008, 130, 041103. [Google Scholar] [CrossRef]
- Morales-Espejel, G.E.; Gabelli, A. Damage Mechanisms of Indentations in Raceways of Rolling Bearings. 2012. Available online: http://evolution.skf.com/damage-mechanisms-of-indentations-in-raceways-of-rolling-bearings/ (accessed on 26 September 2022).
- Harris, T.A.; Kotzalas, M.N. Rolling Bearing Analysis Essential Concepts of Bearing Technology; Wiley: New York, NY, USA, 2007. [Google Scholar]
- Tadina, M.; Boltežar, M. Improved model of a ball bearing for the simulation of vibration signals due to faults during run-up. J. Sound Vib. 2011, 330, 4287–4301. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, Z.; Li, Y.; Zhai, W. Dynamic investigation and alleviative measures for the skidding phenomenon of lubricated rolling bearing under light load. Mech. Syst. Signal Process. 2022, 184, 109685. [Google Scholar] [CrossRef]
- Antaluca, E.; Nélias, D. Contact Fatigue Analysis of a Dented Surface in a Dry Elastic–Plastic Circular Point Contact. Tribol. Lett. 2008, 29, 139–153. [Google Scholar] [CrossRef]
- Johnson, K.L. Contact Mechanics, 1st ed.; Cambridge University Press: London, UK, 1985. [Google Scholar]
- Vakharia, V.; Gupta, V.K.; Kankar, P.K. Nonlinear dynamic analysis of ball bearings due to varying number of balls and centrifugal force. Mech. Mach. Sci. 2015, 21, 1831–1840. [Google Scholar] [CrossRef]
- Cheng, H.; Zhang, Y.; Lu, W.; Yang, Z. Research on ball bearing model based on local defects. SN Appl. Sci. 2019, 1, 1219. [Google Scholar] [CrossRef]
- Yan, P.; Yan, C.; Wang, K.; Wang, F.; Wu, L. 5-DOF Dynamic Modeling of Rolling Bearing with Local Defect considering Comprehensive Stiffness under Isothermal Elastohydrodynamic Lubrication. Shock Vib. 2020, 2020, 9310278. [Google Scholar] [CrossRef]
- Xu, M.; Feng, G.; He, Q.; Gu, F.; Ball, A. Vibration Characteristics of Rolling Element Bearings with Different Radial Clearances for Condition Monitoring of Wind Turbine. Appl. Sci. 2020, 10, 4731. [Google Scholar] [CrossRef]
- Igarashi, T.; Kato, J. Studies on the vibration and sound of defective rolling bearings. Bull. JSME 1985, 28, 492–499. [Google Scholar] [CrossRef]
- Ismail, M.A.A.; Klausen, A. Multiple Defect Size Estimation of Rolling Bearings using Autonomous Diagnosis and Vibrational Jerk. In Proceedings of the 7th World Conference on Structural Control and Monitoring, Qingdao, China, 22–25 July 2018. [Google Scholar]
- Bearing Data Center. Available online: https://engineering.case.edu/bearingdatacenter (accessed on 26 July 2022).




| Parameter | Value |
|---|---|
| Inner race diameter, Do | 25 mm |
| Outer race diameter, Di | 52 mm |
| Pitch diameter, Dp | 39.0398 |
| Ball diameter, db | 7.94004 |
| Number of balls, z | 9 |
| Contact angle, α | 0° |
| Radial clearance, γ | 5.5 µm |
| Load–deflection factor, K | 1.5779 × 1010.5 N/m1.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Atef, M.M.; Khair-Eldeen, W.; Yan, J.; Nassef, M.G.A. Investigating the Combined Effect of Multiple Dent and Bump Faults on the Vibrational Behavior of Ball Bearings. Machines 2022, 10, 1062. https://doi.org/10.3390/machines10111062
Atef MM, Khair-Eldeen W, Yan J, Nassef MGA. Investigating the Combined Effect of Multiple Dent and Bump Faults on the Vibrational Behavior of Ball Bearings. Machines. 2022; 10(11):1062. https://doi.org/10.3390/machines10111062
Chicago/Turabian StyleAtef, Mahmoud M., Wael Khair-Eldeen, Jiwang Yan, and Mohamed G. A. Nassef. 2022. "Investigating the Combined Effect of Multiple Dent and Bump Faults on the Vibrational Behavior of Ball Bearings" Machines 10, no. 11: 1062. https://doi.org/10.3390/machines10111062
APA StyleAtef, M. M., Khair-Eldeen, W., Yan, J., & Nassef, M. G. A. (2022). Investigating the Combined Effect of Multiple Dent and Bump Faults on the Vibrational Behavior of Ball Bearings. Machines, 10(11), 1062. https://doi.org/10.3390/machines10111062







