A Self-Adaptive Multiple Exposure Image Fusion Method for Highly Reflective Surface Measurements

Abstract

Fringe projection profilometry (FPP) has been extensively applied in various fields for its superior fast speed, high accuracy and high data density. However, measuring objects with highly reflective surfaces or high dynamic range surfaces remains challenging when using FPP. A number of multiple exposure image fusion methods have been proposed and successfully improved measurement performance for these kinds of objects. Normally, these methods have a relatively fixed sequence of exposure settings determined by practical experiences or trial and error experiments, which may decrease the efficiency of the entire measurement process and may have less robustness with regard to various environmental lighting conditions and object reflective properties. In this paper, a novel self-adaptive multiple exposure image fusion method is proposed with two areas of improvement relating to adaptively optimizing the initial exposure and the exposure sequence. First, by introducing the theory of information entropy, combined with an analysis of the characterization of fringe image entropy, an adaptive initial exposure searching method is proposed. Then, an exposure sequence generation method based on dichotomy is further described. On the basis of these two improvements, a novel self-adaptive multiple exposure image fusion method for FPP as well as its detailed procedures are provided. Experimental results validate the performance of the proposed self-adaptivity multiple exposure image fusion method via the measurement of objects with differences in surface reflectivity under different ambient lighting conditions.

1. Introduction

Fringe projection profilometry (FPP) has been widely applied in three-dimensional shape measurement in many fields such as manufacturing [1,2], medicine [3], law enforcement [4] and entertainment [5], due to advantages such as its noncontact operation, full-field measurement, high accuracy and high efficiency. However, the measurement of highly reflective surfaces or high dynamic range surfaces using FPP has always been a problem. Capturing surface details in dark areas requires higher camera exposure values, whereas recovering ground truth in bright regions needs lower exposure values. For conventional cameras, this may lead to low contrast fringe regions or saturated regions existing in the captured images. These regions have a low signal–noise ratio, which may further result in missing measurement data or decreasing accuracy. Therefore, finding effective measurement methods for highly reflective or high dynamic surfaces has always been an important research focus in the context of FPP.

Various methods have been proposed to solve this problem. One category of the method, multiple exposure fusion methods, improves measurement performance by capturing fringe images with different camera exposures. Zhang and Yau put forward a high dynamic range scanning method which takes advantage of the merits of pixel-by-pixel phase retrieval for the phase-shifting algorithm [6]. This technique captures a sequence of fringe images with different exposure times. The brightest but not saturated pixels are selected to construct the fused fringe images, which are used to compute the final phase map. Ekstrand and Zhang proposed a method that could evaluate the effect of exposure according to feedback from the reflectivity of the measured object [7]. Defocusing binary projection is introduced to enlarge the camera exposure time selection range. Long et al. presented a method that uses the magnitude of a non-principal frequency component to identify saturated pixels [8]. The magnitude function of the frequency component is presented by Fourier analysis. The magnitude of the non-principal frequency component is deduced and utilized as the saturation criteria.

Another category of the method involves measuring the shiny surfaces by adjusting the projected fringes accordingly. Waddington and Kofman presented a camera-independent method of avoiding image saturation according to modifying projected fringes after complex calibration procedures [9]. Babaie et al. captured fringe images by recursively controlling the intensity of the projection pattern pixel-wisely [10]. The reflected images captured by the camera are used as references. Lin et al. proposed an adaptive method by adjusting the pixel-wise intensity of the projected fringe patterns based on the saturated pixels in the captured images [11].

The third category of method is to extend the dynamic range by using hardware and can be categorized into two types: chip level extension and affiliated hardware extension. In terms of chip level extension, Orly [12], Cheng [13] and Bub [14] proposed different methods to extend the dynamic response range of the pixels. When it comes to the affiliated hardware method, digital micromirror device (DMD) chips [15,16,17,18] and spatial light modulators [19,20] are usually implemented to modulate the intensity and direction of spatial light.

Among all these categories, the multiple exposure fusion methods have become one of the most important research directions thanks to their superior flexibility, high accuracy and hardware-independent characteristics. There are two key factors in the sequence of exposure settings for multiple exposure fusion methods: the initial exposure and the exposure sequence. The initial exposure is considered as the highest value in the exposure sequence, and it is critical for the quality of the fusion images and the overall processing efficiency. A higher initial exposure means more unnecessary series of fringe images have to be captured, which contributes nothing to the quality of the fusion images but makes the overall process longer. A lower initial exposure may lead to poor quality regarding the obtained fusion images. For the exposure sequence, a large sequence with small exposure steps improves the quality of the fusion images, but it requires a longer operating time. A short sequence with large exposure steps may result in lower quality fusion images. There are no such criteria to balance the fusion image quality and the processing efficiency. Thus, the initial exposure and the exposure sequence are very important with regard to the performance of the multiple exposure fusion method.

Current multiple exposure fusion methods always have a relatively fixed sequence of exposure settings which are normally determined by practical experience or multiple trial and error experiments. However, when measuring new objects with differences in surface reflectivity or under different ambient lighting conditions, the initial exposure and the exposure sequence must be adjusted accordingly to ensure multiple exposure fusion performance. In such cases, using trial and error experiments to adjust the initial exposure and the exposure sequence is time-consuming, and the initial exposure and the exposure sequence cannot be precisely optimized based on manual adjustments based on practical experiences. This means that there is a critical demand for self-adaptive, fast and automatic methods to optimize the sequence of exposure settings according to the measured object’s surfaces adaptively, thereby improving the overall processing efficiency as well as the measurement quality.

In order to solve this problem, a novel self-adaptive multiple exposure image fusion method is proposed in this paper. By introducing the information entropy theory into the analysis of the fringe images, which builds a theoretical foundation for the selection of the initial exposure, a self-adaptive initial exposure searching method is first presented. Additionally, an exposure sequence generation method based on dichotomy is proposed. On the basis of the aforementioned two methods, a self-adaptive multiple exposure image fusion method for FPP as well as its detailed procedures are presented. The remainder of this paper is organized as follows. Section 2 presents the principle of the proposed method. Specifically, Section 2.1 presents the initial exposure searching method based on information entropy, Section 2.2 describes the exposure sequence generation method based on dichotomy and Section 2.3 proposes the self-adaptive multiple exposure image fusion method for highly reflective surface measurements. Section 3 presents the experiments and an analysis of the results. Section 4 concludes this paper.

2. The Proposed Method

2.1. Initial Exposure Searching Based on Information Entropy

In the case of multiple exposure image fusion methods, the selection of the initial exposure value is one of the key aspects that determine the measurement performance. A high initial exposure may increase pixel grayscale values in low-reflectivity areas, but it will also increase the number of overexposed pixels. Furthermore, multiple exposure fusion methods generally adopt a high to low approach to vary the exposure values and analyze the fringe images. With a too high initial exposure, more exposure changes are required to obtain a fused image, reducing the overall measurement efficiency. And if the initial exposure is set too low, the quality of the final fused image will be affected, leading to missing data and decreasing accuracy.

The present methods usually select an appropriate initial exposure through multiple experiments or practical experience. However, this kind of method is not very flexible if the illumination environment changes or objects with differences in surface reflectivity are measured because the initial exposure has to be reset correspondingly. This reduces the adaptability of the current multiple exposure methods. Therefore, there is an urgent need to develop a self-adaptive initial exposure searching method to enhance the adaptive capability of current multiple exposure image fusion methods.

2.1.1. Selecting Criteria for Initial Exposure

An appropriate initial exposure value should not cause too many saturated or low gray value pixels in the captured images. As shown in Figure 1, in order to observe the fringe image intensity distribution in different exposure conditions, three simulated images are obtained by adjusting the modulated gray value in low, normal and high exposure conditions. The upper row shows the simulated images, and the down row shows the intensity variation scatter diagram in one pixel row of the images. The scatters diagram in Figure 1a shows that most of the pixels in the image are concentrated in a narrow gray value interval in the case of low exposure. There is little difference in intensity between pixels, which makes the simulated fringe image blurred. Figure 1b shows that the gray value of the fringe image pixels for normal exposure conditions are distributed in the entire interval between 0 and 255, and the stripes can be seen very clearly in the corresponding image. In Figure 1c, it is illustrated that the intensity of most pixels is near 255 since the exposure value is too high. Therefore, the fringe is no longer sinusoidal. An appropriate initial exposure value should maximize the variability between pixels in the acquired images and make the range of the pixels’ gray value as wide as possible. The opposite means that there are too many overflow pixels or too many pixels with low gray values in the obtained initial exposure image. Whereas the former will lead to more adjustment times in terms of the exposure value and a longer measurement time, the latter will easily lead to a reduction in quality in the fusion images, both of which should be avoided.

Based on the above analysis, the selection criterion for the initial exposure value for the multiple exposure image fusion method can be determined. That is, the selected initial exposure value should ensure maximum variability in terms of the pixel grayscale values in the acquired sequence of images. The larger the variability in terms of the pixel gray values in the image, the more obvious the sinusoidal fringe feature is. In FPP, fringe stripes are the carrier for encoding and decoding phase information, which itself is the information required for 3D reconstruction. In other words, maximizing the variance in pixel gray values in an image means maximizing the amount of information in the image. Thus, the criterion for selecting the initial exposure value in the multiple exposure image fusion method can be further clarified, as the initial exposure should be chosen in such a way as to maximize the amount of information in the acquired set of initial exposure value images.

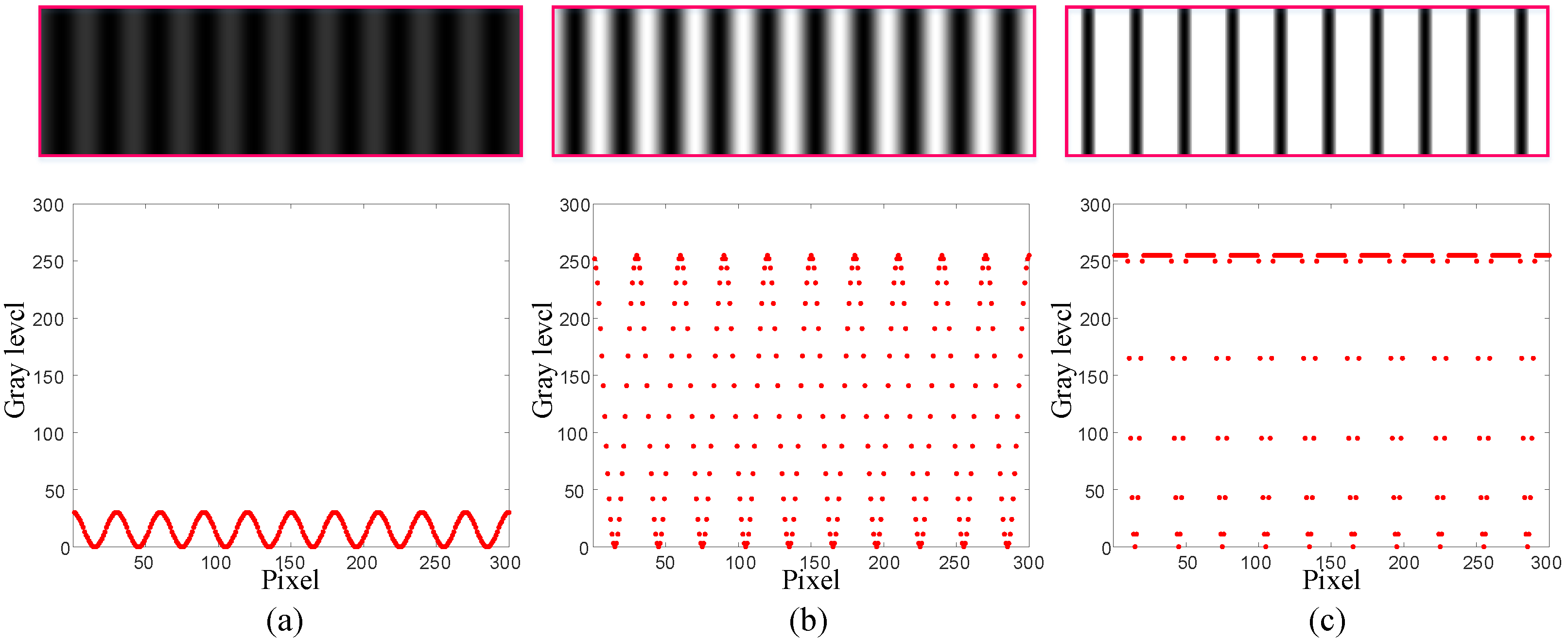
2.1.2. Information Entropy Metric for Initial Exposure Selecting Criteria

As aforementioned, the criterion for selecting the initial exposure value in the multiple exposure image fusion method should be such that the amount of information in the corresponding image sequence at this exposure is maximized. This implies the need to determine a quantitative index for measuring the amount of information in the images.

In physics, the concept of entropy is used to represent the uniformity of energy distribution in space. The more uniformly the energy is distributed, the higher the entropy of the system. Shannon, the founder of information theory, introduced this concept into the field of informatics and proposed the use of information entropy to measure the uncertainty of an information source [21]. Suppose that the probability of occurrence of each event in a probabilistic event set is $p_1$, $p_2$, … $p_n$, respectively, and suppose that there exists such a metric, $H$, that can describe the degree of uncertainty of the information, which can be given as follows [21], where n is the number of the event in the probabilistic event set.

$$H={\displaystyle \sum _{i=1}^n{p}_i {\log }_2\left(\frac{1}{p_i}\right)}$$

(1)

This formula is used to express the metric of information uncertainty in information theory, which is termed information entropy. The magnitude of information entropy can be expressed to express the amount of information in the information source. Specifically, in the field of image processing, the pixel intensity is a probabilistic event in Shannon’s definition of information entropy. The intensity of pixels in an image at different image coordinates is denoted by $X_i$, where $i=1,2,\dots ,k$, $k$ is the number of pixel grayscale levels. Let $E$ be the image information entropy, which can be expressed as follows.

$$E={\displaystyle \sum _{i=1}^k{p}_i {\log }_2\left(\frac{1}{p_i}\right)=p_1 {\log }_2\left(\frac{1}{p_1}\right)+p_2 {\log }_2\left(\frac{1}{p_2}\right)}+\cdots p_k {\log }_2\left(\frac{1}{p_k}\right)$$

(2)

where $p_i$ is the grayscale probability. For an 8-bit depth image, the maximal grayscale is 256 and the maximum image entropy equals 8 but only when the gray levels are evenly distributed in the image, which is not a common case in real applications. For any given scene, the image information entropy will vary with variations in exposure. The amount of information will reach the maximum when the image entropy becomes maximal.

Based on the above analysis, image information entropy can be used as the metric of the amount of information in an image. The greater the image entropy, the more information is contained in the image. Thus, the selection criteria for the initial exposure in the multiple exposure image fusion method can be expressed as that which determines a suitable exposure such that the image information entropy in the acquired image sequence at this exposure value reaches its maximum.

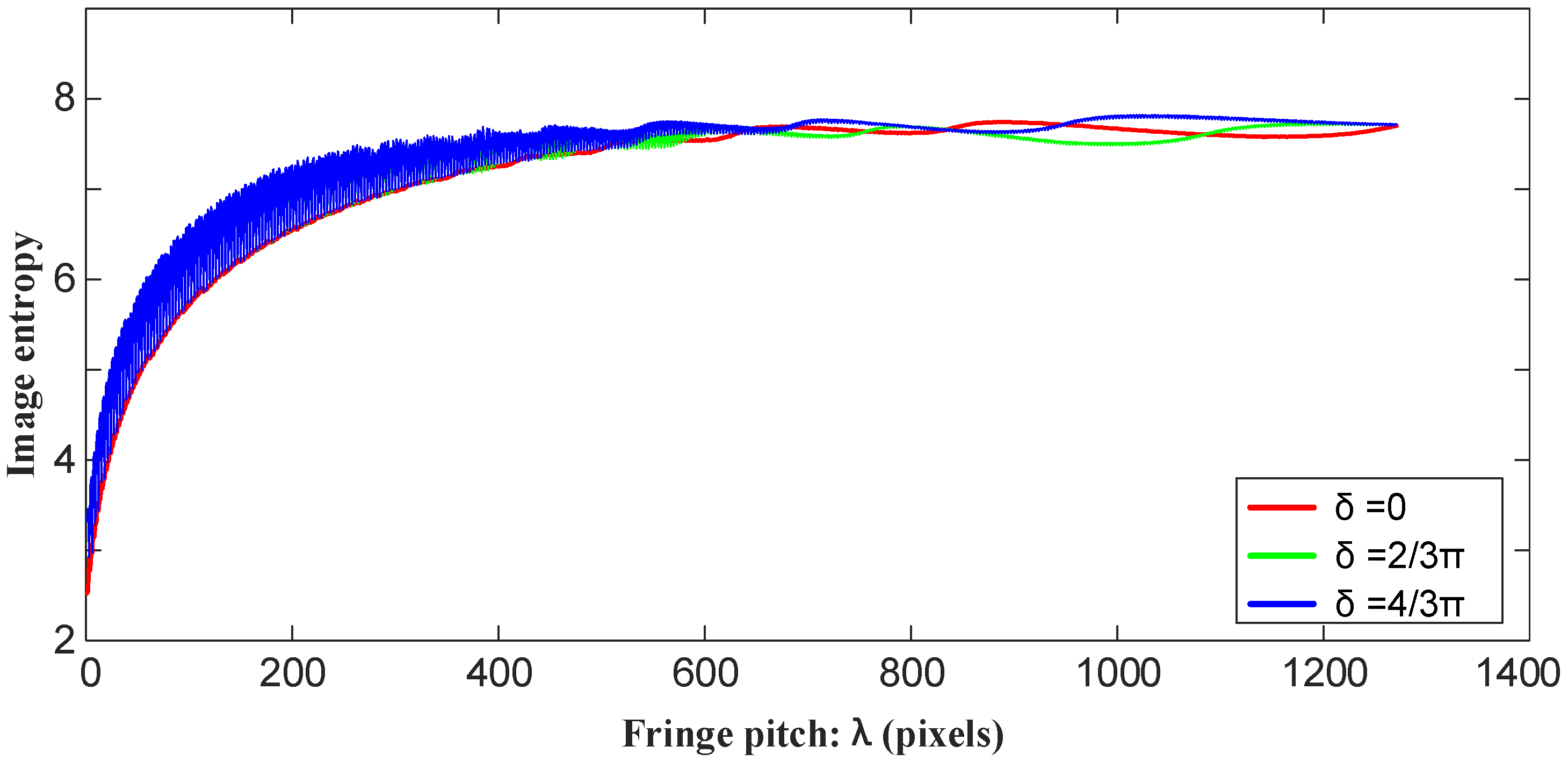
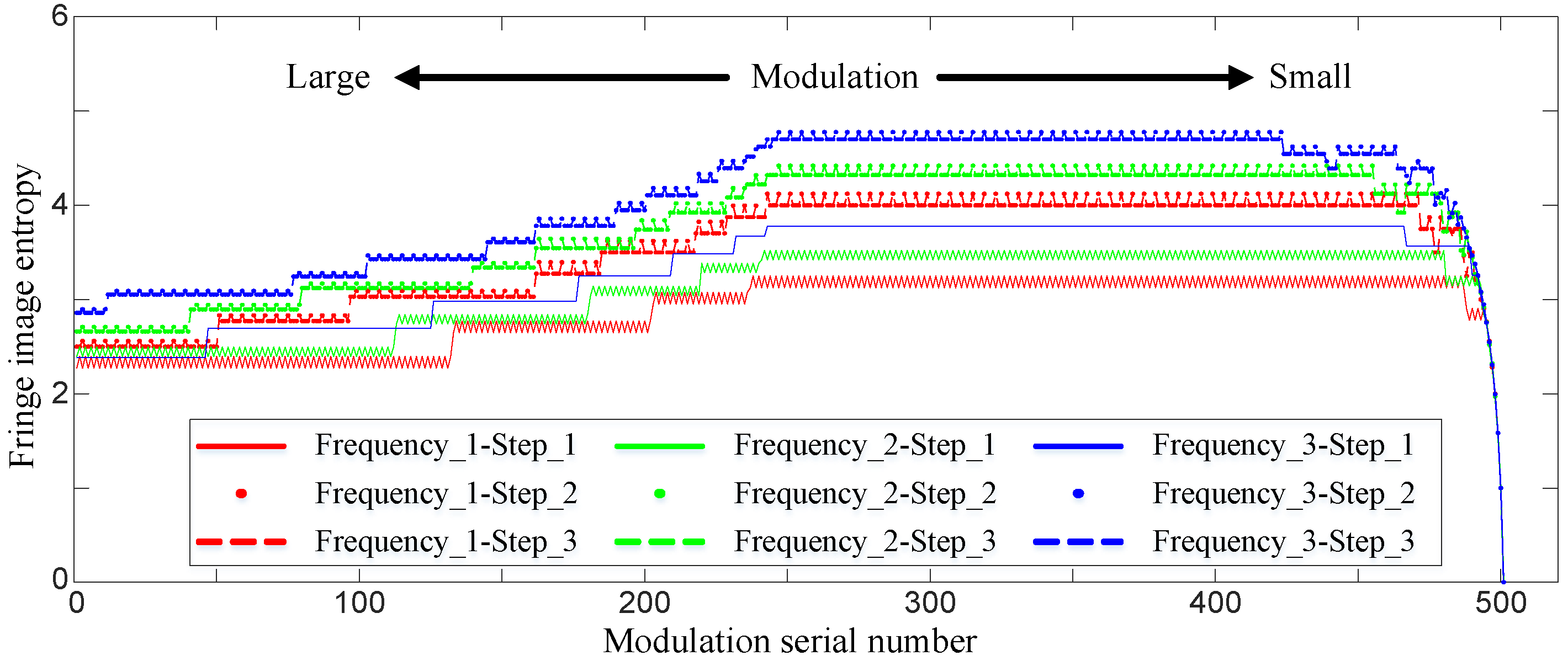
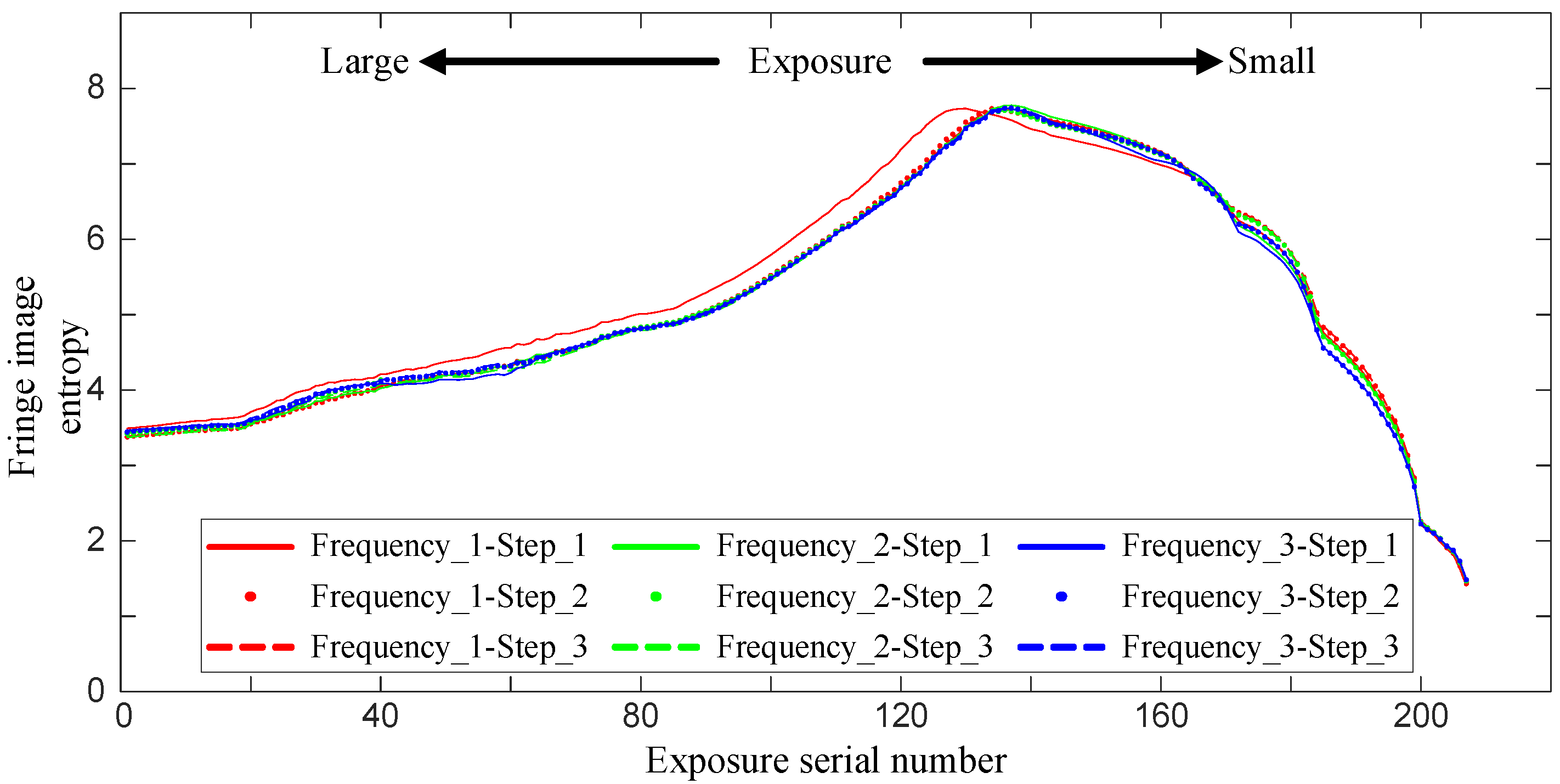
2.1.3. Variation Characteristics for Fringe Image Information Entropy

As one of the most common encoding and decoding methods for FPP, three-frequency three-step phase shifting is adopted in this study. When determining the initial exposure value, in order to improve the algorithm efficiency, the fringe image at a certain frequency should be used as the reference image for the information entropy calculation. This requires the study of the information entropy characteristics of the fringe images at different frequencies, the fringe images with different phase shift steps at the same frequency and the three-frequency three-step phase shift fringe images captured when the exposure value changes.

(1)

Information entropy for multi-frequency fringe images

In the multi-frequency phase-shifting method, the frequency of fringe images is reflected in the stripe pitch used to produce the fringe image. To study the variation in fringe image information entropy for different frequencies, a range of fringe images with varied stripe pitches are artificially produced. According to the Nyquist sampling theorem and further taking into account the effect of noise [22], the minimum stipe pitch is set to 10. The maximum stripe pitch, meanwhile, is set to 1280, since this is the pixel column size for common DMD chips. A total of 1271 fringe images, with the strip pitch $\lambda$ ranging from 10 to 1280, are used for further analysis. The image entropy of each fringe image was calculated, and the results are shown in Figure 2.

As can be seen from the figure, the information entropy of the striped image rises and fluctuates with the increase in the stripe pitch, showing an increasing trend. However, the curve plot has many fluctuation intervals, in which the image information entropy fluctuates to some degree. As the fringe pitch increases, the period of the fluctuation interval also increases gradually. In terms of the variation rate, it can be seen from the figure that in the interval $\lambda \in [10,100]$, the fringe image entropy increases rapidly with the increase in fringe pitch. When it comes to the interval $\lambda \in [600,1280]$, the increasing speed of image information entropy reduces gradually. After that, the image entropy stabilizes between 7 and 8 and fluctuates in a small range.

(2)

Information entropy for three-step phase-shift fringe images

To study the information entropy variation for the phase shifting fringe images concerning the change in fringe pitch, three groups of fringe images with three-step phase shifts (${\delta }_1=0$, ${\delta }_2=2\pi /3$, ${\delta }_3=4\pi /3$) are produced. For each group of fringe images, its incremental step is set to 1, and a total of 3813 fringe images are produced. The information entropy for each phase shift concerning the variation of fringe pitch is presented in Figure 3.

As shown in Figure 3, the information entropy of ${\delta }_1=2\pi /3$ and ${\delta }_2=4\pi /3$ is generally similar to that of ${\delta }_0=0$, which shows the changing characteristics of the composite functions of logarithm and sine functions. There is also a certain degree of fluctuation, with its period becoming larger as the pitch increases. In terms of the fluctuation in amplitude, in the range of $\lambda \in [0,600)$, the curve of ${\delta }_0=0$ results in the smallest amplitude. The fluctuation of the other two curves is larger, and the fluctuation average is above that of $\delta =0$. This means that the phase-shifting images are more sensitive to fringe pitch changes. In most cases, the entropy of the fringe image with phase shift is larger than that of the fringe image without phase shift. For the range of $\lambda \in [600,1280)$, the fringe image entropy changes alternately among the three phase shifts.

(3)

Information entropy for phase-shifting fringe images at different exposures

To further clarify the variation characteristics regarding the information entropy of three-frequency three-step phase-shifting fringe images when the exposure changes, simulation images and real images are used to study the variation characteristics, respectively. Simulated images are used to study the variation characteristics without considering the surface optical properties of the measured object. Then, real images are utilized to verify the applicability of the conclusions drawn from this ideal case.

The encoding scheme of the sinusoidal fringes can be expressed as

$$I=I^{\prime }+I^{″}\cos (\phi (x)+\delta )$$

(3)

where $I$ is the fringe image intensity, $I^{\prime }$ is the average intensity, $I^{″}$ is the intensity modulation, $\phi$ is the principle phase, $x$ is the pixel position and $\delta$ is the phase shift. The variation in intensity of the fringe images with the change in exposure can be simulated by modifying the intensity modulation. In the multiple exposure image fusion method, the exposure values are usually adjusted in the order from the highest to the lowest values to obtain high-quality fused fringe images. Therefore, the light intensity modulation values are also adjusted in the order from high to low. In the simulation, the fringe images are obtained at 500 light intensity modulation values, and the information entropy of a total number of 4500 fringe images at different frequencies and phase shifts are calculated. The results are shown in Figure 4.

As can be seen from the figure, the information entropy of three-frequency three-step fringe images tends to increase and then decrease as the modulation value decreases. Specifically, the information entropy of the fringe images first increases in a step-like manner. After reaching the maximum, it stabilizes in a small range of fluctuation as the modulation value decreases at the beginning and descends rapidly when the modulation value is relatively small. In terms of the speed of reaching the maximum, the larger the fringe pitch is, the later the maximum is reached and the smaller the corresponding modulation. For the same fringe pitch, the image entropy of the two steps with phase shifts reaches the maximum later than that of the step without phase shifts.

To verify the applicability of the above conclusions in a real scene, a white plane was measured using the multiple exposure image fusion method. The exposure was adjusted from a high value to a low value, and three-frequency three-step phase-shifting fringe images at 207 different exposure were captured. The information entropy of the captured fringe images was calculated and the results are shown in Figure 5. As can be seen, with the decrease in the exposure, the fringe image entropy also shows a trend of first increasing and then decreasing. And the larger the fringe pitch, the slower the stripe image entropy reaches its maximum, which is the same as in the results obtained using the simulated fringes.

To enhance the measurement speed of the multiple exposure image fusion method for FPP, one phase-shifting image under a certain frequency should be selected and analyzed as the reference fringe image for the initial exposure calculation. When the information entropy of this reference fringe image reaches the maximum, it should be ensured that the image entropy of all other fringe images is at or adjacent to the maximum. Additionally, in order to obtain the highest possible quality fused fringe images, an as large as possible exposure value is preferred. Based on the above criteria, combined with the analysis results for the variation characteristics of the fringe images’ entropy, the third phase-shifting fringe image with the largest fringe pitch is selected as the reference image for initial exposure calculation.

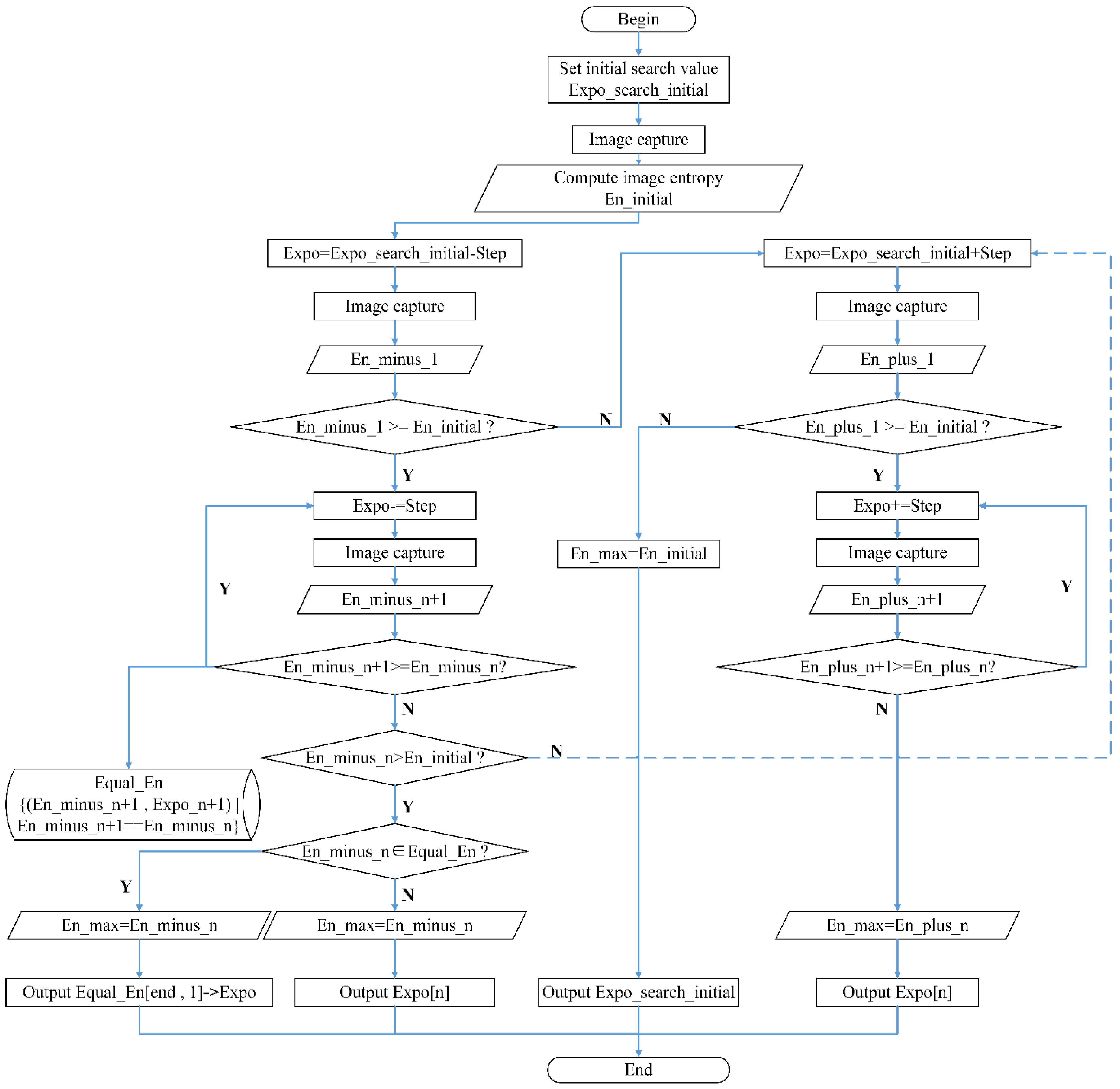
2.1.4. The Initial Exposure Searching Algorithm Based on Information Entropy

Based on the above discussion, the variation characteristics of the fringe image information entropy concerning the change in pitch and exposure are clarified and the reference image used to search the initial exposure is determined. Thus, an adaptive initial exposure searching algorithm based on information entropy for multiple exposure image fusion is proposed in this paper, as shown in Figure 6. The flow of the algorithm as well as its procedures can be detailly presented as follows.

(1)

Manually or automatically set an initial value for exposure searching according to the adjustment range of the camera. This initial value is denoted as $Expo\_search\_initial$.

(2)

Acquire the reference fringe image of the third phase shift with the largest fringe pitch at the initial exposure. Calculate the image information entropy $En\_initial$.

(3)

Search along the direction the exposure reduces. Taking $Step$ as the exposure searching step, let $Expo=Expo\_search\_initial-Step$. Capture the images under this exposure and calculate the entropy, $En\_minor\_\mathit{1}$, for the reference fringe image.

(4)

Determine the searching direction according to the relationship between $En\_minor\_\mathit{1}$ and $En\_initial$. If $En\_minus\_\mathit{1}<En\_initial$, according to the variation characteristics of the fringe image entropy with the change in exposure, it will never reach the maximum in this direction. Therefore, searching in this direction stops and the procedure goes to 8. If $En\_minus\_\mathit{1}\ge En\_initial$, this means that the entropy may reach the maximum in this direction. Continue to search in this direction and proceed to 5).

(5)

Continue to search in the direction of exposure reduction. Reduce the exposure by an interval of $Step$ and calculate the fringe image entropy. Then, compare the two values acquired before and after the adjustment of exposure. If $En\_minus\_n+\mathit{1}\ge En\_minus\_n$, the exposure is further reduced by $Step$ and the loop continues. If the two values are equal, the image entropy and corresponding exposure will be saved to the data set $Equal\_En$ in a form of key–value pair. If $En\_minus\_n+1<En\_minus\_n$, proceed to 6.

(6)

If $En\_minus\_n>Equal\_En$, proceed to 7. Otherwise, the stop searching in the current direction and switch to the opposite direction to that in which the exposure increases. Taking $Expo\_search\_initial$ as the initial exposure searching value, proceed to 8.

(7)

If $En\_minus\_n$ belongs to the data set $Equal\_En$, set $En\_max$ to $Equal\_minus\_n$. Select the exposure value of the first entropy–exposure pair in the last equivalent entropy–exposure pair of $Equal\_En$ as the desired exposure for the maximum entropy. The procedure then ends here. Otherwise, set $En\_max$ equal to $Equal\_minus\_n$ and output the corresponding exposure value. Then the procedure ends.

(8)

Search in the direction the exposure value increases. Let $Expo=Expo\_search\_initial+Step$, capture corresponding fringe images and calculate the image entropy. If $En\_plus\_\mathit{1}\ge En\_initial$, then continue to search in this direction and proceed to 9. Otherwise, let $En\_max=En\_initial$ and output the corresponding exposure, $Expo\_search\_initial$. This means that the initial exposure set at the beginning of the searching algorithm makes the image entropy reach the maximum. The procedure then ends here.

(9)

Continue the searching loop in the direction of rising exposure. Increase the exposure and calculate the image entropy. If $En\_plus\_n+\mathit{1}\ge En\_plus\_n$, increase the exposure and the loop continues. Otherwise, set $En\_max$ to be equal to $En\_plus\_n$. The corresponding exposure, $Expo[\mathit{n}]$, will be outputted and the procedure ends here.

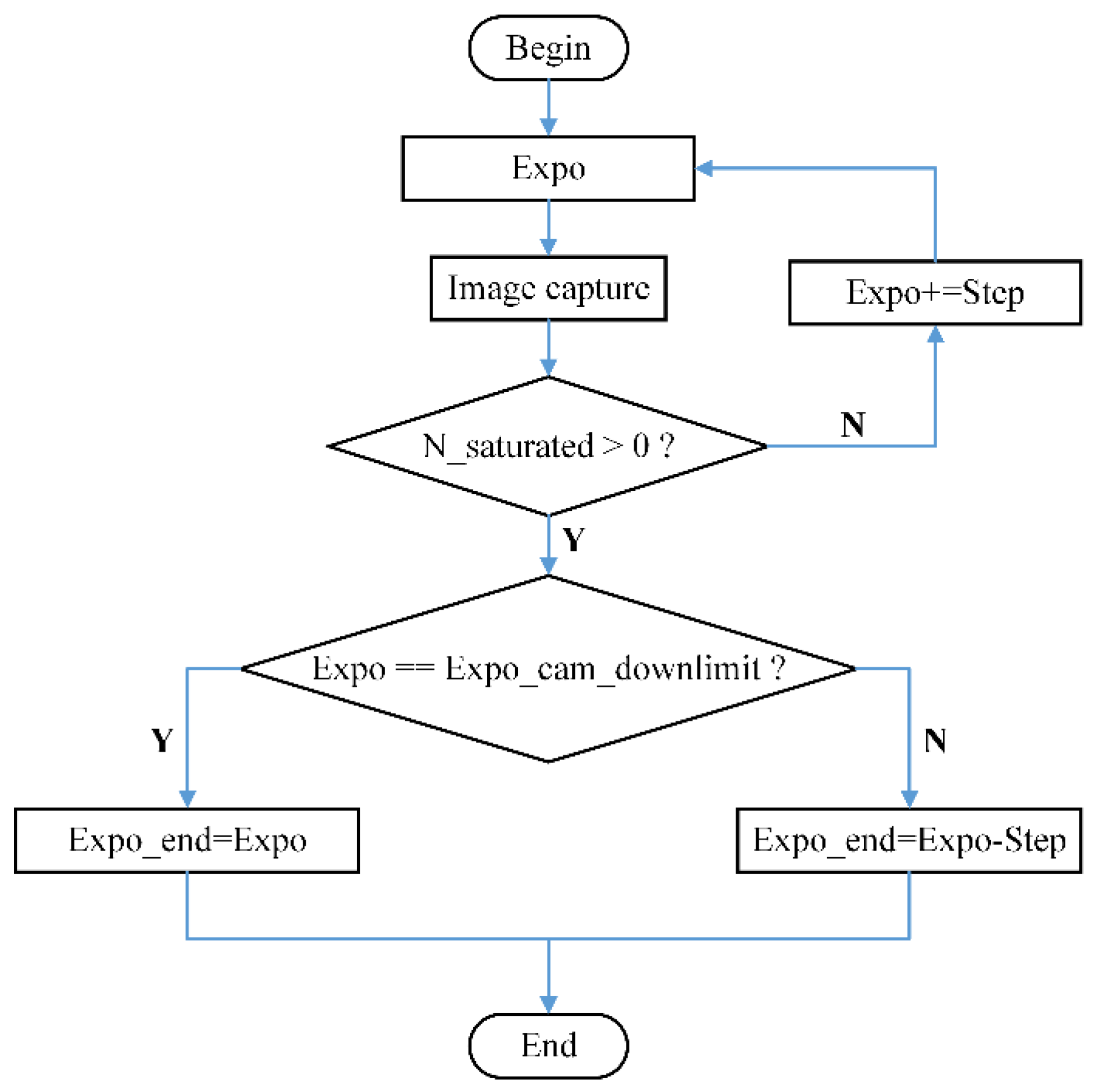
2.2. Exposure Sequence Generation Based on Dichotomy

In the case of multiple exposure fusion methods for highly reflective surface measurements, the selection of a proper exposure sequence is another key factor that affects the measurement effect. In theory, the higher number of exposure value adjustments and the wider the exposure coverage range, the higher the quality of the fusion fringe image. However, from the perspective of improving the measurement efficiency, it is not possible to increase the number of exposure value adjustments indefinitely. When the exposure adjustment step is too small, the change in the number of saturated pixels will become insignificant. A balance between measurement efficiency and fusion image quality is generally achieved through experiments, which seriously reduces the algorithm efficiency. To improve the automation of the multiple exposure method, an exposure sequence generation method based on dichotomy is proposed in this study.

In order to study the variation rule for the saturated pixel number concerning the exposure values for highly reflective metal surfaces, a reflective metal surface was selected for measurements at a range of exposure values. The exposure value was adjusted from high to low in steps of 10 to obtain a raster stripe image at 1481 exposures, and the saturated pixels in the images were counted. As a comparison, the same exposure values parameters were used to measure a white, uniformly scattering plane, and the number of saturated pixels was counted. The results are shown in Figure 7.

Compared to the saturated pixels number variation curve of the metallic highly reflective surface, the curve of the uniform scattering plane has an obvious slope. The reason for this difference is that the uniformly scattering surface has a similar reflectance at all points, and, as the exposure value decreases, the grayscale values of the image pixels also tend to change uniformly. The number of saturated pixels declines rapidly when the exposure value decreases to a certain level. When measuring the metallic highly reflective surface, the existence of a specular reflection lobe and specular reflection crest in the direction of the camera means that there always exists saturated pixels in the images. This leads to a slight variation in the saturated pixel number curve, which suits most of machined metallic surfaces. This makes the procedure suitable for constructing the exposure sequence based on the dichotomy method.

Let the upper limit and lower limit of the exposure be denoted as $Expo\_begin$ and $Expo\_end$, respectively, and suppose that the exposure value in the exposure sequence is more than three. Then, the exposure sequence generation procedure based on dichotomy is proposed as follows.

(1)

Set the desired total number of exposure N and determine $Expo\_begin$ and $Expo\_end$;

(2)

Build the initial exposure sequence $\left\{Expo\_begin,Expo\_end\right\}$. The exposure number in the current exposure sequence is denoted as $Num\_count$;

(3)

Update the exposure sequence. Compute the average of the upper and lower limit of exposure and insert it into the sequence. In this way, the updated exposure sequence S1 can be generated.

$$S1=\left\{Expo\_begin,Expo\_\mathit{1}\_\mathit{1},Expo\_end\right\}$$

(4)

$$Expo\_\mathit{1}\_\mathit{1}=floor[(Expo\_begin+Expo\_end)/\mathit{2}]$$

(5)

(4)

Continue to update the exposure sequence.

$$Expo\_\mathit{2}\_\mathit{1}=floor[(Expo\_begin+Expo\_\mathit{1}\_\mathit{1})/\mathit{2}]$$

(6)

$$Expo\_\mathit{2}\_\mathit{2}=floor[(Expo\_\mathit{1}\_\mathit{1}+Expo\_end)/\mathit{2}]$$

(7)

Then, the updated exposure sequence can be expressed as

$$S2=\left\{Expo\_begin,Expo\_\mathit{2}\_\mathit{1},Expo\_\mathit{1}\_\mathit{1},Expo\_\mathit{2}\_\mathit{2},Expo\_end\right\}$$

(8)

(5)

If $Num\_count>N$, then the procedure ends and outputs the exposure sequence. Otherwise, continue to execute the dichotomy method until the aforementioned inequation works. The final generated exposure sequence can be denoted as $S\_final$.

2.3. Self-Adaptive Multiple Exposure Image Fusion Algorithm for FPP

Based on the previous initial exposure searching procedures based on information entropy and the exposure sequence generation procedures based on dichotomy, a self-adaptive multiple exposure image fusion algorithm for FPP is finally proposed in this section, which is described in detail as follows.

(1)

Determine the beginning and ending exposure values. Determine the initial exposure, $Expo\_initial$, using the method proposed in Section 2.1. Then, the beginning exposure can be given by:

$$Expo\_begin=k\_initial\ast Expo\_initial$$

(9)

where $k\_initial$ is a weighting factor, which is normally greater than one. By using this item, enhance the intensity level of the pixels which are outside the saturated area of the image captured under the beginning exposure.

The procedure to determine the ending exposure, $Expo\_end$, involves analyzing the number of saturated pixels, as shown in Figure 8. Let the current exposure be denoted by $Expo$. Commence the searching procedure by capturing the images at the lower exposure limit of the camera, $Expo\_cam\_lowerlimit$, and calculating the number of saturated pixels, $N\_saturated$. If $N\_saturated$ is greater than zero, and if $Expo=Expo\_cam\_lowerlimit$, then set the ending exposure $Expo\_end$ to be $Expo$. Otherwise, $Expo\_end=Expo-M$,where $M$ is the exposure adjustment step. If the number of saturated pixels is still equal to zero, then $E\mathrm{x}po=Expo+M$. Then, repeat the aforementioned operations will be until the ending exposure is determined. The procedure then ends.

(2)

Generate the exposure sequence automatically. After providing the exposure times, the exposure sequence will be generated by the method proposed in Section 2.2.

(3)

Project the fringes and capture the images according to the generated exposure sequence in Step (2). Suppose $\left\{Expo\_\mathit{1},Expo\_\mathit{2},Expo\_\mathit{3},\dots \dots ,Expo\_n\right\}$ are the n exposure values from the exposure sequence, as shown in Figure 9a, then n groups of images, each of which has nine phase shift fringe images, are captured at each of the exposure values.

(4)

Multiple exposure image fusion. Image fusion starts with the image group of three-frequency three-step fringe images captured at the largest exposure value, $Expo\_1$, by the pixel-by-pixel analysis. If a certain position pixel at this exposure value is not over-exposed in all the nine fringe images of this group, select this pixel, with its intensities in the nine phase shift images, to form the final fused images. Otherwise, if this pixel is overexposed in at least one image of the nine fringe images in this group, then select the image group at a lower exposure value to repeat the above judgment procedures. As shown in Figure 9b, a set of fused three-frequency three-step phase-shifting fringe images for both left and right cameras can finally be obtained in this way.

(5)

Phase decoding. Unwrap the fused three-frequency three-step phase-shifting fringe images and obtain the full-field phase map, as shown in Figure 9c. Details regarding the phase decoding is resented in reference [23].

(6)

Point cloud reconstruction [23]. Compute the disparity map according to the left and right full-field phase map and finally constructed the point cloud, as shown in Figure 9d,e.

Thus, a complete set of the self-adaptive multiple exposure fusion methods for FPP for measuring highly reflective metal surfaces has been established. The self-adaptivity of this method is assured by the initial exposure searching algorithm based on image information entropy and the exposure sequence generation algorithm based on dichotomy. This makes the method more flexible concerning the measurement of surfaces with differences in reflectivity and usable in different lighting environments.

The developed algorithm needs to work in conjunction with FPP systems. It needs the fringe images captured by FPP systems as the inputs for analysis and generates the exposure values as the output to instruct FPP systems to capture the images. This process is repeated during the initial exposure searching and exposure sequence generation. The algorithm can be developed using any programming language depending on how easily it can be integrated into a specific FPP system and make the entire process automatic.

The total cost time of the entire process to determine the optimized initial exposure and exposure sequence mainly depends on the FPP hardware system because the process includes interacting with the FPP hardware to project patterns and capture images. The computational time in terms of analyzing the fringe images is very little. For our system, the entire process is very fast and can output the results within seconds. Once the optimized initial exposure and exposure sequence are obtained, the FPP system can start its measurement according to the exposure values.

3. Experiments and Discussions

To verify the performance of the proposed methods, two experiments were designed and implemented. The first experiment was designed for the verification of the initial exposure searching algorithm and the second was for the verification of the proposed self-adaptive multiple exposure image fusion method for FPP by evaluating the measurement performance. The FPP system had two Basler aca1300-30 gm cameras with resolutions of 1280 × 960.

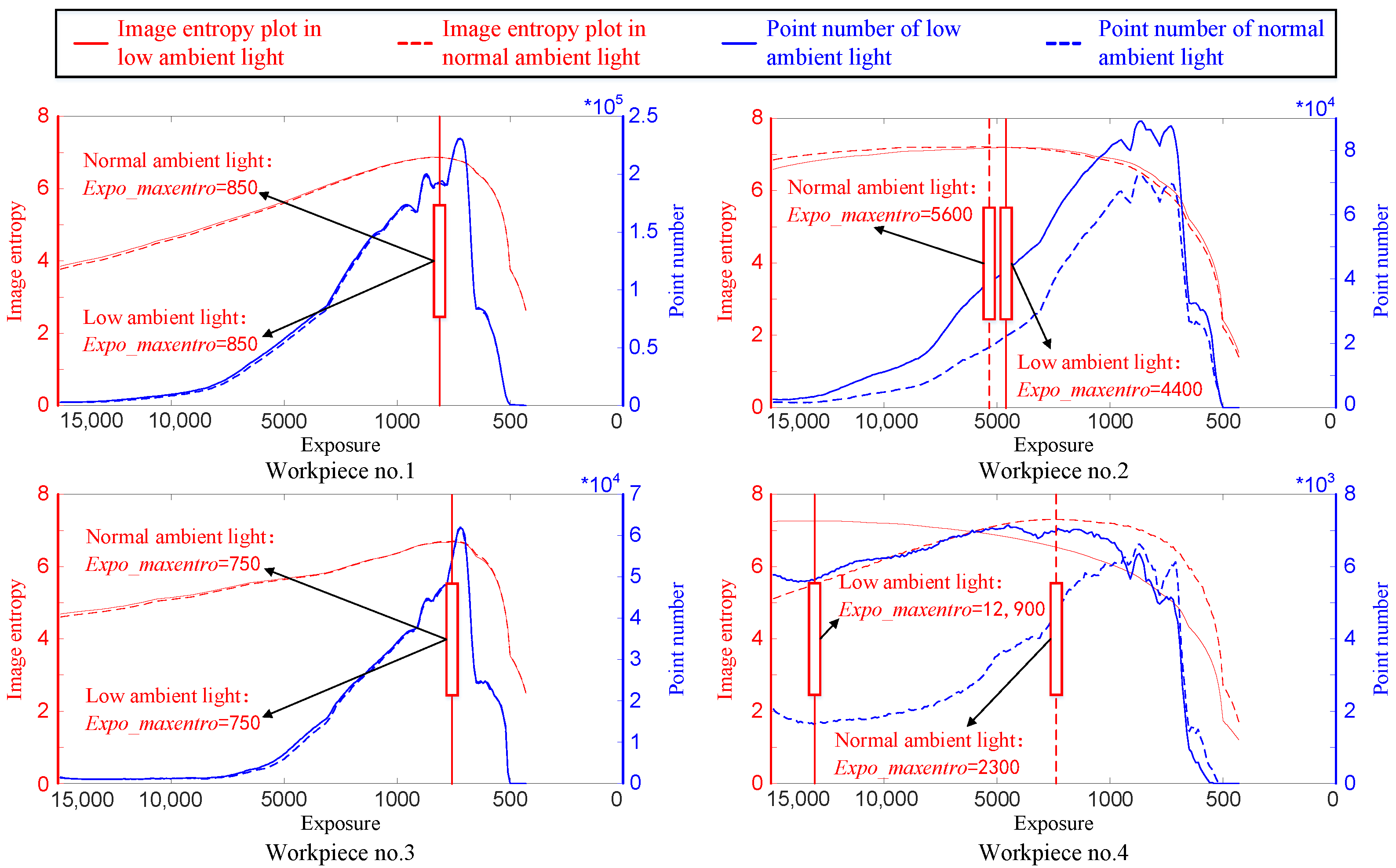
3.1. Adaptivity Verification of the Proposed Initial Exposure Searching Algorithm

To verify the adaptivity and accuracy of the proposed initial exposure searching algorithm based on information entropy, six metal workpieces with different sizes, shapes and surface reflectivity were used as the experimental objects, as shown in Figure 10. The surfaces of workpieces no.1–no.4 are the original machined surfaces, workpiece no.5 is a cylinder after oxidation treatment and workpiece no.6 is an automobile body structural part treated by the oxidation process. Workpieces no.1 to no.4 were utilized to verify algorithm performance in different lighting conditions. The suitability of the algorithm for surfaces with differences in reflectivity was verified by using workpieces no.1 to no.6. Taking these workpieces as the test objects, the algorithm’s adaptivity in different lighting conditions and with differences in surface reflectivity was verified as follows.

3.1.1. Algorithm Adaptivity Verification in Different Ambient Lighting Conditions

To verify the algorithm’s adaptivity in different ambient lighting conditions, workpieces no.1 to no.4 were selected as the experimental objects. The maximum information entropy of the fringe images was searched in ambient lighting and normal ambient lighting, respectively. The ambient light scene is shown in Figure 11.

The fringe image entropy of each workpiece was obtained at a total of 229 exposures to verify the accuracy of the maximum entropy searching algorithm. This exposure sequence decreased from a maximum of 15,000 to a minimum of 20, with a 100-step decrease when the exposure was greater than 1000 and a 10-step decrease when the exposure was less than 1000. Additionally, to observe the relationship between the maximum in terms of the point cloud number and the initial exposure value obtained by the proposed algorithm, the point numbers of the point clouds obtained at these 229 exposures were also counted. The searching algorithm was executed with 5000 as the initial exposure value and 50 as the searching step. The results are shown in Figure 12. The reason why a total of 229 exposures was used is because a complete distribution of image information entropy with respect to the exposure value needed to be obtained. It is considered as a standard to evaluate the accuracy of results concerning the maximum entropy searching algorithm, and thus to further evaluate the proposed initial exposure searching algorithm. Regarding actual measurements, these do not require as many exposures to optimize the initial exposure. Normally, twenty exposures are sufficient to accurately calculate the initial exposures in experiments.

As can be seen from the figure, the maximum value in terms of the fringe image entropy was accurately obtained for each of the workpieces and the corresponding initial exposure value is provided. For workpieces no.1 and no.3, the fringe image entropy variation curves under normal ambient lighting are very close to that under low ambient lighting conditions, and thus the initial exposure values obtained by the searching algorithm in different lighting conditions are equal. The image entropy change curves of workpiece no. 2 show a certain degree of difference between the different lighting conditions, and, thus, the final obtained initial exposure values are also different. And as for workpiece 4, its fringe image entropy change curve obtained in normal ambient lighting is different from that in low ambient illumination. Compared with the image entropy curve in low ambient illumination conditions, the curves in normal ambient illumination arrive at their peak later. The curves in normal ambient illumination descend faster than those in low ambient illumination.

As for the variation characteristics of the point cloud number, it also rises at first and decreases after arriving at the peak. The curve of the point cloud number arrives at the peaks later than the curve of the image entropy. It means that after the fringe image entropy reaches the maximum value, the point cloud number will continue to maintain the trend of increasing and reach the maximum after the exposure value drops to a certain value. This illustrates that the three-frequency three-step phase shift method used in this study is adaptable to lighting conditions and can guarantee decoding quality in a weaker lighting condition. Furthermore, it means that the exposure value corresponding to the maximum point number of the point cloud, denoted by $Expo\_max\_pointnum$, would be less than the initial exposure obtained from the proposed algorithm. This ensures that the exposure, $Expo\_max\_pointnum$, is always within the upper limit and lower limit of the exposure sequence, which helps the fusion algorithm make full use of the fringe images captured at this exposure value. Additionally, it ensures that more pixels with high intensity could be selected for the fused image, which further improves the quality of the full-field phase map and point cloud.

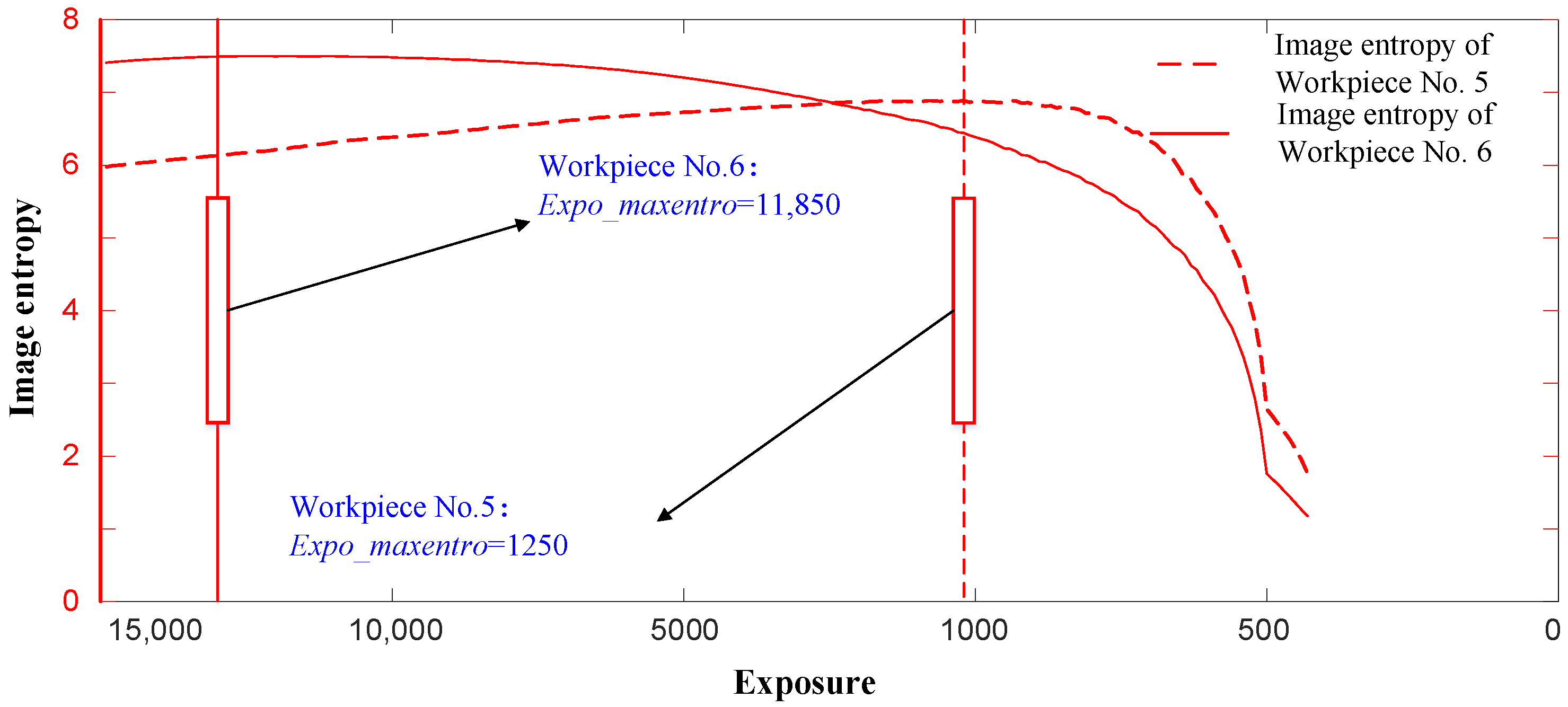
3.1.2. Algorithm Verification for Surfaces with Differences in Reflectivity

In 3.1.1, the performance of the proposed algorithm was verified in different ambient lighting conditions using four workpieces with the original machining surfaces, which were highly reflective. To verify the algorithm’s adaptivity concerning surfaces with differences in reflectivity, experiments were performed with workpieces no. 5 and no. 6, those with oxidized surfaces, under normal lighting conditions. The relevant fringe image entropy curves were produced with the same parameters as those used in 3.1.1. The results are shown in Figure 13.

As can be seen from the figure, the initial exposure value search algorithm found the maximum entropy of the streak image and obtained the corresponding exposure value for both workpieces 5 and 6 with surface oxidation. This, combined with the previous results for the machined original surfaces of workpieces 1–4, demonstrates that the proposed algorithm can successfully find the maximum entropy of the fringe images for measured objects with differences in surface reflectance and can obtain the corresponding exposure value as the initial exposure value. Thus, the proposed initial exposure searching algorithm based on fringe image entropy can adapt to both different ambient lighting conditions and differences in surface reflectivity, which ensures the adaptiveness, robustness and accuracy of the obtained results for the initial exposure value.

3.2. Measurement Verification of the Adaptive Multiple Exposure Fringe Fusion Method

To verify the measurement performance of the proposed adaptive multiple exposure fringe fusion method for FPP, workpieces no.1–no.4 were measured under normal ambient lighting conditions. To demonstrate the algorithm’s performance sufficiently, the original fringe images with maximal entropy obtained in 3.1 were selected to be compared with the fused fringe images. The saturation threshold was set to 250, and the overexposure pixels in the original images are represented in red. The area which failed to secure rational complemented pixels in the fused image is marked by a green color. The image entropy before and after the fusion was calculated, and the results are shown in Figure 14.

As can be seen from the figure, there are overexposure areas, presented in red, in the original fringe images for all four workpieces. This may greatly reduce the sinusoidal intensity distribution in these areas, which leads to significant phase errors during image decoding. In contrast, almost all of these areas are well restored in the fused fringe images, except for a small part of workpiece 1, presented as the green area, which could not be restored because of the extremely high surface reflection. Additionally, there are a large number of areas where the fringe contrast is very low due to the darkness of the image, as shown in the right portion of the images of the four workpieces. The fringe contrast in these areas was significantly improved in the fused images. To evaluate this effect quantitatively, the image entropy, E, was calculated before and after image fusion. It can be seen from the results that the entropy of each fused image is significantly improved compared to the original image, with the improvement being 11.5%, 11.7%, 12.2% and 11.9%, respectively, which means that the fused images can provide more fringe information for later phase decoding, thus improving the quality of the obtained phase map.

Phase unwrapping was performed using these fringe images before and after fringe fusion. The cross sections of the unwrapped phase maps at the same positions were obtained for evaluation, as shown in Figure 15. The quality of the full-field phase maps obtained using fused stripe images was significantly improved compared to the unwrapped results obtained using the original fringe images. Taking workpiece no.1 as an example, in the upper left region of the phase map unwrapped from the original fringe images, there exists a distinct visual fold area. In this area, there is a large region where there is a failure in phase unwrapping because of the strong surface reflection. This folded and black region in the phase map corresponds to the red region of workpiece 1 in Figure 14. It can be seen that there is a large error in this area due to the presence of high reflectivity. On the contrary, the fold areas in the original fringe phase map are effectively eliminated in the fused phase map. As can be seen, all the regions of workpiece 1 have good unwrapping results, except for the extremely highly reflective region marked in green in Figure 14. The quality of the phase maps were also greatly improved for workpieces 2 to 4.

To compare the phase unwrapping error of the original fringe images and the fused fringe images more intuitively, the cross-section data was plotted in Figure 15. The selected section for the phase map before and after the fusion algorithm is marked with the red dotted line and green dotted line, respectively. As can be seen from the phase variation curve, there exists a distinct phase disturbance in the cross-section phase curve of the original phase map. This means that there is an obvious phase error in this area, which would lead to an error in 3D reconstruction. Comparatively, the section phase curve of the fused phase map is smooth, and the quality in terms of phase unwrapping was greatly improved.

As shown in Figure 16, the point cloud was reconstructed based on the original fringe images and the fused fringe images. As can be seen, many points are missing in the reconstructed point cloud reconstructed from the original fringe images. This stems from the phase error which occurred because of the existence of a highly reflective area, which resulted in incorrect matching and matching failure in the stereo match step and further lead to missing point cloud data. In contrast, the completeness of the point cloud reconstructed from the fused fringe images shows a dramatic improvement. The point numbers of the original point cloud and the fused point cloud are given in

Table 1. Point numbers reconstructed from original fringe images and fused fringe images.

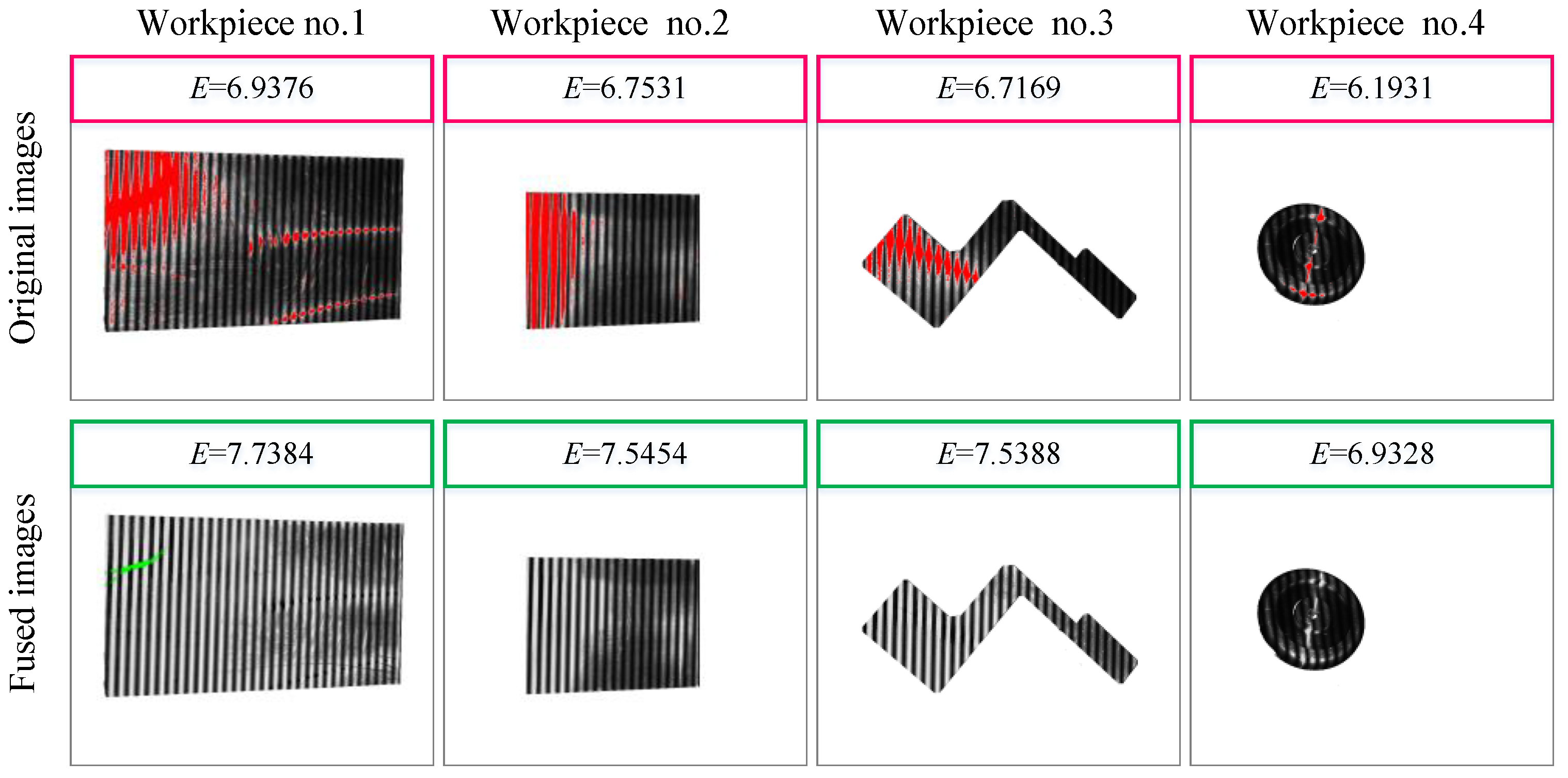
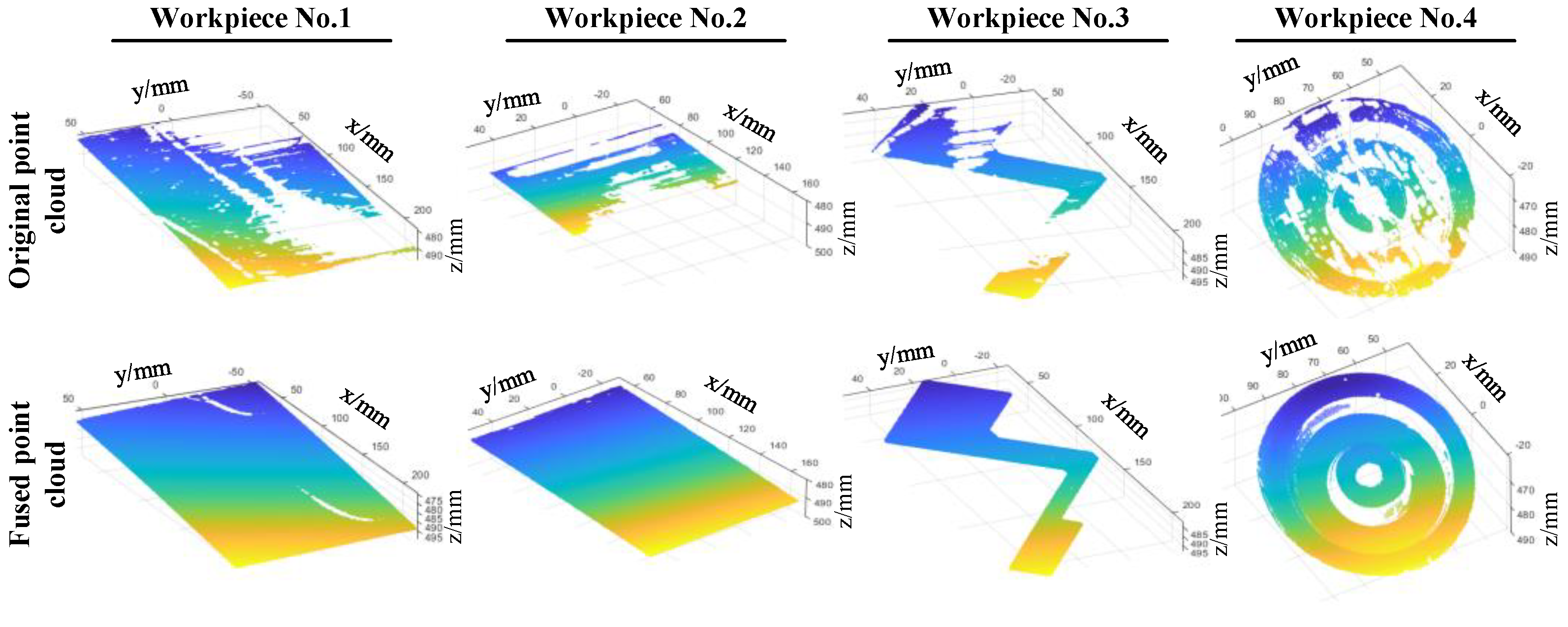
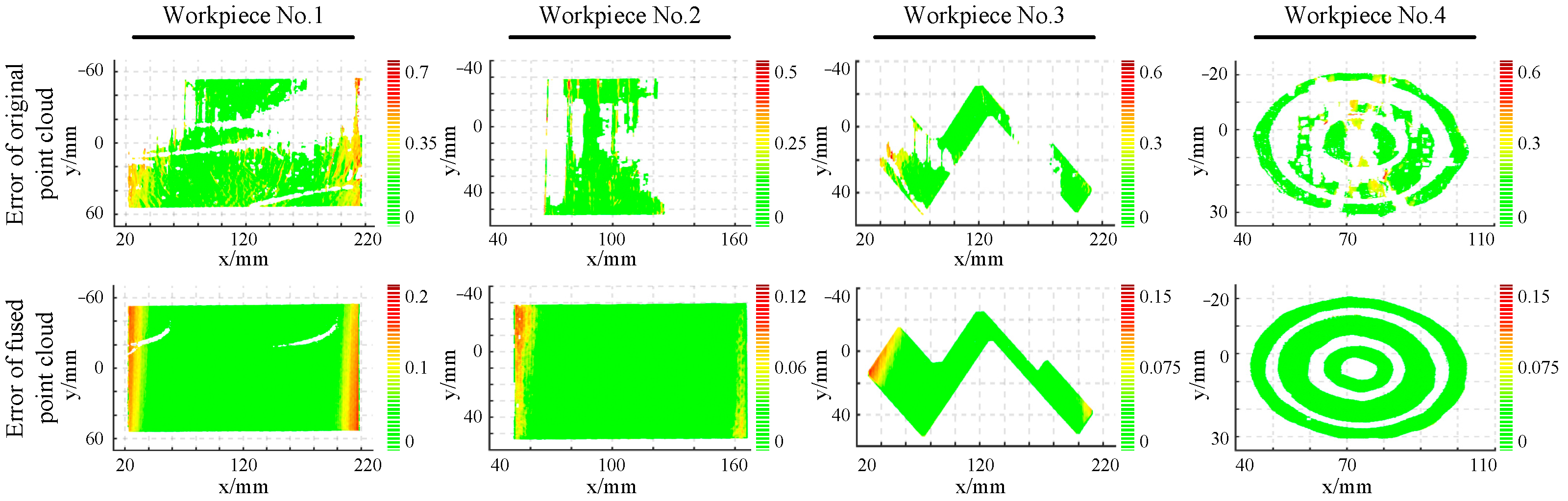
	Workpiece No.1	Workpiece No.2	Workpiece No.3	Workpiece No.4
Initial point cloud	192535	23534	50454	4782
Fused point cloud	418859	129824	98169	33894

.

To analyze the 3D reconstruction results more accurately, the aforementioned point clouds were fitted to obtain the fitting surface as the ground truth. Then, the errors in terms of the point cloud before and after the fusion algorithm was calculated and the color range maps were constructed, as shown in Figure 17. Simultaneously, to quantitatively evaluate the error, the mean error and root mean square error (RMSE) were calculated, as listed in

Table 2. Errors of the point clouds reconstructed from the original and fused images.

	Error Item	Workpiece No.1	Workpiece No.2	Workpiece No.3	Workpiece No.4
Initial point cloud	Mean Error/mm	0.0639	0.0478	0.0537	0.0496
	RMSE/mm	0.1125	0.0942	0.0937	0.0786
Fused point cloud	Mean error/mm	0.0332	0.0308	0.0281	0.0313
	RMSE	0.0358	0.0362	0.0297	0.0344

.

Compared to the point clouds of the original fringe images, the mean errors and RMSEs of the fused point clouds are greatly reduced. For example, the mean errors of the four workpieces are roughly 0.05 mm to 0.06 mm. Whereas the mean errors of the fused point clouds are reduced to approximately 0.03 mm. The RMSE of the original point cloud is roughly 0.09 mm, whereas the RMSE of the fused point cloud is roughly 0.03 mm. This means that the accuracy of the fused point cloud is also improved compared with the original point cloud. This is mainly because the fused fringe images are of, better quality especially in the reflective areas, and, as a result, the point noise can be greatly suppressed.

4. Conclusions

In this paper, a self-adaptive multiple exposure image fusion method has been proposed to solve the challenges of measuring highly reflective surfaces or high dynamic range surfaces for FPP. An adaptive initial exposure searching method has been proposed by introducing the theory of information entropy to the fringe image combined with an analysis of the characterization of fringe image entropy. To generate the proper exposure sequence automatically, an exposure sequence generation algorithm has been proposed, which needs only a small number of parameters for presetting. Based on these two algorithms, a novel self-adaptive multiple exposure image fusion method for FPP as well as its detailed procedures have been provided. To verify the performance of the proposed method, experiments were designed by measuring metal workpieces of different shapes and with differences in surface reflectivity. Compared with current multiple exposure image fusion methods, the experimental results verify the self-adaptivity, efficiency and robustness of the proposed method when measuring for differences in reflectivity and in different ambient lighting conditions.

When measuring different objects with differences in surface reflectivity or in different ambient light conditions, the initial exposure and the exposure sequence must be adjusted accordingly. Most existing multiple exposure image fusion methods typically have a relatively fixed sequence of exposure settings that are determined by practical experience or trial and error experiments. Trial and error experiments used to adjust the sequence of exposure settings are time-consuming, and the initial exposure and the exposure sequence cannot be precisely optimized based on practical experience. Compared with the existing methods, the core novelty and main contribution of the method proposed in this manuscript is that it can optimize the initial exposure and the exposure sequence self-adaptively. This advantage makes the proposed method superior to others in terms of self-adaptivity for variations in surface reflectivity and ambient lighting conditions. It also has the ability to optimize the exposure settings quickly and automatically rather than relying on manually adjustments based on practical experience or performing trial and error experiments.

Although the proposed method works well, a number of issues require further study, for example, the effect of the geometry complexity on measurements has not been studied in detail. In future works, the possibility of applying the proposed solution in structured light measurement systems projecting other kinds of patterns needs to be studied. The influence of the object’s geometric complexity and the intensity of the light on the proposed method need to be studied. The criteria to use when deciding whether to modify the exposure setting or continue using the old one when the relative angle and position between the measured object and the light source changes is another area worthy of attention. Deep learning could also be utilized in the recovery of the saturation areas in the captured images. Methods based on hardware could be studied. For example, taking the super high dynamic range characteristic of the chips into consideration, event-based cameras have great potential when it comes to solving the problem of highly reflective surface measurements.