Experimental Fatigue Evaluation of Bogie Frames on Metro Trains
Abstract
1. Introduction
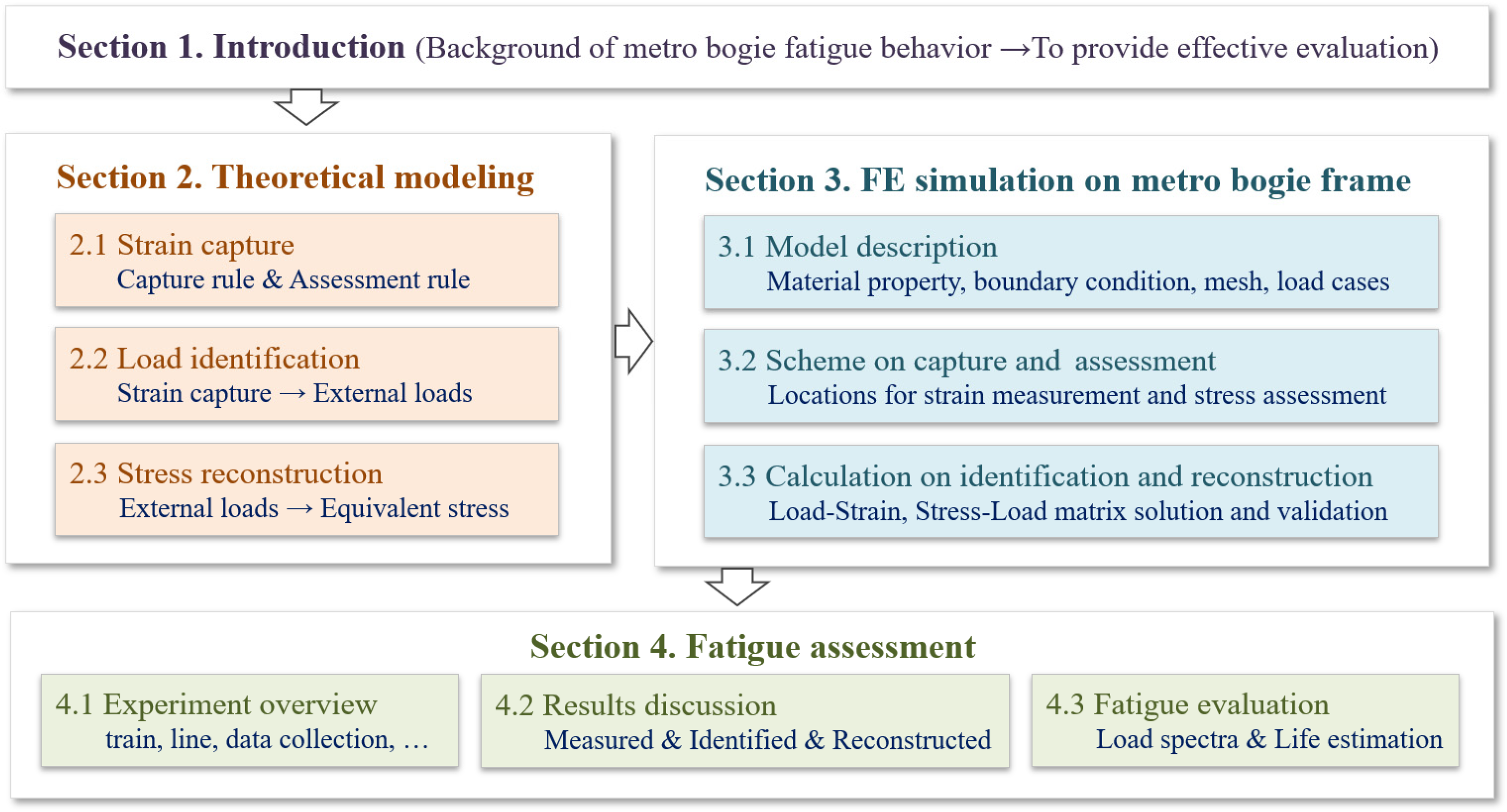
2. Theoretical Modeling
2.1. Strain Capture
2.2. Load Identification
2.3. Stress Reconstruction
3. FE Simulation on Metro Bogie Frame
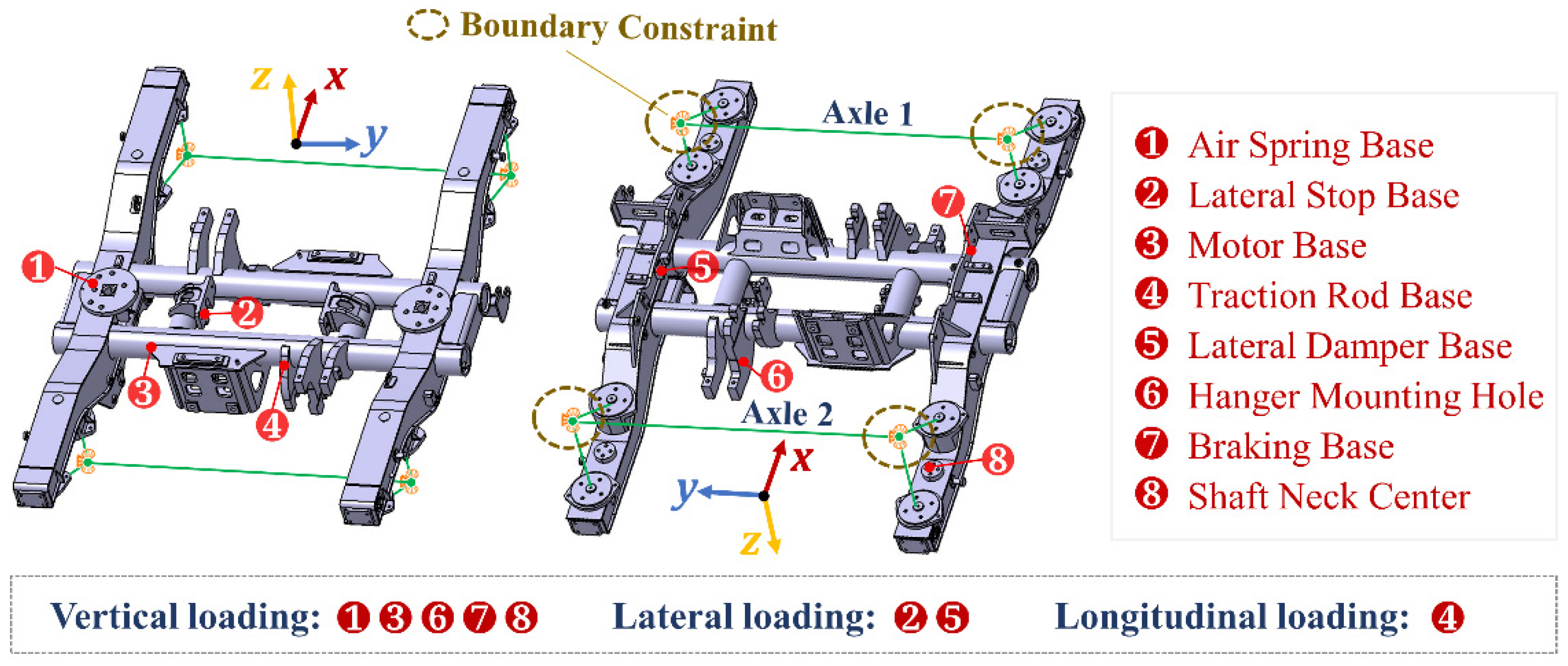
3.1. Model Description
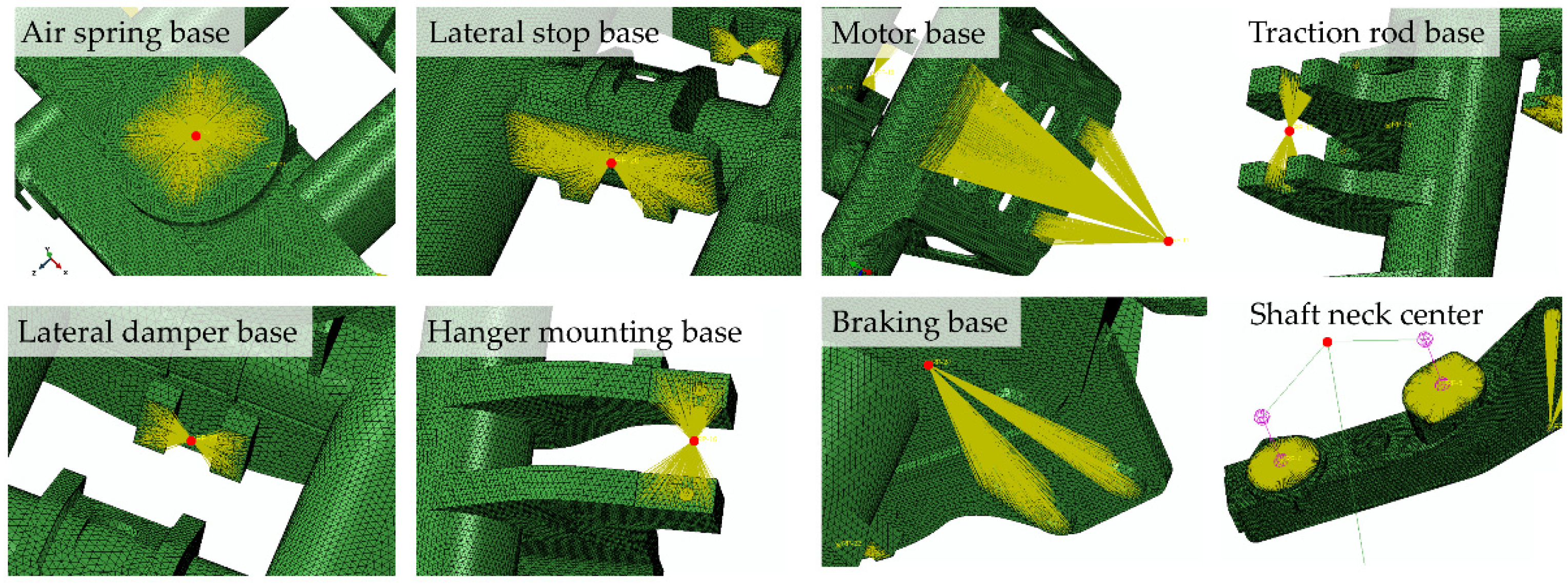
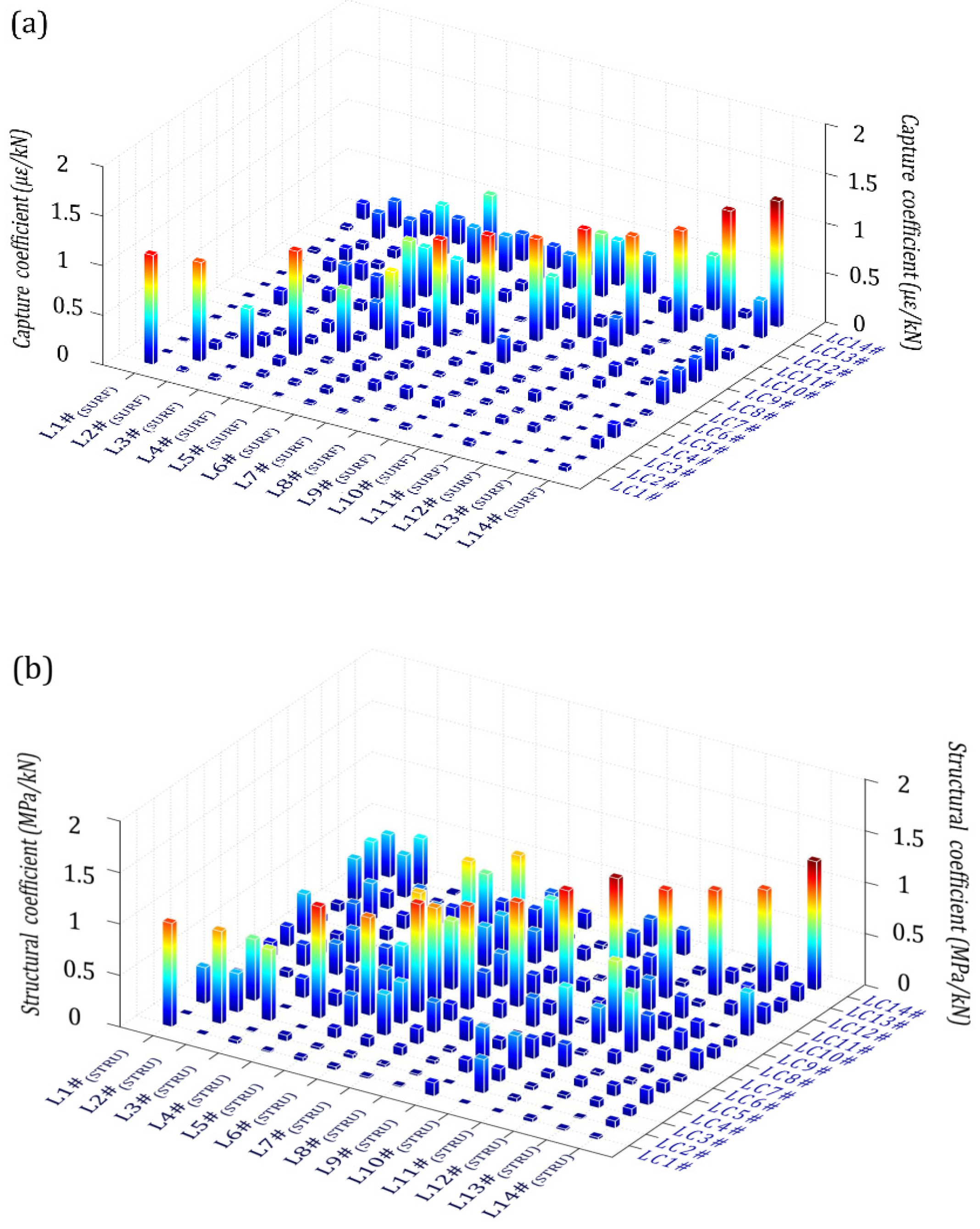
3.2. Scheme on Capture and Assessment
3.3. Calculation on Identification and Reconstruction
3.4. Validation on Load Identification
4. Fatigue Assessment
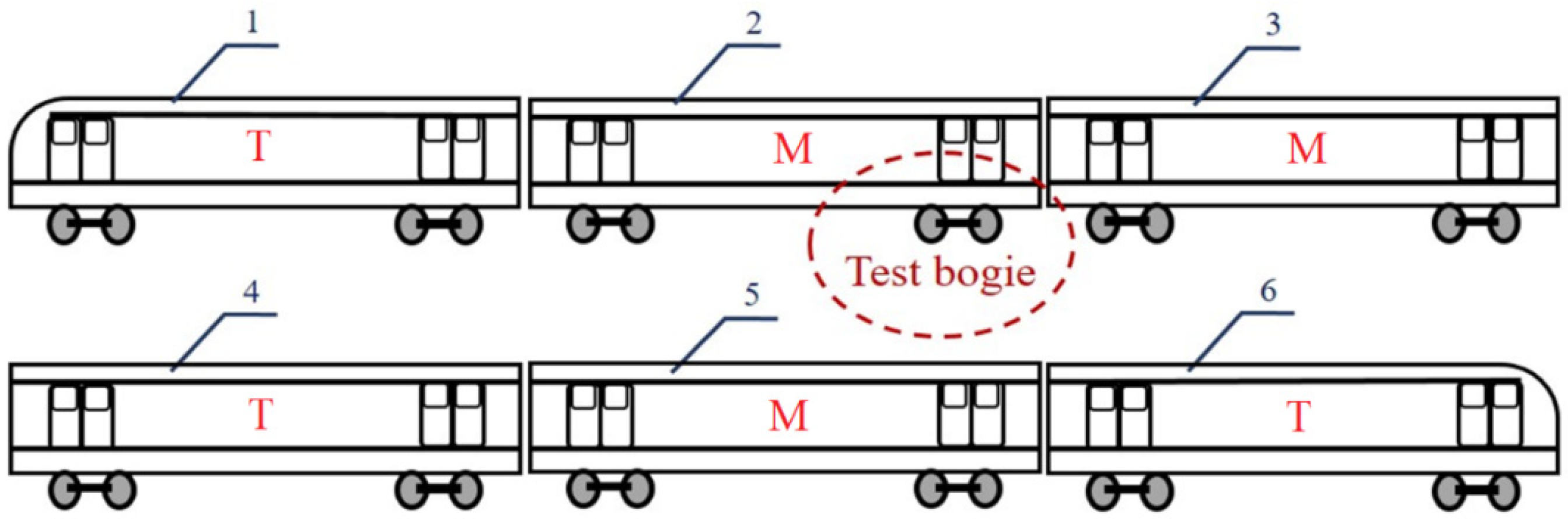
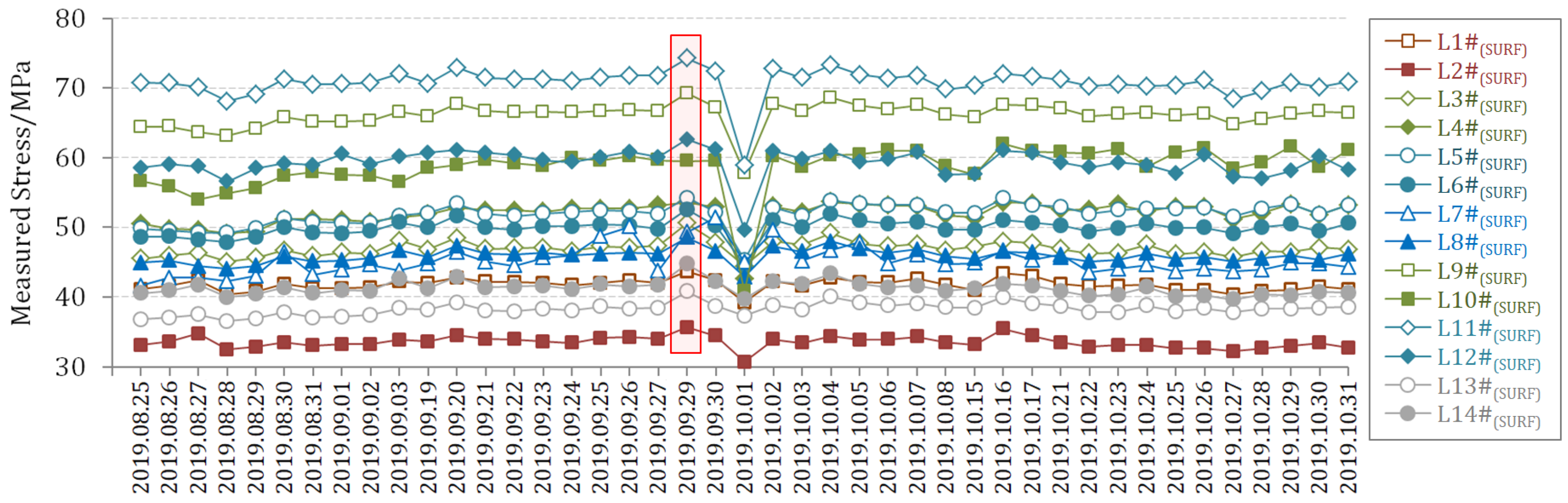
4.1. Experiment Overview
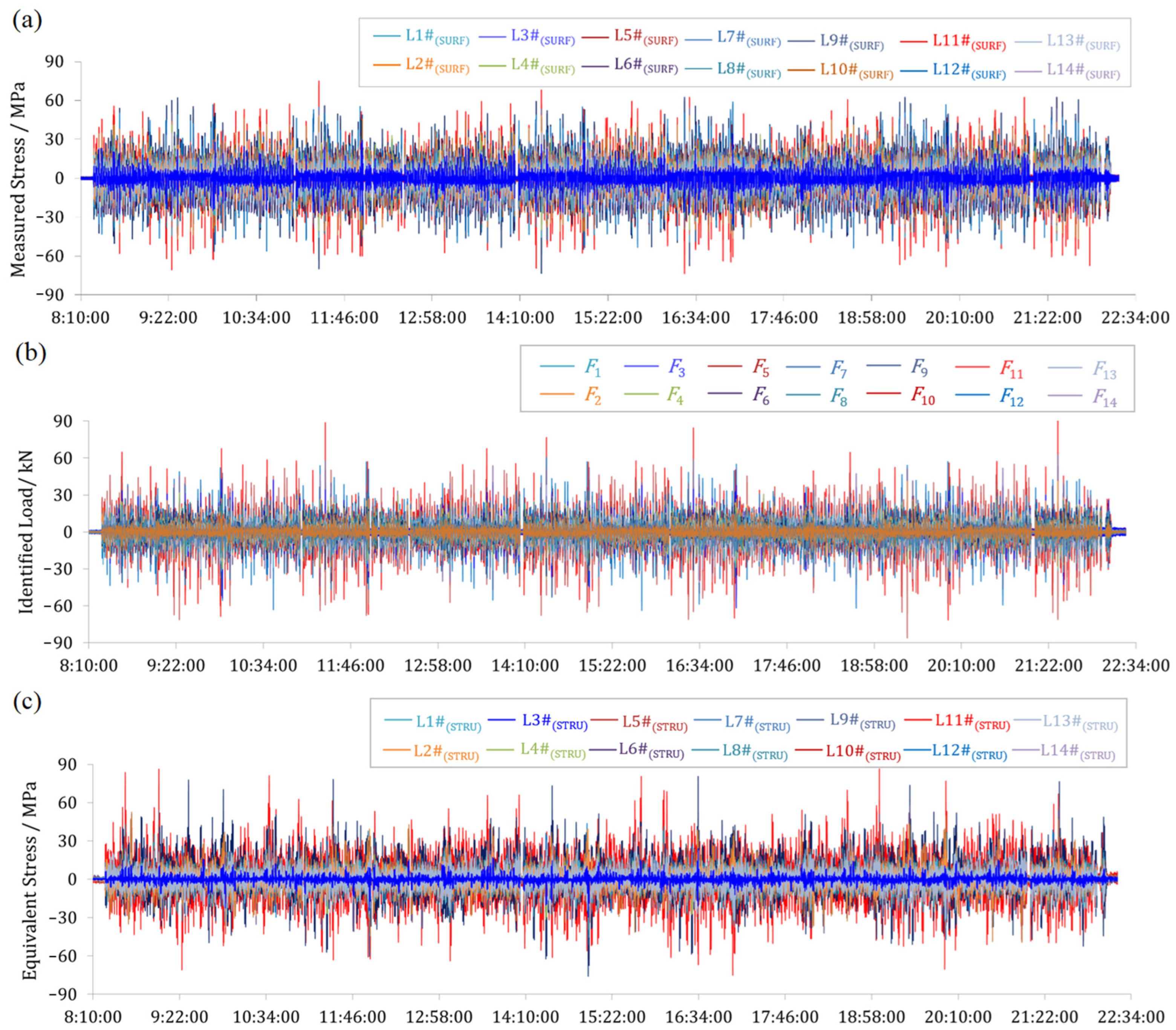
4.2. Results and Discussion
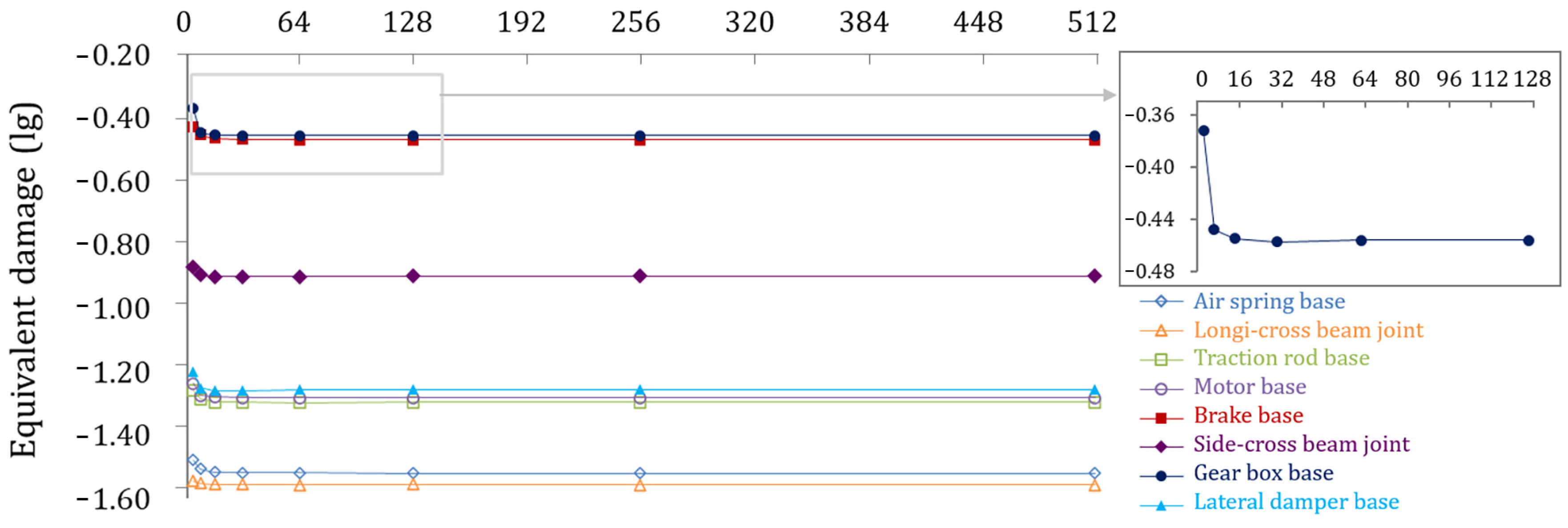
4.3. Fatigue Damage Evaluation
5. Conclusions
- (1)
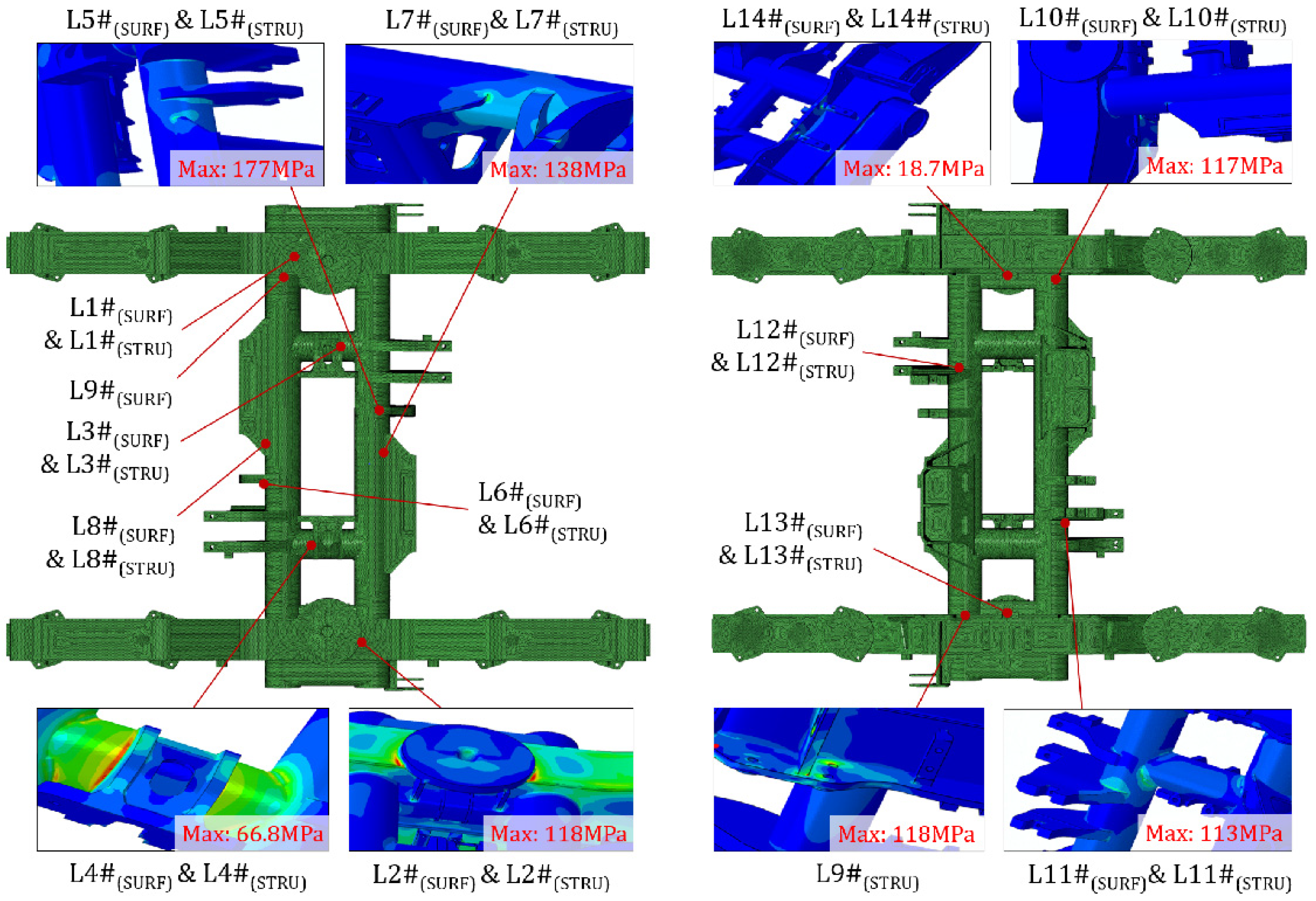
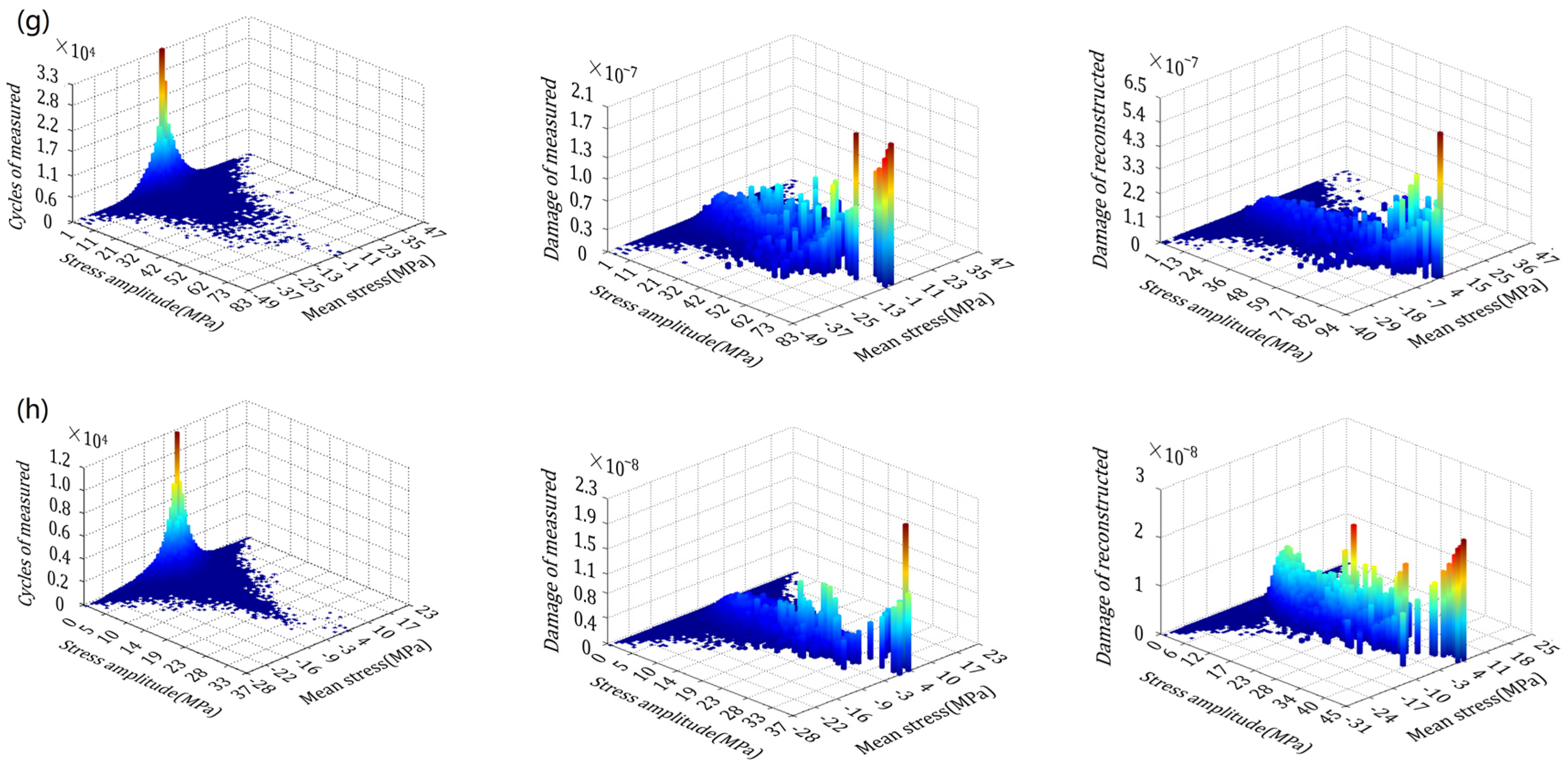
- A structural stress reconstruction model is derived for the metro bogie frame. The locations of the maximum stress under different load cases are obtained, and reasonable positions are selected to arrange the measurement points with assistance from the FEA. Furthermore, the stress distribution of the frame is reconstructed using the calculated transfer relationship between capture points and large stress points. The results reveal that the stresses after reconstruction are generally larger than those before.
- (2)
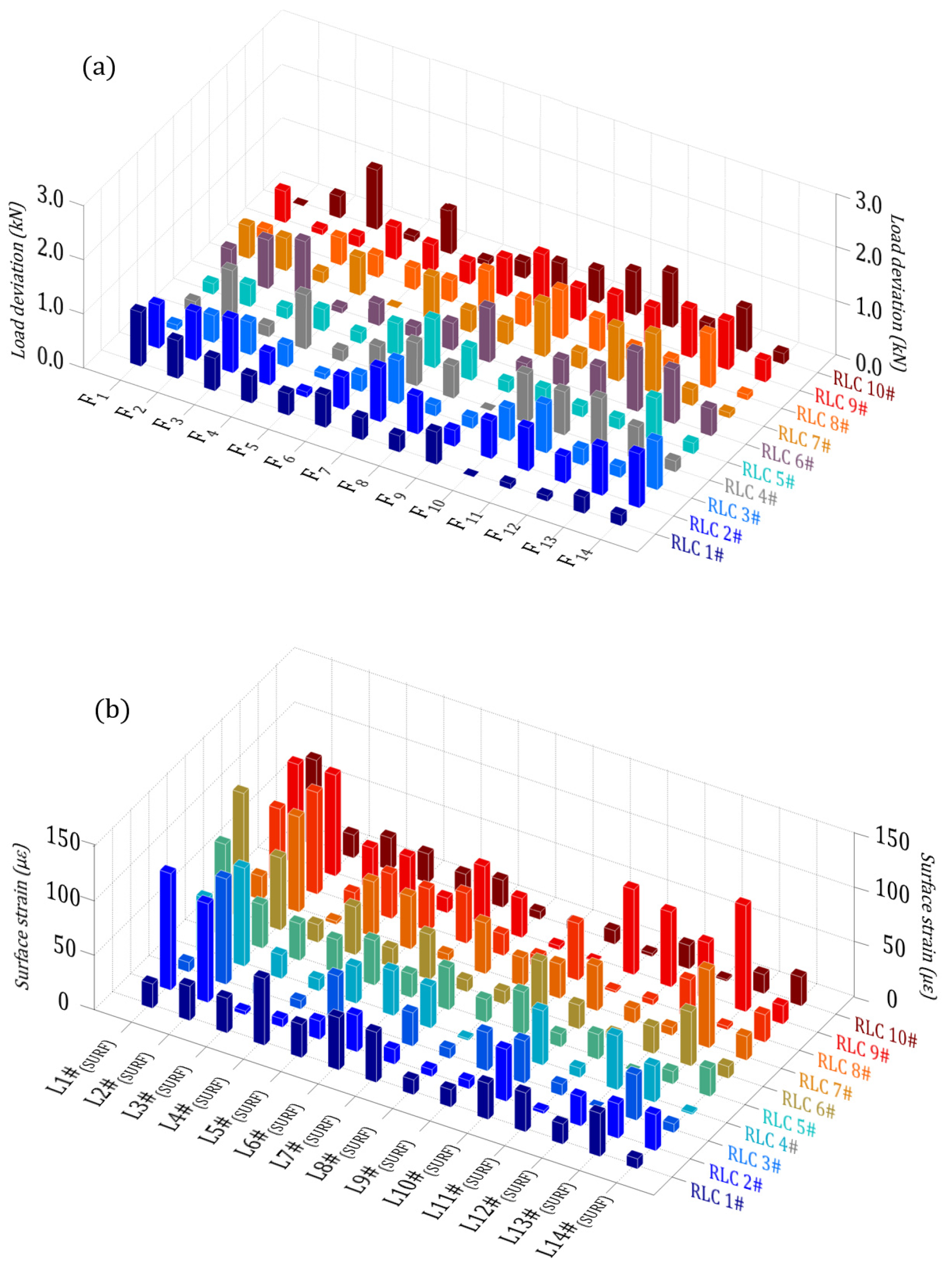
- In light of the relationship between external load and stress in the FE simulation, a load identification model is presented, and the theoretical model is verified by FE simulation under a random load, wherein the maximum deviation does not exceed 1.1 kN, and the minimum deviation is 0 kN. The validation results indicate that there is good agreement between the theoretical model and the numerical simulation.
- (3)
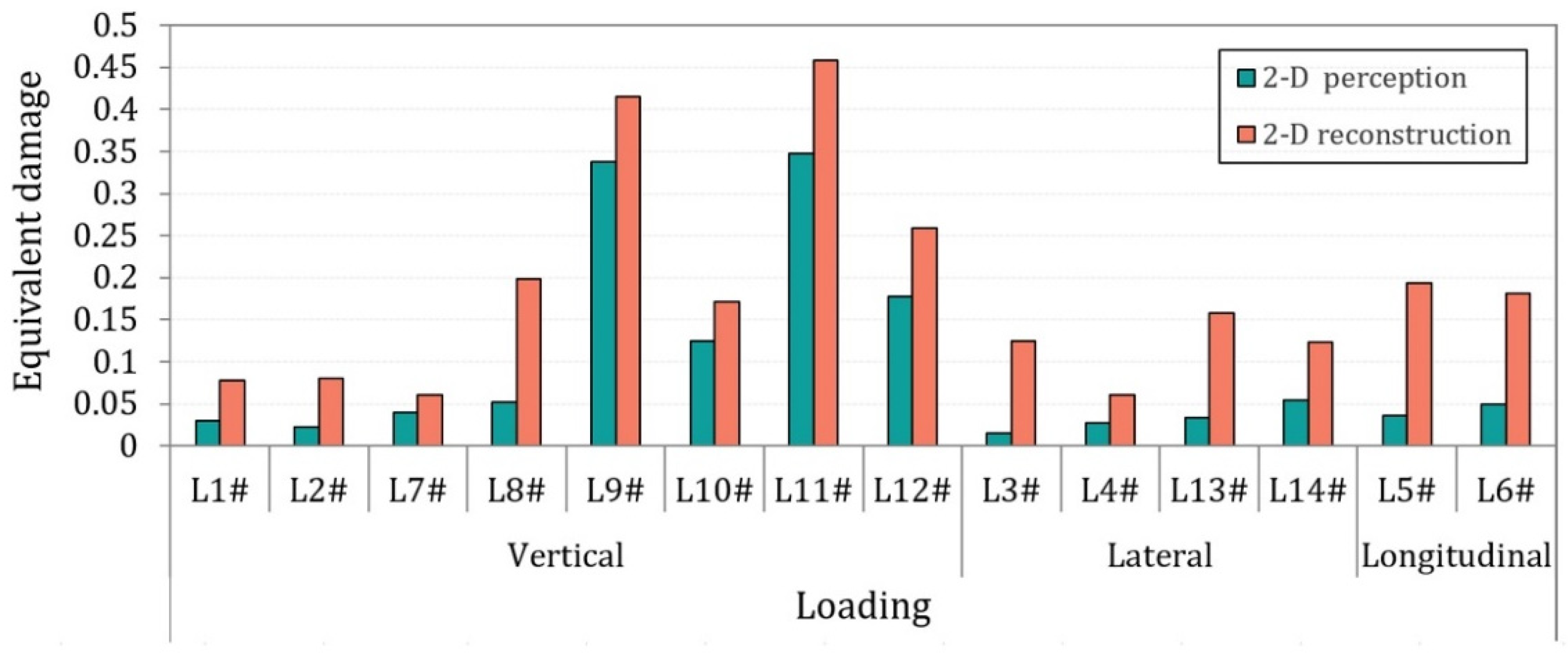
- Time-history data of the motor car bogie frame was obtained through a vehicle test, and the results show that the stress extreme value after reconstruction is greater than the capture. The maximum equivalent damage of reconstructed and captured is 0.46 and 0.35, respectively. The equivalent damage at different load directions is in descending order of vertical load, longitudinal load and lateral load. Hence, much focus should be on the role of vertical loads and the joint action locations of multiple loads.
- (4)
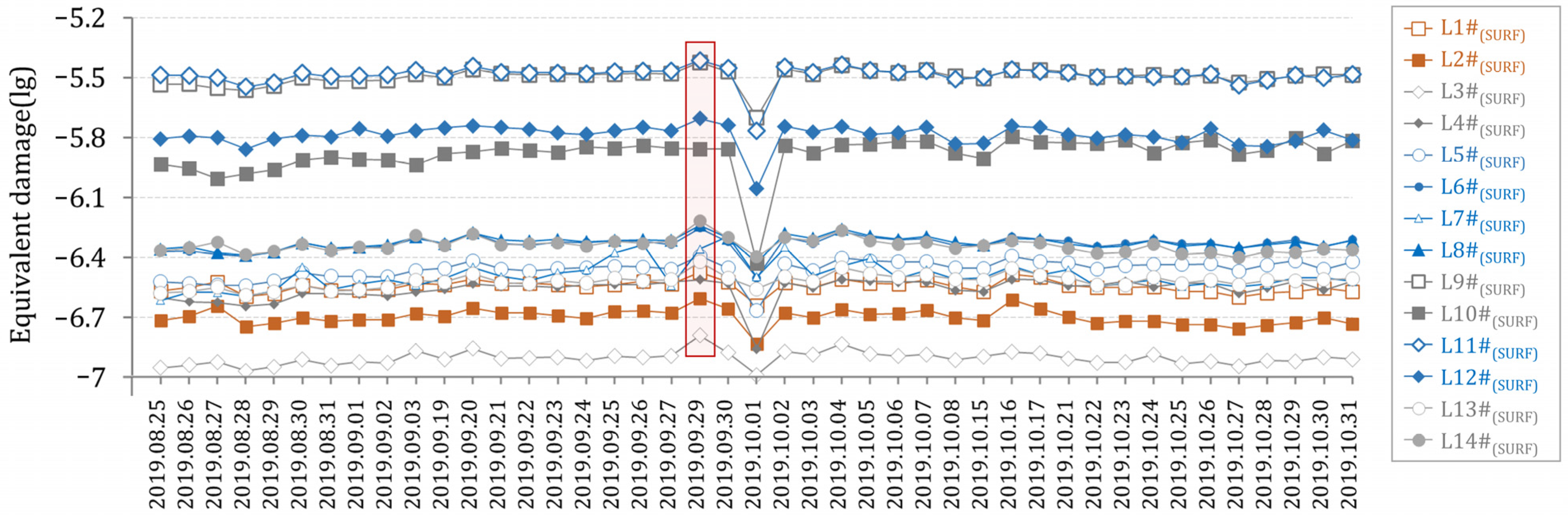
- Equivalent damage is evaluated over two assessment methods in the full life cycle, one using maximum daily dynamic stress damage and another using maximum cumulative damage during the whole test period. Both damage assessment methods are satisfied with the design life of the bogie frame, revealing that the current operating condition does not lead to fatigue damage to the frame.
6. Patents
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Żak, J.; Kurek, D. Multiple Criteria Evaluation of Trams Based on Customers’ Specifications (Expectations) in Selected Countries. Transp. Res. Procedia 2020, 47, 696–703. [Google Scholar] [CrossRef]
- Jing, L.; Liu, K.; Ren, M. The Transient Response of Car Body and Side Windows for High-Speed Trains Passing by Each Other in a Tunnel. Compos. Part B Eng. 2019, 166, 284–297. [Google Scholar] [CrossRef]
- Cubillo, A.; Vermeulen, J.; Rodriguez de la Peña, M.; Collantes Casanova, I.; Perinpanayagam, S. Physics-Based Integrated Vehicle Health Management System for Predicting the Remaining Useful Life of an Aircraft Planetary Gear Transmission. Int. J. Struct. Integr. 2017, 8, 484–495. [Google Scholar] [CrossRef]
- Wang, G.; Wu, C.; Li, S. Effect of Vibration from Highway Vehicle Load on Adjacent Buildings and Its Assessment. IOP Conf. Ser. Earth Environ. Sci. 2019, 267, 052048. [Google Scholar] [CrossRef]
- Ferreiro, S.; Arnaiz, A.; Sierra, B.; Irigoien, I. Application of Bayesian Networks in Prognostics for a New Integrated Vehicle Health Management Concept. Expert Syst. Appl. 2012, 39, 6402–6418. [Google Scholar] [CrossRef]
- Deng, S.J.; Luan, J.Y.; Tang, L.W.; Wang, W. Research of Vehicle Health Management System Framework Design Based on Teds Sensor. In Proceedings of the 2012 International Conference on Quality, Reliability, Risk, Maintenance, and Safety Engineering, Chengdu, China, 15–18 June 2012; pp. 772–775. [Google Scholar] [CrossRef]
- Mizrak, C.; Esen, İ. The Optimisation of Rail Vehicle Bogie Parameters with the Fuzzy Logic Method in Order to Improve Passenger Comfort during Passage over Bridges. Int. J. Heavy Veh. Syst. 2017, 24, 113–139. [Google Scholar] [CrossRef]
- Jin, M.; Kosova, G.; Cenedese, M.; Chen, W.; Singh, A.; Jana, D.; Brake, M.R.W.; Schwingshackl, C.W.; Nagarajaiah, S.; Moore, K.J.; et al. Measurement and Identification of the Nonlinear Dynamics of a Jointed Structure Using Full-Field Data: Part II-Nonlinear System Identification. Mech. Syst. Signal Process. 2022, 166, 108402. [Google Scholar] [CrossRef]
- Deng, L.; Zou, S.; Wang, W.; Kong, X. Fatigue Performance Evaluation for Composite Osd Using Uhpc under Dynamic Vehicle Loading. Eng. Struct. 2021, 232, 111831. [Google Scholar] [CrossRef]
- Xiu, R.; Spiryagin, M.; Wu, Q.; Yang, S.; Liu, Y. Fatigue Life Assessment Methods for Railway Vehicle Bogie Frames. Eng. Fail. Anal. 2020, 116, 104725. [Google Scholar] [CrossRef]
- Wang, H.; Liu, W.; Shang, Y. Fatigue Strength Analysis of Domestic Y25 Bogie Welded Frame Based on Hot Spot Stress. China Railw. Sci. 2013, 34, 66–70. [Google Scholar]
- Lan, Q.; Song, F. Fatigue Simulation of Railway Car Bogie Frame Based on Multi-Body Dynamics and Finite Element Analysis. J. Phys. Conf. Ser. 2021, 1885, 042057. [Google Scholar] [CrossRef]
- Di, J.; Ruan, X.; Zhou, X.; Wang, J.; Peng, X. Fatigue Assessment of Orthotropic Steel Bridge Decks Based on Strain Monitoring Data. Eng. Struct. 2021, 228, 111437. [Google Scholar] [CrossRef]
- Liang, Z.; Chai, J.; Na, S.; Ma, T.; Tang, Y. Validity Analysis of Bridge Health Monitoring Data Based on Deep Learning. J. Chongqing Jiaotong Univ. 2021, 40, 78–83. [Google Scholar]
- Wang, C.; Meng, G.; Yuan, L.; Liu, J. Numerical Simulation Analysis of Fatigue Life of a New High Speed Bus Frame. China Railw. Sci. 2001, 03, 94–98. [Google Scholar]
- Yaohui, L. Study on Fatigue Reliability of Welded Frame of Railway Passenger Car Bogie. Ph.D. Thesis, Southwest Jiaotong University, Chengdu, China, 2011. [Google Scholar]
- Bingrong, M. Fatigue Simulation of Locomotive Body Structure Based on Multi-Body Dynamics and Finite Element Method. Ph.D. Thesis, Southwest Jiaotong University, Chengdu, China, 2007. [Google Scholar]
- Zeng, L.; Zhao, J.; Meng, Y. Vibrational Fatigue Failure Prediction of a Brake Caliper Used for Railway Vehicles Based on Frequency Domain Method. J. Phys. Conf. Ser. 2021, 1948, 012091. [Google Scholar] [CrossRef]
- Zhou, X.; Zhang, X. Thoughts on the Development of Bridge Technology in China. Engineering 2019, 5, 1120–1130. [Google Scholar] [CrossRef]
- Spiroiu, M.A. Reliability Model of Freight Bogie Damper Based on Real Field Data. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1037, 012056. [Google Scholar] [CrossRef]
- Zhang, C.; Fu, Y.; Li, Y.; Li, J. Distributed Dynamic Load Identification of Aircraft Skin Based on Strain Modal Method. Equip. Environ. Eng. 2020, 17, 113–117. [Google Scholar] [CrossRef]
- Coules, H.E.; Smith, D.J.; Abburi Venkata, K.; Truman, C.E. A Method for Reconstruction of Residual Stress Fields from Measurements Made in an Incompatible Region. Int. J. Solids Struct. 2014, 51, 1980–1990. [Google Scholar] [CrossRef]
- Lampone, L.W. A Positive Polynomial Expansion Problem in Minimum Variance Smoothing. SIAM J. Math. Anal. 1978, 9, 500–514. [Google Scholar] [CrossRef]
- Nakamura, T. Local Stress-Field Reconstruction around Holes in a Plate Using Strain Monitoring Data and Stress Function. J. Appl. Mech. 2018, 86, 031005. [Google Scholar] [CrossRef]
- Wang, B.J.; Li, Q.; Ren, Z.S.; Sun, S.G. Improving the Fatigue Reliability of Metro Vehicle Bogie Frame Based on Load Spectrum. Int. J. Fatigue 2020, 132, 105389. [Google Scholar] [CrossRef]
- Tae, K.H. Fatigue Prediction of Spot Welded Joints Using Equivalent Structural Stress. Mater. Des. 2005, 28, 837–843. [Google Scholar]
- HG/T 20580-2011; Specification of Design Base for Steel Chemical Vessels. China Standard Press: Beijing, China, 2011; p. 41.
- TB/T 2368-2005; Test Method for Strength of Power Bogie Frames. China Standard Press: Beijing, China, 2005; p. 18.
- Chandrasekhar, S.; Liu, X. Chapter 3-Advances in Tb/S Superchannels. In Optical Fiber Telecommunications, 6th ed.; Kaminow, I.P., Li, T., Willner, A.E., Eds.; Academic Press: Boston, MA, USA, 2013; pp. 83–119. [Google Scholar]
- Xie, X.Y.; Jin, G.L.; Wang, R.L. Evaluation of Bogie Frame Safety of Shanghai Metro Line 1 by 3d Fem Analysis. AIP Conf. Proc. 2010, 1233, 1140. [Google Scholar]




| Component | Material | Elastic Modulus E (GPa) | Poisson’s Ratio υ | Density ρ (g cm−3) | Yield Stress σys (MPa) | Fatigue Limit σlim (MPa) |
|---|---|---|---|---|---|---|
| Steel plate | Q345 | 206 | 0.3 | 7.85 | 345 | 110 |
| Cross beam | SMA490BW | 206 | 0.3 | 7.85 | 355 | 110 |
| Material | Tensile Strength (MPa) | Yield Strength (MPa) | Elongation (%) |
|---|---|---|---|
| J507 | 490 | 400 | 20 |
| Load Case | Load [28] (Ministry of Railways 2005) Fi(max) (kN) | Load Position | Load Type and Direction |
|---|---|---|---|
| LC1# | −100 | Right air spring base | Vertical load (-Z) |
| LC2# | −100 | Left air spring base | Vertical load (-Z) |
| LC3# | −68.67 | Right lateral stop base | Lateral load (-Y) |
| LC4# | 68.67 | Left lateral stop base | Lateral load (Y) |
| LC5# | 82.4 | Front traction rod base | Longitudinal load (X) |
| LC6# | 82.4 | Rear traction rod base | Longitudinal load (X) |
| LC7# | −28.5 | Front motor base | Vertical load (-Z) |
| LC8# | −28.5 | Rear motor base | Vertical load (-Z) |
| LC9# | 10 | Left braking base | Torsional load (Z) |
| LC10# | 10 | Left shaft neck center | Torsional load (Z) |
| LC11# | −50 | Front gear box base | Vertical load (-Z) |
| LC12# | 50 | Rear gear box base | Vertical load (Z) |
| LC13# | 3 | Left lateral damper base | Lateral load (Y) |
| LC14# | 3 | Right lateral damper base | Lateral load (Y) |
| Location Labels | Location Descriptions |
|---|---|
| L1#(SURF), L1#(STRU) || L2#(SURF), L2#(STRU) | Left || Right air spring base welds |
| L3#(SURF), L3#(STRU) || L4#(SURF), L4#(STRU) | Left || Right lateral stop base welds |
| L5#(SURF), L5#(STRU) || L6#(SURF), L6#(STRU) | Front || Rear traction rod base welds |
| L7#(SURF), L7#(STRU) || L8#(SURF), L8#(STRU) | Front || Rear motor base welds |
| L9#(SURF) || L10#(SURF), L10#(STRU) | Left || Right side-cross beam joint welds |
| L9#(STRU) | Left brake base welds |
| L11#(SURF), L11#(STRU) || L12#(SURF), L12#(STRU) | Front || Rear gear box base welds |
| L13#(SURF), L13#(STRU) || L14#(SURF), L14#(STRU) | Left || Right lateral damper base welds |
| Random Load Case | Load Types | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| F1 | F2 | F3 | F4 | F5 | F6 | F7 | F8 | F9 | F10 | F11 | F12 | F13 | F14 | ||
| RLC1# | GV | −20.6 | 30.7 | −65.7 | 44.8 | 45.4 | 53.3 | 15.6 | 24.3 | 9.9 | 5.8 | −36.7 | 19.7 | 0.5 | 0.5 |
| ID | −19.6 | 31.4 | −65.1 | 45.3 | 45.8 | 53.9 | 16.0 | 24.6 | 10.5 | 5.8 | −36.6 | 19.8 | 0.8 | 0.7 | |
| RLC2# | GV | 93.0 | 92.9 | −8.6 | −9.7 | 21.6 | 50.6 | −12.8 | 6.3 | 7.6 | −7.4 | 10.8 | −27.8 | 0.3 | −1.3 |
| ID | 93.8 | 93.8 | −7.6 | −9.1 | 21.7 | 51.2 | −11.8 | 7.0 | 7.9 | −6.7 | 11.6 | −27.3 | 1.2 | −0.3 | |
| RLC3# | GV | 11.3 | −95.7 | −14.1 | −10.1 | −57.3 | −8.5 | 2.9 | −28.1 | −8.0 | −5.2 | 0.8 | 0.0 | 2.1 | 2.0 |
| ID | 11.4 | −95.2 | −13.5 | −9.7 | −57.2 | −8.2 | 3.7 | −27.9 | −7.8 | −4.6 | 1.7 | 0.3 | 2.3 | 2.9 | |
| RLC4# | GV | 43.6 | 92.6 | −64.8 | −23.9 | 45.8 | 57.6 | 0.5 | 13.5 | −1.5 | −3.3 | 20.9 | 49.7 | 2.6 | −1.9 |
| ID | 43.8 | 93.6 | −64.6 | −22.9 | 46.0 | 58.1 | 1.3 | 14.1 | −1.5 | −2.4 | 21.7 | 50.6 | 3.2 | −1.7 | |
| RLC5# | GV | 75.9 | −35.1 | 57.1 | −22.3 | −72.2 | 27.1 | −18.6 | −8.0 | −0.6 | 3.7 | −11.1 | −4.9 | −0.3 | 2.5 |
| ID | 76.1 | −34.7 | 57.3 | −21.9 | −72.0 | 27.7 | −17.7 | −7.4 | −0.4 | 4.0 | −10.9 | −4.7 | 0.5 | 2.7 | |
| RLC6# | GV | −99.3 | −70.0 | −19.7 | −43.3 | 31.8 | −49.5 | 18.3 | −9.6 | −5.5 | −1.4 | −11.1 | −27.2 | −1.0 | −0.8 |
| ID | −98.8 | −69.1 | −18.6 | −43.2 | 32.2 | −49.3 | 18.8 | −8.6 | −5.3 | −0.9 | −10.5 | −26.1 | 0.0 | −0.3 | |
| RLC7# | GV | −23.0 | 82.1 | −9.8 | 44.5 | 71.9 | 11.0 | 10.0 | 0.9 | 6.4 | 3.3 | −14.0 | 5.0 | 2.3 | 1.6 |
| ID | −22.4 | 82.7 | −9.6 | 45.2 | 71.9 | 11.8 | 10.4 | 1.3 | 7.4 | 3.6 | −13.0 | 6.1 | 2.6 | 1.7 | |
| RLC8# | GV | 60.9 | 90.9 | −39.6 | −39.9 | 52.3 | −47.4 | −6.0 | 15.5 | −1.4 | 9.9 | −5.5 | 40.0 | 2.8 | 2.8 |
| ID | 61.1 | 90.9 | −39.1 | −39.5 | 52.7 | −47.0 | −5.2 | 16.0 | −0.5 | 10.5 | −5.2 | 40.3 | 3.8 | 2.9 | |
| RLC9# | GV | 77.5 | 93.5 | 48.6 | 39.1 | 0.8 | 67.1 | 4.5 | −4.6 | −6.4 | −8.8 | −48.9 | 47.2 | 1.5 | 1.8 |
| ID | 78.1 | 93.6 | 48.8 | 39.7 | 1.3 | 67.5 | 5.2 | −3.6 | −5.8 | −8.1 | −48.2 | 48.1 | 2.4 | 2.2 | |
| RLC10# | GV | −69.3 | −18.2 | −67.4 | −37.0 | 30.9 | 37.3 | −3.7 | −7.7 | 8.6 | 4.1 | 19.9 | −7.0 | 0.2 | −0.2 |
| ID | −69.3 | −17.8 | −66.3 | −36.9 | 31.7 | 37.4 | −3.4 | −7.2 | 9.2 | 4.9 | 20.9 | −6.7 | 1.0 | 0.0 | |
| Structure | S-N Curve Parameter | Limit Cycles (×104) | Design Mileage (km) | Running Mileage (km) | |
|---|---|---|---|---|---|
| m | c | ||||
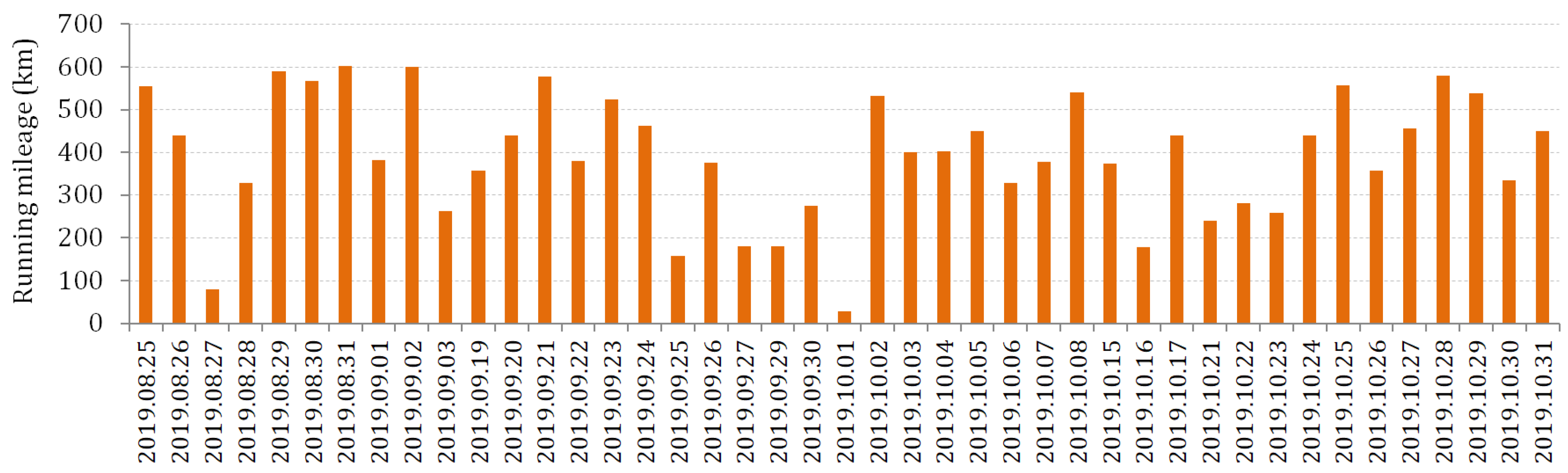
| Base metal | 5 | 4.484 × 1017 | 1000 | 396 × 104 | 16,854 |
| Welding joints | 3.5 | 2.7919 × 1013 | 200 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, W.; Zhang, G.; Wang, H.; Peng, C.; Liu, X.; Xiao, H.; Liang, X. Experimental Fatigue Evaluation of Bogie Frames on Metro Trains. Machines 2022, 10, 1003. https://doi.org/10.3390/machines10111003
Zhou W, Zhang G, Wang H, Peng C, Liu X, Xiao H, Liang X. Experimental Fatigue Evaluation of Bogie Frames on Metro Trains. Machines. 2022; 10(11):1003. https://doi.org/10.3390/machines10111003
Chicago/Turabian StyleZhou, Wei, Gangli Zhang, Hui Wang, Chang Peng, Xiang Liu, Heting Xiao, and Xifeng Liang. 2022. "Experimental Fatigue Evaluation of Bogie Frames on Metro Trains" Machines 10, no. 11: 1003. https://doi.org/10.3390/machines10111003
APA StyleZhou, W., Zhang, G., Wang, H., Peng, C., Liu, X., Xiao, H., & Liang, X. (2022). Experimental Fatigue Evaluation of Bogie Frames on Metro Trains. Machines, 10(11), 1003. https://doi.org/10.3390/machines10111003







