Selection of Constitutive Material Model for the Finite Element Simulation of Pressure-Assisted Single-Point Incremental Forming
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Work
2.2. FE Modelling Work
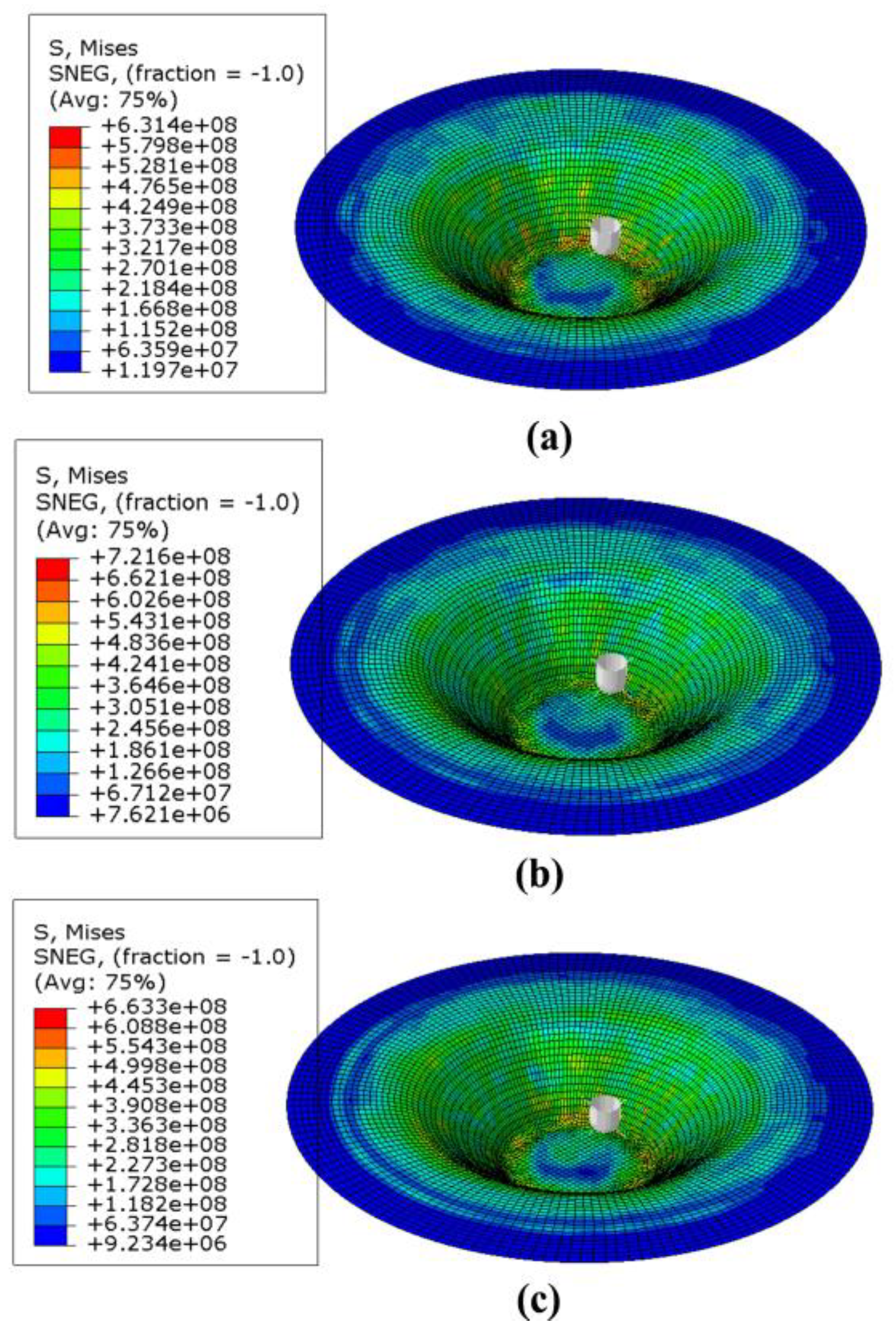
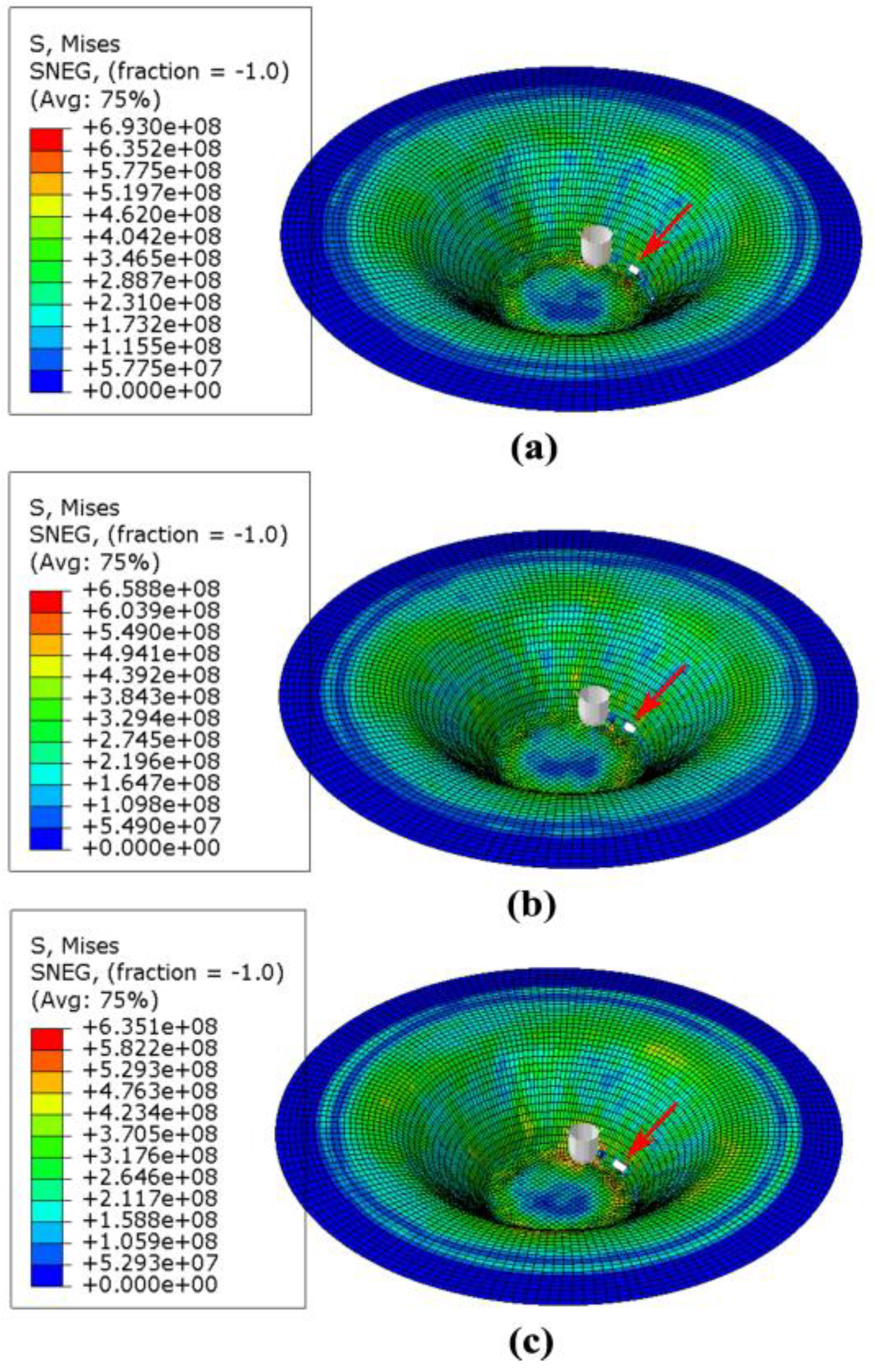
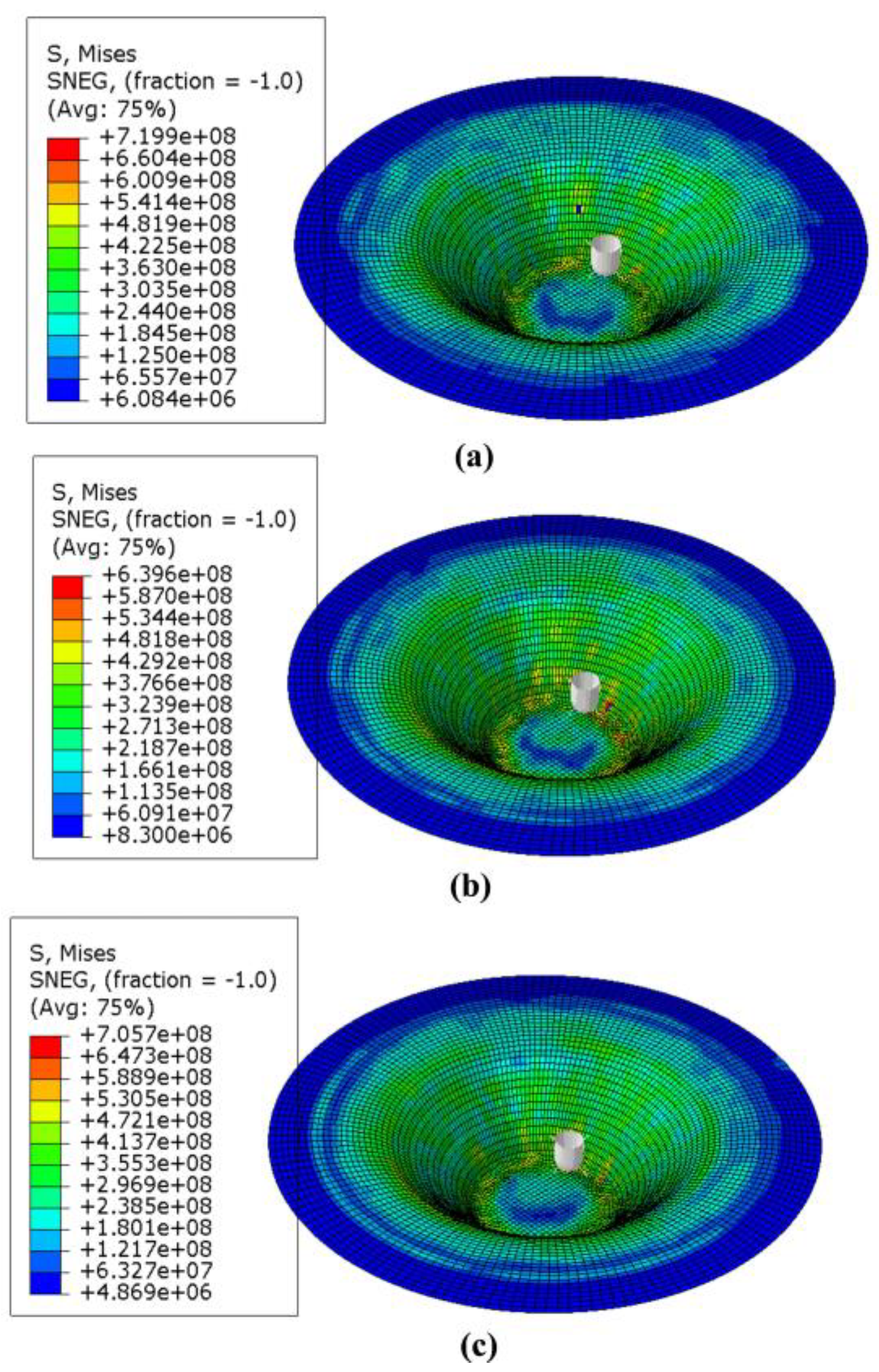
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Martins, P.A.F.; Bay, N.; Skjoedt, M.; Silva, M.B. Theory of Single Point Incremental Forming. CIRP Ann.-Manuf. Technol. 2008, 57, 247–252. [Google Scholar] [CrossRef]
- Abdelhafeez, A.M.; Nemat-Alla, M.M.; El-Sebaie, M.G. FEA of Electromagnetic Forming Using a New Coupling Algorithm. Int. J. Appl. Electromagn. Mech. 2013, 42, 157–169. [Google Scholar] [CrossRef]
- Abdelhafeez, A.M.; Nemat-Alla, M.M.; El-Sebaie, M.G. Finite Element Analysis of Electromagnetic Bulging of Sheet Metals. Int. J. Sci. Eng. Res. 2012, 3, 180–187. [Google Scholar]
- Abdelhafeez, A.M.; Nemat-Alla, M.M.; El-Sebaie, M.G. FEA of Electromagnetic Forming Using a New Coupling Algorithm: Effects of Strain Hardening Properties and Anisotropy. Int. J. Sci. Eng. Res. 2014, 5, 1069–1075. [Google Scholar]
- Emmens, W.C.; Sebastiani, G.; van den Boogaard, A.H. The Technology of Incremental Sheet Forming—A Brief Review of the History. J. Mater. Processing Technol. 2010, 210, 981–997. [Google Scholar] [CrossRef]
- Peter, I.; Fracchia, E.; Canale, I.; Maiorano, R. Incremental Sheet Forming for Prototyping Automotive Modules. Procedia Manuf. 2019, 32, 50–58. [Google Scholar] [CrossRef]
- Duflou, J.R.; Habraken, A.-M.; Cao, J.; Malhotra, R.; Bambach, M.; Adams, D.; Vanhove, H.; Mohammadi, A.; Jeswiet, J. Single Point Incremental Forming: State-of-the-Art and Prospects. Int. J. Mater. 2018, 11, 743–773. [Google Scholar] [CrossRef]
- Scheffler, S.; Pierer, A.; Scholz, P.; Melzer, S.; Weise, D.; Rambousek, Z. Incremental Sheet Metal Forming on the Example of Car Exterior Skin Parts. Procedia Manuf. 2019, 29, 105–111. [Google Scholar] [CrossRef]
- Behera, A.K.; de Sousa, R.A.; Ingarao, G.; Oleksik, V. Single Point Incremental Forming: An Assessment of the Progress and Technology Trends from 2005 to 2015. J. Manuf. Processes 2017, 27, 37–62. [Google Scholar] [CrossRef]
- Kumar, A.; Gulati, V.; Kumar, P.; Singh, V.; Kumar, B.; Singh, H. Parametric Effects on Formability of AA2024-O Aluminum Alloy Sheets in Single Point Incremental Forming. J. Mater. Res. Technol. 2019, 8, 1461–1469. [Google Scholar] [CrossRef]
- McAnulty, T.; Jeswiet, J.; Doolan, M. Formability in Single Point Incremental Forming: A Comparative Analysis of the State of the Art. CIRP J. Manuf. Sci. Technol. 2017, 16, 43–54. [Google Scholar] [CrossRef]
- Kim, T.J.; Yang, D.Y. Improvement of Formability for the Incremental Sheet Metal Forming Process. Int. J. Mech. Sci. 2000, 42, 1271–1286. [Google Scholar] [CrossRef]
- Ambrogio, G.; De Napoli, L.; Filice, L.; Gagliardi, F.; Muzzupappa, M. Application of Incremental Forming Process for High Customised Medical Product Manufacturing. J. Mater. Processing Technol. 2005, 162–163, 156–162. [Google Scholar] [CrossRef]
- Cheng, Z.; Li, Y.; Xu, C.; Liu, Y.; Ghafoor, S.; Li, F. Incremental Sheet Forming towards Biomedical Implants: A Review. J. Mater. Res. Technol. 2020, 9, 7225–7251. [Google Scholar] [CrossRef]
- Habibi, N.; Ramazani, A.; Sundararaghavan, V.; Prahl, U. Failure Predictions of DP600 Steel Sheets Using Various Uncoupled Fracture Criteria. Eng. Fract. Mech. 2018, 190, 367–381. [Google Scholar] [CrossRef]
- Ham, M.; Jeswiet, J. Single Point Incremental Forming and the Forming Criteria for AA3003. CIRP Ann. 2006, 55, 241–244. [Google Scholar] [CrossRef]
- Afonso, D.; de Sousa, R.A.; Torcato, R. Incremental Forming of Tunnel Type Parts. Procedia Eng. 2017, 183, 137–142. [Google Scholar] [CrossRef]
- Moayedfar, M.; Leman, Z.; bin Baharudin, B.T.H.T. Incremental Sheet Forming (ISF) of AISI 316 Stainless Steel Sheet Using CNC Milling Machine. AMR 2014, 939, 322–327. [Google Scholar] [CrossRef]
- Manco, G.L.; Ambrogio, G. Influence of Thickness on Formability in 6082-T6. Int. J. Mater. 2010, 3, 983–986. [Google Scholar] [CrossRef]
- Mugendiran, V.; Gnanavelbabu, A. Comparison of FLD and Thickness Distribution on AA5052 Aluminium Alloy Formed Parts by Incremental Forming Process. Procedia Eng. 2014, 97, 1983–1990. [Google Scholar] [CrossRef]
- Pereira Bastos, R.N.; Alves de Sousa, R.J.; Fernandes Ferreira, J.A. Enhancing Time Efficiency on Single Point Incremental Forming Processes. Int. J. Mater. 2016, 9, 653–662. [Google Scholar] [CrossRef]
- Azevedo, N.G.; Farias, J.S.; Bastos, R.P.; Teixeira, P.; Davim, J.P.; Alves de Sousa, R.J. Lubrication Aspects during Single Point Incremental Forming for Steel and Aluminum Materials. Int. J. Precis. Eng. Manuf. 2015, 16, 589–595. [Google Scholar] [CrossRef]
- Ham, M.; Jeswiet, J. Dimensional Accuracy of Single Point Incremental Forming. Int. J. Mater. 2008, 1, 1171–1174. [Google Scholar] [CrossRef]
- Zhu, H.; Liu, L. Research the CNC Incremental Forming of Straight-Wall Parts Based on a Virtual Auxiliary Body. J. Mater. Processing Technol. 2021, 288, 116841. [Google Scholar] [CrossRef]
- Zhu, H.; Wang, Y.; Kang, J. Research on Combinatorial Optimization of Multidirectional Sheet Postures for Forming Thickness Uniformity. J. Mech. Sci. Technol. 2020, 34, 4251–4261. [Google Scholar] [CrossRef]
- Zhan, X.; Wang, Z.; Li, M.; Hu, Q.; Chen, J. Investigations on Failure-to-Fracture Mechanism and Prediction of Forming Limit for Aluminum Alloy Incremental Forming Process. J. Mater. Processing Technol. 2020, 282, 116687. [Google Scholar] [CrossRef]
- Mirnia, M.J.; Vahdani, M.; Shamsari, M. Ductile Damage and Deformation Mechanics in Multistage Single Point Incremental Forming. Int. J. Mech. Sci. 2018, 136, 396–412. [Google Scholar] [CrossRef]
- Chang, Z.; Chen, J. Investigations on the Deformation Mechanism of a Novel Three-Sheet Incremental Forming. J. Mater. Processing Technol. 2020, 281, 116619. [Google Scholar] [CrossRef]
- Eyckens, P.; Belkassem, B.; Henrard, C.; Gu, J.; Sol, H.; Habraken, A.M.; Duflou, J.R.; Van Bael, A.; Van Houtte, P. Strain Evolution in the Single Point Incremental Forming Process: Digital Image Correlation Measurement and Finite Element Prediction. Int. J. Mater. 2011, 4, 55–71. [Google Scholar] [CrossRef]
- Henrard, C.; Bouffioux, C.; Eyckens, P.; Sol, H.; Duflou, J.R.; Van Houtte, P.; Van Bael, A.; Duchêne, L.; Habraken, A.M. Forming Forces in Single Point Incremental Forming: Prediction by Finite Element Simulations, Validation and Sensitivity. Comput. Mech. 2011, 47, 573–590. [Google Scholar] [CrossRef]
- Essa, K.; Hartley, P. An Assessment of Various Process Strategies for Improving Precision in Single Point Incremental Forming. Int. J. Mater. 2011, 4, 401–412. [Google Scholar] [CrossRef]
- Esmaeilpour, R.; Kim, H.; Park, T.; Pourboghrat, F.; Mohammed, B. Comparison of 3D Yield Functions for Finite Element Simulation of Single Point Incremental Forming (SPIF) of Aluminum 7075. Int. J. Mech. Sci. 2017, 133, 544–554. [Google Scholar] [CrossRef]
- Yan, Z.; Hassanin, H.; El-Sayed, M.A.; Eldessouky, H.M.; Djuansjah, J.; Alsaleh, A.N.; Essa, K.; Ahmadein, M. Multistage Tool Path Optimisation of Single-Point Incremental Forming Process. Materials 2021, 14, 6794. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Shu, C.; Hassan, A.; Attallah, M.M.; Essa, K. Application of Machine Learning on Tool Path Optimisation and Cooling Lubricant in Induction Heating-Assisted Single Point Incremental Sheet Forming of Ti-6Al-4V Sheets. Int. J. Adv. Manuf. Technol. 2022. [Google Scholar] [CrossRef]
- Frikha, S.; Giraud-Moreau, L.; Bouguecha, A.; Haddar, M. Simulation-Based Process Design for Asymmetric Single-Point Incremental Forming of Individual Titanium Alloy Hip Cup Prosthesis. Materials 2022, 15, 3442. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Wang, L.; Zhang, H.; Gu, Y.; Ye, Y. A Novel Algorithm for Thickness Prediction in Incremental Sheet Metal Forming. Materials 2022, 15, 1201. [Google Scholar] [CrossRef] [PubMed]
- Pepelnjak, T.; Sevšek, L.; Lužanin, O.; Milutinović, M. Finite Element Simplifications and Simulation Reliability in Single Point Incremental Forming. Materials 2022, 15, 3707. [Google Scholar] [CrossRef]
- Mulay, A.; Ben, S.; Ismail, S. Lubricant Selection and Post Forming Material Characterization in Incremental Sheet Forming. IOP Conf. Ser. Mater. Sci. Eng. 2020, 967, 012072. [Google Scholar] [CrossRef]
- Diabb, J.; Rodríguez, C.A.; Mamidi, N.; Sandoval, J.A.; Taha-Tijerina, J.; Martínez-Romero, O.; Elías-Zúñiga, A. Study of Lubrication and Wear in Single Point Incremental Sheet Forming (SPIF) Process Using Vegetable Oil Nanolubricants. Wear 2017, 376–377, 777–785. [Google Scholar] [CrossRef]
- Isik, K.; Gerstein, G.; Gutknecht, F.; Clausmeyer, T.; Nürnberger, F.; Maier, H.J.; Tekkaya, A.E. Investigations of Ductile Damage in DP600 and DC04 Deep Drawing Steel Sheets during Punching. Procedia Struct. Integr. 2016, 2, 673–680. [Google Scholar] [CrossRef][Green Version]
- Heibel, S.; Dettinger, T.; Nester, W.; Clausmeyer, T.; Tekkaya, A. Damage Mechanisms and Mechanical Properties of High-Strength Multiphase Steels. Materials 2018, 11, 761. [Google Scholar] [CrossRef] [PubMed]
- Gatea, S.; Ou, H.; Lu, B.; McCartney, G. Modelling of Ductile Fracture in Single Point Incremental Forming Using a Modified GTN Model. Eng. Fract. Mech. 2017, 186, 59–79. [Google Scholar] [CrossRef]
- Yu, H.L.; Jeong, D.Y. Application of a Stress Triaxiality Dependent Fracture Criterion in the Finite Element Analysis of Unnotched Charpy Specimens. Theor. Appl. Fract. Mech. 2010, 54, 54–62. [Google Scholar] [CrossRef]
- Marciniak, Z.; Duncan, J.L.; Hu, S.J. Mechanics of Sheet Metal Forming, 2nd ed.; Butterworth-Heinemann: Oxford, UK, 2002; ISBN 978-0-7506-5300-8. [Google Scholar]


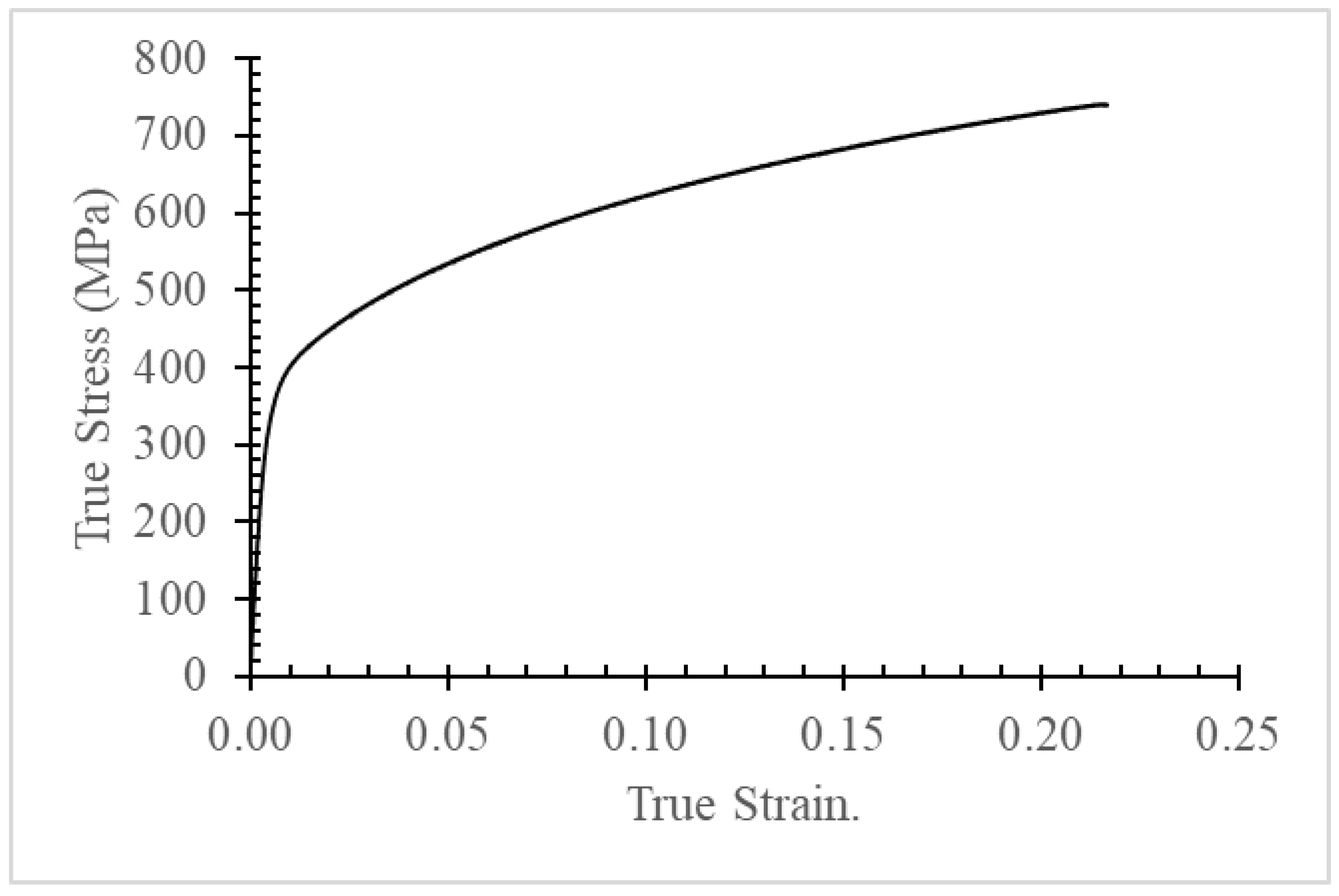


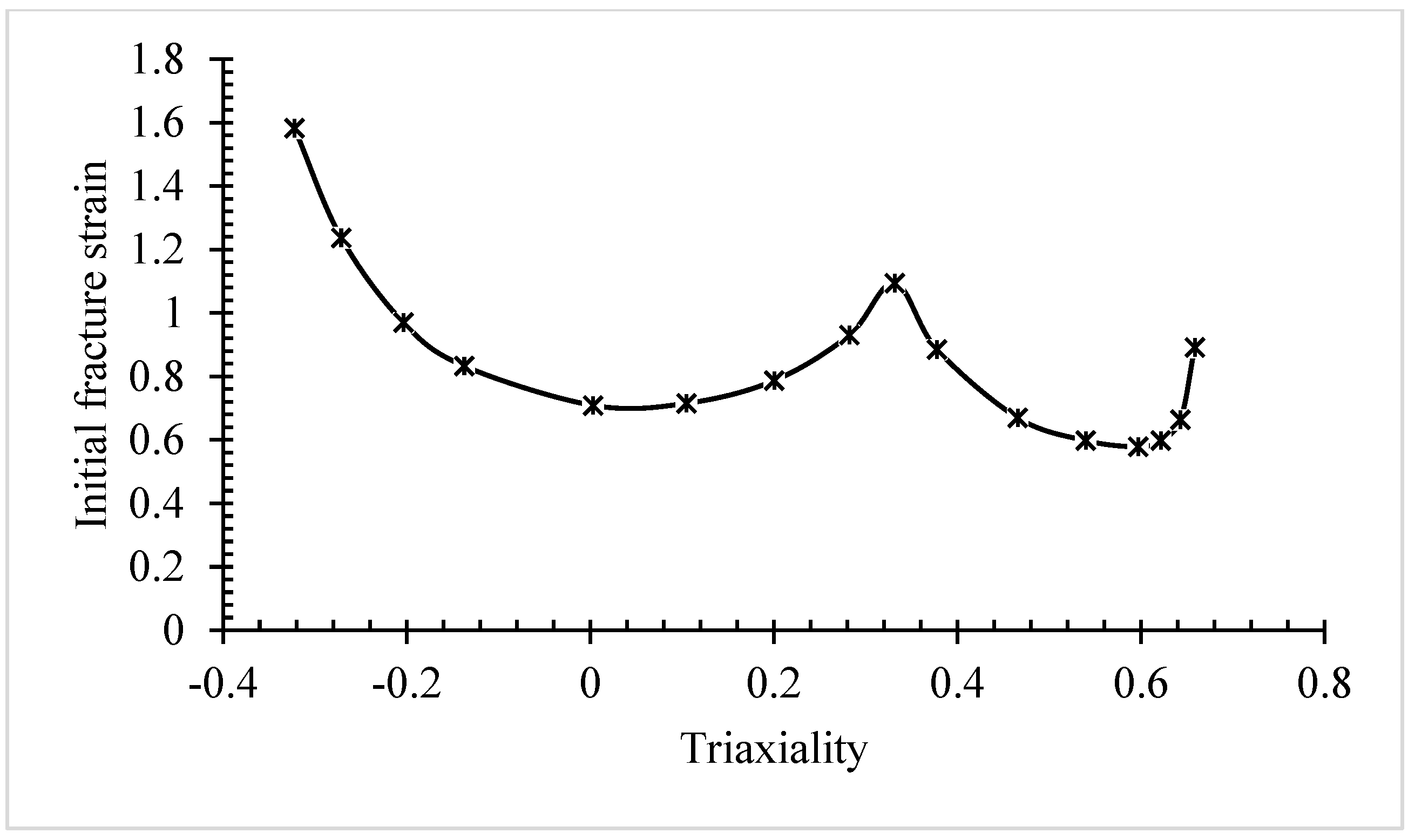
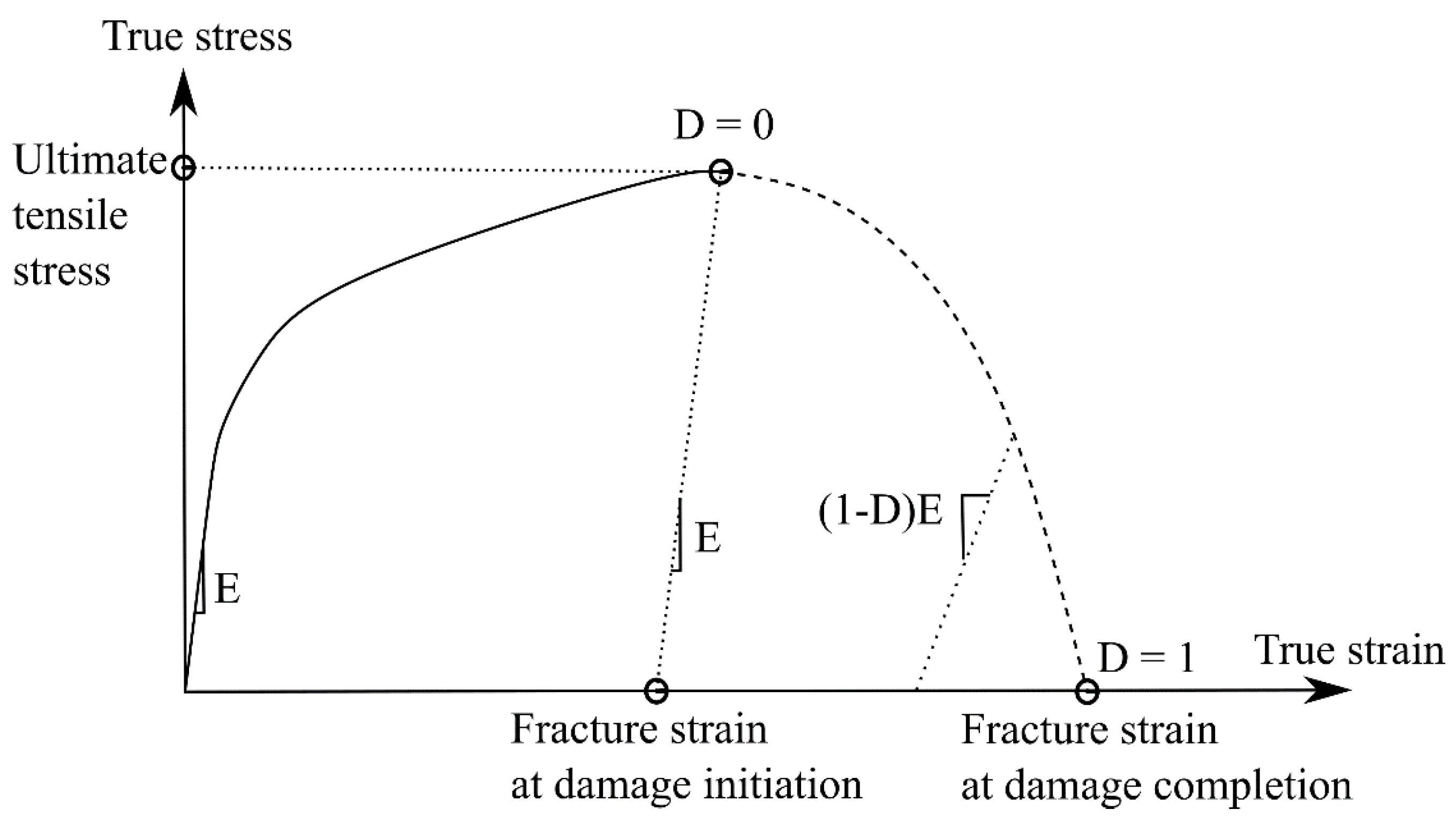
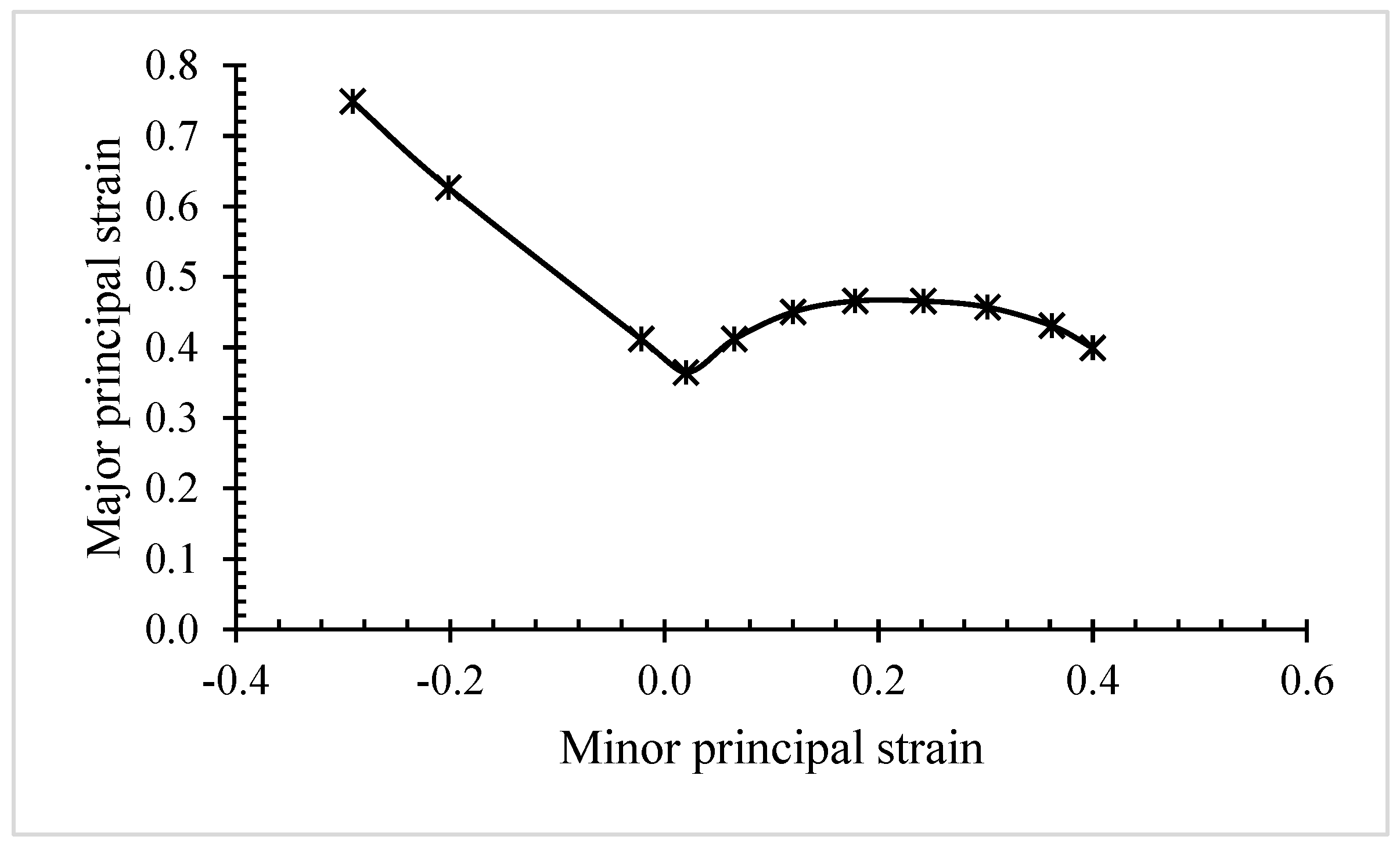



| Tool elemental composition (wt.%) | Al | Fe | Ni | Mn | Cu | Zn | Pb | Sn |
| 5.0 | 2.0 | 1.0 | 2.5 | 60 | 22 | 0.20 | 0.20 | |
| Oil physical Properties | Density (gr/cm³) | Viscosity (mm²/s)at 40 °C | Flash point (°C) | |||||
| 0.92 | 6 | 310 | ||||||
| Workpiece elemental composition (wt.%) | C | Mn | Si | Cr | Al | Ni | P | Cu |
| 0.116 | 1.545 | 0.289 | 0.634 | 0.042 | 0.041 | 0.029 | 0.019 | |
| q1 | q2 | q3 | f0 | fc | ff | fN | SN | εN |
|---|---|---|---|---|---|---|---|---|
| 1.5 | 1 | 2.25 | 0.008 | 0.15 | 0.25 | 0.00062 | 0.1283 | 0.5421 |
| Axial Depth (mm) | Experimental Results | FFLD | GTN | DD | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.0 bar | 0.2 bar | 0.4 bar | 0.0 bar | 0.2 bar | 0.4 bar | 0.0 bar | 0.2 bar | 0.4 bar | 0.0 bar | 0.2 bar | 0.4 bar | |
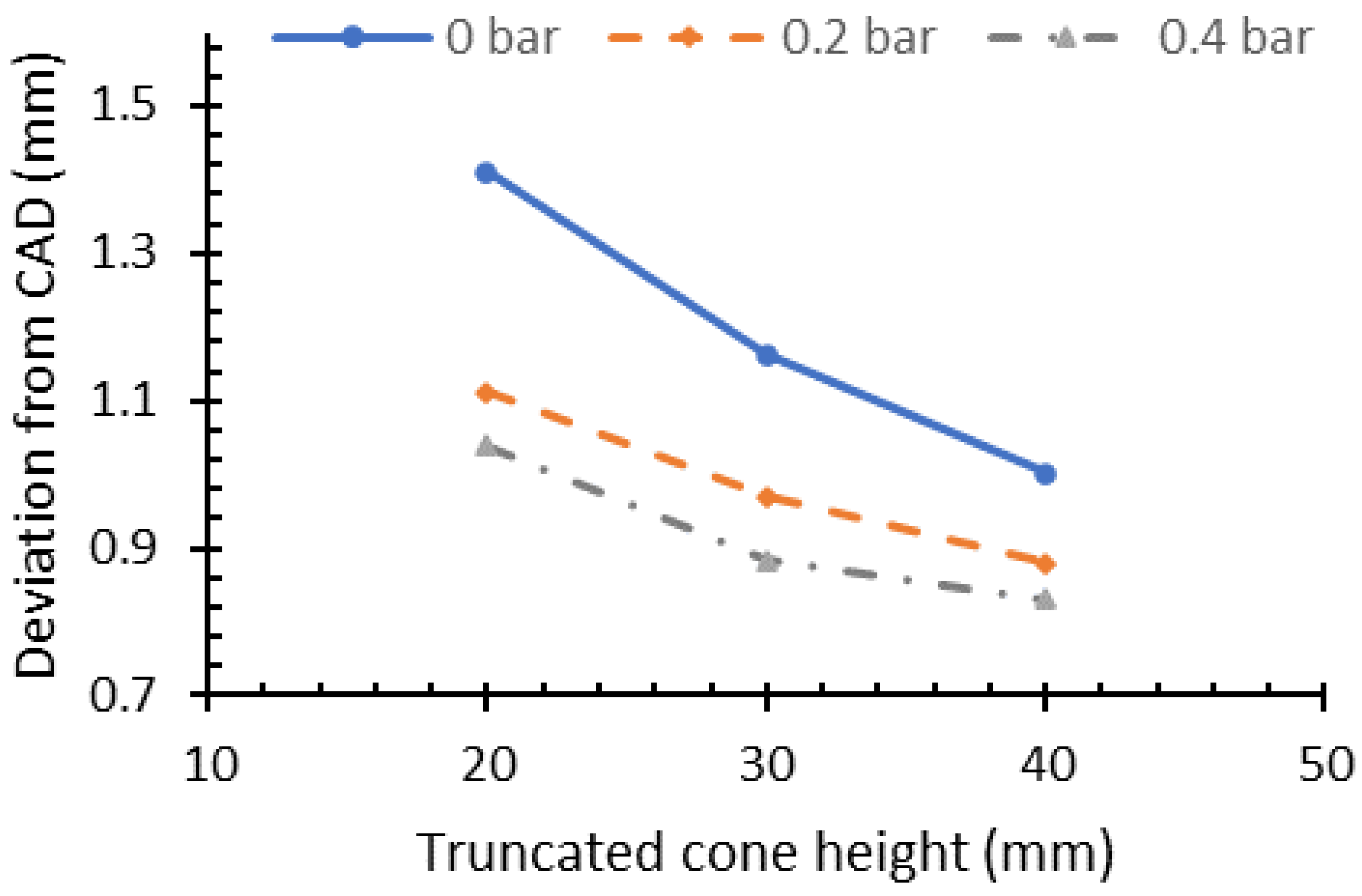
| Variation from CAD (mm) | ||||||||||||
| 20 | 1.4 | 1.11 | 1.03 | 1.39 | 1.12 | 1.01 | 1.42 | 1.21 | 1.05 | 1.38 | 1.06 | 0.99 |
| 30 | 1.1 | 0.96 | 0.88 | 1.16 | 0.95 | 0.86 | 1.17 | 1.04 | 0.89 | 1.13 | 0.93 | 0.86 |
| 40 | 1.01 | 0.88 | 0.83 | 0.99 | 0.86 | 0.81 | 1.10 | 0.92 | 0.84 | 0.94 | 0.86 | 0.83 |
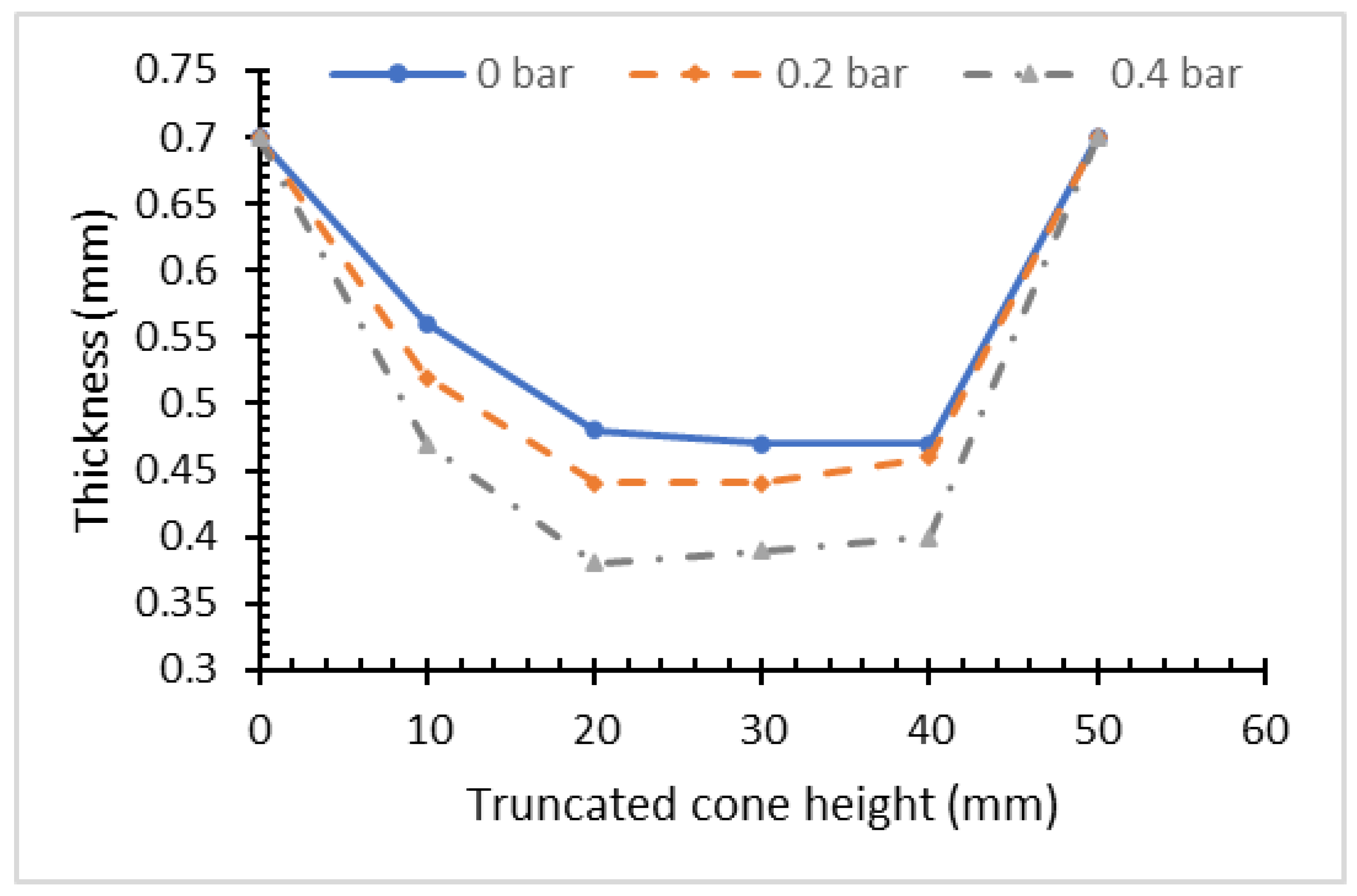
| Thickness (mm) | ||||||||||||
| 10 | 0.56 | 0.52 | 0.47 | 0.56 | 0.51 | 0.46 | 0.51 | 0.50 | 0.44 | 0.53 | 0.50 | 0.44 |
| 20 | 0.48 | 0.44 | 0.38 | 0.47 | 0.43 | 0.37 | 0.44 | 0.41 | 0.36 | 0.46 | 0.41 | 0.36 |
| 30 | 0.47 | 0.44 | 0.39 | 0.46 | 0.43 | 0.38 | 0.45 | 0.40 | 0.37 | 0.47 | 0.42 | 0.39 |
| 40 | 0.47 | 0.46 | 0.41 | 0.47 | 0.45 | 0.40 | 0.46 | 0.44 | 0.37 | 0.45 | 0.43 | 0.38 |
| Material Model | |||
|---|---|---|---|
| Characteristics | FFLD | DD | GTN |
| No-fracture prediction | Yes | Yes | No |
| Thickness discrepancy up to (%) | 3 | 6 | 10 |
| Variation from CAD up to (%) | 10 | 16 | 21 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdelhafeez Hassan, A.; Küçüktürk, G.; Yazgin, H.V.; Gürün, H.; Kaya, D. Selection of Constitutive Material Model for the Finite Element Simulation of Pressure-Assisted Single-Point Incremental Forming. Machines 2022, 10, 941. https://doi.org/10.3390/machines10100941
Abdelhafeez Hassan A, Küçüktürk G, Yazgin HV, Gürün H, Kaya D. Selection of Constitutive Material Model for the Finite Element Simulation of Pressure-Assisted Single-Point Incremental Forming. Machines. 2022; 10(10):941. https://doi.org/10.3390/machines10100941
Chicago/Turabian StyleAbdelhafeez Hassan, Ali, Gökhan Küçüktürk, Hurcan Volkan Yazgin, Hakan Gürün, and Duran Kaya. 2022. "Selection of Constitutive Material Model for the Finite Element Simulation of Pressure-Assisted Single-Point Incremental Forming" Machines 10, no. 10: 941. https://doi.org/10.3390/machines10100941
APA StyleAbdelhafeez Hassan, A., Küçüktürk, G., Yazgin, H. V., Gürün, H., & Kaya, D. (2022). Selection of Constitutive Material Model for the Finite Element Simulation of Pressure-Assisted Single-Point Incremental Forming. Machines, 10(10), 941. https://doi.org/10.3390/machines10100941







