Upgrade of Biaxial Mechatronic Testing Machine for Cruciform Specimens and Verification by FEM Analysis
Abstract
:1. Introduction
- -
- Slow speed for the experiment;
- -
- Fast mode for piston position adjustment.
2. Materials and Methods
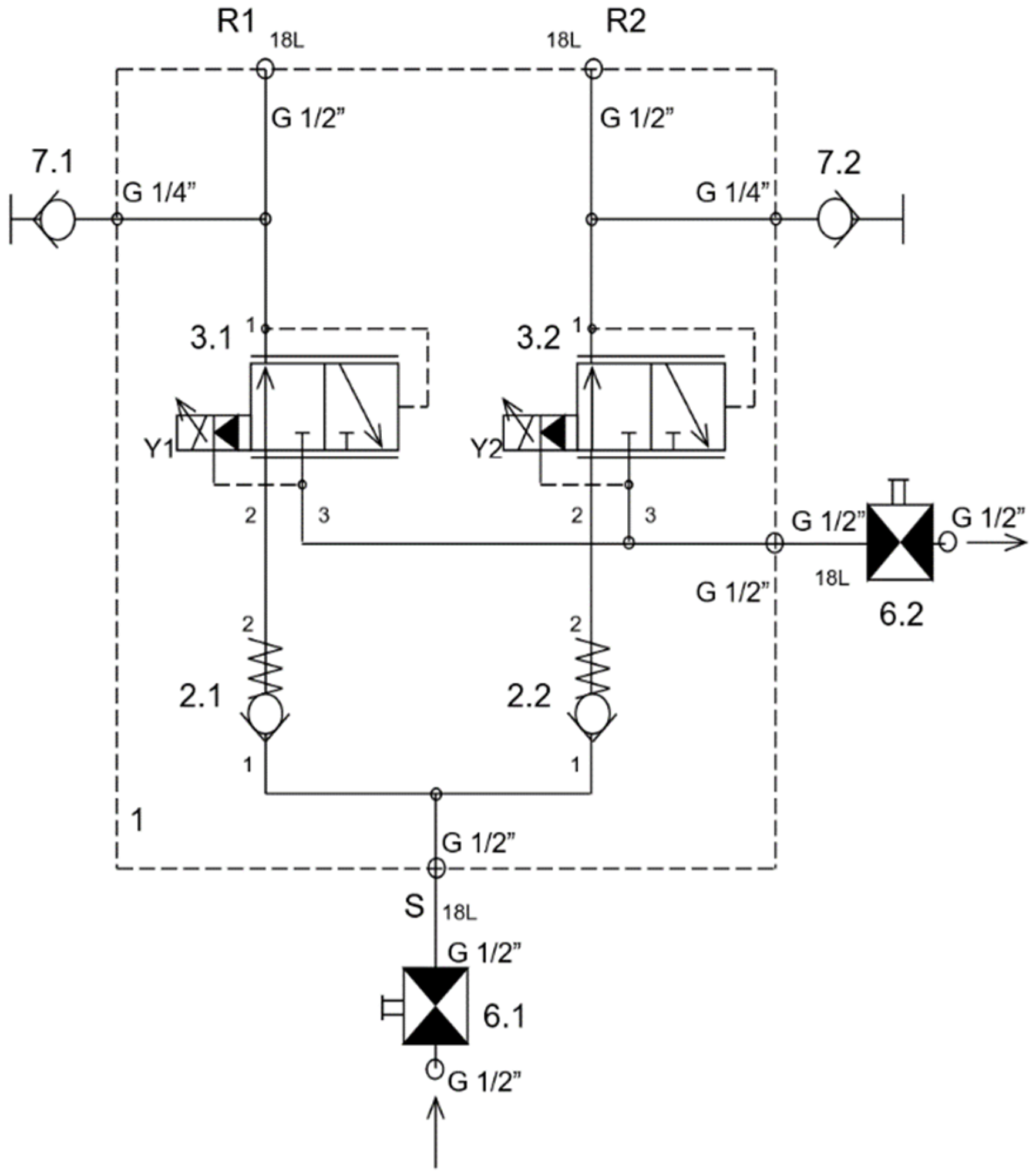
2.1. Technical Realization of the Hydraulic Loading Device
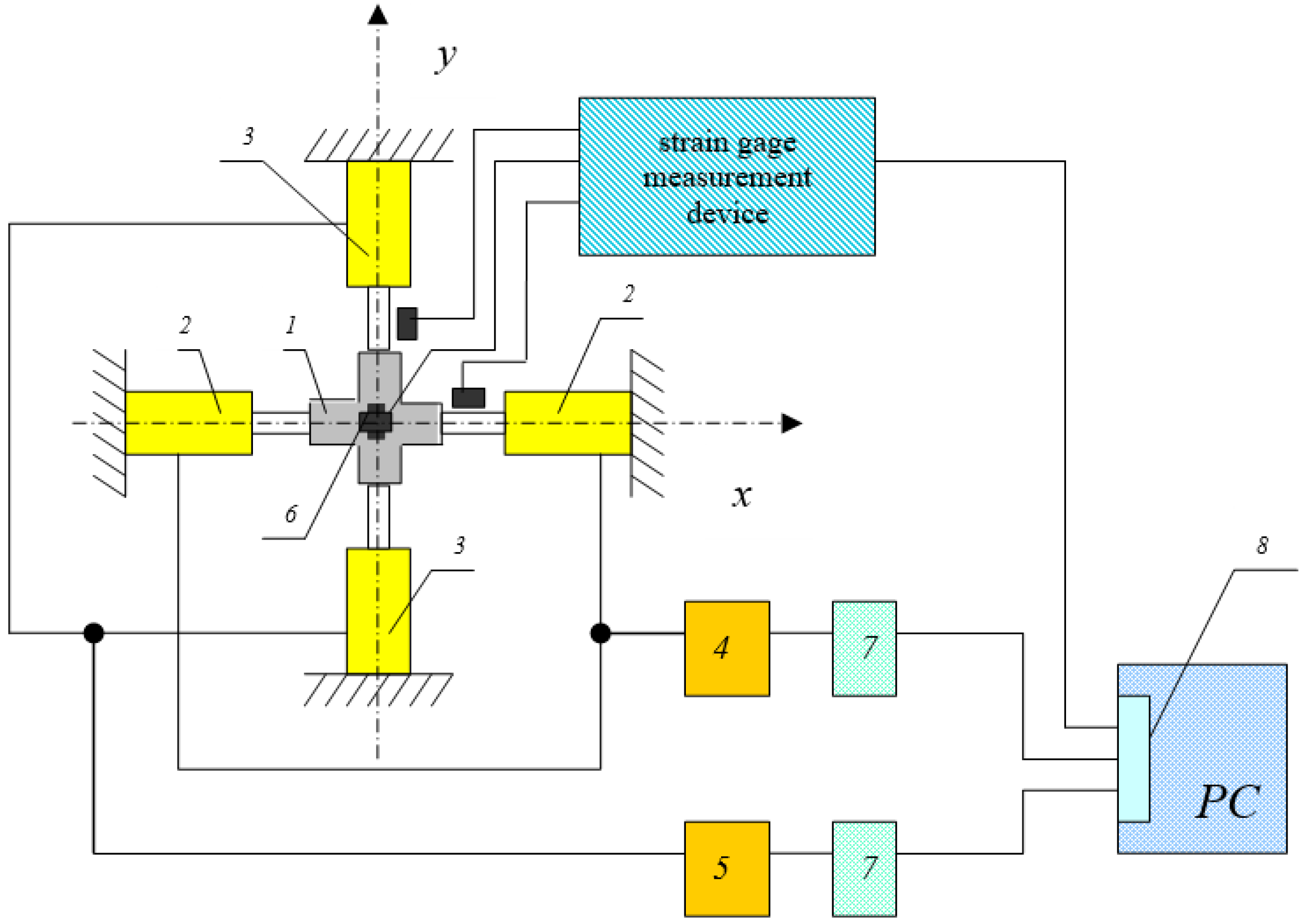
- A hydraulic device for biaxial loading of the cruciform specimens;
- A dynamic strain gauge measurement device for sensing the evolution of the loading forces in the cruciform specimen arms using dynamometers with resistive strain gages;
- An extensometer for measuring the deformation in the central part of the cruciform specimen under biaxial tensile loading.
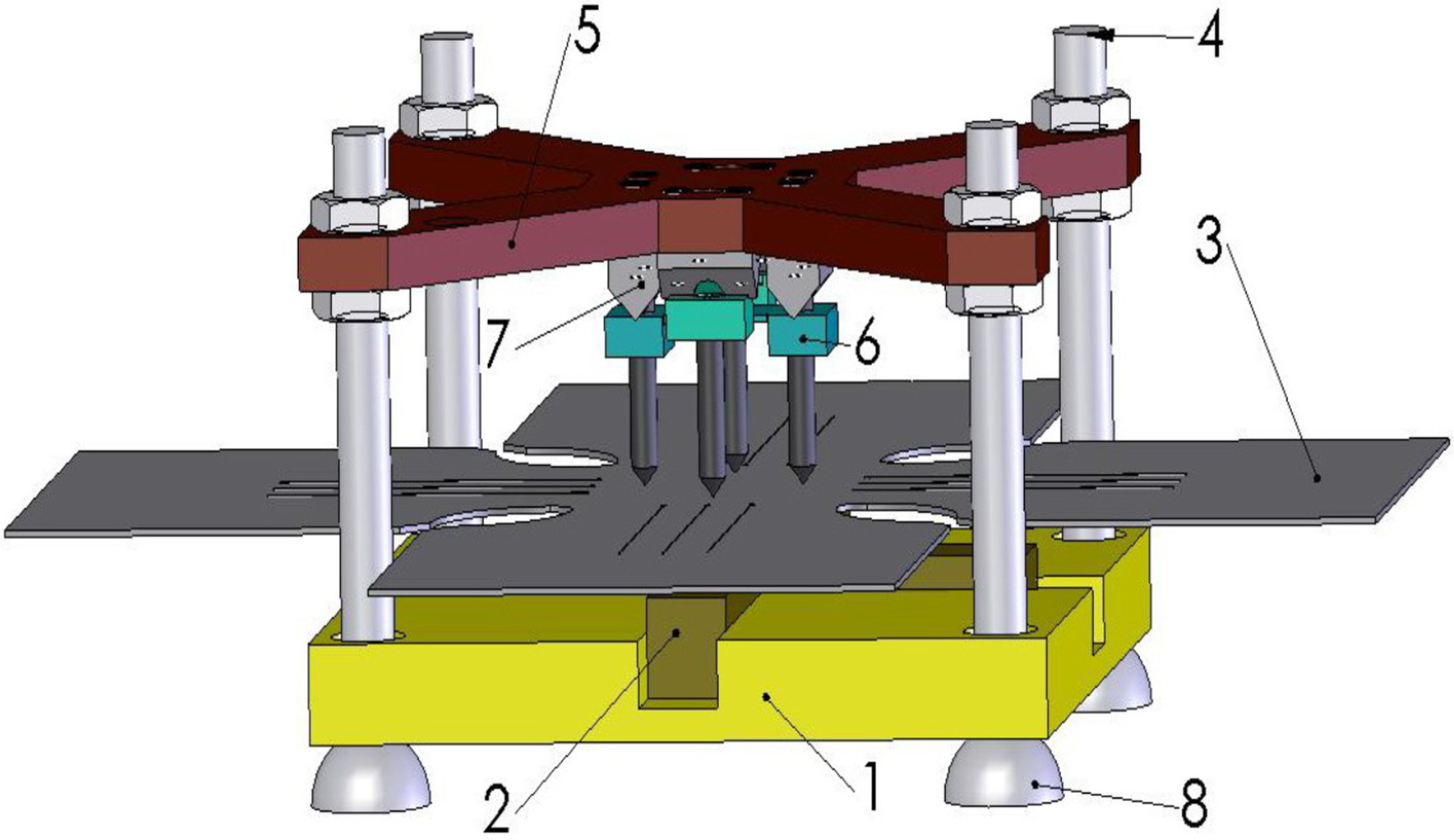
- The hydraulic loading device consists of the following main parts:
- A lamellar hydrogenerator SA33-100;
- Hydraulic cylinders;
- Clamping jaws;
- A guide body;
- Throttling valves;
- A main valve;
- Distributors of working fluid pressure;
- Electrical switches.
2.1.1. Lamellar Hydrogenerator SA3-100
- Power W = 7.5 kW;
- Maximum working fluid flow Q = 40 dm3·min−1;
- Working temperature 50 °C;
- Maximum working pressure of 16 MPa.
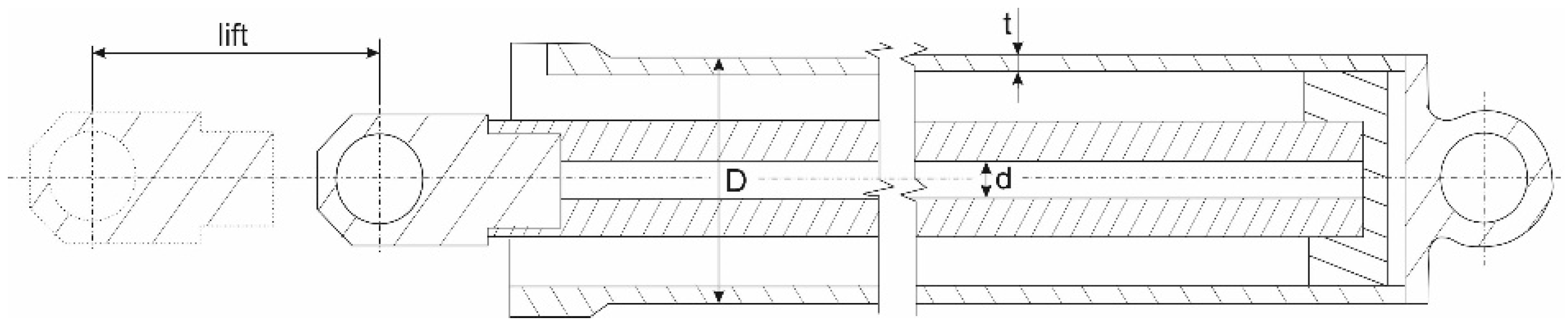
2.1.2. Hydraulic Cylinders and Hoses
- Direction X: D = 63 mm, d = 32 mm, t = 6.5 mm, and lift= 250 mm;
- Direction Y: D = 60 mm, d = 32 mm, t = 6.5 mm, and lift= 100 mm.
2.1.3. Clamping Jaws and Guide Body
2.1.4. Parameters of the Main and Throttle Valves
- Maximum working fluid flow: Q = 30 dm3·min−1;
- Maximum working pressure: P= 35 MPa;
- Maximum working temperature: T = 80 °C.

- Maximum working fluid flow: Q = 1.6 dm3·min−1;
- Maximum working pressure: P= 32 MPa.
2.1.5. Electrical Switches
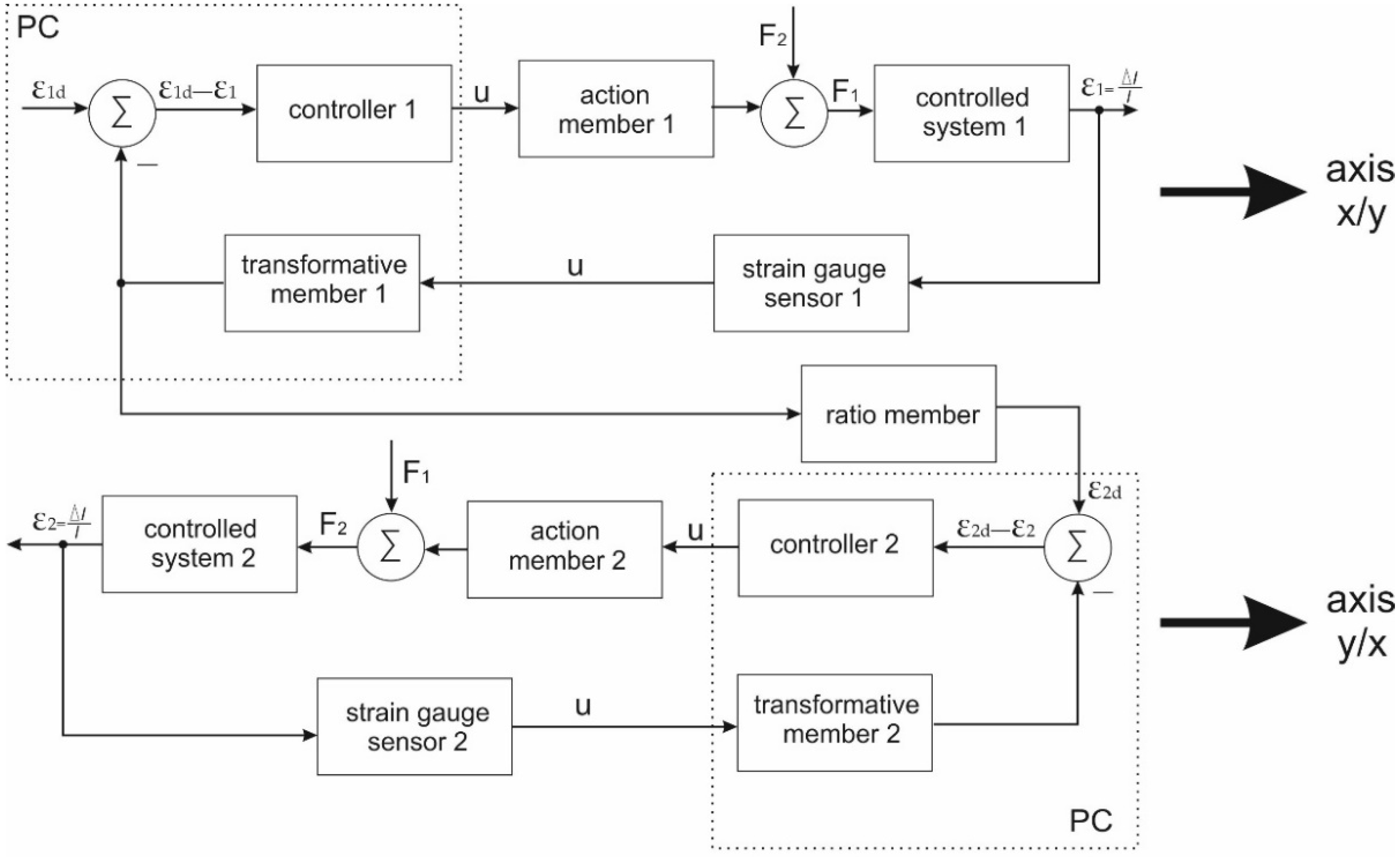
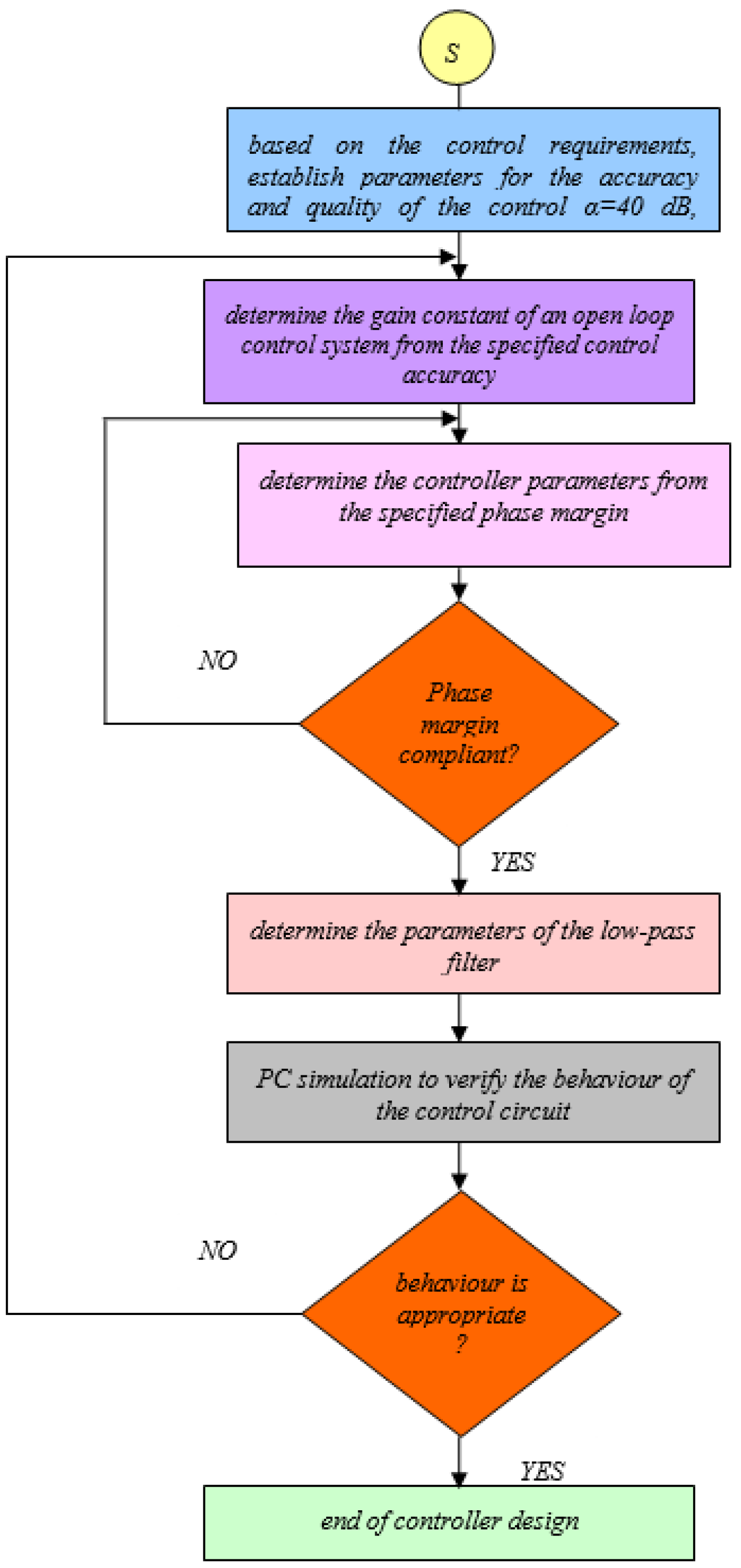
2.2. Load Mechanism Improvement through Regulator Design
- Application of force to the testing specimen;
- Ratio regulation of deformations and mechanical stress;
- That the time change in the deformation will not be greater than prescribed in the relevant norm.
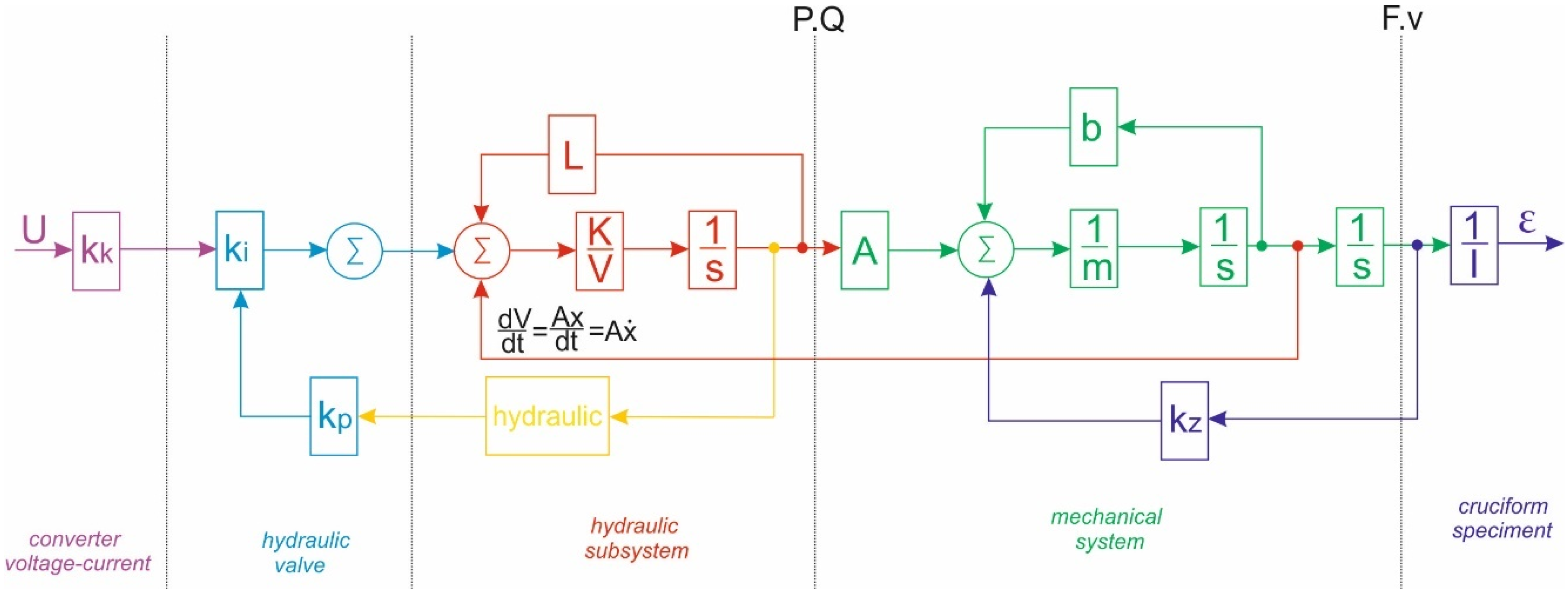
2.2.1. Regulator Design in a Block Diagram
2.2.2. Modernization of the Hydraulic Control Circuit
3. Mathematical Model
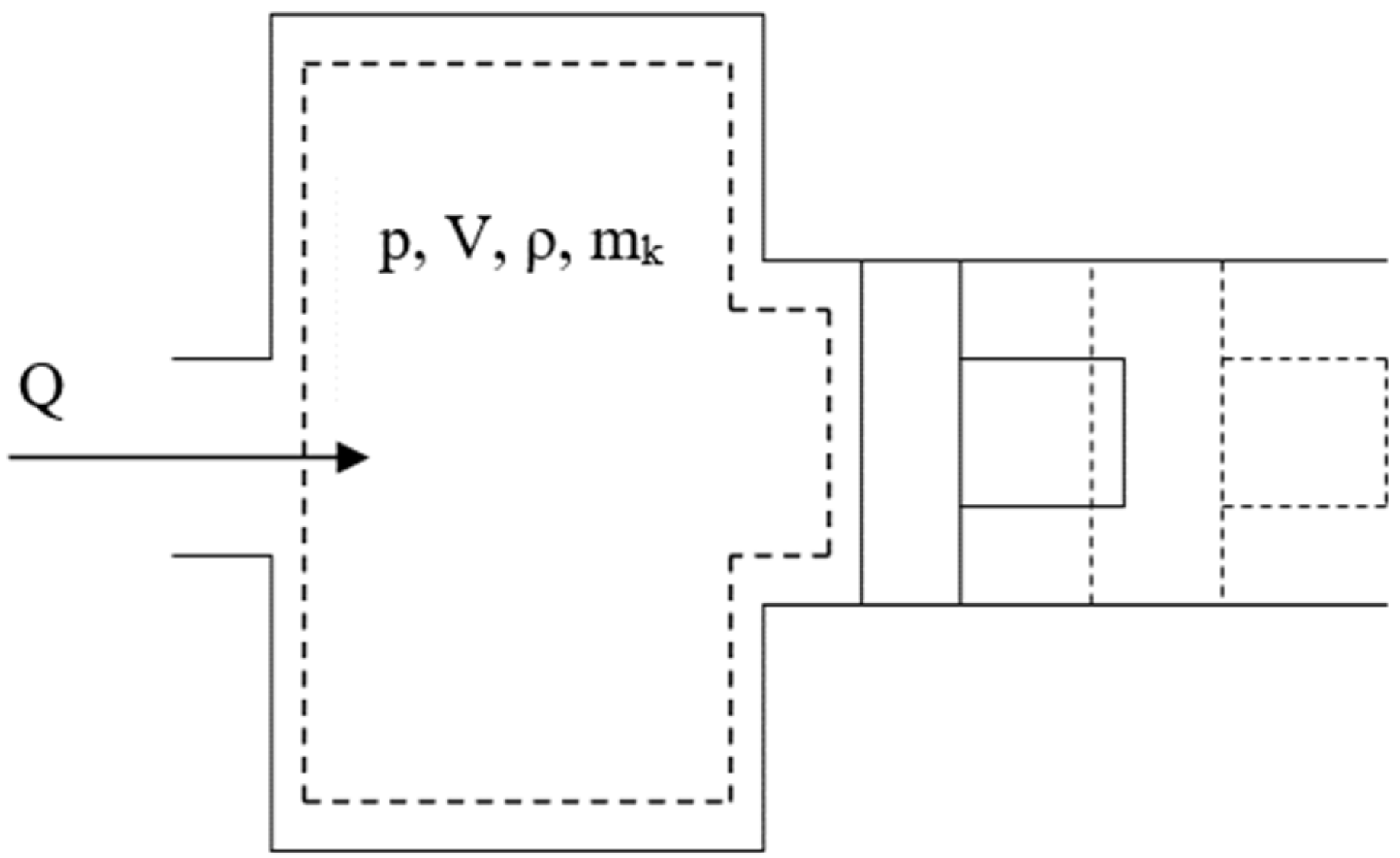
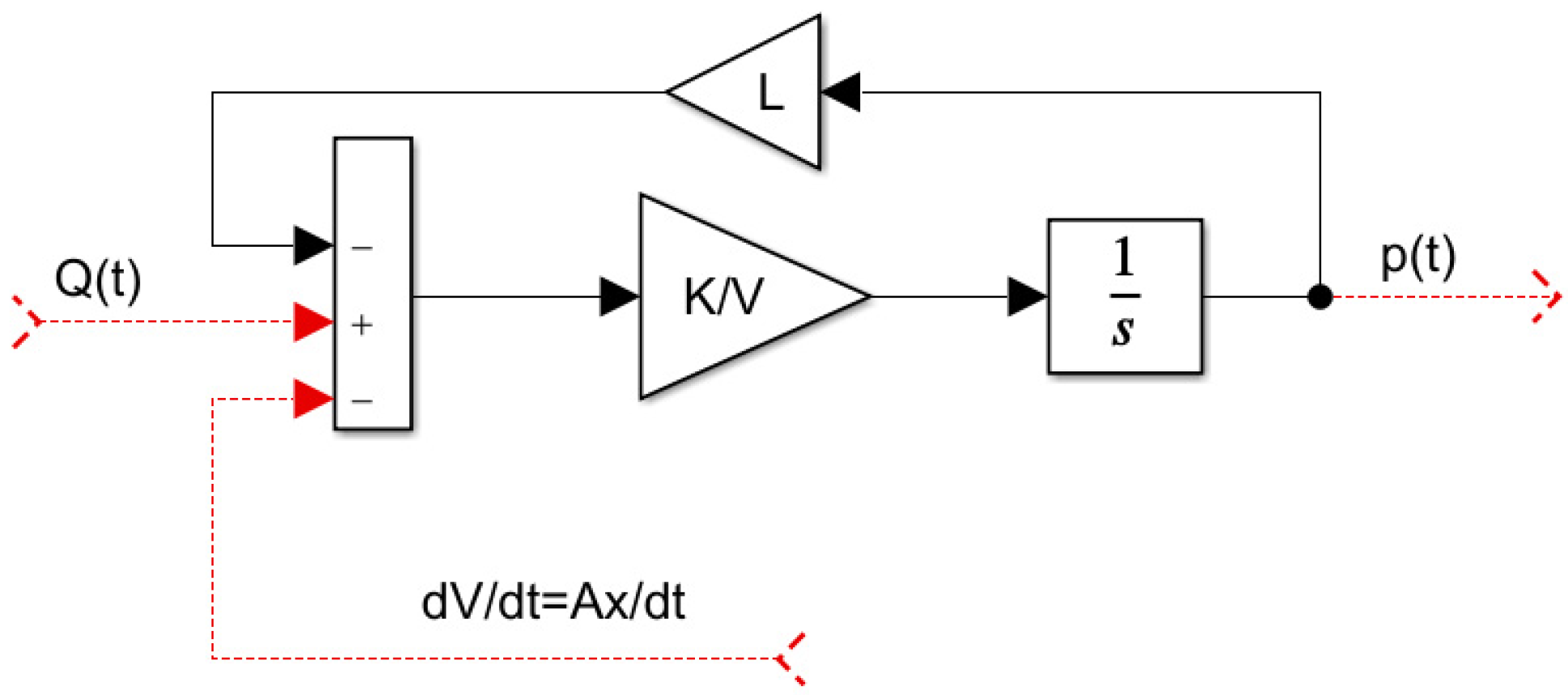
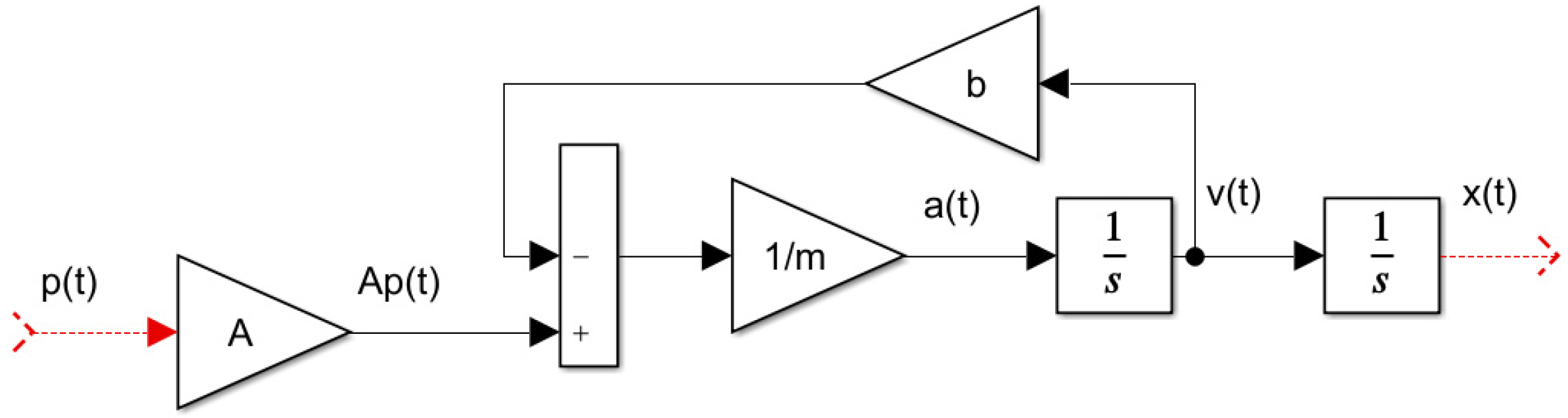
3.1. Mathematical Model of the Electrohydraulic Actuator
3.2. Mathematical Model of the Proportional Pressure-Reducing Valve
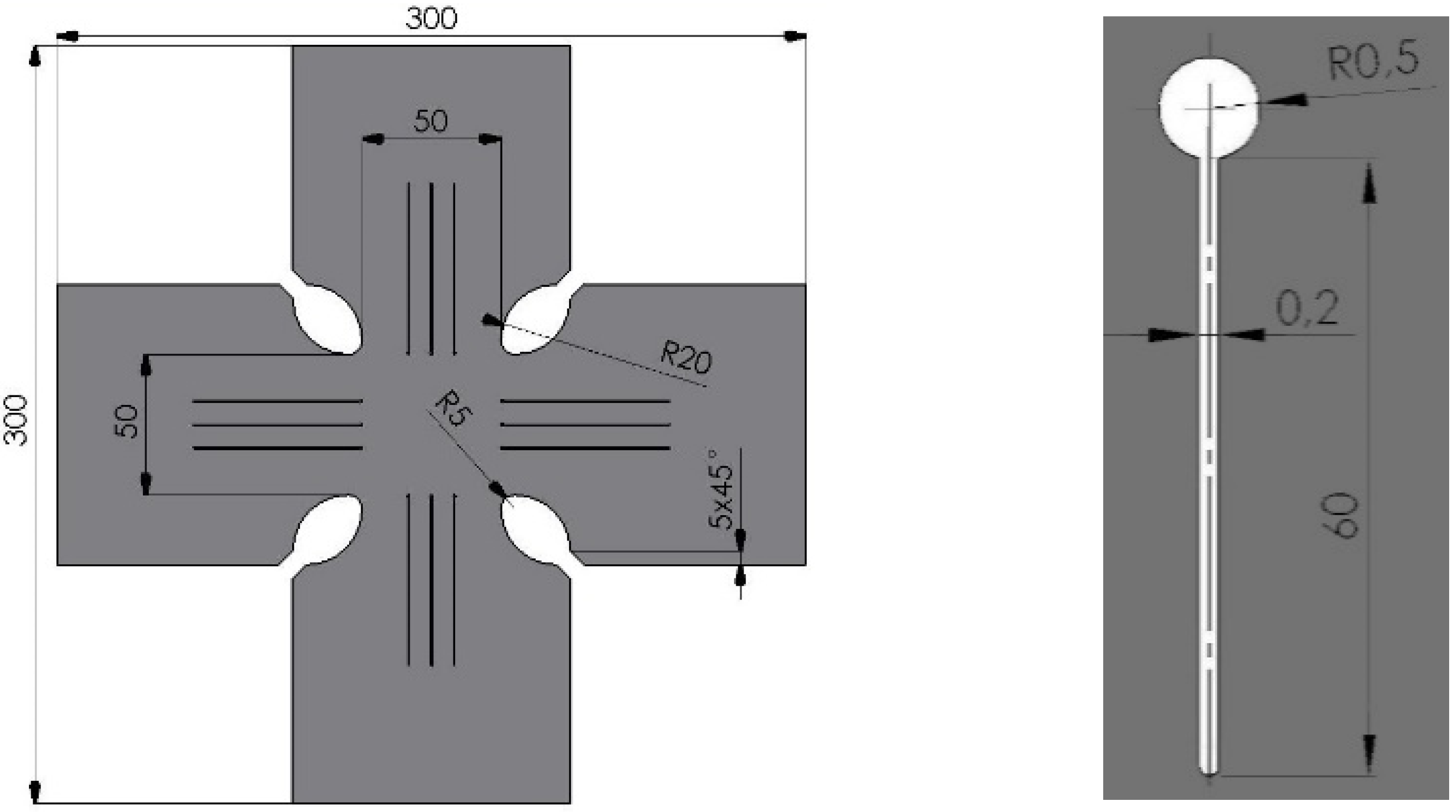
3.3. Mathematical Model of the Cruciform Specimen
3.4. Design of the Resulting Block Diagram of the Control Circuit
4. Results
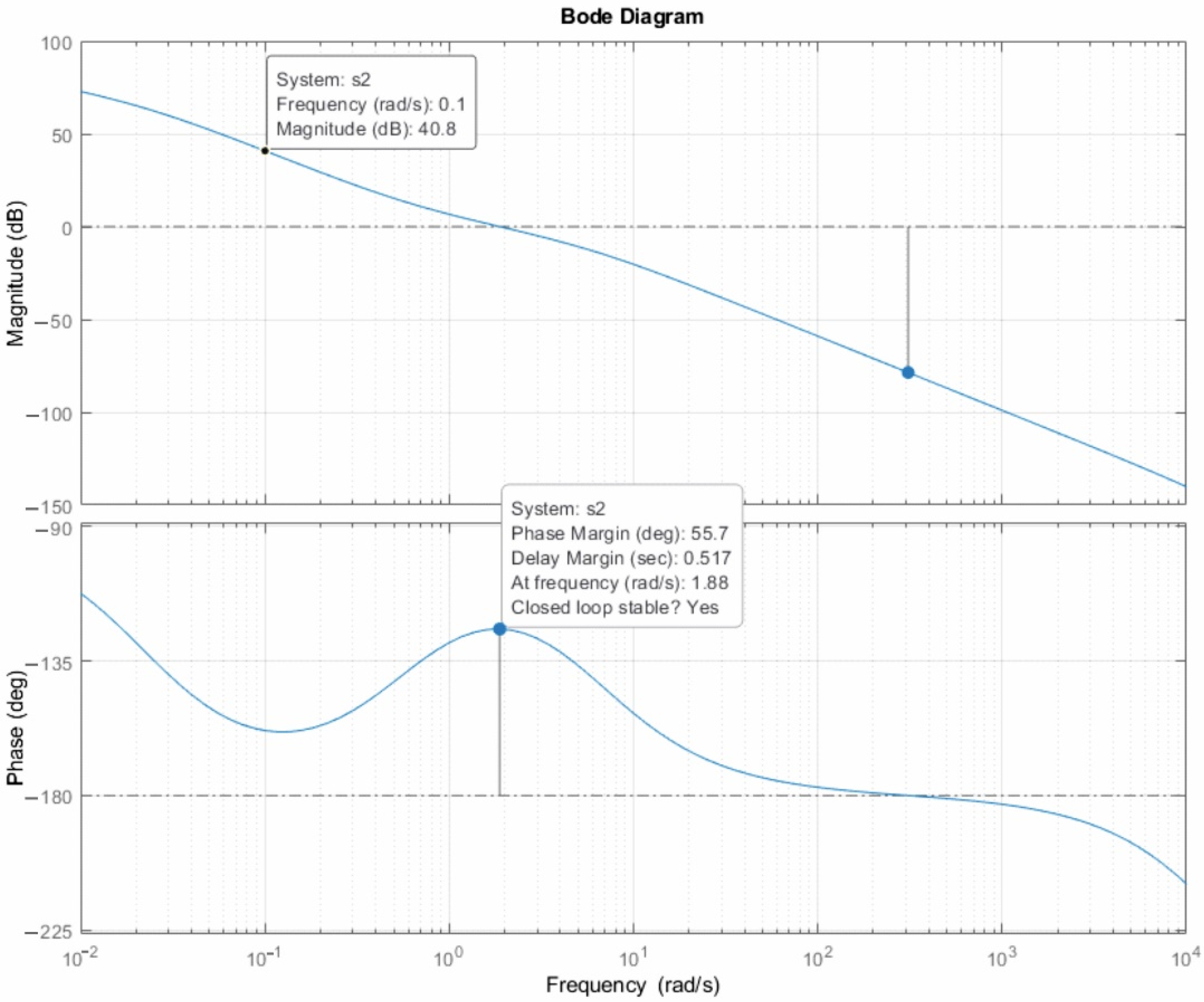
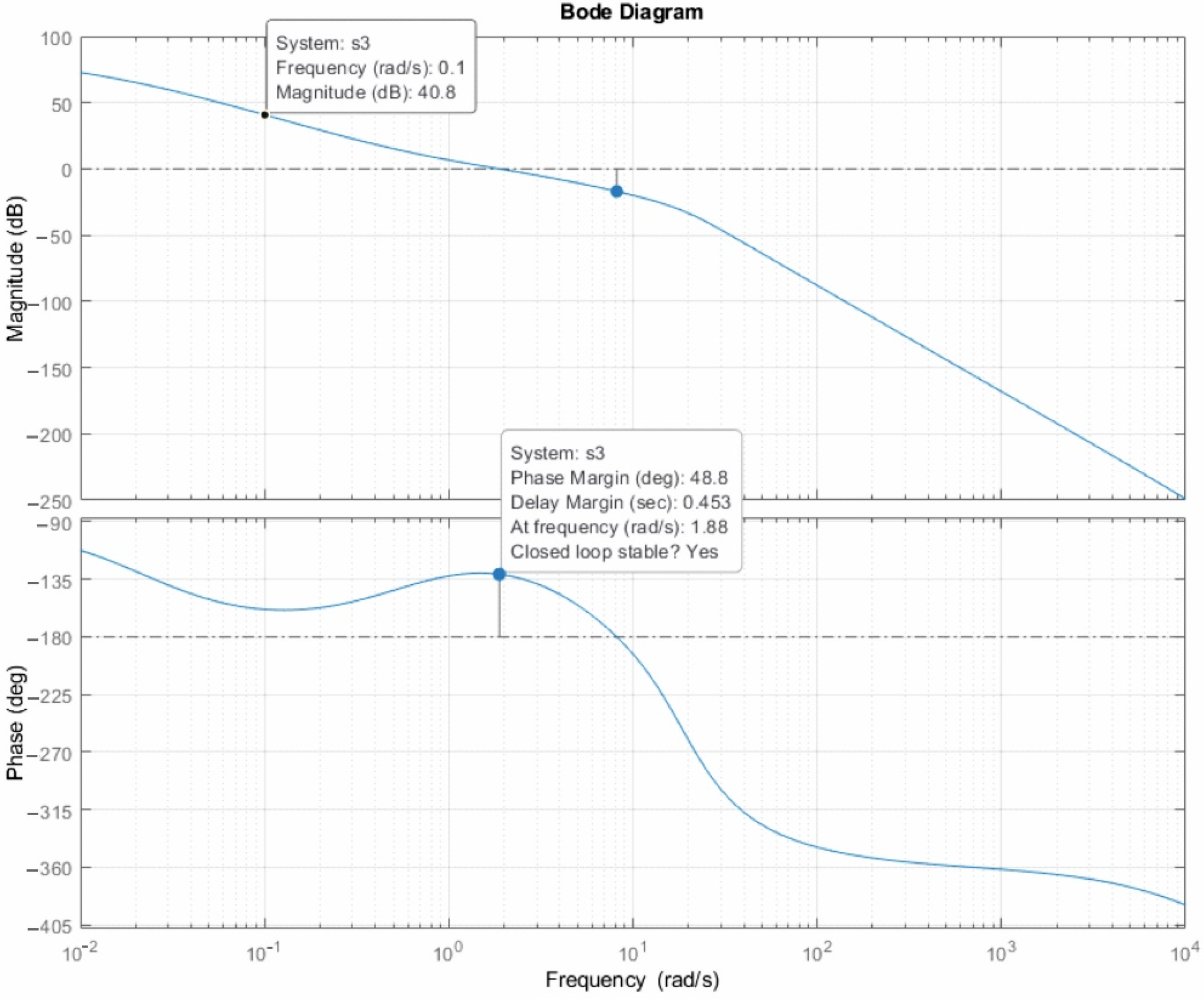
4.1. Design of the Resulting Block Diagram of the Control Circuit
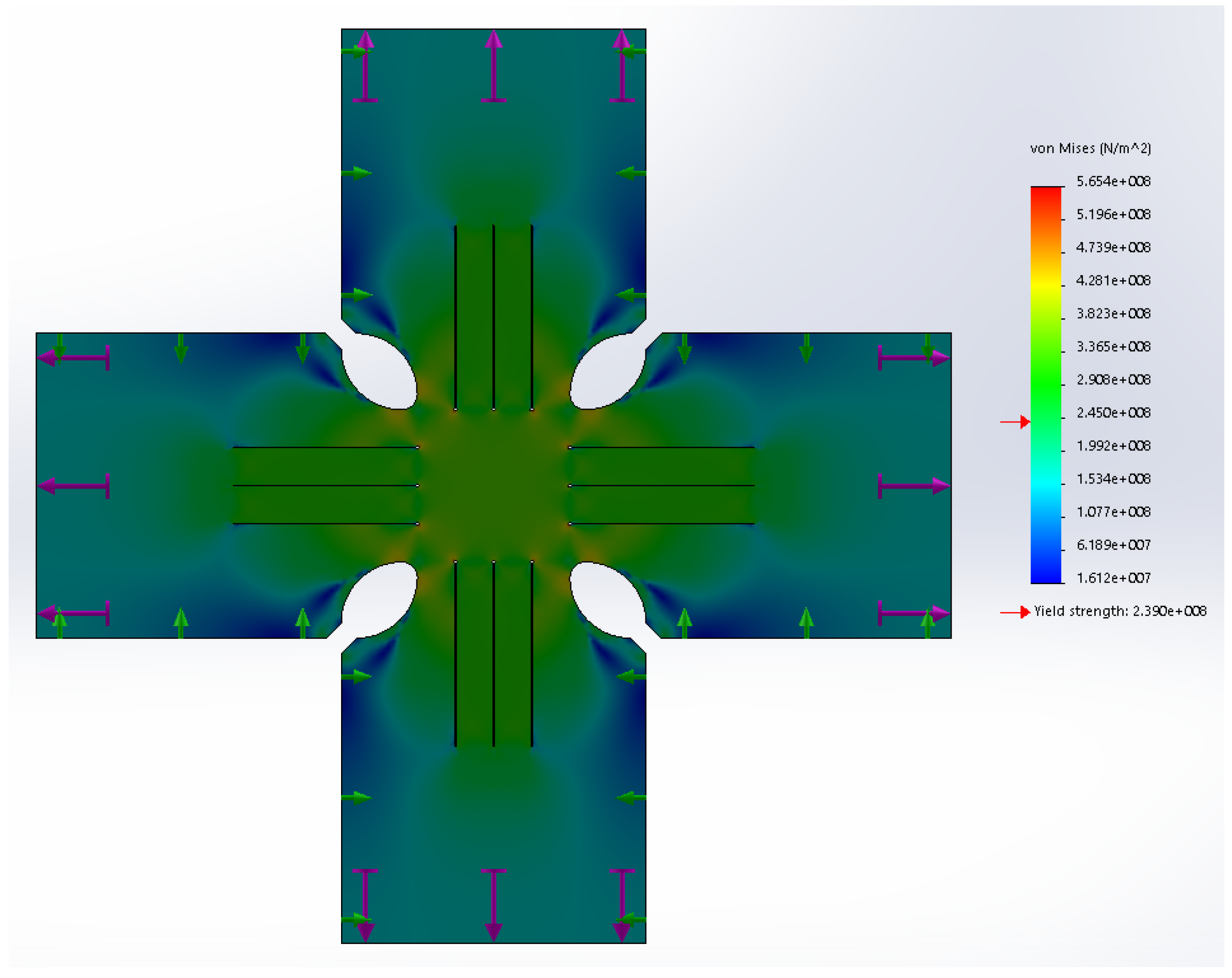
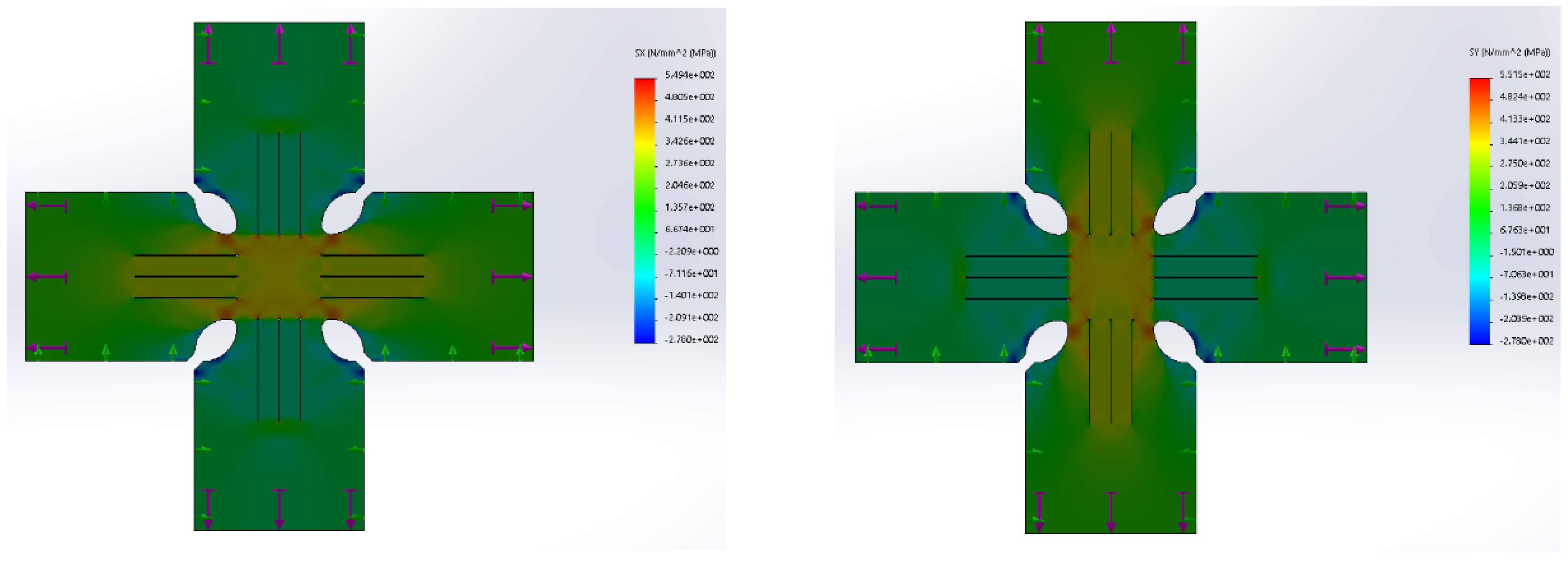
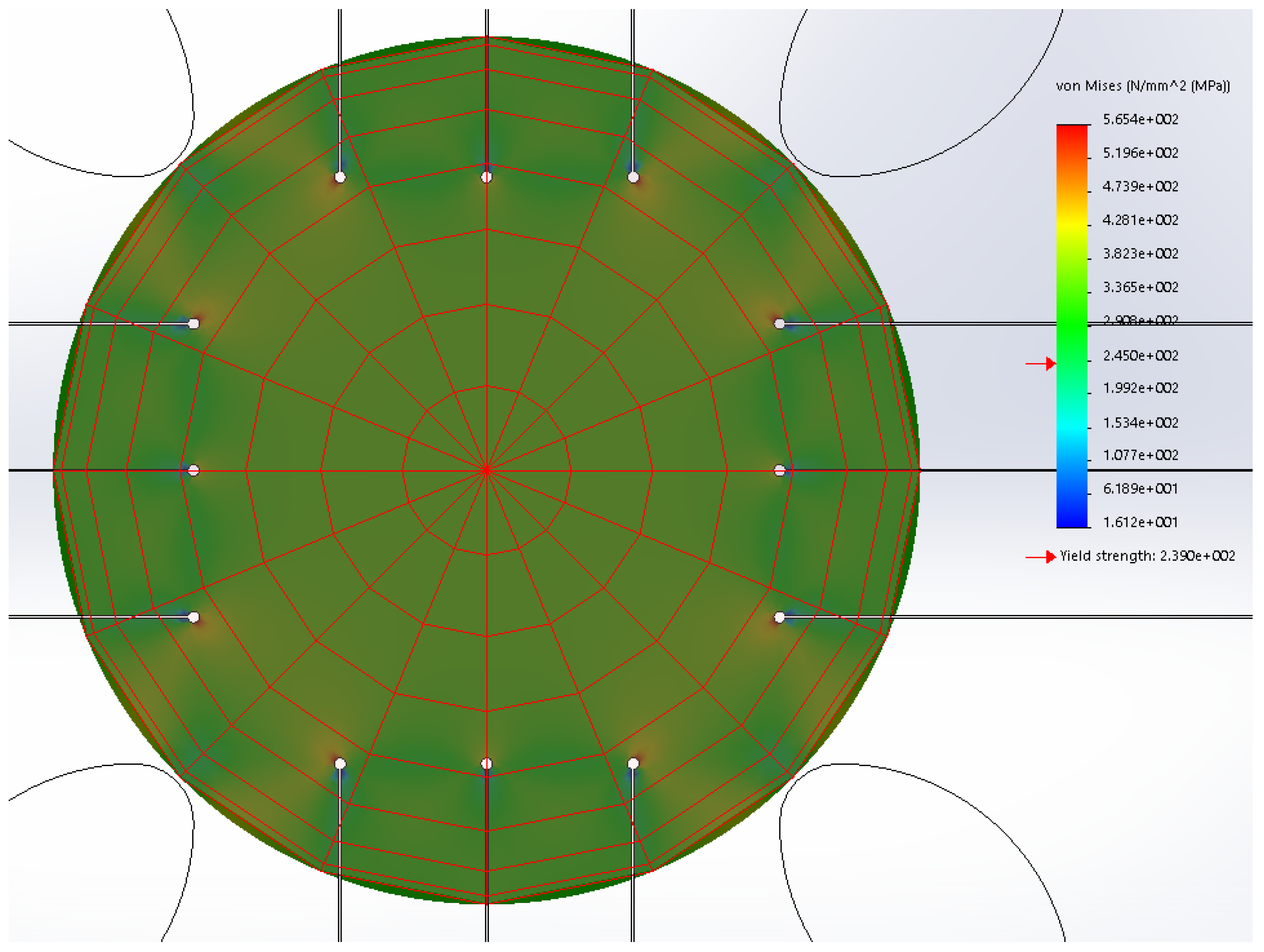
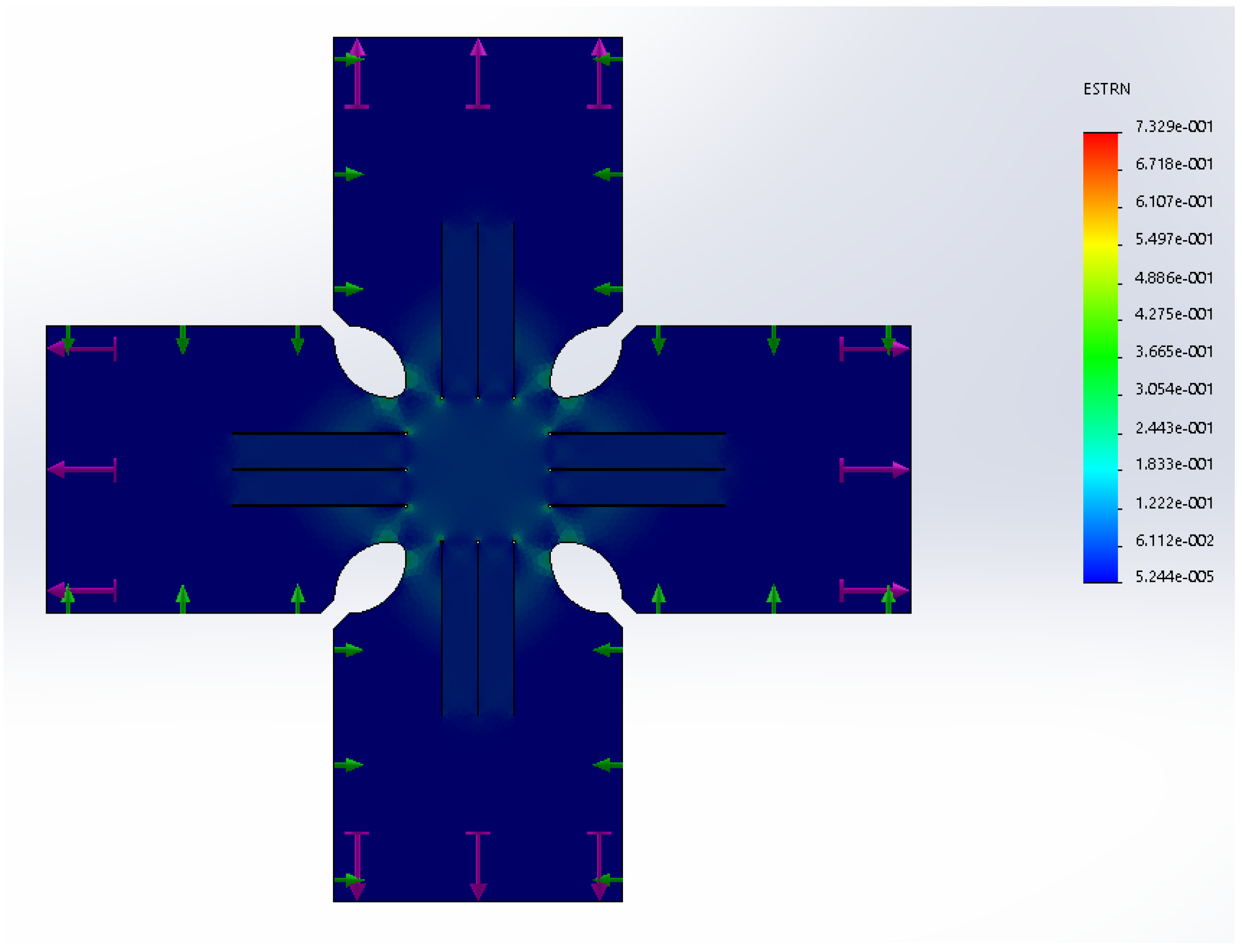
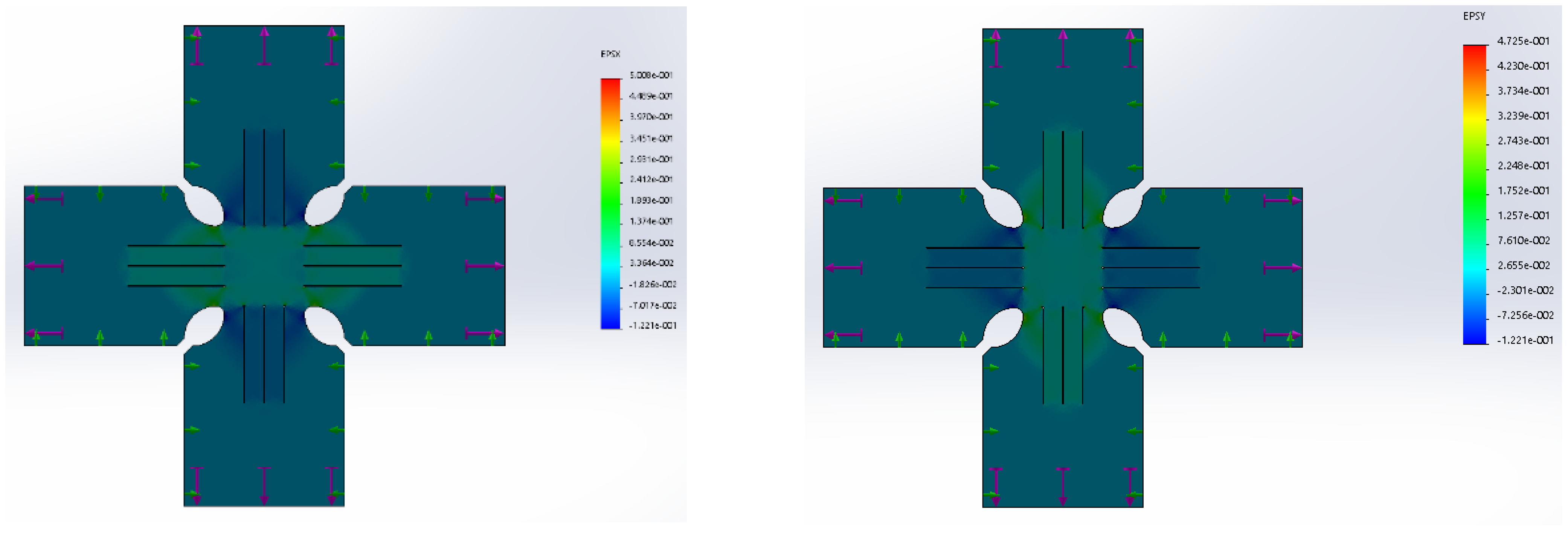
4.2. Nonlinear FEM Simulation of the Specimen Based on the Plasticity Anisotropic Material Model
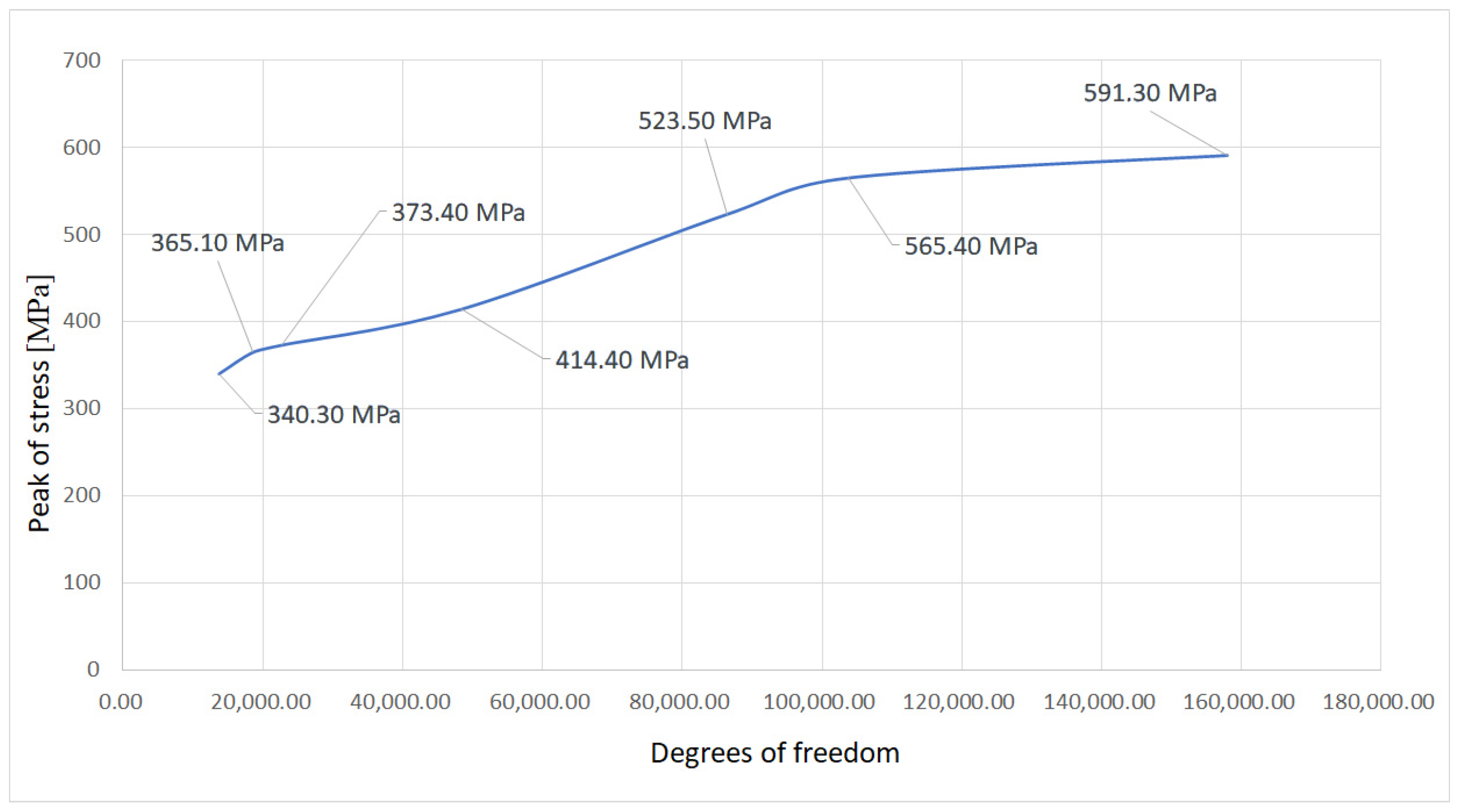
- Several mesh configurations were checked, and the dependence of the change in the peak stress on the change in degrees of freedom was realized, together with the dependence of the peak stress on the change in the number of elements. In this way, the convergence of the mesh was verified, Figure 25;
- The upper limit of the maximum stress was set at which the calculation was still stable without the need for drastic changes in the convergence tolerance and singularity elimination factor;
- The minimum element size was determined based on geometric parameters at 0.078 mm, and the maximum element size was determined based on convergence properties at 2.62 mm.
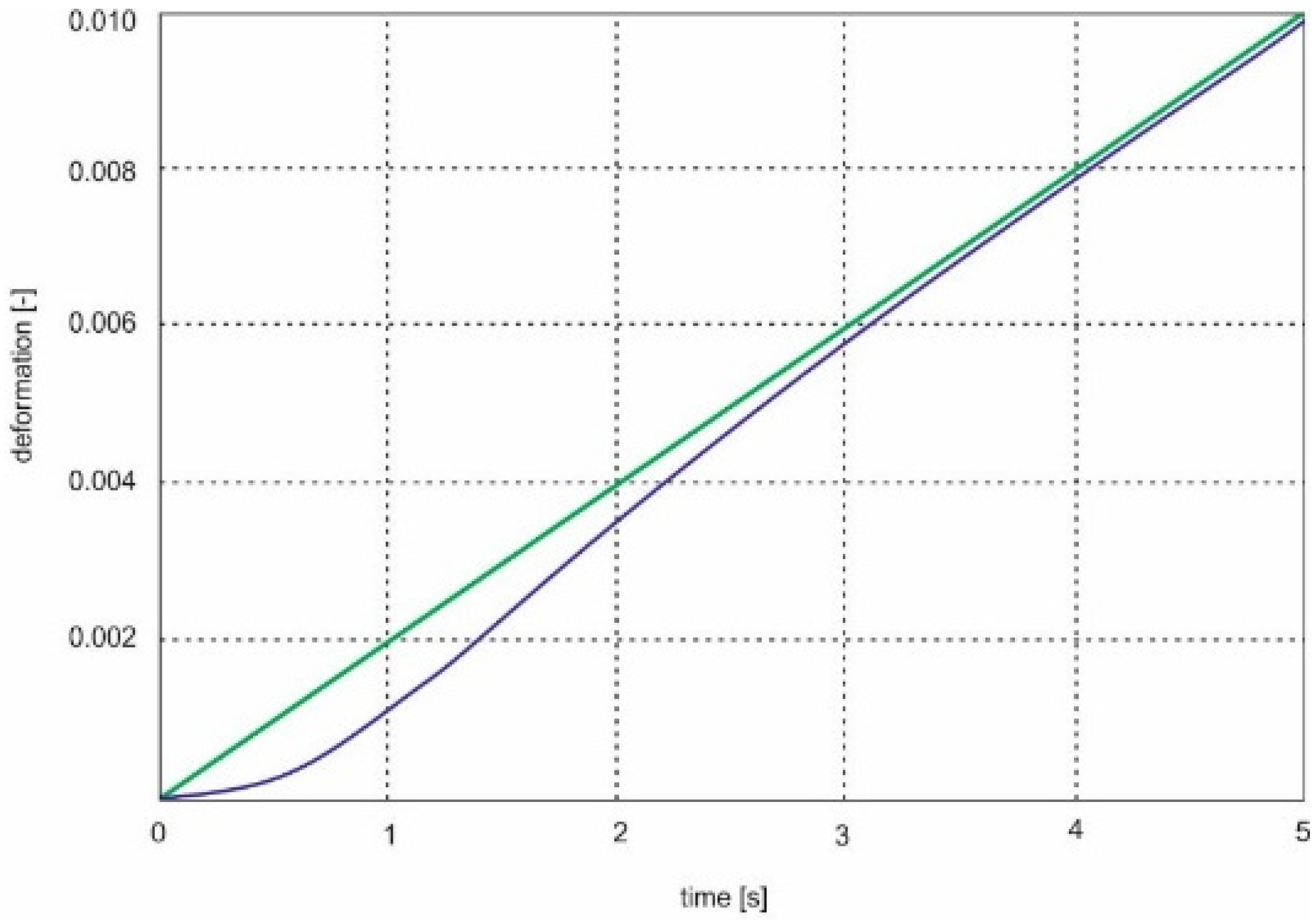
4.3. Experimental Verification of the Closed-Loop Control System and the Plasticity Properties of the Cruciform Specimen
5. Conclusions
- -
- Design of the structure of the control closed-loop circuit at the functional and object level;
- -
- The detailed design of the electrohydraulic part of the loading device at the object level;
- -
- Design of mathematical models within individual elements of the control closed-loop circuit;
- -
- The final closed-loop block diagram and verification of the controlled system;
- -
- Design of a regulator of the control circuit in the frequency domain using the method of shaping the frequency response of an open-loop control circuit;
- -
- The computer simulation of a control closed-loop circuit in the MATLAB/Simulink environment and its evaluation;
- -
- FEM simulation of the cruciform specimen;
- -
- Experimental verification of the closed-loop control system and plasticity properties of the cruciform specimen.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Šimčák, F.; Trebuňa, F.; Hanušovský, J. Evaluation of Plastic Properties of Sheets in Plane Stress States; Skalský dvůr: Lísek, Czech Republic, 2005; ISBN 80-214-2941-0. [Google Scholar]
- Šimčák, F. Inovačné trendy pri zvyšovaní únosnosti karosérií automobilov. Acta Mech. Slovaca 2003, 1, 13–24. [Google Scholar]
- Gambin, W. Plasticity and Textures; Kluver Academic Publisher: Dordrecht, The Netherlands, 2001. [Google Scholar]
- Mises, R.V. Mechanics of plastic deformation of crystals 592. Zeitsch.Angew. J. Appl. Math. Mech. 1928, 8, 161–185. [Google Scholar]
- Hill, R. Mathematical Theory of Plasticity; Oxford University Press: Oxford, UK, 1956. [Google Scholar]
- Hill, R. Constitutive modelling of orthotropic plasticity in sheet metals. J. Mech. Phys. Solids 1990, 38, 405–417. [Google Scholar] [CrossRef]
- Hill, R.A. User-friendly theory of orthotropic plasticity in sheet metals. Int. J. Mech. Sci. 1993, 15, 19–25. [Google Scholar] [CrossRef]
- Hosford, W.F. A 29 eneralized isotropic yield criterion. J. Appl. Mech. 1972, 39, 607–609. [Google Scholar] [CrossRef]
- Gotoh, M. A theory of plastic anisotropy based on a yield function of fourth order. Int. J. Mech. Sci. 1977, 19, 505–520. [Google Scholar] [CrossRef]
- Barlat, F.; Lege, D.J.; Brem, J.C. A six-component yield function for anisotropic materials. Int. J. Plast. 1991, 7, 693–712. [Google Scholar] [CrossRef]
- Pöhlandt, K.; Banabic, D.; Balan, T.; Comsa, D.S.; Müller, W. A new criterion for anisotropic sheet metals. In Proceedings of the 8th International Conference Achievements in the Mechanical and Materials Engineering, Gliwice, Poland; 1999; pp. 33–36. [Google Scholar]
- Šimčák, F.; Hanušovský, J.; Berinštet, V. Experimental determination of yield locus of steel sheets by biaxial tensile test. Acta Mech. Slovaca 2006, 1, 535–542. [Google Scholar]
- Boehler, J.P.; Demmerle, S.; Koss, S. New direct biaxial testing machine for anisotropic materials. Exp. Mech. 1994, 34, 1–9. [Google Scholar] [CrossRef]
- Makinde, A.; Thibodeau, L.; Neale, K.W. Development of an Apparatus for Biaxial Testing Using Cruciform Specimens. Exp. Mech. 1992, 32, 138–144. [Google Scholar] [CrossRef]
- Sheet Metal Structures. Maintenance Manual (MM) or Structural Repair Manual. Available online: https://membefiles.freewebs.com/76/87/106238776/documents/2%20SHEET%20METAL%20STRUCTURES.pdf (accessed on 6 July 2021).
- Kuwabara, T.; Ikeda, S.; Kuroda, K. Measurement and Analysis of Work Hardening of Sheet Metals Under Plane—Strain Tension. J. Mater. Process. Technol. 1998, 80–81, 97–102. [Google Scholar]
- Shimamoto, A.; Shimomura, T.; Nam, J.H. The Development of a Servo Dynamic Biaxial Loading Device. Key Eng. Mater. 2003, 243–244, 99–104. [Google Scholar] [CrossRef]
- Pereira, A.B.; Fernandes, F.A.O.; de Morais, A.B.; Maio, J. Biaxial Testing Machine: Development and Evaluation. Machines 2020, 8, 40. [Google Scholar] [CrossRef]
- Chen, C.; Li, Z.; Xu, C.; Zhu, Z.; Zou, S. Variation of Fracture Toughness with Biaxial Load and T-Stress under Mode I Condition. Appl. Sci. 2022, 12, 9319. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, J.; Zhao, H. Quantifying Alignment Deviations for the In-Plane Biaxial Test System via a Shape-Optimised Cruciform Specimen. Materials 2022, 15, 4949. [Google Scholar] [CrossRef] [PubMed]
- Ru, M.; Lei, X.; Liu, X.; Wei, Y. An Equal-Biaxial Test Device for Large Deformation in Cruciform Specimens. Exp. Mech. 2022, 62, 677–683. [Google Scholar] [CrossRef]
- Wang, S.; Hou, C.; Wang, B.; Wu, G.; Fan, X.; Xue, H. Mechanical responses of L450 steel under biaxial loading in the presence of the stress discontinuity. Int. J. Press. Vessel. Pip. 2022, 198, 104662. [Google Scholar] [CrossRef]
- Corti, A.; Shameen, T.; Sharma, S.; De Paolis, A.; Cardoso, L. Biaxial testing system for characterization of mechanical and rupture properties of small samples. HardwareX 2022, 12, e00333. [Google Scholar] [CrossRef] [PubMed]
- Berinštet, V.; Tomčík, J. Modernization of the experimental workplace for evaluation of elastic-plastic properties of sheet metals in plane stress. Acta Mechanica Slovaca. Techonl. Univerzita-Stroj. Fak. 2005, 12, 69–76. [Google Scholar]
- Medvecká-Beňová, S. Strength analysis of the frame of a trailer. Sci. J. Sil. Univ. Technol. Ser. Transport. 2017, 96, 105–113. [Google Scholar] [CrossRef]
- Airmotive Specialties, Inc. Salinas, CA 93901. Available online: http://www.airmotives.com/index.html (accessed on 18 August 2021).










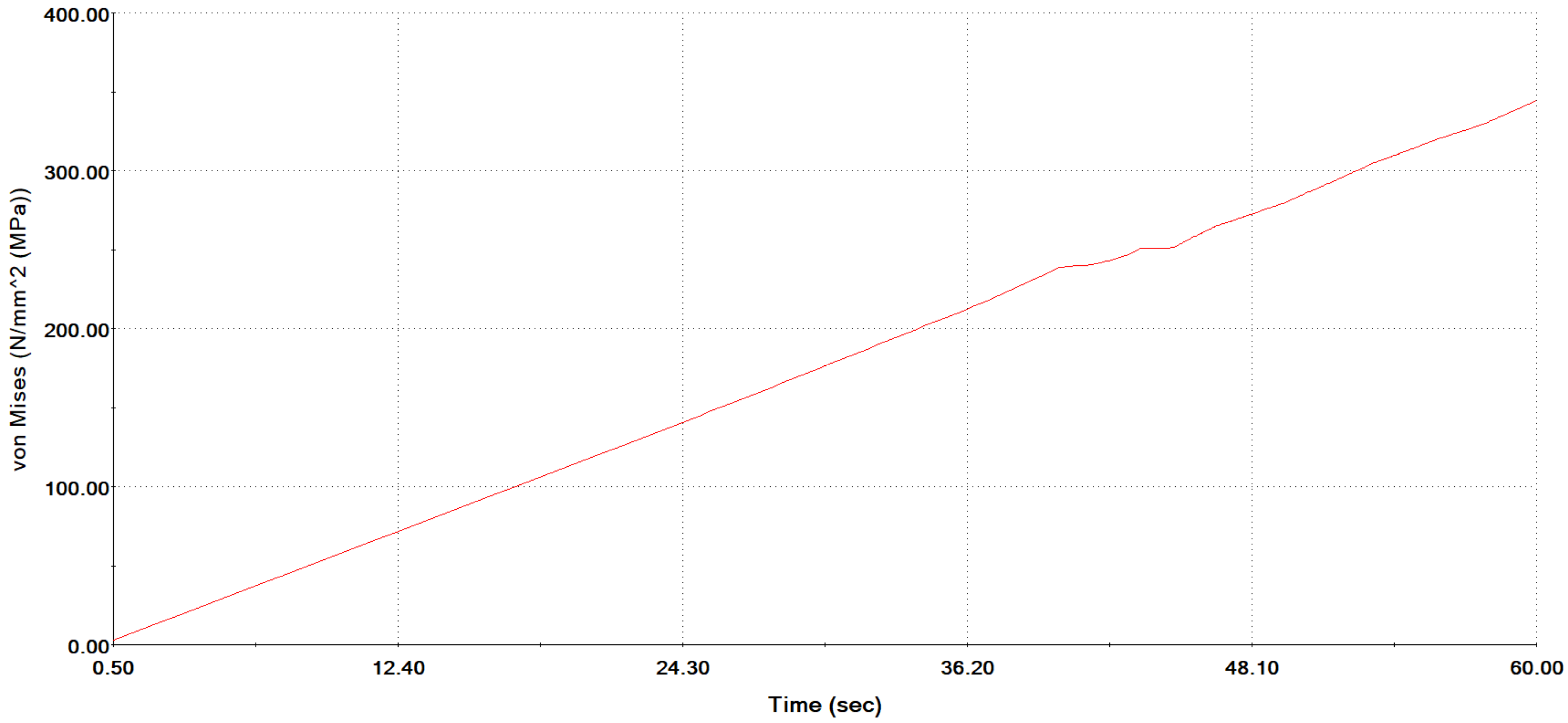
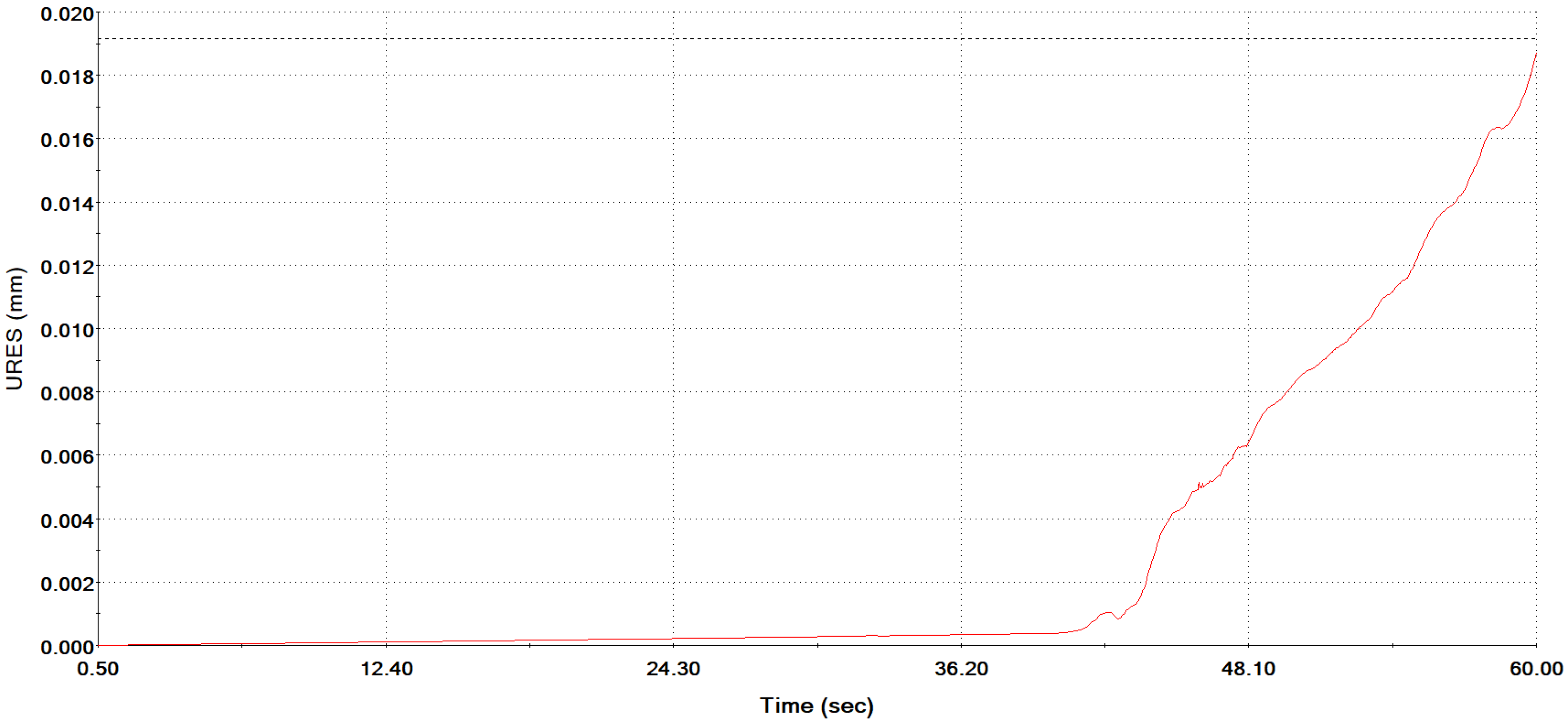

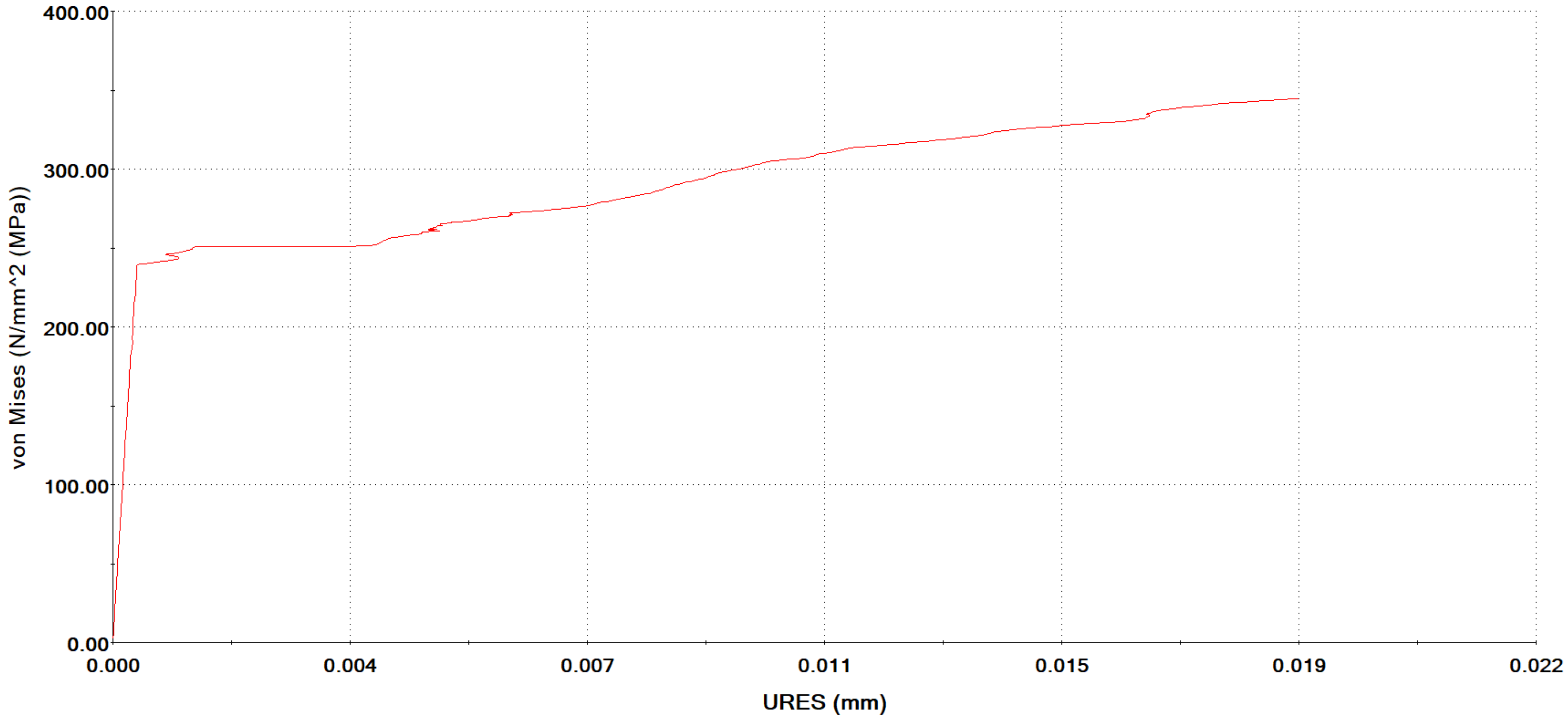



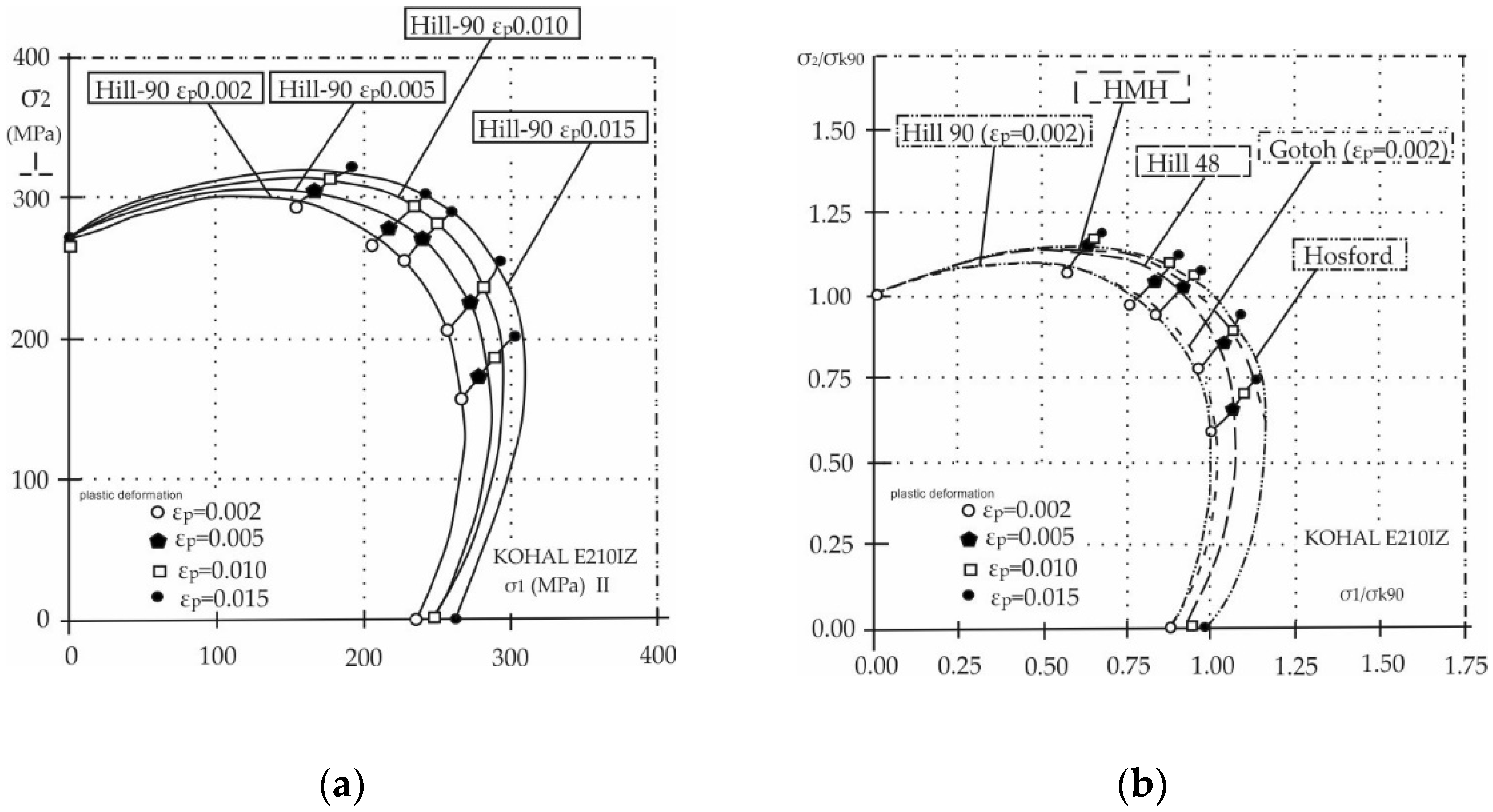
| Selected Step of Simulation | Computed Value—Strain in Plastic Deformation (Center of Specimen) |
|---|---|
| In 100 | |
| In 150 | |
| In 200 | |
| In 250 | |
| In 463 (final) |
| Material | Thickness [mm] | Direction | Rp0.2 [MPa] | Rm [MPa] | A80 [%] | r(20) | r(5) |
|---|---|---|---|---|---|---|---|
| KOHAL E 210 IZ | 1.00 | 0° | 239 | 353 | 37 | 0.91 | 0.86 |
| 45° | 254 | 352 | 38 | 1.03 | 1.09 | ||
| 90° | 267 | 358 | 38 | 1.09 | 1.17 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miková, Ľ.; Prada, E.; Kelemen, M.; Krys, V.; Mykhailyshyn, R.; Sinčák, P.J.; Merva, T.; Leštach, L. Upgrade of Biaxial Mechatronic Testing Machine for Cruciform Specimens and Verification by FEM Analysis. Machines 2022, 10, 916. https://doi.org/10.3390/machines10100916
Miková Ľ, Prada E, Kelemen M, Krys V, Mykhailyshyn R, Sinčák PJ, Merva T, Leštach L. Upgrade of Biaxial Mechatronic Testing Machine for Cruciform Specimens and Verification by FEM Analysis. Machines. 2022; 10(10):916. https://doi.org/10.3390/machines10100916
Chicago/Turabian StyleMiková, Ľubica, Erik Prada, Michal Kelemen, Václav Krys, Roman Mykhailyshyn, Peter Ján Sinčák, Tomáš Merva, and Lukáš Leštach. 2022. "Upgrade of Biaxial Mechatronic Testing Machine for Cruciform Specimens and Verification by FEM Analysis" Machines 10, no. 10: 916. https://doi.org/10.3390/machines10100916
APA StyleMiková, Ľ., Prada, E., Kelemen, M., Krys, V., Mykhailyshyn, R., Sinčák, P. J., Merva, T., & Leštach, L. (2022). Upgrade of Biaxial Mechatronic Testing Machine for Cruciform Specimens and Verification by FEM Analysis. Machines, 10(10), 916. https://doi.org/10.3390/machines10100916









