Modeling, Identification, and Compensation Control of Friction for a Novel Dual-Drive Hydrostatic Lead Screw Micro-Feed System
Abstract
1. Introduction
2. Description and Modeling of System
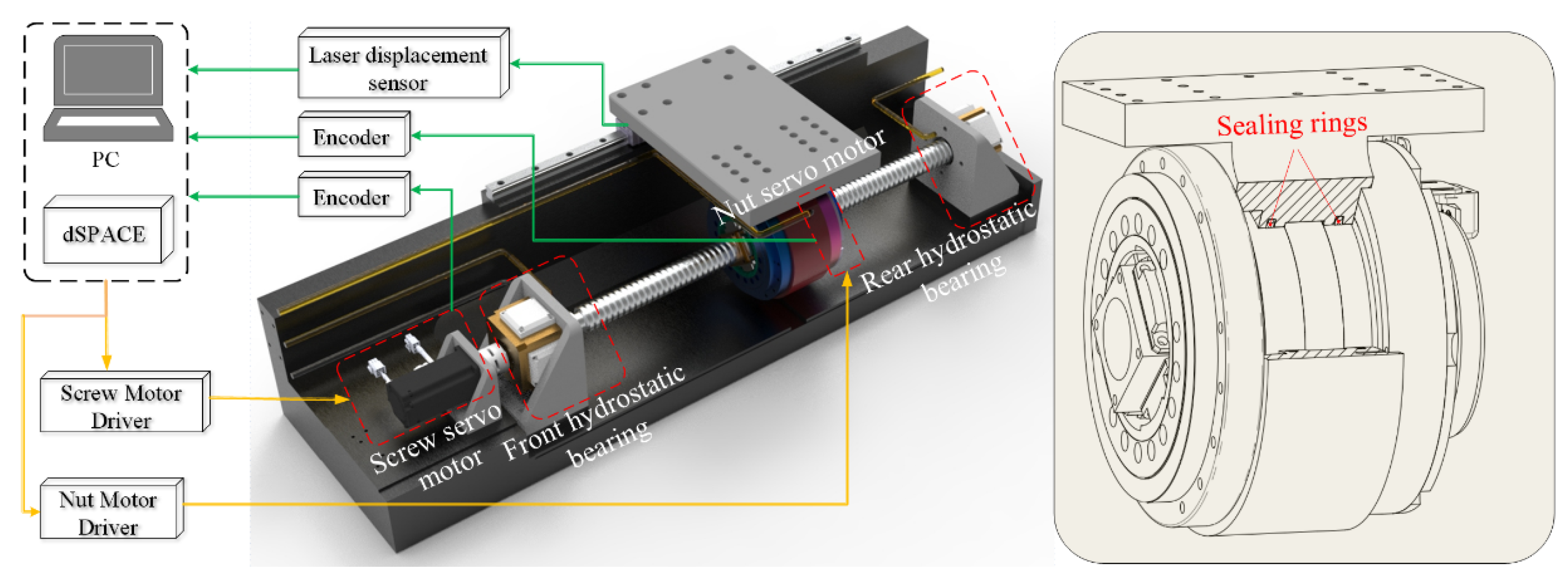
2.1. System Description
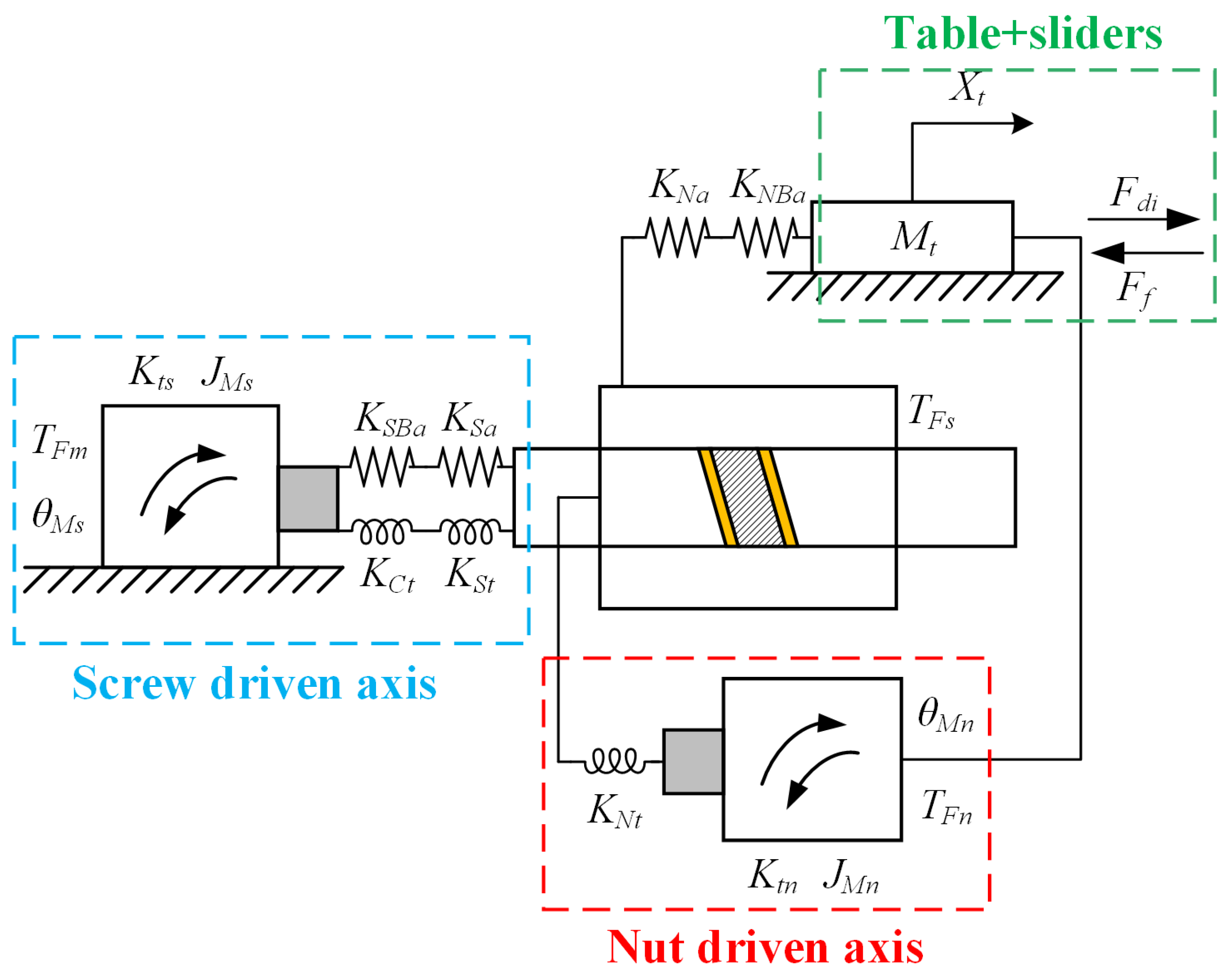
2.2. Dynamic Modeling of the DDHLS
2.3. Modeling of Friction in DDHLS
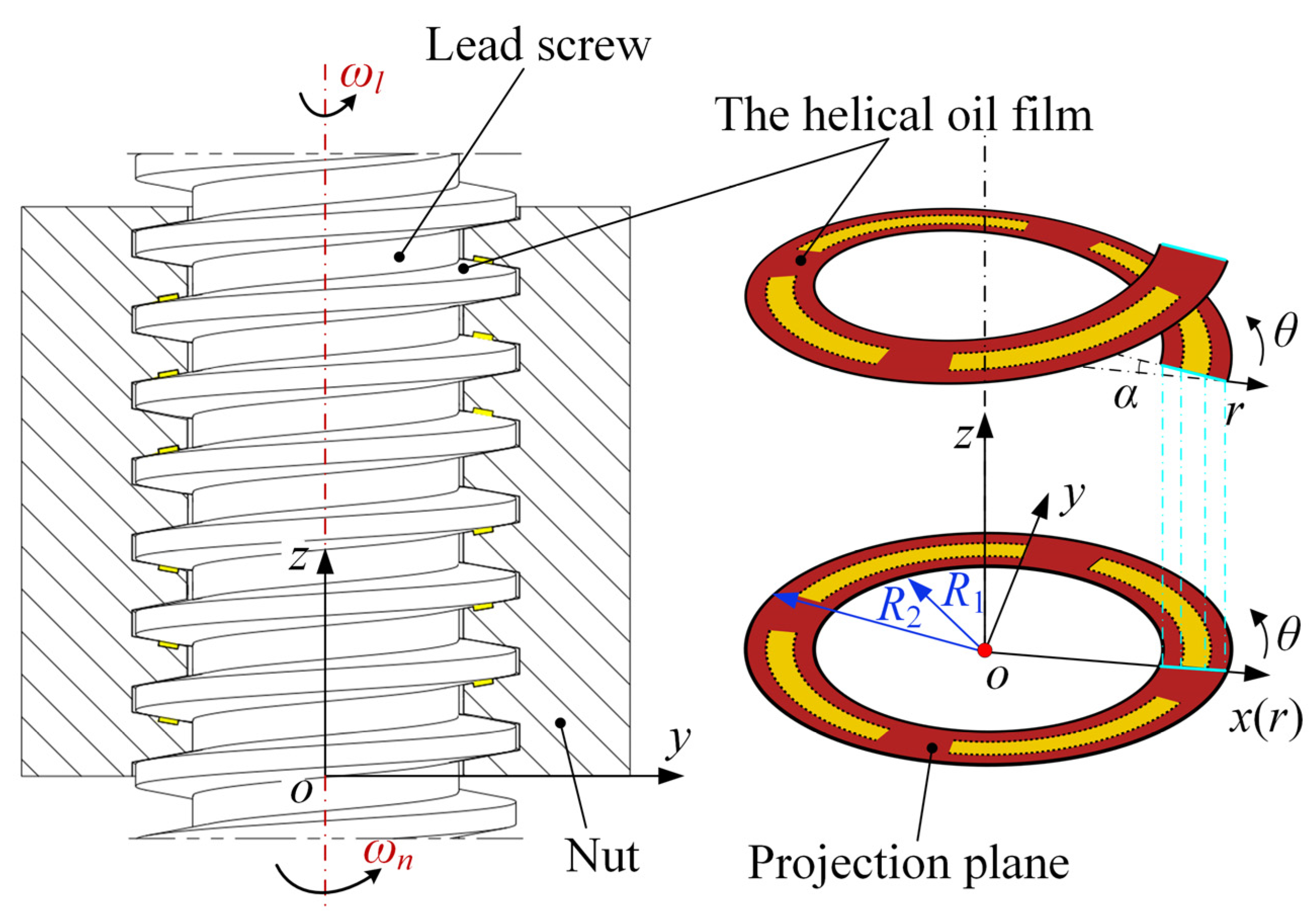
2.3.1. Fluid Friction Modeling
The Hydrostatic Lead Screw
The Front Hydrostatic Bearing
The Rear Hydrostatic Bearing
2.3.2. Fluid Friction Calculation Model Based on Variable Viscosity Theory
2.3.3. Boundary Friction Modeling
3. Friction Identification in DDHLS
3.1. Friction Identification of the Screw Drive Motor
3.2. Identification for the Friction Model of LM Guides
3.3. Identification for the Friction Model of Nut Shaft
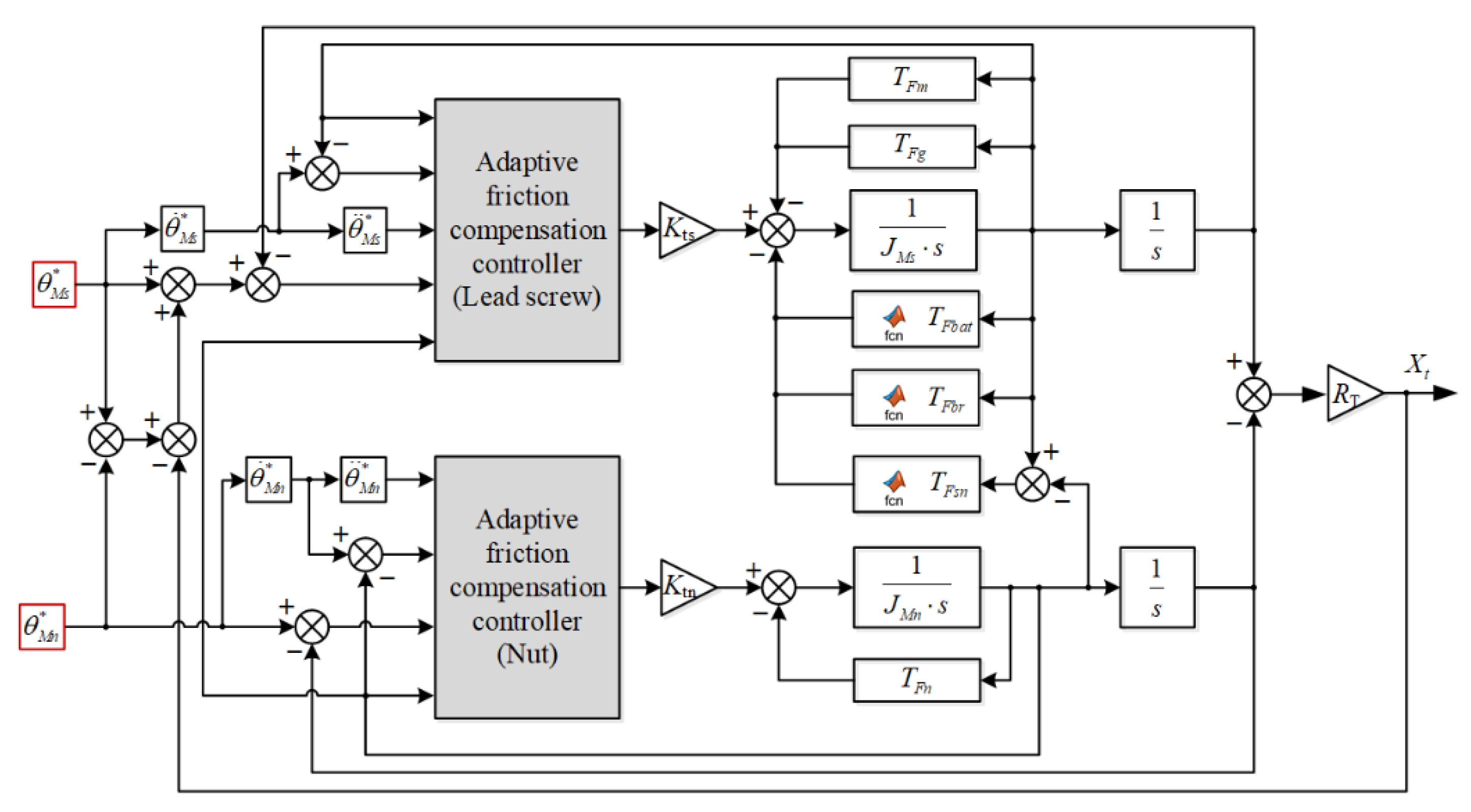
4. Controller Design
5. Experiments and Results
5.1. Experimental Setup
5.2. Fluid Friction Model Estimation
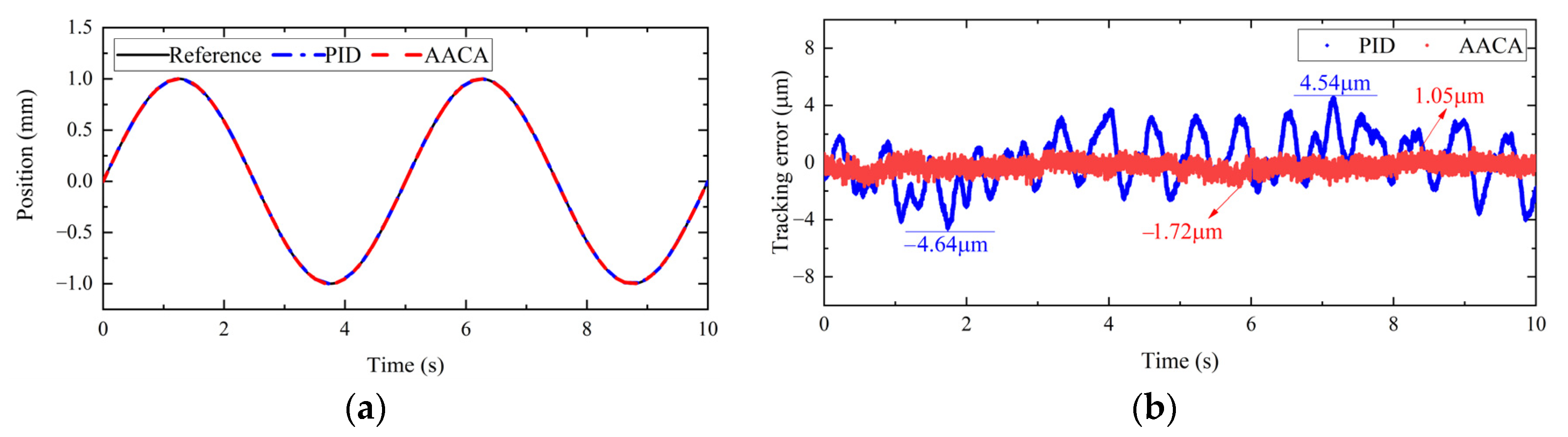
5.3. Friction Compensation
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Yuan, J.; Zhang, F.; Dai, Y.; Kang, R.; Yang, H.; Lv, B. Development Research of Science and Technologies in Ultra-precision Machining Field. J. Mech. Eng. 2010, 46, 161–177. [Google Scholar] [CrossRef]
- Wang, Z.; Feng, X.; Du, F.; Li, H.; Su, Z. A novel method for smooth low-speed operation of linear feed systems. Precis. Eng. 2019, 60, 215–221. [Google Scholar] [CrossRef]
- Du, F.; Zhang, M.; Wang, Z.; Yu, C.; Feng, X.; Li, P. Identification and compensation of friction for a novel two-axis differential micro-feed system. Mech. Syst. Signal Process. 2018, 106, 453–465. [Google Scholar] [CrossRef]
- El-Sayed, H.; Khatan, H. A suggested new profile for externally pressurized power screws. Wear 1975, 31, 141–156. [Google Scholar] [CrossRef]
- Liu, Y.; Feng, X.; Li, Y.; Lu, J.; Su, Z. Research on boundary slip of hydrostatic lead screw under different driving modes. Sci. Rep. 2021, 11, 22307. [Google Scholar] [CrossRef]
- Huang, S.; Liang, W.; Tan, K.K. Intelligent Friction Compensation: A Review. IEEE/ASME Trans. Mechatron. 2019, 24, 1763–1774. [Google Scholar] [CrossRef]
- Indri, M.; Trapani, S. Framework for Static and Dynamic Friction Identification for Industrial Manipulators. IEEE/ASME Trans. Mechatron. 2020, 25, 1589–1599. [Google Scholar] [CrossRef]
- Marques, F.; Flores, P.; Pimenta Claro, J.C.; Lankarani, H.M. A survey and comparison of several friction force models for dynamic analysis of multibody mechanical systems. Nonlinear Dyn. 2016, 86, 1407–1443. [Google Scholar] [CrossRef]
- Breki, A.; Nosonovsky, M. Ultraslow frictional sliding and the stick-slip transition. Appl. Phys. Lett. 2018, 113, 241602. [Google Scholar] [CrossRef]
- Li, F.; Jiang, Y.; Li, T.; Ehmann, K.F. Compensation of dynamic mechanical tracking errors in ball screw drives. Mechatronics 2018, 55, 27–37. [Google Scholar] [CrossRef]
- Lee, C.; Hwang, S.; Nam, E.; Min, B. Identification of mass and sliding friction parameters of machine tool feed drive using recursive least squares method. Int. J. Adv. Manuf. Technol. 2020, 109, 2831–2844. [Google Scholar] [CrossRef]
- Yang, M.; Yang, J.; Ding, H. A two-stage friction model and its application in tracking error pre-compensation of CNC machine tools. Precis. Eng. 2018, 51, 426–436. [Google Scholar] [CrossRef]
- Thenozhi, S.; Sanchez, A.C.; Rodriguez-Resendiz, J. A Contraction Theory-Based Tracking Control Design with Friction Identification and Compensation. IEEE Trans. Ind. Electron. 2022, 69, 6111–6120. [Google Scholar] [CrossRef]
- Dumanli, A.; Sencer, B. Pre-compensation of servo tracking errors through data-based reference trajectory modification. CIRP Ann. 2019, 68, 397–400. [Google Scholar] [CrossRef]
- Sancak, K.; Bayraktaroglu, Z. Observer-Based Friction Compensation in Heavy-Duty Parallel Robot Control. J. Mech. Sci. Technol. 2021, 35, 3693–3704. [Google Scholar] [CrossRef]
- Feng, H.; Qiao, W.; Yin, C.; Yu, H.; Cao, D. Identification and compensation of non-linear friction for a electro-hydraulic system. Mech. Mach. Theory 2019, 141, 1–13. [Google Scholar] [CrossRef]
- Lu, D.; Liu, K.; Zhao, W.; Lu, B. Thermal Characteristics of Water-Lubricated Ceramic Hydrostatic Hydrodynamic Hybrid Bearings. Tribol. Lett. 2016, 63, 23. [Google Scholar] [CrossRef]
- Jiang, R.; Liu, C.; Ning, Y. Control Strategy with Adaptive Friction Torque Compensation for Radar Servo System. J. Mech. Eng. 2019, 18, 187–195. [Google Scholar]
- Li, C.; Chen, Z.; Yao, B. Identification and adaptive robust precision motion control of systems with nonlinear friction. Nonlinear Dyn. 2019, 95, 995–1007. [Google Scholar] [CrossRef]
- Rahmani, M.; Rahman, M.H.; Nosonovsky, M. A new hybrid robust control of MEMS gyroscope. Microsyst. Technol. 2020, 26, 853–860. [Google Scholar] [CrossRef]
- Yu, H.; Feng, X. Dynamic Modeling and Spectrum Analysis of Macro-Macro Dual Driven System. Jilin Water Resour. 2016, 11, 044505. [Google Scholar] [CrossRef]
- Dong, W.; Li, B.; Guo, W.; Zhou, Q. Prediction of different design conditions on comprehensive performance of hydrostatic slide and experimental verification. Int. J. Adv. Manuf. Technol. 2020, 107, 535–547. [Google Scholar] [CrossRef]
- Seeton, C. Viscosity–Temperature Correlation for Liquids. Tribol. Lett. 2006, 1, 67–78. [Google Scholar] [CrossRef]
- Zhao, J.; Gao, D. Influence of Hydraulic Oil Viscosity on Characteristics of Liquid Hydrostatic Slide. China Mech. Eng. 2013, 21, 2847–2851. [Google Scholar]
- Freidovich, L.; Robertsson, A.; Shiriaev, A.; Johansson, R. LuGre-Model-Based Friction Compensation. IEEE Trans. Control Syst. Technol. 2010, 18, 194–200. [Google Scholar] [CrossRef]
- Yao, J.; Deng, W.; Jiao, Z. Adaptive Control of Hydraulic Actuators with LuGre Model-Based Friction Compensation. IEEE Trans. Ind. Electron. 2015, 62, 6469–6477. [Google Scholar] [CrossRef]
- De Wit, C.C.; Olsson, H.; Astrom, K.J.; Lischinsky, P. A new model for control of systems with friction. IEEE Trans. Autom. Control 1995, 3, 419–425. [Google Scholar] [CrossRef]
- Wang, X.; Wang, S. Output torque tracking control of direct-drive rotary torque motor with dynamic friction compensation. J. Frankl. Inst. 2015, 352, 5361–5379. [Google Scholar] [CrossRef]









| Parameters | Value |
|---|---|
| Torsional stiffness of the coupling (KCt) | 4.1 × 106 N·m/rad |
| Torsional stiffness of the screw (KSt) | 8.42 × 106 N·m/rad |
| Axial stiffness of the bearing (KSBa) | 8 × 108 N/m |
| Axial stiffness of the screw (KSa) | 1.73 × 108 N/m |
| Axial stiffness of the nut (KNa) | 5.95 × 108 N/m |
| Axial stiffness of the nut-bearing (KNBa) | 12 × 108 N/m |
| Moment of inertia equivalent to the motor (JS, JN) | 5.92 × 10−3 Kg·m2 |
| Oil supply pressure (Ps) | 3.2 MPa |
| Density of hydraulic oil (ρ) | 876 Kg/m3 |
| Specific heat capacity of hydraulic oil (J) | 1760 Kg·K |
| Parameters | Value |
|---|---|
| Inner radius of the nut (R1) | 14 mm |
| Outer radius of the lead screw (R2) | 20 mm |
| Half angle of thread (α) | 10° |
| Pitch (P) | 8 mm |
| Number of nut threads with helical recesses (N) | 6 |
| Designed axial clearance for the hydrostatic lead screw (h0) | 0.025 mm |
| Parameters | Value | Parameters | Value |
|---|---|---|---|
| ra | 39.03 mm | hb | 0.02 mm |
| rb | 42.2 mm | αbc | 30° |
| rc | 68.4 mm | rA | 17.5 mm |
| rd | 70 mm | rB | 20.7 mm |
| θs | 120° | rC | 33.9 mm |
| hr | 0.5 mm | rD | 35.5 mm |
| Parameters | Value |
|---|---|
| Oil flow of hydrostatic lead screw (qsn) | 0.75 L/min |
| Oil flow of front hydrostatic bearing (qbat) | 0.4 L/min |
| Oil flow of rear hydrostatic bearing (qbr) | 0.25 L/min |
| Parameters | Values | Parameters | Values | ||||
|---|---|---|---|---|---|---|---|
| Serve Motor | LM guide | The Nut Shaft | |||||
| Positive | Negative | Positive | Negative | Positive | Negative | ||
| Ts (N·m) | 0.0608 | −0.10594 | Fs (N) | 17.721 | −18.223 | 16.74 | −12.37 |
| Tc (N·m) | 0.0574 | −0.0558 | Fc (N) | 13.097 | −13.407 | 5.09 | −3.18 |
| θs (r/s) | 0.0082 | −0.0093 | vs (m/s) | 0.0043 | −0.0041 | 0.00792 | −0.00331 |
| σ2 (N·m·s/r) | 0.0006 | 0.0005 | σ2 (N·s/m) | 59.125 | 60.394 | 1.24 | 3.51 |
| σ0 (N·m/r) | 41.34 | σ0 (N/m) | 4.54 × 105 | 1.15 × 106 | |||
| σ1 (N·m·s/r) | 0.22 | σ1 (N·s/m) | 1.87 × 103 | 1.73 × 102 | |||
| Viscosity Types | Estimation Error (N·m) | Estimation Error (°C) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Bearings | Lead Screw | Front Bearing | Rear Bearing | Lead Screw | ||||||
| Max | Mean | Max | Mean | Max | Mean | Max | Mean | Max | Mean | |
| Constant | 0.289 | 0.127 | 0.115 | 0.045 | 5.461 | 2.611 | 1.582 | 0.674 | 0.757 | 0.558 |
| Variable | 0.032 | 0.016 | 0.029 | 0.009 | 0.421 | 0.138 | 0.367 | 0.120 | 0.447 | 0.230 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Feng, X.; Li, P.; Li, Y.; Su, Z.; Liu, H.; Lu, Z.; Yao, M. Modeling, Identification, and Compensation Control of Friction for a Novel Dual-Drive Hydrostatic Lead Screw Micro-Feed System. Machines 2022, 10, 914. https://doi.org/10.3390/machines10100914
Liu Y, Feng X, Li P, Li Y, Su Z, Liu H, Lu Z, Yao M. Modeling, Identification, and Compensation Control of Friction for a Novel Dual-Drive Hydrostatic Lead Screw Micro-Feed System. Machines. 2022; 10(10):914. https://doi.org/10.3390/machines10100914
Chicago/Turabian StyleLiu, Yandong, Xianying Feng, Peigang Li, Yanfei Li, Zhe Su, Haiyang Liu, Ziteng Lu, and Ming Yao. 2022. "Modeling, Identification, and Compensation Control of Friction for a Novel Dual-Drive Hydrostatic Lead Screw Micro-Feed System" Machines 10, no. 10: 914. https://doi.org/10.3390/machines10100914
APA StyleLiu, Y., Feng, X., Li, P., Li, Y., Su, Z., Liu, H., Lu, Z., & Yao, M. (2022). Modeling, Identification, and Compensation Control of Friction for a Novel Dual-Drive Hydrostatic Lead Screw Micro-Feed System. Machines, 10(10), 914. https://doi.org/10.3390/machines10100914






