Non-Probabilistic Reliability Analysis of Robot Accuracy under Uncertain Joint Clearance
Abstract
1. Introduction
2. Mathematical Modeling of Robotic Systems
2.1. Robot System Kinematics Positive Solution
2.2. Reliability Model for Robot Motion Based on Non-Probability Interval Theory
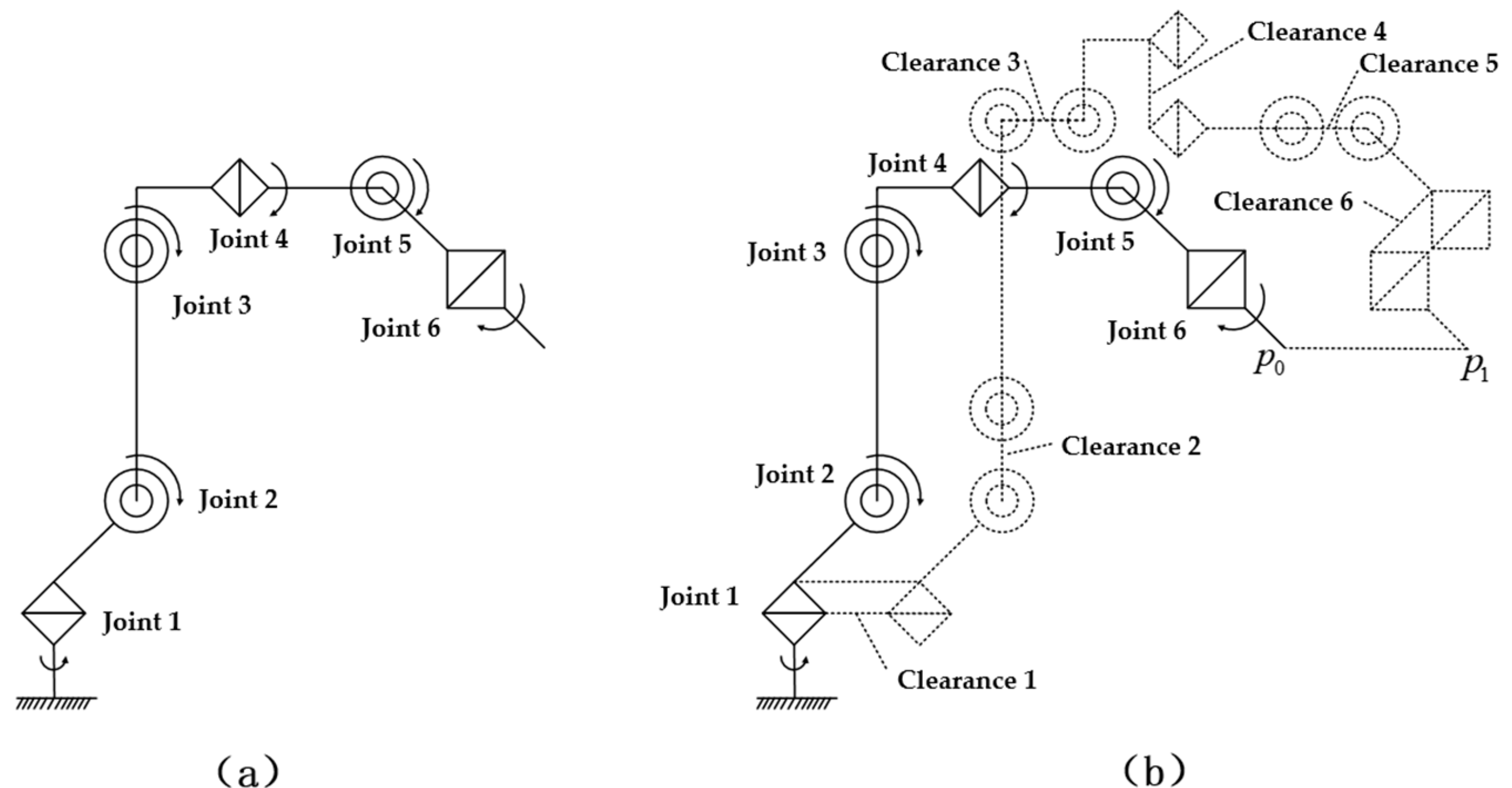
3. Parametric Modeling of 6-Degree-of-Freedom Robots
3.1. Joint Clearance Modeling Ideas
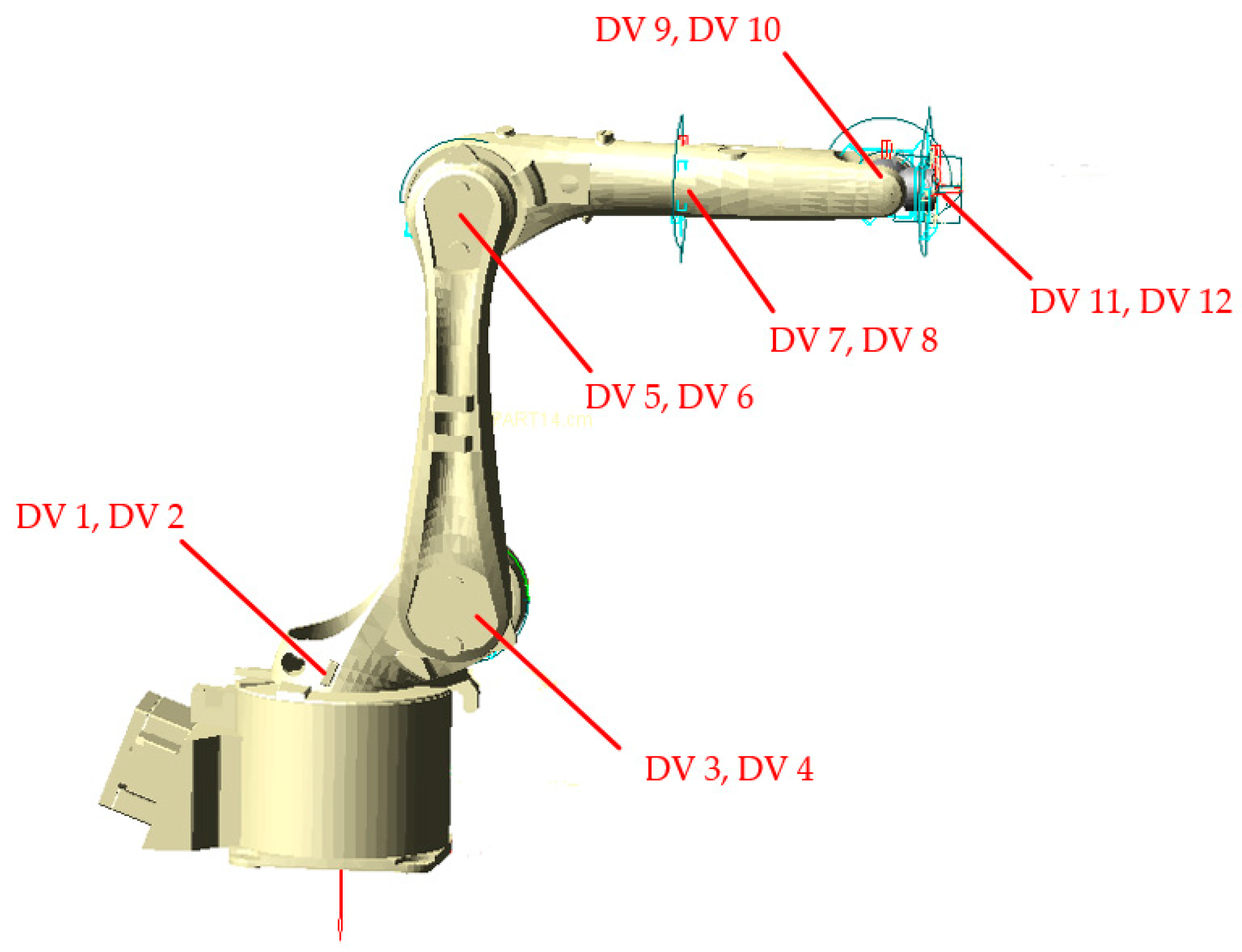
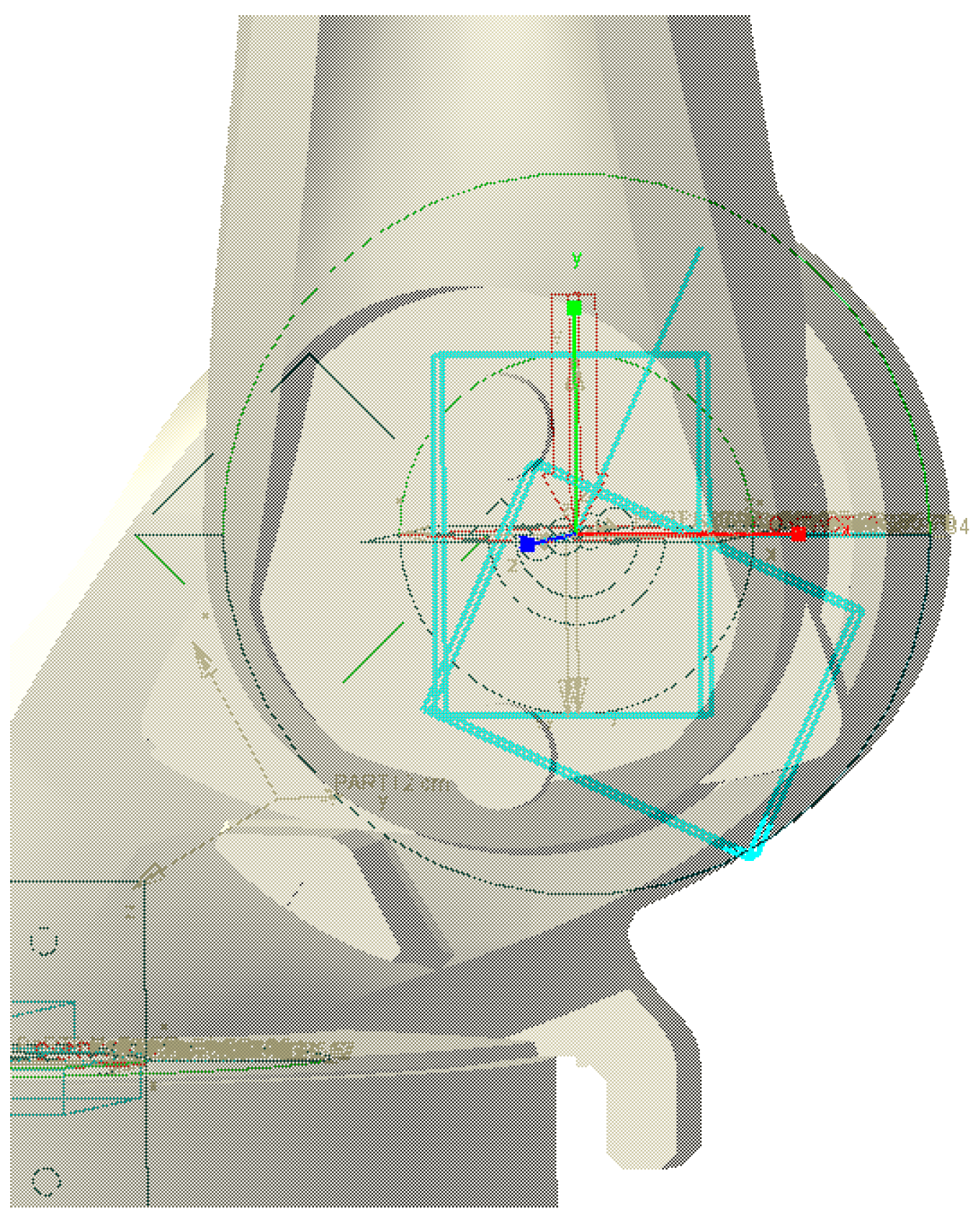
3.2. Parametric Modeling of Joint Clearance
3.3. Setting of Model Drive Parameters
4. Simulation Analysis of Positioning Accuracy of Industrial Robots
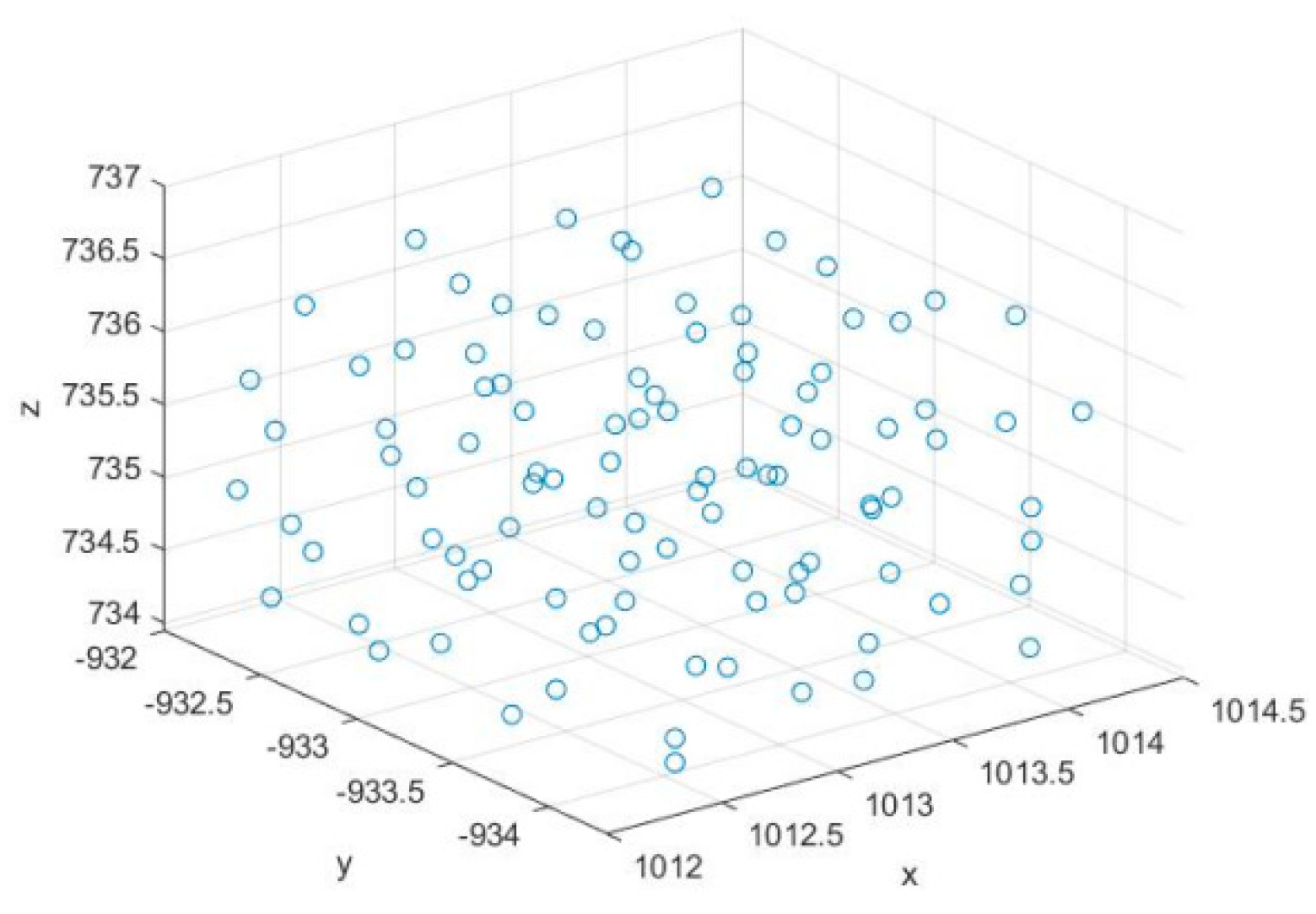
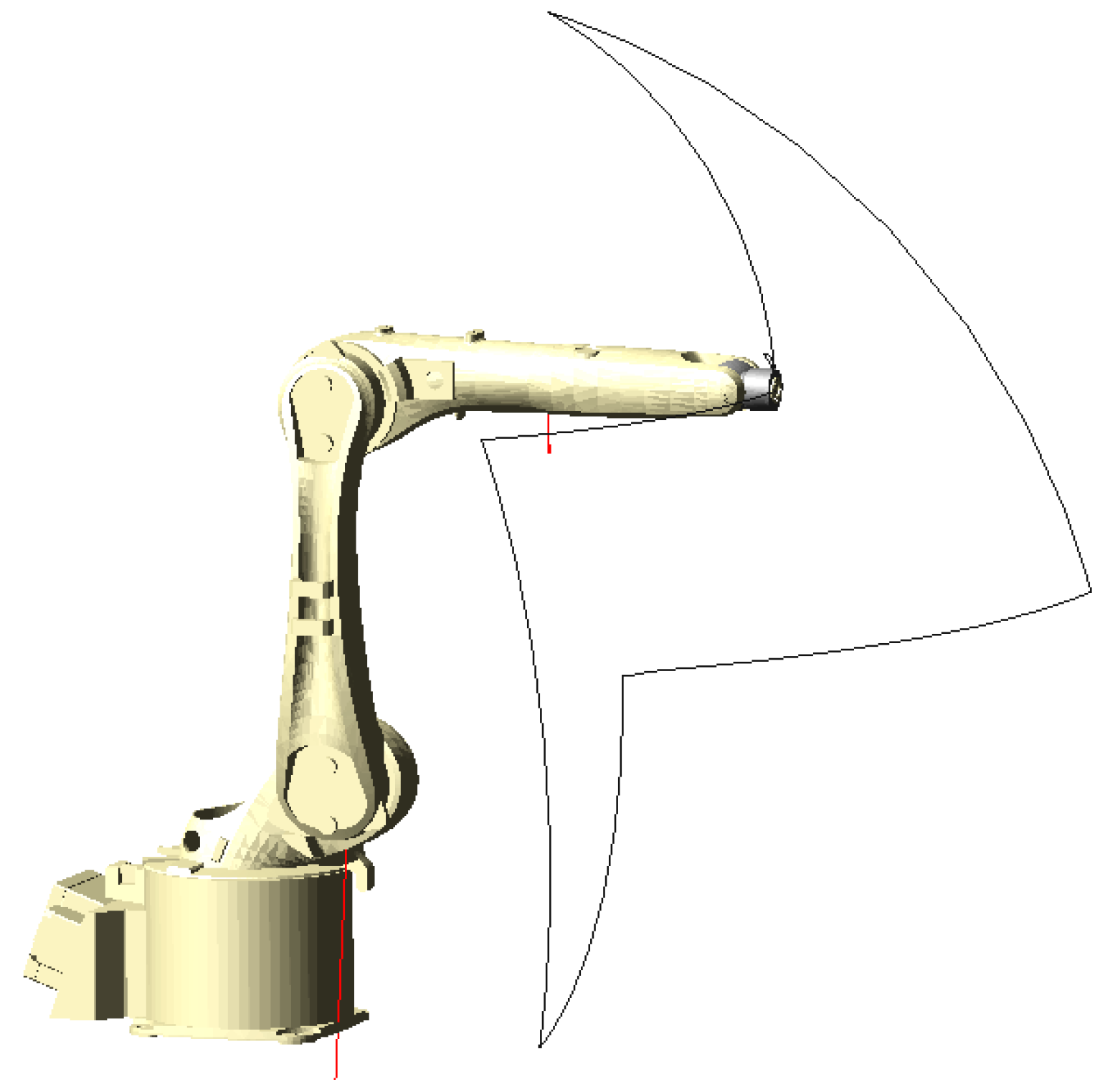
4.1. Analysis of End-Effector Coordinate Points
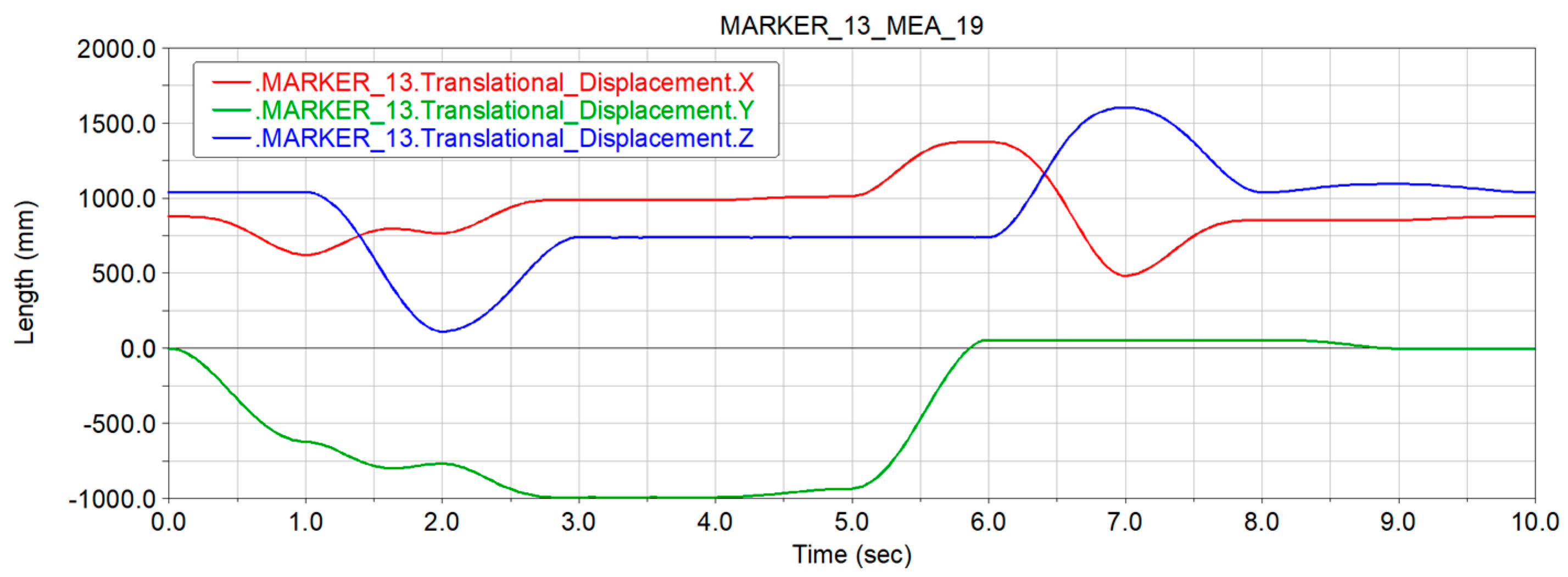
4.2. Analysis of End-Effector Trajectories
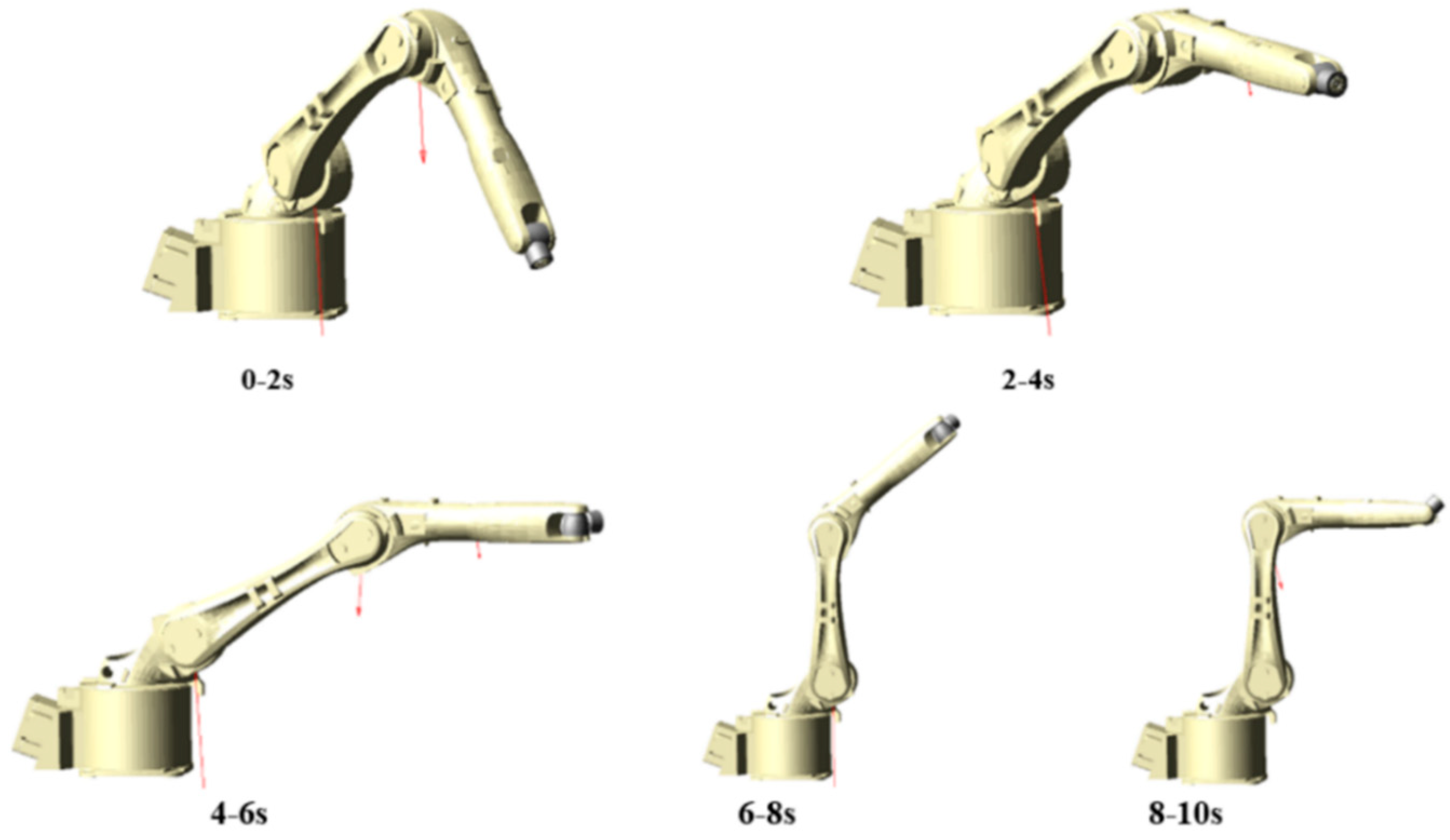
4.3. Analysis of Different Time Periods of Robot End-Effectors
5. Conclusions
- (1)
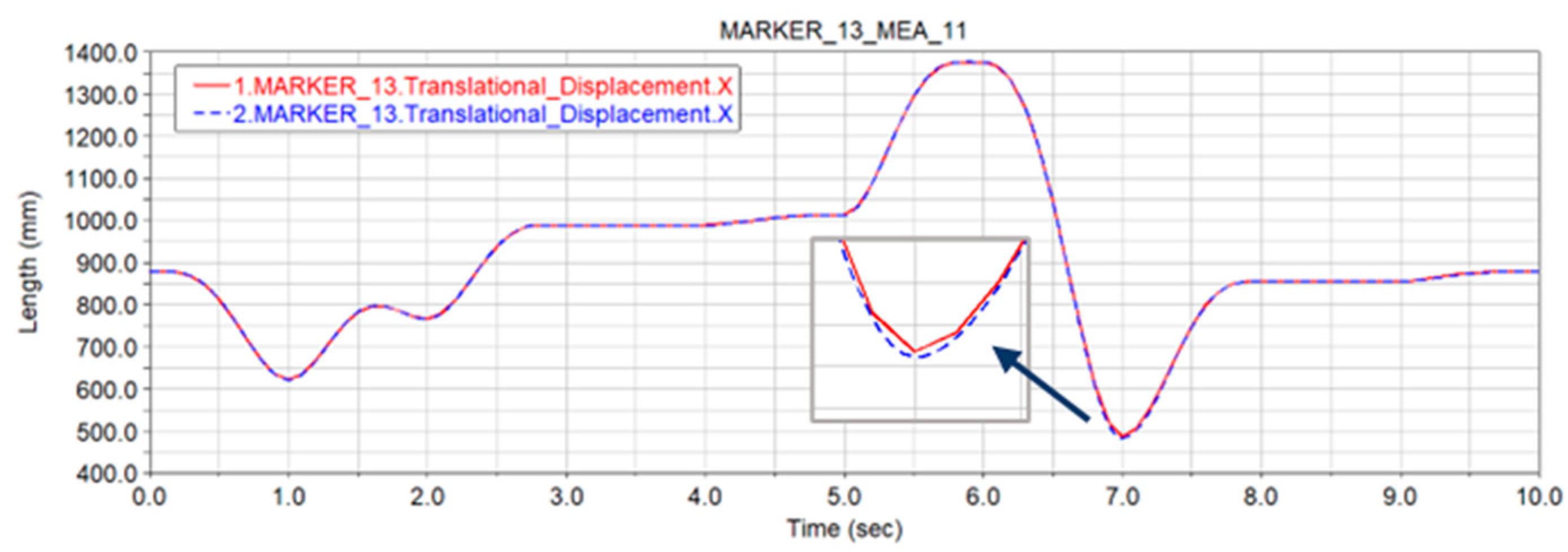
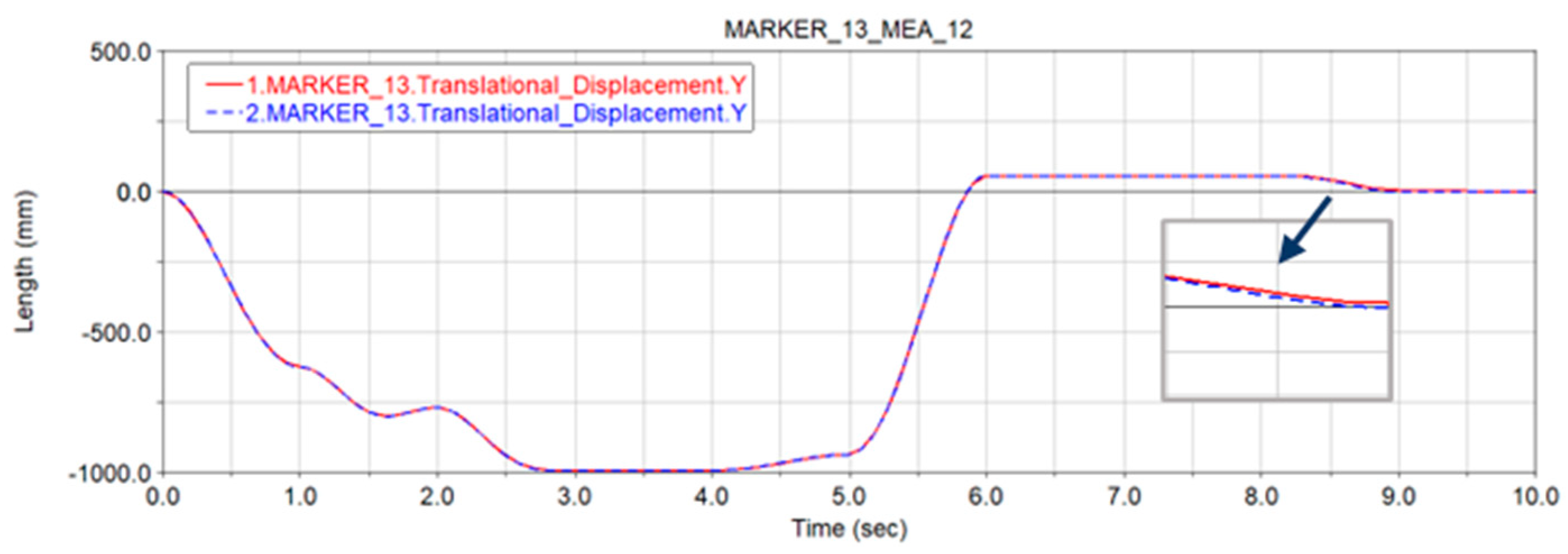
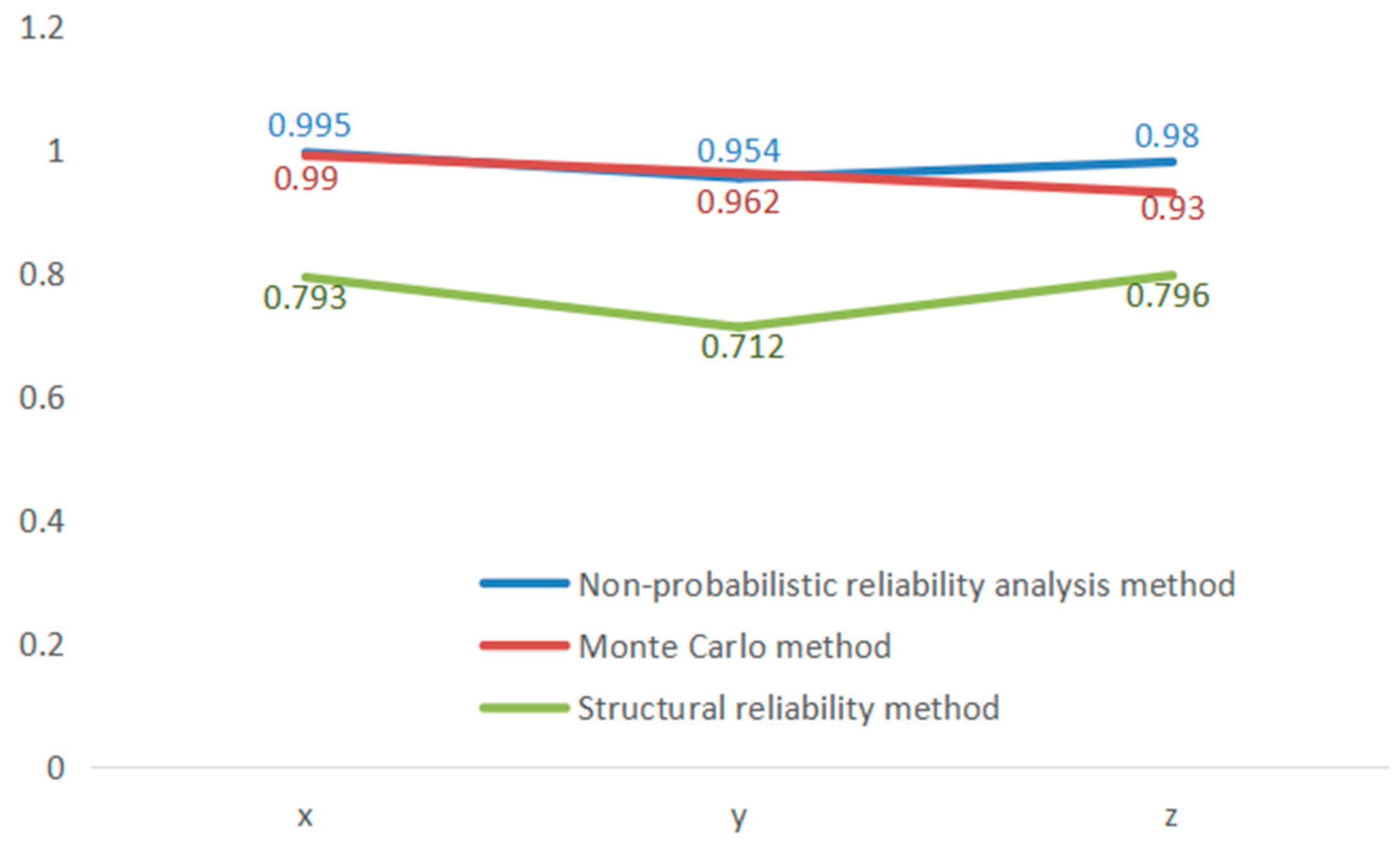
- Non-probabilistic reliability is introduced to analyze the robot position accuracy under the influence of uncertainty considering the joint clearance, and it is found that the method in this paper is consistent with the traditional probabilistic method in evaluating the reliability of the robot end position, but the method in this paper has a lower degree of data requirement and has obvious advantages for the reliability analysis of small sample and information-poor structured systems.
- (2)
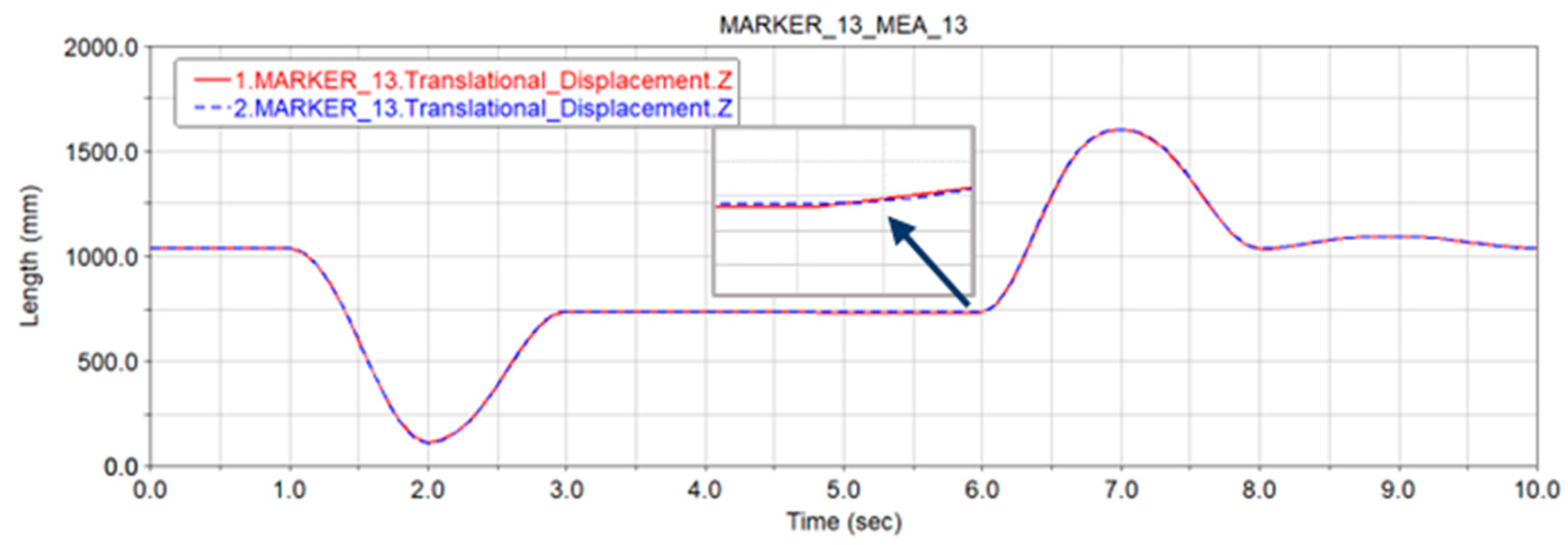
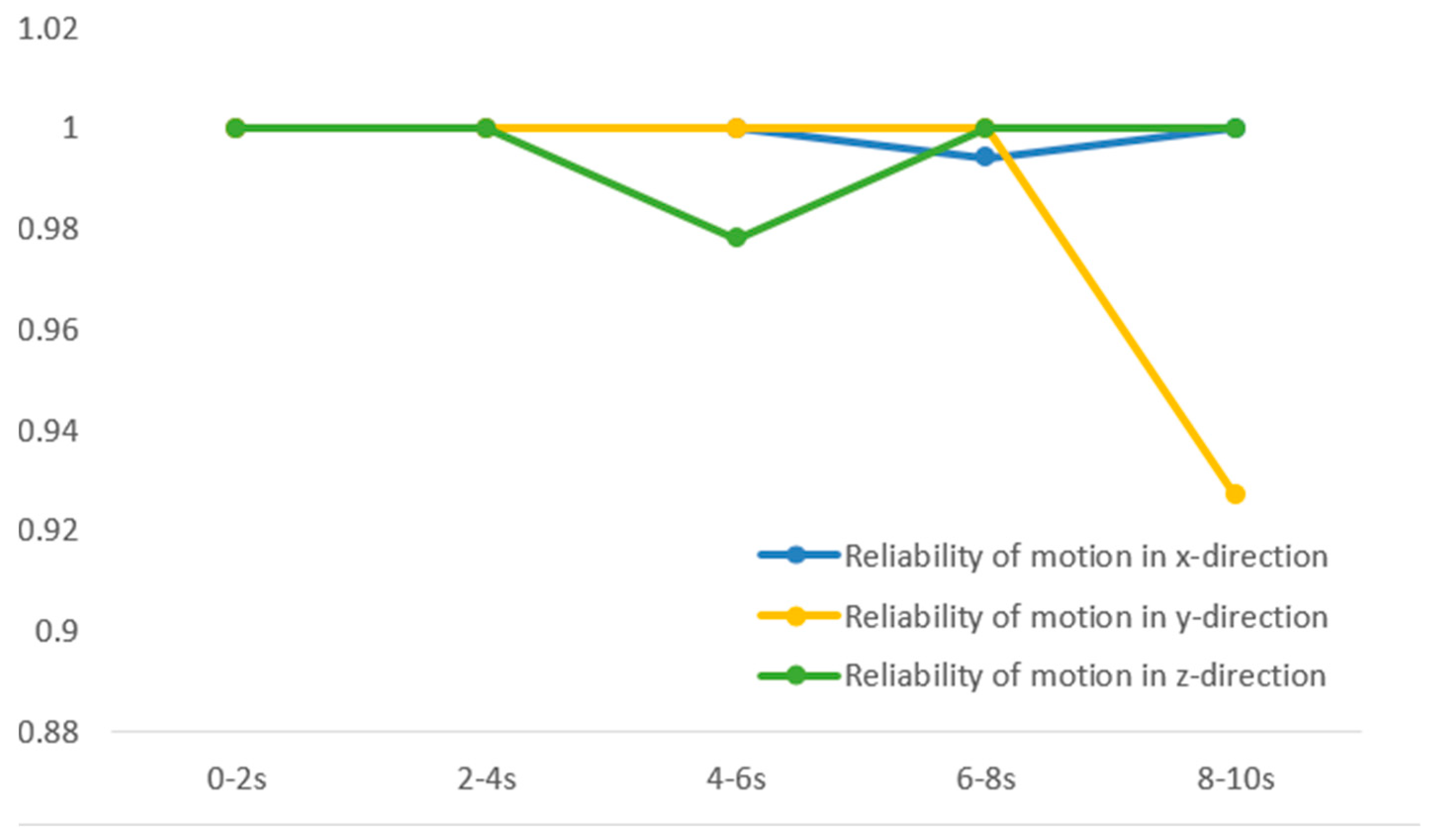
- The simulation analysis of the robot under the influence of the ideal state and uncertain joint clearance parameters is carried out to obtain the displacement error range in each spatial direction, and the reliability analysis based on the non-probability interval theory is carried out. The reliability of the end-effector of the robot is related to the displacement curve. The reliability decreases at the inflection point of the displacement curve and is higher at the smooth displacement curve, and the phenomenon of uneven transition of the displacement curve should be avoided when planning the robot motion trajectory; the reliability of the end-effector is related to its position in the workspace, and the further away from the center of the workspace, the worse the reliability.
- (3)
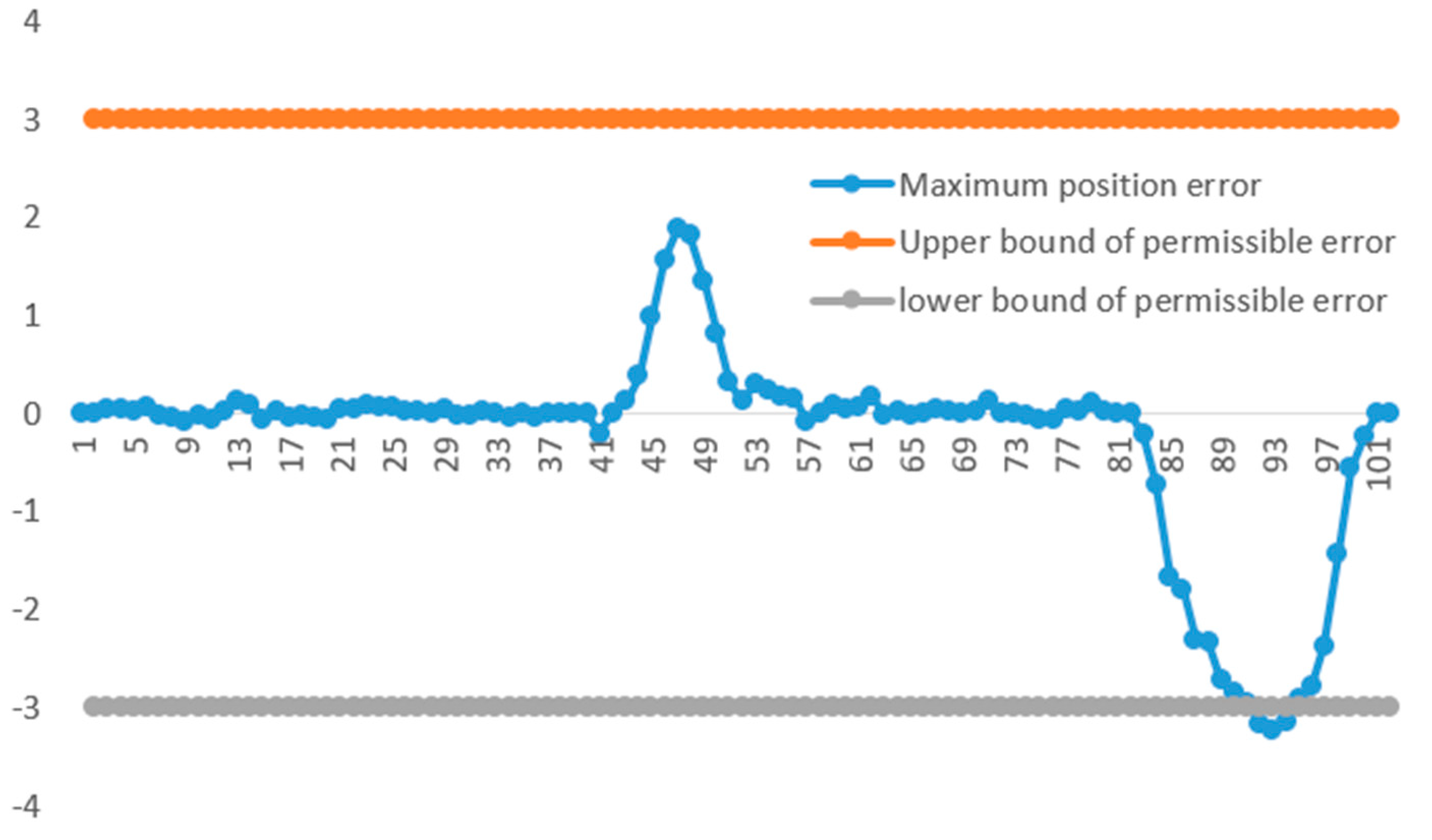
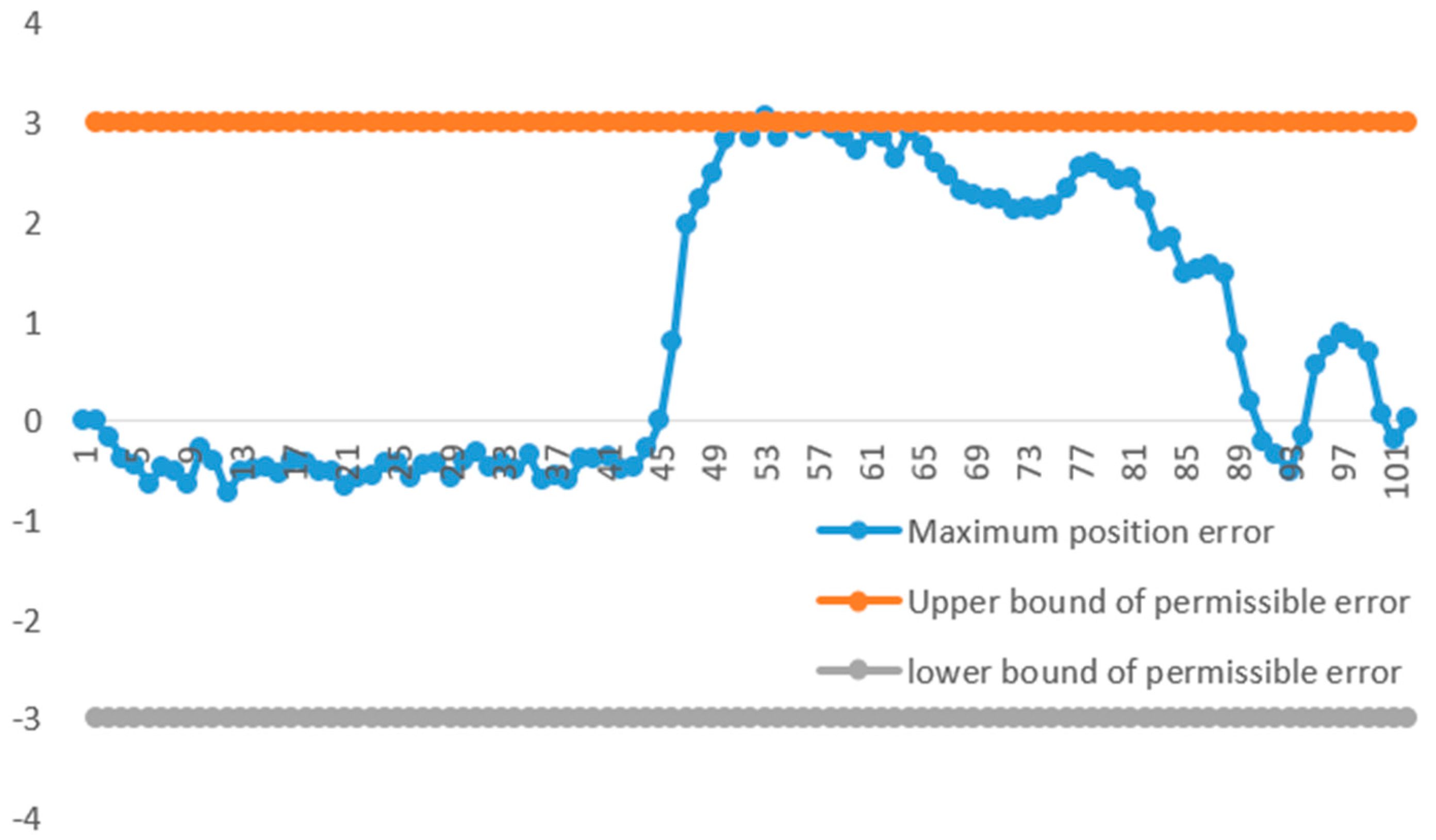
- The motion path is divided into small segments in time, and the reliability of each segment’s motion is analyzed to compare the reliability of the end-effector in different workspace areas corresponding to different time segments, and the conclusion is drawn that the reliability of the end-effector changes in different working regions under the influence of uncertain joint clearance parameters. Based on this conclusion, the research direction of dividing the robot space and partitioning it to establish a non-probability-based reliability calibration model is proposed, which can realize the prediction of the robot end-effector position range and the interval identification of parameters and improve the positioning accuracy and calibration reliability of the robot in the full workspace region.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wu, J.; Tao, Y. Review on Research Status of Positioning Accuracy Reliability of Industrial Robots. China Mech. Eng. 2020, 31, 2180–2188. [Google Scholar] [CrossRef]
- Chen, X.; Wang, T.; Jiang, S. Study of the Dynamic Characteristics of Mechanisms with all Clearance Joints. Mach. Des. Manuf. 2018, 326, 19–22. [Google Scholar] [CrossRef]
- Andrei, L.; Stan, G. The influence of reference position deviation on industrial robots positioning precision. IOP Conf. Ser. Mater. Sci. Eng. 2018, 400, 052004. [Google Scholar] [CrossRef]
- Zi-Qi, Y. Kinematic Error Analysis of Controllable Palletizing Robot. Equip. Manuf. Technol. 2020, 3, 89–93. [Google Scholar] [CrossRef]
- Gu, Y.; Zhang, Y.L.; Zhao, J.L.; Yan, S.Z. Dynamic Characteristics of Free-floating Space Manipulator with Joint Clearance. J. Mech. Eng. 2019, 55, 99–108. [Google Scholar] [CrossRef]
- Jian-Feng, H.; Ying-Long, C.; Jiang-Yi, C. Analysis of Kinematic Accuracy of 3-RRR Mechanism Considering Joint Clearances and Flexible Components. Mach. Tool Hydraul. 2019, 47, 5–8+36. [Google Scholar] [CrossRef]
- Zhang, F.; Yuan, Z. The Study of Coupling Dynamics Modeling and Characteristic Analysis for Flexible Robots with Nonlinear and Frictional Joints. Arab. J. Sci. Eng. 2022, 47, 1–17. [Google Scholar] [CrossRef]
- Li, Y.; Shang, D.; Fan, X.; Liu, Y. Motion Reliability Analysis of the Delta Parallel Robot considering Mechanism Errors. Math. Probl. Eng. 2019, 2019, 1–10. [Google Scholar] [CrossRef]
- Wang, W.; Wang, J.; Lu, G.D. Reliability analysis of manipulator based on fourth-moment estimation. J. Zhejiang Univ. 2018, 52, 1–7+49. [Google Scholar] [CrossRef]
- Jiang, G.J.; Gao, L. Reliability analysis of martial arts arena robot systems based on fuzzy set theory. J. Mech. Sci. Technol. 2018, 32, 5069–5077. [Google Scholar] [CrossRef]
- Icli, C.; Stepanenko, O.; Bonev, I. New method and portable measurement device for the calibration of industrial robots. Sensors 2020, 20, 5919. [Google Scholar] [CrossRef]
- Cui, W.X.; Qu, S.L.; Wen, X.L.; Feng, Y.G. Research on Reliability of Robot Calibration Based on Monte Carlo Method. J. Nanjing Inst. Technol. 2021, 19, 1–6. [Google Scholar] [CrossRef]
- Shang, D.; Li, Y.; Liu, Y.; Cui, S. Research on the Motion Error Analysis and Compensation Strategy of the Delta Robot. Mathematics 2019, 7, 411. [Google Scholar] [CrossRef]
- Qi, J.; Chen, B.; Zhang, D. A calibration method for enhancing robot accuracy through integration of kinematic model and spatial interpolation algorithm. J. Mech. Robot. 2021, 13, 061013. [Google Scholar] [CrossRef]
- Jian-Ping, S.; Jeff, X.; Zhao-Ping, T. Non-probabilistic reliability method for robot position accuracy and calibration. Chin. J. Sci. Instrum. 2018, 39, 109–120. [Google Scholar] [CrossRef]
- Merlet, J.P. Interval Analysis and Reliability in Robotics. Int. J. Reliab. Saf. 2009, 3, 104. [Google Scholar] [CrossRef]
- Lara-Molina, F.A.; Dumur, D. A Fuzzy Approach for the Kinematic Reliability Assessment of Robotic Manipulators. Robotica 2021, 39, 2095–2109. [Google Scholar] [CrossRef]
- Carreras, C.; Walker, I.D. On interval methods applied to robot reliability quantification. Reliab. Eng. Syst. Saf. 2020, 70, 291–303. [Google Scholar] [CrossRef]
- Wu, W.; Rao, S.S. Uncertainty analysis and allocation of joint tolerances in robot manipulators based on interval analysis. Reliab. Eng. Syst. Saf. 2007, 92, 54–64. [Google Scholar] [CrossRef]
- Jorge, S.; Manuel, G. Uncertainty estimation in robot kinematic calibration. Robot. Comput.-Integr. Manuf. 2013, 29, 370–384. [Google Scholar] [CrossRef]
- Chen, S.; Ling, H.; Chen, C.L. Mobile robot localization based on probabilistic fuzzy system. Acad. Conf. Syst. Simul. Technol. Its Appl. 2010, 12, 627–631. [Google Scholar]
- Guo, S.X. and Lu, Z.Z. Procedure for the robust reliability design of structures. Acta Aeronaut. Astronaut. Sin. 2001, 22, 451–453. [Google Scholar] [CrossRef]
- Guo, S.X.; Lu, Z.Z.; Feng, Y.S. A non-probabilistic reliability method for the design of mechanical components. Mech. Sci. Technol. Aerosp. Eng. 2000, 19, 106–107. [Google Scholar] [CrossRef]
- Sun, H.L. Research on some Issues about Interval Model for Structural Reliability Analysis. Ph.D. Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2007. [Google Scholar] [CrossRef]
- Li, L.L.; Zhang, Y.L.; Zhou, X.; Ma, D.J. Structure Non-Probabilistic Reliability Model Based on Interval Analysis. Electr. Energy Manag. Technol. 2014, 8, 1–3. [Google Scholar] [CrossRef]
- Jiang, Y. The Reliability Analysis of 6R Industrial Robot Based on Virtual Prototype Technology. Master Thesis, Anhui Polytechnic University, Wuhu, China, 2017. [Google Scholar]
- Li, H.Z.; Chen, Q.Y.; Zhang, H.W.; Wu, Z.H.; Tang, G.B. Analysis of Kinematic Reliability for SCARA Robots Mechanism Based on ADAMS/Insight. Mach. Des. Res. 2018, 34, 63–66. [Google Scholar] [CrossRef]
- Sun, J.P.; Luo, Y.P.; Tang, Z.P. The Structural Reliability Measurement Method Based on Interval Model. J. Syst. Sci. Math. 2017, 37, 1114–1125. [Google Scholar] [CrossRef]

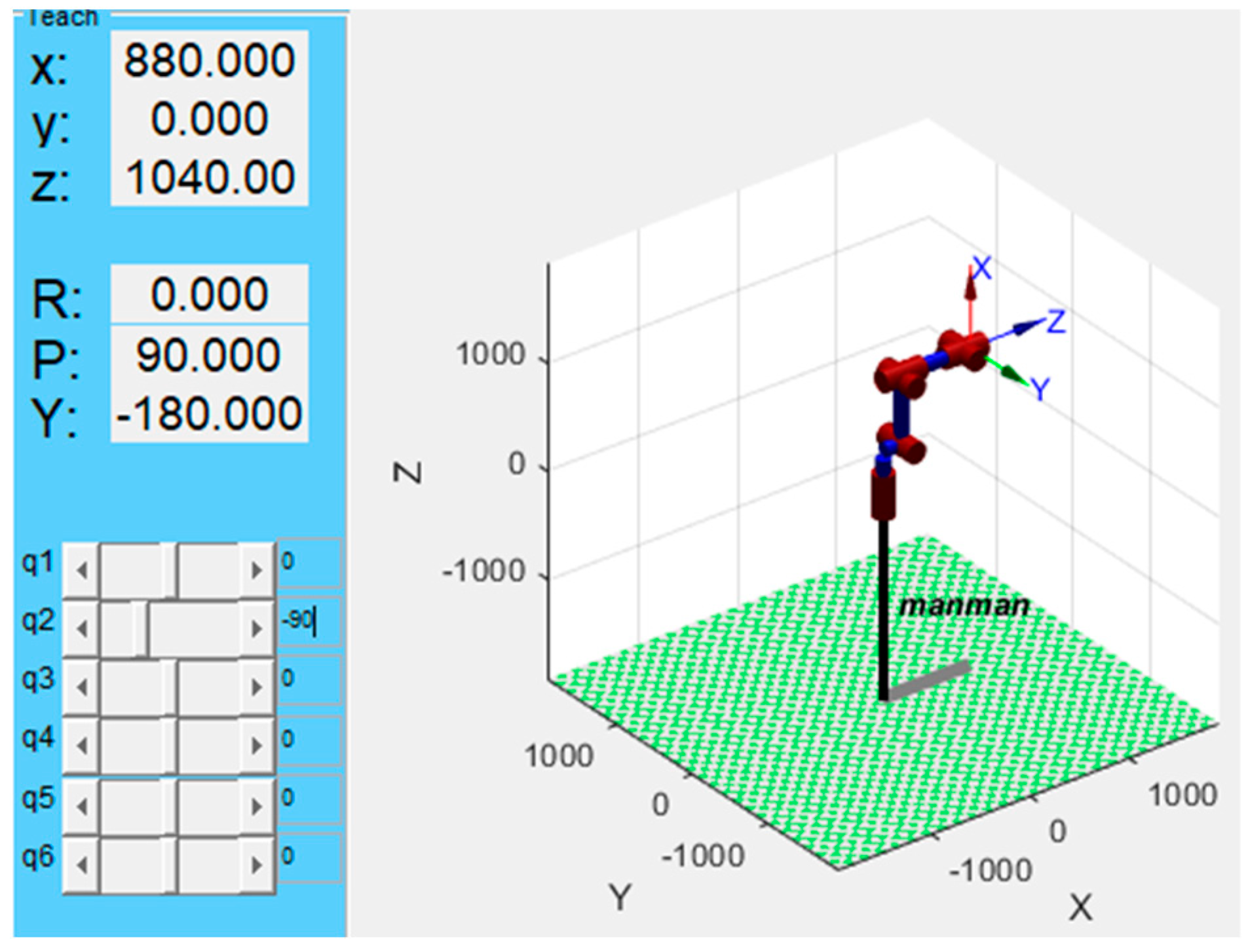
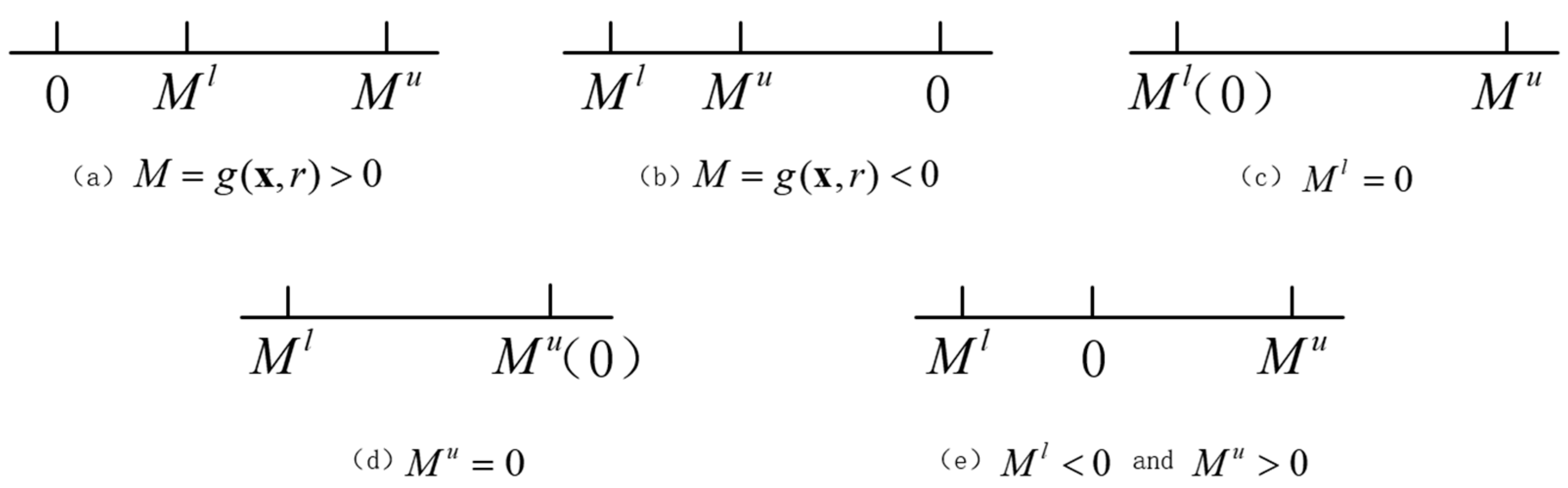
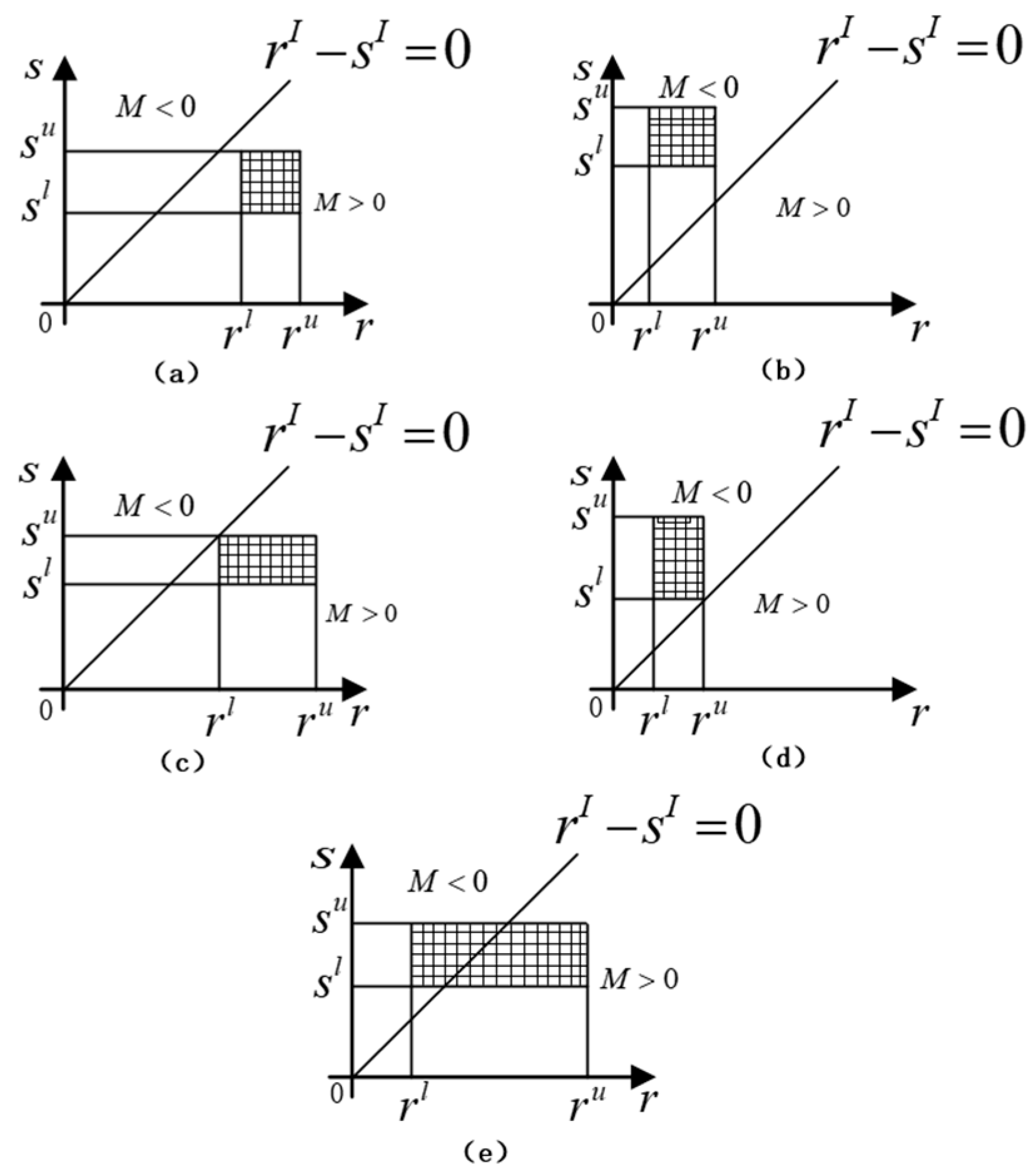
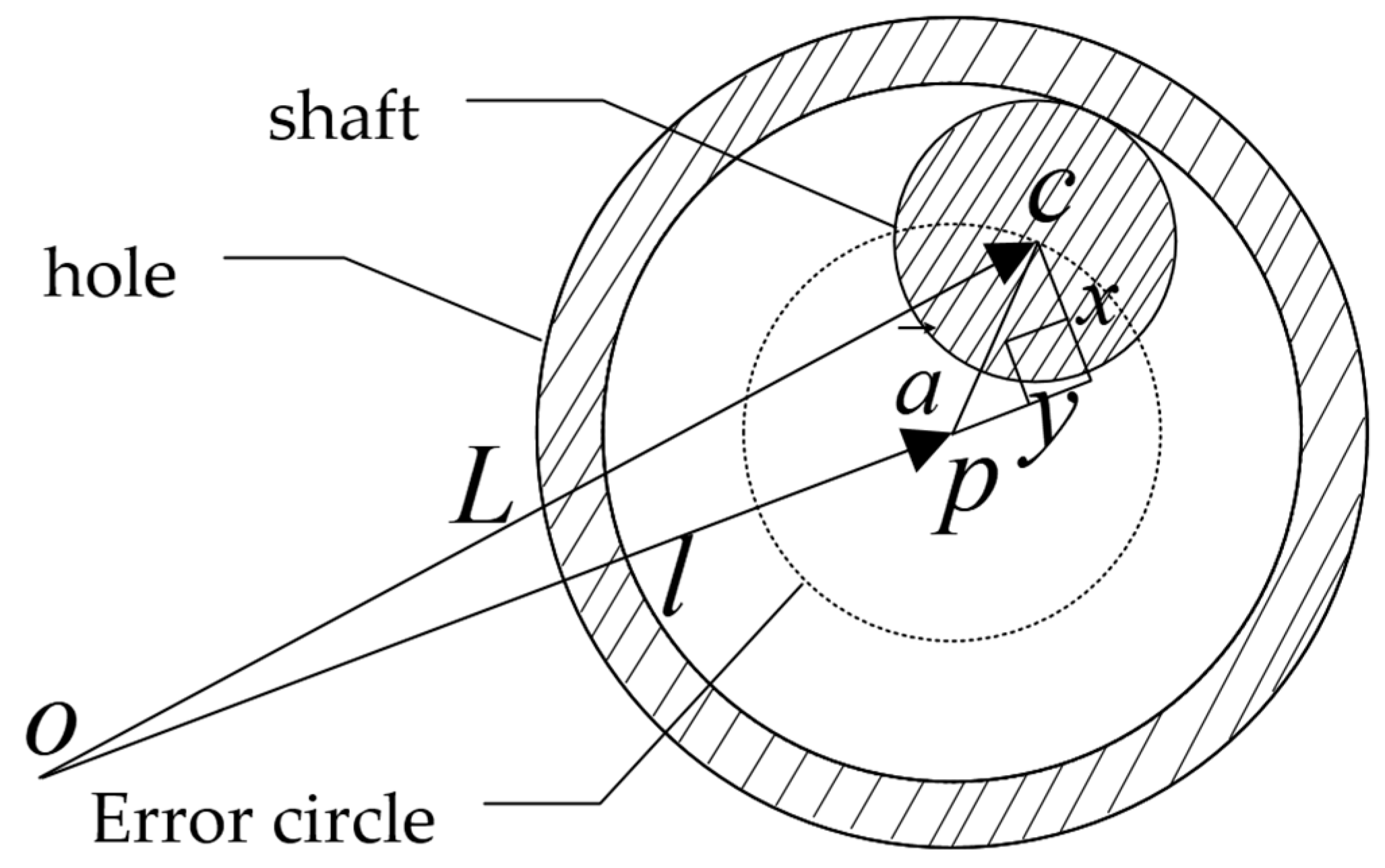

| Joint Range | |||||
|---|---|---|---|---|---|
| 1 | 180 | 400 | −90 | (−170~170) | |
| 2 | 600 | 0 | 0 | (−180~65) | |
| 3 | 40 | 0 | −90 | (−120~165) | |
| 4 | 0 | 620 | 90 | (−180~180) | |
| 5 | 0 | 0 | −90 | (−120~120) | |
| 6 | 0 | 80 | 0 | (−360~360) |
| Variable | Nominal Size /(mm) | Tolerance /(mm) | Upper and Lower Limit Dimensions /(mm) | Maximum Clearance /(mm) | Minimum Clearance /(mm) | Notes |
|---|---|---|---|---|---|---|
| DV 1 | 40 | 0.011 | 39.989,40 | 0.027 | 0 | Radius of base shaft |
| DV 2 | 40 | 0.016 | 40,40.016 | Radius of swivel base hole | ||
| DV 3 | 30 | 0.013 | 30,30.013 | 0.022 | 0 | Radius of swivel base hole |
| DV 4 | 30 | 0.009 | 29.991,30 | Radius of large arm shaft (front end) | ||
| DV 5 | 22.5 | 0.009 | 22.491,22.5 | 0.022 | 0 | Radius of large arm shaft (end) |
| DV 6 | 22.5 | 0.013 | 22.5,22.513 | Radius of small arm rod hole | ||
| DV 7 | 10 | 0.006 | 9.994,10 | 0.015 | 0 | Radius of small arm rod shaft |
| DV 8 | 10 | 0.009 | 10,10.009 | Radius of small armhole (front end) | ||
| DV 9 | 6 | 0.008 | 6,6.008 | 0.013 | 0 | Radius of small armhole (end) |
| DV 10 | 6 | 0.005 | 5.995,6 | Radius of wrist shaft | ||
| DV 11 | 5 | 0.008 | 5,5.008 | 0.013 | 0 | Radius of wrist hole |
| DV 12 | 5 | 0.005 | 4.995,5 | Radius of flange shaft |
| Joint | Connected Components | Constraints (Plane Pairs) | Contact Force | Driving Mode (Point Driving) | Drive Function |
|---|---|---|---|---|---|
| Joint 1 | Base, swivel base | joint_1 | contact_1 | general_motion_1 | STEP(time, 0, 0 d,1, −45 d) + STEP(time, 5, 0 d, 6, 45 d) |
| Joint 2 | Swivel base, large arm | joint_2 | contact_2 | general_motion_2 | STEP(time, 1, 0 d,2 ,60 d) + STEP(time, 6, 0 d, 7, −60 d) |
| Joint 3 | Large arm, small arm rod | joint_3 | contact_3 | general_motion_3 | STEP(time, 2, 0 d, 3, 60 d) + STEP(time, 7, 0 d, 8, −60 d) |
| Joint 4 | Small arm rod, small arm | joint_4 | contact_4 | general_motion_4 | STEP(time, 3, 0 d, 4, 90 d) + STEP(time, 8, 0 d, 9, −90 d) |
| Joint 5 | Small arm, wrist | joint_5 | contact_5 | general_motion_5 | STEP(time, 4, 0 d, 5, 45 d) + STEP(time, 9, 0 d, 10, −45 d) |
| Joint 6 | Wrist, flange | joint_6 | contact_6 | general_motion_6 | STEP(time, 4, 0 d, 5, 180 d) + STEP(time, 9, 0 d, 10, −180 d) |
| Theoretical Coordinates | Range of Error /(mm) | Non-Probability Reliability | Traditional Probabilistic Reliability | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| x | y | z | x | y | z | |||||
| (−45°, −30°, −60°, −90°, −45°, 180°) | 1013.1, −933.109, 735.25 | −1.1424 | −1.077 | −1.0096 | 0.909 | 0.9435 | 0.925 | 0.903 | 0.924 | 0.919 |
| 1.0588 | 1.0428 | 1.1521 | ||||||||
| Time Period | X | Y | Z |
|---|---|---|---|
| 0–2 s | [−0.1667,0.1726] | [−0.1056,0.1183] | [−0.7244,0] |
| 2–4 s | [−0.0255,0.1218] | [−0.2035,0.0717] | [−0.5962,−0.3404] |
| 4–6 s | [−0.0826,0.6975] | [−0.0893,1.8808] | [−0.4825,3.0768] |
| 6–8 s | [−3.0183,0.1457] | [−0.0601,0.1421] | [2.121,2.9081] |
| 8–10 s | [−0.4716,0.0345] | [−3.2367,0.0064] | [−0.4892,1.8582] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, Z.; Peng, J.; Sun, J.; Meng, X. Non-Probabilistic Reliability Analysis of Robot Accuracy under Uncertain Joint Clearance. Machines 2022, 10, 917. https://doi.org/10.3390/machines10100917
Tang Z, Peng J, Sun J, Meng X. Non-Probabilistic Reliability Analysis of Robot Accuracy under Uncertain Joint Clearance. Machines. 2022; 10(10):917. https://doi.org/10.3390/machines10100917
Chicago/Turabian StyleTang, Zhaoping, Jun Peng, Jianping Sun, and Xin Meng. 2022. "Non-Probabilistic Reliability Analysis of Robot Accuracy under Uncertain Joint Clearance" Machines 10, no. 10: 917. https://doi.org/10.3390/machines10100917
APA StyleTang, Z., Peng, J., Sun, J., & Meng, X. (2022). Non-Probabilistic Reliability Analysis of Robot Accuracy under Uncertain Joint Clearance. Machines, 10(10), 917. https://doi.org/10.3390/machines10100917







