Abstract
Three-dimensional (3D) object detection is an important task in the field of machine vision, in which the detection of 3D objects using monocular vision is even more challenging. We observe that most of the existing monocular methods focus on the design of the feature extraction framework or embedded geometric constraints, but ignore the possible errors in the intermediate process of the detection pipeline. These errors may be further amplified in the subsequent processes. After exploring the existing detection framework of keypoints, we find that the accuracy of keypoints prediction will seriously affect the solution of 3D object position. Therefore, we propose a novel keypoints uncertainty prediction network (KUP-Net) for monocular 3D object detection. In this work, we design an uncertainty prediction module to characterize the uncertainty that exists in keypoint prediction. Then, the uncertainty is used for joint optimization with object position. In addition, we adopt position-encoding to assist the uncertainty prediction, and use a timing coefficient to optimize the learning process. The experiments on our detector are conducted on the benchmark. For the two levels of easy and moderate, we achieve accuracy of 17.26 and 11.78 in , and achieve accuracy of 23.59 and 16.63 in , which are higher than the latest method KM3D.
1. Introduction
The understanding of 3D properties of objects in the real world is critical for vision-based autonomous driving and traffic surveillance systems [1,2,3,4,5]. Compared with a two-dimensional (2D) object detection task, the 3D object detection task involves nine degrees of freedom, in which the length, width, height, and pose of the 3D bounding box need to be detected. Currently, there are three main methods for 3D object detection: monocular 3D object detection, stereo-based 3D object detection and LIDAR-based 3D object detection. Among them, the LIDAR-based and the stereo-based detection methods can usually obtain higher detection accuracy with the provision of reliable depth information. However, the radar system has the disadvantages of high cost, high energy consumption, and short service life. On the contrary, the monocular detection method, which is characterized by low cost and low energy consumption, has received extensive attention and attracted researchers to conduct studies in this field. Therefore, our work focuses on the improvements in monocular 3D object detection techniques.
Monocular 3D object detection takes a single RGB image as input, and outputs the pose and dimension of the object in the real world. Due to the lack of depth information, this process is ill-conditioned, and the ambiguity will occur in the process of inverse projection from the 2D image plane to 3D space. Obviously, compared with stereo-based and LIDAR-based methods, the task of monocular 3D object detection is more challenging. Thanks to the powerful feature extraction and parameter regression capabilities of the neural network, some original monocular 3D object detection pipelines [6,7] regress the 3D dimension, orientation and position of an object directly by designing a deep convolutional neural network. However, learning 3D spatial information from planar features of 2D images undoubtedly expands the searching space of parameter learning. Therefore, it is difficult for the deep convolution neural networks to learn effectively without additional auxiliary information. In order to address these challenges, recent works attempt to help the networks learn 3D information better by adding extra information. For example, Mono3D [7] takes advantage of masks to realize instance segmentation. MF3D [8] and ROI-10D [9] use depth information as supervision. However, adding extra information for monocular 3D object detection means more annotation information should be obtained. Fortunately, other scholars try to tackle this problem by using the geometric constraints between 3D space and 2D images, which can narrow the searching space for parameter learning and improve the learning efficiency and detection accuracy.
In our work, we adopt a keypoints-based framework to accomplish the 3D object detection task. In detail, our approach predicts the keypoints projected from the center and corner points of the 3D bounding box. Then, the 3D position of a predicted object is solved by minimizing the re-projection error with supervision of 3D ground-truth. Usually, this method requires a long detection pipeline, resulting in prediction errors in the intermediate process. Unfortunately, the solution of the 3D position depends on the results of previous processes, which will cause the errors to be further amplified and affect the final detection results. Notably, Chen et al. [10] propose to utilize the pairwise relationship of the objects as a constraint to characterize the errors that exist in the detection pipeline. This method greatly improves the detection capability. Considering that the accuracy of keypoints prediction will seriously affect the solution of 3D position, we design an uncertainty prediction module to measure the possible errors at the stage of keypoints prediction. Specifically, by dealing with the coordinates of keypoints, we can obtain some 2D boxes that can be used to extract the regions for describing the features of objects. Then, the network outputs the uncertainty of each object through a series of fully connected neural networks with the 2D box attributes and feature regions as input. Finally, we integrate the uncertainty into 3D position loss for joint optimization. Additionally, we also use a setting of the timing coefficient for more effective training. The subsequent experiments show that our improvements can be beneficial to the 3D detection task. In general, our main contributions are as follows:
- (a).
- A method to predict keypoints uncertainty based on multi-clue fusion.
- (b).
- A strategy to optimize the 3D position by jointly considering the uncertainty.
- (c).
- KUP-Net outperforms the previous methods on the kitti dataset.
2. Materials
Mono-based 3D detection: As an issue of great interest in detection technology, monocular 3D object detection suffers from a lack of depth information when only a single RGB image is available as input. At present, there are two strategies for solving this problem. The first is to use instance segmentation, a prior CAD wireframe model, an independent depth estimation network and other means to assist the monocular vision pipeline in learning geometric information. For example, Chen et al. use the ground plane hypothesis in Mono3D [7] to segment instances, which can improve the detection accuracy by obtaining the contours of the detected objects. In AM3D [11], Ma et al. add an independent depth prediction branch for the monocular 3D object detection pipeline, and the predicted depth information can be converted into point clouds to realize a more efficient detection. In addition, the CAD wireframe models are also widely used to assist the monocular 3D object detection task. For example, DeepMANTA [12] ingeniously combines the keypoints method with CAD prior to prediction of the 3D object information. These methods are not based on a pure monocular image to obtain the 3D information of objects. Although they can improve detection accuracy to a certain extent, the annotation work for extra label information is always laborious and cumbersome. On the contrary, the second strategy only uses a single RGB image and the corresponding ground-truth to complete the detection task, which is different from the above ways. The most representative work is Deep3D [13], in which Mousavian et al. assume that the projection points of the corners in 3D bounding box are all located on the four edges of the 2D bounding box. According to this assumption, they construct the projection constraints based on the 3D–2D relationship of . Inspired by Faster-RCNN [14], M3D-PRN [15] narrows the searching space of geometric information by setting up a series of 3D anchors. Recently, the latest approach RTM3D [16] predicts the projection points of 3D corners based on the well-known 2D object detection framework CenterNet [17]. This concise design causes the outstanding work to become the first real-time algorithm for the monocular 3D object detection task. Subsequently, KM3D [18] adopts a differentiable geometric reasoning module to realize the end-to-end training. Admittedly, the success of these methods is inspiring, but they all ignore the possible errors in the intermediate process due to a long detection pipeline, which has a bad effect on the detection performance.
Uncertainty estimation: When the deep neural network is used to complete various tasks, there will inevitably exist cognitive uncertainty and unpredictable uncertainty [19,20]. In many machine vision tasks, a large number of scholars have begun to consider the impact of uncertainty. For example, in the process of depth regression work, the existence of noise often has a large impact on the final results [19,21]. Regarding this problem, ref. [22] uses uncertainty theory to model the estimation error in depth, which is beneficial to the regression of depth. Similarly, Chen et al. [10] calculate the uncertainty of the distance between objects and the uncertainty of the object location to optimize the prediction of the 3D object position. In addition, for the tasks of trajectory planning [23], pedestrian positioning [24], etc., uncertainty estimation has also been well applied. Our work aims at modeling the uncertainty of keypoints prediction, and then optimizing the position loss under the guidance of uncertainty theory.
3. Methods
In Figure 1, we show the overall structure of our monocular 3D object detector. This detection pipeline follows the one-stage approach [17], which takes RGB images as input and outputs 2D and 3D properties related to the objects. Depending on detection tasks, we can add different components behind the feature map output from the backbone network. For the 2D task, these components mainly include a heatmap, 2D size, and 2D center offset, but the 3D task usually contains a keypoints heatmap, keypoints offset, local orientation, 3D dimension and 3D object confidence. Based on the predicted 3D properties, we follow the practice of [18] and adopt a geometric reasoning module (GRM) to solve the 3D position for objects. Furthermore, we design an uncertainty prediction module for characterizing the errors in the detection pipeline to optimize the 3D object position. Next, we will elaborate on these contents from four aspects: 2D detection, 3D detection, uncertainty prediction module and loss optimization.
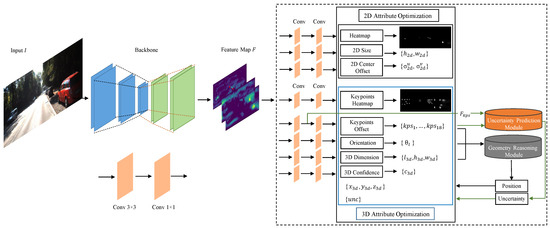
Figure 1.
Overview of our network architecture: the backbone is composed of DLA-34 followed by eight sub-task components, the 3D object position is solved by the geometric reasoning module, and the uncertainty module is used to predict the uncertainty for joint optimization in the position loss.
3.1. 2D Detection
Our detection pipeline uses a single RGB image as input and outputs a global feature map that is used as input to different components of the subsequent detection tasks, where N is a down-sampling factor. Referring to the method of CenterNet [17], we need three sub-functional components to predict the related properties of the 2D bounding box: the object heatmap, 2D box size, and center point offset. Specifically, we apply the convolution kernels of 3 × 3 and 1 × 1 on the F to obtain the object heatmap for determining the category to which the object belongs, where represents three types of objects to be detected: car, pedestrian, and cyclist. Similarly, the 2D box size and the center point offset can be obtained by conducting the same convolution operation.
3.2. 3D Detection
Compared with the 2D detection, the 3D detection is more complicated. As we all know, the projection from 3D space to 2D image plane will result in the loss of depth information. Without auxiliary information, it is ill-conditioned to perform inverse projection from the image plane. Therefore, to restore the more accurate position information for objects, we need to obtain as much 3D information as possible and use geometric constraints to solve the geometric property. In the 3D detection task, the appearance information can be obtained from the feature level, mainly including the object local orientation, keypoints heatmap, keypoints offset, 3D bounding box dimension and 3D confidence. The dimension and orientation properties are visualized in Figure 2.
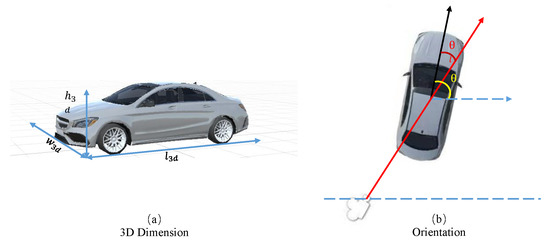
Figure 2.
Illustration of the 3D dimension (a) and orientation (b).
Based on the assumption that vehicles drive on a horizontal road, the global orientation of cars is constant when no motion occurs in the yaw direction. However, with the depth of the object changes in the real world, its local orientation will be changed from the perspective of monocular camera. We follow the suggestion in Deep3D [13] to predict the local orientation for the object. In addition the light angle can be calculated by the camera intrinsic matrix to obtain the global orientation . Similar to the operation of the object heatmap prediction in 2D detection, we need to predict the keypoints heatmap , which represents the projection of the eight corner points and center points of the 3D bounding box on the 2D image plane. At the same time, the keypoints offset are predicted for the subsequent construction of geometric constraints between 3D points and 2D points. Furthermore, the keypoints offset and orientation, dimension and confidence of 3D bounding boxes also need to be acquired for constructing geometric constraints. Therefore, the last two components will be used to obtain the object 3D dimension and the confidence . After the appearance properties of the 3D bounding box have been predicted, it is most important to obtain its geometric property, i.e., its position in 3D space. By using the 3D dimension , orientation O, keypoints offset , we can solve the position through a geometric reasoning module proposed in [18,25,26], which can be expressed as follows:
where is the keypoints coordinate calculated by , and the is:
By solving the pseudo-inverse of SVD, we can obtain the value of with constantly approaching the ground-truth . The details can be seen in the Appendix A.
3.3. Uncertainty Prediction Module
Owing to the prediction uncertainty in neural networks, the prediction results may be subject to errors. Therefore, it is meaningful to take the influence of uncertainty into consideration, which has been confirmed in [20]. In the above Section 3.2, we introduced the 3D detection task, in which the 3D object position is solved by keypoints offset . Considering that the prediction errors of directly affect the accuracy of , it is necessary to construct an error characterization about to jointly optimize position loss. Therefore, we model the uncertainty prediction in a probability framework, and the predicted uncertainty is used to measure the accuracy of the 3D position, which can guide the network to train a better detector. We assume that the object position along each axis of the coordinate conforms to the Laplace distribution defined by and , in which and represent the mean and variance, respectively. The more accurate the object position, the closer the is to ground-truth. The closer the is to 1, the lower the uncertainty. On the contrary, the uncertainty is higher. As shown in Figure 3, we design an uncertainty prediction module. Specifically, by using the , we first solve the nine keypoint coordinates for each object. Then, these coordinates will be used to obtain a series of diagonal points that are constrained within the projection of their corresponding 3D bounding boxes. It should be noted that represent the maximum and minimum values of the nine keypoints along the u direction and the v direction, respectively. Naturally, we can define the 2D keypoints box , in which the center coordinate is and the 2D size is . Due to the not containing the object feature clue, we use the to extract the region of interest with the size of from the feature map that is used to predict the . For each region, a fully connected neural network maps it into a 128-dimensional feature representation . Before sending the position clue of 2D keypoints box to an uncertainty prediction module, we encode it from the low dimension to the high dimension for a better characterization. The encoding method is as follows:
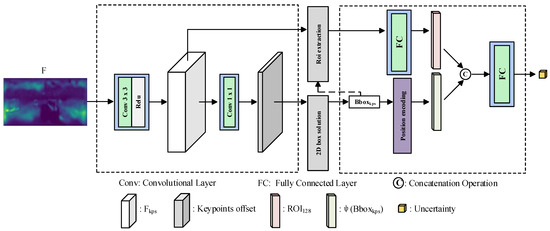
Figure 3.
Flow chart of uncertainty prediction.
In order to fuse together the feature clue and box properties in the same dimension, the 2D box properties should also be encoded into a 128-dimensional vector as shown in Equation (3), where M is set to 16. Finally, and are concatenated into , and then the uncertainty is output through a fully connected neural network. It should be noted that only the uncertainty along the z axis is predicted for optimization and the reasons can be seen in the ablation study. In Algorithm 1, we give a more concise description of the uncertainty prediction process.
| Algorithm 1: The illustration of uncertainty prediction. |
Input: Feature map , Keypoints offset Output: Uncertainty 1: Coordinate solution: keypoints coordinate: 2: Diagonal points acquisition: 3: 2D boxes acquisition: 4: Feature region extraction: 5: Position encoding: 6: Feature fusion: ; concatenate and into 7: Output: 8: END |
3.4. Loss Function
To describe the loss function more clearly, we first explain the 2D and 3D detection loss, respectively, and then give the loss function of the whole pipeline.
By calculating the difference value between , , and their corresponding ground-truth, the 2D loss function can be defined as the three parts of heatmap loss , 2D size loss , and center point offset loss :
In order to solve the imbalance problem between positive and negative samples, we follow [17,27,28] to optimize with focal loss. Considering that the 2D size and the center point offset are easy to regress, we choose L1 loss [29] to optimize and .
Similarly, the 3D loss function is composed of six parts: keypoints heatmap loss , keypoints offset loss , 3D dimension loss , local orientation loss , 3D confidence loss and position loss :
Clearly, the 3D detection task has more regression targets and is more difficult than the 2D detection task. For the term that still has the sample imbalance problem, we optimize it in the same way with . The 3D dimension loss can be better optimized with L1 loss [29]. To optimize more efficiently, we use the depth-guided L1 loss in [18] to dynamically adjust the penalty coefficient. Since the regression of local angle is a multi-modal problem, it is more appropriate to choose multi-bin loss [12] to deal with . The loss of 3D confidence is optimized by calculating the binary cross-entropy between confidence and the 3D IOU score. For the optimization of 3D position loss , we focus on minimizing the re-projection error under the guidance of heteroscedasticity uncertainty theory in [19]:
In constructing the 3D position loss function, we add the prediction uncertainty in a continuous form for joint optimization. The loss function of the whole detection pipeline is defined as:
During the training phase, we empirically set the loss coefficients , , , , to 1, and set the , to 4 and , respectively. The is set to at the beginning and changes with the increase in training epochs. For the coefficient of position loss , we adopt a setting of the timing coefficient, which is similar to that in [30]. This setting makes the position loss added to the whole loss function at the 6th epoch, which can be defined as:
where, and are the lower bound and upper bound for the number of iterations, respectively.
4. Results
4.1. Experimental Setting
As an authoritative dataset, the object detection benchmark [31] is widely applied in the field of 3D object detection to evaluate the performance of detectors. In the dataset, there are 7481 labeled training images and 7518 unlabeled test images for users. According to the suggestion of [7,8,12,32,33], we divide the dataset into , , , and , . This is because the official test set does not give the corresponding annotation information. In our detector, the input images are filled into the size of , and the global feature map output through the backbone network is . Behind the global feature map, eight branches are connected for the 2D detection task and 3D detection task, respectively. The convolution kernels of and are applied on the global feature to obtain output for each component. Keypoints labels for supervision are obtained by projecting 3D truth values of the left and right images, and we use image inversion, image scaling and other technologies to enhance the dataset. The whole training process is realized on i7-8086K CPU and a single 1080Ti GPU, with the batch size of 8. Moreover, we use an Adam [34] optimizer to optimize the parameters of the whole network. The total number of epochs is 180, and the initial learning rate is set to , which is reduced by at 60 and 140 epochs, respectively. In order to demonstrate the performance of our method, we label the detection difficulties in three levels (, , ) based on the level of occlusion, truncation and height of the objects [10,18]. Under the guidance of [13,16], we choose two metrics for 3D detection task: average precision for 3D intersection-over-union() and average precision for bird’s eye view(). If the 2D detection task is needed, average precision for 2D intersection-over-union() and average orientation similarity() are used to evaluate 2D detection performance.
4.2. Experimental Results
Since most of the current works of monocular 3D object detection are devoted to the detection of cars, we first conduct qualitative and quantitative analysis on this category. Then, we show the results of 2D and multi-class detection tasks for a comprehensive evaluation regarding our detector.
4.2.1. Qualitative Results of Cars
To intuitively reflect the effect of our detector, we visualize the 3D detection results of cars. In Figure 4, we choose four scenes to show the visualization of the 3D bounding box and bird’s eye view results of our detector. According to the comparison with ground-truth, we can see that our detector can well distinguish the cars and locate them, which proves the efficiency of our approach.

Figure 4.
Visualization of car category detection in four scenes. In each picture group, we show the ground-truth (a), the output (b) and the bird’s eye view (c) from the left to the right.
4.2.2. Quantitative Results of Cars
We select the representative methods in the field of monocular 3D object detection and some of the latest methods to compare with our approach. The performance metrics for the comparison algorithms are the official metric data provided. As shown in Table 1 and Table 2, we show the comparisons between our approach and other methods under the evaluation of and . Considering that some methods only use for evaluation, we use instead of in and to obtain a more comprehensive comparison result [18]. In the , we choose to obtain a fair comparison result. According to [16], the backbone network can choose -18 [6] and -34 [35], respectively, for the tradeoff of speed or accuracy. Our improvement is not focused on the detection speed, so we only use -34 as the backbone network to achieve higher detection accuracy. Based on the comparison results, we can see that our approach significantly improved detection accuracy at both easy and moderate levels. Therefore, considering the uncertainty in the intermediate process of the detection pipeline plays an effective role in the 3D object detection task.

Table 1.
comparison on , and with a 0.5 and 0.7 IOU threshold: (a) Extra indicates whether there is additional information to assist detection (b) E, M and, H indicate the levels from Easy, Moderate, to Hard. (c) The red, blue, and cyan denote the highest, second highest, and third highest results respectively.

Table 2.
comparison on , and with a 0.5 and 0.7 IOU threshold: (a) Extra indicates whether there is additional information to assist detection (b) E, M and, H indicate the levels from Easy, Moderate, to Hard. (c) The red, blue, and cyan denote the highest, second highest, and third highest results respectively.
4.2.3. Results of 2D and Multi-Class Detection
Besides the results of 3D detection for cars, we also report the ability of our approach to perform 2D and multi-class detection. Similarly, we provide subjective and objective evaluations for the two tasks. In Figure 5 and Figure 6, we qualitatively show the visualization results of 2D detection for cars and 3D detection for pedestrians and cyclists, respectively. Additionally, we also give the corresponding metric values in Table 3 and Table 4, in which Table 3 shows the and for the 2D detection task and Table 4 shows the and for the pedestrian and cyclist detection tasks. Based on these results, we can find that our detector can also be competent for the 2D and multi-class detection tasks.

Figure 5.
Visualization of 2D detection for cars in four scenes. In each picture group, we show the ground-truth (a) and the output (b).

Figure 6.
Visualization of multi-class detection for pedestrians and cyclists in four scenes. In each picture group, we show the ground-truth (a) and the output (b).

Table 3.
Evaluation for 2D detection of cars on by and metrics: E, M, and H indicate the levels from Easy, Moderate, to Hard.

Table 4.
Evaluation for multi-class detection of pedestrian and cyclist on by and metrics: E, M, and H indicate the levels from Easy, Moderate, to Hard.
4.3. Ablation Study
In the above section, we have fully shown the results and efficiency of our method. Next, we will further elaborate on three aspects: timing coefficient, uncertainty prediction mode, and position encoding. By doing this, we can concretely analyze the contribution to each improvement in our work.
4.3.1. Effect of Timing Coefficient
For stable and efficient training, we use a timing coefficient setting for position loss. At the initial training phase, the parameter of the network cannot sufficiently meet the needs of the position solution task, which will lead to a large deviation in position prediction. This large deviation is a disadvantage to the learning and convergence of a multi-task pipeline [22]. Therefore, we propose to use the timing coefficient to decide when to add position loss into the global optimization. Thanks to this strategy, we can provide a set of appropriate initial training parameters for the position optimization. In our work, we optimize the position loss after the fifth epoch, and the loss coefficient changes exponentially with the number of epochs in the following training process. The evaluation details can be seen in Table 5. The accuracy is improved using this setting.

Table 5.
Evaluation for the influences of position encoding (Poe) and timing coefficient (Tic) settings: E, M, and H indicate the levels from Easy, Moderate, to Hard.
4.3.2. Effect of Uncertainty Prediction Mode
According to the division of the 3D coordinate axis, we provide three optional uncertainty terms to jointly optimize the solution of 3D position, namely , and , which represent the uncertainty along the x, y and z axes, respectively. We provide four combinations of these uncertainties according to the process of 3D–2D projection. As shown in Table 6, we find that applying uncertainty prediction only for z-direction can bring better benefits to the detector. In view of this situation, we think that only the depth information is missing along the z axis in the forward projection process. Therefore, predicting the uncertainty is the best choice for our detector.

Table 6.
Evaluation for the influences of uncertainty , , and settings: E, M, and H indicate the levels from Easy, Moderate, to Hard.
4.3.3. Effect of Position Encoding
In the uncertainty prediction module, we use the fusion information of feature clue and 2D position clue as input. Obviously, the feature clue is in a high dimension and the 2D position clue is in a low dimension. If we concatenate the two clues directly, the problem of feature mismatching will emerge. Thus, a position encoding on is necessary. From the results in Table 5, it can be seen that the position encoding in Section 3.3 is useful, which enhances the information representation ability and contributes to the prediction of uncertainty.
5. Discussion
Our approach outperforms the latest method in the levels of easy and moderate of and . Especially in the , the relative improvements of and were achieved in easy and moderate levels, respectively. Compared with the methods using depth information or CAD models in the inference process, the pure-image-based method is higher ill-posed and more difficult to use to improve the detection accuracy. However, a pure-image-based method usually performs better in the real-time requirement for the tasks of automatic driving and complex environment perception.
Although the method based on pure images exhibits better real-time performance, it is obviously unreliable to fit 3D properties only using deep neural networks. Therefore, the design of the keypoints detection framework adds concise and reliable geometric constraints under the condition of real timeliness. However, in KM3D, the features used to predict keypoints is ambiguous. For example, the keypoints of an object in 2D image plane may appear on the other objects or the background region. This ambiguity of features brings uncertainty to keypoints prediction, influencing the accuracy of the 3D object position. Based on this observation, we model the uncertainty of keypoints prediction, and integrate the uncertainty into the 3D position loss, which is advantageous to the learning of parameters and the convergence of training. Unlike previous works [39,40] that apply uncertainty theory in 2D object detection, Monopair introduces uncertainty estimation into 3D object detection for the first time. However, Monopair is designed on a depth prediction architecture, which cannot perform well in real time. Moreover, Monopair does not encode position clues explicitly when predicting the uncertainty, causing the irrelevant regions to have effects on the prediction results. Accordingly, we fuse the feature clue and position clue defined by the keypoints region. In comparison with the method that only use feature clues, our fusion strategy achieves a richer and clearer feature representation.
6. Conclusions
In our work, aiming at the possible errors in the intermediate process of the monocular 3D object detection pipeline, we have constructed an uncertainty prediction module to optimize the solution of the 3D position property. Experiments on the dataset show that our method is effective and outperforms some of the latest algorithms. However, our method does not perform well for the detection of hard samples. Based on this problem, we find that the hard samples have more serious occlusion and truncation problems than easy and moderate samples, and therefore a more accurate module is required to predict uncertainty. Furthermore, better results may be achieved by using different training setups, and readers interested in this can make other attempts. In the following work, we will try to develop a richer and more reliable uncertainty constraint strategy for the detection pipeline by referring to the related methods of automatically encoding the relationship between different objects in natural language processing (NLP) [41,42,43].
Author Contributions
Conceptualization, M.C. and H.Z.; methodology, M.C.; software, M.C.; validation, M.C. and P.L.; formal analysis, M.C.; investigation, M.C.; resources, M.C.; data curation, M.C.; writing—original draft preparation, M.C.; writing—review and editing, M.C., H.Z. and P.L.; visualization, M.C.; supervision, P.L.; project administration, M.C.; funding acquisition, M.C., H.Z. and P.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research is funded by the National Equipment Development Department of China (Grant No. 41401040105) and the National Natural Science Foundation of China (Grant No. U2013210).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors would like to thank the University of Chinese Academy of Sciences for the support.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Based on the reference [18], we transform the Equation (2) into a linear system with the shape of , which can be specifically expressed as:
where A is the keypoints matrix normalized by the intrinsic camera, X is the 3D object position, and B is the corner points matrix normalized by the intrinsic camera. To solve X, we need to obtain the inverse of matrix A. Since A is not a square matrix, we use the SVD operator to transform A to to obtain its pseudo inverse , in which U and V are both unitary matrices. By multiplying with A, we can see that and . Obviously, and .
References
- Li, S.; Yan, Z.; Li, H.; Cheng, K.T. Exploring intermediate representation for monocular vehicle pose estimation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 19–25 June 2021. [Google Scholar]
- Yang, B.; Luo, W.; Urtasun, R. PIXOR: Real-time 3D Object Detection from Point Clouds. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar]
- Qi, C.R.; Litany, O.; He, K.; Guibas, L.J. Deep Hough Voting for 3D Object Detection in Point Clouds. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Korea, 27–28 October 2019. [Google Scholar]
- Peng, W.; Pan, H.; Liu, H.; Sun, Y. IDA-3D: Instance-Depth-Aware 3D Object Detection from Stereo Vision for Autonomous Driving. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 14–19 June 2020. [Google Scholar]
- Ferryman, J.M.; Maybank, S.J.; Worrall, A.D. Visual surveillance for moving vehicles. Int. J. Comput. Vis. 2000, 37, 187–197. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Chen, X.; Kundu, K.; Zhang, Z.; Ma, H.; Urtasun, R. Monocular 3D Object Detection for Autonomous Driving. In Proceedings of the IEEE Conference on Computer Vision & Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Xu, B.; Chen, Z. Multi-level Fusion Based 3D Object Detection from Monocular Images. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar]
- Manhardt, F.; Kehl, W.; Gaidon, A. ROI-10D: Monocular Lifting of 2D Detection to 6D Pose and Metric Shape. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Chen, Y.; Tai, L.; Sun, K.; Li, M. MonoPair: Monocular 3D Object Detection Using Pairwise Spatial Relationships. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 14–19 June 2020. [Google Scholar]
- Ma, X.; Wang, Z.; Li, H.; Zhang, P.; Ouyang, W.; Fan, X. Accurate Monocular 3D Object Detection via Color-Embedded 3D Reconstruction for Autonomous Driving. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Korea, 27–28 October 2019. [Google Scholar]
- Chabot, F.; Chaouch, M.; Rabarisoa, J.; Teulière, C.; Chateau, T. Deep MANTA: A Coarse-to-Fine Many-Task Network for Joint 2D and 3D Vehicle Analysis from Monocular Image. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Mousavian, A.; Anguelov, D.; Flynn, J.; Kosecka, J. 3D Bounding Box Estimation Using Deep Learning and Geometry. In Proceedings of the IEEE conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 1137–1149. [Google Scholar] [CrossRef] [Green Version]
- Brazil, G.; Liu, X. M3D-RPN: Monocular 3D Region Proposal Network for Object Detection. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Korea, 27–28 October 2019. [Google Scholar]
- Li, P.; Zhao, H.; Liu, P.; Cao, F. RTM3D: Real-Time Monocular 3D Detection from Object Keypoints forAutonomous Driving. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020. [Google Scholar]
- Zhou, X.; Wang, D.; Krhenbühl, P. Objects as Points. arXiv 2019, arXiv:1904.07850. [Google Scholar]
- Li, P. Monocular 3D Detection with Geometric Constraints Embedding and Semi-supervised Training. IEEE Robot. Autom. Lett. 2021, 6, 5565–5572. [Google Scholar] [CrossRef]
- Kendall, A.; Gal, Y. What Uncertainties Do We Need in Bayesian Deep Learning for Computer Vision? arXiv 2017, arXiv:1703.04977. [Google Scholar]
- Gal, Y.; Ghahramani, Z. Dropout as a Bayesian Approximation: Representing Model Uncertainty in Deep Learning. In Proceedings of the International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016. [Google Scholar]
- Liu, C.; Gu, J.; Kim, K.; Narasimhan, S.G.; Kautz, J. Neural RGB®D Sensing: Depth and Uncertainty From a Video Camera. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 10978–10987. [Google Scholar] [CrossRef]
- Blundell, C.; Cornebise, J.; Kavukcuoglu, K.; Wierstra, D. Weight Uncertainty in Neural Networks. In Proceedings of the International Conference on Machine Learning, Lille, France, 7–9 July 2015. [Google Scholar]
- Wirges, S.; Reith-Braun, M.; Lauer, M.; Stiller, C. Capturing Object Detection Uncertainty in Multi-Layer Grid Maps. In Proceedings of the 2019 IEEE Intelligent Vehicles Symposium (IV), Paris, France, 9–12 June 2019. [Google Scholar]
- Bertoni, L.; Kreiss, S.; Alahi, A. MonoLoco: Monocular 3D Pedestrian Localization and Uncertainty Estimation. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Korea, 27–28 October 2019. [Google Scholar]
- Giles, M. An Extended Collection of Matrix Derivative Results for Forward and Reverse Mode Algorithmic Dieren Tiation; Oxford University Computing Laboratory: Oxford, UK, 2008. [Google Scholar]
- Ionescu, C.; Vantzos, O.; Sminchisescu, C. Matrix Backpropagation for Deep Networks with Structured Layers. In Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 2965–2973. [Google Scholar] [CrossRef]
- Laine, S.; Aila, T. Temporal Ensembling for Semi-Supervised Learning. arXiv 2016, arXiv:1610.02242. [Google Scholar]
- Lin, T.Y.; Goyal, P.; Girshick, R.; He, K.; Dollár, P. Focal Loss for Dense Object Detection. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017. [Google Scholar]
- Simonelli, A.; Bulò, S.R.R.; Porzi, L.; López-Antequera, M.; Kontschieder, P. Disentangling Monocular 3D Object Detection. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Korea, 27–28 October 2019. [Google Scholar]
- Feng, D.; Rosenbaum, L.; Dietmayer, K. Towards Safe Autonomous Driving: Capture Uncertainty in the Deep Neural Network for Lidar 3D Vehicle Detection. In Proceedings of the 2018 21st International Conference on Intelligent Transportation Systems (ITSC), Maui, HI, USA, 4–7 November 2018. [Google Scholar]
- Geiger, A.; Lenz, P.; Urtasun, R. Are we ready for autonomous driving? The KITTI vision benchmark suite. In Proceedings of the IEEE Conference on Computer Vision & Pattern Recognition, Providence, RI, USA, 16–21 June 2012. [Google Scholar]
- Yu, X.; Choi, W.; Lin, Y.; Savarese, S. Data-Driven 3D Voxel Patterns for Object Category Recognition. In Proceedings of the CVPR 2015, Boston, MA, USA, 7–12 June 2015. [Google Scholar]
- Chen, X.; Kundu, K.; Zhu, Y.; Ma, H.; Fidler, S.; Urtasun, R. 3D Object Proposals using Stereo Imagery for Accurate Object Class Detection. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 40, 1259–1272. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Yu, F.; Wang, D.; Shelhamer, E.; Darrell, T. Deep Layer Aggregation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar]
- Ku, J.; Pon, A.D.; Waslander, S.L. Monocular 3D Object Detection Leveraging Accurate Proposals and Shape Reconstruction. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Li, B.; Ouyang, W.; Sheng, L.; Zeng, X.; Wang, X. GS3D: An Efficient 3D Object Detection Framework for Autonomous Driving. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Qin, Z.; Wang, J.; Lu, Y. Triangulation Learning Network: From Monocular to Stereo 3D Object Detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Choi, J.; Chun, D.; Kim, H.; Lee, H. Gaussian YOLOv3: An Accurate and Fast Object Detector Using Localization Uncertainty for Autonomous Driving. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Korea, 27–28 October 2019. [Google Scholar]
- He, Y.; Zhu, C.; Wang, J.; Savvides, M.; Zhang, X. Bounding Box Regression with Uncertainty for Accurate Object Detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention Is All You Need. In Proceedings of the 31st Conference on Neural Information Processing System, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Zhang, Q.; Yang, Y. ResT: An Efficient Transformer for Visual Recognition. arXiv 2021, arXiv:2105.13677. [Google Scholar]
- Alaparthi, S.; Mishra, M. Bidirectional Encoder Representations from Transformers (BERT): A sentiment analysis odyssey. arXiv 2020, arXiv:2007.01127. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).