Approximate Methods for Solving Linear and Nonlinear Hypersingular Integral Equations
Abstract
1. Introduction
- (1)
- It allows us to extend collocations and mechanical quadratures methods to hypersingular integral equations with non-Riemann integrable right sides;
- (2)
- For linear hypersingular integral equations, it allows one to verify the inverse operator existence and estimate its norm quite easily;
- (3)
- The method is stable with respect to the operator and right hand side perturbations;
- (4)
- The method does not require the existence and reversibility of the nonlinear operator derivative.
2. Continuous Method and Its Convergence Properties
Continuous Method for Solving Operator Equations
- 1.
- The inequalityholds for all .
- 2.
- Inequality (12) is satisfied.
3. An Solution of Hypersingular Integral Equations with the Continuous Method
- (i)
- The above limit exists;
- (ii)
- has at least p derivatives in the neighborhood of the point .
3.1. An Approximate Solution of Linear Hypersingular Integral Equations with Second Order Singularity
- (1)
- Unite the nodes and , denoting them by
- (2)
- Unite the nodes and , denoting them by
- (3)
- Denote the family of basis functions , by ;
- (4)
- Denote by unknowns , .
3.2. Nonlinear Hypersingular Integral Equations
4. Summary and Discussion
- (1)
- The method is applicable for solving linear and nonlinear hypersingular integral equations, whose right-hand sides contain non-Riemann integrable functions.
- (2)
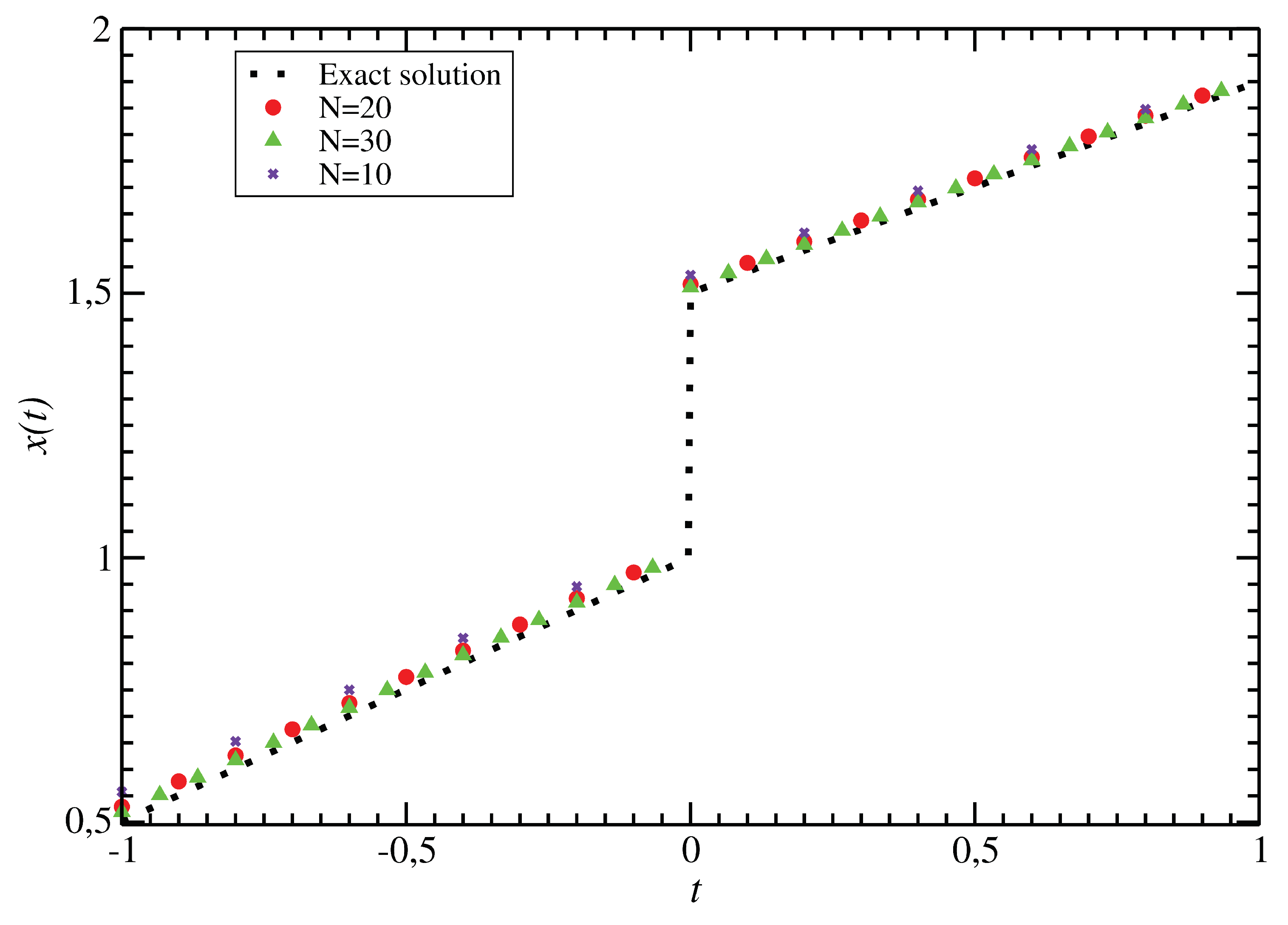
- In Section 3.1 the continuous method is applied to linear hypersingular integral equations with the singularities of the second order. The conditions for the unique solvability of the constructed computing scheme are obtained and the convergence of the sequence of approximate solutions to the exact one is proven. It is shown that for linear hypersingular integral equations, the method converges for sufficiently large N and for .
- (3)
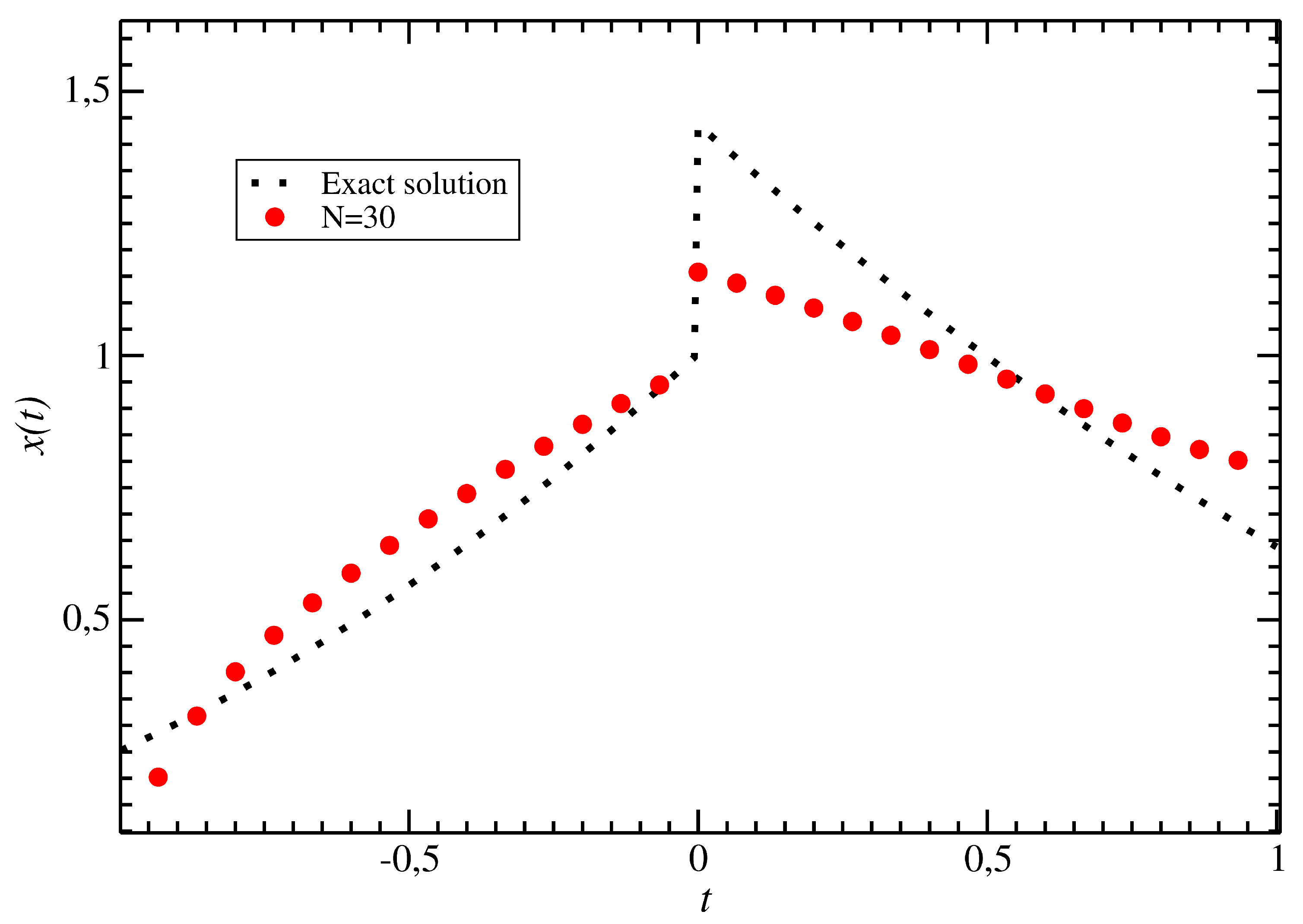
- In Section 3.2 the continuous method is applied to nonlinear hypersingular integral equations with the singularities of the second order. Conditions are given for the convergence of the constructed iterative spline-collocation method to the solution of a nonlinear hypersingular integral equation. It should be noted that the method is applicable to hypersingular integral equations of the first and second kinds.
- 1.
- To obtain a set of convergence conditions owing to logarithmic norm values in various spaces;
- 2.
- To determine the norm of the inverse matrix of an approximate system;
- 3.
- To determine stability boundaries for solutions with respect to variations of kernels and right-hand sides of the equations.
Author Contributions
Funding
Conflicts of Interest
References
- Bogolubov, N.N.; Mesheryakov, V.A.; Tavkhelidze, A.N. An application of Muskhelishvili’s methods in the theory of elementary particles. In Proceedings of the Symposium on Solid Mechanics and Related Problems of Analysis, Metsniereba, Tbilisi; 1971; Volume 1, pp. 5–11. (In Russian). [Google Scholar]
- Brown, D.D.; Jackson, A.D. The Nucleon-Nucleon Interaction; North-Holland: Amsterdam, The Netherlands, 1976. [Google Scholar]
- Faddeev, L.; Takhtajan, L. Hamiltonian Approach to Solution Theory; Springer: Berlin, Germany, 1986. [Google Scholar]
- Ioakimidis, N.I. Two methods for the numerical solution of Bueckher’s singular integral equation for plane elasticity crack problems, Comput. Methods Appl. Mech. Engrg. 1982, 2, 169–177. [Google Scholar] [CrossRef]
- Lifanov, I.K.; Poltavskii, L.N.; Vainikko, G.M. Hypersingular Integral Equations and their Applications; Chapman Hall/CRC: Boca Raton, FL, USA; CRC Press Company: London, UK; New York, NY, USA; Washington, DC, USA, 2004. [Google Scholar]
- Mandal, B.N.; Chakrabarti, A. Applied Singular Integral Equations; CRC Press: Boca Raton, FL, USA, 2011; 260p. [Google Scholar]
- Boykov, I.V.; Boykova, A.I. Analytical methods for solution of hypersingular and polyhypersingular integral equations. arXiv 2019, arXiv:1901.04880v1. [Google Scholar]
- Gakhov, F.D. Boundary Value Problems; Dover Publication: Mineola, NY, USA, 1990; 561p. [Google Scholar]
- Ivanov, V.V. The Theory of Approximate Methods and their Application to the Numerical Solution of Singular Integral Equations; Noordhoff International Publishing: Leiden, The Netherlands, 1976. [Google Scholar]
- Gohberg, I.C.; Fel’dman, I.A. Convolution Equation and Projection Methods for Their Solution; Nauka: Moscow, Russia, 1971; English Translation: Translations of Mathematical Monographss Volume 41; American Mathematical Society: Providence, RI, USA, 1974. [Google Scholar]
- Golberg, M.A. Introduction to the numerical solution of Cauchy singular integral equations. In Mathematical Concepts and Methods in Science and Engineering; Plenum Press: New York, NY, USA, 1990; Volume 42. [Google Scholar]
- Michlin, S.G.; Prossdorf, S. Singular Integral Operatoren; Acad.-Verl.: Berlin, Germany, 1980. [Google Scholar]
- Boykov, I.V. Approximate Methods of Solution of Singular Integral Equations; The Penza State University: Penza, Russia, 2004. (In Russian) [Google Scholar]
- Boykov, I.V. Numerical methods for solutions of singular integral equations. arXiv 1973, arXiv:1610.09611. [Google Scholar]
- Capobiano, M.R.; Criscuolo, G.; Junghanns, P. On the numerical solution of a nonlinear integral equation of Prandtl’s type. In Operator Theory: Advances and Applications; Birkhauser Verlag: Basel, Switzerland, 2005; Volume 160, pp. 53–79. [Google Scholar]
- Oseledets, I.V.; Tyrtyshnicov, E.E. Approximate invention of matrices in the process of solving hypersingular integral equation. Comput. Math. Math. Phys. 2005, 45, 302–313. [Google Scholar]
- Golberg, M.A. The convergence of several algorithms for solving integral equations with finite-part integrals, I. Integral Equ. 1983, 5, 329–340. [Google Scholar] [CrossRef]
- Golberg, M.A. The convergence of several algorithms for solving integral equations with finite-part integrals, II. Integral Equ. 1985, 9, 267–275. [Google Scholar] [CrossRef]
- Lifanov, I.K. Singular Integral Equations and Discrete Vortices; VSP: Utrecht, The Netherlands, 1996. [Google Scholar]
- Boykov, I.V.; Zakharova Yu, F. An approximate solution to hypersingular integro-differential equations. Univ. Proc. Volga Reg. Phys. Math. Sci. Math. 2010, 1, 80–90. (In Russian) [Google Scholar]
- Boykov, I.V.; Boykova, A.I. An approximate solution of hypersingular integral equations with odd singularities of integer order. Univ. Proc. Volga Reg. Phys. Math. Sci. Math. 2010, 3, 15–27. (In Russian) [Google Scholar]
- Boykov, I.V.; Ventsel, E.S.; Boykova, A.I. An approximate solution of hypersingular integral equations. Appl. Numer. Math. 2010, 60, 607–628. [Google Scholar] [CrossRef]
- Boykov, I.V.; Ventsel, E.S.; Roudnev, V.A.; Boykova, A.I. An approximate solution of nonlinear hypersingular integral equations. Appl. Numer. Math. 2014, 86, 1–21. [Google Scholar] [CrossRef]
- Boykov, I.V.; Roudnev, V.A.; Boykova, A.I.; Baulina, O.A. New iterative method for solving linear and nonlinear hypersingular integral equations. Appl. Numer. Math. 2018, 127, 280–305. [Google Scholar] [CrossRef]
- Kaya, A.C.; Erdogan, F. On The Solution of Integral Equations with Strongly Singular Kernels. Quart. Appl. Math. 1987, 95, 105–122. [Google Scholar] [CrossRef]
- Eshkuvatov, Z.K.; Zulkarnain, F.S.; Nik Long, N.M.A.; Muminov, Z. Modified homotopy perturbation method for solving hypersingular integral equations of the first kind. SpringerPlus 2016, 5, 1473. [Google Scholar] [CrossRef]
- Boykov, I.V.; Boykova, A.I.; Syomov, M.A. An approximate solution of hypersingular integral equations of the first kind. Univ. Proc. Volga Reg. Phys. Math. Sci. Math. 2015, 3, 11–27. (In Russian) [Google Scholar]
- Boykov, I.V.; Boykova, A.I. Approximate methods for solving hypersingular integral equations of the first kind with second-order singularities on classes of functions with weights (1-t2)-1/2. Univ. Proc. Volga Reg. Phys. Math. Sci. Math. 2017, 2, 79–90. (In Russian) [Google Scholar]
- Boykov, I.V.; Boykova, A.I. An approximate solution of hypersingular integral equations of the first kind with singularities of the second order on the class of functions with weight ((1-t)/(1+t))±1/2. Univ. Proc. Volga Reg. Phys. Math. Sci. Math. 2019, 3, 76–92. (In Russian) [Google Scholar]
- Lifanov, I.K.; Nenashev, A.S. Hypersingular integral equations and the theory of wire antennas. Diff. Equ. 2005, 41, 126–145. [Google Scholar] [CrossRef]
- Lifanov, I.K.; Nenashev, A.S. Analysis of Some Computational Schemes for a Hypersingular Integral Equation on an Interval. Diff. Equ. 2005, 41, 1343–1348. [Google Scholar] [CrossRef]
- Boykov, I.V. Analytical and numerical methods for solving hypersingular integral equations. Dyn. Syst. 2019, 9, 244–272. (In Russian) [Google Scholar]
- Boikov, I.V. On a continuous method for solving nonlinear operator equations. Differ. Equ. 2012, 48, 1308–1314. [Google Scholar] [CrossRef]
- Daletskii Yu, L.; Krein, M.G. Stability of Solutions of Differential Equations in Banach Space; Nauka: Moscow, Russia, 1970; 536p, English Translation: Translations of Mathematical Monographss, Volume 43; American Mathematical Society: Providence, RI, USA, 1974. (In Russian) [Google Scholar]
- Lozinskii, S.M. Note on a paper by V.S. Godlevskii. Ussr Comput. Math. Math. Phys. 1973, 13, 232–234. [Google Scholar] [CrossRef]
- Boikov, I.V. On the stability of solutions of differential and difference equations in critical cases. Soviet Math. Dokl. 1991, 42, 630–632. [Google Scholar]
- Boikov, I.V. Stability of Solutions of Differential Equations; Publishing House of Penza State University: Penza, Russia, 2008; 24p. (In Russian) [Google Scholar]
- Browder, F.E. Nonlinear mappings of the nonexpansive and accretive type in Banach spaces. Bull. Am. Math. Soc. 1967, 73, 875–882. [Google Scholar] [CrossRef]
- Malkowski, E.; Rakoćević, V. Advanced Functional Analysis; CRS Press, Taylor and Francis Group: Boca Raton, FL, USA, 2019. [Google Scholar]
- Ćirić, L.; Rafiq, A.; Radenović, S.; Rajović, M. Jeong Sheok Ume On Mann implicit iterations for strongly accreative and strongly pseudo-contractive mappings. Appl. Math. Comput. 2008, 198, 128–137. [Google Scholar]
- Todoriević, V. Harmonic Quasiconformal Mappings and Hyperbolic Type Metrics; Springer Nature: Cham, Switzerland, 2019. [Google Scholar]
- Todoriević, V. Subharmonic behavior and quasiconformal mappings. Anal. Math. Phys. 2019, 9, 1211–1225. [Google Scholar] [CrossRef]
- Hadamard, J. Lectures on Cauchy’s Problem in Linear Partial Differential Equations; Dover Publ. Inc.: New York, NY, USA, 1952. [Google Scholar]
- Chikin, L.A. Special cases of the Riemann boundary value problems and singular integral equations. Sci. Notes Kazan State Univ. 1953, 113, 53–105. (In Russian) [Google Scholar]
- Chan, Y.-S.; Fannjiang, A.C.; Paulino, G.H. Integral equations with hypersingular kernels-theory and applications to fracture mechanics. Int. J. Eng. Sci. 2003, 41, 683–720. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Boykov, I.; Roudnev, V.; Boykova, A. Approximate Methods for Solving Linear and Nonlinear Hypersingular Integral Equations. Axioms 2020, 9, 74. https://doi.org/10.3390/axioms9030074
Boykov I, Roudnev V, Boykova A. Approximate Methods for Solving Linear and Nonlinear Hypersingular Integral Equations. Axioms. 2020; 9(3):74. https://doi.org/10.3390/axioms9030074
Chicago/Turabian StyleBoykov, Ilya, Vladimir Roudnev, and Alla Boykova. 2020. "Approximate Methods for Solving Linear and Nonlinear Hypersingular Integral Equations" Axioms 9, no. 3: 74. https://doi.org/10.3390/axioms9030074
APA StyleBoykov, I., Roudnev, V., & Boykova, A. (2020). Approximate Methods for Solving Linear and Nonlinear Hypersingular Integral Equations. Axioms, 9(3), 74. https://doi.org/10.3390/axioms9030074





