Kripke-Style Models for Logics of Evidence and Truth
Abstract
:1. Introduction
- When :
- , : at w the database has only the information that A is true;
- , : at w the database has only the information that A is false;
- , : at w the database has conflicting information about A;
- , : at w the database has no information about A.
- When :
- 5.
- : at w the database has reliable information that A is true;
- 6.
- : at w the database has reliable information that A is false.
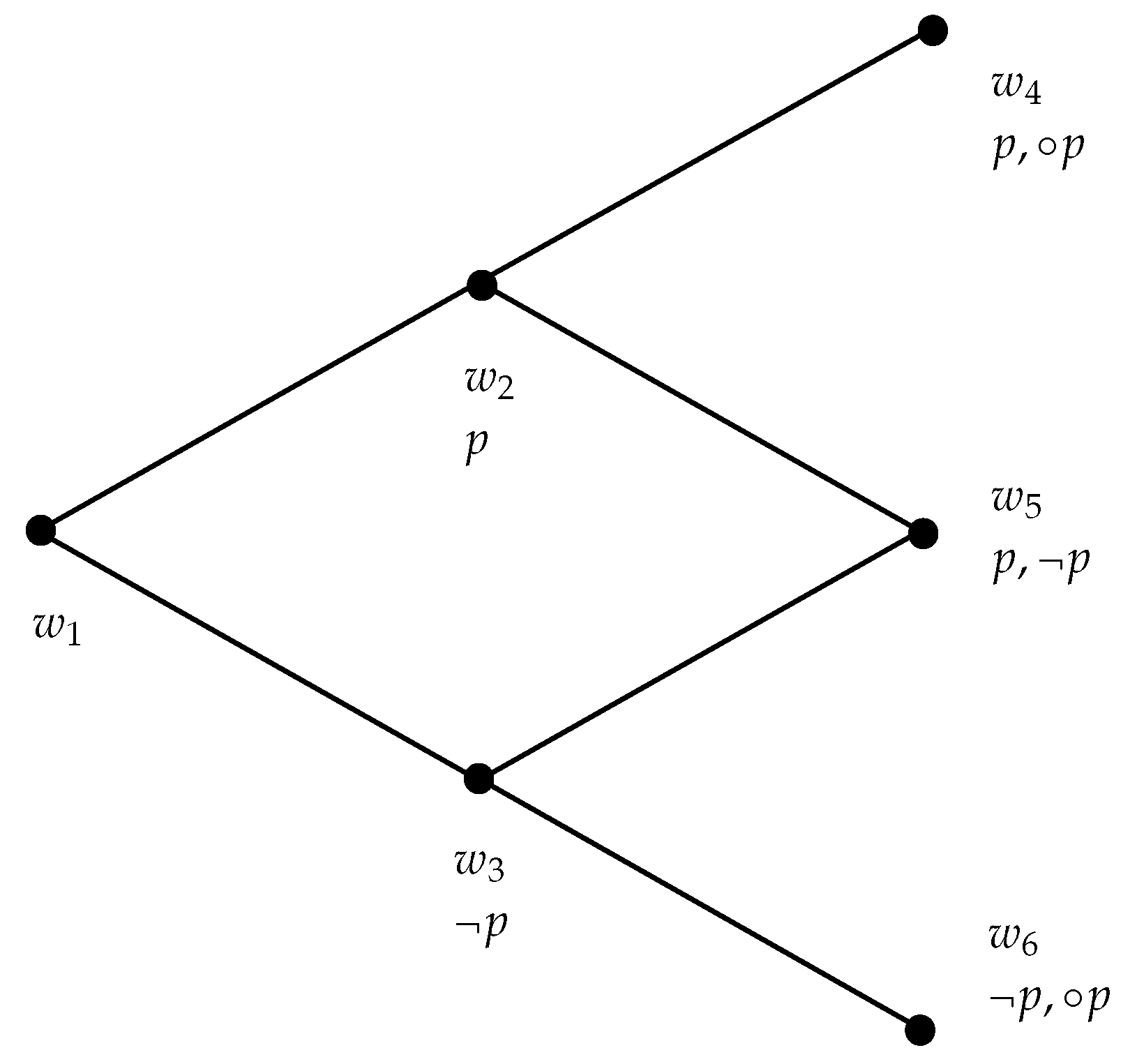
2. The Logic
- 1.
- iff and ;
- 2.
- iff or ;
- 3.
- iff ;
- 4.
- iff or ;
- 5.
- iff and ;
- 6.
- only if exactly one of the following conditions obtains:For every , and ;For every , and ;
- 7.
- iff for every , if , then ;
- 8.
- iff and ;
- P1.
- If , then for every , , for every .
Soudness and Completeness
- 1.
- Δ is nontrivial: , for some ;
- 2.
- Δ is closed: if , then , for every ;
- 3.
- Δ is disjunctive (or prime): if , then or , for every .
- 1.
- iff and ;
- 2.
- iff or ;
- 3.
- iff ;
- 4.
- iff or ;
- 5.
- iff and ;
- 6.
- If , then one of the following conditions obtains:For every regular set , and ;For every regular set , and ;
- 7.
- iff for every regular set , if , then ;
- 8.
- iff and .
- ;
- ;
- is defined by: iff , for every .
3. From to
- 7′.
- iff
- 1.
- iff and ;
- 2.
- iff or ;
- 3.
- iff ;
- 4.
- iff or ;
- 5.
- iff and ;
- 6.
- If , then one of the following conditions obtains:For every regular set , and ;For every regular set , and ;
- 7′.
- iff .
- ;
- ;
- is defined by: iff , for every .
- 1.
- If , then , for every ;
- 2.
- If , then , for every .
4. Persistence Clauses and Information Revision
- and : the information conveyed by A was available at w and it has not been revised in the process of moving from w to (i.e., it remained available);
- and : the information conveyed by A was available at w but it has been revised in the process of moving from w to ;
- and : the information conveyed by A was unavailable at w, nor was it acquired in the process of moving from w to (i.e., it remained unavailable);
- and : the information conveyed by A was unavailable at w but it has been acquired in the process of moving from w to .
4.1. Persistence Conditions
- P1.
- Total non-revisabilityFor every , if , then .
- P2.
- Non-revisability of reliable informationFor every , if , then .
- P3.
- Non-revisability of reliable information and basic informationFor every , if , then ;For every , if , then ;For every , if , then .
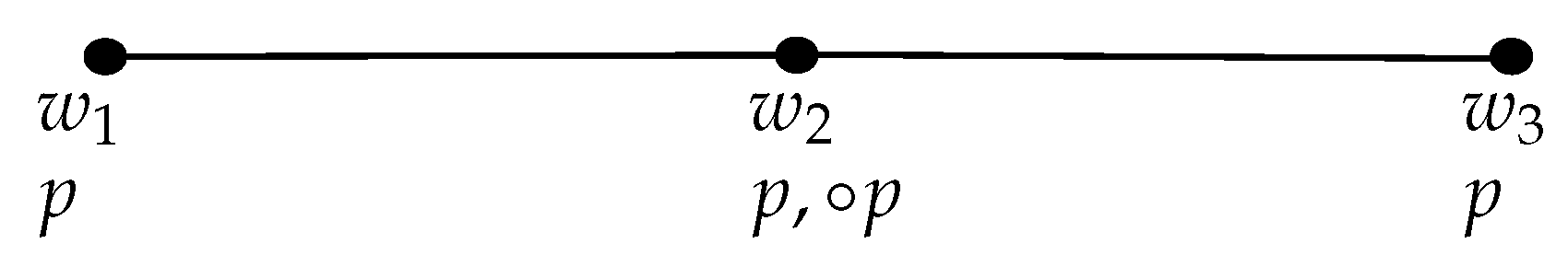 .
.- P2′.
- If , then for every , .
4.2. Adding Persistence to
Soundness and Completeness with Persistence
- ;
- ; and
- is a total function such that for every :
- (I)
- For every such that , and ;
- (II)
- For every such that , and .
- 1.
- iff;
- 2.
- iff;
- 3.
- iff.
- A3.
- ,
- A8.
- .
- i.
- ;
- ii.
- .
5. Some Properties of and
- 1.
- ;
- 2.
- ();
- 3.
- (in only);
- 4.
- (, in only).
- 1.
- Any -formula formed with over behaves classically;
- 2.
- Any -formula formed with over behaves classically.
- 1.
- In , if , then for any formula B formed with over , and for any , B behaves classically in ;
- 2.
- In , assuming persistence for formulas , if , then for any formula B formed with over , and for any , B behaves classically in .
6. Final Remarks and Further Research
Author Contributions
Funding
Conflicts of Interest
References
- Carnielli, W.; Rodrigues, A. An epistemic approach to paraconsistency: A logic of evidence and truth. Synthese 2017, 196, 3789–3813. [Google Scholar] [CrossRef] [Green Version]
- Rodrigues, A.; Bueno-Soler, J.; Carnielli, W. Measuring evidence: A probabilistic approach to an extension of Belnap-Dunn Logic. Synthese 2020. [Google Scholar] [CrossRef]
- Carnielli, W.; Rodrigues, A. On epistemic and ontological interpretations of intuitionistic and paraconsistent paradigms. Log. J. IGPL 2020. [Google Scholar] [CrossRef]
- Carnielli, W.; Coniglio, M.E. Paraconsistent Logic: Consistency, Contradiction and Negation; Springer: Berlin, Germany, 2016. [Google Scholar]
- Carnielli, W.; Coniglio, M.E.; Marcos, J. Logics of Formal Inconsistency. In Handbook of Philosophical Logic; Gabbay, D.M., Guenthner, F., Eds.; Springer: Berlin, Germany, 2007; Volume 14. [Google Scholar]
- Carnielli, W.; Coniglio, M.E.; Rodrigues, A. Recovery operators, paraconsistency and duality. Log. J. IGPL 2019. [Google Scholar] [CrossRef] [Green Version]
- Dunn, J.M. Information in computer science. In Philosophy of Information; Volume 8 of Handbook of the Philosophy of Science; Adriaans, P., van Benthem, J., Eds.; Elsevier: Amsterdam, The Netherlands, 2008; pp. 581–608. [Google Scholar]
- Odintsov, S.; Wansing, H. On the Methodology of Paraconsistent Logic. In Logical Studies of Paraconsistent Reasoning in Science and Mathematics; Andreas, H., Verdée, P., Eds.; Springer: Berlin, Germany, 2016. [Google Scholar]
- Belnap, N.D. How a computer should think. In Contemporary Aspects of Philosophy; Ryle, G., Ed.; Oriel Press: Charleville, UK, 1977. [Google Scholar]
- Belnap, N.D. A useful four-valued logic. In Modern Uses of Multiple Valued Logics; Epstein, G., Dunn, J.M., Eds.; D. Reidel: Dordrecht, The Netherlands, 1977. [Google Scholar]
- Dunn, J.M. Intuitive semantics for first-degree entailments and ‘coupled trees’. Philos. Stud. 1976, 29, 149–168. [Google Scholar] [CrossRef]
- Wansing, H. The Logic of Information Structures; Springer: Berlin, Germany, 1993. [Google Scholar]
- Kapsner, A. Logics and Falsifications; Springer: Berlin, Germany, 2014. [Google Scholar]
- Van Dalen, D. Logic and Structure, 4th ed.; Springer: Berlin, Germany, 2008. [Google Scholar]
- Omori, H.; Wansing, H. 40 years of FDE: An Introductory Overview. In Studia Logica; Springer: Berlin, Germany, 2017; pp. 1021–1049. [Google Scholar]
- Omori, H.; Sano, K. da Costa Meets Belnap and Nelson. In Recent Trends in Philosophical Logic; Ciuni, R., Wansing, H., Willkommen, C., Eds.; Springer: Berlin, Germany, 2014. [Google Scholar]
- Carnielli, W.; Rodrigues, A. On the philosophy and mathematics of the Logics of Formal Inconsistency. In New Directions in Paraconsistent Logic; Springer: Berlin, Germany, 2016. [Google Scholar]
- Marcos, J. Nearly every normal modal logic is paranormal. Log. Anal. 2005, 48, 279–300. [Google Scholar]
- Dodó, A.; Marcos, J. Negative modalities, consistency and determinedness. Electron. Notes Theor. Comput. Sci. 2014, 300, 21–45. [Google Scholar] [CrossRef] [Green Version]
- Odintsov, S. Algebraic semantics for paraconsistent Nelson’s logic. J. Log. Comput. 2003, 4, 453–468. [Google Scholar] [CrossRef]
- Carnielli, W.; Coniglio, M.E.; Rodrigues, A. On formal aspects of the epistemic approach to paraconsistency. In Logic and Philosophy of Logic: Recent Trends in Latin America and Spain; Freund, M., de Castro, M., Ruffino, M., Eds.; College Publications: London, UK, 2018. [Google Scholar]
- Coniglio, M.E.; Figallo-Orellano, A.; Golzio, A.C. Non-deterministic algebraization of logics by swap structures. Log. J. IGPL. forthcoming.
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Antunes, H.; Carnielli, W.; Kapsner, A.; Rodrigues, A. Kripke-Style Models for Logics of Evidence and Truth. Axioms 2020, 9, 100. https://doi.org/10.3390/axioms9030100
Antunes H, Carnielli W, Kapsner A, Rodrigues A. Kripke-Style Models for Logics of Evidence and Truth. Axioms. 2020; 9(3):100. https://doi.org/10.3390/axioms9030100
Chicago/Turabian StyleAntunes, Henrique, Walter Carnielli, Andreas Kapsner, and Abilio Rodrigues. 2020. "Kripke-Style Models for Logics of Evidence and Truth" Axioms 9, no. 3: 100. https://doi.org/10.3390/axioms9030100
APA StyleAntunes, H., Carnielli, W., Kapsner, A., & Rodrigues, A. (2020). Kripke-Style Models for Logics of Evidence and Truth. Axioms, 9(3), 100. https://doi.org/10.3390/axioms9030100






