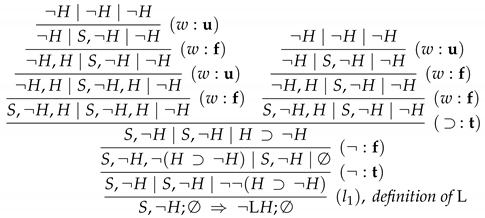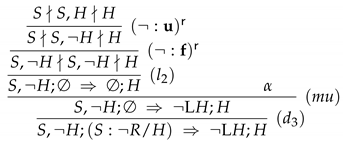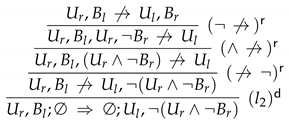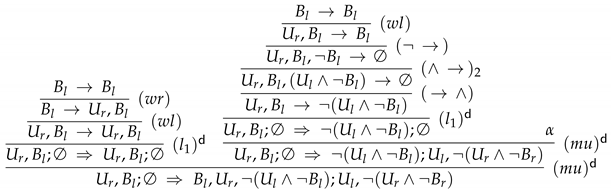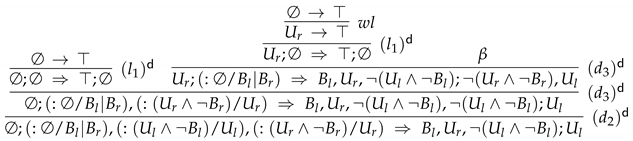Sequent-Type Calculi for Three-Valued and Disjunctive Default Logic
Abstract
1. Introduction
- (i)
- assertional sequents for axiomatising validity in the respective underlying monotonic base logic;
- (ii)
- anti-sequents for axiomatising invalidity for the underlying monotonic logics, taking care of the consistency check of defaults; and
- (iii)
- proper default sequents, for representing nonmonotonic conclusions.
2. Background
2.1. Underlying Monotonic Logics
2.1.1. Classical Propositional Logic
- . (“Inflationaryness”.)
- . (“Idempotency”.)
- implies . (“Monotonicity”.)
2.1.2. Łukasiewicz’s Three-Valued Logic
- the connective “” (“weak negation”), given by
- the unary operators “” (“certainty operator”) and “” (“possibility operator”), defined bywhich, according to Łukasiewicz [11], were first formalised in 1921 by Tarski; and
- the operator “”, given by
- If , then .
- If , then .
- If , then .
- If A is an atomic formula, then .
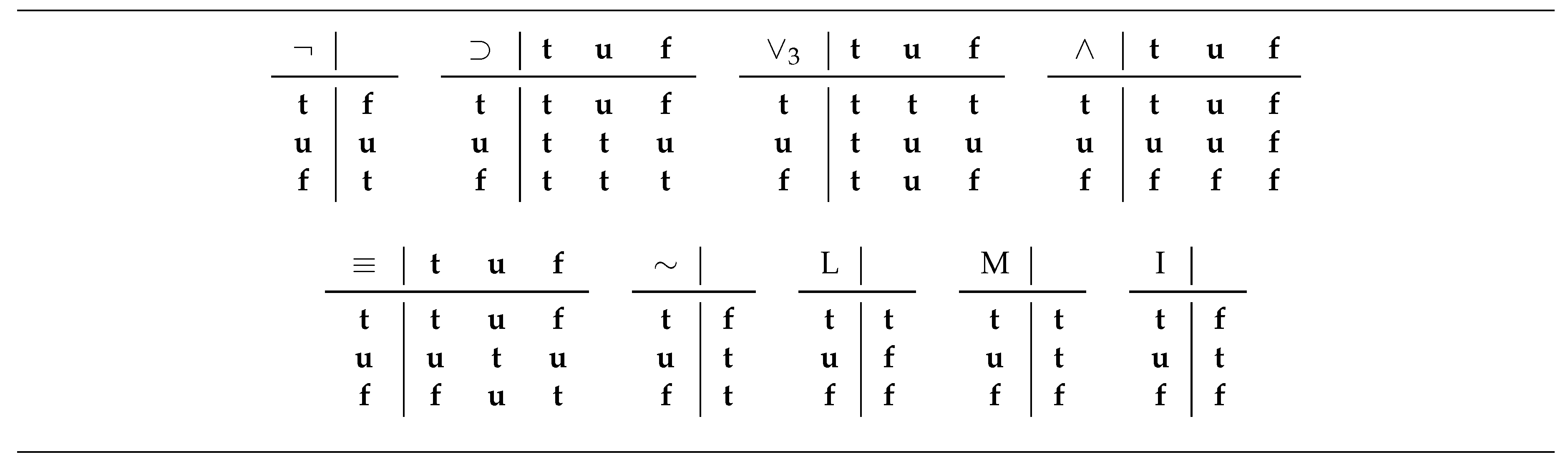
- If , for some formula B, or , for some formulas C and D, then is determined according to the truth tables given in Figure 1 (there, the corresponding truth conditions for the defined connectives are also given).
- .
- , for and .
- , for .
- .
- .
- .
- .
- .
- 1.
- iff is inconsistent (in ).
- 2.
- iff .
2.2. Two Variants of Default Logic
2.2.1. Three-Valued Default Logic
if A is believed, and and are consistent with what is believed, then is asserted.
- .
- .
- If , , , and , then .
- 3’.
- If , , and , then .
- P: “Tony recites passages from Shakespeare”;
- Q: “Tony can read and write”;
- R: “Tony is over seven years old”.
2.2.2. Disjunctive Default Logic
if A is believed and are consistent with what is believed, then one of is asserted.
- .
- .
- If , and , then , for some .
3. A Sequent Calculus for Three-Valued Default Logic
3.1. Postulates of the Calculus
3.1.1. A Sequent Calculus for
- axioms of are sequents of the form
- -
- ,
- -
- ,
- -
- , and
- -
- , where A is a formula;
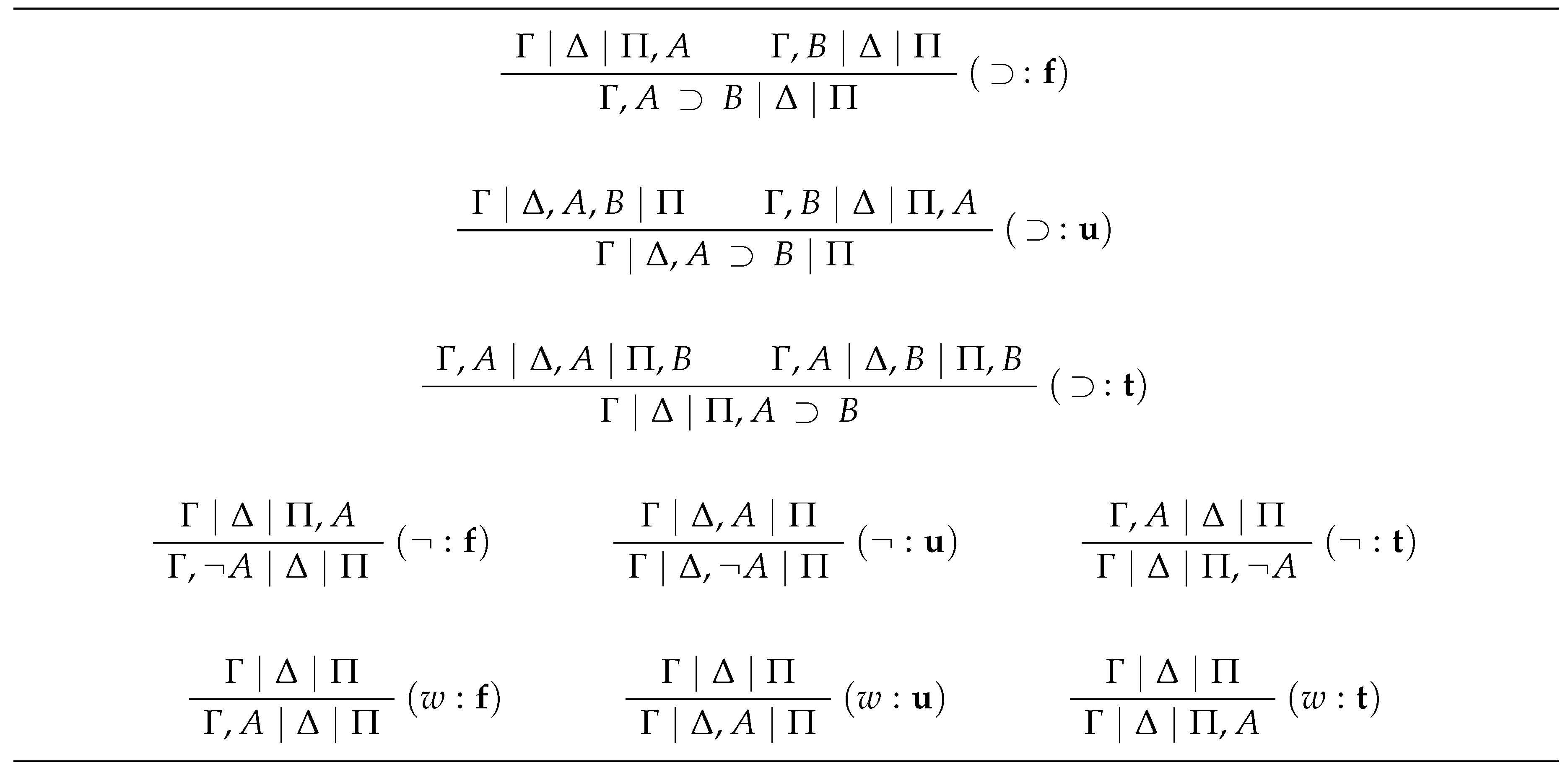
and - the inference rules of are comprised of the rules depicted in Figure 2.
3.1.2. An Anti-Sequent Calculus for
- the axioms of are anti-sequents of the form , where each () is a set of atomic formulas such that , , , and ; and
- the inference rules of are those given in Figure 3.
3.1.3. The Default-Sequent Calculus
- all axioms and inference rules of and ;
- axioms of the form , where Γ is a finite set of formulas of; and
- the inference rules depicted in Figure 4.
- (i)
- rules and combine three-valued sequents and anti-sequents with default sequents, respectively;
- (ii)
- rule is the rule of “monotonic union”—it allows the joining of information in case that no default is present; and
- (iii)
- rules – are the default introduction rules, where rules , , and take care of introducing non-active defaults, whilst rule allows to introduce an active default.
- Proof α:
- Proof β:
3.2. Adequacy of the Calculus
3.2.1. Preparatory Characterisations: Residues and Extensions
- 1.
- .
- 2.
- .
- 3.
- If , then .
- 4.
- If , then .
- 1.
- If , then .
- 2.
- If , then .
- ;
- ; and
- .
3.2.2. Soundness and Completeness of
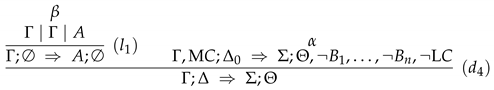
- ;
- there is some such that ; or
- .
- ;
- ; or
- .
- a proof in of ;
- a proof in of ; or
- a proof in of .
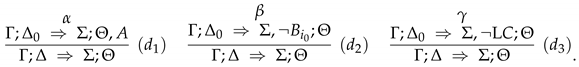
4. A Sequent Calculus for Disjunctive Default Logic
- (i)
- sequents for expressing validity in ;
- (ii)
- anti-sequents for expressing non-tautologies; and
- (iii)
- special default inference rules reflecting brave reasoning in .
4.1. Postulates of the Calculus
4.1.1. The Sequent Calculus
- axioms of are sequents of the form
- -
- ,
- -
- , and
- -
- , where A is a formula;
and - the inference rules of are those given in Figure 5.
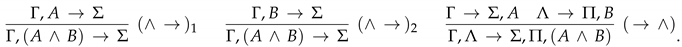
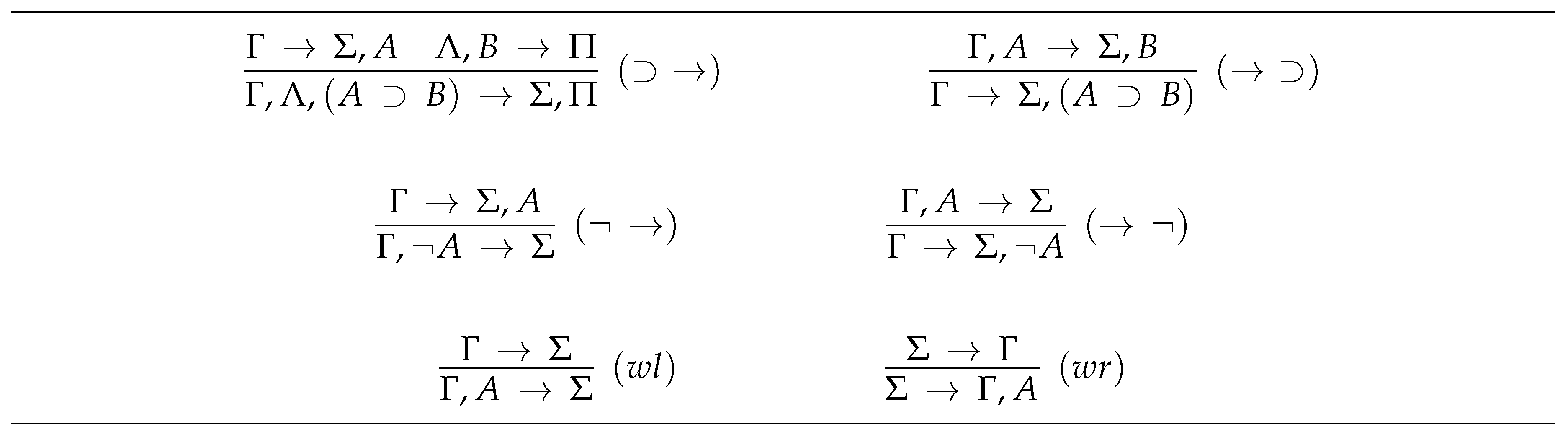
4.1.2. The Anti-Sequent Calculus
- the axioms of are anti-sequents of the form , where Φ and Ψ are disjoint finite sets of atomic formulas such that and ; and
- the inference rules of are those depicted in Figure 6.
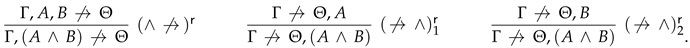
4.1.3. The Default-Sequent Calculus
- all axioms and inference rules of and ;
- axioms of the form , where Γ is a finite set of formulas of ; and
- the inference rules are those depicted in Figure 7.
- (i)
- rules and combine classical sequents and anti-sequents with disjunctive default sequents, respectively;
- (ii)
- rule again allows the joining of information in case that no default is present; and
- (iii)
- rules , , and are the default introduction rules, where rules and take care of introducing non-active defaults, whilst rule allows to introduce an active default.
- Proof α:
- Proof β:
- Proof γ:
4.2. Adequacy of the Calculus
- (i)
- contain W,
- (ii)
- are closed under propositional consequence, and
- (iii)
- are closed under R.
- 1.
- If and , then .
- 2.
- If and , then , for some formula .
- 1.
- If E is an extension of and d is active in E, then E is an extension of , for some .
- 2.
- If E is an extension of the disjunctive default theory , for some , , and , then E is an extension of .
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Reiter, R. A Logic for Default Reasoning. Artif. Intell. 1980, 13, 81–132. [Google Scholar] [CrossRef]
- Moore, R.C. Semantical Considerations on Nonmonotonic Logic. Artif. Intell. 1985, 25, 75–94. [Google Scholar] [CrossRef]
- McCarthy, J. Circumscription—A Form of Non-Monotonic Reasoning. Artif. Intell. 1980, 13, 27–39. [Google Scholar] [CrossRef]
- Gelfond, M.; Lifschitz, V. Classical Negation in Logic Programs and Disjunctive Databases. New Gener. Comput. 1991, 9, 365–385. [Google Scholar] [CrossRef]
- Pearce, D. Equilibrium Logic. Ann. Math. Artif. Intell. 2006, 47, 3–41. [Google Scholar] [CrossRef]
- Minsky, M. A Framework for Representing Knowledge. In Mind Design; Haugeland, J., Ed.; MIT Press: Cambridge, MA, USA, 1975; pp. 95–128. [Google Scholar]
- Bonatti, P.A. Sequent Calculi for Default and Autoepistemic Logic. In Proceedings of the 5th International Workshop on Theorem Proving with Analytic Tableaux and Related Methods (TABLEAUX ’96), Lecture Notes in Computer Science, Terrasini, Palermo, Italy, 15–17 May 1996; Miglioli, P., Moscato, U., Mundici, D., Ornaghi, M., Eds.; Springer: Berlin/Heidelberg, Germany, 1996; Volume 1071, pp. 127–142. [Google Scholar]
- Bonatti, P.A.; Olivetti, N. Sequent Calculi for Propositional Nonmonotonic Logics. ACM Trans. Comput. Log. 2002, 3, 226–278. [Google Scholar] [CrossRef]
- Radzikowska, A. A Three-Valued Approach to Default Logic. J. Appl. Non-Class. Logics 1996, 6, 149–190. [Google Scholar] [CrossRef]
- Gelfond, M.; Lifschitz, V.; Przymusinska, H.; Truszczyński, M. Disjunctive Defaults. In Proceedings of the 2nd International Conference on Principles of Knowledge Representation and Reasoning (KR’91), Cambridge, MA, USA, 22–25 April 1991; Allen, J.F., Fikes, R., Sandewall, E., Eds.; Morgan Kaufmann: Burlington, MA, USA, 1991; pp. 230–237. [Google Scholar]
- Łukasiewicz, J. Philosophische Bemerkungen zu mehrwertigen Systemen des Aussagenkalküls. Comptes Rendus Des Séances De La Société Des Sciences Et Des Lettres De Varsovie Cl III 1930, 23, 51–77. [Google Scholar]
- Łukaszewicz, W. Considerations on Default Logic—An alternative approach. Comput. Intell. 1988, 4, 1–16. [Google Scholar] [CrossRef]
- Schaub, T. On Constrained Default Theories; Technical Report AIDA-92-2; FG Intellektik, FB Informatik, TH Darmstadt: Darmstadt, Germany, 1992. [Google Scholar]
- Delgrande, J.P.; Schaub, T.; Jackson, W.K. Alternative Approaches to Default Logic. Artif. Intell. 1994, 70, 167–237. [Google Scholar] [CrossRef]
- Mikitiuk, A.; Truszczyński, M. Rational Default Logic and Disjunctive Logic Programming. In Proceedings of the 2nd International Workshop on Logic Programming and Non-Monotonic Reasoning (LPNMR’93), Lisbon, Portugal, 28–30 June 1993; Pereira, L.M., Nerode, A., Eds.; MIT Press: Cambridge, MA, USA, 1993; pp. 283–299. [Google Scholar]
- Zhou, Y.; Lin, F.; Zhang, Y. General Default Logic. Ann. Math. Artif. Intell. 2009, 57, 125–160. [Google Scholar] [CrossRef]
- Yue, A.; Ma, Y.; Lin, Z. Four-Valued Semantics for Default Logic. In Proceedings of the 19th Conference of the Canadian Society for Computational Studies of Intelligence (Canadian AI 2006), Lecture Notes in Computer Science, Quebec City, QC, Canada, 7–9 June 2006; Lamontagne, L., Marchand, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2006; Volume 4013, pp. 195–205. [Google Scholar]
- Antoniou, G.; Wang, K. Default Logic. In Handbook of the History of Logic, Volume 8: The Many Valued and Nonmonotonic Turn in Logic; Gabbay, D., Woods, J., Eds.; North-Holland: Amsterdam, The Netherlands, 2007; pp. 517–632. [Google Scholar]
- Beyersdorff, O.; Meier, A.; Thomas, M.; Vollmer, H. The Complexity of Reasoning for Fragments of Default Logic. J. Log. Comput. 2012, 22, 587–604. [Google Scholar] [CrossRef]
- Łukasiewicz, J. O sylogistyce Arystotelesa. Sprawozdania Z Czynności I Posiedzeń Polskiej Akademii Umiejętności 1939, 44, 220–226. [Google Scholar]
- Béziau, J.Y. A Sequent Calculus for Lukasiewicz’s Three-Valued Logic Based on Suszko’s Bivalent Semantics. Bull. Sect. Log. 1999, 28, 89–97. [Google Scholar]
- Avron, A. Classical Gentzen-Type Methods in Propositional Many-Valued Logics. In Beyond Two: Theory and Applications in Multiple-Valued Logics; Fitting, M., Orłowska, E., Eds.; Springer: Berlin/Heidelberg, Germany, 2003; pp. 117–155. [Google Scholar]
- Gentzen, G. Untersuchungen über das logische Schließen I. Math. Z. 1935, 39, 176–210. [Google Scholar] [CrossRef]
- Avron, A. Natural 3-Valued Logics—Characterization and Proof Theory. J. Symb. Log. 1991, 56, 276–294. [Google Scholar] [CrossRef]
- Rousseau, G.S. Sequents in Many Valued Logic I. Fundam. Math. 1967, 60, 23–33. [Google Scholar] [CrossRef][Green Version]
- Zach, R. Proof Theory of Finite-Valued Logics. Master’s Thesis, Technische Universität Wien, Institut für Computersprachen, Wien, Austria, 1993. [Google Scholar]
- Bogojeski, M.; Tompits, H. On Sequent-Type Rejection Calculi for Many-Valued Logics. In Reasoning: Games, Cognition, Logic; Urbański, M., Skura, T., Łupkowski, P., Eds.; College Publications: London, UK, 2020; pp. 193–207. [Google Scholar]
- Łukasiewicz, J. Logika dwuwartościowa. Przegląd Filozoficzny 1921, 23, 189–205. [Google Scholar]
- Łukasiewicz, J. Aristotle’s Syllogistic from the Standpoint of Modern Formal Logic, 2nd ed.; Clarendon Press: Oxford, UK, 1957. [Google Scholar]
- Słupecki, J. Z Badań Nad Sylogistyką Arystotelesa; Wrocławskie Towarzystwo Naukowe: Wrocław, Poland, 1948; Volume 6, pp. 1–30. [Google Scholar]
- Słupecki, J. Funkcja Łukasiewieza. Zesz. Nauk. Uniw. Wrocławskiego Ser. A 1959, 3, 33–40. [Google Scholar]
- Wybraniec-Skardowska, U. Teoria zdań odrzuconych. Zesz. Nauk. Wyższej Szkoły Pedagog. W Opolu Ser. B Stud. I Monogr. 1969, 22, 5–131. [Google Scholar]
- Bryll, G. Kilka uzupelnień teorii zdań odrzuconych. Zesz. Nauk. Wyższej Szkoły Pedagog. W Opolu Ser. B Stud. I Monogr. 1969, 22, 133–154. [Google Scholar]
- Słupecki, J.; Bryll, G.; Wybraniec-Skardowska, U. Theory of Rejected Propositions I. Stud. Log. 1971, 29, 75–115. [Google Scholar] [CrossRef]
- Słupecki, J.; Bryll, G.; Wybraniec-Skardowska, U. Theory of Rejected Propositions II. Stud. Log. 1972, 30, 97–139. [Google Scholar] [CrossRef]
- Tiomkin, M.L. Proving Unprovability. In Proceedings of the Third Annual Symposium on Logic in Computer Science (LICS’88), Scotland, UK, 5–8 July 1988; IEEE Computer Society: Washington, DC, USA, 1988; pp. 22–26. [Google Scholar]
- Bonatti, P.A. A Gentzen System for Non-Theorems; Technical Report CD-TR 93/52; Christian Doppler Labor für Expertensysteme, Technische Universität Wien: Vienna, Austria, 1993. [Google Scholar]
- Goranko, V. Refutation Systems in Modal Logic. Stud. Log. 1994, 53, 299–324. [Google Scholar] [CrossRef]
- Skura, T. A Complete Syntactic Characterization of the Intuitionistic Logic. Rep. Math. Log. 1989, 23, 75–80. [Google Scholar]
- Dutkiewicz, R. The Method of Axiomatic Rejection for the Intuitionistic Propositional Logic. Stud. Log. 1989, 48, 449–459. [Google Scholar] [CrossRef]
- Pinto, L.; Dyckhoff, R. Loop-Free Construction of Counter-Models for Intuitionistic Propositional Logic. In Symposia Gaussiana, Proceedings of the 2nd Gauss Symposium, Conference A: Mathematics and Theoretical Physics, Munich, Germany, 2–7 August 1993; Behara, M., Fritsch, R., Lintz, R.G., Eds.; Walter de Gruyter: Berlin, Germany, 1995; pp. 225–232. [Google Scholar]
- Skura, T. Aspects of Refutation Procedures in the Intuitionistic Logic and Related Modal Systems. Acta Univ. Wratislav. Log. 1999, 20, 1–84. [Google Scholar]
- Skura, T. Refutation Systems in Propositional Logic. In Handbook of Philosophical Logic, 2nd ed.; Gabbay, D., Guenthner, D., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; Volume 16, pp. 115–157. [Google Scholar]
- Skura, T. Refutation Methods in Modal Propositional Logic; Semper: Warszawa, Poland, 2013. [Google Scholar]
- Berger, G.; Tompits, H. On Axiomatic Rejection for the Description Logic . In Declarative Programming and Knowledge Management–Declarative Programming Days (KDPD 2013); Revised Selected Papers; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2014; Volume 8439, pp. 65–82. [Google Scholar]
- Wybraniec-Skardowska, U. On the Notion and Function of the Rejection of Propositions. Acta Univ. Wratislav. Log. 2005, 23, 179–202. [Google Scholar]
- Rosser, J.B.; Turquette, A.R. Many-Valued Logics; North-Holland: Amsterdam, The Netherlands, 1952. [Google Scholar]
- Malinowski, G. Many-Valued Logic and its Philosophy. In Handbook of the History of Logic, Volume 8: The Many Valued and Nonmonotonic Turn in Logic; Gabbay, D., Woods, J., Eds.; North-Holland: Amsterdam, The Netherlands, 2007; pp. 13–94. [Google Scholar]
- Wajsberg, M. Aksjomatyzacja trójwartościowego rachunku zdań. Comptes Rendus Des Séances De La Société Des Sciences Et Des Lettres De Varsovie Cl III 1931, 24, 136–148. [Google Scholar]
- Łukaszewicz, W. Non-Monotonic Reasoning: Formalization of Commonsense Reasoning; Ellis Horwood: Chichester, UK, 1990. [Google Scholar]
- Pearl, J. Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference; Morgan Kaufmann Publishers: Burlington, MA, USA, 1988. [Google Scholar]
- Poole, D. What the Lottery Paradox Tells us about Default Reasoning. In Proceedings of the First International Conference on Principles of Knowledge Representation and Reasoning (KR’89), Toronto, ON, Canada, 15–18 May 1989; Brachman, R.J., Levesque, H.J., Reiter, R., Eds.; Morgan Kaufmann: Burlington, MA, USA, 1989; pp. 333–340. [Google Scholar]
- Lin, F.; Shoham, Y. Epistemic Semantics for Fixed-Points Non-Monotonic Logics. In Proceedings of the Third Conference on Theoretical Aspects of Reasoning about Knowledge (TARK’90), Pacific Grove, CA, USA, 4–7 March 1990; Parikh, R., Ed.; Morgan Kaufmann: Burlington, MA, USA, 1990; pp. 111–120. [Google Scholar]
- Baumgartner, R.; Gottlob, G. Propositional Default Logics Made Easier: Computational Complexity of Model Checking. Theor. Comput. Sci. 2002, 289, 591–627. [Google Scholar] [CrossRef]
- Bonatti, P.A. Sequent Calculi for Default and Autoepistemic Logic; Technical Report CD-TR 93/53; Christian Doppler Labor für Expertensysteme, Technische Universität Wien: Wien, Austria, 1993. [Google Scholar]
- Carnielli, W.A. On Sequents and Tableaux for Many-Valued Logics. J. Non-Class. Log. 1991, 8, 59–76. [Google Scholar]
- Avron, A. The Method of Hypersequents in the Proof Theory of Propositional Non-Classical Logics. In Logic: From Foundations to Applications; Clarendon Press: Oxford, UK, 1996; pp. 1–32. [Google Scholar]
- Hähnle, R. Tableaux for Many-Valued Logics. In Handbook of Tableaux Methods; D’Agostino, M., Gabbay, D., Hähnle, R., Posegga, J., Eds.; Kluwer: Dordrecht, The Netherlands, 1999; pp. 529–580. [Google Scholar]
- Marek, W.; Truszczyński, M. Nonmonotonic Logic: Context-Dependent Reasoning; Springer: Berlin/Heidelberg, Germany, 1993. [Google Scholar]
- Egly, U.; Tompits, H. A Sequent Calculus for Intuitionistic Default Logic. In Proceedings of the 12th Workshop on Logic Programming (WLP’97), Forschungsbericht PMS-FB-1997-10, Institut für Informatik, Ludwig-Maximilians-Universität München, Munich, Germany, 17–19 September 1997; pp. 69–79. [Google Scholar]
- Lupea, M. Axiomatization of Credulous Reasoning in Default Logics using Sequent Calculus. In Proceedings of the 10th International Symposium on Symbolic and Numeric Algorithms for Scientific Computing (SYNASC 2008), Timisoara, Romania, 26–29 September 2008. [Google Scholar]
- Niemelä, I. Implementing Circumscription Using a Tableau Method. In Proceedings of the 12th European Conference on Artificial Intelligence (ECAI’96), Budapest, Hungary, 11–16 August 1996; Wahlster, W., Ed.; John Wiley and Sons: New York, NY, USA, 1996; pp. 80–84. [Google Scholar]
- Amati, G.; Aiello, L.C.; Gabbay, D.; Pirri, F. A Proof Theoretical Approach to Default Reasoning I: Tableaux for Default Logic. J. Log. Comput. 1996, 6, 205–231. [Google Scholar] [CrossRef][Green Version]
- Pearce, D.; de Guzmán, I.P.; Valverde, A. A Tableau Calculus for Equilibrium Entailment. In Proceedings of the 9th International Conference on Automated Reasoning with Analytic Tableaux and Related Methods (TABLEAUX 2000), Lecture Notes in Computer Science, St Scotland, UK, 3–7 July 2000; Dyckhoff, R., Ed.; Springer: Berlin/Heidelberg, Germany, 2000; Volume 1847, pp. 352–367. [Google Scholar]
- Cabalar, P.; Odintsov, S.P.; Pearce, D.; Valverde, A. Partial Equilibrium Logic. Ann. Math. Artif. Intell. 2007, 50, 305–331. [Google Scholar] [CrossRef][Green Version]
- Gebser, M.; Schaub, T. Tableau Calculi for Logic Programs under Answer Set Semantics. ACM Trans. Comput. Log. 2013, 14, 1–40. [Google Scholar] [CrossRef]
- Oetsch, J.; Tompits, H. Gentzen-Type Refutation Systems for Three-Valued Logics with an Application to Disproving Strong Equivalence. In Proceedings of the 11th International Conference on Logic Programming and Nonmonotonic Resoning (LPNMR 2011), Lecture Notes in Computer Science, Vancouver, BC, Canada, 16–19 May 2011; Delgrande, J.P., Faber, W., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; Volume 6645, pp. 254–259. [Google Scholar]

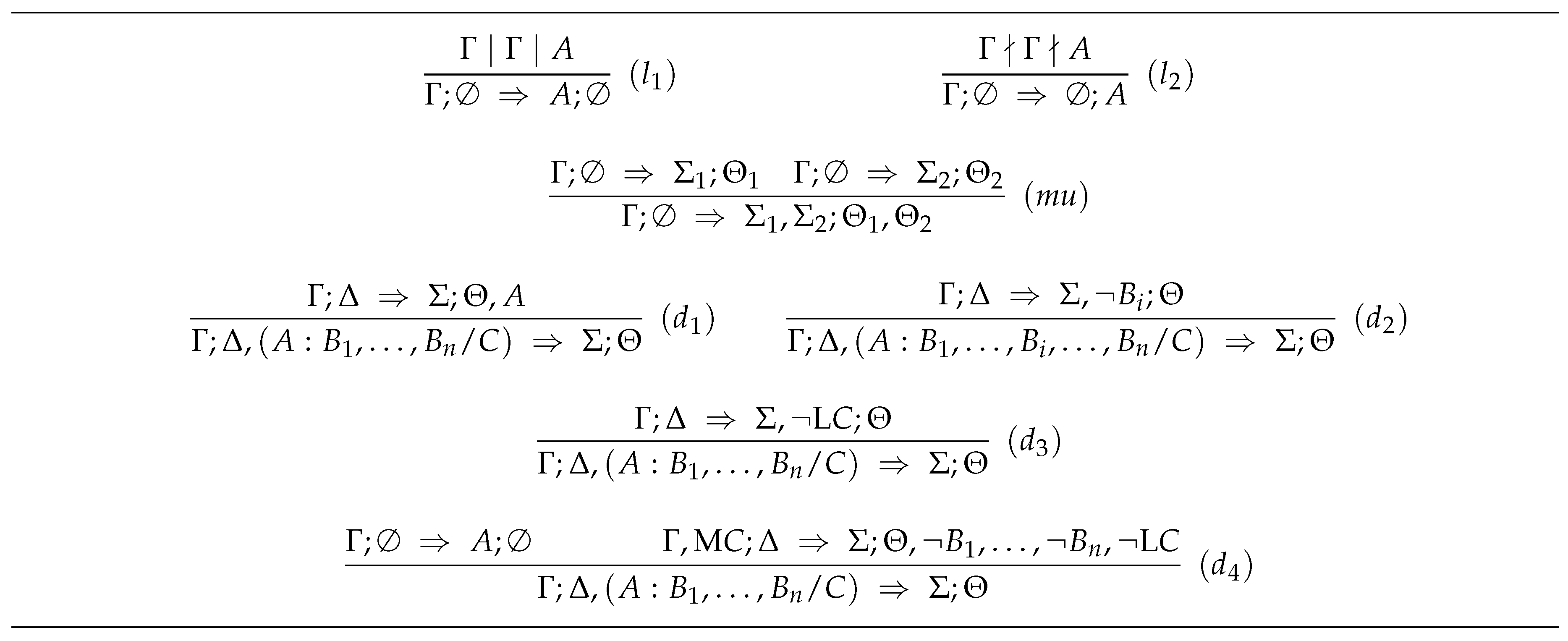
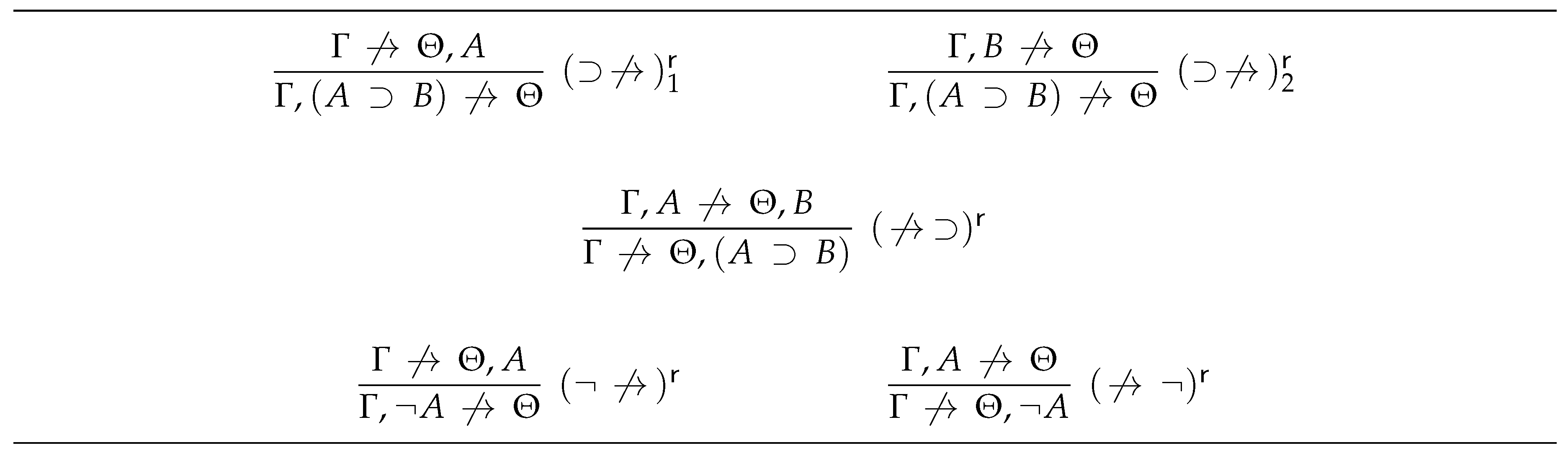
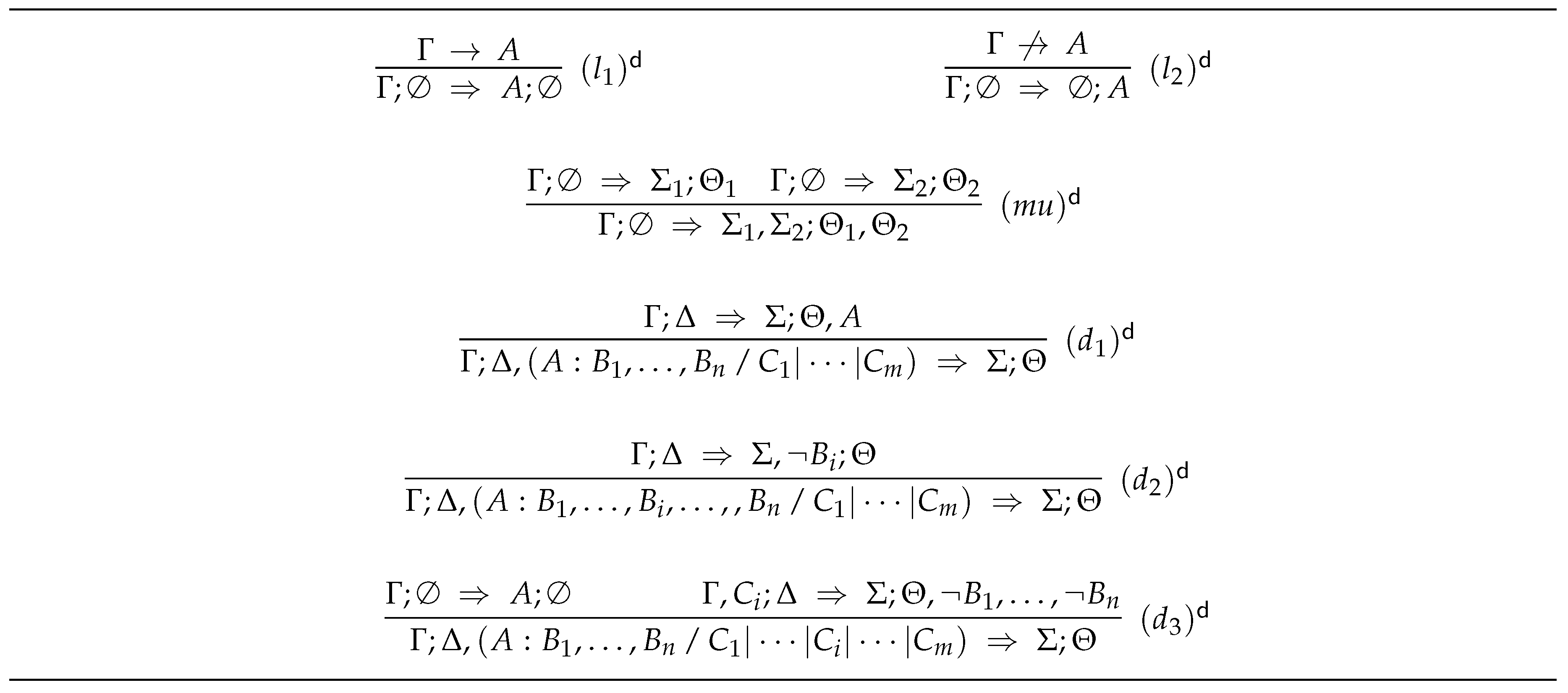
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pkhakadze, S.; Tompits, H. Sequent-Type Calculi for Three-Valued and Disjunctive Default Logic. Axioms 2020, 9, 84. https://doi.org/10.3390/axioms9030084
Pkhakadze S, Tompits H. Sequent-Type Calculi for Three-Valued and Disjunctive Default Logic. Axioms. 2020; 9(3):84. https://doi.org/10.3390/axioms9030084
Chicago/Turabian StylePkhakadze, Sopo, and Hans Tompits. 2020. "Sequent-Type Calculi for Three-Valued and Disjunctive Default Logic" Axioms 9, no. 3: 84. https://doi.org/10.3390/axioms9030084
APA StylePkhakadze, S., & Tompits, H. (2020). Sequent-Type Calculi for Three-Valued and Disjunctive Default Logic. Axioms, 9(3), 84. https://doi.org/10.3390/axioms9030084