Correlations in Two-Qubit Systems under Non-Dissipative Decoherence
Abstract
1. Introduction
2. Theoretical Framework
2.1. Quantum Discord
2.2. Generalized Measures of Correlations
2.2.1. Squared Bures Distance
2.2.2. Squared Hellinger Distance
2.2.3. Quantum Jensen–Shannon Divergence
2.3. Two-Qubit States with Maximally Mixed Marginals
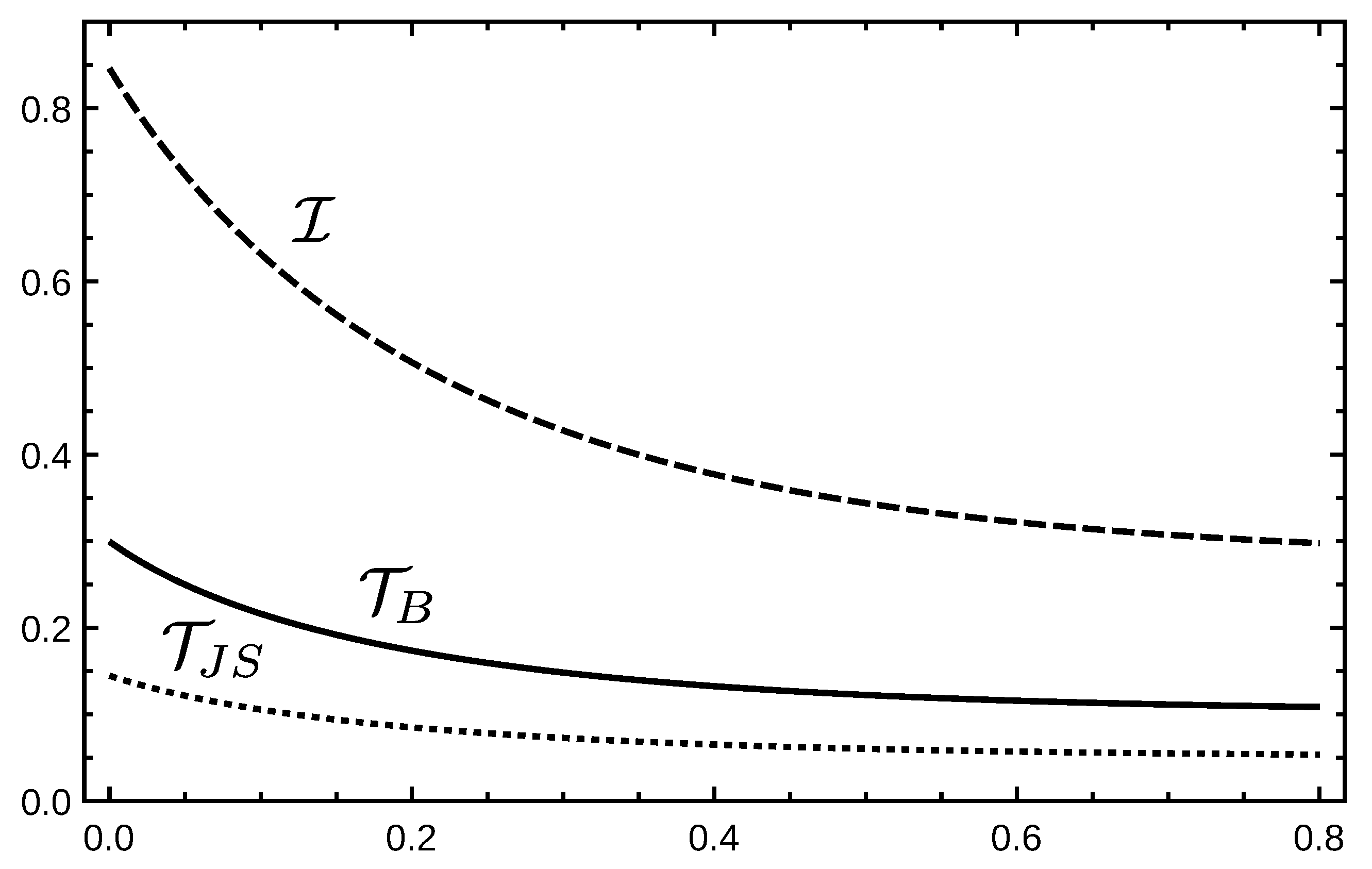
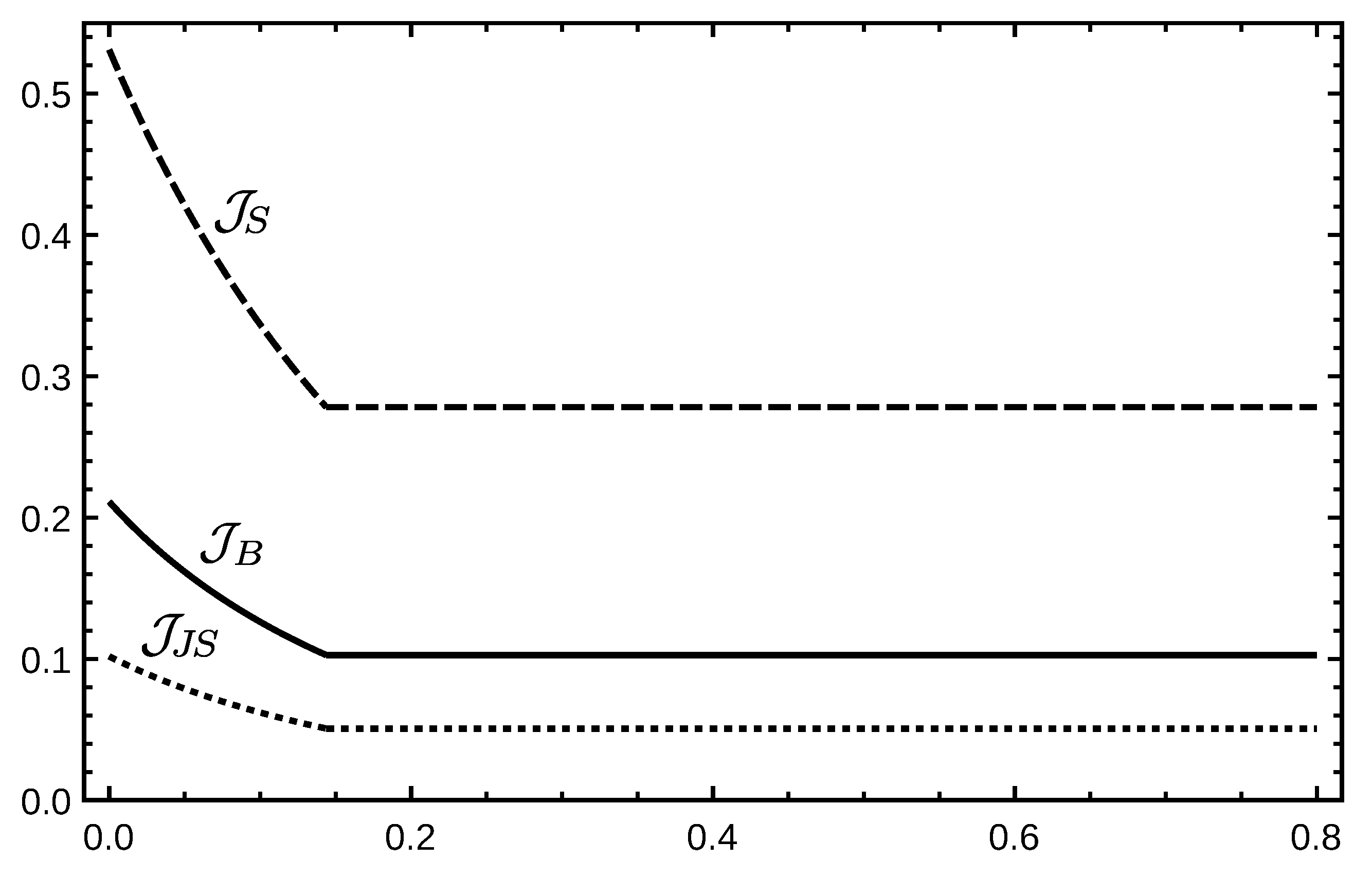
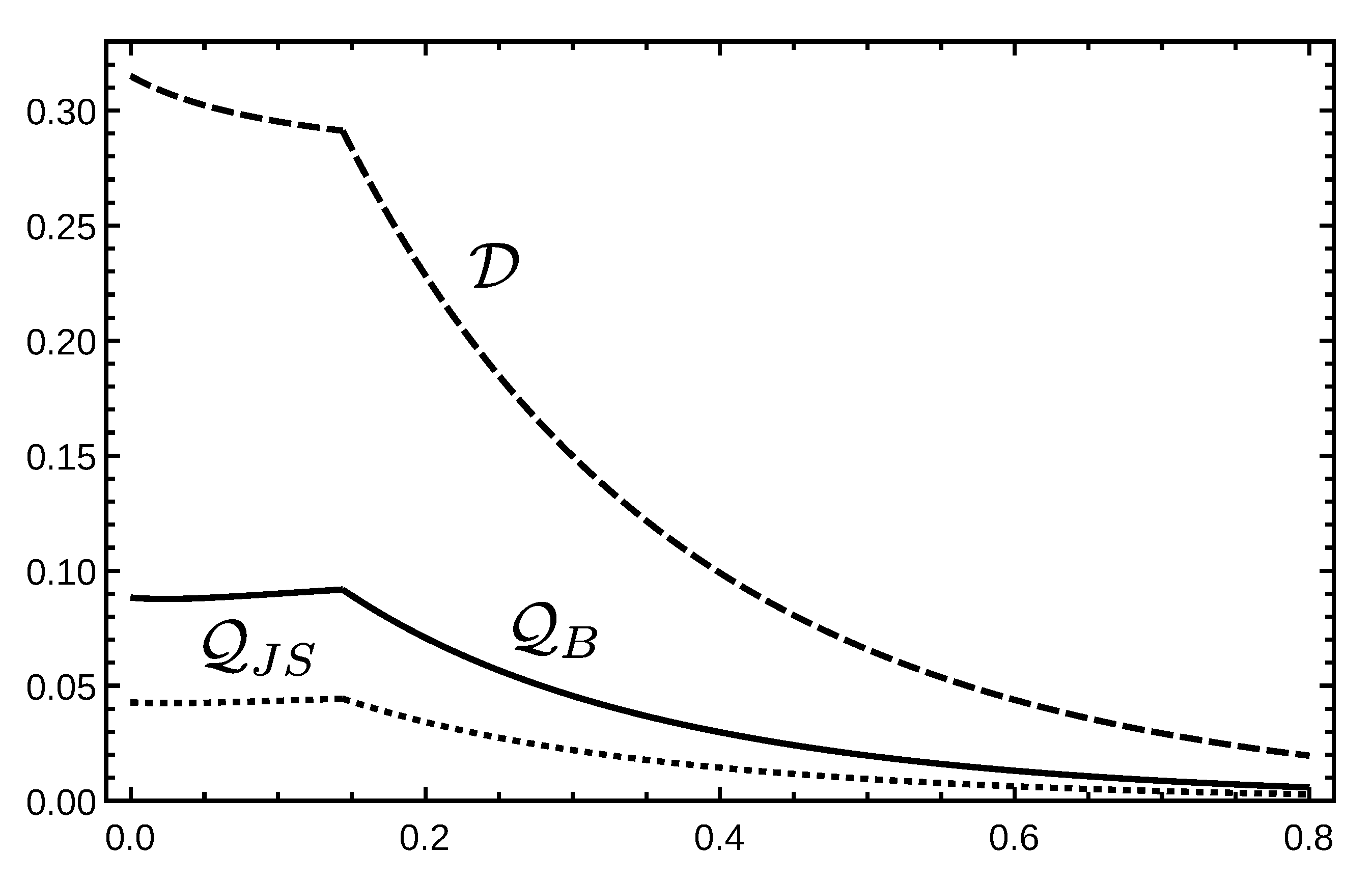
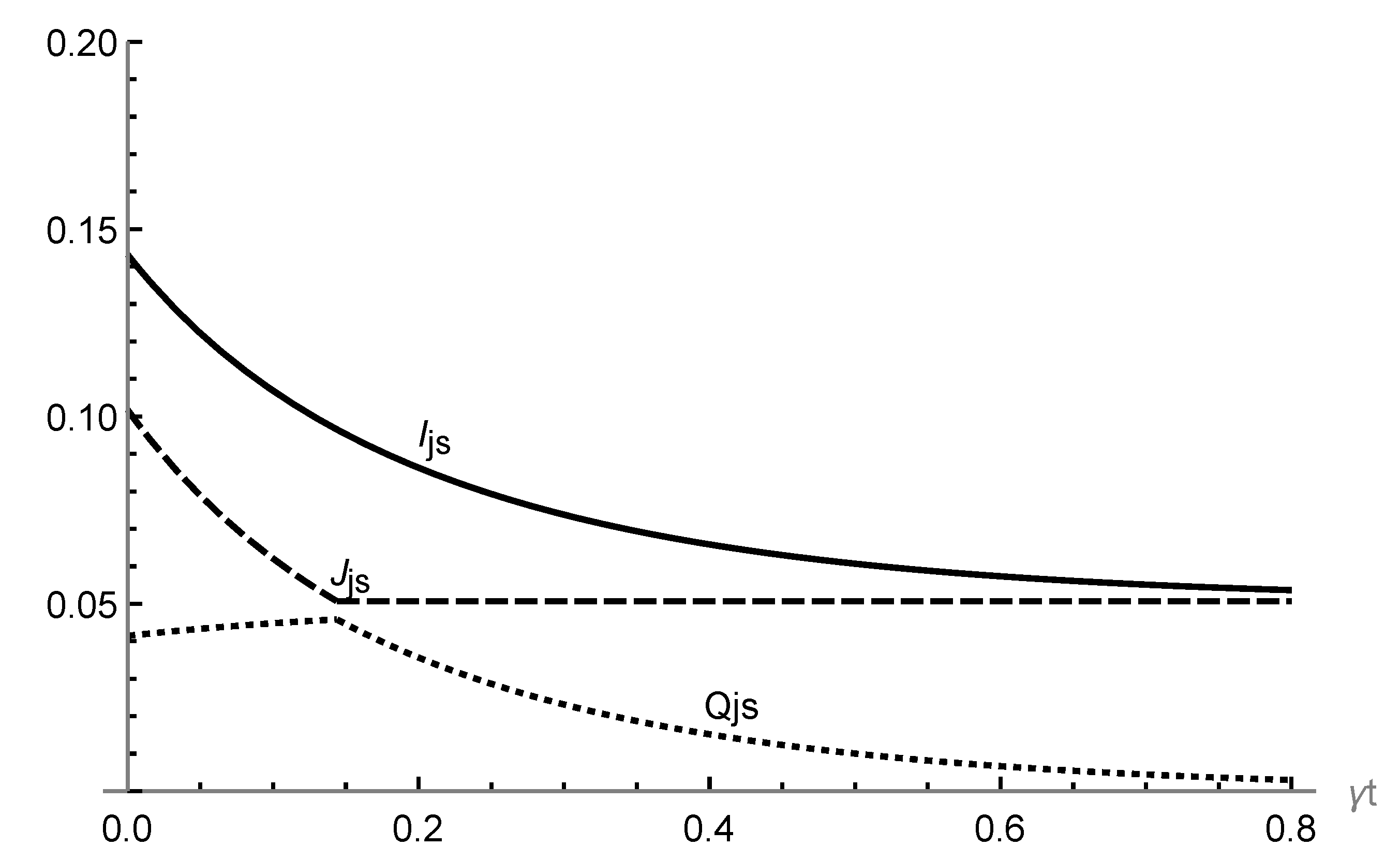
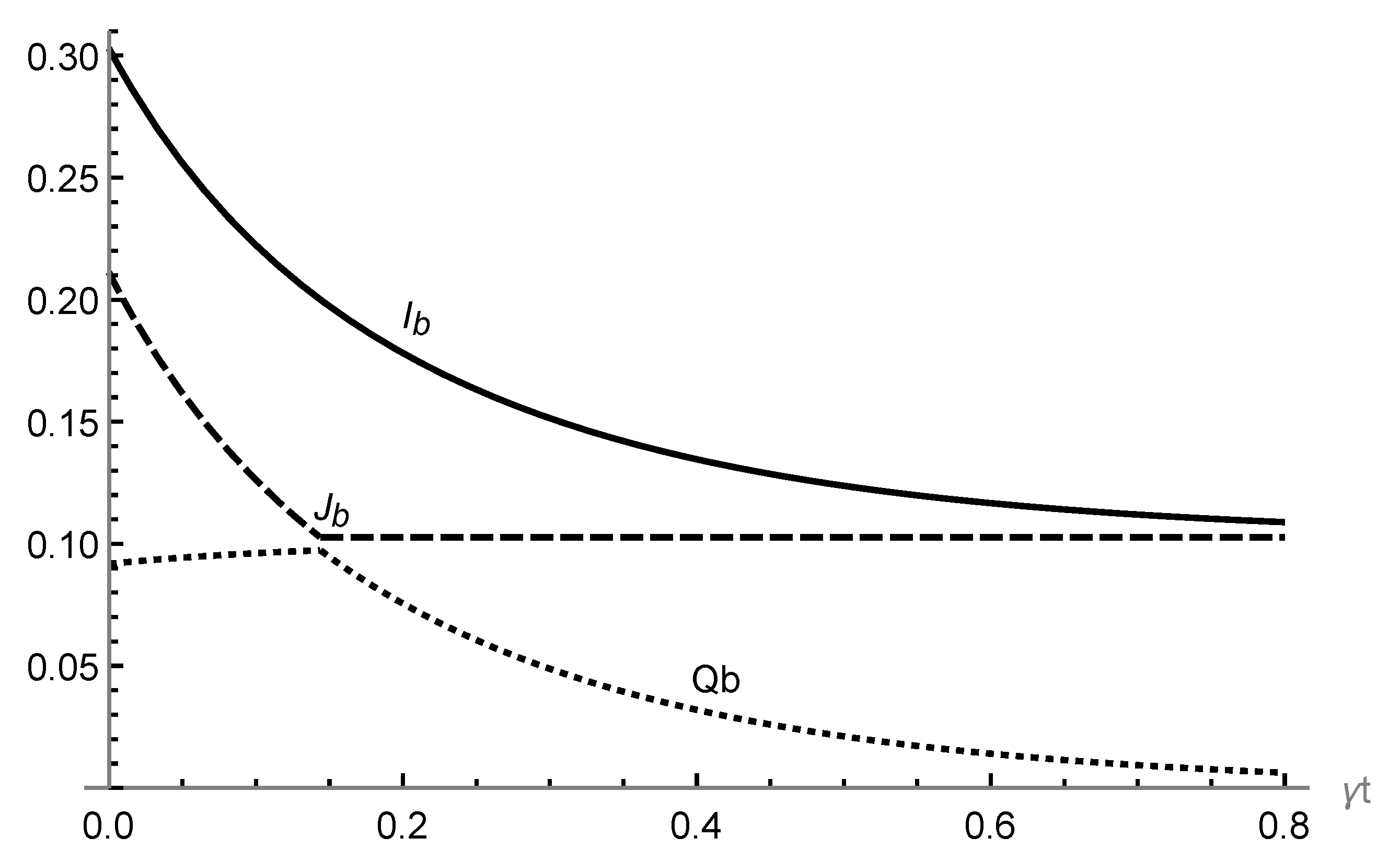
3. Results
- If ⇒, ;
- If ⇒, ;
- If ⇒, .
Behavior of Correlations under Non-Dissipative Decoherence
4. Concluding Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Moore, G.E. Cramming More Components onto Integrated Circuits. Electronics 1965, 38, 114. [Google Scholar] [CrossRef]
- Le Bellac, M. A Short Introduction to Quantum Information and Quantum Computation; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Datta, A.; Shaji, A.; Caves, C.M. Quantum Discord and the Power of One Qubit. Phys. Rev. Lett. 2008, 100, 050502. [Google Scholar] [CrossRef] [PubMed]
- Lanyon, B.P.; Barbieri, M.; Almeida, M.P.; White, A.G. Experimental Quantum Computing without Entanglement. Phys. Rev. Lett. 2008, 101, 200501. [Google Scholar] [CrossRef] [PubMed]
- Knill, E.; Laflamme, R. Power of One Bit of Quantum Information. Phys. Rev. Lett. 1998, 81, 5672. [Google Scholar] [CrossRef]
- Laflamme, R.; Cory, D.; Negrevergne, C.; Viola, L. NMR quantum information processing and entanglement. Quantum Inf. Comp. 2002, 2, 166. [Google Scholar]
- Braunstein, S.L.; Caves, C.M.; Jozsa, R.; Linden, N.; Popescu, S.; Schack, R. Separability of very noisy mixed states and implications for NMR Quantum computing. Phys. Rev. Lett. 1999, 83, 1054. [Google Scholar] [CrossRef]
- Meyer, D.A. Sophisticated Quantum Search Without Entanglement. Phys. Rev. Lett. 2000, 85, 2014. [Google Scholar] [CrossRef] [PubMed]
- Datta, A.; Flammia, S.T.; Caves, C.M. Entanglement and the power of one qubit. Phys. Rev. A 2005, 72, 042316. [Google Scholar] [CrossRef]
- Datta, A.; Vidal, G. Role of entanglement and correlations in mixed-state quantum computation. Phys. Rev. A 2007, 75, 042310. [Google Scholar] [CrossRef]
- Henderson, L.; Vedral, V. Classical, quantum and total correlations. J. Phys. A 2001, 34, 6899. [Google Scholar] [CrossRef]
- Ollivier, H.; Zurek, W.H. Quantum Discord: A Measure of the Quantumness of Correlations. Phys. Rev. Lett. 2001, 88, 017901. [Google Scholar] [CrossRef] [PubMed]
- Modi, K.; Brodutch, A.; Cable, H.; Paterek, T.; Vedral, V. The classical-quantum boundary for correlations: Discord and related measures. Rev. Mod. Phys. 2012, 84, 1655. [Google Scholar] [CrossRef]
- Adesso, G.; Bromley, T.R.; Cianciaruso, M. Measures and applications of quantum correlations. J. Phys. A Math. Theor. 2016, 49, 473001. [Google Scholar] [CrossRef]
- Bosyk, G.M.; Bellomo, G.; Zozor, S.; Portesi, M.; Lamberti, P.W. Unified entropic measures of quantum correlations induced by local measurements. Phys. A Stat. Mech. Appl. 2016, 462, 930–939. [Google Scholar] [CrossRef]
- Rossignoli, R.; Canosa, N.; Ciliberti, L. Generalized entropic measures of quantum correlations. Phys. Rev. A 2010, 82, 052342. [Google Scholar] [CrossRef]
- Rossignoli, R.; Canosa, N.; Ciliberti, L. Quantum correlations and least disturbing local measurements. Phys. Rev. A 2011, 84, 052329. [Google Scholar] [CrossRef]
- Bussandri, D.G.; Majtey, A.P.; Lamberti, P.W.; Osán, T.M. Generalized approach to quantify correlations in bipartite quantum systems. Quantum Inf. Proc. 2019, 18, 57. [Google Scholar] [CrossRef]
- Brodutch, A.; Modi, K. Criteria for measures of quantum correlations. Quantum Inf. Comp. 2012, 12, 721. [Google Scholar]
- Uhlmann, A. The “transition probability” in the state space of a *-algebra. Rep. Math. Phys. 1976, 9, 273. [Google Scholar]
- Jozsa, R. Fidelity for Mixed Quantum States. J. Mod. Opt. 1994, 41, 2315. [Google Scholar] [CrossRef]
- Horodecki, R.; Horodecki, P.; Horodecki, M.; Horodecki, K. Quantum entanglement. Rev. Mod. Phys. 2009, 81, 865. [Google Scholar] [CrossRef]
- Luo, S. Quantum discord for two-qubit systems. Phys. Rev. A 2008, 77, 042303. [Google Scholar] [CrossRef]
- Maziero, J.; Céleri, L.C.; Serra, R.M.; Vedral, V. Classical and quantum correlations under decoherence. Phys. Rev. A 2009, 80, 044102. [Google Scholar] [CrossRef]
- Céleri, L.C.; Maziero, J.; Serra, R.M. Theoretical and experimental aspects of quantum discord and related measures. Int. J. Quantum Inf. 2011, 9, 1837. [Google Scholar] [CrossRef]
- Lo Franco, R.; Bellomo, B.; Maniscalco, S.; Compagno, G. Dynamics of quantum correlations in two-qubit systems within non-Markovian environments. Int. J. Mod. Phys. B 2013, 27, 1345053. [Google Scholar] [CrossRef]
- Ferraro, A.; Aolita, L.; Cavalcanti, D.; Cucchietti, F.M.; Acín, A. Optimal reconstruction of the states in qutrit systems. Phys. Rev. A 2010, 81, 044102. [Google Scholar]
- Cianciaruso, M.; Bromley, T.R.; Roga, W.; Lo Franco, R.; Adesso, G. Universal freezing of quantum correlations within the geometric approach. Sci. Rep. 2015, 5, 10177. [Google Scholar] [CrossRef]
- Girolami, D.; Adesso, G. Quantum discord for general two-qubit states: Analytical progress. Phys. Rev. A 2011, 83, 052108. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bussandri, D.G.; Osán, T.M.; Lamberti, P.W.; Majtey, A.P. Correlations in Two-Qubit Systems under Non-Dissipative Decoherence. Axioms 2020, 9, 20. https://doi.org/10.3390/axioms9010020
Bussandri DG, Osán TM, Lamberti PW, Majtey AP. Correlations in Two-Qubit Systems under Non-Dissipative Decoherence. Axioms. 2020; 9(1):20. https://doi.org/10.3390/axioms9010020
Chicago/Turabian StyleBussandri, Diego G., Tristán M. Osán, Pedro W. Lamberti, and Ana P. Majtey. 2020. "Correlations in Two-Qubit Systems under Non-Dissipative Decoherence" Axioms 9, no. 1: 20. https://doi.org/10.3390/axioms9010020
APA StyleBussandri, D. G., Osán, T. M., Lamberti, P. W., & Majtey, A. P. (2020). Correlations in Two-Qubit Systems under Non-Dissipative Decoherence. Axioms, 9(1), 20. https://doi.org/10.3390/axioms9010020




