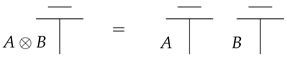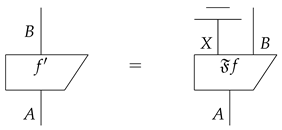Impossibility of Quantum Bit Commitment, a Categorical Perspective
Abstract
1. Introduction
- The length of the proof in Cohn-Gordon [29] is more than two pages. We provide a simpler proof which takes only a few lines.
- The proof in [29] only concerns the qualitative version of the no-go theorem. We formalize and prove the quantitative version of the no-go theorem.
- We show that the impossibility of bit commitment is equivalent to the unitary equivalence of purification in the setting of dagger monoidal categories. This provides an answer to the problem left by Heunen and Kissinger [30].
2. The No-Go Theorem of Quantum Bit Commitment
- The Hilbert space required to describe the protocol is the tensor product of the Hilbert spaces that play a role in the protocol.
- The total system is initially in a pure state.
- Every action taken by a party corresponds to that party performing a unitary operation on the systems in his/her possession.
- Every communication corresponds to a party sending a subset of the systems in his/her possession to the other party.
- (1)
- Two finite-dimensional Hiblert spaces A and B
- (2)
- Two pure states
- (3)
- A quantum operation (i.e., completely positive, trace-preserving super operator) on such that
- 1.
- Commit phase:
- (a)
- Alice chooses the value of the committed bit c and the auxiliary bits .
- (b)
- If , she prepares and sends Bob s qubits, which are chosen to be either or . The value of c is kept secret during the commit phase. If , then Alice sets the ith qubit to be . If , then she sets the ith qubit to be . The value of are also kept secret during the commit phase.
- (c)
- Similarly, if , she prepares and sends Bob s qubits, which are chosen to be either or . If , then Alice sets the ith qubit to be . If , and then she sets the ith qubit to be . The value of are kept secret during the commit phase.
- 2.
- Opening phase:
- (a)
- Bob randomly prepares auxiliary bits . If , and then Bob measures the ith qubit in the basis. If , then Bob measures the ith qubit in the basis.
- (b)
- Alice announces the value of .
- (c)
- Bob accepts Alice’s commitment if and only if, for all indexes with , Bob’s measurement outcome agrees with Alice’s announcement.
- Let and .
- Let , where is the identity operator and is the Pauli X operator.
- Let , where is the Hadamard operator H and is .
- Let be a completely positive map such that
- -
- , where is the completely positive map which represents the measurement on the basis and is the completely positive map which represents the measurement on the basis.
- -
- .
2.1. The Qualitative No-Go Theorem
2.2. The Quantitative No-Go Theorem
3. Bit Commitment in Categorical Quantum Mechanics
- 1.
- a parallel composition operation for objects:
- 2.
- a unit object ; and
- 3.
- a parallel composition operation for morphisms:
- 1.
- ⊗ is associative and unital on objects:
- 2.
- ⊗ is associative and unital on morphisms:
- 3.
- ⊗ and ∘ satisfy the interchange law:.
- identity on objects: ;
- reserves morphisms: ;
- is involutive: ; and
- respects the symmetric monoidal category structure:
3.1. Environment Structure and Purification
- 1.
- We have , and for all objects A and B: .
- 2.
- For morphisms and in , in if and only if in .
- 3.
- For each , there is for some object X such that in . Such an f is called a purification of .

3.2. Bit Commitment in Dagger Monoidal Category
- 1.
- Two objects A and B
- 2.
- Two states in
- 3.
- A morphism on in such that in
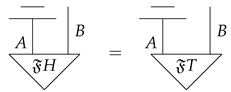
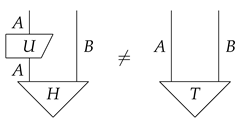
- (1)
- The unitary equivalence of purification is satisfied.
- (2)
- For all bit commitment protocols on , if it is concealing, then it is not binding.
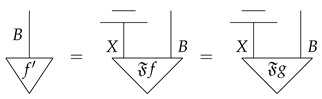
- If , then by the second requirement in the definition of environment structure, we know that . Now, we let . Then, it holds that .
- If , then we design a bit commitment protocol in which . Since , we know this protocol is concealing. Hence, it cannot be binding, which means there is a unitary morphism such that .To conclude, no matter or , the unitary equivalence of purification is satisfied. □
4. Related Work and Discussion
4.1. An Alternative Notion of Bindingness
4.2. Mixed State Formalization of QBC
5. Conclusions and Future Work
- Sikora and Selby [48] formalized bit commitment in generalized probabilistic theories and showed that the no-go theorem holds by presenting a quantitative trade-off between Alice’s and Bob’s cheating probabilities. A comparison between our formalization and theirs will be carried out in the future.
- It was shown by Kent et al. [5,6,7,12] that perfect bit commitment is possible in the theory of relativity. Baez [49] pointed out that, from a categorical perspective, the theory of relativity and quantum theory resemble each other quite well. DMC plays an important role in both theories. In particular, nCob, the DMC which contains manifold as object and cobordism as morphism, plays an important role in general relativity. It will be interesting to formalize bit commitment in nCob and use it to analyze the similarity and difference of quantum theory and the theory of relativity.
- We also plan to apply the axiomatic and graphical language of categorical quantum mechanics in the formal verification of concrete QBC protocols in the future.
- The MLC no-go theorem does not rule out the feasibility of designing secure QBC in practice. Several practically secure QBC protocols have been devised and experimentally implemented in the last decade [50,51,52]. The security of those protocols typically relies on the current technological limitation on non-demolition measurement and long-term quantum memory. The implementation of those protocols often uses quantum optical devices such as nanosecond pulse laser, single mode optical fiber, and Mach–Zehnder interferometer for the generation, communication, and operation of non-entangled photons. With the recent development on the generation and manipulation of entangled photons [53], in the future, we are also interested in implementing QBC protocols based on (low-dimensional) entangled states [9,16].
Author Contributions
Funding
Conflicts of Interest
References
- Bennetta, C.; Brassard, G. Quantum cryptography: Public key distribution and coin tossing. Theor. Comput. Sci. 1984, 560, 175–179. [Google Scholar] [CrossRef]
- Hardy, L.; Kent, A. Cheat Sensitive Quantum Bit Commitment. Phys. Rev. Lett. 2004, 92, 1–4. [Google Scholar] [CrossRef] [PubMed]
- Buhrman, H.; Christandl, M.; Hayden, P.; Lo, H.K.; Wehner, S. Possibility, impossibility, and cheat sensitivity of quantum-bit string commitment. Phys. Rev. A 2008, 78, 1–10. [Google Scholar] [CrossRef]
- Shimizu, K.; Fukasaka, H.; Tamaki, K.; Imoto, N. Cheat-sensitive commitment of a classical bit coded in a block of m × n round-trip qubits. Phys. Rev. A 2011, 84, 1–14. [Google Scholar] [CrossRef]
- Kent, A. Unconditionally secure bit commitment with flying qudits. New J. Phys. 2011, 13, 1–16. [Google Scholar] [CrossRef]
- Kent, A. Unconditionally Secure Bit Commitment by Transmitting Measurement Outcomes. Phys. Rev. Lett. 2012, 109, 130501. [Google Scholar] [CrossRef]
- Lunghi, T.; Kaniewski, J.; Bussières, F.; Houlmann, R.; Tomamichel, M.; Kent, A.; Gisin, N.; Wehner, S.; Zbinden, H. Experimental Bit Commitment Based on Quantum Communication and Special Relativity. Phys. Rev. Lett. 2013, 111, 180504. [Google Scholar] [CrossRef]
- He, G.P. Simplified quantum bit commitment using single photon nonlocality. Quantum Inf. Process. 2014, 13, 2195–2211. [Google Scholar] [CrossRef]
- Li, Y.; Wen, Q.; Li, Z.; Qin, S.; Yang, Y. Cheat sensitive quantum bit commitment via pre- and post-selected quantum states. Quantum Inf. Process. 2014, 13, 141–149. [Google Scholar] [CrossRef]
- Adlam, E.; Kent, A. Device-independent relativistic quantum bit commitment. Phys. Rev. A 2015, 92, 1–9. [Google Scholar] [CrossRef]
- Lunghi, T.; Kaniewski, J.; Bussières, F.; Houlmann, R.; Tomamichel, M.; Wehner, S.; Zbinden, H. Practical Relativistic Bit Commitment. Phys. Rev. Lett. 2015, 115, 030502. [Google Scholar] [CrossRef] [PubMed]
- Verbanis, E.; Martin, A.; Houlmann, R.; Boso, G.; Bussières, F.; Zbinden, H. 24-Hour Relativistic Bit Commitment. Phys. Rev. Lett. 2016, 117, 140506. [Google Scholar] [CrossRef] [PubMed]
- Song, Y.; Yang, L. Practical Quantum Bit Commitment Protocol Based on Quantum Oblivious Transfer. Appl. Sci. 2018, 8, 1990. [Google Scholar] [CrossRef]
- Nagy, M.; Nagy, N. An Information-Theoretic Perspective on the Quantum Bit Commitment Impossibility Theorem. Entropy 2018, 20, 193. [Google Scholar] [CrossRef]
- He, G.P. Unconditionally secure quantum bit commitment based on the uncertainty principle. Proc. R. Soc. Math. Phys. Eng. Sci. 2019, 475, 20180543. [Google Scholar]
- Zhou, L.; Sun, X.; Su, C.; Liu, Z.; Choo, K.R. Game theoretic security of quantum bit commitment. Inf. Sci. 2019, 479, 503–514. [Google Scholar] [CrossRef]
- Brassard, G.; Crépeau, C. Quantum Bit Commitment and Coin Tossing Protocols. In Advances in Cryptology—CRYPTO ’90, Proceedings of the 10th Annual International Cryptology Conference, Santa Barbara, CA, USA, 11–15 August 1990; Menezes, A., Vanstone, S.A., Eds.; Springer: Berlin/Heidelberg, Germany, 1990; pp. 49–61. [Google Scholar]
- Brassard, G.; Crépeau, C.; Jozsa, R.; Langlois, D. A Quantum Bit Commitment Scheme Provably Unbreakable by both Parties. In Proceedings of the 34th Annual Symposium on Foundations of Computer Science, Palo Alto, CA, USA, 3–5 November 1993; IEEE Computer Society: Washington, DC, USA, 1993; pp. 362–371. [Google Scholar] [CrossRef]
- Mayers, D. Unconditionally secure quantum bit commitment is impossible. Phys. Rev. Lett. 1997, 78, 3414–3417. [Google Scholar] [CrossRef]
- Lo, H.K.; Chau, H.F. Is Quantum Bit Commitment Really Possible? Phys. Rev. Lett. 1997, 78, 3410–3413. [Google Scholar] [CrossRef]
- Lo, H.K.; Chau, H.F. Why quantum bit commitment and ideal quantum coin tossing are impossible. Phys. Nonlinear Phenom. 1998, 120, 177–187. [Google Scholar] [CrossRef]
- Yuen, H. Unconditionally Secure Quantum Bit Commitment Is Possible. 2000. Available online: https://arxiv.org/abs/quant-ph/0006109 (accessed on 6 January 2020).
- Yuen, H. Unconditionally Secure Quantum Bit Commitment. 2005. Available online: https://arxiv.org/abs/quant-ph/0505132 (accessed on 6 January 2020).
- Nambu, Y.; Chiba-Kohno, Y. Information-Theoretic Description of No-go Theorem of a Bit Commitment. 2000. Available online: https://arxiv.org/abs/quant-ph/0011068 (accessed on 6 January 2020).
- Spekkens, R.W.; Rudolph, T. Degrees of concealment and bindingness in quantum bit commitment protocols. Phys. Rev. A 2001, 65, 012310. [Google Scholar] [CrossRef]
- He, G.P. Security bound of cheat sensitive quantum bit commitment. Sci. Rep. 2015, 5, 9398. [Google Scholar] [CrossRef] [PubMed]
- D’Ariano, G.M.; Kretschmann, D.; Schlingemann, D.; Werner, R.F. Reexamination of quantum bit commitment: The possible and the impossible. Phys. Rev. A 2007, 76, 032328. [Google Scholar] [CrossRef]
- Chiribella, G.; D’Ariano, G.M.; Perinotti, P.; Schlingemann, D.; Werner, R. A short impossibility proof of quantum bit commitment. Phys. Lett. A 2013, 377, 1076–1087. [Google Scholar] [CrossRef]
- Cohn-Gordon, K. Commitment Algorithms. Master’s Thesis, University of Oxford, Oxford, UK, 2012. [Google Scholar]
- Heunen, C.; Kissinger, A. Can Quantum Theory Be Characterized in Terms of Information-Theoretic Constraints? 2016. Available online: http://homepages.inf.ed.ac.uk/cheunen/publications/2016/cbh/cbh.pdf (accessed on 6 January 2020).
- Clifton, R.; Bub, J.; Halvorson, H. Characterizing Quantum Theory in Terms of Information-Theoretic Constraints. Found. Phys. 2003, 33, 1561–1591. [Google Scholar] [CrossRef]
- Watrous, J. The Theory of Quantum Information; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar]
- Nielsen, M.; Chuang, I. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Abramsky, S.; Coecke, B. A Categorical Semantics of Quantum Protocols. In Proceedings of the 19th IEEE Symposium on Logic in Computer Science (LICS 2004), Turku, Finland, 14–17 July 2004; IEEE Computer Society: Washington, DC, USA, 2004; pp. 415–425. [Google Scholar] [CrossRef]
- Selinger, P. Dagger Compact Closed Categories and Completely Positive Maps: (Extended Abstract). Electr. Notes Theor. Comput. Sci. 2007, 170, 139–163. [Google Scholar] [CrossRef]
- Coecke, B.; Duncan, R. Interacting Quantum Observables. In Automata, Languages and Programming, Proceedigs of the 35th International Colloquium, ICALP 2008, Reykjavik, Iceland, 7–11 July 2008, Part II—Track B: Logic, Semantics, and Theory of Programming & Track C: Security and Cryptography Foundations; Lecture Notes in Computer Science; Aceto, L., Damgård, I., Goldberg, L.A., Halldórsson, M.M., Ingólfsdóttir, A., Walukiewicz, I., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; Volume 5126, pp. 298–310. [Google Scholar] [CrossRef]
- Vicary, J. Categorical Formulation of Finite-dimensional C*-algebras. Electr. Notes Theor. Comput. Sci. 2011, 270, 129–145. [Google Scholar] [CrossRef][Green Version]
- Coecke, B.; Duncan, R. Interacting quantum observables: categorical algebra and diagrammatics. New J. Phys. 2011, 13, 1–85. [Google Scholar] [CrossRef]
- Coecke, B.; Wang, Q.; Wang, B.; Wang, Y.; Zhang, Q. Graphical Calculus for Quantum Key Distribution (Extended Abstract). Electr. Notes Theor. Comput. Sci. 2011, 270, 231–249. [Google Scholar] [CrossRef]
- Selinger, P. Finite Dimensional Hilbert Spaces are Complete for Dagger Compact Closed Categories (Extended Abstract). Electr. Notes Theor. Comput. Sci. 2011, 270, 113–119. [Google Scholar] [CrossRef]
- Coecke, B.; Perdrix, S. Environment and classical channels in categorical quantum mechanics. Log. Methods Comput. Sci. 2012, 8, 1–24. [Google Scholar] [CrossRef]
- Backens, M. The ZX-calculus is complete for stabilizer quantum mechanics. New J. Phys. 2014, 16, 093021. [Google Scholar] [CrossRef]
- Coecke, B.; Kissinger, A. Picturing Quantum Processes: A First Course in Quantum Theory and Diagrammatic Reasoning; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Zhou, L.; Wang, Q.; Sun, X.; Kulicki, P.; Castiglione, A. Quantum technique for access control in cloud computing II: Encryption and key distribution. J. Netw. Comput. Appl. 2018, 103, 178–184. [Google Scholar] [CrossRef]
- Hadzihasanovic, A.; Ng, K.F.; Wang, Q. Two complete axiomatisations of pure-state qubit quantum computing. In Proceedings of the 33rd Annual ACM/IEEE Symposium on Logic in Computer Science, LICS 2018, Oxford, UK, 9–12 July 2018; Dawar, A., Grädel, E., Eds.; ACM: New York, NY, USA, 2018; pp. 502–511. [Google Scholar] [CrossRef]
- Coecke, B.; Heunen, C. Pictures of complete positivity in arbitrary dimension. Inf. Comput. 2016, 250, 50–58. [Google Scholar] [CrossRef]
- Heunen, C. Compactly Accessible Categories and Quantum Key Distribution. Log. Methods Comput. Sci. 2008, 4. [Google Scholar] [CrossRef]
- Sikora, J.; Selby, J. Simple proof of the impossibility of bit commitment in generalized probabilistic theories using cone programming. Phys. Rev. A 2018, 97, 1–5. [Google Scholar] [CrossRef]
- Baez, J. Quantum Quandaries: A Category-Theoretic Perspective. In The Structural Foundations of Quantum Gravity; Rickles, D., French, S., Saatsi, J.T., Eds.; Oxford Scholarship Online: Oxford, UK, 2006. [Google Scholar]
- Danan, A.; Vaidman, L. Practical quantum bit commitment protocol. Quantum Inf. Process. 2012, 11, 769–775. [Google Scholar] [CrossRef]
- Loura, R.; Almeida, A.J.; André, P.S.; Pinto, A.N.; Mateus, P.; Paunković, N. Noise and measurement errors in a practical two-state quantum bit commitment protocol. Phys. Rev. A 2014, 89, 052336. [Google Scholar] [CrossRef]
- Loura, R.; Arsenović, D.c.v.; Paunković, N.; Popović, D.c.v.B.; Prvanović, S. Security of two-state and four-state practical quantum bit-commitment protocols. Phys. Rev. A 2016, 94, 062335. [Google Scholar] [CrossRef]
- Li, C.; Jiang, Z.; Zhang, Y.; Zhang, Z.; Wen, F.; Chen, H.; Zhang, Y.; Xiao, M. Controlled Correlation and Squeezing in Pr3+: Y2SiO5 to Yield Correlated Light Beams. Phys. Rev. Appl. 2017, 7, 014023. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, X.; He, F.; Wang, Q. Impossibility of Quantum Bit Commitment, a Categorical Perspective. Axioms 2020, 9, 28. https://doi.org/10.3390/axioms9010028
Sun X, He F, Wang Q. Impossibility of Quantum Bit Commitment, a Categorical Perspective. Axioms. 2020; 9(1):28. https://doi.org/10.3390/axioms9010028
Chicago/Turabian StyleSun, Xin, Feifei He, and Quanlong Wang. 2020. "Impossibility of Quantum Bit Commitment, a Categorical Perspective" Axioms 9, no. 1: 28. https://doi.org/10.3390/axioms9010028
APA StyleSun, X., He, F., & Wang, Q. (2020). Impossibility of Quantum Bit Commitment, a Categorical Perspective. Axioms, 9(1), 28. https://doi.org/10.3390/axioms9010028