Abstract
Protein folding problem (PFP) consists of determining the functional three-dimensional structure of a target protein. PFP is an optimization problem where the objective is to find the structure with the lowest Gibbs free energy. It is significant to solve PFP for use in medical and pharmaceutical applications. Hybrid simulated annealing algorithms (HSA) use a kind of simulated annealing or Monte Carlo method, and they are among the most efficient for PFP. The instances of PFP can be classified as follows: (a) Proteins with a large number of amino acids and (b) peptides with a small number of amino acids. Several HSA have been positively applied for the first case, where I-Tasser has been one of the most successful in the CASP competition. PEP-FOLD3 and golden ratio simulated annealing (GRSA) are also two of these algorithms successfully applied to peptides. This paper presents an enhanced golden simulated annealing (GRSA2) where soft perturbations (collision operators), named “on-wall ineffective collision” and “intermolecular ineffective collision”, are applied to generate new solutions in the metropolis cycle. GRSA2 is tested with a dataset for peptides previously proposed, and a comparison with PEP-FOLD3 and I-Tasser is presented. According to the experimentation, GRSA2 has an equivalent performance to those algorithms.
1. Introduction
Protein folding problem (PFP) consists of determining the functional three-dimensional structure or native structure (NS) of a target protein. This problem represents an enormous challenge for the scientific community, and although there are significant advances and applications of PFP [1], this problem is far from being solved.
In 1962, Anfinsen developed the thermodynamic hypothesis (TH), which explains how the NS is achieved in every single protein. Anfinsen showed that this structure is, thermodynamically, the most stable; it is entirely determined by the corresponding interatomic interactions. Moreover, TH establishes that the NS is reached when Gibbs free energy is the lowest [2]. The incorrect folding or misfolding of proteins is a relevant factor in diseases produced by infectious agents and neurodegenerative diseases such as Alzheimer’s, Parkinson’s, cystic fibrosis, amyloidosis, and Gaucher disease [3,4,5]. However, for a small set of proteins, the energy of the native structure is not the lowest [6], and probably some constraints are not completely known.
In 1968, the challenge of PFP was made evident by the publication of the so-called Levinthal paradox, which talks about two issues in general: (a) The computational effort of PFP algorithms represents an extremely long execution time for most of the instances, even for very powerful computers; but, (b) in nature, the same instances can be solved almost instantaneously [7]. Thus, to design more efficient algorithms, it is important to solve this challenge.
Traditionally, the experimental methods for finding the tertiary protein structure are X-ray crystallography and nuclear magnetic resonance (NMR). The bad news is that these processes are regularly too expensive and can take a very long time [8]. This kind of experimental method can result in accurate solutions when a computational algorithm provides a close solution to the NS.
NS computational prediction belongs to the NP-hard class, and exact algorithms can take an unacceptable execution time [9]. The problems of this class are considered at least as hard as the hardest NP problems. As a consequence, heuristic algorithms are currently used. These algorithms are focused on finding approximate solutions with fast execution times, but they require an adequate set of their parameters. Thus, designing and tuning heuristic algorithms have become a major PFP challenge in this area.
The algorithms for PFP can be applied in two kinds of instances: (a) Proteins, with 50 or more amino acids, and (b) peptides with a small number of amino acids (2–50). Hybrid simulated annealing algorithms (HSA) use a kind of simulated annealing (SA) or Monte Carlo method, and they are among the most efficient for PFP. Several HSA have been positively applied for the first case, where I-Tasser has shown to be one of the most successful in the CASP competition. In recent years, small proteins or peptides have become very important in pharmaceutical research [10], drug design [11,12], and venom analysis [13]. In this sense, to design algorithms for finding NS with reasonable processing time for peptides is relevant. PEP-FOLD3 [12], and golden ratio simulated annealing (GRSA) [14] are two HSA algorithms successfully applied to peptides. However, the original GRSA only obtain good results in small instances. Also, we note that other very good algorithms reported in CASP competition as Rosetta [15] and Quark [16,17] cannot be easily applied to peptides. In contrast, for I-Tasser [18] and PEP-FOLD3, there are automated protein structure prediction servers available; then, these algorithms can be easily executed for peptides. Other algorithms without a kind of Monte Carlo method have not yet published better results for peptides, and are not considered within the confines of this paper.
This paper presents an enhancement GRSA named GRSA2 for the general application of peptides; we show a comparison of this algorithm with I-Tasser [18] and PEP-FOLD3 [12]. According to the experimentation, the proposed algorithm has an equivalent performance to those algorithms.
The paper is organized as follows: In Section 1, we give a brief explanation of the problem. In Section 2, a background of the area and the main work related to this research are presented. In Section 3, a formal definition of ab initio is discussed. In Section 4, the GRSA algorithm and the soft perturbations are presented. In Section 5, we describe the experimentation made with the selected dataset, and we analyze the results obtained by the proposed algorithms. Finally, Section 6 contains our conclusions.
2. Background
Nowadays, PFP is one of the most critical problems due to its complexity and implications in optimization, computer science, and bioinformatics [19]. According to Dill and MacCallum [20], this problem consists of three different enigmas:
- To design the physical code that aims to determine the interatomic forces of the protein structure for a given amino acid sequence.
- To solve the computational problem of designing an algorithm to predict the native structure from a given amino acid sequence.
- To perform an algorithm for the folding process by nature, which rapidly finds the routes or pathways from an initial solution to the NS or functional structure.
This paper is related to the second of these problems, commonly known in computer science as the protein folding problem, or PFP.
The strategy for solving PFP using only information from the amino acid sequences is known as ab initio and relies on the TH of Anfinsen: This is the approach used in this paper. As we have mentioned before, there are other successful strategies; nevertheless, they cannot be considered as ab initio because they use additional data from the secondary structure or other fragments of proteins. Besides, I-Tasser [18], PEPFOLD3, and Rosetta [15,21] have servers that use these strategies; the former has obtained first place in the CASP12 competition and has a free solver for proteins and peptides. The second server permits the execution of peptides until 36 amino acids. Finally, the last server does not permit the execution of small peptides.
2.1. Computational Methods in PFP
The computational methods applied to the protein folding problem are designed under different approaches, such as homology, threading, and ab initio. The homology method determines a first three-dimensional structure comparing the linear sequence of amino acids’ sequence of the target protein with sequences of other proteins previously solved. This step is usually performed through multiple alignments of the target versus the candidate protein. Once the best homolog structure is found, this pattern is used as a template to determine the final structure of the target protein. In consequence, several homology-modeling tools software for proteins and peptides have been developed [22,23,24]. However, the homology models do not guarantee to solve the whole problem due to the necessity of having an amino acid sequence very similar to the target. When a homologous protein is not found, the threading method (fold recognition) may be used. This method uses templates of known structures already solved and published in databases such as PDB (Proteins Database). There is a set of approaches where threading is applied, for instance: Prospect [25], Hhpred [26], Raptor [27], Eigenthreader [28], and Lomet [29], which is a phase of the I-Tasser suite [18,30]. Nevertheless, homology and threading need patterns information about other proteins previously solved and, in this case, the complete solution of the problem is not guaranteed. In contrast to homology and threading, the ab initio strategy is not limited to the templates because the amino acid sequence is the unique information used for predicting the tertiary structure. Moreover, ab initio represents a real challenge to the scientific community due to its computational complexity, which is NP-hard [31].
There have been many types of computational algorithms applied to the PFP using the ab initio approach [32,33]. Among the most successful are Monte Carlo and SA algorithms. In this sense, HSA algorithms have been used for small peptides obtaining acceptable results [34]. These algorithms are chaotic multi-quenching annealing [35]; the classical simulated annealing using Monte Carlo methods [36]; multiphase simulated annealing algorithm using Boltzmann and Bose–Einstein distributions (MPSABBE) [37]; golden ratio simulated annealing [14]; and parallel evolutionary multi-quenching annealing for protein folding problem [38]. However, all these HSA algorithms have found acceptable solutions only for some peptides. To find the best way to improve this algorithm is not an easy task. Moreover, chemical reaction optimization is a successful metaheuristic for other NP-hard problems [39], which deals with perturbation methods for generating new solutions based on high and low energy particles. These perturbation methods were not used before in ab initio and are considered in this paper.
Additionally, other strategies add the ab initio approach that improves the structure prediction, for instance, Rosetta [15], Touchstone II [40], Quark [16,17], I-Tasser [18], and PEP-FOLD [41]. In this paper, the I-Tasser [18] and PEP-FOLD3 [12] servers for protein structure prediction were used. Also, I-Tasser is one of the most successful in CASP [42]. Additionally, PEP-FOLD3 is a server specialized in peptides [12].
2.2. Simulated Annealing
Kirkpatrick proposed the original simulated annealing algorithm, which uses the metropolis algorithm applied to optimization problems [43]. SA uses an analogy of the process of annealing a metal, and the mechanical statistics approach to solve these problems. Essentially, SA uses the initial and the final temperature parameters and , respectively. Classical SA (Algorithm 1) consists of two cycles; an external cycle that is controlled by the temperature parameter and the metropolis cycle, where a new solution is generated by modifying the previous cycle with a perturbation function (row 6). In Algorithm 1, the next temperature is determined in row 14, where is the parameter for decreasing the current temperature. Simulated annealing introduces a random stage for the acceptance criterion of new solutions (rows 8 to 12), and the difference of energy of two configurations is calculated. At this point, a new solution is accepted when is less than zero; otherwise, a probability distribution function (row 10) is applied to decide whether the solution is accepted or not. As is well known, the complexity of SA is , where depends on the instance size (in our case, the number of variables in each peptide) [44].
| Algorithm 1 Classical Simulated Annealing. |
| 1: SA (, , , ) |
| 2: |
| 3: |
| 4: while do |
| 5: while do |
| 6: |
| 7: |
| 8: if then |
| 9: |
| 10: else if then |
| 11: |
| 12: end |
| 13: end |
| 14: |
| 15: end |
| 16: end |
2.3. Chemical Reaction Optimization
Chemical reaction optimization algorithm (CRO) is a metaheuristic for optimization, inspired by the process of the chemical reactions [39]. A chemical reaction is a change of a substance called reactant into a new one with a different chemical identity. The resulting products have different properties than the reactants. These products will be more stable, and then their energy will be lower. When the substance is heated, the molecules move faster, and when it is cooled, they move slower. A chemical reaction between two molecules can only occur when those molecules collide with each other. If the molecules have a large amount of energy, they will move around faster; when the particles move very fast, they collide with each other. Therefore, if the energy is transferred to the particles, the number of times that the molecules collide with each other will increase. There are two types of collisions [39,45]:
- Unimolecular collisions: When the molecule hits the wall of the container.
- Intermolecular collision: When a molecule collides with other molecules.
CRO presents four different reactions or ways to generate new solutions when a perturbation function is used with an old solution. These collisions are [39]:
- Unimolecular collision (low energy collisions). In this group, we find two reactions:
- On-wall ineffective collision is established as follows [39]:“It represents the situation when a molecule collides with a wall of the container and then bounces away remaining in one single unit”.In GRSA2, the current solution is changed by a new solution obtained by a perturbation function. This operation is equivalent to the classical SA perturbation. Thus, the complexity of GRSA2 is not modified. This operation is implemented in line seven of Algorithm 3, which calls the function soft perturbation or Algorithm 2, explained in Section 4. As we will see, this operation does not add complexity to the classical SA.
- Decomposition. In this case, a molecule (solution) hits a wall and then is divided into several parts. In the GRSA2 algorithm, decomposition is a perturbation operation that generates two new solutions from the current solution. This perturbation is implemented in GRSA2 in lines sixth and seven of Algorithms 2 and 3, respectively. Again, to include this operation in SA for obtaining GRSA2 does not increase the complexity of the new algorithm.
- Intermolecular collision (high energy collisions). This collision has the next elementary reactions:
- Intermolecular ineffective collision. These kinds of reactions occur when multiple molecules collide with each other and then bounce away. The number of molecules remains the same.
- Synthesis. In this reaction, several molecules are fused into a single one.
In this paper, we apply low energy collisions because, according to our previous experimentation, they are the only ones with good performance.
2.4. Analytical Tuning Method
Simulated annealing uses a random walk, which consists of a sequence of possible solutions to the problem. Simulated annealing, like many other algorithms, behaves well when its parameters are correctly tuned. The main parameters are the initial temperature ( also designed ) and the final temperature (). In the classical SA, the temperatures for two consecutive iterations have the relation of the Equation (1) where is another parameter . There are n temperatures and a metropolis cycle for each of them. In SA, every time the temperature changes a new metropolis cycle is started; for the the length of this cycle is . This parameter is the length of the Markov chain (i.e., k times the solution space is explored).
Moreover, an acceptable solution in the metropolis cycle should satisfy the Boltzmann distribution, given by Equation (2). In this equation is a random number from the [0, 1] range, which is used to determine if the solution in the iterative process is or is not accepted as part of the random walk of the algorithm. In other words, represents the acceptance probability of the ith solution for the current temperature and a given variation of the ith solution and the previous one [46].
In this analytical tuning method, the calculations for and are based on the acceptance probability of a new solution P (Sj) and the maximum and minimum cost deterioration . Therefore, to obtain and the calculation is as follows in Equations (3) and (4):
In SA, the metropolis cycle can be considered as a homogeneous Markov chain where the length of the Markov chain means the number of iteration for each k-temperature and the increment in each k-temperature is determined by , where determines the increment for this parameter in the next iteration of the Metropolis cycle. is modified until is reached. When the geometrical cooling schedule of Equations (1) is applied, we can establish Equations (5) and (6):
Then, the number of metropolis cycles can be determined by the variable n as follows in Equation (7):
Now, we obtain the β parameter from Equation (8):
For the last temperature, the length of the metropolis cycle is the longest and is represented by the variable defined by Equation (9):
Then:
Finally, from Equation (10) the parameter is determined by Equation (11)
In this case, the analytical tuning method can be applied to the algorithms proposed in this paper.
3. Ab Initio Definition
In this section, the ab initio definition and the force field used in the protein folding problem are presented.
3.1. Ab Initio Problem in PFP
Protein folding problem is the process of finding the tertiary structure of a protein known as native structure, in which the proteins perform their biological functions correctly. In this paper, ab initio is applied, which is defined as follows [35]:
- Given a sequence of amino acids; , which represents the primary structure of a protein with a set of dihedral angles , and an energy function which represents the free energy or Gibbs energy (G).
- Find the native structure of the protein, such that represents the minimum energy value, where the optimal solution defines the best three-dimensional configuration. The PFP variables are the set of dihedral angles.
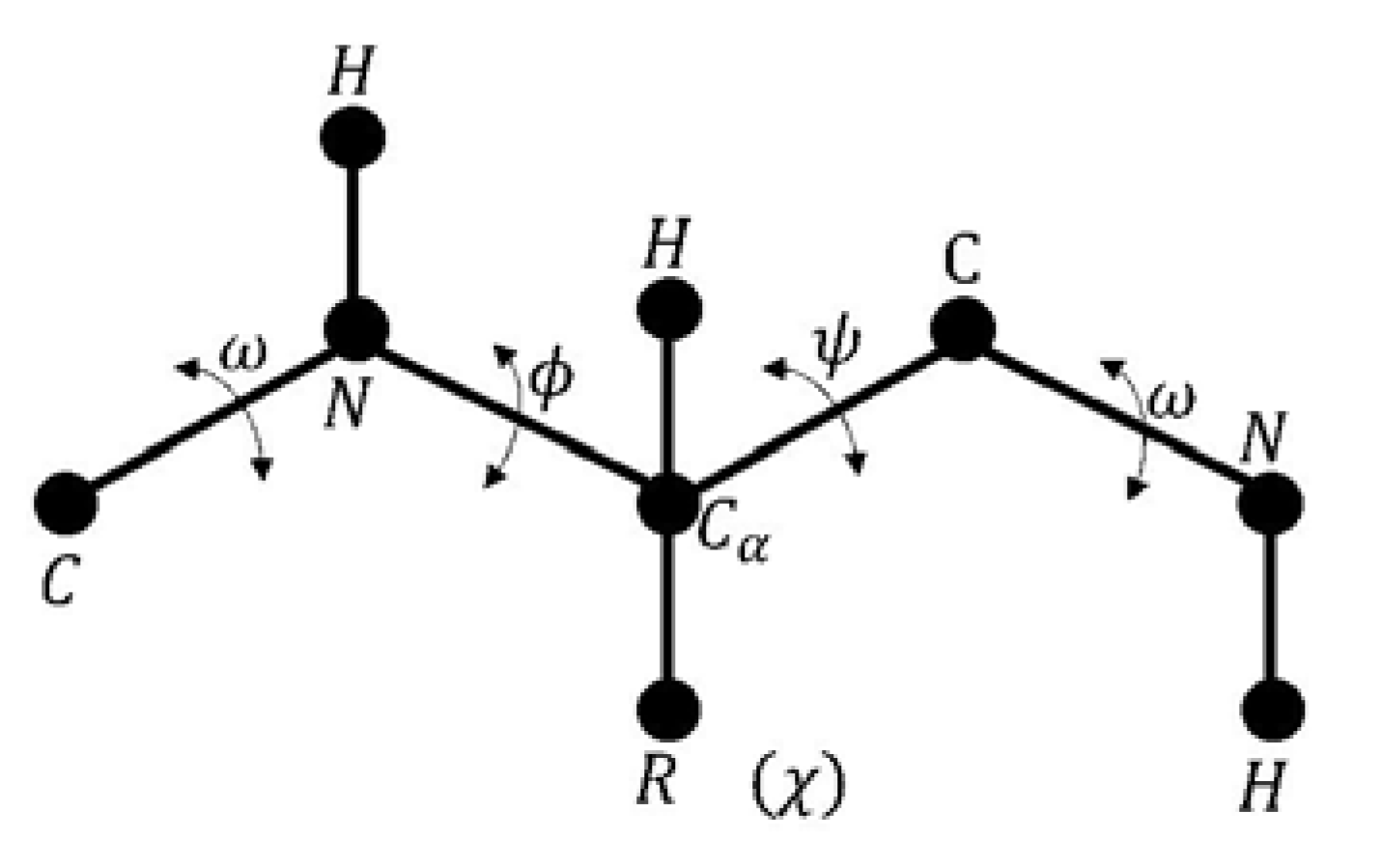
There are four types of torsion angles or dihedral angles as presented in Figure 1. The PFP variables are the set of dihedral angles that satisfy the minimum energy value. Protein atoms are represented in three-dimensional Cartesian coordinates.
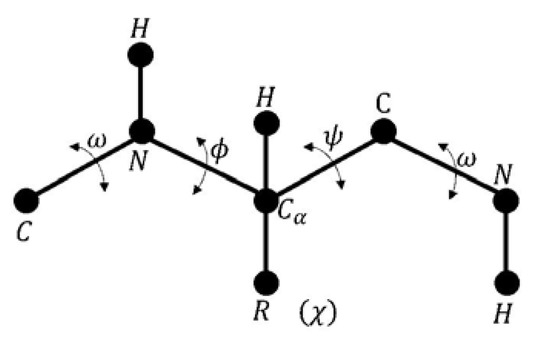
Figure 1.
Representation of the four dihedral angles.
The dihedral angles are defined as follows:
- Phi is the angle between the amino group and the alpha carbon.
- Psi is the angle between the alpha carbon and the carboxyl group.
- Omega is defined for each two consecutive amino acids.
- Chi is defined between the two planes conformed by two consecutive carbon atoms in the radical group.
3.2. Force Field
Force fields or energy functions are used to represent the energy of the protein [47]; examples of these are CHARMM [48], AMBER [47], ECEPP/2 [49], and ECEPP/3 [50]; the latter and ECEPP/2 are the most common. In these force fields, the potential energy is given by the sum of the electrostatic energy, Lennard–Jones, and hydrogen-bond energy for all pairs of atoms in the peptide chain together with the torsion energy for all torsion angles [49]. These terms are shown in Equation (12) through which energy function ECEPP/2 should be minimized to find the NS [49].
where:
- is the distance in between the atoms and .
- and are the parameters of the empirical potentials.
- and are the partial charges on the atoms and , respectively.
- is the dielectric constant, which is usually set to .
- 332 is a factor used to obtain the energy in kcal/mol.
- is the energetic torsion barrier of rotation about the bond .
- is the multiplicity of the torsion angle .
4. An Enhancement of Golden Ratio Simulated Annealing
Metaheuristic applications to PFP have been increasing their importance in the computational biology area due to the large number of conformations that a protein can take. The NS computational prediction can lead to a more efficient and inexpensive process; in fact, the problem belongs to the NP-hard class. As a consequence, metaheuristic algorithms are currently used. These are high-performance methods focused on finding approximate solutions using low execution times. Thus, the correct design and tuning of metaheuristic algorithms have become a significant challenge in the optimization area [9]. Moreover, experimental methods can find more accurate solutions when a computational algorithm provides an approximate solution close to the functional solution. Therefore, it is very advantageous to design heuristics for PFP using ab initio. We describe the proposed GRSA2 below.
4.1. The Enhancement of GRSA
As was mentioned earlier, hybrid simulated annealing algorithms have been used to solve PFP with remarkable results; one of them is the golden ratio (GR) search method. GR is an irrational number known as the aura ratio and represented by the letter Φ used in antiquity to design architectural masterpieces. In modern times, GR has been used as a search strategy [51]. GRSA algorithm is a hybridization of the SA algorithm and the GR method, which has been applied to NP-hard problems such as scheduling [52] and SAT [53]. GRSA was also successfully applied to PFP, obtaining good quality solutions for some peptides [14]. GRSA divides the solution space into sections using the golden number [14].
A remarkable difference between SA and GRSA is the cooling scheme behavior. GRSA uses different values of the parameter , depending on the current temperature, which is cut in some cut-off temperatures calculated using the golden number Φ. This temperature is decremented through the geometric cooling function , and once is reached, a new phase begins where the value of the parameter is updated and another is recalculated. This procedure remains until the number of cuts () is reached. The last phase is executed until the final temperature is reached. In Algorithm 3, we can observe this procedure. GRSA uses two strategies for better performance: Stop criterion and reheat strategy. The reheat strategy (RH) is applied in two phases: (a) At the end of the last GR section, and (b) when the equilibrium is detected.
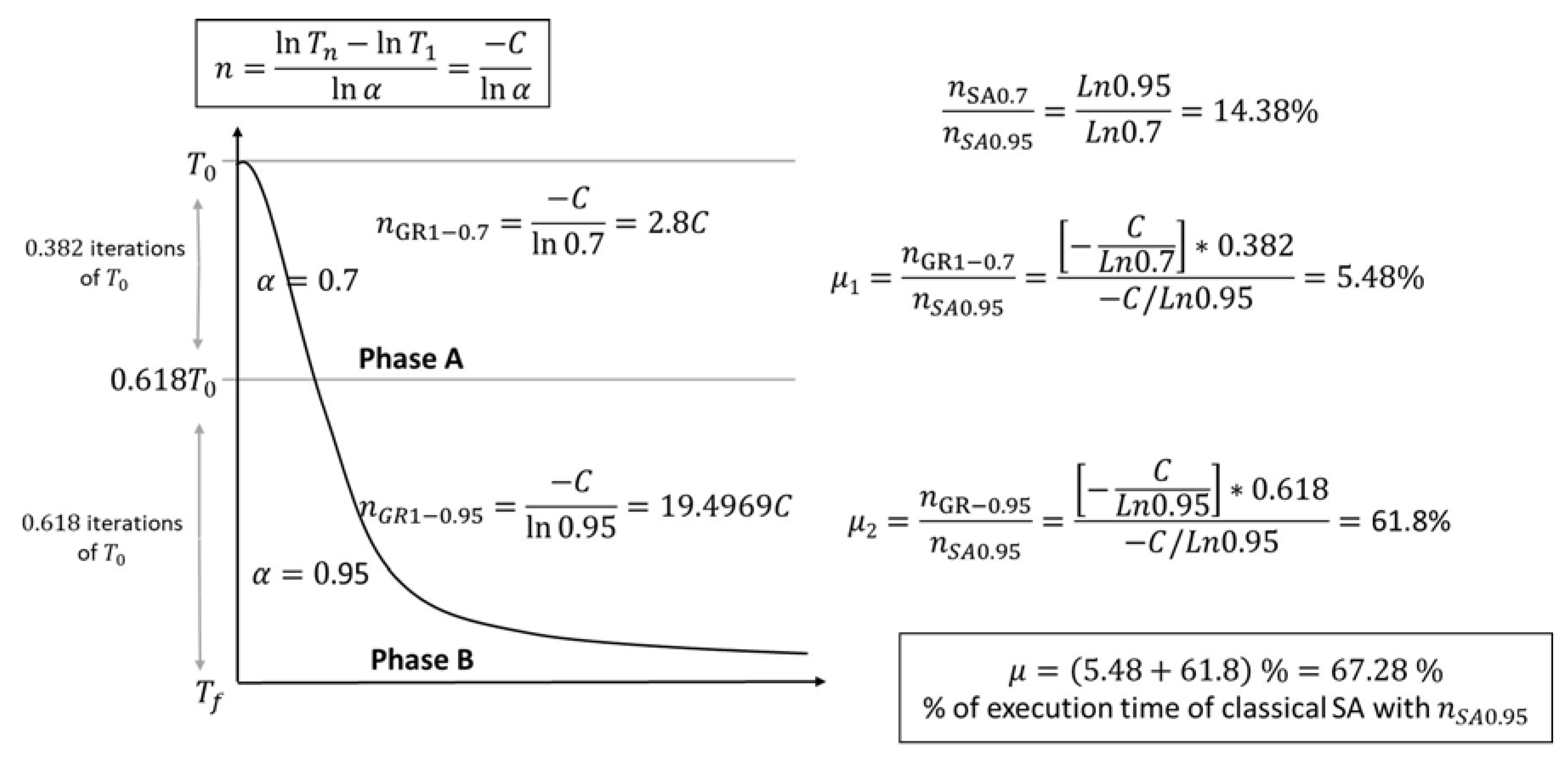
Experimentally, we observed that every time a golden section is executed, the time involved decreases; this reduction is because the GRSA cooling function reaches the final temperature faster. At the top of Figure 2, we have the equation of the number n of iterations required in general for SA; in this equation, for a particular instance, the numerator is a C0 constant determined by the final and initial temperature and respectively. Thus, for any specific instance, the number of iterations is a function of the parameter; then, the execution time decreases by reducing this parameter. To give an idea, with , the time required will be less than 15% of the time used for SA with a normal cooling scheme (using ). On Figure 2 the exact proportion is represented by , and is given as 14.38%. Notice that this relation considers the complete iterations from the to temperatures. In other words, gives the proportion of randomly executed SA two times, both of them until SA converges.
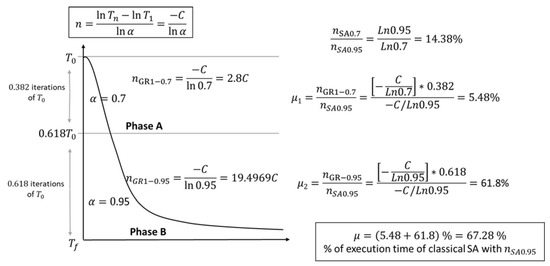
Figure 2.
Example using two values and a cut-off temperature.
If the SA algorithm is executed normally, that is, slowly from to with a high value of alpha (i.e., ), the number of iterations is . In GRSA, the process is executed a certain nGolden number of phases (see Algorithm 3) depending on the number of cut-off temperatures . Figure 2 is an example of GRSA where any cut-off is represented by (updated on line 5 of Algorithm 3). We want to know if a GRSA algorithm with one or more cut-off temperatures makes the processing time greater, lower, or equivalent to SA. As is shown in Figure 2, one cut-off temperature divides the process into phases A and B, which are executed with and , respectively. The time of GRSA will be, in this case, the total processing times of both phases. GRSA for several cuts has the following execution times:
- GRSA with one cut-off temperature:
- The processing time of phase A is multiplied by the fraction of iterations where this phase is executed . Let be the proportion of time of phase A concerning the normal execution time of SA (); as is shown in Figure 2, of .
- The processing time of phase B is given by . Now, the time proportion of phase B for the normal execution of SA is of .
- The total proportion of GRSA processing time compared to SA is .
- GRSA with two or more cut-off temperatures
- Phase A is the same process as case 1 (with ) and uses of .
- Phase B is divided into nGolden sections. For instance, if nGolden equals 2, phase B is divided into two subphases. The new values for the next subsections can be again 0.7 and 0.95 for the next subphases. In other words, each time a subdivision is made, the last subphase will have a new parameter equal to 0.95. The division process continues until nGolden parameter is reached. When nGolden equals 2, the two new subphases (with and ) will have of the execution time of phase B. The proportion of the total processing time (time of phase A plus time of new subphases generated from B) will be of the execution time of SA.
- When nGolden is increased, a reduction of the time is obtained.
- The alpha values can be changed in several ways. Instead of using the last numbers (0.7, 0.95) to divide the subsections, a linear or exponential function for the alphas can be used. In our case, the linear approach was used [14], which gives similar reductions to those previously presented. Experimentation reveals that, in general, a nGolden value lower or equal to five gives good results in the case of peptides.
4.2. Soft Perturbation in GRSA
In this work, the goal was to improve the quality of solutions obtained by GRSA for peptides. Thus, we designed an enhancement of this algorithm by using soft perturbations described before. Next, we present the GRSA2 (Algorithm 3), which takes the amino acid sequences of the target protein (primary structure), to generate an initial solution, which will be modified during the process by the perturbation function. This function is implemented in the metropolis cycle. As was mentioned earlier, GRSA divides the space solution using the GR number, making cuts in the temperature parameter. For each temperature range, the variable is set with a different value in a range of . The main difference between GRSA and GRSA2 is the perturbation process. In the GRSA, the perturbation function randomly chose an angle of the current solution. As a consequence, the new solution is accepted if the energy is better than the current solution. In GRSA2, the current solution is modified with the perturbation function (Algorithm 2. Soft perturbation).
In Algorithm 2, line 2, the variables moleColl and b are used for deciding what type of perturbation will be performed in the metropolis Cycle. In the former, moleColl is defined with a value that will be compared with the variable b using a random number in the range [0, 1]. We have two cases: (a) If , only one molecule is chosen for the perturbance process, and a unimolecular collision will be performed in this case. (b) Otherwise, a high energy perturbation can be applied. In case (a), the Decomposition criterion statement (line 5) is used to allow the algorithm to explore other regions of the solution space after enough local search by soft collisions. If the algorithm has not located a better minimum, it explores other regions of the solution space using decomposition. Otherwise, a soft collision is applied.
The perturbation called decomposition involves a molecule that hits the wall, and it is divided into two new molecules. In the GRSA2, decomposition is performed by applying a circular permutation to the molecule, and two new molecules are created; in other words, two new solutions will be evaluated and their energies are compared with the original molecule energy. SoftCollision involves a molecule that hits the wall and results in a new molecule. In GRSA2, this perturbation is randomly made by selecting the angle of the vector solution; then, the complexity of this operation is O(1). Once a perturbation is applied, the energy of the new molecule (solution) is calculated and compared with the original molecule. Only one of the new solutions generated by the different perturbations is selected (i.e., the solution with the lowest energy), and it continues in the next iteration.
| Algorithm 2 Soft perturbation. |
| 1: SoftPertubation () |
| 2: |
| 3: if then |
| 4: Randomly select one particle |
| 5: if then |
| 6: |
| 7: else if |
| 8: |
| 9: end |
| 10: end |
| 11: end |
In Algorithm 3, we can see the external cycle similar to classical SA. However, the main difference is in the metropolis cycle, which made soft perturbation (explained in Algorithm 2). In particular, the acceptance criterion is given by the potential energy (EP) which is the energy function of the current solution (Enew) and is compared with the current energy (Eold) plus the kinetic energy (EK), which is later updated (line 11, Algorithm 3), in a certain way similar to the threshold accepting algorithm (TA) [54] to accept bad solutions. However, the acceptance criterion is slightly different and is inspired by the CRO algorithm [39]. In addition, the GRSA2 algorithm has a stop criterion based on the least square method wherein a low temperature time window (Tf) is established and the slope (m) of a set of energies is calculated, and when m is lower than a tolerance parameter ε (0.001 in our case), the algorithm is ended. Finally, the alpha value (α) is updated depending on how many golden sections (defined by the variable nGolden) are used. Note that the number of cuts of temperature (Tfp) is indirectly defined in Algorithm 3 by the nGolden parameter are used.
| Algorithm 3 GRSA2. |
| 1: GRSA2 (, , , E, S, , KE, EP nGolden) |
| 2: |
| 3: |
| 4: while do |
| 5: |
| 6: while do |
| 7: |
| 8: EP = Enew |
| 9: if then |
| 10: |
| 11: KE = ((Eold+KE)-EP)*random [0, 1] |
| 12: end if |
| 13: end while |
| 14: if then |
| 15: |
| 16: if then |
| 17: (the algorithm is stopped) |
| 18: end if |
| 19: end if |
| 20: if then |
| 21: |
| 22: |
| 23: else |
| 24: |
| 25: end if |
| 26: end while |
| 27: end |
In general, GRSA2 has two main contributions that improve the performance of GRSA. Firstly, the collision operators used to generate new solutions; specifically, soft perturbations are applied; and finally, the acceptance criterion (similar to threshold annealing algorithm [54]) inspired in the CRO algorithm and used in the metropolis cycle.
The complexity of the GRSA and GRSA2 algorithms is related to the number of iterations for generating new solutions, which is equal or lower than the classical SA; also, the perturbations to generate new solutions for all the three algorithms belong to O(1), the complexity of GRSA and GRSA2 is the same as SA. Note that the acceptance criterion taken from threshold accepting does not modify the complexity of GRSA2. Experimentally, we verified this situation for the case of peptides in the results section (Figure 6) and the processing time of the proposed algorithm is generally shorter than SA.
5. Results
In this section, the experimentation results of the proposed algorithms for peptides and small proteins are discussed. Essentially, we present the instances used to evaluate the proposed algorithms and comparing GRSA2 versus SA, I-Tasser, and PEP-FOLD3 algorithms. The previous comparison has not been made previously.
5.1. Experimental Description
The algorithms presented in this paper were tested with a set of 18 peptides; some of them are very common in the literature, such as the Met-enkephalin (The PDB code is 2LWC) and the Human Proinsulin C-Peptide (1T0C). In Table 1, we show the number of amino acids and variables for these peptides. Met-enkephalin is a very small peptide, which is included here because it is commonly used to test new algorithms for peptides, due to its number of amino acids and the size of the solution space. The Met-enkephalin can be taken as a benchmark for evaluating the efficiency of new algorithms [55]. All the algorithms were executed 30 times for statistical validation. The energy function ECEPP/2 implemented in SMMP is used [49]. The initial and final temperatures used by the algorithms tested were tuned analytically (Section 2.2).

Table 1.
Peptide instances test set.
For the SA algorithm, the parameter was set at 0.95. In the case of GRSA, was tuned using values from 0.75 to 0.95 with five golden ratio sections. The angle used by all the assessed algorithms was fixed at 180°. Furthermore, in addition to the minimal energy quality value, we used two metrics of structural quality usually used for PFP algorithms, the RMSD (Root Mean Square Deviation) and the TM-Score (Template Modeling Score) [56]. RMSD is a structural measure between the native structure and the best-found solution. When RMSD is close to zero, there is a perfect structural similarity between the two compared structures. However, when RMSD is greater than zero, the structural quality is reduced. The metric TM-Score is also used to measure the similarity of structures. Protein pairs with a would indicate that they are mostly within the same fold, while those with a would indicate that they are mainly not within the same fold [57]. RMSD and TM-Score were calculated using TM-Align Server [58], which employs the backbone (Cα).
5.2. Results and Discussion
The results obtained by the proposed algorithms are shown in Table 2, Table 3 and Table 4. Table 2 and Table 3 include information about the average energy of each protein (kcal/mol), average processing time (minutes), RMSD, and TM-Score. In Table 2, the results obtained with the SA algorithm are presented.

Table 2.
Average results of the simulated annealing (SA) algorithm.

Table 3.
Average results of the enhanced golden simulated annealing (GRSA2) algorithm.

Table 4.
The five best RMSD and TM-Score of PEP-FOLD and the enhancement GRSA algorithms.
Finally, the results of GRSA2 algorithm are shown in Table 3. This table shows an improvement in the average energy in most cases.
In Table 2 and Table 3, we can observe how the improvements in energy, RMSD, and TM-Score are not always in favor of a particular algorithm. This situation often occurs in optimization problems, as underlined in the non-free lunch theorem [59].
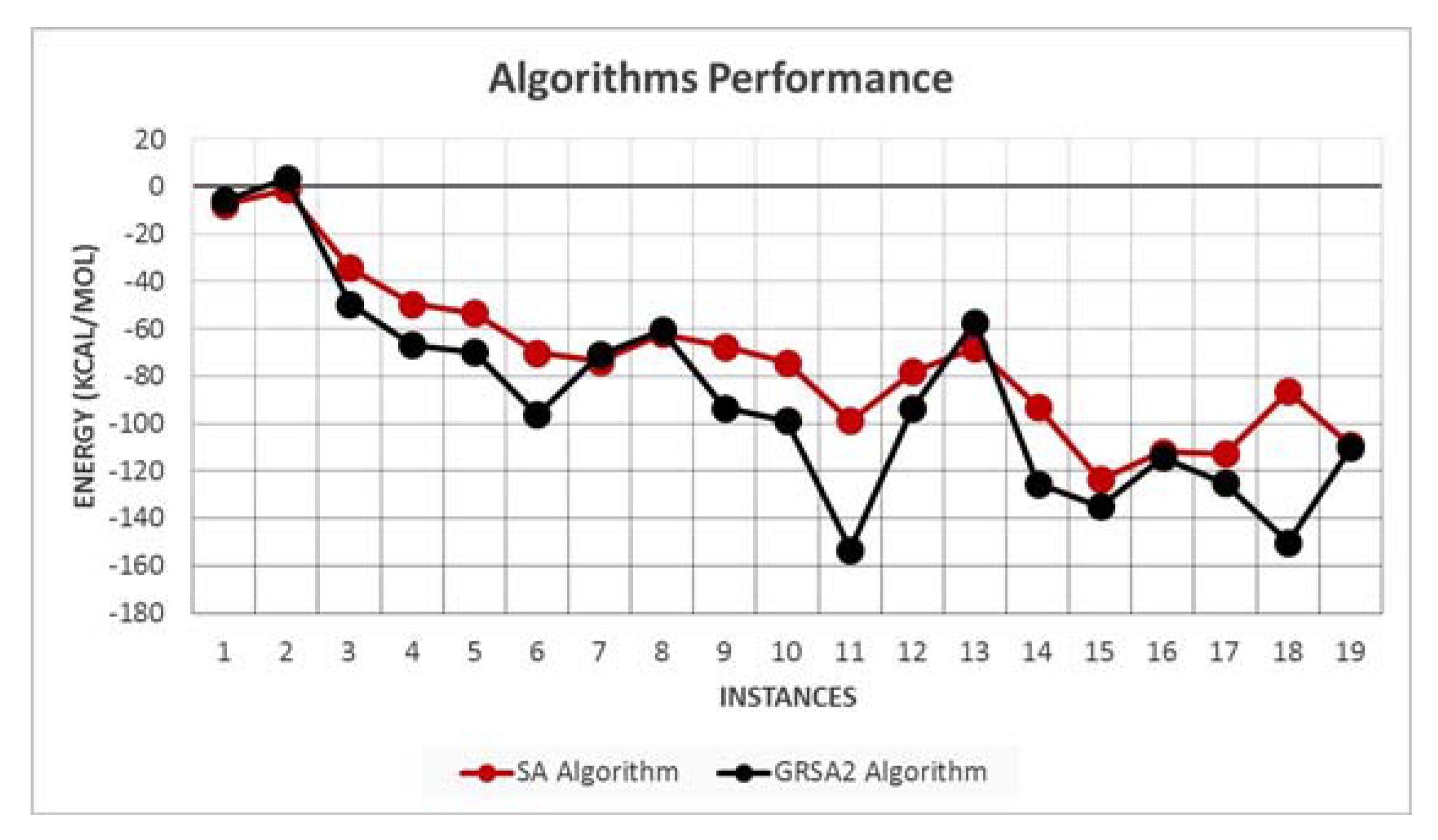
Figure 3 shows the average energy results for nineteen instances. We note that GRSA2 outperforms SA in most cases.
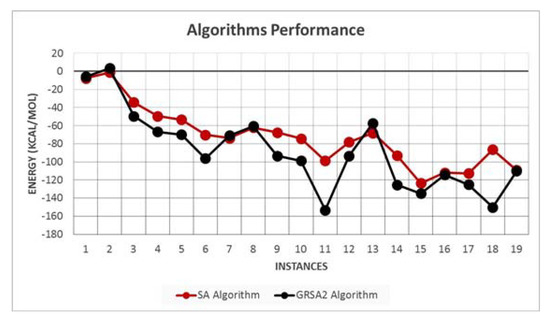
Figure 3.
SA and GRSA2 algorithms performance with energy average results.
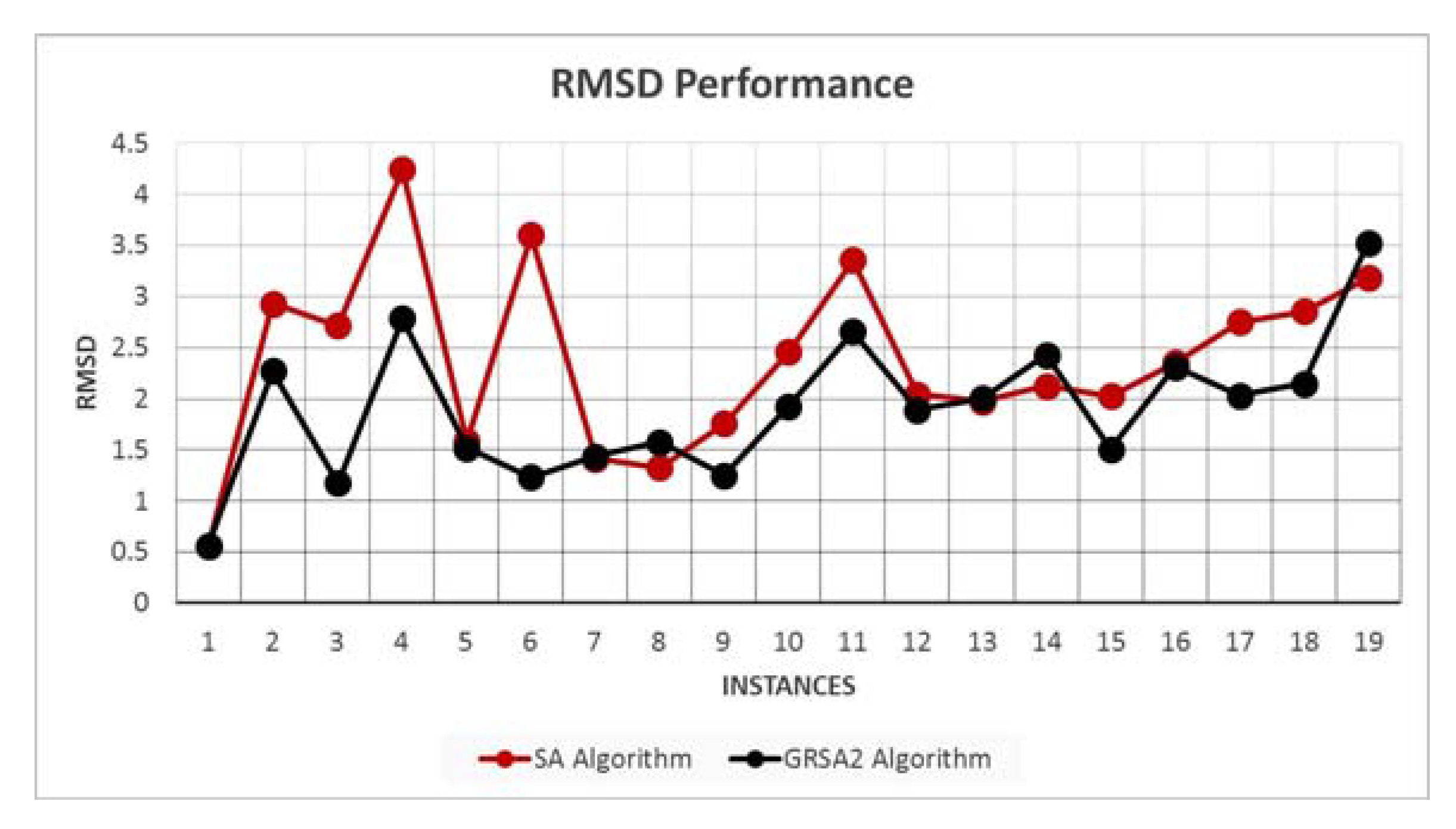
Figure 4 shows the average RMSD results for 19 instances. We note that GRSA2 outperforms SA in most cases.
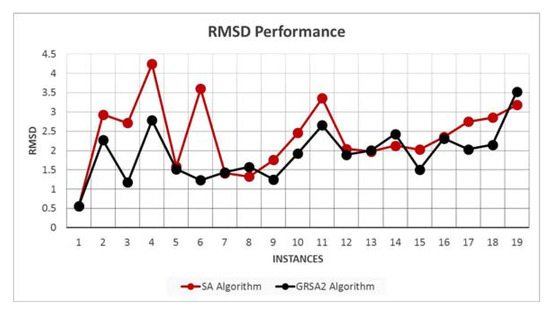
Figure 4.
RMSD performance with average results of SA and GRSA2.
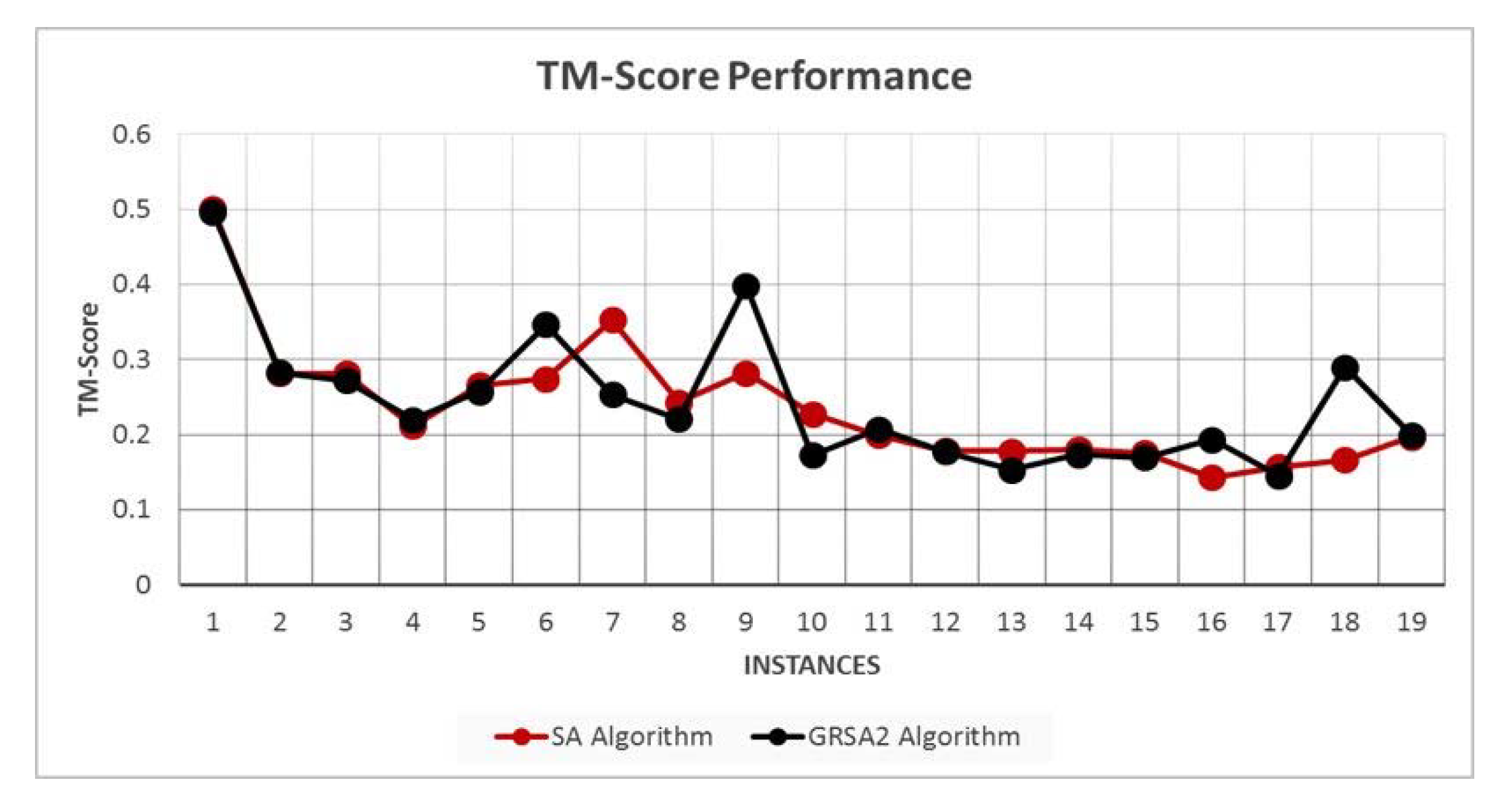
Figure 5 shows the TM-Score average results for nineteen instances. We can observe that GRSA2 and SA algorithms have a similar performance. However, in some cases, GRSA2 outperforms SA.
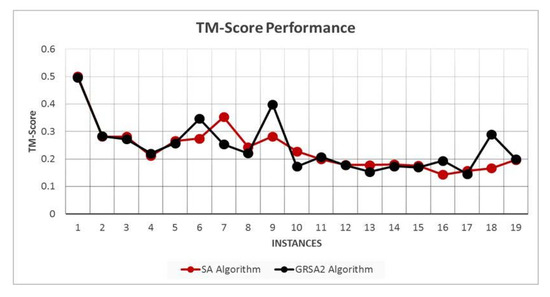
Figure 5.
TM-Score performance with average results.
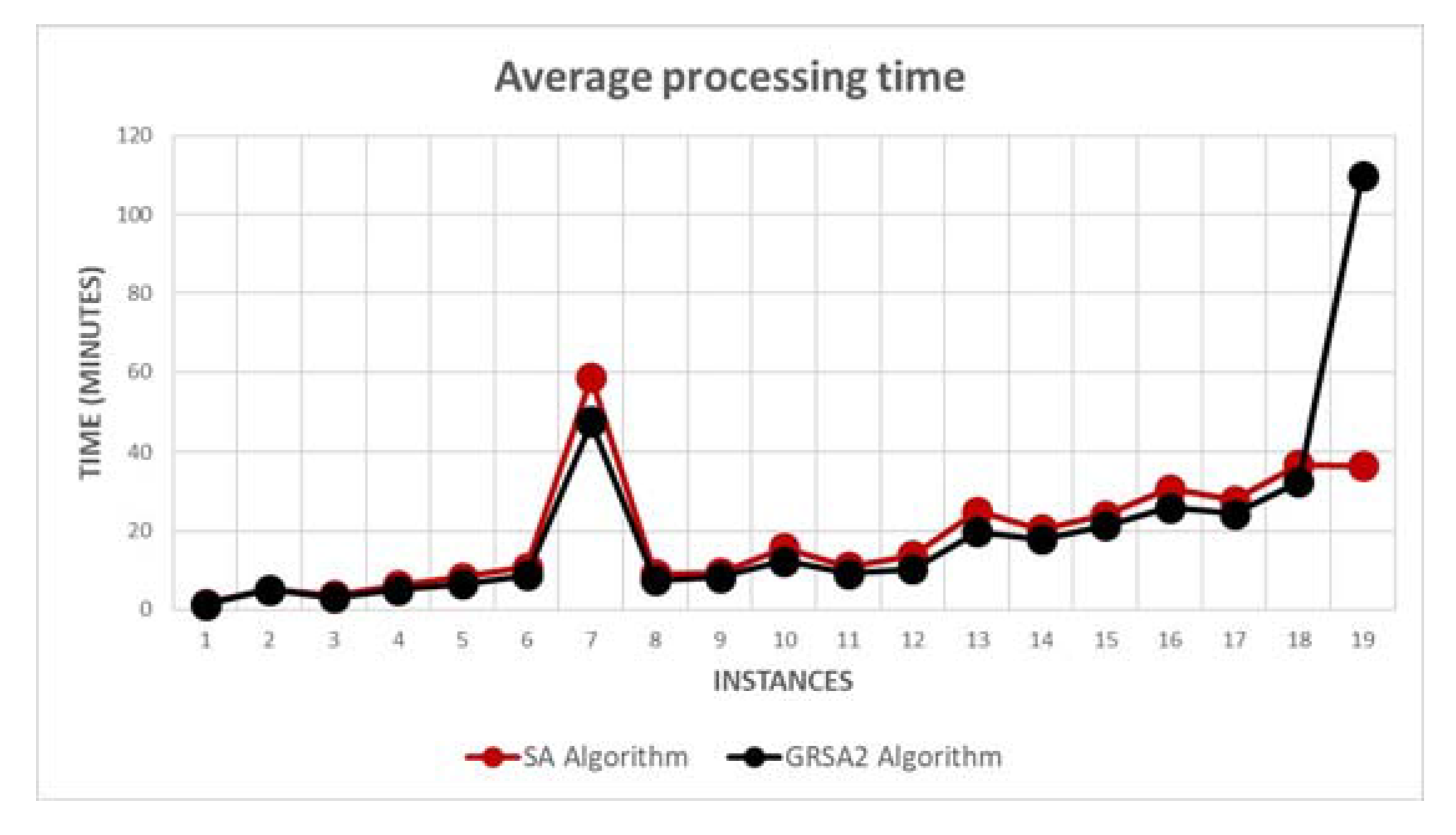
The average processing times for SA and GRSA2 are shown in Figure 6. As we can observe, GRSA2 has a better processing time than the SA algorithm, except in the last instance.
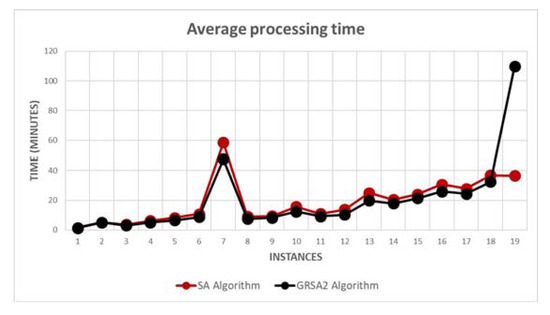
Figure 6.
Average processing time of SA and GRSA2.
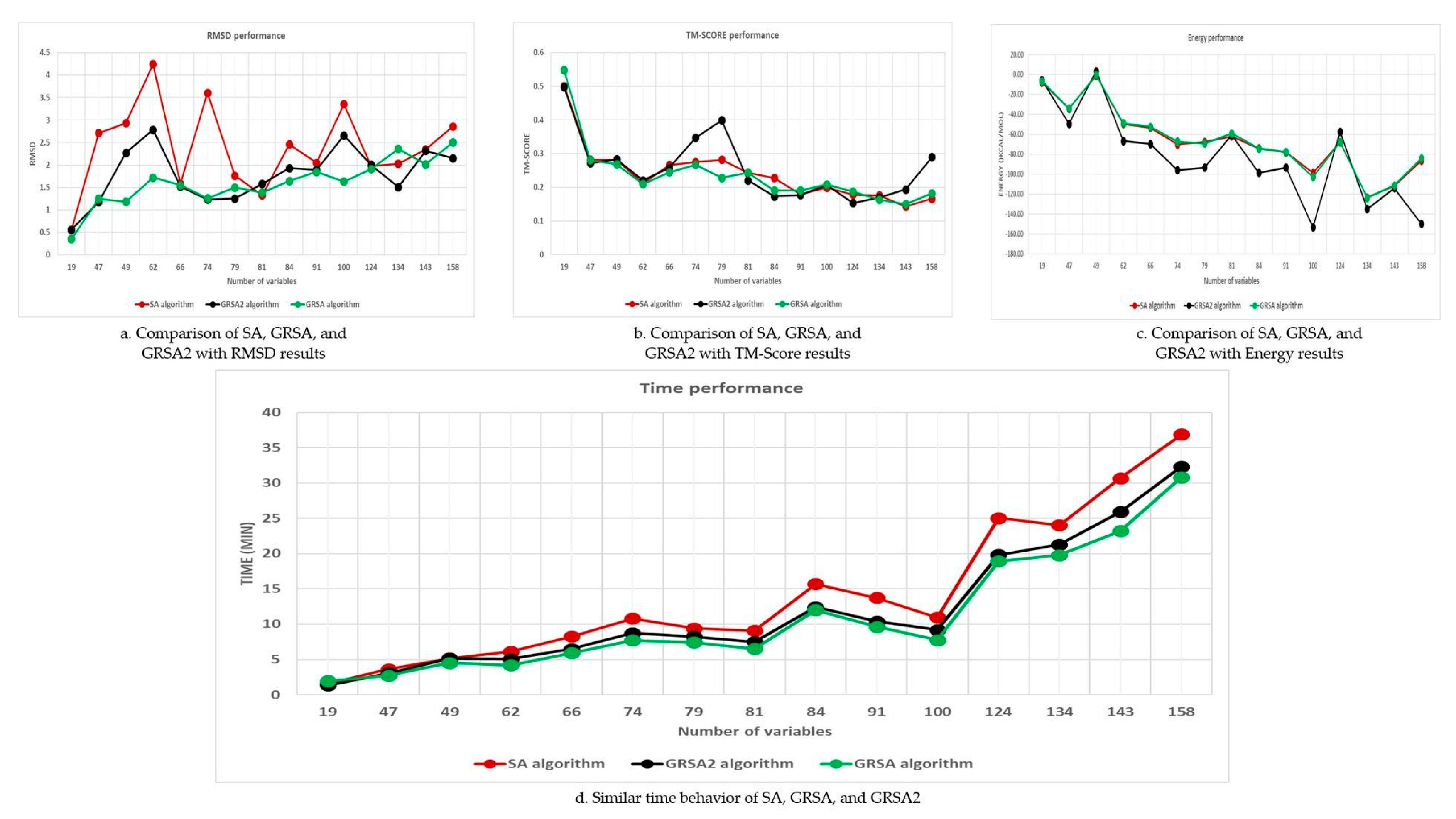
We take a set of 15 peptides of Table 1 ordered by the number of variables to compare the performance of SA with GRSA and GRSA2. Figure 7a,b shows the RMSD and TM-SCORE of the algorithms. We can observe that GRSA and GRSA2, in most cases, have better results than SA. However, according to Figure 7c, it is clear that GRSA2 outperforms SA and GRSA. Finally, Figure 7d shows the execution time f1(n), f2(n), and f3(n) of the three algorithms, SA, GRSA, and GRSA2, respectively. Because f2(n) and f3(n) are lower or equal than f1(n), they belong to the same complexity class [60].
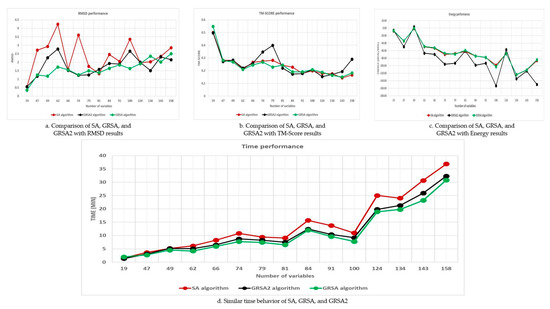
Figure 7.
Performance of the SA, golden ratio simulated annealing (GRSA), and GRSA2.
Table 4 shows the results for 19 instances for peptides reported by PEP-FOLD3 in its server. These peptides have between 5 and 50 amino acids in aqueous solution [12]. Column one contains the instances used for testing the proposed algorithms and PEP-FOLD3. In columns two and three, we present the RMSD average of the five best instances of PEP-FOLD3 and GRSA. Note that in most cases, GRSA2 obtained the best results with respect to RMSD (bold). In columns four and five, we present the TM-Score obtained by these algorithms. Once again, we verify that GRSA obtained the best results. We do not show the processing time of the results obtained by I-Tasser and PEP-FOLD3 servers. This is because these servers do not include this information.
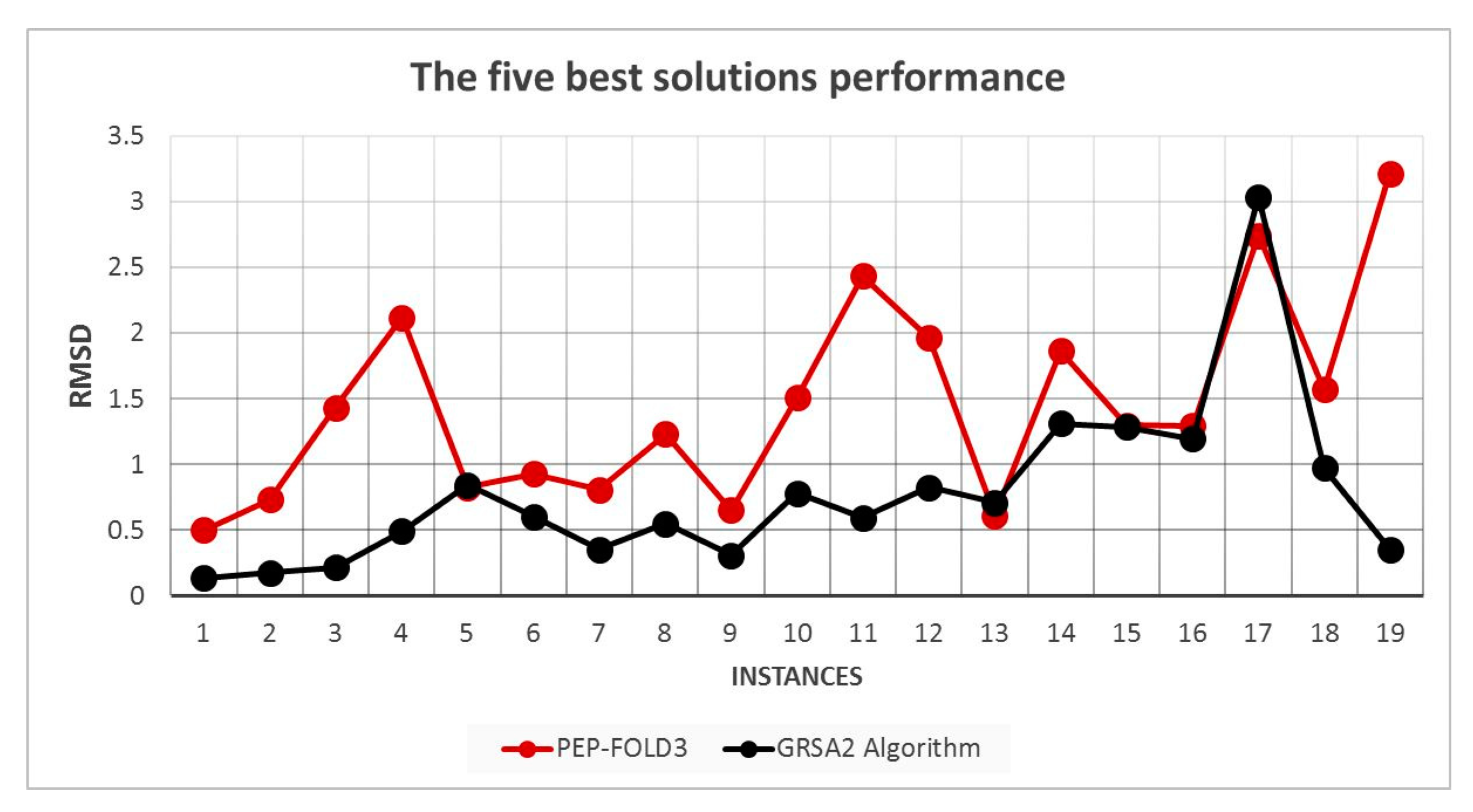
Figure 8 shows the five best RMSD results for 19 instances. We note that GRSA2 outperforms PEP-FOLD3 in most cases.
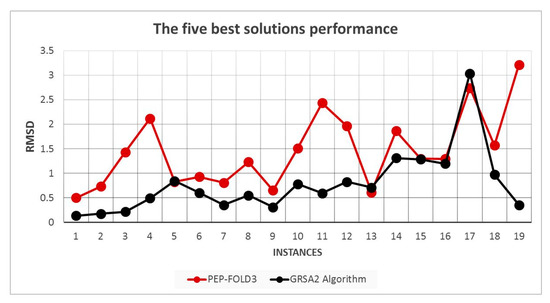
Figure 8.
RMSD performance of the five best solutions.
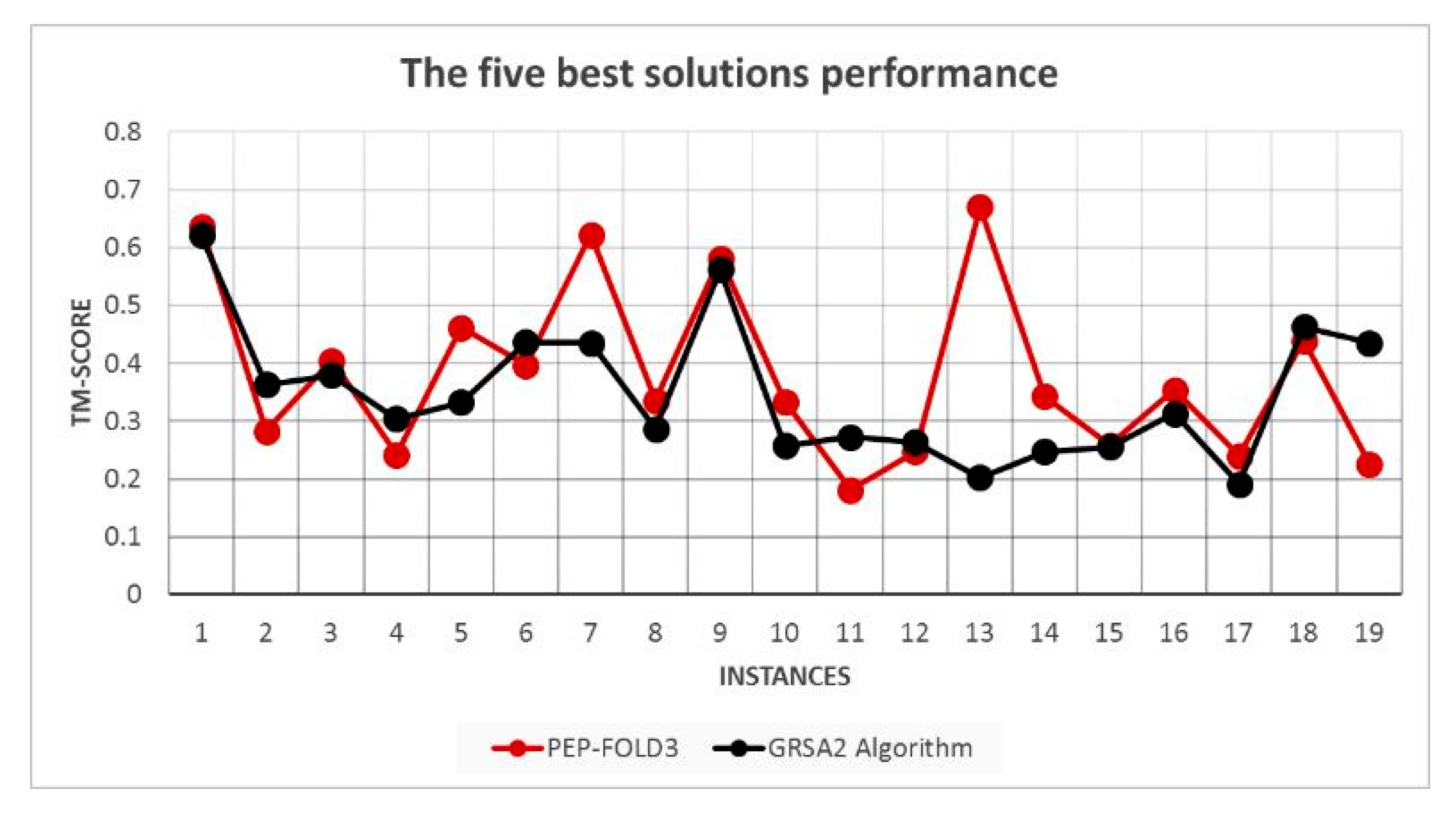
Figure 9 shows the TM-Score of the five best results for 19 instances. We note that GRSA2 and PEP-FOLD have similar performance, although PEP-FOLD3 is the best in most cases.
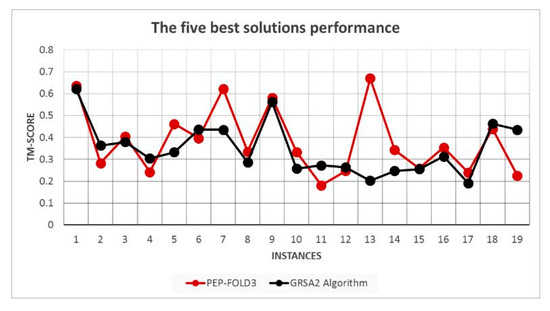
Figure 9.
TM-Score performance of the five best solutions.
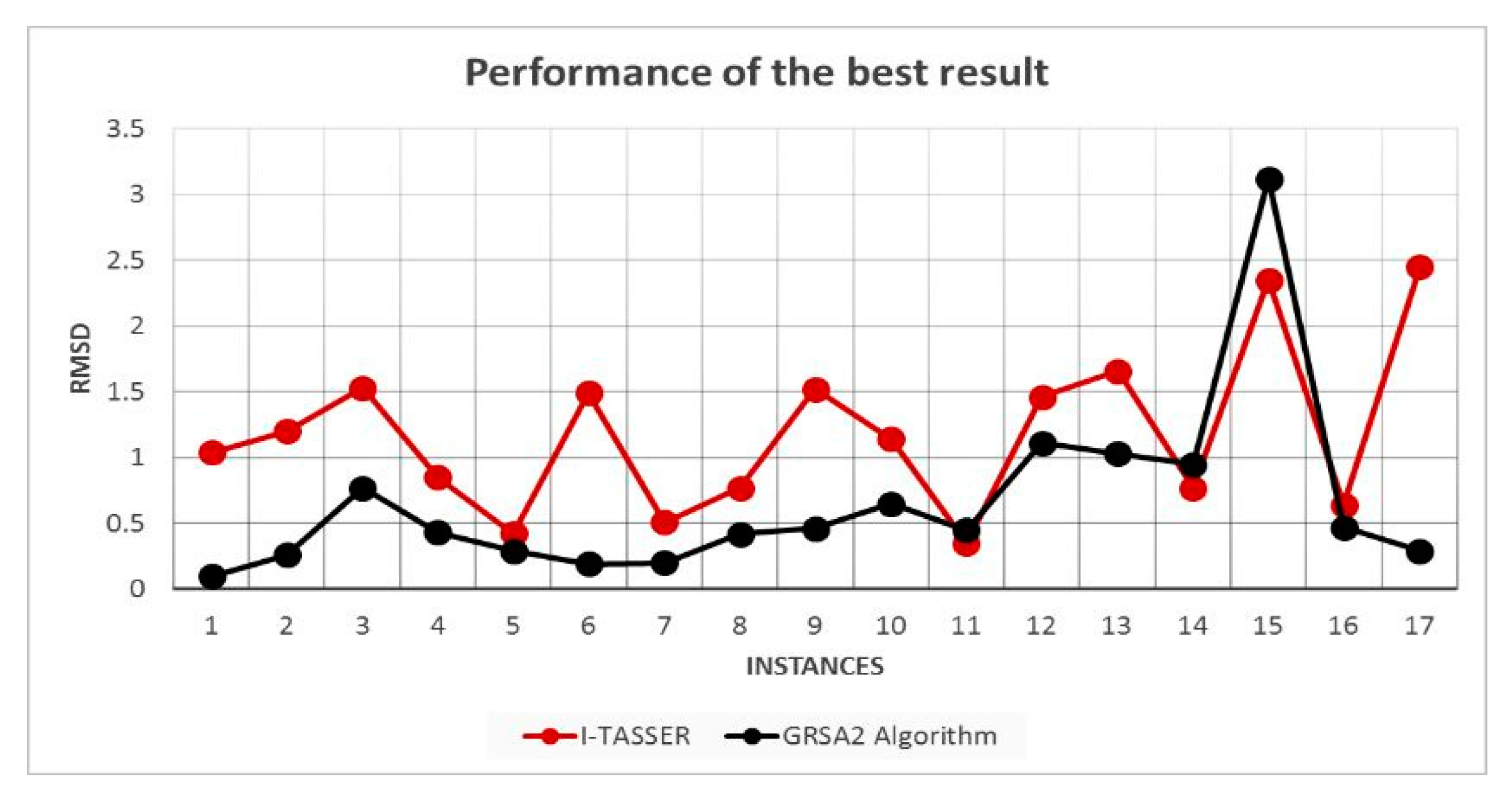
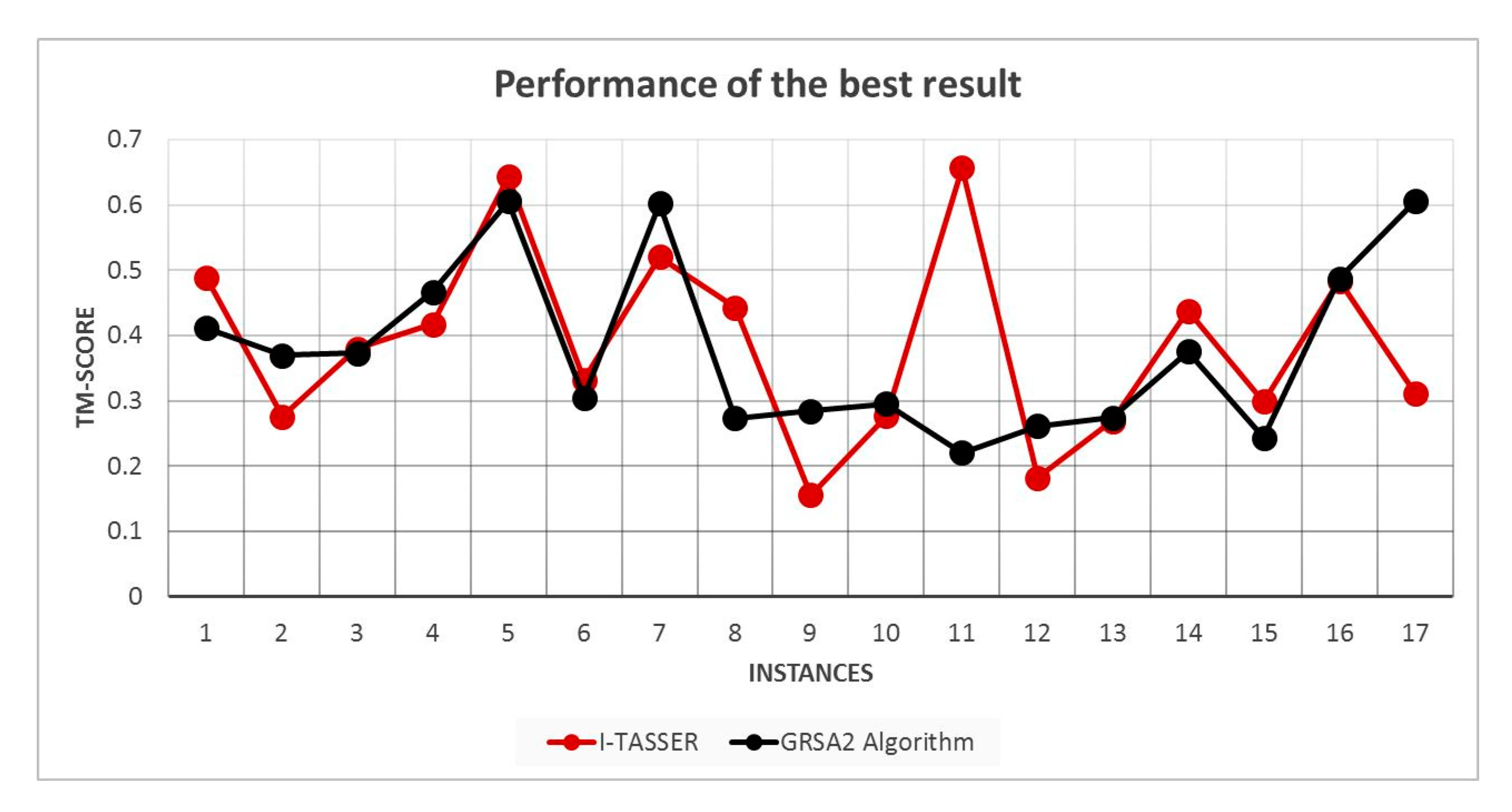
In Figure 10, a comparison of I-Tasser, and GRSA2 using RMSD is presented. In this case, 17 instances are compared because I-Tasser only accepts proteins greater than 10 amino acids. For this reason, 2LWC and 1EGS are discarded. The results presented in Figure 10 show the best result obtained by I-Tasser and GRSA2. We may observe that comparing RMSD results, GRSA2 outperforms I-Tasser in this set of instances. However, in Figure 11, we observe a similar result between I-Tasser and GRSA2 comparing only the best TM-Score in both algorithms.
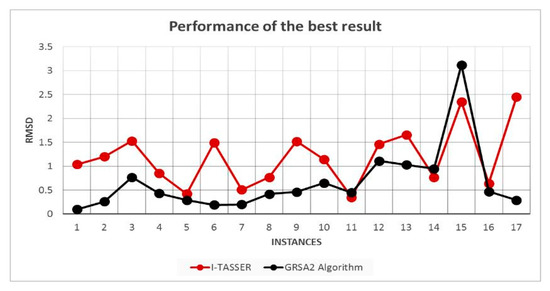
Figure 10.
RMSD comparison of I-Tasser and GRSA2.
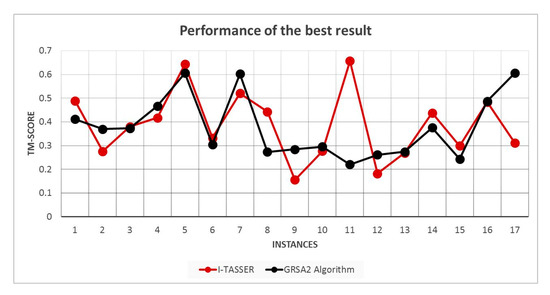
Figure 11.
TM-Score comparison of I-Tasser versus GRSA2.
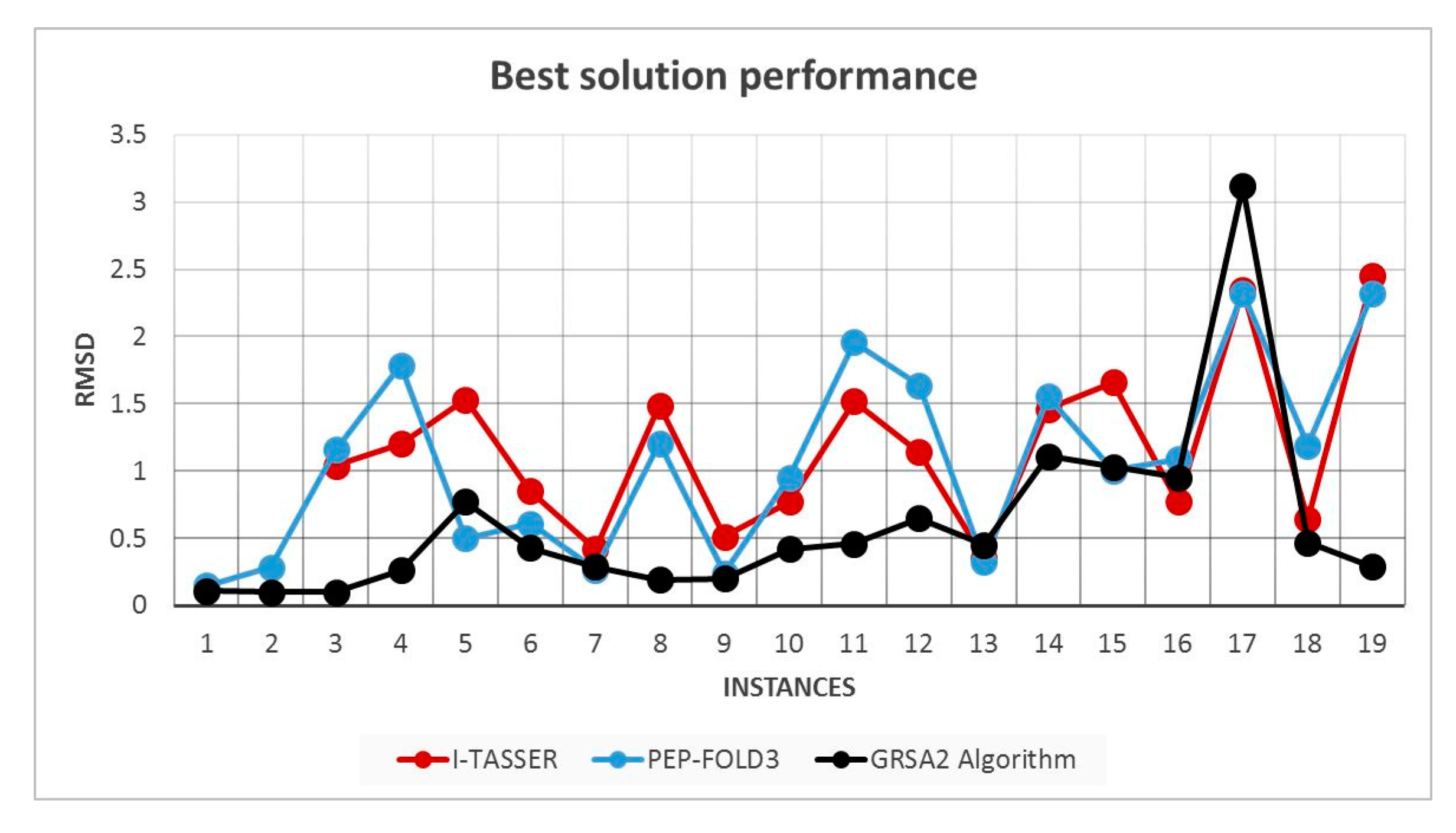
The following comparisons (Figure 12 and Figure 13) are made using RMSD and TM-Score with the best result obtained in the RMSD and I-Tasser algorithms to observe the performance with the set of instances evaluated.
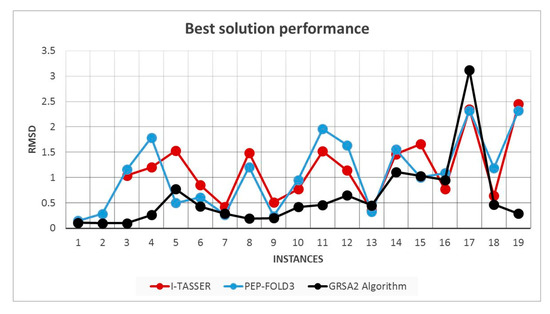
Figure 12.
Best RMSD obtained for I-Tasser, PEP-FOLD3, and GRSA2 algorithms.
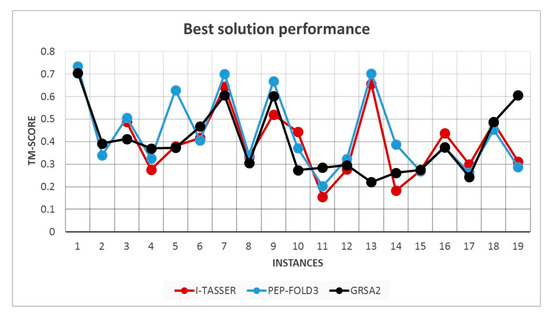
Figure 13.
TM-Score performance of I-Tasser, PEP-FOLD3, and GRSA2.
In Figure 12, the best RMSD solutions of I-Tasser, PEP-FOLD3, and GRSA2 are compared. Note that in most cases, GRSA obtains better results than I-Tasser and PEP-FOLD3.
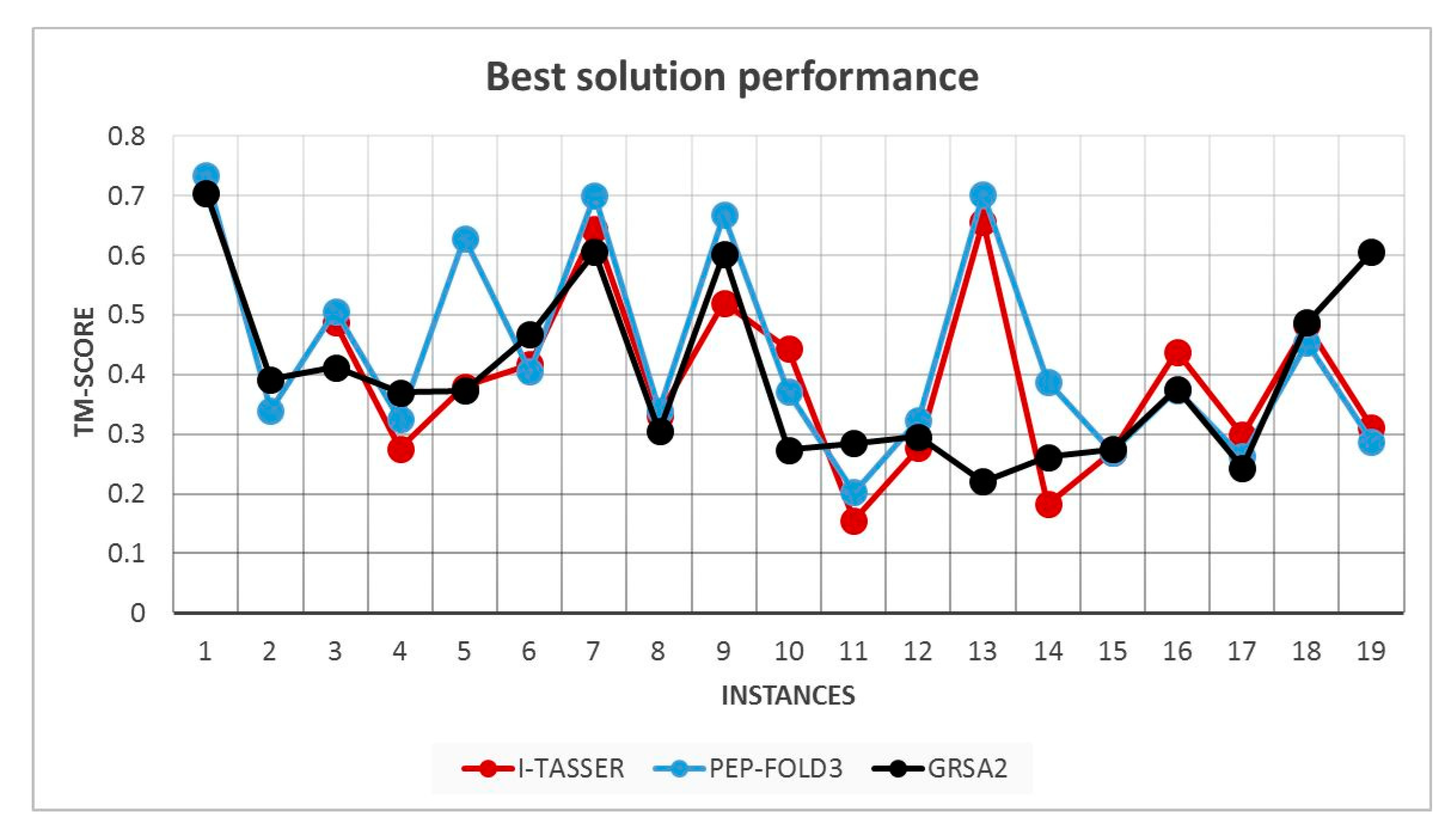
Finally, in Figure 14, the best TM-Score solutions obtained by I-Tasser, PEP-FOLD3, and GRSA are compared. We may observe that PEP-FOLD3, in most cases, is better than GRSA and I-Tasser. However, we should point out that GRSA2 obtain similar or very close results in several instances.
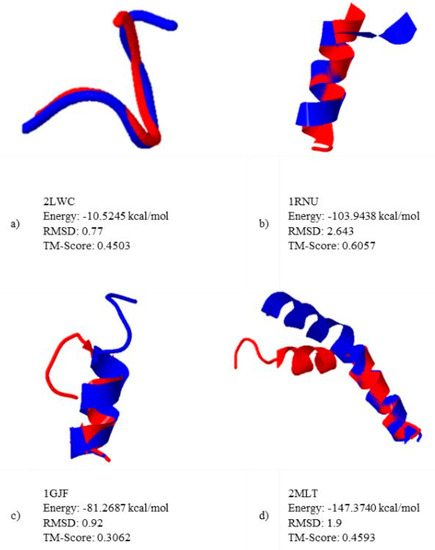
Figure 14.
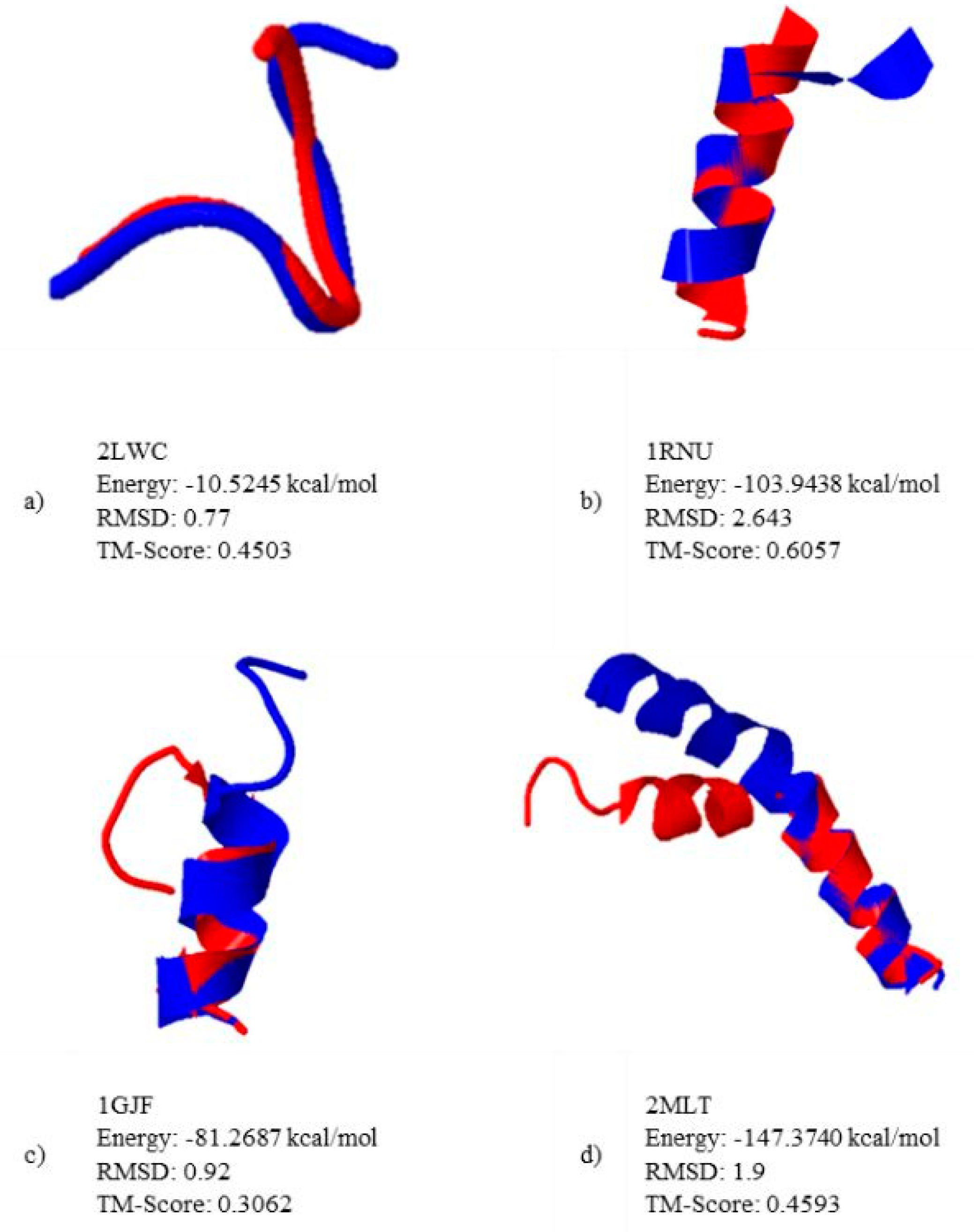
TM-align simulation exemplifying the alignment vs. native structure (NS).
Figure 14 shows a typical alignment of our algorithms and the native structure using the TM-Align server [58]. Four proteins were chosen (in red), and their native structures (in blue) are compared with the results obtained by GRSA. As we mentioned before, the quality of the solution is measured by using energy, the RMSD, and TM-Score values.
Compared to the classic SA algorithm, GRSA2 shows the best performance in virtually all instances using RMSD and TM-Score as a quality metric, as shown in Figure 3, Figure 4 and Figure 5.
Although GRSA2 is an algorithm that does not use any biological information, as mentioned above, the results obtained are competitive and sometimes better than those obtained by the PEP-FOLD3 and I-TASSER servers.
The best RMSD results of GRSA2, I-TASSER, and PEP-FOLD3 are shown in Figure 12, and we can observe that GRSA2 has the best performance. However, when TM-SCORE is also used as a quality metric, PEP-FOLD3 has the best performance for most of the instances. Thus, we made a hypothesis test, and we found that all of the three algorithms are statistically equivalent.
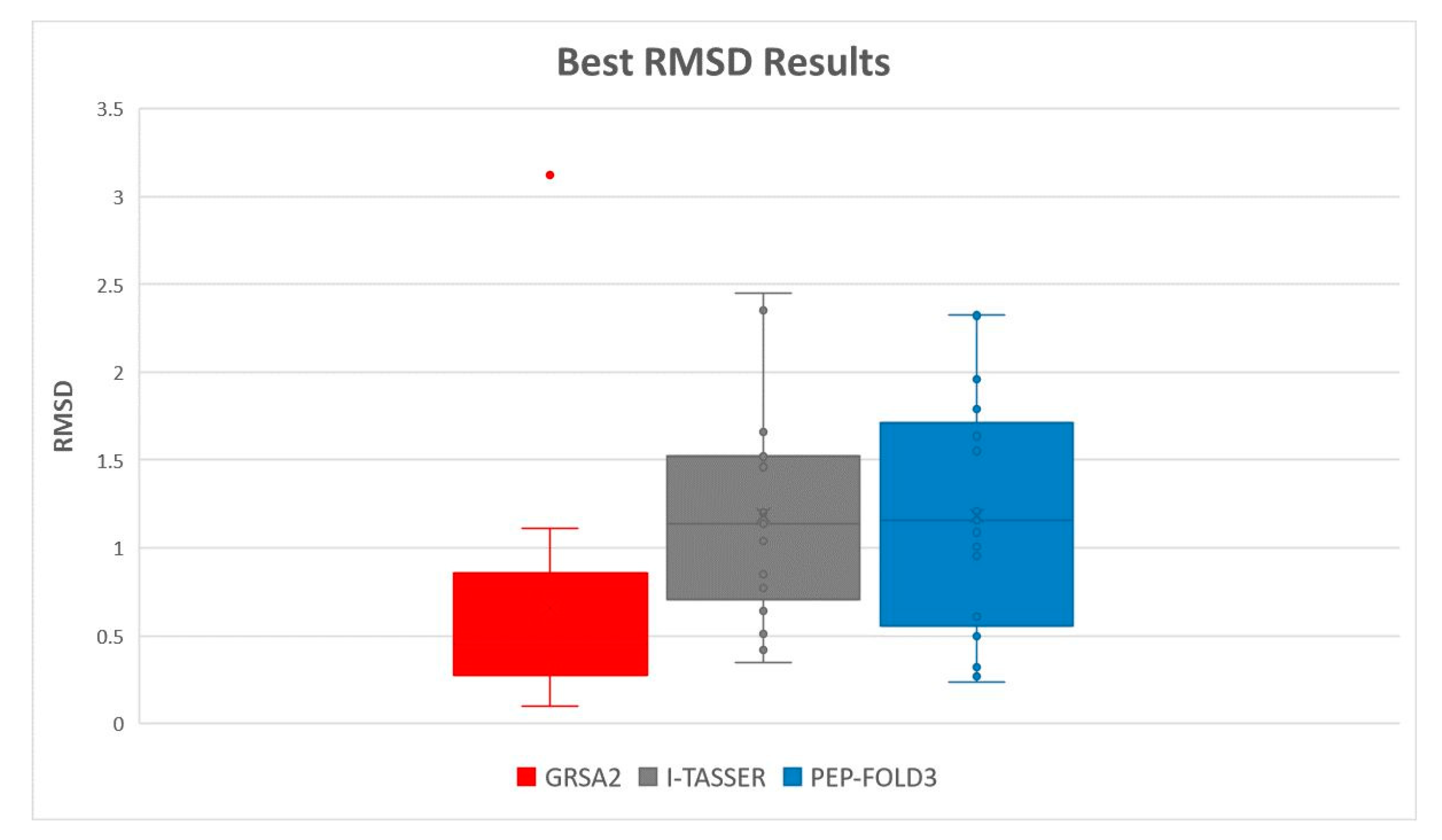
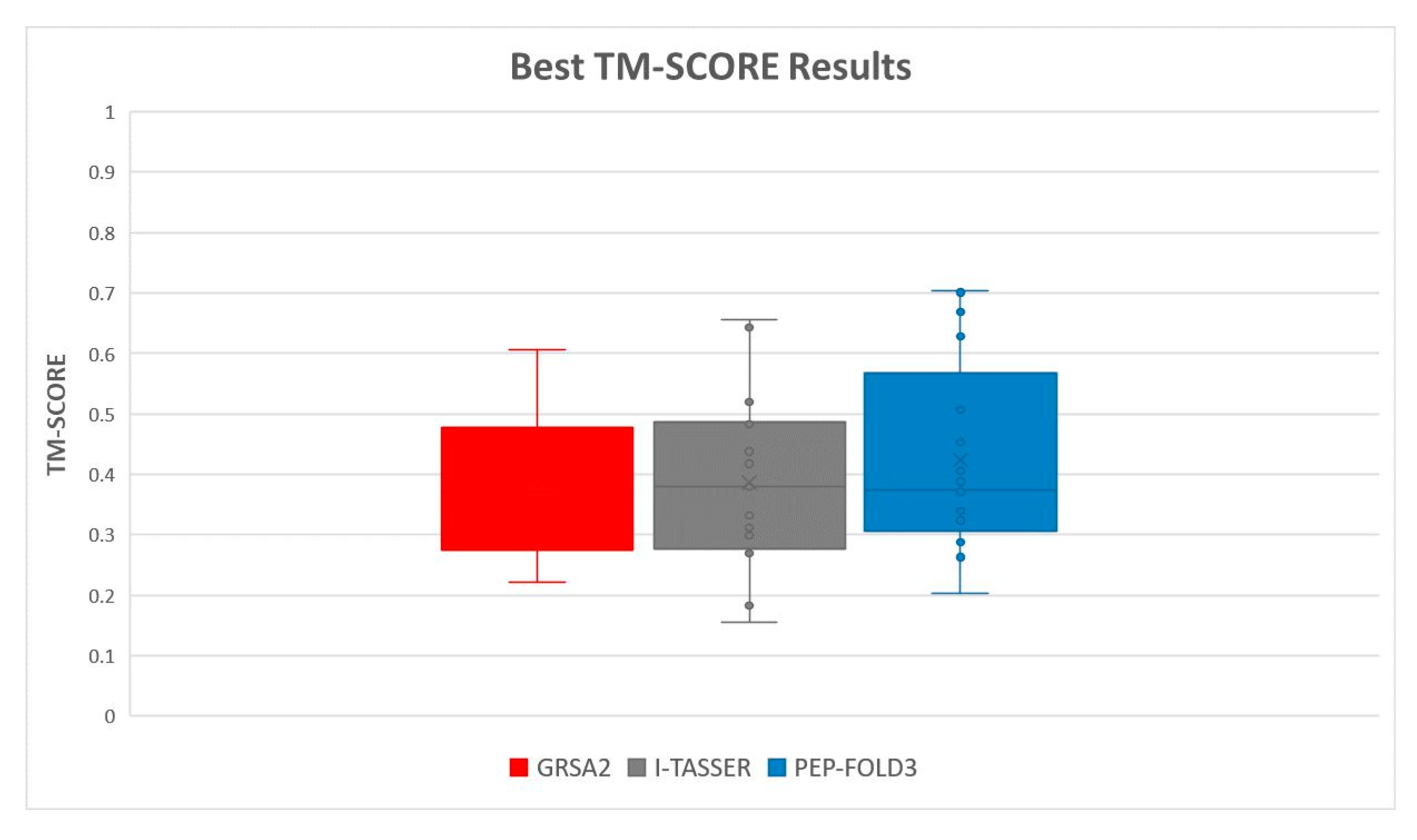
For a better appreciation of the results and the performance of the algorithms, two box diagrams with the best RMSD and TM-SCORE are presented in Figure 15 and Figure 16, respectively. Note that GRSA2 has a very good performance concerning I-TASSER and PEP-FOLD3 algorithms.
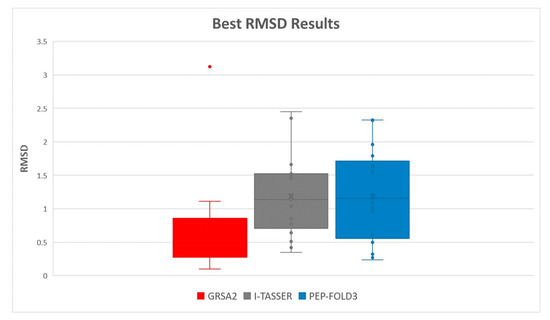
Figure 15.
Best RMSD obtained of I-Tasser, PEP-FOLD3, and GRSA2 algorithms.
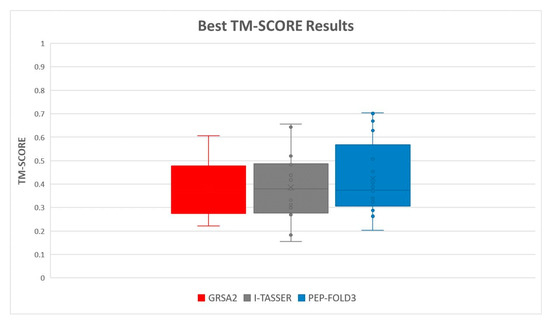
Figure 16.
Best RMSD obtained of I-Tasser, PEP-FOLD3, and GRSA2 algorithms.
Despite the good performance shown by GRSA2, we should mention that this algorithm outperforms I-TASSER and PEP-FOLD3 servers but not in all cases. For instance, in Figure 8, when the TM-SCORE metric is used, a downward trend is observed for cases of less than 10 amino acids, compared to the results obtained by PEP-FOLD3. Also, by comparing it to I-Tasser and PEP-FOLD3, the quality measured with the TM-Score metric for GRSA2 is not the best in most cases (Figure 13 and Figure 16).
6. Conclusions
In this paper, we present the GRSA2 algorithm for the protein folding problem applied to peptides. This algorithm combines the classical features of SA with soft perturbation and acceptance criterion taken CRO algorithm, and for generating new solutions, we use soft particle perturbations proposed in the CRO algorithm. As a result, the simulation process for peptides leads to the tertiary structure close to the native structure and with equivalent quality as the best PFP algorithms.
The proposed algorithms were compared against the classical simulated annealing algorithm, PEP-FOLD3, and I-Tasser. According to the experimentation, the proposed algorithms overpass SA, PEP-FOLD3, and I-Tasser when RMSD is compared. However, when TM-Score is used, the results are similar in some cases, and others are very close. Moreover, according to the experimentation, GRSA2 is statistically equivalent to the other two algorithms PEP-FOLD3 and I-Tasser. In addition, GRSA2 has the advantage that it is simpler and easier to implement than the other algorithms. To be precise, to use GRSA2 is more friendly because this algorithm does not require machine learning techniques or a fragments database.
The GRSA2 algorithm is a simple algorithm because it only uses the sequence of amino acids as input information, which for certain users can be considered advantageous compared to PEP-FOLD3 and I-Tasser, which depend on biological information. On the contrary, it is necessary to further improve the proposed algorithm in such a way that we can obtain better results using the TM-Score metric. Finally, we showed that this new enhancement of GRSA is useful for protein folding problems in the case of peptides. Therefore, we consider the proposed algorithms are relevant because these proteins have many applications in medicine, biotechnology, and other areas. As part of our ongoing work, we are developing a server using GRSA2 for small peptides and other proteins.
Author Contributions
Authors J.F.-S., and J.P.S.-H. contributed equally to the development of this paper. Conceptualization, J.P.S.-H. and J.F.-S.; methodology J.F.-S., J.P.S.-H., and J.J.G.-B.; Software J.P.S.-H., and F.G.M.-N.; validation, J.P.S.-H. and J.F.-S.; formal analysis, F.G.M.-N., and J.J.G.-B.; writing—original draft J.F.-S., and J.P.S.-H.; writing—review and editing, J.F.-S., F.G.M.-N., and J.P.S.-H.
Funding
This research received no external funding.
Acknowledgments
The authors would like to acknowledge with appreciation and gratitude CONACYT and TecNM/Instituto Tecnológico de Ciudad Madero. Also, we acknowledge Laboratorio Nacional de Tecnologías de la Información (LaNTI) for the access to the cluster. Fanny Gabriela Maldonado-Nava would like to thank CONACYT for the PhD. scholarship. Juan Paulo Sánchez Hernández thanks CONACYT for the postdoctoral scholarship program.
Conflicts of Interest
The authors declare that they have no competing interests.
References
- Khoury, G.A.; Smadbeck, J.; Kieslich, C.A.; Floudas, C.A. Protein Folding and de Novo Protein Design for Biotechnological Applications. Trends Biotechnol. 2014, 32, 99–109. [Google Scholar] [CrossRef] [PubMed]
- Anfinsen, C.B. Principles that Govern the Folding of Protein Chains. Science 1973, 181, 223–230. [Google Scholar] [CrossRef] [PubMed]
- Shin, M.H.; Lim, H.S. Screening Methods for Identifying Pharmacological Chaperones. Mol. Biosyst. 2017, 13, 638–647. [Google Scholar] [CrossRef] [PubMed]
- Hou, Z.S.; Ulloa-Aguirre, A.; Tao, Y.X. Pharmacoperone Drugs: Targeting Misfolded Proteins Causing Lysosomal Storage-, ion Channels-, and G protein-coupled receptors-associated conformational disorders. Expert Rev. Clin. Pharmacol. 2018, 11, 611–624. [Google Scholar] [CrossRef] [PubMed]
- Valastyan, J.S.; Lindquist, S. Mechanisms of Protein-folding Diseases at a Glance. Dis. Model. Mech. 2014, 7, 9–14. [Google Scholar] [CrossRef] [PubMed]
- Sohl, J.L.; Jaswal, S.S.; Agard, D.A. Unfolded Conformations of α-lytic Protease are More Stable Than its Native State. Nature 1998, 395, 817–819. [Google Scholar] [CrossRef]
- Levinthal, C. Are There Pathways for Protein Folding. J. Chim. Phys. 1968, 65, 44–45. [Google Scholar] [CrossRef]
- Yee, A.A.; Savchenko, A.; Ignachenko, A.; Lukin, J.; Xu, X.; Skarina, T.; Edwards, A.M. NMR and X-ray crystallography, complementary tools in structural proteomics of small proteins. J. Am. Chem. Soc. 2005, 127, 16512–16517. [Google Scholar] [CrossRef]
- Hart, W.E.; Istrail, S. Robust Proofs of NP-Hardness for Protein Folding: General Lattices and Energy Potentials. J. Comput. Biol. 1997, 4, 1–22. [Google Scholar] [CrossRef]
- Uhlig, T.; Kyprianou, T.; Martinelli, F.G.; Oppici, C.A.; Heiligers, D.; Hills, D.; Verhaert, P. The Emergence of Peptides in the Pharmaceutical Business: From Exploration to Exploitation. EuPA Open Proteom. 2014, 4, 58–69. [Google Scholar] [CrossRef]
- Fosgerau, K.; Hoffmann, T. Peptide Therapeutics: Current Status and Future Directions. Drug Discov. Today 2015, 20, 122–128. [Google Scholar] [CrossRef] [PubMed]
- Lamiable, A.; Thévenet, P.; Rey, J.; Vavrusa, M.; Derreumaux, P.; Tufféry, P. PEP-FOLD3: Faster de Novo Structure Prediction for Linear Peptides in Solution and in Complex. Nucleic Acids Res. 2016, 44, W449–W454. [Google Scholar] [CrossRef] [PubMed]
- Vetter, I.; Davis, J.L.; Rash, L.D.; Anangi, R.; Mobli, M.; Alewood, P.F.; King, G.F. Venomics: A New Paradigm for Natural Products-based Drug Discovery. Amino Acids 2011, 40, 15–28. [Google Scholar] [CrossRef] [PubMed]
- Frausto-Solis, J.; Sánchez-Hernández, J.P.; Sánchez-Pérez, M.; García, E.L. Golden Ratio Simulated Annealing for Protein Folding Problem. Int. J. Comput. Methods 2015, 12, 1550037. [Google Scholar] [CrossRef]
- Rohl, C.A.; Strauss, C.E.M.; Misura, K.M.S.; Baker, D. Protein Structure Prediction Using Rosetta. In Methods in Enzymology; Elsevier: Amsterdam, The Netherlands, 2004; Volume 383, pp. 66–93. [Google Scholar]
- Xu, D.; Zhang, Y. Ab initio Protein Structure Assembly Using Continuous Structure Fragments and Optimized Knowledge-based Force Field. Proteins Struct. Funct. Bioinform. 2012, 80, 1715–1735. [Google Scholar] [CrossRef] [PubMed]
- Xu, D.; Zhang, Y. Toward Optimal Fragment Generations for ab initio Protein Structure Assembly. Proteins Struct. Funct. Bioinform. 2013, 81, 229–239. [Google Scholar] [CrossRef]
- Yang, J.; Yan, R.; Roy, A.; Xu, D.; Poisson, J.; Zhang, Y. The I-TASSER Suite: Protein Structure and Function Prediction. Nat. Methods 2015, 12, 7–8. [Google Scholar] [CrossRef]
- Kennedy, D.; Norman, C. What Don’t We Know? American Association for the Advancement of Science. Science 2005, 309, 75. [Google Scholar] [CrossRef]
- Dill, K.A.; MacCallum, J.L. The Protein-Folding Problem, 50 Years On. Science 2012, 338, 1042–1046. [Google Scholar] [CrossRef]
- Kaufmann, K.W.; Lemmon, G.H.; DeLuca, S.L.; Sheehan, J.H.; Meiler, J. Practically Useful: What the Rosetta Protein Modeling Suite Can Do for You. Biochemistry 2010, 49, 2987–2998. [Google Scholar] [CrossRef]
- Bienert, S.; Waterhouse, A.; de Beer, T.A.; Tauriello, G.; Studer, G.; Bordoli, L.; Schwede, T. The SWISS-MODEL Repository-new Features and Functionality. Nucleic Acids Res. 2017, 45, D313–D319. [Google Scholar] [CrossRef] [PubMed]
- Nielsen, M.; Lundegaard, C.; Lund, O.; Petersen, T.N. CPHmodels-3.0—Remote Homology Modeling Using Structure-guided Sequence Profiles. Nucleic Acids Res. 2010, 38, W576–W581. [Google Scholar] [CrossRef] [PubMed]
- Kelley, L.A.; Mezulis, S.; Yates, C.M.; Wass, M.N.; Sternberg, M.J.E. The Phyre2 Web Portal for Protein Modeling, Prediction and Analysis. Nat. Protoc. 2015, 10, 845–858. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.; Xu, D. Protein Threading Using PROSPECT: Design and Evaluation. Proteins Struct. Funct. Genet. 2000, 40, 343–354. [Google Scholar] [CrossRef]
- Soding, J. Protein Homology Detection by HMM-HMM Comparison. Bioinformatics 2005, 21, 951–960. [Google Scholar] [CrossRef]
- Xu, J.; Li, M.; Kim, D.; Xu, Y. RAPTOR: Optimal Protein Threading by Linear Programming. J. Bioinform. Comput. Biol. 2003, 1, 95–117. [Google Scholar] [CrossRef]
- Buchan, D.W.A.; Jones, D.T. EigenTHREADER: Analogous Protein Fold Recognition by Efficient Contact Map Threading. Bioinformatics 2017, 33, 2684–2690. [Google Scholar] [CrossRef]
- Wu, S.; Zhang, Y. LOMETS: A Local Meta-threading-server for Protein Structure Prediction. Nucleic Acids Res. 2007, 35, 3375–3382. [Google Scholar] [CrossRef]
- Wang, Y.; Virtanen, J.; Xue, Z.; Tesmer, J.J.G.; Zhang, Y. Using Iterative Fragment Assembly and Progressive Sequence Truncation to Facilitate Phasing and Crystal Structure Determination of Distantly Related Proteins. Acta Crystallogr. Sect. D Struct. Biol. 2016, 72, 616–628. [Google Scholar] [CrossRef]
- Unger, R.; Moult, J. Finding the Lowest Free Energy Conformation of a Protein is an NP-hard Problem: Proof and Implications. Bull. Math. Biol. 1993, 55, 1183–1198. [Google Scholar] [CrossRef]
- Dorn, M.E.; Silva, M.B.; Buriol, L.S.; Lamb, L.C. Three-dimensional Protein Structure Prediction: Methods and Computational Strategies. Comput. Biol. Chem. 2014, 53, 251–276. [Google Scholar] [CrossRef] [PubMed]
- Delarue, M.; Koehl, P. Combined Approaches from Physics, Statistics, and Computer Science for ab initio Protein Structure Prediction: Ex Unitate Vires (unity is strength)? F1000Research 2018, 7, 1125. [Google Scholar] [CrossRef] [PubMed]
- Melo-Vega, A.; Frausto-Solís, J.; Castilla-Valdez, G.; Liñán-García, E.; González-Barbosa, J.J.; Terán-Villanueva, D. Protein Folding Problem in the Case of Peptides Solved by Hybrid Simulated Annealing Algorithms. In Fuzzy Logic Augmentation of Neural and Optimization Algorithms: Theoretical Aspects and Real Applications; Springer: Cham, Switzerland, 2018; pp. 141–152. [Google Scholar]
- Frausto-Solis, J.; Liñan-García, E.; Sánchez-Pérez, M.; Sánchez-Hernández, J.P. Chaotic Multiquenching Annealing Applied to the Protein Folding Problem. Sci. World J. 2014, 2014, 1–11. [Google Scholar] [CrossRef]
- Li, Z.; Scheraga, H.A. Monte Carlo-minimization Approach to the Multiple-minima Problem in Protein Folding. Proc. Natl. Acad. Sci. USA 1987, 84, 6611–6615. [Google Scholar] [CrossRef] [PubMed]
- Frausto-Solis, J.; Liñán-García, E.; Sánchez-Hernández, J.P.; González-Barbosa, J.J.; González-Flores, C.; Castilla-Valdez, G. Multiphase Simulated Annealing Based on Boltzmann and Bose-Einstein Distribution Applied to Protein Folding Problem. Adv. Bioinform. 2016, 2016, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Vega, A.M.; Frausto-Solís, J.; García, E.L.; Valdez, G.C.; Barbosa, J.J.G.; Villanueva, D.T.; Hernández, J.P.S. Parallel Evolutionary Multi-Quenching Annealing for Protein Folding Problem. Int. J. Comb. Optim. Probl. Inform. 2018, 9, 41–54. [Google Scholar]
- Lam, A.Y.S.; Li, V.O.K. Chemical Reaction Optimization: A tutorial. Memetic Comput. 2012, 4, 3–17. [Google Scholar] [CrossRef]
- Zhang, Y.; Kolinski, A.; Skolnick, J. TOUCHSTONE II: A New Approach to ab initio Protein Structure Prediction. Biophys. J. 2003, 85, 1145–1164. [Google Scholar] [CrossRef]
- Maupetit, J.; Derreumaux, P.; Tuffery, P. PEP-FOLD: An Online Resource for de Novo Peptide Structure Prediction. Nucleic Acids Res. 2009, 37, W498–W503. [Google Scholar] [CrossRef]
- Kryshtafovych, A.; Monastyrskyy, B.; Fidelis, K.; Moult, J.; Schwede, T.; Tramontano, A. Evaluation of the Template-based Modeling in CASP12. Proteins Struct. Funct. Bioinform. 2018, 86, 321–334. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.; Vecchi, M. Optimization by Simulated Annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Hansen, P.B. Simulated Annealing. In Electrical Engineering and Computer Science Technical Reports; Syracuse University: Syracuse, NY, USA, 1992; Volume 170. [Google Scholar]
- Alatas, B. ACROA: Artificial Chemical Reaction Optimization Algorithm for Global Optimization. Expert Syst. Appl. 2011, 38, 13170–13180. [Google Scholar] [CrossRef]
- Sanvicente-Sánchez, H.; Frausto-Solís, J. A Method to Establish the Cooling Scheme in Simulated Annealing Like Algorithms. In International Conference on Computational Science and Its Applications; Springer: Berlin/Heidelberg, Germany, 2004; pp. 755–763. [Google Scholar]
- Ponder, J.W.; Case, D.A. Force Fields for Protein Simulations. Adv. Protein Chem. 2003, 66, 27–85. [Google Scholar] [PubMed]
- Brooks, B.R.; Bruccoleri, R.E.; Olafson, B.D.; States, D.J.; Swaminathan, S.; Karplus, M. CHARMM: A Program for Macromolecular Energy, Minimization, and Dynamics Calculations. J. Comput. Chem. 1983, 4, 187–217. [Google Scholar] [CrossRef]
- Eisenmenger, F.; Hansmann, U.H.E.; Hayryan, S.; Hu, C.K. [SMMP] A Modern Package for Simulation of Proteins. Comput. Phys. Commun. 2001, 138, 192–212. [Google Scholar] [CrossRef]
- Meinke, J.H.; Mohanty, S.; Eisenmenger, F.; Hansmann, U.H.E. SMMP v. 3.0-Simulating Proteins and Protein Interactions in Python and Fortran. Comput. Phys. Commun. 2008, 178, 459–470. [Google Scholar] [CrossRef]
- Pronzato, L. A Generalized Golden-section Algorithm for Line Search. IMA J. Math. Control Inf. 1998, 15, 185–214. [Google Scholar] [CrossRef]
- Frausto-Solis, J.; Martinez-Rios, F. Golden Annealing Method for Job Shop Scheduling Problem. In Proceedings of the 10th WSEAS International Conference on Mathematical and Computational Methods in Science and Engineering, Bucharest, Romania, 7–9 November 2008; World Scientific and Engineering Academy and Society (WSEAS): Stevens Point, WI, USA, 2008; pp. 374–379. [Google Scholar]
- Frausto-Solis, J.; Martinez-Rios, F. Golden Ratio Annealing for Satisfiability Problems Using Dynamically Cooling Schemes. In International Symposium on Methodologies for Intelligent Systems; Springer: Berlin/Heidelberg, Germany, 2008; pp. 215–224. [Google Scholar]
- Duek, G.; Scheuer, T. Threshold Accepting: A general Purpose Optimization Algorithm Appearing Superior to Simulated Annealing. J. Comput. Phys. 1990, 90, 161–175. [Google Scholar] [CrossRef]
- Zhan, L.; Chen, J.Z.Y.; Liu, W.K. Conformational Study of Met-Enkephalin Based on the ECEPP Force Fields. Biophys. J. 2006, 91, 2399–2404. [Google Scholar] [CrossRef]
- Zhang, Y.; Skolnick, J. Scoring Function for Automated Assessment of Protein Structure Template Quality. Proteins Struct. Funct. Bioinform. 2004, 57, 702–710. [Google Scholar] [CrossRef]
- Xu, J.; Zhang, Y. How Significant is a Protein Structure Similarity with TM-score = 0.5? Bioinformatics 2010, 26, 889–895. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Skolnick, J. TM-align: A Protein Structure Alignment Algorithm Based on the TM-score. Nucleic Acids Res. 2005, 33, 2302–2309. [Google Scholar] [CrossRef] [PubMed]
- Wolpert, D.H.; Macready, W.G. No Free Lunch Theorems for Optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef]
- Papadimitriou, C.H. Computational Complexity; Addison Wesley Longman: Boston, MA, USA, 1994; ISBN 0-201-53082-1. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).