1. Introduction
One of the most famous formulas in mathematics, Euler’s identity,
contains the transcendental numbers
e and
, the imaginary number
i, the constants 0 and 1, and (transcendental) operations. Beautiful, powerful, and surprising, it has influenced many areas of mathematics and theoretical physics.
Euler’s formula states (for
Euler’s formula becomes Euler’s identity):
Another interesting relation appeared in [
1]:
It can also be expressed as:
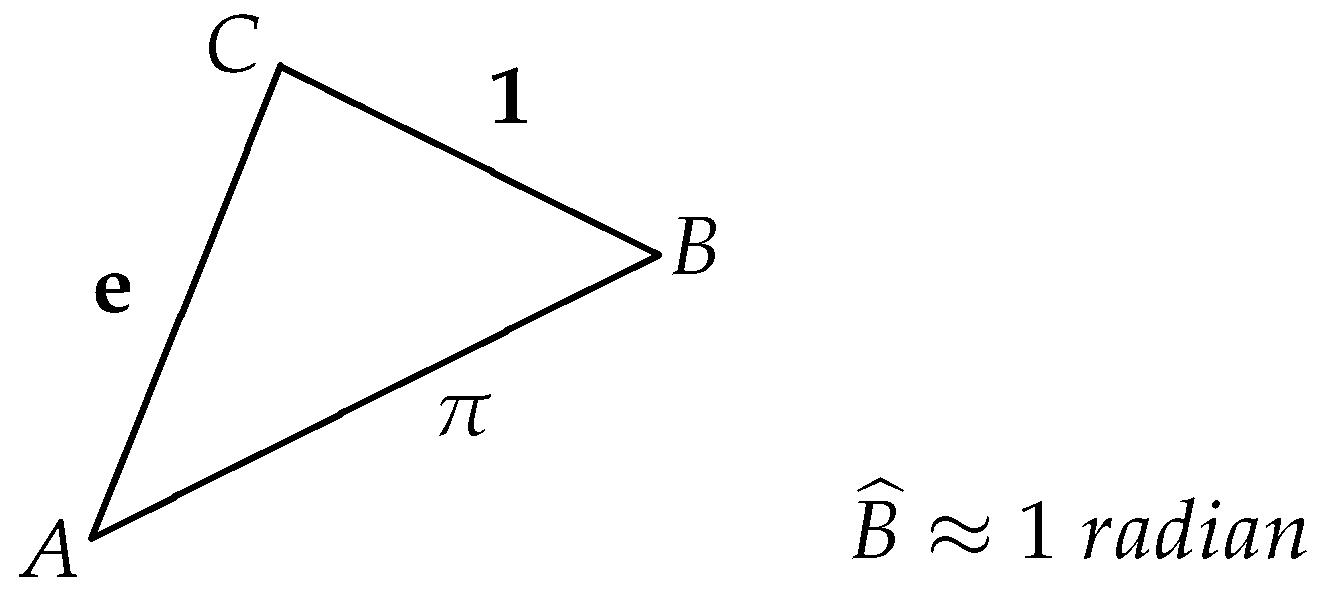
, and it has a geometrical interpretation (see
Figure 1).
Equations (
1) and (
3) can be unified, and we will explain how in
Section 3.
The next section is a survey on transcendental numbers, transcendental functions, transcendental operations, and transcendence (following the ideas from [
2,
3]).
Section 3 deals with identities and inequalities of transcendental numbers. We prove Equation (
3). We also present some open problems.
Section 4 contains two important constructions: solutions to the Yang–Baxter equation both from hyperbolic functions and from material implication. The last section provides conclusions.
2. Transcendence and Transcendental Numbers in Mathematics
The term “transcendence” has been introduced to express issues related to divinity. Implying initially the aforementioned attributes, its use has been used widely in movies, novels, jazz albums, corporations, game brands, poems, internet websites, internet blogs, names of all kinds of doctrines, philosophies, etc. The “trans” prefix comes from Latin, implying a passing through a certain area, and it appears in many (common) words: transport, transparent, translation, transmission, transformation, transplant, transgress, transdisciplinarity, etc.
In the 18th century, Leonhard Euler initiated a discussion about
transcendence in mathematics (see [
4]). Leibniz was the first to refer to transcendence in mathematics (see [
5]). Euler does not refer directly to transcendental numbers (as it happened, subsequently, in the 19th century), but he refers to
transcendental operations. The non-transcendental operations are addition, subtraction, multiplication, division, exponentiation, and rooting (applied to integers and to those numbers that are obtained from them by such operations). These operations are considered to be non-transcendent. They are algebraic operations because all numbers generated in this way are roots of some algebraic equations; we refer to those equations expressed by polynomial structures, where all mentioned operations are applied for a finite number of times (focus on finite) and, as soon as this is not the case, we enter in the field of transcendence. Therefore, in mathematics,
the idea of transcendence is essentially related to the idea of infinity—but not to just any kind of infinity. For Euler, the entrance to mathematical transcendence is through the gate of the differential and integral calculus. Euler considers the exponentiation a to x, the logarithm, and the trigonometric sine/cosine functions as
transcendental functions and operations because they are associated, in one way or another, with the mathematical idea of integrals and with expressions that include an integral (for instance, the logarithm is associated with the integral of dx/x). For Euler, the function log(x) + 7 is transcendent, but log(7) + x is algebraic.
The passing from non-transcendent to transcendent is gradual. Such an assertion deviates us from mathematical rigor but consolidates our understanding. We have in mathematics the situation of irrational numbers, such as the square root of 2. The word “irrational” would suggest transcendence, but it is immediately completed by the word “algebraic,” the negation of “transcendent.” We may consider the algebraic irrationals (an algebraic number is a root of a polynomial equation with integer coefficients) as a passing bridge, or intermediary steps, when passing from non-transcendent to transcendent. It is not rigorous, but it is suggestive. We must add that we talk about rational numbers (such as 2/3 or ) and irrational numbers, and we are tempted to associate such irrational numbers as the square root of 2 with something beyond reason. However, the Latin etymology clarifies the fact that “rational” is seen here as a ratio or as a fraction, where, in a number of the form a/b, a and b are integers, and b is not zero.
Joseph Liouville is the first who managed to encounter an example of transcendental numbers. This important discovery happened in the year 1844. Liouville introduced a class of eponymously named real numbers. A real number x is a Liouville number if there is an integer b greater than or equal to 2 and an infinite sequence of integers (, , …, , …) so that x is the sum of the series that has, as a general term, a ratio between and the power of exponent k! of b. (For b = 10 and = 1 for any k, x becomes Liouville’s constant.) Concerning his numbers (see also Remark 5), Liouville proves that they are not algebraic; they are transcendental. It was the first example of non-algebraic real numbers. Another presentation of Liouville’s numbers consists in approximation by rational numbers: x is a Liouville number if, for any natural number n, there are integers p and q, where q is greater than or equal to 2, and the absolute value of the difference between x and p/q is strictly between zero and the fraction with 1 as the numerator and the value of q to the power of n as the denominator. It is thus clear that Liouville’s numbers have tight approximations by rational numbers. The number e also has tight approximations by rational numbers (see Remark 2). These facts were not expected because they suggest that, in some respects, transcendental numbers are nearer to rational numbers than algebraic irrationals.
The manner in which rational numbers can approach transcendent numbers urges us to see the transcendence process in the infinite range of approximations of transcendental numbers. This situation suggests us to generally regard transcendence as a result of an asymptotic process when all stages are in the terrestrial universe, but the infinite number of stages precludes their being crossed in real time. Such a view increases the likelihood that a sharp border between transcendent and terrestrial is absent.
There are other philosophical enigmas related to mathematical transcendence. One would expect that transcendental numbers, such as or e, would be farther from rational numbers than irrational algebraic numbers. However, in terms of approximation by rational numbers, it seems that this does not happen. It must also be noted that transcendental numbers are greater than algebraic numbers, but “greater” here is a metaphoric extension of such qualification, from finite to infinite. Mathematicians express this by the following statement: “The algebraic numbers form a countable set, while the transcendental numbers form an uncountable set; it is a set of the power of the continuum.”
3. Transcendental Numbers: Identities, Inequalities and Open Problems
The following identities that contain the transcendental numbers
and
are well-known:
These formulas, unified in [
6], can be proved by contour integration.
Other inequalities for
and
(from [
1]) are quite new; here, we list three:
We now prove the last formula, Inequality (
3).
is equivalent to . Now, we use the estimations , , , and , . (This proof was slightly improved by Dr. Cezar Joita.)
Remark 1. Let us consider the two variable complex functions . The formulas (1), (3) and (4) can be unified using the function : Remark 2. Related to Section 2, one could consider the equation which has real solutions for r that are sufficiently small, but the “limit” equation (for ) has no real solutions because The “limit” equation can be interpretated as an inequality:which will be generalized in the next section. The question if is a transcendental number is an open problem. Remark 3. Resembling the problem of squaring the circle, the geometrical interpretation of the formula can be stated as follows: “The perimeter of the circle with diameter π is almost equal (and less) to the perimeter of a square with edges of length e” (see Figure 2). In this case, the area of the circle is greater than the area of the square because . Remark 4. We now present open problems related to .
Let us consider an arbitrary convex closed curve (see, for example, Figure 2), and the center of mass of the body, which corresponds to the domain inside the given curve. The lines going through this center of mass intersect the given curve twice, and they are called diameters. The smallest diameter is represented by d, and the maximum diameter represented by D. - (i)
If L is the length of the given curve, then - (ii)
Moreover, the first inequality becomes equality if and only if the second inequality becomes equality if and only if the given curve is a circle.
- (iii)
If the area of the domain inside the given curve is A, then .
- (iv)
The equation is not completely solved; for example, if the given curve is an ellipse, this equation cannot be solved.
Remark 5. Solving the equation , in which two coefficients are Liouville numbers, by using the quadratic formula is hard; however, one can use the formula in order to solve this equation. The solution can be observed directly.
4. Transcendental Numbers in Mathematical Physics
In some special issues on Hopf algebras, quantum groups, and Yang–Baxter equations, several papers, as well as a feature paper, have covered many topics related to the Yang–Baxter equation, ranging from mathematical physics to Hopf algebras, from Azumaya Monads to quantum computing, and from mathematical logic to Rota–Baxter equations.
The terminology of this section is consistent with those papers.
V is a complex vector space, and are identity maps. We consider a linear map that satisfies and where .
Thus,
satisfies the colored Yang–Baxter equation:
Remark 6. The theory of integrable Hamiltonian systems makes great use of solutions of Equation (7), since coefficients of the power series expansion of such a solution give rise to commuting integrals of motion. For more applications of the mathematical physics of Equation (7), see [7]. There is a version of Equation (
2) for matrices:
and it can be used in order to simplify our proof that
is a solution of Equation (
7); therefore, that proof reduces to checking the equality
.
In dimension two,
J could have the following matrix form (for
):
Thus, we have a generalization of Equation (
1):
In a similar manner, we generalize Inequality (
5) for matrices below (we leave this general case without proof):
A generalization of Equation (
6), with
, was studied in [
8].
Replacing only the condition
with
, the authors of [
9,
10] obtained interesting results (a new realization of doubling degeneracy based on an emergent Majorana operator, new solutions for the Yang–Baxter equation, etc).
With these cases, we enter into the world of quaternions and Clifford algebras.
We present two new theorems below. The first one can be interpreted as a version of Euler’s formula for hyperbolic functions.
Theorem 1. Solutions to the Yang–Baxter equation from hyperbolic functions:
Let be a linear map that satisfies and
Then, satisfies the colored Yang–Baxter equation (Equation (7)). Proof. The equality follows from properties of hyperbolic functions, and , and from and ☐
Remark 7. In dimension two, the matrix form of the above operator J could beThe corresponding matrix for in this case can be expressed as follows:Notice that . Therefore, this formula could be understood as a version of Equation (1) for hyperbolic functions. Theorem 2. Solutions to the Yang–Baxter equation from material implication:
For a Boolean algebra, the map is a solution for the constant Yang–Baxter equation: Proof. The equality implies , but . ☐
Remark 8. Only the self-distributive law from the definition of racks is used in the above proof.
Remark 9. The question if the above theorem holds in more general settings (such as Wajsberg–Algebras, MV–Algebras, and BCK/BCI–Algebras) has led to some interesting investigations (see [11]). 5. Conclusions
The current paper consists of three main parts: a heuristical–phylosophical introduction, a short essay outlining some questions about
and
e, and a section with deep results, where ideas from the previous section may be applied. Our main results are Theorems 1 and 2, the proof by hand of Equation (
3), and the unification of Equations (
1) and (
3). Several open problems are also presented (Remarks 2 and 4).
We used results and concepts from a number of different fields, including algebra, mathematical analysis, mathematical physics, geometry, history of mathematics, numerical analysis, epistemology, and philosophy. The high number of new disciplines behooves one to have a transdisciplinary understanding of the world: a transdisciplinary approach (see [
12,
13,
14,
15]) attempts to discover what is between disciplines, across different disciplines, and beyond all disciplines. Transcendence is a concept that plays an important role in theology, in science, and in art and can be considered beyond all disciplines. The Yang–Baxter equation appears across different disciplines, and mathematical physics is at the border of two disciplines.
The author of [
16] considers two types of scientists: birds, which resemble scientists with a broad vision, who try to unify theories and who obtain results of interest for a large readership, and frogs, which he considers less influential. Solomon Marcus used the terms of Francis Bacon (Novum Organum)— bees and ants—in this matter, and he also refers to spiders, which are scientists that build large networks of results.
We conclude with some historical facts. Euler was born in Basel (on 15 April 1707), and he received his Master of Philosophy from University of Basel. On 17 March 2016, Solomon Marcus passed away.