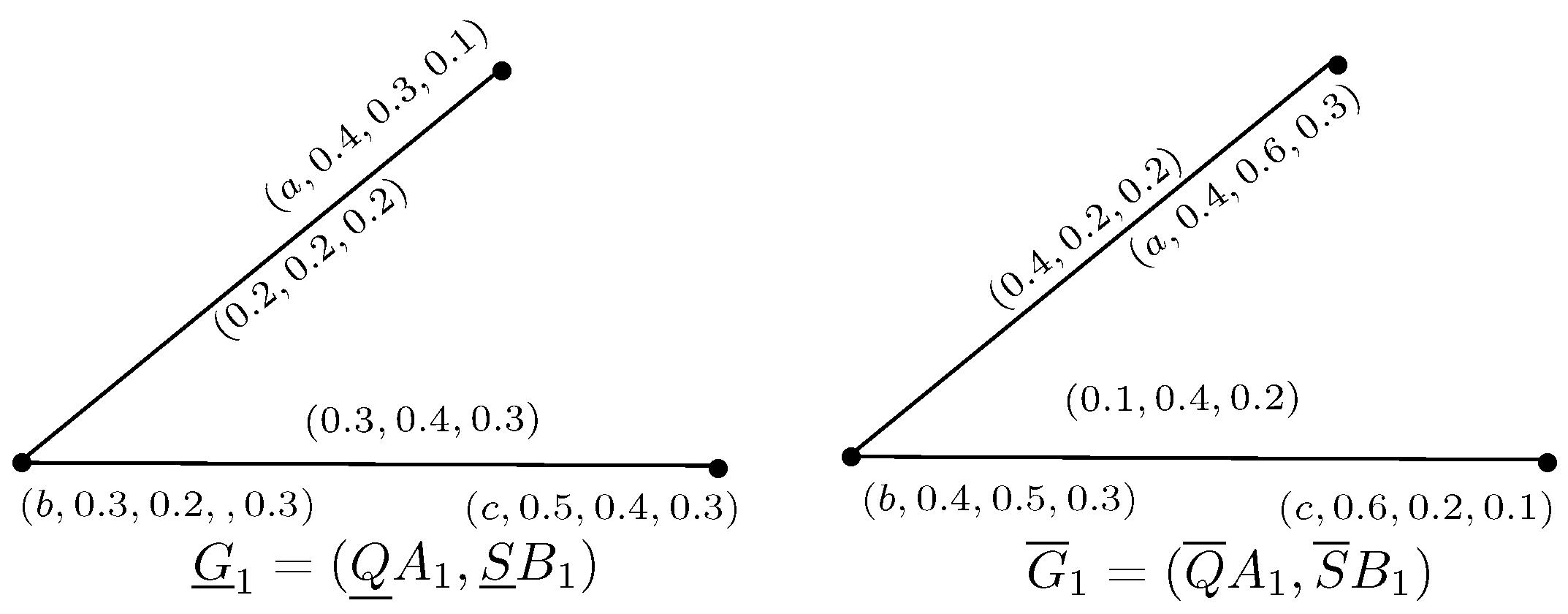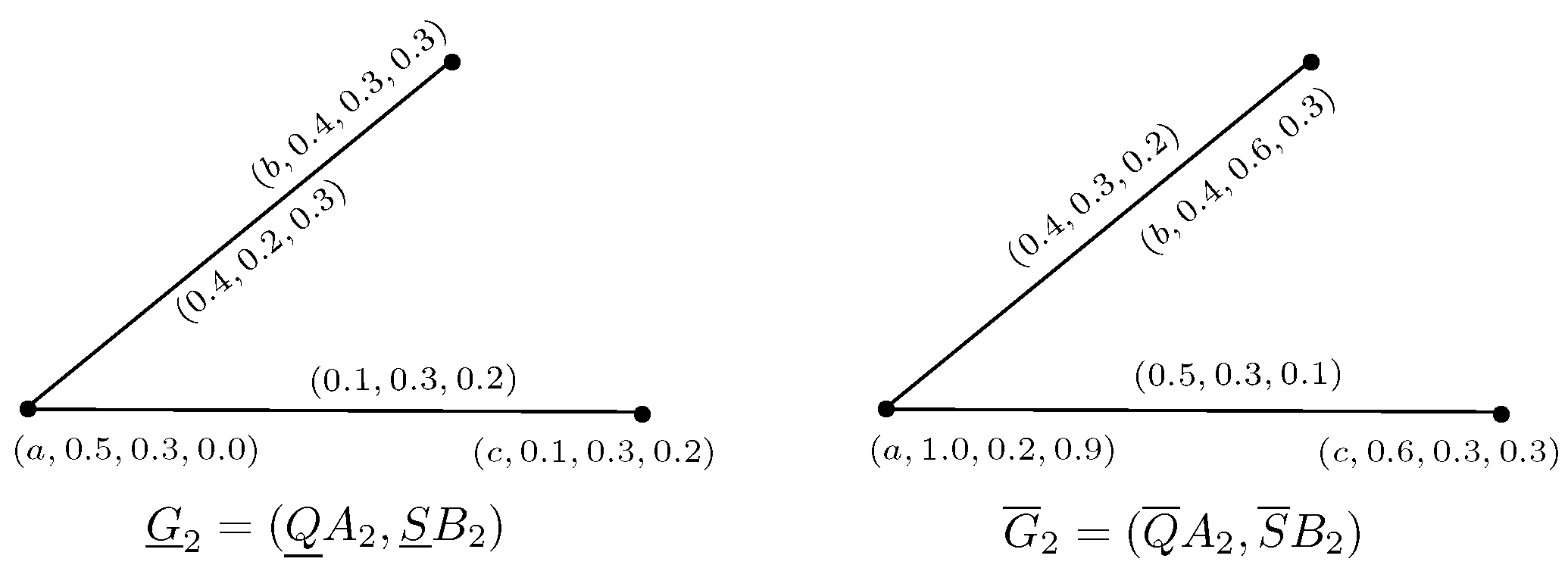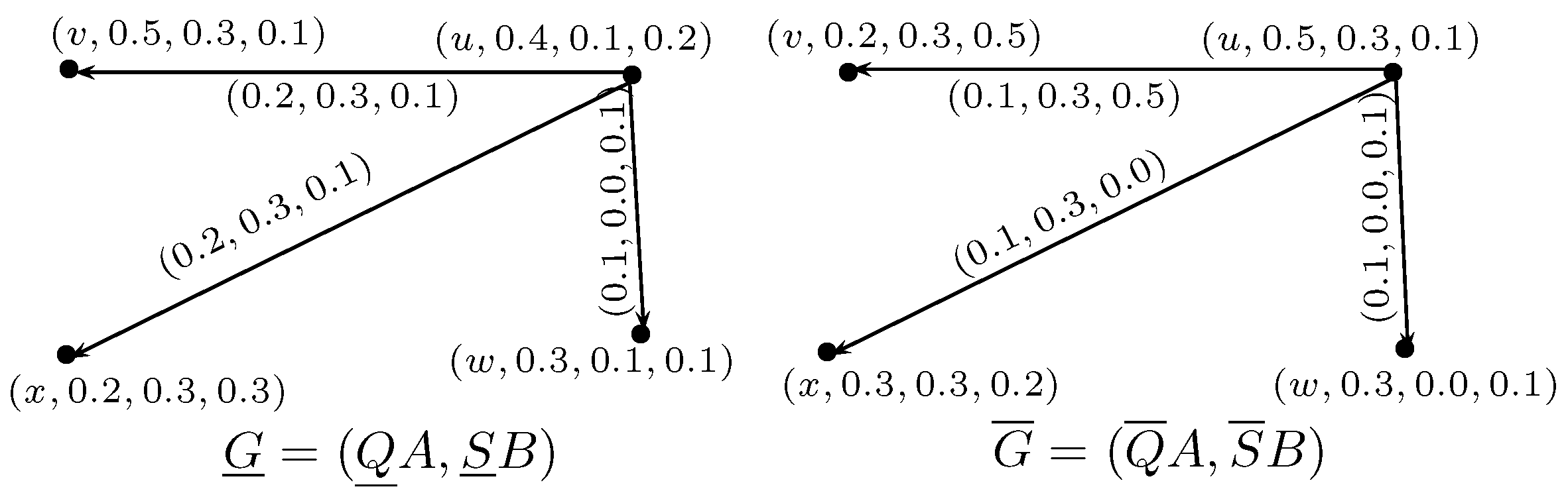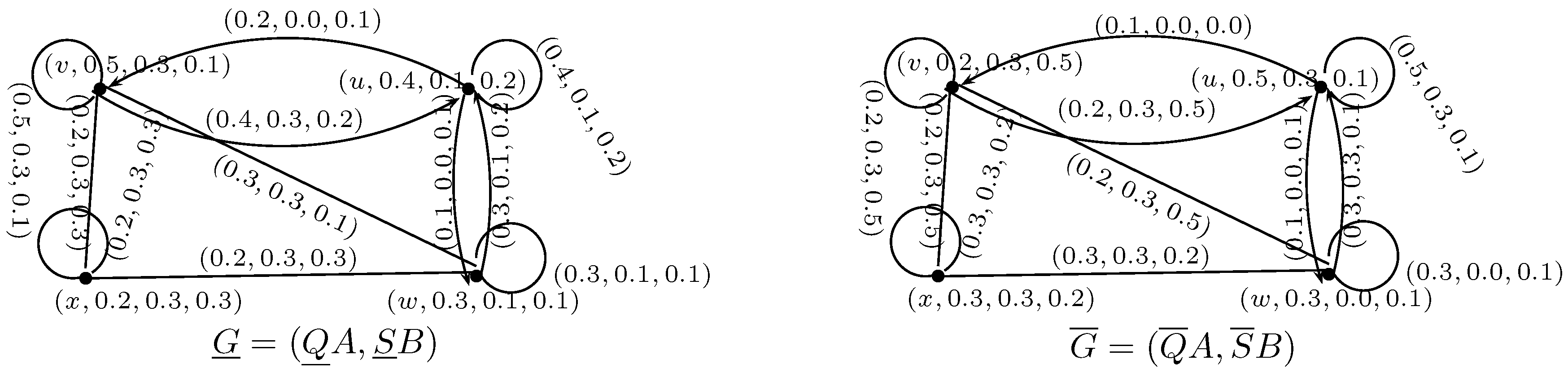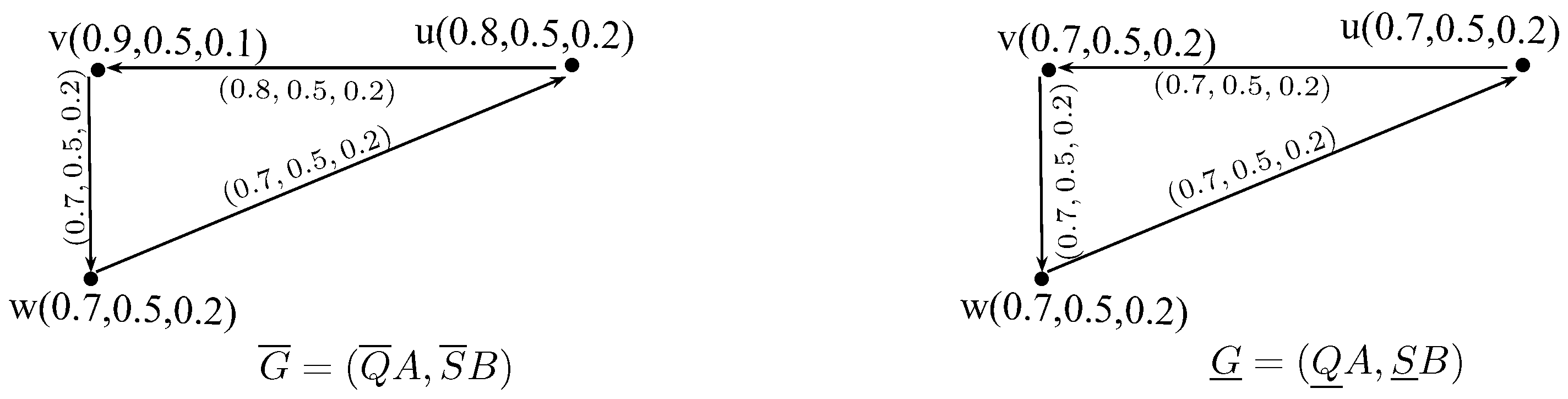Neutrosophic Soft Rough Graphs with Application

Abstract

Neutrosophic sets (NSs) handle uncertain information while fuzzy sets (FSs) and intuitionistic fuzzy sets (IFs) fail to handle indeterminate information. Soft set theory, neutrosophic set theory, and rough set theory are different mathematical models for handling uncertainties and they are mutually related. The neutrosophic soft rough set (NSRS) model is a hybrid model by combining neutrosophic soft sets with rough sets. We apply neutrosophic soft rough sets to graphs. In this research paper, we introduce the idea of neutrosophic soft rough graphs (NSRGs) and describe different methods of their construction. We consider the application of NSRG in decision-making problems. In particular, we develop efficient algorithms to solve decision-making problems.

1. Introduction

Smarandache [1] initiated the concept of neutrosophic set (NS). Smarandache’s NS is characterized by three parts: truth, indeterminacy, and falsity. Truth, indeterminacy and falsity membership values behave independently and deal with problems having uncertain, indeterminant and imprecise data. Wang et al. [2] gave a new concept of single valued neutrosophic sets (SVNSs) and defined the set theoretic operators on an instance of NS called SVNS. Peng et al. [3] discussed the operations of simplified neutrosophic numbers and introduced an outranking idea of simplified neutrosophic numbers.

Molodtsov [4] introduced the notion of soft set (SS) as a novel mathematical approach for handling uncertainties. Molodtsov’s SSs gave us a new technique for dealing with uncertainty from the viewpoint of parameters. Maji et al. [5,6,7] introduced neutrosophic soft sets (NSSs), intuitionistic fuzzy soft sets and fuzzy soft sets (FSSs). In [8], Sahin and Kucuk presented NSS in the form of neutrosophic relations.

Theory of rough set (RS) was proposed by Pawlak [9] in 1982. Rough set theory is used to study the intelligence systems containing incomplete, uncertain or inexact information. The lower and upper approximation operators of RSs are used for managing hidden information in a system. Feng et al. [10] took a significant step to introduce parametrization tools in RSs. Meng et al. [11] provide further discussion of the combination of SSs, RSs and FSs. The existing results of RSs and other extended RSs such as rough fuzzy sets, generalized rough fuzzy sets, soft fuzzy rough sets and intuitionistic fuzzy rough sets based decision-making models have their advantages and limitations [12,13]. In a different way, rough set approximations have been constructed into the intuitionistic fuzzy environment and are known as intuitionistic fuzzy rough sets and rough intuitionistic fuzzy sets [14,15]. Zhang et al. [16,17] presented the notions of soft rough sets, soft rough intuitionistic fuzzy sets, intuitionistic fuzzy soft rough sets, its application in decision-making, and also introduced generalized intuitionistic fuzzy soft rough sets. Broumi et al. [18,19] developed a hybrid structure by combining RSs and NSs, called RNSs, they also presented interval valued neutrosophic soft rough sets by combining interval valued neutrosophic soft sets and RSs. Yang et al. [20] proposed single valued neutrosophic rough sets (SVNRSs) by combining SVNSs and RSs and defined SVNRSs on two universes and established an algorithm for a decision-making problem based on SVNRSs on two universes. Akram and Nawaz [21] have introduced the concept of soft graphs and some operation on soft graphs. Certain concepts of fuzzy soft graphs and intuitionistic fuzzy soft graphs are discussed in [22,23,24]. Akram and Shahzadi [25] have introduced neutrosophic soft graphs. Zafar and Akram [26] introduced a rough fuzzy digraph and several basic notions concerning rough fuzzy digraphs. In this research paper, a neutrosophic soft rough set is a generalization of a neutrosophic rough set, and we introduce the idea of neutrosophic soft rough graphs (NSRGs) that are made by combining NSRSs with graphs and describe different methods of their construction. We consider the application of NSRG in decision-making problems and resolve the problem. In particular, we develop efficient algorithms to solve decision-making problems.

For other notations, terminologies and applications not mentioned in the paper, the readers are referred to [27,28,29,30,31,32,33,34,35].

2. Neutrosophic Soft Rough Information

In this section, we will introduce the notions of neutrosophic soft rough relation (NSRR), and NSRGs.

Definition 1.

Let Y be an initial universal set, $\mathbb{P}$ a universal set of parameters and $\mathbb{M}\subseteq \mathbb{P}$. For an arbitrary neutrosophic soft relation Q over $Y\times \mathbb{M}$, $(Y,\mathbb{M},Q)$ is called neutrosophic soft approximation space (NSAS).

For any NS $A\in \mathcal{N}(\mathbb{M}),$ we define the upper neutrosophic soft rough approximation (UNSRA) and the lower neutrosophic soft rough approximation (LNSRA) operators of A with respect to $(Y,\mathbb{M},Q)$ denoted by $\overline{Q}(A)$ and $\underline{Q}(A),$ respectively as follows:

$$\begin{array}{ccc}\hfill \overline{Q}(A)& =& \{(u,T_{\overline{Q}(A)}(u),I_{\overline{Q}(A)}(u),F_{\overline{Q}(A)}(u))|u\in Y\},\hfill \\ \hfill \underline{Q}(A)& =& \{(u,T_{\underline{Q}(A)}(u),I_{\underline{Q}(A)}(u),F_{\underline{Q}(A)}(u))|u\in Y\},\hfill \end{array}$$

where

$$\begin{array}{ccc}\hfill T_{\overline{Q}(A)}(u)& =& \underset{e\in \mathbb{M}}{\bigvee }\left(T_{Q(A)}(u,e)\wedge T_A(e)\right),I_{\overline{Q}(A)}(u)=\underset{e\in \mathbb{M}}{\bigwedge }\left(I_{Q(A)}(u,e)\vee I_A(e)\right),\hfill \\ \hfill F_{\overline{Q}(A)}(u)& =& \underset{e\in \mathbb{M}}{\bigwedge }\left(F_{Q(A)}(u,e)\vee F_A(e)\right);T_{\underline{Q}(A)}(u)=\underset{e\in \mathbb{M}}{\bigwedge }\left(F_{Q(A)}(u,e)\vee T_A(e)\right),\hfill \\ \hfill I_{\underline{Q}(A)}(u)& =& \underset{e\in \mathbb{M}}{\bigvee }\left((1-I_{Q(A)}(u,e))\wedge I_A(e)\right),F_{\underline{Q}(A)}(u)=\underset{e\in \mathbb{M}}{\bigvee }\left(T_{Q(A)}(u,e)\wedge F_A(e)\right).\hfill \end{array}$$

The pair $(\underline{Q}(A),\overline{Q}(A))$ is called NSRS of A w.r.t $(Y,\mathbb{M},Q),\underline{Q}$ and $\overline{Q}$ are referred to as the LNSRA and the UNSRA operators, respectively.

Example 1.

Suppose that $Y=\{w_1,w_2,w_3,w_4\}$ is the set of careers under consideration, and Mr. X wants to select the best suitable career. $\mathbb{M}=\{e_1,e_2,e_3\}$ is a set of decision parameters. Mr. X describes the “most suitable career" by defining a neutrosophic soft set $(Q,\mathbb{M})$ on Y that is a neutrosophic relation from Y to $\mathbb{M}$ as shown in

Table 1. Neutrosophic soft relation Q.

Q	${\mathit{w}}_{\mathbf{1}}$	${\mathit{w}}_{\mathbf{2}}$	${\mathit{w}}_{\mathbf{3}}$	${\mathit{w}}_{\mathbf{4}}$
$e_1$	$(0.3,0.4,0.5)$	$(0.4,0.2,0.3)$	$(0.1,0.5,0.4)$	$(0.2,0.3,0.4)$
$e_2$	$(0.1,0.5,0.4)$	$(0.3,0.4,0.6)$	$(0.4,0.4,0.3)$	$(0.5,0.3,0.8)$
$e_3$	$(0.3,0.4,0.4)$	$(0.4,0.6,0.7)$	$(0.3,0.5,0.4)$	$(0.5,0.4,0.6)$

.

Now, Mr. X gives the most favorable decision object A, which is an NS on $\mathbb{M}$ defined as follows: $A=\{(e_1,0.5,0.2,0.4),(e_2,0.2,0.3,0.1),(e_3,0.2,0.4,0.6)\}$. By Definition 1, we have

$$T_{\overline{Q}(A)}(w_1)=0.3,I_{\overline{Q}(A)}(w_1)=0.4,F_{\overline{Q}(A)}(w_1)=0.4,$$

$$T_{\overline{Q}(A)}(w_2)=0.4,I_{\overline{Q}(A)}(w_2)=0.2,F_{\overline{Q}(A)}(w_2)=0.4,$$

$$T_{\overline{Q}(A)}(w_3)=0.2,I_{\overline{Q}(A)}(w_3)=0.4,F_{\overline{Q}(A)}(w_3)=0.3,$$

$$T_{\overline{Q}(A)}(w_4)=0.2,I_{\overline{Q}(A)}(w_4)=0.3,F_{\overline{Q}(A)}(w_4)=0.4.$$

Similarly,

$$T_{\underline{Q}(A)}(w_1)=0.4,I_{\underline{Q}(A)}(w_1)=0.4,F_{\underline{Q}(A)}(w_1)=0.3,$$

$$T_{\underline{Q}(A)}(w_2)=0.5,I_{\underline{Q}(A)}(w_2)=0.4,F_{\underline{Q}(A)}(w_2)=0.4,$$

$$T_{\underline{Q}(A)}(w_3)=0.4,I_{\underline{Q}(A)}(w_3)=0.4,F_{\underline{Q}(A)}(w_3)=0.3,$$

$$T_{\underline{Q}(A)}(w_4)=0.5,I_{\underline{Q}(A)}(w_4)=0.4,F_{\underline{Q}(A)}(w_4)=0.5.$$

Thus, we obtain

$$\begin{array}{ccc}\hfill \overline{Q}(A)& =& \{(w_1,0.3,0.4,0.4),(w_2,0.4,0.2,0.4),(w_3,0.2,0.4,0.3),(w_4,0.2,0.3,0.4)\},\hfill \\ \hfill \underline{Q}(A)& =& \{(w_1,0.4,0.4,0.3),(w_2,0.5,0.4,0.4),(w_3,0.4,0.4,0.3),(w_4,0.5,0.4,0.5)\}.\hfill \end{array}$$

Hence, $(\underline{Q}(A),\overline{Q}(A))$ is an NSRS of A.

The conventional neutrosophic soft set is a mapping from a parameter to the neutrosophic subset of the universe and letting $(Q,\mathbb{M})$ be neutrosophic soft set. Now, we present the constructive definition of neutrosophic soft rough relation by using a neutrosphic soft relation S from $\mathbb{M}\times \mathbb{M}=\acute{\mathbb{M}}$ to $\mathcal{N}(Y\times Y=\acute{Y})$, where Y is a universal set and $\mathbb{M}$ be a set of parameters.

Definition 2.

A neutrosophic soft rough relation $(\underline{S}(B),\overline{S}(B))$ on Y is an NSRS, $S:\acute{\mathbb{M}}\to \mathcal{N}(\acute{Y})$ is a neutrosophic soft relation on Y defined by

$$\begin{array}{ccc}\hfill S(e_i{e}_j)& =& \{u_i{u}_j|\exists u_i\in Q(e_i),u_j\in Q(e_j)\},u_i{u}_j\in \acute{Y},\mathit{such}\mathit{that}\hfill \\ \hfill T_S(u_i{u}_j,e_i{e}_j)& \le & min\{T_Q(u_i,e_i),T_Q(u_j,e_j)\}\hfill \\ \hfill I_S(u_i{u}_j,e_i{e}_j)& \le & max\{I_Q(u_i,e_i),I_Q(u_j,e_j)\}\hfill \\ \hfill F_S(u_i{u}_j,e_i{e}_j)& \le & max\{F_Q(u_i,e_i),F_Q(u_j,e_j)\}.\hfill \\ \hfill \mathit{For}\mathit{any}B\in \mathcal{N}(\acute{\mathbb{M}}),B& =& \{\left(e_i{e}_j,T_B(e_i{e}_j),I_B(e_i{e}_j),F_B(e_i{e}_j)\right)u_i{u}_j\in \acute{\mathbb{M}}\},\hfill \\ \hfill T_B(e_i{e}_j)& \le & min\{T_A(e_i),T_A(e_j)\},\hfill \\ \hfill I_B(e_i{e}_j)& \le & max\{I_A(e_i),I_A(e_j)\},\hfill \\ \hfill F_B(e_i{e}_j)& \le & max\{F_A(e_i),F_A(e_j)\}.\hfill \end{array}$$

The UNSA and the LNSA of B w.r.t $(\acute{Y},\acute{\mathbb{M}},S)$ are defined as follows:

$$\overline{S}(B)=\{(u_i{u}_j,T_{\overline{S}(B)}(u_i{u}_j),I_{\overline{S}(B)}(u_i{u}_j),F_{\overline{S}(B)}(u_i{u}_j))|u_i{u}_j\in \acute{Y}\},$$

$$\underline{S}(B)=\{(u_i{u}_j,T_{\underline{S}(B)}(u_i{u}_j),I_{\underline{S}(B)}(u_i{u}_j),F_{\underline{S}(B)}(u_i{u}_j))|u_i{u}_j\in \acute{Y}\},$$

where

$$\begin{array}{ccc}\hfill T_{\overline{S}(B)}(u_i{u}_j)& =& \underset{e_i{e}_j\in \acute{\mathbb{M}}}{\bigvee }\left(T_S(u_i{u}_j,e_i{e}_j)\wedge T_B(e_i{e}_j)\right),\hfill \\ \hfill I_{\overline{S}(B)}(u_i{u}_j)& =& \underset{e_i{e}_j\in \tilde{\mathbb{M}}}{\bigwedge }\left(I_S(u_i{u}_j,e_i{e}_j)\vee I_B(e_i{e}_j)\right),\hfill \\ \hfill F_{\overline{S}(B)}(u_i{u}_j)& =& \underset{e_i{e}_j\in \tilde{\mathbb{M}}}{\bigwedge }\left(F_S(u_i{u}_j,e_i{e}_j)\vee F_B(e_i{e}_j)\right);\hfill \end{array}$$

$$\begin{array}{ccc}\hfill T_{\underline{S}(B)}(u_i{u}_j)& =& \underset{e_i{e}_j\in \acute{\mathbb{M}}}{\bigwedge }\left(F_S(u_i{u}_j,e_i{e}_j)\vee T_B(e_i{e}_j)\right),\hfill \\ \hfill I_{\underline{S}(B)}(u_i{u}_j)& =& \underset{e_i{e}_j\in \tilde{\mathbb{M}}}{\bigvee }\left((1-I_S(u_i{u}_j,e_i{e}_j))\wedge I_B(e_i{e}_j)\right),\hfill \\ \hfill F_{\underline{S}(B)}(u_i{u}_j)& =& \underset{e_i{e}_j\in \tilde{\mathbb{M}}}{\bigvee }\left(T_S(u_i{u}_j,e_i{e}_j)\wedge F_B(e_i{e}_j)\right).\hfill \end{array}$$

The pair $(\underline{S}(B),\overline{S}(B))$ is called NSRR and $\underline{S},\overline{S}:\mathcal{N}(\acute{\mathbb{M}})\to \mathcal{N}(\acute{Y})$ are called the LNSRA and the UNSRA operators, respectively.

Remark 1.

Consider an NS B on $\acute{\mathbb{M}}$ and an NS A on $\mathbb{M}$, according to the definition of NSRR, we get

$$\begin{array}{ccc}\hfill T_{\overline{S}(B)}(u_i{u}_j)& \le & min\{T_{\overline{S}(A)}(u_i),T_{\overline{S}(A)}(u_j)\},\hfill \\ \hfill I_{\overline{S}(B)}(u_i{u}_j)& \le & max\{I_{\overline{S}(A)}(u_i),I_{\overline{S}(A)}(u_j)\},\hfill \\ \hfill F_{\overline{S}(B)}(u_i{u}_j)& \le & max\{F_{\overline{S}(A)}(u_i).F_{\overline{S}(A)}(u_j)\}.\hfill \end{array}$$

Similarly, for LNSRA operator $\underline{S}(B)$,

$$\begin{array}{ccc}\hfill T_{\underline{S}(B)}(u_i{u}_j)& \le & min\{T_{\underline{S}(A)}(u_i),T_{\underline{S}(A)}(u_j)\},\hfill \\ \hfill I_{\underline{S}(B)}(u_i{u}_j)& \le & max\{I_{\underline{S}(A)}(u_i),I_{\underline{S}(A)}(u_j)\},\hfill \\ \hfill F_{\underline{S}(B)}(u_i{u}_j)& \le & max\{F_{\underline{S}(A)}(u_i).F_{\underline{S}(A)}(u_j)\}.\hfill \end{array}$$

Example 2.

Let $Y=\{u_1,u_2,u_3\}$ be a universal set and $\mathbb{M}=\{e_1,e_2,e_3\}$ a set of parameters. A neutrosophic soft set $(Q,\mathbb{M})$ on Y can be defined in tabular form in

Table 2. Neutrosophic soft set $(Q,\mathbb{M})$.

Q	${\mathit{u}}_{\mathbf{1}}$	${\mathit{u}}_{\mathbf{2}}$	${\mathit{u}}_{\mathbf{3}}$
$e_1$	$(0.4,0.5,0.6)$	$(0.7,0.3,0.2)$	$(0.6,0.3,0.4)$
$e_2$	$(0.5,0.3,0.6)$	$(0.3,0.4,0.3)$	$(0.7,0.2,0.3)$
$e_3$	$(0.7,0.2,0.3)$	$(0.6,0.5,0.4)$	$(0.7,0.2,0.4)$

as follows:

Let $E=\{u_1{u}_2,u_2{u}_3,u_2{u}_2,u_3{u}_2\}\subseteq \acute{Y}$ and $L=\{e_1{e}_3,e_2{e}_1,e_3{e}_2\}\subseteq \acute{\mathbb{M}}$.

Then, a soft relation S on E (from L to E) can be defined in

Table 3. Neutrosophic soft relation S.

S	${\mathit{u}}_{\mathbf{1}}{\mathit{u}}_{\mathbf{2}}$	${\mathit{u}}_{\mathbf{2}}{\mathit{u}}_{\mathbf{3}}$	${\mathit{u}}_{\mathbf{2}}{\mathit{u}}_{\mathbf{2}}$	${\mathit{u}}_{\mathbf{3}}{\mathit{u}}_{\mathbf{2}}$
$e_1{e}_3$	$(0.4,0.4,0.5)$	$(0.6,0.3,0.4)$	$(0.5,0.4,0.2)$	$(0.5,0.4,0.3)$
$e_2{e}_1$	$(0.3,0.3,0.4)$	$(0.3,0.2,0.3)$	$(0.2,0.3,0.3)$	$(0.7,0.2,0.2)$
$e_3{e}_2$	$(0.3,0.3,0.2)$	$(0.5,0.3,0.2)$	$(0.2,0.4,0.4)$	$(0.3,0.4,0.4)$

as follows:

Let $A=\{(e_1,0.2,0.4,0.6),(e_2,0.4,0.5,0.2),(e_3,0.1,0.2,0.4)\}$ be an NS on $\mathbb{M}$, then $\overline{S}(A)=\{(u_1,0.4,0.2,0.4),(u_2,0.3,0.4,0.3),(u_3,0.4,0.2,0.3)\},$ $\underline{S}(A)=\{(u_1,0.3,0.5,0.4),(u_2,0.2,0.5,0.6),(u_3,0.4,0.5,0.6)\}.$

Let $B=\{(e_1{e}_3,0.1,0.3,0.5),(e_2{e}_1,0.2,0.4,0.3),(e_3{e}_2,0.1,0.2,0.3)\}$ be an NS on $L,$ then $\overline{S}(B)=\{(u_1{u}_2,0.2,0.3,0.3),(u_2{u}_3,0.2,0.3,0.3),(u_2{u}_2,0.2,0.4,0.3),(u_3{u}_2,0.2,0.4,0.3)\},$ $\underline{S}(B)=\{(u_1{u}_2,0.2,0.4,0.4),(u_2{u}_3,0.2,0.4,0.5),(u_2{u}_2,0.3,0.4,0.5),(u_3{u}_2,0.2,0.4,0.5)\}.$

Hence, $S(B)=(\underline{S}(B),\overline{S}(B))$ is NSRR.

Definition 3.

A neutrosophic soft rough graph (NSRG) on a non-empty V is an 4-ordered tuple $(V,\mathbb{M},Q(A),S(B))$ such that

(i)

$\mathbb{M}$ is a set of parameters,

(ii)

Q is an arbitrary neutrosophic soft relation over $V\times \mathbb{M},$

(iii)

S is an arbitrary neutrosophic soft relation over $\acute{V}\times \acute{\mathbb{M}},$

(vi)

$Q(A)=(\underline{Q}A,\overline{Q}A)$ is an NSRS of A,

(v)

$S(B)=(\underline{S}B,\overline{S}B)$ is an NSRR on $\acute{V}\subset V\times V$,

(iv)

$G=(Q(A),S(B))$ is a neutrosophic soft rough graph, where $\underline{G}=(\underline{Q}A,\underline{S}B)$ and $\overline{G}=(\overline{Q}A,\overline{S}B)$ are lower neutrosophic approximate graph (LNAG) and upper neutrosophic approximate graph (UNAG), respectively of neutrosophic soft rough graph (NSRG) $G=(Q(A),S(B))$.

Example 3.

Let $V=\{v_1,v_2,v_3,v_4,v_5,v_6\}$ be a vertex set and $\mathbb{M}=\{e_1,e_2,e_3\}$ a set of parameters. A neutrosophic soft relation over $V\times \mathbb{M}$ can be defined in tabular form in

Table 4. Neutrosophic soft relation Q.

Q	${\mathit{v}}_{\mathbf{1}}$	${\mathit{v}}_{\mathbf{2}}$	${\mathit{v}}_{\mathbf{3}}$	${\mathit{v}}_{\mathbf{4}}$	${\mathit{v}}_{\mathbf{5}}$	${\mathit{v}}_{\mathbf{6}}$
$e_1$	$(0.4,0.5,0.6)$	$(0.7,0.3,0.5)$	$(0.6,0.2,0.3)$	$(0.4,0.4,0.2)$	$(0.5,0.5,0.6)$	$(0.4,0.5,0.6)$
$e_2$	$(0.5,0.4,0.2)$	$(0.6,0.4,0.5)$	$(0.7,0.3,0.4)$	$(0.5,0.3,0.2)$	$(0.4,0.5,0.4)$	$(0.6,0.5,0.4)$
$e_3$	$(0.5,0.4,0.1)$	$(0.6,0.3,0.2)$	$(0.5,0.4,0.3)$	$(0.6,0.2,0.3)$	$(0.5,0.4,0.4)$	$(0.7,0.3,0.5)$

as follows:

Let $A=\{(e_1,0.5,0.4,0.6),(e_2,0.7,0.4,0.5),(e_3,0.6,0.2,0.5)\}$ be an NS on $\mathbb{M}$, then

$$\begin{array}{ccc}\hfill \overline{S}(A)& =& \{(v_1,0.5,0.4,0.5),(v_2,0.6,0.3,0.5),(v_3,0.7,0.4,0.5),(v_4,0.6,0.2,0.5),(v_5,0.5,\hfill \\ \hfill & & 0.4,0.5),(v_6,0.6,0.3,0.5)\},\hfill \\ \hfill \underline{S}(A)& =& \{(v_1,0.6,0.4,0.5),(v_2,0.5,0.4,0.6),(v_3,0.5,0.4,0.6),(v_4,0.5,0.4,0.5),(v_5,0.6,\hfill \\ \hfill & & 0.4,0.5),(v_6,0.6,0.4,0.5)\}.\hfill \end{array}$$

Let $E=\{v_1{v}_1,v_1{v}_2,v_2{v}_1,v_2{v}_3,v_4{v}_5,v_3{v}_4,v_5{v}_2,v_5{v}_6\}\subseteq \acute{V}$ and $L=\{e_1{e}_3,e_2{e}_1,e_3{e}_2\}\subseteq \acute{\mathbb{M}}$.

Then, a neutrosophic soft relation S on E (from L to E) can be defined in

Table 5. Neutrosophic soft relation S.

S	${\mathit{v}}_{\mathbf{1}}{\mathit{v}}_{\mathbf{1}}$	${\mathit{v}}_{\mathbf{1}}{\mathit{v}}_{\mathbf{2}}$	${\mathit{v}}_{\mathbf{2}}{\mathit{v}}_{\mathbf{1}}$	${\mathit{v}}_{\mathbf{2}}{\mathit{v}}_{\mathbf{3}}$
$e_1{e}_2$	$(0.4,0.4,0.2)$	$(0.4,0.4,0.5)$	$(0.4,0.4,0.5)$	$(0.6,0.3,0.4)$
$e_2{e}_3$	$(0.5,0.4,0.1)$	$(0.4,0.3,0.2)$	$(0.4,0.3,0.2)$	$(0.5,0.3,0.2)$
$e_1{e}_3$	$(0.4,0.4,0.1)$	$(0.4,0.2,0.2)$	$(0.4,0.2,0.2)$	$(0.5,0.3,0.3)$

and

Table 6. Neutrosophic soft relation S.

S	${\mathit{v}}_{\mathbf{3}}{\mathit{v}}_{\mathbf{4}}$	${\mathit{v}}_{\mathbf{4}}{\mathit{v}}_{\mathbf{5}}$	${\mathit{v}}_{\mathbf{5}}{\mathit{v}}_{\mathbf{2}}$	${\mathit{v}}_{\mathbf{5}}{\mathit{v}}_{\mathbf{6}}$
$e_1{e}_2$	$(0.4,0.2,0.2)$	$(0.4,0.4,0.2)$	$(0.4,0.3,0.4)$	$(0.3,0.2,0.3)$
$e_2{e}_3$	$(0.6,0.2,0.4)$	$(0.3,0.2,0.1)$	$(0.4,0.3,0.2)$	$(0.4,0.3,0.4)$
$e_1{e}_3$	$(0.4,0.2,0.3)$	$(0.4,0.3,0.1)$	$(0.5,0.3,0.2)$	$(0.5,0.3,0.5)$

as follows:

$$\begin{array}{ccc}\hfill \mathit{Let}B& =& \{(e_1{e}_2,0.4,0.4,0.5;),(e_2{e}_3,0.5,0.4,0.5),(e_1{e}_3,0.5,0.2,0.5)\}\mathit{be}\mathit{an}\mathit{NS}\mathit{on}L,\mathit{then}\hfill \\ \hfill \overline{S}B& =& \{(v_1{v}_1,0.5,0.4,0.5),(v_1{v}_2,0.4,0.2,0.5),(v_2{v}_1,0.4,0.2,0.5),(v_2{v}_3,0.5,0.3,0.5),\hfill \\ \hfill & & (v_3{v}_4,0.5,0.2,0.5),(v_4{v}_5,0.4,0.3,0.5),(v_5{v}_2,0.5,0.3,0.5),(v_5{v}_6,0.5,0.3,0.5)\},\hfill \\ \hfill \underline{S}B& =& \{(v_1{v}_1,0.4,0.4,0.5)(v_1{v}_2,0.5,0.4,0.4),(v_2{v}_1,0.5,0.4,0.4),(v_2{v}_3,0.4,0.4,0.5),\hfill \\ \hfill & & (v_3{v}_4,0.4,0.4,0.5),(v_4{v}_5,0.4,0.4,0.4),(v_5{v}_2,0.4,0.4,0.5),(v_5{v}_6,0.4,0.4,0.5)\}.\hfill \\ \hfill \mathit{Hence},S(B)& =& (\underline{S}B,\overline{S}B)\mathit{is}\mathit{NSRR}\mathit{on}\acute{V}.\hfill \end{array}$$

Thus, $\underline{G}=(\underline{Q}A,\underline{S}B)$ and $\overline{G}=(\overline{Q}A,\overline{S}B)$ are LNAG and UNAG, respectively, are shown in Figure 1.

Hence, $G=(\underline{G},\overline{G})$ is NSRG.

Definition 4.

Let $G=(V,\mathbb{M},Q,S)$ be a neutrosophic soft rough graph on a non-empty set V. The order of G can be denoted by $\mathbf{O}(G),$ defined by

$$\begin{array}{ccc}\hfill \mathbf{O}(G)& =& \mathbf{O}(\overline{G})+\mathbf{O}(\underline{G}),\mathit{where}\hfill \\ \hfill \mathbf{O}(\overline{G})& =& \sum _{v\in V}\overline{Q}A(v),\mathbf{O}(\underline{G})=\sum _{v\in V}\underline{Q}A(v).\hfill \end{array}$$

The size of neutrosophic soft rough graph G, denoted by $\mathbf{S}(G),$ defined by

$$\begin{array}{ccc}\hfill \mathbf{S}(G)& =& (\mathbf{S}\overline{G}+\mathbf{S}\underline{G}),\mathit{where}\hfill \\ \hfill \mathbf{S}(\overline{G})& =& \sum _{uv\in E}\overline{S}B(uv),\mathbf{S}(\underline{G})=\sum _{uv\in E}\underline{S}B(uv).\hfill \end{array}$$

Example 4.

Let G be a neutrosophic soft rough graph as shown in Figure 1. Then,

$$\begin{array}{ccc}\hfill \mathbf{O}(\overline{G})& =& (3.5,2.0,3.0),\mathbf{O}(\underline{G})=(3.3,2.4,3.2),\hfill \\ \hfill \mathbf{O}(G)& =& \mathbf{O}(\overline{G})+\mathbf{O}(\underline{G})=(6.8,4.4,6.2),\mathit{and}\hfill \\ \hfill \mathbf{S}(\overline{G})& =& (3.2,1.8,3.0)\mathbf{S}(\underline{G})=(2.5,2.4,2.8)\hfill \\ \hfill \mathbf{S}(G)& =& \mathbf{S}(\overline{G})+\mathbf{S}(\underline{G})=(5.7,4.2,5.8).\hfill \end{array}$$

Definition 5.

Let $G_1=({\underline{G}}_1,{\overline{G}}_1)$ and $G_2=({\underline{G}}_2,{\overline{G}}_2)$ be two neutrosophic soft rough graphs on V. The union of $G_1$ and $G_2$ is a neutrosophic soft rough graph $G=G_1\cup G_2=({\underline{G}}_1\cup {\underline{G}}_2,{\overline{G}}_1\cup {\overline{G}}_2)$, where ${\underline{G}}_1\cup {\underline{G}}_2=(\underline{Q}{A}_1\cup \underline{Q}{A}_2,\underline{S}{B}_1\cup \underline{S}{B}_2)$ and ${\overline{G}}_1\cup {\overline{G}}_2=(\overline{Q}{A}_1\cup \overline{Q}{A}_2,\overline{S}{B}_1\cup \overline{S}{B}_2)$ are neutrosophic graphs, such that

(i) 

$\forall v\in Q{A}_1$ but $v\notin Q{A}_2.$

$$\begin{array}{cc}\hfill T_{\overline{Q}{A}_1\cup \overline{Q}{A}_2}(v)=& T_{\overline{Q}{A}_1}(v),T_{\underline{Q}{A}_1\cup \underline{Q}{A}_2}(v)=T_{\underline{Q}{A}_1}(v),\hfill \\ \hfill I_{\overline{Q}{A}_1\cup \overline{Q}{A}_2}(v)=& I_{\overline{Q}{A}_1}(v),I_{\underline{Q}{A}_1\cup \underline{Q}{A}_2}(v)=I_{\underline{Q}{A}_1}(v),\hfill \\ \hfill F_{\overline{Q}{A}_1\cup \overline{Q}{A}_2}(v)=& F_{\overline{Q}{A}_1}(v),F_{\underline{Q}{A}_1\cup \underline{Q}{A}_2}(v)=F_{\underline{Q}{A}_1}(v).\hfill \end{array}$$

(ii) 

$\forall v\notin Q{A}_1$ but $v\in Q{A}_2.$

$$\begin{array}{cc}\hfill T_{\overline{Q}{A}_1\cup \overline{Q}{A}_2}(v)=& T_{\overline{Q}{A}_2}(v),T_{\underline{Q}{A}_1\cup \underline{Q}{A}_2}(v)=T_{\underline{Q}{A}_2}(v),\hfill \\ \hfill I_{\overline{Q}{A}_1\cup \overline{Q}{A}_2}(v)=& I_{\overline{Q}{A}_2}(v),I_{\underline{Q}{A}_1\cup \underline{Q}{A}_2}(v)=I_{\underline{Q}{A}_2}(v),\hfill \\ \hfill F_{\overline{Q}{A}_1\cup \overline{Q}{A}_2}(v)=& F_{\overline{Q}{A}_2}(v),F_{\underline{Q}{A}_1\cup \underline{Q}{A}_2}(v)=F_{\underline{Q}{A}_2}(v).\hfill \end{array}$$

(iii) 

$\forall v\in Q{A}_1\cap \underline{Q}{A}_2$

$$\begin{array}{cc}\hfill T_{\overline{Q}{A}_1\cup \overline{Q}{A}_2}(v)=& max\{T_{\overline{Q}{A}_1}(v),T_{\overline{Q}{A}_2}(v)\},T_{\underline{Q}{A}_1\cup \underline{Q}{A}_2}(v)=max\{T_{\underline{Q}{A}_1}(v),T_{\underline{Q}{A}_2}(v)\},\hfill \\ \hfill I_{\overline{Q}{A}_1\cup \overline{Q}{A}_2}(v)=& min\{I_{\overline{Q}{A}_1}(v),I_{\overline{Q}{A}_2}(v)\},I_{\underline{Q}{A}_1\cup \underline{Q}{A}_2}(v)=min\{I_{\underline{Q}{A}_1}(v),I_{\underline{Q}{A}_2}(v)\},\hfill \\ \hfill F_{\overline{Q}{A}_1\cup \overline{Q}{A}_2}(v)=& min\{F_{\overline{Q}{A}_1}(v),F_{\overline{Q}{A}_2}(v)\},F_{\underline{Q}{A}_1\cup \underline{Q}{A}_2}(v)=min\{F_{\underline{Q}{A}_1}(v),F_{\underline{Q}{A}_2}(v)\}.\hfill \end{array}$$

(iv) 

$\forall vu\in S{B}_1$ but $vu\notin S{B}_2.$

$$\begin{array}{cc}\hfill T_{\overline{S}{B}_1\cup \overline{S}{B}_2}(vu)=& T_{\overline{S}{B}_1}(vu),T_{\underline{S}{B}_1\cup \underline{S}{B}_2}(vu)=T_{\underline{S}{B}_1}(vu),\hfill \\ \hfill I_{\overline{S}{B}_1\cup \overline{S}{B}_2}(vu)=& I_{\overline{S}{B}_1}(vu),I_{\underline{S}{B}_1\cup \underline{S}{B}_2}(vu)=I_{\underline{S}{B}_1}(vu),\hfill \\ \hfill F_{\overline{S}{B}_1\cup \overline{S}{B}_2}(vu)=& F_{\overline{S}{B}_1}(vu),F_{\underline{S}{B}_1\cup \underline{S}{B}_2}(vu)=F_{\underline{S}{B}_1}(vu).\hfill \end{array}$$

(v) 

$\forall vu\notin S{B}_1$ but $vu\in S{B}_2$

$$\begin{array}{cc}\hfill T_{\overline{S}{B}_1\cup \overline{S}{B}_2}(vu)=& T_{\overline{S}{B}_2}(vu),T_{\underline{S}{B}_1\cup \underline{S}{B}_2}(vu)=T_{\underline{S}{B}_2}(vu),\hfill \\ \hfill I_{\overline{S}{B}_1\cup \overline{S}{B}_2}(vu)=& I_{\overline{S}{B}_2}(vu),I_{\underline{S}{B}_1\cup \underline{S}{B}_2}(vu)=I_{\underline{S}{B}_2}(vu),\hfill \\ \hfill F_{\overline{S}{B}_1\cup \overline{S}{B}_2}(vu)=& F_{\overline{S}{B}_2}(vu),F_{\underline{S}{B}_1\cup \underline{S}{B}_2}(vu)=F_{\underline{S}{B}_2}(vu).\hfill \end{array}$$

(vi) 

$\forall vu\in S{B}_1\cap \underline{S}{B}_2$

$$\begin{array}{cc}\hfill T_{\overline{S}{B}_1\cup \overline{S}{B}_2}(vu)=& max\{T_{\overline{S}{B}_1}(vu),T_{\overline{S}{B}_2}(vu)\},T_{\underline{S}{B}_1\cup \underline{S}{B}_2}(vu)=max\{T_{\underline{S}}{B}_1(vu),T_{\underline{S}{B}_2}(vu)\},\hfill \\ \hfill I_{\overline{S}{B}_1\cup \overline{S}{B}_2}(vu)=& min\{I_{\overline{S}{B}_1}(vu),I_{\overline{S}{B}_2}(vu)\},I_{\underline{S}{B}_1\cup \underline{S}{B}_2}(vu)=min\{I_{\underline{S}{B}_1}(vu),I_{\underline{S}{B}_2}(vu)\},\hfill \\ \hfill F_{\overline{S}{B}_1\cup \overline{S}{B}_2}(vu)=& min\{F_{\overline{S}{B}_1}(vu),F_{\overline{S}{B}_2}(vu)\},F_{\underline{S}{B}_1\cup \underline{S}{B}_2}(vu)=min\{F_{\underline{S}{B}_1}(vu),F_{\underline{S}{B}_2}(vu)\}.\hfill \end{array}$$

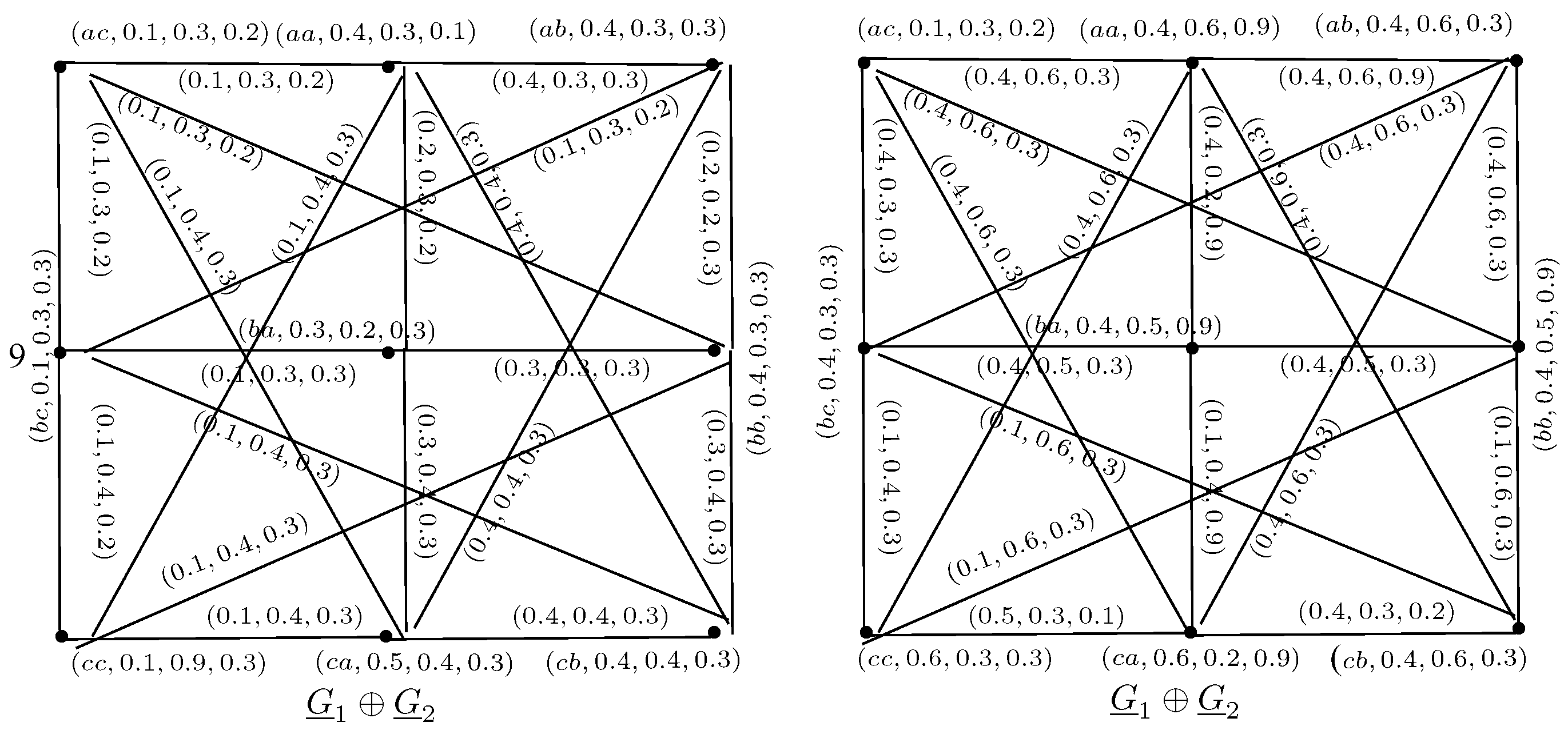
Example 5.

Let $V=\{v_1,v_2,v_3,v_4\}$ be a set of universes, and $\mathbb{M}=\{e_1,e_2,e_3\}$ a set of parameters. Then, a neutrosophic soft relation over $V\times \mathbb{M}$ can be written as in

Table 7. Neutrosophic soft relation Q.

Q	${\mathit{v}}_{\mathbf{1}}$	${\mathit{v}}_{\mathbf{2}}$	${\mathit{v}}_{\mathbf{3}}$	${\mathit{v}}_{\mathbf{4}}$
$e_1$	$(0.5,0.4,0.3)$	$(0.7,0.6,0.5)$	$(0.7,0.6,0.4)$	$(0.5,0.7,0.4)$
$e_2$	$(0.3,0.5,0.6)$	$(0.4,0.5,0.1)$	$(0.3,0.6,0.5)$	$(0.4,0.8,0.2)$
$e_3$	$(0.7,0.5,0.8)$	$(0.2,0.3,0.8)$	$(0.7,0.3,0.5)$	$(0.6,0.4,0.3)$

.

Let $A_1=\{(e_1,0.5,0.7,0.8),(e_2,0.7,0.5,0.3),(e_3,0.4,0.5,0.3)\},$ and $A_2=\{(e_1,0.6,0.3,0.5),(e_2,0.5,0.8,0.2),(e_3,0.5,0.7,0.2)\}$ are two neutrosophic sets on $\mathbb{M}$, Then, $Q(A_1)=(\underline{Q}(A_1),\overline{Q}(A_1))$ and $Q(A_2)=(\underline{Q}(A_2),\overline{Q}(A_2))$ are NSRSs, where

$$\begin{array}{ccc}\hfill \underline{Q}(A_1)& =& \{(v_1,0.5,0.6,0.5),(v_2,0.5,0.5,0.7)(v_3,0.5,0.5,0.7),(v_{4}0.4,0.5,0.5)\},\hfill \\ \hfill \overline{Q}(A_1)& =& \{(v_1,0.5,0.5,0.6),(v_2,0.5,0.5,0.3),(v_3,0.5,0.5,0.5),(v_{4}0.5,0.5,0.3)\},\hfill \\ \hfill \underline{Q}(A_2)& =& \{(v_1,0.6,0.5,0.5),(v_2,0.5,0.7,0.5),(v_3,0.5,0.7,0.5),(v_4,0.5,0.6,0.5)\},\hfill \\ \hfill \overline{Q}(A_2)& =& \{(v_1,0.5,0.4,0.5),(v_2,0.6,0.6,0.2),(v_3,0.6,0.6,0.5),(v_4,0.5,0.7,0.2)\}.\hfill \end{array}$$

Let $E=\{v_1{v}_2,v_1{v}_4,v_2{v}_2,v_2{v}_3,v_3{v}_3,v_3{v}_4\}\subseteq V\times V$, and $L=\{e_1{e}_2,e_1{e}_3,e_2{e}_3\}\subset \acute{\mathbb{M}}$. Then, a neutrosophic soft relation on E can be written as in

Table 8. Neutrosophic soft relation S.

S	${\mathit{v}}_{\mathbf{1}}{\mathit{v}}_{\mathbf{2}}$	${\mathit{v}}_{\mathbf{1}}{\mathit{v}}_{\mathbf{4}}$	${\mathit{v}}_{\mathbf{2}}{\mathit{v}}_{\mathbf{2}}$	${\mathit{v}}_{\mathbf{2}}{\mathit{v}}_{\mathbf{3}}$	${\mathit{v}}_{\mathbf{3}}{\mathit{v}}_{\mathbf{3}}$	${\mathit{v}}_{\mathbf{3}}{\mathit{v}}_{\mathbf{4}}$
$e_1{e}_2$	(0.3, 0.4 ,0.1)	$(0.4,0.4,0.2)$	$(0.4,0.5,0.1)$	$(0.3,0.5,0.4)$	$(0.3,0.4,0.4)$	$(0.4,0.5,0.2)$
$e_1{e}_3$	(0.2 ,0.3 ,0.3)	$(0.4,0.3,0.2)$	$(0.2,0.3,0.5)$	$(0.4,0.3,0.3)$	$(0.5,0.3,0.3)$	$(0.5,0.4,0.3)$
$e_2{e}_3$	(0.2,0.3,0.5)	$(0.3,0.3,0.3)$	$(0.2,0.3,0.1)$	$(0.4,0.3,0.1)$	$(0.3,0.3,0.5)$	$(0.3,0.4,0.3)$

.

Let $B_1=\{(e_1{e}_2,0.5,0.4,0.5),(e_1{e}_3,0.3,0.4,0.5),(e_2{e}_3,0.4,0.4,0.3)\},$ and $B_2=\{(e_1{e}_2,0.5,0.3,0.2),$ $(e_1{e}_3,0.4,0.3,0.3),(e_2{e}_3,0.4,0.6,0.2)\}$ are two neutrosophic sets on L, Then, $S(B_1)=(\underline{S}(B_1),\overline{S}(B_1))$ and $S(B_2)=(\underline{S}(B_2),\overline{S}(B_2))$ are NSRRs, where

$$\begin{array}{ccc}\hfill \underline{S}(B_1)& =& \{(v_1{v}_2,0.3,0.4,0.3),(v_1{v}_4,0.3,0.4,0.4),(v_2{v}_2,0.4,0.4,0.4),(v_2{v}_3,0.3,0.4,0.4),\hfill \\ \hfill & & (v_3{v}_3,0.3,0.4,0.5),(v_3{v}_4,0.3,0.4,0.5)\},\hfill \\ \hfill \overline{S}(B_1)& =& \{(v_1{v}_2,0.3,0.4,0.5),(v_1{v}_4,0.4,0.4,0.3),(v_2{v}_2,0.4,0.4,0.3),(v_2{v}_3,0.4,0.4,0.3),\hfill \\ \hfill & & (v_3{v}_3,0.3,0.4,0.5),(v_3{v}_4,0.4,0.4,0.3)\};\hfill \\ \hfill \underline{S}(B_2)& =& \{(v_1{v}_2,0.4,0.6,0.2),(v_1{v}_4,0.4,0.6,0.3),(v_2{v}_2,0.4,0.6,0.2),(v_2{v}_3,0.4,0.6,0.3),\hfill \\ \hfill & & (v_3{v}_3,0.4,0.6,0.3),(v_3{v}_4,0.4,0.6,0.3)\},\hfill \\ \hfill \overline{S}(B_2)& =& \{(v_1{v}_2,0.3,0.3,0.2),(v_1{v}_4,0.4,0.3,0.2),(v_2{v}_2,0.4,0.3,0.2),(v_2{v}_3,0.4,0.3,0.2),\hfill \\ \hfill & & (v_3{v}_3,0.4,0.3,0.3),(v_3{v}_4,0.4,0.4,0.2)\}.\hfill \end{array}$$

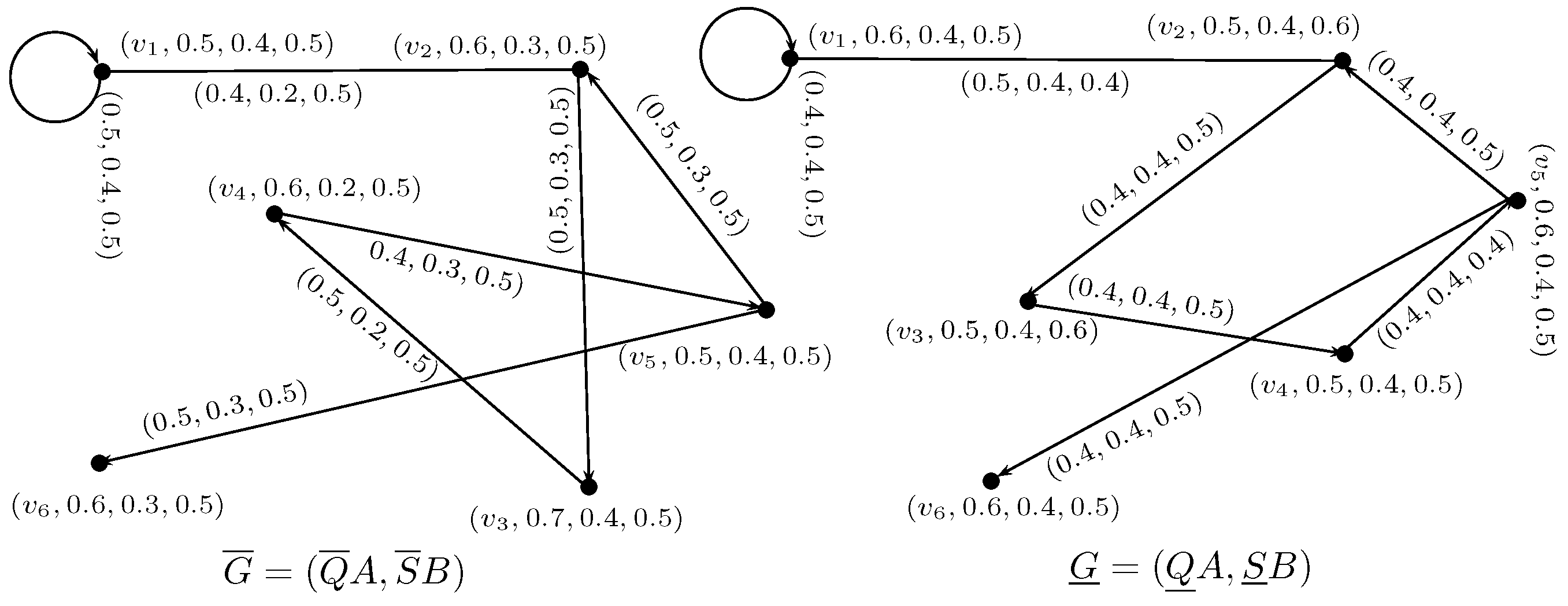
Thus, $G_1=({\underline{G}}_1,{\overline{G}}_1)$ and $G_2=({\underline{G}}_2,{\overline{G}}_2)$ are NSRGs, where ${\underline{G}}_1=(\underline{Q}(A_1),\underline{S}(B_1))$, ${\overline{G}}_1=(\overline{Q}(A_1),\overline{S}(B_1))$ as shown in Figure 2.

${\underline{G}}_2=(\underline{Q}(A_2),\underline{S}(B_2))$, ${\overline{G}}_2=(\overline{Q}(A_2),\overline{S}(B_2))$ as shown in Figure 3.

The union of $G_1=({\underline{G}}_1,{\overline{G}}_1)$ and $G_2=({\underline{G}}_2,{\overline{G}}_2)$ is NSRG $G=G_1\cup G_2=({\underline{G}}_1\cup {\underline{G}}_2,{\overline{G}}_1\cup {\overline{G}}_2)$ as shown in Figure 4.

Definition 6.

Let $G_1=({\underline{G}}_1,{\overline{G}}_1)$ and $G_2=({\underline{G}}_2,{\overline{G}}_2)$ be two NSRGs on V. The intersection of $G_1$ and $G_2$ is a neutrosophic soft rough graph $G=G_1\cap G_2=({\underline{G}}_1\cap {\underline{G}}_2,{\overline{G}}_1\cap {\overline{G}}_2)$, where ${\underline{G}}_1\cap {\underline{G}}_2=(\underline{Q}{A}_1\cap \underline{Q}{A}_2,\underline{S}{B}_1\cap \underline{S}{B}_2)$ and ${\overline{G}}_1\cap {\overline{G}}_2=(\overline{Q}{A}_1\cap \overline{Q}{A}_2,\overline{S}{B}_1\cap \overline{S}{B}_2)$ are neutrosophic graphs, respectively, such that

(i) 

$\forall v\in Q{A}_1$ but $v\notin Q{A}_2.$

$$\begin{array}{cc}\hfill T_{\overline{Q}{A}_1\cap \overline{Q}{A}_2}(v)=& T_{\overline{Q}{A}_1}(v),T_{\underline{Q}{A}_1\cap \underline{Q}{A}_2}(v)=T_{\underline{Q}{A}_1}(v),\hfill \\ \hfill I_{\overline{Q}{A}_1\cap \overline{Q}{A}_2}(v)=& I_{\overline{Q}{A}_1}(v),I_{\underline{Q}{A}_1\cap \underline{Q}{A}_2}(v)=I_{\underline{Q}{A}_1}(v),\hfill \\ \hfill F_{\overline{Q}{A}_1\cap \overline{Q}{A}_2}(v)=& F_{\overline{Q}{A}_1}(v),F_{\underline{Q}{A}_1\cap \underline{Q}{A}_2}(v)=F_{\underline{Q}{A}_1}(v).\hfill \end{array}$$

(ii) 

$\forall v\notin Q{A}_1$ but $v\in Q{A}_2.$

$$\begin{array}{cc}\hfill T_{\overline{Q}{A}_1\cap \overline{Q}{A}_2}(v)=& T_{\overline{Q}{A}_2}(v),T_{\underline{Q}{A}_1\cap \underline{Q}{A}_2}(v)=T_{\underline{Q}{A}_2}(v),\hfill \\ \hfill I_{\overline{Q}{A}_1\cap \overline{Q}{A}_2}(v)=& I_{\overline{Q}{A}_2}(v),I_{\underline{Q}{A}_1\cap \underline{Q}{A}_2}(v)=I_{\underline{Q}{A}_2}(v),\hfill \\ \hfill F_{\overline{Q}{A}_1\cap \overline{Q}{A}_2}(v)=& F_{\overline{Q}{A}_2}(v),F_{\underline{Q}{A}_1\cap \underline{Q}{A}_2}(v)=F_{\underline{Q}{A}_2}(v).\hfill \end{array}$$

(iii) 

$\forall v\in Q{A}_1\cap \underline{Q}{A}_2$

$$\begin{array}{cc}\hfill T_{\overline{Q}{A}_1\cap \overline{Q}{A}_2}(v)=& min\{T_{\overline{Q}{A}_1}(v),T_{\overline{Q}{A}_2}(v)\},T_{\underline{Q}{A}_1\cap \underline{Q}{A}_2}(v)=min\{T_{\underline{Q}{A}_1}(v),T_{\underline{Q}{A}_2}(v)\},\hfill \\ \hfill I_{\overline{Q}{A}_1\cap \overline{Q}{A}_2}(v)=& max\{I_{\overline{Q}{A}_1}(v),I_{\overline{Q}{A}_2}(v)\},I_{\underline{Q}{A}_1\cap \underline{Q}{A}_2}(v)=max\{I_{\underline{Q}{A}_1}(v),I_{\underline{Q}{A}_2}(v)\},\hfill \\ \hfill F_{\overline{Q}{A}_1\cap \overline{Q}{A}_2}(v)=& max\{F_{\overline{Q}{A}_1}(v),F_{\overline{Q}{A}_2}(v)\},F_{\underline{Q}{A}_1\cap \underline{Q}{A}_2}(v)=max\{F_{\underline{Q}{A}_1}(v),F_{\underline{Q}{A}_2}(v)\}.\hfill \end{array}$$

(iv) 

$\forall vu\in S{B}_1$ but $vu\notin S{B}_2.$

$$\begin{array}{cc}\hfill T_{\overline{S}{B}_1\cap \overline{S}{B}_2}(vu)=& T_{\overline{S}{B}_1}(vu),T_{\underline{S}{B}_1\cap \underline{S}{B}_2}(vu)=T_{\underline{S}{B}_1}(vu),\hfill \\ \hfill I_{\overline{S}{B}_1\cap \overline{S}{B}_2}(vu)=& I_{\overline{S}{B}_1}(vu),I_{\underline{S}{B}_1\cap \underline{S}{B}_2}(vu)=I_{\underline{S}{B}_1}(vu),\hfill \\ \hfill F_{\overline{S}{B}_1\cap \overline{S}{B}_2}(vu)=& F_{\overline{S}{B}_1}(vu),F_{\underline{S}{B}_1\cap \underline{S}{B}_2}(vu)=F_{\underline{S}{B}_1}(vu).\hfill \end{array}$$

(v) 

$\forall vu\notin S{B}_1$ but $vu\in S{B}_2$

$$\begin{array}{cc}\hfill T_{\overline{S}{B}_1\cap \overline{S}{B}_2}(vu)=& T_{\overline{S}{B}_2}(vu),T_{\underline{S}{B}_1\cap \underline{S}{B}_2}(vu)=T_{\underline{S}{B}_2}(vu),\hfill \\ \hfill I_{\overline{S}{B}_1\cap \overline{S}{B}_2}(vu)=& I_{\overline{S}{B}_2}(vu),I_{\underline{S}{B}_1\cap \underline{S}{B}_2}(vu)=I_{\underline{S}{B}_2}(vu),\hfill \\ \hfill F_{\overline{S}{B}_1\cap \overline{S}{B}_2}(vu)=& F_{\overline{S}{B}_2}(vu),F_{\underline{S}{B}_1\cap \underline{S}{B}_2}(vu)=F_{\underline{S}{B}_2}(vu).\hfill \end{array}$$

(vi) 

$\forall vu\in S{B}_1\cap \underline{S}{B}_2$

$$\begin{array}{cc}\hfill T_{\overline{S}{B}_1\cap \overline{S}{B}_2}(vu)=& min\{T_{\overline{S}{B}_1}(vu),T_{\overline{S}{B}_2}(vu)\},T_{\underline{S}{B}_1\cap \underline{S}{B}_2}(vu)=min\{T_{\underline{S}}{B}_1(vu),T_{\underline{S}{B}_2}(vu)\},\hfill \\ \hfill I_{\overline{S}{B}_1\cap \overline{S}{B}_2}(vu)=& max\{I_{\overline{S}{B}_1}(vu),I_{\overline{S}{B}_2}(vu)\},I_{\underline{S}{B}_1\cap \underline{S}{B}_2}(vu)=max\{I_{\underline{S}{B}_1}(vu),I_{\underline{S}{B}_2}(vu)\},\hfill \\ \hfill F_{\overline{S}{B}_1\cap \overline{S}{B}_2}(vu)=& max\{F_{\overline{S}{B}_1}(vu),F_{\overline{S}{B}_2}(vu)\},F_{\underline{S}{B}_1\cap \underline{S}{B}_2}(vu)=max\{F_{\underline{S}{B}_1}(vu),F_{\underline{S}{B}_2}(vu)\}.\hfill \end{array}$$

Definition 7.

Let $G_1=({\underline{G}}_1,{\overline{G}}_1)$ and $G_2=({\underline{G}}_2,{\overline{G}}_2)$ be two neutrosophic soft rough graphs on V. The join of $G_1$ and $G_2$ is a neutrosophic soft rough graph $G=G_1+G_2=({\underline{G}}_1+{\underline{G}}_2,{\overline{G}}_1+{\overline{G}}_2)$, where ${\underline{G}}_1+{\underline{G}}_2=(\underline{Q}{A}_1+\underline{Q}{A}_2,\underline{S}{B}_1+\underline{S}{B}_2)$ and ${\overline{G}}_1+{\overline{G}}_2=(\overline{Q}{A}_1+\overline{Q}{A}_2,\overline{S}{B}_1+\overline{S}{B}_2)$ are neutrosophic graph, respectively, such that

(i) 

$\forall v\in Q{A}_1$ but $v\notin Q{A}_2.$

$$\begin{array}{cc}\hfill T_{\overline{Q}{A}_1+\overline{Q}{A}_2}(v)=& T_{\overline{Q}{A}_1}(v),T_{\underline{Q}{A}_1+\underline{Q}{A}_2}(v)=T_{\underline{Q}{A}_1}(v),\hfill \\ \hfill I_{\overline{Q}{A}_1+\overline{Q}{A}_2}(v)=& I_{\overline{Q}{A}_1}(v),I_{\underline{Q}{A}_1+\underline{Q}{A}_2}(v)=I_{\underline{Q}{A}_1}(v),\hfill \\ \hfill F_{\overline{Q}{A}_1+\overline{Q}{A}_2}(v)=& F_{\overline{Q}{A}_1}(v),F_{\underline{Q}{A}_1+\underline{Q}{A}_2}(v)=F_{\underline{Q}{A}_1}(v).\hfill \end{array}$$

(ii) 

$\forall v\notin Q{A}_1$ but $v\in Q{A}_2.$

$$\begin{array}{cc}\hfill T_{\overline{Q}{A}_1+\overline{Q}{A}_2}(v)=& T_{\overline{Q}{A}_2}(v),T_{\underline{Q}{A}_1+\underline{Q}{A}_2}(v)=T_{\underline{Q}{A}_2}(v),\hfill \\ \hfill I_{\overline{Q}{A}_1+\overline{Q}{A}_2}(v)=& I_{\overline{Q}{A}_2}(v),I_{\underline{Q}{A}_1+\underline{Q}{A}_2}(v)=I_{\underline{Q}{A}_2}(v),\hfill \\ \hfill F_{\overline{Q}{A}_1+\overline{Q}{A}_2}(v)=& F_{\overline{Q}{A}_2}(v),F_{\underline{Q}{A}_1+\underline{Q}{A}_2}(v)=F_{\underline{Q}{A}_2}(v).\hfill \end{array}$$

(iii) 

$\forall v\in Q{A}_1\cap \underline{Q}{A}_2$

$$\begin{array}{cc}\hfill T_{\overline{Q}{A}_1+\overline{Q}{A}_2}(v)=& max\{T_{\overline{Q}{A}_1}(v),T_{\overline{Q}{A}_2}(v)\},T_{\underline{Q}{A}_1+\underline{Q}{A}_2}(v)=max\{T_{\underline{Q}{A}_1}(v),T_{\underline{Q}{A}_2}(v)\},\hfill \\ \hfill I_{\overline{Q}{A}_1+\overline{Q}{A}_2}(v)=& min\{I_{\overline{Q}{A}_1}(v),I_{\overline{Q}{A}_2}(v)\},I_{\underline{Q}{A}_1+\underline{Q}{A}_2}(v)=min\{I_{\underline{Q}{A}_1}(v),I_{\underline{Q}{A}_2}(v)\},\hfill \\ \hfill F_{\overline{Q}{A}_1+\overline{Q}{A}_2}(v)=& min\{F_{\overline{Q}{A}_1}(v),F_{\overline{Q}{A}_2}(v)\},F_{\underline{Q}{A}_1+\underline{Q}{A}_2}(v)=min\{F_{\underline{Q}{A}_1}(v),F_{\underline{Q}{A}_2}(v)\}.\hfill \end{array}$$

(iv) 

$\forall vu\in S{B}_1$ but $vu\notin S{B}_2.$

$$\begin{array}{cc}\hfill T_{\overline{S}{B}_1+\overline{S}{B}_2}(vu)=& T_{\overline{S}{B}_1}(vu),T_{\underline{S}{B}_1+\underline{S}{B}_2}(vu)=T_{\underline{S}{B}_1}(vu),\hfill \\ \hfill I_{\overline{S}{B}_1+\overline{S}{B}_2}(vu)=& I_{\overline{S}{B}_1}(vu),I_{\underline{S}{B}_1+\underline{S}{B}_2}(vu)=I_{\underline{S}{B}_1}(vu),\hfill \\ \hfill F_{\overline{S}{B}_1+\overline{S}{B}_2}(vu)=& F_{\overline{S}{B}_1}(vu),F_{\underline{S}{B}_1+\underline{S}{B}_2}(vu)=F_{\underline{S}{B}_1}(vu).\hfill \end{array}$$

(v) 

$\forall vu\notin S{B}_1$ but $vu\in S{B}_2$

$$\begin{array}{cc}\hfill T_{\overline{S}{B}_1+\overline{S}{B}_2}(vu)=& T_{\overline{S}{B}_2}(vu),T_{\underline{S}{B}_1+\underline{S}{B}_2}(vu)=T_{\underline{S}{B}_2}(vu),\hfill \\ \hfill I_{\overline{S}{B}_1+\overline{S}{B}_2}(vu)=& I_{\overline{S}{B}_2}(vu),I_{\underline{S}{B}_1+\underline{S}{B}_2}(vu)=I_{\underline{S}{B}_2}(vu),\hfill \\ \hfill F_{\overline{S}{B}_1+\overline{S}{B}_2}(vu)=& F_{\overline{S}{B}_2}(vu),F_{\underline{S}{B}_1+\underline{S}{B}_2}(vu)=F_{\underline{S}{B}_2}(vu).\hfill \end{array}$$

(vi) 

$\forall vu\in S{B}_1\cap \underline{S}{B}_2$

$$\begin{array}{cc}\hfill T_{\overline{S}{B}_1+\overline{S}{B}_2}(vu)=& max\{T_{\overline{S}{B}_1}(vu),T_{\overline{S}{B}_2}(vu)\},T_{\underline{S}{B}_1+\underline{S}{B}_2}(vu)=max\{T_{\underline{S}}{B}_1(vu),T_{\underline{S}{B}_2}(vu)\},\hfill \\ \hfill I_{\overline{S}{B}_1+\overline{S}{B}_2}(vu)=& min\{I_{\overline{S}{B}_1}(vu),I_{\overline{S}{B}_2}(vu)\},I_{\underline{S}{B}_1+\underline{S}{B}_2}(vu)=min\{I_{\underline{S}{B}_1}(vu),I_{\underline{S}{B}_2}(vu)\},\hfill \\ \hfill F_{\overline{S}{B}_1+\overline{S}{B}_2}(vu)=& min\{F_{\overline{S}{B}_1}(vu),F_{\overline{S}{B}_2}(vu)\},F_{\underline{S}{B}_1+\underline{S}{B}_2}(vu)=min\{F_{\underline{S}{B}_1}(vu),F_{\underline{S}{B}_2}(vu)\}.\hfill \end{array}$$

(vii) 

$\forall vu\in \tilde{E}$, where $\tilde{E}$ is the set of edges joining vertices of $Q{A}_1$ and $Q{A}_2$.

$$\begin{array}{cc}\hfill T_{\overline{S}{B}_1+\overline{S}{B}_2}(vu)=& min\{T_{\overline{Q}{A}_1}(v),T_{\overline{Q}{A}_2}(u)\},T_{\underline{S}{B}_1+\underline{S}{B}_2}(vu)=min\{T_{\underline{Q}{A}_1}(v),T_{\underline{Q}{A}_2}(u)\},\hfill \\ \hfill I_{\overline{S}{B}_1+\overline{S}{B}_2}(vu)=& max\{I_{\overline{Q}{A}_1}(v),I_{\overline{Q}{A}_2}(u)\},I_{\underline{S}{B}_1+\underline{S}{B}_2}(vu)=max\{I_{\underline{Q}{A}_1}(v),I_{\underline{Q}{A}_2}(u)\},\hfill \\ \hfill F_{\overline{S}{B}_1+\overline{S}{B}_2}(vu)=& max\{F_{\overline{Q}{A}_1}(v),F_{\overline{Q}{A}_2}(u)\},F_{\underline{S}{B}_1+\underline{S}{B}_2}(vu)=max\{F_{\underline{Q}{A}_1}(v),F_{\underline{Q}{A}_2}(u)\}.\hfill \end{array}$$

Definition 8.

The Cartesian product of $G_1$ and $G_2$ is a $G=G_1⋉G_2=({\underline{G}}_1⋉{\underline{G}}_2,{\overline{G}}_1⋉{\overline{G}}_2),$ where ${\underline{G}}_1⋉{\underline{G}}_2=(\underline{Q}{A}_1⋉\underline{Q}{A}_2,\underline{S}{B}_1⋉\underline{S}{B}_2)$ and ${\overline{G}}_1⋉{\overline{G}}_2=(\overline{Q}{A}_1⋉\overline{Q}{A}_2,\overline{S}{B}_1⋉\overline{S}{B}_2)$ are neutrosophic digraph, such that

(i) 

$\forall (v_1,v_2)\in Q{A}_1\times Q{A}_2.$

$$\begin{array}{cc}\hfill T_{(\overline{Q}{A}_1⋉\overline{Q}{A}_2)}(v_1,v_2)=& min\{T_{\overline{Q}{A}_1}(v_1),T_{\overline{Q}{A}_2}(v_1)\},T_{(\underline{Q}{A}_1⋉\underline{Q}{A}_2)}(v_1,v_2)=min\{T_{\underline{Q}{A}_1}(v_1),T_{\underline{Q}{A}_2}(v_1)\},\hfill \\ \hfill I_{(\overline{Q}{A}_1⋉\overline{Q}{A}_2)}(v_1,v_2)=& max\{I_{\overline{Q}{A}_1}(v_1),I_{\overline{Q}{A}_2}(v_1)\},I_{(\underline{Q}{A}_1⋉\underline{Q}{A}_2)}(v_1,v_2)=max\{I_{\underline{Q}{A}_1}(v_1),I_{\underline{Q}{A}_2}(v_1)\},\hfill \\ \hfill F_{(\overline{Q}{A}_1⋉\overline{Q}{A}_2)}(v_1,v_2)=& max\{F_{\overline{Q}{A}_1}(v_1),F_{\overline{Q}{A}_2}(v_1)\},F_{(\underline{Q}{A}_1⋉\underline{Q}{A}_2)}(v_1,v_2)=max\{F_{\underline{Q}{A}_1}(v_1),F_{\underline{Q}{A}_2}(v_1)\}.\hfill \end{array}$$

(ii) 

$\forall v_1{v}_2\in S{B}_2,v\in Q{A}_1$.

$$\begin{array}{cc}\hfill T_{(\overline{S}{B}_1⋉\overline{S}{B}_2)}\left((v,v_1)(v,v_2)\right)=& min\{T_{\overline{Q}{A}_1}(v),T_{\overline{S}{B}_2}(v_1{v}_2)\},\hfill \\ \hfill T_{(\underline{S}{B}_1⋉\underline{S}{B}_2)}\left((v,v_1)(v,v_2)\right)=& min\{T_{\underline{Q}{A}_1}(v),T_{\underline{S}{B}_2}(v_1{v}_2)\},\hfill \\ \hfill I_{(\overline{S}{B}_1⋉\overline{S}{B}_2)}\left((v,v_1)(v,v_2)\right)=& max\{I_{\overline{Q}{A}_1}(v),I_{\overline{S}{B}_2}(v_1{v}_2)\},\hfill \\ \hfill I_{(\underline{S}{B}_1⋉\underline{S}{B}_2)}\left((v,v_1)(v,v_2)\right)=& max\{I_{\underline{Q}{A}_1}(v),I_{\underline{S}{B}_2}(v_1{v}_2)\},\hfill \\ \hfill F_{(\overline{S}{B}_1⋉\overline{S}{B}_2)}\left((v,v_1)(v,v_2)\right)=& max\{F_{\overline{Q}{A}_1}(v),F_{\overline{S}{B}_2}(v_1{v}_2)\},\hfill \\ \hfill F_{(\underline{S}{B}_1⋉\underline{S}{B}_2)}\left((v,v_1)(v,v_2)\right)=& max\{F_{\underline{Q}{A}_1}(v),F_{\underline{S}{B}_2}(v_1{v}_2)\}.\hfill \end{array}$$

(iii) 

$\forall v_1{v}_2\in S{B}_1,v\in Q{A}_2$.

$$\begin{array}{cc}\hfill T_{(\underline{S}{B}_1⋉\underline{S}{B}_2)}\left((v_1,v)(v_2,v)\right)=& min\{T_{\underline{S}{B}_1}(v_1{v}_2),T_{\underline{Q}{A}_2}(v)\},\hfill \\ \hfill T_{(\overline{S}{B}_1⋉\overline{S}{B}_2)}\left((v_1,v)(v_2,v)\right)=& min\{T_{\overline{S}{B}_1}(v_1{v}_2),T_{\overline{Q}{A}_2}(v)\},\hfill \\ \hfill I_{(\overline{S}{B}_1⋉\overline{S}{B}_2)}\left((v_1,v)(v_2,v)\right)=& max\{I_{\overline{S}{B}_1}(v_1{v}_2),I_{\overline{Q}{A}_2}(v)\},\hfill \\ \hfill I_{(\underline{S}{B}_1⋉\underline{S}{B}_2)}\left((v_1,v)(v_2,v)\right)=& max\{I_{\underline{S}{B}_1}(v_1{v}_2),I_{\underline{Q}{A}_2}(v)\},\hfill \\ \hfill F_{(\overline{S}{B}_1⋉\overline{S}{B}_2)}\left((v_1,v)(v_2,v)\right)=& max\{F_{\overline{S}{B}_1}(v_1{v}_2),F_{\overline{Q}{A}_2}(v)\},\hfill \\ \hfill F_{(\underline{S}{B}_1⋉\underline{S}{B}_2)}\left((v_1,v)(v_2,v)\right)=& max\{F_{\underline{S}{B}_1}(v_1{v}_2),F_{\underline{Q}{A}_2}(v)\}.\hfill \end{array}$$

Definition 9.

The cross product of $G_1$ and $G_2$ is a neutrosophic soft rough graph $G=G_1⊚G_2=({\underline{G}}_1⊚{\underline{G}}_2,{\overline{G}}_1⊚{\overline{G}}_2),$ where ${\underline{G}}_1⊚{\underline{G}}_2=(\underline{Q}{A}_1⊚\underline{Q}{A}_2,\underline{S}{B}_1⊚\underline{S}{B}_2)$ and ${\overline{G}}_1⊚{\overline{G}}_2=(\overline{Q}{A}_1⊚\overline{Q}{A}_2,\overline{S}{B}_1⊚\overline{S}{B}_2)$ are neutrosophic graphs, respectively, such that

(i) 

$\forall (v_1,v_2)\in Q{A}_1\times Q{A}_2$.

$$\begin{array}{cc}\hfill T_{(\overline{Q}{A}_1⊚\overline{Q}{A}_2)}(v_1,v_2)=& min\{T_{\overline{Q}{A}_1}(v_1),T_{\overline{Q}{A}_2}(v_1)\},T_{(\underline{Q}{A}_1⊚\underline{Q}{A}_2)}(v_1,v_2)=min\{T_{\underline{Q}{A}_1}(v_1),T_{\underline{Q}{A}_2}(v_1)\},\hfill \\ \hfill I_{(\overline{Q}{A}_1⊚\overline{Q}{A}_2)}(v_1,v_2)=& max\{I_{\overline{Q}{A}_1}(v_1),I_{\overline{Q}{A}_2}(v_1)\},I_{(\underline{Q}{A}_1⊚\underline{Q}{A}_2)}(v_1,v_2)=max\{I_{\underline{Q}{A}_1}(v_1),I_{\underline{Q}{A}_2}(v_1)\},\hfill \\ \hfill F_{(\overline{Q}{A}_1⊚\overline{Q}{A}_2)}(v_1,v_2)=& max\{F_{\overline{Q}{A}_1}(v_1),F_{\overline{Q}{A}_2}(v_1)\},F_{(\underline{Q}{A}_1⊚\underline{Q}{A}_2)}(v_1,v_2)=max\{F_{\underline{Q}{A}_1}(v_1),F_{\underline{Q}{A}_2}(v_1)\}.\hfill \end{array}$$

(ii) 

$\forall v_1{u}_1\in S{B}_1,v_2{u}_2\in S{B}_2$.

$$\begin{array}{cc}\hfill T_{(\overline{S}{B}_1⊚\overline{S}{B}_2)}\left((v_1,v_2)(u_1,u_2)\right)=& min\{T_{\overline{S}{B}_1}(v_1{u}_1),T_{\overline{S}{B}_2}(v_1{u}_2)\},\hfill \\ \hfill T_{(\underline{S}{B}_1⊚\underline{S}{B}_2)}\left((v_1,v_2)(u_1,u_2)\right)=& min\{T_{\underline{S}{B}_1}(v_1{u}_1),T_{\underline{S}{B}_2}(v_1{u}_2)\},\hfill \\ \hfill I_{(\overline{S}{B}_1⊚\overline{S}{B}_2}\left((v_1,v_2)(u_1,u_2)\right)=& max\{I_{\overline{S}{B}_1}(v_1{u}_1),I_{\overline{S}{B}_2}(v_1{u}_2)\},\hfill \\ \hfill I_{(\underline{S}{B}_1⊚\underline{S}{B}_2)}\left((v_1,v_2)(u_1,u_2)\right)=& max\{I_{\underline{S}{B}_1}(v_1{u}_1),I_{\underline{S}{B}_2}(v_1{u}_2)\},\hfill \\ \hfill F_{(\overline{S}{B}_1⊚\overline{S}{B}_2}\left((v_1,v_2)(u_1,u_2)\right)=& max\{F_{\overline{S}{B}_1}(v_1{u}_1),F_{\overline{S}{B}_2}(v_1{u}_2)\},\hfill \\ \hfill F_{(\underline{S}{B}_1⊚\underline{S}{B}_2)}\left((v_1,v_2)(u_1,u_2)\right)=& max\{F_{\underline{S}{B}_1}(v_1{u}_1),F_{\underline{S}{B}_2}(v_1{u}_2)\}.\hfill \end{array}$$

Definition 10.

The rejection of $G_1$ and $G_2$ is a neutrosophic soft rough graph $G=G_1|G_2=({\underline{G}}_1|{\underline{G}}_2,{\overline{G}}_1|{\overline{G}}_2),$ where ${\underline{G}}_1|{\underline{G}}_2=(\underline{S}{A}_1|\underline{S}{A}_2,\underline{S}{B}_1|\underline{S}{B}_2)$ and ${\overline{G}}_1|{\overline{G}}_2=(\overline{S}{A}_1|\overline{S}{A}_2,\overline{S}{B}_1|\overline{S}{B}_2)$ are neutrosophic graphs such that

(i) 

$\forall (v_1,v_2)\in Q{A}_1\times Q{A}_2$.

$$\begin{array}{cc}\hfill T_{(\overline{Q}{A}_1|\overline{Q}{A}_2)}(v_1,v_2)=& min\{T_{\overline{Q}{A}_1}(v_1),T_{\overline{Q}{A}_2}(v_2)\},T_{(\underline{Q}{A}_1|\underline{Q}{A}_2)}(v_1,v_2)=min\{T_{\underline{Q}{A}_1}(v_1),T_{\underline{Q}{A}_2}(v_2)\},\hfill \\ \hfill I_{(\overline{Q}{A}_1|\overline{Q}{A}_2)}(v_1,v_2)=& max\{I_{\overline{Q}{A}_1}(v_1),I_{\overline{Q}{A}_2}(v_2)\},I_{(\underline{Q}{A}_1|\underline{Q}{A}_2)}(v_1,v_2)=max\{I_{\underline{Q}{A}_1}(v_1),I_{\underline{Q}{A}_2}(v_2)\},\hfill \\ \hfill F_{(\overline{Q}{A}_1|\overline{Q}{A}_2)}(v_1,v_2)=& max\{F_{\overline{Q}{A}_1}(v_1),F_{\overline{Q}{A}_2}(v_2)\},F_{(\underline{Q}{A}_1|\underline{Q}{A}_2)}(v_1,v_2)=max\{F_{\underline{Q}{A}_1}(v_1),F_{\underline{Q}{A}_2}(v_2)\}.\hfill \end{array}$$

(ii) 

$\forall v_2{u}_2\notin S{B}_2,v\in Q{A}_1$.

$$\begin{array}{cc}\hfill T_{(\overline{S}{B}_1|\overline{S}{B}_2)}\left((v,v_2)(v,u_2)\right)=& min\{T_{\overline{Q}{A}_1}(v),T_{\overline{Q}{A}_2}(v_2),T_{\overline{Q}{A}_2}(u_2)\},\hfill \\ \hfill T_{(\underline{S}{B}_1|\underline{Q}{B}_2)}\left((v,v_2)(v,u_2)\right)=& min\{T_{\underline{Q}{A}_1}(v),T_{\underline{Q}{A}_2}(v_2),T_{\underline{Q}{A}_2}(u_2)\},\hfill \\ \hfill (I_{\overline{S}{B}_1|\overline{S}{B}_2)}\left((v,v_2)(v,u_2)\right)=& max\{I_{\overline{Q}{A}_1}(v),I_{\overline{Q}{A}_2}(v_2),I_{\overline{Q}{A}_2}(u_2)\},\hfill \\ \hfill (I_{\underline{S}{B}_1|\underline{S}{B}_2)}\left((v,v_2)(v,u_2)\right)=& max\{I_{\underline{Q}{A}_1}(v),I_{\underline{Q}{A}_2}(v_2),I_{\underline{Q}{A}_2}(u_2)\},\hfill \\ \hfill (F_{\overline{S}{B}_1|\overline{S}{B}_2)}\left((v,v_2)(v,u_2)\right)=& max\{F_{\overline{Q}{A}_1}(v),F_{\overline{Q}{A}_2}(v_2),F_{\overline{Q}{A}_2}(u_2)\},\hfill \\ \hfill (F_{\underline{S}{B}_1|\underline{S}{B}_2)}\left((v,v_2)(v,u_2)\right)=& max\{F_{\underline{Q}{A}_1}(v),F_{\underline{Q}{A}_2}(v_2),F_{\underline{Q}{A}_2}(u_2)\}.\hfill \end{array}$$

(iii) 

$\forall v_1{u}_1\notin S{B}_1,v\in Q{A}_2$,

$$\begin{array}{cc}\hfill T_{(\underline{S}{B}_1|\underline{S}{B}_2)}\left((v_1,v)(u_1,v)\right)=& min\{T_{\underline{Q}{A}_1}(v_1),T_{\underline{Q}{A}_1}(u_1),T_{\underline{Q}{A}_2}(v)\},\hfill \\ \hfill I_{(\underline{S}{B}_1|\underline{S}{B}_2)}\left((v_1,v)(u_1,v)\right)=& max\{I_{\underline{Q}{A}_1}(v_1),I_{\underline{Q}{A}_1}(u_1),I_{\underline{Q}{A}_2}(v)\},\hfill \\ \hfill F_{(\underline{S}{B}_1|\underline{S}{B}_2)}\left((v_1,v)(u_1,v)\right)=& max\{F_{\underline{Q}{A}_1}(v_1),F_{\underline{Q}{A}_1}(u_1),F_{\underline{Q}{A}_2}(v)\},\hfill \\ \hfill T_{(\overline{S}{B}_1|\overline{S}{B}_2)}\left((v_1,v)(u_1,v)\right)=& min\{T_{\overline{Q}{A}_1}(v_1),T_{\overline{Q}{A}_1}(u_1),T_{\overline{Q}{A}_2}(v)\},\hfill \\ \hfill I_{(\overline{S}{B}_1|\overline{S}{B}_2)}\left((v_1,v)(u_1,v)\right)=& max\{I_{\overline{Q}{A}_1}(v_1),I_{\overline{Q}{A}_1}(u_1),I_{\overline{Q}{A}_2}(v)\},\hfill \\ \hfill F_{(\overline{S}{B}_1|\overline{S}{B}_2)}\left((v_1,v)(u_1,v)\right)=& max\{F_{\overline{Q}{A}_1}(v_1),F_{\overline{Q}{A}_1}(u_1),F_{\overline{Q}{A}_2}(v)\}.\hfill \end{array}$$

(iv) 

$\forall v_1{u}_1\notin \overline{S}{B}_1,v_2{u}_2\notin \overline{S}{B}_2,v_1=u_1.$

$$\begin{array}{cc}\hfill T_{(\underline{S}{B}_1|\underline{S}{B}_2)}\left((v_1,v_2)(u_1,u_2)\right)=& min\{T_{\underline{Q}{A}_1}(v_1),T_{\underline{Q}{A}_1}(u_1),T_{\underline{Q}{A}_2}(v_2),T_{\underline{Q}{A}_2}(u_2)\},\hfill \\ \hfill I_{(\underline{S}{B}_1|\underline{S}{B}_2)}\left((v_1,v_2)(u_1,u_2)\right)=& max\{I_{\underline{Q}{A}_1}(v_1),I_{\underline{Q}{A}_1}(u_1),I_{\underline{Q}{A}_2}(v_2),I_{\underline{Q}{A}_2}(u_2)\},\hfill \\ \hfill F_{(\underline{S}{B}_1|\underline{S}{B}_2)}\left((v_1,v_2)(u_1,u_2)\right)=& max\{F_{\underline{Q}{A}_1}(v_1),F_{\underline{Q}{A}_1}(u_1),F_{\underline{Q}{A}_2}(v_2),F_{\underline{Q}{A}_2}(u_2)\},\hfill \\ \hfill T_{(\overline{S}{B}_1|\overline{S}{B}_2)}\left((v_1,v_2)(u_1,u_2)\right)=& min\{T_{\overline{Q}{A}_1}(v_1),T_{\overline{Q}{A}_1}(u_1),T_{\overline{Q}{A}_2}(v_2),T_{\overline{Q}{A}_2}(u_2)\},\hfill \\ \hfill I_{(\overline{S}{B}_1|\overline{S}{B}_2)}\left((v_1,v_2)(u_1,u_2)\right)=& max\{I_{\overline{Q}{A}_1}(v_1),I_{\overline{Q}{A}_1}(u_1),I_{\overline{Q}{A}_2}(v_2),I_{\overline{Q}{A}_2}(u_2)\},\hfill \\ \hfill F_{(\overline{S}{B}_1|\overline{S}{B}_2)}\left((v_1,v_2)(u_1,u_2)\right)=& max\{F_{\overline{Q}{A}_1}(v_1),F_{\overline{Q}{A}_1}(u_1),F_{\overline{Q}{A}_2}(v_2),F_{\overline{Q}{A}_2}(u_2)\},\hfill \end{array}$$

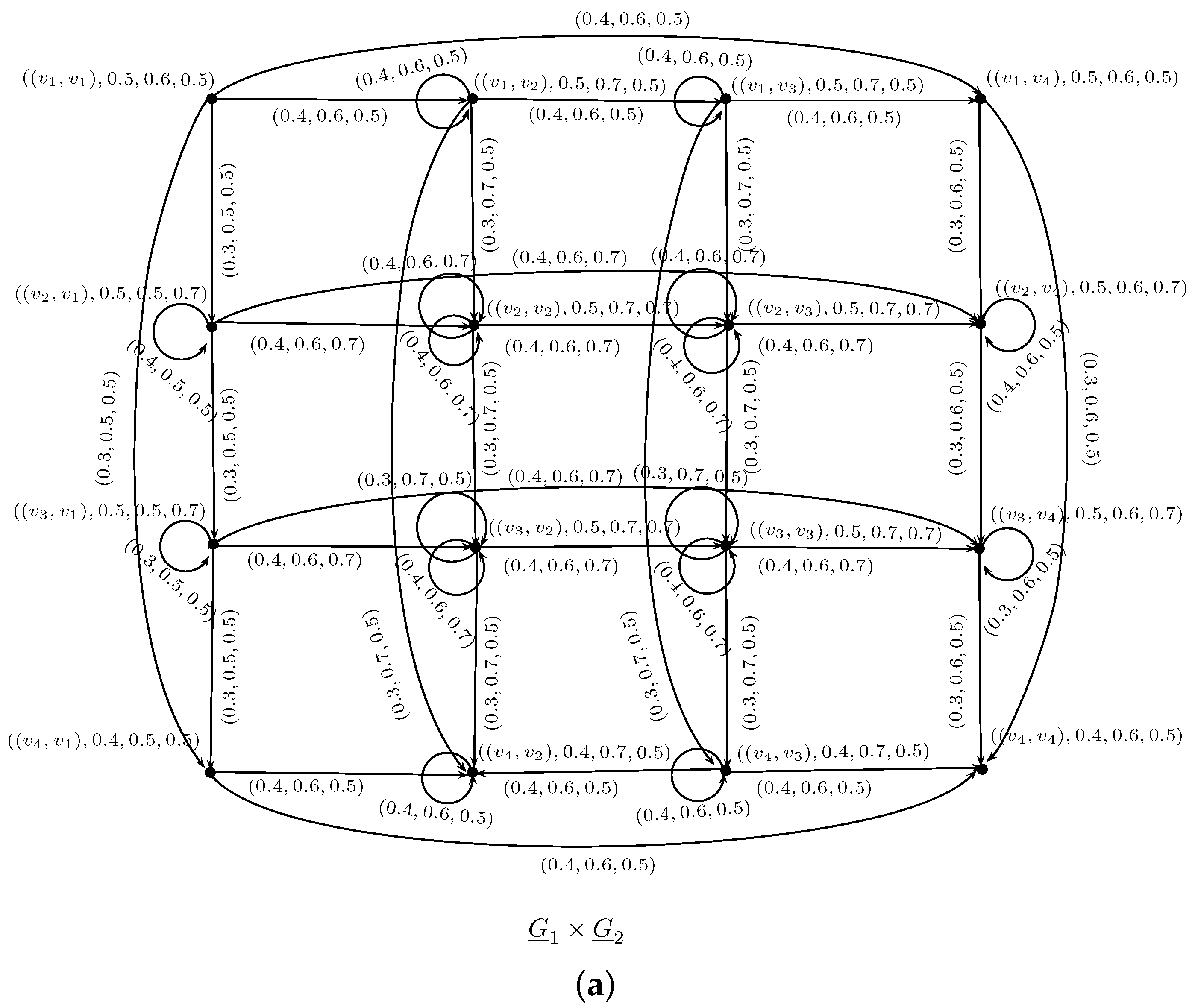
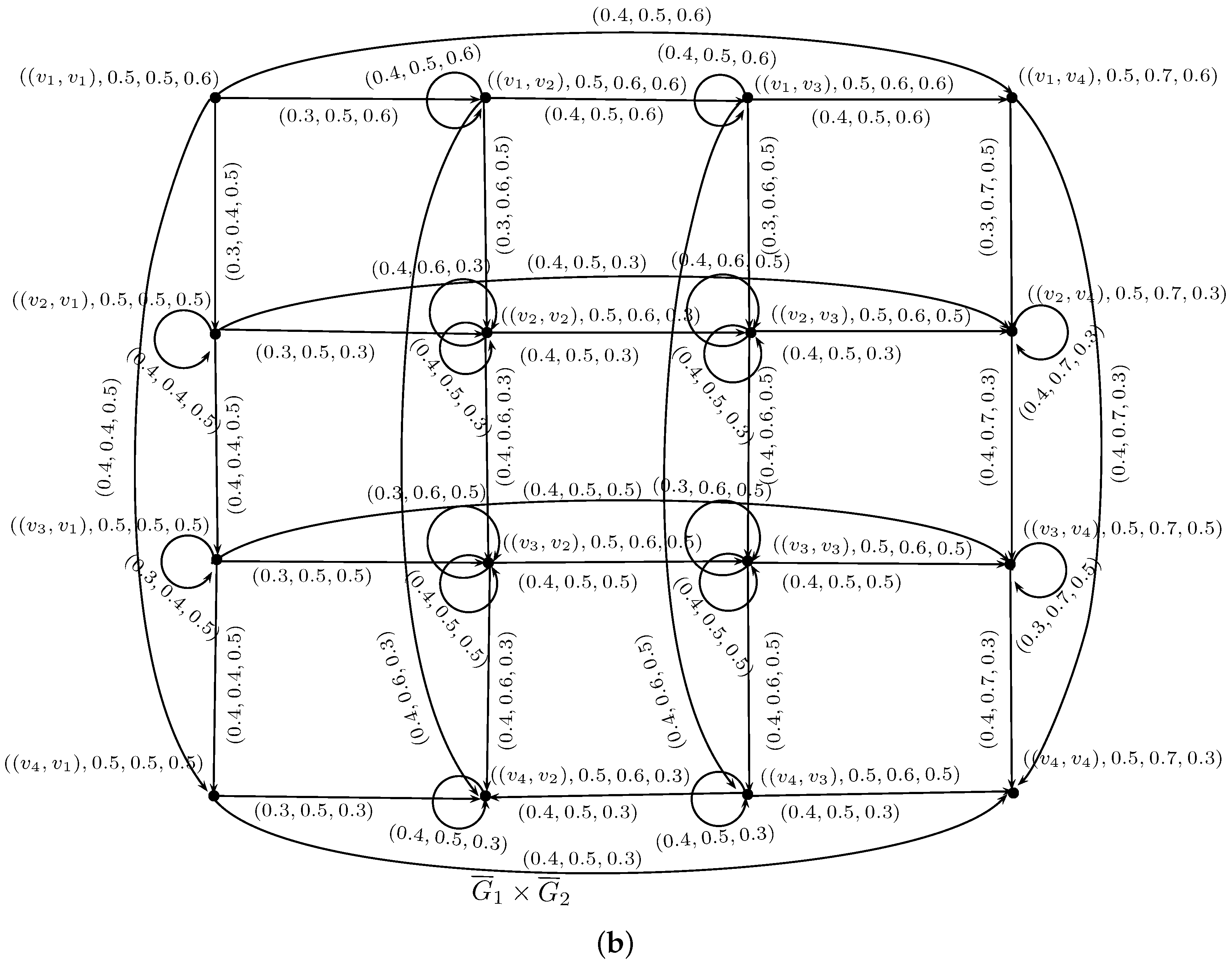
Example 6.

Let $G_1=({\underline{G}}_1,{\overline{G}}_1)$ and $G_2=({\underline{G}}_2,{\overline{G}}_2)$ be two neutrosophic soft rough graphs on V, where ${\underline{G}}_1=(\underline{Q}{A}_1,\underline{S}{B}_1)$ and ${\overline{G}}_1=(\overline{Q}{A}_1,\overline{S}{B}_1)$ are neutrosophic graphs as shown in Figure 2 and ${\underline{G}}_2=(\underline{Q}{A}_2,\underline{S}{B}_2)$ and ${\overline{G}}_2=(\overline{Q}{A}_2,\overline{S}{B}_2)$ are neutrosophic graphs as shown in Figure 3. The Cartesian product of $G_1=({\underline{G}}_1,{\overline{G}}_1)$ and $G_2=({\underline{G}}_2,{\overline{G}}_2)$ is NSRG $G=G_1\times G_2=({\underline{G}}_1\times {\underline{G}}_2,{\overline{G}}_1\times {\overline{G}}_2)$ as shown in Figure 5.

Definition 11.

The symmetric difference of $G_1$ and $G_2$ is a neutrosophic soft rough graph $G=G_1\oplus G_2=({\underline{G}}_1\oplus {\underline{G}}_2,{\overline{G}}_1\oplus {\overline{G}}_2),$ where ${\underline{G}}_1\oplus {\underline{G}}_2=(\underline{Q}{A}_1\oplus \underline{Q}{A}_2,\underline{S}{B}_1\oplus \underline{S}{B}_2)$ and ${\overline{G}}_1\oplus {\overline{G}}_2=(\overline{Q}{A}_1\oplus \overline{Q}{A}_2,\overline{S}{B}_1\oplus \overline{S}{B}_2)$ are neutrosophic graphs, respectively, such that

(i) 

$\forall (v_1,v_2)\in Q{A}_1\times Q{A}_2$.

$$\begin{array}{cc}\hfill T_{(\overline{Q}{A}_1\oplus \overline{Q}{A}_2)}(v_1,v_2)=& min\{T_{\overline{Q}{A}_1}(v_1),T_{\overline{Q}{A}_2}(v_2)\},T_{(\underline{Q}{A}_1\oplus \underline{Q}{A}_2)}(v_1,v_2)=min\{T_{\underline{Q}{A}_1}(v_1),T_{\underline{Q}{A}_2}(v_2)\},\hfill \\ \hfill I_{(\overline{Q}{A}_1\oplus \overline{Q}{A}_2)}(v_1,v_2)=& max\{I_{\overline{Q}{A}_1}(v_1),I_{\overline{Q}{A}_2}(v_2)\},I_{(\underline{Q}{A}_1\oplus \underline{Q}{A}_2)}(v_1,v_2)=max\{I_{\underline{Q}{A}_1}(v_1),I_{\underline{Q}{A}_2}(v_2)\},\hfill \\ \hfill F_{(\overline{Q}{A}_1\oplus \overline{Q}{A}_2)}(v_1,v_2)=& max\{F_{\overline{Q}{A}_1}(v_1),F_{\overline{Q}{A}_2}(v_2)\},F_{(\underline{Q}{A}_1\oplus \underline{Q}{A}_2)}(v_1,v_2)=max\{F_{\underline{Q}{A}_1}(v_1),F_{\underline{Q}{A}_2}(v_2)\}.\hfill \end{array}$$

(ii) 

$\forall v_1{v}_2\in S{B}_2,v\in Q{A}_1$.

$$\begin{array}{cc}\hfill T_{(\overline{S}{B}_1\oplus \overline{S}{B}_2)}\left((v,v_1)(v,v_2)\right)=& min\{T_{\overline{Q}{A}_1}(v),T_{\overline{S}{B}_2}(v_1{v}_2)\},\hfill \\ \hfill T_{(\underline{S}{B}_1\oplus \underline{S}{B}_2)}\left((v,v_1)(v,v_2)\right)=& min\{T_{\underline{Q}{A}_1}(v),T_{\underline{S}{B}_2}(v_1{v}_2)\},\hfill \\ \hfill I_{(\overline{S}{B}_1\oplus \overline{S}{B}_2)}\left((v,v_1)(v,v_2)\right)=& max\{I_{\overline{Q}{A}_1}(v),I_{\overline{S}{B}_2}(v_1{v}_2)\},\hfill \\ \hfill I_{(\underline{S}{B}_1\oplus \underline{S}{B}_2)}\left((v,v_1)(v,v_2)\right)=& max\{I_{\underline{Q}{A}_1}(v),I_{\underline{S}{B}_2}(v_1{v}_2)\},\hfill \\ \hfill F_{(\overline{S}{B}_1\oplus \overline{S}{B}_2)}\left((v,v_1)(v,v_2)\right)=& max\{F_{\overline{Q}{A}_1}(v),F_{\overline{S}{B}_2}(v_1{v}_2)\},\hfill \\ \hfill F_{(\underline{S}{B}_1\oplus \underline{S}{B}_2)}\left((v,v_1)(v,v_2)\right)=& max\{F_{\underline{Q}{A}_1}(v),F_{\underline{S}{B}_2}(v_1{v}_2)\}.\hfill \end{array}$$

(iii) 

$\forall v_1{v}_2\in S{B}_1,v\in Q{A}_2$.

$$\begin{array}{cc}\hfill T_{(\overline{S}{B}_1\oplus \overline{S}{B}_2)}\left((v_1,v)(v_2,v)\right)=& min\{T_{\overline{S}{B}_1}(v_1{v}_2),T_{\overline{Q}{A}_2}(v)\},\hfill \\ \hfill T_{(\underline{S}{B}_1\oplus \underline{S}{B}_2)}\left((v_1,v)(v_2,v)\right)=& min\{T_{\underline{S}{B}_1}(v_1{v}_2),T_{\underline{Q}{A}_2}(v)\},\hfill \\ \hfill I_{(\overline{S}{B}_1\oplus \overline{S}{B}_2)}\left((v_1,v)(v_2,v)\right)=& max\{I_{\overline{S}{B}_1}(v_1{v}_2),I_{\overline{Q}{A}_2}(v)\},\hfill \\ \hfill I_{(\underline{S}{B}_1\oplus \underline{S}{B}_2)}\left((v_1,v)(v_2,v)\right)=& max\{I_{\underline{S}{B}_1}(v_1{v}_2),I_{\underline{Q}{A}_2}(v)\},\hfill \\ \hfill F_{(\overline{S}{B}_1\oplus \overline{S}{B}_2)}\left((v_1,v)(v_2,v)\right)=& max\{F_{\overline{S}{B}_1}(v_1{v}_2),F_{\overline{Q}{A}_2}(v)\},\hfill \\ \hfill F_{(\underline{S}{B}_1\oplus \underline{S}{B}_2)}\left((v_1,v)(v_2,v)\right)=& max\{F_{\underline{S}{B}_1}(v_1{v}_2),F_{\underline{Q}{A}_2}(v)\}.\hfill \end{array}$$

(iv) 

$\forall v_1{u}_1\notin S{B}_1,v_2{u}_2\in S{B}_2$.

$$\begin{array}{cc}\hfill T_{(\overline{S}{B}_1\oplus \overline{S}{B}_2)}\left((v_1,v_2)(u_1,u_2)\right)=& min\{T_{\overline{S}{B}_1}(v_1{u}_1),T_{\overline{Q}{A}_2}(v_2),T_{\overline{Q}{A}_2}(u_2)\},\hfill \\ \hfill T_{(\underline{S}{B}_1\oplus \underline{S}{B}_2)}\left((v_1,v_2)(u_1,u_2)\right)=& min\{T_{\underline{S}{B}_1}(v_1{u}_1),T_{\underline{Q}{A}_2}(v_2),T_{\underline{Q}{A}_2}(u_2)\},\hfill \\ \hfill I_{(\overline{S}{B}_1\oplus \overline{S}{B}_2)}\left((v_1,v_2)(u_1,u_2)\right)=& max\{I_{\overline{S}{B}_1}(v_1{u}_1),I_{\overline{Q}{A}_2}(v_2),I_{\overline{Q}{A}_2}(u_2)\},\hfill \\ \hfill I_{(\underline{S}{B}_1\oplus \underline{S}{B}_2)}\left((v_1,v_2)(u_1,u_2)\right)=& max\{I_{\underline{S}{B}_1}(v_1{u}_1),I_{\underline{Q}{A}_2}(v_2),I_{\underline{Q}{A}_2}(u_2)\},\hfill \\ \hfill F_{(\overline{S}{B}_1\oplus \overline{S}{B}_2)}\left((v_1,v_2)(u_1,u_2)\right)=& max\{F_{\overline{S}{B}_1}(v_1{u}_1),F_{\overline{Q}{A}_2}(v_2),F_{\overline{Q}{A}_2}(u_2)\},\hfill \\ \hfill F_{(\underline{S}{B}_1\oplus \underline{S}{B}_2)}\left((v_1,v_2)(u_1,u_2)\right)=& max\{F_{\underline{S}{B}_1}(v_1{u}_1),F_{\underline{Q}{A}_2}(v_2),F_{\underline{Q}{A}_2}(u_2)\}.\hfill \end{array}$$

(v) 

$\forall v_1{u}_1\notin S{B}_1,v_2{u}_2\in S{B}_2$.

$$\begin{array}{cc}\hfill T_{(\overline{S}{B}_1\oplus \overline{S}{B}_2)}\left((v_1,v_2)(u_1,u_2)\right)=& min\{T_{\overline{Q}{A}_1}(v_1),T_{\overline{Q}{A}_1}(u_1),T_{\overline{S}{B}_2}(v_2{u}_2)\},\hfill \\ \hfill T_{(\underline{S}{B}_1\oplus \underline{S}{B}_2)}\left((v_1,v_2)(u_1,u_2)\right)=& min\{T_{\underline{Q}{A}_1}(v_1),T_{\underline{Q}{A}_1}(u_1),T_{\underline{S}{B}_2}(v_2{u}_2)\},\hfill \\ \hfill I_{(\overline{S}{B}_1\oplus \overline{S}{B}_2)}\left((v_1,v_2)(u_1,u_2)\right)=& max\{I_{\overline{Q}{A}_1}(v_1),I_{\overline{Q}{A}_1}(u_1),I_{\overline{S}{B}_2}(v_2{u}_2)\},\hfill \\ \hfill I_{(\underline{S}{B}_1\oplus \underline{S}{B}_2)}\left((v_1,v_2)(u_1,u_2)\right)=& max\{I_{\underline{Q}{A}_1}(v_1),I_{\underline{Q}{A}_1}(u_1),I_{\underline{S}{B}_2}(v_2{u}_2)\},\hfill \\ \hfill F_{(\overline{S}{B}_1\oplus \overline{S}{B}_2)}\left((v_1,v_2)(u_1,u_2)\right)=& max\{F_{\overline{Q}{A}_1}(v_1),F_{\overline{Q}{A}_1}(u_1),F_{\overline{S}{B}_2}(v_2{u}_2)\},\hfill \\ \hfill F_{(\underline{S}{B}_1\oplus \underline{S}{B}_2)}\left((v_1,v_2)(u_1,u_2)\right)=& max\{F_{\underline{Q}{A}_1}(v_1),F_{\underline{Q}{A}_1}(u_1),F_{\underline{S}{B}_2}(v_2{u}_2)\}.\hfill \end{array}$$

Example 7.

Let $G_1=({\underline{G}}_1,{\overline{G}}_1)$ and $G_2=({\underline{G}}_2,{\overline{G}}_2)$ be two neutrosophic soft rough graphs on V, where ${\underline{G}}_1=(\underline{Q}{A}_1,\underline{S}{B}_1)$ and ${\overline{G}}_1=(\overline{Q}{A}_1,\overline{S}{B}_1)$ are neutrosophic graphs as shown in Figure 6 and ${\underline{G}}_2=(\underline{Q}{A}_2,\underline{S}{B}_2)$ and ${\overline{G}}_2=(\overline{Q}{A}_2,\overline{S}{B}_2)$ are neutrosophic graphs as shown in Figure 7.

The symmetric difference of $G_1$ and $G_2$ is $G=G_1\oplus G_2=({\underline{G}}_1\oplus {\underline{G}}_2,{\overline{G}}_1\oplus {\overline{G}}_2)$, where ${\underline{G}}_1\oplus {\underline{G}}_2=(\underline{Q}{A}_1\oplus \underline{Q}{A}_2,\underline{S}{B}_1\oplus \underline{S}{B}_2)$ and ${\overline{G}}_1\oplus {\overline{G}}_2=(\overline{Q}{A}_1\oplus \overline{Q}{A}_2,\overline{S}{B}_1\oplus \overline{S}{B}_2)$ are neutrosophic graphs as shown in Figure 8.

Definition 12.

The lexicographic product of $G_1$ and $G_2$ is a neutrosophic soft rough graph $G=G_1\odot G_2=({G_1}_{\ast }\odot {G_2}_{\ast },G_1^{\ast }\odot G_2^{\ast }),$ where ${G_1}_{\ast }\odot {G_2}_{\ast }=(\underline{Q}{A}_1\odot \underline{Q}{A}_2,\underline{S}{B}_1\odot \underline{S}{B}_2)$ and $G_1^{\ast }\odot G_2^{\ast }=(\overline{Q}{A}_1\odot \overline{Q}{A}_2,\overline{S}{B}_1\odot \overline{S}{B}_2)$ are neutrosophic graphs, respectively, such that

(i) 

$\forall (v_1,v_2)\in Q{A}_1\times Q{A}_2$.

$$\begin{array}{cc}\hfill T_{(\overline{Q}{A}_1\odot \overline{Q}{A}_2)}(v_1,v_2)=& min\{T_{\overline{Q}{A}_1}(v_1),T_{\overline{Q}{A}_2}(v_2)\},T_{(\underline{Q}{A}_1\odot \underline{Q}{A}_2)}(v_1,v_2)=min\{T_{\underline{Q}{A}_1}(v_1),T_{\underline{Q}{A}_2}(v_2)\},\hfill \\ \hfill I_{(\overline{Q}{A}_1\odot \overline{Q}{A}_2)}(v_1,v_2)=& max\{I_{\overline{Q}{A}_1}(v_1),I_{\overline{Q}{A}_2}(v_2)\},I_{(\underline{Q}{A}_1\odot \underline{Q}{A}_2)}(v_1,v_2)=max\{I_{\underline{Q}{A}_1}(v_1),I_{\underline{Q}{A}_2}(v_2)\},\hfill \\ \hfill F_{(\overline{Q}{A}_1\odot \overline{Q}{A}_2)}(v_1,v_2)=& max\{F_{\overline{Q}{A}_1}(v_1),F_{\overline{Q}{A}_2}(v_2)\},F_{(\underline{Q}{A}_1\odot \underline{Q}{A}_2)}(v_1,v_2)=max\{F_{\underline{Q}{A}_1}(v_1),F_{\underline{Q}{A}_2}(v_2)\}.\hfill \end{array}$$

(ii) 

$\forall v_1{v}_2\in S{B}_2,v\in Q{A}_1$.

$$\begin{array}{cc}\hfill T_{(\overline{S}{B}_1\odot \overline{S}{B}_2)}\left((v,v_1)(v,v_2)\right)=& min\{T_{\overline{Q}{A}_1}(v),T_{\overline{S}{B}_2}(v_1{v}_2)\},\hfill \\ \hfill T_{(\underline{S}{B}_1\odot \underline{S}{B}_2)}\left((v,v_1)(v,v_2)\right)=& min\{T_{\underline{Q}{A}_1}(v),T_{\underline{S}{B}_2}(v_1{v}_2)\},\hfill \\ \hfill I_{(\overline{S}{B}_1\odot \overline{S}{B}_2)}\left((v,v_1)(v,v_2)\right)=& max\{I_{\overline{Q}{A}_1}(v),I_{\overline{S}{B}_2}(v_1{v}_2)\},\hfill \\ \hfill I_{(\underline{S}{B}_1\odot \underline{S}{B}_2)}\left((v,v_1)(v,v_2)\right)=& max\{I_{\underline{Q}{A}_1}(v),I_{\underline{S}{B}_2}(v_1{v}_2)\},\hfill \\ \hfill F_{(\overline{S}{B}_1\odot \overline{S}{B}_2)}\left((v,v_1)(v,v_2)\right)=& max\{F_{\overline{Q}{A}_1}(v),F_{\overline{S}{B}_2}(v_1{v}_2)\},\hfill \\ \hfill F_{(\underline{S}{B}_1\odot \underline{S}{B}_2)}\left((v,v_1)(v,v_2)\right)=& max\{F_{\underline{Q}{A}_1}(v),F_{\underline{S}{B}_2}(v_1{v}_2)\}.\hfill \end{array}$$

(iii) 

$\forall v_1{u}_1\in S{B}_1,v_1{u}_2\in S{B}_2$.

$$\begin{array}{cc}\hfill T_{(\overline{S}{B}_1\odot \overline{S}{B}_2)}\left((v_1,v_1)(u_1,u_2)\right)=& min\{T_{\overline{S}{B}_1}(v_1{u}_1),T_{\overline{S}{B}_2}(v_1{u}_2)\},\hfill \\ \hfill T_{(\underline{S}{B}_1\odot \underline{S}{B}_2)}\left((v_1,v_1)(u_1,u_2)\right)=& min\{T_{\underline{S}{B}_1}(v_1{u}_1),T_{\underline{S}{B}_2}(v_1{u}_2)\},\hfill \\ \hfill I_{(\overline{S}{B}_1\odot \overline{S}{B}_2}\left((v_1,v_1)(u_1,u_2)\right)=& max\{I_{\overline{S}{B}_1}(v_1{u}_1),I_{\overline{S}{B}_2}(v_1{u}_2)\},\hfill \\ \hfill I_{(\underline{S}{B}_1\odot \underline{S}{B}_2)}\left((v_1,v_1)(u_1,u_2)\right)=& max\{I_{\underline{S}{B}_1}(v_1{u}_1),I_{\underline{S}{B}_2}(v_1{u}_2)\},\hfill \\ \hfill F_{(\overline{S}{B}_1\odot \overline{S}{B}_2}\left((v_1,v_1)(u_1,u_2)\right)=& max\{F_{\overline{S}{B}_1}(v_1{u}_1),F_{\overline{S}{B}_2}(v_1{u}_2)\},\hfill \\ \hfill F_{(\underline{S}{B}_1\odot \underline{S}{B}_2)}\left((v_1,v_1)(u_1,u_2)\right)=& max\{F_{\underline{S}{B}_1}(v_1{u}_1),F_{\underline{S}{B}_2}(v_1{u}_2)\}.\hfill \end{array}$$

Definition 13.

The strong product of $G_1$ and $G_2$ is a neutrosophic soft rough graph $G=G_1\otimes G_2=({G_1}_{\ast }\otimes {G_2}_{\ast },G_1^{\ast }\otimes G_2^{\ast }),$ where ${G_1}_{\ast }\otimes {G_2}_{\ast }=(\underline{Q}{A}_1\otimes \underline{Q}{A}_2,\underline{S}{B}_1\otimes \underline{S}{B}_2)$ and $G_1^{\ast }\otimes G_2^{\ast }=(\overline{Q}{A}_1\otimes \overline{Q}{A}_2,\overline{S}{B}_1\otimes \overline{S}{B}_2)$ are neutrosophic graphs, respectively, such that

(i) 

$\forall (v_1,v_2)\in Q{A}_1\times Q{A}_2$.

$$\begin{array}{cc}\hfill T_{(\overline{Q}{A}_1\otimes \overline{Q}{A}_2)}(v_1,v_2)=& min\{T_{\overline{Q}{A}_1}(v_1),T_{\overline{Q}{A}_2}(v_2)\},T_{(\underline{Q}{A}_1\otimes \underline{Q}{A}_2)}(v_1,v_2)=min\{T_{\underline{Q}{A}_1}(v_1),T_{\underline{Q}{A}_2}(v_2)\},\hfill \\ \hfill I_{(\overline{Q}{A}_1\otimes \overline{Q}{A}_2)}(v_1,v_2)=& max\{I_{\overline{Q}{A}_1}(v_1),I_{\overline{Q}{A}_2}(v_2)\},I_{(\underline{Q}{A}_1\otimes \underline{Q}{A}_2)}(v_1,v_2)=max\{I_{\underline{Q}{A}_1}(v_1),I_{\underline{Q}{A}_2}(v_2)\},\hfill \\ \hfill F_{(\overline{Q}{A}_1\otimes \overline{Q}{A}_2)}(v_1,v_2)=& max\{F_{\overline{Q}{A}_1}(v_1),F_{\overline{Q}{A}_2}(v_2)\},F_{(\underline{Q}{A}_1\otimes \underline{Q}{A}_2)}(v_1,v_2)=max\{F_{\underline{Q}{A}_1}(v_1),F_{\underline{Q}{A}_2}(v_2)\}.\hfill \end{array}$$

(ii) 

$\forall v_1{v}_2\in S{B}_2,v\in Q{A}_1$.

$$\begin{array}{cc}\hfill T_{(\overline{S}{B}_1\otimes \overline{S}{B}_2)}\left((v,v_1)(v,v_2)\right)=& min\{T_{\overline{Q}{A}_1}(v),T_{\overline{S}{B}_2}(v_1{v}_2)\},\hfill \\ \hfill T_{(\underline{S}{B}_1\otimes \underline{S}{B}_2)}\left((v,v_1)(v,v_2)\right)=& min\{T_{\underline{Q}{A}_1}(v),T_{\underline{S}{B}_2}(v_1{v}_2)\},\hfill \\ \hfill I_{(\overline{S}{B}_1\otimes \overline{S}{B}_2)}\left((v,v_1)(v,v_2)\right)=& max\{I_{\overline{Q}{A}_1}(v),I_{\overline{S}{B}_2}(v_1{v}_2)\},\hfill \\ \hfill I_{(\underline{S}{B}_1\otimes \underline{S}{B}_2)}\left((v,v_1)(v,v_2)\right)=& max\{I_{\underline{Q}{A}_1}(v),I_{\underline{S}{B}_2}(v_1{v}_2)\},\hfill \\ \hfill F_{(\overline{S}{B}_1\otimes \overline{S}{B}_2)}\left((v,v_1)(v,v_2)\right)=& max\{F_{\overline{Q}{A}_1}(v),F_{\overline{S}{B}_2}(v_1{v}_2)\},\hfill \\ \hfill F_{(\underline{S}{B}_1\otimes \underline{S}{B}_2)}\left((v,v_1)(v,v_2)\right)=& max\{F_{\underline{Q}{A}_1}(v),F_{\underline{S}{B}_2}(v_1{v}_2)\}.\hfill \end{array}$$

(iii) 

$\forall v_1{v}_2\in S{B}_1,v\in Q{A}_2$.

$$\begin{array}{cc}\hfill T_{(\overline{S}{B}_1\otimes \overline{S}{B}_2)}\left((v_1,v)(v_2,v)\right)=& min\{T_{\overline{S}{B}_1}(v_1{v}_2),T_{\overline{Q}{A}_2}(v)\},\hfill \\ \hfill T_{(\underline{S}{B}_1\otimes \underline{S}{B}_2)}\left((v_1,v)(v_2,v)\right)=& min\{T_{\underline{S}{B}_1}(v_1{v}_2),T_{\underline{Q}{A}_2}(v)\},\hfill \\ \hfill I_{(\overline{S}{B}_1\otimes \overline{S}{B}_2)}\left((v_1,v)(v_2,v)\right)=& max\{I_{\overline{S}{B}_1}(v_1{v}_2),I_{\overline{Q}{A}_2}(v)\},\hfill \\ \hfill I_{(\underline{S}{B}_1\otimes \underline{S}{B}_2)}\left((v_1,v)(v_2,v)\right)=& max\{I_{\underline{S}{B}_1}(v_1{v}_2),I_{\underline{Q}{A}_2}(v)\},\hfill \\ \hfill F_{(\overline{S}{B}_1\otimes \overline{S}{B}_2)}\left((v_1,v)(v_2,v)\right)=& max\{F_{\overline{S}{B}_1}(v_1{v}_2),F_{\overline{Q}{A}_2}(v)\},\hfill \\ \hfill F_{(\underline{S}{B}_1\otimes \underline{S}{B}_2)}\left((v_1,v)(v_2,v)\right)=& max\{F_{\underline{S}{B}_1}(v_1{v}_2),F_{\underline{Q}{A}_2}(v)\}.\hfill \end{array}$$

(iv) 

$\forall v_1{u}_1\in S{B}_1,v_1{u}_2\in S{B}_2$.

$$\begin{array}{cc}\hfill T_{(\overline{S}{B}_1\otimes \overline{S}{B}_2)}\left((v_1,v_1)(u_1,u_2)\right)=& min\{T_{\overline{S}{B}_1}(v_1{u}_1),T_{\overline{S}{B}_2}(v_1{u}_2)\},\hfill \\ \hfill T_{(\underline{S}{B}_1\otimes \underline{S}{B}_2)}\left((v_1,v_1)(u_1,u_2)\right)=& min\{T_{\underline{S}{B}_1}(v_1{u}_1),T_{\underline{S}{B}_2}(v_1{u}_2)\},\hfill \\ \hfill I_{(\overline{S}{B}_1\otimes \overline{S}{B}_2}\left((v_1,v_1)(u_1,u_2)\right)=& max\{I_{\overline{S}{B}_1}(v_1{u}_1),I_{\overline{S}{B}_2}(v_1{u}_2)\},\hfill \\ \hfill I_{(\underline{S}{B}_1\otimes \underline{S}{B}_2)}\left((v_1,v_1)(u_1,u_2)\right)=& max\{I_{\underline{S}{B}_1}(v_1{u}_1),I_{\underline{S}{B}_2}(v_1{u}_2)\},\hfill \\ \hfill F_{(\overline{S}{B}_1\otimes \overline{S}{B}_2}\left((v_1,v_1)(u_1,u_2)\right)=& max\{F_{\overline{S}{B}_1}(v_1{u}_1),F_{\overline{S}{B}_2}(v_1{u}_2)\},\hfill \\ \hfill F_{(\underline{S}{B}_1\otimes \underline{S}{B}_2)}\left((v_1,v_1)(u_1,u_2)\right)=& max\{F_{\underline{S}{B}_1}(v_1{u}_1),F_{\underline{S}{B}_2}(v_1{u}_2)\}.\hfill \end{array}$$

Definition 14.

The composition of $G_1$ and $G_2$ is a neutrosophic soft rough graph $G=G_1\left[G_2\right]=({G_1}_{\ast }\left[{G_2}_{\ast }\right],G_1^{\ast }\left[G_2^{\ast }\right]),$ where ${G_1}_{\ast }\left[{G_2}_{\ast }\right]=(\underline{Q}{A}_1\left[\underline{Q}{A}_2\right],\underline{S}{B}_1\left[\underline{S}{B}_2\right])]$ and $G_1^{\ast }\left[G_2^{\ast }\right]=(\overline{Q}{A}_1\left[\overline{Q}{A}_2\right],\overline{S}{B}_1\left[\overline{S}{B}_2\right])$ are neutrosophic graphs, respectively, such that

(i) 

$\forall (v_1,v_2)\in Q{A}_1\times Q{A}_2$.

$$\begin{array}{cc}\hfill T_{(\overline{Q}{A}_1\times \overline{Q}{A}_2)}(v_1,v_2)=& min\{T_{\overline{Q}{A}_1}(v_1),T_{\overline{Q}{A}_2}(v_2)\},T_{(\underline{Q}{A}_1\times \underline{Q}{A}_2)}(v_1,v_2)=min\{T_{\underline{Q}{A}_1}(v_1),T_{\underline{Q}{A}_2}(v_2)\},\hfill \\ \hfill I_{(\overline{Q}{A}_1\times \overline{Q}{A}_2)}(v_1,v_2)=& max\{I_{\overline{Q}{A}_1}(v_1),I_{\overline{Q}{A}_2}(v_2)\},I_{(\underline{Q}{A}_1\times \underline{Q}{A}_2)}(v_1,v_2)=max\{I_{\underline{Q}{A}_1}(v_1),I_{\underline{Q}{A}_2}(v_2)\},\hfill \\ \hfill F_{(\overline{Q}{A}_1\times \overline{Q}{A}_2)}(v_1,v_2)=& max\{F_{\overline{Q}{A}_1}(v_1),F_{\overline{Q}{A}_2}(v_2)\},F_{(\underline{Q}{A}_1\times \underline{Q}{A}_2)}(v_1,v_2)=max\{F_{\underline{Q}{A}_1}(v_1),F_{\underline{Q}{A}_2}(v_2)\}.\hfill \end{array}$$

(ii) 

$\forall v_1{v}_2\in S{B}_2,v\in Q{A}_1$.

$$\begin{array}{cc}\hfill T_{(\overline{S}{B}_1\times \overline{S}{B}_2)}\left((v,v_1)(v,v_2)\right)=& min\{T_{\overline{Q}{A}_1}(v),T_{\overline{S}{B}_2}(v_1{v}_2)\},\hfill \\ \hfill T_{(\underline{S}{B}_1\times \underline{S}{B}_2)}\left((v,v_1)(v,v_2)\right)=& min\{T_{\underline{Q}{A}_1}(v),T_{\underline{S}{B}_2}(v_1{v}_2)\},\hfill \\ \hfill I_{(\overline{S}{B}_1\times \overline{S}{B}_2)}\left((v,v_1)(v,v_2)\right)=& max\{I_{\overline{Q}{A}_1}(v),I_{\overline{S}{B}_2}(v_1{v}_2)\},\hfill \\ \hfill I_{(\underline{S}{B}_1\times \underline{S}{B}_2)}\left((v,v_1)(v,v_2)\right)=& max\{I_{\underline{Q}{A}_1}(v),I_{\underline{S}{B}_2}(v_1{v}_2)\},\hfill \\ \hfill F_{(\overline{S}{B}_1\times \overline{S}{B}_2)}\left((v,v_1)(v,v_2)\right)=& max\{F_{\overline{Q}{A}_1}(v),F_{\overline{S}{B}_2}(v_1{v}_2)\},\hfill \\ \hfill F_{(\underline{S}{B}_1\times \underline{S}{B}_2)}\left((v,v_1)(v,v_2)\right)=& max\{F_{\underline{Q}{A}_1}(v),F_{\underline{S}{B}_2}(v_1{v}_2)\}.\hfill \end{array}$$

(iii) 

$\forall v_1{v}_2\in S{B}_1,v\in Q{A}_2$.

$$\begin{array}{cc}\hfill T_{(\overline{S}{B}_1\times \overline{S}{B}_2)}\left((v_1,v)(v_2,v)\right)=& min\{T_{\overline{S}{B}_1}(v_1{v}_2),T_{\overline{Q}{A}_2}(v)\},\hfill \\ \hfill T_{(\underline{S}{B}_1\times \underline{S}{B}_2)}\left((v_1,v)(v_2,v)\right)=& min\{T_{\underline{S}{B}_1}(v_1{v}_2),T_{\underline{Q}{A}_2}(v)\},\hfill \\ \hfill I_{(\overline{S}{B}_1\times \overline{S}{B}_2)}\left((v_1,v)(v_2,v)\right)=& max\{I_{\overline{S}{B}_1}(v_1{v}_2),I_{\overline{Q}{A}_2}(v)\},\hfill \\ \hfill I_{(\underline{S}{B}_1\times \underline{S}{B}_2)}\left((v_1,v)(v_2,v)\right)=& max\{I_{\underline{S}{B}_1}(v_1{v}_2),I_{\underline{Q}{A}_2}(v)\},\hfill \\ \hfill F_{(\overline{S}{B}_1\times \overline{S}{B}_2)}\left((v_1,v)(v_2,v)\right)=& max\{F_{\overline{S}{B}_1}(v_1{v}_2),F_{\overline{Q}{A}_2}(v)\},\hfill \\ \hfill F_{(\underline{S}{B}_1\times \underline{S}{B}_2)}\left((v_1,v)(v_2,v)\right)=& max\{F_{\underline{S}{B}_1}(v_1{v}_2),F_{\underline{Q}{A}_2}(v)\}.\hfill \end{array}$$

(iv) 

$\forall v_1{u}_1\in S{B}_1,v_1\ne u_2\in Q{A}_2$.

$$\begin{array}{cc}\hfill T_{(\overline{S}{B}_1\times \overline{S}{B}_2)}\left((v_1,v_1)(u_1,u_2)\right)=& min\{T_{\overline{S}{B}_1}(v_1{u}_1),T_{\overline{S}{B}_2}(v_1{u}_2)\},\hfill \\ \hfill T_{(\underline{S}{B}_1\times \underline{S}{B}_2)}\left((v_1,v_1)(u_1,u_2)\right)=& min\{T_{\underline{S}{B}_1}(v_1{u}_1),T_{\underline{S}{B}_2}(v_1{u}_2)\},\hfill \\ \hfill I_{(\overline{S}{B}_1\times \overline{S}{B}_2}\left((v_1,v_1)(u_1,u_2)\right)=& max\{I_{\overline{S}{B}_1}(v_1{u}_1),I_{\overline{S}{B}_2}(v_1{u}_2)\},\hfill \\ \hfill I_{(\underline{S}{B}_1\times \underline{S}{B}_2)}\left((v_1,v_1)(u_1,u_2)\right)=& max\{I_{\underline{S}{B}_1}(v_1{u}_1),I_{\underline{S}{B}_2}(v_1{u}_2)\},\hfill \\ \hfill F_{(\overline{S}{B}_1\times \overline{S}{B}_2}\left((v_1,v_1)(u_1,u_2)\right)=& max\{F_{\overline{S}{B}_1}(v_1{u}_1),F_{\overline{S}{B}_2}(v_1{u}_2)\},\hfill \\ \hfill F_{(\underline{S}{B}_1\times \underline{S}{B}_2)}\left((v_1,v_1)(u_1,u_2)\right)=& max\{F_{\underline{S}{B}_1}(v_1{u}_1),F_{\underline{S}{B}_2}(v_1{u}_2)\}.\hfill \end{array}$$

Definition 15.

Let $G=(\underline{G},\overline{G})$ be a neutrosophic soft rough graph. The complement of G, denoted by $\acute{\underline{G}}=(\acute{\underline{G}},\acute{\overline{G}})$ is a neutrosophic soft rough graph, where $\acute{\underline{G}}=(\acute{\underline{Q}A},\acute{\underline{S}B})$ and $\acute{\overline{G}}=(\acute{\overline{Q}A},\acute{\overline{S}B})$ are neutrosophic graphs such that

(i) 

$\forall v\in QA$.

$$\begin{array}{cc}\hfill \acute{T_{\overline{Q}A}}(v)& =T_{\overline{Q}A(v)},\acute{I_{\overline{Q}A}}(v)=I_{\overline{Q}A(v)},\acute{F_{\overline{Q}A}}(v)=F_{\overline{Q}A(v)},\hfill \\ \hfill \acute{T_{\underline{Q}A}}(v)& =T_{\underline{Q}A(v)},\acute{I_{\underline{Q}A}}(v)=I_{\underline{Q}A(v)},\acute{F_{\underline{Q}A}}(v)=F_{\underline{Q}A(v)}.\hfill \end{array}$$

(ii) 

$\forall v,u\in QA$.

$$\begin{array}{cc}\hfill \acute{T_{\overline{S}B}}(vu)& =min\{T_{\overline{Q}A}(v),T_{\overline{Q}A}(u)\}-T_{\overline{S}B}(vu),\hfill \\ \hfill \acute{I_{\overline{S}B}}(vu)& =max\{I_{\overline{Q}A}(v),I_{\overline{Q}A}(u)\}-I_{\overline{S}B}(vu),\hfill \\ \hfill \acute{F_{\overline{S}B}}(vu)& =max\{F_{\overline{Q}A}(v),F_{\overline{Q}A}(u)\}-F_{\overline{S}B}(vu),\hfill \\ \hfill \acute{T_{\underline{S}B}}(vu)& =min\{T_{\underline{Q}A}(v),T_{\underline{Q}A}(u)\}-T_{\underline{S}B}(vu),\hfill \\ \hfill \acute{I_{\underline{S}B}}(vu)& =max\{I_{\underline{Q}A}(v),I_{\underline{Q}A}(u)\}-I_{\overline{S}B}(vu),\hfill \\ \hfill \acute{F_{\underline{S}B}}(vu)& =max\{F_{\underline{Q}A}(v),F_{\underline{Q}A}(u)\}-F_{\underline{S}B}(vu).\hfill \end{array}$$

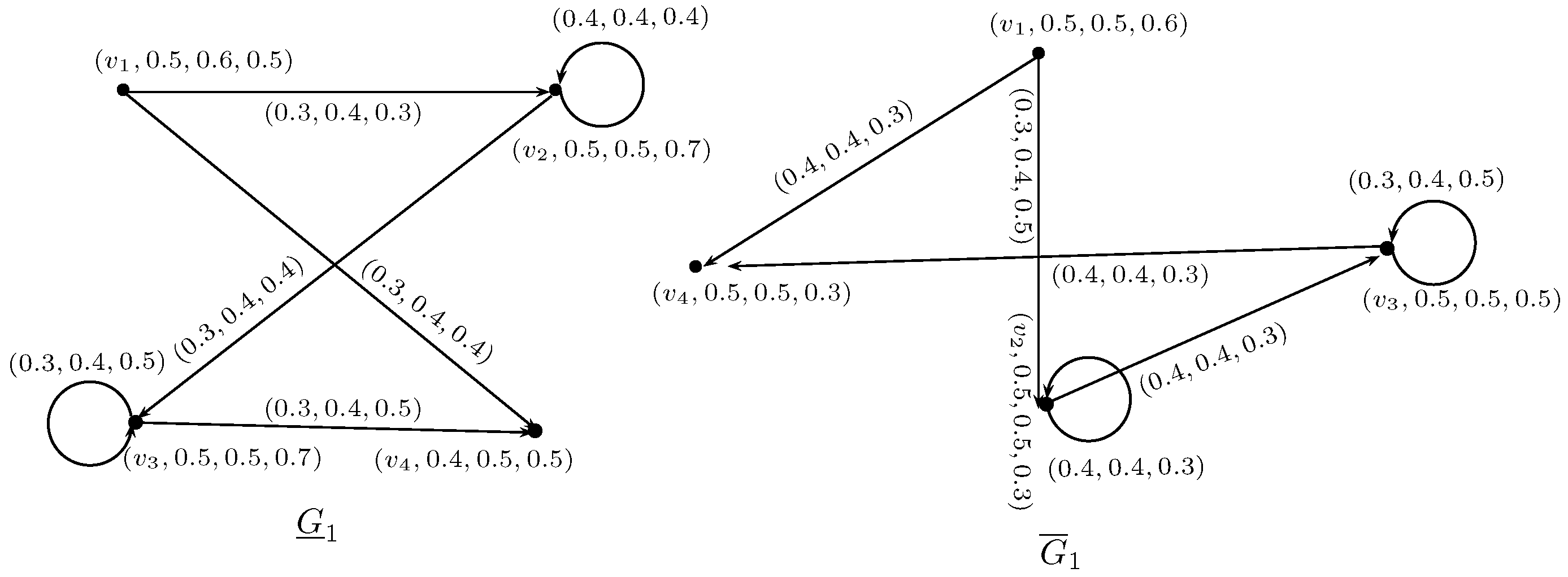
Example 8.

Consider an NSRGs G as shown in Figure 9.

The complement of G is $\acute{G}=(\acute{\underline{G}},\acute{\overline{G}})$ is obtained by using the Definition 15, where $\acute{\underline{G}}=(\acute{\underline{Q}A},\acute{\underline{S}B})$ and $\acute{\overline{G}}=(\acute{\overline{Q}A},\acute{\overline{S}B})$ are neutrosophic graphs as shown in Figure 10.

Definition 16.

A graph G is called self complement, if $G=\acute{\mathbf{G}},$ i.e.,

(i) 

$\forall v\in QA$.

$$\begin{array}{cc}\hfill \acute{T_{\overline{Q}A}}(v)& =T_{\overline{Q}A(v)},\acute{I_{\overline{Q}A}}(v)=I_{\overline{Q}A(v)},\acute{F_{\overline{Q}A}}(v)=F_{\overline{Q}A(v)},\hfill \\ \hfill \acute{T_{\underline{Q}A}}(v)& =T_{\underline{Q}A(v)},\acute{I_{\underline{Q}A}}(v)=I_{\underline{Q}A(v)},\acute{F_{\underline{Q}A}}(v)=F_{\underline{Q}A(v)}.\hfill \end{array}$$

(ii) 

$\forall v,u\in QA$.

$$\begin{array}{cc}\hfill \acute{T_{\overline{S}B}}(vu)& =T_{\overline{S}B}(vu),\acute{I_{\overline{S}B}}(vu)=I_{\overline{S}B}(vu),\acute{F_{\overline{S}B}}(vu)=F_{\overline{S}B}(vu),\hfill \\ \hfill \acute{T_{\underline{S}B}}(vu)& =T_{\underline{S}B}(vu),\acute{I_{\underline{S}B}}(vu)=I_{\underline{S}B}(vu),\acute{F_{\underline{S}B}}(vu)=F_{\underline{S}B}(vu).\hfill \end{array}$$

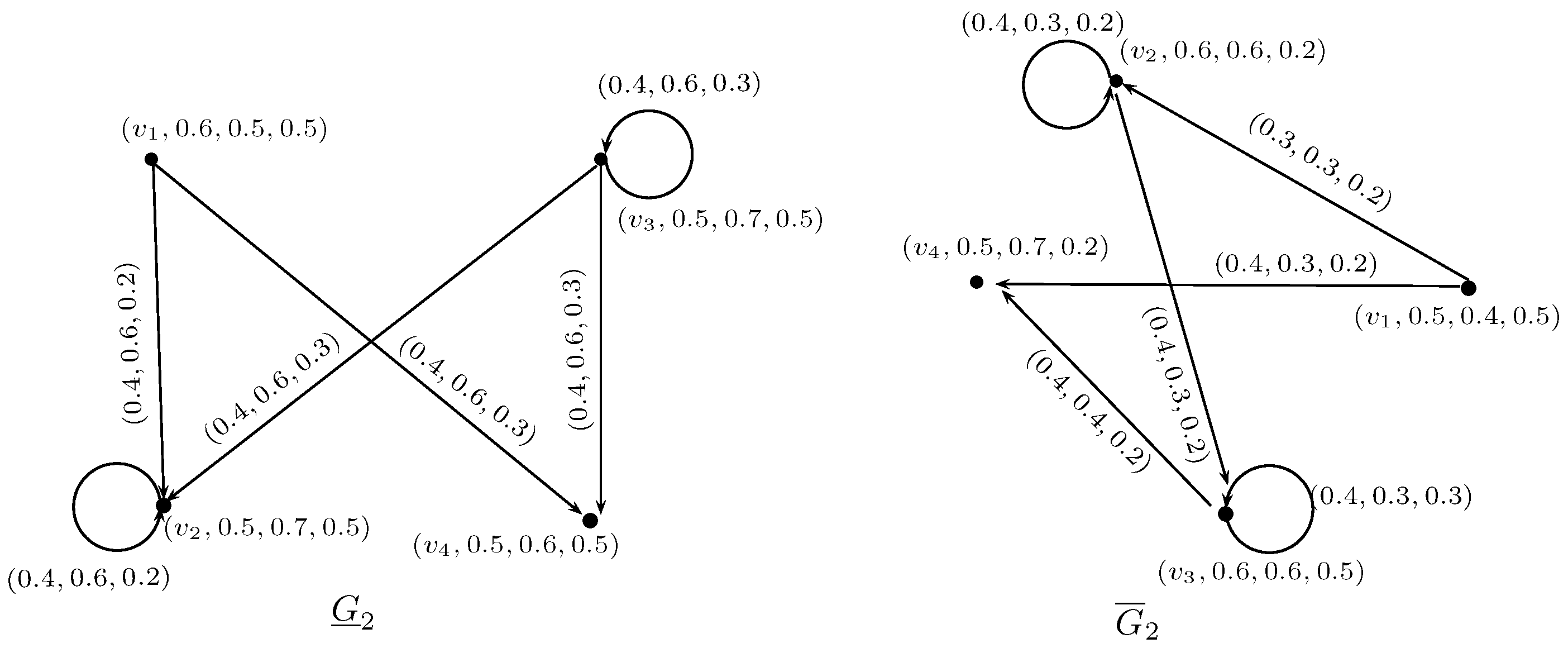
Definition 17.

A neutrosophic soft rough graph G is called strong neutrosophic soft rough graph if $\forall uv\in SB$,

$$\begin{array}{cc}\hfill T_{\overline{S}B}(vu)=& min\{T_{\overline{Q}A}(v),T_{\overline{Q}A}(u)\},I_{\overline{S}B}(vu)=max\{I_{\overline{Q}A}(v),I_{\overline{Q}A}(u)\}),F_{\overline{S}B}(vu)=max\{F_{\overline{Q}A}(v),F_{\overline{Q}A}(u)\},\hfill \\ \hfill T_{\underline{S}B}(vu)=& min\{T_{\underline{Q}A}(v),T_{\underline{Q}A}(u)\},I_{\underline{S}B}(vu)=max\{I_{\underline{Q}A}(v),I_{\underline{Q}A}(u)\},F_{\underline{S}B}(vu)=max\{F_{\underline{Q}A}(v),F_{\underline{Q}A}(u)\}.\hfill \end{array}$$

Example 9.

Consider a graph G such that $V=\{u,v,w\}$ and $E=\{uv,vw,wu\}$ as shown in Figure 11. Let $QA$ be a neutrosophic soft rough set of V and let $SB$ be a neutrosophic soft rough set of E defined in the

Table 9. Neutrosophic soft rough set on V.

V	$\overline{\mathit{Q}}\mathit{A}$	$\underline{\mathit{Q}}\mathit{A}$
u	$(0.8,0.5,0.2)$	$(0.7,0.5,0.2)$
v	$(0.9,0.5,0.1)$	$(0.7,0.5,0.2)$
w	$(0.7,0.5,0.1)$	$(0.7,0.5,0.2)$

and

Table 10. Neutrosophic soft rough set on E.

E	$\overline{\mathit{S}}\mathit{B}$	$\underline{\mathit{S}}\mathit{B}$
$uv$	$(0.8,0.5,0.2)$	$(0.7,0.5,0.2)$
$vw$	$(0.7,0.5,0.1)$	$(0.7,0.5,0.2)$
$wu$	$(0.7,0.5,0.2)$	$(0.7,0.5,0.2)$

, respectively.

Hence, $G=(QA,SB)$ is a strong neutrosophic soft rough graph.

Definition 18.

A neutrosophic soft rough graph G is called a complete neutrosophic soft rough graph if $\forall vu\in QA,$

$$\begin{array}{cc}\hfill T_{\overline{S}B}(vu)=& min\{T_{\overline{Q}A}(v),T_{\overline{Q}A}(u)\},I_{\overline{S}B}(vu)=max\{I_{\overline{Q}A}(v),I_{\overline{Q}A}(u)\},F_{\overline{S}B}(vu)=max\{F_{\overline{Q}A}(v),F_{\overline{Q}A}(u)\},\hfill \\ \hfill T_{\underline{S}B}(vu)=& min\{T_{\underline{Q}A}(v),T_{\underline{Q}A}(u)\},I_{\underline{S}B}(vu)=max\{I_{\underline{Q}A}(v),I_{\underline{Q}A}(u)\},F_{\underline{S}B}(vu)=max\{F_{\underline{Q}A}(v),F_{\underline{Q}A}(u)\}.\hfill \end{array}$$

Remark 2.

Every complete neutrosophic soft rough graph is a strong neutrosophic soft rough graph. However, the converse is not true.

Definition 19.

A neutrosophic soft rough graph G is isolated, if $\forall x,y\in QA$.

$$T_{\underline{S}B}(vu)=0,I_{\underline{S}B}(vu)=0,F_{\underline{S}B}(vu)=0,T_{\overline{S}B}(vu)=0,I_{\overline{S}B}(vu)=0,F_{\overline{S}B}(vu)=0.$$

Theorem 1.

The rejection of two neutrosophic soft rough graphs is a neutrosophic soft rough graph.

Proof. 

Let $G_1=({\underline{G}}_1,{\overline{G}}_1)$ and $G_2=({\underline{G}}_2,{\overline{G}}_2)$ be two NSRGs. Let $G=G_1|G_2=({\underline{G}}_1|{\underline{G}}_2,{\overline{G}}_1|{\overline{G}}_2)$ be the rejection of $G_1$ and $G_2$, where ${\underline{G}}_1|{\underline{G}}_2=(\underline{Q}{A}_1|\underline{Q}{A}_2,\underline{S}{B}_1|\underline{S}{B}_2)$ and ${\overline{G}}_1|{\overline{G}}_2=(\overline{Q}{A}_1|\overline{Q}{A}_2,\overline{S}{B}_1|\underline{S}{B}_2).$ We claim that $G=G_1|G_2$ is a neutrosophic soft rough graph. It is enough to show that $\underline{S}{B}_1|\underline{S}{B}_2$ and $\overline{S}{B}_1|\overline{S}{B}_2$ are neutrosophic relations on $\underline{Q}{A}_1|\underline{Q}{A}_2$ and $\overline{Q}{A}_1|\overline{Q}{A}_2,$ respectively. First, we show that $\underline{S}{B}_1|\underline{S}{B}_2$ is a neutrosophic relation on $\underline{Q}{A}_1|\underline{Q}{A}_2$.

If $v\in \underline{Q}{A}_1$, $v_1{v}_2\notin \underline{S}{B}_2$, then

$$\begin{array}{ccc}\hfill T_{(\underline{S}{B}_1|\underline{S}{B}_2)}((v,v_1)(v,v_2))& =& (T_{\underline{Q}{A}_1}(v)\wedge (T_{\underline{Q}{A}_2}(v_2)\wedge T_{\underline{Q}{A}_2}(v_2)))\hfill \\ \hfill & =& (T_{\underline{Q}{A}_1}(v)\wedge T_{\underline{Q}{A}_2}(v_2))\wedge (T_{\underline{Q}{A}_1}(v)\wedge T_{\underline{Q}{A}_2}(v_2))\hfill \\ \hfill & =& T_{(\underline{Q}{A}_1|\underline{Q}{A}_2)}(v,v_1)\wedge T_{(\underline{Q}{A}_1|\underline{Q}{A}_2)}(v,v_2)\hfill \\ \hfill T_{(\underline{S}{B}_1|\underline{S}{B}_2)}((v,v_1)(v,v_2))& =& T_{(\underline{Q}{A}_1|\underline{Q}{A}_2)}(v,v_1)\wedge T_{(\underline{Q}{A}_1|\underline{Q}{A}_2)}(v,v_2)\hfill \\ \hfill \mathrm{Similarly},I_{(\underline{S}{B}_1|\underline{S}{B}_2)}((v,v_1)(v,v_2))& =& I_{(\underline{Q}{A}_1|\underline{Q}{A}_2)}(v,v_1)\vee I_{(\underline{Q}{A}_1|\underline{Q}{A}_2)}(v,v_2)\hfill \\ \hfill F_{(\underline{S}{B}_1|\underline{S}{B}_2)}((v,v_1)(v,v_2))& =& F_{(\underline{Q}{A}_1|\underline{Q}{A}_2)}(v,v_1)\vee F_{(\underline{Q}{A}_1|\underline{Q}{A}_2)}(v,v_2).\hfill \end{array}$$

If $v_1{v}_2\notin \underline{S}{B}_1$, $v\in \underline{Q}{A}_2$, then

$$\begin{array}{ccc}\hfill T_{(\underline{S}{B}_1|\underline{S}{B}_2)}((v_1,v)(v_2,v))& =& ((T_{\underline{Q}{A}_1}(v_1)\wedge T_{\underline{Q}{A}_1}(v_2))\wedge T_{\underline{Q}{A}_2}(v))\hfill \\ \hfill & =& ((T_{\underline{Q}{A}_1}(v_1)\wedge T_{\underline{Q}{A}_2}(v))\wedge (T_{\underline{Q}{A}_1}(v_2)\wedge T_{\underline{Q}{A}_2}(v)))\hfill \\ \hfill & =& T_{(\underline{Q}{A}_1|\underline{Q}{A}_2)}(v_1,v)\wedge T_{(\underline{Q}{A}_1|\underline{Q}{A}_2)}(v_2,v)\hfill \\ \hfill T_{(\underline{S}{B}_1|\underline{S}{B}_2)}((v_1,v)(v_2,v))& =& T_{(\underline{Q}{A}_1|\underline{Q}{A}_2)}(v_1,v)\wedge T_{(\underline{Q}{A}_1|\underline{Q}{A}_2)}(v_2,v)\hfill \\ \hfill \mathrm{Similarly},I_{(\underline{S}{B}_1|\underline{S}{B}_2)}((v_1,v)(v_2,v))& =& I_{(\underline{Q}{A}_1|\underline{Q}{A}_2)}(v_1,v)\vee I_{(\underline{Q}{A}_1|\underline{Q}{A}_2)}(v_2,v)\hfill \\ \hfill F_{(\underline{S}{B}_1|\underline{S}{B}_2)}((v_1,v)(v_2,v))& =& F_{(\underline{Q}{A}_1|\underline{Q}{A}_2)}(v_1,v)\vee F_{(\underline{Q}{A}_1|\underline{Q}{A}_2)}(v_2,v).\hfill \end{array}$$

If $v_1{v}_2\notin \underline{S}{B}_1$, $u_1,u_2\notin \underline{S}{B}_2,$ then

$$\begin{array}{ccc}\hfill T_{(\underline{S}{B}_1|\underline{S}{B}_2)}((v_1,u_1)(v_2,u_2))& =& ((T_{\underline{Q}{A}_1}(v_1)\wedge T_{\underline{Q}{A}_1}(v_2))\wedge (T_{\underline{Q}{A}_2}(u_1)\wedge T_{\underline{Q}{A}_2}(u_2)))\hfill \\ \hfill & =& (T_{\underline{Q}{A}_1}(v_1)\wedge T_{\underline{Q}{A}_2}(u_1))\wedge (T_{\underline{Q}{A}_1}(v_2)\wedge T_{\underline{Q}{A}_2}(u_2))\hfill \\ \hfill & =& T_{(\underline{Q}{A}_1|\underline{Q}{A}_2)}(v_1,u_1)\wedge T_{(\underline{Q}{A}_1|\underline{Q}{A}_2)}(v_2,u_2)\hfill \\ \hfill T_{(\underline{S}{B}_1|\underline{S}{B}_2)}((v_1,u_1)(v_2,u_2))& =& T_{(\underline{Q}{A}_1|\underline{Q}{A}_2)}(v_1,u_1)\wedge T_{(\underline{Q}{A}_1|\underline{Q}{A}_2)}(u_1,u_2)\hfill \\ \hfill \mathrm{Similarly},I_{(\underline{S}{B}_1|\underline{S}{B}_2)}((v_1,u_1)(v_2,u_2))& =& I_{(\underline{Q}{A}_1|\underline{Q}{A}_2)}(v_1,u_1)\vee I_{(\underline{Q}{A}_1|\underline{Q}{A}_2)}(u_1,u_2)\hfill \\ \hfill F_{(\underline{S}{B}_1|\underline{S}{B}_2)}((v_1,u_1)(v_2,u_2))& =& F_{(\underline{Q}{A}_1|\underline{Q}{A}_2)}(v_1,u_1)\vee F_{(\underline{Q}{A}_1|\underline{Q}{A}_2)}(u_1,u_2).\hfill \end{array}$$

Thus, $\underline{S}{B}_1|\underline{S}{B}_2$ is a neutrosophic relation on $\underline{Q}{A}_1|\underline{Q}{A}_2$. Similarly, we can show that $\overline{S}{B}_1|\overline{S}{B}_2$ is a neutrosophic relation on $\overline{Q}{A}_1|\overline{Q}{A}_2$. Hence, G is a neutrosophic soft rough graph. ☐

Theorem 2.

The Cartesian product of two NSRGs is a neutrosophic soft rough graph.

Proof. 

Let $G_1=({\underline{G}}_1,{\overline{G}}_1)$ and $G_2=({\underline{G}}_2,{\overline{G}}_2)$ be two NSRGs. Let $G=G_1⋉G_2=({\underline{G}}_1⋉{\underline{G}}_2,{\overline{G}}_1⋉{\overline{G}}_2)$ be the Cartesian product of $G_1$ and $G_2$, where ${\underline{G}}_1⋉{\underline{G}}_2=(\underline{Q}{A}_1⋉\underline{Q}{A}_2,\underline{S}{B}_1⋉\underline{S}{B}_2)$ and ${\overline{G}}_1⋉{\overline{G}}_2=(\overline{Q}{A}_1⋉\overline{Q}{A}_2,\overline{S}{B}_1⋉\underline{S}{B}_2).$ We claim that $G=G_1⋉G_2$ is a neutrosophic soft rough graph. It is enough to show that $\underline{S}{B}_1⋉\underline{S}{B}_2$ and $\overline{S}{B}_1⋉\overline{S}{B}_2$ are neutrosophic relations on $\underline{Q}{A}_1⋉\underline{Q}{A}_2$ and $\overline{Q}{A}_1⋉\overline{Q}{A}_2,$ respectively. We have to show that $\underline{S}{B}_1⋉\underline{S}{B}_2$ is a neutrosophic relation on $\underline{Q}{A}_1⋉\underline{Q}{A}_2$.

If $v\in \underline{Q}{A}_1$, $v_1{u}_1\in \underline{S}{B}_2$, then

$$\begin{array}{ccc}\hfill T_{(\underline{S}{B}_1⋉\underline{S}{B}_2)}((v,v_1)(v,u_1))& =& T_{(\underline{Q}{A}_1)}(v)\wedge T_{(\underline{S}{B}_2)}(v_1{u}_1)\hfill \\ \hfill & \le & T_{(\underline{Q}{A}_1)}(v)\wedge (T_{(\underline{Q}{A}_2)}(v_1)\wedge T(\underline{Q}{A}_2)(u_1))\hfill \\ \hfill & =& (T_{(\underline{Q}{A}_1)}(v)\wedge T_{(\underline{Q}{A}_2)}(v_1))\wedge (T_{(\underline{Q}{A}_1)}(v)\wedge T_{(\underline{Q}{A}_2)}(u_1))\hfill \\ \hfill & =& T_{(\underline{Q}{A}_1⋉\underline{Q}{A}_2)}(v,v_1)\wedge T_{(\underline{Q}{A}_1⋉\underline{Q}{A}_2)}(v,u_1)\hfill \\ \hfill T_{(\underline{S}{B}_1⋉\underline{S}{B}_2)}((v,v_1)(v,u_1))& \le & T_{(\underline{Q}{A}_1⋉\underline{Q}{A}_2)}(v,v_1)\wedge T_{(\underline{Q}{A}_1⋉\underline{Q}{A}_2)}(v,u_1)\hfill \\ \hfill \mathrm{Similarly},I_{(\underline{S}{B}_1⋉\underline{S}{B}_2)}((v,v_1)(v,u_1))& \le & I_{(\underline{Q}{A}_1⋉\underline{Q}{A}_2)}(v,v_1)\vee I_{(\underline{Q}{A}_1⋉\underline{Q}{A}_2)}(v,u_1)\hfill \\ \hfill F_{(\underline{S}{B}_1⋉\underline{S}{B}_2)}((v,v_1)(v,u_1))& \le & F_{(\underline{Q}{A}_1⋉\underline{Q}{A}_2)}(v,v_1)\vee F_{(\underline{Q}{A}_1⋉\underline{Q}{A}_2)}(v,u_1).\hfill \end{array}$$

If $v_1{u}_1\in \underline{S}{B}_1$, $z\in \underline{Q}{A}_2$, then

$$\begin{array}{ccc}\hfill T_{(\underline{S}{B}_1⋉\underline{S}{B}_2)}((v_1,z)(u_1,z))& =& T_{(\underline{S}{B}_1)}(v_1{u}_1)\wedge T_{(\underline{Q}{A}_2)}(z)\hfill \\ \hfill & \le & (T_{(\underline{Q}{A}_1)(v_1)\wedge (\underline{Q}{A}_1)}(u_1))\wedge T_{(\underline{Q}{A}_2)}(z)\hfill \\ \hfill & =& T_{(\underline{Q}{A}_1⋉\underline{Q}{A}_2)}(v_1,z)\wedge T_{(\underline{Q}{A}_1⋉\underline{Q}{A}_2)}(u_1,z)\hfill \\ \hfill T_{(\underline{S}{B}_1⋉\underline{S}{B}_2)}((v_1,z)(u_1,z))& \le & T_{(\underline{Q}{A}_1⋉\underline{Q}{A}_2)}(v_1,z)\wedge T_{(\underline{Q}{A}_1⋉\underline{Q}{A}_2)}(u_1,z)\hfill \\ \hfill \mathrm{Similarly},I_{(\underline{S}{B}_1⋉\underline{S}{B}_2)}((v_1,z)(u_1,z))& \le & I_{(\underline{Q}{A}_1⋉\underline{Q}{A}_2)}(v_1,z)\vee I_{(\underline{Q}{A}_1⋉\underline{Q}{A}_2)}(u_1,z)\hfill \\ \hfill F_{(\underline{S}{B}_1⋉\underline{S}{B}_2)}((v_1,z)(u_1,z))& \le & F_{(\underline{Q}{A}_1⋉\underline{Q}{A}_2)}(v_1,z)\vee F_{(\underline{Q}{A}_1⋉\underline{Q}{A}_2)}(u_1,z).\hfill \end{array}$$

Therefore, $\underline{S}{B}_1⋉\underline{S}{B}_2$ is a neutrosophic relation on $\underline{Q}{A}_1⋉\underline{Q}{A}_2$. Similarly, $\overline{S}{B}_1⋉\overline{S}{B}_2$ is a neutrosophic relation on $\overline{Q}{A}_1⋉\overline{Q}{A}_2.$ Hence, G is a neutrosophic rough graph. ☐

Theorem 3.

The cross product of two neutrosophic soft rough graphs is a neutrosophic soft rough graph.

Proof. 

Let $G_1=({\underline{G}}_1,{\overline{G}}_1)$ and $G_2=({\underline{G}}_2,{\overline{G}}_2)$ be two NSRGs. Let $G=G_1⊚G_2=({\underline{G}}_1⊚{\underline{G}}_2,{\overline{G}}_1⊚{\overline{G}}_2)$ be the cross product of $G_1$ and $G_2$, where ${\underline{G}}_1⊚{\underline{G}}_2=(\underline{Q}{A}_1⊚\underline{Q}{A}_2,\underline{S}{B}_1⊚\underline{S}{B}_2)$ and ${\overline{G}}_1⊚{\overline{G}}_2=(\overline{Q}{A}_1⊚\overline{Q}{A}_2,\overline{S}{B}_1⊚\underline{S}{B}_2).$ We claim that $G=G_1⊚G_2$ is a neutrosophic soft rough graph. It is enough to show that $\underline{S}{B}_1⊚\underline{S}{B}_2$ and $\overline{S}{B}_1⊚\overline{S}{B}_2$ are neutrosophic relations on $\underline{Q}{A}_1⊚\underline{Q}{A}_2$ and $\overline{Q}{A}_1⊚\overline{Q}{A}_2,$ respectively. First, we show that $\underline{S}{B}_1⊚\underline{S}{B}_2$ is a neutrosophic relation on $\underline{Q}{A}_1⊚\underline{Q}{A}_2$.

If $v_1{u}_1\in \underline{S}{B}_1$, $v_1{u}_2\in \underline{S}{B}_2$, then

$$\begin{array}{ccc}\hfill T_{(\underline{S}{B}_1⊚\underline{S}{B}_2)}((v_1,v_1)(u_1,u_2))& =& T_{(\underline{S}{B}_1)}(v_1{u}_1)\wedge T_{(\underline{S}{B}_2)}(v_1{u}_2)\hfill \\ \hfill & \le & (T_{(\underline{Q}{A}_1)}(v_1)\wedge T_{(\underline{Q}{A}_1)}(u_1)\wedge (T_{(\underline{Q}{A}_2)}(v_1)\wedge T_{(\underline{Q}{A}_2)}(u_2))\hfill \\ \hfill & =& (T_{(\underline{Q}{A}_1)}(v_1)\wedge T_{(\underline{Q}{A}_2)}(v_1))\wedge (T_{(\underline{Q}{A}_1)}(u_1)\wedge T_{(\underline{Q}{A}_2)}(u_2))\hfill \\ \hfill & =& T_{(\underline{Q}{A}_1⊚\underline{Q}{A}_2)}(v_1,v_1)\wedge T_{(\underline{Q}{A}_1⊚\underline{Q}{A}_2)}(u_1,u_2)\hfill \\ \hfill T_{(\underline{S}{B}_1⊚\underline{S}{B}_2)}((v_1,v_1)(u_1,u_2))& \le & T_{(\underline{Q}{A}_1⊚\underline{Q}{A}_2)}(v_1,v_1)\wedge T_{(\underline{Q}{A}_1⊚\underline{Q}{A}_2)}(v,u_2)\hfill \\ \hfill \mathrm{Similarly},I_{(\underline{S}{B}_1⊚\underline{S}{B}_2)}((v_1,v_1)(u_1,u_2))& \le & I_{(\underline{Q}{A}_1⊚\underline{Q}{A}_2)}(v_1,v_1)\vee I_{(\underline{Q}{A}_1⊚\underline{Q}{A}_2)}(v,u_2)\hfill \\ \hfill F_{(\underline{S}{B}_1⊚\underline{S}{B}_2)}((v_1,v_1)(u_1,u_2))& \le & F_{(\underline{Q}{A}_1⊚\underline{Q}{A}_2)}(v_1,v_1)\vee F_{(\underline{Q}{A}_1⊚\underline{Q}{A}_2)}(v,u_2).\hfill \end{array}$$

Thus, $\underline{S}{B}_1⊚\underline{S}{B}_2$ is a neutrosophic relation on $\underline{Q}{A}_1⊚\underline{Q}{A}_2$. Similarly, we can show that $\overline{S}{B}_1⊚\overline{S}{B}_2$ is a neutrosophic relation on $\overline{Q}{A}_1⊚\overline{Q}{A}_2$. Hence, G is a neutrosophic soft rough graph. ☐

3. Application

In this section, we apply the concept of NSRSs to a decision-making problem. In recent times, the object recognition problem has gained considerable importance. The object recognition problem can be considered as a decision-making problem, in which final identification of objects is founded on a given set of information. A detailed description of the algorithm for the selection of most suitable objects based on an available set of alternatives is given, and purposed decision-making method can be used to calculate lower and upper approximation operators to progress deep concerns of the problem. The presented algorithms can be applied to avoid lengthy calculations when dealing with large number of objects. This method can be applied in various domains for multi-criteria selection of objects.

Selection of Most Suitable Generic Version of Brand Name Medicine

In the pharmaceutical industry, different pharmaceutical companies develop, produce and discover pharmaceutical medicine (drugs) for use as medication. These pharmaceutical companies deals with “brand name medicine” and “generic medicine”. Brand name medicine and generic medicine are bioequivalent, and have a generic medicine rate and element of absorption. Brand name medicine and generic medicine have the same active ingredients, but the inactive ingredients may differ. The most important difference is cost. Generic medicine is less expensive as compared to brand name comparators. Usually, generic drug manufacturers face competition to produce cost less products. The product may possibly be slightly dissimilar in color, shape, or markings. The major difference is cost. We consider a brand name drug “$u=\mathrm{Loratadine}$” used for seasonal allergies medication. Consider

$$\begin{array}{ccc}\hfill V& =& \{u_1=\mathrm{Triamcinolone},u_2=\mathrm{Cetirizine}/\mathrm{Pseudoephedrine},\hfill \\ \hfill & & u_3=\mathrm{Pseudoephedrine},u_4=\mathrm{loratadine}/\mathrm{pseudoephedrine},\hfill \\ \hfill & & u_5=\mathrm{Fluticasone}\}\hfill \end{array}$$

is a set of generic versions of “Loratadine”. We want to select the most suitable generic version of Loratadine on the basis of parameters $e_1=$ Highly soluble, $e_2=$ Highly permeable, $e_3=$ Rapidly dissolving. $\mathbb{M}=\{e_1,e_2,e_3\}$ be a set of paraments. Let Q be a neutrosophic soft relation from V to parameter set M, and describe truth-membership, indeterminacy-membership and false-membership degrees of generic version medicine corresponding to the parameters as shown in

Table 11. Neutrosophic soft set $(Q,M)$.

Q	${\mathit{u}}_{\mathbf{1}}$	${\mathit{u}}_{\mathbf{2}}$	${\mathit{u}}_{\mathbf{3}}$	${\mathit{u}}_{\mathbf{4}}$	${\mathit{u}}_{\mathbf{5}}$
$e_1$	$(0.4,0.5,0.6)$	$(0.5,0.3,0.6)$	$(0.7,0.2,0.3)$	$(0.5,0.7,0.5)$	$(0.6,0.5,0.4)$
$e_2$	$(0.7,0.3,0.2)$	$(0.3,0.4,0.3)$	$(0.6,0.5,0.4)$	$(0.8,0.4,0.6)$	$(0.7,0.8,0.5)$
$e_3$	$(0.6,0.3,0.4)$	$(0.7,0.2,0.3)$	$(0.7,0.2,0.4)$	$(0.8,0.7,0.6)$	$(0.7,0.3,0.5)$

.

Suppose $A=\{(e_1,0.2,0.4,0.5),(e_2,0.5,0.6,0.4),(e_3,0.7,0.5,0.4)\}$ is the most favorable object that is an NS on the parameter set M under consideration. Then, $(\underline{Q}(A),\overline{Q}(A))$ is an NSRS in NSAS $(V,M,Q),$ where

$$\begin{array}{ccc}\hfill \overline{Q}(A)& =& \{(u_1,0.6,0.5,0.4),(u_2,0.7,0.4,0.4),(u_3,0.7,0.4,0.4),(u_4,0.7,0.6,0.5),(u_5,0.7,0.5,0.5)\},\hfill \\ \hfill \underline{Q}(A)& =& \{(u_1,0.5,0.6,0.4),(u_2,0.5,0.6,0.5),(u_3,0.3,0.3,0.5),(u_4,0.5,0.6,0.5),(u_5,0.4,0.5,0.5)\}.\hfill \end{array}$$

Let $E=\{u_1{v}_2,u_1{u}_3,u_4{u}_1,u_2{u}_3,u_5{u}_3,u_2{u}_4,u_2{u}_5\}\subseteq \acute{V}$ and $L=\{e_1{e}_3,e_2{e}_1,e_3{e}_2\}\subseteq \acute{\mathbb{M}}$.

Then, a neutrosophic soft relation S on E (from L to E) can be defined as follows in

Table 12. Neutrosophic soft relation S.

S	${\mathit{u}}_{\mathbf{1}}{\mathit{u}}_{\mathbf{2}}$	${\mathit{u}}_{\mathbf{1}}{\mathit{u}}_{\mathbf{3}}$	${\mathit{u}}_{\mathbf{4}}{\mathit{u}}_{\mathbf{1}}$	${\mathit{u}}_{\mathbf{2}}{\mathit{u}}_{\mathbf{3}}$	${\mathit{u}}_{\mathbf{5}}{\mathit{u}}_{\mathbf{3}}$	${\mathit{u}}_{\mathbf{2}}{\mathit{u}}_{\mathbf{4}}$	${\mathit{u}}_{\mathbf{2}}{\mathit{u}}_{\mathbf{5}}$
$e_1{e}_2$	(0.3, 0.4 ,0.2)	$(0.4,0.4,0.5)$	$(0.4,0.4,0.5)$	$(0.6,0.3,0.4)$	$(0.4,0.2,0.2)$	$(0.4,0.4,0.2)$	$(0.4,0.3,0.4)$
$e_2{e}_3$	(0.5 ,0.4 ,0.1)	$(0.4,0.3,0.2)$	$(0.4,0.3,0.2)$	$(0.3,0.3,0.2)$	$(0.6,0.2,0.4)$	$(0.3,0.2,0.1)$	$(0.3,0.3,0.2)$
$e_1{e}_3$	(0.4,0.4,0.1)	$(0.4,0.2,0.2)$	$(0.4,0.2,0.2)$	$(0.5,0.3,0.3)$	$(0.4,0.2,0.3)$	$(0.4,0.3,0.1)$	$(0.5,0.3,0.2)$

:

Let $B=\{(e_1{e}_2,0.2,0.4,0.5),(e_2{e}_3,0.5,0.4,0.4),(e_1{e}_3,0.5,0.2,0.5)\}$ be an NS on L that describes some relationship between the parameters under consideration; then, $SB=(\underline{S}B,\overline{S}B)$ is an NSRR, where

$$\begin{array}{ccc}\hfill \overline{S}B& =& \{(u_1{u}_2,0.5,0.4,0.4),(u_1{u}_3,0.4,0.2,0.4),(u_4{u}_1,0.4,0.2,0.4),(u_2{u}_3,0.5,0.3,0.4),\hfill \\ \hfill & & (u_5{u}_3,0.5,0.2,0.4),(u_2{u}_4,0.4,0.3,0.4),(u_2{u}_5,0.5,0.3,0.4)\},\hfill \\ \hfill \underline{S}B& =& \{(u_1{u}_2,0.2,0.4,0.4)(u_1{u}_3,0.5,0.4,0.4),(u_4{u}_1,0.5,0.4,0.4),(u_2{u}_3,0.4,0.4,0.5),\hfill \\ \hfill & & (u_5{u}_3,0.2,0.4,0.4),(u_2{u}_4,0.2,0.4,0.4),(u_2{u}_5,0.4,0.4,0.5)\}.\hfill \end{array}$$

Thus, $G=(\underline{G},\overline{G})$ is an NSRG as shown in Figure 12.

In [3], the sum of two neutrosophic numbers is defined.

Definition 20.

[3] Let C and D be two single valued neutrosophic numbers, and the sum of two single valued neutrosophic number is defined as follows:

$$C\oplus D=<T_C+T_D-T_C\times T_D,I_C\times I_D,F_C\times F_D>.$$

(1)

Algorithm 1: Algorithm for selection of most suitable objects

1. Input the number of elements in vertex set $V=\{u_1,u_2,\dots ,u_n\}$. 2. Input the number of elements in parameter set $\mathbb{M}=\{e_1,e_2,\dots ,e_m\}$. 3. Input a neutrosophic soft relation Q from V to $\mathbb{M}$. 4. Input a neutrosophic set A on M. 5. Compute neutrosophic soft rough vertex set $QA=(\underline{Q}A,\overline{Q}(A))$. 6. Input the number of elements in edge set $E=\{u_1{u}_1,u_1{u}_2,\dots ,u_k{u}_1\}$. 7. Input the number of elements in parameter set $\acute{\mathbb{M}}=\{e_1{e}_1,e_1{e}_2,\dots ,e_l{e}_1\}$. 8. Input a neutrosophic soft relation S from $\acute{V}$ to $\acute{\mathbb{M}}$. 9. Input a neutrosophic set B on $\acute{\mathbb{M}}$. 10. Compute neutrosophic soft rough edge set $SB=(\underline{S}B,\overline{S}(B))$. 11. Compute neutrosophic set $\alpha =(T_{\alpha }(u_i),I_{\alpha }(u_i),F_{\alpha }(u_i))$, where $$\begin{array}{ccc}\hfill T_{\alpha }(u_i)& =& T_{\overline{Q}(A)}(u_i)+T_{\underline{Q}(A)}(u_i)-T_{\overline{Q}(A)}(u_i)\times T_{\underline{Q}(A)}(u_i),\hfill \\ \hfill I_{\alpha }(u_i)& =& T_{\overline{Q}(A)}(u_i)\times T_{\underline{Q}(A)}(u_i),\hfill \\ \hfill F_{\alpha }(u_i)& =& F_{\overline{Q}(A)}(u_i)\times F_{\underline{Q}(A)}(u_i).\hfill \end{array}$$ 12. Compute neutrosophic set $\beta =(T_{\beta }(u_i{u}_i),I_{\beta }(u_i{u}_j),F_{\beta }(u_i{u}_j))$, where $$\begin{array}{ccc}\hfill T_{\beta }(u_i{u}_j)& =& T_{\overline{S}(B)}(u_i{u}_j)+T_{\underline{S}(B)}(u_i{u}_j)-T_{\overline{S}(B)}(u_i{u}_j)\times T_{\underline{S}(B)}(u_i{u}_j),\hfill \\ \hfill I_{\beta }(u_i{u}_j)& =& T_{\overline{S}(B)}(u_i{u}_j)\times T_{\underline{S}(B)}(u_i{u}_j),\hfill \\ \hfill F_{\beta }(u_i{u}_j)& =& F_{\overline{S}(B)}(u_i{u}_j)\times F_{\underline{S}(B)}(u_i{u}_j).\hfill \end{array}$$ 13. Calculate the score values of each object $u_i$, and the score function is defined as follows: $$\tilde{S}(u_i)=\sum _{u_i{u}_j\in E}{\displaystyle \frac{T_{\alpha }(u_j)+I_{\alpha }(u_j)-F_{\alpha }(u_j)}{3-(T_{\beta }(u_i{u}_j)+I_{\beta }(u_i{u}_j)-F_{\beta }(u_i{u}_j))}}.$$ 14. The decision is $S_i$ if $S_i=\underset{i=1}{\overset{n}{max}}{\tilde{S}}_i$. 15. If i has more than one value, then any one of $S_i$ may be chosen.

The sum of UNSRS $\overline{Q}A$ and the LNSRS $\underline{Q}A$ and sum of LNSRR $\underline{S}B$ and the UNSRR $\overline{S}B$ are NSs $\overline{Q}A\oplus \underline{Q}A$ and $\overline{S}B\oplus \underline{S}B$, respectively defined by

$$\begin{array}{ccc}\hfill \alpha =\overline{Q}A\oplus \underline{Q}A& =& \{(u_1,0.8,0.3,0.16),(u_2,0.85,0.24,0.2),(u_3,0.79,0.2,0.2),(u_4,0.85,0.36,0.25),\hfill \\ \hfill & & (u_5,0.82,0.25,0.25)\},\hfill \\ \hfill \beta =\overline{S}B\oplus \underline{S}B& =& \{(u_1{u}_2,0.6,0.16,0.16),(u_1{u}_3,0.7,0.8,0.16),(u_4{u}_1,0.7,0.8,0.16),(u_2{u}_3,0.7,\hfill \\ \hfill & & 0.12,0.2),(u_5{u}_3,0.6,0.08,0.16),(u_2{u}_4,0.52,0.12,0.16),(u_2{u}_5,0.7,0.12,0.2)\}.\hfill \end{array}$$

The score function $\tilde{S}(u_k)$ defines for each generic version medicine $u_i\in V$,

$$\tilde{S}(u_i)=\sum _{u_i{u}_j\in E}\frac{T_{\alpha }(u_j)+I_{\alpha }(u_j)-F_{\alpha }(u_j)}{3-(T_{\beta }(u_i{u}_j)+I_{\beta }(u_i{u}_j)-F_{\beta }(u_i{u}_j))}$$

(2)

and $u_k$ with the larger score value $u_k=\underset{i}{max}S(u_i)$ is the most suitable generic version medicine. By calculations, we have

$$\begin{array}{c}\hfill \tilde{S}(u_1)=0.88,\tilde{S}(u_2)=0.69,\tilde{S}(u_3)=0.26\tilde{S}(u_4)=0.57,\mathrm{and}\tilde{S}(u_5)=0.33.\end{array}$$

(3)

Here, $u_1$ is the optimal decision, and the most suitable generic version of “Loratadine” is “Triamcinolone”. We have used software MATLAB (version 7, MathWorks, Natick, MA, USA) for calculating the required results in the application. The algorithm is given in Algorithm 1. The algorithm of the program is general for any number of objects with respect to certain parameters.

4. Conclusions

Rough set theory can be considered as an extension of classical set theory. Rough set theory is a very useful mathematical model to handle vagueness. NS theory, RS theory and SS theory are three useful distinguished approaches to deal with vagueness. NS and RS models are used to handle uncertainty, and combining these two models with another remarkable model of SSs gives more precise results for decision-making problems. In this paper, we have presented the notion of NSRGs and investigated some properties of NSRGs in detail. The notion of NSRGs can be utilized as a mathematical tool to deal with imprecise and unspecified information. In addition, a decision-making method based on NSRGs is proposed. This research work can be extended to (1) Rough bipolar neutrosophic soft sets; (2) Bipolar neutrosophic soft rough sets, (3) Interval-valued bipolar neutrosophic rough sets, and (4) Soft rough neutrosophic graphs.