Abstract
Ordered fuzzy numbers are defined by Kosiński. In this way, he was going to supplement a fuzzy number by orientation. A significant drawback of Kosiński’s theory is that there exist such ordered fuzzy numbers which, in fact, are not fuzzy numbers. For this reason, a fully formalized correct definition of ordered fuzzy numbers is proposed here. Also, the arithmetic proposed by Kosiński has a significant disadvantage. The space of ordered fuzzy numbers is not closed under Kosiński’s addition. On the other hand, many mathematical applications require the considered space be closed under used arithmetic operations. Therefore, the Kosinski’s theory is modified in this way that the space of ordered fuzzy numbers is closed under revised arithmetic operations. In addition, it is shown that the multiple revised sum of finite sequence of ordered fuzzy numbers depends on its summands ordering.
1. Introduction
The ordered fuzzy numbers (OFNs) were introduced by Kosiński and his associates in a series of papers [1,2,3,4] as an extension of the notion of fuzzy numbers (FNs). For this reason, ordered fuzzy numbers are increasingly called Kosinski’s numbers [5,6]. The monograph [7] is a competent source of information about the contemporary state of knowledge on OFN.
OFNs have already begun to find their use in operations research applied in economics and finance. Examples of such applications can already be found in the works [8,9,10,11,12].
It is a common view that the theory of fuzzy sets is very extensive and very helpful in many applications. On the other hand, the previous Kosiński’s theory of ordered fuzzy number is poor (see [7]). Thus, it is obvious that considerations with use the theory fuzzy sets may be much more fruitful. Kosiński [4] has shown that there exist improper OFNs which cannot be represented by a pair of FN and orientation. It means that we cannot apply any knowledge of fuzzy sets to solve practical problems described by improper OFN. Therefore, considerations with improper use of OFNs may not be fruitful. Thus, the main purpose of this article is to revise Kosiński’s theory. The presented study limits the family of all OFNs to the family of all proper OFNs which are represented by a pair of FN and orientation. This goal will be achieved by modifying the OFNs’ definition.
Kosiński [1,2,3] has determined OFNs’ arithmetic as an extension of results obtained by Goetschel and Voxman [13] for fuzzy numbers. Moreover, Kosiński [4] has shown that there exist such proper OFNs that their Kosiński’s sum is equal to an improper OFN. This means that the family of all proper OFNs is not closed under Kosiński’s addition. On the other hand, most mathematical applications require the considered objects’ family be closed under used arithmetic operations. For this reason, the revised arithmetic is introduced for OFNs.
The linear space of FNs is usually determined using dot product and sum [14] defined by means of the Zadeh’s Extension Principle [15,16,17]. The last goal of this paper is to investigate the linear space of OFNs determined by dot products and revised sums of OFNs. In this article, the discussion on linear space properties is limited due to exploration the perceived disadvantages associated with the revised sums. Many mathematical applications require the finite multiple sums to be independent on summands ordering. Any associative and commutative sum satisfies this property. Therefore, the associativity and commutativity of revised sum will also be considered. All considerations are based on three counterexamples with use of trapezoidal or triangle OFNs. This approach is sufficient to falsify theses formulated for the general case of OFNs. On the other hand, all previously known uses of ordered fuzzy number uses are limited to applications of trapezoidal OFNs.
2. Elements of Fuzzy Numbers Theory
Zadeh [18] introduced the fuzzy sets theory to deal with linguistic variables problems. A fuzzy set is an extension of a crisp set. The crisp sets use only the notions of a full membership or non-membership, whereas fuzzy sets allow partial membership.
Objects of any cognitive-application activities are elements of the predefined space . The basic tool for imprecise classification of these elements is the notion of fuzzy set described by its membership function , as the set of ordered pairs
In multi-valued logic terms, the value of membership function is interpreted as the true value of the sentence . By we denote the family of all fuzzy subsets of the space . In this work, the following notions will be applied for analyzing any fuzzy subset:
- -
- cut of the fuzzy subset determined for each by dependence
- -
- support closure of the fuzzy subset given in a following way
An imprecise number is a family of values in which each considered value belongs to it to a varying degree. A commonly accepted model of imprecise number is the fuzzy number, defined as a fuzzy subset of the real line . The most general definition of fuzzy number is given as follows:
Definition 1.
[14] The fuzzy number (FN) is such a fuzzy subset with bounded support closure that it is represented by its upper semi-continuous membership function satisfying the conditions:
The set of all FN we denote by the symbol .
Dubois and Prade [19] first introduced the arithmetic operations on FN. In this paper, the symbol means one of the usual arithmetic operations: addition , subtraction , multiplication , and division . We assume that are represented respectively by their membership functions . In [19] any arithmetic operation on is extended to arithmetic operation on by means of the identity
where we have
These arithmetic operations are coherent with the Zadeh’s Extension Principle [15,16,17].
Among other things, Dubois and Prade [20] have distinguished a special type of representation of FN called -type FN which may be generalized in a following way.
Definition 2.
Let us assume that for any nondecreasing sequence the left reference function and the right reference function are upper semi-continuous monotonic functions satisfying the condition
Then the identity
defines the membership function of the FN which is called LR-type FN (LR-FN).
Let us note that this identity describes additionally extended notation of numerical intervals, which is used in this work.
Remark 1.
In original version of the Dubois–Prade definition [20] LR-FN was defined only for the case of any sequence fulfilling the condition
and reference functions given as continuous surjections.
Further generalizations have resulted from requirements imposed by the needs of individual applications.
Goetschel and Voxman [13] showed that the Definition 1 can be replaced by following an equivalent definition of FN:
Definition 3
[13]. FN is such fuzzy subset with bounded support closure that it fulfils the condition
Then Goetschel and Voxman [4] prove the following theorems:
Theorem 1
[13]. For any FN :
If a pair of functions fulfils the conditions (12)–(15) then it is called a pair of Goetschel–Voxman functions.
Theorem 2
[13]. For any pair of Goetschel–Voxman functions there exists exactly one such FN that the condition (11) is fulfilled.
Therefore, the pair of Goetschel–Voxman functions representing FN will be denoted by the symbol .
Definition 4.
For any upper semi-continuous and nondecreasing function its lower pseudo-inverse function is given by the identity
Definition 5.
For any upper semi-continuous and nonincreasing function its lower pseudo-inverse function is given by the identity
In a special case, we can conclude that:
Theorem 3
[13]. For any LR-FN additionally:
The next theorem is proved in [13] with the use of following notions:
Definition 6.
For any bounded continuous and nondecreasing function its upper pseudo-inverse function is given by the identity
Definition 7.
For any bounded continuous and nonincreasing function its upper pseudo-inverse function is given by the identity
Theorem 4
[13]. For any pair of Goetschel–Voxman functions additionally fulfilling condition (18) there exists exactly one such LR-FN that condition (11) is fulfilled and we have
We assume that are represented respectively by their pairs of Goetschel–Voxman functions . Goetschel and Voxman [13] have proved that if is given by the identity (6) then we have and
Let us note that if the bounded continuous and monotonic function is bijection then we have
3. Kosiński’s Ordered Fuzzy Numbers
The concept of ordered fuzzy numbers (OFN) was introduced by Kosiński and his co-writers in the series of papers [1,2,3,4] as an extension of concept of FN. Thus, any OFN should be determined by (1) as a fuzzy subset in the real line . On the other hand, Kosiński has defined OFN as a ordered pair of functions from the interval into . This pair is not a fuzzy subset in . Thus, we cannot accept Kosiński’s original terminology. Then again, the intuitive Kosiński’s approach to the notion of OFN is very useful. For these reasons, a revised definition of OFN, which fully corresponds with the intuitive Kosiński’s will be presented below. The OFN concept of number is closely linked to the following ordered pair.
Definition 8.
For any sequence , the Kosiński’s pair is defined as any ordered pair of monotonic continuous surjections and fulfilling the condition
Remark 2.
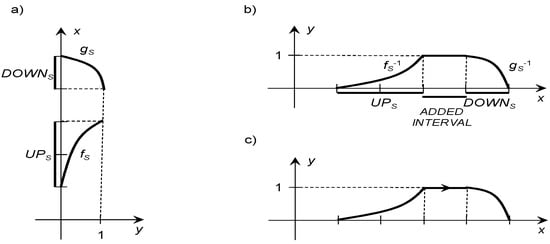
In the original final version of the Kosiński’s definition [4], the OFN is defined as ordered pair of continuous bijections and . Because OFN defined in such a way, is not fuzzy set, in Definition 8 Kosiński’s term of OFN was replaced by the term “Kosiński’s pair”. Moreover, Kosiński has assumed implicitly that the sequence fulfils the condition (10) or the condition
Kosiński marked the additional conditions of the above definition only on graphs. Some example of such Kosiński’s graphs are presented in Figure 1.

Figure 1.
(a) Positively oriented Kosiński’s pair; (b) Membership function of FN determined by positive oriented OFN; (c) Arrow denotes the positive orientation of OFN. Source: [4].
For any Kosiński pair the function is called the up-function. Then the function is called the down-function. The up-function and the down-function are collectively referred to as Kosiński’s maps.
Note that Kosiński developed his theory without using the results obtained by Goetschel and Voxman [13]. In this article, thanks to the use of these results, we can generalize Kosiński’s theory to the case when Kosiński’s maps are continuous surjections. This generalization is needed for individual applications.
By means of Goetschel–Voxman results, we can define OFN in such manner which fully corresponds to the intuitive OFN definition by Kosiński.
Definition 9.
For any sequence the Kosiński’s pair determines Kosiński’s ordered fuzzy number (K’s-OFN) defined explicitly by its membership relation given by (9).
The above definition is coherent to the intuitive Kosiński’s approach of the OFN notion. Therefore, we agree with other scientists [5,6] that the OFN should be called the Kosiński’s number. The space of all K’s-OFN is denoted by the symbol. For any OFN, its up-function is denoted by the symbol and its down-function is denoted by the symbol .
Any sequence satisfies exactly one of the following conditions
If condition (28) is fulfilled then the K’s-OFN has a positive orientation. For this case, an example of graphs of Kosiński’s maps is presented on the Figure 1a. Then the graph of membership function of FN is presented in Figure 1b. The graph of K’s-OFN membership function with positive orientation is shown in Figure 1c. The membership function of K’s-OFN has an extra arrow denoting the orientation, which provides supplementary information. Positively oriented K’s-OFN is interpreted as such imprecise number, which may increase. The space of all positively oriented OFN is denoted by the symbol. An example of positively oriented K’s-OFN is presented in Figure 2a.
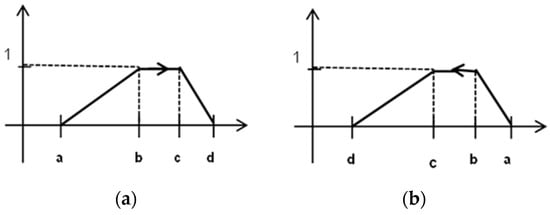
Figure 2.
The membership function of K’s-OFN with: (a) positive orientation, (b) negative orientation. Source: Own elaboration
If the condition (29) is fulfilled, then the K’s-OFN has a negative orientation. Negatively oriented K’s-OFN is interpreted as such imprecise number, which may decrease. The space of all negatively oriented OFN is denoted by the symbol. Some example of negatively oriented K’s-OFN is presented in the Figure 2b. If condition (30) is fulfilled, then the K’s-OFN describes which is not oriented.
If the sequence is not monotonic, then the membership relation is not a function. Then, this membership relation cannot be considered as a membership function of any fuzzy set. Therefore, for any non-monotonic sequence the K’s-OFN is called an improper K’s-OFN [4].An example of negatively oriented improper K’s-OFN is presented in Figure 3. The remaining K’s-OFNs are called proper ones. Some examples of proper K’s-OFNs are presented in Figure 2.
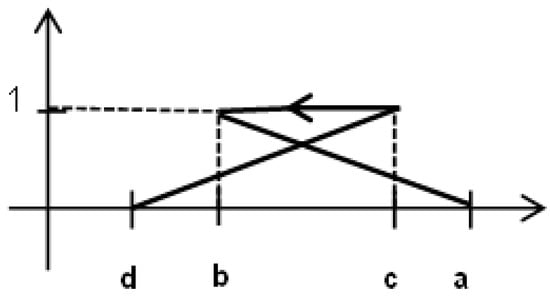
Figure 3.
Membership relation of improper K’s-OFN . Source: Own elaboration.
The difference relation between K’s-OFN and crisp zero is defined in the following way
We assume that are represented respectively by their Kosiński’s pairs. Any arithmetic operation on is extended by Kosiński to arithmetic operation on by means of the identity
where we have
The division is defined only for K’s-OFN .
The above Kosinski’s definition of arithmetic operations is coherent with the Goetschel and Voxman identity (24). On the other hand, due to the significant expansion of the arithmetic operations domain, Kosiński’s definition is an important extension of the identity (24). Therefore, the above defined arithmetic operations will be called Kosiński’s operations.
Due to (24), it is very easy to check that if proper K’s-OFNs have identical orientation then results obtained by Kosiński’s arithmetic are identical with the results obtained by means of arithmetic introduced by Dubois and Prade [19]. Moreover, Kosiński [4] has shown that if K’s-OFNs have different orientation then results obtained by his arithmetic may be different form results obtained by arithmetic introduced by Dubois and Prade [19].
All our further considerations will be illustrated by examples with use of the following type of K’s-OFNs.
Definition 10.
For any sequence Kosiński’s trapezoidal ordered fuzzy number (K’s-TrOFN) is defined explicitly by its membership relation given by the identity
Examples of proper K’s-TrOFNs are presented in Figure 2. An example of improper K’s-TrOFN is given in Figure 3. For any K’s-TrOFN its up-function and down-function are given by the identities
Among other things, it implies, that for any triple of K’s-TrOFN we have
4. Revision of the Kosiński’s Theory
In general, if OFN is determined by such membership relation which is not a function then, it is called an improper OFN. On the other hand, if OFN is determined by such a membership relation that it is a function then it is called a proper OFN. Only in case of a proper OFN can we apply all knowledge of fuzzy sets to solve practical problems described by OFN. In this way, our practical considerations will be more fruitful. Therefore, in my opinion, limiting the OFNs’ family to the family of proper OFNs is useful and absolutely necessary. Thus, the cognitive paradigm of limiting the OFNs’ family to the family of proper OFNs is well justified. For this reason, the revised definition of OFN is proposed as follows.
Definition 11.
For any monotonic sequence the Kosiński’s pair determines an ordered fuzzy number (OFN) defined explicitly by its membership function given by (9).
It is obvious that any above defined OFN is proper. In agreement with the above definition, any proper K’s-TrOFN is called a trapezoidal ordered fuzzy number (TrOFN). The space of all OFNs, the space of positively oriented OFNs, and the space of negatively oriented OFNs, are respectively denoted by the symbols . Thus we can now note the following relationships:
- Any K’s-OFN belonging to is improper.
- Any K’s-OFN belonging to is proper.
- , .
Let us look now at the following case.
Counterexample 1.
Let us calculate the Kosiński’s sum of TrOFNs and . Due to the identity (37), we have
It means that the sum of TrOFNs may be equal to improper K’s-TrOFN.
Similarly, the above conclusion was obtained by Kosiński [4]. We can generalize this conclusion as follows:
Conclusion:
The space of all OFNs is not closed under Kosiński’s operations.
Therefore, we ought to modify arithmetic of OFN in such a way that the space of all OFN will be closed under revised arithmetic operations.
Let us consider the OFNs described as follows
Any arithmetic operations on is extended now to revised arithmetic operation on by the identity
where we have
Example 1.
Some cases of modified sum are presented below. Let us observe that in all these cases the Kosiński’s sum does not exist.
Theorem 5.
Any revised arithmetic operation satisfies the condition
Proof.
We take into account such OFNs described by (38) that the condition (39) is fulfilled. Let K’s-OFN be given by the identity (32).Then, according to (33), the sum is described by K’s-OFN , where the sequence is determined by Equations (40)–(43) and the Kosiński’s pair is determined by (32). Additionally, let us note that
If then the sequence is monotonic. For this reason, it is sufficient to consider the following three cases
For case (51), by (44) and (45), we obtain
Thanks to this, from Equations (46), (47), and we obtain following conclusions
All this together implies that for the case (51) we have
For case (52), given by (44) and (45), we obtain
Then using (46), (47), , and we obtain
It implies that also for the case (52) we have (54). For the case (53) we have . It means that the condition (53) implies the condition (51). The proof is completed. □
Along with the Kosiński’s definition (32) and (33) and the Goetschel–Voxman combined together, the thesis the above theorem shows that the revised arithmetic operations are well defined for each corresponding operation on .
Theorem 6.
If for any pair the K’s-OFN is calculated by (32) then the OFN determined by (39) is given as follows
where we have
Proof.
The identity (57) immediately follows (46) together with (33) and (41). Similarly, taking into account (47) together with (33) and (42) we obtain the identity (58).
If then any OFN . It implies that and because we have
Taking into account all above simple conclusions, we obtain which is in accordance with the Theorem 5 If , then we ought to consider the following 10 cases
For case (59), we see that if then any OFN Thus, we obtain
We see that and . For case (60), we notice that if then any OFN Thus we obtain
We see that and . For case (61), we see that if and then any OFN Thus we obtain
We see that and . For case (62), we notice that if then any OFN and if then any OFN Thus we obtain
We see that and . For case (63), we notice that if then any OFN and if then any OFN Thus we obtain
We see that and . For case (64), we notice that if then any OFN and if then any OFN Thus we obtain
We see that and . For case (65), we notice that if then any OFN and if then any OFN Thus we obtain
We see that and . For case (66), we notice that if then any OFN Thus we obtain
We see that and . For case (67), we notice that if then any OFN Thus we obtain
We see that and . For case (68), we notice that if and then any OFN Thus we obtain
We see that and . For each above considered case, we have obtained results by means of the identities (44) and (45). The proof is completed. ☐
The space of all OFNs is closed under revised arithmetic operations. The last theorem shows that results obtained by using revised arithmetic operations are the best approximations of results obtained by means of Kosiński’s arithmetic operations.
5. Linear Space of Ordered Fuzzy Numbers
Let us presume the OFNs described by (38). For any pair, we define its dot product in a following way
Let us note that, equivalently, we can define the dot product as follows
because of the sequence is always a monotonic one.
The sum of OFNs is determined by revised addition defined by (39). The main link between the revised addition and the Kosiński’s addition is described in the Theorem 5. Here, we can indicate further additional relationships between the revised addition and the Kosiński’s addition . Because for every OFNs the sequence is always nondecreasing, we can say that
Because for every OFNs the sequence is always nonincreasing, we can say that
If the sum is determined by revised addition , then for any OFN its opposite element is defined by the identity
Then the neutral element is described as follows
For Kosiński’s addition its opposite elements and neutral elements are determined in the same way [4]. The identities (39)–(47) together with the commutativity of addition imply that the revised addition is commutative. The addition of FN and the Kosiński’s sum of OFN are associative and commutative [4,13,19]. The associativity of revised addition of will be investigated using the following special kind of TrOFN.
Definition 12.
For any monotonic sequence a triangular OFN (TOFN) is defined by the identity
Let us take into account the following counterexample.
Counterexample 2.
Let the following four TOFN be given by
The number of different ways of associating three applications of the addition operator is equal the Catalan number . Therefore, we have the following five different associations of four summands [21]
In [22], it is shown that we have
Many mathematical applications require a finite multiple sum to be independent of summands’ ordering. Any associative and commutative sum satisfies this property. The results of above counterexample prove that revised addition of OFN is not associative. Therefore, we should check whether the multiple sum determined by depends on its summands’ ordering.
Counterexample 3.
For all permutations of TOFN described in the Counterexample 2, we determine their multiple sum. In [22], it is shown that
The results of above counterexample prove that multiple sum calculated using addition depends on its summands’ ordering.
6. Conclusions
The main goals of the article have been achieved as follows. The Definition 11 describes the OFN in a way that any OFN is proper. The arithmetic operations are revised using the identities (38)–(47). The assumption of conditions (44) and (45) guarantees that the family of all proper OFN is closed under revised arithmetic operations. An interpretation of the revised operations is described by Theorem 6, which shows that results obtained using revised arithmetic operations are the best approximation of results obtained by means of Kosiński’s arithmetic operations. Thanks to this, we can apply all knowledge of fuzzy sets to solve practical problems described by proper OFN.
Unfortunately, the OFN linear space has one annoying drawback. Counterexample 3 shows that multiple sum determined by revised addition, depends on its summands’ ordering. Therefore, the summands ordering should be clearly defined for each practical application of the multiple sum of finite sequence of OFN. This summands ordering must be sufficiently justified in the field of application. Some examples of such justification can be found in [23]. This proves that from a practical view point, the revised sum is useful in applications despite the fact that it is dependent on its summands’ ordering.
Further research on the OFN theory should be devoted to the following problems:
- -
- preorders on the family of all proper OFNs;
- -
- equations determined by OFNs;
- -
- imprecision measurement for OFN;
- -
- reorientation of OFN.
Acknowledgments
The author is very grateful to the anonymous reviewers for their insightful and constructive comments and suggestions. Using these comments allowed me to improve this article.
Conflicts of Interest
The author declares no conflicts of interest.
References
- Kosiński, W.; Słysz, P. Fuzzy numbers and their quotient space with algebraic operations. Bull. Pol. Acad. Sci. 1993, 41, 285–295. [Google Scholar]
- Kosiński, W.; Prokopowicz, P.; Ślęzak, D. Fuzzy Numbers with Algebraic Operations: Algorithmic Approach; Klopotek, M., Wierzchoń, S.T., Michalewicz, M., Eds.; Physica Verlag: Heidelberg, Germany, 2002. [Google Scholar]
- Kosiński, W.; Prokopowicz, P.; Ślęzak, D. Ordered fuzzy numbers. Bull. Pol. Acad. Sci. 2003, 51, 327–339. [Google Scholar]
- Kosiński, W. On fuzzy number calculus. Int. J. Appl. Math. Comput. Sci. 2006, 16, 51–57. [Google Scholar]
- Prokopowicz, P.; Pedrycz, W. The directed compatibility between ordered fuzzy numbers—A base tool for a direction sensitive fuzzy information processing. Artif. Intell. Soft Comput. 2015, 119, 249–259. [Google Scholar]
- Prokopowicz, P. The directed inference for the Kosinski’s fuzzy number model. In Proceedings of the Second International Afro-European Conference for Industrial Advancement; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Prokopowicz, P.; Czerniak, J.; Mikołajewski, D.; Apiecionek, Ł.; Slezak, D. Theory and Applications of Ordered Fuzzy Number; Springer: Berlin, Germany, 2017. [Google Scholar]
- Kacprzak, D.; Kosiński, W.; Kosiński, W.K. Financial stock data and ordered fuzzy numbers. In Proceedings of the International Conference on Artificial Intelligence and Soft Computing; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Marszałek, A.; Burczyński, T. Ordered fuzzy candlesticks. In Theory and Applications of Ordered Fuzzy Number; Prokopowicz, P., Czerniak, J., Mikołajewski, D., Apiecionek, Ł., Slezak, D., Eds.; Springer: Berlin, Germany, 2017. [Google Scholar]
- Roszkowska, E.; Kacprzak, D. The fuzzy SAW and fuzzy TOPSIS procedures based on ordered fuzzy numbers. Inf. Sci. 2016, 369, 564–584. [Google Scholar] [CrossRef]
- Łyczkowska-Hanćkowiak, A. Behavioural present value determined by ordered fuzzy number. SSRN Electr. J. 2017. [Google Scholar] [CrossRef]
- Piasecki, K. Expected return rate determined as oriented fuzzy number. In Proceedings of the 35th International Conference Mathematical Methods in Economics; Prazak, P., Ed.; Gaudeamus: Hradec Kralove, Czech, 2017. [Google Scholar]
- Goetschel, R.; Voxman, W. Elementary fuzzy calculus. Fuzzy Set. Syst. 1986, 18, 31–43. [Google Scholar] [CrossRef]
- Dubois, D.; Prade, H. Fuzzy real algebra: Some results. Fuzzy Set. Syst. 1979, 2, 327–348. [Google Scholar] [CrossRef]
- Zadeh, L.A. The concept of a linguistic variable and its application to approximate reasoning. Part I. Information linguistic variable. Expert Syst. Appl. 1975, 36, 3483–3488. [Google Scholar]
- Zadeh, L.A. The concept of a linguistic variable and its application to approximate reasoning. Part II. Inf. Sci. 1975, 8, 301–357. [Google Scholar] [CrossRef]
- Zadeh, L.A. The concept of a linguistic variable and its application to approximate reasoning. Part III. Inf. Sci. 1975, 9, 43–80. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Dubois, D.; Prade, H. Operations on fuzzy numbers. Int. J. Syst. Sci. 1978, 9, 613–629. [Google Scholar] [CrossRef]
- Dubois, D.; Prade, H. Fuzzy Sets and Systems: Theory and Applications; Academic Press: New York, NY, USA, 1980. [Google Scholar]
- Koshy, T. Catalan Numbers with Applications; Oxford University Press: London, UK, 2008. [Google Scholar]
- Łyczkowska-Hanćkowiak, A.; Piasecki, K. On some difficulties in the addition of trapezoidal ordered fuzzy numbers. arXiv, 2017; arXiv:1710.03541. [Google Scholar]
- Łyczkowska-Hanćkowiak, A.; Piasecki, K. Present value of portfolio of assets with present values determined by trapezoidal ordered fuzzy numbers. Oper. Res. Decis. (under review).
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).