1. Introduction
In a conflicting multi-criteria problem, there is no unique solution that could optimize all the criteria simultaneously. The conflicting multi-criteria problem gives a set of Pareto solutions. Each Pareto solution is defined as a trade-off solution between the conflicting criteria, where it is not possible to achieve the best score of a criterion without downgrading the score of some other criteria.
The multi-criteria decision-making (MCDM) analysis contains a number of decision-making steps including weighting of criteria and ranking of alternatives. The weighting of criteria can reflect the individual preferences of the Decision-Maker. The weighted sum of the objectives leads to an aggregate function to be optimized. Eckenrode [
1] implemented this approach to optimize an air-defence system. The selection of the alternatives was based on the individual preferences of 24 experts who considered six criteria.
The Analytic Hierarchy Process (AHP) proposed by Saaty [
2] also involves human judgement in evaluations. According to AHP, the MCDM problem is split into a hierarchy with the goal, decision criteria and alternatives. Then, it uses the expert judgement to be converted into a numerical evaluation. The AHP is widely used in the decision-making process (e.g., [
3,
4,
5,
6,
7]). Zaidan et al. [
8] integrated the AHP method with other MCDM techniques to select the right software for open-source electronic medical record. The Analytic Network Process (ANP) also proposed by Saaty [
9] represents some modification of the AHP. The ANP interprets the AHP hierarchy as a network. In contrast to the AHP, the decision criteria in the AHP are supposed to be independent from each another. This technique has been used in a number of publications (e.g., [
10,
11,
12,
13]).
The Multi-Attribute Utility Theory (MAUT) by Keeney and Raiffa [
14] represents a classical approach in MCDM analysis. This is a structured methodology based on the utility axioms introduced by von Neumann and Morgenstern. In the algorithm, a utility value is assigned to each action whilst quantifying all individual preferences. Some examples of the use of MAUT in the decision-making can be found in [
15]. In turn, the Elimination and Choice Expressing Reality (ELECTRE) by Roy is an outranking approach that is used to discard unacceptable alternatives. This approach was modified in PROMETHEE (Preference Ranking Organization Method for Enrichment Evaluations) by Brans and Vincke [
16]. PROMETHEE exists in three versions: the PROMETHEE I (partial ranking), the PROMETHEE II (complete ranking) and the PROMETHEE-GAIA (geometrical analysis for interactive aid). Several authors applied the outranking techniques in MCDM problems (e.g., [
17,
18,
19]).
The genetic algorithm (GA) has also been used for MCDM problems (e.g., [
20,
21,
22,
23,
24]). It is widely used thanks to its universal nature. A problem with GA is that it generates a large number of solutions that are mostly redundant. Wang and Yang [
25] used the particle swarm optimization (PSO) to determine a ranking for MCDM problems. Particle swarm is capable of improving the search ability of GA thanks to its better convergence to the Pareto frontier. However, as noted in [
25], PSO requires significant computational time.
There is a number of techniques related to the ranking of available alternatives that are presented by the Pareto solutions. In all these techniques, the ranking is based on a metric introduced in the criteria space. The Technique for Order Preference by Similarity to the Ideal Solution (TOPSIS) was first proposed by Hwang and Yoon [
26]. The original TOPSIS method presumed priori weights for criteria to be specified by the Decision-Maker. The TOPSIS approach is based on an individual evaluation score that depends on the distances from the alternative to the ideal and anti-ideal solutions. This type of evaluation is obviously the best for the non-conflicting multi-criteria problems, where the alternative that is the closest to the ideal solution is also the farthest from the anti-ideal solution. However, in a conflicting multi-criteria problem, such an assumption cannot always be realized. This drawback in TOPSIS is addressed in a few papers [
27,
28,
29]. It was Kao [
29] who practically suggested to measure the distance in
norm instead of
-norm implemented in the conventional TOPSIS method to overcome the inconsistency problem. TOPSIS has been widely used in MCDM due to its simplicity (e.g., [
30,
31,
32,
33]). The VlseKriterijuska Optimizacija I Komoromisno Resenje (VIKOR) algorithm proposed by Opricovic [
27] is based on the compromise programming with weights to be prescribed to the performances by the Decision-Maker. Such weights are subjective and depend on how adequately such quantitative characteristics reflect the individual preferences of the Decision-Maker.
The real-life design is usually related to the inevitable uncertainties in the input data, parameters, etc. The uncertainty in the MCDM problem includes the imprecision of criteria values, vagueness in the importance of criteria (weights) and dealing with qualitative, linguistic or incomplete information.
The concept of fuzziness, first introduced by Zadeh [
34], is proved to be an efficient tool to include the uncertainties in the MCDM problems. Numerous fuzzy MCDM methods have been developed, including [
35,
36,
37,
38,
39,
40,
41,
42]. They utilize the fuzzy numbers in the formulation of their fuzzy MCDM methods. There are two ways used in solving the fuzzy MCDM problems [
43]. One way to solve the fuzzy MCDM problem is based on utilizing the fuzzy MCDM method [
44,
45]. Another way is reduced to the defuzzification of the fuzzy MCDM problem and solving it by a conventional MCDM method [
46]. The defuzzification process converts the fuzzy numbers into crisp values. In both ways, the defuzzification process is essential, since the MCDM solution must provide a crisp result. Many defuzzification methods can be used including the center of sum and the center of gravity [
47,
48]. The fuzzy methodology was extended to the TOPSIS method [
30,
49,
50,
51] and VIKOR algorithm [
52,
53]. Several researchers used the fuzzy TOPSIS method for different applications including the selection problem [
37,
54,
55,
56] and the performance evaluation [
40,
57,
58,
59,
60]. Wang et al. [
28] proposed merging the fuzzy TOPSIS and the fuzzy AHP to surpass the problem. A few authors also explored the VIKOR algorithm to solve the fuzzy MCDM problem [
61,
62]. The trade-off ranking method [
63] suggested by Jaini and Utyuzhnikov selects the least compromise solution as the best option. In contrast to the TOPSIS and VIKOR methodologies, the trade-off ranking method is based on the overall evaluation score of an alternative with respect to all other alternatives by taking into account the position of each Pareto solution in the criteria space. This strategy is nonlocal and essentially different from the VIKOR and TOPSIS methodologies.
The current paper is focused on the ranking of alternatives in the MCDM problems with conflicting criteria. The trade-off ranking method has been modified for a conflicting fuzzy environment. The approach is compared against the fuzzy TOPSIS and VIKOR methodologies. The paper is organized as follows. The next section briefly describes the fuzzy MCDM problem and its ranking application, the arithmetics of fuzzy numbers used throughout the paper, as well as the fuzzy VIKOR and TOPSIS methods. The background of the proposed fuzzy trade-off ranking method and its algorithms are discussed in
Section 3. The approach is realized in both the fuzzy and defuzzification ways. In
Section 4, a numerical example is presented to illustrate the application of the fuzzy trade-off ranking. The comparisons of the results are also given there. Lastly, the conclusions of the paper are discussed in
Section 5.
3. Trade-Off Ranking Method
As mentioned in the Introduction, the trade-off ranking method is developed to solve the MCDM problem with conflicting criteria. Such a problem gives a set of Pareto solutions. Eventually, the DM has to choose only one solution out of many. Therefore, an evenly distributed Pareto set is important in the trade-off ranking method. The evenness property gives a sufficient set of solutions that represents the whole Pareto solutions for the DM to make a decision in a limited time. Such a Pareto set can be obtained, in particular, by the Directed Search Domain (DSD) algorithm [
70].
In a fuzzy MCDM problem, the simplest way of solving the problem is by defuzzification, in which the fuzziness is dissolved at an early stage of the decision-making process. The defuzzification process turns the fuzzy numbers into a crisp value.
Thus, the first task in solving the fuzzy MCDM problem is to defuzzify the alternative performance and the weight of each criterion using Equation (12). Each defuzzification is then denoted as and , respectively.
After the defuzzification process, the ranking of the alternatives is then calculated using a conventional trade-off ranking method described below.
3.1. Trade-Off Ranking Method with Defuzzification
The trade-off ranking method is utilised to give a solution with the least compromise as the best option. To measure the value of compromise, the distance formula is used to calculate the trade-off between the alternatives.
First, the algorithm starts with the normalization of
and
, respectively, by the formula:
The normalization guarantees that the range of normalized triangular fuzzy numbers belongs to [0,1] and eliminates the units of criteria functions.
It is to be noted that the triangular fuzzy numbers are considered for the sake of simplicity because of the lack of information on the uncertainties. However, the technique can be extended to more sophisticated approximations straightforward.
Next, the extreme solutions,
, are determined. The extreme solutions are the solutions with the best value in at least one criterion. Thus, a
k-th extreme solution is the alternative with the optimal
j-th criterion such as:
The benefit criteria are the criteria to be maximized such as profit, while the cost criteria are the ones to be minimized such as price.
The trade-off ranking method has two levels of selection. The first level is the trade-off between each alternative and the extreme solutions. Before we determine the first level of the selection, the distance between an alternative
and an extreme solution is calculated. Such a distance, denoted as
, is calculated using the
-metric distance:
Then, the first level of trade-off is calculated using equation
The ranking is determined by the value of where the least value holds the highest ranking.
The extreme solutions are chosen to be the reference point since they are the optimal solutions for each single-criterion problem. An alternative with the least has the least trade-off with the extreme solutions. In a conflicting multi-criteria problem, it is not possible to have a solution that simultaneously satisfies all criteria. Therefore, having the alternative that is the closest to the optimal value of most criteria, if not all, is considered to be a relevant compromise solution. In the case of the same value of , the second level of selection is considered that takes into account a compromise with the other alternatives.
The distance between the alternatives is calculated using equation:
where
, known as the weighted performance of alternative
i in criterion
j.
The second level of trade-off is then calculated using equation:
The least value of denotes the least value of compromise in terms of the alternative differences. Therefore, an alternative with the lowest value of is defined as the best trade-off solution among the alternatives with the same value of .
To illustrate the application of the trade-off ranking method, consider an example of buying a share investment with two conflicting criteria, low risk and high return. Note that, in a conflicting multi-criteria problem, it is impossible to optimize both criteria simultaneously. However, there are usually two extreme opportunities: (i) low risk with a low return; and (ii) high risk with a high return. These two extreme opportunities are known as the extreme solutions. With these two options, the solution would depend on the DM preferences, either towards a low risk or a high return per investment. Suppose there are other options between the two extreme solutions. Conveniently, the DM usually prefers a trade-off between the two criteria. In this example, if the DM preferences towards both criteria are equal, the trade-off ranking method is able to give the best compromise solution as the best choice.
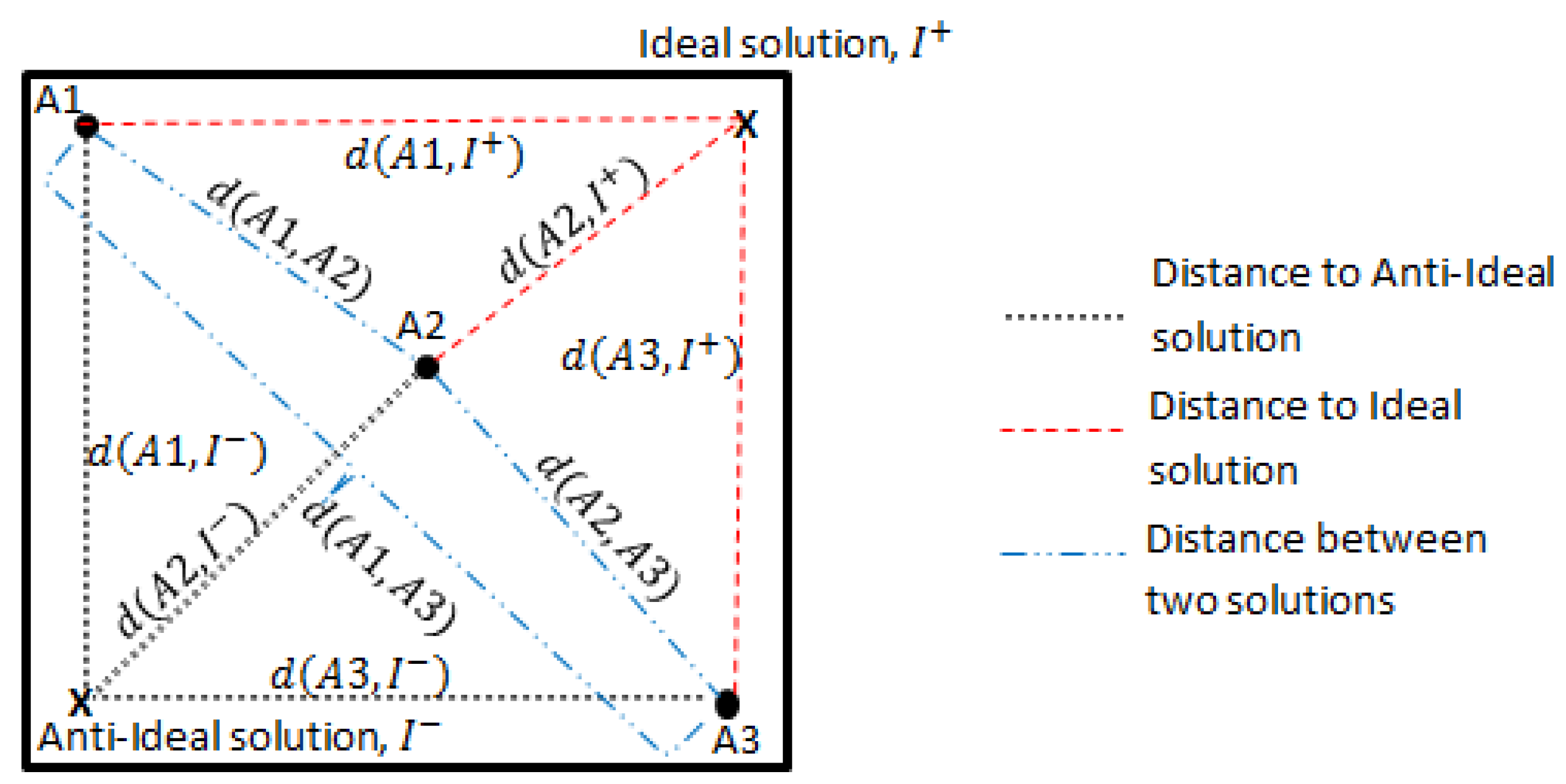
The concepts of distance measure in TOPSIS and the trade-off ranking method are illustrated in
Figure 3.
Figure 3 shows the difference in the distance measure between TOPSIS and the trade-off ranking method in evaluating three Pareto alternatives
and
. TOPSIS uses the distance between an alternative to the ideal/anti-ideal solutions as a ranking measure, which are denoted in
Figure 3 as
and
, respectively, for
. In turn, the trade-off ranking method uses the distance between an alternative to the extreme solutions or other alternatives to determine the ranking. In
Figure 3, such distances are marked as
and
. The ranking determination in the trade-off ranking method depends on the sum of the distances between those alternatives. The example in
Figure 3 also shows that alternative
, which is the closest to the ideal solution, is also the closest to the anti-ideal solution compared to alternatives
and
. In this case, the property of the TOPSIS method to have the best solution as the closest to the ideal solution and the farthest to the anti-ideal solution is violated.
3.2. Fuzzy Trade-Off Ranking Method
Another way to solve the fuzzy MCDM problem is using the fuzzy MCDM method. In this approach, the fuzzy numbers are processed until the end of the algorithms. As such, the fuzzy information is preserved and the final solution is more accurate. In a fuzzy MCDM method, the distance formula between fuzzy numbers (11) is used for the ranking determination. An algorithm for the fuzzy trade-off ranking (FTOR) method is presented in the following steps:
4. Numerical Example: Personnel Selection Problem
Consider a numerical example of the personnel selection problem where five benefit criteria are considered in selecting one of three candidates,
, for the post of system analysis engineer [
30]. The criteria considered are stated as follows:
Emotional steadiness, ;
Oral communication skill, ;
Personality, ;
Past experience, ;
Self-confidence, .
Here, the fuzzy trade-off ranking, fuzzy TOPSIS and fuzzy VIKOR methods are used to solve the personnel selection problem. Suppose the rating process of each alternative and the weight of each criterion are made by three DMs. The results of the rating evaluations are shown in
Table 3 and
Table 4. The rating value is described by the linguistic terms expressed in the triangular fuzzy numbers as seen in
Table 1 and
Table 2.
Formulae (
1) and (2) are applied to the data in
Table 3 and
Table 4, respectively, in order to find the average performance of the alternative and the average weight of each criterion. The fuzzy decision matrix of the problem is then given in
Table 5.
The defuzzified decision matrix using Formula (12) is given in
Table 6.
This problem aims to maximize all the criteria. However, the conflicting situation arises since none of the candidates possessed the best in all criteria. More details can be seen in
Table 6. According to
Table 6, candidate
is ranked second in criteria
,
,
and
. Meanwhile, candidate
is ranked first in criterion
. Furthermore, candidate
is ranked first out of two criteria, which are
and
, but ranked third in two other criteria,
and
. Meanwhile, candidate
is ranked the best in two criteria,
and
, but the worst in three other criteria, which are
,
and
.
The normalized defuzzified decision matrix by the trade-off ranking method, Formula (
13), is given in
Table 7.
Referring to
Table 7 and using Formula (
14), the extreme solutions for the trade-off ranking method are determined. As an example, an alternative with the optimal value in criterion
is the fifth extreme solution for the problem, i.e.,
since
.
After calculating the data in
Table 7, using Formulae (
15) and (
16), and the data in
Table 5 with Formulae (
17) and (
18), the ranking by the trade-off method with defuzzification and the fuzzy trade-off ranking are given in
Table 8. As can be observed in
Table 8, the best candidate ranked by the fuzzy trade-off is candidate
. In addition, it is also the best candidate ranked by the pre-defuzzification approach in the trade-off ranking method. Note that, even though candidate
is only ranked first in one criterion, he/she is not ranked the worst in the other criteria. Thus, this candidate has the most balanced traits, i.e., the least compromise, out of all five criteria compared to
and
.
Table 9 shows the results of the fuzzy trade-off
and the defuzzification trade-off
. The indifference in the ranking by the trade-off method with defuzzification and the fuzzy trade-off ranking method is due to the small range of fuzziness in the triangular fuzzy numbers and small differences in the criteria ratings. The crisp values of the fuzzy numbers given in
Table 6 significantly close to their middle values,
, presented in
Table 5. A graphical explanation for this statement is given in
Figure 4.
The triangular fuzzy numbers of each criterion for alternative
and their respective crisp values are shown in
Figure 4. As can be seen, the crisp values are situated close to the middle values of the triangular fuzzy numbers. Hence, there is a small difference in the
and
values for each alternative and indifference in the ranking solutions. In the fuzzy MCDM problem, the final result is a crisp value since the MCDM method must provide a deterministic solution.
Next, consider the ranking by fuzzy VIKOR as given in
Table 10. The fuzzy ranking
in the fuzzy VIKOR method gives a partial ranking since the first position in
is not confirmed (Step 5 in
Section 2.4).
In the case of ranking by VIKOR defuzzification, the final decision is the set of compromise solutions {
,
,
} (Step 8 in
Section 2.4). Eventually, since there are only three options, the defuzzification ranking by VIKOR gives a set of solutions with all three options. The results obtained by the fuzzy VIKOR are given in
Table 11.
Next, the ranking by the fuzzy TOPSIS is given in
Table 12. This method also identifies candidate
as the best candidate.
As can be seen from
Table 12, alternative
is the closest to the ideal solution (
). However, it is not the farthest from the anti-ideal solution (
). In fact, the alternative farthest from the anti-ideal solution is
(
). It shows that the concept of the TOPSIS method, to have the best solution that is the closest to the ideal and the farthest from the anti-ideal solutions, is not realized in this conflicting multi-criteria problem.
Now, suppose the DM have changed their preferences towards each criterion. The new DM’s preferences, presented by the linguistic variables, are given in
Table 13. According to
Table 1, as well as Formulae (2) and (12), the fuzzy and defuzzified weights associated with the new preferences are shown in
Table 14.
As can be seen from
Table 14, the DM now prefer criterion
(emotional steadiness) and criterion
(past experience) more than the other criteria. The results by each fuzzy MCDM method for the new criteria weights are given in
Table 15.
From the results in
Table 15, the best candidate by the fuzzy trade-off ranking method is candidate
. Note that candidate
is ranked the lowest with the previous criteria weights. The difference is related to DM’s preferences. In the previous problem, DM’s preferences towards each criterion are quite equal (
Table 7). However, in the new weights problem, the DM prefer criteria
and
more than the others. According to
Table 7, candidate
possesses the best score in both criteria preferred by the DMs. Hence, it is now regarded as the best choice. In turn, the worst candidate is
since this candidate is ranked the lowest in both criteria
and
.
Meanwhile, the fuzzy VIKOR method gives a set of compromise solutions as a final ranking result for the new weights case. As for the fuzzy TOPSIS, the best option for the new weights is the same as in the previous weights case, i.e., candidate . The difference now is in the results such that the alternative that is closer to the ideal solution () is also farther from the anti-ideal solution ().
5. Conclusions
A fuzzy trade-off ranking method for the fuzzy MCDM problem has been proposed. The approach has been utilised to find the best solution to the fuzzy conflicting multi-criteria problem. The fuzzy trade-off ranking method is able to capture the solution with the least compromise. It is also able to comprehend DM’s preferences in a conflicting MCDM problem. The algorithm takes into account the position of an alternative with respect to the other alternatives. Therefore, in contrast to other techniques, the ranking analysis is nonlocal. The proposed methodology has been compared against two well known fuzzy methods, VIKOR and TOPSIS, in application to the personnel selection problem.
In contrast to the fuzzy trade-off ranking method, the fuzzy TOPSIS method is an individual performance method, where an alternative is only compared against the ideal/anti-ideal solutions, which are artificial solutions. Such a ranking calculation is the best for the MCDM problem, where an alternative that is close to the ideal solution is also far from the anti-ideal solution. However, in a conflicting MCDM problem, such an assumption is not always realized. The best solution that is the closest to the ideal solution may not be the farthest from the anti-ideal solution. On the contrary, the fuzzy VIKOR gives a similar solution as the fuzzy trade-off ranking since the fuzzy VIKOR was also developed to tackle the conflicting MCDM problems. However, in some problems, as shown in the numerical example, the fuzzy VIKOR gives a set of compromise solutions rather than one single solution. In that matter, the DM still has to choose one solution out of the compromise set proposed by the fuzzy VIKOR method. In future work, the approach will be applied to a wider range of data including continuous, ordinal and categorical variables. More practical problems will be considered. Comparisons with other available ranking techniques are also needed. The final selection of the ranking method depends on the preferences of the Decision-Maker. Systematic comparison of the available techniques for different classes of problems should be valuable.