Abstract
Hough transform (HT) is a useful tool for both pattern recognition and image processing communities. In the view of pattern recognition, it can extract unique features for description of various shapes, such as lines, circles, ellipses, and etc. In the view of image processing, a dozen of applications can be handled with HT, such as lane detection for autonomous cars, blood cell detection in microscope images, and so on. As HT is a straight forward shape detector in a given image, its shape detection ability is low in noisy images. To alleviate its weakness on noisy images and improve its shape detection performance, in this paper, we proposed neutrosophic Hough transform (NHT). As it was proved earlier, neutrosophy theory based image processing applications were successful in noisy environments. To this end, the Hough space is initially transferred into the NS domain by calculating the NS membership triples (T, I, and F). An indeterminacy filtering is constructed where the neighborhood information is used in order to remove the indeterminacy in the spatial neighborhood of neutrosophic Hough space. The potential peaks are detected based on thresholding on the neutrosophic Hough space, and these peak locations are then used to detect the lines in the image domain. Extensive experiments on noisy and noise-free images are performed in order to show the efficiency of the proposed NHT algorithm. We also compared our proposed NHT with traditional HT and fuzzy HT methods on variety of images. The obtained results showed the efficiency of the proposed NHT on noisy images.
1. Introduction
The Hough transform (HT), which is known as a popular pattern descriptor, was proposed in sixties by Paul Hough [1]. This popular and efficient shape based pattern descriptor was then introduced to the image processing and computer vision community in seventies by Duda and Hart [2]. The HT converts image domain features (e.g., edges) into another parameter space, namely Hough space. In Hough space, every points () on a straight line in the image domain, corresponds a point ().
In the literature, there have been so many variations of Hough’s proposal [3,4,5,6,7,8,9,10,11,12,13,14]. In [3], Chung et al. proposed a new HT based on affine transformation. Memory-usage efficiency was provided by proposed affine transformation, which was in the center of Chung’s method. Authors targeted to detect the lines by using slope intercept parameters in the Hough space. In [4], Guo et al. proposed a methodology for an efficient HT by utilizing surround-suppression. Authors introduced a measure of isotropic surround-suppression, which suppresses the false peaks caused by the texture regions in Hough space. In traditional HT, image features are voted in the parameter space in order to construct the Hough space. Thus, if an image has more features (e.g., texture), construction of the Hough space becomes computationally expensive. In [5], Walsh et al. proposed the probabilistic HT. Probabilistic HT was proposed in order to reduce the computation-cost of the traditional HT by using a selection step. The selection step in probabilistic HT approach just considered the image features that contributed the Hough space. In [6], Xu et al. proposed another probabilistic HT algorithm, called randomized HT. Authors used a random selection mechanism to select a number of image domain features in order to construct the Hough space parameters. In other words, only the hypothesized parameter set was used to increment the accumulator. In [7], Han et al. used the fuzzy concept in HT (FHT) for detecting the shapes in noisy images. FHT enables detecting shapes in noisy environment by approximately fitting the image features avoiding the spurious detected using the traditional HT. The FTH can be obtained by one-dimensional (1-D) convolution of the rows of the Hough space. In [8], Montseny et al. proposed a new FHT method where edge orientations were considered. Gradient vectors were considered to enable edge orientations in FHT. Based on the stability properties of the gradient vectors, some relevant orientations were taken into consideration, which reduced the computation burden, dramatically. In [9], Mathavan et al. proposed an algorithm to detect cracks in pavement images based on FHT. Authors indicated that due to the intensity variations and texture content of the pavement images, FHT was quite convenient to detect the short lines (cracks). In [10], Chatzis et al. proposed a variation of HT. In the proposed method, authors first split the Hough space into fuzzy cells, which were defined as fuzzy numbers. Then, a fuzzy voting procedure was adopted to construct the Hough domain parameters. In [11], Suetake et al. proposed a generalized FHT (GFHT) for arbitrary shape detection in contour images. The GFHT was derived by fuzzifying the vote process in the HT. In [12], Chung et al. proposed another orientation based HT for real world applications. In the proposed method, authors filtered out those inappropriate edge pixels before performing their HT based methodology. In [13], Cheng et al. proposed an eliminating- particle-swarm-optimization (EPSO) algorithm to reduce the computation cost of HT. In [14], Zhu et al. proposed a new HT for reducing the computation complexity of the traditional HT. The authors called their new method as Probabilistic Convergent Hough Transform (PCHT). To enable the HT to detect an arbitrary object, the Generalized Hough Transform (GHT) is the modification of the HT using the idea of template matching [15]. The problem of finding the object is solved by finding the model’s position, and the transformation’s parameter in GHT.
The theory of neutrosophy (NS) was introduced by Smarandache as a new branch of philosophy [16,17]. Different from fuzzy logic, in NS, every event has not only a certain degree of truth, but also a falsity degree and an indeterminacy degree that have to be considered independently from each other [18]. Thus, an event or entity {A} is considered with its opposite {Anti-A} and the neutrality {Neut-A}. In this paper, we proposed a novel HT algorithm, namely NHT, to improve the line detection ability of the HT in noisy environments. Specifically, the neutrosophic theory was adopted to improve the noise consistency of the HT. To this end, the Hough space is initially transferred into the NS domain by calculating the NS memberships. A filtering mechanism is adopted that is based on the indeterminacy membership of the NS domain. This filter considers the neighborhood information in order to remove the indeterminacy in the spatial neighborhood of Hough space. A peak search algorithm on the Hough space is then employed to detect the potential lines in the image domain. Extensive experiments on noisy and noise-free images are performed in order to show the efficiency of the proposed NHT algorithm. We further compare our proposed NHT with traditional HT and FHT methods on a variety of images. The obtained results show the efficiency of the proposed NHT on both noisy and noise-free images.
The rest of the paper is structured as follows: Section 2 briefly reviews the Hough transform and fuzzy Hough transform. Section 3 describes the proposed method based on neutrosophic domain images and indeterminacy filtering. Section 4 describes the extensive experimental works and results, and conclusions are drawn in Section 5.
2. Previous Works
In the following sub-sections, we briefly re-visit the theories of HT and FHT. The interested readers may refer to the related references for more details about the methodologies.
2.1. Hough Transform
As it was mentioned in the introduction section, HT is a popular feature extractor for image based pattern recognition applications. In other definitions, HT constructs a specific parameter space, called Hough space, and then uses it to detect the arbitrary shapes in a given image. The construction of the Hough space is handled by a voting procedure. Let us consider a line given in an image domain as;
where k is the slope and b is the intercept. Figure 1 depicts such a straight line with ρ and θ in image domain. In Equation (1), if we replace with , then we then obtain the following equation;
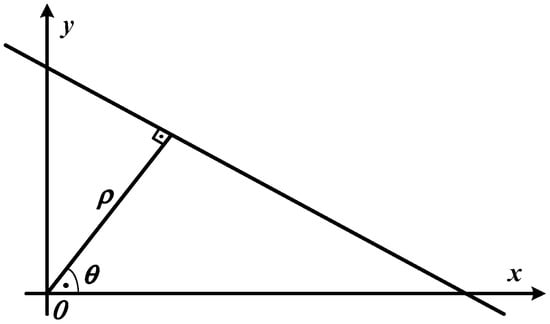
Figure 1.
A straight line in an image domain.
If we re-write the Equation (2), as shown in Equation (3), the image domain data can be represented in the Hough space parameters.
Thus, a point in the Hough space can specify a straight line in the image domain. After Hough transform, an image I in the image domain is transferred into Hough space, which is denoted as IHT.
2.2. Fuzzy Hough Transform
Introducing fuzzy concept into HT is arisen due to the lines that are not straight in the image domain [19]. In other words, traditional HT only considers the pixels that align on a straight line and non-straight lines detection with HT becomes challenging. Non-straight lines generally occur due to the noise or discrepancies in pre-processing operations, such as thresholding or edge detection. FHT aims to alleviate this problem by applying a strategy. In this strategy, closer the pixel to any line contributes more to the corresponding accumulator array bin. As it was mentioned in [7], the application of the FHT can be achieved by two successive steps. In the first step, the traditional HT is applied to obtain the Hough parameter space. In the second step, a 1-D Gaussian function is used to convolve the rows of the obtained Hough parameter space. The 1-D Gaussian function is given as following;
where defining the width of the 1-D Gaussian function.
3. Proposed Method
3.1. Neutrosophic Hough Space Image
An element in NS is defined as: let as a set of alternatives in neutrosophic set. The alternative Ai is , where , , and are the membership values to the true, indeterminate, and false set.
A Hough space image IHT is mapped into neutrosophic set domain, denoted as INHT, which is interpreted using THT, IHT, and FHT. Given a pixel in IHT, it is interpreted as . , , and represent the memberships belonging to foreground, indeterminate set, and background, respectively [20,21,22,23,24,25,26,27].
Based on the Hough transformed value and local neighborhood information, the true membership and indeterminacy membership are used to describe the indeterminacy among local neighborhood as:
where and are the HT values and its gradient magnitude at the pixel of on the image INHT.
3.2. Indeterminacy Filtering
A filter is defined based on the indeterminacy and is used to remove the effect of indeterminacy information for further segmentation, whose the kernel function is defined as follows:
where is the standard deviation value where is defined as a function that is associated to the indeterminacy degree. When the indeterminacy level is high, is large and the filtering can make the current local neighborhood more smooth. When the indeterminacy level is low, is small and the filtering takes a less smooth operation on the local neighborhood.
An indeterminate filtering is taken on to make it more homogeneous.
where is the indeterminate filtering result, and are the parameters in the linear function to transform the indeterminacy level to standard deviation value.
3.3. Thresholding Based on Histogram in Neutrosophic Hough Image
After indeterminacy filtering, the new true membership set in Hough space image become homogenous, and the clusters with high HT values become compact, which is suitable to be identified. A thresholding method is used on to pick up the clustering with high HT values, which respond to the lines in original image domain. The thresholding value is automatic determined by the maximum peak on this histogram of the new Hough space image.
where is the threshold value that is obtained from the histogram of .
In the binary image after thresholding, the object regions are detected and the coordinators of their center are identified as the parameters of the detected lines. Finally, the detected lines are found and recovered in the original images using the values of .
4. Experimental Results
In order to specify the efficiency of our proposed NHT, we conducted various experiments on a variety of noisy and noise-free images. Before illustration of the obtained results, we opted to show the effect of our proposed NHT on a synthetic image. All of the necessary parameters for NHT were fixed in the experiments where the sigma parameter and the window size of the indeterminacy filter were chosen as 0.5 and 7, respectively. The value of a and b in Equation (11) are set as 0.5 by the trial and error method.
In Figure 2, a synthetic image, its NS Hough space, detected peaks on NS Hough space and the detected lines illustration are illustrated below.
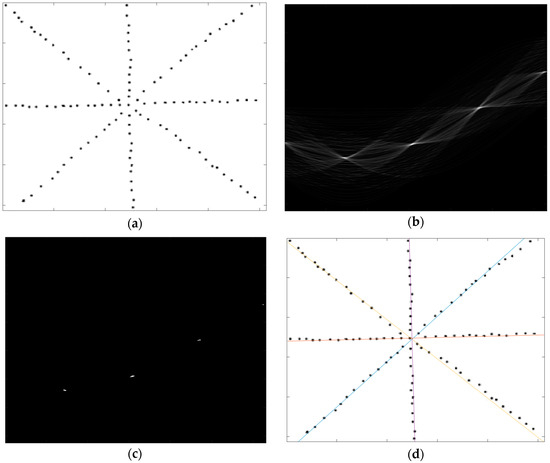
Figure 2.
Application of the neutrosophic Hough transform (NHT) on a synthetic image, (a) input synthetic image; (b) neutrosophy (NS) Hough space; (c) Detected peaks in NS Hough space; and, (d) Detected lines.
As seen in Figure 2a, we constructed a synthetic image, where four dotted lines were crossed in the center of image. The lines are designed not to be perfectly straight in order to test the proposed NHT. Figure 2b shows the NS Hough space of the input image. As seen in Figure 2b, each image point in the image domain corresponds to a sinus curve in NS Hough space, and the intersections of these sinus curves indicate the straight lines in the image domain. The intersected curves regions, as shown in Figure 2b, were detected based on the histogram thresholding method and the exact location of the peaks was determined by finding the center of the region. The obtained peaks locations are shown in Figure 2c. The obtained peak locations were then converted to lines and the detected lines were superimposed in the image domain, as shown in Figure 2d.
We performed the above experiment one more time when the input synthetic image was corrupted with noise. With this experiment, we can investigate the behavior of our proposed NHT on noisy images. To this end, the input synthetic image was degraded with a 10% salt & pepper noise. The degraded input image can be seen in Figure 3a. The corresponding NS Hough space is depicted in Figure 3b. As seen in Figure 3b, the NS Hough space becomes denser when compared with the Figure 2b, because the all of the noise points contributed the NS Hough space. The thresholded the NS Hough space is illustrated in Figure 3c, where four peaks are still visible. Finally, as seen in Figure 3d, the proposed method can detect the four lines correctly in a noisy image. We further experimented on some noisy and noise-free images, and the obtained results were shown in Figure 4. While the images in the Figure 4a column show the input noisy and noise-free images, in Figure 4b column, we give the obtained results. As seen in the results, the proposed NHT is quite effective for both noisy and noise-free images. All of the lines were detected successfully. In addition, as shown in the first row of Figure 4, the proposed NHT could detect the lines that were not straight perfectly.
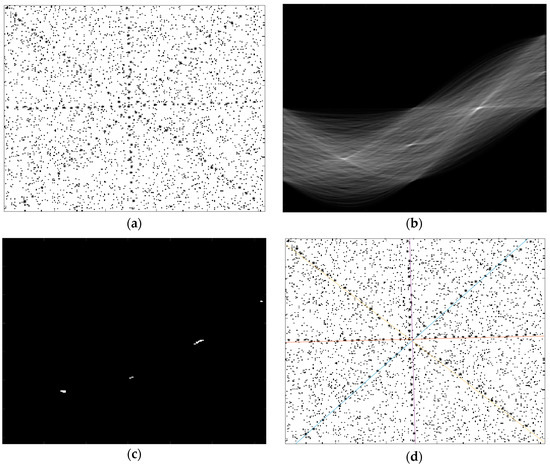
Figure 3.
Application of the NHT on a noisy synthetic image, (a) input noisy synthetic image; (b) NS Hough space; (c) Detected peaks in NS Hough space; and, (d) Detected lines.
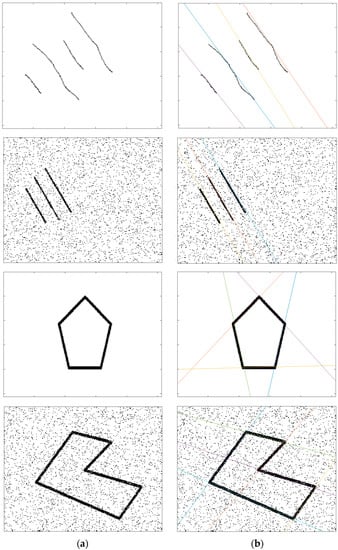
Figure 4.
Application of the NHT on a noisy synthetic image, (a) input noisy and noise-free synthetic image; (b) Detected lines with proposed NHT.
As the proposed NHT was quite good in detection of the lines in both noise and noise-free synthetic images, we performed some experiments on gray scale real-world images. The obtained results were indicated in Figure 5. Six images were used and obtained lines were superimposed on the input images. As seen from the results, the proposed NHT yielded successful results. For example, for the images of Figure 5a,c–f, the NHT performed reasonable lines. For the chessboard image (Figure 5b), only few lines were missed.

Figure 5.
Various experimental results for gray scale real-world images (a–f).
We further compared the proposed NHT with FHT and the traditional HT on a variety of noisy images and obtained results were given in Figure 6. The first column of Figure 6 shows the HT performance, the second column shows the FHT achievements, and final column shows the obtained results with proposed NHT.
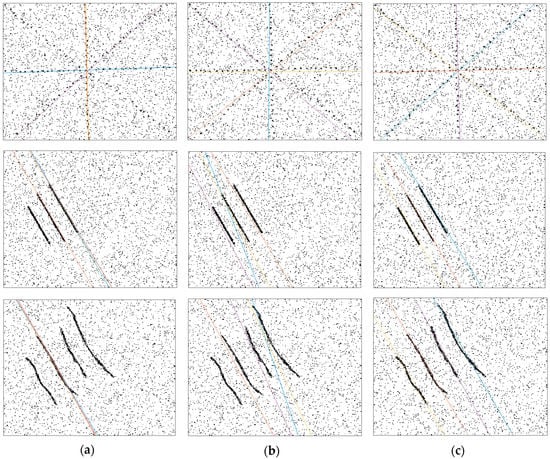
Figure 6.
Comparison of NHT with Hough transform (HT) and FHT on noisy images (a) HT results; (b) FHT results and (c) NHT results.
With visual inspection, the proposed method obtained better results than HT and FHT. Generally, HT missed one or two lines in the noisy environment. Especially for the noisy images that were given in the third row of Figure 6, HT just detected one line. FHT generally produced better results than HT. FHT rarely missed lines but frequently detected the lines in the noisy images due to its fuzzy nature. In addition, the detected lines with FHT were not on the ground-truth lines, as seen in first and second rows of Figure 6. NHT detected all of the lines in all noisy images that were given Figure 6. The detected lines with NHT were almost superimposed on the ground-truth lines as we inspected it visually. In order to evaluate the comparison results quantitatively, we computed the F-measure values for each method, which is defined as:
where precision is the number of correct results divided by the number of all returned results. The recall is the number of correct results divided by the number of results that should have been returned.
To this end, the detected lines and the ground-truth lines were considered. A good line detector produces an F-measure percentage, which is close to 100%, while a poor one produces an F-measure value that is closer to 0%. As Figure 6 shows the comparison results, the corresponding F-measure values were tabulated in Table 1. As seen in Table 1, the highest average F-measure value was obtained by the proposed NHT method. The second highest average F-measure value was obtained by FHT. The worst F-measure values were produced by HT method.

Table 1.
F-measure percentages for compared methods.
We also experimented on various noisy real-world images and compared the obtained results with HT and FHT achievements. The real-world images were degraded with a 10% salt & pepper noise. The obtained results were given in Figure 7. The first, second, and third columns of Figure 7 show the HT, FHT, and NHT achievement, respectively. In addition, in the last column of Figure 7, the running times of each method for each image were given for comparison purposes.


Figure 7.
Comparison of NHT with HT and FHT on noisy images (a) HT results; (b) FHT results; and, (c) NHT results.
As can be seen in Figure 7, the proposed NHT method is quite robust against noise and can able to find the most of the true lines in the given images. In addition, with a visual inspection, the proposed NHT achieved better results than the compared HT and FHT. For example, for the image, which is depicted in the first row of Figure 7, the NHT detected all of the lines. FHT almost detected the lines with error. However, HT only detected just one line and missed the other lines. Similar results were also obtained for the other images that were depicted in the second and third rows of the Figure 7. In addition, for a comparison of the running times, it is seen that there is no significant differences between the compared methods running times.
5. Conclusions
In this paper, a novel Hough transform, namely NHT, was proposed, which uses the NS theory in voting procedure of the HT algorithm. The proposed NHT is quite efficient in the detection of the lines in both noisy and noise-free images. We compared the performance achievement of proposed NHT with traditional HT and FHT methods on noisy images. NHT outperformed in line detection on noisy images. In future works, we are planning to extend the NHT on more complex images, such natural images, where there are so many textured regions. In addition, Neutrosophic circular HT will be investigated in our future works.
Author Contributions
Ümit Budak, Yanhui Guo, Abdulkadir Şengür and Florentin Smarandache conceived and worked together to achieve this work.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hough, P.V.C. Method and Means for Recognizing. US Patent 3,069,654, 25 March 1960. [Google Scholar]
- Duda, R.O.; Hart, P.E. Use of the Hough transform to detect lines and curves in pictures. Commun. ACM 1972, 15, 11–15. [Google Scholar] [CrossRef]
- Chung, K.L.; Chen, T.C.; Yan, W.M. New memory- and computation-efficient Hough transform for detecting lines. Pattern Recognit. 2004, 37, 953–963. [Google Scholar] [CrossRef]
- Guo, S.; Pridmore, T.; Kong, Y.; Zhang, X. An improved Hough transform voting scheme utilizing surround suppression. Pattern Recognit. Lett. 2009, 30, 1241–1252. [Google Scholar] [CrossRef]
- Walsh, D.; Raftery, A. Accurate and efficient curve detection in images: The importance sampling Hough transform. Pattern Recognit. 2002, 35, 1421–1431. [Google Scholar] [CrossRef]
- Xu, L.; Oja, E. Randomized Hough transform (RHT): Basic mechanisms, algorithms, and computational complexities. CVGIP Image Underst. 1993, 57, 131–154. [Google Scholar] [CrossRef]
- Han, J.H.; Koczy, L.T.; Poston, T. Fuzzy Hough transform. Patterns Recognit. Lett. 1994, 15, 649–658. [Google Scholar] [CrossRef]
- Montseny, E.; Sobrevilla, P.; Marès Martí, P. Edge orientation-based fuzzy Hough transform (EOFHT). In Proceedings of the 3rd Conference of the European Society for Fuzzy Logic and Technology, Zittau, Germany, 10–12 September 2003. [Google Scholar]
- Mathavan, S.; Vaheesan, K.; Kumar, A.; Chandrakumar, C.; Kamal, K.; Rahman, M.; Stonecliffe-Jones, M. Detection of pavement cracks using tiled fuzzy Hough transform. J. Electron. Imaging 2017, 26, 053008. [Google Scholar] [CrossRef]
- Chatzis, V.; Ioannis, P. Fuzzy cell Hough transform for curve detection. Pattern Recognit. 1997, 30, 2031–2042. [Google Scholar] [CrossRef]
- Suetake, N.; Uchino, E.; Hirata, K. Generalized fuzzy Hough transform for detecting arbitrary shapes in a vague and noisy image. Soft Comput. 2006, 10, 1161–1168. [Google Scholar] [CrossRef]
- Chung, K.-L.; Lin, Z.-W.; Huang, S.-T.; Huang, Y.-H.; Liao, H.-Y.M. New orientation-based elimination approach for accurate line-detection. Pattern Recognit. Lett. 2010, 31, 11–19. [Google Scholar] [CrossRef]
- Cheng, H.-D.; Guo, Y.; Zhang, Y. A novel Hough transform based on eliminating particle swarm optimization and its applications. Pattern Recognit. 2009, 42, 1959–1969. [Google Scholar] [CrossRef]
- Zhu, L.; Chen, Z. Probabilistic Convergent Hough Transform. In Proceedings of the International Conference on Information and Automation, Changsha, China, 20–23 June 2008. [Google Scholar]
- Ballard, D.H. Generalizing the Hough Transform to Detect Arbitrary Shapes. Pattern Recognit. 1981, 13, 111–122. [Google Scholar] [CrossRef]
- Smarandache, F. Neutrosophy: Neutrosophic Probability, Set, and Logic; ProQuest Information & Learning; American Research Press: Rehoboth, DE, USA, 1998; 105p. [Google Scholar]
- Smarandache, F. Introduction to Neutrosophic Measure, Neutrosophic Integral and Neutrosophic Probability; Sitech Education Publishing: Columbus, OH, USA, 2013; 55p. [Google Scholar]
- Smarandache, F. A Unifying Field in Logics Neutrosophic Logic. In Neutrosophy, Neutrosophic Set, Neutrosophic Probability, 3rd ed.; American Research Press: Rehoboth, DE, USA, 2003. [Google Scholar]
- Vaheesan, K.; Chandrakumar, C.; Mathavan, S.; Kamal, K.; Rahman, M.; Al-Habaibeh, A. Tiled fuzzy Hough transform for crack detection. In Proceedings of the Twelfth International Conference on Quality Control by Artificial Vision (SPIE 9534), Le Creusot, France, 3–5 June 2015. [Google Scholar]
- Guo, Y.; Şengür, A. A novel image segmentation algorithm based on neutrosophic filtering and level set. Neutrosophic Sets Syst. 2013, 1, 46–49. [Google Scholar]
- Guo, Y.; Xia, R.; Şengür, A.; Polat, K. A novel image segmentation approach based on neutrosophic c-means clustering and indeterminacy filtering. Neural Comput. Appl. 2017, 28, 3009–3019. [Google Scholar] [CrossRef]
- Karabatak, E.; Guo, Y.; Sengur, A. Modified neutrosophic approach to color image segmentation. J. Electron. Imaging 2013, 22, 013005. [Google Scholar] [CrossRef]
- Guo, Y.; Sengur, A. A novel color image segmentation approach based on neutrosophic set and modified fuzzy c-means. Circuits Syst. Signal Process. 2013, 32, 1699–1723. [Google Scholar] [CrossRef]
- Sengur, A.; Guo, Y. Color texture image segmentation based on neutrosophic set and wavelet transformation. Comput. Vis. Image Underst. 2011, 115, 1134–1144. [Google Scholar] [CrossRef]
- Guo, Y.; Şengür, A.; Tian, J.W. A novel breast ultrasound image segmentation algorithm based on neutrosophic similarity score and level set. Comput. Methods Programs Biomed. 2016, 123, 43–53. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.; Sengur, A. NCM: Neutrosophic c-means clustering algorithm. Pattern Recognit. 2015, 48, 2710–2724. [Google Scholar] [CrossRef]
- Guo, Y.; Şengür, A. A novel image segmentation algorithm based on neutrosophic similarity clustering. Appl. Soft Comput. 2014, 25, 391–398. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).