1. Introduction
Corporate financial decision making is the process of identifying and then choosing the best of alternatives in capital budgeting, capital structure and/or working capital, in order to meet some objective or objectives of the firm. When there are several objectives (such as in the stakeholder theory), or a single objective defined by several attributes (such as in the balance scorecard concept), then a multi-criteria decision analysis method is needed. This paper is concerned with the optimal decision making in corporate financial management. In particular, it is concerned with two issues around this. The first issue is the interesting dichotomy in the academic literature regarding the flexibility of management in corporate financial decision making. The second issue is the use of residual income as an accounting basis for managerial compensation contracts.
With regard to the first issue, corporate financial decisions may be made amongst contemporaneous alternatives (at the same point in time) or amongst inter-temporal alternatives (at different points in time) and, often, the choice between contemporaneous alternatives will depend, in part, on what inter-temporal alternatives also exist. Decision making amongst inter-temporal alternatives is further complicated with the uncertainty of not knowing what will happen in the future and so, the decision-making process takes on a strategic perspective based on certain flexibilities corporate financial managers may have to make vary their decisions contingent on how uncertainty plays out. These managerial flexibilities have been termed “real options” by academics and strategic value or strategic options by corporate executives, and real option analysis has become the premier methodology for analyzing corporate financial decision making amongst inter-temporal alternatives. The real options literature takes a single objective—the maximization of firm value—and views managerial flexibility as value creating since it allows firms to capture the potential benefits of optimal decisions to be made in the future. In other words, the potential benefits of optimally exercised real options represent additional value above what is accounted for by traditional evaluative methods like Net Present Value (
NPV) analysis. Proponents of the real options approach to capital budgeting therefore argue that projects with such flexibilities should be valued more that similar projects without these flexibilities. This view of managerial flexibility being value enhancing is at odds with the literature on agency problems which tends to consider this very same managerial flexibility as potentially destroying value. Managers with incentives that are not aligned to the interests of outside investors (stockholders and bondholders) will use any flexibility that is present to pursue other objectives, usually to the detriment of the outside investors. If these adverse incentives cannot be controlled in some way, then the firm is better off sticking to projects that do not afford any flexibility. This paper is an attempt to combine and reconcile the above two streams of the literature by presenting a model of real options in the presence of the agency problem of adverse incentives. Thus, a key question we address is:
when will the presence of real options be value enhancing and when will it be value reducing? This is an issue that surprisingly relatively few papers in the literature have considered. One paper to address this issue is Cottrell and Calistrate (2000) [
1] and Feingold and Vasma (2014) [
2] who examine incentive compensation contracts for optimal technological upgrades or liquidation policies.
There are many corporate decisions made by management that are important, but in this paper, we shall focus on the capital budgeting decision and the presence of real options in capital investment projects. Given these real options and the potential for them to be abused by management, the second issue this paper is concerned with is the use of residual income (such as Economic Value Added (EVA) is a registered trademark of Stern Stewart & Co (New York, NY, USA). Note that at the time the EVA was developed, the company was called Stern & Stewart) as an accounting measure on which to base managerial compensation in order to induce the right investment incentives. From Fortune Magazine to academic journals in Economics and Operations Management, residual income based incentive plans have been touted as a way to align managers’ interest with that of shareholders when making investment decisions. For example, Stern (1990) [
3], Malmi and Ikaheimo (2003) [
4], and Lin and Zhilin (2008) [
5] have shown that companies adopting EVA as a base for executive compensation significantly increase their performance. Lehn and Makhija (1997) [
6] examine various performance measures for CEOs and their results suggest that labor markets assess CEOs on the basis of EVA™. Robertson and Batsakis (1999) [
7] find that investors respond favorably to companies that adopt an EVA-based compensation plan for their managers. Sharma and Kumar (2010) [
8] provide an overview of the literature on the EVA™ model and its applications. Unfortunately, these incentive plans are almost always geared towards guiding the manager into taking only those projects which have traditional
NPV that is positive. As Greene (1998) [
9] noted, when it comes to valuing real options, the EVA™ approach is deficient. One key problem with residual income based incentive plans is that implementation of such plans require the estimation of a constant risk adjusted cost of capital, and as Myers and Turnbull (1977) [
10] and Sick (1989) [
11] have pointed out, when an investment project contains real options, the relevant cost of capital will tend to be stochastic (An easy way to understand this is to consider that the relevant beta will now be a weighted average of two different component betas, with the weights themselves being stochastic). Furthermore, Rogerson (1997) [
12] has noted that using the firm’s cost-of-capital does not recognize the fact that managers may have personal hurdle rates that differ from the firm’s cost-of-capital. This paper addresses this problem by first determining the incentive compatible cost-of-capital for any given manager when the agency characteristics of that manager are known.
Agency theory predicts that if shareholders’ and managers’ interests are not in alignment, then managers are likely to engage in activities detrimental to the welfare of the firm’s shareholders (Jensen and Meckling 1976 [
13]). For example, Stulz (1990) [
14], Masulis, Wang, and Xie (2007) [
15], and Hope and Thomas (2008) [
16] have documented a well-known agency problem termed managerial “empire building”, where managers have a tendency to grow the firm beyond its optimal size in order to increase their personal status, power, or prestige. Jensen (1986) [
17] argues that firms with free cash flows and low growth prospects are the ones most prone to agency costs, and Richardson (2006) [
18] argue that managers pursuing other interests, including self-interest at the expense of shareholders may use waste excess free cash flows to make bad corporate investments. As in Rogerson, we then seek to determine if there is a particular cost-of-capital that, in a real options setting, will provide the correct incentives for all managers whose utility increases with the residual income. Contrary to Rogerson, in the presence of real options we do not find this to be the case. Instead we find that in general, a range of incentive compatible costs-of-capital exists across all managerial investment horizons but not across all managerial hurdle rates.
Another related paper that is similar in spirit to Rogerson is Dutta and Reichelstein (2002) [
19] who analyze managerial incentives for investment decisions when there is private information about the projects profitability. In a traditional
NPV setting, they find that investment incentives can be aligned through an appropriate depreciation rate leaving flexibility to control the moral hazard problem related to effort. Unfortunately, we cannot directly compare the results we obtain in our real options setting to theirs since they allow for a constant risk adjusted cost-of-capital, and we do not.
The rest of the paper is organized as follows.
Section 2 develops the real options capital budgeting model and compares it with the traditional model that is still more widely used (and taught).
Section 3 introduces the agency problem of adverse incentives which essentially leads to suboptimal exercise of the real options. It then is demonstrated that if this agency problem is severe enough, the real options
NPV of a project may actually fall below the traditional
NPV. Hence, real options may not always be value enhancing.
Section 3 also introduces the use of residual income as an incentive measure.
Section 4 develops this notion of residual income or, EVA™, by assuming that one of the managerial agency characteristics is unknown. Using numerical examples this section investigates whether there is a unique incentive compatible cost-of-capital that exists across all managerial investment horizons and all managerial hurdle rates.
Section 5 concludes. Evidence is collected in the appendices.
2. The Model
The model we develop in this paper is a variation of the normally distributed cash flow model of real options discussed in Sick (1989) [
11]. It is also a continuous time version of the discrete time model utilized by Dutta and Reichelstein (2002) [
19]. We consider an investment project that is to be undertaken although the analysis developed may be easily used to evaluate the existing assets of the firm. Let the systematic cash flows of the investment project follow the diffusion process (We use the term systematic to denote that the cash flows have some correlation to the market. Since this correlation is not perfect, there is still a diversifiable portion of the risk of these cash flows. Hence here, we distinguish between the terms systematic and undiversifiable):
where the initial cash flow is
. Here,
represents the systematic cash flow level at time
t,
μ is the drift rate or expected change in the systematic cash flow,
σ is volatility of the systematic cash flow changes, and
Wt is a standard Brownian motion process defined on probability space Ω and probability measure
endowed with the usual Brownian filtration. We assume that the time
t total operating cash flow
Ct is comprised of the systematic cash flow
and an unsystematic component
where
represents some unobservable action or effort on the part of the manager who undertakes the project and impacts on the distribution of the unsystematic cash flow
. The effort
is costly to the manager and we denote the expected value of
conditional on
, as
which is the same for
t. For now, we will assume that the level of effort is known (induced through some wage mechanism) and suppress the effort argument. We will comment further about the effort level in a later section after address the implication of basing the wage mechanism on residual income. Based on the solution to the stochastic differential equation above, we get that the random operating cash flow generated by the investment project at time
t is
where
has a standard normal distribution with mean zero and variance
t. The dispersion of information in our model is given in the assumption below.
Assumption 1. The operating cash flows are assumed to be observable to all, but the unsystematic component is only observed by the manager (inside agent). However, the parameters of the dynamics of the systematic cash flows, C, μ and, σ are common knowledge.
Thus, as in Dutta and Reichelstein (2002) [
19], outside investors are able to observe only the total cash flows and cannot distinguish between those related to the project and those related to the manager’s personal effort. Note that the process for the total operating cash flows allows for the possibility of their becoming negative as is the case for most real world situations. This possibility of negative cash flows is important, because it implies that in general, there will not be a constant risk-adjusted rate of return. That is, if the cash flows at any time
t, are reinvested back into the firm, the expected instantaneous return, denoted as
is
which, of course, will change as the level of cash flows change. This point has been noted by several authors including Sick (1989) [
11] who provides an example as to how the use of a constant risk-adjusted rate of return is erroneous due to a random time varying beta of the underlying asset. With no constant risk-adjusted rate of return, valuation of these cash flows must proceed by other means and we do so by making the following assumption.
Assumption 2. The financial markets contain a complete set of securities, or at least securities that span the risk of the project.
Given, Assumption 2, if we denote the market price of the risk embedded in the cash flows as
θ, then it is well known that by applying risk neutral valuation, the current market value of these cash flows is given by
where
r is the risk-free rate, and where the expectation
is taken under a new probability measure
, equivalent to P with a Radon–Nikodym derivative (That is,
and is assumed to satisfy the Novikov condition)
defined as the exponential martingale:
The probability measure
is termed the risk neutral probability measure and, by Assumption 2, the
in this measure is unique. Typically (for example, see Dixit and Pindyck (1994) [
20], (p. 115))
will be equal to the market price of risk multiplied by the amount of systematic in the operating cash flows,
z, where this amount is measured by the correlation between
z and the risk embedded in the aggregate market. That is
The market price of risk , the expected change in cash flow μ and the volatility of the cash flow change σ represent the primitives of the model and are exogenously given. Implementation of this model, will therefore require their estimation from data that enables the forecasting of operating cash flows and data from a proxy for the market. By definition, the unsystematic component of the cash flows has zero correlation to the market and so its risk is not priced by the market.
2.1. The Traditional NPV Approach
Consider that the investment opportunity generating these cash flows has a current capital cost of
I0. We assume that once the investment project is operational, its cash flows continue on forever (unless the project is sold for some salvage value which is a special case of what is discussed in the next section). The traditional approach to assessing this project is then to discount the cash flows to infinity and subtract this cost. That is
It can be shown that this becomes
This representation is nothing more than a certainty-equivalent representation, where under certainty equivalence the expected cash flow change becomes
, and cash flows are discounted at the risk-free rate. Sick (1989) [
11] arrives at a similar representation. It is clear that since the cash flows of the firm are allowed to be negative, if we wish to rigorously ensure that the present value (which is a market value) of these cash flows does not become negative we would have to impose certain restriction. One obvious and intuitive restriction would to require
μ/
σ >
θ or in other words, that the project’s stand-alone price of systematic risk be greater than its market price of risk (Recall that we have distinguished between the terms systematic and non-diversifiable. Therefore, a project’s stand-alone systematic risk consists of its diversifiable and non-diversifiable risk. Keeping this in mind we can see that the restriction
μ/
σ >
θ in fact, makes sense). A second (and more troublesome) restriction would be the requirement that (
even if the cash flows became negative. Practically, this second restriction will only have a noticeable impact for projects with extremely high volatility and so since it would change the dynamics of
, we have not incorporated it explicitly into the analysis (In fact, the ability to shut down operations when cash flows become sufficiently negative is a real option which will be analyzed in the next section. Furthermore, there is positive probability that the firm’s cash flows will never fall to such a level (see Karatzas and Shreve (1991) [
21] (p. 197)). Finally, it is also straight forward to see that if the cash flows are risk-less or if their risk is orthogonal to the market risk, then the
NPV of the project will simply be
2.2. The Real Options Approach
The real options approach recognizes that the investment project may have the flexibility (at the discretion of whomever is managing the project) to expand or contract at some point in time in the future as uncertainty is resolved. We model this by allowing the firm to expand (or contract) its systematic stochastic cash flows from to if the existing cash flows hit an upper (lower) level B at some random time in the future . Note that for bounded expansion (contraction), α satisfies 1 < α ≤ M (0 ≤ α < 1) for some finite number M and that the expansion (contraction) will involve a capital expenditure (recovery) of IB.
The current market value of the investment’s cash flows is given by:
This representation is similar to that of the seminal work by Leland (1994) [
22] where he examines the optimal leverage position when default is determined endogenously as the result of an optimal decision policy carried out by equity holders. The first part of the expression reflects the cash flows prior to expansion (contraction). The second part reflects cash flows after the expansion has occurred at the random time
. The third part reflects the investment (recovery) made at the random time
in order to effect the expansion (contraction), where
. The approach here is general enough to capture abandonment options such as in McDonald and Siegel (1985) [
23] or Dixit and Pindyck (1994) [
20] by setting
α equal to zero and
IB equal to salvage value. Note, that
IB can be easily generalized to be an increasing function of
α or of time. The boundary
B is initially assumed to be constant and we will later verify that this assumption is valid.
Using the first passage time density
f(
C, B, t) of the cash flow process to the boundary
B, it can be shown that the evaluation of the above representation for
V0 leads to the below closed form expression:
where
and
The first two parts of the expression for V0 is the traditional NPV value. The third and fourth parts comprise the real options value of the investment and are analogous to a financial options framework where the option value is the discounted future cash flows net of exercise price conditional on the option being “in-the-money”. We can interpret as the discounted probability of exercising the option and we point out that is the expected time (under certainty-equivalence) to exercising the real option.
For the rest of the paper we will focus on an expansion option which implies that α > 1, and B > C which implies that .
2.3. Optimal Exercise of Real Options
As mentioned in the introduction, the real options approach considers managerial flexibility to be value enhancing. This is because the real options approach implicitly assumes that any real options that are present will be exercised optimally. Assuming this to be true, we can determine the optimal exercise boundary and consequently, the “first best” value of the project.
In order to obtain the optimal boundary, we apply the smooth pasting (or high-contact) condition to the real option valuation expression. This condition is the requirement that at the optimal boundary the connection between the value of the real option before expansion and the value of the real option after expansion is tangential which means that their derivatives (w.r.t. cash flows) equate (For an argument on the appropriateness of the smooth pasting condition, see Dixit and Pyndick [
20] (1994, Chapter 4). See also Sick (1989) [
11] for an intuitive explanation). The boundary obtained by applying smooth pasting has the property that it maximizes the value of the real option for any given initial cash flow level
C such that
and thus another way of obtaining the optimal boundary is to maximize the real option component in the expression given above (w.r.t.
B). We shall, however, employ the former approach. Since the unsystematic cash flows are not impacted by the real option, then if expansion occurs at some time
t, after expansion the real option value is simply the
NPV of the expansion which is
The derivative of this w.r.t. cash flow is
. If we denote the real option value at time
t as
ROVt, then the smooth pasting condition is
It can be shown that this optimal boundary, denoted as
B*, is
It is important to note that this boundary represents a level of the systematic cash flows and, as we had initially assumed, is in fact constant. Note that under the traditional
NPV rule, expansion will occur once the
NPV is positive. Using this, we get that the boundary for this rule denoted as
BNPV, is
Comparing this with the real options boundary, we can see that, since the third component of
B* is non-negative, it is generally not optimal to invest as soon as the
NPV of expansion is positive and that the more volatile the cash flows of the project (i.e., greater
σ), the longer is the optimal waiting period. We should also note that when
, then
which results in the expected conclusion that at the optimal boundary
In other words, the real option representation given above satisfies the well-known “value-matching” condition. The approach we have used differs from the usual approach (for example see Dixit and Pindyck (1994) [
20]) which generally uses an American option valuation approach. Although the result is the same, this approach allows for a more intuitive interpretation and will permit the development of the adverse managerial incentives considered below.
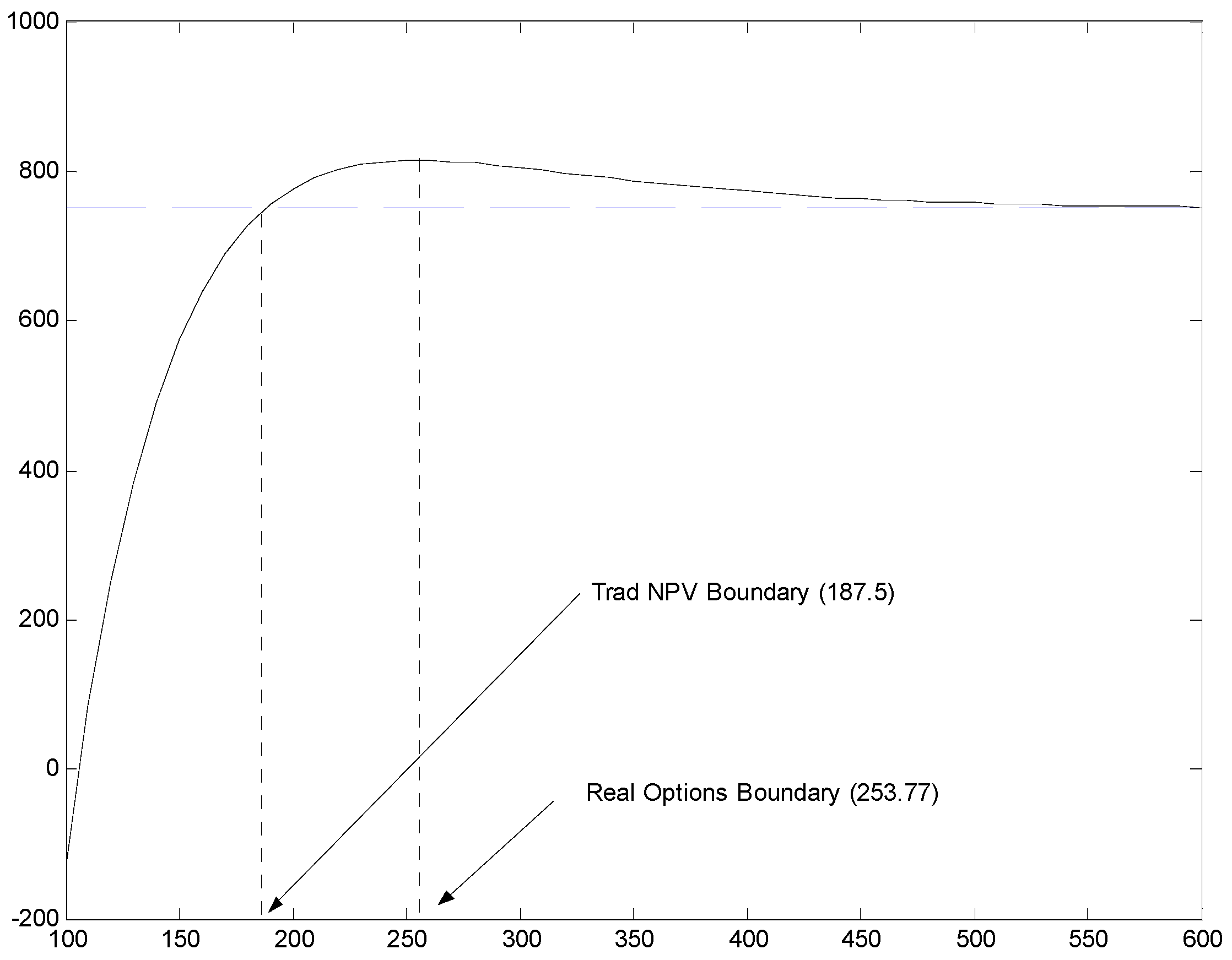
Figure 1 shows how the value of the project changes as the boundary changes assuming that
, and given the following parameters:
- -
Initial cash flow, C = 100
- -
Risk-free interest rate, r = 0.05
- -
Expected periodic cash flow change, μ = 5
- -
Volatility of cash flow changes, σ = 7.5
- -
Price of risk of cash flows, θ = 0.25
- -
Expansion factor, α = 1.5
- -
Initial Capital Expenditure, I0 = 2500
- -
Add-on Capital Expenditure, IB = 2500
Using the representation above, the optimal expansion boundary is 253.77, giving a project (net) value of 824.89 as compared to its traditional
NPV value of 750 and a real options value of 74.89. Note that if expansion is to be delayed till a point where the systematic cash flows exceed 253.77, then the value of the project will be less than is “first best” value even though there may still be some value added above its traditional
NPV. However, if the project is to be expanded when systematic cash flows are between 100 and 180.50, the value of the project will fall below 750. In other words, for premature early exercise, the value of the firm may actually fall below the traditional
NPV value. Thus, if managers have the incentive to exercise early, then real options may actually be value destroying. We may interpret premature early exercise as a form of
over investment and sub-optimal delayed exercise as a form of
under investment. Hence, in this framework, the boundary at which managers decide to expand captures over or under investment incentives.
Table 1 shows how the firm value and optimal boundary is affected by
IB,
μ,
σ,
θ, and
α.The key conclusion from this analysis is that whereas financial options are limited liability securities, real options can have negative value, since there are no arbitrage restrictions that prohibit exercising out-of-the-money real options. Modern corporate finance recognizes that managers with other objectives than just firm value maximization may therefore have the incentive to over or under invest and so there is a potential for real options to be advantageous or disadvantageous depending on how aligned or adverse the manager’s incentives are. We address the issue of managerial incentives in detail in the next section. Note however, that the optimal boundary does not depend on the unsystematic cash flow and therefore that wage mechanism used to influence the manager’s effort will not impact on the expansion decision.
3. Multiple Objectives and the Agency Problem of Adverse Incentives
If the systematic cash flows were observable, then a compensation contract for the manager could be designed “forcing” the optimal exercise of the real option. However, the presence of the unobservable unsystematic cash flows means that the wage mechanism will have to be based on some other observable quantity and the incentives of the manager become important. We focus on the use of some measure of the operating income as a quantity on which to base compensation contracts in order to align managers’ incentives with those of outside investors in the firm.
Aside from the moral hazard of costly effort, there are many reasons why managers of firms may have different incentives to act other than maximizing firm value and may therefore not exercise real options optimally. That is, even if there were no problem in engendering optimal effort, managers could still have the other objectives resulting in an incentive to invest in, expand, or contract operations sub-optimally. One obvious reason is that although firms are assumed to have unlimited life spans, managers generally have limited planning horizon. This may be due to managers’ perception of a limited employment horizon with any particular firm, or it may be due to their perception of their own mortality, or it may simply be due to a boundedness in their rationality that restricts them from considering states of nature beyond a certain time frame.
Jensen and Meckling (1976) [
13] have suggested that another reason managers may not maximize firm value is that they have the tendency to want to always increase the size of firms, even beyond their optimal size. Still another reason is that managers may have different levels of risk aversion than the owners. We summarize and capture all these reasons by saying that the alternate objectives of managers are captured by a limited horizon and a particular internal hurdle rate which the managers use to assess investments. As Rogerson (1997) [
12] put it, managers may invest inefficiently “because their personal cost of capital is higher than the firms or because they have a shorter time horizon than the firm”.
The impact of this agency problem is that expansion boundary which a particular manager considers personally optimal will, in general, differ from the “true” optimal boundary B*. At one extreme, the manager’s boundary may be so much larger than B* that all real option value will effectively be destroyed. Worse, however, is the other extreme where the manager’s boundary is so low that not only is all real option valued destroyed, but some traditional NPV value may also be lost.
To account for managerial incentives, we denote the manager’s investment horizon as T, and personal hurdle rate as R. As the hurdle rate R captures any risk aversion on the part of the manager, we make the following assumption.
Assumption 3. The manager’s utility (from wages) is a weakly increasing function of the expected discounted residual cash flows of the firm within the managers time horizon T, and with discounting done at the manager’s personal hurdle rate R.
Under certain circumstances, Assumption 3 can be derived by imposing a monotone likelihood ratio condition on the impact of the effort choice of the manager on the joint distribution of the cash flows. Note that by “time horizon”, we mean a constant limited time frame beyond which the manager is either incapable or unwilling to consider. We do not mean a constant future date that approaches as time passes. Hence at any point in time the manager considers up to
T years into the future and no more. By “residual”, we mean after a charge for the capital investment has been deducted. It is obvious that if operating cash flows do not have a capital cost component for the investment made, Assumption 3 means that the manager will generally have the incentive to always immediately (and sub-optimally) exercise expansion options. In fact, it is precisely due to such adverse incentives that firms base managerial compensation on accounting measures such as residual income or EVA™ which allocate investment expenditures over time. In the context of the model in this paper, the residual income, denoted as
, is defined similar to Balachandran and Mohanram (2012) [
24], as:
where
R* is the relevant cost-of-capital or so called capital charge and
It is the current book value of the capital assets used for the project. In terms of a depreciation rate
δ it is clear that
What may not be so clear is the relationship between
R* and
. To understand the relationship, as in Rogerson (1997) [
12], we introduce an imputed interest rate
i which we define as an interest rate in terms of units of real assets (hence imputed). That is, one may think of
i as borrowing
x units of some asset at time
t and paying
xi units of the asset at time
t + 1 as an interest charge. This may be compared to the cost of capital
R* which is always in terms of units of currency—the numeraire in the financial markets. Now, consider borrowing one unit of the asset for a promised interest of
i units in the next period. We assume the loan is perpetual so no return of principal is necessary. At the end of one period, if the asset has depreciated (relative to currency) at a rate
, the
i units will have a market value of
units of currency. Alternatively, one could have initially sold the unit of the asset and invested at the (opportunity) cost-of-capital
R*. Therefore, for there to be an equilibrium between the real asset markets and the financial markets, we must have the following
Definition 1. The cost-of-capital is related to the rate of depreciation and the imputed interest rate i by:
In some sense the above definition is similar to a carrying-cost definition of the cost of capital and we can interpret the imputed interest rate as the real required rate of return on the assets. Note, that according to this definition, firms using the traditional net operating income (EBIT) as the residual income will implicitly be setting , which implies an imputed interest of .
From Assumption 3 and the definition for
R* above, given
i and
δ, the manager will therefore view the net present value of the cash flows of any project as:
It can be shown that this leads to the below closed form expression:
where
and where
F(
t,
μ) represents the probability of hitting the boundary by time
t, given a drift of
μ. From [
25] Harrison (1985) we have obtained that
and
where
N(·) is the cumulative normal density function. It is important to remember that
represents the manager’s personal (and non-tradable)
NPV valuator when evaluating projects and by itself has no meaning as a market value. Furthermore, in a very real sense, the flexibility to expand the systematic cash flows of the project is considered by the financial markets as a particular real option, and by the manager as a
completely different real option. Hence to the manager, the optimal boundary
will be the cash flow level that optimizes the internal option and this will, in general not be the same boundary that optimizes the external option. By differentiating with respect to
C and imposing the smooth pasting condition, it can be shown directly that
is linear w.r.t.
R* and has the representation:
where (denoting derivatives w.r.t.
C with a “prime”)
and
Note that the intercept term does not depend on the rate of depreciation. It is the boundary level of cash flows at which the manager would exercise the real option if the allocated capital charge were zero (or equivalently, if the imputed interest rate were zero). Depending on the time horizon, could be negative (for shorter horizons) or positive (for longer horizons). This means that if no capital charge is allocated, expansion could occur even when current cash flows are negative. is invariably positive which implies that as the cost-of-capital used to compute residual income is increased, it will push up the manager’s expansion boundary or in other words, it will give the manager the incentive to delay expansion. Conversely, if one wanted to encourage the manager to expand sooner rather than .later, a lower R* should be employed.
Project Market Values
In basing compensation on residual income, the rate of depreciation δ and the imputed interest rate i will be choice variables that define the class of compensation schemes. Suppose that the firm chooses an arbitrary depreciation rate, and bases managerial compensation on some arbitrary cost-of-capital (such as a CAPM based cost-of-capital) rather than an incentive aligning cost-of-capital. This corresponds to some arbitrary combination of imputed interest and depreciation rates. The possibility of suboptimal exercise of the real options implies that if outside investors knew the manager’s hurdle rate R and time horizon T, as well as the imputed interest and depreciation rates i and δ, they could forecast the level of . Since will in general differ from the true optimal , the impact of adverse incentives on firm valuation will therefore be that the project will be valued at this level and, upon announcement that the firm is taking on the project, an NPV lower than the optimal NPV will be added on to the existing market value of the firm. As pointed out in the previous section, this NPV may actually be lower than the traditional NPV and hence the presence of the real option combined with adverse incentives may actually destroy value.
Given a general compensation mechanism satisfying Assumption 2, the managerial boundary can be viewed as a trade-off between the benefits of expansion: Expanded systematic cash flows, and the costs of expansion: allocated capital charges. The greater the benefits are relative to the costs, the more likely it is that the manager will expand early, or in other words, the lower will be . Similarly, the greater the costs are relative to the benefits, the higher will be .For a fixed rate of depreciation, the linear relationship between and R* implies that for any particular manager, a cost-of-capital R* will result in one and only one expansion boundary that, at the margin, reflects the cost benefit trade off.
How might one expect this trade off, and hence the expansion boundary of systematic cash flows, to be affected by the manager’s hurdle rate or investment horizon? Intuitively, for a fixed investment horizon, greater hurdle rates imply greater levels of aversion to risk and hence lower perceived net benefits. That is, since the cash flows are stochastic but the allocated charge is not, increasing the discount rates will impact more on the benefits than the costs. We should therefore expect that as the manager’s hurdle rate increases, expansion will be delayed which means that the boundary will pushed up.
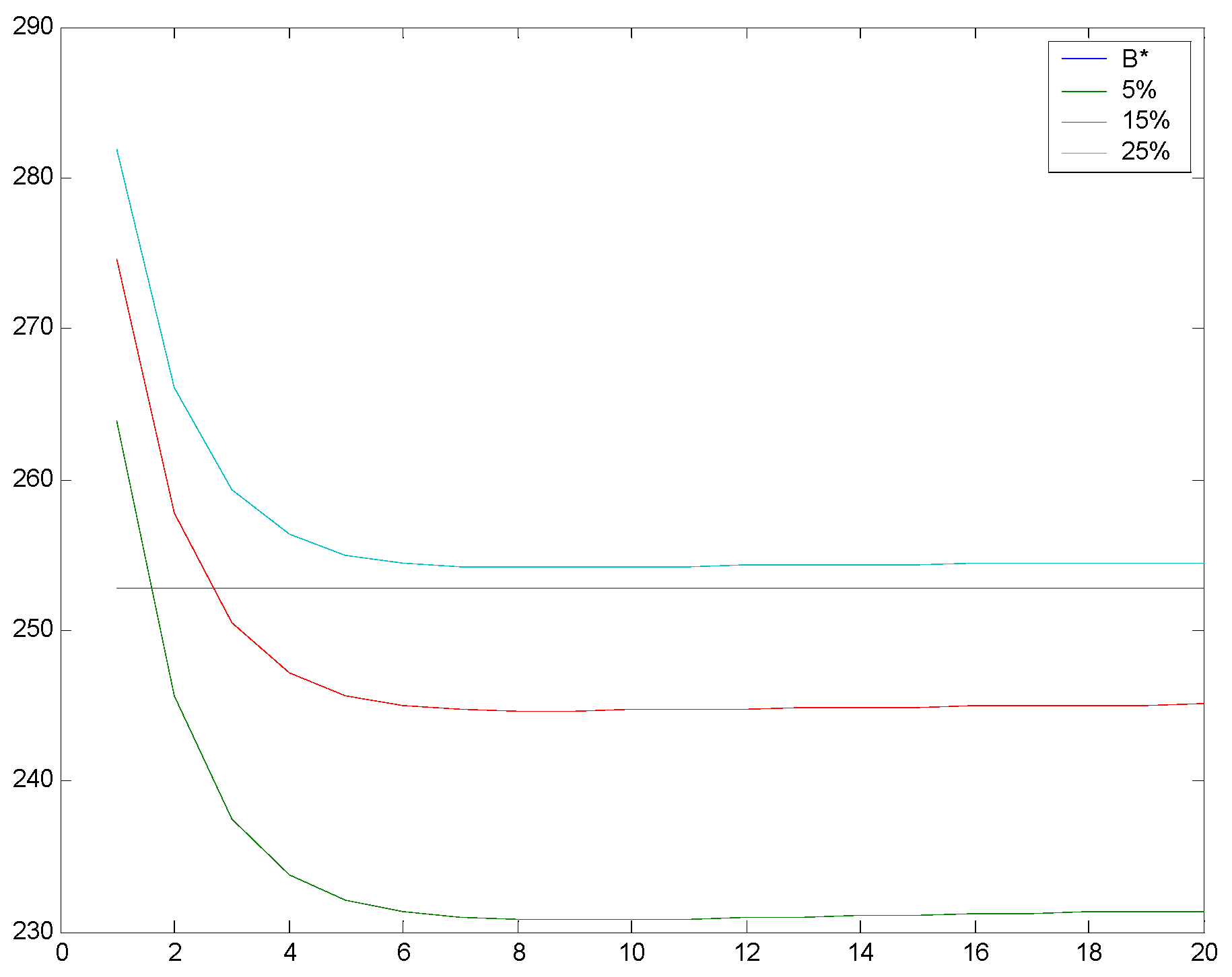
Figure 2 confirms this intuition. Using the parameters
C = 100,
I0 =
IB = 2500,
μ = 5,
σ = 5,
T = 10,
α = 1.7,
δ = 0.25 and
R* = 0.065, it shows that the real options boundary increases as hurdle rates increase and that at a hurdle rate of about 6%, the optimal boundary and the manager’s boundary coincide.
Figure 1 also shows that the curves for different time horizons are almost identical implying that manager’s with different horizons may tend to behave in the same manner.
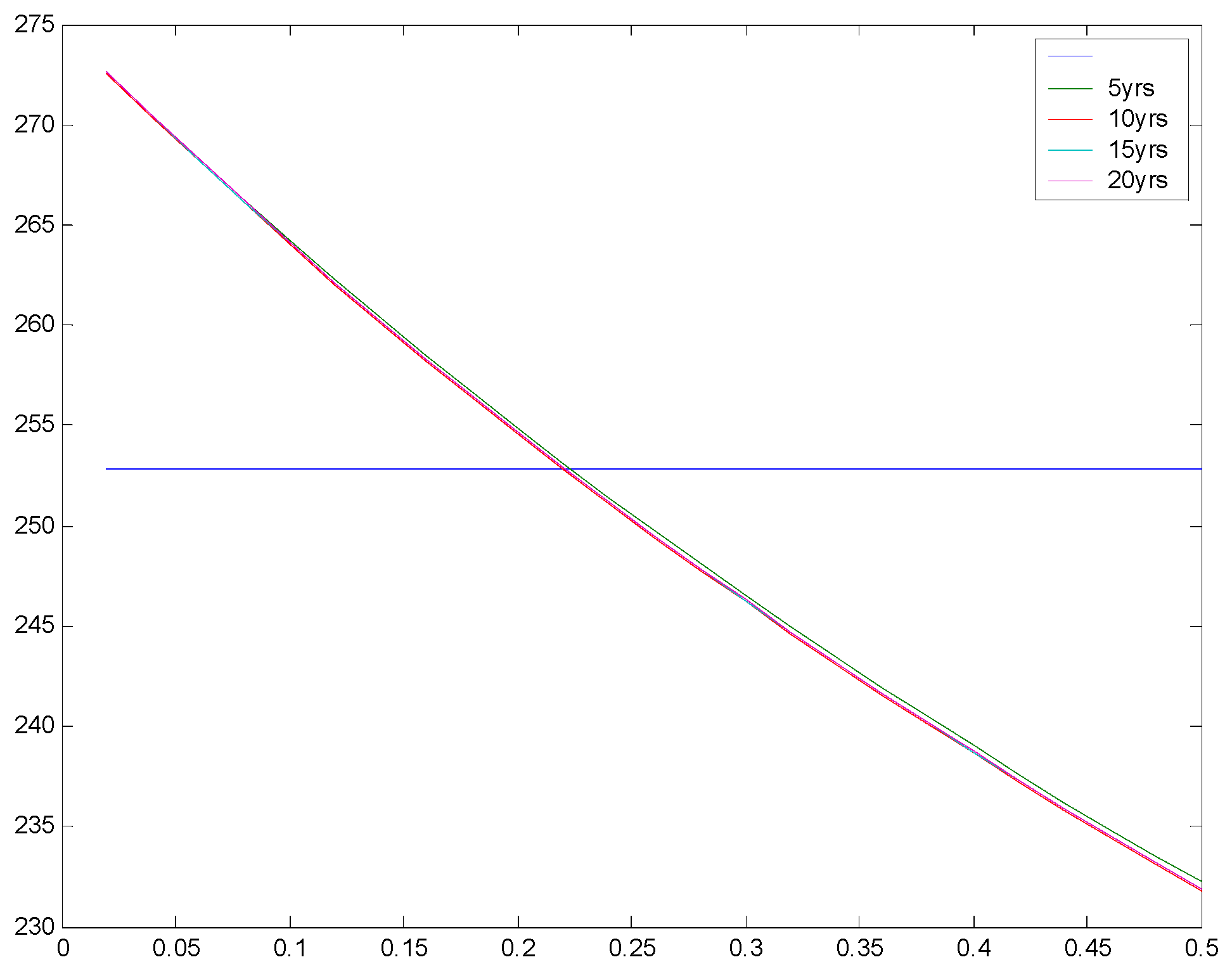
Figure 3 further demonstrates this finding. Using the same parameters as above, it shows that as the manager’s investment horizon increases, the expansion boundary declines. The reason for this is that for a fixed hurdle rate, an increasing time horizon implies reduced future capital bases and hence lower allocated capital charge. Thus there is a greater net benefit. However, we see that for horizons beyond about seven years the effect is flat. That is, managers with the same hurdle rate but different investment horizons will tend to respond to a particular cost-of-capital in the same manner.
For a fixed managerial investment horizon, greater depreciation implies a lower capital base and hence lower costs. Thus we might expect that the manager will have more of an incentive to expand early and the expansion boundary to decline.
Figure 4 shows how
responds to depreciation. We indeed observe declining expansion boundaries, but again, we see that managers with different horizons have very little difference in their boundaries.
If the depreciation rate were predetermined, then for any particular manager there would be a unique R*, termed the incentive compatible cost-of-capital, for which . This in turn would correspond to a unique imputed interest i. However, by definition, residual income is an accounting construct and both the depreciation and imputed interest are design accounting variables. As the rate of depreciation increases for a given manager’s finite horizon, there is a greater incentive to exercise the real option early. On the other hand, increased imputed interest charges give the manager the incentive to delay exercise. Thus, the high rates of depreciation can be countered with high imputed interest rates in order to force the manager to optimally exercise the real option. We can conclude from this that for each pair of investment horizons and personal discount rates {T,R}, there is a curve, representing particular combinations of i and δ for which . Along this curve, the project will achieve full market valuation. Hence, if all information is available, the selection of a combination along this curve will be incentive aligning. We describe this curve as the optimal iso-incentive curve for the given parameters {T,R}. In the next section, we examine the situation when all information is not common knowledge.
4. Incentive Compatible Cost-of-Capital
So far, we have assumed that
R and
T are known. However, it is likely that at least one of these will be information private to the manager. Rogerson (1997) [
12] also examines a case managerial characteristics is unobservable and concludes that efficient investment is induced if and only if the risk adjusted cost-of-capital for the firm’s existing assets is used to allocate investment expenditure. However, in the context of our model, and in particular in the presence of real options, a constant risk adjusted cost-of-capital for the firm’s existing assets may no longer have any meaning in the evaluation of new projects.
To determine analytically if there is an incentive-compatible cost-of-capital that covers all managers, we would need to ask if there exists a combination of
i and
δ such that for this combination,
for all
T or for all
R. Graphically, this would mean that if we plotted the optimal iso-incentive curves for various time horizons or for various hurdle rates, they would all intersect (or merge) at some point(s). To investigate this point, we plot iso-incentive curves for various
T and
R.
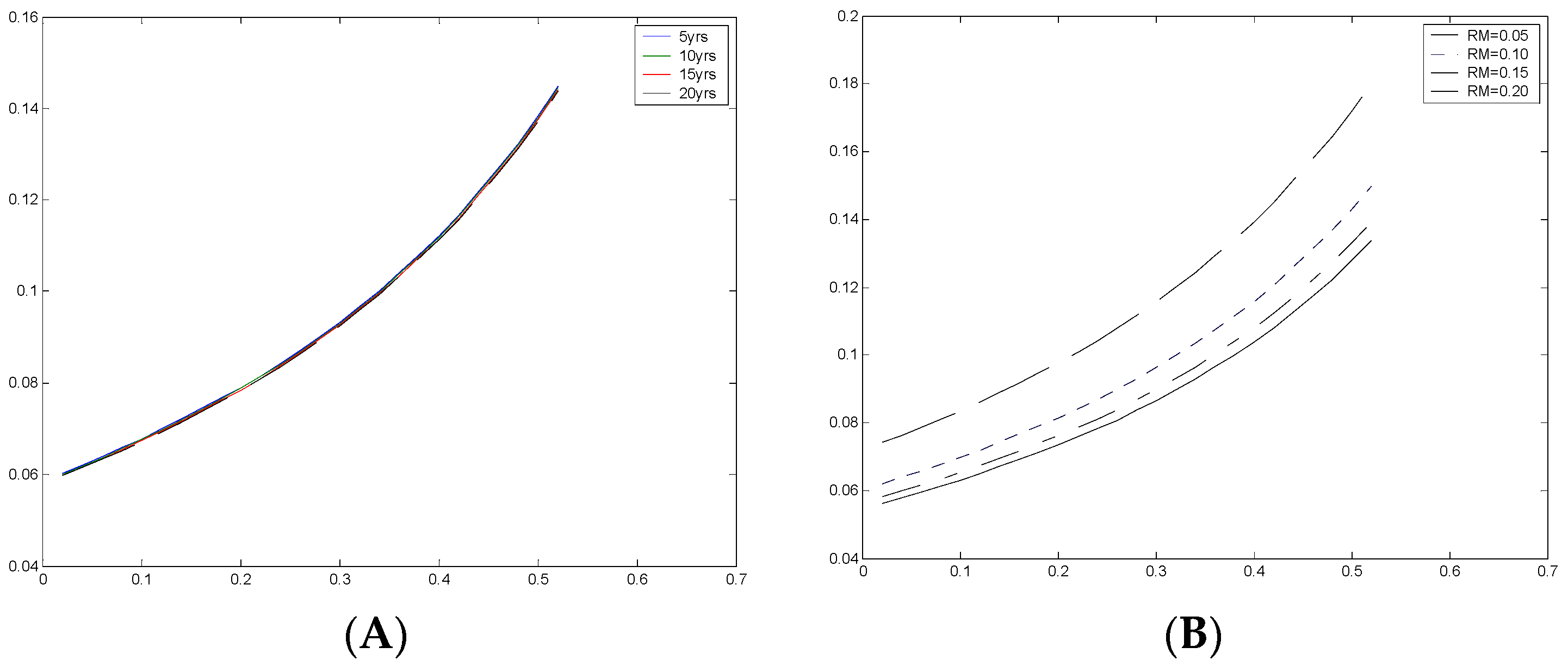
Figure 5A plots optimal iso-incentive curves for managerial time horizons of 5 years, 10 years, 15 years, and 20 years using the parameters from the previous section. As we can see, they almost all lie on the same line. This holds for projects with various levels of
μ (mean cash flow changes), and for low levels of
σ (volatility of cash flow changes). Although not shown, we can report that for very high levels of volatility, managers with different horizons separate out themselves.
Figure 5B plots optimal iso-incentive curves for managerial hurdle rates of 5%, 10%, 15%, and 20%. As we can see, there is no common cross-over point which implies that there is no one
i and
δ combination (and hence no unique
R*) that is incentive compatible for all managerial types. This contrasts with Rogerson (1997) [
12] who found in a somewhat different setting, that for the traditional
NPV, there is a unique
R* that induces proper incentives for all managers.
The end result is that the incentive compatible cost-of-capital is project specific in that it depends on the parameters of the project. This is much the same as choosing a cost-of-capital to fit the “risk” of the project. However, we see that it must also be specific to the personal hurdle rate of the manager, but it need not be specific to the investment horizon. Since this cost-of-capital is chosen simultaneously with the applicable depreciation rate, we are still left with a large amount of latitude. Presumably, we can utilize this latitude to further seek to create the right effort incentives by combining particular levels of depreciation with the corresponding incentive compatible cost-of-capital.
Figure 6A sets the managerial hurdle rate to 12% and plots the incentive compatible cost-of-capital. It is interesting to note that the rate of depreciation is generally higher that the corresponding cost-of-capital. Furthermore, as the rate of depreciation approaches 100%, the incentive compatible cost-of-capital goes to 7.13% (but is actually undefined for
δ = 1%).
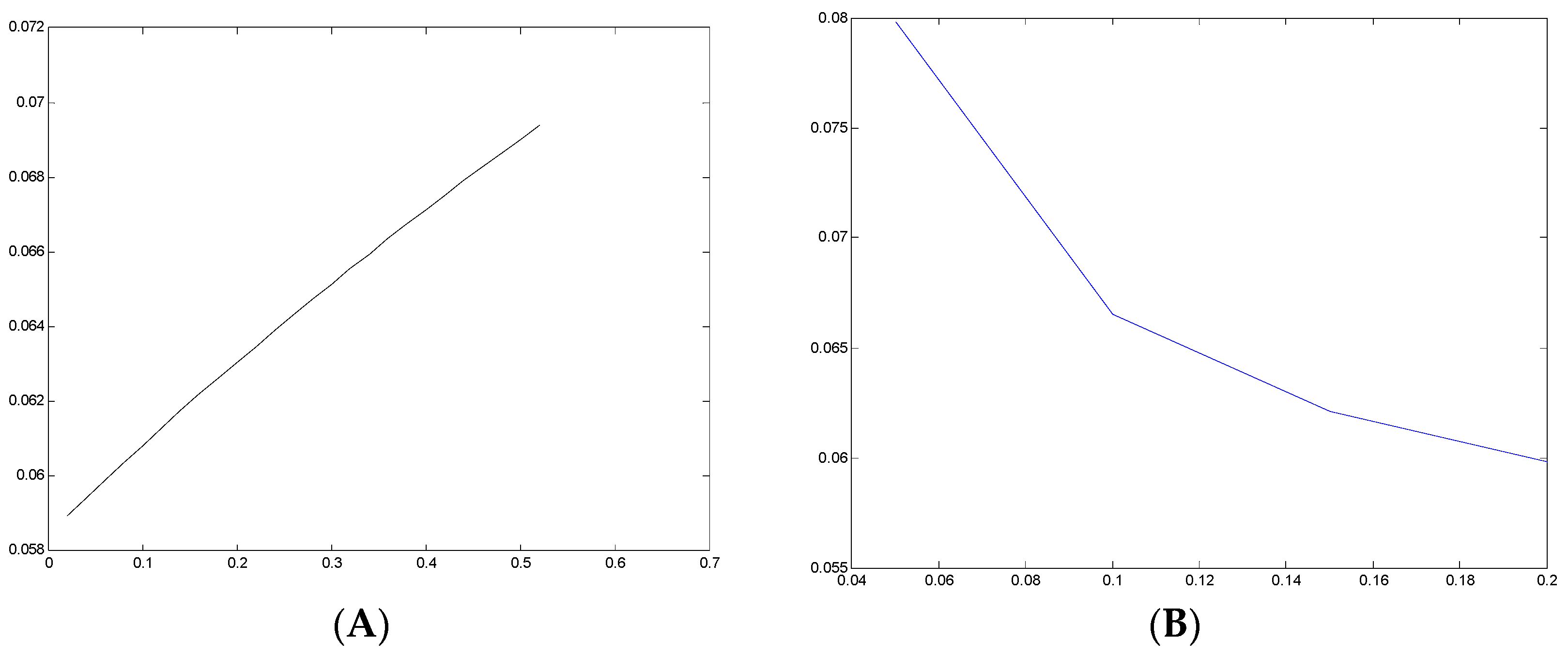
Figure 6B shows how the incentive-compatible cost-of-capital changes with hurdle rate when the depreciation rate is set to 26%. As is expected, lower hurdle rates require greater capital charges in order to induce the right expansion incentives.
Finally, inducing proper effort
ε from the manager will entail solving a standard principal agent problem using the restricted class of linear wage contract obtained above from inducing the correct expansion boundary. The important paper by Holmstrom and Milgrom (1987) [
26] has shown that under fairly general conditions, if the principal is risk neutral and the agent is risk averse with a von-Neumann Morgenstern Constant Absolute Risk Aversion (CARA) utility function, the optimal wage contract will be linear in wages. For more general utility functions, this may not be the case. For example, the Prospect Theory in Kahneman and Tversky (1979) [
27] and Tversky and Kahneman (1992) [
28] indicates that a manager’s utility function is differs on the domains of gains and losses, which may result in the optimal contract being a piece-wise linear function, kinked at some endogenous reference point. That said, these alternative formulations and their solutions, which will be third-best in nature, are beyond the scope of this paper and we relegate it to future research (In addition, in terms of practical application, the mean cash flow change,
μ, and the volatility of cash flow changes,
σ, may (likely) not be known a prior but may be filtered out using some version of a hidden Markov model (HMM) filter as in Elliott, Aggoun and Moore (1982) [
29] and while the model in this paper assumes that the mean and variance are given, it may be possible to extend the model using HMM methods. However, that is beyond the scope of the paper).