Hybrid Beamforming via Fourth-Order Tucker Decomposition for Multiuser Millimeter-Wave Massive MIMO Systems

Abstract

To enhance the spectral efficiency of hybrid beamforming in millimeter-wave massive MIMO systems, the problem is formulated as a high-dimensional non-convex optimization under constant modulus constraints. A novel algorithm based on fourth-order tensor Tucker decomposition is proposed. Specifically, the frequency-domain channel matrices are structured into a fourth-order tensor to explicitly capture the couplings across the spatial, frequency, and user domains. To tackle the non-convexity induced by constant modulus constraints, the analog precoder and combiner are derived by solving a truncated-rank Tucker decomposition problem through the Alternating Direction Method of Multipliers and Alternating Least Squares schemes. Subsequently, in the digital domain, the Regularized Block Diagonalization algorithm is integrated with the subcarrier and user factor matrices—obtained from the tensor decomposition—along with the water-filling strategy to design the digital precoder and combiner, thereby achieving a balance between multi-user interference suppression and noise enhancement. The proposed tensor-based algorithm is demonstrated through simulations to outperform existing state-of-the-art schemes. This work provides an efficient and mathematically sound solution for hybrid beamforming in dense multi-user scenarios envisioned for sixth-generation mobile communications.

1. Introduction

With the sixth-generation mobile communication era, demands for larger capacity and higher rates are pursued [1]. Millimeter-wave (mmWave)and even terahertz frequency bands will be adopted. Simultaneously, the small wavelength characteristic of mmWave is recognized as an inherent advantage for deploying massive MIMO systems [2,3]. However, mmWave is characterized by severe path loss and poor penetration. This deficiency is compensated in mmWave massive MIMO systems through beamforming to focus energy [4]. Although superior performance is offered by traditional fully digital beamforming, an independent radio frequency (RF) chain is required for each antenna, leading to hardware complexity and power consumption that grow exponentially with the number of antennas. Hybrid (HBF) beamforming technology, achieved through the decomposition of beamforming into joint analog-digital domain optimization, has been recognized as the critical solution for balancing spectral efficiency and hardware implementation costs in multi-user dense communication systems [5].

HBF is recognized for significantly reducing system power consumption and hardware complexity while high-bandwidth, high-data-rate, low-latency communication services are delivered [6,7], with its spectral efficiency approaching the performance upper bound of fully digital beamforming. However, the optimization problem is rendered inherently non-convex due to the high coupling between digital and analog beamforming domains, combined with the constant modulus constraints (CMC) of analog beamforming and transmit power constraints [8]. A principal solution approach is implemented by leveraging the sparse nature of mm Wave MIMO channels through alternating optimization of the transmit precoder and receive combiner matrices; this optimization is approached by first identifying a locally optimal precoder solution, subsequently solving the updated matrix equations for the corresponding optimal combiner, and progressively iterating to optimize all four transceiver matrices [9,10]. In [11], the base station (BS) precoding matrix and per-user combining matrix are designed through gradual minimization of the mean square error (MSE) to minimize the bit error rate (BER) in downlink multi-user transmissions. In [12], an iterative algorithm employing alternating minimization (AltMin) and manifold optimization is proposed to solve the non-convex weighted minimum mean square error (WMMSE) problem with established convergence guarantees. Nevertheless, conventional approaches are characterized by requiring numerous iterations leading to slow convergence, being prone to suboptimal solutions, and critically not accounting for multidimensional information such as intra-cell multi-user interference management—constituting the primary challenge for future.

To overcome the limitations of matrix-based methods in capturing the inherent multidimensional structure of channels, tensor decomposition theory provides a powerful mathematical framework [13,14]. As a higher-order generalization of matrices, tensors offer a natural and efficient representation for multi-domain data encountered in mmWave massive MIMO systems, inherently revealing correlations among spatial, frequency, and user domains. Among various tensor decomposition models, the Tucker decomposition is particularly suitable for this task [15]. It enables the direct processing of high-dimensional data without structural information loss caused by matricization. Unlike the canonical polyadic (CP) decomposition [16], which requires identical column ranks across all factor matrices, the Tucker model allows different modes (e.g., antennas, subcarriers, users) to have distinct ranks. This flexibility is essential for accurately characterizing the varying degrees of freedom in each domain within hybrid beamforming problems. By performing a truncated-rank Tucker decomposition on the constructed channel tensor, a new approach is provided for designing an analog precoder and combiner under CMC. Meanwhile, the resulting frequency-domain and user correlation matrices can be used to design digital precoder and combiner.

mmWave channels (30–300 GHz) are characterized by substantial bandwidth advantages, which has driven the exploration of orthogonal frequency division multiplexing (OFDM) systems. In such systems, wide bandwidth channels are decomposed into multiple mutually orthogonal narrowband subchannels. This decomposition motivates the application of OFDM’s frequency-flat subchannels to mmWave massive MIMO systems, where the multidimensional structure of multiuser OFDM can be effectively addressed through tensor decomposition techniques. Prior implementations of tensor decomposition have been applied to channel estimation and hybrid precoding design in beamforming systems. Specifically, in [17], phase rotation is incorporated into factor matrices of tensor-based orthogonal matching pursuit (OMP) algorithms to mitigate grid constraint-induced energy leakage; in [18], high-rank four-dimensional canonical polyadic decomposition with Vandermonde constraints on three factor matrices is introduced for efficient subpath parameter estimation in sub-6G channel modeling; while in [19], subcarrier channel matrices are represented as a third-order tensor to fully exploit channel information across all subcarriers via tensor decomposition. Although spectral efficiency approaching fully digital beamforming is achieved, these methods are characterized by critical dependency on RF chain count.

In HBF technology, designing is required for the analog precoding matrix and its combiner, digital precoding and its combiner, followed by joint optimization of both. Simultaneously, OFDM systems are equipped with numerous subcarriers, and mmWave massive MIMO systems are deployed with hundreds to thousands of antennas to serve more users. Addressing this problem necessitates tensor decomposition tools for processing high-dimensional data [20,21]. For hybrid beamforming in multi-user OFDM systems, employing tensor decomposition naturally characterizes multi-user interference and directly captures the coupling relationships of multidimensional parameters (spatial domain, temporal domain, frequency domain, user dimension, etc.) [22], enabling the joint optimization of inter-user beams through decomposition to enhance spectral efficiency.

Proposed in this paper is an HBF design method based on joint optimization of Tucker Decomposition of a Fourth-Order Tensor and the RBD algorithm for mmWave massive MIMO multi-user OFDM systems. Through hybrid tensor decomposition and RBD interference management, noise is effectively suppressed, spectral efficiency approaching fully digital performance is achieved, and an effective solution is provided for mmWave massive MIMO multi-user OFDM systems by the algorithm.

The main contributions of this article are concluded as follows.

• A unified fourth-order tensor channel modeling framework is established to overcome the dimensionality separation limitation of conventional matrix-based methods. This model cohesively integrates the spatial, frequency-domain, and user dimensions. A novel analog beamforming design scheme is subsequently proposed, wherein the analog precoder and combiner are derived from the factor matrices of a truncated-rank Tucker decomposition. The inherent non-convexity arising from the constant modulus constraints is effectively resolved using an Alternating Direction Method of Multipliers (ADMM)-based projection technique.
• A digital beamforming scheme is developed by utilizing the outcomes of the tensor decomposition. The subcarrier and user factor matrices, obtained through the Alternating Least Squares (ALS) algorithm, are systematically integrated with the Regularized Block Diagonalization (RBD) technique and water-filling power allocation strategy. This integration enables precise interference management and effective noise suppression, thereby significantly enhancing the overall spectral efficiency.
• Simulation experiments validate the impact of different parameters on the spectral efficiency performance of the HBF design in this paper. Simultaneously, simulation experiments verify that the proposed algorithm can still achieve satisfactory performance under low-resolution phase shifters.

The remainder of this paper is organized as follows: Section 2 presents the channel model, system framework, and methodological approach; Section 3 elaborates the HBF system design, computational complexity analysis, and numerical validation of spectral efficiency performance; Section 4 concludes the study and outlines future research directions.

2. Signal Model and Problem Formulation

This section introduces the channel and system model for HBF technology and gives the Tucker decomposition of a fourth-order tensor model.

2.1. Tucker Decomposition of a Fourth-Order Tensor

Tucker decomposition is a higher-order generalization of principal component analysis (PCA) [23,24], which decomposes a tensor into the product of a core tensor and corresponding matrices for each dimension. The truncated rank—($R_1,R_2,R_3,R_4$) fourth-order tensor a is defined as follows:

$$\begin{array}{cc}\hfill \mathcal{X}& \approx \mathcal{G}\times {}_1\mathbf{U}^{\left(1\right)}\times {}_2\mathbf{U}^{\left(2\right)}\times {}_3\mathbf{U}^{\left(3\right)}\times {}_4\mathbf{U}^{\left(4\right)}\hfill \\ & =\sum _{r_1=1}^{R_1}\sum _{r_2=1}^{R_2}\sum _{r_3=1}^{R_3}\sum _{r_4=1}^{R_4}{g}_{r_1{r}_2{r}_3{r}_4}{\mathbf{u}}_{r_1}^{\left(1\right)}\circ {\mathbf{u}}_{r_2}^{\left(1\right)}\circ {\mathbf{u}}_{r_3}^{\left(3\right)}\circ {\mathbf{u}}_{r_4}^{\left(4\right)}\hfill \end{array}$$

(1)

where $\mathcal{X}\in {\mathbb{C}}^{I_1\times I_2\times I_3\times I_4}$ is a fourth-order tensor, $\mathcal{G}\in {\mathbb{C}}^{R_1\times R_2\times R_3\times R_4}$ is the core tensor; ${\mathbf{U}}^{\left(1\right)}\in {\mathbb{C}}^{I_1\times R_1},{\mathbf{U}}^{\left(2\right)}\in {\mathbb{C}}^{I_2\times R_2},{\mathbf{U}}^{\left(3\right)}\in {\mathbb{C}}^{I_3\times R_3},$ and ${\mathbf{U}}^{\left(4\right)}\in {\mathbb{C}}^{I_4\times R_4}$ are the factor matrices for the four modalities, respectively, and are mutually orthogonal; ∘ is the outer product operation; and  ${\times }_{\mathrm{n}}$ is the n-modal product.

$$\begin{array}{cc}\hfill \underset{\mathcal{G},{\mathbf{U}}^{\left(1\right)},{\mathbf{U}}^{\left(2\right)},{\mathbf{U}}^{\left(3\right)},{\mathbf{U}}^{\left(4\right)}}{min}& {∥\mathcal{X}-\mathcal{G}{\times }_1{\mathbf{U}}^{\left(1\right)}{\times }_2{\mathbf{U}}^{\left(2\right)}{\times }_3{\mathbf{U}}^{\left(3\right)}{\times }_4{\mathbf{U}}^{\left(4\right)}∥}_F^2\hfill \\ \hfill \mathrm{s}.\mathrm{t}.& {\mathbf{U}}^{\left(n\right)\mathrm{H}}{\mathbf{U}}^{\left(n\right)}={\mathbf{I}}_{R_n},\forall n\in \{1,2,3,4\}\hfill \end{array}$$

(2)

The requirement for decomposition is defined by four factor matrices with varying ranks across dimensions for hybrid beamforming design, rendering CP decomposition unsuitable due to its requirement for identical column ranks in all factor matrices. Concurrently, when compared to Singular Value Decomposition (SVD), Tucker decomposition enables direct processing of high-dimensional data without structural information loss induced by matricization. Although non-unique solutions are provided by Tucker decomposition, exclusive focus is placed on fourth-order Tucker decomposition applications in hybrid beamforming systems in this study. Adoption of a feasible decomposition instance herein compromises neither the validity nor the research outcomes. According to the number of users, data streams, and subcarriers, truncated rank ($R_1,R_2,R_3,R_4$) is reasonably set to jointly characterize multi-dimensional features including spatial, frequency-domain, and user dimensions, thereby enabling hybrid beamforming design.

2.2. System Model

Considering a downlink multi-user massive MIMO-OFDM system employing a fully-connected architecture, both the BS and user equipment utilize planar antenna arrays (UPA) with square configurations. The base station is equipped with $N_t$ transmit antennas and $N_t^{RF}$ RF chains, serving K users over m subcarriers. The channel model adopts the Extended Saleh-Valenzuela model. User equipment is configured with $N_r$ transmit antennas and $N_r^{RF}$ RF chains, with $N_s$ data streams transmitted per subcarrier, satisfying $N_t^{RF}\le N_t, N_r^{RF}\le N_r,$$N_s=N_r^{RF}, K{N}_s=N_t^{RF}$, The HBF system model is shown in Figure 1.

The received signal at the k-th user for the m-th subcarrier is

$${\stackrel{⌢}{y}}_k\left[m\right] = \sqrt{{\rho }_k}{\mathbf{W}}_{BB,k}^{\mathrm{H}}\left[m\right]{\mathbf{W}}_{RF,k}^{\mathrm{H}}{\mathbf{H}}_k\left[m\right]{\mathbf{F}}_{RF}{\mathbf{F}}_{BB}\left[m\right]x\left[m\right] + {\mathbf{W}}_{BB,k}^{\mathrm{H}}\left[m\right]{\mathbf{W}}_{RF,k}^{\mathrm{H}}{\mathbf{n}}_k\left[m\right]$$

(3)

where $x\left[m\right]$ is the symbol vector for the m-th subcarrier, $x\left[m\right]\in {\mathbb{C}}^{K{N}_s\times 1}$, ${\stackrel{⌢}{y}}_k$$\left[m\right]$ is the symbol vector for the k-th user and m-th subcarrier, ${\stackrel{⌢}{y}}_k \in {\mathbb{C}}^{N_s\times 1}$, ${\mathbf{n}}_k\left[m\right]$ is additive white Gaussian noise, ${\mathbf{n}}_k\left[m\right] \in {\mathbb{C}}^{N_r\times 1}$ is independent and identically distributed (i.i.d.), ${\mathbf{n}}_k\left[m\right] ~ \mathcal{C}\mathcal{N}(0, {\sigma }_n^2{\mathbf{I}}_{N_r})$, $\sqrt{{\rho }_k}$ is the power gain factor, ${\Vert {\mathbf{F}}_{RF}{\mathbf{F}}_{BB}\left[m\right]\Vert }_{\mathrm{F}}^2 = P_T$ is the total transmit power per subcarrier, digital precoder at the BS is performed separately for the N_s data streams of K users, ${\mathbf{F}}_{BB}\left[m\right] = \left[{\mathbf{F}}_{BB,1}\right[m],\cdots ,{\mathbf{F}}_{BB,k}[m\left]\right] \in {\mathbb{C}}^{N_t^{RF}\times K{N}_s}$; the digital combiner for the k-th user is ${\mathbf{W}}_{BB,k} \in {\mathbb{C}}^{N_r^{RF}\times K{N}_s}$, the analog precoder at the BS is common to all subcarriers; the analog precoder and combiner satisfy constant modulus constraints $\left|{\mathbf{F}}_{RF}\right(i, j\left)\right| = 1/\sqrt{N_t}, \left|{\mathbf{W}}_{RF}\right(i, j\left)\right| = 1/\sqrt{N_r}, {\mathbf{F}}_{RF} \in {\mathbb{C}}^{N_t\times N_t^{RF}},{\mathbf{W}}_{RF,k} \in {\mathbb{C}}^{N_r\times N_r^{RF}}$ this paper adopts an OFDM system where each subcarrier channel is a narrowband flatfading channel; the frequency-domain channel matrix for the k-th user and m-th subcarrier is ${\mathbf{H}}_k\left[m\right],{\mathbf{H}}_k\left[m\right] \in {\mathbb{C}}^{N_r\times N_t}$.

2.3. Problem Statement

The spectral efficiency formula adopted in this paper is as follows [25]:

$$R_k\left[m\right]={log}_2\left|{\mathbf{I}}_{{\mathbf{N}}_{\mathbf{s}}}+{\displaystyle \frac{{\rho }_k}{{\sigma }_n^2}}{\mathbf{U}}_k^{-1}{\mathbf{V}}_{k,m}{\mathbf{V}}_{k,m}^{\mathrm{H}}\right|$$

(4)

where ${\mathbf{V}}_{k,m}={\mathbf{W}}_{k,m}^H{\mathbf{H}}_k\left[m\right]{\mathbf{F}}_{k,m}$, ${\mathbf{W}}_{k,m}={\mathbf{W}}_{RF,k}{\mathbf{W}}_{BB,k}\left[m\right]$, ${\mathbf{F}}_{k,m}={\mathbf{F}}_{RF}{\mathbf{F}}_{BB,k}\left[m\right]$, ${\mathbf{U}}_k={\displaystyle \frac{{\rho }_k}{{\sigma }_n^2}}{\displaystyle \sum _{i\ne k}^K}{\mathbf{W}}_{k,m}^{\mathrm{H}}{\mathbf{H}}_k\left[m\right]{\mathbf{F}}_{i,m}{\mathbf{F}}_{i,m}^{\mathrm{H}}{\mathbf{H}}_k^{\mathrm{H}}\left[m\right]{\mathbf{W}}_{k,m}+{\mathbf{W}}_{k,m}^{\mathrm{H}}{\mathbf{W}}_{k,m}$, the objective of this paper is to maximize spectral efficiency in multi-user massive MIMO-OFDM systems, the optimized spectral efficiency formula is as follows:

$$\begin{array}{cc}\hfill \underset{{\mathbf{F}}_{\mathrm{RF}},{\mathbf{W}}_{\mathrm{RF}},{\mathbf{F}}_{\mathrm{BB}}\left[m\right],{\mathbf{W}}_{\mathrm{BB}}\left[m\right]}{max}& {\displaystyle \frac{1}{M}}\sum _{m=1}^M{R}_k\left[m\right]\hfill \\ \hfill \mathrm{s}.\mathrm{t}.& {∥{\mathbf{F}}_{\mathrm{RF}}{\mathbf{F}}_{\mathrm{BB}}\left[m\right]∥}_{\mathrm{F}}^2=P_{\mathrm{T}}\hfill \\ \hfill & \left|{\mathbf{F}}_{\mathrm{RF}}\left(i,j\right)\right|=1/\sqrt{N_t}\hfill \\ \hfill & \left|{\mathbf{W}}_{\mathrm{RF}}\left(i,j\right)\right|=1/\sqrt{N_r}\hfill \end{array}$$

(5)

Due to the CMC of $\left|{\mathbf{F}}_{RF}\left(i,j\right)\right|$ and $\left|{\mathbf{W}}_{RF}\left(i,j\right)\right|$ and the transmit power constraint, this problem is formulated as a convex optimization problem. Alternating optimization is adopted for iterative solution. Specifically, the analog precoder and digital precoder are alternately optimized, where analog precoder optimization is transformed into several subproblems. In [26], the analog precoding solution problem is converted into $N_r^{RF}$ independent subproblems. Problem (5) is decomposed into $K{N}_S$ consecutive Tucker rank—(1,1) approximation subproblems, then Tucker2 decomposition is adopted. During analog precoder and combiner design, truncated-rank Tucker decomposition of a fourth-order tensor is first employed in this paper, with ADMM and ALS algorithms being utilized to decompose Problem (5) into optimization of core tensor and factor matrices. Through the dimensionality reduction property of tensor decomposition, noise-dominated subspaces are eliminated, effective signal power is enhanced, and capacity loss caused by traditional methods is avoided.

Secondly, during digital precoder design, multi-user interference is targeted to be overcome and noise to be suppressed. Nonlinear techniques are generally employed to achieve this goal, thereby improving spectral efficiency. In [27], the RCD algorithm is demonstrated to balance multi-user interference suppression and noise mitigation compared to the BD algorithm. In [28], a generalized zero-forcing approach is implemented through two-stage SVD-based nullspace projection to eliminate interference. The RBD algorithm is employed in our work, where SVD decomposition of the interference matrix enables explicit interference suppression while avoiding noise amplification from over-projection. Simultaneously, frequency-domain and user-domain factor matrices derived from Tucker decomposition are leveraged to precisely coordinate multi-user interference. Water-filling power allocation is integrated to further enhance spectral efficiency, prioritizing high-gain subchannels to maximize signal-to-noise ratios. This comprehensive strategy ultimately achieves elevation of the system’s spectral efficiency.

2.4. Extended Saleh-Valenzuela Channel Model

mmWave channels are predominantly characterized by line-of-sight (LOS) propagation and spatial sparsity [29,30]. The Extended Saleh-Valenzuela channel model is adopted in this work, wherein propagation paths with similar angular distributions and proximate delays are grouped into distinct scattering clusters. $N_c$ scattering clusters are defined, each comprising $N_p$ propagation paths. The frequency-domain channel response for the k-th user at the m-th subcarrier is mathematically represented as:

$${\mathbf{H}}_k\left(m\right)=\sqrt{{\displaystyle \frac{N_r{N}_t}{N_c{N}_p}}}\underset{c=1}{\sum ^{N_c}}\times \underset{p=1}{\sum ^{N_p}}{\gamma }_{cp}^i{\mathbf{a}}_r\left({\theta }_{cp}^k,{\varphi }_{cp}^k\right){\mathbf{a}}_{\mathbf{t}}^{\mathrm{H}}\left({\vartheta }_{cp}^k,{\phi }_{cp}^k\right)e^{{\displaystyle \frac{-j2\pi i\left(m-1\right)}{M}}}$$

(6)

where ${\gamma }_{cp}^i\sim \mathcal{C}\mathcal{N}\left(0,{\sigma }_{\gamma ,c}^2\right)$ is the complex gain of the p-th path in the c-th scattering cluster, ${\mathbf{a}}_r\left({\theta }_{cp}^k,{\varphi }_{cp}^k\right)$ and ${\mathbf{a}}_t^{\mathrm{H}}\left({\vartheta }_{cp}^k,{\phi }_{cp}^k\right)$ are the array responses at the user receiver and BS transmitter, respectively, ${\theta }_{cp}^k$, ${\varphi }_{cp}^k$ are the arrival azimuth and elevation angles from the base station to the p-th path of the c-th cluster, ${\vartheta }_{cp}^k,{\phi }_{cp}^k$ are the departure azimuth and elevation angles from the base station to the p-th path of the c-th cluster. Under UPA antenna configuration with half-wavelength antenna spacing, let ${\sum }_{c=1}^{N_c}{\gamma }_{cp}^2=\sqrt{N_r{N}_t/N_c{N}_p}$ satisfy the normalization factor $\mathbb{E}\left[{\Vert {\mathbf{H}}_k\left[m\right]\Vert }_F^2\right] = N_r{N}_t$, transmitter size is $\sqrt{N_t}\times \sqrt{N_t}$, receiver size is $\sqrt{N_r}\times \sqrt{N_r}$ Here it is assumed that the number of user scattering clusters, propagation paths, and angular spread are consistent. The antenna array responses at the BS and user equipment are:

$$\begin{gathered} {{\mathbf{a}}_{\mathrm{UPA}}(\vartheta ,\phi ) = \frac{1}{\sqrt{N_t}}[1,\cdots , {\mathrm{e}}^{j\frac{2\pi }{\lambda }d(p\sin \vartheta \sin \phi +q\cos \phi )}, \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\cdots , {\mathrm{e}}^{j\frac{2\pi }{\lambda }d\left(\right(\sqrt{N_t}-1)\sin \vartheta \sin \phi +(\sqrt{N_t}\left)\cos \phi \right)}]}^{\mathrm{T}} \end{gathered}$$

(7)

$$\begin{gathered} {{\mathbf{a}}_{\mathrm{UPA}}(\mathit{\theta },\mathit{\varphi }) = \frac{1}{\sqrt{N_r}}[1,\cdots , {\mathrm{e}}^{j\frac{2\pi }{\lambda }d(p\sin \mathit{\theta }\sin \mathit{\varphi }+q\cos \mathit{\varphi })}, \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\cdots , {\mathrm{e}}^{j\frac{2\pi }{\lambda }d\left(\right(\sqrt{N_r}-1)\sin \mathit{\theta }\sin \mathit{\varphi }+(\sqrt{N_r})\cos \mathit{\varphi })}]}^{\mathrm{T}} \end{gathered}$$

(8)

where λ is the signal wavelength, d is the spacing between antenna elements, and satisfies $0 \le p< \sqrt{Nr}-1, 0 \le q< \sqrt{Nr}-1$

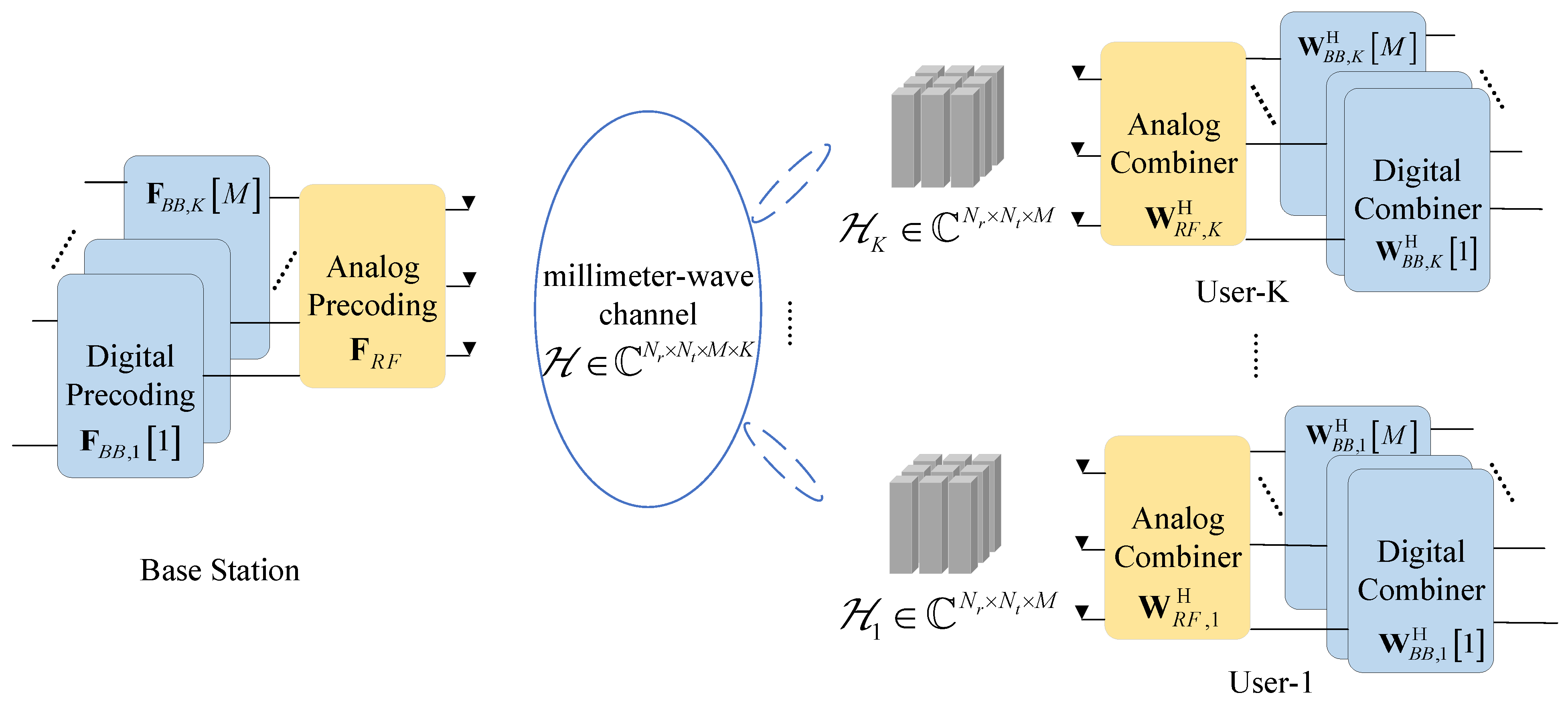
3. HBF Design

This paper presents a HBF framework based on joint Tucker decomposition of fourth-order tensors and RBD. Compared with conventional HBF designs, the proposed approach integrates channel state information, user-specific characteristics, and frequency-domain resources through a unified tensor model. Frequency-domain and user-domain factor matrices are utilized for digital beamformer optimization to achieve precise interference suppression. The detailed designs of analog and digital beamforming architectures are elaborated in subsequent sections.

3.1. Analog Precoder and Combiner

Through Tucker decomposition of a fourth-order tensor, the design of analog precoder and combiner is transformed into phase extraction and quantization of the transmitter-side factor matrices ${\mathbf{U}}^{\left(1\right)},{\mathbf{U}}^{\left(2\right)}$. This method significantly reduces computational complexity while ensuring hardware feasibility. Moreover, the decomposed factor matrices of the frequency domain and the user domain provide the optimization space for subsequent digital precoder. First, analog precoder and combiner are designed via truncated-rank Tucker decomposition of a fourth-order tensor. First, the channel tensor $\mathcal{H}\in {\mathbb{C}}^{N_r\times N_t\times M\times K}$ is built, with core tensor $\mathcal{G}\in {\mathbb{C}}^{K{N}_s\times K{N}_s\times M\times K}$. The four factor matrices obtained from its truncated-rank decomposition are analog precoder and combiner, subcarrier correlation matrix, and user correlation matrix, respectively. Tucker decomposition of a fourth-order tensor achieves interference suppression through multi-dimensional joint optimization without requiring per-stream alternating optimization. The channel model is then expressed as follows:

$$\mathcal{H}\approx \mathcal{G}{\times }_1{\mathbf{W}}_{RF}{\times }_2{\mathbf{F}}_{RF}{\times }_3\mathbf{C}{\times }_4\mathbf{D}$$

(9)

where $\mathbf{C}$ is the subcarrier factor matrix, $\mathbf{D}$ is the user factor matrix. The problem of Tucker decomposition of a fourth-order tensor for the channel is transformed into the solving process of analog precoder and combiner. Under the assumption of perfect channel state information (CSI), Although channel estimation for mmWave massive MIMO systems is challenging, several high-precision low-complexity methods have been proposed [31,32]. Let the channel tensor be denoted as $\mathcal{H}\in {\mathbb{C}}^{N_r\times N_t\times M\times K}$. Our objective is to minimize ${∥\mathcal{H}-\tilde{\mathcal{H}}∥}^2$. By optimizing the design variables ${\mathbf{W}}_{RF},{\mathbf{F}}_{RF},\mathbf{C},\mathbf{D}$, subject to hardware constraints during the design of the analog precoder and combiner.

$$\begin{array}{cc}\hfill \underset{\mathcal{G},{\mathbf{W}}_{\mathrm{RF}},{\mathbf{F}}_{\mathrm{RF}},M,K}{min}& {∥\mathcal{H}-\mathcal{G}{\times }_1{\mathbf{W}}_{\mathrm{RF}}{\times }_2{\mathbf{F}}_{\mathrm{RF}}{\times }_3\mathbf{C}{\times }_4\mathbf{D}∥}^2\hfill \\ \hfill \mathrm{s}.\mathrm{t}.& \left|{\mathbf{F}}_{\mathrm{RF}}(i,j)\right|={\displaystyle \frac{1}{\sqrt{N_t}}},\forall i,j\hfill \\ \hfill & \left|{\mathbf{W}}_{\mathrm{RF}}(i,j)\right|={\displaystyle \frac{1}{\sqrt{N_r}}},\forall i,j\hfill \\ \hfill & {\mathbf{C}}^{\mathrm{H}}\mathbf{C}={\mathbf{I}}_M\hfill \\ \hfill & {\mathbf{D}}^{\mathrm{H}}\mathbf{D}={\mathbf{I}}_K\hfill \end{array}$$

(10)

The CMC on the analog precoder and combiner render Equation (10) a non-convex optimization problem. To address this, we deploy the ADMM, which effectively handles the non-convexity induced by CMC. Compared to conventional per-stream optimization methods, this approach significantly reduces computational complexity. Within the ADMM framework, we employ alternating least squares (ALS) to iteratively optimize factor matrices while updating the core tensor as follows:

$$\mathcal{G}=\mathcal{H}{\times }_1{\mathbf{W}}_{RF}^{†}{\times }_2{\mathbf{F}}_{RF}^{†}{\times }_3{\mathbf{C}}^{†}{\times }_4{\mathbf{D}}^{†}$$

(11)

where † denotes pseudoinverse. By performing SVD decomposition on the unfolding of the tensor, the factor matrices are updated. The tensor $\mathcal{H}{\times }_1{\mathbf{W}}_{RF}^{\mathsf{H}}{\times }_2{\mathbf{F}}_{RF}^{\mathsf{H}}{\times }_4{\mathbf{D}}^{\mathsf{H}}$ is unfolded along mode-3 to obtain matrix ${\mathbf{H}}_{\left(3\right)}\in {\mathbb{C}}^{M\times \left(K{N}_r{N}_t\right)}$, defined as.

$${\mathbf{H}}_{\left(3\right)}={\left(\mathrm{H}{\times }_1{\mathbf{W}}_{\mathrm{RF}}^{\mathrm{H}}{\times }_2{\mathbf{F}}_{\mathrm{RF}}^{\mathsf{H}}{\times }_4{\mathbf{D}}^{\mathrm{H}}\right)}_{\left(3\right)}$$

(12)

where ${\left(.\right)}_{\left(3\right)}$ denotes the mode-3 unfolding operation of the tensor, which unfolds the third dimension (subcarrier dimension) into matrix rows and other dimensions (user, antenna) into columns. By performing SVD decomposition and taking the top M left singular vectors:

$$\mathbf{C}=\mathrm{SV}{\mathrm{D}}_M\left({\mathbf{H}}_{\left(3\right)}\right)$$

(13)

The tensor $\mathcal{H}{\times }_1{\mathbf{W}}_{RF}^{\mathrm{H}}{\times }_2{\mathbf{F}}_{RF}^{\mathrm{H}}{\times }_3{\mathbf{C}}^{\mathrm{H}}$ is unfolded along mode-4 to obtain matrix ${\mathbf{H}}_{\left(4\right)}\in {\mathbb{C}}^{K\times \left(N_r{N}_{t}M\right)}$, defined as

$${\mathbf{H}}_{\left(4\right)}={\left(\mathcal{H}{\times }_1{\mathbf{W}}_{RF}^{\mathrm{H}}{\times }_2{\mathbf{F}}_{RF}^{\mathrm{H}}{\times }_3{\mathbf{C}}^{\mathrm{H}}\right)}_{\left(4\right)}$$

(14)

By performing SVD decomposition and taking the top K left singular vectors:

$$\mathbf{D}=\mathrm{SV}{\mathrm{D}}_K\left({\mathbf{H}}_{\left(4\right)}\right)$$

(15)

Theauxiliary variables ${\mathbf{Z}}_W$ and ${\mathbf{Z}}_F$ and dual variables U_F and U_W are introduced, decomposing the constraint problem of constant modulus into solvable sub-problems. The objective function is:

$$\begin{array}{c}min{∥{\mathbf{Y}}_F-{\mathbf{F}}_{RF}{\mathbf{H}}_{\left(2\right)}∥}_F^2+{\displaystyle \frac{\rho }{2}}{∥{\mathbf{F}}_{RF}-{\mathbf{Z}}_F+{\mathbf{U}}_F∥}_F^2\hfill \\ min{∥{\mathbf{Y}}_W-{\mathbf{W}}_{RF}{\mathbf{H}}_{\left(1\right)}∥}_F^2+{\displaystyle \frac{\rho }{2}}{∥{\mathbf{W}}_{RF}-{\mathbf{Z}}_W+{\mathbf{U}}_W∥}_F^2\hfill \end{array}$$

(16)

where ${\mathbf{Y}}_F={\left(\mathcal{G}{\times }_1{\mathbf{W}}_{RF}{\times }_3\mathbf{C}{\times }_4\mathbf{D}\right)}_{\left(2\right)}$, ${\mathbf{Y}}_W={\left(\mathcal{G}{\times }_2{\mathbf{F}}_{RF}{\times }_3\mathbf{C}{\times }_4\mathbf{D}\right)}_{\left(1\right)}$, and the solution is obtained as follows:

$$\begin{array}{c}{\mathbf{F}}_{\mathrm{RF}}^{\mathrm{new}}={\left({\mathbf{Y}}_F{\mathbf{Y}}_F^{\mathrm{H}}+\rho {\mathbf{I}}_{N_t^{\mathrm{RF}}}\right)}^{-1}{\left({\mathbf{Y}}_F{\mathbf{H}}_{\left(2\right)}^{\mathrm{H}}+\rho \left({\mathbf{Z}}_F-{\mathbf{U}}_F\right)\right)}^{\mathrm{H}}\hfill \\ {\mathbf{W}}_{\mathrm{RF}}^{\mathrm{new}}={\left({\mathbf{Y}}_W{\mathbf{Y}}_W^{\mathrm{H}}+\rho {\mathbf{I}}_{K{N}_r^{\mathrm{RF}}}\right)}^{-1}{\left({\mathbf{Y}}_W{\mathbf{H}}_{\left(1\right)}^{\mathrm{H}}+\rho \left({\mathbf{Z}}_W-{\mathbf{U}}_W\right)\right)}^{\mathrm{H}}\hfill \end{array}$$

(17)

To satisfy the CMC, phase extraction and normalization are performed on ${\mathbf{F}}_{RF}^{new},{\mathbf{W}}_{RF}^{new}$

$$\begin{array}{c}{\mathbf{Z}}_F={\displaystyle \frac{1}{\sqrt{N_t}}}exp\left(j·\angle \left({\mathbf{F}}_{RF}^{new}+{\mathbf{U}}_F\right)\right)\hfill \\ {\mathbf{Z}}_W={\displaystyle \frac{1}{\sqrt{N_r}}}exp\left(j·\angle \left({\mathbf{W}}_{RF}^{new}+{\mathbf{U}}_W\right)\right)\hfill \end{array}$$

(18)

The dual variable is updated to rigorously enforce the constant modulus constraint:

$$\begin{array}{c}{\mathbf{U}}_F^{\left(t+1\right)}={\mathbf{U}}_F^{\left(t\right)}+({\mathbf{F}}_{RF}^{new}-{\mathbf{Z}}_F^{\left(t+1\right)})\hfill \\ {\mathbf{U}}_W^{\left(t+1\right)}={\mathbf{U}}_W^{\left(t\right)}+({\mathbf{W}}_{RF}^{new}-{\mathbf{Z}}_W^{\left(t+1\right)})\hfill \end{array}$$

(19)

Convergence Judgment

$$\left\{\begin{array}{c}re{s}_F={\displaystyle \frac{{\mathbf{F}}_{RF}^{\mathrm{new}}-{\mathbf{F}}_{RFF}}{{\mathbf{F}}_{RFF}}}\\ re{s}_W={\displaystyle \frac{{\mathbf{W}}_{RF}^{\mathrm{new}}-{\mathbf{W}}_{RFF}}{{\mathbf{W}}_{RFF}}}\\ re{s}_C={\displaystyle \frac{\mathbf{C}-{\mathbf{C}}_{\mathrm{prev}F}}{{\mathbf{C}}_{\mathrm{prev}F}}}\\ re{s}_D={\displaystyle \frac{\mathbf{D}-{\mathbf{D}}_{\mathrm{prev}F}}{{\mathbf{D}}_{\mathrm{prev}F}}}\end{array}\right.$$

(20)

Collaborative optimization of analog precoder and combiners in mmWave massive MIMO systems is achieved by this algorithm through joint Tucker decomposition of a fourth-order tensor channel model using ALS and ADMM algorithms. Frequency-domain and factor matrices are yielded through the decomposition to participate in subsequent digital precoder and combiner design. After each iteration, an economy-size QR decomposition is executed, which fundamentally resolves beam pattern distortion caused by constant modulus constraints, thereby ensuring array gain. The algorithm flow of analog beamforming is presented in Algorithm 1.

Algorithm 1 Design of analog beamforming based on Joint ADMM-ALS decomposition

1: Randomly initialization: ${\mathbf{Z}}_F,{\mathbf{U}}_F,{\mathbf{W}}_{RF}^{\left(0\right)},{\mathbf{F}}_{RF}^{\left(0\right)},{\mathbf{C}}^{\left(0\right)},{\mathbf{D}}^{\left(0\right)}$ 2: Zero matrix: ${\mathbf{Z}}_W,{\mathbf{U}}_W$, Set $max\_iter,\epsilon$ 3: for$iter=1$to$max\_iter$do 4:    ALS: Core tensor update: 5:    $\mathcal{G}=\mathcal{H}{\times }_1{\left({\mathbf{W}}_{RF}\right)}^{†}{\times }_2{\left({\mathbf{F}}_{RF}\right)}^{†}{\times }_3{\mathbf{C}}^{†}{\times }_4{\mathbf{D}}^{†}$ 6:    $\mathbf{C}=\mathrm{SV}{\mathrm{D}}_M\left({\mathbf{H}}_{\left(3\right)}\right)$ 7:    $\mathbf{D}=\mathrm{SV}{\mathrm{D}}_K\left({\mathbf{H}}_{\left(4\right)}\right)$ 8:    ADMM: Analog matrices solution: 9:    ${\mathbf{F}}_{\mathrm{RF}}^{\mathrm{new}}={\left({\mathbf{Y}}_F{\mathbf{Y}}_F^{\mathrm{H}}+\rho {\mathbf{I}}_{N_t^{\mathrm{RF}}}\right)}^{-1}{\left({\mathbf{Y}}_F{\mathbf{H}}_{\left(2\right)}^{\mathrm{H}}+\rho \left({\mathbf{Z}}_F-{\mathbf{U}}_F\right)\right)}^{\mathrm{H}}$ 10:    ${\mathbf{W}}_{\mathrm{RF}}^{\mathrm{new}}={\left({\mathbf{Y}}_W{\mathbf{Y}}_W^{\mathrm{H}}+\rho {\mathbf{I}}_{K{N}_r^{\mathrm{RF}}}\right)}^{-1}{\left({\mathbf{Y}}_W{\mathbf{H}}_{\left(1\right)}^{\mathrm{H}}+\rho \left({\mathbf{Z}}_W-{\mathbf{U}}_W\right)\right)}^{\mathrm{H}}$ 11:    ${\mathbf{Z}}_F={\displaystyle \frac{1}{\sqrt{N_t}}}exp\left(j·\angle ({\mathbf{F}}_{RF}^{new}+{\mathbf{U}}_F)\right)$ 12:    ${\mathbf{Z}}_W={\displaystyle \frac{1}{\sqrt{N_r}}}exp\left(j·\angle \left({\mathbf{W}}_{RF}^{new}+{\mathbf{U}}_W\right)\right)$ 13:    Update ${\mathbf{U}}_F$, ${\mathbf{U}}_W$, according to (19) 14:    if $max(re{s}_F,re{s}_W,re{s}_C,re{s}_D)<\epsilon$, then 15:       break loop 16:    end if 17:    Update ${\mathbf{F}}_{RF}$, ${\mathbf{W}}_{RF}$, according to (17) 18: end for 19: Output: ${\mathbf{F}}_{RF},{\mathbf{W}}_{RF},\mathbf{C},\mathbf{D}$

3.2. Digital Precoder and Combiner

In digital precoder and combiner design, consideration must be given to the multi-user interference (MUI) problem. Traditional SVD algorithms cannot be applied for direct handling of multi-user interference, while the BD algorithm requires orthogonal user channels—a condition difficult to satisfy in practical scenarios. The RCD algorithm is characterized by slow convergence and susceptibility to local optima. Therefore, the RBD algorithm [33] is adopted, where a regularization term is introduced based on the BD framework, enabling further suppression of MUI in the digital domain while noise amplification is avoided and spectral efficiency is significantly improved.

During the design of digital precoders and combiners in this work, the frequency-domain correlation matrix $\mathbf{C}$ and user correlation matrix $\mathbf{D}$, derived from Tucker decomposition of a fourth-order tensor, are fully exploited. Precise suppression of dominant interferers is prioritized while avoiding excessive suppression of non-dominant interference components. Building upon analog pre-beamforming, multi-user interference is effectively canceled, inter-user interference is mitigated, signal-to-noise ratio is enhanced, and near-optimal power allocation is realized. For the k-th user at the m-th subcarrier, the post-combining equivalent channel is constructed as follows:

$${\mathbf{H}}_{\mathrm{eff},k}\left[m\right]={\mathbf{W}}_{RF,k}^{\mathrm{H}}{\mathbf{H}}_k\left[m\right]{\mathbf{F}}_{RF}$$

(21)

Construct the Interference Matri,

$${\mathbf{H}}_{\mathrm{e},\mathrm{eff},k}\left[m\right]=\left[\begin{array}{c}\sqrt{{\rho }_1}{\omega }_1{\mathbf{H}}_{\mathrm{eff},1}\left[m\right]\\ ⋮\\ \sqrt{{\rho }_{k-1}}{\omega }_{k-1}{\mathbf{H}}_{\mathrm{eff},k-1}\left[m\right]\\ \sqrt{{\rho }_{k+1}}{\omega }_{k+1}{\mathbf{H}}_{\mathrm{eff},\mathrm{k}+1}\left[m\right]\\ ⋮\\ \sqrt{{\rho }_K}{\omega }_K{\mathbf{H}}_{\mathrm{eff},K}\left[m\right]\end{array}\right]$$

(22)

where ${\omega }_u=\sqrt{D\left(u,k\right)C\left(m,m\right)/K}$, $\mathbf{C}$ denotes the subcarrier weighting matrix and $\mathbf{D}$ represents the user weighting matrix. The user factor $\mathbf{D}\left(u,k\right)$ enables effective quantification of interference intensity. Compared with the equal-weighting scheme, this approach achieves precise suppression of dominant interference sources. Subsequently, a primary digital precoder is designed to construct an interference null space, enabling ${\mathbf{H}}_{\mathrm{e},\mathrm{eff},k}\left[m\right]{\mathbf{F}}_a\approx 0$ to nearly eliminate multiuser interference completely. Compared with the BD algorithm, this approach preserves more degrees of freedom. To derive the null-space projection matrix, SVD is performed on ${\widehat{\mathbf{H}}}_{\mathrm{eff},k}\left[m\right]$, to extract the right singular vectors.

$${\mathbf{F}}_a=\mathrm{null}({\mathbf{H}}_{\mathrm{e},\mathrm{eff},k}\left[m\right]={\mathbf{V}}_{\mathrm{interf}}(:,\mathrm{end}-N_s+1:\mathrm{end})$$

(23)

Then, when designing the digital precoder, to enhance interference suppression, frequency-domain and user factors are introduced. $\mathbf{D}(k,k)$ can enhance independent user signals, $\mathrm{C}(m,m)$ can enhance high-quality subcarrier weights, then SVD decomposition is performed.

$$\begin{array}{c}{\mathbf{H}}_{\mathrm{proj}}={\mathbf{H}}_{\mathrm{eff},k}{\mathbf{F}}_a\hfill \\ g_k=\mathbf{D}(k,k)\mathbf{C}(m,m)\hfill \\ {\mathbf{H}}_{\mathrm{proj}}={\mathbf{U}}_{\mathrm{proj}}{\Sigma }_{\mathrm{proj}}{\mathbf{V}}_{\mathrm{proj}}^H\hfill \end{array}$$

(24)

The water-filling algorithm is introduced to design the secondary digital precoder [34]. According to singular values of the equivalent baseband channel (channel quality indicators), limited power is intelligently allocated to high-quality subchannels to suppress noise.

$$p_i=max\left(\mu -{\displaystyle \frac{{\sigma }_n^2}{{\sigma }_i^2}},0\right)$$

(25)

$${\mathbf{F}}_b={\mathbf{V}}_{\mathrm{proj}}(:,1:N_s)\sqrt{P}$$

(26)

Then the complete digital precoder is as follows:

$${\mathbf{F}}_{BB,k}={\mathbf{F}}_a{\mathbf{F}}_b$$

(27)

The digital combiner similarly features a secondary structure. By performing SVD decomposition on the weighted equivalent channel, left singular vectors are extracted.

$$\begin{array}{c}{\mathbf{W}}_{BB,k}={\mathbf{U}}_{\mathrm{comb}}\left(:,1:N_s\right)\hfill \\ \left[{\mathbf{U}}_{\mathrm{comb}},{\Sigma }_{\mathrm{comb}}\right]=\mathrm{SVD}\left(g_k{\mathbf{H}}_{\mathrm{eff},k}\right)\hfill \end{array}$$

(28)

$${\mathbf{F}}_{BB,k}\left[m\right]=\sqrt{P_T}{\displaystyle \frac{{\mathbf{F}}_{BB,k}\left[m\right]}{{∥{\mathbf{F}}_{RF}{\mathbf{F}}_{BB,k}\left[m\right]∥}_2}}$$

(29)

In the digital domain, balanced control of interference and noise is achieved through regularized projection and optimal power allocation. Frequency-domain and user-domain factor matrices are introduced to enhance high-quality subcarriers and precisely suppress interference, significantly improving spectral efficiency in dense user scenarios.

3.3. Complexity Analysis

We proceed to analyze the computational complexity of the proposed HBF technique based on fourth-order Tucker decomposition. For the analog precoding stage, the complexity is $\mathcal{O}(I_{ALS+ADMM}M{K}^2{N}_r^2{N}_t^2+M^{2}K{N}_r^2{N}_t^2+K^3{N}_s^3)$. For the digital precoding stage, the complexity is $\mathcal{O}\left(M{K}^2{N}_r{N}_t{N}_s\right)$. The overall algorithm complexity is $\mathcal{O}(I_{ALS+ADMM}M{K}^2{N}_r^2{N}_t^2+M^{2}K{N}_r^2{N}_t^2+K^3{N}_s^3+M{K}^2{N}_r{N}_t{N}_s)$. Analog precoding complexity is higher in our algorithm due to the higher-order Tucker decomposition and subcarrier scaling in wideband scenarios. Digital precoding complexity is similar to hybrid Tucker2 and hybrid SOTS. The hybrid Tucker2 fits small antenna arrays. Hybrid SOTS fits medium-scale arrays. Despite marginally higher overall complexity, our algorithm provides superior interference suppression. It is ideal for massive MU-MIMO with abundant subcarriers and users when computational resources allow. The Computational Complexity Comparison are shown in

Table 1. Computational complexity comparison.

Schemes	Analog Precoding Complexity	Digital Precoding Complexity
proposed hybrid design	$\mathcal{O}(N_{ALS+ADMM}M{K}^2{N}_r^2{N}_t^2+M^{2}K{N}_r^2{N}_t^2+K^3{N}_s^3)$	$\mathcal{O}\left(M{K}^2{N}_r{N}_t{N}_s\right)$
hybrid Tucker2	$\mathcal{O}\left(I_{ALS}K{N}_s\left(N_t^2{N}_r{M}^2+N_t^3\right)\right)$	$\mathcal{O}\left(M{K}^2{N}_r{N}_t{N}_s\right)$
hybrid SOTS	$\mathcal{O}(I_{\mathrm{CCD}}{K}^2{N}_s{N}_t^3+MK{N}_r{N}_t^2)$	$\mathcal{O}\left(M{K}^2{N}_r{N}_t{N}_s\right)$

.

3.4. Simulation Results and Comparisons

In this section, simulation results are presented to evaluate the performance of our proposed algorithm and compare it with prior algorithms. Under the assumption of perfect CSI availability, SNR for all users, and identical numbers of scattering clusters, propagation paths, and antenna array orientations, each experiment yields results averaged over 500 Monte Carlo channel realizations. Key simulation parameters are summarized in

Table 2. The simulation parameters and environment.

Parameter/Condition	Value/Description
Antenna Array Orientation	${15}^{\circ }$
Antenna Element Spacing	$\lambda /2$
Number of Scattering Clusters and Propagation Paths in mmWave Channel	$N_c=4$, $N_p=8$
Number of Subcarriers	32
$\epsilon$	0.001
$\max \_\mathrm{iter}$	50
Noise Power	$-50\mathrm{dBm}$

.

Experimental comparisons are conducted between the proposed algorithm and the hybrid Tucker2 [27] and hybrid SOTS [28] methods. While practical OFDM systems typically employ 128 or more subcarriers, we configure the number of subcarriers as M = 32 due to computational constraints, particularly those imposed by the hybrid SOTS implementation. This parameter configuration does not compromise the validity of the experimental findings.

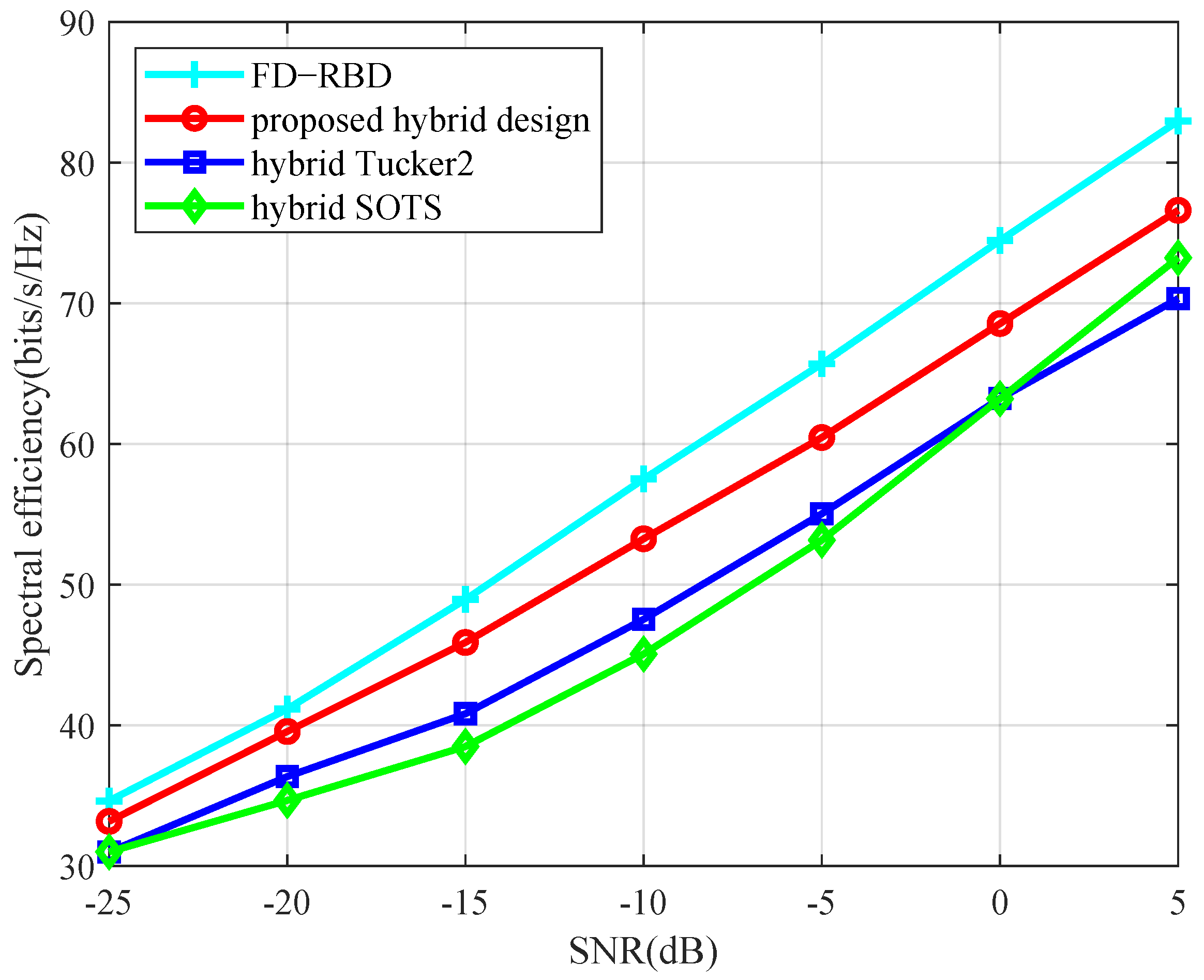
In the first experiment, the spectral efficiency performance of the system is evaluated under different SNR is evaluated. Assuming a mm Wavemassive MIMO system with $N_t=100$, $N_r=16$ antennas and $M=32$ subcarriers, number of RF chains $N_t^{RF}=16, N_r^{RF}=4$, number of users $K=4$, and number of data streams $N_S=4$. In Figure 2, Compared with hybrid Tucker2 and hybrid SOTS under identical simulation conditions, the FD-RBD scheme—characterized by the absence of analog beamforming—omits frequency- and user-domain factor matrices in its design. This fully-digital beamforming approach, derived by removing the analog beamforming component from our proposed algorithm, requires dedicated RF chains per antenna element, resulting in substantially higher hardware and computational complexity than HBF architectures. While FD-RBD serves as the performance upper bound benchmark, the core objective of hybrid solutions is to approach this bound with controlled complexity. Our proposed algorithm demonstrates superior spectral efficiency over competing methods, achieving performance levels approaching those of the fully-digital RBD benchmark. Spectral Efficiency Performance Comparison (SNR = 5 dB) are shown in

Table 3. Spectral efficiency performance comparison (SNR = 5 dB).

Schemes	Spectral Efficiency (Bits/s/Hz)	CI Radius (±)	95% CI Range	Gain vs. Baseline
proposed hybrid design	76.61	0.22	[76.39, 76.83]	-
hybrid SOTS	73.23	0.30	[72.93, 73.53]	3.38
hybrid Tucker2	70.33	0.26	[70.07, 70.59]	6.28

.

At 5 dB SNR, the proposed algorithm achieves a spectral efficiency of 76.61 ± 0.22 bits/s/Hz ($95\%$ confidence interval). This represents gains of 3.38 bits/s/Hz and 6.28 bits/s/Hz over hybrid Tucker2 and hybrid SOTS, respectively. With the narrowest confidence interval width (0.22 bits/s/Hz) observed in the comparative study, the proposed scheme demonstrates enhanced robustness against channel stochastic variations while approaching the theoretical limit of fully-digital beamforming (82.96 bits/s/Hz). The performance superiority over both hybrid Tucker2 and hybrid SOTS is statistically significant.

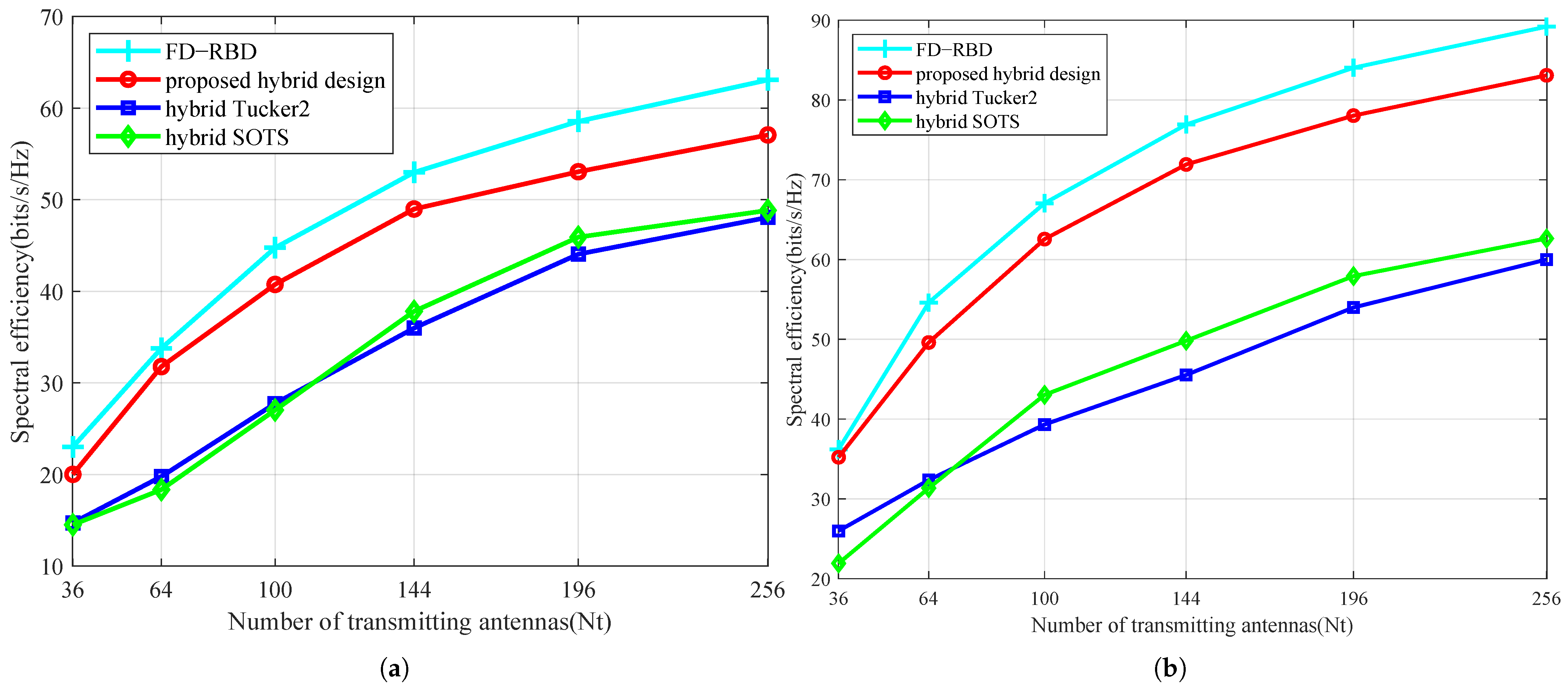
The second experiment evaluated the relationship between system spectral efficiency and transmitting and receiving antennas, setting parameters $N_r=16$, $N_t^{RF}=9, N_t^{RF}=3$, user number $K=3$, and data stream number $N_S=3$. In Figure 3, at 5 dB SNR, $N_t=256$, the proposed algorithm achieves spectral efficiency gains of 20.45 bits/s/Hz and 23.09 bits/s/Hz over hybrid SOTS and hybrid Tucker2, respectively. These results demonstrate consistent superiority of our algorithm in spectral efficiency across the evaluated SNR range.

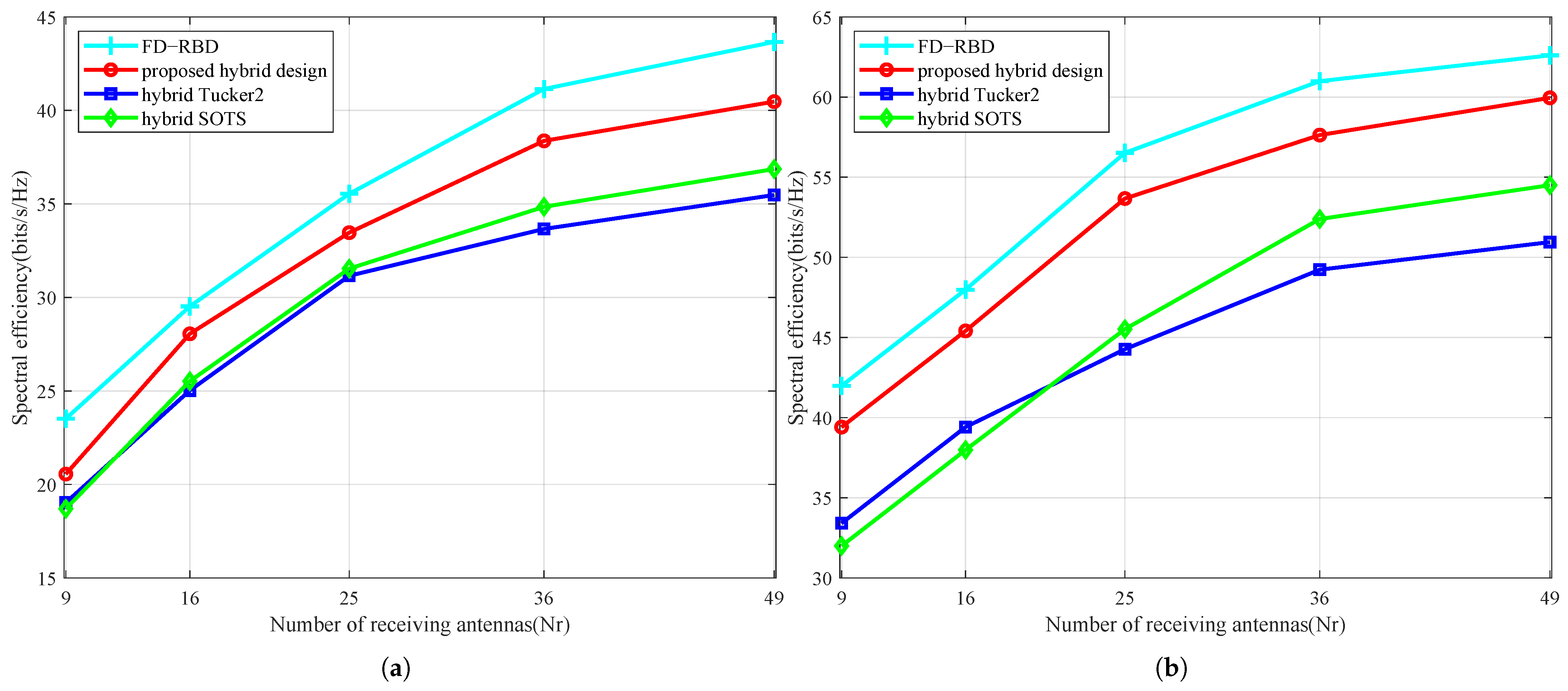
We then tested the impact of receive antennas on spectral efficiency, setting the parameter $N_t=100$ with all other parameters consistent with the second experiment. In Figure 4, conducting tests at SNR = −15 dB and SNR = 5 dB. At −15 dB with $N_r=36$, the spectral efficiency is 3.52 bits/s/Hz higher than the hybrid SOTS algorithm and 4.71 bits/s/Hz higher than the hybrid Tucker2 algorithm. The results indicate that our algorithm exhibits superior spectral efficiency compared to other algorithms.

In both Experiment 2 and 3, the spectral efficiency of HBF algorithms exhibits strong sensitivity to the number of transmit antennas but weak dependence on receive antennas. This occurs because: Spatial degrees of freedom are dominated by the transmit array, where increasing transmit antennas enhances interference suppression and precoding gain through high-precision beam energy focusing, yielding logarithmic growth in spectral efficiency; Receive antennas primarily provide diversity gain, yet under fixed data-stream constraints, surplus antennas remain underutilized; The sparsity of mmWave multipath channels makes transmit beamforming critical, as additional transmit antennas precisely match angle-domain paths while extra receive antennas offer diminishing returns in path capture capability. Consequently, HBF spectral efficiency demonstrates higher sensitivity to transmit antenna scaling.

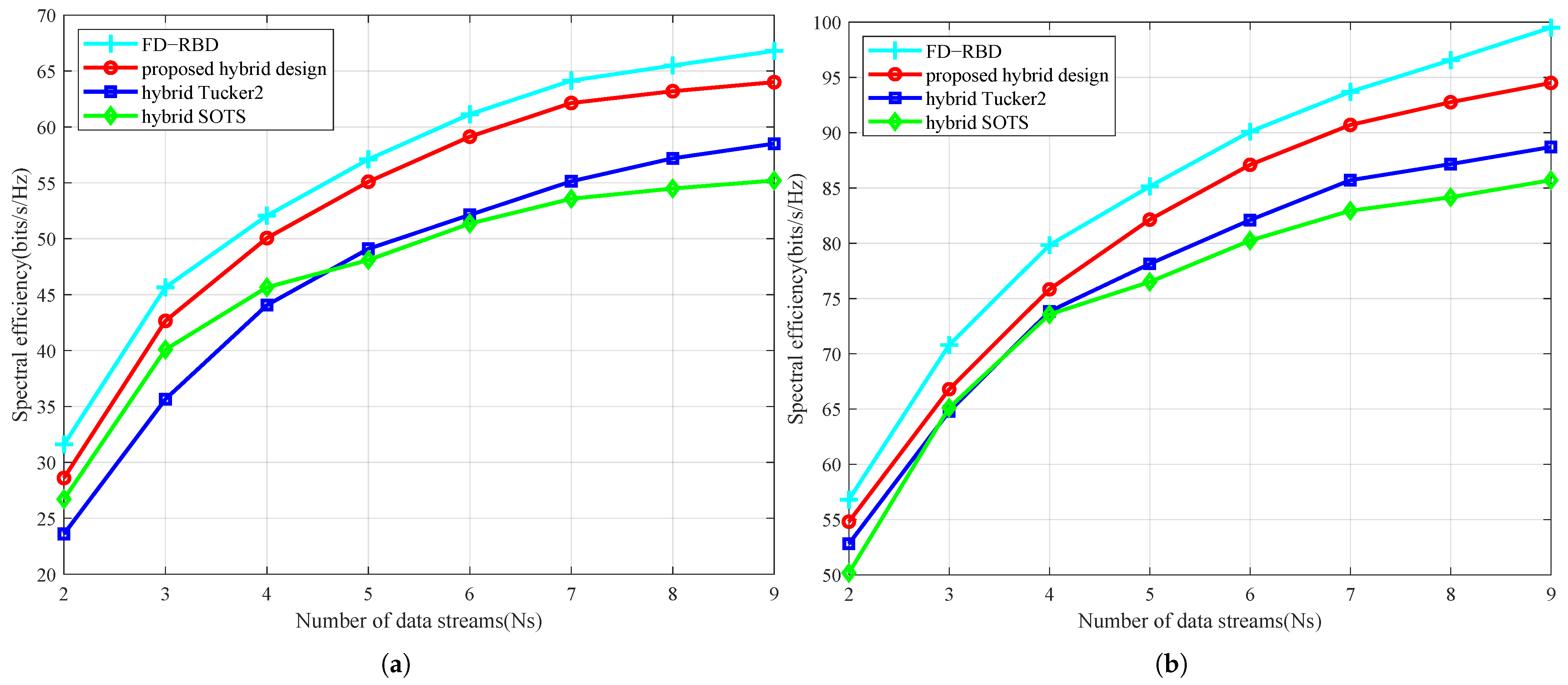
Then spectral efficiency performance under different data streams is simulated in Figure 5. Parameters are set as $N_t=100,N_r=48$. $K=4$. At −15 dB SNR with $N_S=6$, the proposed algorithm achieves spectral efficiency improvements of 7.78 bits/s/Hz over hybrid SOTS and 7.02 bits/s/Hz over hybrid Tucker2. At 5 dB SNR with $N_S=6$, it maintains superior gains of 6.86 bits/s/Hz and 5.01 bits/s/Hz against these benchmarks respectively. These results demonstrate consistent performance dominance across tested conditions. Moreover, with increasing data streams, our algorithm not only outperforms competitors but also approaches fully-digital beamforming performance, attributed to enhanced utilization of RF chains and strengthened interference suppression that eliminates multi-user interference. Consequently, the proposed architecture proves particularly effective in high-data-stream scenarios.

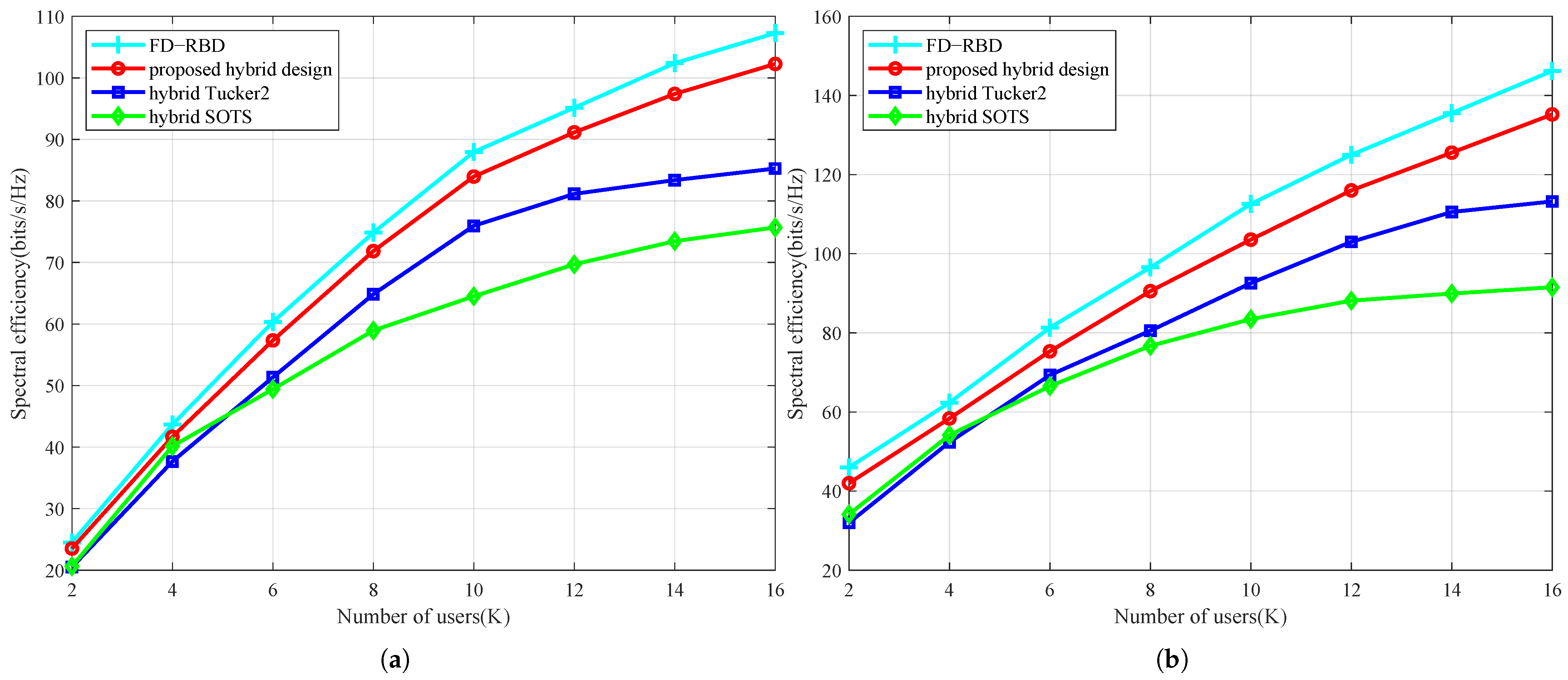
Below, spectral efficiency performance under different users is evaluated in Figure 6. Parameters are set as, $N_t=100,N_r=36$, $N_r^{RF}=2$, $N_S=2$. At −15 dB SNR with $K=16$ users, the proposed algorithm achieves spectral efficiency gains of 26.57 bits/s/Hz over hybrid SOTS and 17.02 bits/s/Hz over hybrid Tucker2. At 5 dB SNR with $K=16$, it demonstrates superior improvements of 43.69 bits/s/Hz and 22.13 bits/s/Hz against these benchmarks respectively. This significant outperformance in dense-user scenarios confirms the algorithm’s advantage over existing HBF designs, increased user count enables precise suppression of dominant interferers through frequency- and user-domain factor matrices while avoiding over-suppression of weak interference sources, thereby establishing particular efficacy for hybrid beamforming in dense-user communication systems.

Finite phase-shifter resolution causes phase discretization, leading to beam pattern gain degradation. With ideal continuous-phase shifters, spectral efficiency remains uncompromised. Thus while higher resolution improves spectral efficiency, practical hardware constraints impose fundamental limits. Simulations validate phase-shifter resolution impact on our algorithm’s spectral efficiency under Parameter Set $N_t=100, N_r=16$, $N_t^{RF}=16, N_r^{RF}=4, N_S=4, K=4,$ SNR = 5 dB. In Figure 7, our method achieves $99.5\%$ of the ideal spectral efficiency at 6-bit resolution, whereas hybrid Tucker2 and hybrid SOTS require 5-bit and 7-bit resolutions respectively for comparable performance. This demonstrates marginally higher resolution sensitivity than hybrid Tucker2 but lower than hybrid SOTS, enabling spectral efficiency requirements to be met with moderate-resolution hardware.

4. Conclusions

This paper establishes a theoretical hybrid beamforming framework by organically integrating fourth-order Tucker tensor decomposition into the RBD algorithm. The proposed scheme provides a mathematically rigorous solution to the high-dimensional non-convex optimization problem under constant modulus constraints, effectively unifying the spatial, frequency, and user domains. The analog beamforming design, obtained through a tailored ADMM-ALS solution, derives the precoder and combiner from the decomposed factor matrices. The digital design further incorporates these factor matrices into the RBD algorithm combined with a water-filling strategy, achieving precise interference management and optimal power allocation. Simulation results confirm that the proposed tensor-based theory not significantly enhances spectral efficiency and resource utilization, but also demonstrates strong robustness under practical hardware impairments, offering a feasible technical pathway for 6G ultra-massive MIMO systems with dense user configurations.

Future research can be conducted along the following two directions:

• Investigate the beamforming technology of this algorithm under RIS to expand its application domains;
• As the current algorithm relies on ideal channel assumptions, explore precise millimeter-wave channel estimation methods or beam alignment techniques to support algorithm implementation.