Abstract
In various research domains, researchers frequently encounter multiple datasets pertaining to the same subjects, with one dataset providing explanatory variables for the others. To address this structure, we introduce the Binary 3-way PARAFAC Partial Least Squares (Bin-3-Way-PARAFAC-PLS), a novel multiway regression method. This method is specifically engineered for scenarios involving a three-way real-valued explanatory data array and a matrix of binary response data. We detail the algorithm’s implementation and illustrate its practical application. Furthermore, we describe biplot representations to aid in result interpretation. The accompanying software necessary for implementing the method is also provided. Finally, the proposed method’s utility in real-world problem-solving is demonstrated through its application to a psychological dataset.
MSC:
62A09; 62-08; 62H30; 62H99
1. Introduction
The prediction of a dependent variable () based on a set of multidimensional independent variables () has attracted significant interest across various fields. A commonly used approach for this prediction is Partial Least Squares (PLS) [1,2,3], which was originally developed for continuous data. PLS identifies a set of linear combinations of the predictor variables that exhibit the highest correlation with the response variables.
Multiway data, also known as higher-order data or tensors, has become increasingly common in various areas of our information society, such as bioinformatics [4], chemometrics [5], neuropsychology [6], and personality research [7]. In the context of multiway data, a ‘way’ represents one of the dimensions along which the data is structured. For example, in a dataset with three dimensions, these might be subjects, variables, and occasions. The term ‘mode’ is used to specify the type of entity associated with each dimension. Typically, the number of ways and modes are equal as in a three-dimensional dataset where each way corresponds to a different entity type (e.g., subjects, variables, and occasions). However, there are scenarios where the number of modes is less than the number of ways. An example is a two-mode, three-way dataset where one entity type occurs in more than one dimension. This occurs, for example, when objects are compared across multiple subjects, resulting in a data structure where the same objects are repeated across dimensions [8,9]. To analyze these types of data, traditional methods based on Principal Component Analysis (PCA) [10] have been extended to accommodate the complexity of higher-dimensional structures. Techniques such as Tucker decomposition [11,12,13] and PARAFAC decomposition [14,15,16] are among the most widely used. Tucker decomposition generalizes PCA by decomposing the data into a core tensor and factor matrices, with each factor matrix corresponding to one of the modes of the tensor [17]. On the other hand, PARAFAC decomposes the tensor into a sum of component tensors, where each component is a rank-1 tensor.
Given the prevalence of this type of data, Partial Least Squares (PLS) has been extended to accommodate such data structures, facilitating the prediction of from , where and/or are three-way data arrays. Specifically, Bro [18] first combined the PARAFAC three-way analysis method with the PLS method. This method, called multilinear PLS (N-PLS), is thus a mixture of a trilinear model (PARAFAC) and PLS [19]. Subsequently, Bro et al. [20] proposed a modification of the above model that aims not to improve the prediction of the dependent variables but rather to improve the modeling of the independent variables. To achieve this, they rely on the distinction between low-rank and subspace approximation inherent in the PARAFAC and Tucker3 models. More recently, Sparse N-Way Partial Least Squares with L1 penalization has been proposed [21,22], which aims to achieve lower prediction errors by filtering out variable noise, while improving the interpretability and utilization of the N-PLS method.
The methods discussed earlier are designed for scenarios where both predictors and responses are continuous. When the response matrix contains binary variables, Partial Least Squares Discriminant Analysis (PLS-DA) [23] is often employed, which essentially fits a PLS regression to a dummy or fictitious variable. Bastien et al. [24] introduced a PLS model for a single binary response, analogous to the PLS-1 model. Later, Vicente-Gonzalez and Vicente-Villardon [25] proposed the PLS-BLR method, a Partial Least Squares method for situations where the responses are binary and the predictors are continuous. Subsequently, they extended this approach to address cases where both the predictors and the responses are binary [26], introducing additional adaptations to handle this more complex scenario. This method, known as Binary Partial Least Squares Regression (BPLSR), further broadens the applicability of Partial Least Squares methods in analyzing binary data structures. These approaches extend PLS generalized linear regression [24] from a single response variable (PLS1) to multiple responses (PLS2), incorporating dimension reduction—a feature not present in the original method. In the context of genomic data, other studies [27,28] applied Iteratively Re-weighted Least Squares (IRWLS) to handle binary responses with numerical predictors.
A notable gap in the current methodological landscape is the lack of suitable regression approaches for binary response variables within three-way data structures. Although tensor regression models with low-rank constraints have been widely developed for continuous outcomes, extending them to binary responses is limited. Specifically, existing methods rarely combine the interpretability of multilinear models with an adequate probabilistic framework for binary data.
To fill this gap, we propose Bin-3-Way-PARAFAC-PLS, an extension of the N-PLS method designed to handle scenarios with binary dependent variables and three-way predictor arrays. The method integrates key features from N-PLS and PLS-BLR, incorporating a PARAFAC decomposition to reduce dimensionality while maintaining interpretability. Although the proposed method is currently designed and tested for three-way data arrays, its underlying principles hold the potential for generalization to N-way configurations. In addition, to facilitate the interpretation of the results and the identification of explanatory variables most strongly associated with the responses, we propose the use of biplot-based visualizations. Specifically, we combine logistic biplot methods [29,30] with interactive biplots [31] to graphically assess prediction quality and enhance the practical utility of the model.
The paper is structured as follows: Section 2 provides a brief overview of the PLS methods, followed by the introduction of the Bin-3-Way-PARAFAC-PLS method in Section 3, which allows PLS analysis of a matrix of binary responses alongside a three-way data array of explanatory variables. An algorithm for calculating model parameters is outlined in this section. Section 4 introduces a biplot method for visual assessment of the results obtained with Bin-3-Way-PARAFAC-PLS. Section 5 illustrates the application of the proposed method, and finally Section 6 offers concluding remarks and outlines potential future research directions.
2. A Brief Overview of PLS Models for Continuous Data
In this work, scalars are denoted by italic lowercase, vectors by bold lowercase, matrices by bold uppercase, and three-way data arrays by underlined bold uppercase. The letters I, J, K, and L are used to denote the dimension of different orders. The abbreviations for the different PLS models are Bi/Tri-PLS-1/2/3, where the prefix (Bi/Tri) indicates the order of and the last number (1/2/3) indicates the order of , e.g., Bi-PLS3 refers to PLS with as a data matrix and as a 3-way data array.
Let us begin with a brief overview of bi-PLS1. Let and be column-centered (and scaled if necessary) matrices. The bi-PLS1 algorithm consists of two main steps. In the first step for each component, a rank-one model of and is constructed. Then, in a second step, these models are subtracted from and , resulting in residuals. From these residuals, a new set of components is obtained. The goal is therefore to find a one-component model of such that where and are the scores and the weights, respectively. This is performed by maximizing the following function:
where .
It can be verified that the value of the above expression is maximal when
This is the normalized direction maximizing , equivalent to the first left singular vector of . Once the first component is obtained, and are deflated and the second component is sought following the same process.
Similarly, when is a three-way data array, the goal of the algorithm is to maximize the covariance between and . Let be the mode-1 unfolding of tensor [32], then it is a matter of finding latent spaces and that maximize the covariance between and so that can be written as
Here, ⊙ denotes the Khatri–Rao product (column-wise Kronecker product) [33], is a matrix of residuals and S is the number of components. The above decomposition corresponds to the PARAFAC model for three-way arrays.
In this case the function to be maximized is
To obtain the component weights and , we construct the matrix as follows:
This matrix is then decomposed using singular value decomposition (SVD), from which and are extracted as the first left and right singular vectors, respectively.
Given the number of components S, the full algorithm for the Tri-PLS1 model is as follows (see Algorithm 1):
| Algorithm 1 Tri-PLS1 for S components |
|
When there are several dependent variables , can be expressed as
where is the matrix of scores, is the loading matrix, and is a matrix of residuals.
The model is estimated such that the covariance between and is maximized. The prediction model between and can be expressed as
where the matrix represents the regression coefficients.
The algorithm that implements the Tri-PLS2 model for S components is as follows (see Algorithm 2):
| Algorithm 2 Tri-PLS2 for S components. |
|
3. Bin-3-Way-PARAFAC-PLS
The previous linear model is invalid, and a logit transformation must be performed if the response matrix is binary. In this case, the expected values of the binary response are probabilities, and the logit function is used as the link function. Let , then
where is a vector of ones of length I.
This equation is a generalization of Equation (4), but it now requires a vector with intercepts for each variable, given that binary matrices cannot be centered in the same way as continuous matrices. Each probability can be expressed as
The procedure for estimating the parameters of the model is similar to that described in [25]. The cost function in this case is as follows:
The objective is to estimate the parameters , , and that minimize the value of the above cost function. There are no closed-form solutions for this optimization problem; therefore, an iterative approach is employed, in which a sequence of progressively smaller values for the loss function is generated with each iteration. The gradient method is applied iteratively, solving for one component at a time while keeping the others fixed. The update for each parameter is as follows:
for a chosen .
The corresponding gradients are
where is a vector of ones of length I.
Step-by-Step Description of the BIN-Tri-PLS2 Algorithm
The BIN-Tri-PLS2 algorithm estimates model parameters through an iterative procedure, applied component by component. For each latent component, the method alternately updates the individual scores and the logistic regression coefficients , keeping previously extracted components fixed to ensure orthogonality. Since the response matrix is binary and cannot be centered, the intercept vector is estimated as a separate preliminary step.
A common issue in logistic regression is separation, where response variables can be perfectly predicted by linear combinations of the predictors. This leads to instability or divergence in maximum likelihood estimates [34]. To address this, we include a Ridge penalty in the optimization process [35], which improves convergence and numerical stability.
Ridge penalization is particularly well suited in our case because we employ a gradient-based optimization procedure, which requires the penalty function to be differentiable. While Lasso is often used for variable selection, its non-differentiability makes it unsuitable for gradient-based methods. Ridge regularization, by contrast, ensures smooth convergence while helping to mitigate separation. Although the penalty influences parameter estimates, we have observed that the overall model results and interpretations remain consistent across different regularization strategies.
The overall procedure can be summarized as follows:
- Intercept estimation: Estimate the intercept vector using gradient descent, minimizing the logistic loss until convergence. This step establishes baseline probabilities without incorporating predictors.
- Component extraction: For each latent component (s), the following sub-steps are iteratively performed:
- Score Initialization: Randomly initialize individual scores ().
- Projection Direction Calculation: Compute the projection directions of the predictor three-way array using PARAFAC decomposition.
- Coefficient Estimation and Score Refinement: Estimate the logistic regression coefficients () via gradient descent, and iteratively update until both converge.
- Predicted Probabilities Update: After each update of or , recompute the predicted probabilities () for all observations and responses.
- Predictor Three-way Deflation: Deflate the predictor three-way array after extracting each component.
- Final Model Output: Once all S latent components have been extracted, the algorithm terminates.
The resulting BIN-Tri-PLS2 algorithm, integrating the Tri-PLS2 framework with the gradient-based estimation procedure for binary outcomes, is formally summarized below (see Algorithm 3).
| Algorithm 3 Bin-Tri-PLS2 for S components |
|
The regression coefficients of the response variables on the observed variables can be obtained as follows:
where , (i.e., are the regression coefficients with respect to the observed variables).
This algorithm is implemented in the package BinNPLS developed in R 4.2.1 [36], which is publicly available at https://github.com/efb2711/Bin-NPLS (accessed on 15 June 2025).
From a computational perspective, the Bin-3-Way-PARAFAC-PLS algorithm involves several steps that contribute to its overall complexity. The most demanding operations include the construction of the matrix , where each entry is computed as , with a cost of . Additionally, a singular value decomposition (SVD) of this matrix is performed to extract the weights of the second and third modes; depending on the implementation, this operation has a complexity of approximately .
Another significant component is the estimation of the logistic regression parameters through gradient descent. This requires computing predicted probabilities , along with the gradients with respect to , , and , which involves operations over all individuals and response variables, yielding a computational cost of per iteration. Furthermore, the Khatri–Rao product is used to construct the loading matrix , and its multiplication with the unfolded tensor adds to the overall cost.
Considering that these operations are repeated for each of the S components, the total computational complexity per full pass of the algorithm can be roughly estimated as
This expression suggests that the algorithm is computationally feasible for small- to moderate-sized datasets.
4. Bin-3-Way-PARAFAC-PLS Biplot
In this section, a biplot representation is proposed for the graphical visualization of the results obtained by the Bin-3-Way-PARAFAC-PLS algorithm. It begins with a brief review of the biplot for continuous data to introduce the biplot for binary data, known as the logistic biplot. The combination of the PLS-biplot [37] with the logistic biplot [29,30] and the interactive biplot [31] for three-way data will result in the proposed Bin-3-Way-PARAFAC-PLS biplot.
4.1. Classical Biplot
The biplot was originally introduced by Gabriel [38] and later extended by Gower and Hand [39] to visualize relationships between variables and observations in multivariate datasets. It has since been widely adopted across diverse fields such as ecology, chemometrics, and the social sciences, owing to its ability to provide a comprehensive graphical representation of both observations and variables simultaneously in a low-dimensional space. A more recent and comprehensive overview of biplot methods can be found in [40].
A fundamental aspect of matrix decomposition is that any matrix with rank R can be decomposed into two matrices, () and (), such that . This decomposition enables the assignment of vectors (row markers) to each of the I rows of and vectors (column markers) to each of its J columns, thereby providing a representation of using vectors in an R-dimensional space. In the case of matrices with rank two, this representation occurs in a two-dimensional space (plane), but for higher-rank matrices, an approximation in a reduced-dimensional space (either 2 or 3 dimensions) is obtained such that .
This factorization, usually achieved by singular value decomposition (SVD), facilitates the representation of the matrix in a space of reduced dimension such that . Geometrically, this means that the projection of a row marker onto the vector representing a variable approximates the individual’s value on that variable and allows individuals to be ordered by it. Interpretation also extends to the angles formed by two variables or the distances between individuals. The angles between variables in a biplot represent their correlations or associations. If two variables form a small angle, this indicates a strong positive correlation between them, while a large angle indicates a weaker or negative correlation. The distances between individuals (observations) in a biplot reflect their similarities or dissimilarities based on the values of the variables. Closer distances indicate greater similarity, while further distances indicate greater dissimilarity.
4.2. Logistic Biplot
While classical linear biplots approximate the data matrix by factorizing its expected values into the product of two low-rank matrices, logistic biplots extend this framework to model binary data by linking the expected probabilities to a low-dimensional representation through the logit function.
This extension was initially proposed by Vicente-Villardón et al. [29] as an adaptation of classical biplots for binary data matrices. Further methodological developments have been introduced in subsequent years, including enhancements for logistic biplots by Demey et al. [30] and Babativa-Márquez and Vicente-Villardón [41]. In addition, related biplot techniques have been formulated for other types of categorical data, such as ordinal data [42] and nominal data [43]. A detailed description and further applications of logistic biplots can also be found in Vicente-Gonzalez and Vicente-Villardon [25], Vicente-Gonzalez et al. [26].
Given a binary matrix and its expected value , we have that
Aside from the constant vector , which is necessary because binary matrices cannot be centered, this equation yields a biplot on a logit scale
and these logit values can then be converted into estimated probabilities using the inverse logit (logistic) function, allowing for a probabilistic interpretation of the biplot.
By projecting the row coordinate onto the column vector , one obtains—up to an additive constant—the expected value on the logit scale for the entry in the matrix . This constant, , shifts the logit function to determine the threshold at which the logit equals zero or any specified value, and thus adjusts the corresponding probability accordingly.
The geometry of the logistic biplot is similar to that of the continuous biplot, with the distinction that it predicts probabilities. Projecting the row markers onto column markers yields the expected probability for each entry. In this case, it is necessary that the column vectors be accompanied by scales indicating the probabilities. Sometimes, reduced prediction scales are employed to simplify the presentation, where a dot represents a probability of and an arrow represents a probability of . This approach not only reveals the direction in which the probability increases but also offers insights into discriminant power, with shorter arrows typically signifying lower discriminant power of the associated variable.
To illustrate the interpretability of the logistic biplot, we use a subset of the Mushroom dataset from the UCI Machine Learning Repository [44]. This dataset contains categorical information about physical characteristics of mushroom species, including shape, color, surface, and odor. For this example, we select only the variables related to the cap and gill features of the mushrooms, such as cap shape, cap surface, cap color, bruises, odor, gill attachment, gill spacing, gill size, and gill color. All variables are transformed into binary indicators.
Using this subset of data, we construct a logistic biplot, which provides a joint representation of the rows and columns of the data matrix in a two-dimensional space. This visualization summarizes the structure of the data, allowing for simultaneous interpretation of both individuals and variables. Mushrooms that appear close to each other in the plot share similar profiles based on the selected characteristics.
The angles between variable vectors can be interpreted as indicative of the correlation between them. Acute angles suggest a strong positive association, whereas right or near-right angles indicate little to no correlation. Conversely, obtuse angles imply a strong negative relationship between the corresponding variables.
To provide an initial visualization of the data structure and its relationship with the selected characteristics, we construct a reduced logistic biplot (Figure 1). The Mushroom dataset contains 8124 samples (individual mushrooms), each represented as a point in the plot. The arrows correspond to the binary variables related to cap and gill features, and indicate the direction in which the probability of the corresponding characteristic increases. The arrows are drawn from a baseline probability of 0.5 up to 0.75.
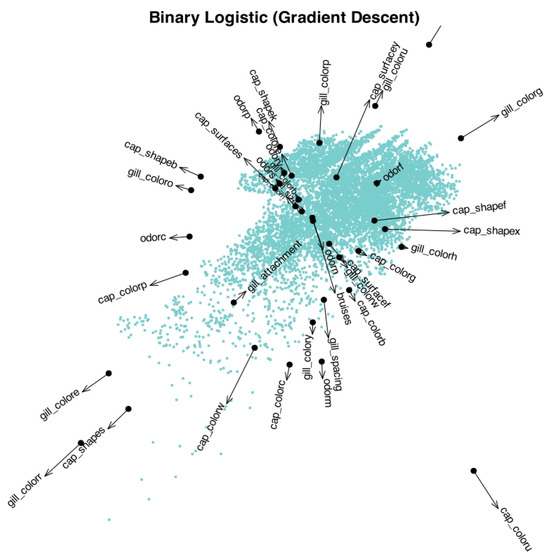
Figure 1.
Reduced logistic biplot showing mushrooms (points) and selected binary characteristics (arrows). Arrows are scaled to represent probability values from 0.5 to 0.75.
Although the overall cloud of points does not reveal clearly separated clusters, valuable insights can still be drawn from the relationships between individuals and variables. In particular, several characteristics appear to be unlikely for the majority of mushrooms, as indicated by the direction and length of the corresponding vectors. Among these, the following traits stand out as particularly improbable:
- gill_color: green, red, orange, and yellow
- cap_shape: sunken and bell
- cap_color: pink, white, and cinnamon
- odor: creosote and musty
- gill_spacing: crowded
In a logistic biplot, the expected probability of presence for each characteristic can be approximated by projecting each individual (point) orthogonally onto the corresponding arrow. The point marked on each arrow indicates the location where the predicted probability is 0.5, which typically serves as a threshold for classification. Individuals projected beyond this point, in the direction of the arrow, are expected to exhibit the characteristic, while those projected before it are expected not to.
These types of visual representations can be generated using the MultibiplotR package [45], which provides flexible tools for constructing logistic biplots. In addition to plotting individuals and variables jointly, the package allows for the projection of observations onto variable directions to estimate predicted probabilities. It also supports the visualization of cluster structures overlaid on the biplot, enhancing the interpretability of complex patterns in multivariate data.
To facilitate the interpretation of relationships between variables, we present a second biplot focused exclusively on the variables, omitting the representation of individual observations. This version includes reference scales along the arrows to support a more precise understanding of the underlying geometry. Only variables with a representation quality above 85% on the first two dimensions are included in the plot.
It is important to note that the underlying computations are performed using the full dataset and the complete set of variables. However, restricting the graphical representation to a subset of well-represented variables results in a cleaner, more interpretable plot that highlights the most informative patterns.
The scaled logistic biplot focusing on variable relationships (Figure 2) reveals several distinct association patterns. A strong and direct relationship is observed between the variables odor_fishy and odor_pungent, indicating that these two odor types tend to co-occur. Both are also strongly and inversely associated with cap_color_purple, suggesting that mushrooms with either a fishy or pungent odor are unlikely to exhibit a purple cap color.
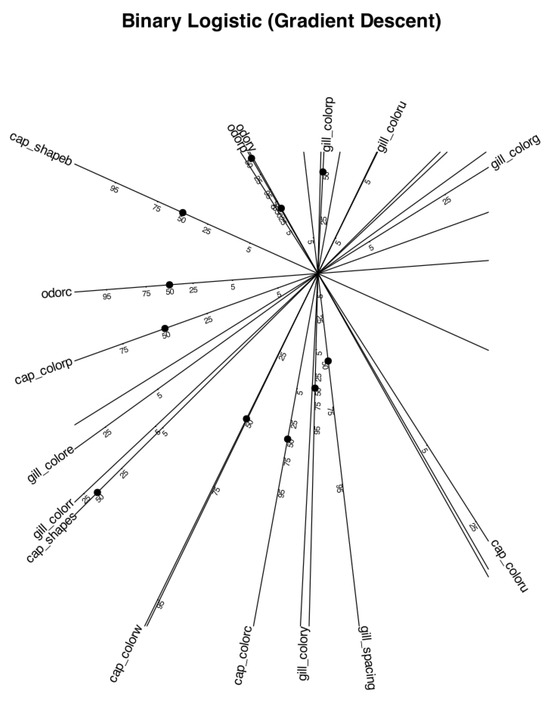
Figure 2.
Scaled logistic biplot showing relationships between selected binary variables with representation quality above 85%. Arrows include reference scales to support interpretation of relative distances and angles. Individual observations are omitted for clarity.
Additionally, odor_fishy and odor_pungent show moderate direct associations with gill_color_purple, gill_color_pink, and cap_shape_bell. At the same time, they exhibit moderate inverse associations with gill_spacing_crowded, gill_color_yellow, and cap_color_cinnamon, reinforcing a coherent pattern of mutual relationships across multiple morphological features.
Another interesting pattern emerges between cap_color_white and gill_color_purple, which show a very strong inverse association. This suggests that mushrooms with a white cap are highly unlikely to have purple gills, reflecting a mutually exclusive relationship between these two traits.
A separate and distinct group of variables emerges, centered around gill_color_red, which is strongly and directly associated with gill_color_green and cap_shape_sunken, and inversely associated with gill_color_gray. This second cluster of variables appears to be largely independent from the first group described above, as indicated by the approximate orthogonality of the corresponding vectors in the biplot.
In summary, the variable-focused logistic biplot provides a clear and interpretable geometric representation of the main relationships among morphological traits in the dataset. By focusing on variables with high representation quality and excluding individual observations, the visualization emphasizes the most relevant patterns and potential biological constraints. This exploratory insight lays the foundation for more targeted analyses or for guiding future model refinement using real-world data.
4.3. Interactive Biplot
If is a three-way data array , it can be decomposed, e.g., via a PARAFAC decomposition, such that the mode-1 matricization can be written as . From this decomposition, a biplot can be constructed where the row markers are and the column markers are . In this biplot, each combination of levels from two of the modes is represented by a single marker. For example, when the second and third modes are combined, there will be column markers. The interpretation of interactive biplots is analogous to that of classical biplots, as they also provide an approximation of the values within the data matrix on the appropriate scale).
Given that the number of column markers, , can be large, making a single biplot of all of them can be unclear. Therefore, one of the modes is fixed and a separate biplot representation is generated for each level of that fixed mode. For example, if the second mode is fixed, there would be J biplot representations, each containing K variables.
4.4. Bin-3-Way-PARAFAC-PLS Biplot (Triplot)
The factorization of the matrix in Equation (2) yields a biplot whose row markers are the rows of the matrix and whose column markers are derived from . Furthermore, a logistic biplot of the binary matrix can also be constructed from Equation (5), where the row markers also correspond to the rows of . Combining these two biplots, there are three sets of markers: individual scores (from ), markers for the response variables (from and ), and markers for the predictors (from ). The combined display of all these markers is called a triplot. In this case, individuals can be projected onto vectors corresponding to binary response variables and continuous explanatory variables, yielding expected probabilities and values for each continuous variable.
In summary, the triplot facilitates the analysis of relationships among explanatory variables, identifies which explanatory variables are more influential in predicting response variables, and enables the approximation of individual values for both types of variables. In the case of binary variables, this approximation represents the probability that the individual exhibits that response.
5. Illustrative Application
An important goal of psychology is to investigate the relationship between individuals’ reactions to specific situations and their inherent traits or dispositions [46]. It is plausible to assume that people’s reactions to certain scenarios can provide information about their personality traits. Therefore, we will conduct a Bin-3-Way-PARAFAC-PLS analysis on a dataset comprising, on the one hand, individuals’ reactions to certain situations and, on the other hand, their personality traits.
The simulated dataset consists of a data array (persons × emotions × situations), capturing the emotions people feel when faced with the situations considered, and a binary data matrix (persons × dispositions), indicating whether or not they exhibit certain personality traits. The situations considered are “Argue with someone”, “Partner leaves you”, “Someone lies about you”, “Give a bad speech”, “Fail an exam” and “Write a bad paper”. The possible responses are “Other anger”, “Shame”, “Love”, “Grief”, “Fear”, “Guilt” and “Self-anger”. Finally, the personality traits considered are “Fear of rejection”, “Kindness”, “Importance of others’ judgments”, “Altruism”, “Neuroticism”, “Being strict with oneself”, “Low self-esteem”, “Conscientiousness”, and “Depression”. The continuous dataset has been appropriately centered and normalized. The aim of the analysis is to predict individuals’ personality traits from the way they react to certain situations, using the proposed Bin-Tri-PLS2 method.
The variance of the predictors explained by the decomposition is shown in Table 1.

Table 1.
Eigenvalues and explained variance percentages for the first two principal components.
It can be seen that the first two dimensions explain 67.01% of the variance of the predictors.
The components obtained are interpreted by examining the content of the entities of the different modes that score high on the component under study. When examining the component scores for emotional responses and situations (see Table 2 and Table 3), the first component can be interpreted as an interpersonal dimension. Situations that involve relational conflicts, such as “Argue with someone”, “Partner leaves you”, or “Someone lies about you”, score highly on this component. These situations tend to elicit emotions like shame and other-directed anger, which are inherently social and typically arise in the real or imagined presence of others. In contrast, the second component appears to reflect an intrapersonal dimension, as it is more strongly associated with situations implying personal failure or self-evaluation (e.g., “Giving a bad speech”, “Fail an exam”, or “Writing a bad paper”). These scenarios are linked to emotions such as guilt, self-anger, and sorrow, which involve internal moral or evaluative processes.

Table 2.
Component matrix for the response scales (matrix ), resulting from the Bin-3-Way-PARAFAC-PLS (values exceeding 0.4 in absolute value are in bold).

Table 3.
Component values for the situations (matrix ), resulting from the Bin-3-Way-PARAFAC-PLS (values exceeding 0.4 in absolute value are in bold).
Table 4 presents several fit measures for the binary response variables, including a likelihood-ratio test comparing the model to the null model, three pseudo R-squared coefficients (Nagelkerke, Cox-Snell, and McFadden), and the percentage of correctly classified cases. The Bin-3-Way-PARAFAC-PLS model achieved an overall classification accuracy of 81.94%.

Table 4.
Goodness-of-fit statistics for logistic models per variable.
To provide a more comprehensive evaluation of classification performance, standard classification metrics, including precision, recall, specificity, and F1-score are reported in Table 5. The total values reported in the last row of the table are obtained from a single global confusion matrix constructed by aggregating predictions across all binary response variables. Specifically, the overall numbers of true positives, false positives, true negatives, and false negatives were computed by summing over all subjects and all variables. The global precision, recall (sensitivity), specificity, and F1-score are then derived from this aggregated confusion matrix. Thus, unlike the per-variable results, which are based on individual confusion matrices, the ‘Total’ row corresponds to a micro-averaged evaluation of classification performance. The table indicates that most variables achieve high precision and recall values, indicating effective identification of positive cases with few false positives and false negatives. For example, fear of rejection, kindness, and importance of others’ judgments demonstrate perfect recall (1.0) alongside relatively high precision (0.75), reflecting reliable classification. In contrast, altruism exhibits lower precision (0.5) and zero specificity, which suggests a higher rate of false positives in this category. Overall, the overall scores demonstrate good classifier performance, with an average F1-score of 0.84, balancing precision and recall across variables.

Table 5.
Classification performance measures per variable.
To complement the summary measures in Table 5, representative confusion matrices are provided for selected variables. For instance, Table 6 shows the confusion matrix for Neuroticism, where both positive and negative cases are mostly classified correctly, resulting in high precision and specificity. In contrast, Table 7 presents the confusion matrix for Altruism, where all positive cases were correctly identified (sensitivity = 1), but none of the negative cases are classified correctly (specificity = 0), leading to a high number of false positives. These examples highlight how confusion matrices provide valuable insights into the types of errors (off-diagonal elements) made by the model, complementing the aggregated performance metrics [47].

Table 6.
Confusion matrix for the variable Neuroticism.

Table 7.
Confusion matrix for the variable Altruism.
For the graphical visualization of the results obtained from the Bin-3-Way-PARAFAC-PLS analysis, biplots are employed. To facilitate clearer interpretation, especially given the large number of variables to be represented, separate biplots are presented for each situation, including the associated responses and personality traits. It is important to note that in this triplot, the probabilities of binary variables are depicted with a dot representing a probability of 0.5, and an arrow indicating a probability of 0.75.
Figure 3 displays six separate biplots, one for each situational context. In each biplot, psychological dispositions are represented as red vectors, response variables as black vectors, and individual participants as green points.These biplots reveals that individuals 5, 6, 7, and 8 share very similar personality traits (“Depression”, “Conscientiousness”, “Low self esteem”, “Being strict to oneself”, and “Neuroticism”). These traits are also present in person 4 but to a lesser extent. Furthermore, these personality traits are evidently highly correlated. The remaining individuals are characterized by being kind, altruistic, importance of others’ judgments, and fearful of rejection. Similarly, these personality traits are closely related to each other.
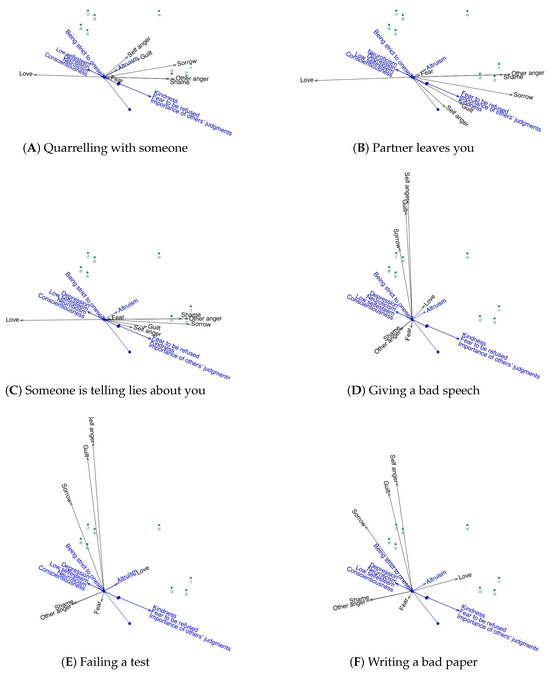
Figure 3.
Logistic biplots for the six emotional scenarios under study. Each panel shows the joint representation of emotional responses (black vectors), psychological dispositions (blue vectors), and individual participants (green points). Labels (A) through (F) correspond to the following: (A) Quarreling with someone. (B) Partner leaves you. (C) Someone is telling lies about you. (D) Giving a bad speech. (E) Failing a test. (F) Writing a bad paper.
When analyzing the reactions to the different situations, similarities emerge among the situations “Giving a bad speech”, “Fail an exam” and “Writing a bad paper”. In all cases, people who react to these situations by feeling “Sorrow”, “Self-anger” or “Guilt” are characterized by the following personality traits: “Depression”, “Conscientiousness”, “Low self esteem” and “Being strict to oneself”. Conversely, the situations “Argue with someone”, “Partner leaves you” and “Someone lies about you” exhibit similar emotional response patterns. People who experience “Other anger”, “Shame”, and “Sorrow” in these situations are characterized by their kindness, by the importance of others’ judgments, and by their fear of rejection.
For the construction and visualization of the biplots, we use the MultbiplotR package [45], which is available on CRAN at https://cran.r-project.org/web/packages/MultBiplotR (accessed on 15 June 2025). A reproducible example of the R 4.2.1 code used for the analysis is provided in Appendix A.
6. Conclusions
In this paper, we present a generalization of the N-PLS model for binary response matrices, named Bin-3-Way-PARAFAC-PLS. To the best of our knowledge, there is currently no model in the literature that addresses this specific situation. Furthermore, we also provide an algorithm for efficiently computing all parameters of the model. The algorithm has been implemented in an R 4.2.1 package, BinNPLS, which is freely available at https://github.com/efb2711/Bin-NPLS (accessed on 15 June 2025).
Beyond its practical utility, the proposed Bin-3-Way-PARAFAC-PLS model addresses a significant methodological gap in the existing literature. Although tensor regression models with low-rank constraints have been extensively studied for continuous responses, their adaptation to binary outcomes in three-way data structures remains limited. This work provides a novel solution by integrating PARAFAC decomposition with a probabilistic framework for binary data, enhancing both interpretability and predictive performance. This contribution is particularly relevant for scenarios involving binary responses and structured, multiway predictors, for which few tailored methods currently exist.
For the visualization and interpretation of the results obtained from the proposed model, we suggest the use of a biplot method, to facilitate the understanding of relationships between explanatory variables and response variables.
To validate the efficacy and utility of the proposed model, we applied it to a personality trait analysis dataset. The results demonstrate the model’s ability to yield significant insights in this domain.
While the Bin-3-Way-PARAFAC-PLS method is currently limited to three-way data arrays, future research should explore its generalization to N-way data arrays. Extending the approach to handle N-way structures would significantly broaden its applicability and versatility. However, such an extension entails several challenges, including a substantial increase in computational complexity due to the increasing number of parameters and the higher-dimensional optimization space. These factors could negatively impact the scalability and convergence behavior of the algorithm, particularly when dealing with large-scale or high-dimensional data. Moreover, parameter identifiability becomes more problematic as the number of modes increases, especially in the context of non-Gaussian responses such as binary outcomes.
Another promising avenue for future research involves the use of the Tucker3 model instead of the PARAFAC model for the decomposition of the three-way data array, which could potentially enhance the model’s flexibility and performance. The use of Tucker decomposition as an alternative to PARAFAC offers greater modeling flexibility, as it allows for a different number of components in each mode. However, this added flexibility comes at the cost of increased model complexity, primarily stemming from the presence of a core tensor that complicates interpretation and inflates the number of parameters to estimate. These aspects may also lead to identifiability and overfitting issues if not properly regularized. Future research could focus on developing efficient optimization strategies and robust model selection criteria tailored to the Tucker framework, especially in the context of binary response data.
Additionally, exploring scenarios where the binary response is a three-way array or extending to two multiway binary arrays would further expand the model’s applicability.
Author Contributions
Conceptualization, E.F.-B.; Methodology, E.F.-B. and L.V.-G.; Software, E.F.-B.; Validation, E.F.-B. and L.V.-G.; Formal analysis, E.F.-B.; Investigation, E.F.-B. and L.V.-G.; Resources, E.F.-B.; Data curation, E.F.-B.; Writing—original draft, E.F.-B. and L.V.-G.; Writing—review & editing, E.F.-B., L.V.-G. and A.E.S.; Visualization, E.F.-B. and L.V.-G.; Supervision, E.F.-B.; Project administration, E.F.-B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The dataset analyzed during the current study is available in the GitHub repository (version 1.0.1, https://github.com/efb2711/Bin-NPLS, accessed on 15 June 2025). Also, the proposed algorithm is implemented in R 4.2.1 [36]. It is available at https://github.com/efb2711/Bin-NPLS (accessed on 15 June 2025).
Conflicts of Interest
The author declares no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
Appendix A. Code for Reproducing the Analysis
The R 4.2.1 code required to implement the Bin-3-Way-PARAFAC-PLS analysis using the BinNPLS and MultBiplotR packages is shown below.
- # Install devtools package if not already installed
- install . packages ("devtools")
- # Load devtools package
- library (";devtools")
- # Install BinNPLS package from GitHub
- install_github ("efb2711/BinNPLS")
- # Install MultBiplot package if not already installed
- install . packages ("MultBiplotR")
- # Load necessary libraries
- library ("BinNPLS")
- library ("MultBiplotR")
- # Perform BIN-3-Way-PARAFAC-PLS analysis
- X<- as . matrix (X3way)
- pls <-NPLSRBin(Y,X,8,7,6,9)
- # Create a biplot of the results
- plsbip=Biplot.PLSRBIN (pls)
- plot (plsbip)
References
- Wold, S.; Ruhe, A.; Wold, H.; Dunn, W.J., III. The Collinearity Problem in Linear Regression. The Partial Least Squares (PLS) Approach to Generalized Inverses. SIAM J. Sci. Stat. Comput. 1984, 5, 735–743. [Google Scholar] [CrossRef]
- Höskuldsson, A. PLS regression methods. J. Chemom. 1988, 2, 211–228. [Google Scholar] [CrossRef]
- de Jong, S. SIMPLS—An alternative approach to partial least-squares regression. Chemom. Intell. Lab. Syst. 1993, 18, 251–263. [Google Scholar] [CrossRef]
- Li, L.; Yan, S.; Bakker, B.M.; Hoefsloot, H.; Chawes, B.; Horner, D.; Rasmussen, M.A.; Smilde, A.K.; Acar, E. Analyzing postprandial metabolomics data using multiway models: A simulation study. BMC Bioinform. 2024, 25, 94. [Google Scholar] [CrossRef]
- Murphy, K.R.; Stedmon, C.A.; Graeber, D.; Bro, R. Fluorescence spectroscopy and multi-way techniques. PARAFAC. Anal. Methods 2013, 5, 6557–6566. [Google Scholar] [CrossRef]
- Escudero, J.; Acar, E.; Fernández, A.; Bro, R. Multiscale entropy analysis of resting-state magnetoencephalogram with tensor factorisations in Alzheimer’s disease. Brain Res. Bull. 2015, 119, 136–144. [Google Scholar] [CrossRef]
- Reitsema, A.M.; Jeronimus, B.F.; van Dijk, M.; Ceulemans, E.; van Roekel, E.; Kuppens, P.; de Jonge, P. Distinguishing dimensions of emotion dynamics across 12 emotions in adolescents’ daily lives. Emotion 2023, 23, 1549. [Google Scholar] [CrossRef]
- Coombs, C. A Theory of Data. Psychol. Rev. 1960, 67, 143–159. [Google Scholar] [CrossRef] [PubMed]
- Carroll, J.D.; Arabie, P. Multidimensional scaling. In Measurement, Judgment and Decision Making; Elsevier: Amsterdam, The Netherlands, 1998; pp. 179–250. [Google Scholar] [CrossRef]
- Pearson, K. LIII. On lines and planes of closest fit to systems of points in space. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1901, 2, 559–572. [Google Scholar] [CrossRef]
- Kroonenberg, P.M. Three-Mode Principal Component Analysis: Theory and Applications; DSWO: Leiden, The Netherlands, 1983. [Google Scholar]
- Tucker, L.R. Some mathematical notes on three-mode factor analysis. Psychometrika 1966, 31, 279–311. [Google Scholar] [CrossRef]
- Tucker, L.R. The extension of factor analysis to three-dimensional matrices. In Contributions to Mathematical Psychology; Frederiksen, N., Gulliksen, H., Eds.; Holt, Rinehart and Winston: New York, NY, USA, 1964; pp. 109–127. [Google Scholar]
- Hitchcock, F.L. The expression of a tensor or a polyadic as a sum of products. J. Math. Phys. 1927, 6, 164–189. [Google Scholar] [CrossRef]
- Harshman, R.A. Foundations of the parafac procedure: Models and conditions for an explanatory multi-modal factor analysis. UCLA Work. Pap. Phon. 1970, 16, 1–84. [Google Scholar]
- Carroll, J.D.; Chang, J.J. Analysis of individual differences in multidimensional scaling via an N-way generalization of “Eckart-Young” decomposition. Psychometrika 1970, 35, 283–319. [Google Scholar] [CrossRef]
- Smilde, A.K.; Bro, R.; Geladi, P. Multi-Way Analysis: Applications in the Chemical Sciences; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Bro, R. Multiway calibration. Multilinear PLS. J. Chemom. 1996, 10, 47–61. [Google Scholar] [CrossRef]
- Smilde, A. Comments on multilinear PLS. J. Chemom. 1997, 11, 367–377. [Google Scholar] [CrossRef]
- Bro, R.; Smilde, A.; de Jong, S. On the difference between low-rank and subspace approximation: Improved model for multi-linear PLS regression. Chemom. Intell. Lab. Syst. 2001, 58, 3–13. [Google Scholar] [CrossRef]
- Hervás, D.; Prats-Montalbán, J.; Lahoz, A.; Ferrer, A. Sparse N-way partial least squares with R package sNPLS. Chemom. Intell. Lab. Syst. 2018, 179, 54–63. [Google Scholar] [CrossRef]
- Hervás, D.; Prats-Montalbán, J.; García-Cañaveras, J.; Lahoz, A.; Ferrer, A. Sparse N-way partial least squares by L1-penalization. Chemom. Intell. Lab. Syst. 2019, 185, 85–91. [Google Scholar] [CrossRef]
- Barker, M.; Rayens, W. Partial least squares for discrimination. J. Chemom. 2003, 17, 166–173. [Google Scholar] [CrossRef]
- Bastien, P.; Vinzi, V.E.; Tenenhaus, M. PLS generalised linear regression. Comput. Stat. Data Anal. 2005, 48, 17–46. [Google Scholar] [CrossRef]
- Vicente-Gonzalez, L.; Vicente-Villardon, J.L. Partial Least Squares Regression for Binary Responses and Its Associated Biplot Representation. Mathematics 2022, 10, 2580. [Google Scholar] [CrossRef]
- Vicente-Gonzalez, L.; Frutos-Bernal, E.; Vicente-Villardon, J.L. Partial Least Squares Regression for Binary Data. Mathematics 2025, 13, 458. [Google Scholar] [CrossRef]
- Bazzoli, C.; Lambert-Lacroix, S. Classification based on extensions of LS-PLS using logistic regression: Application to clinical and multiple genomic data. BMC Bioinform. 2018, 19, 314. [Google Scholar] [CrossRef] [PubMed]
- Fort, G.; Lambert-Lacroix, S. Classification using partial least squares with penalized logistic regression. Bioinformatics 2005, 21, 1104–1111. [Google Scholar] [CrossRef]
- Vicente-Villardon, J.; Galindo-Villardón, M.P.; Blazquez-Zaballos, A. Logistic Biplots. In Multiple Correspondence Analysis and Related Methods; Chapman and Hall/CRC: Boca Raton, FL, USA, 2006; pp. 503–521. [Google Scholar]
- Demey, J.R.; Vicente-Villardon, J.L.; Galindo-Villardón, M.P.; Zambrano, A.Y. Identifying molecular markers associated with classification of genotypes by External Logistic Biplots. Bioinformatics 2008, 24, 2832–2838. [Google Scholar] [CrossRef] [PubMed]
- Carlier, A.; Kroonenberg, P. Decompositions and biplots in three-way correspondence analysis. Psychometrika 1996, 61, 355–373. [Google Scholar] [CrossRef]
- Kiers, H. Towards a standardized notation and terminology in multiway analysis. J. Chemom. 2000, 14, 105–122. [Google Scholar] [CrossRef]
- Rao, C.R.; Mitra, S.K. Generalized inverse of a matrix and its applications. In Proceedings of the Sixth Berkeley Symposium on Mathematical Statistics and Probability; University of California Press: Oakland, CA, USA, 1972; Volume 1, pp. 601–620. [Google Scholar]
- Albert, A.; Anderson, J.A. On the existence of maximum likelihood estimates in logistic regression models. Biometrika 1984, 71, 1–10. [Google Scholar] [CrossRef]
- Cessie, S.L.; Houwelingen, J.V. Ridge estimators in logistic regression. J. R. Stat. Soc. Ser. C Appl. Stat. 1992, 41, 191–201. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2023. [Google Scholar]
- Oyedele, O.F.; Lubbe, S. The construction of a partial least-squares biplot. J. Appl. Stat. 2015, 42, 2449–2460. [Google Scholar] [CrossRef]
- Gabriel, K.R. The biplot graphic display of matrices with application to principal component analysis. Biometrika 1971, 58, 453–467. [Google Scholar] [CrossRef]
- Gower, J.C.; Hand, D. Biplots; Monographs on Statistics and Applied Probability; Chapman and Hall: London, UK, 1996; Volume 54, 277p. [Google Scholar]
- Gower, J.C.; Lubbe, S.G.; Le Roux, N.J. Understanding Biplots; John Wiley and Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Babativa-Márquez, J.G.; Vicente-Villardón, J.L. Logistic Biplot by Conjugate Gradient Algorithms and Iterated SVD. Mathematics 2021, 9, 2015. [Google Scholar] [CrossRef]
- Vicente-Villardón, J.L.; Hernández Sánchez, J.C. Logistic Biplots for Ordinal Data with an Application to Job Satisfaction of Doctorate Degree Holders in Spain. arXiv 2014. [Google Scholar] [CrossRef]
- Hernández-Sánchez, J.C.; Vicente-Villardón, J.L. Logistic biplot for nominal data. Adv. Data Anal. Classif. 2017, 11, 307–326. [Google Scholar] [CrossRef][Green Version]
- Lichman, M.; Bache, K. UCI Machine Learning Repository; University of California, Irvine, School of Information and Computer Sciences: Irvine, CA, USA, 2013. [Google Scholar]
- Vicente-Villardon, J.L.; Vicente-Gonzalez, L.; Frutos Bernal, E. MultBiplotR: Multivariate Analysis Using Biplots in R; R package version 1.6.14; Universidad de Salamanca: Salamanca, Spain, 2024. [Google Scholar]
- Van Coillie, H.; Van Mechelen, I.; Ceulemans, E. Multidimensional individual differences in anger-related behaviors. Personal. Individ. Differ. 2006, 41, 27–38. [Google Scholar] [CrossRef]
- Barranco-Chamorro, I.; Carrillo-Garcia, R.M. Techniques to deal with off-diagonal elements in confusion matrices. Mathematics 2021, 9, 3233. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).