A Novel Poisson–Weibull Model for Stress–Strength Reliability Analysis in Industrial Systems: Bayesian and Classical Approaches

Abstract

Industrial systems often rely on specialized redundant systems to enhance reliability and prevent unexpected failures. This study introduces a novel three-parameter model, the Poisson–Weibull distribution (PWD), and discovers its various key properties. The primary focus of the study is to develop stress–strength (SS) model based on this newly developed distribution. Parameter estimation for both the PWD and SS models is carried out using maximum likelihood estimation (MLE) and Bayesian estimation techniques. Given the complexity of the proposed distribution, numerical approximation techniques are employed to obtain reliable parameter estimates. A comprehensive simulation study employing the Monte Carlo simulation (MCS) and Markov Chain Monte Carlo (MCMC) examines the behavior of the PWD and SS model parameters under various scenarios. The development of the SS model enhances understanding of the PWD’s dynamics while providing practical insights into its real-life applications and limitations. The effectiveness of the proposed distribution and the SS reliability measure is established through applications to real-life data sets.

1. Introduction

The field of reliability engineering is vast and has extensively examined stress–strength (SS) models under various proposed distributions. Wang et al. [1] proposed a generalized SS model, while Ghitany et al. [2] estimated SS reliability under the power Lindley distribution. Jose et al. [3] used the discrete phase-type distribution for SS reliability estimation, and Panahi et al. [4] explored the SS model under the Lomax distribution. Empirical studies include Sharma et al. [5], who analyzed real-world head and neck cancer data for SS reliability estimation, and Morris et al. [6], who provided simulation-based evaluations of statistical methods. Willis et al. [7] employed the Newton–Raphson iteration for MLE in a bivariate random effects model, while Sabry et al. [8] estimated SS reliability using Monte Carlo simulation. Recent advancements include Elbatal et al. [9], who analyzed SS reliability for various distributions under progressive type-II censoring with Binomial removal, while Alharbi et al. [10] focused on the estimation of SS reliability using classical and Bayesian methods with progressively first-failure censored data from an inverse Pareto distribution.

Despite this extensive body of work, there remains an open question: How can discrete event occurrences such as shocks, recoveries, or failure attempts be systematically integrated into continuous lifetime models? To address this, Alsadat et al. [11] proposed the Poisson Rayleigh Distribution (PRD) that incorporates a discrete Poisson component within the structure of a continuous Rayleigh model.

Distributions such as PRD are motivated by real-world systems with event-triggered deterioration, such as a drone with multiple battery backups or a medical device whose risk of failure increases with prior stress events. In such cases the continuous distribution models the underlying lifetime, e.g., time to complete system failure, while the Poisson component captures the number of discrete triggering events, such as shocks, failed recovery attempts, or independent component breakdowns. Each such event may reduce overall system reliability, thereby affecting the time-to-failure.

The probability mass function (PMF) of the Poisson distribution is given by

$$P\left[N=n\right]=\left\{\begin{array}{c}{e}^{-\lambda }, n=1, \lambda \ge 0\\ {\displaystyle \frac{e^{-\lambda }. {\lambda }^{\left(n-1\right)}}{\left(n-1\right)!}}, \lambda \ge 0; n=\mathrm{2,3},\dots \end{array}\right.$$

(1)

where $\lambda$ is the average rate of occurrence, and $n$ is the number of events.

In this research, the use of the Weibull distribution extends the Poisson–Rayleigh framework by introducing an additional shape parameter b, allowing the hazard rate to vary flexibly. This flexibility enables the modeling of systems where the risk of failure may increase, decrease or remain constant over time, a behavior the Rayleigh distribution cannot capture due to its fixed value for b, equal to 2.

While the Rayleigh distribution is suitable for systems with quadratic hazard rates, e.g., idealized mechanical systems, real-world systems often exhibit more complex lifetime behavior. The Weibull distribution’s adaptability makes it more suitable for practical reliability modeling across diverse application domains. From an inferential standpoint, our model enables learning not just the rate of failure but also the evolution of failure risk over time. This enhances interpretability and decision-making in preventative maintenance and risk assessment.

The reliability function of the Weibull distribution, representing the likelihood of a system surviving beyond a given time $x$ is

$${\overline{F}}_c\left(x\right)=e^{-( {x/\alpha )}^b},$$

(2)

where $\alpha$ is the scale parameter, and $b$ is the shape parameter.

This innovative distribution is further extended to develop a stress–strength (SS) reliability model, where failure occurs when stress exceeds strength. The PWD introduces a flexible non-monotone hazard rate function, enabling researchers to model complex temporal dynamics and provide deeper insights into system behavior. By comparing the reliability of two systems or components, the SS model offers valuable insights into the probability of a system withstanding a given stress and the interference area between their lifetime distributions, indicating relative reliability. To ensure robust parameter estimation, the study employs both Bayesian and non-Bayesian methods to fit the PWD and SS models to real-world data, showcasing their practical applicability in reliability analysis.

The formation of the study is presented as follows: Section 2 develops the PWD and its corresponding SS model, Section 3 discusses various properties of the PWD, Section 4 presents the parameter estimation methods, Section 5 demonstrates the performance of the PWD and SS models through a simulation study, and Section 6 evaluates their performance using Bayesian and non-Bayesian estimation techniques.

2. Formation of the Poisson–Weibull Distribution and Stress–Strength Model

In this section the development of the proposed model PWD is described along with its graphical representation, followed by the derivation of the SS model.

2.1. Poisson–Weibull Distribution (PWD)

To develop the PWD, Marshall–Olkin [12] method is considered as given,

$$\overline{F}\left(x;\alpha , b,\lambda \right)={\sum }_{n=1}^{\infty }[ {\left\{\overline{F_c}\left(x; \alpha , b\right)\right\}}^n.P(N=n) ],$$

(3)

where $\overline{F}\left(x;\alpha , b,\lambda \right)$ is the reliability function of the proposed PWD, and ${\overline{F}}_c\left(x;\alpha ,\beta \right)$ is the reliability function of the two-parameter Weibull distribution given in Equation (2) and $P(N=n)$ is the PMF of the Poisson distribution given in Equation (1). Substituting these into Equation (3), and after some simplifications, we get

$$\overline{F}\left(x\right)={\overline{F}}_c\left(x\right) \left[e^{-\lambda \left\{1-{\overline{F}}_c\left(x\right)\right\}}\right],$$

or alternatively,

$$\overline{F}\left(x\right)=e^{-({x/\alpha )}^b} \left[e^{-\lambda \left\{1-e^{-({x/\alpha )}^b}\right\}}\right].$$

Finally, we get reliability function of the PWD as

$$\overline{F}\left(x\right)=e^{-({x/\alpha )}^b-\lambda (1-e^{-{\left(x/\alpha \right)}^b})}.$$

(4)

The complement of the reliability function given in Equation (4) gives the cumulative distribution function (CDF) of the PWD,

$$F\left(x\right)=1-e^{-({x/\alpha )}^b-\lambda (1-e^{-{\left(x/\alpha \right)}^b})}.$$

(5)

Taking the derivative of the CDF in Equation (5), we get the probability density function (PDF) of the PWD as

$$f\left(x\right)=(b/\alpha ){\left(x/\alpha \right)}^{b-1}{e}^{-2{\left(x/\alpha \right)}^b+\lambda \left(e^{-{\left(x/\alpha \right)}^b}-1\right)}\left(e^{{\left(x/\alpha \right)}^b}+\lambda \right), x>0; \alpha , b, \lambda >0$$

or

$$f\left(x\right)=(b/\alpha ){\left(x/\alpha \right)}^{b-1}{e}^{{-\left(x/\alpha \right)}^b-\lambda \left(1-e^{-{\left(x/\alpha \right)}^b}\right)}\left(1+\lambda e^{{-\left(x/\alpha \right)}^b}\right), x>0; \alpha , b, \lambda >0.$$

(6)

The function given in Equation (6) has the following characteristic:

• In Equation (6) for $b=1$, the PWD is reduced to Poisson-exponential distribution (PED); for $\lambda =0,$ PWD reduces to the Weibull distribution, and when $b=1, and \lambda =0,$ PWD reduces to the exponential distribution, see

  Table 1. Some special cases of the Poisson–Weibull distribution (PWD).

  Fixed Parameters	Distribution
  $b=1$	Poisson-exponential distribution
  $\lambda =0$	Weibull distribution
  $b=1, \lambda =0$	Exponential distribution

  .
• In the transformation given in Equation (3), the probability mass function (PMF) of the Poisson distribution is applied when $n\ge$ 2.
• In the Poisson–Weibull distribution (PWD), λ represents the rate of occurrence of events relevant to the final event of interest.
• If λ equals 1, the PWD would not accurately represent the events relevant to the final event, as the occurrence of the event of interest would not be influenced by the occurrence of events relevant to it.

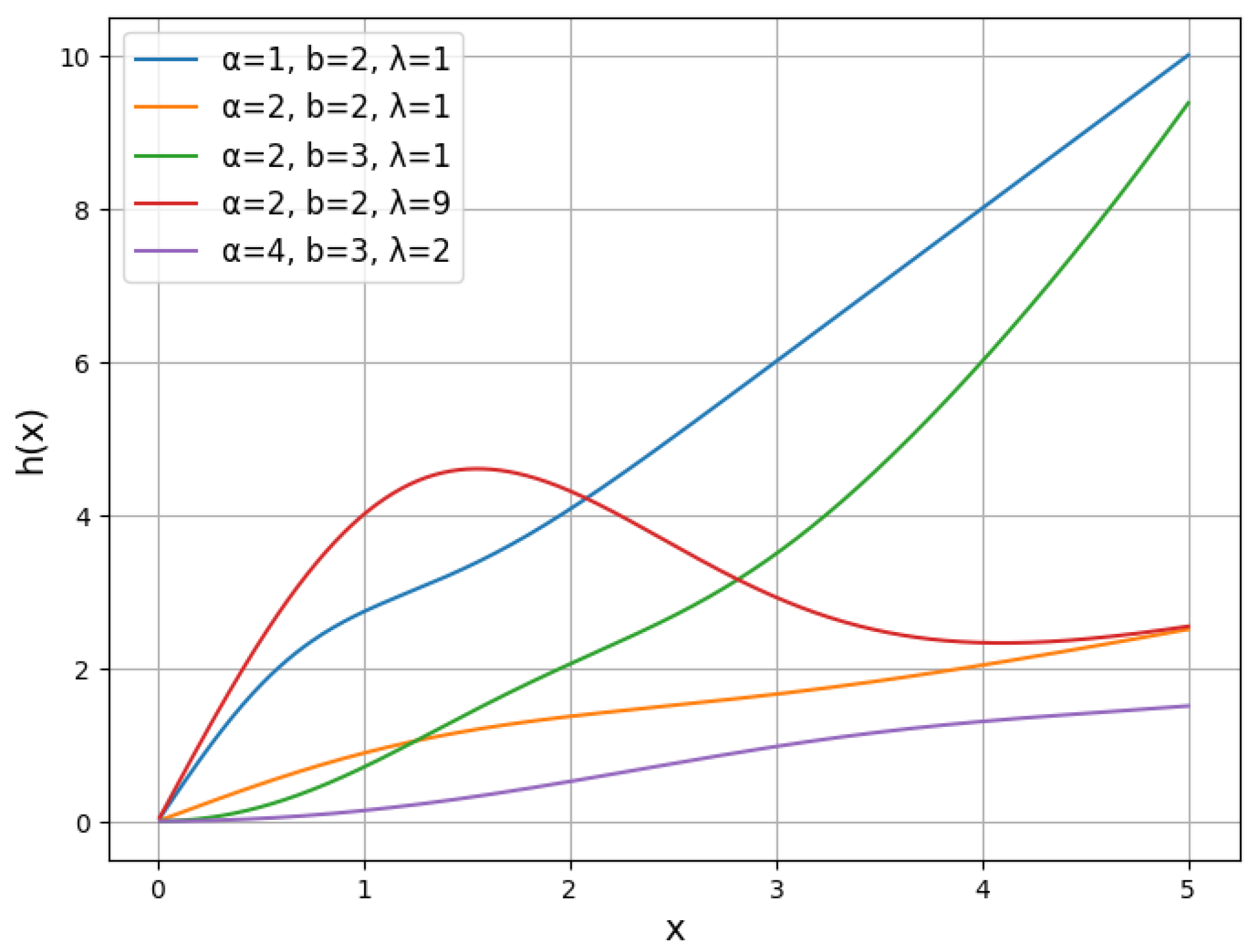
Figure 1a is for different combinations of parametric values and shows right/positive skewed shapes but at $\alpha =2, b=6 and \lambda =1$ it shows symmetric shape. Figure 1b shows right/positive skewed shapes for fixed $\lambda , b and$ changing $\alpha$. Figure 1c shows positive skewed or symmetric shapes for fixed $\lambda , \alpha$ and changing $b.$ Figure 1d shows only positive skewed shapes for fixed $b, \alpha$ and changing $\lambda$. Overall, from Figure 1, it is observed that PWD shows a variety of shapes, mostly positively skewed, occasionally symmetric for different values of its parameters, and displays flat, normal, and high-peaked distributions.

2.2. Stress–Strength Reliability Model

In this section, the SS model is derived by using the PWD developed in Section 2.1. The SS model $R=P\left(Y<X\right)$ is estimated when the random variable $X~PWD\left({\alpha }_1,b_{1,}{\lambda }_1\right)$ and $Y~PWD\left({\alpha }_2,b_{2,}{\lambda }_2\right)$. The SS model denoted by R is given as follows,

$$R={\int }_0^{\infty }p\left(Y<X|X=x\right)f_X\left(x\right)dx.$$

(7)

Since $p\left(Y<X|X=x\right)=F_Y\left(x\right)$, Equation (7) can be written as

$$R={\int }_0^{\infty }{F}_Y\left(x\right)f_X\left(x\right)dx.$$

(8)

Substituting the expressions for $F_Y\left(x\right)$ and $f_X\left(x\right)$ in Equation (8), we get

$$R={\int }_0^{\infty }(b_1/{\alpha }_1){\left(x/{\alpha }_1\right)}^{b_1-1}{e}^{-2{\left(x/{\alpha }_1\right)}^{b_1}+{\lambda }_1\left(e^{-{\left(x/{\alpha }_1\right)}^{b_1}}-1\right)}\left(e^{{\left(x/{\alpha }_1\right)}^{b_1}}+{\lambda }_1\right)\left(1-e^{-({x/{\alpha }_2)}^{b_2}+{\lambda }_2(e^{-{\left(x/{\alpha }_2\right)}^{b_2}}-1)}\right)dx.$$

(9)

Due to the complex nature of this integral, $R$ cannot be expressed in a closed form. However, numerical methods, such as Monte Carlo simulations can be used to approximate $R$. These methods involve sampling from the distributions and estimating the integral through repeated trials, providing an effective way to handle the complexity of the SS reliability model.

3. Properties of PWD

In this section some statistical properties including moments, skewness, kurtosis, quantile function, mode, median, certain reliability measures such as hazard rate function, reversed hazard rate function, cumulative hazard rate function, odd function, mill ratio, and elasticity function of the PWD are derived.

If X is a random variable that follows PWD given in Equation (6), then the $rth$ moments of X are obtained by

$$E{\left(X\right)}^r={\displaystyle \frac{b}{\alpha }}{\int }_0^{\infty }{x}^r{\left(x/\alpha \right)}^{b-1}{e}^{{-\left(x/\alpha \right)}^b}{e}^{-\lambda (1-e^{{-\left(x/\alpha \right)}^b})}[1+\lambda e^{{-\left(x/\alpha \right)}^b}].$$

(10)

Applying exponential series $e^{-\theta }=\sum _{x=0}^{\infty }{\displaystyle \frac{{\theta }^n}{x!}}$ in Equation (10) and after some simplifications we get

$$e^{-\lambda (1-e^{{-\left(x/\alpha \right)}^b})}={\sum }_{i=0}^{\infty }{\displaystyle \frac{{\left(-1\right)}^i{\lambda }^i}{i!}}{(1-e^{{-\left(x/\alpha \right)}^b})}^i.$$

(11)

Using the binomial expansion in Equation (11), we get

$${(1-e^{{-\left(x/\alpha \right)}^b})}^i={\sum }_{j=0}^i{(-1)}^j\left({\displaystyle \genfrac{}{}{0pt}{}{i}{j}}\right)e^{{-j\left(x/\alpha \right)}^b}.$$

(12)

Substituting the results of Equations (11) and (12) into Equation (10) and simplifying them, we get

$${\mu }_r^{\prime }=E{\left(X\right)}^r={\sum }_{i=0}^{\infty }{\sum }_{j=0}^i{\displaystyle \frac{{\left(-1\right)}^{i+j}{\lambda }^i}{i!}}\left({\displaystyle \genfrac{}{}{0pt}{}{i}{j}}\right){\alpha }^r\Gamma ({\displaystyle \frac{r}{b}}+1)\left[{\left(j+1\right)}^{-{\displaystyle \frac{r}{b}}-1}+{\lambda (j+2)}^{-{\displaystyle \frac{r}{b}}-1}\right].$$

(13)

The numerical values for the mean, variance, skewness, and kurtosis are calculated for different values of parameters using moments given in Equation (13) and shown in

Table 2. Effects on summary statistics for varying $\alpha$ with fixed $b$ and $\lambda$.

$\mathbf{Parameters} \left(\mathit{\alpha },\mathit{b},\mathit{\lambda }\right)$	Mean	Variance	Skewness	Kurtosis
(1, 2, 1)	0.63	0.32	0.59	2.76
(2, 2, 1)	1.26	1.30	0.56	2.73
(3, 2, 1)	1.90	2.88	0.59	2.75
(4, 2, 1)	2.53	5.14	0.59	2.74
(5, 2, 1)	3.16	8.04	0.59	2.74
(6, 2, 1)	3.79	11.61	0.58	2.74
(7, 2, 1)	4.42	15.80	0.58	2.74
(8, 2, 1)	5.06	20.56	0.59	2.75
(9, 2, 1)	5.69	26.05	0.59	2.74

,

Table 3. Effects on summary statistics for varying $b$ with fixed $\alpha$ and $\lambda$.

$\mathbf{Parameters} \left(\mathit{\alpha },\mathit{b},\mathit{\lambda }\right)$	Mean	Variance	Skewness	Kurtosis
(2, 1, 1)	1.26	2.29	2.76	14.92
(2, 2, 1)	1.26	1.20	0.56	2.73
(2, 3, 1)	1.26	1.12	0.02	1.72
(2, 4, 1)	1.26	1.05	−0.19	1.49
(2, 5, 1)	1.26	1.02	−0.31	1.41
(2, 6, 1)	1.26	1.00	−0.38	1.38
(2, 7, 1)	1.26	0.99	−0.43	1.37
(2, 8, 1)	1.26	0.98	−0.45	1.33
(2, 9, 1)	1.26	0.97	−0.45	1.31

and

Table 4. Effects on summary statistics for varying $\lambda$ with fixed $\alpha$ and $b$.

$\mathbf{Parameters} \left(\mathit{\alpha },\mathit{b},\mathit{\lambda }\right)$	Mean	Variance	Skewness	Kurtosis
(2, 2, 1)	1.26	1.30	0.56	2.73
(2, 2, 2)	0.86	0.95	0.97	3.56
(2, 2, 3)	0.63	0.66	1.27	4.49
(2, 2, 4)	0.49	0.48	1.40	5.11
(2, 2, 5)	0.40	0.36	1.50	5.33
(2, 2, 6)	0.33	0.28	1.58	5.61
(2, 2, 7)	0.28	0.23	1.56	5.42
(2, 2, 8)	0.25	0.19	1.65	5.75
(2, 2, 9)	0.22	0.16	1.73	5.42

. The formulas for calculating both using moments are given as follows:

$$skew\left(X\right)= {\displaystyle \frac{{\mu }_3-3\mu {\sigma }^2-{\mu }^3}{{\sigma }^3}},$$

and

$$kurt\left(X\right)={\displaystyle \frac{{\mu }_4-4\mu {\mu }_3+{6\mu }^2{\sigma }^2+{6\mu }^4}{{\sigma }^4}}.$$

• In Table 2, for fixed values of $b \mathrm{a}\mathrm{n}\mathrm{d} \lambda$, as $\alpha$ increases, the mean and variance increase, while skewness and kurtosis are not significantly affected.
• In Table 3, for fixed values of $\alpha \mathrm{a}\mathrm{n}\mathrm{d} \lambda$, as $b$ increases, the mean does not change, variance decreases, skewness shifts from right to left, and peakedness moves from leptokurtic to platykurtic.
• In Table 4, for fixed values of $\alpha \mathrm{a}\mathrm{n}\mathrm{d} b$, as $\lambda$ increases, the mean and variance decrease, right skewness increases, and peakedness shifts towards leptokurtic.

The quantile function Q(p), when a random variable follows PWD, is as follows

$$1-e^{-{\left({\displaystyle \frac{Q\left(p\right)}{\alpha }}\right)}^b}{e}^{-\lambda \left(1-e^{-{\left({\displaystyle \frac{Q\left(p\right)}{\alpha }}\right)}^b}\right)}=p, \to e^{-{\left({\displaystyle \frac{Q\left(p\right)}{\alpha }}\right)}^b}{e}^{{\lambda e}^{-{\left({\displaystyle \frac{Q\left(p\right)}{\alpha }}\right)}^b}}=e^{\lambda \left(1-p\right)}.$$

Let, $z\left(p\right)=\lambda e^{-{\left({\displaystyle \frac{Q\left(p\right)}{\alpha }}\right)}^b}$, then $e^{-{\left({\displaystyle \frac{Q\left(p\right)}{\alpha }}\right)}^b}={\displaystyle \frac{1}{\lambda }}z\left(p\right)$, → ${\displaystyle \frac{1}{\lambda }}z\left(p\right)e^{z\left(p\right)}=(1-p)e^{\lambda }$,

or

$$z\left(p\right)=\omega \left[\lambda e^{\lambda }(1-p)\right].$$

Substituting expression for $z\left(p\right)$ and simplifying gives the following form for the quantile function:

$$Q\left(p\right)= \alpha {\left[-ln\left\{{\displaystyle \frac{1}{\lambda }}\omega (\lambda e^{\lambda }(1-p))\right\}\right]}^{{\displaystyle \frac{1}{b}}}.$$

(14)

The three quantiles of the PWD are computed as

$$Q_1=\alpha {\left[-ln\left\{{\displaystyle \frac{1}{\lambda }}\omega (\lambda e^{\lambda }(0.75))\right\}\right]}^{{\displaystyle \frac{1}{b}}},$$

$$Median=\alpha {\left[-ln\left\{{\displaystyle \frac{1}{\lambda }}\omega (\lambda e^{\lambda }(0.5))\right\}\right]}^{{\displaystyle \frac{1}{b}}},$$

and

$$Q_3=\alpha {\left[-ln\left\{{\displaystyle \frac{1}{\lambda }}\omega (\lambda e^{\lambda }(0.25))\right\}\right]}^{{\displaystyle \frac{1}{b}}}.$$

The mode for the PWD is the solution of the following expression

$${\displaystyle \frac{\delta f\left(x\right)}{\delta x}}={\displaystyle \frac{b-1}{x}}-{\displaystyle \frac{{bx}^{b-1}}{{\alpha }^b}}-{\displaystyle \frac{\lambda b{x}^{b-1}{e}^{-{\left(x/\alpha \right)}^b}}{{\alpha }^b}}=0,$$

for which

$${\displaystyle \frac{{\delta }^{2}f\left(x\right)}{\delta x^2}}=-{\displaystyle \frac{\left(b-1\right)}{x^2}}-{\displaystyle \frac{{b\left(b-1\right)x}^{b-2}}{{\alpha }^b}}-{\displaystyle \frac{{\lambda b\left(b-1\right)x}^{b-2}{e}^{-{\left(x/\alpha \right)}^b}}{{\alpha }^b}}-{\displaystyle \frac{{{\lambda }^2{b}^{2}e}^{-{\left(x/\alpha \right)}^b}}{{\alpha }^{2b}}}<0.$$

Therefore, the mode can be numerically calculated from the equation $x={\displaystyle \frac{{\alpha }^{b}b\left(1+\lambda e^{-{\left(x/\alpha \right)}^b}\right)}{\left(b-1\right)}}$.

If X is a random variable that follows PWD, then the hazard rate function (HRF) for the PWD is

$$h\left(x;\alpha ,b,\lambda \right)=\left(b/\alpha \right){\left(x/\alpha \right)}^{b-1}\left(1+\lambda e^{-{\left(x/\alpha \right)}^b}\right).$$

(15)

The reverse hazard rate function (RHRF)for the PWD is

$$r\left(x; \alpha , b,\lambda \right)={\displaystyle \frac{\left(b/\alpha \right){\left(x/\alpha \right)}^{b-1}{e}^{{-\left(x/\alpha \right)}^b-\lambda \left(1-e^{-{\left(x/\alpha \right)}^b}\right)}\left(1+\lambda e^{{-\left(x/\alpha \right)}^b}\right)}{1-e^{-\left(x/\alpha \right)-\lambda \left(1-e^{-{\left(x/\alpha \right)}^b}\right)}}}.$$

The cumulative hazard rate function (CHRF) of the PWD is

$$H\left(x\right)={\left(x/\alpha \right)}^b+\lambda \left(1-e^{-{\left(x/\alpha \right)}^b}\right).$$

The odd function (OF), mills ratio (MR), and elasticity function (EF) for the PWD are given, respectively, as

$$O\left(x\right)={\displaystyle \frac{1-e^{-\left(x/\alpha \right)-\lambda \left(1-e^{-{\left(x/\alpha \right)}^b}\right)}}{e^{-\left(x/\alpha \right)-\lambda \left(1-e^{-{\left(x/\alpha \right)}^b}\right)}}},$$

$$M\left(x\right)={\displaystyle \frac{\alpha }{b{\left(x/\alpha \right)}^{b-1}\left(1+\lambda e^{{-\left(x/\alpha \right)}^b}\right)}},$$

and

$$\epsilon \left(x\right)={\displaystyle \frac{\left(b/\alpha \right){x\left(x/\alpha \right)}^{b-1}{e}^{{-\left(x/\alpha \right)}^b-\lambda \left(1-e^{-{\left(x/\alpha \right)}^b}\right)}\left(1+\lambda e^{{-\left(x/\alpha \right)}^b}\right)}{\left[1-e^{-\left(x/\alpha \right)-\lambda \left(1-e^{-{\left(x/\alpha \right)}^b}\right)}\right]}}.$$

Shannon Entropy of PWD does not have a closed form solution because the logarithm of $f\left(x\right)$ becomes quite complex. However, the following form for the entropy can be numerically integrated using fixed values for PWD parameters.

$$SE\left(X\right)=-{\int }_0^{\infty }f\left(x\right)logf\left(x\right)dx.$$

Let $X~PWD({\alpha }_1,b_1,{\lambda }_1)$ and $Y~PWD({\alpha }_2,b_2,{\lambda }_2)$. Then the usual stochastic ordering is

$$X{\le }_{st}Y iff {\overline{F}}_X\left(x\right)\le {\overline{F}}_Y\left(x\right)$$

For PWD the survival function is

$$\overline{F}\left(x\right)=e^{{-\left(x/\alpha \right)}^b. \left[1-\lambda \left(1-e^{{-\left(x/\alpha \right)}^b}\right)\right]}.$$

So, for stochastic ordering,

$$X{\le }_{st}Y if \forall x>0, e^{{-\left({\displaystyle \frac{x}{{\alpha }_1}}\right)}^{b_1}. \left[1-{\lambda }_1\left(1-e^{{-\left({\displaystyle \frac{x}{{\alpha }_1}}\right)}^{b_1}}\right)\right]}\le e^{{-\left({\displaystyle \frac{x}{{\alpha }_2}}\right)}^{b_2}. \left[1-{\lambda }_2\left(1-e^{{-\left({\displaystyle \frac{x}{{\alpha }_2}}\right)}^{b_2}}\right)\right]}.$$

Let $X_{1:n}\le X_{2:n}\le \cdots \le X_{n:n}$ be the order statistics of an i.i.d. sample $X_1,X_2,\dots ,X_n~PWD(\alpha ,b,\lambda )$.

The PDF of the r-th order statistic $X_{r:n}$ is

$$\begin{gathered} F_{X_r}\left(x\right)={\displaystyle \frac{n!}{\left(r-1\right)!\left(n-r\right)!}}{\left[1-e^{{-(x/\alpha )}^b-\lambda (1-e^{{-(x/\alpha )}^b})}\right]}^{r-1}{\left[e^{{-(x/\alpha )}^b-\lambda (1-e^{{-(x/\alpha )}^b})}\right]}^{n-r}\times (b \\ /\alpha ){(x/\alpha )}^{b-1}{e}^{{-(x/\alpha )}^b}\left[b\lambda {(x/\alpha )}^b+1\right] \end{gathered}$$

Figure 2 shows the HRF for the PWD non-monotone behavior. Non-monotone hazard rates can be used to model diseases or treatments where the risk of failure or relapse initially decreases, for example, the hazard rate may initially decrease during a recovery period, but later increase due to aging or long-term side effects. For certain products, the hazard rate might be high at the beginning due to early failures or manufacturing defects, then decrease or remain stable during a normal operating period, and finally increase again as the product ages, i.e., due to wear-out failures. During software testing, the failure rate might initially increase as issues are identified, then decrease as they are solved, but may spike again as new features are added. The proposed distribution is capable of modeling risks like forest fires or floods, where hazard rates can increase due to seasonal influences, then decrease, and possibly increase again due to external factors like climate change.

4. Estimation of Parameters

In this section the parameters of the PWD and SS are estimated using the maximum likelihood estimation (MLE) and Bayesian estimation method.

4.1. MLE for PWD

Given a random sample $X_1,X_2,\dots , X_n$ arising from PWD, the likelihood function is formulated as follows:

$$\begin{gathered} L\left(\alpha ,b,\lambda \right)=n\left(\mathit{log}\left(b\right)-\mathit{log}\left(\alpha \right)\right)+\left(b-1\right){\sum }_{i=1}^{n}log\left(x_i/\alpha \right)+log{\sum }_{i=1}^n\left(e^{{\left(x_i/\alpha \right)}^b}+\lambda \right)-2{\sum }_{i=1}^n{\left(x_i/\alpha \right)}^b+ \\ \lambda {\sum }_{i=1}^n\left(-e^{{-\left(x_i/\alpha \right)}^b}-1\right). \end{gathered}$$

(16)

To find the MLE of $\alpha , b,$ and $\lambda$, we need to solve the following partial derivate equations by setting them to zero. As mentioned, MLE of $\alpha , b,$ and $\lambda$ are obtained by solving the non-linear equations ${\displaystyle \frac{\partial L}{\partial \alpha }}=0$, ${\displaystyle \frac{\partial L}{\partial b}}=0,$ and ${\displaystyle \frac{\partial L}{\partial \lambda }}=0$. These can only be solved through iterative numerical approximation methods. In this work, the L-BFGS-B algorithm was used for this purpose.

L-BFGS-B

In this study, we employ the limited-memory Broyden–Fletcher–Goldfarb–Shanno with bounds (L-BFGS-B) algorithm for parameter estimation under the frequentist framework. This is a quasi-Newton optimization method specifically designed for problems involving a large number of parameters and box constraints (i.e., lower and upper bounds on parameters).

Traditional Newton-based methods require the Hessian matrix and its inverse to determine the optimal step direction and size. However, computing and storing the full Hessian is computationally expensive, especially for large problems. Quasi-Newton methods, like BFGS, overcome this by building an approximation of the inverse Hessian using gradient information.

The L-BFGS-B variant further improves efficiency by retraining only a limited number of past gradient and parameter updates, hence the name “limited-memory”. The “B” in L-BFGS-B indicates its ability to handle box constraints, which is important in our setting because parameters like scale, shape, and rate must remain positive.

In this study, L-BFGS-B is used to minimize the negative log-likelihood function derived from PWD and obtain the MLE of parameters. This algorithm is implemented in R using the optima function with method set to “L-BFGS-B”. This allows us to specify the lower bounds for all parameters and ensure that parameter estimates remain within the valid domain of the distribution. The complete implementation code, including simulation and optimization, is provided at this link: https://github.com/hadiqa-b/pwd-paramater-estimation (accessed on 15 June 2025).

4.2. MLE for SS

To get the likelihood for the SS model, the following formula is used:

$$L= {\prod }_{i=1}^{n}f\left(x_i;a_1, b_1,{\lambda }_1\right){\prod }_{j=1}^{m}f\left(y;a_2, b_2,{\lambda }_2\right).$$

Inputting the PDF of PWD in the likelihood gives the form for calculating the stress–strength likelihood

$$\begin{gathered} L_{SS}=n\left(\mathit{log}\left(b_1\right)-\mathit{log}\left({\alpha }_1\right)\right)+\left(b_1-1\right){\sum }_{i=1}^{n}log\left({\displaystyle \frac{x_i}{{\alpha }_1}}\right)+log{\sum }_{i=1}^n\left(e^{{\left({\displaystyle \frac{x_i}{{\alpha }_1}}\right)}^{b_1}}+{\lambda }_1\right)-2{\sum }_{i=1}^n{\left({\displaystyle \frac{x_i}{{\alpha }_1}}\right)}^{b_1}+ \\ {\lambda }_1{\sum }_{i=1}^n\left(e^{{-\left({\displaystyle \frac{x_i}{{\alpha }_1}}\right)}^{b_1}}-1\right)+m\left(\mathit{log}\left(b_2\right)-\mathit{log}\left({\alpha }_2\right)\right)+\left(b_2-1\right){\sum }_{j=1}^{m}log\left({\displaystyle \frac{y_j}{{\alpha }_2}}\right)+log{\sum }_{j=1}^m\left(e^{{\left({\displaystyle \frac{y_j}{{\alpha }_2}}\right)}^{b_2}}+{\lambda }_2\right)- \\ 2{\sum }_{j=1}^m{\left({\displaystyle \frac{y_j}{{\alpha }_2}}\right)}^{b_2}+{\lambda }_2{\sum }_{j=1}^m\left(e^{{-\left({\displaystyle \frac{y_j}{{\alpha }_2}}\right)}^{b_2}}-1\right). \end{gathered}$$

(17)

MLE of ${\alpha }_1,b_1,{\lambda }_1,{\alpha }_2,b_2$ and ${\lambda }_2$, are obtained by solving the non-linear equations ${\displaystyle \frac{\partial L_{SS}}{\partial {\alpha }_1}}=0$, ${\displaystyle \frac{\partial L_{SS}}{\partial b_1}}=0$, ${\displaystyle \frac{\partial L_{SS}}{\partial {\lambda }_1}}=0,{\displaystyle \frac{\partial L_{SS}}{\partial {\alpha }_2}}=0,{\displaystyle \frac{\partial L_{SS}}{\partial b_2}}=0,\mathrm{a}\mathrm{n}\mathrm{d} {\displaystyle \frac{\partial L_{SS}}{\partial {\lambda }_2}}=0$. These can only be solved through iterative numerical approximation methods. In this work, the L-BFGS-B algorithm was used for this purpose due to its capability for solving large-scale optimization problems with bound constraints.

4.3. Bayesian Estimation for PWD

To perform Bayesian inference, we incorporate prior distributions for the parameters $\alpha , b, \mathrm{a}\mathrm{n}\mathrm{d} \lambda$. The Gamma distribution is presumptively applied due to its adaptability. Using h₁, q₁, h₂, q₂, h₃, q₃ as hyperparameters, following are the priors for PWD parameters

$$\pi \left(\alpha |h_1,q_1\right)\propto {\alpha }^{h_1-1}{e}^{-q_1\alpha },$$

(18)

$$\pi \left(b|h_2,q_2\right)\propto b^{h_2-1}{e}^{-q_{2}b},$$

(19)

and

$$\pi \left(\lambda |h_3,q_3\right)\propto {\lambda }^{h_3-1}{e}^{-q_3\lambda },$$

(20)

The joint prior distribution of $\alpha , b, \mathrm{a}\mathrm{n}\mathrm{d} \lambda$ from Equations (18)–(20) is given by

$$g\left(\alpha , b, \lambda \right) \propto {\alpha }^{h_1-1}{e}^{-q_1\alpha } b^{h_2-1}{e}^{-q_{2}b}{\lambda }^{h_3-1}{e}^{-q_3\lambda }.$$

(21)

Using Bayes’ theorem, the posterior incorporating the updated priors is

$$\pi \left(\alpha ,b,\lambda |\mathit{x},h_1,q_1,h_2,q_2,h_3,q_3\right)\propto L\left(\mathit{x}|\alpha ,b,\lambda \right)g\left(\alpha ,b,\lambda \right).$$

(22)

Using Equations (17), (21) and (22), the posterior density for PWD is

$$\begin{gathered} \pi \left(\alpha ,b,\lambda |x,h_1,q_1,h_2,q_2,h_3,q_3\right) \propto n\left(\mathit{log}\left(b\right)-\mathit{log}\left(\alpha \right)\right)+\left(b-1\right){\sum }_{i=1}^{n}log\left({\displaystyle \frac{x_i}{\alpha }}\right)+log{\sum }_{i=1}^n\left(e^{{\left({\displaystyle \frac{x_i}{\alpha }}\right)}^b}+\lambda \right)- \\ 2{\sum }_{i=1}^n{\left({\displaystyle \frac{x_i}{\alpha }}\right)}^b+\lambda {\sum }_{i=1}^n\left(-e^{{-\left({\displaystyle \frac{x_i}{\alpha }}\right)}^b}-1\right)\times {\alpha }^{h_1-1}{e}^{-q_1\alpha } b^{h_2-1}{e}^{-q_{2}b}{\lambda }^{h_3-1}{e}^{-q_3\lambda }. \end{gathered}$$

(23)

Minimizing the squared error loss (SEL) provides Bayes estimators, which are the posterior means of the parameters

$${\widehat{\alpha }}_{SEL}=E\left[\alpha \right|\mathit{x},h_1,q_1,h_2,q_2,h_3,q_3],$$

$${\widehat{b}}_{SEL}=E\left[b\right|\mathit{x},h_1,q_1,h_2,q_2,h_3,q_3],$$

and

$${\widehat{\lambda }}_{SEL}=E\left[\lambda \right|\mathit{x},h_1,q_1,h_2,q_2,h_3,q_3].$$

${\widehat{\alpha }}_{SEL}$, ${\widehat{b}}_{SEL},$ and ${\widehat{\lambda }}_{SEL}$ cannot be stated in closed form; however, the Bayes estimate can be roughly approximated using the Monte Carlo Markov Chain (MCMC) method. To do this, the conditional distributions of $\alpha , b,$ and $\lambda$ must be first acquired. The conditional distribution of the parameters, incorporating the hyperparameters, can be derived from the joint posterior distribution,

$$\pi \left(\alpha |b,\lambda ,h_1,q_1\right)\propto \pi \left(\alpha ,b,\lambda \right|\mathit{x},h_1,q_1,h_2,q_2,h_3,q_3),$$

$$\pi \left(b|\alpha ,\lambda ,h_2,q_2\right)\propto \pi \left(\alpha ,b,\lambda \right|\mathit{x},h_1,q_1,h_2,q_2,h_3,q_3),$$

and

$$\pi \left(\lambda |b,\alpha ,h_3,q_3\right)\propto \pi \left(\alpha ,b,\lambda \right|\mathit{x},h_1,q_1,h_2,q_2,h_3,q_3).$$

Using conditional distributions, MCMC methods can generate samples from the posterior distribution, enabling the estimation of, $\alpha , b,$ and $\lambda$. The approximate Bayes estimates obtained from MCMC provide a practical approach to parameter estimation when closed-form solutions are not available.

MCMC

Bayesian estimation was implemented using MCMC via the Hamilton Monte Carlo (HMC) algorithm with No-U-Turn Sampler (NUTS), as implemented in the rstan package in R. The Stan model was specified explicitly using the stan function, and posterior samples were drawn using 5 parallel chains, each with 20,000 iterations, including warm-up samples for adaptation.

The squared error loss Bayes estimator corresponds to the posterior mean, which was computed directly from the posterior samples for each parameter. This aligns with the principle that under squared loss, the Bayes estimator minimized the expected posterior loss.

Posterior diagnostics and visualization were performed using the bayesplot and ggplot2 packages, including trace plots, density plots, and credible intervals. All analyses were executed in a standard desktop environment.

The complete R code and model specification are provided at this link: https://github.com/hadiqa-b/pwd-paramater-estimation (accessed on 15 June 2025).

4.4. Bayesian Estimation for SS

The joint prior density function of $\alpha , b,$ and $\lambda$ can be written as

$$g\left({\alpha }_1, b_1, {\lambda }_1,{\alpha }_2, b_2, {\lambda }_2\right) \propto {{\alpha }_1}^{h_1-1}{e}^{-q_1{\alpha }_1}{{\alpha }_2}^{h_3-1}{e}^{-q_1{\alpha }_2} {b_1}^{h_2-1}{e}^{-q_2{b}_1}{b_2}^{h_4-1}{e}^{-q_4{b}_2}{{\lambda }_1}^{h_3-1}{e}^{-q_3{\lambda }_1}{{\lambda }_2}^{h_6-1}{e}^{-q_6{\lambda }_2},$$

(24)

where the hyperparameters h₁, q₁, h₂, q₂, h₃, q₃, h₄, q₄, h₅, q₅, h₆, and q₆ represent the prior knowledge about the unknown parameters.

The posterior distribution of $\alpha , b,$ and $\lambda$ are expressed by combining the likelihood function with the joint prior distribution, as follows:

$$\begin{array}{cc}\hfill \pi ({\alpha }_1, b_1, {\lambda }_1,{\alpha }_2, b_2,& {\lambda }_2|x,h_1,q_1,h_2,q_2,h_3,q_3, h_4,q_4,h_5,q_5,h_5,q_5)\hfill \\ & \propto n\left(\mathit{log}\left(b_1\right)-\mathit{log}\left({\alpha }_1\right)\right)+\left(b_1-1\right)\sum _{i=1}^{n}log\left({\displaystyle \frac{x_i}{{\alpha }_1}}\right)+log\sum _{i=1}^n\left(e^{{\left({\displaystyle \frac{x_i}{{\alpha }_1}}\right)}^{b_1}}+{\lambda }_1\right)-2\sum _{i=1}^n{\left({\displaystyle \frac{x_i}{{\alpha }_1}}\right)}^{b_1}\hfill \\ & +{\lambda }_1\sum _{i=1}^n\left(-e^{{-\left({\displaystyle \frac{x_i}{{\alpha }_1}}\right)}^{b_1}}-1\right) \times {{\alpha }_1}^{h_1-1}{e}^{-q_1{\alpha }_1} {b_1}^{h_2-1}{e}^{-q_2{b}_1}{{\lambda }_1}^{h_3-1}{e}^{-q_3{\lambda }_1}\hfill \\ & + m\left(\mathit{log}\left(b_2\right)-\mathit{log}\left({\alpha }_2\right)\right)+\left(b_2-1\right)\sum _{j=1}^{m}log\left({\displaystyle \frac{y_j}{{\alpha }_2}}\right)+log\sum _{j=1}^m\left(e^{{\left({\displaystyle \frac{y_j}{{\alpha }_2}}\right)}^{b_2}}+{\lambda }_2\right)-2\sum _{j=1}^m{\left({\displaystyle \frac{y_j}{{\alpha }_2}}\right)}^{b_2}\hfill \\ & +{\lambda }_2\sum _{j=1}^m\left(-e^{{-\left({\displaystyle \frac{y_j}{{\alpha }_2}}\right)}^{b_2}}-1\right) \times {{\alpha }_2}^{h_4-1}{e}^{-q_4{\alpha }_2} {b_2}^{h_5-1}{e}^{-q_5{b}_2}{{\lambda }_2}^{h_6-1}{e}^{-q_6{\lambda }_2}.\hfill \end{array}$$

(25)

The Bayes estimator of the SS parameters can be found by minimizing the SEL. However, due to the complex form of the joint posterior distribution, the posterior mean cannot be solved analytically. Therefore, the posterior means must be numerically approximated using Markov Chain Monte Carlo (MCMC) sampling from the conditional distributions of the Bayes parameters.

5. Simulation Study

In this section, a simulation study is presented for the (i) PWD (MLE and Bayesian) and (ii) SS (MLE and Bayesian). To perform the simulation for MLE, Monte Carlo simulation (MCS) is conducted, and to perform the simulation for Bayesian, Monte Carlo Markov Chain (MCMC) simulation is conducted.

A thorough description of the MCS algorithm for complete sample scenarios is provided in this section.

5.1. Performance Evaluation Metrics

To assess the quality of the estimators in this study, two widely used metrics are employed, namely Relative Bias (RB) and Mean Squared Error (MSE).

5.1.1. RB

RB quantifies the systematic deviation of the estimator from the true parameter value. It is computed as

$$RB={\displaystyle \frac{1}{R}}\sum _{i=1}^R\left({\displaystyle \frac{{\widehat{\theta }}_i-\theta }{\theta }}\right)$$

where ${\widehat{\theta }}_i$ is the estimate from the $i^{rh}$ replication, $\theta$ is the true parameter, and $R$ is the total number of replications. A lower RB value indicates lower bias.

5.1.2. MSE

MSE reflects both the variance and bias of the estimator. It is calculated as

$$MSE={\displaystyle \frac{1}{R}}\sum _{i=1}^R{\left({\widehat{\theta }}_i-\theta \right)}^2$$

Lower MSE values signify higher estimation accuracy. In this study, MSE captures the combined effect of estimator variability and its deviation from the true parameter values.

5.2. PWD Simulation

The Monte Carlo Simulation (MCS) technique is used to evaluate the performance of both MLE and Bayesian estimation methods under the PWD using complete data.

Following the steps of the algorithm below, we perform the simulation study for the PWD.

Step 1: Assume various values for PWD parameters

$$\left(\alpha ,b,\lambda \right)=\left(\mathrm{2,2},1\right), \left(\mathrm{2,2},1.5\right), \left(\mathrm{2,2},3\right), \left(\mathrm{2,3},1\right), \left(\mathrm{2,3},1.5\right), \left(\mathrm{2,3},3\right), \left(\mathrm{3,2},1\right), \left(\mathrm{3,2},1.5\right), (\mathrm{3,2},3).$$

Step 2: Choose sample size n = 25, 75 and 150.

Step 3: Create a random sample using the PWD quantile function.

Step 4: Use L-BFGS-B to obtain estimates for MLE parameters and draw posterior samples for Bayesian estimation using MCMC.

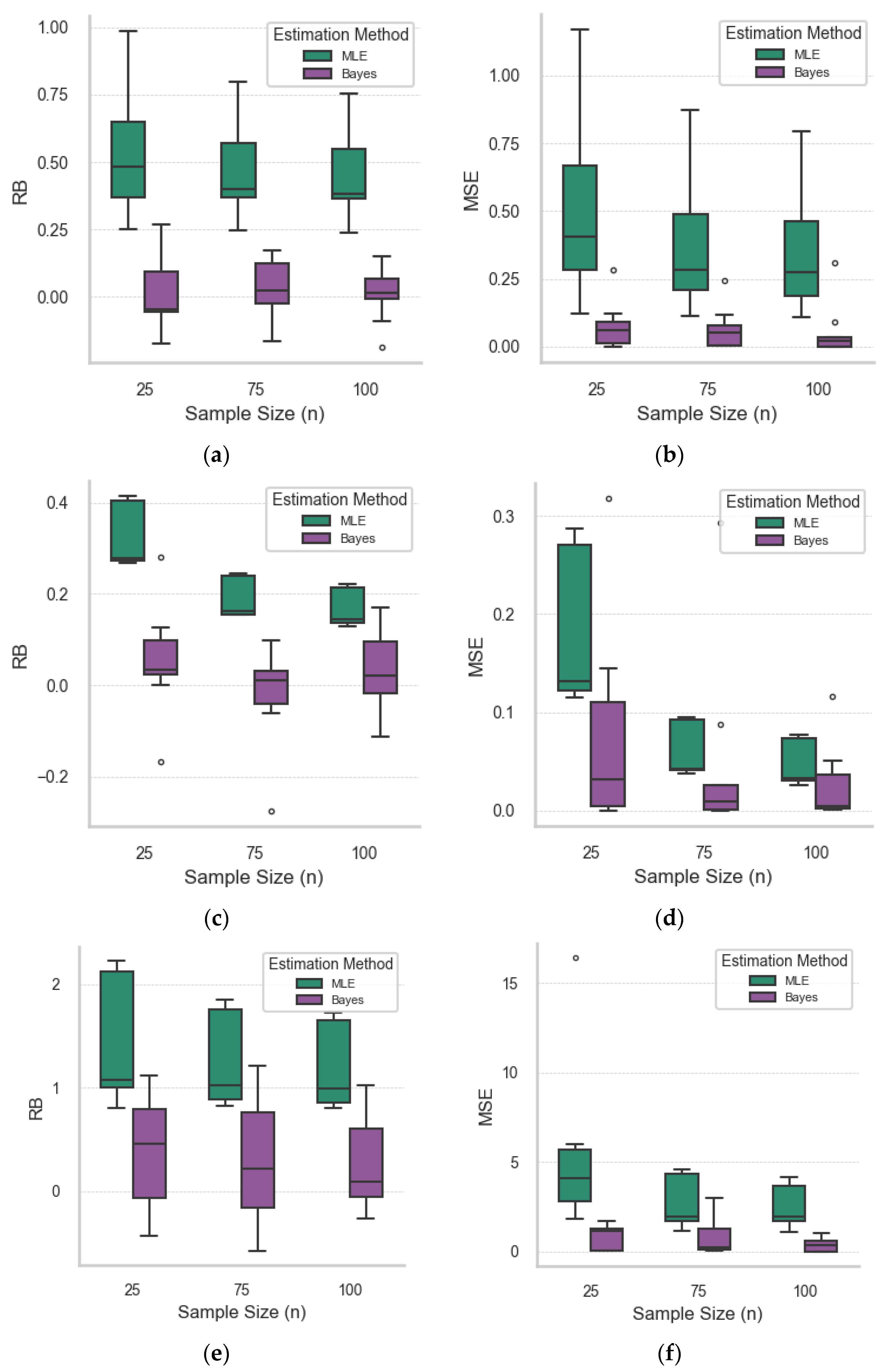
Figure 3 provides a visual comparison of RB and MSE across varying sampling sizes for each parameter presented in

Table 5. RB and MSE for MLE and Bayesian estimates of PWD when $\alpha =2, b=2$, and $\lambda =1, 1.5, 3$.

Parameters			$\mathit{n}$		MLE		Bayes
$\mathit{\alpha }$	$\mathit{b}$	$\mathit{\lambda }$			RB	MSE	RB	MSE
2	2	1	25	$\alpha$	0.3710	0.2848	0.1210	0.0586
				$b$	0.2723	0.1243	0.0987	0.0390
				$\lambda$	0.8098	1.8512	1.1244	1.2642
			75	$\alpha$	0.3707	0.2782	0.1225	0.0600
				$b$	0.1634	0.0422	0.0799	0.0255
				$\lambda$	0.8770	1.7053	0.8538	0.7291
			100	$\alpha$	0.3629	0.2719	0.0890	0.0316
				$b$	0.1482	0.0341	−0.112	0.0503
				$\lambda$	0.8604	1.6868	0.6013	0.3615
		1.5	25	$\alpha$	0.4357	0.4052	−0.048	0.0095
				$b$	0.2692	0.1203	0.0340	0.0046
				$\lambda$	1.0111	2.9694	0.7399	1.2318
			75	$\alpha$	0.3989	0.2837	0.1147	0.0526
				$b$	0.1608	0.0409	0.0080	0.0002
				$\lambda$	1.0273	1.9701	0.2476	0.2380
			100	$\alpha$	0.3843	0.2763	0.0687	0.0189
				$b$	0.1442	0.0326	0.0216	0.0018
				$\lambda$	0.9917	1.9451	0.6651	0.9953
		3	25	$\alpha$	0.6598	0.5385	−0.173	0.1204
				$b$	0.2785	0.1319	0.0269	0.0029
				$\lambda$	2.1204	5.5484	0.0699	0.0440
			75	$\alpha$	0.5726	0.4314	−0.026	0.0028
				$b$	0.1539	0.0373	0.0137	0.0007
				$\lambda$	1.8563	4.5700	−0.154	0.215
			100	$\alpha$	0.5269	0.3799	−0.090	0.0331
				$b$	0.1392	0.0302	0.0231	0.0021
				$\lambda$	1.7283	4.1329	0.0238	0.0051

,

Table 6. RB and MSE for MLE and Bayesian estimates of PWD when $\alpha =2, b=3$, and $\lambda =1, 1.5, 3$.

Parameters			$\mathit{n}$		MLE		Bayes
$\mathit{\alpha }$	$\mathit{b}$	$\mathit{\lambda }$			RB	MSE	RB	MSE
2	3	1	25	$\alpha$	0.2517	0.1193	0.2668	0.2849
				$b$	0.4084	0.2795	0.1266	0.1444
				$\lambda$	0.8715	16.4181	1.0615	1.1268
			75	$\alpha$	0.2457	0.1121	0.1705	0.1162
				$b$	0.2452	0.0949	0.0317	0.009
				$\lambda$	0.8883	1.8388	1.2178	1.4831
			100	$\alpha$	0.2394	0.1097	0.1523	0.0928
				$b$	0.2223	0.0766	−0.021	0.0041
				$\lambda$	0.8709	1.8268	1.0254	1.0514
		1.5	25	$\alpha$	0.2990	0.1473	−0.012	0.0006
				$b$	0.4039	0.2707	0.024	0.0052
				$\lambda$	1.0063	2.8327	0.7963	1.4267
			75	$\alpha$	0.2677	0.1178	0.1393	0.0776
				$b$	0.2413	0.0920	0.0099	0.0008
				$\lambda$	1.0249	1.9426	0.7605	1.3016
			100	$\alpha$	0.2564	0.1126	0.0534	0.0114
				$b$	0.2165	0.0733	0.0079	0.0005
				$\lambda$	0.9910	1.9347	0.5131	0.5925
		3	25	$\alpha$	0.4832	0.2900	−0.051	0.0106
				$b$	0.4133	0.2869	0.0005	2.2 × 10−6
				$\lambda$	2.1271	5.7022	−0.059	0.0323
			75	$\alpha$	0.3956	0.2105	0.0191	0.0014
				$b$	0.2399	0.0918	0.0988	0.0879
				$\lambda$	1.8286	4.4989	−0.117	0.1252
			100	$\alpha$	0.3674	0.1871	0.0165	0.001
				$b$	0.2142	0.0728	−0.017	0.0026
				$\lambda$	1.7191	4.0768	−0.171	0.2636

and

Table 7. R RB and MSE for MLE and Bayesian estimates of PWD when $\alpha =3, b=2$, and $\lambda =1, 1.5, 3$.

Parameters			$\mathit{n}$		MLE		Bayes
$\mathit{\alpha }$	$\mathit{b}$	$\mathit{\lambda }$			RB	MSE	RB	MSE
3	2	1	25	$\alpha$	0.5987	0.8333	0.0937	0.0791
				$b$	0.2935	0.1386	0.2818	0.3177
				$\lambda$	1.0736	4.0872	0.4637	0.215
			75	$\alpha$	0.5002	0.5345	0.0216	0.0042
				$b$	0.1628	0.0446	−0.061	0.0151
				$\lambda$	0.8264	1.4279	0.2154	0.0464
			100	$\alpha$	0.5745	0.6341	−0.007	0.0004
				$b$	0.1295	0.0302	0.0952	0.0363
				$\lambda$	0.8037	1.5823	0.0956	0.0091
		1.5	25	$\alpha$	0.6487	0.6694	−0.055	0.0275
				$b$	0.2684	0.1149	−0.166	0.1103
				$\lambda$	1.1441	2.6365	−0.113	0.0288
			75	$\alpha$	0.5894	0.4890	−0.056	0.0287
				$b$	0.1550	0.0403	−0.040	0.0065
				$\lambda$	0.9288	1.1790	−0.155	0.0542
			100	$\alpha$	0.5494	0.4623	−0.004	0.0001
				$b$	0.1368	0.0287	0.0958	0.0367
				$\lambda$	0.8539	1.0782	−0.053	0.0065
		3	25	$\alpha$	0.9846	1.1684	−0.101	0.0927
				$b$	0.2736	0.1225	0.0888	0.0316
				$\lambda$	2.2253	6.0045	−0.433	1.688
			75	$\alpha$	0.7961	0.8730	−0.164	0.2442
				$b$	0.1554	0.0415	−0.274	0.2926
				$\lambda$	1.7564	4.3284	−0.574	2.971
			100	$\alpha$	0.7525	0.7928	−0.185	0.3081
				$b$	0.1310	0.0264	0.1707	0.1166
				$\lambda$	1.6484	3.6874	−0.264	0.6280

. MLE estimators display a consistent and expected reduction in MSE with increasing n, affirming their asymptotic properties. In contrast, Bayesian estimation demonstrates superior performance in small samples, particularly for parameters α and b. This is because the Bayesian approach incorporates prior information, which helps stabilize estimates when data is scarce, a phenomenon often referred to as regularization.

However, for the Poisson rate parameter λ, Bayesian estimation shows fluctuating MSE across sample sizes. This instability arises because λ governs latent event counts that are not directly observed in the data. In small samples, the prior exerts a strong influence, sometimes improving the estimation by preventing overfitting. But as the sample size increases, the likelihood starts to dominate, and the estimate of λ becomes more reliant on data which may still offer limited or noisy information, particularly when λ interacts with the shape parameter b. This leads to posterior distributions that are skewed, multimodal, or unstable, especially when λ is large, which can manifest as MSE fluctuations.

Overall, while Bayesian methods benefit from their built-in prior structure in small-sample contexts, particularly for α and b, they struggle with stability for λ even as the sample size grows. MLE, in contrast, becomes more consistent with increasing n, especially for λ, as it relies entirely on the data.

5.3. Simulation for Stress–Strength Parameters

Following the steps of the algorithm below, we perform the simulation study for the stress–strength parameters of the PWD.

• Step 1: Assume various values for PWD parameters.
• Case 1: ${\alpha }_1=2,b_1=2,{\lambda }_1=1,{\alpha }_2=3,b_2=2,{\lambda }_2=1.5,$
• Case 2: ${\alpha }_1=2,b_1=3,{\lambda }_1=1,{\alpha }_2=3,b_2=3,{\lambda }_2=1.5,$
• Case 3: ${\alpha }_1=0.7,b_1=2.5,{\lambda }_1=4,{\alpha }_2=4,b_2=1.5,{\lambda }_2=2$.
• Step 2: Choose sample sizes n = 25, 75, and 150, while for m = 30, 80, and 120.
• Step 3: Create random samples for both $x_i$ and $y_j$ using the PWD quantile function.
• Step 4: Use L-BFGS-B to obtain estimates for MLE parameters and MCMC sampling to get Bayesian estimates.

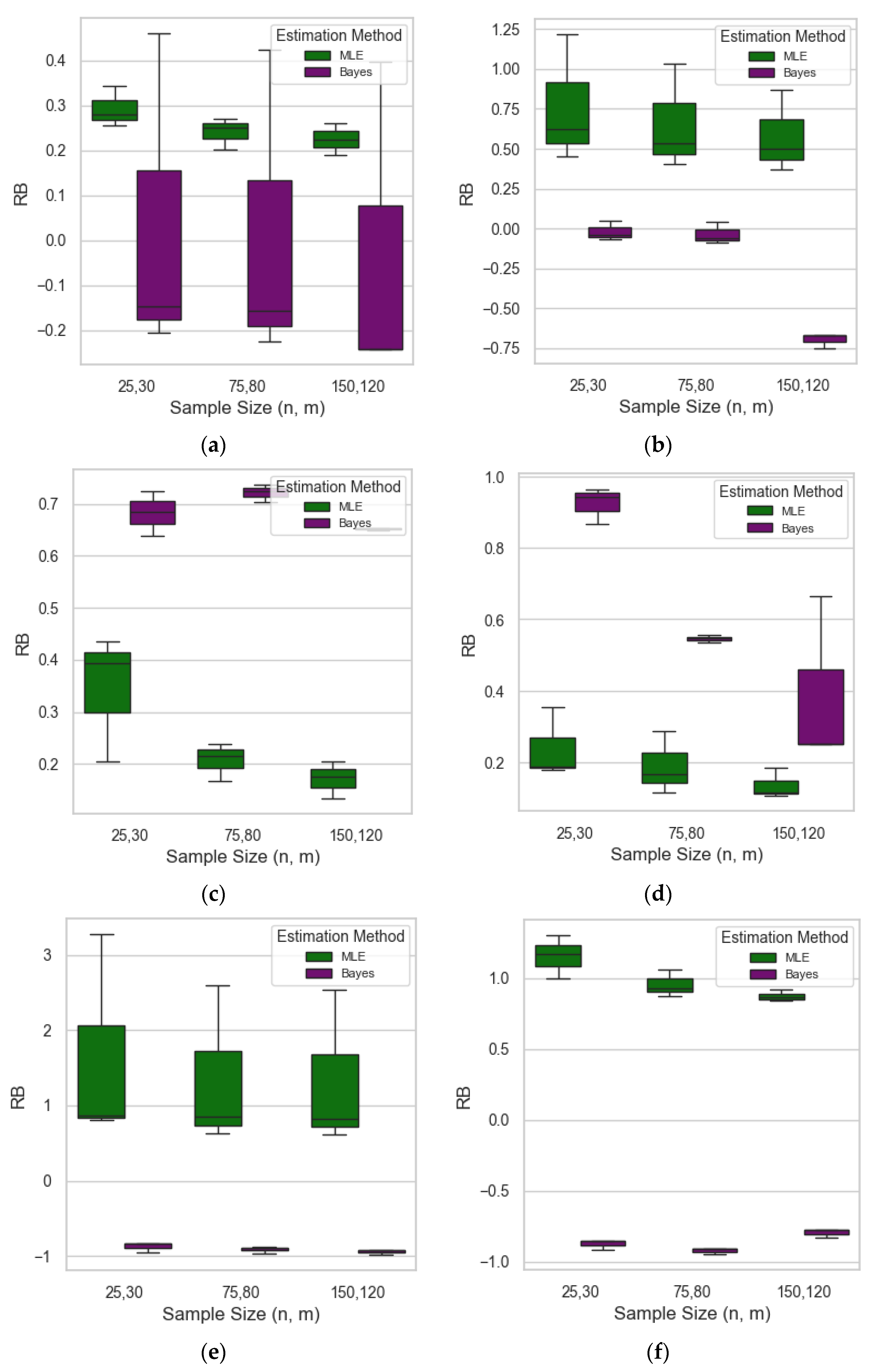
The results from

Table 8. RB and MSE for MLE and Bayesian estimates of SS for Case 1.

			MLE		Bayesian
Case	n, m	Parameters	RB	MSE	RB	MSE
1	25, 30	${\alpha }_1$	0.3432	0.1749	−0.2054	0.1689
		$b_1$	0.2045	0.0625	0.7250	2.1029
		${\lambda }_1$	0.8008	0.8803	−0.8328	0.6935
		${\alpha }_2$	0.6202	0.6356	−0.0648	0.0378
		$b_2$	0.1872	0.0598	0.9635	3.713
		${\lambda }_2$	1.167	2.2309	−0.8554	1.6464
	75, 80	${\alpha }_1$	0.2713	0.1082	−0.2244	0.2014
		$b_1$	0.1681	0.0419	0.7362	2.1681
		${\lambda }_1$	0.6292	0.6299	−0.8836	0.7808
		${\alpha }_2$	0.534	0.4136	−0.0856	0.0659
		$b_2$	0.168	0.045	0.5569	1.2409
		${\lambda }_2$	0.8716	1.1658	−0.9097	1.8622
	150, 120	${\alpha }_1$	0.26	0.0975	−0.2420	0.2344
		$b_1$	0.1341	0.0302	0.6534	1.7077
		${\lambda }_1$	0.6133	0.5893	−0.9192	0.8450
		${\alpha }_2$	0.4985	0.3221	−0.6659	3.9912
		$b_2$	0.1163	0.0215	0.2511	0.2523
		${\lambda }_2$	0.8618	0.9085	−0.7781	1.3623

,

Table 9. RB and MSE for MLE and Bayesian estimates of SS for Case 2.

			MLE		Bayesian
Case	n, m	Parameters	RB	MSE	RB	MSE
2	25, 30	${\alpha }_1$	0.2804	0.1798	−0.1464	0.0857
		$b_1$	0.4347	0.3001	0.6381	3.6651
		${\lambda }_1$	0.8707	2.6426	−0.8388	0.7037
		${\alpha }_2$	0.4514	0.3099	−0.0427	0.0164
		$b_2$	0.3541	0.2229	0.8647	6.7308
		${\lambda }_2$	0.9954	1.6244	−0.8534	1.6590
	75, 80	${\alpha }_1$	0.2506	0.1209	−0.1575	0.0992
		$b_1$	0.2392	0.08	0.7043	4.4643
		${\lambda }_1$	0.8455	1.6911	−0.8871	0.7869
		${\alpha }_2$	0.4018	0.2697	−0.0574	0.0296
		$b_2$	0.2867	0.1234	0.5349	2.5757
		${\lambda }_2$	0.9281	1.6082	−0.9084	1.8569
	150, 120	${\alpha }_1$	0.2245	0.0797	−0.2420	0.2344
		$b_1$	0.2047	0.065	0.6534	1.7077
		${\lambda }_1$	0.8161	1.2049	−0.9192	0.8450
		${\alpha }_2$	0.372	0.2004	−0.6659	3.9912
		$b_2$	0.1839	0.0572	0.2511	0.2523
		${\lambda }_2$	0.8415	1.0525	−0.7781	1.3623

and

Table 10. RB and MSE for MLE and Bayesian estimates of SS for Case 3.

			MLE		Bayesian
Case	n, m	Parameters	RB	MSE	RB	MSE
3	25, 30	${\alpha }_1$	0.2562	0.0713	0.4596	0.1035
		$b_1$	0.3927	0.2434	0.6850	2.9333
		${\lambda }_1$	3.2694	11.2682	−0.9557	14.6146
		${\alpha }_2$	1.2159	1.8799	0.0521	0.0435
		$b_2$	0.1796	0.0448	0.9408	1.9916
		${\lambda }_2$	1.299	2.0815	−0.9185	3.3752
	75, 80	${\alpha }_1$	0.2021	0.0493	0.4237	0.0879
		$b_1$	0.2157	0.0786	0.7236	3.2729
		${\lambda }_1$	2.5916	8.0887	−0.9701	15.0582
		${\alpha }_2$	1.0368	1.512	0.0441	0.0311
		$b_2$	0.1153	0.022	0.5451	0.6685
		${\lambda }_2$	1.0591	1.6022	−0.9468	3.5860
	150, 120	${\alpha }_1$	0.1903	0.046	0.3961	0.0769
		$b_1$	0.175	0.0436	0.6483	2.6271
		${\lambda }_1$	2.5322	7.8405	−0.9793	15.3457
		${\alpha }_2$	0.8672	1.0781	−0.7503	9.0079
		$b_2$	0.1064	0.0815	0.6651	0.9955
		${\lambda }_2$	0.9153	1.2134	−0.8336	2.7797

and the corresponding boxplots in Figure 4 provide insights into the performance of MLE and Bayesian estimators for SS parameters of the PWD.

In general, both MLE and Bayesian estimators show decreasing RB values as samples sizes increase, confirming the asymptotic unbiasedness of both methods. However, the Bayesian RB exhibits more variability, particularly in small samples and for parameters such as ${\lambda }_1$ and ${\lambda }_2$. This reflects the impact of the prior information, which dominates in small samples, sometimes resulting in shrinkage or overcorrection. Parameters ${\lambda }_1$ and ${\lambda }_2$ consistently show high bias, particularly in Case 3. This is consistent with known limitations of PWD where likelihood surfaces for these parameters can be flat and poorly behaved. The plots in Figure 4e,f show that the Bayesian posterior for ${\lambda }_1$ and ${\lambda }_2$ sometimes concentrate below zero, violating the theoretical support of the distribution. This may reflect multimodality or numerical instability in posterior sampling.

MSE generally decreases for larger sample sizes, as expected. For most parameters, Bayesian estimators outperform MLE in smaller samples due to the regularizing effect of the prior, especially for parameters ${\alpha }_1,{\alpha }_2,$ and $b_1$. However, Bayesian MSE remains volatile for $\lambda$-parameters, especially in Case 3. This suggests poor identifiability and posterior instability for those parameters under certain configurations of the stress–strength model. In a few cases (e.g., $b_1,b_2$) the Bayesian MSE starts higher but improves rapidly as sample size increases, becoming competitive or even better than MLE in medium-to-large samples.

Case 3, with more extreme parameter values, shows the largest bias and MSE for both estimation methods. This highlights the limitations of the PWD in modeling stress–strength when the scale or shape parameters differ drastically between the stress and strength components. Cases 1 and 2, with moderate configurations, show more stable behavior, especially for MLE. Bayesian estimation still shows fluctuation in some parameters, suggesting sensitivity to prior assumptions or posterior geometry.

6. Real-Life Applications

This section presents a real-life application of the proposed models in an industrial context, divided into two subsections. The first subsection describes the modeling of the Poisson–Weibull Distribution (PWD), while the second subsection demonstrates the modeling of the SS model. The PWD is applied to precipitation data (measured in inches) for Minneapolis/St. Paul, while the SS model is applied to failure times for two types of electrical insulation subjected to continuous voltage.

6.1. Modeling of the PWD

Data Description: To demonstrate the modeling capabilities of the Poisson–Weibull Distribution (PWD), the distribution is fitted to real-life application-based data in the industrial context. The data set consists of 30 observations of March precipitation (in inches) recorded in Minneapolis/St. Paul. The observed values are as follows: 0.77, 1.74, 0.81, 1.20, 1.95, 1.20, 0.47, 1.43, 3.37, 2.20, 3.00, 3.09, 1.51, 2.10, 0.52, 1.62, 1.31, 0.32, 0.59, 0.81, 2.81, 1.87, 1.18, 1.35, 4.75, 2.48, 0.96, 1.89, 0.90, and 2.05.

6.1.1. MLE Results

The fitted models are compared using several criteria: the Akaike Information Criterion (AIC), the Hannan–Quinn Information Criterion (HQIC), the Kolmogorov–Smirnov distance (KS), and the p-values of the KS statistic.

The Poisson–Weibull Distribution (PWD) is compared with the following distributions: Power Rayleigh (PoR) [13], Marshal-Olkin Kumaraswamy moment exponential (MOKWME) [14], Marshall–Olkin Alpha Power Rayleigh (MOAPR) [15] Extended Odd Weibull Rayleigh (EOWR) [16] and Gompertz Lomax (GL) [17].

Figure 5 shows the relative histogram with the fitted PWD, along with the fitted cumulative distribution function (CDF) compared to the empirical CDF, as well as the P-P plots of the data set. The graphical goodness-of-fit results in these figures support the results summarized in

Table 11. PWD performance comparison with other distributions.

Models	Estimated Parameters						Test Statistic
		λ	B	α	δ	$\mathit{\theta }$	KS	p-Value	AIC	BIC	HQIC
PWD	Estimates	1.5687	2.0892	2.7079	-----	-----	0.052	0.9999	82.5356	86.7392	83.8804
	SE	2.5385	0.3044	1.2539	-----	-----
PoR	Estimates	0.9044	1.7804	------	------	-----	0.0689	0.9988	122.8754	125.6778	123.7719
	SE	0.1246	0.2557	------	------	-----
MOKWME	Estimates	0.3154	2.0811	------	0.4209	1.4901	0.0744	0.9963	84.0541	89.6589	85.8471
	SE	0.4032	1.6355	------	0.6408	1.3657
EOWR	Estimates	1.4018	3.8097	------	0.5644	-----	0.0721	0.9977	102.5666	106.7701	103.9113
	SE	0.8265	6.1518	------	0.6101	-----
GL	Estimates	4.9941	0.5928	-------	0.5456	0.6572	0.930	0.9576	88.3289	93.9337	90.1219
	SE	5.5811	0.6892	-------	0.5533	0.9295
MOAPR	Estimates	13.1738	0.0968	-------	1.8334	-----	0.0613	0.9999	82.6000	86.8036	83.9448
	SE	56.3147	0.3535	------	0.8998	-----

. Figure 6 shows the likelihood contour plots, confirming that the estimated parameters are in the region of highest likelihood.

Based on the goodness-of-fit test results, the PWD performs exceptionally well as it has the lowest KS statistic (0.052), indicating the best fit among the other well-known distributions. The AIC, BIC, and HQIC values are competitive, with only PR distribution having slightly better AIC and HQIC values.

Therefore, the PWD stands out as having a better fit to the data, making it a robust choice compared to other distributions such as Power Rayleigh (PoR), Marshall–Olkin Kumaraswamy moment exponential (MOKWME), Extended Odd Weibull Rayleigh (EOWR), Gompertz Lomax (GL), and Marshall–Olkin Alpha Power Rayleigh (MOAPR). Its superior performance in terms of the KS statistics and p-value highlights its effectiveness in modeling the given data set.

6.1.2. Bayesian Results

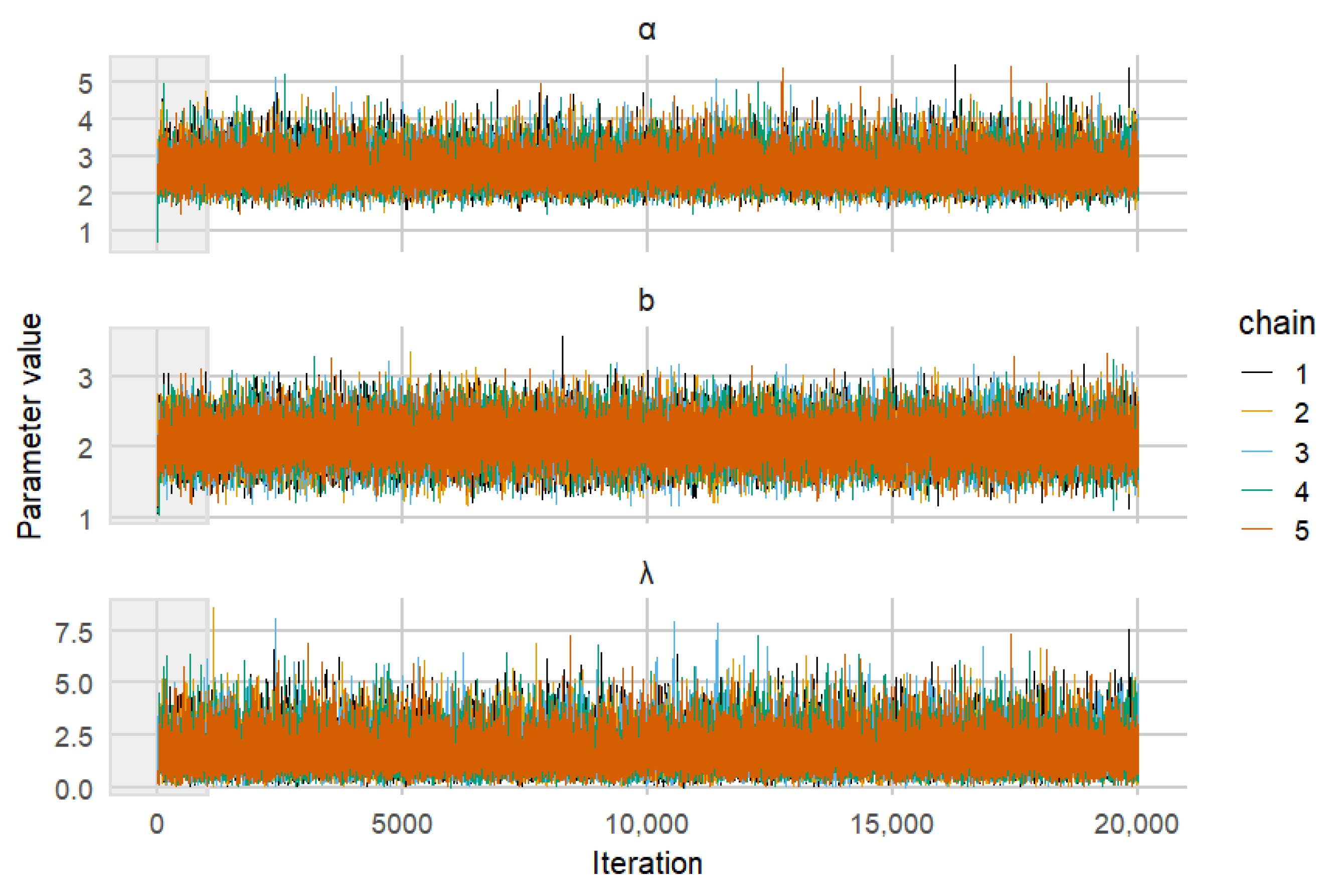
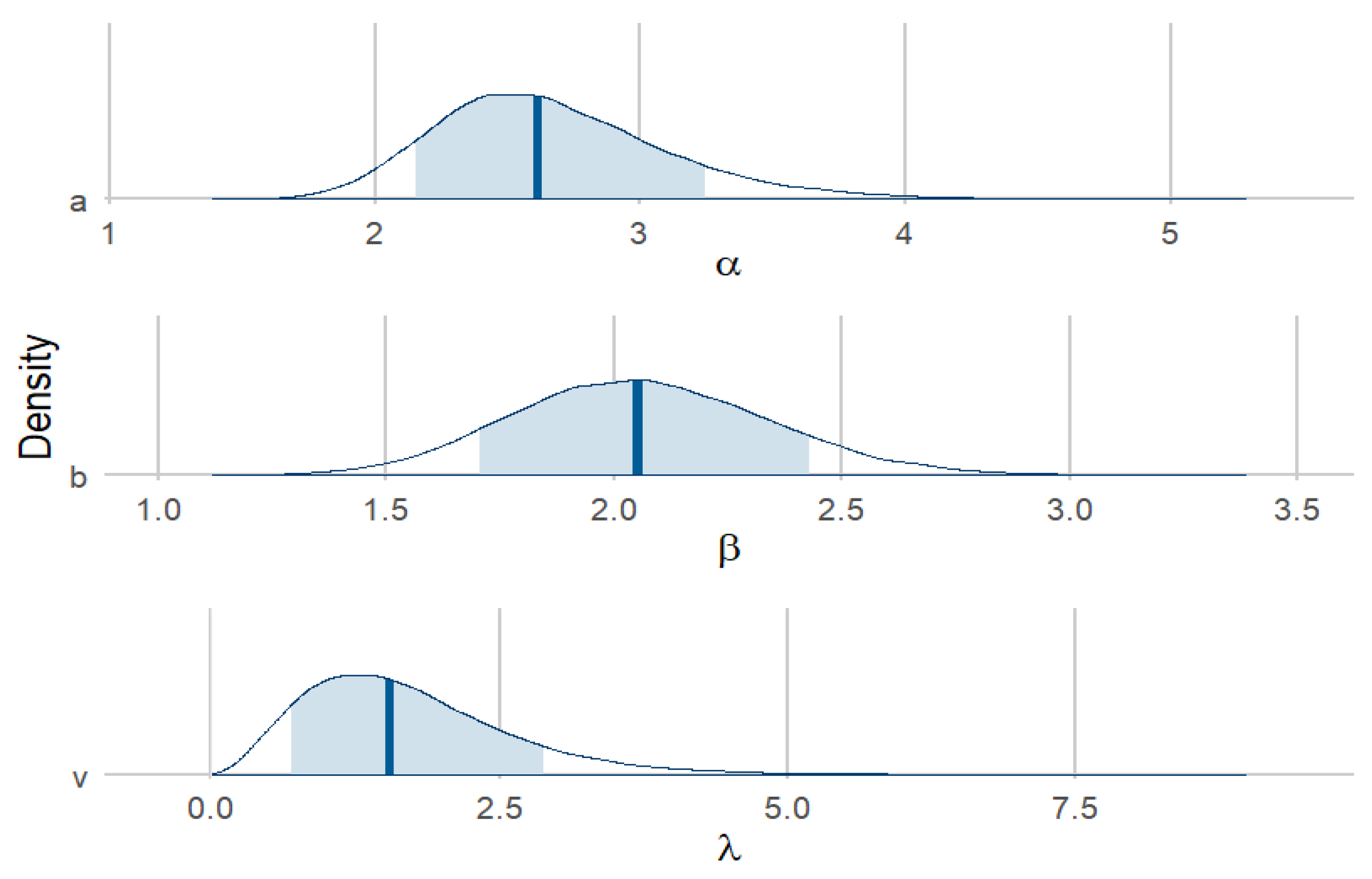
To monitor the convergence of the MCMC results, trace plots of the posterior distributions of the parameter values have been generated, as shown in Figure 7. Trace plots are a crucial diagnostic tool in MCMC analysis, providing visual representation of the sampled values across iterations. By examining these plots, the convergence performance across chains can be evaluated. In Figure 7, each line represents a different parameter chain over the course of the simulations.

The trace plots indicate there is no major divergence among any of the chains, suggesting that the MCMC algorithm has reached a stable state and is sampling from the target posterior distribution effectively. Consistent and overlapping traces across different chains is an indication of good mixing and convergence.

In addition to the trace plots, Figure 8 shows the histograms of the parameter estimates for the marginal posterior densities, based on values from five chains. These histograms allow the examination of the distribution of parameter estimates and assess their symmetry and consistency with the theoretical posterior density functions. The histograms in Figure 8 show that the posterior distributions are symmetric, further validating the reliability of the MCMC results.

Overall, the trace plots and histograms together provide robust evidence that MCMC chains have converged and that the posterior distributions have been accurately estimated.

Table 12. MLE and Bayesian estimation results for the observed precipitation in Minneapolis/St. Paul, measured in inches.

	MLE		Bayesian
	Estimates	SE	Bayes	SE
α	2.70	1.25	2.67	0.43
B	2.08	0.30	2.06	0.28
Λ	1.56	2.53	1.69	0.88

presents the point estimates and the standard errors of PWD for MLE and Bayesian estimation. From these results, we can conclude that the Bayesian method has performed better.

6.2. Modeling of SS

This section discusses the SS reliability measures applied to a real lifetime data set in an industrial application, and the parameters are estimated based on MLE and Bayesian estimation.

To demonstrate the performance of the SS model, we use the following real-world data set. The following are the failure times for two different kinds of electrical insulation under a continuous voltage in an experiment (measured in seconds). Thirty pieces of each type were tested.

Type 1: 0.097, 0.014, 0.03, 0.134, 0.240, 0.084, 0.146, 0.024, 0.045, 0.004, 0.099, 0.277, 0.472, 0.094, 0.023, 0.146, 0.030, 0.031, 0.104, 0.105, 0.036, 0.065, 0.022, 0.098, 0.178, 0.059, 0.014, 0.007, 0.007, 0.286.

Type 2: 0.084, 0.236, 0.315, 0.199, 0.252, 0.103, 0.455, 0.135, 0.348, 0.321, 0.166, 0.04, 0.027, 0.519, 0.017, 0.821, 0.942, 0.27, 0.008, 0.03, 0.177, 0.268, 0.18, 0.796, 0.245, 0.703, 0.045, 0.314, 0.281, 0.652.

6.2.1. Results Based on MLE

The contour plots shown in Figure 9 demonstrate that there is a unique solution for all parameters ${\alpha }_1, b_1,{\lambda }_1, {\alpha }_2, b_2,$ and ${\lambda }_2$. These plots indicate that all parameter estimates, except ${\lambda }_1$ and ${\lambda }_2$, lie within the region of maximum likelihood.

The plots reveal a limitation of the SS model under the PWD for the parameters ${\lambda }_1$ and ${\lambda }_2$. If the value with the highest likelihood for ${\lambda }_1$ and ${\lambda }_2$ falls below 0, then the value cannot be estimated because all parameters of the PWD are required to be non-negative. This limitation underscores the challenges in estimating these parameters accurately within the constraints of the PWD framework.

6.2.2. Results Based on Bayesian Estimation

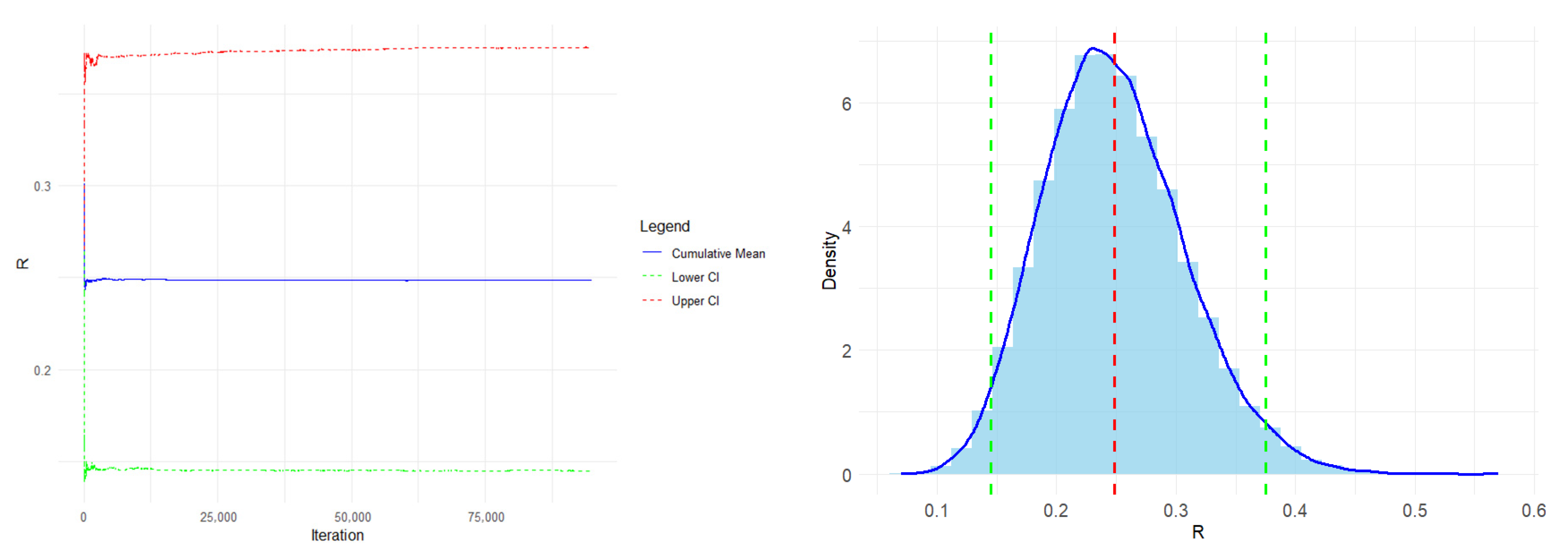
To assess the convergence and robustness at the start of the Bayesian parameter estimates and derived reliability measure, we present MCMC trace plots (Figure 10) and cumulative mean and posterior density diagnostics (Figure 11). The parameters are labeled as for ${\alpha }_1, b_1,{\lambda }_1, {\alpha }_2, b_2,$ and ${\lambda }_2$, respectively.

Each plot shows the sampled values of a parameter over 20,000 iterations for five different chains. All chains mix well, i.e., they overlap significantly and explore the parameter space without a single chain getting stuck in a particular region, and the lack of drifts in the chains suggests that MCMC algorithm has reached convergence.

It is also noted that the chains are stable, with fluctuations around a consistent mean value for each parameter which indicates that the parameter estimates are not subject to significant autocorrelation. Chains for ${\lambda }_1$ and ${\lambda }_2$ show higher variability than the chains of other parameters; however, the chains do not exhibit any drift, confirming convergence despite variability.

Figure 11(left) shows the cumulative mean, the lower confidence interval, and the upper confidence interval of the stress–strength reliability measure across iterations. The cumulative mean stabilizes around 0.25 after a few thousand iterations, indicating convergence. The upper and lower confidence intervals also stabilize, indicating consistent bounds.

Figure 11(right) shows the posterior distribution of $R$ with a density plot. The vertical dashed lines represent the lower and upper confidence intervals, while the red line indicates the mean. The distribution is approximately symmetric and bell-shaped, centered around 0.25, with most values between 0.1 and 0.4. This supports the robustness and reliability of the parameter estimates obtained through the MCMC method.

In

Table 13. Comparison of MLE and Bayesian estimates for observed failure times for two different kinds of electrical insulation.

	MLE				Bayesian
	Estimates	SE	Lower	Upper	Estimates	SE	Lower	Upper
${\alpha }_1$	0.14	0.10	−0.06	0.35	0.19	0.06	0.11	0.35
$b_1$	1.09	0.20	0.70	1.49	1.13	0.10	1.00	1.37
${\lambda }_1$	0.80	1.78	−2.69	4.30	0.64	0.49	0.02	1.83
${\alpha }_2$	0.31	0.20	−0.09	0.72	0.59	0.20	0.33	1.07
$b_2$	1.11	0.32	0.47	1.74	1.21	0.14	1.011	1.53
${\lambda }_2$	0.01	1.25	−2.45	2.47	0.89	0.68	0.04	2.54
R	0.220		0.105	0.335	0.248		0.145	0.373

, it is seen that the Bayesian estimates have lower standard errors and thus are better at predicting the true values for the parameters.

7. Conclusions

In this article, a new lifetime probability density function called the Poisson–Weibull Distribution (PWD) using Marshall–Olkin [12] technique is developed. The Weibull distribution models the lifetime of the main system, while the Poisson distribution accounts for sudden external shocks or drifts that may cause failure. Several properties of the PWD have been developed. Density plots and the HRF plot show that PWD is flexible to model a variety of data sets suitable for non-monotone HRF.

Extending this study, PWD is used to develop a stress–strength (SS) reliability model. When the distributions represent the lifetimes of the objects under study, the area where these two distributions interfere provides insight into which object is more reliable. The study employs both Bayesian and non-Bayesian methods to estimate the parameters of the PWD and the SS model when fitted to real-world data. MCS and MCMC technique is used to estimate the parameters by using the Bayesian estimation for both models PWD and SS. Real-world applications demonstrated the practical relevance of the proposed models.

Despite the strengths of the PWD and SS models, certain limitations should be acknowledged. The estimation of the parameter $\lambda$ showed consistent bias in simulations, especially under small sample sizes, suggesting the need for improved estimation techniques or informative priors.

Future work may focus on exploring alternative prior structures to reduce estimation bias in Bayesian inference, incorporating censoring schemes to better model estimation of truncated data, and evaluating model under misspecification to test robustness.