Edge Fault-Tolerant Strong Menger Edge Connectivity of Folded Crossed Cubes

Abstract

A graph is called strongly Menger-edge connected (SME-connected) if any two vertices are connected by as many edge-disjoint paths as their smaller degree. For positive integers t and r, a graph G is called t-edge-fault-tolerant SME-connected (t-EFT-SME-connected) of order r if $G-F$ is SME-connected for any set F of edges in G with $\left|F\right|\le t$ and $\delta (G-F)\ge r$. We show that the n-dimensional folded crossed cube is $(n-1)$-EFT-SME-connected of order 1 and $(3n-5)$-EFT-SME-connected of order 2. Let $p(G,f)$ and $p^M(G,f)$ be the probabilities that G is connected and SME-connected when f edges are faulted randomly, respectively. We perform a numerical simulation on $p(G,f)$ and $p^M(G,f)$ for a five-dimensional folded crossed cube and folded hypercube. The numerical results show that, in addition to their same edge connectivity and SME connectivity, these two graphs have almost the same values of $p(G,f)$ and $p^M(G,f)$ for every f. This hints that, although the ‘edge-cross’ pattern in a hypercube-based graph can shorten the mean vertex distance, the ‘edge-cross’ is not a necessary pattern for strengthening the connectivity of the graph.

1. Introduction

The failure of nodes/processors or links is generally inevitable in large-scale networks and computing systems. Therefore, evaluating the reliability of large-scale networks or systems has become an essential issue. To evaluate the reliability, a number of fault tolerance models have been introduced, among which the notion of connectivity plays an important role.

The topology of a network is typically represented by a graph, in which vertices are used to depict nodes (or processors), and edges depict communication links. In graph theory, many types of connectivity were introduced from both theoretical and practical sides. The edge connectivity is one of the classical connectivities, which has been applied as a key measure on the reliability of a network. The edge connectivity is defined as the maximum number of faulty edges (deleted edges) that guarantees the connection of the graph. Precisely, the edge connectivity $\lambda \left(G\right)$ of a graph G is the largest k such that the removal of any s edges from the graph with $s<k$ does not disconnect the graph. This means that higher edge connectivity may guarantee higher reliability of a network in the sense of link failures.

We note that, by the definition, $\lambda \left(G\right)$ is not greater than the minimum degree of G since the removal of all the edges incident with a vertex of minimum degree will disconnect the graph. In this sense, the edge connectivity $\lambda \left(G\right)$ does not really satisfactorily reflect the connectivity between the vertices with larger degrees. On the other hand, by the celebrated Menger’s Max-Flow Min-Cut Theorem, a graph G that is k-edge-connected is equivalent to that G having at least k edge-disjoint paths between any two vertices of G. This provides us a nice way to consider the connectivity of a graph G in terms of edge-disjoint paths. From practical point of view, in a network with a larger number of edge-disjoint paths between any two vertices, more efficient routing can be achieved using vertex-disjoint paths, providing parallel routing and high fault tolerance, increasing the efficiency of data transmission, and decreasing transmission time [1]. In fact, various types of such connectivity were introduced to meet practical requirements; see [2,3,4,5]. Particularly, a connected graph is called strongly Menger edge-connected (SME-connected) [2,4] if any two vertices are connected by as many paths as their smaller degree. In this sense, an SME-connected network exhibits relatively well-balanced connectivity in the sense of vertex degrees, which not only guarantee the traditional edge connectivity but also as many edge-disjoint paths as possible between any two vertices. To see this, let us consider an instance. Let $G_1$ and $G_2$ be two graphs, as illustrated in Figure 1. We can see that $G_1$ and $G_2$ are both 2-edge-connected. Further, $G_1$ is SME-connected while $G_2$ is not because there are no three edge-disjoint paths connecting u and v in $G_2$.

Theoretically, the traditional edge connectivity and SME connectivity ensure the maximum number of edges whose removal guarantees the connection between two vertices. However, in practical applications, even if more edges are faulted, a graph may still remain connected or SME-connected. Therefore, in the sense of edge fault tolerance, is it then natural to quantify the effect of edge faults (edge removal) or, in the sense of a probability model, to consider the probability that a graph is still connected or SME-connected when a given number of edges are faulted? To this end, for a graph G, we denote by $p(G,f)$ and $p^M(G,f)$ the probabilities that G is edge-connected and SME-connected when f edges are faulted (removed) randomly, respectively.

Further, when edge faults occur at random under a uniform distribution, it is unlikely that the resulting graph after removing the faulty edges remains a single vertex or a vertex with a very small degree if the number of faulty edges is not too “large”. In this sense, Gu et al. [5] introduced the concept of t-edge-fault-tolerant SME-connected of order r as follows.

Definition 1 

([5]). For positive integers t and r, a connected graph G is t-edge-fault-tolerant SME-connected (t-EFT-SME-connected) of order r if each pair of vertices u and v in $G-F$ are connected by $min\{$${\mathit{deg}}_{G-F}\left(u\right),$${\mathit{deg}}_{G-F}\left(v\right)\}$ edge-disjoint paths for every $F\subseteq E\left(G\right)$ with $\left|F\right|\le t$ and $\delta (G-F)\ge r$, where $\delta (G-F)$ is the minimum degree of $G-F$ and ${deg}_{G-F}\left(u\right)$ is the degree of u in $G-F$.

From the definition above, we can see that the EFT-SME connectivity reflects the tolerance of SME connectivity of a network with edge faults. Further, we note that the notion of t-EFT-SME connectivity of order 2 is particularly called t-conditional EFT-SME-connected [6].

Due to their attractive structural properties such as simple labeling scheme, higher connectivity, higher fault-tolerance and routing capabilities, and lower regular vertex degree, hypercube-like networks have been known as the classic topologies of a network and widely used as many classical real-world multiprocessor systems [7,8,9,10] and other applications [5,11,12,13]. The  SME connectivity and t-EFT-SME connectivity were also studied on various types of hypercube-like networks [3], such as hypercube [4], crossed cube [14,15,16] balanced hypercube [17], augmented cube [18] and augmented k-ary n-cube [19].

We consider another type of hypercube-based network, namely the folded crossed cube [11] (see Definition 3 for a detailed definition) or folded crossed hypercube $FC{Q}_n$ [20], which is constructed from a crossed cube by adding an edge joining each pair of complementary vertices. Therefore, a folded crossed cube has one more degree than a hypercube-like network of the same dimensions. It is also known that the edge connectivity of a folded crossed cube equals its regular vertex degree [11], implying that every folded crossed cube is SME-connected since it is regular. In fact, the folded crossed cube inherits many nice topological properties of both the folded hypercube $F{Q}_n$ [6] (obtained from a hypercube by adding an edge joining each pair of complementary vertices) and the crossed cube, such as high-performance and low-cost architecture [20], short diameter, short mean internode distance, better fault tolerance and better message traffic density [11,21], and  super connectivity [22]. In addition, the g-extra connectivity [23,24], g-component diagnosability and g-good neighbor diagnosability [25], and the star-structure connectivity [26] of the folded crossed cubes were also studied in the literature.

In this paper, we consider the SME and EFT-SME connectivities of folded crossed cubes. The rest of the article is organised as follows. In the following section, we introduce some necessary terminologies, notations and the formal definition of a folded crossed cube. In Section 3, we show that the n-dimensional folded crossed cube $FC{Q}_n$ is $(n-1)$-EFT-SME edge-connected of order 1 and $(3n-5)$-EFT-SME connected of order 2, and the upper bounds $n-1$ and $3n-5$ are both the best possible. In comparison, in Section 4, we also performed a numerical simulation on the two probabilities $p(G,f)$ and $p^M(G,f)$ for the folded crossed cube $FC{Q}_n$ and the folded cube $F{Q}_n$. Our numerical results show that, in addition to their same edge connectivity and the same SME connectivity, $FC{Q}_5$ and $F{Q}_5$ have almost the same values of $p(G,f)$ and $p^M(G,f)$ for every f. This implies that, compared with the folded hypercube, although the ‘edge-cross’ pattern in folded crossed cube shortens the mean internode distance [20], it does not strengthen the connectivity of the graph. Finally, the numerical results also show that, in contrast to the line graph of the generalized hypercube, both the folded crossed cube and the folded cube maintain nice SME connectivity when a number of edges are faulted.

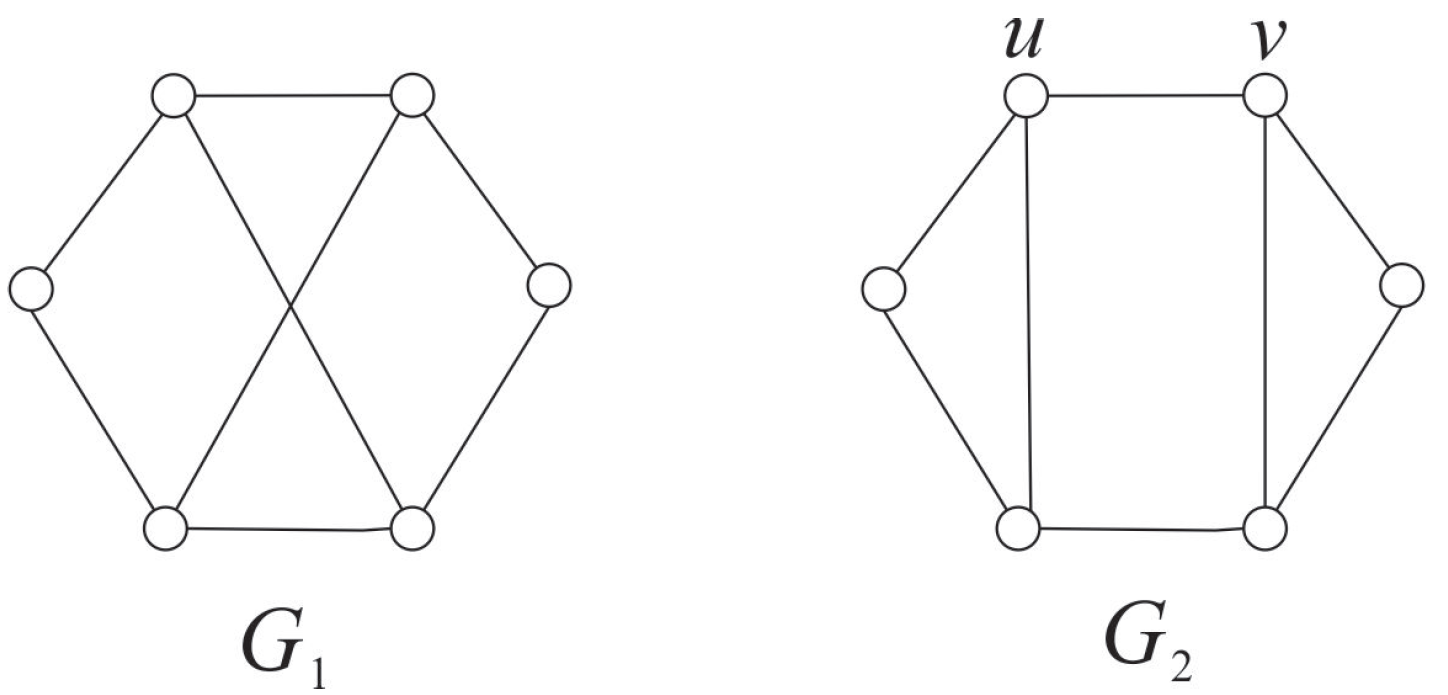
2. Preliminaries

We begin with some elementary notations. Let $G=\left(V\right(G),E(G\left)\right)$ be a simple connected graph where $V\left(G\right)$ and $E\left(G\right)$ denote its vertex set and edge set, respectively. For a vertex $x\in V\left(G\right)$, we denote by $N_G\left(x\right)=\{y:xy\in E\left(G\right)\}$ the neighbor set of x and by ${\mathit{deg}}_G\left(x\right)=\left|N_G\left(x\right)\right|$ the degree of x. In particular, if ${deg}_G\left(x\right)=k$ for every $x\in V\left(G\right)$, then the graph is called k-regular. Let $\delta \left(G\right)=min\{$${deg}_G\left(x\right)|x\in V\left(G\right)\}$ denote the minimum degree of G. For two disjoint subgraphs or vertex sets $H_1$, $H_2$ of G, we use $E_G(H_1,H_2)$ the edges with one endpoint in $H_1$ and the other in $H_2$. For a subset $F\subset V\left(G\right)\cup E\left(G\right)$, the subgraph obtained from G by deleting F is denoted by $G-F$. For any two vertices $x,y$ in $V\left(G\right)$, a $(x,y)$-path is a sequence of distinct vertices $(y_0,y_1,\cdots ,y_k)$ such that $x=y_0,y=y_k$, and $x_i{y}_{i+1}\in E\left(G\right)$ for $0\le i\le k-1$. An edge set $F\subset E\left(G\right)$ is a $(x,y)$-edge cut if $G-F$ has no $(x,y)$-path.

Two binary $\{0,1\}$-strings $x=x_1{x}_0$ and $y=y_1{y}_0$ are said to be pair-related if and only if $(x,y)\in \left\{\right(00,00),(10,10),(01,11),(11,01\left)\right\}$ and are denoted by $x\sim y$. For a positive integer n, the n-dimensional crossed cube ($C{Q}_n$) is recursively defined as follows:

Definition 2 

([14,15]). The vertices of $C{Q}_n$ are binary $\{0,1\}$-strings of length n. $C{Q}_1$ is the complete graph $K_2$ on two vertices 0 and 1. $C{Q}_2$ consists of four vertices $00,01,10$ and 11, and four edges $(00,01),(01,11),(11,10)$ and $(10,00)$. For $n\ge 3$, $C{Q}_n$ consists of $C{Q}_{n-1}^0$ and $C{Q}_{n-1}^1$ obtained from $C{Q}_{n-1}$ by adding 0 and 1 as the the first bit in the string of each vertex in $C{Q}_{n-1}$, respectively. Two vertices $x=0x_{n-2}{x}_{n-3}\cdots x_1{x}_0\in V\left(C{Q}_{n-1}^0\right)$ and $y=1y_{n-2}{y}_{n-3}\dots y_1{y}_0\in V\left(C{Q}_{n-1}^1\right)$ are adjacent in $C{Q}_n$ if and only if

(1) 

$x_{n-2}=y_{n-2}$ if n is even,

(2) 

$x_{2i+1}{x}_{2i}\sim y_{2i+1}{y}_{2i}$ for i with $0\le i<\lfloor (n-1)/2\rfloor$.

For convenience, we call the edges between $C{Q}_{n-1}^0$ and $C{Q}_{n-1}^1$ the cross edges of $C{Q}_n$. It is clear that the cross edges form a perfect matching of $C{Q}_n$. Based on $C{Q}_n$, we now give the formal definition of n-dimensional folded crossed cube ($FC{Q}_n$) as follows:

Definition 3 

([20]). $FC{Q}_n$ is the graph obtained from $C{Q}_n$ by adding an edge, called the complementary edge, between every two complementary vertices.

$$x=x_{n-1}{x}_{n-2}\cdots x_0\mathit{and}\overline{x}={\overline{x}}_{n-1}{\overline{x}}_{n-2}\cdots {\overline{x}}_0,\mathit{where}{\overline{x}}_i=1-x_i,i\in \{0,1,\dots ,n-1\}.$$

Figure 2 illustrates $C{Q}_3$ and $FC{Q}_3$. By the definition, it is clear that $FC{Q}_n$ is an $(n+1)$-regular graph with $2^n$ vertices and $(n+1)2^{n-1}$ edges. For a graph G, let $\kappa \left(G\right)$ be the connectivity of G, that is, the minimum cardinality of a set F of vertices in G such that $G-F$ is disconnected.

The properties introduced below will be used to prove the lemmas in Section 3.

Lemma 1 

([16]). For any integer n, we have $\kappa \left(C{Q}_n\right)=\lambda \left(C{Q}_n\right)=n$.

Lemma 2 

([11]). $\kappa \left(FC{Q}_n\right)=n+1$.

3. The EFT-SME Connectivity of Folded Crossed Cubes

In this section, we study the EFT-SME connectivity of folded crossed cubes $FC{Q}_n$, that is, the tolerance of SME connectivity of folded crossed cubes with edge faults.

Firstly, since $\kappa \left(G\right)\le \lambda \left(G\right)\le \delta \left(G\right)$ for any graph G, by Lemma 2, we have $\lambda \left(FC{Q}_n\right)=n+1$ and, hence, $FC{Q}_n$ is SME-connected as it is $(n+1)$-regular, which could be viewed as the SME connectivity of $FC{Q}_n$ with no edge faults. In the sense of edge fault tolerance, it is then natural to consider its SME connectivity with edge faults. Recall that an SME-connected graph must be connected by the definition. Therefore, if we consider the EFT-SME connectivity, the remaining graph when the faulty edges are removed must have a minimum degree at least 1, or in terms of EFT-SME connectivity of order r, we must have $r\ge 1$. We first give our result for $r=1$ as follows:

Theorem 1. 

For any integer n with $n\ge 3$, $FC{Q}_n$ is $(n-1)$-EFT-SME-connected of order 1.

Remark 1. 

The upper bound $n-1$ in Theorem 1 is the best possibility. Let $u_0\in V\left(FC{Q}_n\right)$, $u\in N_{FC{Q}_n}\left(u_0\right)$ and let v be a vertex not adjacent to $u_0$. Let $F=E(u_0,N_{FC{Q}_n}\left(u_0\right)\setminus \left\{u\right\})$, then $\left|F\right|=n$. It is clear that ${deg}_{FC{Q}_n-F}\left(u\right)={deg}_{FC{Q}_n-F}\left(v\right)=n+1$ but $FC{Q}_n-F$ does not have $(n+1)$ edge-disjoint paths between u and v, meaning that $FC{Q}_n$ is not n-EFT-SME-connected of order 1.

For the case when $r=2$, recall that a t-EFT-SME-connected graph of order 2 is also called t-conditional EFT-SME-connected graph. Before giving our results, we introduce two results related to the conditional EFT-SME connectivities of hypercube-like graph $H{L}_n$ (see [3,9,27] for its definition) and folded hypercube $F{Q}_n$ (the graph obtained from hypercube $Q_n$ by adding an edge between every pair of two complementary vertices, [3,4]).

Theorem 2 

([3]). For any $n\ge 3$, $H{L}_n$ is $(3n-8)$-conditional EFT-SME-connected and the upper bound $3n-8$ is optimal.

We note that $H{L}_n$ is an n-regular graph, which includes a large number of hypercube-like graphs such as the hypercube, Möbius cube and crossed cube, etc. For $(n+1)$-regular graph $F{Q}_n$, the upper bound $3n-8$ could be increased to $3n-5$, as follows:

Theorem 3 

([6]). For any $n\ge 5$, $F{Q}_n$ is $(3n-5)$-conditional EFT-SME-connected, and the upper bound $3n-5$ is optimal.

For folded crossed cubes $FC{Q}_n$, we now give its EFT-SME connectivity of order 2 as follows:

Theorem 4. 

For any integer n with $n\ge 5$, $FC{Q}_n$ is $(3n-5)$-EFT-SME-connected of order 2.

Remark 2. 

The upper bound $3n-5$ in Theorem 4 is the best possibility. Let $C=u{u}_1{u}_2{u}_3$ be a cycle of length four in $FC{Q}_n$ and $w\in N_{FC{Q}_n}\left(u_1\right)\setminus \{u,u_2\}$. Let $F={\bigcup }_{i=1}^{3}E(u_i,N_{FC{Q}_n}\left(u_i\right))\setminus \{E\left(C\right)\cup (u_1,w)\}$. Then, $\left|F\right|=3n-4$. Let $v\in V\left(FC{Q}_n\right)\setminus {\bigcup }_{i=1}^3{N}_{FC{Q}_n}\left(u_i\right)$, then ${deg}_{FC{Q}_n-F}\left(u\right)={deg}_{FC{Q}_n-F}\left(v\right)=n+1$. It can be seen that $FC{Q}_n-F$ does not have $(n+1)$-edge-disjoint paths between u and v. Thus, $FC{Q}_n$ is not $(3n-4)$-EFT-SME-connected of order 2.

Theorems 1 and 3 shows that the folded cube $F{Q}_n$ and the folded crossed cube $FC{Q}_n$ have not only the same edge connectivity $n+1$ but also the same EFT-SME connectivity of order 2. In addition, we will perform a numerical simulation in the following section to see that $F{Q}_n$ and $FC{Q}_n$ have almost the same probability that they are connected (or SME-connected) when f ($f\ge n+1$) edges are faulted.

We give our proofs of Theorems 1 and 4 in Appendix A. Since an $FC{Q}_n$ is constructed from two $C{Q}_{n-1}$ and, moreover, the $C{Q}_{n-1}$ is a particular graph of the class $H{L}_{n-1}$, the following lemmas are necessary for our proof.

Lemma 3 

([12]). For any positive integer n, $C{Q}_n$ is super-edge-connected. That is, for any $S\subseteq E\left(C{Q}_n\right)$ with $\left|S\right|=n$, $C{Q}_n-S$ is connected or has a component H with $\left|V\left(H\right)\right|=2^n-1$.

Lemma 4 

([27]). For any n with $n\ge 2$ and $S\subseteq E\left(H{L}_n\right)$ with $\left|S\right|\le 2n-3$, $H{L}_n-S$ has a component H such that $\left|V\left(H\right)\right|\ge 2^n-1$.

Lemma 5 

([3]). For any n with $n\ge 4$ and $S\subseteq E\left(H{L}_n\right)$ with $\left|S\right|\le 3n-5$, $H{L}_n-S$ has a component H such that $\left|V\left(H\right)\right|\ge 2^n-2$.

Lemma 6 

([3]). For any n with $n\ge 4$ and $S\subseteq E\left(H{L}_n\right)$ with $\left|S\right|\le 4n-9$, $H{L}_n-S$ has a component H such that $\left|V\left(H\right)\right|\ge 2^n-3$.

4. Numerical Simulation and Conclusions Remark

As mentioned in Section 1, the edge connectivity and EFT-SME connectivity of a graph reflect only the worst-case that the graph is disconnected when a number of edges are faulted. In this section we focus on the problem: what will happen if more edges are faulted? Specifically, we investigate the two measurements $p(G,f)$ and $p^M(G,f)$, that is, the probabilities that G is connected and SME-connected, respectively, when f edges are faulted randomly. Indeed, determining the exact values of $p(G,f)$ and $p^M(G,f)$ is in general much difficult. Instead, we will perform a numerical simulation on ${\lambda }_f\left(G\right)$ and ${\lambda }_f^M\left(G\right)$, the numbers of connected graphs and SME-connected graphs when f edges are faulted, by which we give the numerical analyses of $p(G,f)$ and $p^M(G,f)$. Practically, we choose $FC{Q}_5$ and $F{Q}_5$ as the instances for our simulation because they have the same regularity, the same edge connectivity and the same EFT-SME connectivity of order 2.

Since $FC{Q}_5$ and $F{Q}_5$ are 6-regular and 6-edge-connected with 32 vertices and 96 edges, they are connected if less than 6 edges are faulted and disconnected if more than 65 edges are faulted. In our simulation, for each integer f with $6\le f\le 65$, we choose 2000 random graphs obtained from the original graph by removing f edges that are generated randomly, called the faulty edge sets.

The next step of the simulation is to count the connected graphs and SME-connected graphs among the 2000 random graphs, that is, the values of ${\lambda }_f\left(G\right)$ and ${\lambda }_f^M\left(G\right)$. For connectivity, we note that two vertices u and v of a graph G of order n are connected if and only if the element $(u,v)$ (the element at the u-th row and v-th column) in the matrix $A^{n-2}+A^{n-1}$ is not 0, where A is the adjacency matrix of G. For SME connectivity, by its definition and the Max-Flow Min-Cut Theorem, a graph G is SME-connected if and only if G has no two vertices u and v, and an edge cut F with $\left|F\right|<min\left\{d\right(u),d(v\left)\right\}$, such that F separates the two vertices u and v. Since $FC{Q}_5$ and $F{Q}_5$ are 6-regular, the vertex degrees of the 2000 random graphs are not greater than 6. This means that if such edge cut F exists, it must consist of at most 5 edges. Further, to decrease the time-complexity, for each of the 2000 random graphs, we choose 10,000 edge subsets that are generated randomly, instead of choosing all the possible edge sets with at most 5 edges.

In terms of ${\lambda }_f\left(G\right)$ and ${\lambda }_f^M\left(G\right)$, it is clear that $p(G,f)={\lambda }_f\left(G\right)/2000$ and $p^M(G,f)={\lambda }_f^M\left(G\right)/2000$.

We now give our algorithm for the values of ${\lambda }_f\left(G\right)$ and ${\lambda }_f^M\left(G\right)$ for each f with $6\le f\le 65$ as Algorithm 1.

Algorithm 1 The values of ${\lambda }_f\left(G\right)$ and ${\lambda }_f^M\left(G\right)$ for each f with $6\le f\le 65$.

Input: A (the adjacency matrix of G); for $6\le f\le 65$, $F_f=\{F_{f1},F_{f2},\cdots ,F_{f2000}\}$ (the class of 2000 randomly generated faulty edge sets with f edges, represented as matrices); for $f=6:65$ Initialization: ${\lambda }_f=0,{\lambda }_f^M=0$ for $i=1:2000$ if ${(A-F_{fi})}^{31}+{(A-F_{fi})}^{30}$ has no 0 elements then ${\lambda }_f={\lambda }_f+1$ and let $E_{fi}=:\{E_{fi}^1,\dots ,E_{fi}^{10,000}\}$ (the class of 10,000 randomly generated edge subsets of $A-F_{fi}$ with at most 5 edges) for j = 1:10,000 if ${(A-F_{fi}-E_{fi}^j)}^{31}+{(A-F_{fi}-E_{fi}^j)}^{30}$ has a 0 element $(s,t)$ satisfies $min\{d\left(s\right),d\left(t\right)\}>|E_{fi}^j|$ break, let $i=i+1$ else $j=j+1$ if for all j, ${(A-F_{fi}-E_{fi}^j)}^{31}+{(A-F_{fi}-E_{fi}^j)}^{30}$ has no 0 element $(s,t)$ satisfies $min\{d\left(s\right),d\left(t\right)\}>|E_{fi}^j|$ then ${\lambda }_f^M={\lambda }_f^M+1$ else  $i=i+1$ output ${\lambda }_f$ output ${\lambda }_f^M$

The time complexity of above algorithm is as follows:

Time Complexity

Outer Loop: Iterates over f from 6 to 65, resulting in 60 iterations.

Middle Loop: For each f, iterates over 2000 faulty edge sets $F_{fi}$, leading to 2000 iterations.

Inner Loop: For each $F_{fi}$, generates up to 10,000 random edge subsets $E_{fi}^j$, contributing 10,000 iterations.

Matrix Operations: Each evaluation of whether ${(A-F_{fi}-E_{fi}^j)}^{31}+{(A-F_{fi}-E_{fi}^j)}^{30}$ contains zero elements involves matrix exponentiation and addition. For an $n\times n$ adjacency matrix, each exponentiation operation has a complexity of $O\left(n^3\right)$ using standard matrix multiplication, while matrix addition is $O\left(n^2\right)$. Given the computation of both the 31st and 30th powers, the total cost per evaluation is $O\left(61n^3\right)$.

Thus, the overall worst-case time complexity is

$$T\left(n\right)=60\times 2000\times 10,000\times O\left(61n^3\right)=O(7.32\times {10}^{10}{n}^3).$$

We can see that, although the coefficient $7.32\times {10}^{10}$ is large, the above time complexity is of polynomial-time in n, which could be potentially applied to larger networks.

By applying the algorithm above on $FC{Q}_5$ and $F{Q}_5$ with $f=6,7,\dots ,66$, we list the numerical results in

Table 1. The numerical results of ${\lambda }_f,{\lambda }_f^M,p(FC{Q}_5,f),p^M(FC{Q}_5,f)$.

f	16	17	18	19	20	21	22	23	24	25	26	27	28
${\lambda }_f$	2000	2000	2000	2000	1999	1996	1994	1991	1989	1978	1983	1979	1970
${\lambda }_f^M$	2000	1998	1998	1994	1995	1993	1983	1977	1972	1960	1941	1925	1906
$p_f$	1	1	1	1	0.9995	0.998	0.997	0.9955	0.9945	0.989	0.9915	0.9895	0.985
$p_f^M$	1	0.999	0.999	0.997	0.9975	0.9965	0.9915	0.9885	0.986	0.98	0.9705	0.9625	0.953
$\mathit{f}$	29	30	31	32	33	34	35	36	37	38	39	40	41
${\lambda }_f$	1968	1955	1948	1934	1927	1904	1878	1860	1839	1794	1772	1709	1690
${\lambda }_f^M$	1878	1823	1784	1711	1643	1597	1477	1389	1271	1156	1071	878	755
$p_f$	0.984	0.9775	0.974	0.967	0.9635	0.952	0.939	0.93	0.9195	0.897	0.886	0.8545	0.845
$p_f^M$	0.939	0.9115	0.892	0.8555	0.8215	0.7985	0.7385	0.6945	0.6355	0.578	0.5355	0.439	0.3775
$\mathit{f}$	42	43	44	45	46	47	48	49	50	51	52	53	54
${\lambda }_f$	1650	1583	1523	1423	1361	1272	1214	1117	1029	934	857	738	653
${\lambda }_f^M$	620	481	381	250	159	103	75	32	23	8	4	0	0
$p_f$	0.825	0.7915	0.7615	0.7115	0.6805	0.636	0.607	0.5585	0.5145	0.467	0.4285	0.369	0.3265
$p_f^M$	0.31	0.2405	0.1905	0.125	0.0795	0.0515	0.0375	0.016	0.0115	0.004	0.002	0	0
$\mathit{f}$	55	56	57	58	59	60	61	62	63	64	65	-	-
${\lambda }_f$	533	427	334	262	205	121	84	44	22	11	1	-	-
${\lambda }_f^M$	0	0	0	0	0	0	0	0	0	0	0	-	-
$p_f$	0.2665	0.2135	0.167	0.131	0.1025	0.0605	0.042	0.022	0.011	0.0055	0.0005
$p_f^M$	0	0	0	0	0	0	0	0	0	0	0	-	-

and

Table 2. The numerical results of ${\lambda }_f,{\lambda }_f^M,p(F{Q}_5,f),p^M(F{Q}_5,f)$.

f	16	17	18	19	20	21	22	23	24	25	26	27	28
${\lambda }_f$	2000	1999	1998	1996	1996	1996	1994	1990	1990	1986	1983	1976	1971
${\lambda }_f^M$	1999	1998	1996	1994	1993	1986	1978	1971	1972	1948	1939	1928	1899
$p_f$	1	0.999	0.999	0.998	0.998	0.998	0.997	0.995	0.995	0.993	0.9915	0.988	0.986
$p_f^M$	0.999	0.999	0.998	0.997	0.997	0.993	0.989	0.990	0.986	0.974	0.970	0.964	0.950
$\mathit{f}$	29	30	31	32	33	34	35	36	37	38	39	40	41
${\lambda }_f$	1971	1958	1945	1931	1923	1901	1879	1864	1838	1815	1781	1763	1663
${\lambda }_f^M$	1882	1838	1794	1727	1676	1558	1478	1422	1295	1160	1036	914	775
$p_f$	0.990	0.979	0.9725	0.970	0.962	0.951	0.940	0.932	0.919	0.9075	0.891	0.882	0.832
$p_f^M$	0.941	0.919	0.897	0.864	0.838	0.779	0.739	0.711	0.648	0.580	0.518	0.457	0.388
$\mathit{f}$	42	43	44	45	46	47	48	49	50	51	52	53	54
${\lambda }_f$	1623	1580	1534	1475	1354	1306	1250	1121	1015	933	831	727	646
${\lambda }_f^M$	619	465	342	283	176	98	73	35	14	8	2	0	0
$p_f$	0.812	0.790	0.767	0.738	0.677	0.653	0.625	0.561	0.508	0.467	0.416	0.364	0.323
$p_f^M$	0.310	0.233	0.171	0.142	0.088	0.049	0.037	0.018	0.007	0.004	0.001	0	0
$\mathit{f}$	55	56	57	58	59	60	61	62	63	64	65	-	-
${\lambda }_f$	538	461	319	264	180	134	101	47	20	12	2	-	-
${\lambda }_f^M$	0	0	0	0	0	0	0	0	0	0	0	-	-
$p_f$	0.269	0.231	0.160	0.132	0.09	0.067	0.051	0.024	0.01	0.006	0.001
$p_f^M$	0	0	0	0	0	0	0	0	0	0	0	-	-

and illustrate the probabilities $p(G,f)$ and $p^M(G,f)$ as in Figure 3.

From the numerical results, we can see that $FC{Q}_5$ and $F{Q}_5$ have almost the same values of $p(G,f)$ and $p^M(G,f)$ for every f either.

Compared with the traditional edge connectivity, it is clear that the SME connectivity is a stronger version of connectivities, which may vary from different graphs even if they have the same edge connectivity. For this reason, we consider the average ratio $r\left(G\right)$ of the number of SME-connected graphs to that of the connected graphs when the number of edges is faulted in G, where $G\in \{FC{Q}_5,F{Q}_5\}$, i.e.,

$$r\left(FC{Q}_5\right)={\displaystyle \frac{{\sum }_{f=6}^{65}{p}^M(FC{Q}_5,f)\left(\genfrac{}{}{0pt}{}{96}{f}\right)}{{\sum }_{f=6}^{65}p(FC{Q}_5,f)\left(\genfrac{}{}{0pt}{}{96}{f}\right)}}=0.554.$$

and

$$r\left(F{Q}_5\right)={\displaystyle \frac{{\sum }_{f=6}^{65}{p}^M(F{Q}_5,f)\left(\genfrac{}{}{0pt}{}{96}{f}\right)}{{\sum }_{f=6}^{65}p(F{Q}_5,f)\left(\genfrac{}{}{0pt}{}{96}{f}\right)}}=0.548.$$

Conclusions Remark

In this paper, we studied the connectivity of the folded crossed cube $FC{Q}_n$ from both theoretical and numerical analyses. Due to its its nice structure, that is, the hypercube-based structure, $FC{Q}_n$, has actually high connectivity and SME connectivity. In comparison, we also performed a numerical simulation on the two probabilities $p(G,f)$ and $p^M(G,f)$ for the folded crossed cube $FC{Q}_n$ and the folded cube $F{Q}_n$. We note that $FC{Q}_n$ has much shorter mean internode distance than that of $F{Q}_n$ [20]. However, our numerical results show that, in addition to their same edge connectivity and the same SME connectivity, $FC{Q}_5$ and $F{Q}_5$ have almost the same values of $p(G,f)$ and $p^M(G,f)$ for every f. This implies that, compared with the folded hypercube, although the ‘crossed’ pattern of edges in folded crossed cube shorten the mean internode distance, it does not strengthen the connectivity of the graph.

Finally, by the numerical results, we also give the average ratio $r\left(FC{Q}_n\right)=0.554$ and $r\left(F{Q}_n\right)=0.548$, which are much higher than 0.0475, the average ratio of the line graph of the generalized hypercube $FC{Q}_n$ [13]. This means that both the folded crossed cube and the folded cube maintain nice SME connectivity when a number of edges are faulted.