Abstract
Understanding psychological change requires a quantitative framework capable of capturing the complex and dynamic relationships among personal constructs. Personal Construct Psychology emphasizes the hierarchical reorganization of bipolar constructs, yet existing qualitative methods inadequately model the reciprocal and graded influences involved in such change. This paper introduces the Presence–Balance (PB) space, a centrality measure for constructs represented within Fuzzy Cognitive Maps (FCMs). FCMs model cognitive systems as directed, weighted graphs, allowing for nuanced analysis of construct interactions. The PB space operationalizes two orthogonal dimensions: Presence, representing the overall connectivity and activation of a construct, and Implication Balance, quantifying the directional asymmetry between influences exerted and received. By formalizing Hinkle’s hierarchical theory within a rigorous mathematical framework, the PB space enables precise identification of constructs that drive or resist transformation. This dual-dimensional model provides a structured method for analyzing personal construct systems, supporting both theoretical exploration and clinically relevant interpretations in the study of psychological change.
Keywords:
Fuzzy Cognitive Maps (FCMs); graph theory; centrality measures; psychological change; personal construct psychology MSC:
05C07
1. Introduction
1.1. Psychological Change and Personal Construct Systems
Grasping psychological change requires a detailed understanding of the complex interplay of meanings individuals construct to interpret and anticipate their experiences. Personal Construct Psychology (PCP) [1] conceptualizes cognition as a system of bipolar constructs—such as “happy–sad” or “assertive–submissive”—through which individuals organize meaning and anticipate events. Kelly proposed that people operate like naive scientists, constantly testing and revising their constructed systems in light of new experiences, a process he called constructive alternativism [2]. Psychological change therefore corresponds to the reorganization of these personal networks through the adaptation or generation of constructs [3].
A personal construct is, fundamentally, a cognitive discriminant—a bipolar framework that helps an individual differentiate between categories of events, people, or experiences. Constructs are idiographic and subjective: they shape perception and action in idiosyncratic ways (e.g., “friendly vs. unfriendly”, “secure vs. risky”) and are deployed flexibly based on context [4]. This idiographic orientation foregrounds the person rather than the trait, distinguishing PCP from nomothetic traditions.
PCP places particular emphasis on the individual-level dynamics of change. Constructs exist within an organized hierarchical system, constrained by their range of convenience and permeability, which modulates adaptation to new events [1]—providing a sophisticated yet qualitatively oriented theory of personal change. Although mechanisms like anxiety (arising when faced with novel constructs) and hostility (when individuals rigidly defend failing constructs) are theorized [5], PCP lacks explicit formal models quantifying inter-construct influences and predicting systemic effects.
While Kelly’s repertory grid and laddering techniques [6,7] advanced the elicitation and mapping of personal constructs—often identifying supraordinate constructs that lend stability to the system—these methods remain largely qualitative and unidirectional in nature [8]. Hierarchical laddering presupposes a tree-like influence structure, making it insufficient to model the complex reciprocal and graded interdependencies observed in cognitive systems [9,10].
This gap sets the stage for quantitative formalizations—particularly the interrogation of reciprocal, graded influences across constructs—providing a basis for both theoretical precision and clinical intervention. In this context, tools such as the Weighted Implication Grid (WimpGrid) and subsequent graph-theoretic models [11] offer transformative possibilities, operationalizing PCP’s idiographic essence into analytically tractable cognitive networks.
1.2. The WimpGrid: A Quantitative Framework for Modeling Psychological Change
To overcome the limitations of traditional PCP methods, the WimpGrid was developed as a psychometric instrument that bridges constructivist theory and quantitative modeling [11]. The WimpGrid generalizes the logic of the Implication Grid by enabling the modeling of reciprocal, graded influences among constructs. It is designed to elicit, structure, and mathematically represent how individuals anticipate the consequences of modifying aspects of their self-concept.
The WimpGrid protocol begins with the elicitation of bipolar personal constructs that define the participant’s individual meaning system [12,13]. Each participant generates a unique set of constructs, expressed in their own terms, reflecting how they personally interpret and evaluate their experience. For each construct, the participant provides ratings for two key psychological states: the Self-Now, reflecting their perceived current state, and the Ideal-Self, representing their aspirational or desired psychological configuration. These ratings are assigned on a semantic differential scale, with bipolar endpoints corresponding to opposing poles of each construct (e.g., “Anxious” vs. “Calm”). While the WimpGrid supports flexible scale designs, the most commonly used formats include 3-point, 7-point, or 9-point scales. The choice of scale length can influence measurement sensitivity and participant cognitive load, and differences among these options have been empirically explored in the context of construct elicitation and rating reliability [14].
Subsequently, participants are asked to consider a series of hypothetical self-states in which one construct is purposefully changed (e.g., becoming “totally calm” or “totally unhealthy”) and to estimate how this change might propagate to the remaining constructs. These anticipated influence judgments are systematically recorded in the WimpGrid matrix (see Figure 1), where rows represent constructs, and columns correspond to hypothetical selves arising from isolated changes in each construct.
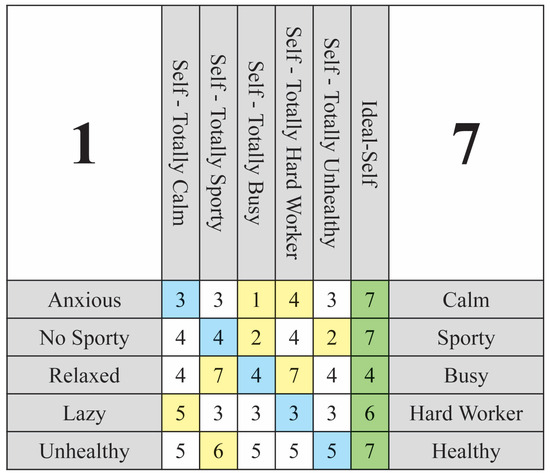
Figure 1.
Weigthed Implication Grid (WimpGrid) Score Matrix (Scale 1–7) used to elicit and structure the individual’s personal construct system. Each row corresponds to a bipolar construct (e.g., Anxious–Calm), and each column represents a hypothetical self: the first five columns depict imagined selves resulting from targeted changes in each construct, while the sixth column represents the Ideal-Self. Cells are filled with self-assigned ratings from 1 to 7, where 1 denotes complete alignment with the left pole and 7 with the right pole. Blue cells indicate the participant’s current Self-Now scores; green cells indicate their Ideal-Self scores; yellow cells highlight constructs where the participant anticipates significant change if another construct is modified.
From this matrix, a computational procedure derives a weight matrix that encodes the perceived causal influence of each construct on the others. The resulting structure can be represented as a directed, weighted graph—an idiographic cognitive network in which nodes are constructs and edges denote inferred influence magnitudes. These graphs serve as the basis for computing psychological metrics such as construct centrality, emotional coherence, and resistance to change [15].
In this way, the WimpGrid formalizes the dynamic logic of personal construct systems, enabling the study of psychological change as an emergent phenomenon within interconnected networks. This methodological innovation not only retains the idiographic richness of PCP but also provides a mathematically tractable framework for exploring individual cognitive transformation.
1.3. Modeling Personal Construct System Through Fuzzy Cognitive Maps
To systematically represent the reciprocal and graded interrelations between constructs, Kosko [16] introduced Fuzzy Cognitive Maps (FCMs), a formalism in which cognitive elements are represented as nodes connected by directed, weighted edges that encode perceived causal influences [17]. FCMs are dynamic graph-based models capable of capturing feedback loops, non-linear propagation, and self-regulation, making them especially compatible with PCP’s anticipatory and systemic logic [18,19,20,21].
Within this framework, the WimpGrid emerges as a highly structured method for empirically eliciting FCMs from individual meaning systems. Unlike classical FCM construction—often based on expert consensus or theoretical assumptions—the WimpGrid anchors each network in the participant’s own psychological representations. Through systematic exploration of hypothetical construct modifications, the WimpGrid yields personalized, weighted networks that reflect how the individual anticipates causal relationships within their internal system of constructs [22]. This procedure transforms abstract constructivist theory into a computationally precise model of cognitive dynamics.
Recent theoretical developments in belief and concept networks—such as those by Rodriguez et al. [23], Dalege et al. [24], and Chopard et al. [25]—have provided powerful formal frameworks for modeling the formation, coherence, and evolution of belief systems. These models leverage insights from computational sociology, statistical mechanics, and constraint satisfaction to describe how beliefs stabilize or shift under social and cognitive pressures. They offer valuable tools for understanding belief dynamics at both individual and collective levels, particularly in contexts involving norm formation, cognitive dissonance, and social conformity. Likewise, work by Bhatia and Golman [26] advances our understanding of bidirectional constraint satisfaction in decision making, modeling how individuals resolve competing demands within structured cognitive environments.
Nevertheless, these approaches tend to operate at a more abstract or nomothetic level, often grounded in formal logic or agent-based modeling assumptions. As such, they may overlook the nuanced, idiographic variability found in individual meaning systems—a central concern in PCP. In this context, our model is not intended to replace these theoretical contributions but to complement them by offering a methodologically grounded, person-centered approach rooted in empirical elicitation. By focusing on subjectively meaningful constructs, our framework aims to extend these broader models with tools that are sensitive to the interpretive and experiential texture of psychological change.
In contrast, the WimpGrid offers a person-centered modeling approach grounded in subjectively meaningful constructs, thereby preserving the idiographic richness of PCP. Rather than assuming shared ontologies or normative constructs, it captures how individuals uniquely perceive and organize psychological meaning. This idiographic emphasis distinguishes it from nomothetic FCM applications and aligns it more closely with clinical and personalized assessment contexts.
Yet, even within individualized FCMs, identifying the most influential constructs—the nodes that most powerfully shape the psychological system—remains analytically nontrivial. While classical centrality measures from graph theory, such as in-degree, out-degree, closeness, and eigenvector centralities [27,28], have been adapted to psychological network analyses [29,30], they were originally conceived for abstract or social networks, not for modeling cognitive systems grounded in subjective personal meaning. These metrics lack theoretical alignment with the epistemological foundations of PCP, and they do not account for the constructivist, idiographic, and interpretive nature of psychological change. As such, they provide limited insight into the functional significance of constructs within a personal system of meaning.
1.4. PB Space: A Framework for Personal Construct Centrality
Building on the limitations outlined above, we introduce the Presence–Balance (PB) space: a novel, geometrically grounded framework designed to quantify the centrality of constructs within personal meaning systems modeled via the WimpGrid. The PB space emerges as a response to the need for analytical tools that are both theoretically consistent with PCP and capable of capturing the dynamic, idiographic structure of individual cognitive networks.
The conceptual roots of PB space lie in the work of Hinkle [8], who emphasized the hierarchical organization of constructs. Hinkle proposed that supraordinate constructs exert greater influence on psychological functioning and are more resistant to change. However, his original formulation was qualitative, unidirectional, and dependent on tree-like hierarchies that may not reflect the reciprocal, networked nature of actual construct systems [9,10]. The PB space generalizes and formalizes these intuitions within a continuous, bidimensional space.
This framework decomposes each construct’s position in the network into two orthogonal dimensions:
- Presence, which reflects the overall engagement of a construct within the system, is calculated as the sum of its in-degree and out-degree. It captures the construct’s general prominence or embeddedness in the network.
- Implication Balance, which measures the directional asymmetry of influence. This index identifies whether a construct predominantly exerts influence on others or is itself influenced—quantifying its functional role as a driver or receptor in the system.
Together, these indices enable a nuanced analysis of constructs not just as static nodes but as active agents within dynamic, self-referential cognitive systems. The PB space therefore bridges a critical methodological gap: it provides a theoretically coherent, mathematically rigorous, and clinically interpretable means of analyzing individual cognitive topologies derived from WimpGrid data.
The objective of this article is to formally define the mathematical structure of the PB space, analyze its geometric and algebraic properties, and demonstrate its potential through selected empirical applications. By doing so, we aim to advance the modeling of psychological change within idiographic construct systems, offering tools for both research insight and therapeutic intervention grounded in the epistemology of PCP.
2. Mathematical Foundations
To analyze psychological change, it is essential to establish a formal mathematical framework that captures the relational structure of personal constructs and their dynamic implications. The following foundations define a graph-theoretic model of psychological meaning making based on the representation of constructs as vectors in bounded spaces, the simulation of hypothetical transformations, and the computation of influence weights between constructs. This section explains how self-perception, ideal goals, and construct interactions can be encoded as algebraic objects and how these structures enable the construction of an FCM that reflects the individual’s psychological topology. The psychological data required to instantiate this model were obtained through the WimpGrid interview protocol [11], a structured assessment methodology to generate personal construct systems. These mathematical definitions provide the basis for deriving a directed graph of meaning relations and for quantifying the centrality and hierarchical role of each construct in psychological change.
2.1. FCM of Psychological Change
To formalize the representation of psychological change, we begin by defining the algebraic objects that capture the structure of an individual’s personal construct system. These objects serve as the foundation for constructing a FCM, where constructs are modeled as nodes, and perceived causal influences among them are represented as weighted directed edges. This mathematical framework enables the translation of qualitative self-perception and Ideal-Self evaluation, as elicited through the WimpGrid interview [11], into a structured and analyzable model. In what follows, we introduce the definitions and axioms necessary to construct such a map, starting from the self and Ideal-Self vectors and culminating in a weight matrix that encodes the system of cognitive implications.
Definition 1.
The Self-Now of the individual can be represented as a vector , where n is the number of constructs elicited in the WimpGrid interview, and each component corresponds to the individual’s Self-Now score on construct i within their personal construct system.
Remark 1.
The notation represents the n-dimensional space, where each coordinate corresponds to a construct elicited. Each score is bounded within the interval , ensuring a normalized representation of personal meanings. A value of indicates complete alignment with the left pole of the construct, while a value of 1 represents complete alignment with the right pole. Intermediate values correspond to positions between the two poles of the construct, reflecting varying degrees of association.
Definition 2.
The Ideal-Self of the individual can be defined as a vector , where n is the number of constructs elicited in the WimpGrid interview, and each component corresponds to the individual’s Ideal Self score on construct i within their personal construct system.
Definition 3.
The hypothetical situations vector encodes the direction of simulated psychological change for each construct elicited in the WimpGrid interview, where n is the number of constructs. Each component represents the direction in which construct i is hypothetically altered during the simulation and is computed from the Self-Now vector and the Ideal-Self vector according to the following rule:
Remark 2.
This formulation reflects the operational logic of the WimpGrid: if the construct has a defined self-position (), the hypothetical self shifts to the opposite pole (i.e., maximal contrast). If the self is neutral () but the ideal has a defined direction, then the hypothetical change follows the ideal’s orientation. In the absence of any directional preference ( and ), the model assigns a default shift toward the right pole of the construct.
Definition 4.
The hypothetical states of the individual (referred to as Hypothetical-Selves) can be represented using a matrix , where each entry represents the hypothetical score assigned to construct i under the influence of hypothetical situation j.
Remark 3.
The diagonal entries are arbitrarily defined as the components of the Self-Now vector for the purposes of subsequent mathematical computations.
Axiom 1
(Linearity of Change). It is assumed that there exists a linear relationship between the proposed change in the hypothetical situation and the declared change in the construct j as a result of the influence of the construct i, denoted by . Specifically, this relationship is expressed as
Remark 4.
The linearity assumption encapsulated in Equation (2) implies that the influence of construct i on construct j can be fully captured through a single proportionality coefficient . This assumption simplifies the system’s complexity by reducing non-linear dynamics to a manageable linear framework, making it amenable to graph-theoretic and algebraic analysis. While this formulation enables tractable modeling of inter-construct dynamics within a cognitive system, it relies on a linear approximation that may not capture more complex non-linear or context-dependent psychological processes. Future work may explore extensions incorporating non-linear or threshold-based influence mechanisms.
Definition 5
(Weight Matrix). Given the current state vector , the hypothetical intensity vector , and the matrix of Hypothetical-Selves , the weight matrix is defined such that each entry quantifies the sensitivity of construct j to changes in construct i. This weight is computed as
under the assumption of the Linearity of Change Axiom, which posits a proportional relationship between changes in constructs.
Remark 5.
The matrix M encodes the hypothetical responses of each construct when others are perturbed. Specifically, represents the predicted value of construct j when construct i is shifted to its hypothetical state . The numerator captures the resulting change in construct j, while the denominator quantifies the intensity of the hypothetical change in construct i. Their ratio expresses the influence of i over j assuming linear propagation, in accordance with the Axiom (1).
Example 1.
Given the score matrix in Figure 1, we can operationalize it as follows:
Applying a rescaling transformation from the interval to , we obtain a normalized matrix defined as follows:
Using the normalized matrix and applying Weight Matrix Calculation (5), we can calculate the self vector , the ideal vector , the hypothetical situations vector , and the weight matrix W. They are defined in the following example:
Definition 6.
Given a weight matrix , a self vector , and an ideal vector , there exists a directed graph such that we have the following:
- , where each vertex corresponds to a construct.
- , where if and only if .
- assigns attributes to vertices, where .
- assigns weights to edges, where .
Figure 2 illustrates the directed graph G constructed from the data presented in Example (1), displaying both the edge weights and the node attributes associated with each construct.
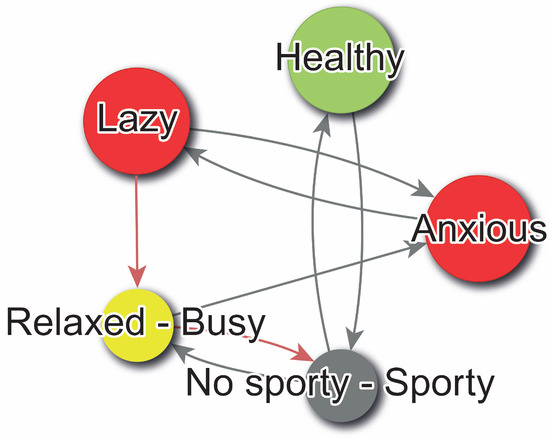
Figure 2.
Directed graph representation of the personal construct system derived from the weight matrix W in Example (1). Each node corresponds to a bipolar construct, positioned and styled according to its psychological attributes. Node color encodes congruence with the Ideal-Self: green indicates full congruence (), red indicates discrepancy (), yellow marks undefined ideal values (), and gray indicates undefined self-perception (). Node size reflects the absolute self-score , representing the construct’s salience in current self-identity. Directed edges represent cognitive implications, with black denoting a direct relationship () and red an inverse relationship (). Edge thickness encodes the absolute weight , reflecting the strength of influence. This graph provides an interpretable structural summary of the Fuzzy Cognitive Map (FCM), supporting both visual intuition and algebraic analysis of psychological change dynamics. Graph generated using WimpTools [31].
The resulting graph G provides a visual and mathematical representation of the relationships between constructs. The directed edges encode the influences derived from W, while the node attributes enrich the graph with the self and ideal scores, allowing for a comprehensive analysis of both structural relationships and individual goals.
2.2. PB Space
Definition 7.
Let be a vertex of the graph G, and let denote the weights associated with the edges of G. We define two measures for the vertex , the in-degree and the out-degree , as follows:
Remark 6.
Axiom 2
(Vertex Balance). Let be a vertex in the graph G. The implication balance of is determined by the relationship between its in-degree and out-degree and is defined as follows:
- is said to be supraordinate if , meaning the vertex exerts more influence (outputs) than it receives (inputs).
- is said to be subordinate if , meaning the vertex is more influenced by other vertices (inputs) than it influences them (outputs).
- is said to be neutral if , meaning the vertex has an equal balance of influence received (inputs) and exerted (outputs).
Remark 7.
The concept of balance described here is inspired by the framework introduced by Hinkle [8], who suggested that constructs exerting greater influence on a system, while themselves being less influenced, should be considered more supraordinate. This psychological principle naturally extends to vertices within a graph, where the balance between inputs and outputs characterizes their role.
Definition 8
(Presence–Balance Transformation). Let be a directed graph, where each vertex has an in-degree and an out-degree . The Presence–Balance ( PB ) index for vertex is defined by the following linear transformation:
Remark 8.
This transformation corresponds to a counterclockwise rotation of the vector. It produces two interpretable indices:
- Presence (): The total connectivity of node , computed as , which projects the degree vector onto the axis.
- Implication Balance (): The asymmetry between outgoing and incoming connections, computed as , projecting onto the axis.
The PB space visualization (Figure 3) thus provides a concise and interpretable summary of the relational dynamics within personal construct systems. By clearly distinguishing constructs according to their centrality and hierarchical roles, this geometric framework not only facilitates theoretical understanding but also supports targeted clinical interventions. Clinicians can readily identify influential constructs that serve as critical leverage points for therapeutic change, enabling a systematic and strategically informed approach to psychological intervention.
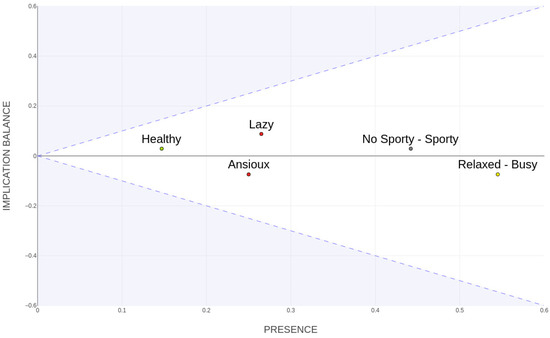
Figure 3.
Presence-Balance (PB) space representation of the psychological constructs from Example (1). Each construct is plotted by its Presence (, horizontal axis) and Balance (, vertical axis). The shaded region indicates the theoretical boundary imposed by the PB transformation. Constructs toward the upper area act more as sources of influence, while those in the lower area are more influenced by others.
2.3. Properties of the PB Space
This section presents a formal characterization of the PB space. The analysis is organized into two parts. First, we demonstrate that the PB space satisfies the defining properties of a two-dimensional convex cone in . Second, we examine the projection as a limiting representation of all possible weighted directed graphs of increasing order n, assuming continuous-valued edge weights in the range .
2.3.1. Bounding Theorem and Geometric Constraint
Theorem 1.
All points resulting from this transformation satisfy the following constraint:
Proof.
Non-negativity of P. Since , it follows that
The bounding inequality is defined as
Boundary cases. Equality holds in the following cases:
- If , i.e., the node is a pure source, then .
- If , i.e., the node is a pure sink, then .
□
2.3.2. Geometric Formulation
Any point in the PB space results from a linear transformation applied to the normalized counts of in-degree and out-degree connections of a construct in an FCM. As shown above, each point satisfies
This inequality defines a conic region in , with its vertex at the origin and bounded by the rays and . At , balance necessarily vanishes, yielding the origin. As P increases, the admissible range of B expands symmetrically.
Definition 9.
The PB space is defined as the following set:
This constraint arises naturally from the linear transformation applied to the node in-strength and out-strength in a weighted directed graph. Since both quantities are defined as non-negative sums of edge weights, it follows that and for all projected nodes. Therefore, the image of any FCM under the PB transformation lies within C.
Theorem 2
(Convex Cone Structure). The set C defined in Definition (9) satisfies the axioms of a convex cone.
Proof.
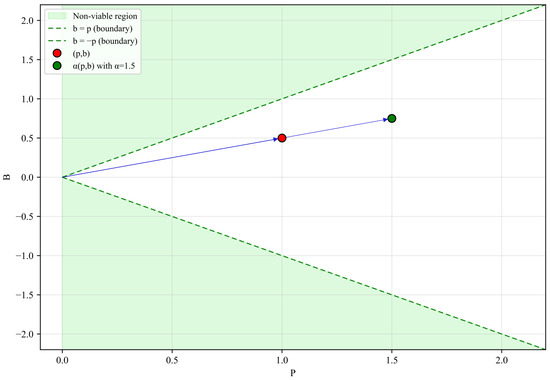
We prove that C satisfies the three fundamental properties:
1. Closure under non-negative scalar multiplication. Let and . Then,
Figure 4 illustrates this property: scaling a vector in preserves cone membership.

Figure 4.
Closure under scalar multiplication (Theorem 2, Property 1).
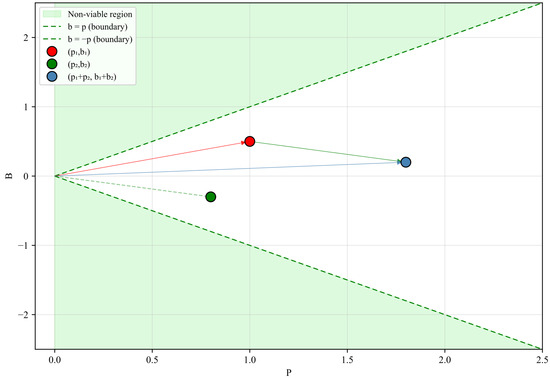
2. Closure under vector addition. Let . Then,
Figure 5 exemplifies vector addition within .

Figure 5.
Exemplification of vector addition (Theorem 2, Property 2).
3. Closure under convex combinations. Let , and define
Then,
□
Figure 6 exemplifies convex combinations in .
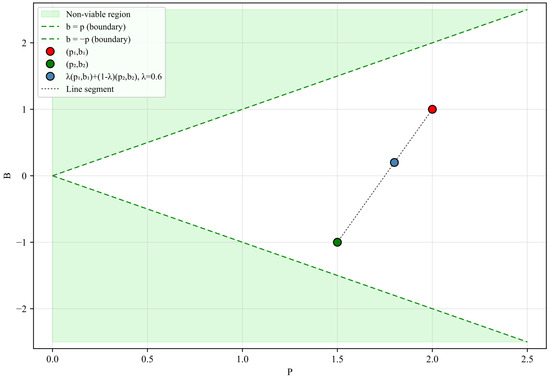
Figure 6.
Convex combinations (Theorem 2, Property 3).
2.3.3. Graph Projections and Asymptotic Behavior
Theorem 3
(Asymptotic Density). Let denote the set of all possible FCMs of order n, where each directed edge can take any value in . Each node maps to a pair via the transformation described above. For fixed n, the projection of is a compact, continuous, non-convex subset of C. As , the union of projections densely fills C.
Proof.
Compactness and continuity. Since the projection is a continuous function of the compact set , its image is compact.
Non-convexity. Consider and the following points:
- (source: )
- (balanced: )
Both are achievable. Their midpoint requires . However, in any 3-node graph, we have the following:
- Achieving A requires a node with (max out-strength).
- Achieving C requires another node with (max connections).
This exhausts all edge slots, leaving no capacity for a node with at M. Thus, .
Asymptotic density. Let be the PB space defined by . Then, for any and any , there exists and a fuzzy cognitive map of order n such that the projection of contains a node satisfying .
Let and be arbitrary. Define
By construction, due to . Our goal is to realize node strengths within an additive error that guarantees in PB space.
Let and be arbitrary. Define
Then, if we construct a node with approximate in-strength and out-strength, satisfying
it follows by linearity of the PB transformation that
To achieve such an approximation, note that any desired value of can be represented as the sum of outgoing connections with weight 1, plus a residual outgoing edge with weight , provided this residual exceeds . The same construction applies symmetrically for by selecting incoming edges in an analogous manner.
Define
and choose
This choice of n ensures that there are enough nodes to provide the required number of incoming and outgoing connections without violating the no-self-loop constraint inherent to the graph definition.
To complete the construction, assign all other edge weights in to values strictly less than . This guarantees that their cumulative contribution to the in-strength or out-strength of the approximating node remains below and does not affect the targeted precision.
Thus, we have constructed a graph containing a node with approximate strengths within of and, consequently, a projection within of in the PB space. Since and are arbitrary, the density of projections in C follows as .
Hence, its projection lies within distance of in the PB space. Since and are arbitrary, the union of projections over increasing n is dense in C. □
3. Discussion
3.1. Applications
The PB space, defined as a bidimensional convex and self-dual cone, admits several analytically grounded applications within the modeling of personal construct systems:
- (a)
- Identification of hub constructs: The PB space constructs located in the high-P region and exhibiting high Mahalanobis distance from the centroid can be interpreted as structural hubs within the cognitive system. To ensure interpretive validity, the analysis is restricted to constructs with , and the Mahalanobis distance is computed relative to the empirical covariance structure of this subset. Constructs exceeding a predefined threshold (e.g., percentile) are identified as hubs, reflecting both prominence and deviation from the system’s central configuration.
- (b)
- Dynamic trajectories and attractors: The convex geometry of the PB space allows for the analysis of simulated activation dynamics derived from fuzzy cognitive maps. Trajectories projected within the cone may exhibit convergence toward fixed points or bounded regions, interpretable as cognitive attractor states. These attractors may correspond to stable interpretative configurations, enabling formal study of equilibrium, rigidity, or response to perturbation in personal construct systems.
- (c)
- Test-retest stability assessment: The geometric structure also supports the quantification of temporal stability across repeated assessments. Displacement of constructs in the PB space can be evaluated using Euclidean or Mahalanobis distances, allowing researchers to distinguish between stable core constructs and volatile peripheral ones. This approach provides an idiographic measure of consistency that is sensitive to both structural position and system-wide distribution.
Each application benefits from the formal constraints of the PB space, enabling statistically consistent and geometrically interpretable operations within a reduced-dimensional framework.
3.2. Limitations and Future Research Directions
- (a)
- Dimensionality reduction: The projection onto the PB plane reduces a potentially high-dimensional system of construct interrelations to two summary dimensions. While this facilitates visualization and analysis, it also entails a loss of information. Further investigation is required to assess which properties of the original system are preserved or distorted by the transformation and whether the PB space can be extended to higher-dimensional analogues.
- (b)
- Lack of evaluative distance representation: The PB projection reflects the structural connectivity of constructs within a fuzzy cognitive map, encoding their total influence (Presence) and directional balance (Balance). However, it does not represent the evaluative proximity or distance of constructs relative to an ideal self or desired pole. This distinction is particularly relevant in clinical or developmental applications, where the salience of a construct may depend not only on its centrality but also on its alignment with aspirational goals. Future research could explore hybrid projections that integrate both structural and evaluative dimensions or combine the PB space with discrepancy-based metrics.
- (c)
- Sectorisation of the PB space: A systematic partitioning of the cone into theoretically meaningful sub-regions (e.g., high-P/high-B, high-P/low-B, low-P core) could clarify how individuals construe the functional roles of their constructs. Future studies should examine whether constructs occupying different sectors correspond to distinct experiential categories—such as guiding principles, adaptive resources, or latent concerns—and how transitions between sectors relate to processes of psychological change.
- (d)
- Empirical validation: Finally, while the PB space has shown promising utility in exploratory analyses—such as the identification of central constructs, attractors, or system stability—its empirical validation remains an open line of inquiry. Initial case applications of WimpGrid-based FCM modeling have been conducted in diverse contexts, including clinical supervision in psychotherapy [33] and case formulation [34], where PB coordinates helped identify therapeutically relevant leverage points. Ongoing validation efforts are currently being carried out in a broader psychometric study focused on the predictive value of WimpGrid indices with respect to psychological well-being and change readiness; preliminary findings are available in an open-access preprint hosted on OSF [15]. Future research should further assess how constructs identified as central or supraordinate in PB space correspond to external psychological variables such as symptom severity, functional outcomes, or response to intervention.
4. Conclusions
This article has introduced the PB space as a bidimensional, self-dual convex cone that provides a compact and analytically tractable geometric embedding for personal construct systems modeled via Fuzzy Cognitive Maps (FCMs). The model defines two orthogonal coordinates:
where denote the in- and out-strengths of construct i. These coordinates capture, respectively, the overall connectivity (Presence) and the directional asymmetry (Balance) of each construct.
The PB transformation satisfies a bounding theorem (), which ensures that all construct projections lie within a convex, self-dual cone. This space is closed under positive scaling, vector addition, and convex combination. An asymptotic density theorem further establishes that as the number of constructs increases, the projections of admissible FCMs densely fill the cone, confirming the completeness of PB space as a codomain for influence-based representations.
Key contributions of this work include the following:
- The derivation of a closed-form expression for the weight matrix W from WimpGrid interview data, based on an explicit linearity axiom.
- The demonstration that define a dual coordinate system of a self-dual cone, thus enabling the application of convex geometric methods—such as optimization, clustering, and partitioning—within the PB plane.
- The construction of a geometric map in which every construct is uniquely located by its coordinates, enabling systematic, visual, and quantitative characterisation of an individual’s personal construct system.
Conceptually, the PB framework advances idiographic psychological modeling by embedding two key aspects of meaning systems into a unified analytic space: the overall salience of each construct (Presence) and its functional role as either a driver or receiver of influence (Balance). This dual metric supports immediate visual identification of pivotal constructs, facilitates the detection of cognitive asymmetries, and opens new avenues for geometry-based interpretation of personal meaning structures—including attractor analysis, region-based segmentation, and trajectory tracking over time.
Taken together, these contributions extend the mathematical foundations of cognitive network analysis and offer a rigorous, interpretable bridge between constructivist theory and contemporary quantitative modeling. Future research may explore non-linear variants of the PB framework, integrate distance-based evaluations with respect to ideal states, and empirically test whether transitions within PB space predict clinically relevant psychological change.
Author Contributions
Conceptualization, A.S., C.H.-M., L.A.S. and L.B.; methodology, A.S. and C.H.-M.; software, A.S.; validation, A.S., C.H.-M., L.A.S. and L.B.; formal analysis, A.S. and C.H.-M.; writing—original draft preparation, A.S. and C.H.-M.; writing—review and editing, A.S., C.H.-M., L.A.S. and L.B.; visualization, A.S. and C.H.-M.; supervision, L.A.S. and L.B.; project administration, L.A.S. and L.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| FCM | Fuzzy Cognitive Map |
| PCP | Personal Construct Psychology |
| PB | Presence–Balance |
| WimpGrid | Weighted Implication Grid |
References
- Kelly, G.A. The Psychology of Personal Constructs; Norton: New York, NY, USA, 1955. [Google Scholar]
- Botella, L.; Feixas, G. Teoría de los Constructos Personales: Aplicaciones a la Práctica Psicológica; FPCEE Blanquerna: Barcelona, Spain, 1998. [Google Scholar] [CrossRef]
- Procter, H.; Winter, D.A. Personal and Relational Construct Psychotherapy; Palgrave Macmillan: London, UK, 2020. [Google Scholar]
- Winter, D.A.; Viney, L.L. Personal Construct Psychotherapy: Advances in Theory, Practice and Research; Whurr Publishers: London, UK, 2007. [Google Scholar]
- Chiari, G.; Nuzzo, M.L. Personal construct theory within psychological constructivism. In Personal Construct Theory: A Psychology for the Future; Walker, B.M., Costigan, J., Eds.; The Australian Psychological Society: Melbourne, Australia, 1996; pp. 25–54. [Google Scholar]
- Fransella, F.; Bell, R.; Bannister, D. A Manual for Repertory Grid Technique; John Wiley & Sons: Chichester, UK, 2004. [Google Scholar]
- Neimeyer, R.A.; Hagans, C.L. Revisiting the Repertory Grid: Applications in Clinical Practice and Research. In Child and Adolescent Therapy: Cognitive-Behavioral Procedures; Kendall, P.C., Ed.; Guilford Press: New York, NY, USA, 2002; pp. 365–394. [Google Scholar]
- Hinkle, D.N. The Change of Personal Constructs from the Viewpoint of a Theory of Construct Implications. Ph.D. Thesis, Ohio State University, Columbus, OH, USA, 1965. [Google Scholar]
- Bell, R.C. Did Hinkle prove laddered constructs are superordinate? A re-examination of his data suggests not. Pers. Constr. Theory Pract. 2014, 11, 1–4. [Google Scholar]
- Korenini, B. What do Hinkle’s data really say about laddering? Pers. Constr. Theory Pract. 2016, 13–20. [Google Scholar]
- Sanfeliciano, A.; Sául, L.A.; Botella, L. Weighted implication grid: A graph-theoretic approach to modelling psychological change. Front. Psychol. 2025; in press. [Google Scholar]
- Leitner, L.M. Interview methodologies for construct elicitation: Searching for the core. In Anticipating Personal Construct Psychology; Epting, F.R., Landfield, A.W., Eds.; University of Nebraska Press: Lincoln, NE, USA, 1985; pp. 292–305. [Google Scholar]
- Epting, F.R.; Probert, J.S.; Pittman, S.D. Alternative strategies for construct elicitation: Experimenting with experience. Int. J. Pers. Constr. Psychol. 1993, 6, 79–98. [Google Scholar] [CrossRef]
- Metzler, A.E.; Gorden, H.; Neimeyer, G.J. The effect of repertory grid scale size and rating direction on structural measures of differentiation. J. Constr. Psychol. 2002, 15, 95–107. [Google Scholar] [CrossRef]
- Sanfeliciano, A.; Saúl, L.A. Exploring the Personal Construction of Psychological Change via Graph Theory: Validation of the Weighted Implication Grid [Preprint]. OSF Preprint. 2025. Available online: https://osf.io/hr85t (accessed on 20 June 2025).
- Kosko, B. Fuzzy cognitive maps. Int. J. Man-Mach. Stud. 1986, 24, 65–75. [Google Scholar] [CrossRef]
- Wang, L.X.; Mendel, J.M. Generating fuzzy rules by learning from examples. IEEE Trans. Syst. Man Cybern. 1992, 22, 1414–1427. [Google Scholar] [CrossRef]
- Botella, L. La Construcción del Cambio Terapéutico: Terapia Constructivista Integradora en la Práctica Clínica; Desclée De Brouwer: Paris, France, 2020. [Google Scholar]
- Tsadiras, A.K. Fuzzy cognitive maps for decision support in social systems. J. Syst. Res. Behav. Sci. 2008, 25, 285–293. [Google Scholar]
- Felix, G.; Nápoles, G.; Falcon, R.; Vanhoof, K. A review on methods and software for fuzzy cognitive maps. Artif. Intell. Rev. 2019, 52, 1707–1737. [Google Scholar] [CrossRef]
- Papageorgiou, E.I.; Froelich, W. Application of Fuzzy Cognitive Maps in Social Theories and Modeling Social Complexity. Int. J. Fuzzy Syst. 2019, 21, 364–377. [Google Scholar] [CrossRef]
- Saúl, L.A.; Sanfeliciano, A.; Botella, L.; Perea, R.; Gonzalez-Puerto, J.A. Fuzzy Cognitive Maps as a Tool for Identifying Cognitive Conflicts That Hinder the Adoption of Healthy Habits. Int. J. Environ. Res. Public Health 2022, 19, 1411. [Google Scholar] [CrossRef]
- Rodriguez, N.; Bollen, J.; Ahn, Y.Y. Collective Dynamics of Belief Evolution under Cognitive Coherence and Social Conformity. PLoS ONE 2016, 11, e0165910. [Google Scholar] [CrossRef]
- Dalege, J.; Galesic, M.; Olsson, H. Networks of Beliefs: An integrative theory of individual- and social-level belief dynamics. Psychol. Rev. 2024, 132, 253–290. [Google Scholar] [CrossRef]
- Chopard, B.; Raynaud, F.; Stalhandske, J. A Model for the Formation of Beliefs and Social Norms Based on the Satisfaction Problem (SAT). Entropy 2025, 27, 358. [Google Scholar] [CrossRef]
- Bhatia, S.; Golman, R. Bidirectional Constraint Satisfaction in Rational Strategic Decision Making. J. Math. Psychol. 2019, 88, 48–57. [Google Scholar] [CrossRef]
- Freeman, L.C. A set of measures of centrality based on betweenness. Sociometry 1977, 40, 35–41. [Google Scholar] [CrossRef]
- Bonacich, P. Power and centrality: A family of measures. Am. J. Sociol. 1987, 92, 1170–1182. [Google Scholar] [CrossRef]
- Özesmi, U.; Özesmi, S.L. Ecological models based on people’s knowledge: A multi-step fuzzy cognitive mapping approach. Ecol. Model. 2004, 176, 43–64. [Google Scholar] [CrossRef]
- Borsboom, D.; Cramer, A.O.J. Network analysis: An integrative approach to the structure of psychopathology. Annu. Rev. Clin. Psychol. 2013, 9, 91–121. [Google Scholar] [CrossRef]
- Sanfeliciano, A.; Saúl, L. WimpTools, version 1.0.0. WimpTools: A Graph-Theoretical R Toolbox for Modeling Psychological Change. Zenodo: Geneva, Switzerland, 2025. [CrossRef]
- Borgatti, S.P. Centrality and network flow. Soc. Netw. 2005, 27, 55–71. [Google Scholar] [CrossRef]
- Saúl, L.A.; Botella, L.; Sanfeliciano, A. Utilización de mapas cognitivos borrosos en supervisión clínica en psicoterapia [Use of Fuzzy Cognitive Maps in Clinical Supervision in Psychotherapy]. Rev. Psicoter. 2023, 34, 133–148. [Google Scholar] [CrossRef]
- Botella, L.; Barrado, E.; Sanfeliciano, A.; Saúl, L.A. Formulación de caso mediante mapas cognitivos borrosos: Bases conceptuales y metodológicas y ejemplo de caso [Case formulation using fuzzy cognitive maps: Conceptual and methodological basis and case study]. Rev. Psicoter. 2022, 33, 79–110. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).