A Novel p-Norm-Based Ranking Algorithm for Multiple-Attribute Decision Making Using Interval-Valued Intuitionistic Fuzzy Sets and Its Applications
Abstract
1. Introduction
1.1. Review of Existing Studies
1.2. Motivation and a Brief Overview of the Present Research
- (1)
- Numerous methods ([7,16,26,27]; see Section 5 for more details) discussed in the existing literature exhibit several notable shortcomings. The shortcomings, presented in the methods [7,16,26,27], include (i) division by zero and (ii) avoiding Definition 4. As a result, these methodologies fall short in delivering an equitable and rational ranking order for the diverse array of alternatives under consideration.
- (2)
- There is an unequivocal necessity for an efficient and appropriate score function tailored to s, which can consistently and reliably manage comparable and incomparable decision data.
1.3. Key Contributions and Organizing Structure
- (1)
- We introduce a for s with robust properties. This function incorporates the concept of the unknown portion of an and two flexible parameters, and , where and . The advantage of these parameters is that varying their values can aid in ordering alternatives.
- (2)
- Several numerical examples are provided to demonstrate the usefulness, effectiveness, and credibility of the that was formulated.
- (3)
- We develop an algorithm to provide a comprehensive solution to decision-making problems by incorporating the p-distance and the proposed .
- (4)
- We showcase the effectiveness of the proposed algorithm by presenting multiple numerical examples. Additionally, our algorithm is used to identify the best investment company.
2. Preliminaries
- (i)
- If and in , then reduces to an intuitionistic fuzzy number ().
- (ii)
- If and , then reduces to a fuzzy number ().
- (iii)
- If and in , then reduces to an interval value fuzzy number ().
- (i)
- ,
- (ii)
- ,
- (iii)
- ,
- (iv)
- ,
- (v)
- ;
- The accuracy function, proposed by Ye [9], is
- The accuracy function, proposed by Nayagam et al. [10], is
- The score function, proposed by Bai [11], is
- The score function, proposed by Nayagam et al. [12], is
- The score function, proposed by Selvaraj and Majumdar [13], is
- The score function proposed by Chen and Tsai [14] is
- The score function, proposed by Chen and Yu [15], is
3. A Novel for s with Robust Properties: A Generalized Approach
3.1. Shortcomings of Many Existing Score and Accuracy Functions
- The functions and give the values and .
- The function produces .
- The function gives the values .
- The computed values are .
- The function gives .
- The function presents .
- The function provides .
- The and functions result in and , respectively.
- The function produces .
- The function yields .
- The function gives . The function yields .
- The function produces .
- The functions and yield and , respectively.
- The function yields .
- The function gives .
- The function produces .
3.2. Novel for s
3.3. Championing the Significance of the Novel
4. Algorithm for Based on Proposed and -Distance
4.1. Formulation and Auxiliary Results
4.2. A Novel Algorithm for the Current
- Step 1.
- The aim of this step is to build up a normalized decision matrix from the matrix , where
- Step 2.
- This step computes the weighted decision matrix from the matrix and the assigned weight vector , where each is represented by an . The th entry of is given bywhich is obtained by using property (ii) (Definition 3).
- Step 3.
- By utilizing the proposed and the matrix , the score alternative matrix is calculated for each i, where with and .
- Step 4.
- For each , we find a row vector . Then, based on Definition 9 and obtained vectors , we calculate p-distance corresponding to each as follows:
- Step 5.
- Based on Definition 10 and the calculated s, we determine a of alternatives. The smaller the p-distance , the better the of alternative , where .
- Benefits and Limitations
- This algorithm provides the solution steps to solve an problem in the context. In such decision-making problems, the expert focuses not only on the behavior of the fuzzy decision matrix (a matrix in which each entry is shown by an ) but also provides attribute weight information in terms of s.
- We calculate a row vector for each alternative score matrix. The advantage of these vectors is that we define a p-distance to check the overall performance of each alternative. Definition 10 states that a small value of the p-distance represents better performance of an alternative in a set of feasible alternatives.
- The proposed is utilized in this algorithm to obtain reasonable decision results. The use of this function permits a sensitivity analysis with respect to the parameter in order to find an effective measure of s.
- This research avoids group perceptions to provide more realistic decision opinions.
- The used in this algorithm has some limitations for parameter . For , this function does not work effectively. For example, if and and , then . This shows that the function does not provide a for and , even though the two numbers are different from each other.
- The present algorithm can be strengthened by including the concept of the negative ideal alternative ().
- A method will be proposed to determine attribute weights precisely, which will ensure a smoother decision-making process.
4.3. Numerical Examples
- Step 1.
- This step is not applicable because each attribute is of the benefit type. Consequently, .
- Step 2.
- According to , the weights for the attributes are given asThen, we calculate the weighted decision matrix , presented in Table 5.
- Step 3.
- By utilizing the proposed , we construct the score matrix for , presented in Table 6.
- Step 4.
- Utilizing (18), the value for is calculated for , where . The calculated values are
- Step 5.
- Step 4 produces the following sequence:This yields the following:Thus, is the most preferable.
- Step 1.
- This step is not applicable because each attribute is of the benefit type. Consequently, .
- Step 2.
- According to , the weights for attributes are given asThen, we calculate the weighted decision matrix , presented in Table 8.
- Step 3.
- By utilizing the proposed , we construct the score matrix for , presented in Table 9.
- Step 4.
- Utilizing (18), the value for is calculated for where . The calculated values are
- Step 5.
- Step 4 produces the following sequence:This yields the following:Thus, is the most preferable.
- Step 1.
- This step is not applicable because each attribute is of the benefit type. Consequently, .
- Step 2.
- According to , the weights for attributes are given asThen, we calculate the weighted decision matrix , presented in Table 11.
- Step 3.
- By utilizing the proposed , we construct the score matrix for , presented in Table 12.
- Step 4.
- Utilizing (18), the value for is calculated for , where . The calculated values are
- Step 5.
- Step 4 produces the following sequence:This yields the following:Thus, is the most preferable.
- Step 1.
- This step is not applicable because each attribute is of the benefit type. Consequently, .
- Step 2.
- According to , the weights for attributes are given asThen, we calculate the weighted decision matrix , as presented in Table 14.
- Step 3.
- By utilizing the proposed , we construct the score matrix for , as presented in Table 15.
- Step 4.
- Utilizing (18), the value for is calculated for where . The calculated values are
- Step 5.
- Step 4 produces the following sequence:This yields the following:Thus, is the most preferable.
- Step 1.
- This step is not applicable because each attribute is of the benefit type. Consequently, .
- Step 2.
- According to , the weights for attributes are given asThen, we calculate the weighted decision matrix , as presented in Table 17.
- Step 3.
- By utilizing the proposed , we construct the score matrix for , presented in Table 18.
- Step 4.
- Utilizing (18), the value for is calculated for , where . The calculated values are
- Step 5.
- Step 4 produces the following sequence:This yields the following:Hence, each alternative has an equal ranking.
- Step 1.
- This step is not applicable because each attribute is of the benefit type. Consequently, .
- Step 2.
- According to , the weights for attributes are given asThen, we calculate the weighted decision matrix , as presented in Table 20.
- Step 3.
- By utilizing the proposed , we construct the score matrix for , presented in Table 21.
- Step 4.
- Utilizing (18), the value for is calculated for , where . The calculated values are
- Step 5.
- Step 4 produces the following sequence:This yields the following:Thus, is the most preferable.
- Step 1.
- This step is not applicable because each attribute is of the benefit type. Consequently, .
- Step 2.
- According to , the weights for attributes are given asThen, we calculate the weighted decision matrix , as presented in Table 23.
- Step 3.
- By utilizing the proposed , we construct the score matrix for , presented in Table 24.
- Step 4.
- Utilizing (18), the value for is associated with where . The calculated values are
- Step 5.
- Step 4 produces the following sequence:This yields the following:Thus, is the most preferable.
5. Comparisons and Advantages
5.1. Comparisons and Advantages with Example 10
- Kumar and Chen [16] presented a connection number-based approach to address an problem. However, their method produced an unreasonable of () for the given data, as the attribute values of and are distinct. To address this issue, Definition 4 is applied, revealing the s of () and () in the pairs and , respectively. These results differed from the calculated ones, rendering the Kumar and Chen method unreliable. In contrast, our proposed method yielded a of () that not only addressed the limitations of the Kumar and Chen method but also justified Definition 4.
- The method in [7] is based on the mean and variance of score matrices for values, while the approach in [25] employs a score function along with a non-linear programming model. The existing methods in [7,25], establish a of (). In harmony with our proposed approach, both s not only adhere to the criteria defined in Definition 4 but also converge on the same top-ranked alternative.
5.2. Comparisons and Advantages with Example 11
- Kumar and Chen [16] developed a connection number-based method for addressing an problem. Kumar and Chen’s approach [16] yielded the () for the given decision problem. However, upon employing Definition 4, it became evident that this method is incapable of providing a consistent . Our proposed algorithm, on the other hand, produced a of (), which satisfies both relationships () and ().
5.3. Comparisons and Advantages with Example 12
- The obtained from Kumar and Chen’s method [16] for the given data is (), which appears unreasonable since the attribute values for these alternatives are distinct. In contrast, our proposed algorithm ranks the alternatives as (), thereby addressing the limitation of Kumar and Chen’s method.
- Chen and Tsai [7] proposed a methodology for solving problems that utilizes the score function of s, along with the mean and variance of the resulting score matrices. The proposed algorithm yields a of (), whereas the existing method [7] produces a of (). Despite the differences, both methods successfully differentiate between the rankings of , and .
5.4. Comparisons and Advantages with Example 13
- Li [26] proposed a nonlinear programming methodology based on the framework to solve problems, where both the ratings of alternatives and the weights of attributes are represented using sets. The method given in [26] suffers from the issue of “division by zero,” rendering it incapable of generating a reliable ranking. However, our proposed algorithm effectively overcomes this shortcoming.
- The methodologies presented in [7,16,25,29,30,31,32,33] are considered for comparison to demonstrate the credibility of our proposed approach. These methods are designed to address problems within the context and are based on various concepts, including the mean and variance, non-linear programming models, probability density functions, U-quadratic distribution, Beta distribution, etc. The proposed algorithm gives the best alternative that is consistent with the alternative obtained from existing methods in [7,16,25,29,30,31,32,33].
5.5. Comparisons and Advantages with Example 14
- To address problems, Li [26] proposed a nonlinear programming methodology based on the framework, while Zhao and Zhang [27] developed a method utilizing an accuracy function and the weighted averaging operator. The existing methods [26,27] are unable to solve this problem due to issue with “division by zero”. However, our proposed algorithm effectively addresses this shortcoming.
5.6. Comparisons and Advantages with Example 15
- The novel approaches presented in [7,21,22,25,27] are developed within the context, with some methods based on concepts such as probability density functions and z-score decision matrix. Our proposed algorithm yields the same as that produced by the existing methods outlined in [7,21,22,25,27]. While the method suggested by Li [26] is unable to generate the for this problem.
- The above comparisons show the reliability of the proposed algorithm.
5.7. Comparisons and Advantages with Example 16
- Chen and Tsai’s method, as outlined in [7], initially established a of () for the given decision making problem. However, upon a thorough examination of matrix , it became apparent that the attribute values associated with , , and for alternatives and exhibited notable differences. This discrepancy indicated that and should not be considered equal in their ranking. In contrast, our proposed algorithm produced a of (), effectively rectifying the limitation identified in [7].
- Chen and Hsu [25] proposed a method in which attribute weights are determined using a non-linear programming model, and combined with a score function to derive the . The proposed algorithm yields a of (), whereas the existing method [25] produces a of (). Despite the differences, both methods successfully differentiate between the rankings of and .
6. Applicability of Proposed Algorithm
- Step 1.
- This step is not applicable because each attribute is of the benefit type. Consequently, .
- Step 2.
- According to , the weights for attributes are given asThen, we calculate the weighted decision matrix , as presented in Table 26.
- Step 3.
- By utilizing the proposed , we construct the score matrix for , as presented in Table 27.
- Step 4.
- Utilizing (18), the value for is calculated for where . The calculated values are
- Step 5.
- Step 4 produces the following sequence:This yields the following:Thus, is the most preferable.
- (i)
- Both kinds (subjective [21,22] and objective [4,6,25]) for describing attribute weight information are used in the approaches given in Table 28 in order to create an effective comparative analysis. However, in the present algorithm, the attribute weight information is subjectively given. But the proposed solution steps are completely different from the steps given in the existing approaches.
- (ii)
- In contrast to Kumar and Chen’s [22] inability to discern a within the given numerical data, the remaining approaches consistently mirror the elucidated by our suggested algorithm. These findings lend credence to the robustness and reliability of the proposed algorithm.
7. Conclusions
7.1. Main Outcomes of the Present Research
- (i)
- A was constructed with its robust properties to measure s for solving decision-making problems. The main features of this function are as follows: (a) This function incorporates the degree of uncertainty presented in an ; (b) it contains two flexible parameters, and , with the relation and ; (c) the efficacy of this function was demonstrated through various numerical examples that indicate its preference over the past s.
- (ii)
- An algorithm was contrived for the using the decision framework. This algorithm utilizes the concept of the p-distance of each alternative score matrix relative to the to effectively accomplish the ’s task. The novelties of the algorithm are as follows: (a) it is simple to implement, i.e., the algorithm running time is very short; (b) a program for this algorithm is given in Python to handle the numerical problems smoothly; (c) the p-distance is computed for each alternative, which plays a crucial role in ranking the alternatives.
- (iii)
- The implementation and advantages of the suggested algorithm are demonstrated through numerous comparative examples.
7.2. Management Insights and Computer Software
- (i)
- It is effective and flexible to include the p-distance of alternatives to the problems. The use of the values of p-distances cooperates for prioritizing alternatives accurately.
- (ii)
- faces many challenges in assigning precise numerical weights to different attributes due to the complex and uncertain nature of the information. Therefore, in this work, the attribute weights are represented by s.
- (iii)
- A practical problem was successfully modeled and solved by using the proposed algorithm. A comprehensive comparative analysis is also provided to show the advantages of the algorithm.
- (iv)
- To calculate the numerical results accurately, Python software (version 3.12.3) was used throughout this paper. The results are presented in Appendix A.
7.3. Future Scope and Limitations
- (i)
- In future studies, the present algorithm can be used for solving problems in other fuzzy and uncertain environments, such as picture fuzzy and linguistic interval-valued intuitionistic fuzzy contexts.
- (ii)
- (iii)
- The present algorithm can be strengthened by including the concept of the negative ideal alternative ().
- (iv)
- The present algorithm ranks the alternatives in problems only; it can be expanded to solve group decision-making problems.
- (v)
- A method will be proposed to determine attribute weights precisely, ensuring a smoother decision-making process.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Python Code
| Listing A1. Python code. |
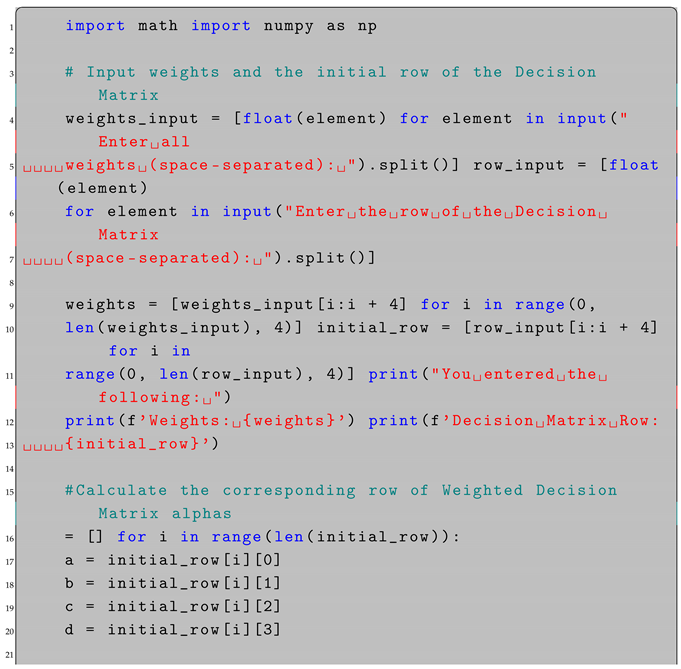  |
References
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Atanassov, K.T. lntuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Atanassov, K.; Gargov, G. Interval-valued intuitionistic fuzzy sets. Fuzzy Sets Syst. 1989, 31, 343–349. [Google Scholar] [CrossRef]
- Garg, H. A new generalized improved score function of interval-valued intuitionistic fuzzy sets and applications in expert systems. Appl. Soft Comput. 2016, 38, 988–999. [Google Scholar] [CrossRef]
- Wan, S.; Dong, J. Decision Making Theories and Methods Based on Interval-Valued Intuitionistic Fuzzy Sets; Springer Nature: Singapore, 2020. [Google Scholar]
- Kumar, S.; Kumar, M. A game theoretic approach to solve multiple group decision making problems with interval-valued intuitionistic fuzzy decision matrices. Int. J. Manag. Sci. Eng. Manag. 2021, 16, 34–42. [Google Scholar] [CrossRef]
- Chen, S.-M.; Tsai, C.-A. Multiattribute decision making using novel score function of interval-valued intuitionistic fuzzy values and the means and the variances of score matrices. Inf. Sci. 2021, 577, 748–768. [Google Scholar] [CrossRef]
- Xu, Z.S. Methods for aggregating interval-valued intuitionistic fuzzy information and their application to decision making. Control Decis. 2007, 22, 215–219. [Google Scholar]
- Ye, J. Multicriteria fuzzy decision-making method based on a novel accuracy function under interval-valued intuitionistic fuzzy environment. Expert Syst. Appl. 2009, 36, 6899–6902. [Google Scholar] [CrossRef]
- Nayagam, V.L.G.; Muralikrishnan, S.; Sivaraman, G. Multi-criteria decision-making method based on interval-valued intuitionistic fuzzy sets. Expert Syst. Appl. 2011, 38, 1464–1467. [Google Scholar] [CrossRef]
- Bai, Z.-Y. An interval-valued intuitionistic fuzzy TOPSIS method based on an improved score function. Sci. World J. 2013, 2013, 879089. [Google Scholar] [CrossRef]
- Nayagam, V.L.G.; Jeevaraj, S.; Dhanasekaran, P. An intuitionistic fuzzy multi-criteria decision-making method based on nonhesitance score for interval-valued intuitionistic fuzzy sets. Soft Comput. 2018, 21, 7077–7082. [Google Scholar] [CrossRef]
- Selvaraj, J.; Majumdar, A. A new ranking method for interval-valued intuitionistic fuzzy numbers and its application in multi-criteria decision-making. Mathematics 2021, 9, 2647. [Google Scholar] [CrossRef]
- Chen, S.-M.; Tsai, K.-Y. Multiattribute decision making based on new score function of interval-valued intuitionistic fuzzy values and normalized score matrices. Inf. Sci. 2021, 575, 714–731. [Google Scholar] [CrossRef]
- Chen, S.-M.; Yu, S.-H. Multiattribute decision making based on novel score function and the power operator of interval-valued intuitionistic fuzzy values. Inf. Sci. 2022, 606, 763–785. [Google Scholar] [CrossRef]
- Kumar, K.; Chen, S.M. Multiattribute decision making based on interval-valued intuitionistic fuzzy values, score function of connection numbers, and the set pair analysis theory. Inf. Sci. 2021, 551, 100–112. [Google Scholar] [CrossRef]
- Wang, Z.; Xiao, F.; Ding, W. Interval-valued intuitionistic fuzzy Jenson-Shannon divergence and its application in multi-attribute decision making. Appl. Intell. 2022, 52, 16168–16184. [Google Scholar] [CrossRef]
- Ohlan, A. Novel entropy and distance measures for interval-valued intuitionistic fuzzy sets with application in multi-criteria group decision-making. Int. J. Gen. Syst. 2022, 51, 413–440. [Google Scholar] [CrossRef]
- Senapati, T.; Mesiar, R.; Simic, V.; Iampan, A.; Chinram, R.; Ali, R. Analysis of interval-valued intuitionistic fuzzy Aczel-Alsina geometric aggregation operators and their aplication to multiple attribute decision-making. Axioms 2022, 11, 258. [Google Scholar] [CrossRef]
- Shen, Q.; Zhang, X.; Lou, J.; Liu, Y.; Jiang, Y. Interval-valued intuitionistic fuzzy multi-attribute second-order decision making based on partial connection numbers of set pair analysis. Soft Comput. 2022, 26, 10389–10400. [Google Scholar] [CrossRef]
- Patra, K. An improved ranking method for multi attributes decision making problem based on interval valued intuitionistic fuzzy values. Cybern. Syst. 2022, 54, 648–672. [Google Scholar] [CrossRef]
- Kumar, K.; Chen, S.M. Multiattribute decision making based on converted decision matrices, probability density functions, and interval-valued intuitionistic fuzzy values. Inf. Sci. 2021, 554, 313–324. [Google Scholar] [CrossRef]
- Shi, X.; Ali, Z.; Mahmood, T.; Liu, P. Power aggregation operators of interval-valued Atanassov-intuitionistic fuzzy sets based on Aczel-Alsina t-norm and t-conorm and their applications in decision making. Int. J. Comput. Intell. Syst. 2023, 16, 43. [Google Scholar] [CrossRef]
- Zhong, Y.; Zhang, H.; Cao, L.; Li, Y.; Qin, Y.; Luo, X. Power Muirhead mean operators of interval-valued intuitionistic fuzzy values in the framework of Dempster-Shafer theory for multiple criteria decision-making. Soft Comput. 2023, 27, 763–782. [Google Scholar] [CrossRef]
- Chen, S.M.; Hsu, M.H. Multiple attribute decision making based on novel score function of interval-valued intuitionistic fuzzy values, score matrix, and nonlinear programming model. Inf. Sci. 2023, 645, 119332. [Google Scholar] [CrossRef]
- Li, D.F. TOPSIS-based nonlinear-programming methodology for multiattribute decision making with interval-valued intuitionistic fuzzy sets. IEEE Trans. Fuzzy Syst. 2010, 18, 299–311. [Google Scholar] [CrossRef]
- Zhao, Z.; Zhang, Y. Multiple attribute decision making method in the frame of interval-valued intuitionistic fuzzy sets. In Proceedings of the Eighth International Conference on Fuzzy Systems and Knowledge Discovery, Shanghai, China, 26–28 July 2011; pp. 192–196. [Google Scholar]
- Balakrishnan, A.V. Applied Functional Analysis; Springer: Berlin/Heidelberg, Germany, 1980. [Google Scholar]
- Chen, S.M.; Huang, Z.C. Multiattribute decision making based on interval-valued intuitionistic fuzzy values and linear programming methodology. Inf. Sci. 2017, 381, 341–351. [Google Scholar] [CrossRef]
- Chen, S.M.; Han, W.H. An improved MADM method using interval-valued intuitionistic fuzzy values. Inf. Sci. 2018, 467, 489–505. [Google Scholar] [CrossRef]
- Chen, S.M.; Fan, K.Y. Multiattribute decision making based on probability density functions and the variances and standard deviations of largest ranges of evaluating interval-valued intuitionistic fuzzy values. Inf. Sci. 2019, 490, 329–343. [Google Scholar] [CrossRef]
- Chen, S.M.; Chu, Y.C. Multiattribute decision making based on U-quadratic distribution of intervals and the transformed matrix in interval-valued intuitionistic fuzzy environments. Inf. Sci. 2020, 537, 30–45. [Google Scholar] [CrossRef]
- Chen, S.M.; Liao, W.T. Multiple attribute decision making using Beta distribution of intervals, expected values of intervals, and new score function of interval-valued intuitionistic fuzzy values. Inf. Sci. 2021, 579, 863–887. [Google Scholar] [CrossRef]
- Komal. Archimedean t-norm and t-conorm based intuitionistic fuzzy WASPAS method to evaluate health-care waste disposal alternatives with unknown weight information. Appl. Soft Comput. 2023, 146, 110751. [Google Scholar]
- Gokasar, I.; Pamucar, D.; Deveci, M.; Ding, W. A novel rough numbers based extended MACBETH method for the prioritization of the connected autonomous vehicles in real-time traffic management. Expert Syst. Appl. 2023, 211, 118445. [Google Scholar] [CrossRef]
| Abbreviation | Definition |
|---|---|
| Accuracy function | |
| Decision maker | |
| Generalized score function | |
| Intuitionistic fuzzy set | |
| Interval-valued intuitionistic fuzzy | |
| Interval-valued intuitionistic fuzzy number | |
| Interval-valued intuitionistic fuzzy set | |
| Multiple-attribute decision making | |
| Multiple-attribute group decision making | |
| Negative ideal alternative | |
| Positive ideal alternative | |
| Preference order | |
| Score function | |
| Set pair analysis |
| Example No. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| and | |||||||||
| for | |||||||||
| and | |||||||||
| for | |||||||||
| and | |||||||||
| for | |||||||||
| … | |||||
|---|---|---|---|---|---|
| … | |||||
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| … |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kumar, S.; Mondal, S.R.; Tyagi, R. A Novel p-Norm-Based Ranking Algorithm for Multiple-Attribute Decision Making Using Interval-Valued Intuitionistic Fuzzy Sets and Its Applications. Axioms 2025, 14, 722. https://doi.org/10.3390/axioms14100722
Kumar S, Mondal SR, Tyagi R. A Novel p-Norm-Based Ranking Algorithm for Multiple-Attribute Decision Making Using Interval-Valued Intuitionistic Fuzzy Sets and Its Applications. Axioms. 2025; 14(10):722. https://doi.org/10.3390/axioms14100722
Chicago/Turabian StyleKumar, Sandeep, Saiful R. Mondal, and Reshu Tyagi. 2025. "A Novel p-Norm-Based Ranking Algorithm for Multiple-Attribute Decision Making Using Interval-Valued Intuitionistic Fuzzy Sets and Its Applications" Axioms 14, no. 10: 722. https://doi.org/10.3390/axioms14100722
APA StyleKumar, S., Mondal, S. R., & Tyagi, R. (2025). A Novel p-Norm-Based Ranking Algorithm for Multiple-Attribute Decision Making Using Interval-Valued Intuitionistic Fuzzy Sets and Its Applications. Axioms, 14(10), 722. https://doi.org/10.3390/axioms14100722






