Three Problems for Decision Rule Systems from Closed Classes

Abstract

The study of the relationships between DRSs (Decision Rule Systems) and DTs (Decision Trees) is of considerable interest in computer science. In this paper, we consider classes of DRSs that are closed under specific operations. First, we examine classes that are closed under the operation of the removal of features and analyze the functions characterizing the worst-case dependence of the minimum depth of DDTs (Deterministic Decision Trees) and NDTs (Nondeterministic Decision Trees), solving the task of finding all true DRs in a DRS on the number of different features in the system. Second, we extend our analysis to classes that are closed under the removal of features and rules, studying the worst-case behavior of the minimum DT depth for the task of finding at least one true DR. Third, we investigate classes closed under the removal of features and rules in the context of finding all right-hand sides of true DRs. We prove that, in all three cases, the corresponding functions characterizing the worst-case minimum depth of DTs are either bounded from above by a constant or grow linearly.

1. Introduction

DTs (Decision Trees) [1,2,3,4,5] and DRSs (Decision Rule Systems) [6,7,8,9,10,11] are common tools for structuring and expressing knowledge. They act as classifiers, providing predictions for unseen cases, and are also employed as algorithms in diverse domains such as fault diagnosis, combinatorial optimization, and beyond. Among classification and knowledge representation models, DTs and DRSs stand out for their high level of interpretability [12,13]. Exploring the connections and transformations between DTs and DRSs has become an important focus of research within computer science.

In this work, we examine classes of DRSs that are closed under certain operations. The operation of feature removal is natural: if we have a DRS but cannot work with one of its features because it is unavailable for some reason, we can remove this feature from the DR and try to work with the resulting DRS. Similarly, rule removal is a fundamental operation that allows us to disregard certain DRs while maintaining the structure of the system.

One of the main tasks associated with a DRS is to find, given a tuple of feature values, all DRs that are true on this tuple (that have a true left-hand side). To solve this task, we use DDTs (Deterministic Decision Trees) and NDTs (Nondeterministic Decision Trees). In addition, we consider two related tasks: finding at least one true DR in a DRS and finding all right-hand sides of true DRs.

For an arbitrary closed class of DRSs, we investigate functions that describe, in the worst-case scenario, how the minimal depth of DDTs and NDTs required to solve these problems depends on the number of distinct features in the system. Specifically, we analyze the task of finding all true DRs in classes closed under the removal of features, the task of finding at least one true DR in classes closed under the removal of features and rules, and the task of finding all right-hand sides of true DRs in classes closed under the same operations. We prove that, in all three cases, the behavior of these functions is such that they are bounded from above by a constant value or have linear growth.

In this paper, we continue to develop a syntactic approach to the study of the relationships between DRSs and DTs, outlined in [14,15]. This method relies on the assumption that we have access only to the DRS itself, without the underlying input data. An overview of earlier research in this area is presented primarily in one book [16]. In that book, we considered all three tasks: finding all true DRs, finding at least one true DR, and finding all right-hand sides of true DRs. However, unlike in this paper, we did not consider NDTs and classes of DRSs closed under specific operations.

Note that this paper is an extension of two conference papers: in [17], we analyzed the problem of finding all realizable rules, and in [18], we studied the problem of finding at least one realizable rule.

The structure of the paper is as follows. In Section 2, we provide the key definitions and notation, which are closely aligned with those in [16]. Section 3 is devoted to the presentation of the main results. Finally, Section 4 presents brief conclusions.

2. Definitions

This section introduces the notation and key definitions for DRSs and DTs.

2.1. DRSs—Decision Rule Systems

Let $N_0=\{0,1,2,\dots \}$ and $F=\{f_i:i\in N_0\}$. Elements of the set F will be called features. Let $k\in N_0\setminus \{0,1\}$. Let $E_k=\{0,1,\dots ,k-1\}$.

Let $E{S}_k$ represent the set of equation systems of the form

$$\{f_{i_1}=v_1,\dots ,f_{i_m}=v_m\},$$

where $m\in N_0$, $f_{i_1},\dots ,$$f_{i_m}\in F$ and $v_1,\dots ,v_m\in E_k$. We say that the system is inconsistent if there exist indices $t,p\in 1,\dots ,m$ with $t\ne p$, such that $i_t=i_p$ but $v_t\ne v_p$. Otherwise, the system of equations will be consistent.

Definition 1.

A k-DR (Decision Rule) is defined as an expression of the form

$$(f_{i_1}=v_1)\wedge \dots \wedge (f_{i_m}=v_m)\to \sigma ,$$

where $m\in N_0\setminus \left\{0\right\}$, $f_{i_1},\dots ,f_{i_m}$ are pairwise different features from F, $v_1,\dots ,$$v_m\in E_k$, and $\sigma \in N_0$.

This DR will be denoted by r. The expression $(f_{i_1}=v_1)\wedge \dots \wedge (f_{i_m}=v_m)$ is referred to as the left-hand side, while the value $\sigma$ is termed the right-hand side of r. The integer m is called the length of the DR and is written as $l\left(r\right)$. Let $Ft\left(r\right)=\{f_{i_1},\dots ,f_{i_m}\}$ and $K\left(r\right)=\{f_{i_1}=v_1,\dots ,f_{i_m}=v_m\}$. Two DRs, $r_1$ and $r_2$, will be called equal if $K\left(r_1\right)=K\left(r_2\right)$ and the right-hand sides of the DRs $r_1$ and $r_2$ are equal.

Definition 2.

A k-DRS (Decision Rule System) S is defined as a finite set of k-DRs.

We define $Ft\left(S\right)={\bigcup }_{r\in S}F\left(r\right)$, $D\left(S\right)$ as the set of right-hand sides of all DRs in S, and $l\left(S\right)=max\left\{l\right(r):r\in S\}$ for a nonempty DRS S. If $S=\varnothing$, then $Ft\left(S\right)=D\left(S\right)=\varnothing$ and $l\left(S\right)=0$.

Let $S\ne \varnothing$ and $Ft\left(S\right)=\{f_{j_1},\dots ,f_{j_n}\}$, where $j_1<\dots <j_n$. For $\overline{v}=(v_1,\dots ,v_n)\in E_k^n$, denote $K(S,\overline{v})=\{f_{j_1}=v_1,\dots ,f_{j_n}=v_n\}$.

A DR $r\in S$ is said to be true for a tuple $\overline{v}\in E_k^{\left|Ft\right(S\left)\right|}$ whenever $K\left(r\right)\subseteq K(S,\overline{v})$. We denote by $S\left(\overline{v}\right)$ the subset of S consisting of all such rules that hold for $\overline{v}$.

Definition 3.

All Rules task for a DRS S: given a tuple $\overline{v}\in E_k^{\left|Ft\right(S\left)\right|}$, determine the subset of rules $S\left(\overline{v}\right)$. This task will be denoted by $\mathcal{AR}\left(S\right)$.

Definition 4.

Some Rules task for a DRS S: given a tuple $\overline{v}\in E_k^{\left|Ft\right(S\left)\right|}$, determine a subset $Z\subseteq S$ such that

• Every rule in Z is true for the $\overline{v}$;
• If $Z=\varnothing$, then no rule from S is true for $\overline{v}$.

We denote this task as $\mathcal{SR}\left(S\right)$.

Definition 5.

All Decisions task for a DRS S: given $\overline{v}\in E_k^{\left|Ft\right(S\left)\right|}$, determine a subset $Z\subseteq S$ such that

• Every rule in Z is true for the $\overline{v}$;
• For every $\sigma \in D\left(S\right)\setminus D\left(Z\right)$, any DR from S with the right-hand side equal to σ is not true for the tuple $\overline{v}$.

We denote this task as $\mathcal{AD}\left(S\right)$.

We now define the operation of removal of a feature $f_i\in Ft\left(S\right)$ from the DRSS. Let $r\in S$. If $f_i\notin Ft\left(r\right)$, then denote $r_{f_i}=r$. If $f_i\in Ft\left(r\right)$, then denote by $r_{f_i}$ the DR derived from r by the removal from the left-hand side of r the equality containing the feature $f_i$. We denote $S\left(f_i\right)=\{r_{f_i}:r\in Ft\left(S\right),l\left(r_{f_i}\right)>0\}$. The DRS $S\left(f_i\right)$ is the result of applying to S the operation of removal feature $f_i$.

The operation of removal of a rule from the DRS S is defined in a natural way: we can remove from S an arbitrary DR.

Later, we will consider two types of closed classes of DRSs: classes of k-DRSs closed under the removal of features and classes of k-DRSs closed under the removal of features and rules.

It is easy to see that the empty DRS belongs to any closed class.

2.2. DTs—Decision Trees

A finite rooted directed tree is a finite directed tree with exactly one vertex that has no incoming edges, referred to as the root. Vertices with no outgoing edges are called leaves, while those that are neither root nor leaves are termed internal vertices. A complete path is a sequence $\xi =u_1,e_1,\dots ,u_m,e_m,u_{m+1}$ where $u_1$ is the root, $u_{m+1}$ is a leaf, and each $e_i$ connects $u_i$ to $u_{i+1}$ for $i=1,\dots ,m$.

Consider S to be a nonempty k-DRS.

Definition 6.

A DT (Decision Tree) over the DRS S is a finite rooted labeled directed tree $\mathcal{G}$ with at least two vertices, such that

• The root and its outgoing edges are not labeled;
• Every internal vertex of $\mathcal{G}$ is labeled by a feature from $Ft\left(S\right)$, and the edges leaving it are labeled by elements of $E_k$;
• Each leaf of $\mathcal{G}$ is labeled by a subset of S.

Definition 7.

A DT $\mathcal{G}$ over S is termed a DDT (Deterministic Decision Tree) if exactly one edge leaves from the root and, at every internal vertex, the outgoing edges are labeled with pairwise distinct labels.

Let $\mathcal{G}$ be a DT over S. Denote by $CP\left(\mathcal{G}\right)$ the set of all complete paths in the DT $\mathcal{G}$. For a complete path $\xi =u_1,e_1,\dots ,u_m,e_m,u_{m+1}$, we associate an equation system $K\left(\xi \right)\in E{S}_k$. If $m=1$ and $\xi =u_1,e_1,u_2$, then $K\left(\xi \right)=\varnothing$. For $m\ge 2$, each vertex $u_j$ ($j=2,\dots ,m$) is labeled by a feature $f_{i_j}$, and the edge $e_j$ is labeled with a value $v_j\in E_k$. In this case, $K\left(\xi \right)=\{f_{i_2}=v_2,\dots ,f_{i_m}=v_m\}$. We denote by $\tau \left(\xi \right)$ the collection of DRs attached to the leaf $u_{m+1}$.

Let $\mathcal{G}$ be a DT over S, $\overline{v}\in E_k^{\left|Ft\right(S\left)\right|}$, and $\xi \in CP\left(\mathcal{G}\right)$. The path $\xi$ is said to accept the tuple $\overline{v}$ whenever $K\left(\xi \right)\subseteq K(S,\overline{v})$.

For each of the three tasks under consideration, we give definitions of DTs that solve them nondeterministically. After each definition, we add some explanations about a complete path $\xi$ accepting a tuple $\overline{v}$ in a DT $\mathcal{G}$ that solves the task. In particular, these definitions and explanations entail Remarks 1, 2, and 3 below.

Definition 8.

We say that $\mathcal{G}$ nondeterministically solves the task $\mathcal{AR}\left(S\right)$ if, for every tuple $\overline{v}\in E_k^{\left|Ft\right(S\left)\right|}$, there exists a complete path $\xi \in CP\left(\mathcal{G}\right)$ that accepts $\overline{v}$, and each complete path ξ with a consistent equation system $K\left(\xi \right)$ satisfies the following:

• For every $r\in \tau \left(\xi \right)$, we have $K\left(r\right)\subseteq K\left(\xi \right)$.
• For every $r\in S\setminus \tau \left(\xi \right)$, the union $K\left(r\right)\cup K\left(\xi \right)$ is inconsistent.

In this situation, $\mathcal{G}$ is referred to as an NDT (Nondeterministic Decision Tree) solving $\mathcal{AR}\left(S\right)$.

Let $\mathcal{G}$ solve the task $\mathcal{AR}\left(S\right)$ nondeterministically, $\xi \in CP\left(\mathcal{G}\right)$, $\overline{v}\in E_k^{\left|Ft\right(S\left)\right|}$, and $\xi$ accept $\overline{v}$. This means that $K\left(\xi \right)\subseteq K(S,\overline{v})$. From this, it follows that $K\left(\xi \right)$ is consistent. Then, for any DR $r\in \tau \left(\xi \right)$, we have $K\left(r\right)\subseteq K\left(\xi \right)$ and $K\left(r\right)\subseteq K(S,\overline{v})$. Therefore, r is true for $\overline{v}$.

We also have that, for any DR $r\in S\setminus \tau \left(\xi \right)$, the system of equations $K\left(r\right)\cup K\left(\xi \right)$ is inconsistent. Since $K\left(\xi \right)\subseteq K(S,\overline{v})$, it follows that $K\left(r\right)\cup K(S,\overline{v})$ is also inconsistent. Therefore, r is not true for $\overline{v}$. Thus, $\tau \left(\xi \right)=S\left(\overline{v}\right)$.

Remark 1.

Let $\mathcal{G}$ solve the task $\mathcal{AR}\left(S\right)$ nondeterministically, $\xi \in CP\left(\mathcal{G}\right)$, $\overline{v}\in E_k^{\left|Ft\right(S\left)\right|}$, and ξ accept $\overline{v}$. Then, $\tau \left(\xi \right)=S\left(\overline{v}\right)$.

Definition 9.

We say that $\mathcal{G}$ nondeterministically solves the task $\mathcal{SR}\left(S\right)$ if, for every tuple $\overline{v}\in E_k^{\left|Ft\right(S\left)\right|}$, there exists a complete path $\xi \in CP\left(\mathcal{G}\right)$ that accepts $\overline{v}$, and each complete path ξ with consistent $K\left(\xi \right)$ satisfies the following:

• For each $r\in \tau \left(\xi \right)$, we have $K\left(r\right)\subseteq K\left(\xi \right)$.
• If $\tau \left(\xi \right)=\varnothing$, then $K\left(r\right)\cup K\left(\xi \right)$ is inconsistent for every $r\in S$.

In this case, $\mathcal{G}$ is called an NDT (Nondeterministic Decision Tree) that solves $\mathcal{SR}\left(S\right)$.

Let $\mathcal{G}$ solve the task $\mathcal{SR}\left(S\right)$ nondeterministically, $\xi \in CP\left(\mathcal{G}\right)$, $\overline{v}\in E_k^{\left|Ft\right(S\left)\right|}$, and $\xi$ accept $\overline{v}$. This means that $K\left(\xi \right)\subseteq K(S,\overline{v})$. From this, it follows that $K\left(\xi \right)$ is consistent. Then, for any DR $r\in \tau \left(\xi \right)$, we have $K\left(r\right)\subseteq K\left(\xi \right)$ and $K\left(r\right)\subseteq K(S,\overline{v})$. Therefore, r is true for $\overline{v}$.

If $\tau \left(\xi \right)=\varnothing$, then for any DR $r\in S$, the system of equations $K\left(r\right)\cup K\left(\xi \right)$ is inconsistent. Since $K\left(\xi \right)\subseteq K(S,\overline{v})$, it follows that $K\left(r\right)\cup K(S,\overline{v})$ is also inconsistent. Therefore, r is not true for $\overline{v}$.

Definition 10.

We say that $\mathcal{G}$ nondeterministically solves the task $\mathcal{AD}\left(S\right)$ if, for every tuple $\overline{v}\in E_k^{\left|Ft\right(S\left)\right|}$, there exists a complete path $\xi \in CP\left(\mathcal{G}\right)$ that accepts $\overline{v}$, and each complete path ξ with consistent $K\left(\xi \right)$ satisfies the following:

• For all $r\in \tau \left(\xi \right)$, we have the relation $K\left(r\right)\subseteq K\left(\xi \right)$.
• If $r\in S\setminus \tau \left(\xi \right)$ and the right-hand side of r does not belong to the set $D\left(\tau \right(\xi \left)\right)$, then the system of equations $K\left(r\right)\cup K\left(\xi \right)$ is inconsistent.

In this case, $\mathcal{G}$ is called an NDT (Nondeterministic Decision Tree) that solves $\mathcal{AD}\left(S\right)$.

Let $\mathcal{G}$ solve the task $\mathcal{AD}\left(S\right)$ nondeterministically, $\xi \in CP\left(\mathcal{G}\right)$, $\overline{v}\in E_k^{\left|Ft\right(S\left)\right|}$, and $\xi$ accept $\overline{v}$. This means that $K\left(\xi \right)\subseteq K(S,\overline{v})$. From this, it follows that $K\left(\xi \right)$ is consistent. Then, for any DR $r\in \tau \left(\xi \right)$, we have $K\left(r\right)\subseteq K\left(\xi \right)$ and $K\left(r\right)\subseteq K(S,\overline{v})$. Therefore, r is true for $\overline{v}$.

If $r\in S\setminus \tau \left(\xi \right)$ and the right-hand side of r is not contained in $D\left(\tau \right(\xi \left)\right)$, then the union $K\left(r\right)\cup K\left(\xi \right)$ is inconsistent. Because $K\left(\xi \right)\subseteq K(S,\overline{v})$, this implies that $K\left(r\right)\cup K(S,\overline{v})$ is also inconsistent. Therefore, r is not true for $\overline{v}$.

Remark 2.

Let $\mathcal{T}\in \{\mathcal{AR},\mathcal{SR},\mathcal{AD}\}$, $\mathcal{G}$ solve the task $\mathcal{T}\left(S\right)$ nondeterministically, $\xi \in CP\left(\mathcal{G}\right)$, $\overline{v}\in E_k^{\left|Ft\right(S\left)\right|}$, ξ accept $\overline{v}$, and $\tau \left(\xi \right)=\varnothing$. Then, for any DR $r\in S$, the system of equations $K\left(r\right)\cup K\left(\xi \right)$ is inconsistent, and the DR r is not true for $\overline{v}$.

Remark 3.

Let $\mathcal{T}\in \{\mathcal{AR},\mathcal{SR},\mathcal{AD}\}$, $\mathcal{G}$ solve the task $\mathcal{T}\left(S\right)$ nondeterministically, $\xi \in CP\left(\mathcal{G}\right)$, $\overline{v}\in E_k^{\left|Ft\right(S\left)\right|}$, ξ accept $\overline{v}$, and $S\left(\overline{v}\right)=\varnothing$. Then, $\tau \left(\xi \right)=\varnothing$.

Definition 11.

Let $\mathcal{T}\in \{\mathcal{AR},\mathcal{SR},\mathcal{AD}\}$. We say that $\mathcal{G}$ solves the task $\mathcal{T}\left(S\right)$ deterministically if it is a DDT (Deterministic Decision Tree) that also solves task $\mathcal{T}\left(S\right)$ in the nondeterministic sense. In this case, $\mathcal{G}$ is referred to as a DDT solving $\mathcal{T}\left(S\right)$.

Definition 12.

For each complete path $\xi \in CP\left(\mathcal{G}\right)$, let $h\left(\xi \right)$ denote the number of internal nodes along ξ. The value $h\left(\mathcal{G}\right)=max\left\{h\right(\xi ):\xi \in CP(\mathcal{G}\left)\right\}$ is defined as the depth of the DT $\mathcal{G}$.

Let S be a nonempty k-DRS and let $\mathcal{T}\in \mathcal{AR},\mathcal{SR},\mathcal{AD}$. Define $h_{\mathcal{T}}^d\left(S\right)$ as the minimum depth of a DDT over S that solves $\mathcal{T}\left(S\right)$, and $h_{\mathcal{T}}^a\left(S\right)$ as the minimum depth of an NDT over S that solves $\mathcal{T}\left(S\right)$. For the empty system $S=\varnothing$, we set $h_{\mathcal{T}}^d\left(S\right)=h_{\mathcal{T}}^a\left(S\right)=0$.

3. Main Results

Let $\mathcal{T}\in \{\mathcal{AR},\mathcal{SR},\mathcal{AD}\}$, and C be a class of k-DRSs closed under the removal of features if $\mathcal{T}=\mathcal{AR}$; otherwise, C is a class of k-DRSs closed under the removal of features and rules. In this section, we investigate the functions $H_{C,\mathcal{T}}^d:N_0\to N_0$ and $H_{C,\mathcal{T}}^a:N_0\to N_0$, which are defined as follows. Let $n\in N_0$, then

$$\begin{array}{cc}\hfill H_{C,\mathcal{T}}^d\left(n\right)& =max\{h_{\mathcal{T}}^d\left(S\right):S\in C,|Ft\left(S\right)|\le n\},\hfill \\ \hfill H_{C,\mathcal{T}}^a\left(n\right)& =max\{h_{\mathcal{T}}^a\left(S\right):S\in C,|Ft\left(S\right)|\le n\}.\hfill \end{array}$$

These functions characterize the minimum depth of DTs solving the task $\mathcal{T}$ for systems from the closed class C growthin the worst case with the growth of the number of different features in the DRSs. In the case of the function $H_{C,\mathcal{T}}^d$, we consider DDTs, and in the case of the functions $H_{C,\mathcal{T}}^a$, we consider NDTs. We begin by establishing several auxiliary results.

Lemma 1.

For any k-DRS S and $\mathcal{T}\in \{\mathcal{AR},\mathcal{SR},\mathcal{AD}\}$, the inequality $h_{\mathcal{T}}^d\left(S\right)\le \left|Ft\left(S\right)\right|$ holds.

Proof. 

If the DRS S is empty, then $h_{\mathcal{T}}^d\left(S\right)=\left|Ft\left(S\right)\right|=0$. Let S be a nonempty DRS. It is easy to show that we can construct a DDT solving the task $\mathcal{T}\left(S\right)$ by the sequential computation of all features from $Ft\left(S\right)$. The depth of this DT is equal to $\left|Ft\right(S\left)\right|$. Thus, $h_{\mathcal{T}}^d\left(S\right)\le \left|Ft\left(S\right)\right|$. □

Lemma 2.

Let $\mathcal{T}\in \{\mathcal{AR},\mathcal{SR},\mathcal{AD}\}$, and C be a class of k-DRSs closed under the removal of features if $\mathcal{T}=\mathcal{AR}$; otherwise, C is a class of k-DRSs closed under the removal of features and rules. Then, for any $n\in N_0$, the values $H_{C,\mathcal{T}}^d\left(n\right)$ and $H_{C,\mathcal{T}}^a\left(n\right)$ are defined and the inequalities $0\le H_{C,\mathcal{T}}^a\left(n\right)\le H_{C,\mathcal{T}}^d\left(n\right)\le n$ hold.

Proof. 

Let $S\in C$. If the DRS S is empty, then $h_{\mathcal{T}}^a\left(S\right)=h_{\mathcal{T}}^d\left(S\right)=\left|Ft\left(S\right)\right|=0$. Let S be a nonempty DRS. It is clear that any DDT solving the task $\mathcal{T}\left(S\right)$ is an NDT solving the task $\mathcal{T}\left(S\right)$. Therefore $h_{\mathcal{T}}^a\left(S\right)\le h_{\mathcal{T}}^d\left(S\right)$. From Lemma 1, it follows that $h_{\mathcal{T}}^d\left(S\right)\le \left|Ft\left(S\right)\right|$. From all of the above, the statement of the lemma follows. □

Lemma 3.

Let $\mathcal{T}\in \{\mathcal{AR},\mathcal{SR},\mathcal{AD}\}$, and C be a class of k-DRSs closed under the removal of features if $\mathcal{T}=\mathcal{AR}$; otherwise, C is a class of k-DRSs closed under the removal of features and rules. If the value $\left|Ft\right(S\left)\right|$ for DRSs $S\in C$ is bounded from above by a positive constant b, then for any $n\in N_0$,

$$0\le H_{C,\mathcal{T}}^a\left(n\right)\le H_{C,\mathcal{T}}^d\left(n\right)\le b.$$

Proof. 

Let the value $\left|Ft\right(S\left)\right|$ for DRSs $S\in C$ be bounded from above by a positive constant b. Using Lemma 1, we obtain that for any $S\in C$, $h_{\mathcal{T}}^d\left(S\right)\le \left|Ft\left(S\right)\right|\le b$. Therefore, $H_{C,\mathcal{T}}^d\left(n\right)\le b$ for any $n\in N_0$. Using Lemma 2, we obtain that $0\le H_{C,\mathcal{T}}^a\left(n\right)\le H_{C,\mathcal{T}}^d\left(n\right)\le b$ for any $n\in N_0$. □

Lemma 4.

Let C be a class of k-DRSs closed under the removal of features, and let the value $\left|Ft\right(S\left)\right|$ for systems $S\in C$ not be bounded from above. If the value $l\left(S\right)$ for systems $S\in C$ is not bounded from above, then for any $n\in N_0\setminus \left\{0\right\}$, there exists a DRS $S^{\prime }$ from C with $\left|Ft\right(S^{\prime }\left)\right|=n$ that contains a DR of the length n.

Proof. 

Let $n\in N_0\setminus \left\{0\right\}$. Let S be a system from C such that $l\left(S\right)\ge n$, and r be a DR from S, the length of which is at least n. We remove from r (and from $S)$ $l\left(r\right)-n$ features and obtain a DR $r^{\prime }$ of the length n. We also remove from S all features that do not belong to the set $Ft\left(r^{\prime }\right)$. As a result, we obtain a DRS $S^{\prime }$ from C with $\left|Ft\right(S^{\prime }\left)\right|=n$ containing the DR $r^{\prime }$ of length n. □

Lemma 5.

Let C be a class of k-DRSs closed under the removal of features, and the value $\left|Ft\right(S\left)\right|$ for systems $S\in C$ be not bounded from above. If the value $l\left(S\right)$ for system $S\in C$ is bounded from above, then for any $n\in N_0\setminus \left\{0\right\}$, there is a DRS $S^{*}$ from C with $\left|Ft\right(S^{*}\left)\right|=n$ that contains n DRs of length 1 with pairwise different features.

Proof. 

Let the value $l\left(S\right)$ for DRSs $S\in C$ be bounded from above by a positive integer l.

Let $t\in N_0\setminus \left\{0\right\}$ and $S\in C$. We denote by $S_t$ the set of DRs from S, the length of which is equal to t. We know that the value $\left|Ft\right(S\left)\right|$ for DRSs $S\in C$ is not bounded from above by a constant. We now show that there exists $t\in \{1,\dots ,l\}$ for which the value $\left|Ft\right(S_t\left)\right|$ for DRSs $S\in C$ is not bounded from above by a constant. Assume the contrary. Then, there exists a positive constant b such that, for any $t\in \{1,\dots ,l\}$, the value $\left|Ft\right(S_t\left)\right|$ for DRSs $S\in C$ is at most b. It is clear that $\left|Ft\right(S_t\left)\right|=0$ if $t>l$. Therefore, for any $S\in C$, $\left|Ft\left(S\right)\right|\le |Ft\left(S_1\right)|+\dots +|Ft\left(S_l\right)|$. As a result, we obtain that $\left|Ft\right(S\left)\right|\le bl$ for any $S\in C$, which is impossible.

We denote by $t_0$ the minimum number $t\in \{1,\dots ,l\}$ for which the value $\left|Ft\right(S_t\left)\right|$ for DRSs $S\in C$ is not bounded from above by a constant. We will show that $t_0=1$.

Let $S\in C$ and $r\in S$. The set $Ft\left(r\right)$ will be called the type of the DR r. For $f_i\in Ft\left(S\right)$, we denote by $d_{f_i}\left(S\right)$ the number of DRs $\rho \in S$ with pairwise different types such that $f_i\in Ft\left(\rho \right)$. Denote $d\left(S\right)=max\{d_{f_i}\left(S\right):f_i\in Ft\left(S\right)\}$.

First, we consider the case when the value $d\left(S_{t_0}\right)$ for DRSs $S\in C$ is bounded from above by a positive integer d. Let $n\in N_0\setminus \left\{0\right\}$ and S be a DRS from C for which $|Ft\left(S_{t_0}\right)|\ge nd(t_0-1)$. Denote $Q=S_{t_0}$. Choose a feature $f_{i_1}\in Ft\left(Q\right)$ and remove from the DRSs Q and S all features with the exception of $f_{i_1}$, which belong to DRs $\rho \in Q$, such that $f_{i_1}\in Ft\left(\rho \right)$. As a result, we remove at most $d(t_0-1)$ features and obtain DRSs $Q^1$ and $S^1$. One can show that $|Ft\left(Q^1\right)|\ge (n-1)d(t_0-1)$, $d\left(Q^1\right)\le d$, and $l\left(Q^1\right)\le t_0$. If $n>1$, choose a feature $f_{i_2}\in Ft\left(Q^1\right)$ different from $f_{i_1}$ and remove from the DRSs $Q^1$ and $S^1$ all features with the exception of $f_{i_2}$, which belong to DRs $\rho \in Q^1$ such that $f_{i_2}\in Ft\left(\rho \right)$. We denote by $Q^2$ and $S^2$ the obtained DRSs, etc. We repeat the described procedure n times and obtain DRSs $Q^n$ and $S^n$. In each of these DRSs, there are n pairwise different features $f_{i_1},\dots ,f_{i_n}$ and n DRs $r_1,\dots ,r_n$ such that, for $j=1,\dots ,n$, $l\left(r_j\right)=1$ and $Ft\left(r_j\right)=\left\{f_{i_j}\right\}$. Moreover, $S^n\in C$. Since n is an arbitrary number from $N_0\setminus \left\{0\right\}$, we obtain that the value $\left|Ft\right(S_1\left)\right|$ for DRSs $S\in C$ is not bounded from above by a constant. Therefore, $t_0=1$.

We now consider the case when the value $d\left(S_{t_0}\right)$ for DRSs $S\in C$ is not bounded from above by a constant. We will prove that $t_0=1$. Let us assume the contrary: $t_0>1$. Let $n\in N_0\setminus \left\{0\right\}$. Choose a DRS $S\in C$ such that $d\left(S_{t_0}\right)\ge n^{t_0-1}$. Let $f_i\in Ft\left(S_{t_0}\right)$ and $d_{f_i}\left(S_{t_0}\right)=d\left(S_{t_0}\right)$. Remove the feature $f_i$ from the DRS S. As a result, we obtain a DRS $S^{\prime }$ from C, which contains a number of DRs of the length $t_0-1$. Let us show that these DRs contain at least n pairwise different features. Let us assume the contrary: the considered DRs contain only $m<n$ pairwise different features. Then, the number of different types of DRs of length $t_0$ in S that contain the feature $f_i$ is at most the number of different subsets of the cardinality $t_0-1$ of the set of considered m features, which is at most $m^{t_0-1}$. Evidently, $m^{t_0-1}<n^{t_0-1}$, but this is impossible, since $d_{f_i}\left(S_{t_0}\right)\ge n^{t_0-1}$. Taking into account that n is an arbitrary number from $N_0\setminus \left\{0\right\}$, we obtain that the value $\left|Ft\right(S_{t_0-1}\left)\right|$ for DRSs $S\in C$ is not bounded from above by a constant. We obtained the contradiction. Thus, $t_0=1$.

Let $n>0$ and S be a DRS from C for which $\left|Ft\right(S_1\left)\right|\ge n$. We remove from S all features with the exception of n pairwise different features from $Ft\left(S_1\right)$. We denote by $S^{*}$ the obtained DRS from C. It is clear that $\left|Ft\right(S^{*}\left)\right|=n$ and $S^{*}$ contains n DRs $r_1,\dots ,r_n$ of length 1 with pairwise different features. □

We will now formulate and prove the main results of this paper.

Theorem 1.

Let C be a class of k-DRSs closed under the removal of features. Then

(a) If the value $\left|Ft\right(S\left)\right|$ for DRSs $S\in C$ is bounded from above by a positive constant b, then $0\le H_{C,\mathcal{AR}}^a\left(n\right)\le H_{C,\mathcal{AR}}^d\left(n\right)\le b$ for any $n\in N_0$.

(b) Otherwise, $H_{C,\mathcal{AR}}^a\left(n\right)=H_{C,\mathcal{AR}}^d\left(n\right)=n$, for any $n\in N_0$.

Proof. 

(a) This statement follows from Lemma 3.

(b) Let the value $\left|Ft\right(S\left)\right|$ for DRSs $S\in C$ be not bounded from above by a positive constant. We now consider two possibilities.

(b.1) Let the value $l\left(S\right)$ for DRSs $S\in C$ be not bounded from above by a constant. Let $n\in N_0$. We now show that $H_{C,\mathcal{T}}^a\left(n\right)\ge n$. It is clear that $H_{C,\mathcal{T}}^a\left(0\right)=0$. Let $n>0$. From Lemma 4, it follows that there exists a DRS $S^{\prime }$ from C with $\left|Ft\right(S^{\prime }\left)\right|=n$ containing a DR $r^{\prime }$ of the length n.

Let $\mathcal{G}$ be an NDT over $S^{\prime }$ that solves the task $\mathcal{AR}\left(S^{\prime }\right)$ and satisfies $h\left(\mathcal{G}\right)=h_{\mathcal{AR}}^a\left(S^{\prime }\right)$. Consider a tuple $\overline{v}\in E_k^n$ for which the DR $r^{\prime }$ is true. Then there exists a complete path $\xi \in CP\left(\mathcal{G}\right)$ that accepts the tuple $\overline{v}$. By Remark 1, the set $\tau \left(\xi \right)$ associated with the leaf of $\xi$ coincides with $S\left(\overline{v}\right)$, the set of rules in S that are true for $\overline{v}$. In particular, $r^{\prime }\in \tau \left(\xi \right)$. Hence, it follows that the relation $K\left(r^{\prime }\right)\subseteq K\left(\xi \right)$ holds, and therefore $h\left(\xi \right)\ge n$ and $h_{\mathcal{AR}}^a\left(S^{\prime }\right)=h\left(\mathcal{G}\right)\ge n$. Since $\left|Ft\right(S^{\prime }\left)\right|=n$, we obtain $H_{C,\mathcal{AR}}^a\left(n\right)\ge n$. From Lemma 2 we have $H_{C,\mathcal{AR}}^a\left(n\right)=H_{C,\mathcal{AR}}^d\left(n\right)=n$.

(b.2) Let the value $l\left(S\right)$ for DRSs $S\in C$ be bounded from above by a positive integer l. Let $n\in N_0$. We now show that $H_{C,\mathcal{T}}^a\left(n\right)\ge n$ for any $n\in N_0$. It is clear that $H_{C,\mathcal{T}}^a\left(0\right)=0$. Let $n>0$. From Lemma 5, this implies the existence of a DRS $S^{*}$ from C with $\left|Ft\right(S^{*}\left)\right|=n$ that contains n DRs $r_1,\dots ,r_n$ of length 1 with pairwise different features.

Let $\mathcal{G}$ be an NDT over $S^{*}$, which solves the task $\mathcal{AR}\left(S^{*}\right)$ and for which $h\left(\mathcal{G}\right)=h_{\mathcal{AR}}^a\left(S^{*}\right)$. Let $\overline{v}\in E_k^n$ be a tuple for which the DRs $r_1,\dots ,r_n$ are true. Then there exists a path $\xi \in CP\left(\mathcal{G}\right)$, which accepts the tuple $\overline{v}$. From Remark 1, it follows that the set $\tau \left(\xi \right)$ attached to the leaf vertex of $\xi$ coincides with the set $S\left(\overline{v}\right)$ of DRs from S that are true for the tuple $\overline{v}$. In particular, $\{r_1,\dots ,r_n\}\subseteq \tau \left(\xi \right)$. From here it follows that the relation $K\left(r_j\right)\subseteq K\left(\xi \right)$ holds for $j=1,\dots ,n$. Therefore $h\left(\xi \right)\ge n$ and $h_{\mathcal{AR}}^a\left(S^{*}\right)=h\left(\mathcal{G}\right)\ge n$. Taking into account that $\left|Ft\right(S^{*}\left)\right|=n$, we obtain $H_{C,\mathcal{AR}}^a\left(n\right)\ge n$. From Lemma 2 it follows that $H_{C,\mathcal{AR}}^a\left(n\right)=H_{C,\mathcal{AR}}^d\left(n\right)=n$. □

Theorem 2.

Let $\mathcal{T}\in \{\mathcal{SR},\mathcal{AD}\}$, and C be a class of k-DRSs closed under the removal features and rules. Then,

(a) If the value $\left|Ft\right(S\left)\right|$ for DRSs $S\in C$ is bounded from above by a positive constant b, then $0\le H_{C,\mathcal{T}}^a\left(n\right)\le H_{C,\mathcal{T}}^d\left(n\right)\le b$ for any $n\in N_0$.

(b) Otherwise, $H_{C,\mathcal{T}}^a\left(n\right)=H_{C,\mathcal{T}}^d\left(n\right)=n$, for any $n\in N_0$.

Proof. 

(a) This statement follows from Lemma 3.

(b) Let the value $\left|Ft\right(S\left)\right|$ for DRSs $S\in C$ be not bounded from above by a positive constant. We now consider two possibilities.

(b.1) Let the value $l\left(S\right)$ for DRSs $S\in C$ be not bounded from above by a constant. Let $n\in N_0$. We now show that $H_{C,\mathcal{T}}^a\left(n\right)\ge n$. It is clear that $H_{C,\mathcal{T}}^a\left(0\right)=0$. Let $n>0$. From Lemma 4, it follows that there exists a DRS $S^{\prime }$ from C with $\left|Ft\right(S^{\prime }\left)\right|=n$ containing a DR $r^{\prime }$ of length n. Denote by $S^{″}$ the DRS obtained from $S^{\prime }$ by removal of all DRs with the exception of $r^{\prime }$. Then, $S^{″}\in C$.

Let $\mathcal{G}$ be an NDT over $S^{″}$, which solves the task $\mathcal{T}\left(S^{″}\right)$ and for which $h\left(\mathcal{G}\right)=h_{\mathcal{T}}^a\left(S^{″}\right)$. Let $\overline{v}\in E_k^n$ be a tuple for which the DR $r^{\prime }$ is true. Then there exists a path $\xi \in CP\left(\mathcal{G}\right)$, which accepts the tuple $\overline{v}$. Using Remark 2 and taking into account that there is only $r^{\prime }$, and it is true for $\overline{v}$, we obtain $\tau \left(\xi \right)=\left\{r^{\prime }\right\}$. From here, we have $K\left(r^{\prime }\right)\subseteq K\left(\xi \right)$. Therefore, $h\left(\xi \right)\ge n$ and $h_{\mathcal{T}}^a\left(S^{″}\right)=h\left(\mathcal{G}\right)\ge n$. Since $\left|Ft\right(S^{″}\left)\right|=n$, we obtain $H_{C,\mathcal{T}}^a\left(n\right)\ge n$. From Lemma 2 it follows that $H_{C,\mathcal{T}}^a\left(n\right)=H_{C,\mathcal{T}}^d\left(n\right)=n$.

(b.2) Let the value $l\left(S\right)$ for DRSs $S\in C$ be bounded from above by a positive integer l. Let $n\in N_0$. We now show that $H_{C,\mathcal{T}}^a\left(n\right)\ge n$ for any $n\in N_0$. It is clear that $H_{C,\mathcal{T}}^a\left(0\right)=0$. Let $n>0$. From Lemma 5, it follows that there exists a DRS $S^{*}$ from C with $\left|Ft\right(S^{*}\left)\right|=n$ that contains n DRs $r_1,\dots ,r_n$ of the length 1 with pairwise different features. Denote by $S^{**}$ the DRS obtained from $S^{*}$ by removal of all DRs with the exception of $r_1,\dots ,r_n$. Then, $S^{**}\in C$.

Let $\mathcal{G}$ be an NDT over $S^{**}$, which solves the task $\mathcal{T}\left(S^{**}\right)$ and for which $h\left(\mathcal{G}\right)=h_{\mathcal{T}}^a\left(S^{**}\right)$. Let $\overline{v}\in E_k^n$ be a tuple for which all the DRs $r_1,\dots ,r_n$ are not true. Then, there exists a path $\xi \in CP\left(\mathcal{G}\right)$, which accepts the tuple $\overline{v}$. Using Remark 3, we obtain $\tau \left(\xi \right)=\varnothing$. By Remark 2, we see that $K\left(\xi \right)\cup K\left(r_j\right)$ is inconsistent for $j=1,\dots ,n$. Therefore $h\left(\xi \right)\ge n$ and $h_{\mathcal{T}}^a\left(S^{**}\right)=h\left(\mathcal{G}\right)\ge n$. Taking into account that $\left|Ft\right(S^{**}\left)\right|=n$, we obtain $H_{C,\mathcal{T}}^a\left(n\right)\ge n$. From Lemma 2 it follows that $H_{C,\mathcal{T}}^a\left(n\right)=H_{C,\mathcal{T}}^d\left(n\right)=n$. □

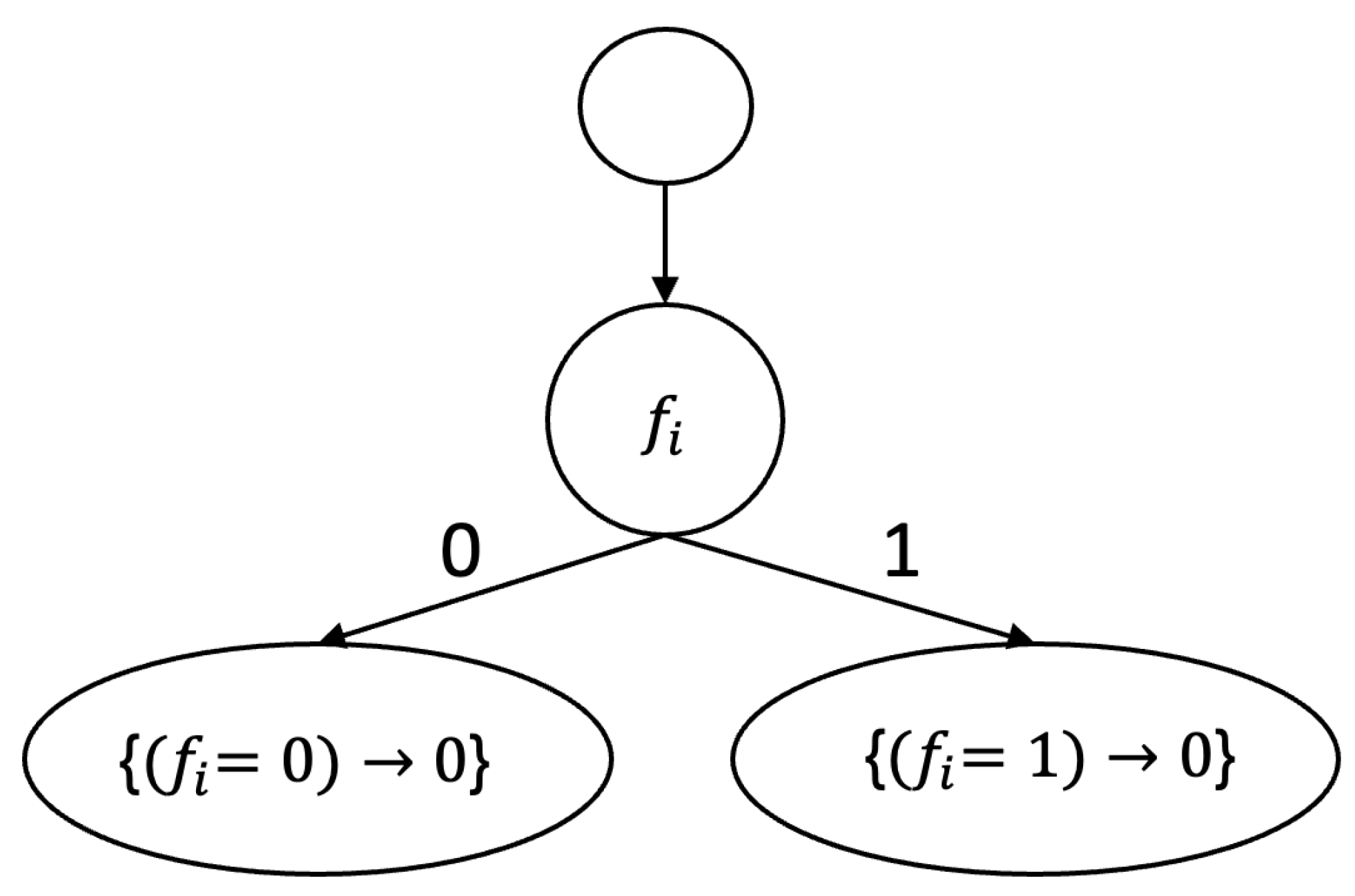
Let $\mathcal{T}\in \{\mathcal{SR},\mathcal{AD}\}$, and C be a class of DRS closed under the operation of removal of features only. We now show that in this case the functions $H_{C,\mathcal{T}}^a$ and $H_{C,\mathcal{T}}^d$ can be bounded from above by a constant even if the value $\left|Ft\right(S\left)\right|$ for DRSs $S\in C$ is not bounded from above by a constant.

Let B be a finite subset of the set $F=\{f_i:i\in N_0\}$. Denote $S_B=\{(f_i=0)\to 0,(f_i=1)\to 0:i\in B\}$. Let us consider the class $C=\{S_B:B\mathrm{is}\mathrm{a}\mathrm{finite}\mathrm{subset}\mathrm{of}A\}$ of 2-DRSs. One can show that the class C is closed under the removal of features, and the value $\left|Ft\right(S_B\left)\right|$ for DRSs $S_B\in C$ is not bounded from above by a constant. Let $S_B\in C$, B be nonempty, and $f_i\in B$. Then, the DDT depicted in Figure 1 solves the task $\mathcal{T}\left(S_B\right)$. Therefore, the functions $H_{C,\mathcal{T}}^a$ and $H_{C,\mathcal{T}}^d$ are bounded from above by the constant 1.

4. Conclusions

In this paper, for arbitrary closed classes of DRSs, we investigated the functions characterizing the worst-case dependence of the minimum depth of DDTs and NDTs on the number of different features in the DRS for three tasks:

• Finding all true DRs in a DRS, considering classes closed under the removal of features operation.
• Determining whether at least one true DR exists, considering classes closed under the removal of features and rules.
• Finding all right-hand sides of true DRs in a DRS, considering classes closed under the removal of features and rules.

It was proven that, in all three cases, the functions describing the worst-case depth of DTs are either bounded from above by a constant or grow linearly. In the future, we plan to extend this study to further tasks of DRSs and DTs.