High-Order Time–Space Compact Difference Methods for Semi-Linear Sobolev Equations
Abstract
1. Introduction
2. Two-Level High-Order Compact Difference Method
2.1. The Two-Level High-Order Compact Difference Method
2.1.1. The Numerical Method Derivation
| Algorithm 1 The computational implementation of HOCDM (14) and (15) |
, |
2.1.2. The Convergence of the Two-Level HOCDM
3. Richardson Extrapolation Technique
| Algorithm 2 The computational implementation of the Richardson extrapolation method ((14) and (15), (33)) |
|
4. The Three-Level HOCDM
4.1. Derivation of the Three-Level HOCDM
| Algorithm 3 The computational implementation of the three-level HOCDM ((50)–(54)) |
|
4.2. The Convergence of the Three-Level HOCDM
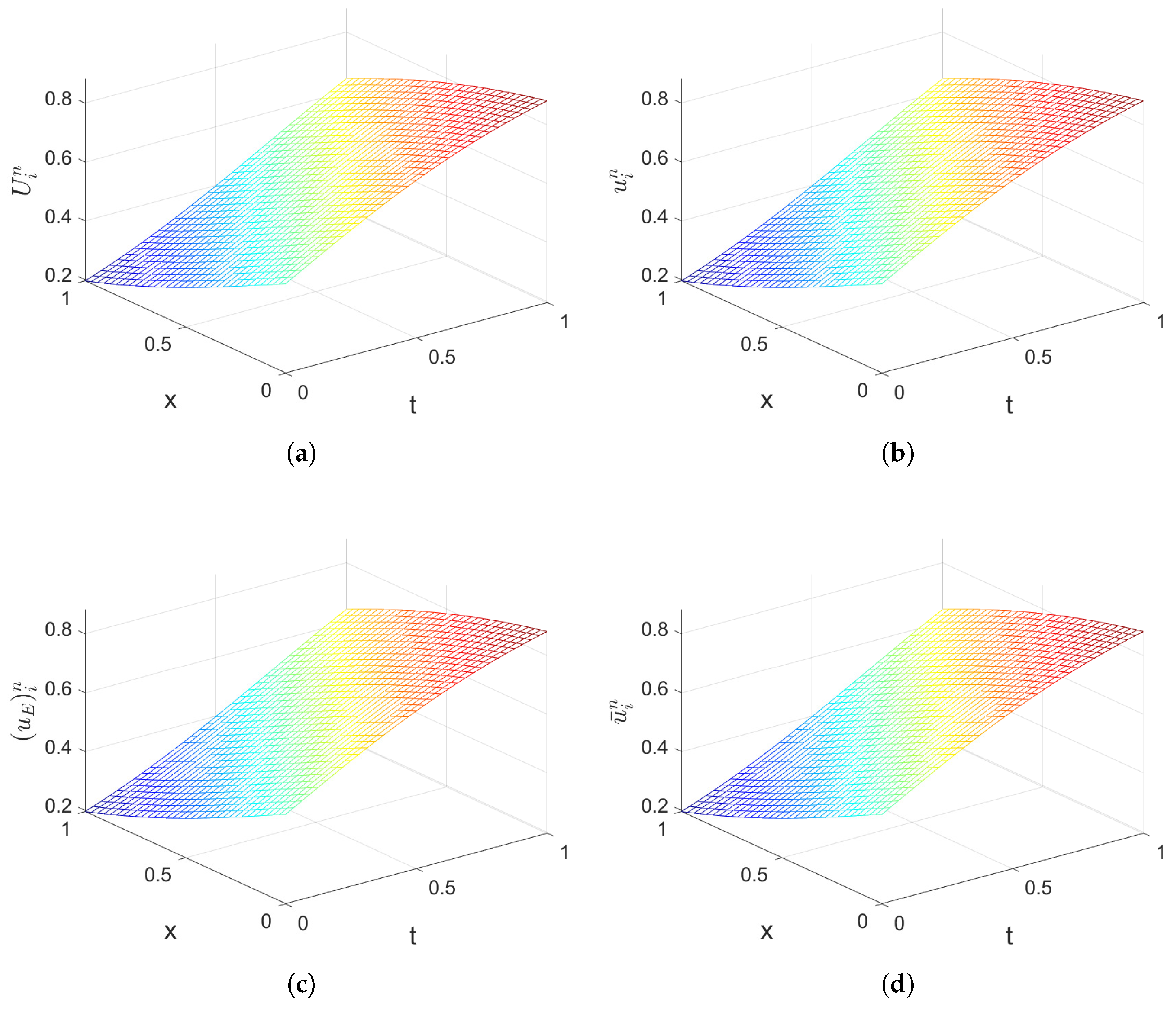
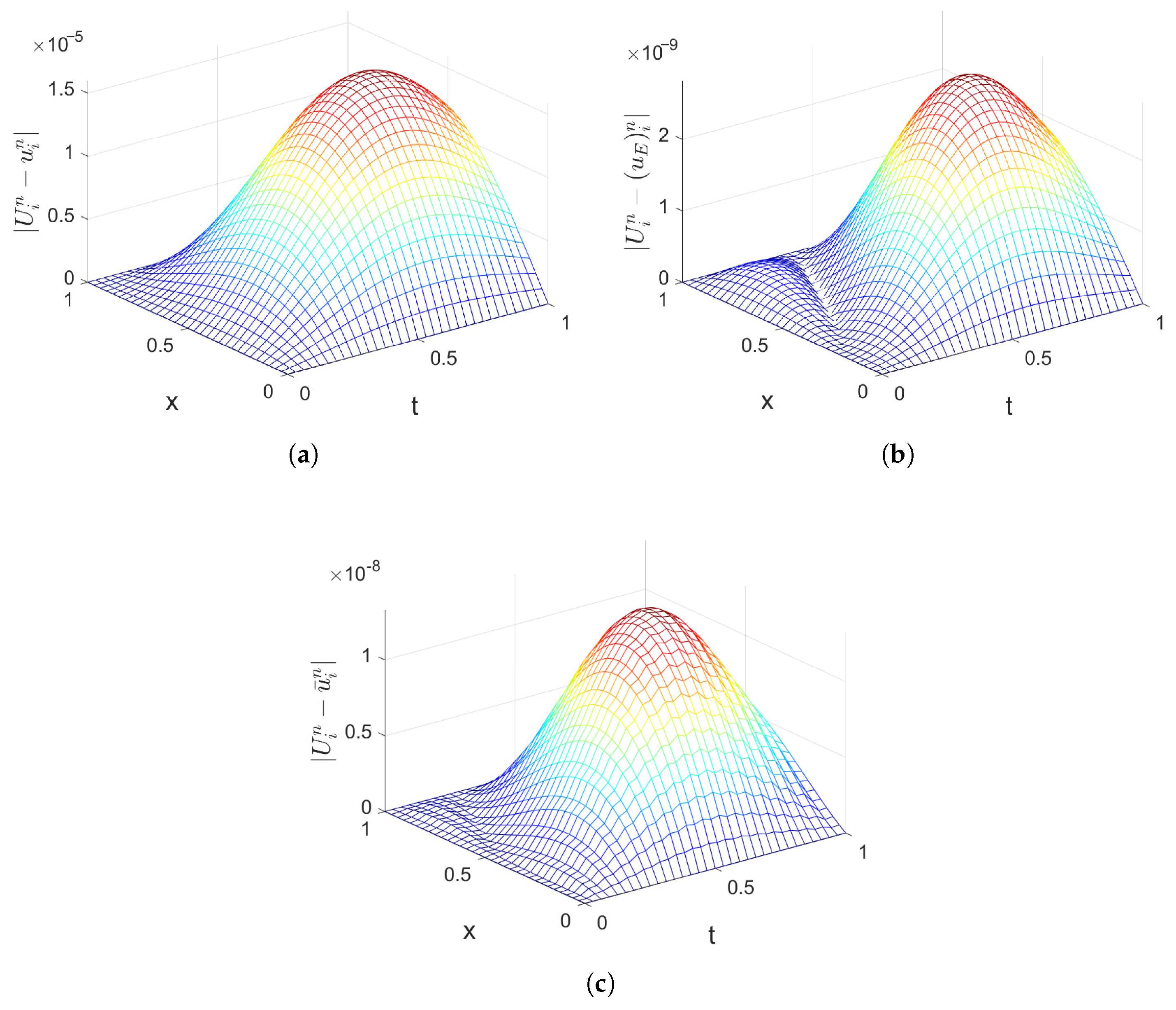
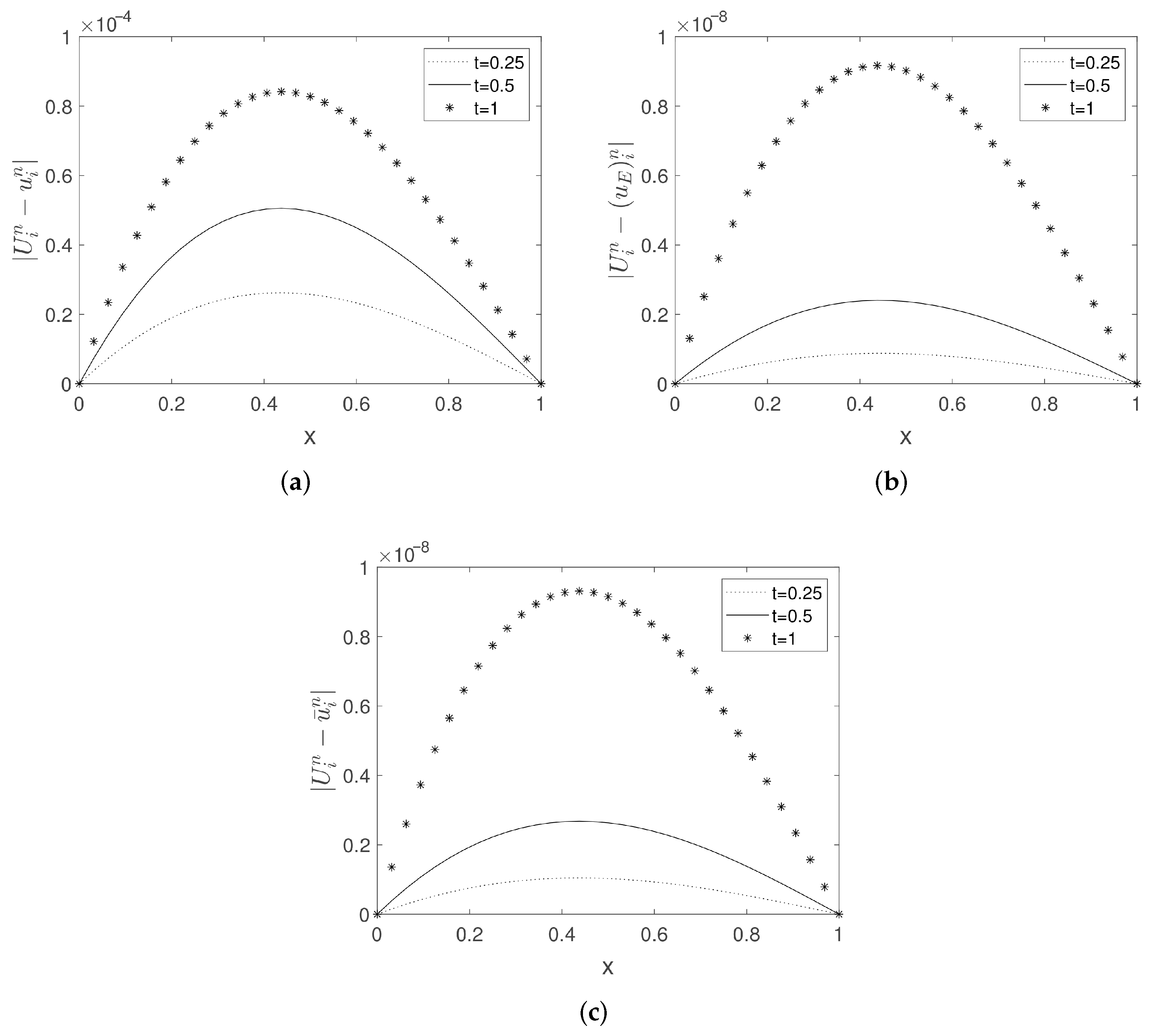
5. Numerical Experiments
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Barenblatt, G.; Zheltov, I.; Kochina, I. Basic concepts in the theory of seepage of homogeneous liquids in fissured rocks. J. Appl. Math. Mech. 1960, 24, 1286–1303. [Google Scholar] [CrossRef]
- Shi, D. On the initial boundary value problem of nonlinear the equation of the migratiion of the moisture in soil. Acta Math. Appl. Sin. 1990, 13, 31–38. [Google Scholar]
- Ting, T.W. A cooling process according to two-temperature theory of heat conduction. J. Math. Anal. Appl. 1974, 45, 23–31. [Google Scholar] [CrossRef]
- Gu, H. Characteristic finite element methods for nonlinear sobolev equations. Appl. Math. Comput. 1999, 102, 51–62. [Google Scholar] [CrossRef]
- Gao, F.; Cui, J.; Zhao, G. Weak galerkin finite element methods for sobolev equation. J. Comput. Appl. Math. 2017, 317, 188–202. [Google Scholar] [CrossRef]
- Tran, T.; Duong, T.B. A posteriori error estimates with the finite element method of lines for a sobolev equation. Numer. Meth. Partial Differ. Equ. 2005, 21, 521–535. [Google Scholar] [CrossRef]
- Zeng, Y.; Luo, Z. The reduced-dimension technique for the unknown solution coefficient vectors in the Crank-Nicolson finite element method for the sobolev equation. J. Math. Anal. Appl. 2022, 513, 126207. [Google Scholar] [CrossRef]
- Abbaszadeh, M.; Dehghan, M. Interior penalty discontinuous Galerkin technique for solving generalized Sobolev equation. Appl. Numer. Math. 2020, 154, 172–186. [Google Scholar] [CrossRef]
- Wang, J.; Li, Q. Superconvergence analysis of a linearized three-step backward differential formula finite element method for nonlinear Sobolev equation. Math. Meth. Appl. Sci. 2019, 42, 3359–3376. [Google Scholar] [CrossRef]
- Xu, Y.; Zhou, Z.; Zhao, J. Conforming Virtual Element Methods for Sobolev Equations. J. Sci. Comput. 2022, 93, 32. [Google Scholar] [CrossRef]
- Liu, W.; Chen, Y.P.; Liang, Q. Unified analysis of conforming and nonconforming virtual element methods for nonlinear Sobolev equations. Calcolo 2025, 62, 7. [Google Scholar] [CrossRef]
- Tang, S.; Li, H.; Yin, B. A space-time spectral method for multi-dimensional Sobolev equations. J. Math. Anal. Appl. 2021, 499, 124937. [Google Scholar] [CrossRef]
- Jin, S.; Luo, Z. A collocation spectral method for two-dimensional Sobolev equations. Bound. Value Probl. 2018, 2018, 83. [Google Scholar] [CrossRef]
- Dehghan, M.; Shafieeabyaneh, N.; Shafieeabyaneh, M. Application of spectral element method for solving Sobolev equations with error estimation. Appl. Numer. Math. 2020, 158, 439–462. [Google Scholar] [CrossRef]
- Kumar, R.; Baskar, S. B-spline quasi-interpolation based numerical methods for some sobolev type equations. J. Comput. Appl. Math. 2016, 292, 41–66. [Google Scholar] [CrossRef]
- Yu, X.; Wang, M. Efficient spectral and spectral element methods for Sobolev equation with diagonalization technique. Appl. Numer. Math. 2024, 201, 265–281. [Google Scholar] [CrossRef]
- Dehghan, M.; Hooshyarfarzin, B.; Abbaszadeh, M. Proper orthogonal decomposition Pascal polynomial-based method for solving Sobolev equation. Int. J. Numer. Methods Heat Fluid Flow. 2022, 32, 2506–2542. [Google Scholar] [CrossRef]
- Chen, X.L.; Duan, J.Q.; Li, D.F. A newton linearized compact finite difference scheme for one class of sobolev equations. Numer. Meth. Partial Differ. Equ. 2018, 34, 1093–1112. [Google Scholar] [CrossRef]
- Zhang, Q.F.; Qin, Y.F.; Sun, Z.Z. Linearly compact scheme for 2D sobolev equation with burgers’s type nonlinearity. Numer. Algorithms 2022, 91, 1081–1114. [Google Scholar] [CrossRef]
- Li, X.; Rui, H. A block-centered finite difference method for the nonlinear Sobolev equation on nonuniform rectangular grids. Appl. Math. Comput. 2019, 363, 124607. [Google Scholar] [CrossRef]
- Xia, H.; Luo, Z.D. An optimized finite difference Crank-Nicolson iterative scheme for the 2D Sobolev equation. Adv. Differ. Equ. 2017, 2017, 196. [Google Scholar] [CrossRef]
- Wang, X.; Fu, H.F. Two linearized second-order block-centered finite difference methods for nonlinear Sobolev equations. Comput. Appl. Math. 2023, 42, 222. [Google Scholar] [CrossRef]
- Haq, S.; Ali, I. Approximate solution of two-dimensional Sobolev equation using a mixed Lucas and Fibonacci polynomials. Eng. Comput. 2022, 38, S2059–S2068. [Google Scholar] [CrossRef]
- Mishra, S.; Pany, A. Completely discrete schemes for 2D Sobolev equations with Burgers’ type nonlinearity. Numer. Algorithms 2022, 90, 963–987. [Google Scholar] [CrossRef]
- Singh, A.; Cheng, H.; Kumar, N.; Jiwari, R. A high order numerical method for analysis and simulation of 2D semilinear Sobolev model on polygonal meshes. Math. Comput. Simul. 2025, 227, 241–262. [Google Scholar] [CrossRef]
- Chen, H.; Nikan, O.; Qiu, W.; Avazzadeh, Z. Two-grid finite difference method for 1D fourth-order Sobolev-type equation with Burgers’ type nonlinearity. Math. Comput. Simul. 2023, 209, 248–266. [Google Scholar] [CrossRef]
- Zhang, J.; Qin, Y.F.; Zhang, Q.F. Maximum error estimates of two linearized compact difference schemes for two-dimensional nonlinear Sobolev equations. Appl. Numer. Math. 2023, 184, 253–272. [Google Scholar] [CrossRef]
- Hirsh, R.S. Higher order accurate difference solutions of fluid mechanics problems by a compact differencing technique. J. Comput. Phys. 1975, 19, 90–109. [Google Scholar] [CrossRef]
- Li, Q.Y.; Wang, N.C.; Yi, D.Y. Numerical Analysis; Tsinghua University Pres: Beijing, China, 2008. [Google Scholar]
- Sun, Z.Z. Numerical Solutions of Partial Differential Equations; Science Press: Beijing, China, 2012. [Google Scholar]
- Sun, Z.Z.; Zhang, Z.B. A linearized compact difference scheme for a class of nonlinear delay partial differential equations. Appl. Math. Model. 2013, 37, 742–752. [Google Scholar] [CrossRef]
| Algorithm 1 | Algorithm 2 | Algorithm 3 | ||||
|---|---|---|---|---|---|---|
| 2.4000 × | – | 2.2309 × | – | 4.1279 × | – | |
| 1.0000 × | 2.05 | 4.2737 × | 4.08 | 5.5682 × | 4.94 | |
| 5.7672 × | 2.02 | 1.3382 × | 4.04 | 1.5581 × | 4.43 | |
| 3.6789 × | 2.01 | 5.4221 × | 4.02 | 6.5961 × | 3.85 | |
| 2.5503 × | 2.01 | 2.6240 × | 4.01 | 2.8509 × | 4.60 | |
| h | Algorithm 1 | Algorithm 2 | Algorithm 3 | |||
|---|---|---|---|---|---|---|
| 4.7675 × | – | 4.7711 × | – | 4.7711 × | – | |
| 9.3562 × | 4.02 | 9.3928 × | 4.01 | 9.3929 × | 4.01 | |
| 2.9319 × | 4.03 | 2.9654 × | 4.01 | 2.9681 × | 4.00 | |
| 1.1783 × | 4.09 | 1.2155 × | 4.00 | 1.2152 × | 4.00 | |
| 5.4931 × | 4.19 | 5.8431 × | 4.02 | 5.8620 × | 4.00 | |
| Algorithm 4 ( | Algorithm 2 () | Algorithm 3 () | ||||
|---|---|---|---|---|---|---|
| 3.4186 × | – | 1.5330 × | – | 1.5263 × | – | |
| 2.2410 × | 3.93 | 9.5549 × | 4.00 | 9.7483 × | 3.97 | |
| 1.4007 × | 4.00 | 6.0070 × | 3.99 | 6.1049 × | 4.00 | |
| 8.7545 × | 4.00 | 3.7538 × | 4.00 | 3.8101 × | 4.00 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hou, B.; Wang, T.; Deng, G.; Wang, Z. High-Order Time–Space Compact Difference Methods for Semi-Linear Sobolev Equations. Axioms 2025, 14, 646. https://doi.org/10.3390/axioms14080646
Hou B, Wang T, Deng G, Wang Z. High-Order Time–Space Compact Difference Methods for Semi-Linear Sobolev Equations. Axioms. 2025; 14(8):646. https://doi.org/10.3390/axioms14080646
Chicago/Turabian StyleHou, Bo, Tianhua Wang, Guoqu Deng, and Zhi Wang. 2025. "High-Order Time–Space Compact Difference Methods for Semi-Linear Sobolev Equations" Axioms 14, no. 8: 646. https://doi.org/10.3390/axioms14080646
APA StyleHou, B., Wang, T., Deng, G., & Wang, Z. (2025). High-Order Time–Space Compact Difference Methods for Semi-Linear Sobolev Equations. Axioms, 14(8), 646. https://doi.org/10.3390/axioms14080646






