Approximation by Power Series of Functions
Abstract
1. Introduction
2. Power Series Built from Functions
3. Expansions
3.1. Scaling
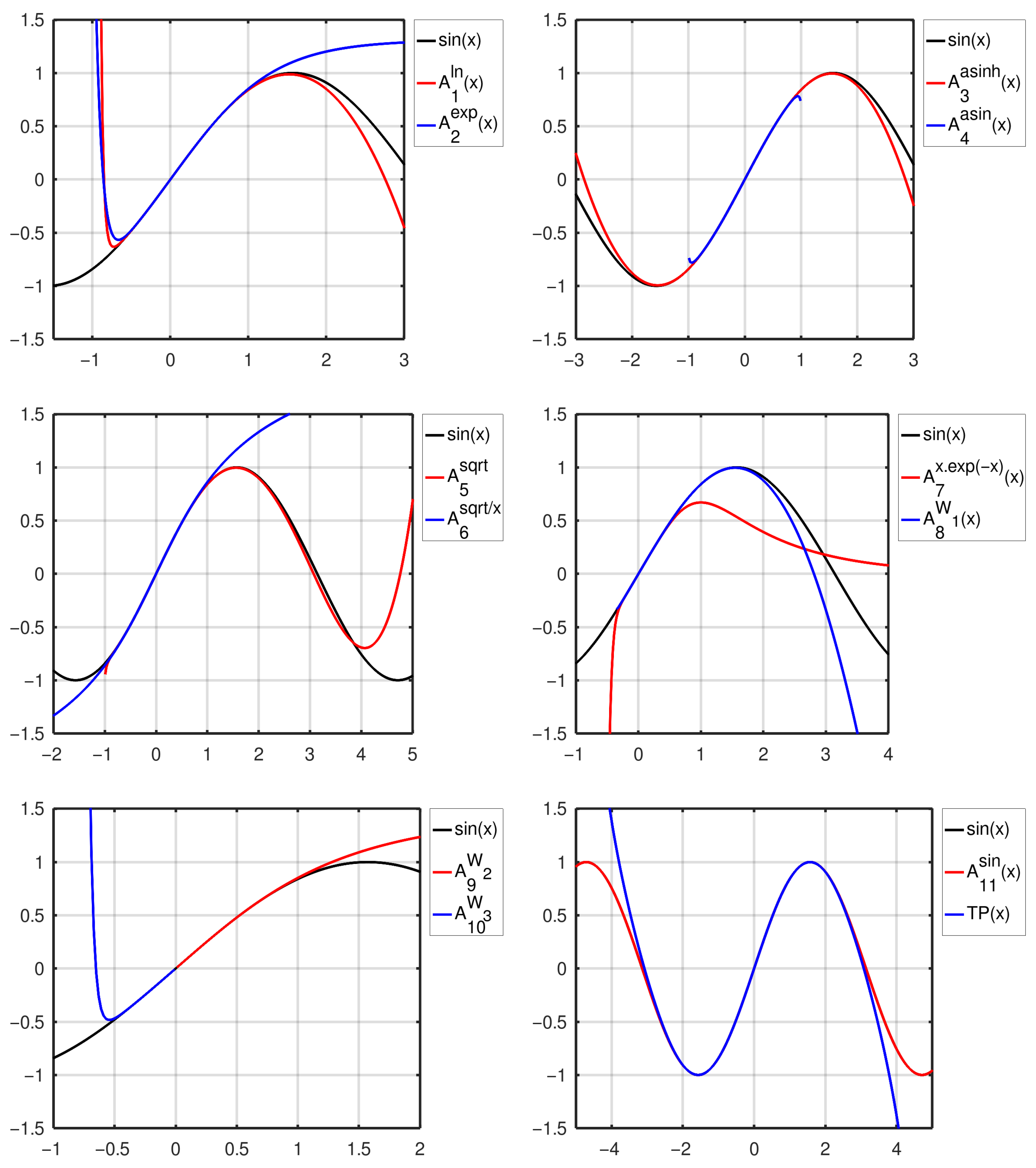
3.2. List
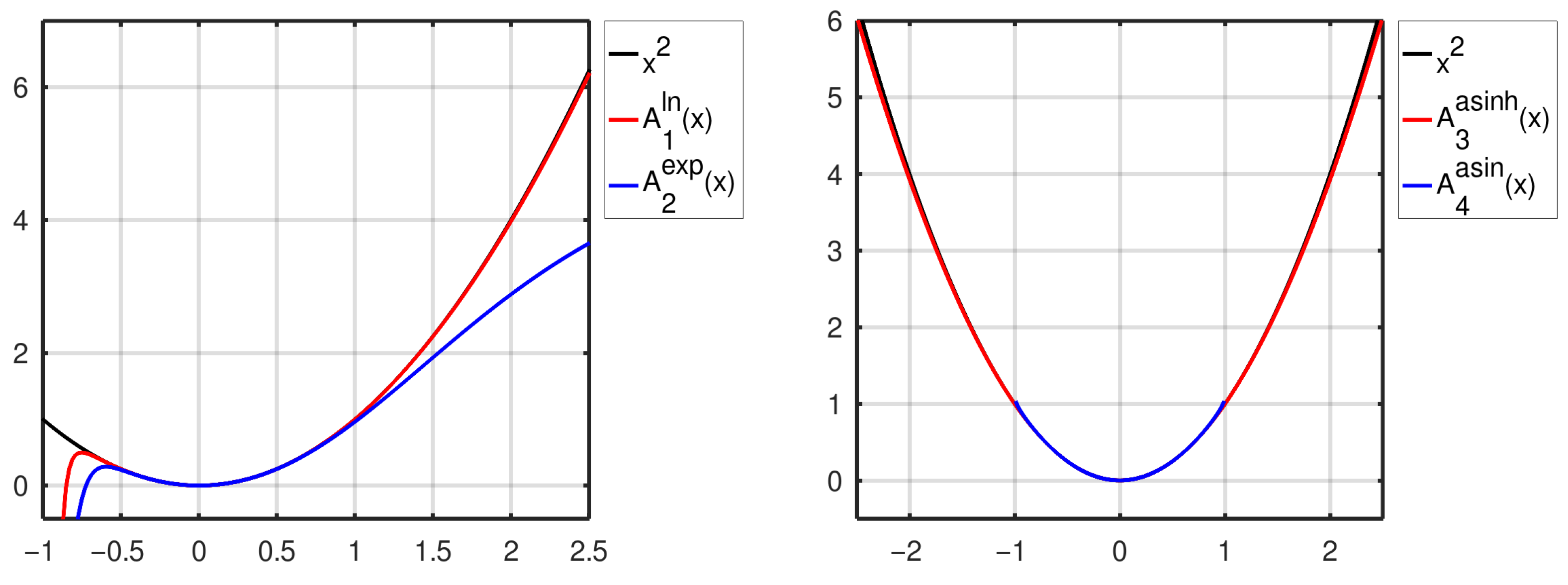
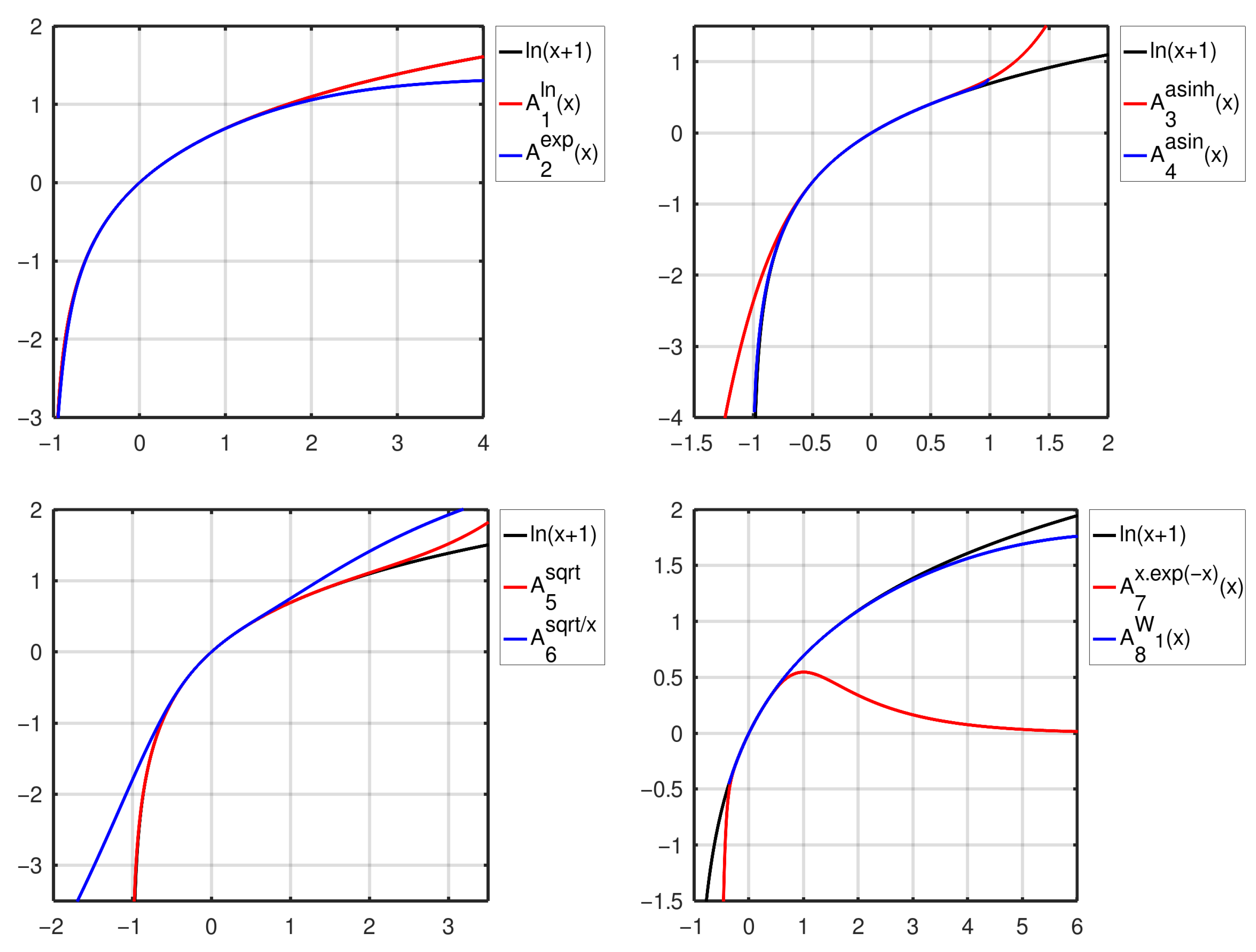
- Logarithm-based expansion ()
- Exponential-based expansion ()
- Expansion with the inverse hyperbolic sine ()
- Arcus-sine-based expansion ()
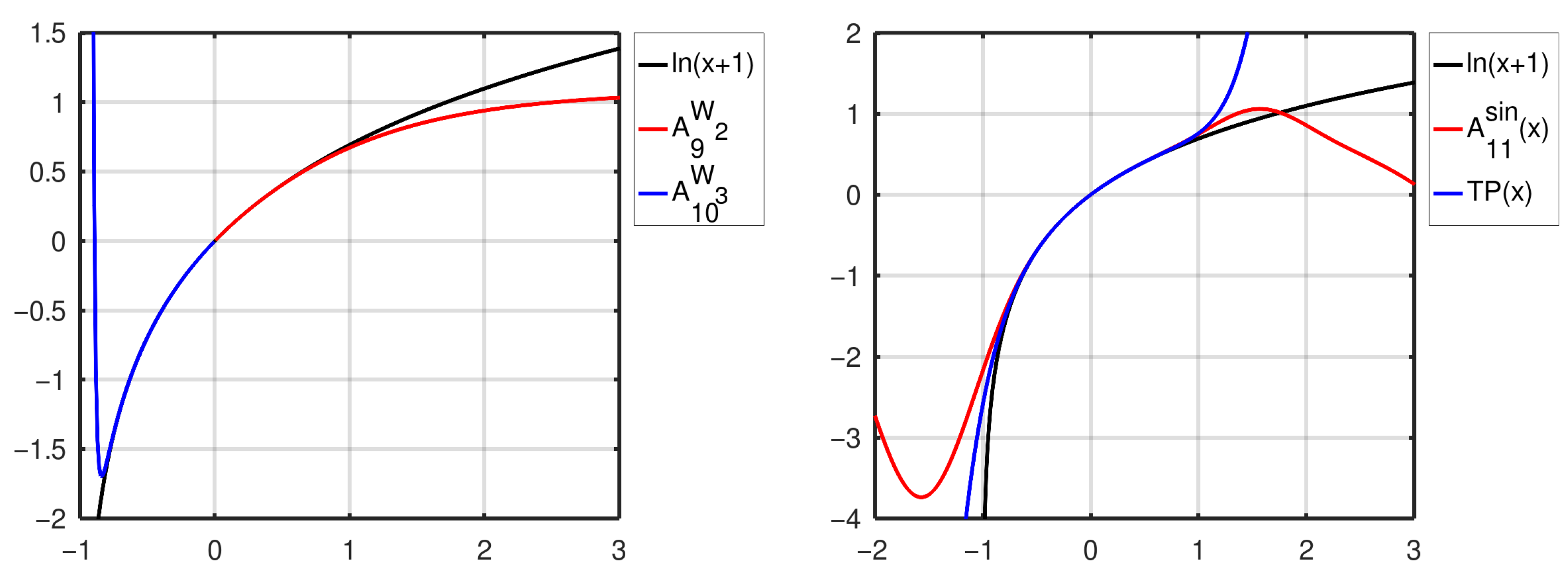
- Expansion in powers of ()Notable special cases (polynomial and rational) for , . For , the TP is constructed.
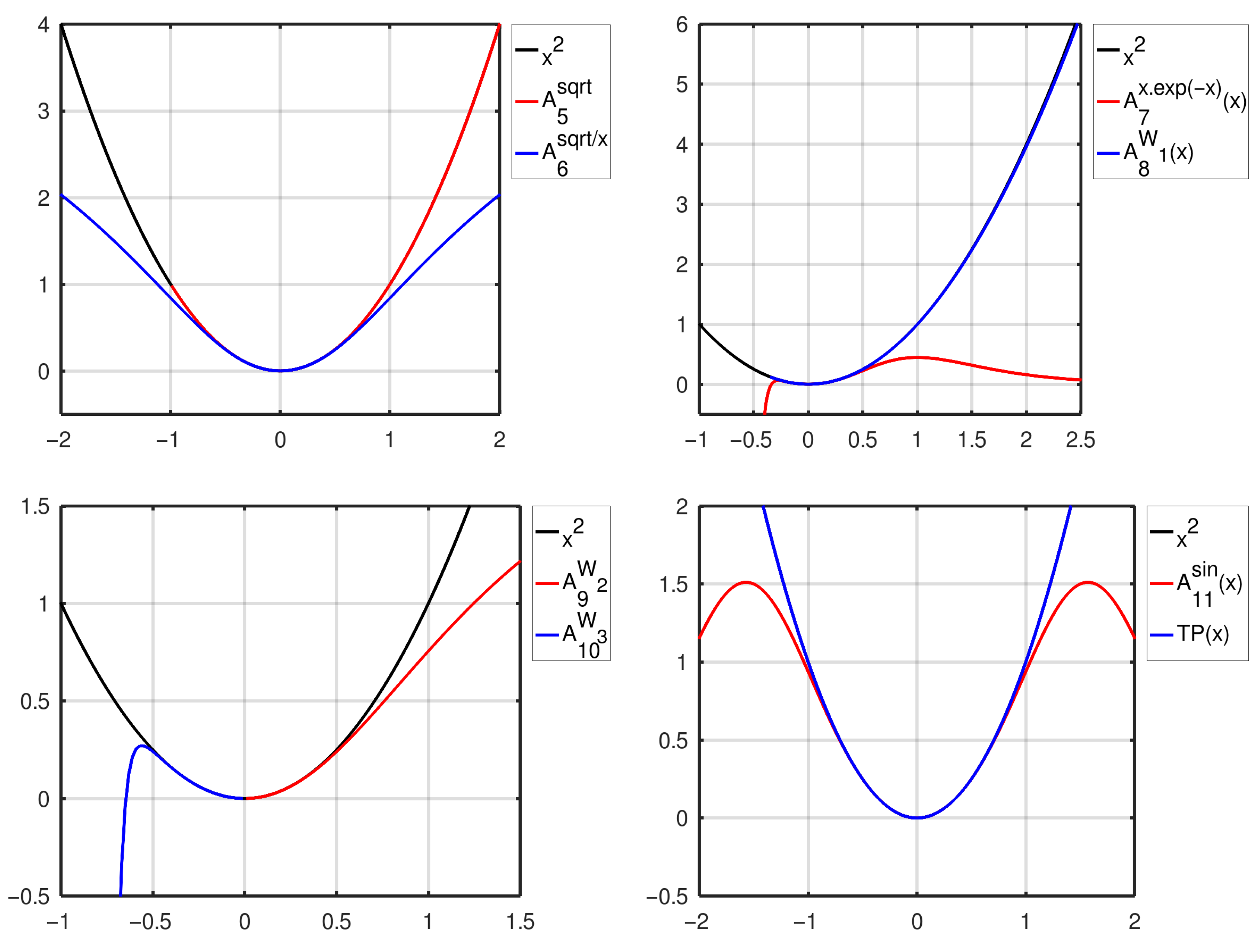
- Expansion with a fraction including the square root ()
- Powers of ()
- Expansion with the Lambert function ()
- Second expansion with the Lambert function ()As readily seen from the argument of the function W (which is defined from to ∞), this approximation is valid in the right neighborhood of zero . A formal approach using and may tempt one to conclude that vanishes everywhere; however, this is not true. The argument of W is not a bijective function; thus, for , the principal branch W is not the appropriate inverse function, which implies that becomes non-trivial. An elementary analogy is , which is identically zero for but is non-constant for .
- Third expansion with the Lambert function ()As readily seen from the argument of the function W, this approximation is valid in the left neighborhood of zero (and the function is there non-trivial; see the previous case).
- Powers of sine ()where is the Kronecker delta and % is the modulo operation. This expansion has many similarities with [7] and represents a Fourier series whose standard form can be obtained by applying trigonometric power formulas to terms.
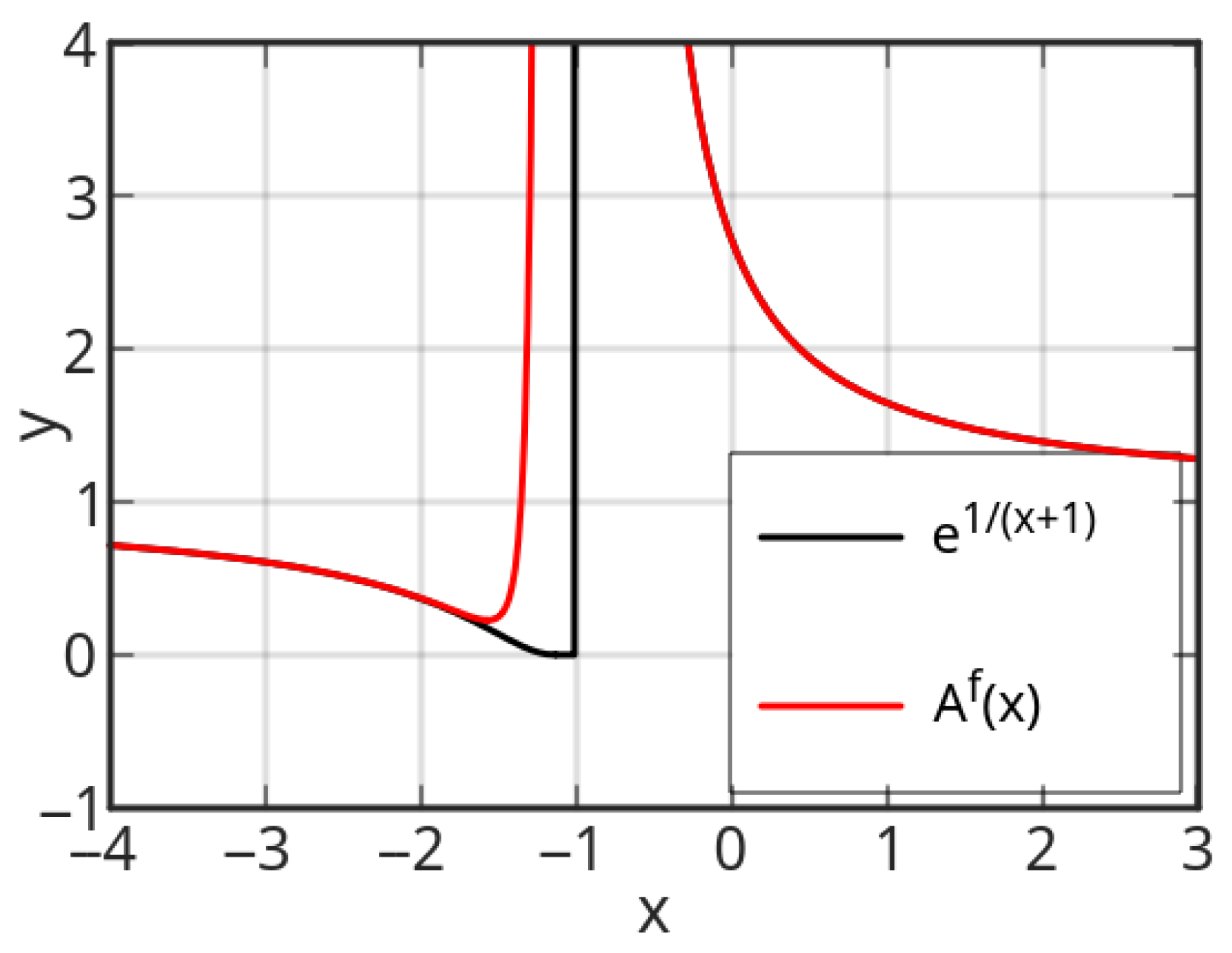
3.3. Non-Elementary g
4. Discussion and Remarks
4.1. Plots
4.2. Convergence
4.3. Examples
5. Applications
5.1. Approximating the Principal Part of Laurent Series
- Using series (21), one is able to approximate the principal part from the knowledge of its derivatives. This is different from the recipe for the Laurent series, where the coefficients are determined by the path integral around the expansion point. It is true that the derivatives contain, through analytic continuation, all information about the function and path integral values included, but we are not aware of a formula linking the Laurent series coefficients to the derivatives in a given point.
- Considering a general function and acknowledging that is a rather specific set of functions, the series (21) have a unique convergence behavior with respect to that, to our knowledge, no other derivative-matching expansion possesses—namely, they converge to the function everywhere, the non-analytic point excepted. The Taylor series reach only the singularity, which determines its convergence radius. The Neumann series of the Bessel functions, if interpreted as a derivative-matching approximation, behaves identically to the Taylor series (see [9], 16.2, “Pincherle’s theorem”). The powers of sines can be also arranged so as to fit the derivatives [7] (covered also in this text; see (19)), but this series is periodic and therefore cannot converge everywhere to f. The Padé approximants look promising; nevertheless, a ratio of two polynomials can only fit a finite number of derivatives.
5.2. Numerical Applications
| N | 3 | 7 | 10 | 20 |
Numerical Evaluation of the Lambert W Function
- Choosing an interval may seem to be a fine-tuning method that suits us; nevertheless interval-based evaluations are very common in numerical applications and one can observe that the selected concurrency methods use this too. It is expected that one method will converge rapidly in one interval, while a different one will converge rapidly in another. This was, of course, true in our case: we conducted an expansion at .
- We do not provide a full implementation of the W function for all possible arguments; we conducted a “feasibility study”. Implementation could be based on the intervals covering the double-precision domain, with expansions for each of them, and can form part of dedicated research.
- Our system is IntelR Core™ i7-4770×8, Ubuntu 24.04.3 LTS, and the C/C++ code is compiled with a c++ (Ubuntu 13.3.0-6ubuntu2~24.04) 13.3.0 compiler. However, we carried out a relative comparison; therefore, we believe our results are system-independent.
- We provide a computer program as an addition to this text in the Supplementary Material. It contains three .cpp files: main.cpp is the executable, the alpha_20.cpp contains our method beta_20, and lambert_w.cpp contains the dw0c method of [12]. The two other methods (GSL, Boost) were linked from external libraries.
- Our approach, of course, requires a trade-off between the execution time (number of terms in the series) and the length of the interval in which full precision is achieved. If the terms up to are included, then the necessary precision is reached for ; this is our choice. We also test , where (method betaShort in alpha_20.cpp). Here, the full precision interval is small .
- We did not investigate the theoretical properties of our approach (e.g., the convergence radius) beyond providing the necessary precision.
| Method | GSL | Boost | Dwc0 | ||
| 42.31 s | - | 144.52 s | 42.51 s | 17.04 s | |
| - | - | 0.29 | 0.99 | 2.48 | |
| 41.32 s | 15.25 s | 177.63 s | 49.12 s | 17.09 s | |
| 0.37 | - | 0.09 | 0.31 | 0.89 |
- The Dwc0 is not easily scalable to a different precision. If a new precision standard is required (long double), completely new rational expressions need to be found. In our case, we just increased the number of terms.
- We believe it may sometimes be advantageous to have a justified, converging mathematical expression that has also a rapidly converging numerical implementation.
6. Summary, Conclusions, and Outlook
- The expansions are genuinely new; they have (in general) a different domain of convergence and a different convergence rate to the Taylor series. As a matter of fact they can be, by substitution, related to the Taylor series to investigate their properties. The latter statement does not alter the validity of the former.
- One finds, among the expansions, purely rational or polynomial expressions, namely Formula (13) for . Being based only on four basic arithmetic operations, they are well suited as practical approximations in computer- or human-performed calculations.
- Even more expansions are based on functions that are part of processor instruction sets (for common architectures) and thus can be rapidly evaluated on a computer. This leads to such expansions having realistic application potential.
Supplementary Materials
Funding
Data Availability Statement
Conflicts of Interest
References
- Liptaj, A. General Approach to Function Approximation. Mathematics 2024, 12, 3702. [Google Scholar] [CrossRef]
- Qi, F.; Niu, D.W.; Lim, D.; Yao, Y.H. Special values of the Bell polynomials of the second kind for some sequences and functions. J. Math. Anal. Appl. 2020, 491, 124382. [Google Scholar] [CrossRef]
- Qi, F. Taylor’s series expansions for real powers of two functions containing squares of inverse cosine function, closed-form formula for specific partial Bell polynomials, and series representations for real powers of π. Demonstr. Math. 2022, 55, 710–736. [Google Scholar] [CrossRef]
- Qi, F. Explicit formulas for partial Bell polynomials, Maclaurin’s series expansions of real powers of inverse (hyperbolic) cosine and sine, and series representations of powers of π. Preprint 2025. [Google Scholar] [CrossRef]
- Khelifa, S.; Cherruault, Y. Nouvelle identité pour les polynômes de Bell. Maghreb Math. Rev. 2000, 9, 115–123. [Google Scholar]
- Abbas, M.; Bouroubi, S. On new identities for Bell’s polynomials. Discret. Math. 2005, 293, 5–10. [Google Scholar] [CrossRef]
- Butzer, P.L.; Schmidt, K.; Stark, E.; Vogt, L. Central factorial numbers; their main properties and some applications. Numer. Funct. Anal. Optim. 1989, 10, 419–488. [Google Scholar] [CrossRef]
- Joshi, S. Discrete Calculus—Summing ∑k=1n+1k(n+1)k(-k+n+1)!. Mathematics Stack Exchange. 22 November 2015. Available online: https://math.stackexchange.com/q/1541208 (accessed on 15 August 2025).
- Watson, G.N. A Treatise on the Theory of Bessel Functions; Cambridge University Press: Cambridge, UK, 1922; Volume 3. [Google Scholar]
- Intel Corporation®. Intel 64 and IA-32 Architectures Software Developer’s Manual Combined, Volumes:1, 2A, 2B, 2C, 2D, 3A, 3B, 3C, 3D and 4. 2022. Available online: https://www.intel.com/content/www/us/en/content-details/782158/intel-64-and-ia-32-architectures-software-developer-s-manual-combined-volumes-1-2a-2b-2c-2d-3a-3b-3c-3d-and-4.html (accessed on 18 August 2025).
- Arm Limited. ArmR Compiler, version 6.6. Armasm User Guide. Arm Limited: Cambridge, UK, 2020.
- Fukushima, T. Precise and fast computation of Lambert W function by piecewise minimax rational function approximation with variable transformation. Preprints 2020. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liptaj, A. Approximation by Power Series of Functions. Axioms 2025, 14, 645. https://doi.org/10.3390/axioms14080645
Liptaj A. Approximation by Power Series of Functions. Axioms. 2025; 14(8):645. https://doi.org/10.3390/axioms14080645
Chicago/Turabian StyleLiptaj, Andrej. 2025. "Approximation by Power Series of Functions" Axioms 14, no. 8: 645. https://doi.org/10.3390/axioms14080645
APA StyleLiptaj, A. (2025). Approximation by Power Series of Functions. Axioms, 14(8), 645. https://doi.org/10.3390/axioms14080645




