Modulation Instability and Abundant Exact Solitons to the Fractional Mathematical Physics Model Through Two Distinct Methods
Abstract
1. Introduction
Fractional Derivative
2. Methodologies
2.1. The Function Method
2.2. Description of Modified Simplest Equation (MSE) Method
3. Mathematical Analysis and Exact Wave Solutions
3.1. Exact Solitons by Function Method
3.2. Exact Wave Solutions by MSE Method
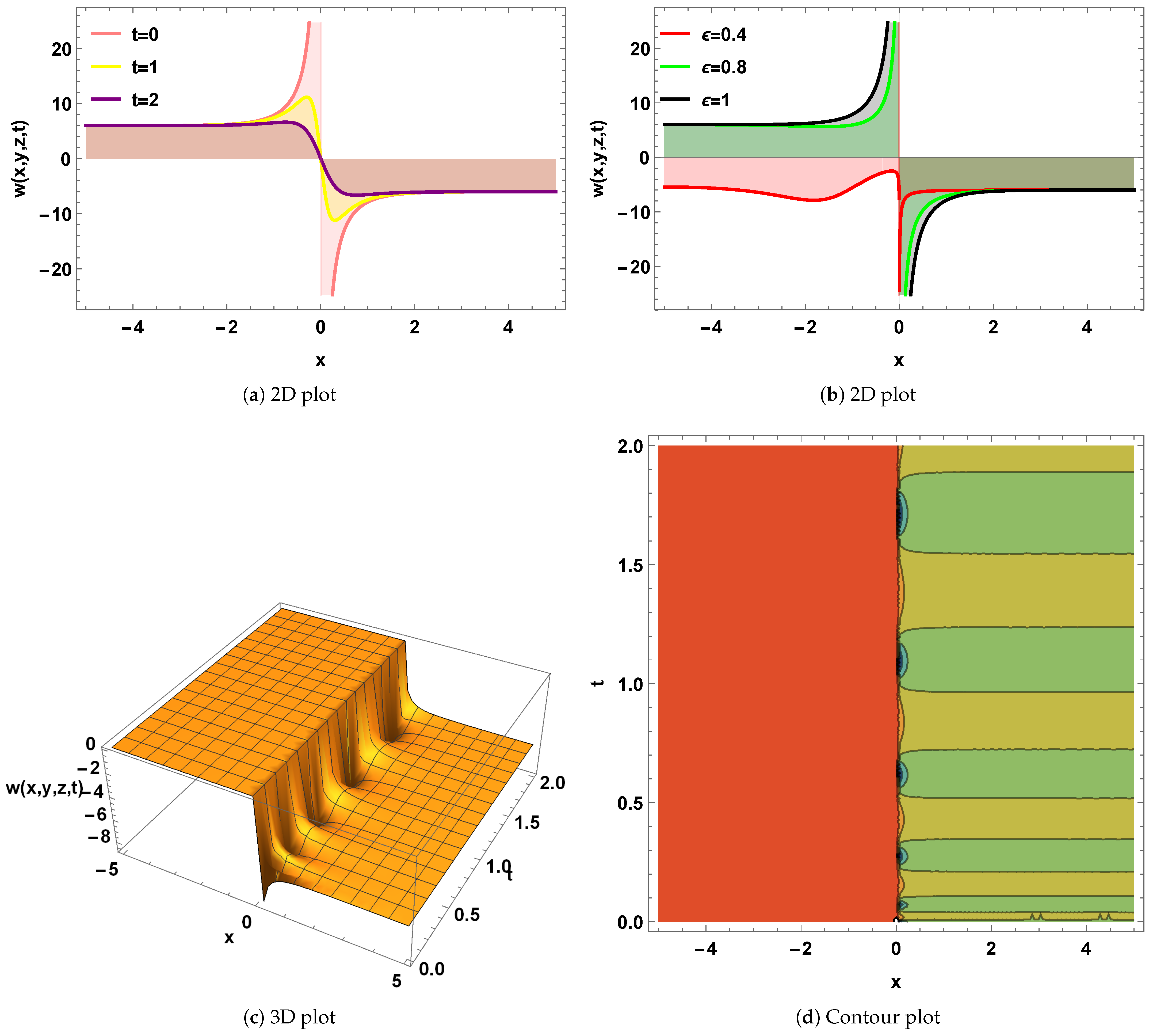
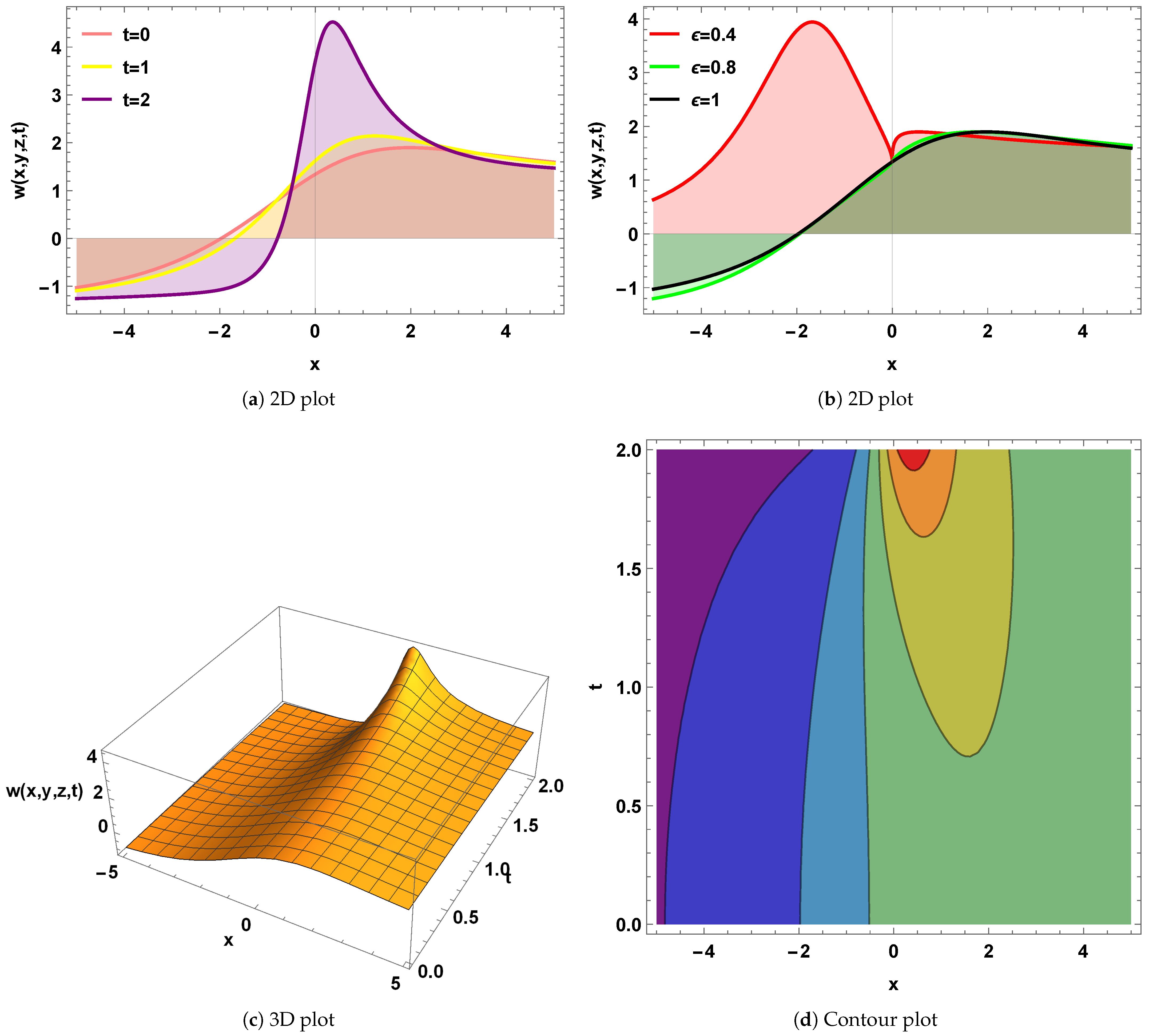
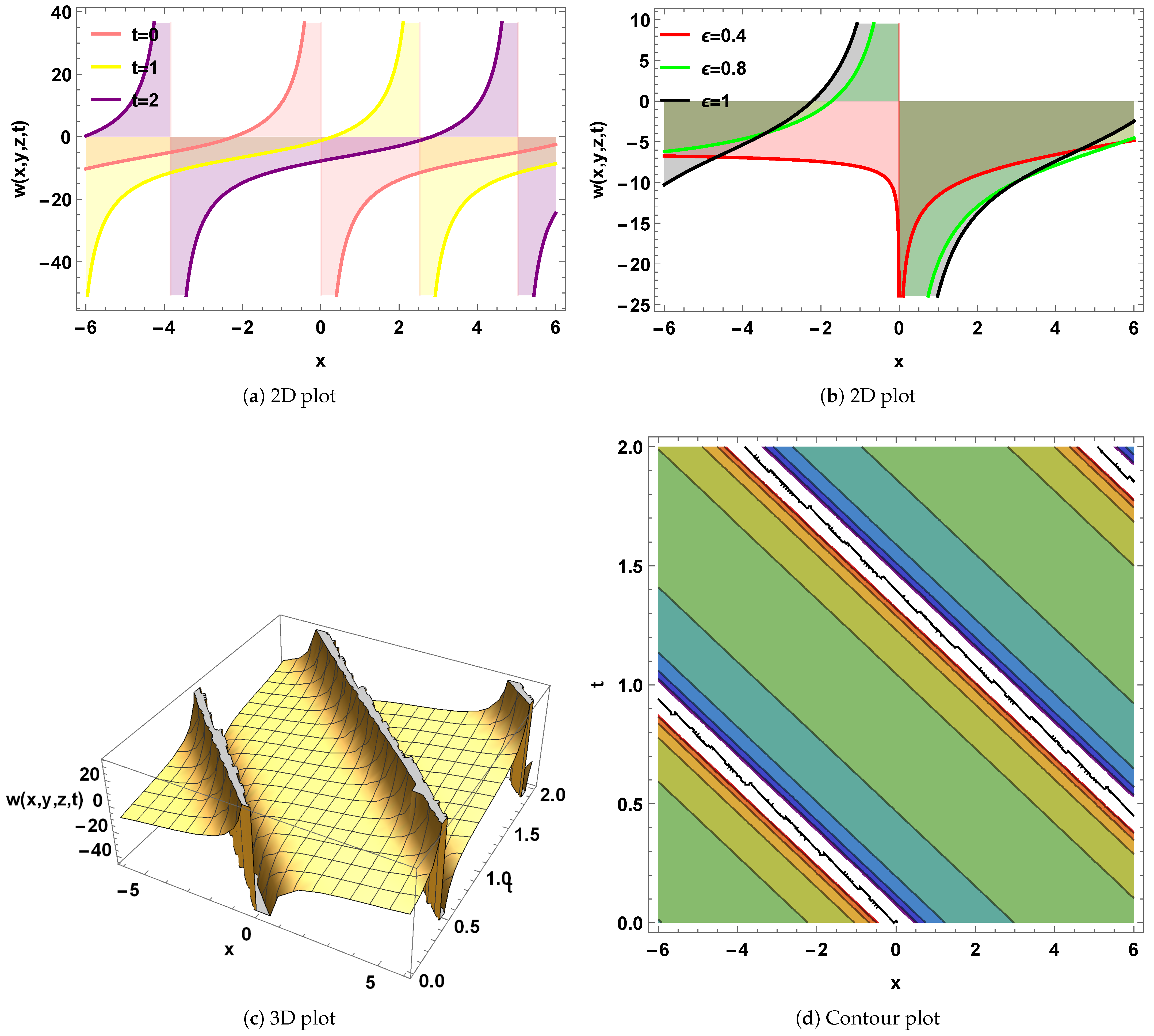
4. Graphical Interpretation
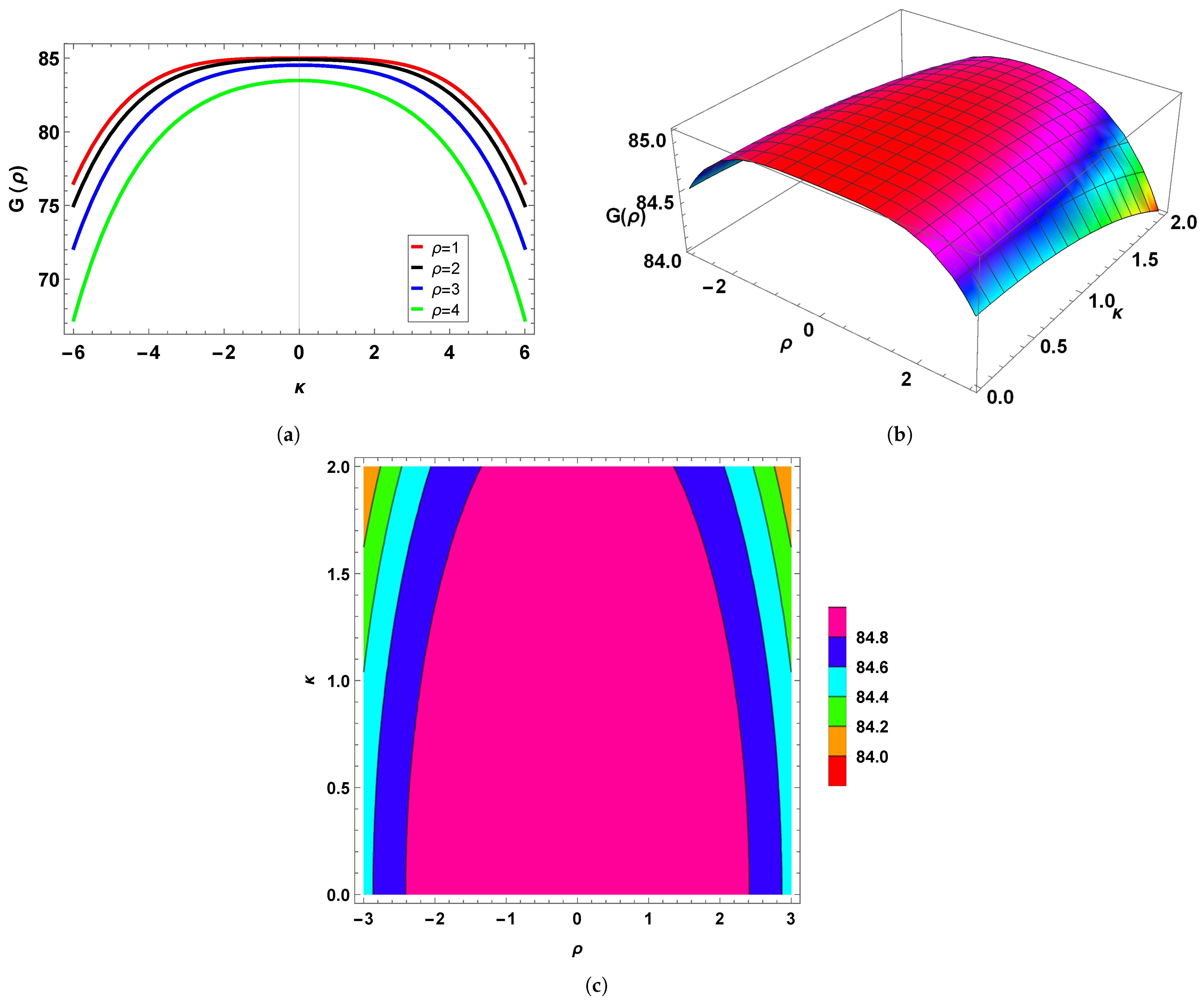
5. Modulation Instability (MI) Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Khater, M.M.A.; Ghanbari, B.; Nisar, K.S.; Kumar, D. Novel exact solutions of the fractional Bogoyavlensky–Konopelchenko equation involving the Atangana-Baleanu-Riemann derivative. Alex. Eng. J. 2020, 59, 2957–2967. [Google Scholar] [CrossRef]
- Ali, H.M.; Ali, A.S.; Mahmoud, M.; Abdel-Aty, A.-H. Analytical approximate solutions of fractional nonlinear Drinfeld–Sokolov–Wilson model using modified Mittag–Leffler function. J. Ocean. Eng. Sci. 2022. [Google Scholar] [CrossRef]
- Zafar, A.; Raheel, M.; Ali, M.R.; Myrzakulova, Z.; Bekir, A.; Myrzakulov, R. Exact Solutions of M-Fractional Kuralay Equation via Three Analytical Schemes. Symmetry 2023, 15, 1862. [Google Scholar] [CrossRef]
- Demirbilek, U.; Ala, V.; Mamedov, K.R. Exact solutions of conformable time fractional Zoomeron equation via IBSEFM. Appl. Math. J. Chin. Univ. 2021, 36, 554–563. [Google Scholar] [CrossRef]
- Hong, B.; Wang, J. Exact solutions for the generalized Atangana-Baleanu-Riemann fractional (3 + 1)-Dimensional Kadomtsev–Petviashvili equation. Symmetry 2022, 15, 3. [Google Scholar] [CrossRef]
- Almatrafi, M.B. Solitary Wave Solutions to a Fractional-Order Fokas Equation via the Improved Modified Extended Tanh-Function Approach. Mathematics 2024, 13, 109. [Google Scholar] [CrossRef]
- Fadhal, E.; Akbulut, A.; Kaplan, M.; Awadalla, M.; Abuasbeh, K. Extraction of exact solutions of higher order Sasa-Satsuma equation in the sense of beta derivative. Symmetry 2022, 14, 2390. [Google Scholar] [CrossRef]
- Sahoo, S.; Saha Ray, S.; Abdou, M.A.M.; Inc, M.; Chu, Y.-M. New soliton solutions of fractional Jaulent-Miodek system with symmetry analysis. Symmetry 2020, 12, 1001. [Google Scholar] [CrossRef]
- Rabie, W.B.; Ahmed, H.M.; Ismail, M.F.; Wazwaz, A.-M.; Syied, A.A.; Abd-Elmonem, A.; Abdalla, N.S.E.; Abbas, W.; Ibrahim, M.A. Investigation of a novel exact wave solution structure in nonlinear thermoelasticity using modern techniques. Results Phys. 2025, 70, 108148. [Google Scholar] [CrossRef]
- Mahmood, A.; Rehman, H.U.; Razzaq, S.; Rashid, J.; Rezazadeh, H.; Karaca, Y.; Hosseinzadeh, M.A. Exact solutions of cubic-quintic-septimal nonlinear Schrödinger wave equation. Opt. Quantum Electron. 2024, 56, 1096. [Google Scholar] [CrossRef]
- Murad, M.A.S.; Ismael, H.F.; Sulaiman, T.A. Various exact solutions to the time-fractional nonlinear Schrödinger equation via the new modified Sardar sub-equation method. Phys. Scr. 2024, 99, 085252. [Google Scholar] [CrossRef]
- Torvattanabun, M.; Khansai, N.; Sirisubtawee, S.; Koonprasert, S.; Tuan, N.M. New Exact Traveling Wave Solutions of the (3 + 1)-Dimensional Chiral Nonlinear Schrodinger Equation Using Two Reliable Techniques: Annual Meeting in Mathematics 2023. Thai J. Math. 2024, 22, 145–163. [Google Scholar]
- Raheel, M.; Zafar, A.; Inc, M.; Tala-Tebue, E. Optical solitons to time-fractional Sasa-Satsuma higher-order non-linear Schrödinger equation via three analytical techniques. Opt. Quantum Electron. 2023, 55, 307. [Google Scholar] [CrossRef]
- Eslami, M.; Matinfar, M.; Asghari, Y.; Rezazadeh, H.; Abduridha, S.A.J. Diverse exact soliton solutions for three distinct equations with conformable derivatives via expa function technique. Opt. Quantum Electron. 2024, 56, 846. [Google Scholar] [CrossRef]
- Qawaqneh, H.; Altalbe, A.; Bekir, A.; Tariq, K.U. Investigation of soliton solutions to the truncated M-fractional (3+ 1)-dimensional Gross-Pitaevskii equation with periodic potential. AIMS Math. 2024, 9, 23410–23433. [Google Scholar] [CrossRef]
- Sheikh, M.A.N.; Taher, M.A.; Hossain, M.M.; Akter, S.; Harun-Or-Roshid. Variable coefficient exact solution of Sharma–Tasso–Olver model by enhanced modified simple equation method. Partial. Differ. Equations Appl. Math. 2023, 7, 100527. [Google Scholar] [CrossRef]
- Razzaq, W.; Habib, M.; Nadeem, M.; Zafar, A.; Khan, I.; Mwanakatwea, P.K. Solitary wave solutions of conformable time fractional equations using modified simplest equation method. Complexity 2022, 1, 8705388. [Google Scholar] [CrossRef]
- Murad, M.A.S.; Iqbal, M.; Arnous, A.H.; Yildirim, Y.; Jawad, A.J.M.; Hussein, L.; Biswas, A. Optical dromions for Radha–Lakshmanan model with fractional temporal evolution by modified simplest equation. J. Opt. 2024, 1–10. [Google Scholar] [CrossRef]
- Kuo, C.-K. New solitary solutions of the Gardner equation and Whitham–Broer–Kaup equations by the modified simplest equation method. Optik 2017, 147, 128–135. [Google Scholar] [CrossRef]
- Ahmad, I.; Ahmad, S.-u.-I.; Kutlu, K.; Ilyas, H.; Hussain, S.I.; Rasool, F. On the dynamical behavior of nonlinear Fitzhugh–Nagumo and Bateman–Burger equations in quantum model using Sinc collocation scheme. Eur. Phys. J. Plus 2021, 136, 1108. [Google Scholar] [CrossRef]
- Qasim, M.; Fengping, Y.; Baber, M.Z. Explicit wave solutions profile of (3 + 1)-dimensional Bateman–Burgers equation via bilinear neural network method. Eur. Phys. J. Plus 2025, 140, 224. [Google Scholar] [CrossRef]
- Saengcharoenthaworn, W.; Chinviriyasit, S. The analytical solutions of Bateman-Burgers equation. PBRU Sci. J. 2023, 20, 48–53. [Google Scholar]
- Alhawatmeh, A.; Bataineh, M.A.; Alashqar, N.; Khalil, R. Atomic solutions to Bateman-Burgers type equation via tensor products. Partial. Differ. Equations Appl. Math. 2025, 13, 101102. [Google Scholar] [CrossRef]
- Gaber, A.A.; Wazwaz, A.-M.; Mousa, M.M. Similarity reductions and new exact solutions for (3 + 1)-dimensional B–B equation. Mod. Phys. Lett. 2024, 38, 2350243. [Google Scholar] [CrossRef]
- Zinat, N.; Hussain, A.; Kara, A.H.; Zaman, F.D. Lie group analysis and conservation laws for the time-fractional 3D Bateman–Burgers equation. Afr. Mat. 2025, 36, 73. [Google Scholar] [CrossRef]
- Akour, A.N.; Jaradat, E.K.; Mahadeen, A.A.; Jaradat, O.K. Describing Bateman-Burgers equation in one and two dimensions using Homotopy perturbation method. J. Interdiscip. Math. 2023, 26, 271–283. [Google Scholar] [CrossRef]
- Sulaiman, T.A.; Yel, G.; Bulut, H. M-fractional solitons and periodic wave solutions to the Hirota-Maccari system. Mod. Phys. Lett. B 2019, 33, 1950052. [Google Scholar] [CrossRef]
- Sousa, J.V.D.; Oliveira, E.C.D. A new truncated M-fractional derivative type unifying some fractional derivative types with classical properties. Int. J. Anal. Appl. 2018, 16, 83–96. [Google Scholar] [CrossRef]
- Ali, A.T.; Hassan, E.R. General expa-function method for nonlinear evolution equations. Appl. Math. Comput. 2010, 217, 451–459. [Google Scholar] [CrossRef]
- Zayed, E.M.E.; Al-Nowehy, A.G. Generalized kudryashov method and general expa function method for solving a high order nonlinear schrödinger equation. J. Space Explor. 2017, 6, 120. [Google Scholar]
- Hosseini, K.; Ayati, Z.; Ansari, R. New exact solutions of the Tzitzéica-type equations in non-linear optics using the expa function method. J. Mod. Opt. 2018, 65, 847–851. [Google Scholar] [CrossRef]
- Rehman, S.; Ahmad, J. Modulation instability analysis and optical solitons in birefringent fibers to RKL equation without four wave mixing. Alex. Eng. J. 2021, 60, 1339–1354. [Google Scholar] [CrossRef]
- Alomair, A.; Naim, A.S.A.; Bekir, A. Exploration of Soliton Solutions to the Special Korteweg–De Vries Equation with a Stability Analysis and Modulation Instability. Mathematics 2024, 13, 54. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alsharidi, A.K.; Bekir, A. Modulation Instability and Abundant Exact Solitons to the Fractional Mathematical Physics Model Through Two Distinct Methods. Axioms 2025, 14, 617. https://doi.org/10.3390/axioms14080617
Alsharidi AK, Bekir A. Modulation Instability and Abundant Exact Solitons to the Fractional Mathematical Physics Model Through Two Distinct Methods. Axioms. 2025; 14(8):617. https://doi.org/10.3390/axioms14080617
Chicago/Turabian StyleAlsharidi, Abdulaziz Khalid, and Ahmet Bekir. 2025. "Modulation Instability and Abundant Exact Solitons to the Fractional Mathematical Physics Model Through Two Distinct Methods" Axioms 14, no. 8: 617. https://doi.org/10.3390/axioms14080617
APA StyleAlsharidi, A. K., & Bekir, A. (2025). Modulation Instability and Abundant Exact Solitons to the Fractional Mathematical Physics Model Through Two Distinct Methods. Axioms, 14(8), 617. https://doi.org/10.3390/axioms14080617






