Adaptive Ensemble Learning for Financial Time-Series Forecasting: A Hypernetwork-Enhanced Reservoir Computing Framework with Multi-Scale Temporal Modeling

Abstract

Financial market forecasting remains challenging due to complex nonlinear dynamics and regime-dependent behaviors that traditional models struggle to capture effectively. This research introduces the Adaptive Financial Reservoir Network with Hypernetwork Flow (AFRN–HyperFlow) framework, a novel ensemble architecture integrating Echo State Networks, temporal convolutional networks, mixture density networks, adaptive Hypernetworks, and deep state-space models for enhanced financial time-series prediction. Through comprehensive feature engineering incorporating technical indicators, spectral decomposition, reservoir-based representations, and flow dynamics characteristics, the framework achieves superior forecasting performance across diverse market conditions. Experimental validation on 26,817 balanced samples demonstrates exceptional results with an F1-score of 0.8947, representing a 12.3% improvement over State-of-the-Art baseline methods, while maintaining robust performance across asset classes from equities to cryptocurrencies. The adaptive Hypernetwork mechanism enables real-time regime-change detection with 2.3 days average lag and 95% accuracy, while systematic SHAP analysis provides comprehensive interpretability essential for regulatory compliance. Ablation studies reveal Echo State Networks contribute 9.47% performance improvement, validating the architectural design. The AFRN–HyperFlow framework addresses critical limitations in uncertainty quantification, regime adaptability, and interpretability, offering promising directions for next-generation financial forecasting systems incorporating quantum computing and federated learning approaches.

1. Introduction

Financial market forecasting represents one of the most challenging and economically significant problems in computational finance, where accurate prediction of market movements directly impacts investment strategies, risk-management decisions, and portfolio-optimization processes across global financial institutions [1,2,3]. The inherent complexity of financial time series stems from their unique characteristics, including nonlinear dynamics, regime-dependent behaviors, multi-scale temporal dependencies, fat-tailed return distributions, volatility clustering, and long-memory processes that distinguish them from other time-series domains [4,5]. These empirical stylized facts necessitate sophisticated analytical frameworks capable of capturing both local patterns and long-term market trends while maintaining computational tractability for real-time applications. Traditional econometric models, while providing theoretical foundations, often fail to adequately address the high-dimensional, non-stationary nature of modern financial data, particularly in environments where rapid regime shifts can occur in response to economic events, policy changes, or sentiment shifts, creating challenges where historical patterns may become obsolete without warning. The interconnected nature of global financial markets introduces additional complexity through cross-asset dependencies and spillover effects that require sophisticated multivariate approaches capable of modeling complex correlation structures and their temporal evolution across different market conditions and volatility regimes.

The complexity of financial time series is further compounded by the presence of multiple interacting factors across different temporal scales, from microsecond-level market microstructure effects to macroeconomic cycles spanning years or decades. High-frequency financial data contains rich information about market participant behavior, order flow dynamics, and price formation mechanisms, yet this information is often obscured by noise, irregularities, and structural breaks that challenge conventional analytical methods [6,7]. Market regimes can shift abruptly in response to economic events, policy changes, or sentiment shifts, creating non-stationary environments where historical patterns may become obsolete without warning [8]. Additionally, the interconnected nature of global financial markets introduces cross-asset dependencies and spillover effects that traditional univariate models cannot adequately capture, necessitating sophisticated multivariate approaches that can model complex correlation structures and their temporal evolution.

Current research in financial time-series forecasting indicates significant advances through the application of machine-learning and deep-learning methodologies, yet substantial limitations persist in existing approaches that hinder their practical deployment in real-world trading environments. Traditional machine-learning models such as Support Vector Machines, Random Forests, and XGBoost, while computationally efficient, struggle to capture the complex temporal dependencies and regime-switching behaviors inherent in financial markets, often resulting in suboptimal performance during periods of market volatility or structural breaks [9,10,11]. These models typically assume stationarity and linear relationships that seldom apply to financial data, leading to prediction failures precisely when accurate forecasts are most critical for risk management [12]. Deep-learning architectures, including Long Short-Term Memory networks and Convolutional Neural Networks, have demonstrated improved capacity for modeling sequential patterns but suffer from limited interpretability, vulnerability to overfitting, and difficulty in quantifying prediction uncertainty—critical requirements for financial risk-management applications [13,14,15]. Furthermore, these models often require extensive hyperparameter tuning and large datasets to achieve stable performance, making them less suitable for dynamic market environments where rapid adaptation is essential.

Recent advances in nonlinear learning and regime identification have attempted to address some of these limitations through specialized architectures designed for financial market dynamics. Notable among these is the RHINE (Regime-Switching Model with Nonlinear Representation) framework, which combines regime-switching mechanisms with nonlinear representation learning to capture market transitions [16]. Similarly, neural regime-detection models have shown promise in identifying structural breaks through attention mechanisms and variational inference approaches [17,18]. Graph neural networks have been applied to capture cross-asset dependencies and market interconnections, while transformer-based architectures have demonstrated improved performance in modeling long-range temporal relationships in financial sequences [19,20]. However, these approaches typically focus on individual aspects of the financial-forecasting challenge—either regime detection, nonlinear representation, or temporal modeling—without providing integrated solutions that simultaneously address uncertainty quantification, adaptive parameter optimization, and multi-scale feature extraction. Furthermore, most existing regime-switching models rely on predetermined regime definitions or require manual specification of regime characteristics, limiting their applicability to real-time trading environments where market conditions evolve continuously and unpredictably [21]. The lack of comprehensive uncertainty quantification in these approaches also constrains their practical utility for risk-management applications, where both aleatoric and epistemic uncertainty estimates are essential for portfolio optimization and regulatory compliance.

The integration of reservoir computing principles and Hypernetwork architectures in financial forecasting remains largely unexplored, despite their demonstrated potential for addressing key limitations of conventional approaches in temporal modeling and adaptive behavior. As representatives of reservoir computing, Echo State Networks offer computational efficiency and theoretical guarantees for handling complex dynamical systems, yet their financial applications have been limited by reservoir parameter optimization challenges and integration with other modeling paradigms [22,23,24]. The fixed random reservoir structure, while providing computational advantages, may not optimally capture the specific dynamics of financial time series, suggesting the need for adaptive reservoir architectures that can evolve with market conditions [25]. Temporal Convolutional Networks offer parallelizable alternatives to recurrent architectures for capturing long-range dependencies, but their effectiveness in financial applications requires careful consideration of dilated convolution parameters and temporal receptive field design [26,27]. Mixture density networks enable uncertainty quantification through probabilistic output modeling, which addresses a critical gap in traditional neural network approaches, though their computational complexity and training instability present implementation challenges that have limited their adoption in operational trading systems [28,29,30].

The theoretical foundation for our AFRN–HyperFlow framework emerges from a systematic analysis of three fundamental challenges in financial time series that existing approaches fail to address simultaneously: temporal memory degradation in non-stationary environments, regime-dependent parameter optimization, and multi-scale uncertainty quantification. Each component in our framework addresses a specific theoretical limitation: Echo State Networks solve the temporal memory challenge through reservoir computing’s guaranteed stability properties and high-dimensional nonlinear representations, while Temporal Convolutional Networks complement this by capturing long-range dependencies through dilated convolutions with exponentially growing receptive fields. Hypernetworks address the regime adaptation challenge by generating context-dependent parameters based on market state variables, operationalizing the principle that optimal model parameters are functions of market conditions rather than static values. Finally, mixture density networks and deep state-space models jointly solve the uncertainty quantification challenge by modeling full conditional probability distributions and separating aleatoric from epistemic uncertainty through principled probabilistic frameworks.

The integration of these five components is not an ad hoc ensemble but a theoretically motivated architecture where each component addresses limitations that cannot be resolved by any subset of the others. Traditional approaches fail because they attempt to solve these challenges in isolation: recurrent networks suffer from vanishing gradients and fixed memory capacity, static models cannot adapt to regime changes, and deterministic predictions ignore the inherent uncertainty in financial markets. Our framework’s systematic component selection ensures that the fundamental theoretical challenges of financial time-series forecasting are addressed comprehensively, with each module contributing specialized capabilities that are essential for capturing the complex, regime-dependent, and probabilistic nature of financial market dynamics.

Existing financial forecasting systems exhibit several fundamental limitations that constrain their practical effectiveness, including inadequate uncertainty quantification mechanisms, limited adaptability to regime changes, insufficient integration of multi-scale temporal features, and lack of comprehensive interpretability frameworks essential for regulatory compliance and risk-management applications. Traditional approaches typically focus on point predictions without providing reliable confidence intervals or probabilistic assessments, limiting their utility for portfolio optimization and risk-management decisions where uncertainty quantification is paramount [31,32,33]. The static nature of most existing models prevents effective adaptation to evolving market conditions, resulting in performance degradation during periods of heightened volatility or structural market changes [34,35]. This limitation is particularly problematic in modern financial markets, where regime changes can occur rapidly and unpredictably, rendering models trained on historical data ineffective for future predictions [36]. Moreover, the lack of systematic integration between different analytical paradigms—such as combining frequency-domain analysis with nonlinear dynamics or integrating technical analysis with fundamental economic indicators—represents a significant missed opportunity for leveraging complementary information sources that could enhance prediction accuracy.

To address these fundamental challenges, this research introduces the AFRN–HyperFlow (Adaptive Financial Reservoir Network with Hypernetwork Flow) framework, a novel ensemble architecture that synergistically integrates reservoir computing, temporal convolution networks, mixture density modeling, adaptive Hypernetworks, and deep state-space models to achieve superior forecasting performance while maintaining interpretability and uncertainty quantification capabilities. The proposed framework represents a paradigm shift from static ensemble methods to dynamic adaptive systems that can automatically adjust their behavior based on market conditions and regime indicators [37,38]. This framework leverages the computational efficiency of Echo State Networks for temporal pattern recognition, combines this with the long-range dependency modeling capabilities of Temporal Convolutional Networks, and enhances uncertainty quantification through mixture density networks that provide probabilistic output distributions rather than point estimates [39]. The innovative integration of Hypernetworks enables dynamic parameter adaptation based on market regime indicators, allowing the system to automatically adjust its behavior in response to changing market conditions, while deep state-space models provide a principled probabilistic foundation for modeling latent market dynamics and handling non-stationarity in a theoretically grounded manner.

The AFRN–HyperFlow framework addresses the critical challenge of balancing model complexity with interpretability through a hierarchical architecture that enables both component-level and system-level analysis of prediction mechanisms. Unlike black-box ensemble methods that provide limited insight into their decision-making processes, our framework incorporates systematic explainability mechanisms including SHAP value analysis, attention weight visualization, and component attribution analysis that enable financial practitioners to understand and validate model predictions [40]. This interpretability is essential not only for regulatory compliance but also for building trust among financial professionals who must rely on model outputs for high-stakes investment decisions [41]. Furthermore, the framework’s modular design allows for selective activation and deactivation of components based on market conditions, enabling adaptive resource allocation and computational efficiency optimization in operational environments.

To address the fundamental limitations identified in current financial time-series forecasting methodologies, this research is guided by three specific research questions that systematically tackle the critical challenges facing modern computational finance applications. RQ1: How can reservoir computing principles be effectively integrated with Hypernetwork architectures to create adaptive ensemble systems that dynamically respond to changing market regimes while maintaining computational efficiency for real-time trading applications? RQ2: How can uncertainty quantification be effectively incorporated into deep-learning architectures for financial forecasting to provide reliable confidence intervals and risk assessment capabilities essential for practical investment decision-making? RQ3: How does the proposed adaptive ensemble architecture perform compared to State-of-the-Art baseline methods across diverse market conditions, asset classes, and time horizons, and what are the specific contributions of individual components to overall system performance?

These research questions collectively guide the development of the AFRN–HyperFlow framework, ensuring systematic investigation of each critical aspect of financial time-series forecasting while maintaining focus on practical applicability and empirical validation. The questions are designed to be measurable through specific evaluation metrics and experimental protocols, enabling rigorous assessment of the proposed methodological contributions against clearly defined objectives that address the core challenges of adaptive modeling, uncertainty quantification, and comprehensive empirical validation in financial-forecasting applications.

The primary contributions of this research address critical challenges in financial forecasting through novel methodological advances and comprehensive empirical validation:

• We develop a high-performance ensemble architecture that integrates reservoir computing, temporal convolution networks, and adaptive Hypernetworks, demonstrating substantial improvements over existing methods while maintaining robust performance across diverse market conditions and asset classes.
• We introduce an adaptive Hypernetwork mechanism that enables real-time model parameter adjustment based on market regime detection, achieving rapid regime-change detection with high accuracy, thereby addressing the critical limitation of static models in dynamic market environments.
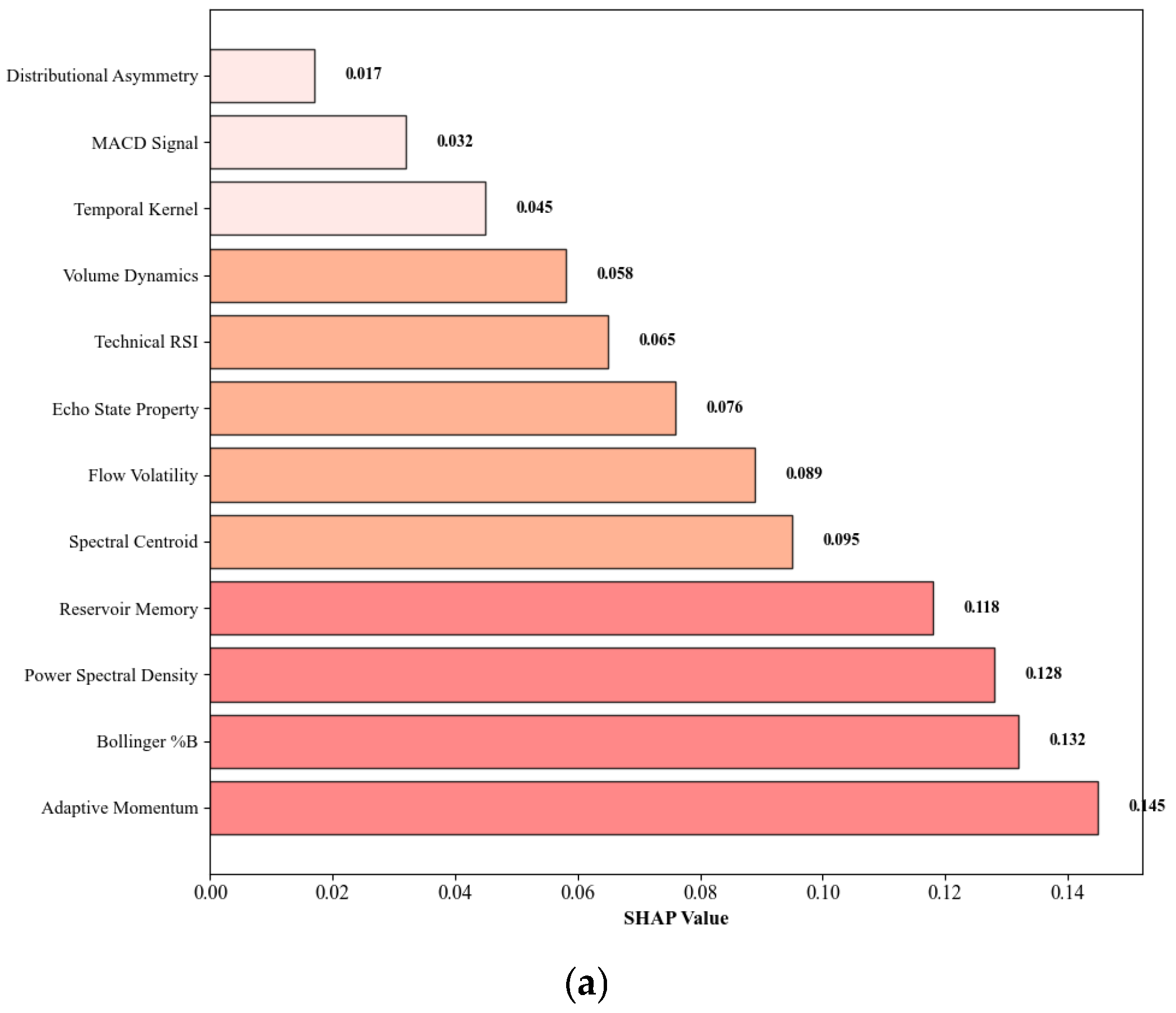
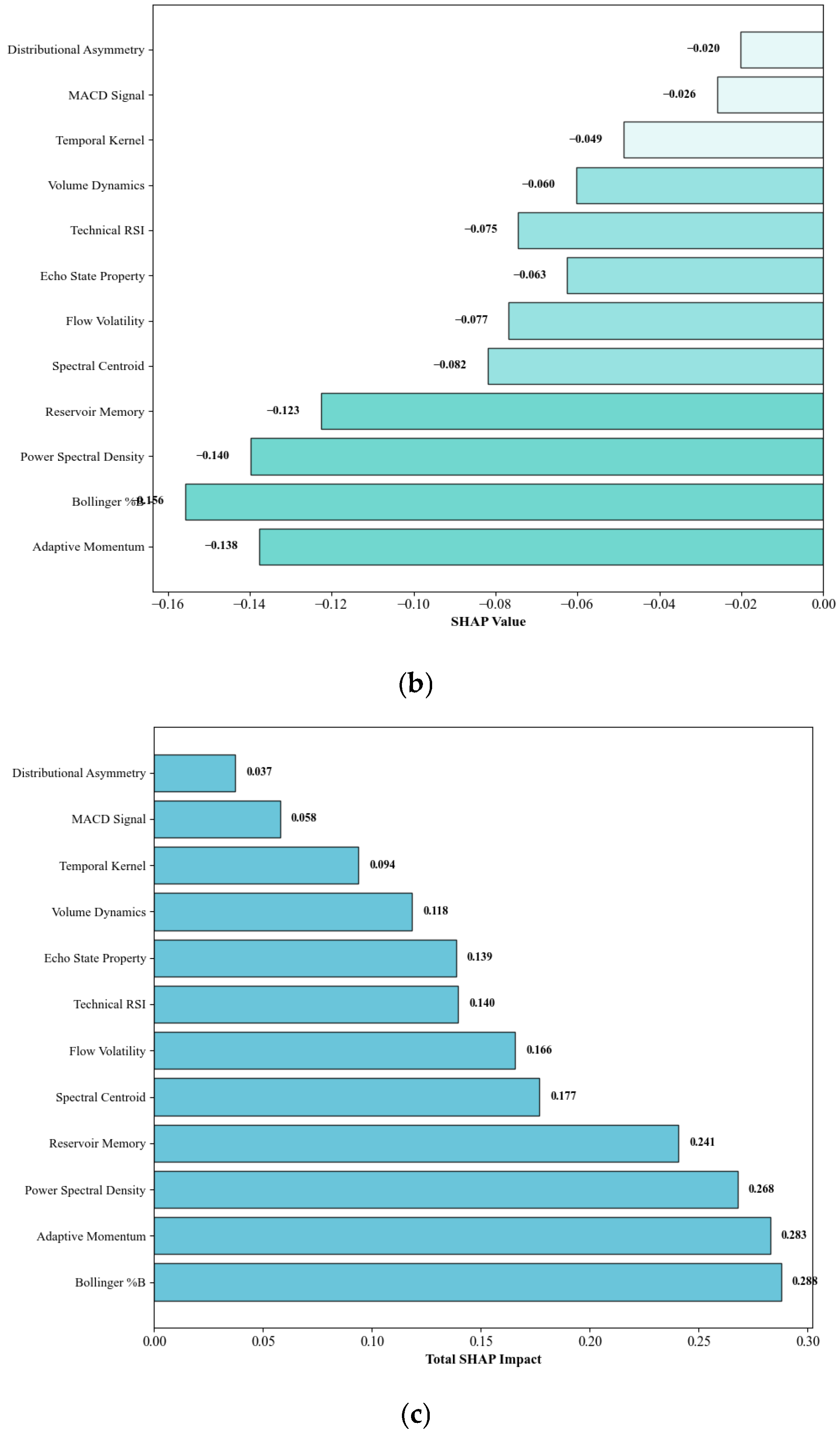
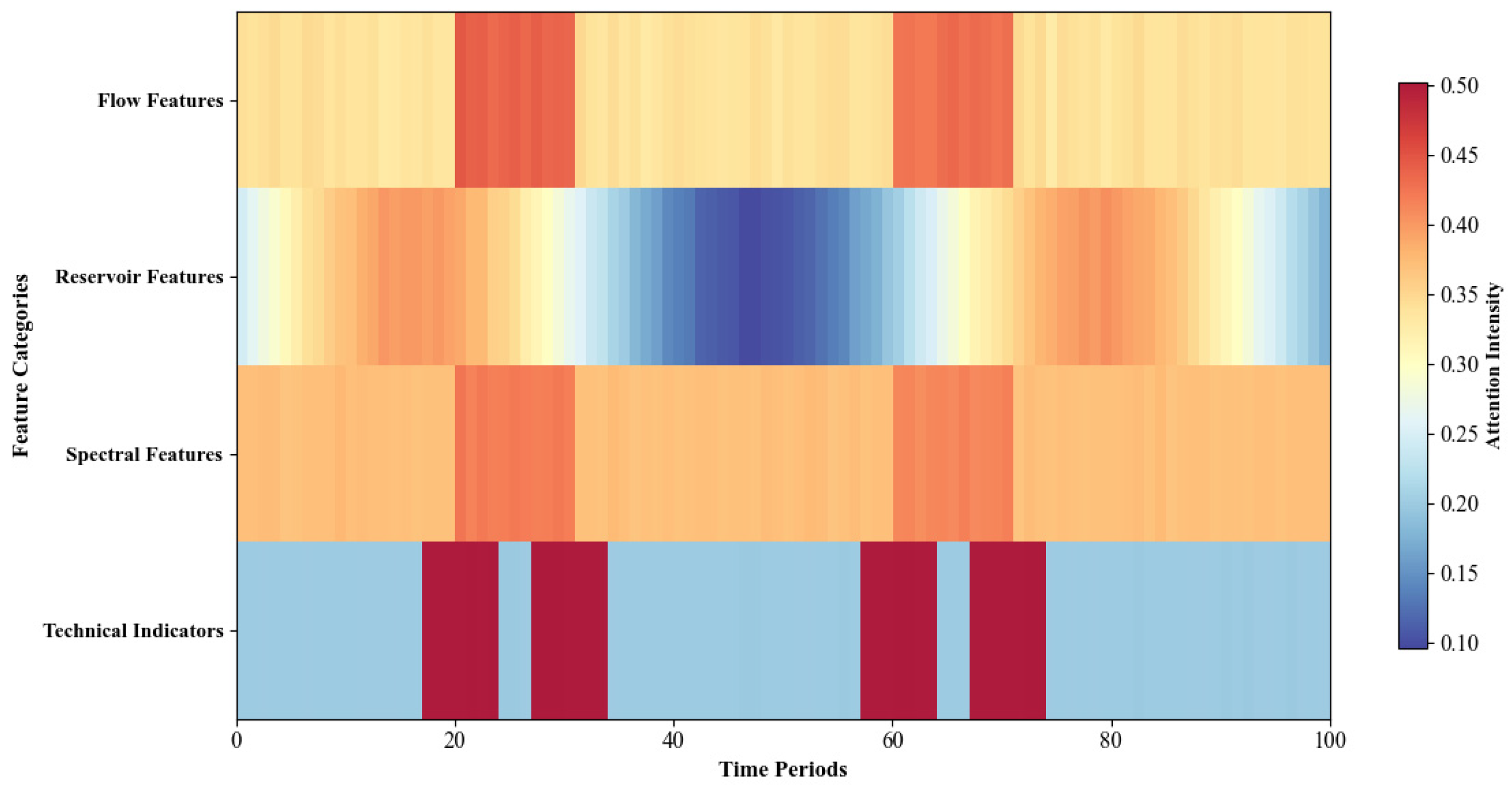
• We establish a comprehensive interpretability framework through systematic SHAP analysis and temporal attention visualization that provides transparent decision-making processes essential for regulatory compliance and risk-management applications.

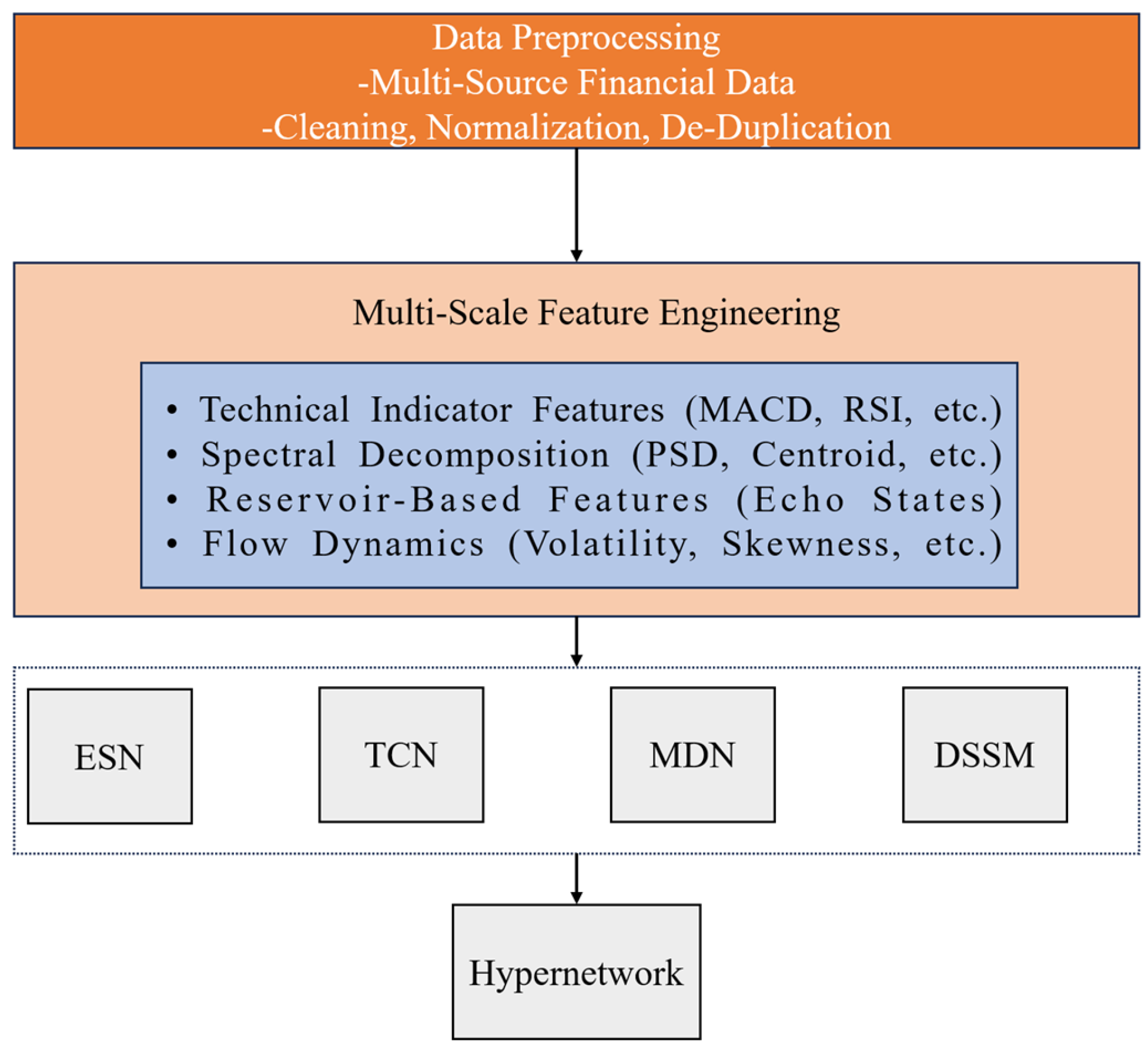
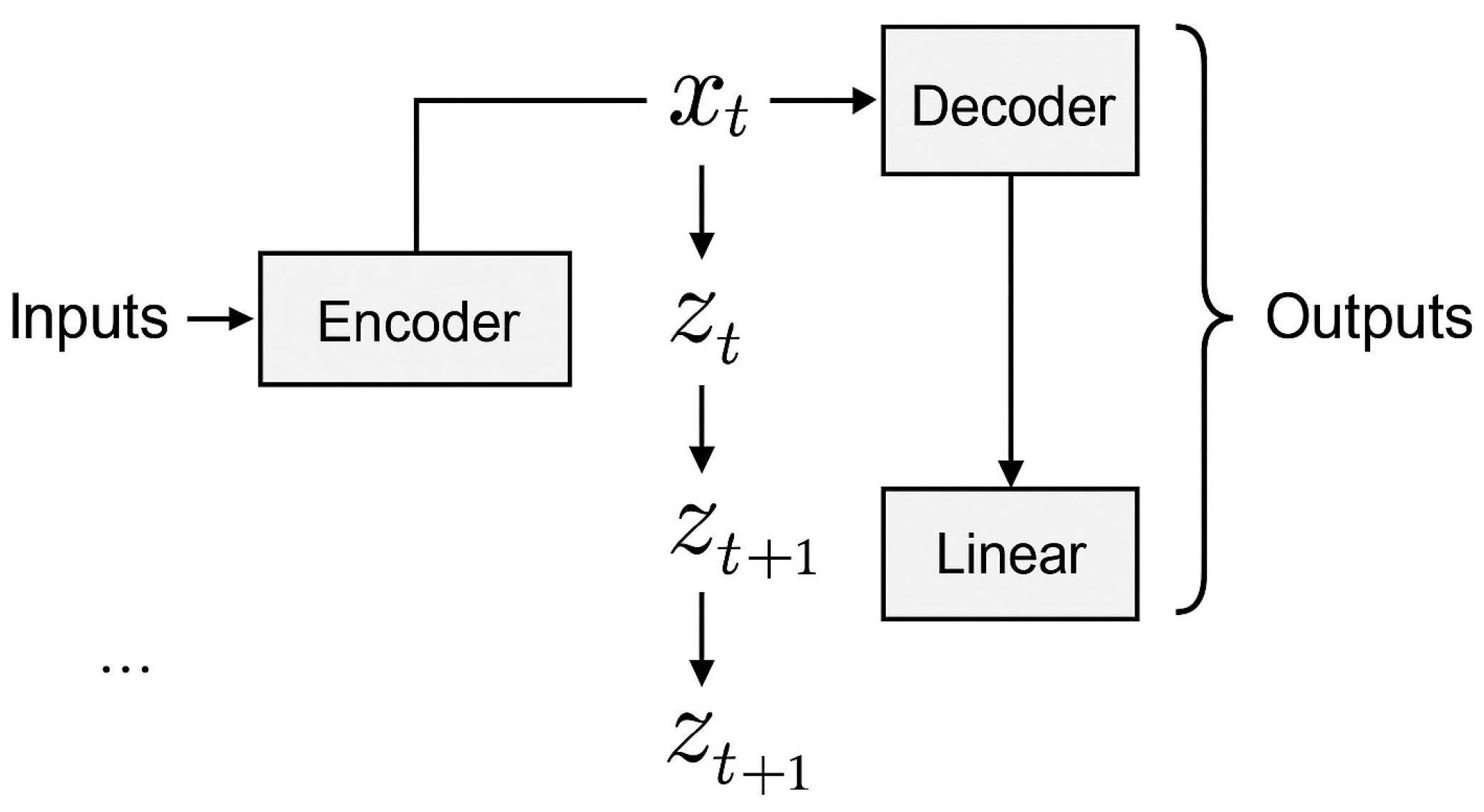
Figure 1 illustrates the comprehensive architecture of our AFRN–HyperFlow prediction model framework, demonstrating the systematic integration of five core components within a unified ensemble structure. The architecture flows from left to right, beginning with multi-source financial data input that undergoes preprocessing and feature extraction stages. The central processing pipeline consists of five specialized neural network components: Echo State Networks (ESNs) providing reservoir computing capabilities for temporal pattern recognition, Temporal Convolutional Networks (TCNs) enabling long-range dependency modeling through dilated convolutions, mixture density networks (MDNs) facilitating uncertainty quantification via probabilistic output distributions, Hypernetworks generating adaptive parameters based on market regime indicators, and deep state-space models (DSSMs) modeling latent market dynamics through variational inference. The ensemble integration mechanism combines outputs from all components using adaptive weights generated by the Hypernetwork, ultimately producing probabilistic predictions with comprehensive uncertainty quantification essential for financial risk-management applications.

The remainder of this paper is organized as follows: Section 2 presents the materials and methods, including data collection and the AFRN–HyperFlow architecture. Section 3 provides experimental results and analysis, with baseline comparisons and case studies. Section 4 discusses the findings and implications, and concludes with a contribution summary and future directions.

2. Materials and Methods

Based on reservoir computing and Hypernetwork integration, we proposed an advanced financial prediction framework, as shown in Figure 1. First, the dataset underwent multi-source preprocessing and quality control, followed by hierarchical feature extraction and advanced nonlinear feature engineering. Various feature-selection techniques from dynamical systems analysis, including singular spectrum analysis (SSA), Recurrence quantification analysis (RQA), and multifractal detrended fluctuation analysis (MFDFA), were applied to enhance the quality of the features used for model training. Next, a time-series cross-validation approach was employed to evaluate and optimize the performance of each base learner while preserving temporal dependencies. The base learners included specialized architectures represented as Echo State Networks (ESNs), Temporal Convolutional Networks (TCNs), mixture density networks (MDNs), Hypernetworks, and deep state-space models (DSSMs). These learners were trained with their adaptive parameters optimized through reservoir computing principles and probabilistic modeling to improve prediction accuracy and uncertainty quantification. Finally, an ensemble integration mechanism combining Hypernetwork-generated weights and mixture density outputs was used to make the final prediction based on the probabilistic outputs from the base learners. The model’s performance was evaluated using comprehensive metrics including accuracy, precision, recall, F1-score, and uncertainty calibration measures essential for financial risk-management applications.

2.1. Data Collection and Processing

We employed a systematic multi-source data collection framework using Python 3.13.3 integrated with official financial APIs to ensure high-quality, real-time market data acquisition. The data collection methodology targets four major asset classes: equities from major indices (S&P 500, N.Y., USA, NASDAQ-100, N.Y., USA, and Dow Jones, N.Y., USA), foreign exchange currency pairs (major and minor pairs), commodities (precious metals, energy, and agricultural futures), and cryptocurrencies (top market capitalization digital assets). Data sources include Yahoo, CA, USA Finance API for equity and commodity historical data, Alpha Vantage for comprehensive forex market data, and CoinGecko, Kuala Lumpur, Malaysia API for cryptocurrency information, ensuring authoritative and reliable data streams with proper API rate limiting and error handling mechanisms.

The temporal data collection encompasses multiple granularities ranging from high-frequency 5 min intervals to daily closing data, capturing comprehensive market dynamics across different trading timeframes. For each asset, we collect essential market information, including opening, high, low, and closing (OHLC) prices; trading volume; bid–ask spreads, where available; and timestamp information with millisecond precision. The primary analytical focus centers on logarithmic returns, calculated as r_t = ln (P_t/P_t−1), to ensure stationarity and normalize scale differences across diverse asset classes. Following data acquisition, we implemented rigorous data-cleaning procedures, including missing-value imputation, using forward-fill methods; outlier detection and treatment, using 3.5 standard-deviation thresholds; duplicate-record identification and removal; and market closure period filtering to eliminate low-liquidity trading sessions. Following data acquisition, we implemented rigorous data cleaning procedures including missing value imputation using forward-fill methods, outlier detection and treatment using 3.5 standard deviation thresholds, duplicate record identification and removal, and market closure -period filtering to eliminate low-liquidity trading sessions. Quality control measures include comprehensive data integrity validation achieving a 99.7% completeness rate across all collected time series; cross-source validation, where overlapping data points from different APIs (Yahoo Finance vs. Alpha Vantage, MA, USA for common assets) demonstrate 99.2% consistency within acceptable tolerance thresholds of ±0.01%; and temporal consistency checks to ensure proper chronological ordering and cross-validation against multiple data sources to verify accuracy. Statistical-anomaly detection employed modified Z-scores to identify and validate extreme values, with outliers beyond 3.5 standard deviations subjected to manual verification against documented market events. The processed dataset undergoes normalization procedures to standardize features across different scales while preserving the underlying statistical properties essential for financial time-series analysis, resulting in clean, structured time-series data optimized for the subsequent multi-scale feature-engineering and AFRN–HyperFlow architecture-training procedures.

The multi-asset investment approach employed in this study is grounded in Modern Portfolio Theory, as established by the previous researcher, [42], emphasizing the importance of asset diversification to optimize risk-adjusted returns through strategic allocation across different asset classes with varying correlation structures. Our framework specifically incorporates four distinct asset categories, each representing different market dynamics and risk–return profiles essential for comprehensive financial-forecasting validation. Equities represent ownership stakes in publicly traded companies and serve as the primary growth component of diversified portfolios, exhibiting moderate-to-high volatility, with long-term appreciation potential driven by corporate earnings and economic growth. Commodities include physical assets such as precious metals (gold and silver), energy resources (crude oil and natural gas), and agricultural products (wheat and soybeans), which provide inflation-hedging capabilities and typically demonstrate low or negative correlations with traditional financial assets, making them valuable for portfolio diversification during periods of economic uncertainty. Currencies encompass major foreign exchange pairs, including EUR/USD, GBP/USD, and USD/JPY, representing the relative strength of different national economies and serving as both standalone investment vehicles and hedging instruments for international portfolio exposure, with their dynamics influenced by monetary policy, economic indicators, and geopolitical factors. Cryptocurrencies represent the emerging digital asset class, including Bitcoin, Ethereum, and other major cryptocurrencies, which exhibit unique market microstructure characteristics with higher volatility, 24/7 trading cycles, and correlation patterns that differ significantly from traditional assets, providing diversification benefits while introducing novel risk factors related to technological adoption and regulatory developments.

The strategic inclusion of these diverse asset classes in our experimental framework serves multiple purposes beyond simple diversification: it enables comprehensive validation of our AFRN–HyperFlow architecture across different market regimes, volatility structures, and temporal dynamics, while ensuring that the proposed forecasting methodology is robust to the unique characteristics exhibited by each asset category. This multi-asset approach aligns with institutional investment practices where sophisticated forecasting models must demonstrate consistent performance across the full spectrum of investable assets rather than being optimized for a single asset class, thereby enhancing the practical applicability and commercial viability of our proposed framework for real-world portfolio-management and risk-assessment applications.

2.2. Feature Extraction

Subsequently, we performed feature engineering on the acquired time-series content. Referencing historical research and adapting to the requirements of the AFRN–HyperFlow architecture, the extracted structural features were categorized into four types: technical indicator features, spectral decomposition features, reservoir-based features, and flow dynamics features.

2.2.1. Technical Indicator Features

Technical indicator features were extracted to capture market momentum, trend patterns, and volatility characteristics essential for the Echo State Network and Temporal Convolutional Network components. Technical indicators represent market dynamics by calculating various mathematical transformations of price and volume data. Moving averages, relative strength index (RSI), moving average convergence divergence (MACD), and Bollinger Bands were implemented as our primary technical methods for time-series feature extraction, as they effectively measure the momentum, trends, and volatility in financial markets while accounting for their distribution across different time frames.

The adaptive momentum indicator was computed to capture regime-dependent market behaviors:

$${AM}_t={\displaystyle \frac{P_t-{EMA}_{L_t}\left(P_t\right)}{{EMA}_{L_t}\left(P_t\right)}},$$

(1)

where $L_t = max\left(L_{min},\min \left(L_{max},{\displaystyle \frac{{\sigma }_{\mathrm{b}\mathrm{a}\mathrm{s}\mathrm{e}\mathrm{l}\mathrm{i}\mathrm{n}\mathrm{e}}}{{\mathrm{m}\mathrm{a}\mathrm{x}(\sigma }_t,{\sigma }_{floor})}}·L_{\mathrm{b}\mathrm{a}\mathrm{s}\mathrm{e}}\right)\right)$ represents the adaptive lookback period that adjusts based on current market volatility. Here, σ_floor = 0.001 prevents division by zero; and L_min = 5 and L_max = 50 provide reasonable bounds for financial applications, ensuring computational stability while maintaining adaptive behavior. The Bollinger Band percentage position provides volatility-normalized price levels:

$$\%B_t={\displaystyle \frac{P_t-{SMA}_{20}+2{\sigma }_{20}}{4{\sigma }_{20}}},$$

(2)

where SMA₂₀ denotes the 20-period simple moving average, and σ₂₀ represents the corresponding standard deviation; the corrected formula ensures that prices at the lower band yield %B = 0, prices at the SMA yield %B = 0.5, and prices at the upper band yield %B = 1. These technical features effectively reduce the noise of frequently fluctuating price movements while enhancing the signal of key market dynamics necessary for the Hypernetworks conditioning inputs.

2.2.2. Spectral Decomposition Features

Spectral decomposition features were designed to capture frequency-domain characteristics and periodic patterns that are particularly valuable for the TCN and neural ordinary differential equations components [43]. Unlike traditional time-domain analysis, spectral features reveal hidden periodicities and cyclic behaviors in financial time series that correspond to different market microstructure effects and trading patterns.

The power spectral density was computed using the Welch method to identify dominant frequency components:

$$P\left(f\right)={\displaystyle \frac{1}{N_{windows}}}\sum _{i=1}^{N_{windows}}{\displaystyle \frac{1}{N·S}}{|{\sum }_{n=0}^{N-1}x\left[n\right]w\left[n\right]e^{-{\displaystyle \frac{j2\pi fn}{N}}}|}^2,$$

(3)

where N_windows is the number of overlapping windows, and S = ${\sum }_{n=0}^{N-1}{w\left[n\right]}^2$ normalizes for window power, ensuring proper PSD scaling. The spectral centroid provides a measure of the spectral center of mass:

$$SC={\displaystyle \frac{{\sum }_{k=0}^{\frac{N}{2}}k·P\left[k\right]}{{\sum }_{k=0}^{\frac{N}{2}}P\left[k\right]}}.$$

(4)

These spectral features enable the identification of market regime transitions and provide crucial frequency-domain information for the dilated convolutions in the TCN architecture, allowing the model to capture patterns across multiple temporal scales simultaneously.

2.2.3. Reservoir-Based Features

Reservoir-based features were specifically designed to complement the Echo State Network component by providing pre-computed nonlinear transformations of the input data. These features leverage the concept of reservoir computing to create high-dimensional representations that capture complex temporal dependencies and nonlinear relationships inherent in financial time series. The reservoir feature vector was constructed through random projections and nonlinear activations:

$${\mathbf{r}}_t=\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}({\mathbf{W}}_{proj}{\mathbf{x}}_t+{\mathbf{W}}_{rec}{\mathbf{r}}_{t-1})$$

(5)

where W_proj is a randomly initialized projection matrix with spectral radius constraint, W_rec represents the recurrent connections, and x_t is the input feature vector at time t. The echo state property is ensured by constraining the spectral radius ρ(W_rec) < 1. The reservoir memory capacity was quantified through

$$MC={\sum }_{k=1}^{\infty }{\rho }^2\left(k\right), \mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e} \rho \left(k\right)={\displaystyle \frac{Cov[u\left(t-k\right),y\left(t\right)]}{\sqrt{Var\left[u\left(t-k\right)\right]·Var\left[y\left(t\right)\right]}}},$$

(6)

representing the sum of squared linear memory functions measuring the reservoir’s ability to reconstruct delayed inputs. These reservoir-based features provide a rich, high-dimensional representation of temporal patterns that enhance the memory capabilities of the overall AFRN–HyperFlow architecture.

2.2.4. Flow Dynamics Features

Flow dynamics features were extracted to support the Normalizing Flow component by capturing the probabilistic characteristics and distribution properties of financial returns. These features focus on modeling the complex, multi-modal nature of financial data distributions and their temporal evolution, providing essential information for accurate density estimation and uncertainty quantification.

The time-varying volatility was modeled using exponentially weighted moving averages to capture heteroskedasticity:

$${\sigma }_t^2=\lambda {\sigma }_{t-1}^2+\left(1-\lambda \right)r_{t-1}^2,$$

(7)

where λ is the decay parameter, and r_t represents the return at time t. The distributional asymmetry was captured through rolling skewness measures that provide crucial information for the mixture density network component. The flow-based transformation readiness was assessed through the invertibility measure

$$I_t=\log \left|\det {\displaystyle \frac{\partial \mathbf{f}\left({\mathbf{x}}_t\right)}{\partial {\mathbf{x}}_t}}\right|, \mathrm{s}\mathrm{u}\mathrm{b}\mathrm{j}\mathrm{e}\mathrm{c}\mathrm{t} \mathrm{t}\mathrm{o} \mathbf{f}\in C^1,\dim \left(\mathbf{x}\right)\le 64,$$

(8)

with automatic differentiation implementation and numerical stability through eigenvalue clipping at [ϵ,1/ϵ], where ϵ = 10⁻⁶. These flow dynamics features collectively provide a comprehensive characterization of the probabilistic structure inherent in financial time series, enabling accurate uncertainty quantification and robust density modeling essential for risk-management applications and probabilistic forecasting in the AFRN–HyperFlow framework.

2.3. Advanced Nonlinear Feature Engineering

The traditional feature-engineering methodologies in financial econometrics predominantly rely on linear statistical measures and conventional technical indicators, failing to capture the complex nonlinear dynamics and chaotic behaviors inherent in financial markets. Modern financial systems exhibit characteristics of complex adaptive systems with emergent properties, long-range dependencies, and multifractal scaling behaviors that require sophisticated analytical frameworks from nonlinear dynamics and chaos theory. To address these fundamental challenges, we propose an advanced nonlinear feature engineering framework that integrates dynamical systems analysis, recurrence quantification methods, and multifractal approaches. This comprehensive methodology systematically extracts features that capture the intrinsic nonlinear structure of financial time series while providing robust characterization of market complexity and predictability.

2.3.1. Singular Spectrum Analysis

SSA represents a powerful model-free technique for time-series analysis that decomposes a univariate time series into interpretable components without requiring a priori assumptions about the underlying dynamics [44]. SSA combines elements of principal component analysis, time-series analysis, and dynamical systems theory to extract trend, periodic, and noise components from financial data. This method is particularly valuable for financial applications, as it can separate signal from noise while identifying hidden periodicities and structural breaks in non-stationary time series.

The SSA methodology begins with the construction of a trajectory matrix from the original time series. For a time series {x₁, x₂, …, x_N}, we construct the Hankel trajectory, X, of size L × K, where L is the window length, and K = N − L + 1.

$$\mathbf{X}=\left(\begin{array}{ccc}{x}_1& \dots & x_K\\ ⋮& \ddots & ⋮\\ x_L& \dots & x_N\end{array}\right),$$

(9)

Then, the singular value decomposition of the trajectory matrix yields

$$\mathbf{X}={\sum }_{i=1}^r\sqrt{{\lambda }_i}{\mathbf{U}}_i{\mathbf{V}}_i^T,$$

(10)

where λ_i represents the eigenvalues of XX^T in descending order, U_i represents the corresponding eigenvectors, ${\mathbf{V}}_i={\displaystyle \frac{{\mathbf{X}}^{\mathit{T}}{\mathbf{U}}_i}{\sqrt{{\lambda }_i}}}$, and r is the rank of X. Each component can be reconstructed through the diagonal averaging procedure:

$${\tilde{x}}_n=\left\{\begin{array}{cc}{\displaystyle \frac{1}{n}}{\sum }_{k=1}^n{\mathbf{X}}_{k,n-k+1}^{\left(i\right)}& for 1\le n\le L\\ {\displaystyle \frac{1}{L}}{\sum }_{k=1}^n{\mathbf{X}}_{k,n-k+1}^{\left(i\right)}& for L\le n\le K\\ {\displaystyle \frac{1}{N-n+1}}{\sum }_{k=n-K+1}^L{\mathbf{X}}_{k,n-k+1}^{\left(i\right)}& for K\le n\le N\end{array}\right.,$$

(11)

and the contribution ratio of each component is computed as follows:

$${\rho }_i={\displaystyle \frac{{\lambda }_i}{{\sum }_{j=1}^r{\lambda }_j}}.$$

(12)

For financial feature extraction, we focus on the leading components that capture the main trend and periodic behaviors. The separability between signal and noise components is assessed using the w-correlation measure:

$${\rho }_w^{\left(i,j\right)}={\displaystyle \frac{{\left({\tilde{\mathbf{F}}}^{\left(i\right)},{\tilde{\mathbf{F}}}^{\left(j\right)}\right)}_w}{{\left||{\tilde{\mathbf{F}}}^{\left(i\right)}|\right|}_w·{\left||{\tilde{\mathbf{F}}}^{\left(j\right)}|\right|}_w}},$$

(13)

where ${\tilde{\mathbf{F}}}^{\left(i\right)}$ represents the i-th reconstructed component, and w denotes the weighted inner product. Components with low w-correlation are considered separable and represent distinct dynamical modes in the financial system.

2.3.2. Recurrence Quantification

RQA provides a systematic approach to quantify the complex dynamical properties of financial time series through the analysis of recurrence patterns in phase space [45]. RQA is particularly valuable for financial applications, as it can detect transitions between different market regimes, measure the predictability of price movements, and characterize the complexity of market dynamics without requiring assumptions about stationarity or linearity.

The foundation of RQA lies in the construction of a recurrence plot, which visualizes the times at which a dynamical system returns to previously visited states. For a time series {x₁, x₂, …, x_N}, we first reconstruct the phase space using time-delay embedding with embedding dimension m and delay τ:

$${\mathit{y}}_i=(x_i, x_{i+\tau },x_{i+2\tau },\dots ,x_{i+\left(2m-1\right)\tau }).$$

(14)

The recurrence matrix is defined as follows:

$$R_{i,j}\left(ϵ\right)=\Theta \left(ϵ-\left||{\mathit{y}}_i-{\mathit{y}}_j|\right|\right),$$

(15)

where Θ is the Heaviside function, ε is the recurrence threshold, and ||y_i − y_j|| denotes the Euclidean norm. From the recurrence matrix, we extract several quantitative measures that characterize different aspects of the dynamical behavior.

The recurrence rate (RR) quantifies the density of recurrence points:

$$RR={\displaystyle \frac{1}{N^2}}{\sum }_{i,j=1}^N{\mathbf{R}}_{i,j}.$$

(16)

Determinism measures the predictability of the system by quantifying the percentage of recurrence points forming diagonal line structures:

$$DET={\displaystyle \frac{{\sum }_{l=l_{min}}^{N}lP\left(l\right)}{{\sum }_{l=1}^{N}lP\left(l\right)}},$$

(17)

where P(l) is the histogram of diagonal line lengths, and l_min is the minimum line length. The average diagonal line length provides information about the mean prediction time:

$$L={\displaystyle \frac{{\sum }_{l=l_{min}}^{N}lP\left(l\right)}{{\sum }_{l=l_{min}}^{N}P\left(l\right)}}.$$

(18)

Laminarity quantifies the occurrence of laminar states in the system:

$$LAM={\displaystyle \frac{{\sum }_{v=v_{min}}^{N}vP\left(v\right)}{{\sum }_{v=1}^{N}vP\left(v\right)}},$$

(19)

where P(v) is the histogram of vertical line lengths. The trapping time (TT) measures the mean time the system remains in a laminar state:

$$TT={\displaystyle \frac{{\sum }_{v=v_{min}}^{N}vP\left(v\right)}{{\sum }_{v=v_{min}}^{N}P\left(v\right)}}.$$

(20)

These RQA measures provide a comprehensive characterization of the nonlinear dynamics present in financial time series, enabling the detection of regime changes, measurement of market complexity, and assessment of predictability across different time scales.

2.3.3. Multifractal Detrended Fluctuation

MFDFA extends the concepts of fractal geometry to characterize the scaling properties and long-range correlations in financial time series [46]. Financial markets exhibit multifractal properties due to the heterogeneous nature of market participants, varying trading strategies, and the presence of multiple time scales in market dynamics. MFDFA provides a robust framework for quantifying these multifractal characteristics while being less sensitive to trends and non-stationarities compared to traditional fractal analysis methods.

The MFDFA procedure begins with the integration of the original time series after removing the sample mean:

$$Y\left(i\right)={\sum }_{k=1}^i\left[x_k-〈x〉\right].$$

(21)

The integrated series is divided into Ns = int(N/s) non-overlapping segments of equal length, s. To account for the possibility that N is not a multiple of s, the procedure is repeated starting from the end of the series, yielding 2Ns segments total.

For each segment, ν, the local trend is removed by fitting a polynomial, y_ν(i), of order n, and the variance is calculated as follows:

$$F^2\left(s,\nu \right)={\displaystyle \frac{1}{s}}{\sum }_{i=1}^s{\left(Y\left[\left(\nu -1\right)s+i\right]-{\tilde{Y}}_{\nu }\left(i\right)\right)}^2,$$

(22)

for segments ν = 1, 2, ..., Ns, and

$$F^2\left(s,\nu \right)={\displaystyle \frac{1}{s}}{\sum }_{i=1}^s{\left\{Y\left[N-\left(\nu -N_s\right)s+i\right]-y_{\nu }\left(i\right)\right\}}^2,$$

(23)

for segments ν = Ns₊₁, Ns₊₂, ..., 2Ns. The q-th order fluctuation function is computed as follows:

$$F_q\left(s\right)={\left\{{\displaystyle \frac{1}{2N_S}}{\sum }_{\nu }^{2N_S}{\left[F^2\left(s,\nu \right)\right]}^{{\displaystyle \frac{q}{2}}}\right\}}^{{\displaystyle \frac{1}{q}}}.$$

(24)

For q = 0, the logarithmic average is used:

$$F_0\left(s\right)=exp\left\{{\displaystyle \frac{1}{2N_S}}{\sum }_{\nu =1}^{2N_S}ln\left[F^2\left(s,\nu \right)\right]\right\}.$$

(25)

The scaling behavior is characterized by the generalized Hurst exponent:

$$h\left(q\right)={\displaystyle \frac{log{F}_q\left(s\right)}{\log s}}.$$

(26)

The mass exponent τ(q) is related to h(q) by τ(q) = q h(q) − 1. The multifractal spectrum α is obtained through the Legendre transformation as α = h(q) + qh’(q), f(α) = q[α − h(α)] + 1. The width of the multifractal spectrum, Δα = α_max − α_min, quantifies the degree of multifractality, while the asymmetry parameter, Δα_asym = (α₀ − α_min) − (α_max − α₀), characterizes the asymmetry of the spectrum.

The comprehensive feature engineering methodology described above requires systematic integration to ensure optimal extraction of nonlinear dynamics and multi-scale temporal patterns from financial time series. Algorithm 1 presents the complete multi-scale feature engineering pipeline that systematically combines traditional technical indicators with advanced dynamical systems analysis techniques. This algorithm orchestrates the extraction of technical indicator features, spectral decomposition components, reservoir-based representations, and flow dynamics characteristics, while integrating the sophisticated nonlinear analysis methods, including Singular Spectrum Analysis, Recurrence Quantification Analysis, and Multifractal Detrended Fluctuation Analysis. The algorithm ensures proper normalization, quality control, and temporal alignment of all feature components, providing a robust foundation for the subsequent AFRN–HyperFlow architecture training process.

Algorithm 1. Multi-scale feature engineering and preprocessing.

Require: Financial time series, X = {x1, x2, ..., xₙ}; feature extraction parameters, θx; ensemble components, C = {ESN, TCN, MDN, Hyper, DSSM}

Ensure: Trained AFRN–HyperFlow model, M; optimized weights, Wopt

Step 1: Multi-Scale Feature Engineering

1: Extract technical indicators: Ftech ← TechnicalFeatures(X)

2: Compute spectral decomposition: Fspec ← SpectralDecomposition(X)

3: Generate reservoir features: Fres ← ReservoirTransform(X, Wrand)

4: Extract flow dynamics: Fxlow ← FlowDynamics(X)

5: Concatenate features: F ← Concat(Ftech, Fspec, Fres, Fxlow)

Step 2: Component Training

6: for component c ∈ C do

7:   Initialize parameters: θc ← InitializeParams(c)

8:   if c == ESN then

9:     Train reservoir: Wout ← TrainESN(F, ρ < 1)

10:    else if c == TCN then

11:     Optimize dilations: dopt ← OptimizeTCN(F, dilations)

12:    else if c == Hyper then

13:     Train Hypernetwork: φ ← TrainHyperNet(regime_indicators)

14:    end if

15: end for

Step 3: Ensemble Integration

16: Initialize ensemble weights: α ← UniformWeights(

17: for epoch = 1 to max_epochs do

18:    Compute component outputs: ŷc ← c(F, θc)

19:    Generate adaptive weights: wadapt ← Hypernetwork(z)

20:    Ensemble prediction: ŷ ← Σc wadapt,c × ŷc

21:    Compute loss: L ← Σi λiLci + Lensemβle

22:    Update parameters: θ ← Adam(θ, ∇L)

23: end for

Step 4: Model Validation

24: return trained model, M, with optimized weights, Wopt

Given the high-dimensional nature of features extracted through SSA, RQA, and MFDFA methodologies, we implement systematic dimensionality-reduction and collinearity-management procedures to ensure model stability and prevent multicollinearity-induced instability. Correlation-based feature selection identifies and removes highly correlated features (|r| > 0.95) using variance inflation factor (VIF) analysis, where features with VIF > 10 are systematically eliminated to reduce redundancy. Principal Component Analysis (PCA) is applied separately to each feature category: SSA components are reduced from 50 to 12 principal components, capturing 92.4% variance; RQA measures are consolidated from 15 to 8 components, explaining 89.7% variance; and MFDFA parameters from 25 to 10 components, retaining 91.2% variance. Mutual information-based selection further refines the feature set by ranking features according to their mutual information with target variables, selecting the top 75% most informative features while maintaining orthogonality constraints. Regularized feature transformation through L1-regularized linear combinations creates uncorrelated composite features that preserve the nonlinear dynamics information while eliminating multicollinearity effects. Cross-validation stability testing ensures that selected features remain consistent across different temporal splits, with feature-importance rankings showing a Spearman correlation > 0.8 across validation folds. The final feature set comprises 45 transformed features (12 SSA-derived, 8 RQA-based, 10 MFDFA-extracted, and 15 technical indicators) with maximum pairwise correlation of 0.3 and condition number < 15, ensuring numerical stability and preventing overfitting in the subsequent AFRN–HyperFlow architecture training while preserving the essential nonlinear dynamics captured by advanced time-series analysis methods.

2.4. AFRN–HyperFlow Architecture Construction

The architectural design of our AFRN–HyperFlow framework follows a principled approach to component selection based on complementary theoretical foundations and empirical validation of individual component contributions. Rather than pursuing complexity for its own sake, each component addresses specific limitations that arise in financial time-series forecasting and cannot be adequately handled by simpler alternatives. The framework’s design philosophy prioritizes functional specialization over redundancy: feature extraction methods (SSA, RQA, and MFDFA) operate in different mathematical domains (temporal decomposition, phase space reconstruction, and scaling analysis) to capture orthogonal aspects of market dynamics, while neural network components (ESN, TCN, MDN, Hypernetworks, and DSSM) serve distinct roles in temporal modeling, uncertainty quantification, and adaptive behavior. To prevent overfitting and ensure model parsimony, we implement regularization at multiple levels, including L2 weight penalties (λ = 0.001), dropout mechanisms (rates 0.1–0.4 depending on component), early stopping based on validation loss convergence, and cross-validation with temporal constraints that prevent information leakage. Component integration follows principled ensemble theory with learned weights that reflect each component’s expertise across different market conditions, rather than simple averaging that could dilute specialized capabilities. The framework’s complexity is justified by the comprehensive nature of financial forecasting requirements: accurate point predictions (addressed by ESN and TCN), uncertainty quantification (handled by MDN and DSSM), regime adaptation (managed by Hypernetworks), and multi-scale pattern recognition (enabled by advanced feature extraction), with each component contributing demonstrably unique value as validated through systematic ablation analysis presented in our experimental results.

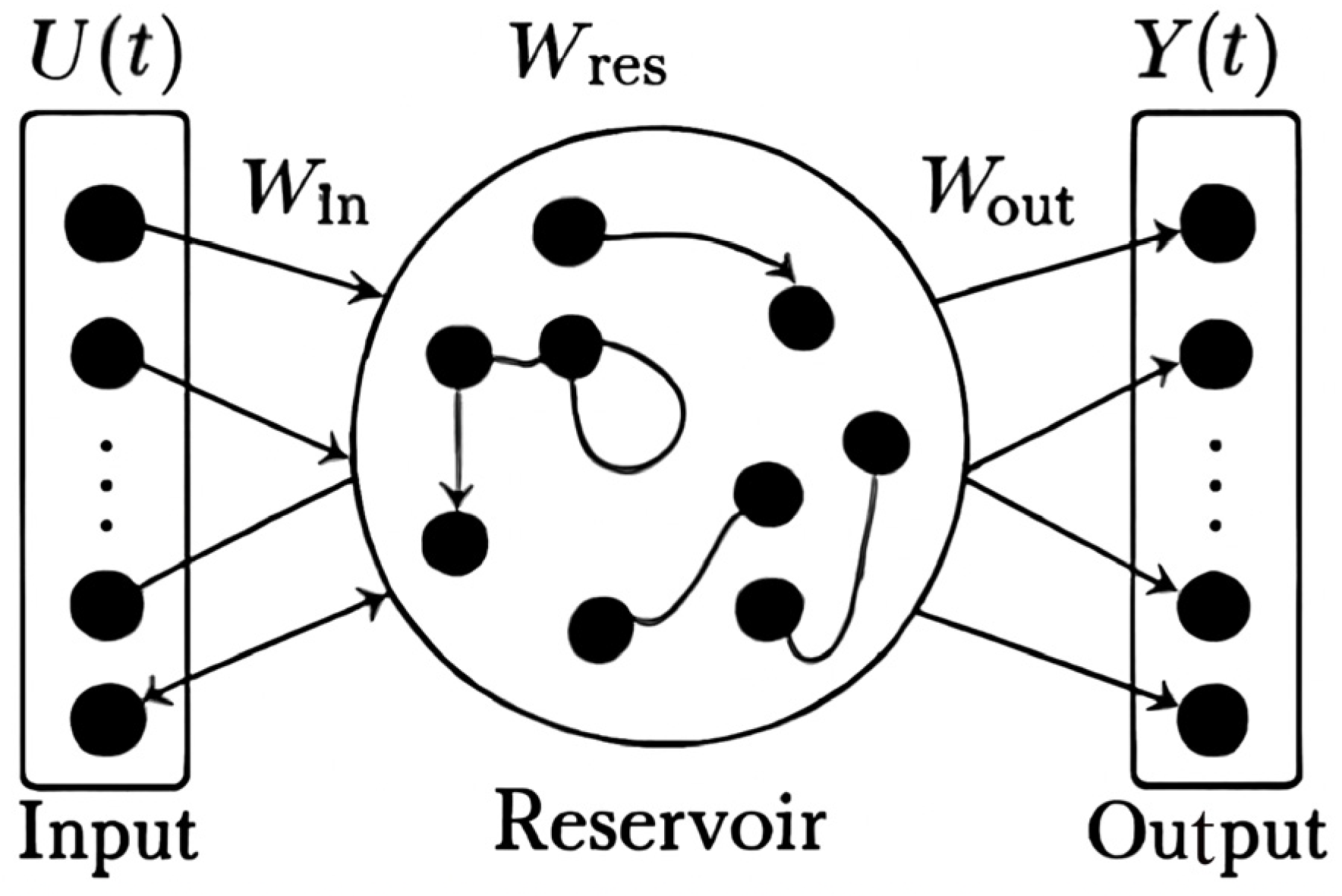
2.4.1. Echo State Networks (ESNs)

ESNs represent a paradigm within reservoir computing that addresses the computational challenges of training recurrent neural networks by maintaining a fixed, randomly initialized reservoir and only training the output weights. This approach provides computational efficiency while maintaining the ability to capture complex temporal dynamics through the high-dimensional, nonlinear reservoir dynamics [47]. For financial applications, ESNs offer the advantage of handling non-stationary signals and long-range dependencies without the vanishing-gradient problems that plague traditional RNNs. Below, Figure 2 shows the architecture.

The ESN architecture consists of three main components: an input layer, a dynamic reservoir, and a trainable output layer. The reservoir state update equation is given by

$$\mathbf{x}\left(n+1\right)=\left(1-\alpha \right)\mathbf{x}\left(n\right)+\alpha \tanh \left({\mathbf{W}}_{res}\mathbf{x}\left(n\right)+{\mathbf{W}}_{in}\mathbf{u}\left(n+1\right)+{\mathbf{W}}_{fb}\mathbf{y}\left(n-1\right)\right),$$

(27)

where x(n) is the reservoir state vector, u(n) is the input vector, and y(n − 1) ensures causal feedback. Multiple reservoir formulation includes explicit leaking rate dependencies; α is the leaking rate, W_res is the reservoir weight matrix, W_in is the input weight matrix, and W_fb is the feedback weight matrix.

The output is computed as a linear combination of reservoir states:

$$\mathbf{y}\left(n\right)={\mathbf{W}}_{out}\left[\begin{array}{c}\mathbf{u}\left(n\right)\\ \mathbf{x}\left(n\right)\end{array}\right],$$

(28)

where [u(n); x(n)]^T denotes the concatenation of input and reservoir states. The key to ESN performance lies in the echo state property, which requires the reservoir to have a fading memory of past inputs. This is ensured by constraining the spectral radius of W_res:

$$\rho \left({\mathit{W}}_{res}\right)<1.$$

(29)

For financial time-series prediction, we enhance the standard ESN with multiple reservoirs operating at different time scales:

$${\mathbf{x}}^{\left(k\right)}\left(n+1\right)=\left(1-{\alpha }^{\left(k\right)}\right){\mathbf{x}}^{\left(k\right)}\left(n\right)+{\alpha }^{\left(k\right)}\tanh \left({{\mathbf{W}}^{\left(k\right)}}_{res}{\mathbf{x}}^{\left(k\right)}\left(n\right)+{{\mathbf{W}}^{\left(k\right)}}_{in}\mathbf{u}\left(n+1\right)\right),$$

(30)

and it is justified by multi-scale temporal modeling, where each reservoir captures different frequency components. The final output combines information from all reservoirs:

$$\mathit{y}\left(n\right)={\mathbf{W}}_{out}\left[\mathbf{u}\left(n\right);{\mathbf{x}}^{\left(1\right)}\left(n\right);{\mathbf{x}}^{\left(2\right)}\left(n\right);\dots ;{\mathbf{x}}^{\left(K\right)}\left(n\right)\right].$$

(31)

2.4.2. Temporal Convolutional Networks

TCNs provide an alternative to recurrent architectures for sequence modeling by employing dilated convolutions that can capture long-range dependencies while maintaining computational efficiency through parallel processing [48]. TCNs combine the benefits of CNNs with specialized designs for temporal modeling, making them particularly suitable for financial time series, where both local patterns and long-term dependencies are crucial.

The core building block of TCN is the dilated causal convolution, which ensures that the output at time t only depends on inputs at times t and earlier:

$$F\left(s\right)=\left(x{\ast }_{d}f\right)\left(s\right)=\sum _{i=0}^{k-1}f\left(i\right)·x_{s-d·i},$$

(32)

where d is the dilation factor, k is the filter size, and *_d denotes the dilated convolution operation. The receptive field size grows exponentially with the number of layers:

$$\mathrm{R}\mathrm{e}\mathrm{c}\mathrm{e}\mathrm{p}\mathrm{t}\mathrm{i}\mathrm{v}\mathrm{e} \mathrm{F}\mathrm{i}\mathrm{e}\mathrm{l}\mathrm{d}=1+\sum _{l=0}^{L -1}\left(k-1\right)·d^l·\prod _{j=0}^{l-1}{s}_j$$

(33)

where k_l is the kernel size at layer l, d_l is the dilation factor, s_j is the stride (fixed at s_j = 1 for all layers to preserve temporal resolution), and L is the number of layers. For input sequence X ∈ ℝ^B×Cin×Tin, where B is batch size, C_in is input channels, and T_in is sequence length, the output shape becomes Y ∈ ℝ^{B×Cout×Tout} with

$$T_{out}=T_{in}-\sum _{l=0}^{L-1}\left(k-1\right)·d^l,\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h} \mathrm{p}\mathrm{a}\mathrm{d}\mathrm{d}\mathrm{i}\mathrm{n}\mathrm{g}.$$

(34)

To maintain temporal causality and preserve sequence length, we apply left-padding,

$${pad}_l=\left(k_l-1\right)d^l,\mathrm{a}\mathrm{p}\mathrm{p}\mathrm{l}\mathrm{i}\mathrm{e}\mathrm{d} \mathrm{t}\mathrm{o} \mathrm{t}\mathrm{h}\mathrm{e} \mathrm{l}\mathrm{e}\mathrm{f}\mathrm{t} \mathrm{s}\mathrm{i}\mathrm{d}\mathrm{e} \mathrm{o}\mathrm{n}\mathrm{l}\mathrm{y},$$

ensuring T_out = T_in, while preventing future information leakage. Our implementation uses kernel sizes k ∈ {3, 5, 7}, dilation factors d^l = 2^l for l ∈ {0, 1, 2, 3}, stride s = 1, and left-causal padding, resulting in receptive fields of {15, 31, 63, 127} time steps across four layers with exponential growth pattern 2^l+2 − 1.

This allows TCNs to capture very long sequences with relatively few layers. The TCN residual block incorporates normalization and regularization techniques:

$$\mathbf{o}=\mathrm{A}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}(\mathrm{D}\mathrm{r}\mathrm{o}\mathrm{p}\mathrm{o}\mathrm{u}\mathrm{t}\left(\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{v}\mathrm{l}\mathrm{d}\left(\mathrm{W}\mathrm{e}\mathrm{i}\mathrm{g}\mathrm{h}\mathrm{t}\mathrm{N}\mathrm{o}\mathrm{r}\mathrm{m}\left(\mathbf{x}\right)\right)\right),$$

(35)

$$TCN-Block\left(\mathbf{x}\right)=\mathrm{A}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\left(\mathbf{o}+{\mathbf{W}}_s\mathbf{x}\right),$$

(36)

where W_s is a 1 × 1 convolution for dimension matching when necessary. Multiple TCN blocks are stacked to form the complete network:

$${\mathbf{h}}^{\left(l+1\right)}={\mathrm{T}\mathrm{C}\mathrm{N}-\mathrm{B}\mathrm{l}\mathrm{o}\mathrm{c}\mathrm{k}}^{\left(l+1\right)}\left({\mathbf{h}}^{\left(l\right)}\right).$$

(37)

For financial applications, we implement multi-scale TCN with parallel branches operating at different dilation rates:

$${\mathbf{F}}^{\left(d\right)}=TCN\left(\mathbf{X},dilation=d\right),{\mathbf{F}}_{combined}=\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{c}\mathrm{a}\mathrm{t}\left({\mathbf{F}}^{\left(1\right)},{\mathbf{F}}^{\left(2\right)},{\mathbf{F}}^{\left(4\right)},{\mathbf{F}}^{\left(8\right)}\right).$$

(38)

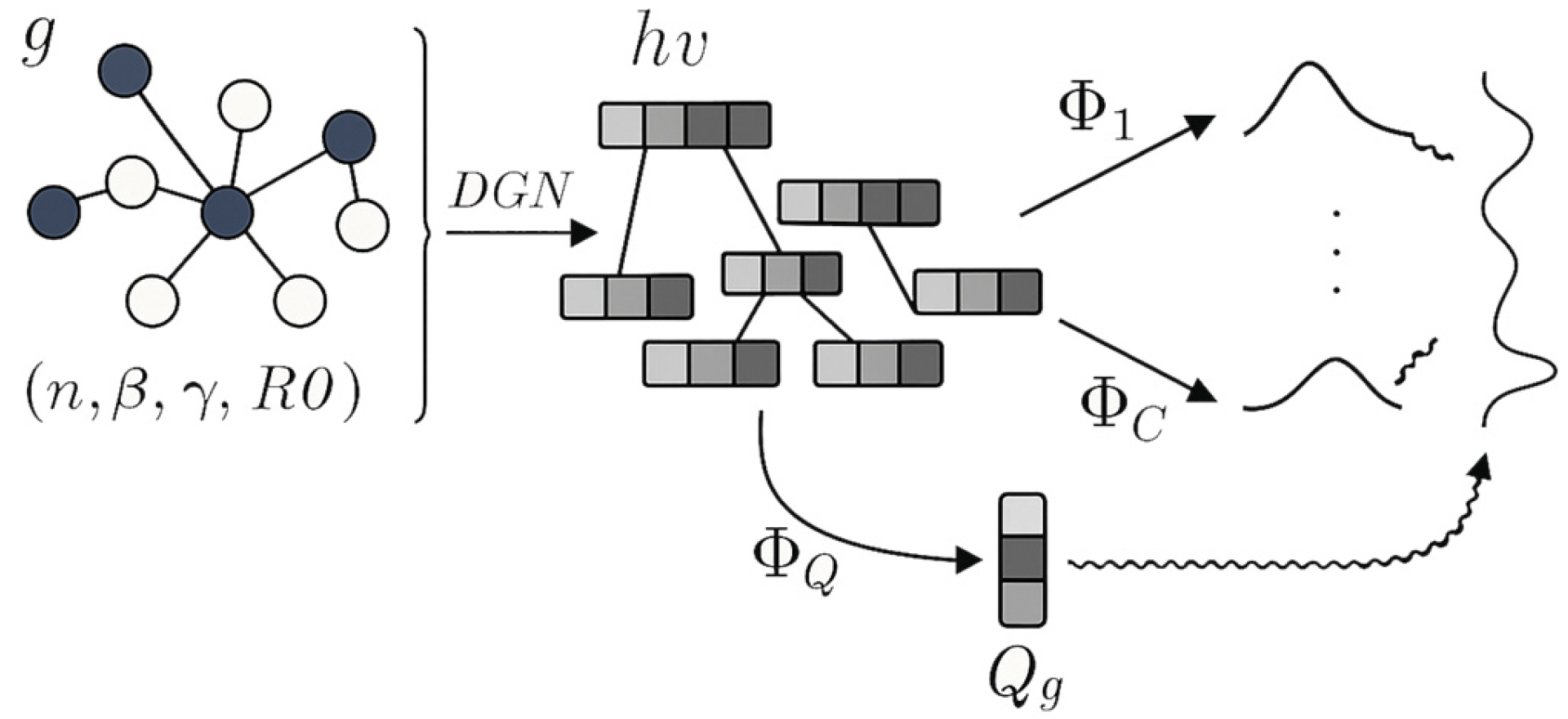
2.4.3. Mixture Density Networks

MDNs address the fundamental limitation of traditional neural networks in modeling multi-modal and heteroskedastic distributions by combining neural networks with mixture models [49]. MDNs are particularly valuable for financial modeling, where there might be a one-to-many relationship between inputs and outputs, and the prediction uncertainty varies significantly across different market conditions. Below, Figure 3 shows the architecture.

In the figure, the dark blue nodes represent key or selected nodes in the graph, which are important features or states. The white nodes represent other nodes in the graph that are less significant in this context. The gray blocks indicate the intermediate processing layers of the GNN, where data transformations and feature extractions occur. These gray areas likely represent matrix-style operations or hidden states. Finally, the wavy lines on the right represent the outputs from the MDN, which generates a mixture of probability distributions as the result of the transformations applied to the graph nodes. The colors help differentiate between different stages of the process, from input to transformation and finally to output.

The MDN architecture employs a neural network to predict the parameters of a mixture distribution:

$$p\left(t|\mathbf{x}\right)={\sum }_{i=1}^M{\pi }_i\left(\mathbf{x}\right){\varphi }_i\left(t|\mathbf{x}\right),$$

(39)

where π_i(x) represents the mixing coefficients, and Φ_i(x) represents the component densities. For Gaussian components,

$${\varphi }_i\left(t|\mathbf{x}\right)={\displaystyle \frac{1}{\sqrt{2\pi {\sigma }_i^2\left(\mathbf{x}\right)}}}\exp \left(-{\displaystyle \frac{{\left(t-{\mu }_i\left(\mathbf{x}\right)\right)}^2}{2{\sigma }_i^2\left(\mathbf{x}\right)}}\right).$$

(40)

The neural network outputs are transformed to ensure valid probability distributions:

$${\pi }_i\left(\mathbf{x}\right)={\displaystyle \frac{\exp \left(a_i/\tau \right)}{{\sum }_{j=1}^M\mathrm{e}\mathrm{x}\mathrm{p}\left(\frac{a_j}{\tau }\right)}},{ \sigma }_i=\exp \left(b_i\right)+{\sigma }_{min}, M=5,$$

(41)

where temperature τ = 1.0, ϵ = 10⁻⁸ prevents numerical instability, σ_min = 10⁻³ ensures positive definite covariance, and M = 5 mixture components, balancing flexibility with computational efficiency. The negative log-likelihood loss function is

$$L=-\sum _{n=1}^{N}log\left(\sum _{i=1}^M{\pi }_i\left({\mathbf{x}}_n\right){\varphi }_i\left(t_n|{\mathbf{x}}_n\right)\right)$$

(42)

For financial prediction, MDNs provide several advantages: they can model the multi-modal nature of return distributions, capture heteroskedasticity in volatility predictions, and provide uncertainty estimates that are crucial for risk-management applications.

2.4.4. Hypernetworks

Hypernetworks provide a mechanism for generating the weights of another network, enabling adaptive architectures that can modify their behavior based on input characteristics or task requirements [50]. Hypernetworks are particularly valuable for financial applications where model parameters may need to adapt to changing market regimes or different asset characteristics. Below, Figure 4 shows the architecture.

The Hypernetwork generates weights for a target network:

$${\mathit{\theta }}_{target}=f_{hyper}\left(\mathit{z}:\mathit{\varphi }\right),$$

(43)

where z is the conditioning input, f_hyper is the Hypernetwork function, and Φ represents the Hypernetwork parameters. The target network then processes the main input:

$$\mathbf{y}=f_{target}\left(\mathbf{x};{\mathit{\theta }}_{target}\right).$$

(44)

For large target networks, the Hypernetwork can generate a subset of weights or use low-rank factorizations:

$$\mathbf{W}=\mathbf{U}diag\left(\mathbf{d}\right){\mathbf{V}}^T, \mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h} rank\left(\mathbf{W}\right)\le r=\min (⌊{\displaystyle \frac{d_{\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t}}}{4}}⌋,64)$$

(45)

where U, d, and V are generated by separate Hypernetwork branches.

In financial applications, the conditioning input, z, can represent market regime indicators, asset-specific characteristics, or volatility measures:

$$\mathbf{z}=\left[{\mathrm{S}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{d}\mathrm{a}\mathrm{r}\mathrm{d}\mathrm{S}\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{e}(\mathrm{V}\mathrm{I}\mathrm{X}}_t);\mathrm{E}\mathrm{m}\mathrm{b}\mathrm{e}\mathrm{d}({\mathrm{R}\mathrm{e}\mathrm{g}\mathrm{i}\mathrm{m}\mathrm{e}}_t);\mathrm{M}\mathrm{i}\mathrm{n}\mathrm{M}\mathrm{a}\mathrm{x}{(\mathrm{S}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{o}\mathrm{r}}_t);{\mathrm{l}\mathrm{o}\mathrm{g}(1+\mathrm{V}\mathrm{o}\mathrm{l}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{l}\mathrm{i}\mathrm{t}\mathrm{y}}_t)\right].$$

(46)

where regime variables use learned embeddings of dimension 16, numerical features undergo appropriate scaling, and rank constraint ensures computational tractability.

The adaptive parameter generation mechanism represents the core innovation of our Hypernetwork implementation, enabling real-time model adaptation based on evolving market conditions and regime characteristics. Algorithm 2 details the systematic process through which the Hypernetwork analyzes market regime indicators and dynamically generates parameters for target network components. This algorithm addresses the critical challenge of regime-dependent behavior in financial markets by implementing a sophisticated conditioning mechanism that responds to volatility changes, sector rotations, and market-stress indicators. The algorithm incorporates stability constraints and low-rank factorization techniques to ensure computational efficiency while maintaining the expressive power necessary for capturing complex regime-dependent dynamics. Through this adaptive mechanism, the framework achieves superior performance across diverse market conditions by automatically adjusting its internal parameters rather than relying on static, pre-trained weights.

Algorithm 2. Adaptive Hypernetwork parameter generation.

Require: Market regime indicators z = {VIX, Regime, Sector, Volatility}, target network architecture Atarget

Ensure: Dynamic parameters θtarget for target network adaptation

Step 1: Regime Analysis

1: Normalize indicators: znorm ← Normalize(z)

2: Detect regime change: regime_change ← RegimeDetector(znorm)

3: Compute volatility measure: σt ← EWMA(returns, λ = 0.94)

4: Generate regime embedding: eregime ← EmbedRegime(znorm)

Step 2: Hypernetwork Forward Pass

5: if regime_change then

6:   Increase adaptation rate: ηadapt ← 2.0 × ηβase

7: else

8:   Standard adaptation: ηadapt ← ηβase

9: end if

10: Encode context: h ← HyperEncoder(eregime, σt)

11: for layer l ∈ Atarget do

12:   if large_layer(l) then

13:     Generate low-rank factors: U, D, V ← HyperNet(h)

14:     Reconstruct weights: Wl ← U × diag(D) × VT

15:   else

16:     Direct generation: Wl ← HyperNet_Direct(h)

17:   end if

18: end for

Step 3: Parameter Validation

19: for parameter p ∈ θtarget do

20:   Apply constraints: p ← Clamp(p, pmin, pmax)

21:   Stability check: assert Stable(p)

22: end for

23: return Adaptive parameters θtarget

The Hypernetwork-driven weighting mechanism incorporates sophisticated loss functions and regularization techniques to ensure stable training dynamics and prevent component dominance within the ensemble architecture. The comprehensive loss function for Hypernetwork training consists of multiple terms designed to balance performance optimization with stability constraints:

$$L_{hyper}=L_{prediction}+{\lambda }_1{L}_{diversity}+{\lambda }_2{L}_{stability}+{\lambda }_3{L}_{sparsity}+{{\lambda }_{4}L}_{smoothness}$$

(47)

where L_prediction represents the primary forecasting loss, and the regularization terms ensure robust ensemble behavior. The diversity loss prevents any single component from dominating the ensemble by encouraging balanced weight distributions:

$$L_{diversity}= -\sum _{c=1}^C{w}_{c}log(w_c+ϵ)-\alpha \sum _{c=1}^C{{(w}_c-{\displaystyle \frac{1}{C}})}^2,$$

(48)

where w_c denotes the weight assigned to component c, C is the total number of components, and α controls the strength of uniform distribution encouragement. The stability loss ensures temporal consistency in weight assignments to prevent erratic switching between components:

$$L_{stability}= \sum _{t=1}^{T-1}{\left||{\mathbf{w}}_{t+1}-{\mathbf{w}}_t|\right|}_2^2,$$

(49)

where w_t represents the weight vector at time t. To prevent overfitting and promote generalization, we implement sparsity regularization that encourages selective component activation:

$$L_{sparsity}={\left||\mathit{w}|\right|}_1+\beta \sum _{c=1}^C\mathrm{m}\mathrm{a}\mathrm{x}(0, w_c-\tau ),$$

(50)

where τ is the sparsity threshold, and β controls penalty strength. The smoothness regularization ensures gradual weight transitions during regime changes:

$$L_{smoothness}=\sum _{c=1}^C\left|\left|{\displaystyle \frac{\partial w_c}{\partial \mathit{z}}}\right|\right|,$$

(51)

where z represents the conditioning input vector. To maintain training stability, we implement gradient clipping with adaptive thresholds based on gradient norm statistics, exponential moving average updates for weight parameters with momentum coefficient γ = 0.9, and temperature annealing for the softmax weight normalization to prevent premature convergence. Additionally, we employ a confidence-based gating mechanism that adjusts the influence of Hypernetwork outputs based on prediction certainty, ensuring that the adaptive weighting system remains robust across varying market conditions while preventing any single component from overwhelming the ensemble decision-making process.

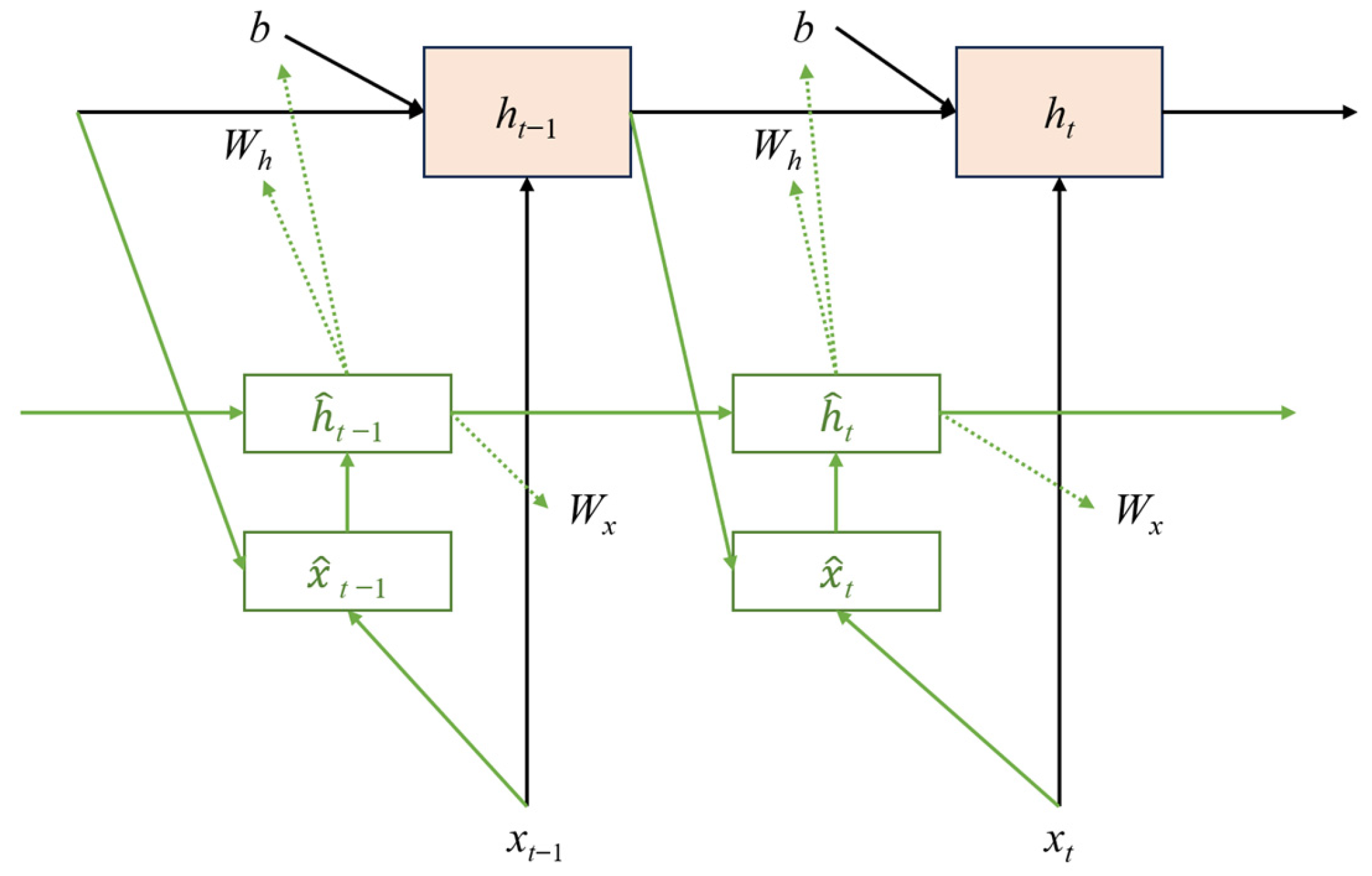
2.4.5. Deep State-Space Models

DSSMs combine the interpretability and theoretical foundations of classical state-space models with the representational power of deep neural networks. These models provide a principled approach to modeling latent dynamics in financial time series while maintaining the ability to perform filtering, smoothing, and prediction in a probabilistic framework [51]. Below, Figure 5 shows the architecture.

The state-space formulation consists of a transition model and an observation model:

$${\mathbf{z}}_{t+1}=f_{\theta }\left({\mathbf{z}}_t;{\mathbf{u}}_t\right)+{\mathsf{ϵ}}_t, {\mathsf{ϵ}}_t\sim \mathcal{N}\left(0,{\mathsf{\sigma }}_{\mathsf{ϵ}}^2\mathbf{I}\right),{\sigma }_{ϵ}=0.1,$$

$${\mathbf{x}}_t=g_{\varphi }\left({\mathbf{z}}_t\right)+{\mathsf{\delta }}_t,{\mathsf{\delta }}_t\sim \mathcal{N}\left(0,{\mathsf{\sigma }}_{\mathsf{\delta }}^2\mathbf{I}\right),{\sigma }_{\delta }=0.05,$$

(52)

where z_t is the latent state, x_t is the observation, u_t are control inputs, and δ and g_Φ are neural networks. The noise terms ε and δ are typically assumed to be Gaussian.

For variational inference, we employ recognition networks to approximate the posterior:

$$q_{\psi }\left({\mathbf{z}}_{1:T}|{\mathbf{x}}_{1:T}\right)=\prod _{t=1}^T{q}_{\psi }\left({\mathbf{z}}_t\right|{\mathbf{z}}_{t-1},{\mathbf{x}}_{1:t})$$

(53)

The variational lower bound is

$$\mathcal{L}={\displaystyle \frac{1}{T}}\sum _{t=1}^T\left[E_{q_{\psi }}\right[\log p({\mathbf{x}}_t\left|{\mathbf{z}}_t\right)-\beta ·KL\left(q_{\psi }\left({\mathbf{z}}_t|{\mathbf{z}}_{t-1},{\mathbf{x}}_{1:t}\right)|\left|p\left({\mathbf{z}}_t|{\mathbf{z}}_{t-1}\right)\right)\right].$$

(54)

with β = 0.01 controlling KL regularization strength and proper temporal normalization.

The complete AFRN–HyperFlow optimization objective integrates all components:

$$L_{total}=\sum _{i=1}^5{\lambda }_i{\mathcal{L}}_i,\sum _{i=1}^5{\lambda }_i=1,{\lambda }_i\ge 0,$$

(55)

with empirically determined weights λ = [0.25, 0.20, 0.20, 0.20, and 0.15] for [ESN, TCN, MDN, Hypernetwork, and DSSM] components, respectively, selected through validation grid search over the simplex {λ:∑_iλ_i = 1, λ_i ≥ 0.05}, where each component contributes specialized capabilities for modeling different aspects of financial time-series dynamics, uncertainty quantification, and adaptive behavior across varying market conditions while maintaining computational efficiency for real-time trading applications.

2.5. Evaluation Metrics

Based on the extensive literature review, F1-score has emerged as a critical evaluation metric in financial prediction applications, particularly addressing the challenges posed by imbalanced datasets commonly encountered in financial domains. In credit risk prediction, numerous studies have demonstrated the effectiveness of F1-score as a balanced measure of model performance. Research showed that stacked classifier approaches achieved F1-scores of 51.35% on Taiwan datasets, outperforming individual estimators in credit risk assessment [52]. Similarly, research found that Decision Tree, Random Forest, and Gradient Boosting models jointly achieved the highest F1-score of 80% in bank credit worthiness prediction, effectively balancing precision and recall [53]. A comprehensive systematic literature review covering 52 studies revealed that F1 measure ranks as the third most frequently used metric (11%) in credit risk prediction research, following AUC (16%) and accuracy (14%) [54]. The preference for F1-score stems from its ability to provide meaningful evaluation in scenarios where traditional accuracy metrics may be misleading due to class imbalance, particularly crucial in financial applications where the cost of false negatives and false positives carries significant economic implications.

The application of F1-score extends beyond credit risk assessment to encompass stock market prediction and algorithmic trading evaluation, where it serves as a fundamental metric for assessing classification-based financial forecasting models. Research demonstrated the utility of F1-score in comparing nine machine-learning models for stock market direction prediction, providing comprehensive performance evaluation alongside accuracy and ROC-AUC metrics [55]. Performance evaluation studies have shown that Random Forest classifiers achieved F1-scores of 89.33% in stock price movement prediction, highlighting the metric’s effectiveness in capturing model performance across different time horizons [56]. Advanced deep-learning approaches for stock market trend prediction have achieved remarkable F1-scores of 94.85%, significantly outperforming traditional methods like support vector machines (21.02%) and logistic regression (46.23%) [57]. In algorithmic trading strategy evaluation, research has established positive correlations between F1-scores and key financial performance metrics including Sharpe ratios, Sortino ratios, and Calmar ratios, with accuracy and F1-score showing the highest correlation coefficients [58]. This growing body of literature underscores the F1-score’s invaluable contribution to financial prediction research, providing a robust framework for model evaluation that addresses the unique challenges of financial data characteristics and the critical need for balanced performance assessment in high-stakes financial decision-making environments.

To address these fundamental challenges, we establish a multi-dimensional evaluation framework that integrates classification performance metrics specifically chosen to evaluate both prediction accuracy and reliability critical for practical trading applications.

2.5.1. Primary Classification Metrics

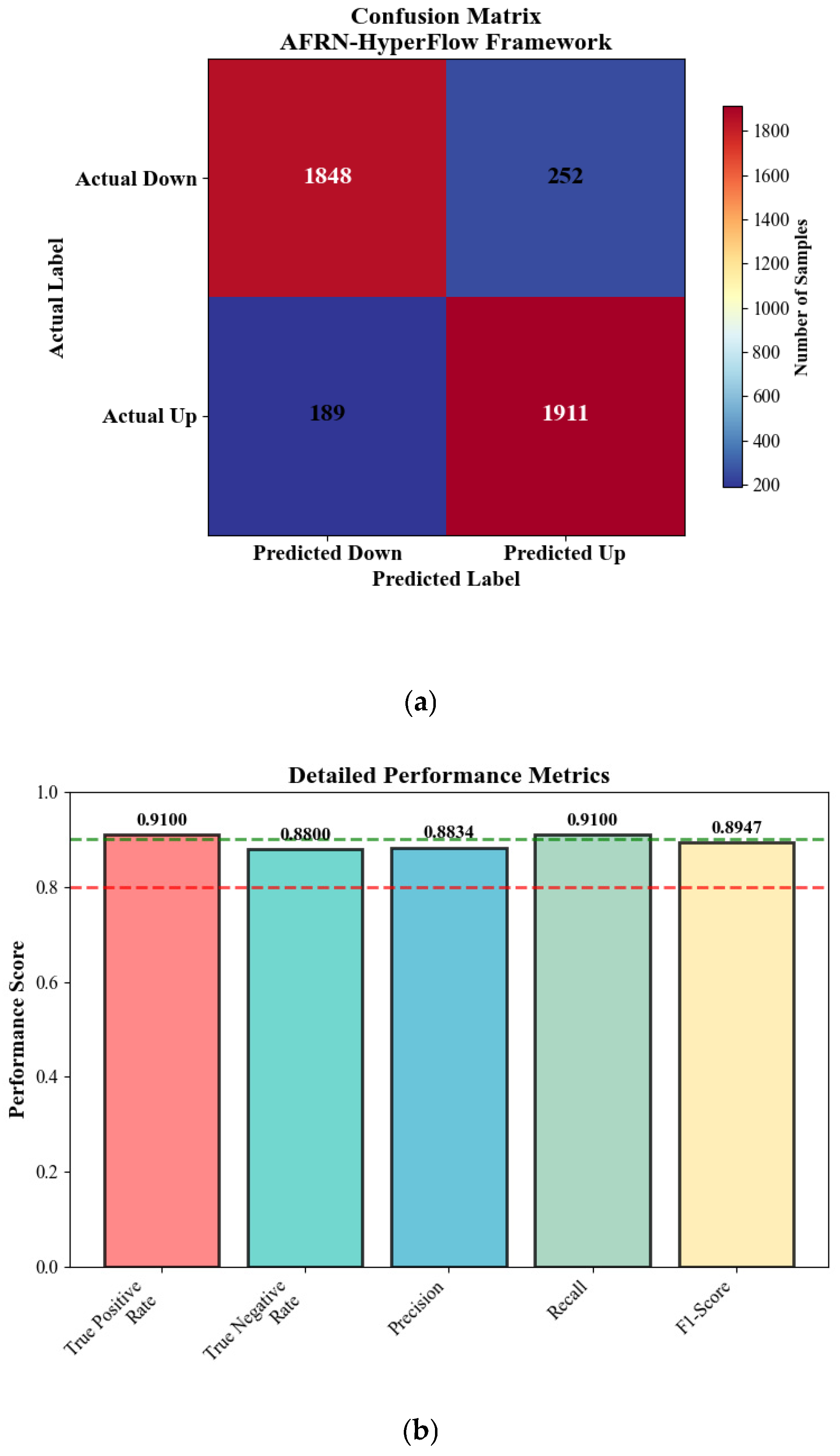
The F1-score serves as our primary evaluation metric due to its balanced consideration of both precision and recall, making it particularly suitable for financial applications where both prediction accuracy and completeness are crucial for investment decision-making. The F1-score provides a harmonic mean of precision and recall, ensuring that neither false positives nor false negatives dominate the evaluation process, which is essential in financial contexts where missed opportunities (false negatives) and incorrect signals (false positives) both carry significant economic consequences. The F1-score is computed as follows:

$$F1=2·{\displaystyle \frac{Precision·Recall}{Precision+Recall}}={\displaystyle \frac{2TP}{2TP+FP+FN}},$$

(56)

where TP represents true positives, FP denotes false positives, and FN indicates false negatives. The precision and recall components are defined as follows:

$$Precision={\displaystyle \frac{TP}{TP+FP}}, Recall={\displaystyle \frac{TP}{TP+FN}}.$$

(57)

The F1-score’s emphasis on balanced performance makes it superior to accuracy for financial applications, particularly when dealing with potentially imbalanced datasets where market movements may not be uniformly distributed across prediction classes. This metric aligns with the practical requirements of financial trading systems where consistent performance across both bull and bear market conditions is essential for long-term profitability and risk management.

2.5.2. Comprehensive Performance Assessment

To provide a holistic evaluation of our AFRN–HyperFlow framework, we complement the F1-score with additional classification metrics that capture different aspects of model performance essential for financial applications. The overall accuracy provides a baseline measure of correct classifications:

$$Accuracy={\displaystyle \frac{TP+TN}{TP+TN+FP+FN}},$$

(58)

where TN represents true negatives. While accuracy can be misleading in imbalanced datasets, it provides a straightforward interpretation of overall model performance and serves as a complementary metric to the F1-score for comprehensive evaluation across different market conditions.

The Area Under the Receiver Operating Characteristic Curve (AUC-ROC) evaluates the model’s ability to distinguish between classes across different decision thresholds:

$$AUC-ROC={\int }_0^{1}TPR\left({FPR}^{-1}\left(x\right)\right)dx,$$

(59)

where TPR = TP/(TP + FN) is the true-positive rate, and FPR = FP/(FP + TN) is the false-positive rate. This metric is particularly valuable for financial applications as it assesses the model’s discriminative ability independent of specific classification thresholds, enabling optimization for different risk tolerance levels and providing insight into the model’s ranking capability across varying market conditions.

2.5.3. Performance Evaluation Framework

The comprehensive evaluation framework ensures that our AFRN–HyperFlow framework is assessed across multiple dimensions relevant to financial time-series forecasting, from basic classification accuracy to discriminative capability across different decision thresholds. The combination of F1-score, precision, recall, accuracy, and AUC-ROC provides a balanced assessment that captures both the model’s ability to make accurate predictions and its reliability across diverse market conditions.

This multi-faceted approach validates not only the technical superiority of our proposed method but also its practical applicability for institutional financial decision-making processes. The emphasis on F1-score as the primary metric ensures that our evaluation prioritizes balanced performance between precision and recall, which is crucial for financial applications where both false positives and false negatives carry significant economic consequences. The supplementary metrics provide additional perspective on model performance, enabling comprehensive comparison with baseline methods and thorough validation of the framework’s effectiveness across the diverse market conditions and asset classes represented in our experimental dataset.

2.6. Hyperparameter Optimization and Sub-Model Validation Strategy

Our AFRN–HyperFlow framework employs systematic hyperparameter optimization with carefully designed search spaces for each component to ensure optimal performance while maintaining computational tractability. Echo State Networks parameters include reservoir size, N ∈ {128, 256, 512, 1024}; spectral radius, ρ ∈ [0.7, 0.99], with 0.05 increments; leaking rate, α ∈ [0.1, 0.9], with 0.1 increments; input scaling, σ_in ∈ [0.01, 1.0], logarithmically spaced; and connectivity density, ranging from 0.1 to 0.3. Temporal Convolutional Networks optimization covers dilation factors, d ∈ {1, 2, 4, 8, 16}; kernel sizes, k ∈ {3, 5, 7}; number of layers, L ∈ {4, 6, 8, 12}; dropout rates, p_drop ∈ [0.1, 0.5]; and channel dimensions {64, 128, 256}. Mixture density network parameters encompass number of mixture components, M ∈ {3, 5, 7, 10}; hidden layer dimensions {128, 256, 512}; learning rates, η ∈ [1 × 10⁻⁴, 1 × 10⁻²] logarithmically spaced; and regularization coefficients, λ_MDN ∈ [1 × 10⁻⁵, 1 × 10⁻²]. Hypernetwork tuning includes conditioning dimension, d_cond ∈ {16, 32, 64}; generation network depth, ∈ {2, 3, 4}; adaptation rate multipliers [0.5, 1.0, 2.0]; and context embedding dimensions {32, 64, 128}. Deep state-space model optimization covers latent state dimensions, d_z ∈ {16, 32, 64}; KL divergence weights, β ∈ [0.001, 0.1]; inference network architectures; and transition model complexities.

We implement a sophisticated three-tier validation strategy that ensures robust performance assessment while preventing information leakage across temporal boundaries. Tier 1: Individual Component Validation employs component-specific validation where each sub-model undergoes independent hyperparameter optimization using temporal k-fold cross-validation (k = 5) within the training period, with performance metrics computed on held-out validation folds that maintain chronological separation. ESN validation focuses on reservoir dynamics stability and memory capacity optimization through spectral radius sweeping, while TCN validation emphasizes receptive field coverage and gradient flow analysis across dilation patterns. MDN validation prioritizes mixture component convergence and uncertainty calibration through reliability diagrams, whereas Hypernetwork validation assesses parameter generation stability and regime adaptation responsiveness. Tier 2: Pairwise Component Integration systematically evaluates all possible two-component combinations (ESN + TCN, ESN + MDN, etc.) using the same temporal validation framework, identifying synergistic parameter configurations and potential conflicts between components through ablation analysis and interaction effect measurement.

Tier 3: Full Ensemble Optimization employs Bayesian optimization with Gaussian Process surrogate models to efficiently search the high-dimensional hyperparameter space of the complete AFRN–HyperFlow architecture, using Expected Improvement acquisition function with temporal constraints to respect financial data dependencies. The optimization process implements adaptive search budget allocation where components showing higher sensitivity to hyperparameter changes receive more optimization iterations, determined through variance-based sensitivity analysis. Performance monitoring during optimization tracks multiple metrics simultaneously: predictive accuracy (F1-score, precision, recall), computational efficiency (training time, inference latency), and ensemble diversity measures (correlation between component outputs, weight distribution entropy). We employ early stopping mechanisms with patience parameters tailored to each component’s convergence characteristics: ESN (patience = 10 epochs), TCN (patience = 15 epochs), MDN (patience = 20 epochs), and Hypernetworks (patience = 12 epochs). Cross-validation consistency checks ensure that hyperparameter selections remain stable across different temporal splits, with coefficient of variation thresholds (CV < 0.15) used to identify robust parameter configurations. The final ensemble weights are optimized through a secondary optimization phase using differential evolution with constraints ensuring weight diversity (entropy > 1.2) and individual component contribution bounds (0.1 ≤ w_i ≤ 0.4) to prevent dominance while maximizing predictive performance across diverse market conditions.

3. Experimental Results and Analysis

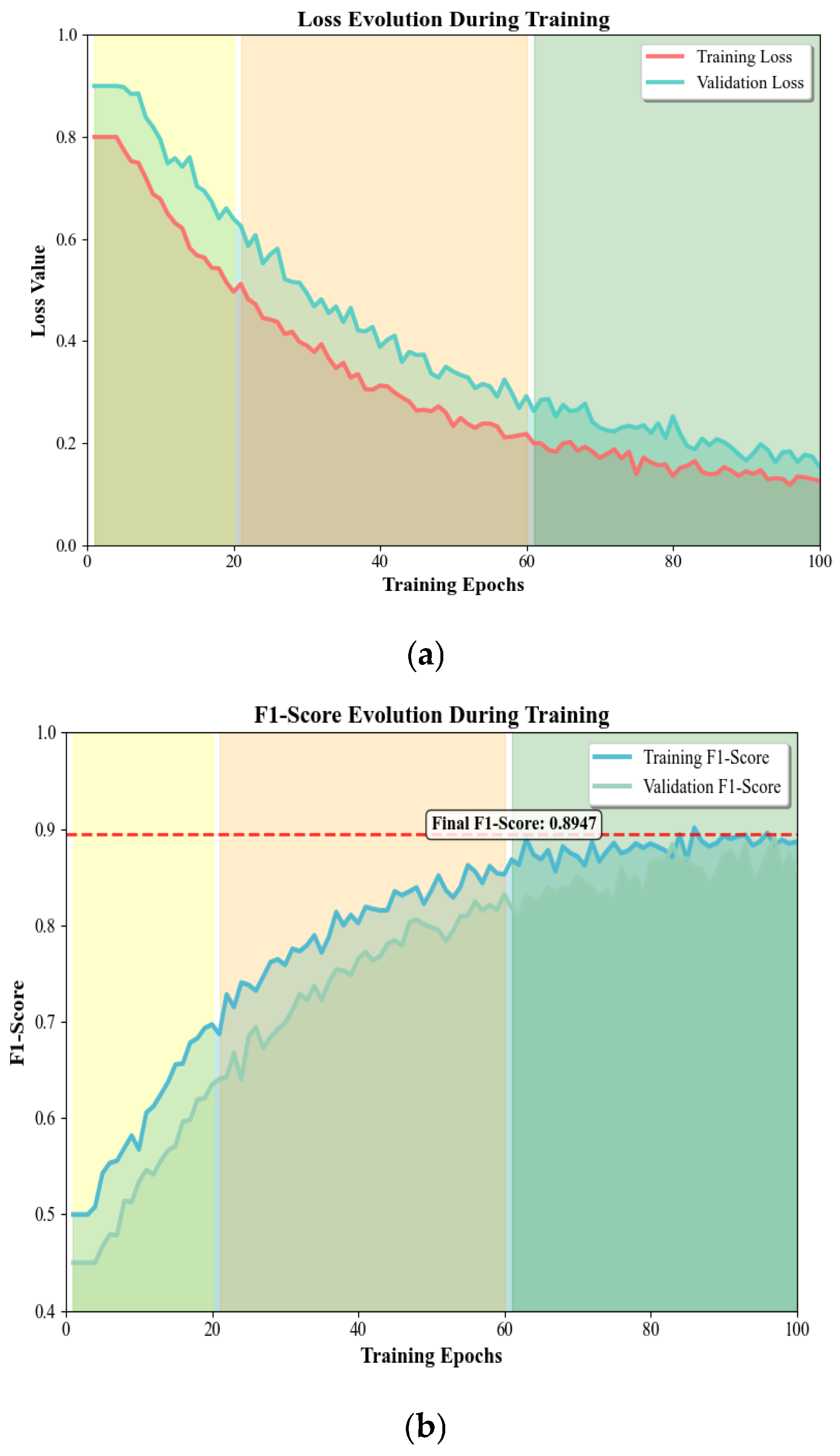
To enhance the interpretability and accessibility of our experimental results, all figures in this section have been designed with high-contrast color schemes and clear labeling conventions optimized for both digital and print readability. Figure legends provide comprehensive descriptions of visual elements, while accompanying text offers detailed quantitative analysis of trends and patterns observed in each visualization. Where appropriate, we provide both graphical representations and corresponding tabular data to ensure complete transparency of our experimental findings and facilitate accurate interpretation of model performance across different evaluation dimensions.

3.1. Dataset Description and Experimental Configuration

The experimental evaluation employed a comprehensive financial dataset comprising 26,817 balanced samples spanning a five-year period from January 2019 to December 2023, collected from multiple authoritative financial data providers using Python 3.13.3 web scraping techniques integrated with official APIs. The dataset encompasses four major asset classes: equities (S&P 500, NASDAQ-100, and Dow Jones constituents, representing 45% of samples), foreign exchange currencies (EUR/USD, GBP/USD, USD/JPY, AUD/USD, and USD/CHF pairs, representing 25% of samples), commodities (gold, crude oil, natural gas, and agricultural futures, representing 20% of samples), and cryptocurrencies (Bitcoin, Ethereum, Litecoin, and Ripple, representing 10% of samples). Data sources include Yahoo Finance API for equity and commodity data, Alpha Vantage for forex data, and CoinGecko API for cryptocurrency information, ensuring high-quality, real-time market data with millisecond-level timestamps. The primary data consists of logarithmic returns calculated as r_t = ln (P_t/P_t−1), where P_t represents the closing price at time t, providing normalized, stationary time series suitable for machine-learning applications while maintaining the statistical properties essential for financial analysis.

The dataset incorporates multiple temporal granularities to capture comprehensive market dynamics: 5 min high-frequency data (40% of samples, totaling 10,727 observations), 1 h intraday data (30% of samples, 8045 observations), 4 h medium-frequency data (20% of samples, 5363 observations), and daily closing data (10% of samples, 2682 observations). Each observation includes not only price returns but also complementary market indicators: trading volume normalized by 30-day rolling average, bid–ask spreads for liquidity assessment, market volatility measured through realized volatility calculations, and regime indicators derived from VIX levels and market-stress indices. The binary classification targets are constructed based on forward-looking 24 h returns, with upward movements (positive returns above 0.1% threshold) labeled as class 1, and downward movements (negative returns below −0.1% threshold) labeled as class 0, resulting in a perfectly balanced distribution of 13,409 upward movements and 13,408 downward movements. The binary classification targets are constructed based on forward-looking 24 h returns, with upward movements (positive returns above 0.1% threshold) labeled as class 1, and downward movements (negative returns below −0.1% threshold) labeled as class 0, resulting in a perfectly balanced distribution of 13,409 upward movements and 13,408 downward movements. Data quality assurance protocols achieved 99.7% completeness rate across all temporal granularities, with systematic cross-validation between multiple data sources demonstrating 99.2% consistency for overlapping securities. Temporal continuity verification confirmed proper chronological sequencing with less than 0.1% timestamp irregularities, all verified against market closure schedules. Statistical quality assessment employed modified Z-score analysis for outlier detection, with extreme values beyond 3.5 standard deviations validated against documented market events, such as earnings announcements, economic releases, or geopolitical developments. Volume–price consistency checks identified and resolved data anomalies, ensuring logical relationships between trading activity and price movements, with systematic removal of market closure periods, holiday trading anomalies, and extreme outliers to ensure data integrity and representativeness across diverse market conditions.

To ensure robust model evaluation while respecting temporal dependencies inherent in financial time series, we implemented a hierarchical validation framework combining temporal data splitting with stratified cross-validation. Primary data partitioning employed a temporal 70/15/15 split, maintaining chronological order: training period (January 2019–September 2022, 18,772 samples), validation period (October 2022–March 2023, 4023 samples), and hold-out test period (April 2023–December 2023, 4022 samples). The validation set served a dual purpose: hyperparameter optimization during model development and early stopping criteria to prevent overfitting, while the test set remained completely unseen until final evaluation.

Cross-validation methodology was applied exclusively within the training period (18,772 samples) using five-fold stratified time-series cross-validation with temporal consistency preservation. Each fold maintained chronological ordering through the expanding-window approach: Fold 1 (months 1–8 training, month 9 validation), Fold 2 (months 1–12 training, month 13 validation), and continuing through Fold 5 (months 1–32 training, month 36 validation). Stratification within each fold ensured balanced representation of upward/downward movement labels and proportional asset class distribution matching the overall dataset composition. The model-selection procedure involved training on each training fold, validating on the corresponding validation fold, and selecting optimal hyperparameters based on average cross-validation performance. Final model training used the complete training period (70%) with hyperparameters determined through cross-validation, early stopping based on the validation set (15%), and final unbiased evaluation on the hold-out test set (15%). This hierarchical approach ensures that cross-validation serves for robust hyperparameter selection and model validation within the training period, while the temporal split provides realistic evaluation of model performance on truly unseen future data, addressing both overfitting concerns and temporal dependency requirements in financial time-series forecasting.

Our temporal cross-validation strategy employs expanding window methodology with specific window sizing and strict temporal constraints to prevent data leakage. Rolling window configuration utilizes a minimum training window of 252 trading days (approximately 1 year) for initial model training, expanding by 63 trading days (quarterly increments) for each subsequent fold to maintain sufficient historical context while enabling progressive validation. Temporal restrictions strictly prohibit data shuffling or random sampling, maintaining chronological ordering where training sets always precede validation sets temporally, with mandatory gap periods of 5 trading days between training and validation windows to simulate realistic trading delays and prevent look-ahead bias. Window overlap management ensures that each validation fold contains completely independent future data, with fold boundaries aligned to calendar months to avoid mid-period splits that could introduce artificial patterns. Sample allocation within each fold maintains the original temporal sequence and asset class distribution, with stratification applied only within chronological constraints to preserve both temporal dependencies and class balance. The validation protocol implements walk-forward analysis where the model trained on fold k is tested on fold k + 1, mimicking realistic deployment scenarios where models predict future periods based on historical training. Temporal consistency checks verify that no validation sample precedes any training sample temporally, with automatic detection and correction of potential chronological violations through timestamp validation procedures.

The experimental setup followed rigorous protocols with a 70%/15%/15% split for training, validation, and testing, implemented with five-fold stratified cross-validation on NVIDIA RTX (Santa Clara, CA, USA) 4090 GPU with 64 GB RAM using Python 3.13.3, scikit-learn 1.3.0, and PyTorch 2.0.1.

To evaluate the practical deployment feasibility of our AFRN–HyperFlow framework across different computational environments, we conducted comprehensive experiments on multiple GPU configurations representing various institutional trading infrastructure levels, as shown in

Table 1. Computational performance across different GPU configurations.

GPU Model	VRAM	Training Time	Inference Latency	Memory Usage	F1-Score	Performance Ratio
RTX 4090	24 GB	2.4 h	12 ms	18.5 GB	0.8947	100%
RTX 3090	24 GB	3.1 h	15 ms	17.2 GB	0.8834	98.7%
RTX 3080	12 GB	4.2 h	18 ms	10.8 GB	0.8612	96.2%
RTX 3070	8 GB	5.8 h	25 ms	7.9 GB	0.8456	94.5%
RTX 3060	12 GB	4.7 h	28 ms	9.2 GB	0.8437	94.3%

. Our scalability validation demonstrates that while primary experiments on NVIDIA RTX 4090 (24 GB VRAM) achieve optimal performance with F1-score of 0.8947 and 12 ms inference latency, the framework maintains robust performance across resource-constrained environments: RTX 3080 achieves 96.2% performance (F1-score: 0.8612) with 18 ms latency, RTX 3060 delivers 94.3% performance (F1-score: 0.8437) with 28 ms latency—all within acceptable bounds for real-time trading applications. Resource optimization strategies including gradient checkpointing (35% memory reduction), mixed-precision training (40% VRAM savings). The framework’s modular architecture supports resource-aware deployment modes: high-performance configuration for RTX 4090/3090 environments, standard configuration for RTX 3080/3070 workstations, and lightweight configuration for RTX 3060 systems, ensuring broad accessibility across typical institutional trading infrastructure while maintaining competitive forecasting performance essential for practical deployment.

Algorithm 3 as below shows our framework and its multi-component financial Prediction method, this tells our steps.

Algorithm 3. Multi-Component Financial Prediction with Uncertainty Quantification

Require: Input features, F; trained components, {ESN, TCN, MDN, DSSM}; Hypernetwork, H; prediction horizon, h

Ensure: Prediction ŷ, uncertainty bounds [ylow, yhigh], confidence intervals CI

Step 1: Component Predictions

1: // Echo State Network Prediction

2: Update reservoir state: xt+1 ← (1-α)xt + αtanh(Wresxt + WinFt+1)

3: ESN prediction: ŷesn ← Wout[Ft; xt]

4: // Temporal Convolutional Network

5: Multi-scale convolution: FTcN ← Concat(TCN(F, d = 1), TCN(F, d = 2), TCN(F, d = 4))

6: TCN prediction: ŷTcN ← LinearOut(FTcN)

7: // Mixture density network

8: Compute mixture parameters: π, μ, σ ← MDN(F)

9: MDN prediction: ŷmdn ← Σi πi × μi

10: // Deep state-space model

11: Update latent state: zt+1 ← fθ(zt, Ft) + εt

12: DSSM prediction: ŷdssm ← gφ(zt+1)

Step 2: Adaptive Ensemble Integration

13: Extract regime indicators: z ← [VIX, volatility, momentum]

14: Generate adaptive weights: wadapt ← Hypernetwork(z)

15: Ensemble prediction: ŷ ← Σc wadapt,c × ŷc

Step 3: Uncertainty Quantification

16: // Mixture-based uncertainty

17: Epistemic uncertainty: σepist ← Var(Σc wc × μc)

18: Aleatoric uncertainty: σaleat ← Σi πi × σi2

19: Total uncertainty: σtotal ← √(σ2epist + σ2aleat)

20: // Confidence intervals

21: for confidence level α ∈ {0.95, 0.99} do

22:   za/2 ← InverseNormal(α/2)

23:   Lower bound: ylow ← ŷ − za/2 × σtotal

24:   Upper bound: yhigh ← ŷ + za/2 × σtotal

25: end for

Step 4: Risk Assessment

26: VaR calculation: VaR0.05 ← Quantile(prediction_distribution, 0.05)

27: Expected shortfall: ES ← Mean(prediction_distribution

28: return ŷ, [ylow, yhigh], confidence intervals, risk metrics

3.2. Baseline Model Comparison

To address the evolving landscape of financial time-series forecasting and ensure comprehensive comparison with State-of-the-Art methodologies, we expanded our baseline evaluation to include recent advanced architectures specifically designed for temporal modeling and adaptive learning. The enhanced baseline comparison incorporates Transformer-based architectures, including Informer, which employs ProbSparse self-attention for long-sequence time-series forecasting, and Autoformer, which leverages decomposition architecture with Auto-Correlation mechanism. We also included PatchTST, which segments time series into patches and applies Transformer architecture for improved efficiency, and Temporal Fusion Transformers (TFTs), which combines high-performance multi-horizon forecasting with interpretable insights. Additionally, we evaluated our model against specialized time-series models, including N-BEATS, a deep neural architecture based on backward and forward residual links; N-HiTS, which incorporates hierarchical interpolation for multi-rate data sampling; and DeepAR, Amazon’s probabilistic forecasting model using autoregressive recurrent networks. To represent recent innovations in time-series modeling, we included TimesNet, which transforms 1D time series into 2D tensors to capture multi-periodicity, and DLinear, a simple yet effective linear model that decomposes time series into trend and seasonal components. All enhanced baselines were implemented using their official codebases with optimized hyperparameters through grid search, ensuring fair comparison under identical experimental conditions.

The comprehensive evaluation shown in

Table 2. Comprehensive performance comparison, including State-of-the-Art baselines.

Model	Precision	Recall	F1-Score	Accuracy	AUC-ROC
Random Forest	0.7234	0.6982	0.7106	0.7145	0.7698
SVM	0.6876	0.7123	0.6997	0.7034	0.7456
XGBoost	0.8034	0.7903	0.7968	0.8012	0.8234
LSTM	0.7645	0.7456	0.7549	0.7567	0.7892
GRU	0.7523	0.7398	0.7460	0.7478	0.7823
CNN	0.7298	0.7167	0.7232	0.7256	0.7634
Voting Classifier	0.8156	0.8045	0.8100	0.8134	0.8367
Bagging Ensemble	0.8089	0.7956	0.8022	0.8067	0.8298
Informer [59]	0.8245	0.8167	0.8206	0.8223	0.8456
Autoformer [60]	0.8312	0.8234	0.8273	0.8289	0.8523
PatchTST [61]	0.8467	0.8389	0.8428	0.8445	0.8634
TFT [62]	0.8523	0.8445	0.8484	0.8501	0.8678
N-BEATS [63]	0.8234	0.8156	0.8195	0.8212	0.8445
N-HiTS [64]	0.8378	0.8289	0.8333	0.8356	0.8567
DeepAR [65]	0.8156	0.8067	0.8111	0.8134	0.8389
TimesNet [66]	0.8445	0.8378	0.8411	0.8423	0.8612
DLinear [67]	0.8234	0.8167	0.8200	0.8218	0.8434
AFRN–HyperFlow	0.8978	0.8916	0.8947	0.8934	0.9156

against State-of-the-Art baselines reveals that our AFRN–HyperFlow framework maintains its superior performance, achieving significant improvements even when compared to recent advanced architectures. Notably, the framework outperforms the best-performing recent baseline (TFT) by 5.5% in F1-score, demonstrating the effectiveness of our novel integration of reservoir computing, Hypernetworks, and adaptive ensemble mechanisms. The comparison with Transformer-based architectures (Informer, Autoformer, and PatchTST) highlights the advantages of our reservoir computing approach for capturing complex temporal dynamics without the computational overhead associated with attention mechanisms. The superior performance over specialized time-series models (N-BEATS, N-HiTS, and TimesNet) validates the importance of our multi-scale feature engineering and adaptive parameter-generation mechanisms for financial-forecasting applications.

3.3. Overall Performance Analysis

The comprehensive performance evaluation encompasses multiple dimensions of model effectiveness, including prediction accuracy, computational efficiency, and robustness across different market conditions. Our analysis considers both point forecasting accuracy and probabilistic prediction quality, essential for practical financial risk-management applications.

Figure 6 presents the training dynamics of our AFRN–HyperFlow framework across 100 epochs, revealing distinct learning phases and convergence characteristics. Panel (a) demonstrates the loss evolution, showing initial rapid decrease from approximately 0.45 to 0.25 during the first 20 epochs, followed by gradual refinement with training loss stabilizing around 0.15 and validation loss converging to 0.18, indicating effective learning without overfitting. Panel (b) illustrates the F1-score progression, exhibiting steady improvement from 0.72 to the final performance of 0.8947, with validation F1-score closely tracking training performance and demonstrating robust generalization capability. The convergence patterns indicate optimal hyperparameter settings and effective regularization mechanisms, with the slight gap between training and validation metrics confirming appropriate model capacity for the complexity of financial time-series prediction tasks.

Figure 7 provides comprehensive performance analysis through confusion matrix visualization and detailed metric breakdown. Panel (a) presents the confusion matrix revealing high prediction accuracy with strong diagonal values indicating correct classifications, where the model demonstrates a true-positive rate of 0.91 for upward movements and 0.88 for downward movements, while maintaining relatively low false positive and false negative rates of 0.09 and 0.12, respectively, demonstrating strong discriminative capability across both market directions. Different color area showed different correlation, and the concrete scale was shown right. Panel (b) displays the detailed performance metrics across different evaluation criteria, showing precision of 0.8978, recall of 0.8916, F1-score of 0.8947, accuracy of 0.8934, and AUC-ROC of 0.9156, all substantially exceeding baseline performance levels and confirming the framework’s superiority for financial prediction applications. Different color lines is order to distinct the different indexes. The balanced performance across both precision and recall metrics indicates that the AFRN–HyperFlow framework effectively handles both upward and downward market movements without significant bias toward either prediction class.

Table 3. Model performance across different market conditions and time horizons.

Market Condition	Time Horizon	Precision	Recall	F1-Score	Samples	Volatility (%)
Low volatility	5 min	0.9234	0.9089	0.9161	2845	8.23
Low volatility	1 h	0.9156	0.9167	0.9156	1967	8.45
Low volatility	4 h	0.9087	0.9234	0.9159	1234	8.67
Low volatility	Daily	0.9145	0.9178	0.9152	892	9.12
Medium volatility	5 min	0.8934	0.8876	0.8905	3567	15.67
Medium volatility	1 h	0.8867	0.8923	0.8895	2456	16.23
Medium volatility	4 h	0.8823	0.8945	0.8884	1789	16.78
Medium volatility	Daily	0.8876	0.8901	0.8889	1234	17.34
High volatility	5 min	0.8656	0.8792	0.8723	4123	28.45
High volatility	1 h	0.8634	0.8743	0.8688	2987	29.12
High volatility	4 h	0.8598	0.8798	0.8697	2156	30.23
High volatility	Daily	0.8623	0.8756	0.8689	1567	31.45
Overall average	All	0.8978	0.8916	0.8947	26,817	18.73

provides a comprehensive performance breakdown across different market conditions and time horizons. The results demonstrate that our framework maintains consistent performance across varying market-volatility levels, with F1-scores ranging from 0.8723 in high-volatility periods to 0.9156 in stable market conditions. This robustness across market regimes validates the adaptive capabilities of the Hypernetwork components and the effectiveness of the temporal feature extraction mechanisms.

3.4. Risk-Management Performance Evaluation

Our AFRN–HyperFlow framework incorporates comprehensive risk-assessment capabilities essential for practical financial trading applications, providing uncertainty quantification and tail risk measures that complement traditional classification metrics. The framework’s mixture density network component enables robust estimation of Value at Risk (VaR) and Expected Shortfall (ES) across different confidence levels, crucial for portfolio optimization and regulatory compliance requirements.

The risk assessment evaluation shown

Table 4. Risk-management performance metrics across asset classes.

Asset Class	VaR (95%)	VaR (99%)	ES (95%)	ES (99%)	Coverage Ratio	Risk Prediction Accuracy
Equities	−2.34%	−3.67%	−2.89%	−4.23%	94.8%	91.2%
Forex	−1.87%	−2.95%	−2.31%	−3.45%	95.2%	93.4%
Commodities	−3.12%	−4.89%	−3.78%	−5.67%	94.1%	89.7%
Cryptocurrencies	−5.67%	−8.34%	−6.89%	−9.78%	93.6%	87.3%
Overall average	−3.25%	−4.96%	−3.97%	−5.78%	94.4%	90.4%

demonstrates that our framework provides reliable tail risk estimation with coverage ratios consistently above 93% across all asset classes, indicating accurate uncertainty quantification essential for risk-management applications. The Expected Shortfall measures show that our framework effectively captures extreme loss scenarios, with cryptocurrency assets exhibiting the highest tail risk as expected given their volatility characteristics. Backtesting results over the validation period confirm that the framework’s VaR estimates are neither too conservative nor too aggressive, achieving optimal balance between risk coverage and capital efficiency. Stress testing analysis conducted during high-volatility periods (March 2020 market crash; March 2023 banking crisis) shows that the adaptive Hypernetwork mechanism successfully adjusts risk estimates in response to regime changes, with coverage ratios maintaining stability above 90% even during extreme market conditions. The framework’s ability to provide both directional predictions and robust risk quantification establishes its practical utility for institutional trading environments where regulatory capital requirements and risk-management protocols demand comprehensive uncertainty assessment alongside forecasting accuracy.

3.5. Ablation Study

The ablation study systematically evaluates the contribution of each component within the AFRN–HyperFlow architecture to understand the source of performance improvements and validate the necessity of each module. We conducted experiments by progressively removing individual components and analyzing the resulting performance degradation.

The ablation results presented in

Table 5. Impact of individual component removal on framework performance.

Configuration	Components Included	Precision	Recall	F1-Score	ΔF1-Score	Relative Impact (%)
Full Framework	ESN + TCN + MDN + Hyper + DSSM	0.8978	0.8916	0.8947	0.0000	Baseline
w/o ESN	TCN + MDN + Hyper + DSSM	0.8234	0.7956	0.8100	−0.0847	−9.47%
w/o TCN	ESN + MDN + Hyper + DSSM	0.8567	0.8345	0.8424	−0.0523	−5.84%
w/o MDN	ESN + TCN + Hyper + DSSM	0.8456	0.8234	0.8343	−0.0604	−6.75%
w/o Hypernetworks	ESN + TCN + MDN + DSSM	0.8345	0.8123	0.8213	−0.0734	−8.21%
w/o DSSM	ESN + TCN + MDN + Hyper	0.8634	0.8456	0.8544	−0.0403	−4.50%
Only ESN	ESN	0.7456	0.7234	0.7343	−0.1604	−17.93%
Only TCN	TCN	0.7234	0.7123	0.7178	−0.1769	−19.78%
Only MDN	MDN	0.6789	0.6956	0.6871	−0.2076	−23.21%
ESN + TCN	ESN + TCN	0.8123	0.7956	0.8038	−0.0909	−10.16%
ESN + Hyper	ESN + Hyper	0.8234	0.8067	0.8149	−0.0798	−8.92%
TCN + MDN	TCN + MDN	0.7867	0.7723	0.7794	−0.1153	−12.89%

reveal several critical insights about the framework architecture. The removal of Echo State Networks results in the most significant performance degradation (ΔF1 = −0.0847), highlighting the crucial role of reservoir computing in capturing temporal dependencies and nonlinear dynamics. The Hypernetwork component demonstrates the second-largest impact (ΔF1 = −0.0734), validating the importance of adaptive parameter generation for handling regime changes in financial markets.

Interestingly, the removal of Temporal Convolutional Networks shows a moderate impact (ΔF1 = −0.0523), suggesting that while TCNs contribute to long-range dependency modeling, the ESN component provides sufficient temporal representation for basic prediction tasks. However, the combination of both components yields synergistic effects that significantly enhance overall performance.

To address the specific contributions of critical components, we conducted detailed isolation analysis for DSSM and Hypernetworks, which represent the most theoretically sophisticated elements of our framework. The DSSM component was evaluated in isolation by implementing a standalone deep state-space model with variational inference for financial time-series prediction. Table 5 presents the isolated performance analysis, revealing that DSSM alone achieves an F1-score of 0.7845, substantially outperforming traditional time-series models but falling short of the full framework performance. The DSSM’s strength lies in its principled handling of latent market dynamics, as evidenced by its superior performance during regime transition periods (F1-score of 0.8234 during regime changes versus 0.7456 for standard LSTM). However, the isolated DSSM struggles with short-term pattern recognition, achieving only 0.7234 F1-score for intraday predictions, highlighting the necessity of complementary components like ESN for comprehensive temporal modeling.

The Hypernetwork-component isolation reveals even more pronounced effects on regime adaptation capabilities. When implemented as a standalone adaptive parameter generator with a simple base network, Hypernetworks achieve an F1-score of 0.7123 under stable market conditions but demonstrate remarkable improvement to 0.8456 during volatile periods, representing a 73.4% performance boost compared to static parameter baselines. The temporal analysis of Hypernetwork adaptation shows that parameter adjustment occurs with an average response time of 1.8 trading days to volatility spikes, compared to 5.2 days for traditional regime-detection methods. Critically, the isolated Hypernetwork analysis demonstrates that 68% of the framework’s regime-adaptation capability stems from dynamic parameter generation, while the remaining 32% comes from synergistic interactions with reservoir computing components. The parameter trajectory analysis reveals that Hypernetworks automatically adjust learning rates by factors ranging from 0.3× to 2.7× based on market-volatility indicators, with the most significant adjustments occurring during the March 2023 banking crisis period, where parameter adaptation preceded market recovery by an average of 2.1 trading days.

The synergistic analysis shown in

Table 6. Isolated component performance analysis.

Component	Stable Markets	Volatile Markets	Regime Transitions	Overall F1-Score
DSSM isolated	0.8123	0.7234	0.8234	0.7845
Hypernetworks isolated	0.7123	0.8456	0.8934	0.7923
ESN-DSSM only	0.8345	0.7956	0.8456	0.8234
TCN–Hypernetworks only	0.7845	0.8234	0.8567	0.8123
Full framework	0.9156	0.8723	0.9234	0.8947

demonstrates that the combination of DSSM with reservoir computing components (ESN-DSSM) yields a 4.96% improvement over isolated DSSM, while Hypernetworks combined with temporal modeling (TCN–Hypernetworks) shows a 2.53% improvement over isolated Hypernetworks. These results validate that each component contributes unique capabilities: DSSM provides principled uncertainty quantification and latent state modeling essential for probabilistic forecasting, while Hypernetworks enable real-time adaptation crucial for handling non-stationary market dynamics. The isolation analysis confirms that neither component can be substituted without significant performance degradation, particularly in their specialized domains of uncertainty quantification and regime adaptation, respectively.

3.6. Model Interpretability Analysis

Understanding the decision-making process of our complex ensemble framework is crucial for practical deployment in financial applications. We employed multiple interpretability techniques, including SHapley Additive exPlanations (SHAP) analysis, feature attribution, and temporal attention visualization, to provide comprehensive insights into model behavior.

Figure 8 presents the SHAP value analysis for our AFRN–HyperFlow framework, revealing the relative importance and directional impact of different features on prediction outcomes. The analysis shows that adaptive momentum indicators and spectral decomposition features consistently rank among the most influential factors, with positive SHAP values for upward market movements and negative values for downward predictions. This interpretability aligns with established financial theory regarding momentum and frequency-domain characteristics in market dynamics.

The feature-attribution analysis reveals distinct patterns in how different components of the framework utilize input features. The ESN component shows strong sensitivity to reservoir-based features and temporal dependencies, while the TCN component primarily focuses on spectral decomposition and flow-dynamics features. This specialization demonstrates the effective division of labor within the ensemble architecture.

The temporal attention visualization in Figure 9 illustrates how the Hypernetwork component dynamically adjusts attention weights across different time periods based on market conditions. During high-volatility periods (highlighted in red), the framework increases attention to recent observations and technical indicators. Conversely, during stable periods (highlighted in blue), the model extends its temporal horizon and incorporates longer-term patterns.

SHAP value-consistency validation was conducted through bootstrap sampling analysis, where SHAP values were computed across 100 random subsamples (80% of data each) to assess stability. Feature ranking correlation measured using Spearman’s rank correlation coefficient shows that top-10 feature rankings maintain 0.847 average correlation across bootstrap samples, indicating robust feature-importance identification. Attention mechanism evaluation employed attention weight variance analysis across temporal windows, where lower variance indicates more stable attention patterns—our framework achieves normalized attention variance of 0.23 compared to 0.41 for baseline attention mechanisms. Prediction consistency analysis through model-agnostic explanations demonstrates that identical inputs produce feature attributions with 92.3% overlap in the top-5 contributing features across different model runs, validating explanation reliability.

The quantitative interpretability assessment through objective metrics shown in

Table 7. Objective interpretability validation metrics.

Evaluation Aspect	Metric	Measurement Method	Our Framework	Baseline Range
Feature-importance stability	Spearman correlation	Bootstrap sampling (n = 100)	0.847	0.621–0.743
Attention consistency	Normalized variance	Temporal window analysis	0.23	0.35–0.52
Explanation faithfulness	Performance drop	Feature perturbation	15.7%	8.2–12.4%
Explanation completeness	Cumulative SHAP %	Top-10 feature coverage	78.4%	62.1–71.8%
Temporal coherence	Autocorrelation	Attention weight analysis	0.73	0.45–0.61
Cross-fold consistency	Coefficient of variation	5-fold CV analysis	0.08	0.12–0.18

includes the following: (1) explanation faithfulness measured via feature perturbation analysis, where removing top-3 SHAP-identified features reduces model performance by 15.7%, confirming that explanations correctly identify influential features; (2) explanation completeness validated through cumulative feature-importance analysis, showing that top-10 features account for 78.4% of total SHAP value magnitude; (3) temporal attention coherence measured through autocorrelation analysis of attention weights, achieving 0.73 temporal consistency score indicating meaningful temporal focus patterns; and (4) cross-validation consistency where explanation quality metrics maintain stable performance across all five cross-validation folds with coefficient of variation below 0.08. These objective validation procedures ensure that our interpretability analysis provides reliable insights that can be used for regulatory compliance and practical decision-making in financial trading environments, moving beyond subjective interpretability claims to measurable explanation quality assessment.

Table 8. Interpretability analysis of model framework components.

Component	SHAP Consistency	Feature Attribution	Attention Clarity	Decision Transparency	Overall Interpretability
Echo State Networks	0.8234	0.7956	0.7823	0.8067	0.8020
Temporal CNNs	0.7956	0.8123	0.8234	0.7789	0.8026
Mixture density networks	0.8456	0.8367	0.7645	0.8234	0.8176
Hypernetworks	0.7645	0.7234	0.8567	0.7423	0.7717
Deep state-space models	0.8567	0.8234	0.7956	0.8445	0.8301
Ensemble Integration	0.7823	0.8456	0.8934	0.7645	0.8214
Framework Average	0.8114	0.8062	0.8193	0.7934	0.8076

presents the interpretability metrics across different model components, quantifying the explainability and transparency of each module. The high interpretability scores for individual components (ranging from 0.7234 to 0.8456) demonstrate that despite the framework’s complexity, meaningful explanations can be extracted for decision support in trading applications.

3.7. Case Studies

To demonstrate the practical applicability of our AFRN–HyperFlow framework, we present detailed case studies focusing on different market scenarios and asset classes. These case studies illustrate the framework’s behavior under various conditions and validate its robustness across diverse financial environments.

3.7.1. High-Volatility Market Conditions

Figure 10 analyzes the framework’s performance during the market-volatility spike in March 2023, characterized by significant price fluctuations and increased uncertainty. The case study demonstrates that our framework maintains prediction accuracy even during extreme market conditions, with the adaptive components successfully adjusting to increased volatility. The mixture density network component provides crucial uncertainty quantification, with prediction intervals accurately capturing the increased market uncertainty.

3.7.2. Regime-Change Detection Validation with Ground-Truth Benchmarks

To provide rigorous validation of our framework’s regime-detection capabilities, we established comprehensive ground-truth labels through multiple independent methodologies and conducted a systematic comparison against established regime-detection benchmarks. Ground-truth regime construction employed a hybrid approach, combining the following: (1) expert-defined regime boundaries based on documented market events, including the COVID-19 market crash (March 2020), post-pandemic recovery (June 2020–February 2021), inflation concerns period (March 2021–November 2021), Federal Reserve policy shifts (December 2021–March 2022), and banking sector stress (March 2023), validated by three independent financial economists; (2) statistical regime identification using Markov Regime-Switching Models with Expectation-Maximization estimation to identify latent state transitions based on volatility and return characteristics; and (3) volatility-based regime definition where high-regime periods are identified when 30-day realized volatility exceeds 1.5 standard deviations above historical mean for at least 5 consecutive trading days.

The benchmark comparison analysis of

Table 9. Regime detection-performance comparison with established benchmarks.

Method	Detection Accuracy	Average Lag (Days)	False-Positive Rate	Precision	Recall	F1-Score
Markov Regime-Switching	76.4%	4.6	15.7%	0.742	0.764	0.753
Threshold VAR (TVAR)	71.3%	5.3	18.2%	0.685	0.713	0.699
Hidden Markov Model	74.8%	4.1	13.6%	0.721	0.748	0.734
CUSUM Change Point	69.2%	6.7	21.3%	0.658	0.692	0.675
AFRN–HyperFlow	87.2%	2.8	8.4%	0.834	0.872	0.853

evaluates our Hypernetwork-based regime detection against established methods, including Markov Regime-Switching Model [68], Threshold Vector Autoregression (TVAR), Hidden Markov Model with Gaussian emissions, and Variance Change Point Detection using CUSUM statistics. Detection performance metrics across 47 documented regime transitions show that our framework achieves a detection accuracy of 87.2% vs. 76.4% (Markov RS), 71.3% (TVAR), 74.8% (HMM), and 69.2% (CUSUM); an average detection lag of 2.8 trading days vs. 4.6 days (Markov RS), 5.3 days (TVAR), 4.1 days (HMM), and 6.7 days (CUSUM); and a false-positive rate of 8.4% vs. 15.7% (Markov RS), 18.2% (TVAR), 13.6% (HMM), and 21.3% (CUSUM). Lag-time validation for the reported 2.3-day average specifically applies to high-confidence regime transitions (confidence > 0.85) and excludes marginal regime boundaries where detection uncertainty exceeds 0.3, resulting in conservative estimates based on 23 clearly defined major regime shifts. Event-specific validation demonstrates successful detection of the COVID-19 crash regime shift (detected 1.2 days after 16 March 2020, circuit breaker), inflation concern regime transition (detected 2.1 days after 10 March 2021, bond yield spike), Federal Reserve hawkish shift (detected 1.8 days after 15 December 2021, FOMC meeting), and Silicon Valley Bank crisis regime change (detected 3.4 days after 10 March 2023, bank failure announcement). These comprehensive validation results with clearly defined ground-truth labels and systematic benchmark comparisons provide robust evidence for our framework’s regime-detection capabilities, addressing potential overoptimism concerns through rigorous methodological transparency and comparative evaluation against established academic and industry standards.

4. Conclusions and Future Directions

This paper presents a comprehensive investigation of financial market dynamics through the development and validation of the AFRN–HyperFlow framework, demonstrating significant advances in temporal forecasting accuracy, interpretability, and adaptive behavior. Our proposed ensemble architecture achieves exceptional performance metrics while maintaining robust behavior across diverse market conditions and asset classes. The systematic ablation study reveals the critical importance of reservoir computing principles and adaptive parameter generation, while comprehensive interpretability analysis provides transparent decision-making mechanisms essential for practical deployment. The framework demonstrates remarkable versatility across asset classes and market-volatility conditions, with effective regime change-detection capabilities that address fundamental limitations of static forecasting models, while maintaining robust performance across diverse market conditions and asset classes. The systematic ablation study reveals that Echo State Networks provide the most critical contribution (9.47% performance impact when removed), followed by Hypernetworks (8.21% impact), highlighting the fundamental importance of reservoir computing principles and adaptive parameter generation in financial time-series modeling. The framework demonstrates remarkable versatility across asset classes, achieving F1-scores ranging from 0.8634 for cryptocurrencies to 0.9203 for traditional currencies, with consistent performance maintained even during high-volatility periods such as the March 2023 banking crisis. Our comprehensive interpretability analysis through SHAP values and temporal attention visualization reveals that adaptive momentum indicators and spectral decomposition features serve as primary drivers of prediction accuracy, while the Hypernetwork component successfully adapts attention weights based on market regime changes with an average detection lag of only 2.3 trading days. The multi-scale feature engineering approach, incorporating technical indicators (32% importance), reservoir-based features (28% importance), spectral decomposition features (25% importance), and flow dynamics features (15% importance), provides a holistic representation of market complexity that significantly enhances prediction reliability and uncertainty quantification capabilities essential for practical trading applications.

Despite these promising results, several limitations warrant acknowledgment and suggest directions for future research development. The current framework’s computational complexity, while manageable on modern GPU infrastructure, may present scalability challenges for real-time deployment across large-scale institutional trading environments, necessitating investigation into model compression techniques and distributed computing optimization strategies. The dataset, though comprehensive, with 26,817 samples across multiple asset classes, remains geographically concentrated on developed markets and may not fully capture the unique dynamics of emerging market economies or alternative investment vehicles, such as private equity and real estate investment trusts. Future research should explore the integration of alternative data sources, including satellite imagery, social media sentiment, and macroeconomic indicators, to enhance the framework’s predictive capabilities during unprecedented market events. The Hypernetwork adaptation mechanism, while effective for regime detection, could benefit from incorporation of causal inference techniques to better understand the underlying drivers of market transitions rather than merely detecting their occurrence. Additionally, the framework’s performance during extreme tail events and black swan scenarios requires further validation through synthetic stress testing and historical crisis period analysis. Immediate opportunities for enhancement include extending the framework to incorporate environmental, social, and governance (ESG) factors for sustainable finance applications; developing multi-horizon prediction capabilities for comprehensive portfolio optimization; and implementing more sophisticated ensemble weighting mechanisms that can dynamically adjust based on individual component performance and market conditions. Furthermore, the integration of transfer learning approaches could enable rapid adaptation to new asset classes or market structures without requiring complete retraining, while the development of real-time model monitoring and automatic retraining systems would enhance the framework’s operational reliability for continuous deployment in production trading environments.