Analytical Approximations as Close as Desired to Special Functions
Abstract
1. Introduction
2. Known Approximation Techniques
3. Methodology
| Algorithm 1 Global Analytical Approximation Construction |
| Require: Objective function ; desired range (possibly extending to ). |
| Ensure: No divergences or singularities exist in the middle of the range; if so, apply the algorithm recursively on subranges excluding them. |
|
4. Walk-Through Example: Fermi Gas Pressure
4.1. Zero Chemical Potential
4.2. Nonzero Chemical Potential
5. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. List of Analytical Approximations
Appendix A.1. Error Function
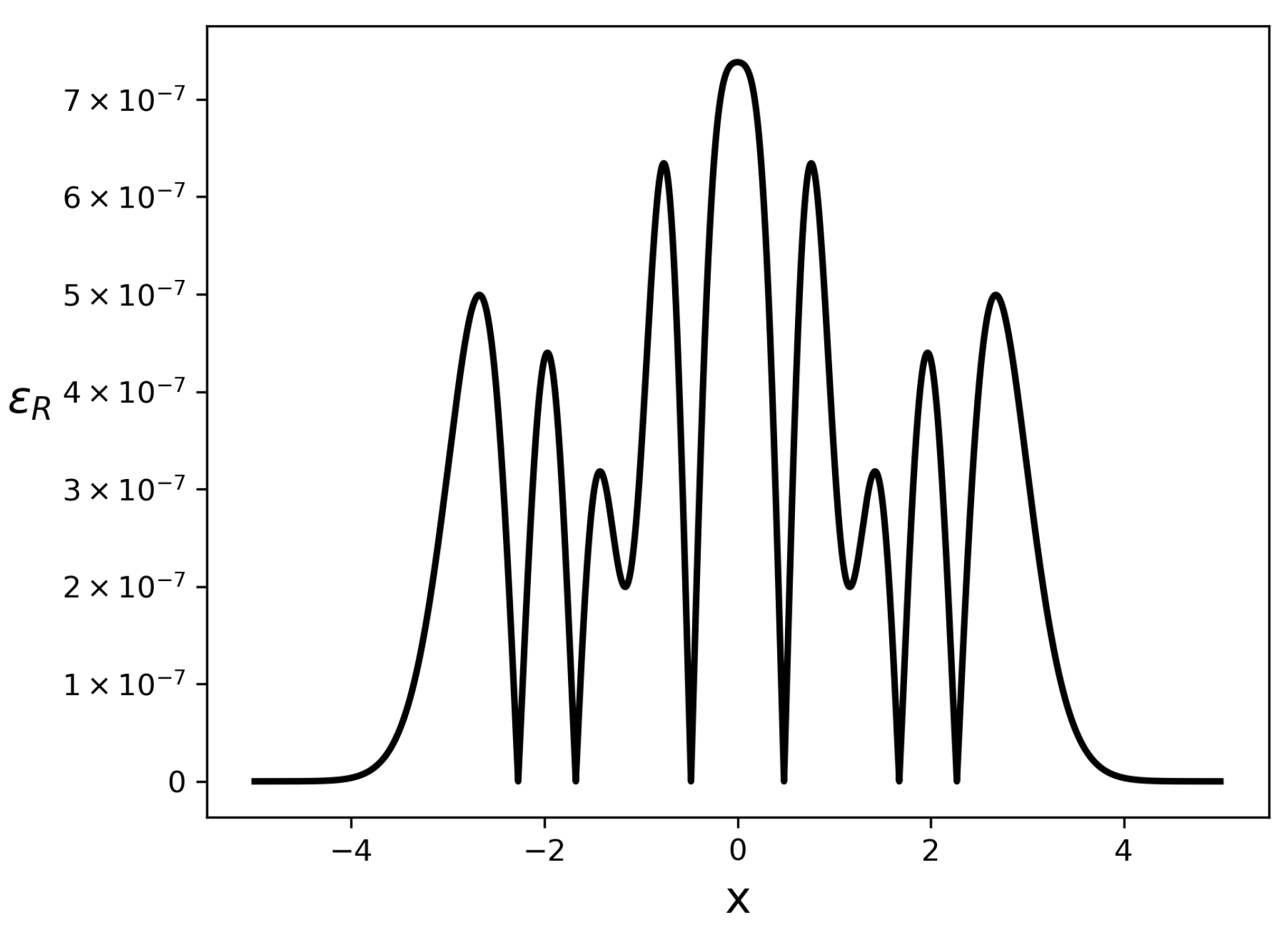
Appendix A.2. Approximation of
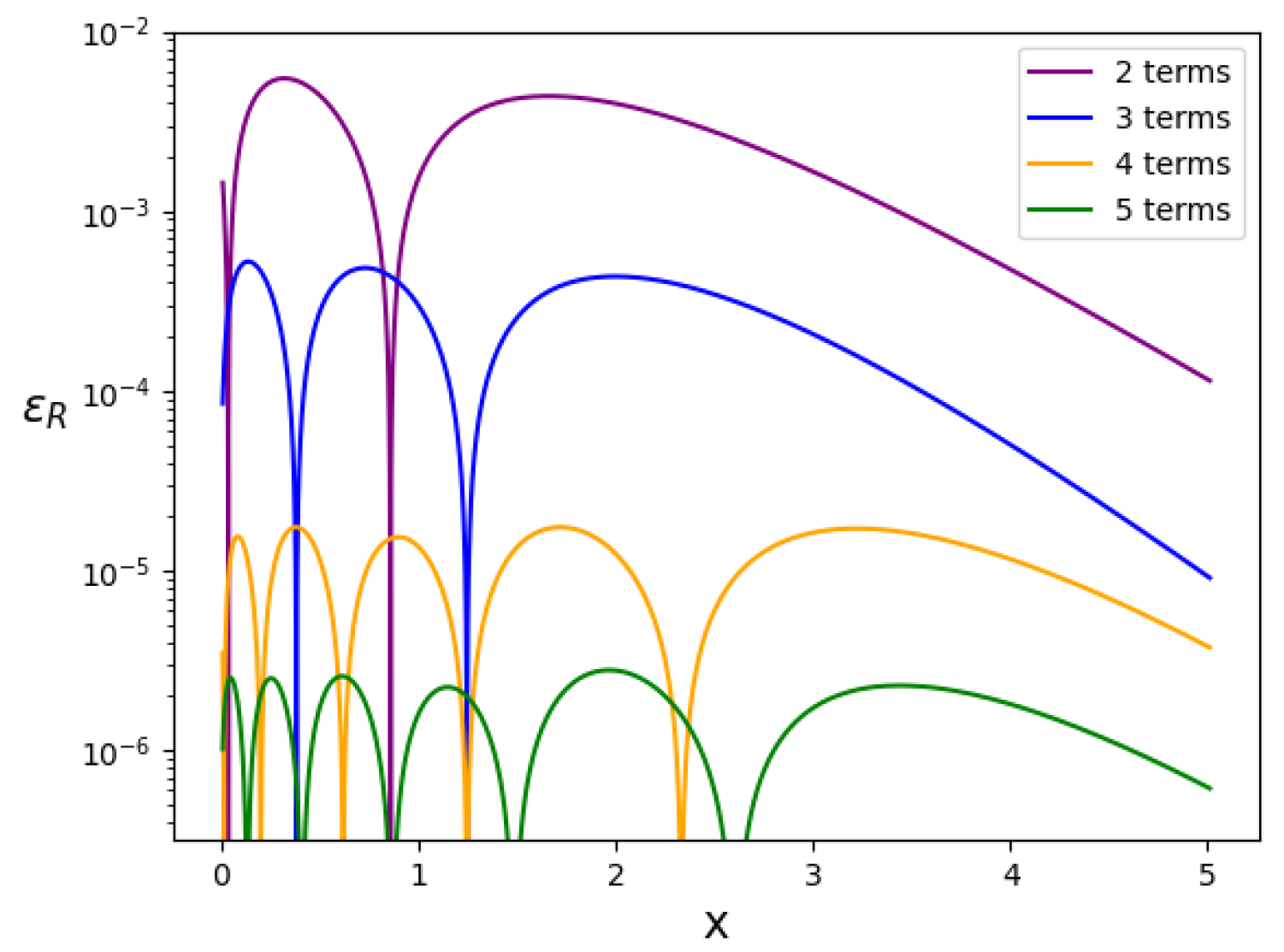
Appendix A.3. The Modified Bessel of the Second Kind (x)
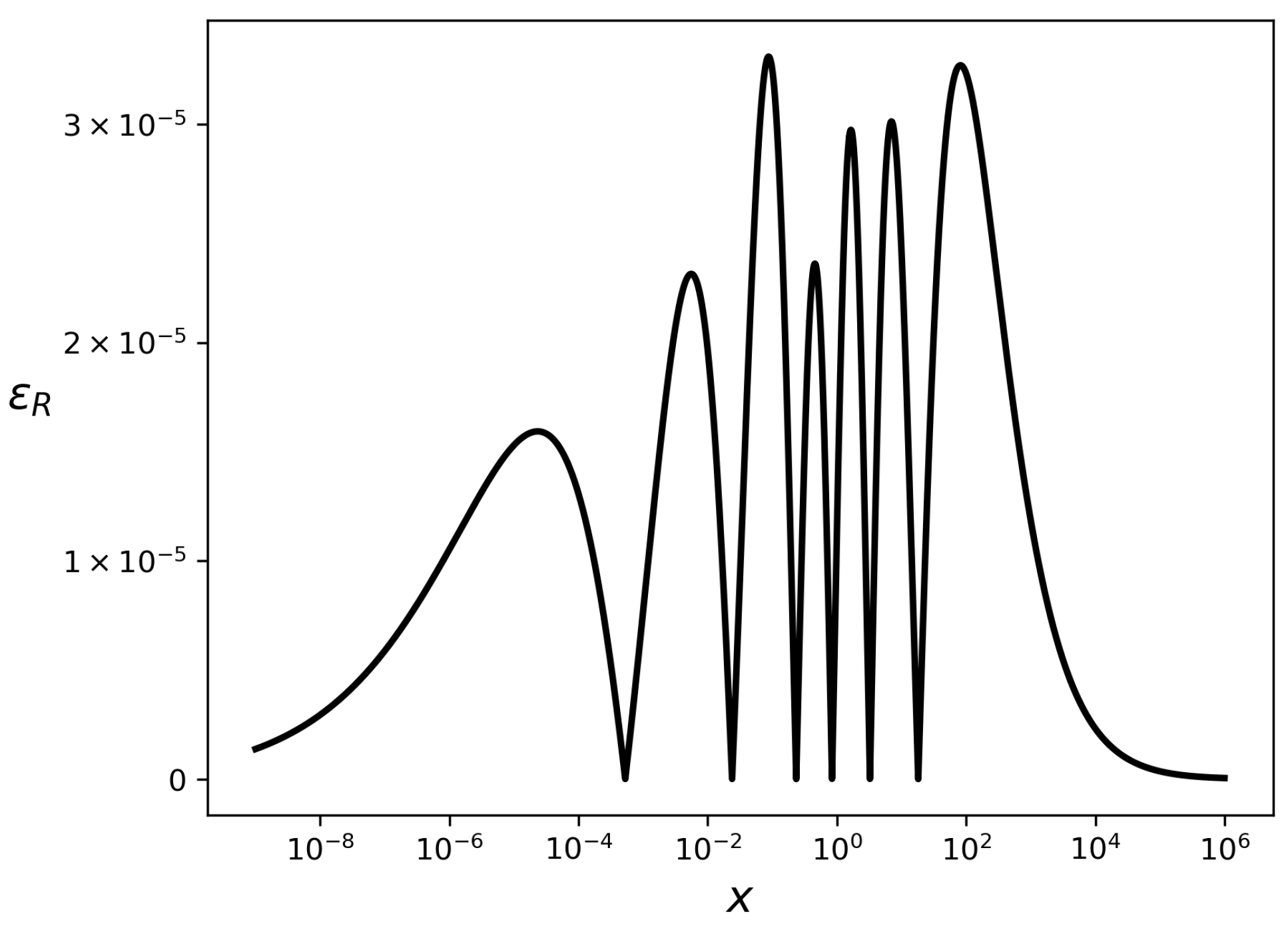
Appendix A.4. PolyLog and Fermi–Dirac Integrals
| s | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1/3 | 5 | −1.2 | 0.49 | 663 | −227 | 3.371 | 139 | −10.5 | 46 | 236 | 9.7 | 286 | −10 | −1.66 | |
| 1/2 | 7.7 | −0.67 | 0.057 | 473 | −23 | 3.376 | 58 | -7.4 | −212 | 241 | 9 | 312 | −11 | −1.24 | |
| 2/3 | 11.8 | −1.1 | 0.09 | 519 | 28 | 3.58 | 57 | −5.2 | −547 | 255 | 7.9 | 346 | −12.7 | −1.13 | |
| 4/3 | 1.4732 | 0.125 | 0.00198 | 5.4 | 12.1 | 1.02 | 10.84 | 4.37 | 13 | 135.1 | 11.79 | 404 | −10.8 | −1.885 | |
| 3/2 | 1.52 | 0.0964 | 0.0011 | 15.35 | 28.15 | 1.1931 | 20 | 6.596 | −94.5 | 131.8 | 11.86 | 443.67 | −11.46 | −2.152 | |
| 5/3 | 3.02 | 0.196 | 0.0093 | 37.8 | 57.3 | 0.9295 | 33.17 | 8.74 | 50.6 | 116 | 12 | 476 | −11.8 | −1.283 | |
| 2 | 24 | −0.17 | 0.128 | 100.8 | 132 | 0.5685 | 63.5 | 13.14 | 300 | 88.6 | 11.6 | 541 | −13 | −0.775 | |
| 5/2 | 32.2 | 38.7 | 38.8 | 9.75 | 22.3 | 1.206 | 13 | 6.82 | 103.6 | 71.7 | 10 | 651 | −15.3 | 0.12638 | |
| 3 | 26.569 | 26.69 | 15.88 | 34.7 | 62.38 | 0.253 | 27.33 | 10.18 | 633.79 | 30.8 | 7.64 | 681.3 | −17.2 | 0.25076 | |
| 7/2 | 42.95 | 36.9 | 12.34 | 85.5 | 122.17 | 1.197 | 49.79 | 12.114 | 516.26 | 19.4 | 5.8 | 768.2 | −20.8 | 0.3759 | |
| 4 | 103.84 | 92.24 | 19.97 | 26.76 | 17.39 | 7.02 | 13.8 | 3.58 | −164 | 33 | 5.4 | 1050 | −27 | 0.50028 | |
| 9/2 | 9.774 | 2.909 | 0 | 235 | 326 | 0.091 | 126.2 | 15.65 | 715.8 | −16.4 | 2.6 | 711.8 | −28 | 1.25 | |
| 5 | 70.4 | 60.6 | 8.25 | 1855 | 836 | 3 | 179 | 14.3 | 202 | −19 | 1 | 229 | −24.6 | 0.7488 | |
| 11/2 | 149 | 76.3 | 4.63 | 1012 | 887 | −34.2 | 284 | 28.3 | 342 | −29.9 | 1.36 | 206 | −18.8 | 0.8758 | |
| 6 | 233.98 | 112.86 | 7.98 | 10.3 | 11 | −1 | 7 | 1.81 | 2004 | −24 | 2.8 | 1981 | −30 | 1.00017 | |
| 13/2 | 280.6 | 122.3 | 5.132 | 22 | 20 | −82 | 9 | 22.7 | 809 | −48 | 1.3 | 629 | −39 | 1.124 |
Appendix A.5. Synchrotron Functions
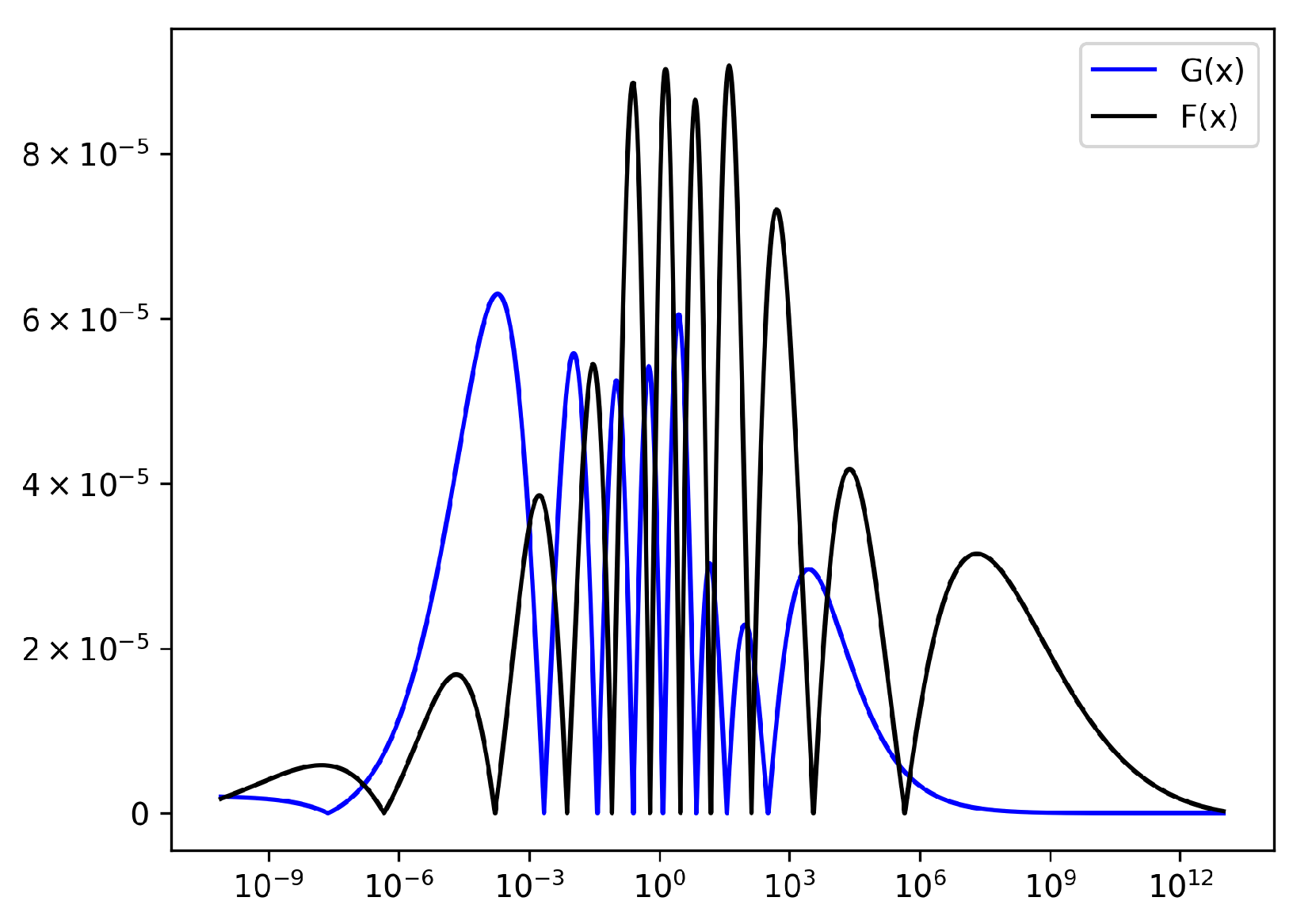
References
- Geng, Z.; Abdulah, S.; Sun, Y.; Ltaief, H.; Keyes, D.E.; Genton, M.G. GPU-Accelerated Modified Bessel Function of the Second Kind for Gaussian Processes. In Proceedings of the ISC High Performance 2025 Research Paper Proceedings (40th International Conference), Hamburg, Germany, 10–13 June 2025; pp. 1–12. [Google Scholar]
- Shah, D.K.; Vyawahare, V.A.; Sadanand, S. Artificial neural network approximation of special functions: Design, analysis and implementation. Int. J. Dyn. Control 2025, 13, 7. [Google Scholar] [CrossRef]
- Chahrour, I.; Wells, J. Comparing machine learning and interpolation methods for loop-level calculations. SciPost Phys. 2022, 12, 187. [Google Scholar] [CrossRef]
- Robinson, D.; Avestruz, C.; Gnedin, N.Y. On the minimum number of radiation field parameters to specify gas cooling and heating functions. Open J. Astrophys. 2025, 8, 76. [Google Scholar] [CrossRef]
- Baumann, D. Cosmology; Cambridge University Press: Cambridge, UK, 2022. [Google Scholar]
- Orly, A. Supplementary Mathematica Notebook for Analytical Closed-form Expressions, Close as Desired to Special Functions. 2024. Available online: https://github.com/AvivBinyaminOrly/Analytical-Approximations (accessed on 19 May 2024).
- Arfken, G.B.; Weber, H.J.; Harris, F.E. Mathematical Methods for Physicists: A Comprehensive Guide, 7th ed.; Academic Press: Burlington, MA, USA, 2012. [Google Scholar]
- López, J.L.; Temme, N.M. Two-Point Taylor Expansions of Analytic Functions. Stud. Appl. Math. 2002, 109, 297–311. [Google Scholar] [CrossRef]
- Baker, G.A., Jr. Essentials of Padé Approximants; Academic Press: New York, NY, USA, 1975. [Google Scholar]
- Pozzi, A. Applications of Pade’ Approximation Theory in Fluid Dynamics; World Scientific: Singapore, 1994. [Google Scholar]
- Prévost, M.; Rivoal, T. Application of Padé approximation to Euler’s constant and Stirling’s formula. Ramanujan J. 2021, 54, 177–195. [Google Scholar] [CrossRef]
- Bultheel, A. Applications of Padé approximants and continued fractions in systems theory. In Mathematical Theory of Networks and Systems; Springer: Berlin/Heidelberg, Germany, 2005; pp. 130–148. [Google Scholar]
- Baker, G.A., Jr.; Gammel, J.L. (Eds.) The Padé Approximant in Theoretical Physics; Academic Press: New York, NY, USA, 1971. [Google Scholar]
- Jordan, K.D.; Kinsey, J.L.; Silbey, R. Use of Pade approximants in the construction of diabatic potential energy curves for ionic molecules. J. Chem. Phys. 1974, 61, 911–917. [Google Scholar] [CrossRef]
- Basdevant, J.L. The Padé approximation and its physical applications. Fortschritte der Physik 1972, 20, 283–331. [Google Scholar] [CrossRef]
- Samuel, M.A.; Ellis, J.; Karliner, M. Comparison of the Pade approximation method to perturbative QCD calculations. Phys. Rev. Lett. 1995, 74, 4380. [Google Scholar] [CrossRef] [PubMed]
- Baker, G.A., Jr.; Graves-Morris, P. Padé Approximants; Cambridge University Press: Cambridge, UK, 1996; Volume 59. [Google Scholar]
- Bender, C.M.; Orszag, S.A. Advanced Mathematical Methods for Scientists and Engineers I: Asymptotic Methods and Perturbation Theory; Springer: New York, NY, USA, 1999. [Google Scholar]
- Winitzki, S. Uniform approximations for transcendental functions. In Proceedings of the International Conference on Computational Science and Its Applications (ICCSA 2003), Montreal, QC, Canada, 18–21 May 2003; pp. 780–789. [Google Scholar]
- Meijering, E. A chronology of interpolation: From ancient astronomy to modern signal and image processing. Proc. IEEE 2002, 90, 319–342. [Google Scholar] [CrossRef]
- De Boor, C. A Practical Guide to Splines; Springer New York: New York, NY, USA, 1978; Volume 27. [Google Scholar]
- Phillips, G.M. Interpolation and Approximation by Polynomials; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2003; Volume 14. [Google Scholar]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Linka, K.; Schäfer, A.; Meng, X.; Zou, Z.; Karniadakis, G.E.; Kuhl, E. Bayesian physics informed neural networks for real-world nonlinear dynamical systems. Comput. Methods Appl. Mech. Eng. 2022, 402, 115346. [Google Scholar] [CrossRef]
- Liu, Z.; Yang, Y.; Cai, Q. Neural network as a function approximator and its application in solving differential equations. Appl. Math. Mech. 2019, 40, 237–248. [Google Scholar] [CrossRef]
- Yang, S.; Ting, T.O.; Man, K.L.; Guan, S.U. Investigation of neural networks for function approximation. Procedia Comput. Sci. 2013, 17, 586–594. [Google Scholar] [CrossRef]
- Holmes, M.H. Introduction to Perturbation Methods; Springer: New York, NY, USA, 2012; Volume 20. [Google Scholar]
- O’Malley, R.E., Jr. The Method of Matched Asymptotic Expansions and Its Generalizations. In Historical Developments in Singular Perturbations; Springer: Cham, Switzerland, 2014; pp. 53–121. [Google Scholar]
- Koch, B.; Olmo, G.J.; Riahinia, A.; Rincón, Á.; Rubiera-Garcia, D. Quasi-normal modes and shadows of scale-dependent regular black holes. arXiv 2025, arXiv:2506.15944. [Google Scholar]
- Maass, F.; Martin, P.; Olivares, J. Analytic approximation to Bessel function J 0 (x). Comput. Appl. Math. 2020, 39, 222. [Google Scholar] [CrossRef]
- Maass, F.; Martin, P. Precise analytic approximations for the Bessel function J1 (x). Results Phys. 2018, 8, 1234–1238. [Google Scholar] [CrossRef]
- Martin, P.; Maass, F. Accurate analytic approximation to the Modified Bessel function of Second Kind K0(x). Results Phys. 2022, 35, 105283. [Google Scholar] [CrossRef]
- Karasiev, V.V.; Chakraborty, D.; Trickey, S.B. Improved analytical representation of combinations of Fermi–Dirac integrals for finite-temperature density functional calculations. Comput. Phys. Commun. 2015, 192, 114–123. [Google Scholar] [CrossRef]
- Turbiner, A.V.; del Valle, J.C. Anharmonic oscillator: A solution. J. Phys. A Math. Theor. 2021, 54, 295204. [Google Scholar] [CrossRef]
- Wang, X.; Yan, L.; Zhang, Q. Research on the Application of Gradient Descent Algorithm in Machine Learning. In Proceedings of the 2021 International Conference on Computer Network, Electronic and Automation (ICCNEA), Xi’an, China, 24–26 September 2021; pp. 11–15. [Google Scholar]
- Kroese, D.P.; Rubinstein, R.Y. Monte carlo methods. Wiley Interdiscip. Rev. Comput. Stat. 2012, 4, 48–58. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential evolution–a simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef]
- Johansson, F. Mpmath: A Python Library for Arbitrary-Precision Floating-Point Arithmetic (Version 0.14). 2010. Available online: http://code.google.com/p/mpmath/ (accessed on 7 January 2024).
- Khvorostukhin, A.S. Simple way to the high-temperature expansion of relativistic Fermi-Dirac integrals. Phys. Rev. D 2015, 92, 096001. [Google Scholar] [CrossRef]
- Fowlie, A. A fast C++ implementation of thermal functions. Comput. Phys. Commun. 2018, 228, 264–272. [Google Scholar] [CrossRef]
- Curtin, D.; Meade, P.; Ramani, H. Thermal resummation and phase transitions. Eur. Phys. J. C 2018, 78, 787. [Google Scholar] [CrossRef]
- Li, T.; Zhou, Y.F. Strongly first order phase transition in the singlet fermionic dark matter model after LUX. J. High Energy Phys. 2014, 2014, 102. [Google Scholar] [CrossRef]
- Gouttenoire, Y. Beyond the Standard Model Cocktail: A Modern and Comprehensive Review of the Major Open Puzzles in Theoretical Particle Physics and Cosmology with a Focus on Heavy Dark Matter. arXiv 2023, arXiv:2312.00032. [Google Scholar]
- Kolb, E.W.; Turner, M.S. The Early Universe; Addison-Wesley: Redwood City, CA, USA, 1990. [Google Scholar]
- Klajn, B. Exact high temperature expansion of the one-loop thermodynamic potential with complex chemical potential. Phys. Rev. D 2014, 89, 036001. [Google Scholar] [CrossRef]
- Joyce, W.B.; Dixon, R.W. Analytic approximations for the Fermi energy of an ideal Fermi gas. Appl. Phys. Lett. 1977, 31, 354–356. [Google Scholar] [CrossRef]
- Selvakumar, C.R. Approximations to Fermi-Dirac integrals and their use in device analysis. Proc. IEEE 1982, 70, 516–518. [Google Scholar] [CrossRef]
- Koroleva, O.N.; Mazhukin, A.V.; Mazhukin, V.I.; Breslavskiy, P.V. Analytical approximation of the Fermi-Dirac integrals of half-integer and integer orders. Math. Models Comput. Simul. 2017, 9, 383–389. [Google Scholar] [CrossRef]
- Longair, M.S. High Energy Astrophysics, 3rd ed.; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Fouka, M.; Ouichaoui, S. Analytical fits to the synchrotron functions. Res. Astron. Astrophys. 2013, 13, 680. [Google Scholar] [CrossRef]
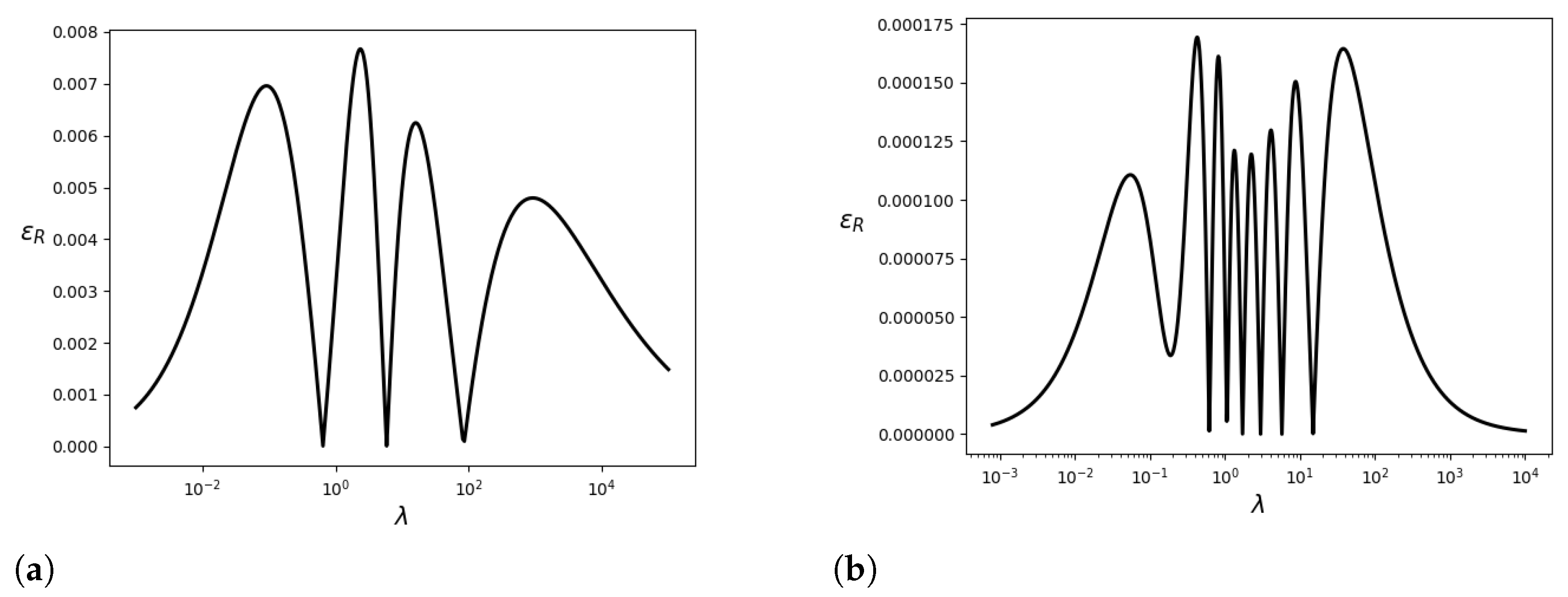
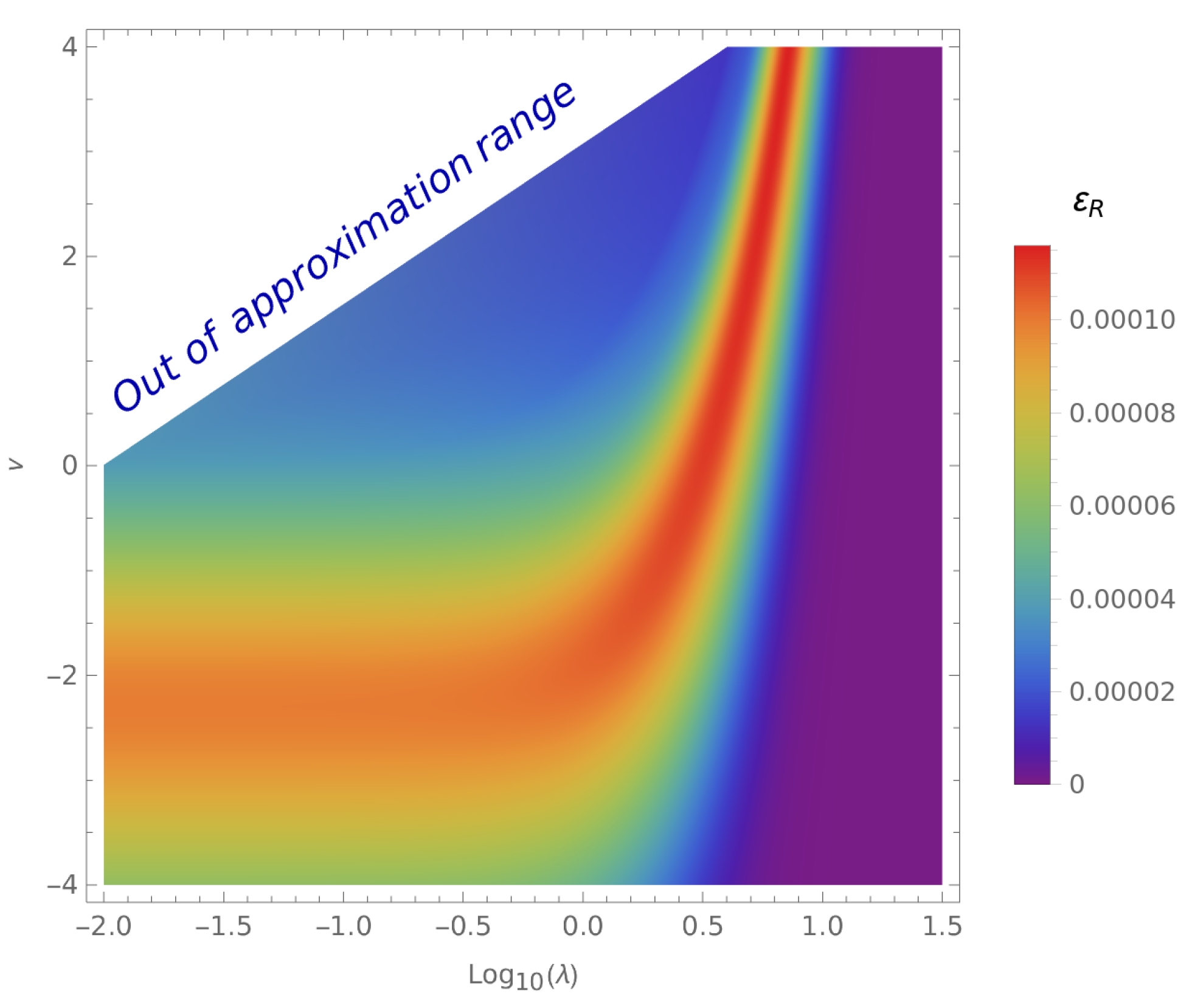
| Technique | Pros | Cons | Single Analytical Expression | Global Domain |
|---|---|---|---|---|
| Taylor and Asymptotic Expansion | Simple to implement; results are often pre-derived and widely available in the literature. | Accurate near the expansion point, but can quickly diverge. | ✔ | × |
| Padé Approximants | Superior to Taylor series in terms of convergence across the domain and in its ability to capture pole behaviors. | Cannot reproduce generic functional behaviors (e.g., logarithmic, exponential); can introduce spurious poles. | × | |
| Chebyshev Polynomials and Remez Algorithm | Excellent for limited domains; specialized for achieving uniform accuracy. | Cannot reproduce generic functional behaviors (e.g., logarithmic, exponential). | ✔ | × |
| Spline Interpolation | Highly flexible and smooth for interpolating a set of data points. | Results in a piecewise function, not a single analytical expression; can have high memory usage. May oscillate or overfit with noisy data. | × | ✔ |
| Neural Networks | Acts as a universal function approximator that can learn from data. | A “black box“ model, not an analytical formula; requires significant data and training; can have long evaluation time and high memory usage. | × | ✔ |
| MPQA Approach | Achieves near-optimal approximation parameters. Does not require numerical minimization. | Approximation structure construction/variation is limited by the solvability of asymptotic matching equations. | ✔ | ✔ |
| This Work | Achieves optimal approximation parameters; approximation structure construction/variation is both automatic and unlimited by asymptotic matching solvability. | Requires numerical minimization. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Orly, A. Analytical Approximations as Close as Desired to Special Functions. Axioms 2025, 14, 566. https://doi.org/10.3390/axioms14080566
Orly A. Analytical Approximations as Close as Desired to Special Functions. Axioms. 2025; 14(8):566. https://doi.org/10.3390/axioms14080566
Chicago/Turabian StyleOrly, Aviv. 2025. "Analytical Approximations as Close as Desired to Special Functions" Axioms 14, no. 8: 566. https://doi.org/10.3390/axioms14080566
APA StyleOrly, A. (2025). Analytical Approximations as Close as Desired to Special Functions. Axioms, 14(8), 566. https://doi.org/10.3390/axioms14080566





