Extremal Permanents of Laplacian Matrices of Unicyclic Graphs

Abstract

The extremal problem of Laplacian permanents of graphs is a classical and challenging topic in algebraic combinatorics, where the inherent #P-complete complexity of permanent computation renders this pursuit particularly intractable. In this paper, we determine the upper and lower bounds of permanents of Laplacian matrices of unicyclic graphs, and the corresponding extremal graphs are characterized. Furthermore, we also determine the upper and lower bounds of permanents of Laplacian matrices of unicyclic graphs with given girth, and the corresponding extremal graphs are characterized.

1. Introduction

Let $G=\left(V\right(G),E(G\left)\right)$ be a simple connected graph with vertex set $V\left(G\right)=\{v_1,v_2,\dots ,v_n\}$ and edge set $E\left(G\right)=\{e_1,e_2,\dots ,e_m\}$. Suppose the degree of vertex $v_i$ equals $d\left(v_i\right)$ (simply written as $d_i$) for $i=1,2,\dots ,n$. The Laplacian matrix $L\left(G\right)=\left[l_{ij}\right]$ is defined by

$$l_{ij}=\left\{\begin{array}{cc}{d}_i\hfill & \mathrm{if}i=j,\hfill \\ -1,\hfill & \mathrm{if}{v}_i\mathrm{and}{v}_j\mathrm{are}\mathrm{adjacent},\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

The matrix $Q\left(G\right)$ is called the signless Laplacian matrix of G whose entries are the absolute values of the entries of $L\left(G\right)$. The Laplacian matrix has been the object of considerable study, stimulated in part by Fiedler’s algebraic connectivity [1] and in part by applications in chemistry [2], statistics [3], and parallel algorithms for sparse matrix computations [4].

For an $n\times n$ matrix $M=\left[a_{ij}\right](i,j\in 1,2,3,\dots ,n)$, the permanent is defined as

$$\mathrm{per}\left(M\right)=\sum _{\varphi }\prod _{i=1}^n{a}_{i\varphi \left(i\right)},$$

where the sum is taken over all permutations $\varphi$ of the set $\{1,2,3,\dots ,n\}$. In general, the problem of evaluating the permanent of a given matrix is known to be very difficult and was proved to be a #P-complete problem [5]. In view of the computational difficulty, a considerable number of researchers have been devoted to the determination of good bounds for permanents for matrices; see [6,7,8]. Often, the problem of determining the upper bound or lower bound of the permanent over a certain class of matrices is the same as that of maximizing or minimizing the permanent over the same class of matrices. Brualdi and Goldwasser [9] characterized the bounds of the permanents of the Laplacian matrix (simply written as Laplacian permanents) of trees or of trees with given graph parameters. Geng et al. [10,11] obtained the lower bounds of the Laplacian permanents of trees with graph parameters (such as numbers of pendent vertices, maximum degree, and domination number), and the corresponding extremal graphs were characterized. Perhaps due to the notorious computational intractability of the permanent, this work seems to have stalled.

A unicyclic graph G is a simple connected graph in which the number of edges is equal to the number of vertices. This implies that a unicyclic graph contains exactly one cycle. Li and Zhang [12,13] characterized the upper and lower bounds for signless Laplacian permanents of unicyclic graphs, and they characterized lower bounds for signless Laplacian permanents of unicyclic graphs with given girth or diameter. Vrba [14] proved that the Laplacian permanents and signless Laplacian permanents are equal for bipartite graphs. This means that the bound of the Laplacian permanents for non-bipartite unicyclic graphs is unknown, i.e.,

Problem 1.

Determining bounds for the Laplacian permanents of non-bipartite unicyclic graphs.

In this paper, our interest is to characterize the bounds of the Laplacian permanents of unicyclic graphs or unicyclic graphs with given graph parameters, and at the same time, provide the solution to Problem 1. For the sake of convenience, we will first introduce several definitions and notations. Let $C_n$, $P_n$, $S_n$ and $K_n$ denote the cycle, path, star, and complete graph, respectively, each having n vertices. Let $S_n^{*}$ be a graph constructed by attaching $n-3$ pendent edges to a vertex of $C_3$; see Figure 1. Let $S_{n,k}^{*}$ be a graph formed by attaching $n-k$ pendent edges to a vertex of $C_k$; see Figure 1. We denote by $C_{n,k}$ a graph obtained by joining a vertex of $C_k$ to an end vertex of $P_{n-k}$; see Figure 1. Denote the set of unicyclic graphs with n vertices by ${\mathcal{U}}_n$, and let ${\mathcal{U}}_{n,k}$ denote the set of unicyclic graphs on n vertices with girth k. Let $S\subseteq V\left(G\right)$ be a vertex subset. We use $L_S\left(G\right)$ to denote the principal submatrix of $L\left(G\right)$ that is formed by deleting the rows and columns corresponding to all vertices of $S\subseteq V\left(G\right)$. In particular, if $S=v$ with $v\in V\left(G\right)$, then $L_v\left(G\right)$ is simply written as $L_v\left(G\right)$. $V\left(C\right)$ denotes the vertex set of the induced cycle C of G. Let $G-e$ and $G-v$ be the graphs obtained by removing the edge e and vertex v from G, respectively. Based on the above definitions and notations, the main results we have obtained in this paper are as follows.

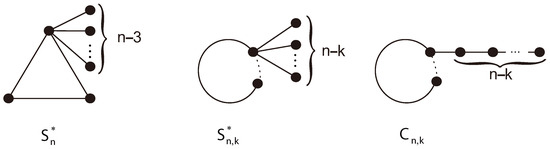
Figure 1. Graphs $S_n^{*}$, $S_{n,k}^{*}$ and $C_{n,k}$.

Theorem 1.

Let $G\in {\mathcal{U}}_n$ be a unicyclic graph with n vertices. Then

$$\begin{array}{c}\hfill 10n-18\le \mathrm{per}L\left(G\right)\le {(1+\sqrt{2})}^n+{(1-\sqrt{2})}^n+2\times {(-1)}^n,\end{array}$$

(1)

where the left equality holds if and only if $G=S_n^{*}$, and the right equality holds if and only if $G=C_n$.

Theorem 2.

Let $G\in {\mathcal{U}}_{n,k}$ be a unicyclic graph with n vertices and girth k. Then

$$\begin{array}{c}\hfill \mathrm{per}L\left(S_{n,k}^{*}\right)\le \mathrm{per}L\left(G\right)\le \mathrm{per}L\left(C_{n,k}\right),\end{array}$$

(2)

where the left equality holds if and only if $G=S_{n,k}^{*}$, and the right equality holds if and only if $G=C_{n,k}$.

To help readers understand Theorems 1 and 2, we have enumerated all unicyclic graphs with five vertices (see Figure 2), whose permanents are $\mathrm{per}L\left(U_5^1\right)=40$, $\mathrm{per}L\left(U_5^2\right)=32$, $\mathrm{per}L\left(U_5^3\right)=56$, $\mathrm{per}L\left(U_5^4\right)=60$, and $\mathrm{per}L\left(U_5^5\right)=80$, respectively. Observing the structures of $U_5^2$, $U_5^3$, and $U_5^5$, we have $U_5^2=S_5^{*}=S_{5,3}^{*}$, $U_5^3=C_{5,3}$, and $U_5^5=C_5$. It is easy to see that $\mathrm{per}L\left(U_5^5\right)$ is the largest and $\mathrm{per}L\left(U_5^2\right)$ is the smallest, which is consistent with Theorem 1. For the case where the girth is 3, it is similarly easy to observe that $\mathrm{per}L\left(U_5^3\right)$ is the largest and $\mathrm{per}L\left(U_5^2\right)$ is the smallest, and this is consistent with Theorem 2.

Figure 2. All unicyclic graphs with five vertices.

The organization of this paper is structured as follows. In Section 2, we will introduce some lemmas. In Section 3, we will present the proof of Theorem 1. Precisely, the upper and lower bounds of the Laplacian permanents of unicyclic graphs are ascertained. In Section 4, the proof of Theorem 2 will be given, wherein the upper and lower bounds of the Laplacian permanents of unicyclic graphs with a specified girth are determined. In Section 5, a brief summary is provided.

2. Preliminary

In this section, several lemmas are crucial for the description and proof of our subsequent results. We list them as follows.

Lemma 1.

Let $M=\left(m_{ij}\right)$, where $i,j=1,2,\dots ,n$, be an $n\times n$ square matrix. Then

$$\begin{array}{c}\hfill \mathrm{per}M=\sum _i{m}_{ij}\mathrm{per}{M}_{ij}\mathrm{and}\mathrm{per}M=\sum _j{m}_{ij}\mathrm{per}{M}_{ij}.\end{array}$$

Lemma 2

([15]). Let M be a positive semidefinite matrix. Then

$$\begin{array}{c}\hfill \mathrm{per}M\ge 0.\end{array}$$

Lemma 3

([9]). Let T be a tree with n vertices. Then

$$\begin{array}{c}\hfill \mathrm{per}L\left(T\right)\ge 2(n-1)withequalityifandonlyifT=S_n.\end{array}$$

Lemma 4

([9]). Let T be a tree with n vertices. Then

$$\begin{array}{c}\hfill \mathrm{per}L\left(T\right)\le {\displaystyle \frac{2-\sqrt{2}}{2}}{(1+\sqrt{2})}^n+{\displaystyle \frac{2+\sqrt{2}}{2}}{(1-\sqrt{2})}^{n}withequalityifandonlyifT=P_n.\end{array}$$

Lemma 5

([9]). Let $P_n$ be the path with n vertices. Let $B_n$ be the matrix obtained from $L\left(P_{n+1}\right)$ by eliminating row and column of one of the end vertices. Then

(i) 

$\mathrm{per}{B}_n={\displaystyle \frac{1}{2}}{(1+\sqrt{2})}^n+{\displaystyle \frac{1}{2}}{(1-\sqrt{2})}^n$,

(ii) 

$\mathrm{per}L\left(P_n\right)=\mathrm{per}{B}_{n-1}+\mathrm{per}{B}_{n-2}$$(n\ge 3)$,

(iii) 

$\mathrm{per}{B}_n=2\mathrm{per}{B}_{n-1}+\mathrm{per}{B}_{n-2}$$(n\ge 3)$,

where $\mathrm{per}{B}_0=1$.

Lemma 6

([9]). Let G be a graph with n vertices. Then

$$\begin{array}{c}\hfill \mathrm{per}Q\left(G\right)\ge \mathrm{per}L\left(G\right)withequalityifandonlyifGisabipartitegraph.\end{array}$$

Lemma 7

([12]). Let G be a unicyclic graph with n vertices. Then

$$\begin{array}{c}\hfill \mathrm{per}Q\left(G\right)\le {(1+\sqrt{2})}^n+{(1-\sqrt{2})}^n+2withequalityifandonlyifG=C_n.\end{array}$$

Lemma 8

([16]). Let G be a simple graph, v be a vertex of graph G, ${\mathcal{C}}_G\left(v\right)$ be the set of cycles in graph G that contain vertex v, and $N\left(v\right)$ denote the neighborhood of v. Then

$$\begin{array}{c}\hfill \mathrm{per}L\left(G\right)=d\left(v\right)\mathrm{per}{L}_v\left(G\right)+\sum _{u\in N\left(v\right)}\mathrm{per}{L}_{vu}\left(G\right)+2\sum _{C\in {\mathcal{C}}_G\left(v\right)}{(-1)}^{\left|V\right(C\left)\right|}\mathrm{per}{L}_{V\left(C\right)}\left(G\right).\end{array}$$

Lemma 9

([16]). Let G be a simple connected graph with $\left|V\right(G\left)\right|\ge 3$. Suppose that $e=uv\in E\left(G\right)$ and ${\mathcal{C}}_G\left(e\right)$ is the set of cycles containing the edge e in G. Then

$$\begin{array}{ccc}\hfill \mathrm{per}L\left(G\right)& =& \mathrm{per}L(G-e)+\mathrm{per}{L}_v(G-e)+\mathrm{per}{L}_u(G-e)\hfill \\ & & +2\mathrm{per}{L}_{uv}\left(G\right)+2\sum _{C\in {\mathcal{C}}_G\left(e\right)}{(-1)}^{\left|V\right(C\left)\right|}\mathrm{per}{L}_{V\left(C\right)}\left(G\right).\hfill \end{array}$$

Lemma 10

([16]). Let G be a simple connected graph with $\left|V\right(G\left)\right|\ge 3$. Suppose that $v\in V\left(G\right)$ and S is a proper subset of $V\left(G\right)$ satisfying $v\notin S$. Then

$$\begin{array}{ccc}\hfill \mathrm{per}{L}_S\left(G\right)& =& d\left(v\right)\mathrm{per}{L}_{S\cup \left\{v\right\}}\left(G\right)+\sum _{{\displaystyle \genfrac{}{}{0pt}{}{uv\in E\left(G\right)}{u\notin S}}}\mathrm{per}{L}_{S\cup \{u,v\}}\left(G\right)\hfill \\ & & +2\sum _{{\displaystyle \genfrac{}{}{0pt}{}{C\in {\mathcal{C}}_G\left(v\right)}{V\left(C\right)\cap S=\varnothing }}}{(-1)}^{\left|V\right(C\left)\right|}\mathrm{per}{L}_{V\left(C\right)\cup S}\left(G\right).\hfill \end{array}$$

Lemma 11

([16]). Let G be a simple connected graph with $\left|V\right(G\left)\right|\ge 3$. If v is a pendant vertex of G, and u is the vertex adjacent to v. Then each of the following holds.

(i) 

$\mathrm{per}{L}_v\left(G\right)=\mathrm{per}L(G-v)+\mathrm{per}{L}_u(G-v)$,

(ii) 

$\mathrm{per}{L}_u(G-v)=\mathrm{per}{L}_{uv}\left(G\right),$

(iii) 

$\mathrm{per}L\left(G\right)=\mathrm{per}L(G-v)+2\mathrm{per}{L}_u(G-v).$

Lemma 12

([17]). Let T be a tree with $n(n\ge 3)$ vertices, and $v\in V\left(T\right)$. Then

$$\begin{array}{c}\hfill d_v\mathrm{per}{L}_v\left(T\right)<\mathrm{per}L\left(T\right)\le 2d_v\mathrm{per}{L}_v\left(T\right).\end{array}$$

Lemma 13.

Let T be a tree with n vertices. Then every term in the expansion of $\mathrm{per}L\left(T\right)$, and the permanent of every principal submatrix of $L\left(T\right)$, is non-negative.

Proof. 

Suppose that $V\left(T\right)=\{v_1$, $v_2$, …, $v_n\}$. Consider a term $a_{1\varphi \left(1\right)}{a}_{2\varphi \left(2\right)}\dots a_{n\varphi \left(n\right)}$ in the expansion of $\mathrm{per}L\left(T\right)$, where $a_{ij}$ is the $(i,j)$-entry of $L\left(T\right)$. Note that $a_{ii}=d\left(v_i\right)$, and when $i\ne j$, if $v_i{v}_j\in E\left(T\right)$, then $a_{ij}=-1$; otherwise $a_{ij}=0$. Hence if $a_{1\varphi \left(1\right)}{a}_{2\varphi \left(2\right)}\dots a_{n\varphi \left(n\right)}\ne 0$, then $j=\varphi \left(j\right)$ or $v_j{v}_{\varphi \left(j\right)}\in E\left(T\right)$ for all $j\in \{1,\dots ,n\}$. We think of $\varphi$ as a product of disjoint cycles. Each cycle corresponds to either $a_{ii}$ or $a_{ij}{a}_{ji}$, where $a_{ii}>0$ and $a_{ij}{a}_{ji}=1>0$. Hence, we deduce that each term in the Laplace expansion of $\mathrm{per}L\left(T\right)$ is a non-negative integer. By the definitions of $\mathrm{per}{L}_S\left(T\right)$, and each term in the Laplace expansion of $\mathrm{per}L\left(T\right)$ is a non-negative integer, we obtain that each term in the Laplace expansion of $\mathrm{per}{L}_S\left(T\right)$ is also a non-negative integer. □

Lemma 14

([17]). Let T be a tree with $n(n\ge 3)$ vertices, and let v be a pendant vertex of T, $u\in V\left(T\right)$, $d\left(u\right)\ge 2$. Then

$$\begin{array}{c}\hfill \mathrm{per}{L}_u\left(T\right)<\mathrm{per}{L}_v\left(T\right).\end{array}$$

Lemma 15.

Let T be a tree with n vertices, $v\in V\left(T\right)$, $d\left(v\right)=i$. Let $T_j$ be the connected components of $T-v$. Denote $T_j+v$ as the subgraph of T induced by $V\left(T_j\right)\cup \left\{v\right\}$($j=1,2,\dots ,i$). Then

$$\begin{array}{c}\hfill \mathrm{per}{L}_v\left(T\right)=\mathrm{per}{L}_v(T_1+v)\times \mathrm{per}{L}_v(T_2+v)\times \dots \times \mathrm{per}{L}_v(T_i+v).\end{array}$$

Proof. 

The matrix $L\left(T\right)$ has the following form

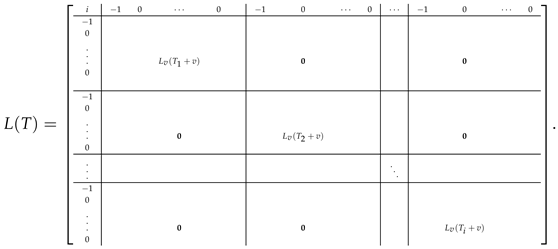By Lemma 1, it can be shown that

$$\begin{array}{c}\hfill \mathrm{per}{L}_v\left(T\right)=\mathrm{per}{L}_v(T_1+v)\times \mathrm{per}{L}_v(T_2+v)\times \dots \times \mathrm{per}{L}_v(T_i+v).\end{array}$$

□

Lemma 16.

Let T be a tree with $n(n\ge 2)$ vertices. Let v be a pendant vertex of T. Then

$$\begin{array}{c}\hfill \mathrm{per}{L}_v\left(T\right)\le \mathrm{per}{B}_{n-1}withequalityifandonlyifT=P_n.\end{array}$$

Proof. 

We are to prove the lemma by induction on $\left|V\right(T\left)\right|$. If $\left|V\right(T\left)\right|=2,3,4$, it can be easily verified through simple calculations that the conclusion holds. Assume it is true for $\left|V\right(T\left)\right|<n$ with $n\ge 5$, and let $\left|V\right(T\left)\right|=n$. Let u be the neighbor of v. According to Lemma 11, we have $\mathrm{per}{L}_v\left(T\right)=\mathrm{per}L(T-v)+\mathrm{per}{L}_u(T-v).$

Suppose that $d\left(u\right)=2$. By the induction hypothesis, we have $\mathrm{per}{L}_u(T-v)\le \mathrm{per}{B}_{n-2}$. By Lemma 4, we have

$$\begin{array}{ccc}\hfill \mathrm{per}{L}_v\left(T\right)& =& \mathrm{per}L(T-v)+\mathrm{per}{L}_u(T-v)\hfill \\ & \le & \mathrm{per}L\left(P_{n-1}\right)+\mathrm{per}{B}_{n-2}\hfill \\ & =& \mathrm{per}{B}_{n-2}+\mathrm{per}{B}_{n-3}+\mathrm{per}{B}_{n-2}\hfill \\ & =& \mathrm{per}{B}_{n-1}.\hfill \end{array}$$

Suppose that $d\left(u\right)>2$. By Lemma 14, we have

$$\begin{array}{c}\hfill \mathrm{per}{L}_u(T-v)\le \mathrm{per}{L}_{v_1}(T-v),\end{array}$$

where $v_1$ is a pendant vertex of $T-v$. By the induction hypothesis, we have

$$\mathrm{per}{L}_{v_1}(T-v)\le \mathrm{per}{B}_{n-2}.$$

Hence $\mathrm{per}{L}_v\left(T\right)\le \mathrm{per}{B}_{n-1}$. □

3. Proof of Theorem 1

In this section, we will give the proof of Theorem 1. Before proceeding to the proof of Theorem 1, we first introduce some lemmas.

Lemma 17.

Let G be a unicyclic graph with n$(n\ge 3)$ vertices. If $v_1$ is a pendant vertex of G, and $v_2$ is the vertex adjacent to $v_1$. Then

$$\mathrm{per}{L}_{\{v_1,v_2\}}\left(G\right)\ge d_3\dots d_n,$$

where $d_i$ is the degree of $v_i$$(i=1,2,\dots ,n)$.

Proof. 

Let $T_j$ be the connected component of $G-\{v_1,v_2\}$. Denote $T_j+v_2$ as the subgraph of G induced by $V\left(T_j\right)\cup \left\{v_2\right\}(j=2,\dots ,d_2-1)$. The matrix $L\left(G\right)$ has the following form

Suppose that $v_2$ is the vertex of the unique cycle in G. By Lemmas 1 and 15, we have

$$\begin{array}{c}\hfill \mathrm{per}{L}_{\{v_1,v_2\}}\left(G\right)=\mathrm{per}{L}_{v_2}(T_2+v_2)\times \mathrm{per}{L}_{v_2}(T_3+v_2)\times \dots \times \mathrm{per}{L}_{v_2}(T_{d_2-1}+v_2).\end{array}$$

By the definition of $T_j+v_2$, $T_j+v_2$ is either a tree or a unicyclic graph with $v_2$ on the unique cycle in $T_j+v_2$. If $T_j+v_2$ is a tree, by Lemma 13, each term of $\mathrm{per}{L}_{v_2}(T_j+v_2)$ is a non-negative integer. If $T_j+v_2$ is a unicyclic graph with $v_2$ on the unique cycle in $T_j+v_2$, then $L_{v_2}(T_j+v_2)$ can be regarded as a principal submatrix of the Laplacian matrix of a tree; thus, by Lemma 13, each term of $\mathrm{per}{L}_{v_2}(T_i+v_2)$ is a non-negative integer. Moreover, since the product of principal diagonal element is a term in the Laplace expansion of $L_{v_2}(T_j+v_2)$, it follows that $\mathrm{per}{L}_{v_2}(T_j+v_2)(2\le j\le d_2-1)$ is greater than or equal to the product of the principal diagonal element. Hence $\mathrm{per}{L}_{\{v_1,v_2\}}\left(G\right)\ge d_3\dots d_n.$

Suppose that $v_2$ is not a vertex of the unique cycle in G. Let $v_i$ be vertex of the unique cycle in G. By Lemma 10, we have

$$\begin{array}{ccc}\hfill \mathrm{per}{L}_{\{v_1,v_2\}}\left(G\right)& =& d\left(v_i\right)\mathrm{per}{L}_{\{v_1,v_2\}\cup \left\{v_i\right\}}\left(G\right)+\sum _{{\displaystyle \genfrac{}{}{0pt}{}{v_i{v}_j\in E\left(G\right)}{j>2}}}\mathrm{per}{L}_{\{v_1,v_2\}\cup \{v_i,v_j\}}\left(G\right)\hfill \\ & & +2\times {(-1)}^{\left|V\right(C\left)\right|}\mathrm{per}{L}_{V\left(C\right)\cup \{v_1,v_2\}}\left(G\right).\hfill \end{array}$$

From the arguments as above, we know that each term in the Laplace expansions of $\mathrm{per}{L}_{\{v_1,v_2\}\cup \left\{v_i\right\}}\left(G\right)$, $\mathrm{per}{L}_{\{v_1,v_2\}\cup \{v_i,v_j\}}\left(G\right)$, and $\mathrm{per}{L}_{V\left(C\right)\cup \{v_1,v_2\}}\left(G\right)$ is non-negative. Hence, each of $\mathrm{per}{L}_{\{v_1,v_2\}\cup \left\{v_i\right\}}\left(G\right)$, $\mathrm{per}{L}_{\{v_1,v_2\}\cup \{v_i,v_j\}}\left(G\right)$, and $\mathrm{per}{L}_{V\left(C\right)\cup \{v_1,v_2\}}\left(G\right)$ is greater than the product of its main diagonal elements. This implies that $d\left(v_i\right)\mathrm{per}{L}_{\{v_1,v_2\}\cup \left\{v_i\right\}}\left(G\right)\ge d_3\dots d_n$. By the structure of G, we know that $\left|V\right(C_k\left)\right|\ge 3$. We can definitely find a vertex $v_f$ (different from $v_i$ and $v_j$) on the unique cycle of G such that

$$\mathrm{per}{L}_{\{v_1,v_2\}\cup \{v_i,v_j,v_f\}}\left(G\right)\ge 2\times \mathrm{per}{L}_{V\left(C\right)\cup \{v_1,v_2\}}\left(G\right).$$

Hence

$$|\sum _{v_i{v}_j\in E\left(G\right)}\mathrm{per}{L}_{\{v_1,v_2\}\cup \{v_i,v_j\}}{\left(G\right)|\ge |2\times (-1)}^{\left|V\right(C\left)\right|}\mathrm{per}{L}_{V\left(C\right)\cup \{v_1,v_2\}}\left(G\right)|.$$

By Lemma 10, we obtain that

$$\begin{array}{ccc}\hfill \mathrm{per}{L}_{\{v_1,v_2\}}\left(G\right)& =& d\left(v_i\right)\mathrm{per}{L}_{\{v_1,v_2\}\cup \left\{v_i\right\}}\left(G\right)+\sum _{{\displaystyle \genfrac{}{}{0pt}{}{v_i{v}_j\in E\left(G\right)}{j>2}}}\mathrm{per}{L}_{\{v_1,v_2\}\cup \{v_i,v_j\}}\left(G\right)\hfill \\ & & +2\times {(-1)}^{\left|V\right(C\left)\right|}\mathrm{per}{L}_{V\left(C\right)\cup \{v_1,v_2\}}\left(G\right)\ge d_3\dots d_n.\hfill \end{array}$$

□

Lemma 18.

Let n be a positive integer. Then

$$\mathrm{per}L\left(C_n\right)={(1+\sqrt{2})}^n+{(1-\sqrt{2})}^n+2\times {(-1)}^n.$$

Proof. 

Let $e=uv$ be an edge of $C_n$. By Lemma 9, we have

$$\begin{array}{ccc}\hfill \mathrm{per}L\left(C_n\right)& =& \mathrm{per}L(C_n-e)+\mathrm{per}{L}_v(C_n-e)+\mathrm{per}{L}_u(C_n-e)\hfill \\ & & +2\mathrm{per}{L}_{uv}\left(C_n\right)+2\sum _{C\in {\mathcal{C}}_{C_n}\left(e\right)}{(-1)}^n\hfill \\ & =& \mathrm{per}L\left(P_n\right)+2\mathrm{per}{B}_{n-1}+2\mathrm{per}{L}_{uv}\left(C_n\right)+2\times {(-1)}^n.\hfill \end{array}$$

Let $A_n$ be the matrix obtained by deleting the first row and column of $L\left(C_{n+1}\right)$. Then, expanding the permanent of $A_n$ along the first row we obtain

$$\begin{array}{c}\hfill \mathrm{per}{A}_n=2\mathrm{per}{A}_{n-1}+\mathrm{per}{A}_{n-2}(n\ge 3).\end{array}$$

(3)

This recurrence relation along with $\mathrm{per}{A}_1=2$ and $\mathrm{per}{A}_2=5$ determines $\mathrm{per}{A}_n$ for all $n\ge 1$. For later use we define $\mathrm{per}{A}_0=1$ so that (3) holds for all $n=2$ as well. This recurrence relation can be solved using standard procedures to obtain the following formula:

$$\begin{array}{c}\hfill \mathrm{per}\left(A_n\right)={\displaystyle \frac{1}{2\sqrt{2}}}[{(1+\sqrt{2})}^{n+1}-{(1-\sqrt{2})}^{n+1}].\end{array}$$

(4)

By Lemmas 4 and 5 and (4), we have

$$\mathrm{per}L\left(C_n\right)={(1+\sqrt{2})}^n+{(1-\sqrt{2})}^n+2\times {(-1)}^n.$$

□

Lemma 19.

Let n be a positive integer. Then

$$\mathrm{per}L\left(S_n^{*}\right)=10n-18.$$

Proof. 

Let $e=uv$ be an edge of $S_n^{*}$, where $d\left(u\right)=d\left(v\right)=2$. By Lemmas 3 and 9, we have

$$\begin{array}{ccc}\hfill \mathrm{per}L\left(S_n^{*}\right)& =& \mathrm{per}L(S_n^{*}-e)+\mathrm{per}{L}_v(S_n^{*}-e)+\mathrm{per}{L}_u(S_n^{*}-e)\hfill \\ & & +2\mathrm{per}{L}_{uv}\left(S_n^{*}\right)+2\sum _{C\in {\mathcal{C}}_{S_n^{*}}\left(e\right)}{(-1)}^3\hfill \\ & =& \mathrm{per}L\left(S_n\right)+\mathrm{per}{L}_v\left(S_n\right)+\mathrm{per}{L}_u\left(S_n\right)+2\mathrm{per}{L}_{uv}\left(S_n\right)-2\hfill \\ & =& 2(n-1)+2\left[2\right(n-2)+1]+2\left[2\right(n-3)+2]-2\hfill \\ & =& 2n-2+4n-8+2+4n-12+4-2\hfill \\ & =& 10n-18.\hfill \end{array}$$

□

Next, we give the proof of Theorem 1.

Proof of Theorem 1.

First, we prove the right inequality in (2). Suppose that G contains a unique cycle of even length. Then, G is a bipartite graph. By Lemmas 6 and 7, the conclusion holds. Next we consider G contains a unique cycle of odd length. Suppose $G\ne C_n$, and $e=uv$ is an edge of the unique cycle in G. By Lemma 9, we have

$$\begin{array}{ccc}\hfill \mathrm{per}L\left(G\right)& =& \mathrm{per}L(G-e)+\mathrm{per}{L}_v(G-e)+\mathrm{per}{L}_u(G-e)\hfill \\ & & +2\mathrm{per}{L}_{uv}\left(G\right)+2\sum _{C\in {\mathcal{C}}_G\left(e\right)}{(-1)}^{\left|V\right(C\left)\right|}\mathrm{per}{L}_{V\left(C\right)}\left(G\right).\hfill \end{array}$$

(5)

It is obvious that the graph $G-e$ is a tree with n vertices. Therefore, by Lemmas 4, 5, 11, and 16, we have

$$\begin{array}{cc}& \mathrm{per}L(G-e)\le \mathrm{per}L\left(P_n\right),\\ & \mathrm{per}{L}_v(G-e)\le \mathrm{per}\left(B_{n-1}\right),\\ & \mathrm{per}{L}_u(G-e)\le \mathrm{per}\left(B_{n-1}\right),\\ & \mathrm{per}{L}_{uv}(G-e)<\mathrm{per}L\left(A_{n-2}\right),\\ & (-1)\mathrm{per}{L}_{V\left(C\right)}\left(G\right)\le -1.\end{array}$$

Hence

$$\begin{array}{ccc}\hfill \mathrm{per}L\left(G\right)& <& \mathrm{per}L\left(P_n\right)+2\mathrm{per}\left(B_{n-1}\right)+2\mathrm{per}L\left(A_{n-2}\right)\hfill \\ & =& {(1+\sqrt{2})}^n+{(1-\sqrt{2})}^n-2.\hfill \end{array}$$

Hence, for any $G\in {\mathcal{U}}_n$, we have

$$\begin{array}{ccc}\hfill \mathrm{per}L\left(G\right)& \le & \mathrm{per}L\left(P_n\right)+2\mathrm{per}\left(B_{n-1}\right)+2\mathrm{per}L\left(A_{n-2}\right)\hfill \\ & =& {(1+\sqrt{2})}^n+{(1-\sqrt{2})}^n+2\times {(-1)}^n.\hfill \end{array}$$

Next, we prove the left inequality in (2) by induction on $\left|V\right(G\left)\right|=n$. If $n=3$, since G is unicyclic graph, it follows from the definition of unicyclic graph that G is isomorphic to $C_3$. Hence, in this case our result holds. Next, we consider the case where $n\ge 4$. Assume that the result holds for $\left|V\right(G\left)\right|<n$. We will prove that it holds for $\left|V\right(G\left)\right|=n$. Suppose that there is no pendant vertex in G, then $G=C_n$. Obviously, $\mathrm{per}L\left(G\right)\ge 10n-18$. Therefore, assume that the unicyclic graph G has at least one pendant vertex $v_1$, and denote its neighbor by $v_2$. By Lemma 11, we have

$$\begin{array}{c}\hfill \mathrm{per}L\left(G\right)=\mathrm{per}L(G-v_1)+2\mathrm{per}{L}_{\{v_1,v_2\}}\left(G\right).\end{array}$$

(6)

Since $G-v_1\in {\mathcal{U}}_{n-1}$, by the induction hypothesis, we have

$$\begin{array}{c}\hfill \mathrm{per}L(G-v_1)\ge 10(n-1)-18=\mathrm{per}L\left(S_{n-1}^{*}\right).\end{array}$$

(7)

Suppose that $G\cong S_n^{*}$; the left inequality in (2) holds.

Suppose that $G\ncong S_n^{*}$. This implied that there is no vertex in G such that its degree is at least $n-1$. Hence

$$\begin{array}{c}\hfill d_3+d_4+\dots +d_{n-1}+d_n\ge 2n-(n-2+1)=n+1,\end{array}$$

(8)

where $d_i$ is the degree of $v_i$$(i=1,2,\dots ,n)$. By Lemma 17, we have

$$\begin{array}{c}\hfill 2\mathrm{per}{L}_{\{v_1,v_2\}}\left(G\right)\ge 2d_3\dots d_n.\end{array}$$

(9)

Since $G\in {\mathcal{U}}_n$, there are at least three vertices in G with a degree of at least 2, obviously, $d_2\ge 2$. Now assume that $v_s$ and $v_t$ are vertices in G satisfying $d_s\ge 2$ and $d_t\ge 2$$(2<s<t\le n)$. Suppose that $d_s=d_t=2$. Then there must exist a vertex $v_k(\ne v_2)$ such that $d_k\ge 2$. Otherwise $d_3+d_4+\dots +d_{n-1}+d_n=2+2+(n-4)=n<n+1$, which contradicts to (8). Therefore, by (9), we have

$$\begin{array}{c}\hfill 2\mathrm{per}{L}_{v_1{v}_2}\left(G\right)\ge 2d_s{d}_t{d}_k\ge 16.\end{array}$$

(10)

Suppose that $d_s\ge 2$ and $d_t>2$. By (9), we obtain that

$$\begin{array}{c}\hfill 2\mathrm{per}{L}_{v_1{v}_2}\left(G\right)\ge 2d_s{d}_t\ge 12.\end{array}$$

(11)

By (6), (7), (10), and (11), we have

$$\begin{array}{c}\hfill \mathrm{per}L\left(G\right)\ge 10(n-1)-18+12=10n-16>10n-18.\end{array}$$

The proof of the theorem is completed. □

4. Proof of Theorem 2

In this section, we will give the proof of Theorem 2. Before proceeding to the proof of Theorem 2, we first prove some lemmas.

Lemma 20.

Let n and k be positive integers. Then

$$\begin{array}{cc}& \mathrm{per}L\left(S_{n,k}^{*}\right)={\displaystyle \frac{1}{\sqrt{2}}}\times [{(1+\sqrt{2})}^{k-1}\times ((n-k+2)+(n-k+1)\sqrt{2})-{(1-\sqrt{2})}^{k-1}\\ & \times ((n-k+2)-(n-k+1)\sqrt{2}){]+2(-1)}^k.\end{array}$$

Proof. 

Assume that $u\in V\left(\left(S_{n,k}^{*}\right)\right)$ and $d\left(u\right)=n-k+2$. By Lemma 8, we have

$$\begin{array}{ccc}\hfill \mathrm{per}L\left(S_{n,k}^{*}\right)& =& d\left(u\right)\mathrm{per}{L}_u\left(S_{n,k}^{*}\right)+\sum _{v\in N\left(u\right)}\mathrm{per}{L}_{vu}\left(S_{n,k}^{*}\right)\hfill \\ & & +2\sum _{C\in {\mathcal{C}}_{S_{n,k}^{*}}\left(u\right)}{(-1)}^{\left|V\right(C\left)\right|}\mathrm{per}{L}_{V\left(C\right)}\left(S_{n,k}^{*}\right)\hfill \\ & =& (n-k+2)\mathrm{per}{A}_{k-1}+2\mathrm{per}{A}_{k-2}+{(-1)}^k\times 2+(n-k)\mathrm{per}{A}_{k-1}\hfill \\ & =& (2n-2k+2)\mathrm{per}{A}_{k-1}+2\mathrm{per}{A}_{k-2}+{(-1)}^k\times 2\hfill \\ & =& {\displaystyle \frac{1}{\sqrt{2}}}\times [{(1+\sqrt{2})}^{k-1}\times ((n-k+2)+(n-k+1)\sqrt{2})-{(1-\sqrt{2})}^{k-1}\hfill \\ & & \times ((n-k+2)-(n-k+1)\sqrt{2}){]+2(-1)}^k.\hfill \end{array}$$

The proof of the lemma is completed. □

Lemma 21.

Let n and k be positive integers. Then

$$\begin{array}{ccc}\hfill \mathrm{per}L\left(C_{n,k}\right)& =& {\displaystyle \frac{3}{4}}{(1+\sqrt{2})}^n+{\displaystyle \frac{3}{4}}{(1-\sqrt{2})}^n+[{\displaystyle \frac{1}{4}}{(1-\sqrt{2})}^k+{(-1)}^k]{(1+\sqrt{2})}^{n-k}\hfill \\ & +& [{\displaystyle \frac{1}{4}}{(1+\sqrt{2})}^k+{(-1)}^k]{(1-\sqrt{2})}^{n-k}.\hfill \end{array}$$

Proof. 

Suppose $e=uv$ is an edge of the unique cycle in $C_{n,k}$ and $d\left(u\right)=3$. By Lemma 9, we have

$$\begin{array}{ccc}\hfill \mathrm{per}L\left(C_{n,k}\right)& =& \mathrm{per}L(C_{n,k}-e)+\mathrm{per}{L}_v(C_{n,k}-e)+\mathrm{per}{L}_u(C_{n,k}-e)\hfill \\ & & +2\mathrm{per}{L}_{uv}\left(C_{n,k}\right)+2\sum _{C\in {\mathcal{C}}_{C_{n,k}}\left(e\right)}{(-1)}^{\left|V\right(C\left)\right|}\mathrm{per}{L}_{V\left(C\right)}\left(C_{n,k}\right)\hfill \\ & =& \mathrm{per}L\left(P_n\right)+\mathrm{per}{B}_{n-1}+\mathrm{per}{B}_{n-k}\mathrm{per}{B}_{k-1}\hfill \\ & & +2\mathrm{per}{A}_{k-2}\mathrm{per}{B}_{n-k}+2{(-1)}^k\mathrm{per}{B}_{n-k}.\hfill \end{array}$$

By Lemmas 4, 5 and (3), we have

$$\begin{array}{ccc}\hfill \mathrm{per}L\left(C_{n,k}\right)& =& {\displaystyle \frac{3}{4}}{(1+\sqrt{2})}^n+{\displaystyle \frac{3}{4}}{(1-\sqrt{2})}^n+[{\displaystyle \frac{1}{4}}{(1-\sqrt{2})}^k+{(-1)}^k]{(1+\sqrt{2})}^{n-k}\hfill \\ & & +[{\displaystyle \frac{1}{4}}{(1+\sqrt{2})}^k+{(-1)}^k]{(1-\sqrt{2})}^{n-k}.\hfill \end{array}$$

□

Definition 1.

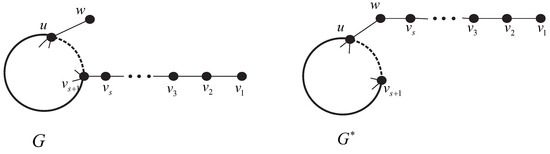
Let G be a unicyclic graph. Suppose that $P_{s+1}=v_1{v}_2\dots v_{s+1}$ is a pendant path of G satisfying $s\ge 1$, $d\left(v_1\right)=1$, and $d\left(v_{s+1}\right)\ge 3$. Assume $w(\ne v_1)$ is a pendant vertex of G. $U_{n-s-1}$ is a unicyclic graph obtained from G by deleting the vertices $v_1,v_2,\dots ,v_s$ and w. Let $G^{*}$ be a unicyclic graph obtained from G by deleting the edge $v_s{v}_{s+1}$ and adding the edge $w{v}_s$. These resulting graphs are illustrated in Figure 3. We say $G^{*}$ is obtained from G by  Operation 1.

Figure 3. $G\Rightarrow G^{*}$ by operation 1.

Lemma 22.

Let G and $G^{*}$ be two graphs defined as above. Then

$$\begin{array}{c}\hfill \mathrm{per}L\left(G^{*}\right)\ge \mathrm{per}L\left(G\right).\end{array}$$

Proof. 

Firstly, we assume that $v_{s+1}w\notin E\left(G\right)$. Given a proper sequence of the vertices of G: $v_1,v_2,\dots ,v_s,v_{s+1},w,\dots$, we have

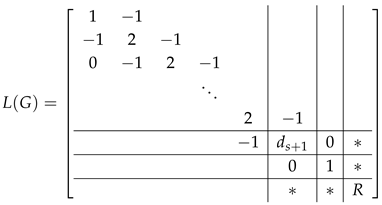and

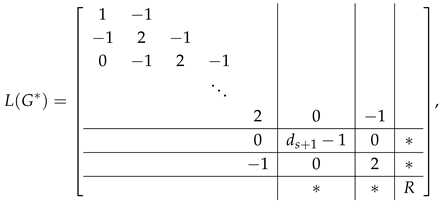where R is a matrix obtained from $L\left(G\right)$ by eliminating the first $s+2$ rows and $s+2$ columns. Let $M_1$(resp. $M_2$) be a matrix obtained from $L\left(G\right)$ (resp. $L\left(G^{*}\right)$) by eliminating the first s rows and s columns. Let $N_1$ (resp. $N_2$) denote the matrix obtained by deleting the first row and first column from $M_1$ (resp. the second row and second column from $M_2$). By Lemma 1, we have

$$\mathrm{per}{M}_1=\mathrm{per}{M}_2+\mathrm{per}{N}_1-\mathrm{per}{N}_2.$$

By expanding the permanent of $L\left(G\right)$ (resp. $L\left(G^{*}\right)$) along the first s rows we obtain

$$\begin{array}{ccc}\hfill \mathrm{per}L\left(G\right)& =& \mathrm{per}{B}_s·\mathrm{per}{M}_1+\mathrm{per}{B}_{s-1}·\mathrm{per}{N}_1,\hfill \\ \hfill \mathrm{per}L\left(G^{*}\right)& =& \mathrm{per}{B}_s·\mathrm{per}{M}_2+\mathrm{per}{B}_{s-1}·\mathrm{per}{N}_2.\hfill \end{array}$$

Hence

$$\begin{array}{ccc}\hfill \mathrm{per}L\left(G^{*}\right)-\mathrm{per}L\left(G\right)& =& \mathrm{per}{B}_s(\mathrm{per}{M}_2-\mathrm{per}{M}_1)+\mathrm{per}{B}_{s-1}(\mathrm{per}{N}_2-\mathrm{per}{N}_1)\hfill \\ & =& \mathrm{per}{B}_s(\mathrm{per}{N}_2-\mathrm{per}{N}_1)+\mathrm{per}{B}_{s-1}(\mathrm{per}{N}_2-\mathrm{per}{N}_1)\hfill \\ & =& (\mathrm{per}{B}_s+\mathrm{per}{B}_{s-1})\times (\mathrm{per}{N}_2-\mathrm{per}{N}_1)\hfill \\ & =& \mathrm{per}L\left(P_{s+1}\right)\times (\mathrm{per}{N}_2-\mathrm{per}{N}_1).\hfill \end{array}$$

(12)

By Lemma 2, we have $\mathrm{per}R\ge 0$. Note that $\mathrm{per}{N}_1<2\mathrm{per}R$ and $\mathrm{per}{N}_2>(d_{s+1}-1)\mathrm{per}R$. Hence

$$\begin{array}{c}\hfill \mathrm{per}{N}_2-\mathrm{per}{N}_1>(d_{s+1}-1)\mathrm{per}R-2\mathrm{per}R=(d_{s+1}-3)\mathrm{per}R\ge 0.\end{array}$$

(13)

By (12) and (13), we have $\mathrm{per}L\left(G^{*}\right)\ge \mathrm{per}L\left(G\right)$.

Now, let $v_{s+1}w\in E\left(G\right)$. Similarly, given a proper sequence of the vertices of G: $v_1,v_2,\dots ,v_s,v_{s+1},w,\dots$, we have

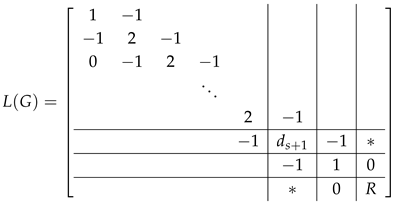and

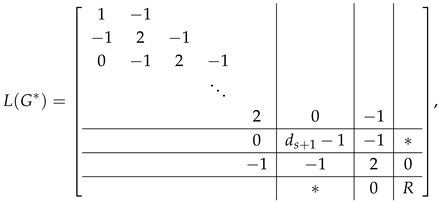where R is a matrix obtained from $L\left(G\right)$ by eliminating the first $s+2$ rows and $s+2$ columns. Let $M_1$(resp. $M_2$) be a matrix obtained from $L\left(G\right)$ (resp. $L\left(G^{*}\right)$) by eliminating the first s rows and s columns. Let $N_1$ (resp. $N_2$) denote the matrix obtained by deleting the first row and first column from $M_1$ (resp. the second row and second column from $M_2$). By Lemma 1, we have

$$\mathrm{per}{M}_1=\mathrm{per}{M}_2+\mathrm{per}{N}_1-\mathrm{per}{N}_2.$$

By expanding the permanent of $L\left(G\right)$ (resp. $L\left(G^{*}\right)$) along the first s rows we obtain

$$\begin{array}{ccc}\hfill \mathrm{per}L\left(G\right)& =& \mathrm{per}{B}_s·\mathrm{per}{M}_1+\mathrm{per}{B}_{s-1}·\mathrm{per}{N}_1,\hfill \\ \hfill \mathrm{per}L\left(G^{*}\right)& =& \mathrm{per}{B}_s·\mathrm{per}{M}_2+\mathrm{per}{B}_{s-1}·\mathrm{per}{N}_2.\hfill \end{array}$$

Hence

$$\begin{array}{ccc}\hfill \mathrm{per}L\left(G^{*}\right)-\mathrm{per}L\left(G\right)& =& \mathrm{per}{B}_s(\mathrm{per}{M}_2-\mathrm{per}{M}_1)+\mathrm{per}{B}_{s-1}(\mathrm{per}{N}_2-\mathrm{per}{N}_1)\hfill \\ & =& \mathrm{per}{B}_s(\mathrm{per}{N}_2-\mathrm{per}{N}_1)+\mathrm{per}{B}_{s-1}(\mathrm{per}{N}_2-\mathrm{per}{N}_1)\hfill \\ & =& (\mathrm{per}{B}_s+\mathrm{per}{B}_{s-1})\times (\mathrm{per}{N}_2-\mathrm{per}{N}_1)\hfill \\ & =& \mathrm{per}L\left(P_{s+1}\right)\times (\mathrm{per}{N}_2-\mathrm{per}{N}_1).\hfill \end{array}$$

(14)

By Lemma 2, we have $\mathrm{per}R\ge 0$. Note that $\mathrm{per}{N}_1=\mathrm{per}R$ and $\mathrm{per}{N}_2>(d_{s+1}-1)\mathrm{per}R$. Hence

$$\begin{array}{c}\hfill \mathrm{per}{N}_2-\mathrm{per}{N}_1>(d_{s+1}-1)\mathrm{per}R-\mathrm{per}R=(d_{s+1}-2)\mathrm{per}R\ge 0.\end{array}$$

(15)

By (14) and (15), we have $\mathrm{per}L\left(G^{*}\right)\ge \mathrm{per}L\left(G\right)$. □

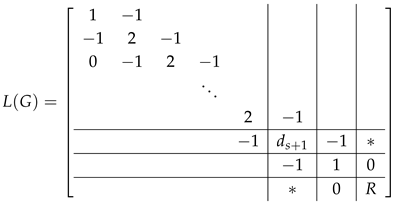
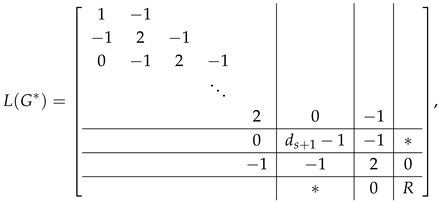
Proof of Theorem 2.

We prove the left inequality by induction on n. Set $G\cong S_{k,k}^{*}$. By Lemma 20, our result holds in this case. Set $G\ncong S_{k,k}^{*}$. Assume that the conclusion holds for all $\left|V\right(G\left)\right|<n$. Next, we prove that the conclusion holds when $\left|V\right(G\left)\right|=n$. Suppose that $v_1$ is a pendant vertex of G, and $v_1$ is adjacent to $v_2$. By Lemma 11, we have

$$\begin{array}{ccc}\hfill \mathrm{per}L\left(G\right)& =& \mathrm{per}L(G-v_1)+2\mathrm{per}{L}_{\{v_1,v_2\}}\left(G\right)\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill \mathrm{per}L\left(S_{n,k}^{*}\right)& =& \mathrm{per}L\left(S_{n-1,k}^{*}\right)+2\mathrm{per}{A}_{k-1}.\hfill \end{array}$$

Since $G-v_1\in {\mathcal{U}}_{n-1,k}$, by the induction hypothesis, we have

$$\begin{array}{c}\hfill \mathrm{per}L(G-v)\ge \mathrm{per}L\left(S_{n-1,k}^{*}\right).\end{array}$$

To prove that the conclusion holds, it suffices to prove that $\mathrm{per}{L}_{v_1{v}_2}\left(G\right)\ge \mathrm{per}{A}_{k-1}$. We distinguish two cases in the following.

Case 1. There exists at least one pendant vertex attached to the induced cycle $C_k$ in G. In this case, suppose that $v_2\in V\left(C_k\right)$, and the other vertices of the induced cycle $C_k$ in G are labeled by $v_{n-k+1},v_{n-k+2},\dots ,v_{n-1},v_n$. Then, $L_{\{v_1,v_2\}}\left(G\right)$ contains a submatrix $H_0$, where

$$H_0=\left[\begin{array}{c}\begin{array}{ccccc}{d}_{n-k+1}& -1& \dots & 0& 0\\ -1& d_{n-k+2}& \dots & 0& 0\\ ⋮& ⋮& \ddots & ⋮& ⋮\\ 0& 0& \dots & d_{n-1}& -1\\ 0& 0& \dots & -1& d_n\end{array}\end{array}\right].$$

By proof of Lemma 17, we have $L_{\{v_1,v_2\}}\left(G\right)$ as a submatrix of the Laplacian matrix of a tree; hence, each term of $\mathrm{per}{L}_{\{v_1,v_2\}}\left(G\right)$ is non-negative. Hence, $\mathrm{per}{L}_{\{v_1,v_2\}}\left(G\right)\ge \mathrm{per}{H}_0\ge \mathrm{per}{A}_{k-1}$.

Case 2. A pendant vertex attached to the induced cycle $C_k$ in G does not exist. In this case, by an appropriate labeling of the vertices of G, the vertices of the induced cycle $C_k$ are labeled successively by $v_{n-k},v_{n-k+1},\dots ,v_{n-1},v_n$. By Lemma 10, we have

$$\begin{array}{ccc}\hfill \mathrm{per}{L}_{\{v_1,v_2\}}\left(G\right)& =& d\left(v_{n-k}\right)\mathrm{per}{L}_{\{v_1,v_2\}\cup \left\{v_{n-k}\right\}}\left(G\right)\hfill \\ & & +\sum _{v_{n-k}{v}_i\in E\left(G\right)}\mathrm{per}{L}_{\{v_1,v_2\}\cup \{v_{n-k},v_i\}}\left(G\right)\hfill \\ & & +2\times {(-1)}^{\left|V\right(C\left)\right|}\mathrm{per}{L}_{V\left(C\right)\cup \{v_1,v_2\}}\left(G\right).\hfill \end{array}$$

Since each term of $\mathrm{per}{L}_{\{v_1,v_2\}\cup \left\{v_{n-k}\right\}}\left(G\right)$ is non-negative and $L_{\{v_1,v_2\}\cup \left\{v_{n-k}\right\}}\left(G\right)$ has a submatrix $H_0$, we have

$$\mathrm{per}{L}_{\{v_1,v_2\}\cup \left\{v_{n-k}\right\}}\left(G\right)\ge \mathrm{per}{H}_0\ge \mathrm{per}{A}_{k-1}.$$

By the proof of Lemma 17, we have

$$\sum _{v_{n-k}{v}_i\in E\left(G\right)}\mathrm{per}{L}_{\{v_1,v_2\}\cup \{v_{n-k},v_i\}}\left(G\right)\ge 2\mathrm{per}{L}_{V\left(C\right)\cup \{v_1,v_2\}}\left(G\right).$$

Hence

$$\mathrm{per}{L}_{\{v_1,v_2\}}\left(G\right)\ge \mathrm{per}{L}_{\{v_1,v_2\}\cup \left\{v_{n-k}\right\}}\left(G\right)\ge \mathrm{per}{H}_0\ge \mathrm{per}{A}_{k-1}.$$

In conclusion,

$$\mathrm{per}{L}_{\{v_1,v_2\}}\left(G\right)\ge \mathrm{per}{A}_{k-1}.$$

Next, we prove the right inequality. Suppose that the graph G has exactly one pendant vertex. By $G\in {\mathcal{U}}_{n,k}$, according to the properties of this graph class, we can conclude that $G\cong C_{n,k}$, and thus the theorem holds. Suppose that G has at least two pendent vertices. In the first step, by Operation 1, the subtrees hanging on the vertex in induced cycle $C_k$ of G are transformed into paths with the corresponding number of vertices. Repeated applications of Operation 1, transform all subtrees hanging on the vertex in induced cycle $C_k$ of G into pendant paths. In the second step, by applying Operation 1 to merge the aforementioned pendant paths, we successfully derive the extremal graph $C_{n,k}$. By Lemma 22, it can be known that the right inequality holds. □

5. Conclusions

In this work, we establish rigorous bounds for Laplacian permanents of unicyclic graphs and provide a complete resolution to Problem 1. Meanwhile, we completely characterize the bounds of unicyclic graphs with a given girth. Notably, our derived bounds for Laplacian permanents differ fundamentally from those established by Li and Zhang [12] for unsigned Laplacian permanents in analogous graph structures. The bounds presented in this paper accurately express the value of the Laplacian permanent of unicyclic graphs, which is extremely difficult given that the computation of the Laplacian matrix permanent is #P-complete. Additionally, they provide an effective theoretical basis for researching the accuracy of permanent approximation algorithms. Building upon Brualdi’s open problem regarding matrix permanents [9], we identify several promising research directions in this domain. Specifically, characterizing extremal values of Laplacian permanents under structural constraints including fixed matching numbers, bipartition parameters, and diameter bounds emerges as particularly compelling. These problems will constitute the primary focus of subsequent investigations, potentially yielding new insights into the combinatorial properties of graph permanents.