On Subprojectivity of Goldie Torsion Modules

Abstract

Recently, the concept of subprojectivity domains for modules has been introduced as a means of quantifying the level of projectivity exhibited by a module. In this research article, we focus on the subprojectivity domain of Goldie torsion modules. In particular, we establish that a ring denoted as R is classified as right nonsingular if and only if the subprojectivity domain of each Goldie torsion module is closed under submodules. In addition, we demonstrate that a right C-ring is a right nonsingular ring if and only if every module possesses an epic ecf-flat envelope, which is further equivalent to each Goldie torsion module having an epic projective envelope.

1. Introduction

In this article, we assume that all rings are associative with an identity, and all modules are unital right modules. Throughout the text, unless explicitly stated otherwise, the symbol R represents a ring. The notations $E\left(A\right)$, $Soc\left(A\right)$, $Z\left(A\right)$, and $Z_2\left(A\right)$ denote the injective hull, socle, singular, and Goldie torsion submodule of a module A, respectively. We use the term $Mod-R$ to refer to the category of all right modules over a ring R. For comprehensive definitions, theorems, and notations, we recommend consulting the references [1,2,3].

A submodule A of an R-module X is considered essential (or large) in X if, for any non-zero submodule B of X, their intersection $A\cap B$ is non-zero. Within an R-module X, the singular submodule $Z\left(X\right)$ is defined as the set of elements $x\in X$ satisfying $xJ=0$ for some essential right ideal J of R. If $Z\left(X\right)$ equals the entire module X, then X is referred to as a singular module. Conversely, if $Z\left(X\right)$ is zero, then X is termed a nonsingular module. The Goldie torsion submodule, also known as the second singular submodule $Z_2\left(X\right)$, of a module X is defined as $Z(X/Z\left(X\right))=Z_2\left(X\right)/Z\left(X\right)$. That is, the second singular submodule $Z_2\left(M\right)$ of M is the preimage of the singular submodule of the factor module $M/Z\left(M\right)$. The functor Z is a left exact preradical, which in general is not a radical. However, $Z_2$ is a left exact radical, known as the singular radical of X. If a module X coincides with its second singular submodule, namely $X=Z_2\left(X\right)$, it is called a Goldie torsion module (or $Z_2$-torsion module). Notably, every singular module is trivially a Goldie torsion module. For more details, see [4,5].

The collection of Goldie torsion modules forms a torsion class within Goldie torsion theory, and this class is generated by all singular modules. On the other hand, the class of nonsingular modules corresponds to the torsion-free class in the same torsion theory. Notably, for any right nonsingular ring R, the singular submodule and the second singular submodule of any right R-module X coincide. The class of Goldie torsion modules exhibits closure properties under submodules, factor modules, extensions, and arbitrary direct sums. In contrast, the class of nonsingular modules demonstrates closure under submodules, direct products, extensions, and injective envelopes. For further information, the reader is referred to Chapter 1 of [6].

A submodule B of A is said to be closed in A if B has no proper essential extension in A. The concept of closed submodules has been extensively investigated in the context of torsion theory, as documented in works such as [7]. Another generalization of closed submodules, termed s-closed submodules, has also been studied [8]. An s-closed submodule of a module A is one for which the quotient module $A/B$ is nonsingular. It is worth noting that every s-closed submodule is closed, and any closed submodule of a nonsingular module is s-closed, as established in ([9], Lemma 2.3).

In the context of short exact sequences, denoted by $0\to X{\to }^{\beta }Y\to Z\to 0$, a sequence is considered closed (or s-closed) exact if the image of the map $\beta$ yields a closed (or s-closed) submodule in Y. The class of closed short exact sequences forms a proper class, following Buchsbaum’s definition. However, it should be noted that the class of s-closed short exact sequences may not necessarily be a proper class, as demonstrated in ([10], Example 3.1). In order to examine the minimal proper class encompassing all short exact sequences determined by s-closed submodules, the notion of an es-closed submodule was introduced in [10].

A submodule A of a module Y is defined as es-closed in Y if there exists a submodule B of Y such that $B\cap A=0$ and the quotient module ${\displaystyle \frac{Y}{B\oplus A}}$ is nonsingular. When considering a short exact sequence $0\to X{\to }^{\beta }Y\to Z\to 0$, the sequence is referred to as es-closed if the image of the map $\beta$ yields an es-closed submodule in Y. It has been established in ([10], Proposition 3.4) that a submodule A of a module Y is es-closed in Y if and only if the sequence $Hom(G,Y)\to Hom(G,Y/A)\to 0$ is exact for every Goldie torsion module G ([10], Propositions 3.3–3.4).

An R-module S is considered flat if the kernel of any epimorphism $N\to S$ is pure in N. In other words, the induced map $Hom(G,N)\to Hom(G,S)$ is an epimorphism for any finitely presented R-module G ([11], 34.5). Building upon the concept of flat modules, various torsion-theoretic versions of flat modules have been introduced and explored (see, for instance, [12]). An R-module M is termed an es-closed flat module (or simply a ecf-module) if the kernel of any epimorphism $N\to M$ is es-closed in N. In other words, every short exact sequence ending with Y is an es-closed sequence [10]. Examples of ecf-modules include nonsingular modules and projective modules.

Projective modules are fundamental concepts in ring and module theory, as well as in homological algebra. They play a crucial role in understanding the structure of modules over a ring and characterizing certain rings in terms of these modules. Recently, many authors have studied these concepts from different perspectives. A module M is said to be N-projective (or projective relative to N) if for every monomorphism $g:K\to M$ and every homomorphism $f:K\to N$, there exists a homomorphism $h:M\to N$ with $hg=f$. By definition, an R-module M is projective if and only if it is projective relative to every module in $Mod-R$. In order to consider the extent to which a given module is projective in the sense that projective modules are the most projective, the notion of a projectivity domain is employed, as defined in ([13], §16). The projectivity domain of M is defined to be the class of those right R-modules N such that M is projective relative to N, and this is denoted by ${\mathfrak{Pr}}^{-1}\left(M\right)$. It follows that M is projective if and only if ${\mathfrak{Pr}}^{-1}\left(M\right)=Mod-R$. Note that the projectivity domain of every R-module contains the class of all semisimple modules. In [14], it was shown that, for any ring R, there exist R-modules whose projectivity domains consist of only semisimple modules. Following [14], such modules are called p-poor modules. Recent research has focused on various aspects of projectivity domains. In particular, modules whose projectivity domains are contained within the class of all pure-split modules were investigated in [15]. The projectivity domains of simple modules over commutative rings were examined in [16], while [17] explored the projectivity domains of pure-projective modules.

In contrast to the notion of relative projectivity, the notion of a subprojectivity domain was first introduced in [18], enabling the study of module projectivity from a new perspective. Specifically, given two modules S and T, we say that S is T-subprojective if, for every epimorphism $g:K\to T$ and every homomorphism $f:S\to T$, there exists a homomorphism $h:S\to K$ such that $gh=f$. In other words, S can be mapped to T via a composition with the epimorphism g. For a given module Y, its subprojectivity domain, denoted by ${\underline{\mathfrak{Pr}}}^{-1}\left(Y\right)$, consists of all modules X for which Y is X-subprojective. In other words, the subprojectivity domain of Y encompasses all modules X that can be mapped to Y through suitable homomorphisms. It is worth noting that a module is projective if and only if its subprojectivity domain includes all modules, indicating the broadest possible range of subprojectivity. In recent studies, the projectivity of finitely generated modules has been analyzed through the lens of subprojectivity domains in [19]. Objects possessing minimal (sub)projectivity domains within exact categories were explored in [20]. Additionally, subprojectivity was investigated within the broader framework of abelian categories in [21,22].

In this paper, our focus was on studying the key properties of the subprojectivity domain of Goldie torsion modules. Our findings include the following: The subprojectivity domain of every Goldie torsion module is closed under submodules if and only if R is a right nonsingular ring. The arbitrary product of any ecf-modules is an ecf-module if and only if the subprojectivity domain of any Goldie torsion module is closed under arbitrary products. Moreover, we establish that a right C-ring R is a right nonsingular ring if and only if every Goldie torsion module has an epic projective envelope. In the last section, we study the family of subprojectivity domains of Goldie torsion modules.

2. On Subprojectivity of Goldie Torsion Modules

Let us open this section with the following proposition, which gives the characterization of an ecf-module.

Proposition 1

([10], Proposition 4.1). A module S is an ecf-module if and only if there is an es-closed sequence $0\to T\to P\to S\to 0$ with P ecf-module.

It is evident that a nonsingular module is an ecf-module, but the converse needs not hold in general. For instance, if R is not a right nonsingular ring, then there exists a projective right R-module P that is an ecf-module but not nonsingular. We will now establish a useful proposition that will aid in proving that every Goldie torsion module has an epic projective envelope on a nonsingular ring.

Proposition 2

([10], Proposition 4.14). For any arbitrary ring R, the following statements are equivalent:

(i) 

R is a right nonsingular ring.

(ii) 

ecf-modules are nonsingular.

(iii) 

ecf-modules are closed under submodules.

(iv) 

Every right ideal of R is an ecf-module.

The next result clarifies how the structure of a right nonsingular ring influences the subprojectivity domain of a Goldie torsion module.

Lemma 1.

Let R be a ring. Then, R is a right nonsingular ring if and only if the subprojectivity domain of every Goldie torsion R-module is closed under submodules.

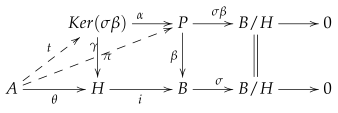
Proof. 

Let R be a right nonsingular ring. Consider a Goldie torsion R-module A that is B-subprojective for an R-module B. Let $i:H\to B$ be an inclusion homomorphism, where H is a submodule of B.

Now, let us introduce an epimorphism $\beta :P\to B$, where P is a free module. We can then construct the following commutative diagram:

Now, $B\in {\underline{\mathfrak{Pr}}}^{-1}\left(A\right)$ implies the existence of a homomorphism $\gamma :A\to P$ such that $i\theta =\beta \gamma$, where $\theta :A\to H$ is any homomorphism. Clearly, $\sigma \beta \gamma =\sigma i\theta =0$. Therefore, using the factor theorem, we obtain a homomorphism $t:A\to ker\left(\sigma \beta \right)$ such that $\alpha t=\gamma$, where $\alpha :ker\left(\sigma \beta \right)\to P$ is the inclusion homomorphism. In addition, since $i\theta =\beta \gamma =\beta \alpha t=i\pi t$ and i is an inclusion homomorphism, then $\theta =\pi t$. Note that P is ecf-flat, and hence the submodule $Ker\left(\sigma \beta \right)$ of P is an ecf-module by Proposition 2. Thus, by ([23], Proposition 2.1), we can conclude that $H\in {\underline{\mathfrak{Pr}}}^{-1}\left(A\right)$, as desired.

For the converse, let us assume that the subprojectivity domain of every Goldie torsion module is closed under submodules. In particular, this implies that $Z\left(R_R\right)\in {\underline{\mathfrak{Pr}}}^{-1}\left(Z\left(R_R\right)\right)$, since $Z\left(R_R\right)$ is a submodule of $R_R$ and $R_R\in {\underline{\mathfrak{Pr}}}^{-1}\left(Z\left(R_R\right)\right)$. By definition, this means that $Z\left(R_R\right)$ is projective according to ([18], Proposition 2.4). However, the only projective singular module is the zero module. Therefore, we conclude that $Z\left(R_R\right)=0$. Hence, we have established the desired result.

Corollary 1.

Let R be a right nonsingular ring, S be a singular R-module, and T be an arbitrary R-module. Then, $T\in {\underline{\mathfrak{Pr}}}^{-1}\left(S\right)$ if and only if $Z_2\left(T\right)\in {\underline{\mathfrak{Pr}}}^{-1}\left(S\right)$.

Proof. 

If $T\in {\underline{\mathfrak{Pr}}}^{-1}\left(S\right)$, then $Z_2\left(T\right)\in {\underline{\mathfrak{Pr}}}^{-1}\left(S\right)$ by Lemma 1. Conversely, assume that $Z_2\left(T\right)\in {\underline{\mathfrak{Pr}}}^{-1}\left(S\right)$. Consider the short exact sequence $0\to Z_2\left(T\right)\to T\to T/Z_2\left(T\right)\to 0$. Let us point out that $T/Z_2\left(T\right)$ is nonsingular, and so it is an ecf-module. Now, the claim follows from the fact that ${\underline{\mathfrak{Pr}}}^{-1}\left(S\right)$ is closed under extension. □

Let $\mathcal{C}$ be a class of R-modules and M be an R-module. A homomorphism $\sigma :M\to X$ is defined as a $\mathcal{C}$-preenvelope if $X\in \mathcal{C}$ and for each $Y\in \mathcal{C}$, the induced map $\mathrm{Hom}(\sigma ,Y):{\mathrm{Hom}}_R(X,Y)\to {\mathrm{Hom}}_R(M,Y)$ is an epimorphism. A $\mathcal{C}$-preenvelope $\sigma :M\to X$ is referred to as a $\mathcal{C}$-envelop module if $g\sigma =\sigma$ for every endomorphism $g:X\to X$.

A module S is said to be simple-projective if, for every simple (singular) module T, any homomorphism $\mu :T\to S$ can be factored through a Goldie torsion-free module K (see [24]). In other words, S is simple-projective if and only if T is S-subprojective for every (singular) simple module T. As a result, ecf-modules are considered simple-projective, due to their property of being subprojective for all (singular) simple modules T.

A ring R is referred to as a right C-ring if $R/I$ is semiartinian for every essential right ideal I of R (see, for example, ([4], 10.10)). On the other hand, a ring R is considered a right PS-ring if the socle $Soc\left(R_R\right)$ is projective [25]. It is worth noting that any right nonsingular ring is also a right PS-ring.

The theorem below presents a new characterization of right nonsingular rings using the projective envelope of Goldie torsion modules.

Theorem 1.

The equivalence of the following statements holds for any right C-ring R:

(i) 

R is a right nonsingular ring.

(ii) 

Every module has an epic ecf-module envelope.

(iii) 

Every Goldie torsion module has an epic projective envelope.

(iv) 

ecf-modules are closed under submodules.

Proof. 

$\left(i\right)\Rightarrow \left(ii\right)$ Since R is right PS, every right module has an epic simple-projective envelope by ([24], Theorem 3.7). We claim that simple-projective modules and ecf-modules are the same. As we noted before, ecf-modules are simple-projective. Now let S be a simple-projective module. By Proposition 2 and the nonsingularity of R, it suffices to show that S is nonsingular. Assume the contrary, that S is not nonsingular. Then, S has a nonzero singular submodule, say G. By our hypothesis, R is a right C-ring, and so G is semiartinian. Then there is a simple submodule V of G. Then, since S is simple-projective, V is simple-projective as a submodule of S by ([24], Theorem 3.7). But V is both simple and simple-projective, and so it must be projective by ([24], Remark 2.2(3)). This contradicts the fact that V is a nonzero singular. Hence, S must be nonsingular.

$\left(ii\right)\Rightarrow \left(iii\right)$ Let G be a Goldie torsion module. By $\left(ii\right)$, there exists an epic ecf-module envelope $\mu :G\to K$. There exists an epimorphism $\sigma :P\to K$ with P a free module. Since K is ecf-module, there exists a $\lambda :G\to P$ such that $\sigma \lambda =\mu .$ Again, since P is an ecf-module and $\mu :G\to K$ is an ecf-module envelope, there is a homomorphism $\beta :K\to P$ such that $\beta \mu =\lambda$. Since $\mu$ is epic and $\mu =\sigma \lambda =\sigma \beta \mu$, then $\sigma \beta =1_K$. This implies that $P\cong K\oplus X$ for some R-module X. Then, K is a projective module. Therefore, $\mu$ is an epic projective envelope of $G.$

$\left(iii\right)\Rightarrow \left(iv\right)$ Let Y be an flat module and A a submodule of Y. Let G be a Goldie torsion module and $f:G\to A$ any homomorphism. Given that Y is an ecf-module, we can find a homomorphism $\pi :G\to F$ such that $h\pi =if$ holds for any epimorphism $h:F\to Y$ with F being a free module. Additionally, according to the hypothesis, G possesses an epic projective envelope $g:G\to P$, with P being a projective module. Consequently, there exists a homomorphism $\theta :P\to F$ such that $\theta g=\pi$. It is important to note that $f=if=h\pi =h\theta g$ where $i:A\hookrightarrow Y$ represents the inclusion homomorphism. Then, $ker\left(g\right)\subset ker\left(f\right)$. By the factor theorem, we have an epimorphism $\psi :P\to A$ such that $\psi g=f$. There exists an epimorphism $\beta :T\to A$ with T free. By the projectivity of P, we have $\gamma :P\to T$ such that $\beta \gamma =\psi .$ Then, $f=\psi g=\left(\beta \gamma \right)g=\beta \left(\gamma g\right)$. Therefore, A is an ecf-module, as desired. Finally, $\left(iv\right)\Rightarrow \left(i\right)$ is an immediate using Proposition 2. □

Lemma 2.

The following statements are equivalent:

(i) 

Arbitrary products of ecf-module modules are ecf-modules.

(ii) 

For any Goldie torsion module G, ${\underline{\mathfrak{Pr}}}^{-1}\left(G\right)$ is closed under an arbitrary product.

(iii) 

An arbitrary product of projective modules is an ecf-module.

Proof. 

$\left(i\right)\Rightarrow \left(ii\right)$ Let G be a Goldie torsion module and ${\left\{Y_j\right\}}_{j\in J}$ be a set of modules in ${\underline{\mathfrak{Pr}}}^{-1}\left(G\right)$. Let $\alpha ={\left({\alpha }_j\right)}_{j\in J}:G\to {\prod }_{j\in J}{Y}_j$ be a homomorphism. There is a projective module $P_j$ and an epimorphism ${\theta }_j:P_j\to Y_j$ for every $j\in J$. $Y_j\in {\underline{\mathfrak{Pr}}}^{-1}\left(G\right)$ implies the existence of a homomorphism ${\gamma }_j:G\to P_j$ such that ${\alpha }_j={\theta }_j{\gamma }_j$ for every $j\in J$. We can define a homomorphism $\theta :{\prod }_{j\in J}{P}_j\to {\prod }_{j\in J}{Y}_j$ via $\theta {\left(x_j\right)}_{j\in J}={\left({\theta }_j\left(x_j\right)\right)}_{j\in J}$. Then, $\theta$ is an epimorphism and $\theta \gamma =\alpha$, which $\gamma ={\left({\gamma }_j\right)}_{j\in J}:G\to {\prod }_{j\in J}{P}_j$ is a homomorphism. From the hypothesis, observe that ${\prod }_{j\in J}{P}_j$ is an ecf-module. Then, G is ${\prod }_{j\in J}{Y}_j$-subprojective by ([23], Proposition 2.1).

The implications of $\left(ii\right)\Rightarrow \left(i\right)$ and $\left(i\right)\Rightarrow \left(iii\right)$ are straightforward. $\left(iii\right)\Rightarrow \left(i\right)$ Let ${\left\{B_j\right\}}_{j\in J}$ be a set of ecf-modules and ${\left\{P_j\right\}}_{j\in J}$ be a set of projective modules. By assumption, ${\prod }_{j\in J}{P}_j$ is an ecf-module. To see the continuation of the proof, we follow a similar proof as $\left(i\right)\Rightarrow \left(ii\right)$, then apply ([23], Proposition 2.1). Consequently, ${\prod }_{j\in J}{B}_j\in {\underline{\mathfrak{Pr}}}^{-1}\left(G\right)$ for every Goldie torsion module G. This means that the arbitrary product ${\prod }_{j\in J}{B}_j$ is an ecf-module, as desired. □

Proposition 3.

Let U be an injective module and G be any Goldie torsion module. Then, $U\in {\underline{\mathfrak{Pr}}}^{-1}\left(G\right)$ if and only if $Z_2\left(U\right)\in {\underline{\mathfrak{Pr}}}^{-1}\left(G\right)$.

Proof. 

Suppose that $U\in {\underline{\mathfrak{Pr}}}^{-1}\left(G\right)$. Consider the short exact sequence $0\to Z_2\left(U\right)\to U\to U/Z_2\left(U\right)\to 0$. Since $U/Z_2\left(U\right)$ is a nonsingular module, it follows that $Z_2\left(U\right)$ is closed in U by ([9], Lemma 2.3). Note that every closed submodule of every injective module is injective. Hence, $U=Z_2\left(U\right)\oplus K$ for some submodule K of U. Since $U\in {\underline{\mathfrak{Pr}}}^{-1}\left(G\right)$ and ${\underline{\mathfrak{Pr}}}^{-1}\left(G\right)$ is closed under direct summands, $Z_2\left(U\right)\in {\underline{\mathfrak{Pr}}}^{-1}\left(G\right)$. Conversely, assume that $Z_2\left(U\right)\in {\underline{\mathfrak{Pr}}}^{-1}\left(G\right)$. Consider the short exact sequence $0\to Z_2\left(U\right)\to U\to U/Z_2\left(U\right)\to 0$. Here, $U/Z_2\left(U\right)\in {\underline{\mathfrak{Pr}}}^{-1}\left(G\right)$ because $U/Z_2\left(U\right)$ is nonsingular. Since ${\underline{\mathfrak{Pr}}}^{-1}\left(G\right)$ is closed under extensions, $U\in {\underline{\mathfrak{Pr}}}^{-1}\left(G\right)$. □

The proof of the next proposition is straightforward, so we skip it.

Proposition 4.

Let R be a right nonsingular ring. An R-singular module Z is M-subprojective if and only if $Hom(Z,M)=0$ for any R-module $M.$

Proposition 5.

Let R be a right nonsingular ring, let S be any singular R-module and M be any R-module. If S is M-subprojective, then $S/A$ is M-subprojective for any submodule A of $S.$

Proof. 

If S is M-subprojective, then $Hom(S,M)=0$ by Proposition 4. Using the factor theorem, it follows that $Hom(S/A,M)=0$, and hence $S/A$ is M-subprojective, as desired. □

Modules whose subprojectivity domain is as small as possible are referred to as projectively indigent (p-indigent) in [18]. According to ([10], Proposition 3.4.), the smallest subprojectivity domain for a Goldie torsion module must contain the class of all ecf-flat modules.

Definition 1.

We will refer to a Goldie torsion module X as gp-indigent if its subprojectivity domain consists precisely of ecf-modules. In other words, a Goldie torsion module X is gp-indigent if and only if ${\underline{\mathfrak{Pr}}}^{-1}\left(X\right)=\{Y\in Mod-R\mid Y\mathit{is}\mathit{an}\mathit{ecf}\text{-}\mathit{module}\}$.

The following result follows directly from the definition of ecf-flat modules.

Proposition 6.

${\bigcap }_{X\in \mathcal{G}}{\underline{\mathfrak{Pr}}}^{-1}\left(X\right)=\{Y\in Mod-R\mid Y\mathit{is}\mathit{ecf}\text{-}\mathit{flat}\}$, where $\mathcal{G}$ is the class of all Goldie torsion modules.

The existence of gp-indigent modules can be characterized by the following proposition.

Proposition 7.

Suppose that R is a right nonsingular ring and $\mathcal{F}$ is the set of all representatives of cyclic singular R-modules. Then, ${\oplus }_{G_i\in \mathcal{F}}{G}_i$ is gp-indigent.

Proof. 

Let $\mathcal{F}$ be the set of all representatives of cyclic singular modules, and let $X\in {\underline{\mathfrak{Pr}}}^{-1}\left({\oplus }_{G_i\in \mathcal{F}}{G}_i\right)$. According to Proposition 4 and the nonsingularity of R, we can conclude that $X\in {\underline{\mathfrak{Pr}}}^{-1}\left(G_i\right)$ for each cyclic singular module $G_i$ in $\mathcal{F}$. By ([6], Theorem 1.2.14), it follows that $Hom(G_i,X)=0$ for each cyclic singular module $G_i$. Therefore, X is a nonsingular module. Consequently, X is also ecf-flat. □

Proposition 8.

Let R be a right nonsingular ring, and let $\mathcal{F}$ be the set of all representatives of simple singular R-modules. Then, ${\oplus }_{G_i\in \mathcal{F}}{G}_i$ is gp-indigent if and only if R is right C-ring.

Proof. 

For the sufficiency, suppose that $X\in {\underline{\mathfrak{Pr}}}^{-1}\left({\oplus }_{G_i\in \mathcal{F}}{G}_i\right)$. This means that $X\in {\underline{\mathfrak{Pr}}}^{-1}\left(G_i\right)$ for each simple singular module $G_i$ in $\mathcal{F}$. Using Proposition 4 and the nonsingularity of R, we can conclude that $Hom(G_i,X)=0$.

Assume, for contradiction, that $Z\left(X\right)\ne 0$. Since R is a right C-ring, this implies that $Hom(G_i,Z\left(X\right))\ne 0$ for some $G_i\in \mathcal{F}$. However, this contradicts the fact that $Hom(G_i,X)=0$ for all $G_i\in \mathcal{F}$. Therefore, we must have $Z\left(X\right)=0$, which means that X is a nonsingular module. By Proposition 2, we can conclude that X is ecf-flat, as desired. The necessity follows directly from Proposition 4 and the given assumption. □

3. Subprojectivity Profile of Goldie Torsion Modules

This section is dedicated to exploring the family of subprojectivity domains associated with Goldie torsion modules. A class $\mathcal{A}$ of R-modules is termed sp-portfolio if there exists an R-module M such that $\mathcal{A}$ coincides with ${\underline{\mathfrak{Pr}}}^{-1}\left(M\right)$. The (right) subprojective profile, often abbreviated as sp-profile, of a class $\mathcal{M}$ of modules is defined as

$$\mathfrak{spP}\left(\mathcal{M}\right)=\left\{\mathcal{A}\subseteq \mathrm{Mod}-R:\mathcal{A}={\underline{\mathfrak{Pr}}}^{-1}\left(M\right)\mathrm{for}\mathrm{some}M\in \mathcal{M}\right\}.$$

Since the zero module 0 in ${\mathcal{T}}_G$, ${\underline{\mathfrak{Pr}}}^{-1}\left(0\right)=Mod-R\in \mathfrak{spP}\left({\mathcal{T}}_G\right)$. Note that we do not know whether the class $\mathcal{ECF}$ of ecf-modules is an sp-portfolio in general. But if R is right nonsingular, the class $\mathcal{ECF}$ is in ${\mathcal{T}}_G$ by Proposition 7. $\mathfrak{spP}\left({\mathcal{T}}_G\right)$ is always contained in $\mathfrak{spP}(Mod-R)$; it is natural to ask when these two classes coincide. The next lemma addresses this question.

A submodule A of an R-module B is called closed in B if it does not have any proper essential extension within B. A module M is defined as CS if all its closed submodules are direct summands. Furthermore, M is termed $\Sigma$-CS if every direct sum of copies of M is itself a $CS$ module. The ring R is considered right $\Sigma$-$CS$ if and only if every projective right R-module is $CS$ [5].

Lemma 3.

If R is a right Σ-CS ring, then $\mathfrak{spP}\left({\mathcal{T}}_G\right)=\mathfrak{spP}(Mod-R)$. In particular, the converse holds if R is right nonsingular.

Proof. 

It is clear that $\mathfrak{spP}\left({\mathcal{T}}_G\right)\subseteq \mathfrak{spP}(Mod-R)$. Let us assume that ${\underline{\mathfrak{Pr}}}^{-1}\left(X\right)\in \mathfrak{spP}(Mod-R)$ for some right R-module X. By ([26], Theorem II), the module X decomposes as a direct sum $X=P\oplus Z$, where P is projective and Z is singular. It follows that ${\underline{\mathfrak{Pr}}}^{-1}\left(X\right)={\underline{\mathfrak{Pr}}}^{-1}\left(P\right)\cap {\underline{\mathfrak{Pr}}}^{-1}\left(Z\right)=Mod-R\cap {\underline{\mathfrak{Pr}}}^{-1}\left(Z\right)={\underline{\mathfrak{Pr}}}^{-1}\left(Z\right)\in \mathfrak{spP}\left({\mathcal{T}}_G\right).$

Now, assume that R is a right nonsingular ring. Since $\mathfrak{spP}\left({\mathcal{T}}_G\right)=\mathfrak{spP}(Mod-R)$, we have $\mathcal{ECF}={\bigcap }_{\mathcal{A}\in \mathfrak{spP}\left({\mathcal{T}}_G\right)}\mathcal{A}={\bigcap }_{\mathcal{A}\in \mathfrak{spP}(Mod-R)}\mathcal{A}=\mathcal{PR},$ by ([18], Proposition 2.8) and ([27], Proposition 1).

Let K be a closed submodule of a projective module F. We claim that K is a direct summand of F. By ([9], Lemma 2.3(b)), the quotient $F/K$ is nonsingular. Since every nonsingular module is ec-flat, it follows from the preceding paragraph that $F/K$ is projective. Hence, K is a direct summand of F, as claimed. □

A ring R is called a right SI-ring if every singular right R-module is injective. A ring R is a right SI-ring if and only if every R is right nonsingular and every singular right R-module is semisimple ([5], Corollary 7.16).

Proposition 9.

If R is a right SI-ring, then $\mathfrak{spP}\left({\mathcal{T}}_G\right)=\mathfrak{spP}\left(\mathcal{SS}\right),$ where $\mathcal{SS}$ is the class of all semisimple modules.

Proof. 

Let M be a semisimple module. Then, we can write $M=M_1\oplus M_2,$ where $M_1$ is the sum of singular simple modules and $M_2$ is the sum of projective simple modules. Recall that both the class of Goldie torsion modules and the class of projective modules are closed under direct sums. Hence, $M_1$ is a Goldie torsion module and $M_2$ is projective. By this decomposition, we have ${\underline{\mathfrak{Pr}}}^{-1}\left(M\right)={\underline{\mathfrak{Pr}}}^{-1}\left(M_1\right)\cap {\underline{\mathfrak{Pr}}}^{-1}\left(M_2\right)={\underline{\mathfrak{Pr}}}^{-1}\left(M_1\right)\cap \mathrm{Mod}\text{-}R={\underline{\mathfrak{Pr}}}^{-1}\left(M_1\right)\in \mathfrak{spP}\left({\mathcal{T}}_G\right),$ where the last inclusion follows from ([18], Proposition 2.10). Therefore, $\mathfrak{spP}\left(\mathcal{SS}\right)\subseteq \mathfrak{spP}\left({\mathcal{T}}_G\right)$.

Conversely, let N be a Goldie torsion module. Since R is a right SI-ring, N is singular and semisimple. Thus, $\mathfrak{spP}\left({\mathcal{T}}_G\right)\subseteq \mathfrak{spP}\left(\mathcal{SS}\right),$ completing the proof. □

Example 1.

Let $\mathbb{K}$ be any field. For $n\in \mathbb{N}$, let $R_n=T_n\left(\mathbb{K}\right)$ denote the ring of all upper triangular $n\times n$ matrices with entries in $\mathbb{K}$. $R_n$ is a (left and right) hereditary Artinian serial ring by ([5], Example 13.6). Since $R_n$ is right nonsingular, $R_n$ is right (and left) Σ-CS ring by ([26], Theorem 4.6). Then, $\mathfrak{spP}\left({\mathcal{T}}_G\right)=\mathfrak{spP}(Mod-R_n)$ by Lemma 3. In particular, if $n=2$, $R_2$ is a (left and right) SI-ring by ([5], Example 13.6). There are exactly two simple right $R_2$-modules: $S_1$ and $S_2$.

The module $S_1$ is projective simple since $P_1=e_{11}{R}_2\cong S_1,$ where $P_1$ is the indecomposable projective module corresponding to the idempotent $e_{11}$. The module $S_2$ is not projective. Therefore, among the simple right $R_2$-modules, exactly one, namely $S_2$, is non-projective. Since $R_2$ is right Σ-CS and $S_2$ is unique non-projective simple module, ${\underline{\mathfrak{Pr}}}^{-1}\left(S_2\right)=\mathcal{PR}$, where $\mathcal{PR}$ is the class of all projective right $R_2$-modules. Thus, $\mathfrak{spP}\left({\mathcal{T}}_G\right)=\mathfrak{spP}(Mod-R_2)=\mathfrak{spP}\left(\mathcal{SS}\right)=\{Mod-R,\mathcal{PR}\}$ by Proposition 9.

We now turn our attention to the cases where the class $\mathfrak{spP}\left({\mathcal{T}}_G\right)$ consists of only one or two elements, and examine the structural consequences for the ring R in such situations. Recall that every simple module is either singular or projective, and that a ring R is semisimple Artinian if and only if every simple module is projective.

Proposition 10.

The following conditions are equivalent for a ring R.

1. 

R is a semisimple Artinian ring.

2. 

$\mathfrak{spP}\left({\mathcal{T}}_G\right)=\{Mod-R\}$

3. 

$\left|\mathfrak{spP}\left({\mathcal{T}}_G\right)\right|=1$

Proof. 

$\left(1\right)\Rightarrow \left(2\right)$ Assume that R is a semisimple Artinian ring. Then, every right R-module is projective. In particular, the zero module 0 has the largest possible subprojectivity domain, that is, $spd\left(0\right)=Mod-R.$ Since 0 is the only module in ${\mathcal{T}}_G$, it follows that $\mathfrak{spP}\left({\mathcal{T}}_G\right)=\{Mod-R\}.$ $\left(2\right)\Rightarrow \left(3\right)$ The implication is immediate, as (2) ensures that every subprojectivity domain in ${\mathcal{T}}_G$ is equal to $Mod-R$.

$\left(3\right)\Rightarrow \left(1\right)$ Assume that ${\underline{\mathfrak{Pr}}}^{-1}\left(U\right)=Mod-R$ for every $U\in {\mathcal{T}}_G$, and we aim to show that R is semisimple Artinian. It suffices to show that every simple right R-module is projective. Note that the zero module 0 belongs to ${\mathcal{T}}_G$, and hence by assumption, ${\underline{\mathfrak{Pr}}}^{-1}\left(0\right)=Mod-R\in \mathfrak{spP}\left({\mathcal{T}}_G\right).$ Suppose, for contradiction, that there exists a simple right R-module U which is not projective. Then, U must be singular. Since $U\in {\mathcal{T}}_G$, the assumption gives ${\underline{\mathfrak{Pr}}}^{-1}\left(U\right)=Mod-R.$ In particular, $U\in {\underline{\mathfrak{Pr}}}^{-1}\left(U\right)$, which implies that U is projective, a contradiction. Therefore, every simple module must be projective, and hence R is semisimple Artinian. □

After a single-element profile, we state the following natural result for a two-element profile.

Proposition 11.

The following conditions are equivalent for a non-semisimple Artinian ring R.

1. 

Every Goldie torsion right R-module is either projective or gp-indigent.

2. 

Every Goldie torsion right R-module is either ecf-module or gp-indigent.

3. 

$\mathfrak{spP}\left({\mathcal{T}}_G\right)=\{\mathcal{ECF},Mod-R\}$.

4. 

$\left|\mathfrak{spP}\left({\mathcal{T}}_G\right)\right|=2$.

Proof. 

The implications $\left(1\right)\Rightarrow \left(2\right)\Rightarrow \left(3\right)\Rightarrow \left(4\right)$ are trivial, and $\left(2\right)\Rightarrow \left(1\right)$ follows by the fact that every Goldie torsion ecf-module is projective. Finally, $\left(4\right)\Rightarrow \left(2\right)$ follows by Proposition ([27], Proposition 1) because all subprojectivity domains of non-projective Goldie torsion right R-modules must be the same by assumption. □

Proposition 12.

Let R be a right PS ring. The following conditions are equivalent:

(i) 

There is a singular simple gp-indigent right R-module.

(ii) 

R is a right nonsingular right C-ring with a unique (up to isomorphism) singular simple R-module.

Proof. 

$\left(i\right)\Rightarrow \left(ii\right)$ Suppose that N is a singular simple right R-module which is gp-indigent. Since N is gp-indigent and $Hom(N,A)=0$ for each simple R-module A, which is not isomorphic to N, it follows that N is unique (up to isomorphism) singular simple R-module. In view of this uniqueness, every non-projective simple right R-module is gp-indigent. By ([27], Corollary 1), R is a right nonsingular right C-ring. $\left(ii\right)\Rightarrow \left(i\right)$ follows directly by ([27], Corollary 1). □

The profile $\mathfrak{spP}\left({\mathcal{T}}_G\right)$ with two or three elements forms a chain, since every pair of elements is comparable. It has been shown that if $\mathfrak{spP}\left({\mathcal{T}}_G\right)$ consists of exactly two elements, then the ring R is either right nonsingular or right Kasch by ([27], Proposition 5). We extend this result in the following manner.

Proposition 13.

If $\mathfrak{spP}\left({\mathcal{T}}_G\right)$ forms a chain, then R possesses, up to isomorphism, a unique singular simple right R-module. Moreover, R is either a right nonsingular ring or a right Kasch ring.

Proof. 

Recall that every simple module is either a Goldie torsion or projective. Let A and B be two non-isomorphic simple right R-modules. Then, $Hom(A,B)=Hom(B,A)=0$. This implies that $A\in {\underline{\mathfrak{Pr}}}^{-1}\left(B\right)$ and $B\in {\underline{\mathfrak{Pr}}}^{-1}\left(A\right)$.

Assume that both A and B are singular simple modules. Since $\mathfrak{spP}\left({\mathcal{T}}_G\right)$ is a chain, we have either ${\underline{\mathfrak{Pr}}}^{-1}\left(A\right)\subseteq {\underline{\mathfrak{Pr}}}^{-1}\left(B\right)$ or ${\underline{\mathfrak{Pr}}}^{-1}\left(B\right)\subseteq {\underline{\mathfrak{Pr}}}^{-1}\left(A\right)$. In either situation, one of the modules A or B must be projective, which contradicts our assumption that both are singular. Therefore, R has, up to isomorphism, a unique singular simple right R-module, say A.

Now consider $Hom(A,R)$. If $Hom(A,R)\ne 0$, then R is a right Kasch ring.

If instead $Hom(A,R)=0$, then R is a right PS-ring. We claim that in this case R must be right nonsingular. Suppose, on the contrary, that R is not right nonsingular. Then, there exists a singular right ideal I of R. Since $Hom(A,R)=0$, it follows that $Hom(A,I)=0$, and thus $I\in {\underline{\mathfrak{Pr}}}^{-1}\left(A\right)$. As $\mathfrak{spP}\left({\mathcal{T}}_G\right)$ is a chain, we have either ${\underline{\mathfrak{Pr}}}^{-1}\left(I\right)\subseteq {\underline{\mathfrak{Pr}}}^{-1}\left(A\right)$ or ${\underline{\mathfrak{Pr}}}^{-1}\left(A\right)\subseteq {\underline{\mathfrak{Pr}}}^{-1}\left(I\right)$. If ${\underline{\mathfrak{Pr}}}^{-1}\left(I\right)\subseteq {\underline{\mathfrak{Pr}}}^{-1}\left(A\right)$, then the class of injective modules $\mathcal{IN}$ contains ${\underline{\mathfrak{Pr}}}^{-1}\left(A\right)$, because I embeds in a projective module by ([28], Lemma 2.2). This would imply that A embeds in R by the same lemma, contradicting $Hom(A,R)=0$. Therefore, this inclusion cannot occur.

On the other hand, if ${\underline{\mathfrak{Pr}}}^{-1}\left(A\right)\subseteq {\underline{\mathfrak{Pr}}}^{-1}\left(I\right)$, then I would be I-subprojective, implying that I is projective. But this contradicts the fact that I is singular. Thus, both cases lead to contradictions, and we conclude that R is a right nonsingular ring. □

If $\mathfrak{spP}\left({\mathcal{T}}_G\right)$ forms a chain, then by Proposition 13, R has a unique (up to isomorphism) singular simple right R-module. This singular simple module plays a fundamental role in our investigation. In what follows, whenever R possesses a unique singular simple module (up to isomorphism), we denote it by $\mathcal{U}$.

By Proposition 13, it is natural in the remainder of this paper to restrict our attention to right Kasch or right PS rings for which $\mathfrak{spP}\left({\mathcal{T}}_G\right)$ is a chain.

Recall that a max ring is a ring in which every nonzero module contains a maximal submodule. An R-module M is said to be coatomic if every proper submodule of M is contained in some maximal submodule. Note that every finitely generated module over any ring is coatomic. Furthermore, by ([2], Exercises 9.7.9 (c)), a module M is semisimple if and only if it is coatomic and every maximal submodule of M is a direct summand of M. Finally, a ring R is a right max ring if and only if every right R-module is coatomic.

Theorem 2.

Let R be a right PS ring. Let $\mathcal{CA}$ be the class of all coatomic right R-modules. The following conditions are equivalent:

1. 

R is a right nonsingular right C-ring with a unique (up to isomorphism) singular simple R-module.

2. 

$\mathfrak{spP}(\mathcal{CA}\cap {\mathcal{T}}_G)=\{\mathcal{ECF},Mod-R\}$.

3. 

$\left|\mathfrak{spP}(\mathcal{CA}\cap {\mathcal{T}}_G)\right|=2$.

Proof. 

$\left(1\right)\Rightarrow \left(2\right)$. Assume that R is a right nonsingular right C-ring with a unique (up to isomorphism) singular simple module $\mathcal{U}$, and let $M\in \mathcal{CA}\cap {\mathcal{T}}_G$. If $M=0$, then clearly ${\underline{\mathfrak{Pr}}}^{-1}\left(M\right)=Mod-R$. Suppose $M\ne 0$. Since M is not projective, and $M\in \mathcal{CA}$, there exists a maximal submodule N of M such that $M/N\cong \mathcal{U}$. Otherwise, M would be semisimple and hence projective by ([2], Exercises 9.7.9(c)), contradicting $M\in {\mathcal{T}}_G$. By Proposition 5, we have ${\underline{\mathfrak{Pr}}}^{-1}\left(M\right)\subseteq {\underline{\mathfrak{Pr}}}^{-1}\left(\mathcal{U}\right)$. As $\mathcal{U}$ is gp-indigent by Proposition 12, it follows that M is gp-indigent.

$\left(2\right)\Rightarrow \left(3\right)$ is immediate.

$\left(3\right)\Rightarrow \left(1\right)$ Since the zero module lies in $\mathcal{CA}\cap {\mathcal{T}}_G$, we have $Mod-R\in \mathfrak{spP}(\mathcal{CA}\cap {\mathcal{T}}_G)$. Let A and B be two nonisomorphic singular simple modules. Then, A and B are in $\mathcal{CA}\cap {\mathcal{T}}_G$. By our assumption, ${\underline{\mathfrak{Pr}}}^{-1}\left(A\right)={\underline{\mathfrak{Pr}}}^{-1}\left(B\right)$. Since $Hom(A,B)=Hom(B,A)=0$, it follows that at least one of A or B must be projective, a contradiction. Thus, there exists a unique (up to isomorphism) singular simple module, say $\mathcal{U}$. Assume R is not a right nonsingular, i.e., $Z\left(R\right)\ne 0$, and let $0\ne a\in Z\left(R\right)$. Then, $aR$ is a singular cyclic module, and hence it belongs to $\mathcal{CA}\cap {\mathcal{T}}_G$. By (3), ${\underline{\mathfrak{Pr}}}^{-1}\left(aR\right)={\underline{\mathfrak{Pr}}}^{-1}\left(\mathcal{U}\right)$. As R is a right PS-ring, we have $Hom(\mathcal{U},aR)=0$, which implies that $aR$ is projective, contradicting with the singularity of $aR$. Hence, R is right nonsingular.

To show that R is a right C-ring, suppose there exists a singular cyclic module C with $Soc\left(C\right)=0$. Then, $C\in \mathcal{CA}\cap {\mathcal{T}}_G$, and hence ${\underline{\mathfrak{Pr}}}^{-1}\left(C\right)={\underline{\mathfrak{Pr}}}^{-1}\left(\mathcal{U}\right)$ by (3). Since $Hom(\mathcal{U},C)=0$, it follows that C is projective, again a contradiction. Thus, every singular cyclic module has a nonzero socle, and R is a right C-ring. □

Corollary 2.

Let R be a right PS ring. The following conditions are equivalent:

1. 

$\mathfrak{spP}\left({\mathcal{T}}_G\right)=\{\mathcal{ECF},Mod-R\}$.

2. 

$\left|\mathfrak{spP}\left({\mathcal{T}}_G\right)\right|=2$.

3. 

R is a right nonsingular right C-ring with a unique (up to isomorphism) singular simple R-module, and every singular module is coatomic.

Proof. 

$\left(1\right)\iff \left(2\right)$ is clear.

$\left(1\right)\Rightarrow \left(3\right)$ By Proposition 12, the ring R is a right nonsingular right C-ring with a unique (up to isomorphism) singular simple R-module $\mathcal{U}$. Let M be a singular module that is not coatomic. Then, M has a submodule A such that $Rad(M/A)=M/A$, which implies that $Hom(M/A,\mathcal{U})=0$. Note that singular modules are closed under quotients, and hence $M/A$ is also singular. By assumption, $\mathcal{U}\in {\underline{\mathfrak{Pr}}}^{-1}(M/A)=\mathcal{ECF}$, and thus $\mathcal{U}$ is projective. This contradicts the singularity of $\mathcal{U}$. Therefore, every singular module is coatomic.

$\left(3\right)\Rightarrow \left(1\right)$ This follows directly from Corollary 2. □

As a generalization of V-rings, the GV-ring has been introduced in [29]. A ring R is called a right GV-ring if all simple singular right modules are injective.

Lemma 4.

Let R be a right GV-ring. If $\mathfrak{spP}\left({\mathcal{T}}_G\right)$ is a chain, then R is a right max ring.

Proof. 

By Proposition 13, R is either a right nonsingular ring or a right Kasch ring, and in both cases, R has a unique (up to isomorphism) singular simple right R-module, denoted by $\mathcal{U}$.

If R is a right Kasch ring, then R must be semisimple Artinian since, as a right GV-ring, every simple module is a direct summand of R.

Now, assume R is right nonsingular. In this case, we have $Hom(\mathcal{U},R)=0$. To prove that R is a right max ring, let M be a nonzero right R-module. We claim that $Rad\left(M\right)\ne M$. Suppose, for contradiction, that $Rad\left(M\right)=M$. Then, it follows that $Hom(M,\mathcal{U})=0$. Consider any finitely generated submodule K of M. Since $\mathcal{U}$ is injective and $Hom(M,\mathcal{U})=0$, we also have $Hom(K,\mathcal{U})=0$.

By our assumptions, every simple module is either projective or isomorphic to $\mathcal{U}$. Therefore, every maximal submodule of K is a direct summand. By ([2], Exercise 9(c), p. 239), this implies that K is semisimple. Recall that a module is semisimple if and only if all its finitely generated submodules are semisimple ([11], 20.3). Thus, M itself is semisimple. Since $Hom(M,\mathcal{U})=0$, M cannot have any composition factors isomorphic to $\mathcal{U}$, meaning that M must be projective. But then $Rad\left(M\right)$ is strictly smaller than M, contradicting the assumption $Rad\left(M\right)=M$. This contradiction confirms that $Rad\left(M\right)\ne M$, showing that R is a right max ring. □

Lemma 5.

Let R be a non-right Kasch ring. If $\mathfrak{spP}\left({\mathcal{T}}_G\right)$ is a chain, then ${\underline{\mathfrak{Pr}}}^{-1}\left(Z\right)\subseteq {\underline{\mathfrak{Pr}}}^{-1}\left(\mathcal{U}\right)$ for each coatomic non-projective Goldie torsion module Z.

Proof. 

Let Z be a coatomic, non-projective Goldie torsion module. Assume that ${\underline{\mathfrak{Pr}}}^{-1}\left(\mathcal{U}\right)$ is properly contained in ${\underline{\mathfrak{Pr}}}^{-1}\left(Z\right)$, that is, ${\underline{\mathfrak{Pr}}}^{-1}\left(\mathcal{U}\right)⊊{\underline{\mathfrak{Pr}}}^{-1}\left(Z\right)$. Then there exists a module K such that $K\in {\underline{\mathfrak{Pr}}}^{-1}\left(Z\right)$ but $K\notin {\underline{\mathfrak{Pr}}}^{-1}\left(\mathcal{U}\right)$. This implies that $Hom(\mathcal{U},K)\ne 0$. Recall from Proposition 13 that R is right nonsingular and that $\mathcal{U}$ is the unique singular simple right R-module, up to isomorphism. By the nonsingularity of R, we have $Hom(Z,K)=0$. Since $Hom(\mathcal{U},K)\ne 0$, we may assume, without loss of generality, that $\mathcal{U}$ is a submodule of K. By Proposition 2, this implies $\mathcal{U}\in {\underline{\mathfrak{Pr}}}^{-1}\left(Z\right)$. Consequently, $Hom(Z,\mathcal{U})=0$. Thus, every simple quotient of Z is projective. By ([2], Exercises 9.7.9 (c)), it follows that Z is semisimple. Since $\mathcal{U}$ is the unique singular simple module and $Hom(Z,\mathcal{U})=0$, all simple summands of Z must be projective. Therefore, Z itself is projective.

This contradicts the assumption that Z is non-projective. Hence, our initial assumption was false, and we conclude that ${\underline{\mathfrak{Pr}}}^{-1}\left(Z\right)\subseteq {\underline{\mathfrak{Pr}}}^{-1}\left(\mathcal{U}\right)$ for every coatomic, non-projective Goldie torsion module Z. □

Corollary 3.

Let R be a max-ring that is not Kasch. If $\mathfrak{spP}\left({\mathcal{T}}_G\right)$ is a chain, then ${\underline{\mathfrak{Pr}}}^{-1}\left(\mathcal{U}\right)$ is a maximal element in $\mathfrak{spP}\left({\mathcal{T}}_G\right)$.