Modal Regression Estimation by Local Linear Approach in High-Dimensional Data Case
Abstract
1. Introduction
2. The Conditional Mode and Its Local Linear Estimator
3. Main Results
- (B1)
- For any , and there exists a function such that:
- (B2)
- The functions is of class and satisfies the following Lipschitz condition:where denotes a neighborhood of .
- (B3)
- The kernel is a positive and differentiable function which is supported within , and such that:is a positive definite matrix.
- (B4)
- The bandwidth satisfies:
4. On the Potential Impact of the Contribution
- Comparison with existing approachesIn an earlier contribution [36], we have investigated robust mode estimation under a functional single-index structure, employing the local constant method. Alternatively, in this study, we examine local linear estimation for the same model under a general functional framework. Firstly, observe that the topic of the present contribution can be viewed as a generalization of [36], in the sense that the local constant constitutes a particular case of the local linear approach, and the functional single index structure is a special case of the general functional structure. Moreover, it is well documented (see, for instance, [27]) that the local linear method has many advantages over the Nadaraya–Watson (the local constant method). Particularly, the local linear estimation is usually used to reduce the bias and the boundary effect of the Nadaraya–Watson method. So, the use of the local linear method instead of the standard kernel method substantially improves the prediction accuracy. On the other hand, it is widely recognized that the single-index model reduces analytical complexity by projecting functional covariates onto a univariate index. Thus, it transforms the functional data analysis problem into a one-dimensional real data issue. This oversimplification is unusual in practice, as it ignores potentially influential higher-dimensional interactions. Our generalized framework of this contribution circumvents this limitation. From a practical point of view, the kernel estimator assumes that the nonparametric model is flat within the neighborhood of the location point, which leads to suboptimal prediction. In contrast, the local linear method assumes that the model has a linear approximation in the neighborhood of the location point, which is more realistic and improves the prediction results.
- On the bias reductionAs mentioned in the previous comment, the behavior of the bias term is one of the main reasons for adopting the local linear method. Although the asymptotic behavior of the bias term is usually linked to the smoothness assumptions of the nonparametric model, this term can be significantly improved in the local linear approach. This beneficial characteristic is related to the weighting functions in the local linear estimator (see [27] in the non-functional case). A similar statement can be deduced in the functional case. Specifically, under standard conditions, the local linear approach offers a better bias term compared to the Nadaraya–Watson [36]. Indeed, this improvement is also due to the specific weighting functions implemented in . It is clear that the leading term of the Bahadur representation of such thatwhereandUsing the same analytical arguments as in [37], we prove that the first part of the bias term can be reduced to . In conclusion, although the local linear and the Nadaraya–Watson (NW) estimators share similar asymptotic properties, the local linearity of the model and the weighting functions of the LLE method allow us to improve the bias term in certain situations.
- On the applicability of the estimatorOf course, the simple use of the estimator greatly depends on choosing its parameters easily. Since the estimator is derived from quantile regression, there are multiple cross-validation methods available for selecting the parameters, particularly the bandwidth parameters associated with the functional component. First, for a given subset of real positive numbers, we consider the cross-validation criterion used by [38].where denotes a local empirical quantile and is the conditional quantile estimator at after excluding this observation from the sample. Secondly, we apply the cross-validation approach that was utilized by [39]Additionally, various other methods can be utilized, such as the least squares cross-validation technique suggested by [6]:Of course, the diversity of selection methods makes the estimator easier to implement in practice.
5. Computational Part
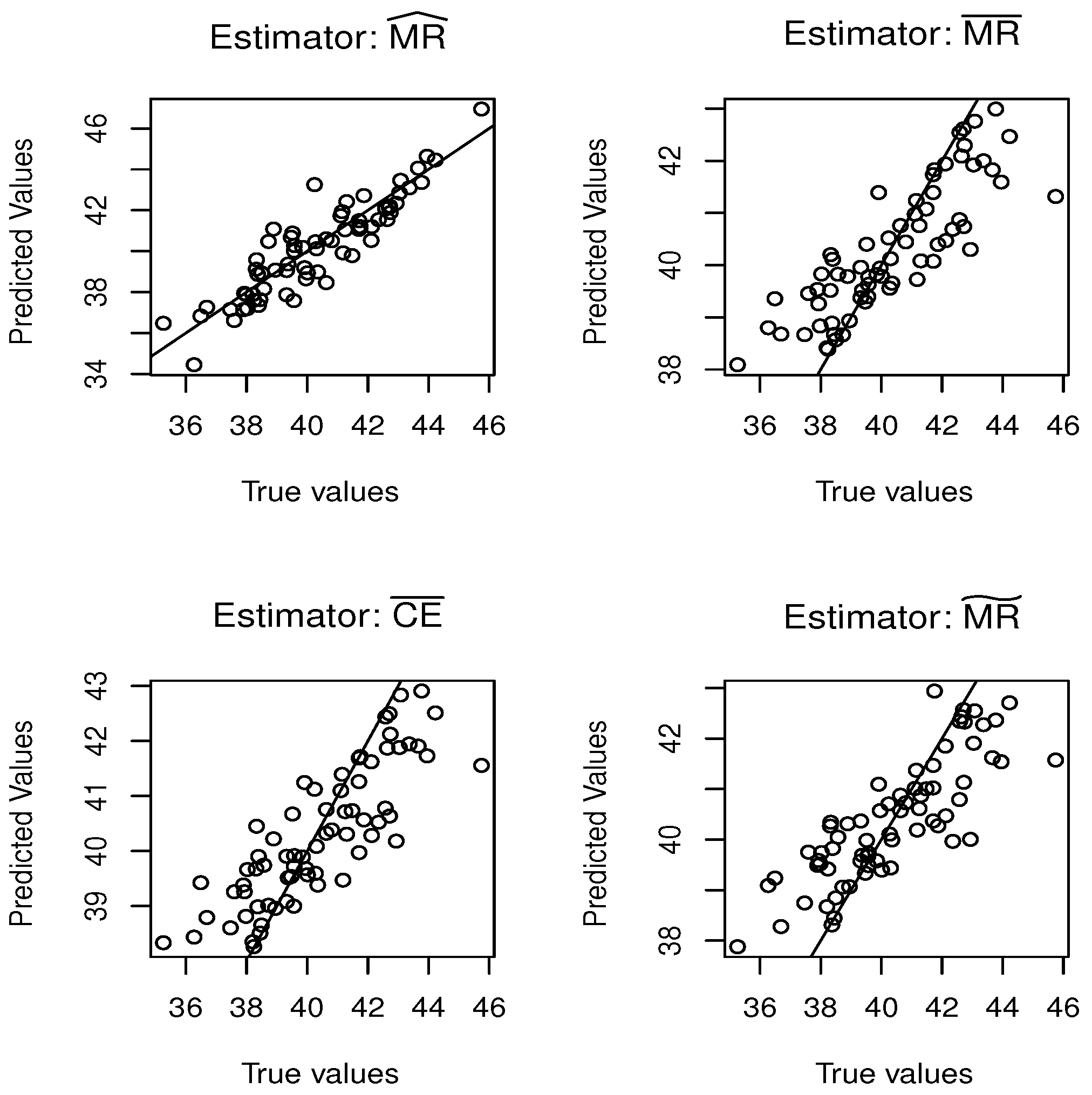
5.1. Simulation Study
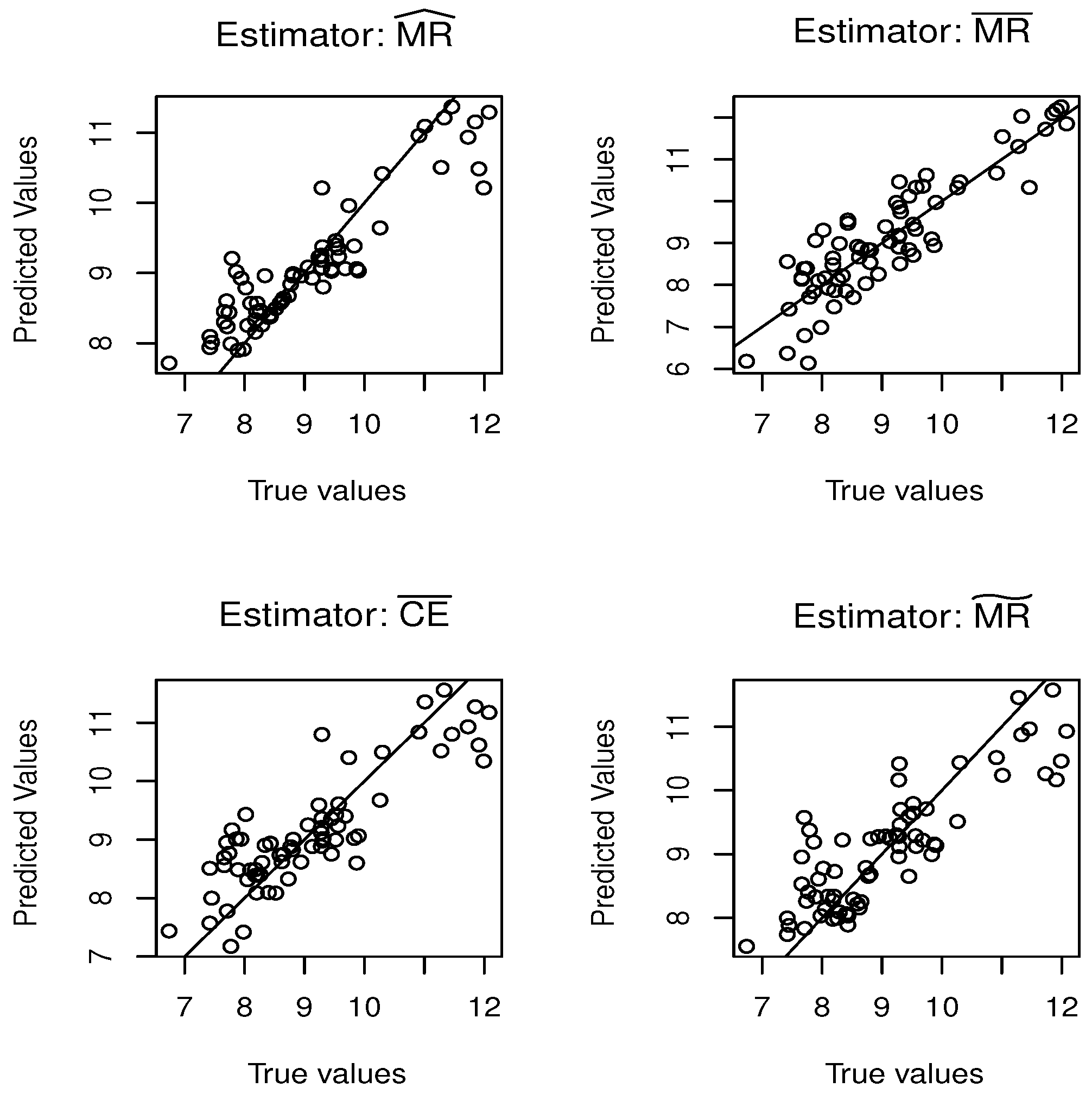
5.2. Real Data Application
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Proofs of Intermediate Results
References
- Ramsay, J.O.; Silverman, B.W. Functional Data Analysis, 2nd ed.; Springer: New York, NY, USA, 2005. [Google Scholar]
- Ferraty, F.; Vieu, P. Nonparametric Functional Data Analysis. Theory and Practice; Springer Series in Statistics; Springer: New York, NY, USA, 2006. [Google Scholar]
- Xu, Y. Functional Data Analysis. In Springer Handbook of Engineering Statistics; Springer: London, UK, 2023; pp. 67–85. [Google Scholar]
- Ahmed, M.S.; Frévent, C.; Génin, M. Spatial Scan Statistics for Functional Data. In Handbook of Scan Statistics; Springer: New York, NY, USA, 2024; pp. 629–645. [Google Scholar]
- Collomb, G.; Härdle, W.; Hassani, S. A note on prediction via estimation of the conditional mode function. J. Stat. Plan. Inference 1986, 15, 227–236. [Google Scholar] [CrossRef]
- Quintela-Del-Rio, A.; Vieu, P. A nonparametric conditional mode estimate. J. Nonparametr. Stat. 1997, 8, 253–266. [Google Scholar] [CrossRef]
- Ioannides, D.; Matzner-Løber, E. A note on asymptotic normality of convergent estimates of the conditional mode with errors-in-variables. J. Nonparametr. Stat. 2004, 16, 515–524. [Google Scholar] [CrossRef]
- Louani, D.; Ould-Saïd, E.L.I.A.S. Asymptotic normality of kernel estimators of the conditional mode under strong mixing hypothesis. J. Nonparametr. Stat. 1999, 11, 413–442. [Google Scholar] [CrossRef]
- Bouzebda, S.; Khardani, S.; Slaoui, Y. Asymptotic normality of the regression mode in the nonparametric random design model for censored data. Commun. Stat. Theory Methods 2023, 52, 7069–7093. [Google Scholar] [CrossRef]
- Bouzebda, S.; Didi, S. Some results about kernel estimators for function derivatives based on stationary and ergodic continuous time processes with applications. Communications in Statistics. Theory Methods 2022, 51, 3886–3933. [Google Scholar] [CrossRef]
- Ferraty, F.; Laksaci, A.; Vieu, P. Estimating some characteristics of the conditional distribution in nonparametric functional models. Stat. Inference Stoch. Process. 2006, 9, 47–76. [Google Scholar] [CrossRef]
- Bouzebda, S.; Chaouch, M.; Laïb, N. Limiting law results for a class of conditional mode estimates for functional stationary ergodic data. Math. Methods Stat. 2016, 25, 1066–5307. [Google Scholar] [CrossRef]
- Ezzahrioui, M.H.; Ould-Saïd, E. Asymptotic normality of a nonparametric estimator of the conditional mode function for functional data. J. Nonparametr. Stat. 2008, 20, 3–18. [Google Scholar] [CrossRef]
- Ezzahrioui, M.H.; Saïd, E.O. Some asymptotic results of a non-parametric conditional mode estimator for functional time-series data. Stat. Neerl. 2010, 64, 171–201. [Google Scholar] [CrossRef]
- Dabo-Niang, S.; Kaid, Z.; Laksaci, A. Asymptotic properties of the kernel estimate of spatial conditional mode when the regressor is functional. AStA Adv. Stat. Anal. 2015, 99, 131–160. [Google Scholar] [CrossRef]
- Bouanani, O.; Laksaci, A.; Rachdi, M.; Rahmani, S. Asymptotic normality of some conditional nonparametric functional parameters in high-dimensional statistics. Behaviormetrika 2019, 46, 199–233. [Google Scholar] [CrossRef]
- Azzi, A.; Belguerna, A.; Laksaci, A.; Rachdi, M. The scalar-on-function modal regression for functional time series data. J. Nonparametr. Stat. 2024, 36, 503–526. [Google Scholar] [CrossRef]
- Stone, C.J. Consistent nonparametric regression. Ann. Stat. 1977, 5, 595–620. [Google Scholar] [CrossRef]
- Koenker, R.; Zhao, Q. Conditional quantile estimation and inference for ARCH models. Econom. Theory 1996, 12, 793–813. [Google Scholar] [CrossRef]
- Hallin, M.; Lu, Z.; Yu, K. Local linear spatial quantile regression. Bernoulli 2009, 15, 659–686. [Google Scholar] [CrossRef]
- Cardot, H.; Crambes, C.; Sarda, P. Quantile regression when the covariates are functions. J. Nonparametr. Stat. 2005, 17, 841–856. [Google Scholar] [CrossRef]
- Wang, H.; Ma, Y. Optimal subsampling for quantile regression in big data. Biometrika 2021, 108, 99–112. [Google Scholar] [CrossRef]
- Jiang, Z.; Huang, Z. Single-index partially functional linear quantile regression. Commun. Stat.-Theory Methods 2024, 53, 1838–1850. [Google Scholar] [CrossRef]
- Dabo-Niang, S.; Kaid, Z.; Laksaci, A. Spatial conditional quantile regression: Weak consistency of a kernel estimate. Rev. Roum. Math. Pures Appl. 2012, 57, 311–339. [Google Scholar]
- Chowdhury, J.; Chaudhuri, P. Nonparametric depth and quantile regression for functional data. Bernoulli 2019, 25, 395–423. [Google Scholar] [CrossRef]
- Mutis, M.; Beyaztas, U.; Karaman, F.; Lin Shang, H. On function-on-function linear quantile regression. J. Appl. Stat. 2025, 52, 814–840. [Google Scholar] [CrossRef] [PubMed]
- Fan, J. Local Polynomial Modelling and Its Applications: Monographs on Statistics and Applied Probability 66; Routledge: Abingdon-on-Thames, UK, 2018. [Google Scholar]
- Rachdi, M.; Laksaci, A.; Demongeot, J.; Abdali, A.; Madani, F. Theoretical and practical aspects of the quadratic error in the local linear estimation of the conditional density for functional data. Comput. Stat. Data Anal. 2014, 73, 53–68. [Google Scholar] [CrossRef]
- Baíllo, A.; Grané, A. Local linear regression for functional predictor and scalar response. J. Multivar. Anal. 2009, 100, 102–111. [Google Scholar] [CrossRef]
- Barrientos-Marin, J.; Ferraty, F.; Vieu, P. Locally modelled regression and functional data. J. Nonparametr. Stat. 2010, 22, 617–632. [Google Scholar] [CrossRef]
- Berlinet, A.; Elamine, A.; Mas, A. Local linear regression for functional data. Ann. Inst. Stat. Math. 2011, 63, 1047–1075. [Google Scholar] [CrossRef]
- Demongeot, J.; Laksaci, A.; Madani, F.; Rachdi, M. Functional data: Local linear estimation of the conditional density and its application. Statistics 2013, 47, 26–44. [Google Scholar] [CrossRef]
- Messaci, F.; Nemouchi, N.; Ouassou, I.; Rachdi, M. Local polynomial modelling of the conditional quantile for functional data. Stat. Methods Appl. 2015, 24, 597–622. [Google Scholar] [CrossRef]
- Laksaci, A.; Ould Saïd, E.; Rachdi, M. Uniform consistency in number of neighbors of the k NN estimator of the conditional quantile model. Metrika 2021, 84, 895–911. [Google Scholar] [CrossRef]
- Ota, H.; Kato, K.; Hara, S. Quantile regression approach to conditional mode estimation. Electron. J. Stat. 2019, 13, 3120–3160. [Google Scholar] [CrossRef]
- Almulhim, F.A.; Alamari, M.B.; Bouzebda, S.; Kaid, Z.; Laksaci, A. Robust Estimation of L 1-Modal Regression Under Functional Single-Index Models for Practical Applications. Mathematics 2025, 13, 602. [Google Scholar] [CrossRef]
- Belarbi, F.; Chemikh, S.; Laksaci, A. Local linear estimate of the nonparametric robust regression in functional data. Stat. Probab. Lett. 2018, 134, 128–133. [Google Scholar] [CrossRef]
- Iglesias Pérez, M.D.C. Estimación de la función de distribución condicional en presencia de censura y truncamiento: Una aplicación al estudio de la mortalidad en pacientes diabéticos. Estad. Esp. 2003, 45, 275–302. [Google Scholar]
- Yuan, M. GACV for quantile smoothing splines. Comput. Stat. Data Anal. 2006, 50, 813–829. [Google Scholar] [CrossRef]
- Panchbhai, K.G.; Lanjewar, M.G. Portable system for cocoa bean quality assessment using multi-output learning and augmentation. Food Control 2025, 174, 111234. [Google Scholar] [CrossRef]

| Cond. Dist. | Model | CURVES | |||
|---|---|---|---|---|---|
| Normal | Hom.model | Smooth | 0.0258 | 0.0897 | 0.1672 |
| Rough | 0.1067 | 0.4676 | 0.5679 | ||
| Normal | Het.model | Smooth | 0.2672 | 0.7426 | 1.0578 |
| Rough | 0.3617 | 1.2725 | 1.8811 | ||
| Laplace | Hom. model | Smooth | 0.4257 | 0.6150 | 0.6317 |
| Rough | 0.9804 | 1.0922 | 1.1788 | ||
| Laplace | Het. model | Smooth | 0.8967 | 1.6824 | 1.7088 |
| Rough | 0.9176 | 2.4521 | 2.6588 | ||
| Weibull | Hom. model | Smooth | 0.5179 | 1.5005 | 1.5446 |
| Rough | 0.8399 | 2.4873 | 2.7098 | ||
| Weibull | Het. model | Smooth | 0.7840 | 1.6253 | 1.4102 |
| Rough | 0.9705 | 3.3567 | 4.3456 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Almulhim, F.A.; Alamari, M.B.; Laksaci, A.; Kaid, Z. Modal Regression Estimation by Local Linear Approach in High-Dimensional Data Case. Axioms 2025, 14, 537. https://doi.org/10.3390/axioms14070537
Almulhim FA, Alamari MB, Laksaci A, Kaid Z. Modal Regression Estimation by Local Linear Approach in High-Dimensional Data Case. Axioms. 2025; 14(7):537. https://doi.org/10.3390/axioms14070537
Chicago/Turabian StyleAlmulhim, Fatimah A., Mohammed B. Alamari, Ali Laksaci, and Zoulikha Kaid. 2025. "Modal Regression Estimation by Local Linear Approach in High-Dimensional Data Case" Axioms 14, no. 7: 537. https://doi.org/10.3390/axioms14070537
APA StyleAlmulhim, F. A., Alamari, M. B., Laksaci, A., & Kaid, Z. (2025). Modal Regression Estimation by Local Linear Approach in High-Dimensional Data Case. Axioms, 14(7), 537. https://doi.org/10.3390/axioms14070537






