1. Introduction
In real life, people are often faced with situations that require them to make decisions in a state of uncertainty. According to Liu [
1], there are two ways to deal with indeterminacy. Probability theory is the most well-known theory and is inevitable in situations when the frequencies are extremely close to the distribution function. On the other hand, when there is no sample available to approximate a probability distribution, probability theory never permits exact solutions. For instance, we are unable to determine the strength of the existing bridge. Consequently, finding sufficient sample data for some events may be challenging. In order to determine the probability that each event would occur under these conditions, we must rely on the domain experts. In order to address these types of situations, Liu [
2] looked into the uncertainty theory idea. While probability theory is based on the frequency of random events, uncertainty theory is based on the degree of confidence. We apply the principle of uncertainty to effectively address both fuzziness and randomness. In recent times, an aspect of mathematics referring to uncertainty theory has been used to model human uncertainty. Liu proposed a revised version of this speculative idea [
3]. Furthermore, Liu used this theory of uncertainty in sequences and showed convergence in mean, distribution, measure and almost sure convergence to prove the property of convergence of uncertain measures. By widening the idea of real uncertain variables into complex uncertain variables, Peng [
4] provided uncertainty theory a new approach, which Chen et al. [
5] further developed. Datta and Tripathy [
6] made further generalizations to their approach by introducing double sequences of complex uncertain variables. After that, You [
7] mentioned the uniformly almost sure convergence of complex uncertain sequences in 2009. Classical convergence demands all terms of a sequence to closely approach a limit, and statistical convergence allows for occasional deviations—making it ideal for uncertain data environments. By integrating statistical convergence with uncertainty theory, we can better understand the long-term behavior of complex uncertain sequences, which is essential in many practical applications—such as engineering, data modeling and control systems. It is often necessary to approximate complex or uncertain functions when exact forms are unknown. When dealing with noisy or missing sensor data in engineering systems, complex uncertain sequences provide reliable means to model such uncertainties. The concept of lacunary almost statistical convergence ensures accurate approximation even if some data points stray from expected values. Nonetheless, applying this method requires careful selection of sequence gaps and uncertainty profiles, which can be difficult with limited data. Practical application is strengthened by incorporating expert knowledge and dynamic adjustment techniques. Classical methods of approximation rely heavily on deterministic models and well-defined convergence. However, in environments filled with uncertainty, these traditional methods may fall short. This is where the combination of uncertainty theory and statistical convergence becomes especially powerful. Numerous mathematicians have contributed to this field, examining its properties and extending its scope; see ([
8,
9,
10]) and many more. By studying how uncertain sequences behave and converge, we gain new tools for constructing and evaluating approximations in situations where classical techniques cannot be applied reliably. This work aims to contribute to this growing area by extending the idea of convergence to complex uncertain variables and exploring its implications for function approximation in uncertain environments. Throughout the paper, we take
and
as real numbers and natural numbers, respectively.
2. Preliminaries
The notion of statistical convergence, a generalization of the classical notion of convergence, was first introduced by Zygmund in the inaugural edition of his celebrated monograph, published in Warsaw in 1935 [
11] and independently by Steinhaus [
12] and Fast [
13]. This concept was later revisited independently by Schoenberg [
14]. Unlike classical convergence, which requires that all but finitely many terms of a sequence lie within an arbitrarily small neighborhood of the limit, statistical convergence relaxes this requirement. Instead, it considers a sequence convergent if the density of terms satisfying the convergence criterion approaches unity. This broader framework enables the study of sequences beyond the constraints of traditional convergence.
Every convergent sequence is statistically convergent. But the converse need not be true in general.
Example 1. Define a sequence byi.e., x=. For this we first observe that (since is non-zero only when k is a square).
Therefore, Thus, the sequence is statistically convergent, but it is evident that it is not convergent as it is finitely oscillating.
A real sequence
is said to be statistically convergent to a real number
z if for a given
> 0,
Later, Tripathy and Nath [
10] used complex uncertain sequences to study statistical convergence.
Now, we present some definitions of uncertainty theory given by (Liu [
1]).
Definition 1. Consider ℓ to be a algebra on a nonempty set Ω. A mapping is called an uncertain measure if it satisfies
- (i)
;
- (ii)
;
- (iii)
For each countable sequence of
where each element is called an event. The triplet is known as uncertainty space. Liu [15] discovered the product criteria of an uncertain measure for compound events as follows: - (iv)
Let be an uncertainty space where The product uncertain measure is a measure satisfying
Definition 2. The uncertain variable z is a measurable function from to the set of real numbers, i.e., for any Borel set B of real numbers, the setis an event. Definition 3. The uncertainty distribution ϕ of an uncertain variable z is defined as Definition 4. The expected value E of an uncertain variable z is defined asonly if one of the two integrals is finite. Chen et al. [
5] presented a notion in complex uncertain sequences, which is shown below.
Definition 5. The complex uncertain sequence is said to be almost surely convergent to ζ if ∃Λ
with such thatfor every Definition 6. The complex uncertain sequence is said to be convergent in measure to ζ if∀ε
Definition 7. The complex uncertain sequence is said to be convergent in mean to ζ if Definition 8. If are uncertainty distributions of uncertain variables , respectively, then a complex uncertain sequence is convergent in distribution to ζ if∀
at which is continuous. Definition 9. The complex uncertain sequence is uniformly almost surely convergent to ζ if ∃ a sequence of events with approaching zero such that converges uniformly to ζ in for fixed
Remark 1. Suppose for and we getas an uncertain variable. The concept of lacunary sequences was introduced by Freedman et al. [
16]. A lacunary sequence is an increasing non-negative integer sequence
with
and
as
. Throughout the paper, the intervals determined by
r will be denoted by
, and later, we refer to Fridy and Orhan [
17] to introduce the concept of lacunary statistical convergence. A real sequence
is said to be lacunary statistically convergent to a number L if for a given
Kişi and Ünal [
9] studied lacunary statistical convergence for complex uncertain sequences.
Almost convergence was first defined by Lorentz [
18] in 1948 using the idea of a Banach limit. A bounded sequence
is known to be almost convergent to a number z if and only if
uniformly in
k for some
z ∈
.
For fundamental theorems in functional analysis and summability theory, readers may refer to recent textbooks [
19,
20], while further insights on almost convergence and related topics can be found in [
21,
22,
23,
24]. Savaş [
25], by using fuzzy numbers, introduced the concept of “almost convergence”, which was further generalized by Saha, Tripathy and Roy [
26] by introducing almost convergence of complex uncertain sequences. In 2021, Das et al. introduced the concept of almost convergence for complex uncertain sequences in both double [
27] and triple sequences [
6]. Following this, Raj et al. [
28] introduced the concept of almost
-statistical convergence for complex uncertain sequences. In 2023, Nath et al. [
29] proposed the concept of strongly almost convergence in sequences of complex uncertain variables. More recently, Das et al. [
30] established a relationship between convergence and almost convergence of complex uncertain sequences. Motivated from these works, we introduce the concept of lacunary almost statistical convergence of order
for complex uncertain sequences via measure, mean, distribution, almost sure convergence and uniformly almost sure convergence and establish some relationships among these notions. Furthermore, when the converse of a theorem does not hold, a counterexample is provided to support the result.
3. Main Results
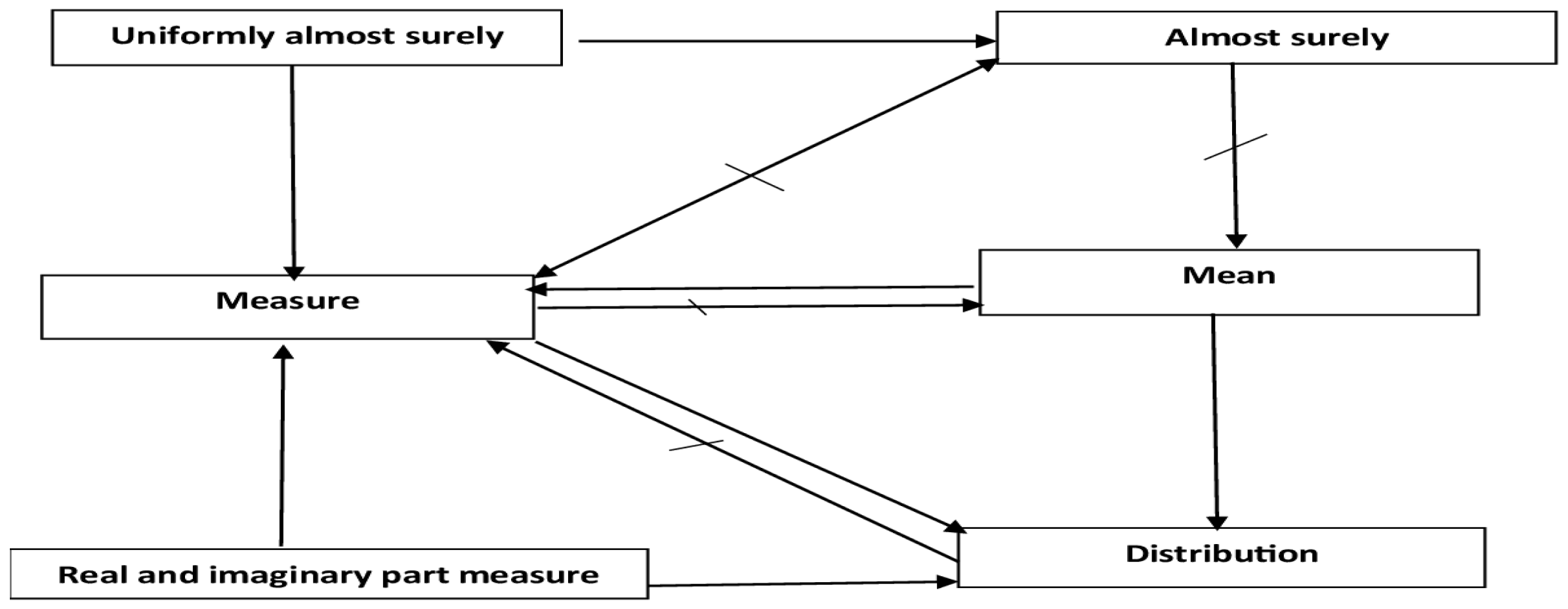
In this section, we present the relationship between complex uncertain sequences by using lacunary almost statistical convergence. (Figure of Interrelationships can be seen in
Figure 1):
Definition 10. The complex uncertain sequence is known to be lacunary almost statistically convergent of order α in concert with almost sure convergence to ζ if there exists an event Λ
with (Λ
) = 1 such thatuniformly in k and ∀
where Λ
represents an uncertain event, (Λ) = 1 and
. Definition 11. The complex uncertain sequence is known to be lacunary almost statistically convergent of order α in measure to ζ if ∀
ε, , Definition 12. The complex uncertain sequence is known to be lacunary almost statistically convergent of order α in mean to ζ if ∀
, ε Definition 13. If the are uncertainty distributions of uncertain variables , respectively, then the complex uncertain sequence lacunary almost statistically converges in distribution to ζ if for every ε ,for all v = a+ib at which ϕ is continuous. Definition 14. The complex uncertain sequence is known to be lacunary almost statistically convergent of order α and uniformly almost surely convergent to ζ if for every ε∃
and a sequence of events such thatwhere represents a sequence of events. Lemma 1.
Let be a non-negative uncertain variable (i.e., for all ), and let be any positive number. Then, the uncertain measure of the set where is at least a satisfies Proof. Define the set
, and let
denote its indicator function:
Since
for all
, we have
Taking the expected value of both sides yields
Using the linearity of expectation and the fact that
, we get
Dividing both sides by
a gives
This completes the proof. □
Theorem 1. If the uncertain sequence is lacunary almost statistically convergent in mean to ζ, then it is also lacunary almost statistically convergent in measure to ζ. But the converse does not hold, in general.
Proof. Suppose the uncertain sequence
is lacunary almost statistically convergent in mean to
. Then, for every
, we have
Now, using Markov’s inequality, we get
Hence,
This implies
as
. Thus, the sequence is lacunary almost statistically convergent in measure to
. This proves the result. Now, for the converse we may illustrate by the example given below. □
Example 2. Consider the uncertainty space with and a set function an uncertain measure satisfying the three axioms of uncertainty and having uncertain measurable functions as follows: Now, we define the complex uncertain variablefor and Then, for some given small number ε and we have So, the sequence is lacunary almost statistically convergent in measure to ζ.
However, for j, k ≥2 the uncertainty distribution of the uncertain variable is
Thus, the sequence is not lacunary almost statistically convergent in mean to ζ.
Theorem 2. If and are the real and imaginary parts of the sequence , respectively, and both are lacunary almost statistically convergent of order in measure to ϱ and ς, respectively, then the sequence is also lacunary almost statistically convergent of order in measure to .
Proof. The sequences
and
are lacunary almost statistically convergent in measure to
and
. Then,
, and we get
and
where
and
.
Also, by letting
it follows from the contrapositive argument that if this norm is at least
, then at least one of the components
or
must deviate from its limit by at least
.
Therefore, we get the inclusion
Using the subadditivity of an uncertain measure, it follows that
This implies that the sequence is lacunary almost statistically convergent in measure to . □
Theorem 3. If and are the real and imaginary parts of the sequence , respectively, and both are lacunary almost statistically convergent of order in measure to ϱ and ς, respectively, then the sequence is lacunary almost statistically convergent of order in distribution to .
Proof. Consider
to be a given point of continuity for a complex uncertain distribution
. Then, for any
,
, we have
By the subadditivity axiom, we get
since
and
are lacunary almost statistically convergent in measure to
and
, respectively. For a given
and
, we have
and
For any
and
, assuming
and the fact that distribution function
is right continuous, we get
On the other hand,
which means that
For a preassigned
and
So, we have
for any
Taking
we get
From inequalities (
1) and (
2), we have that
is lacunary almost statistically convergent in distribution to
as
. The converse of the above theorem is not true. □
Remark 2. Lacunary almost statistical convergence of order in distribution does not imply lacunary almost statistical convergence of order in measure. An explanation is provided in the following example.
Example 3. Consider the uncertainty space to be with Define the complex uncertain variable as Define for Then, and ζ have the same distribution as follows: Since each the values taken by are exactly the same as those taken by , just with opposite signs. However, because the distribution only depends on the probability (or uncertain measure) of these values and not on their signs, the distributions of and are the same. This is why the sequence converges in distribution to . So, is lacunary almost statistically convergent of order in distribution to ζ.
Hence, is not lacunary almost statistically convergent of order in measure to ζ.
Corollary 1. If the uncertain sequence is lacunary almost statistically convergent of order in measure to , then the uncertain sequence is also lacunary almost statistically convergent of order in distribution.
Proof. By using Theorems 2 and 3, we can easily prove the desired result. □
Corollary 2. Lacunary almost statistical convergence of order in mean implies lacunary almost statistical convergence of order in distribution.
Proof. By using Corollary 1 and Theorem 1, we can easily prove the desired result. □
Remark 3. If the uncertain sequence is lacunary almost statistically convergent of order almost surely to ζ, then it does not imply lacunary almost statistical convergence of order in mean. Now, let us look at an example given below.
Example 4. Consider the uncertainty space to be with
Define the complex uncertain variables byfor and Thus, the sequence is lacunary almost statistically convergent almost surely to Considerwhere is an uncertainty distribution of . So, the sequence is not lacunary almost statistically convergent of order in mean to ζ.
Remark 4. If the complex uncertain sequence is lacunary almost statistically convergent of order almost surely to ζ, then it may not be lacunary almost statistically convergent of order in measure. Here is an example to demonstrate this.
Example 5. Consider the uncertainty space to be
Now, we define the complex uncertain variable asfor and Then, the sequence is lacunary almost statistically convergent of order almost surely to ζ. Also, for , we getas . Thus, is not lacunary almost statistically convergent of order in measure to ζ. Remark 5. If the uncertain sequence is lacunary almost statistically convergent of order in measure to ζ, then it may not be lacunary almost statistically convergent of order almost surely. Let us consider an example, which is given below.
Example 6. Consider the uncertainty space to be with a Borel - algebra and to be the Lebesgue measure. For the positive integer , there is an integer o such that where N is an integer between 0 and .
The complex uncertain variable is defined asfor and For some given and one can have Thus, is lacunary almost statistically convergent in measure to ζ. Further, we have for Therefore, sequence is also lacunary almost statistically convergent in mean to ζ. As, for any there exists an infinite number of closed intervals that are of the form containing , where represents an uncertain event, () = 1.
Thus, is not lacunary almost statistically convergent of order almost surely to
Proposition 1.
The complex uncertain sequence is lacunary almost statistically convergent of order almost surely and uniformly in k to if and only if for every and , Proof. Suppose that the sequence
converges to
almost surely and uniformly in
k in the sense of lacunary almost statistical convergence of order
. Then, there exists a set
with
such that for every
and every
, there exists
such that
This implies
Define the set
Then, clearly,
. By the duality axiom of an uncertain measure, we have
Now, fix any
and define the event
Then, clearly,
for all
. Therefore, the number of indices
for which
becomes negligible in lacunary density of order
, that is,
This gives the desired result. Conversely, suppose that for every
and
, we have
Then, for each fixed
, define
and we have
for “almost all”
j in lacunary density of order
. Define the set
Then, for each
, there exists
such that for infinitely many
j,
so
must belong to infinitely many
. But since the set of
with
has lacunary density of order
equal to zero, it follows that
. Hence, there exists a subset
with
such that for each
,
that is,
converges to
uniformly in
k and almost surely in the sense of lacunary statistical convergence of order
. □
Proposition 2.
The complex uncertain sequence is lacunary almost statistically convergent of order uniformly almost surely to if and only if for every and , we have Proof. Suppose that
is lacunary almost statistically convergent of order
uniformly almost surely to
. Then, there exists a set
such that
for arbitrary
, and on
, we have uniform convergence in
k, i.e., for every
, there exists
such that
This implies that for such
and any
,
and hence
So, for sufficiently large
r, the number of such
with this measure exceeding
becomes negligible:
Conversely, suppose the above condition holds. For each
, let
and define
. Then, for each
ℓ, the condition gives
This implies that for each
ℓ, there exists a set
such that
and for all
, there exists
such that
Define the exceptional set
On , the sequence converges uniformly in k to , i.e., the convergence is uniform almost surely. Therefore, is lacunary almost statistically convergent of order uniformly almost surely to . □
Theorem 4.
If the complex uncertain sequence is lacunary almost statistically convergent of order uniformly almost surely to , then the sequence is lacunary almost statistically convergent of order almost surely to .
Proof. By Proposition 2, for every
and
, we have
Now, fix any
. Observe that for each
,
Taking the union over
and applying the uncertainty measure, we obtain
Therefore, the set
is contained in
Since the lacunary density of order of the right-hand set tends to zero as , the same holds for the left-hand set. Hence, is lacunary almost statistically convergent of order almost surely to . □
Theorem 5. If the complex uncertain sequence is lacunary almost statistically convergent of order uniformly almost surely to , then the sequence is lacunary almost statistically convergent of order in measure to .
Proof. By Proposition 2, for every
and
, we have
Now, observe that for any fixed
k and
, we have
Taking the uncertainty measure on both sides yields
Thus, the index set
is a subset of the index set in Proposition 2, which has lacunary density of order
tending to zero. Hence,
is lacunary almost statistically convergent of order
in measure to
. □