Quantum-Inspired Attention-Based Semantic Dependency Fusion Model for Aspect-Based Sentiment Analysis

Abstract

Aspect-Based Sentiment Analysis (ABSA) has gained significant popularity in recent years, which emphasizes the aspect-level sentiment representation of sentences. Current methods for ABSA often use pre-trained models and graph convolution to represent word dependencies. However, they struggle with long-range dependency issues in lengthy texts, resulting in averaging and loss of contextual semantic information. In this paper, we explore how richer semantic relationships can be encoded more efficiently. Inspired by quantum theory, we construct superposition states from text sequences and utilize them with quantum measurements to explicitly capture complex semantic relationships within word sequences. Specifically, we propose an attention-based semantic dependency fusion method for ABSA, which employs a quantum embedding module to create a superposition state of real-valued word sequence features in a complex-valued Hilbert space. This approach yields a word sequence density matrix representation that enhances the handling of long-range dependencies. Furthermore, we introduce a quantum cross-attention mechanism to integrate sequence features with dependency relationships between specific word pairs, aiming to capture the associations between particular aspects and comments more comprehensively. Our experiments on the SemEval-2014 and Twitter datasets demonstrate the effectiveness of the quantum-inspired attention-based semantic dependency fusion model for the ABSA task.

1. Introduction

ABSA focuses on identifying sentiment polarities towards specific aspects within a given text, enabling fine-grained understanding of user opinions. Unlike general sentiment analysis, ABSA requires models to precisely align sentiment expressions with their corresponding aspect terms. This task is inherently complex due to the variability and ambiguity in natural language. Sentiment-related information is often scattered across the sentence, and not all contextual words are equally relevant to the target aspect. In many cases, only a few context words directly influence the sentiment orientation for a given aspect, while others serve as noise or distractors. Accurately capturing the aspect-context alignment is essential for reliable sentiment classification.

With the growth of product reviews and social media, ABSA has been widely used in many practical applications to provide more detailed and valuable insights by analyzing sentiment at a granular level. Traditional approaches struggle with this granularity, and even early deep learning models often treat all words with equal or fixed importance. A more selective mechanism is therefore needed to align aspect terms with their corresponding expressions of opinion. In response, attention mechanisms have emerged as an effective solution, allowing models to dynamically focus on the most informative parts of the context with respect to each aspect. For example, Tang et al. [1] deeply analyzed the correlation between contextual vocabulary and aspect-specific and Long Short-Term Memory (LSTM) networks, and significantly optimized the performance of the model by introducing differential attention weights. These weights accurately reflect the relative importance of contextual vocabulary in particular aspects of sentiment judgement. Subsequently, numerous studies have utilized the attention mechanism to meticulously delineate the intricate relationships between aspect terms and contextual opinion words. Since then some researchers have also used syntactic dependency trees to obtain richer structural and syntactic information. Dependency trees, as a kind of graph-structured data, can be better used to capture semantic knowledge using Graph Neural Networks (GNNs). Therefore, most of the recent work [2,3] on dependency trees is related to GNNs. In the context of the ABSA task, several studies have employed Graph Convolutional Networks (GCNs) in conjunction with pre-trained language models to integrate semantic and syntactic information to varying extents. However, the neighborhood aggregation mechanism inherent in GCNs often results in the averaging or dilution of the contextual information associated with aspectual words. Additionally, when addressing dependency relationships to construct dependency tree models, each layer of GNNs updates the node representation through message passing from neighboring nodes. This computation scales linearly with both the size of the graph and the number of layers, resulting in a computational cost that is significantly higher than the dot product computation utilized in attention mechanisms. While GNNs offer certain advantages in explicitly modeling dependencies, their drawbacks—including high computational complexity, reliance on graph structure, and limited capacity to manage long-distance dependencies—render them less efficient and flexible than attention mechanisms in some scenarios. Furthermore, the interpretability of these classical neural network models is frequently called into question.

Since most of the models mentioned above use real values to represent their features, the sparsity of the weight distribution is also an issue to be considered. Since complex-valued vectors have richer representation capabilities, some quantum probability-driven networks have been proposed in recent years to model different levels of semantic units by extending word embeddings to complex-valued representations. Compared to real vectors, complex vectors inherently offer greater representational flexibility by encoding both magnitude and phase, which is especially beneficial for capturing contextual nuances and interference effects in language. This has led to growing interest in quantum-inspired approaches that naturally adopt complex-valued vector spaces for linguistic modeling. Drawing inspiration from quantum theory, such methods aim to provide a more structured and interpretable framework, where semantic units are not just embedded in continuous spaces but are also governed by probabilistic and superpositional principles. Based on this background, Li et al. [4] constructed a complex-valued network for question–answer tasks, and Chen et al. [5] proposed a quantum entanglement module to learn inseparable correlation information between word states, confirming the richness and interpretability of the entanglement theory for semantic feature encoding. Yu et al. [6] constructed quantum entanglement-based sentence representations entangling two consecutive conceptual words together, and proposed two dimensionality reduction models using numerical computation of tensor multiplication to mine more semantic information. In addition to quantum entanglement, quantum coherence is another central concept in quantum theory, which provides unique inspiration for language systems. It is a fundamental concept in quantum theory that not only characterizes the quantum properties of the single-partite quantum state but also describes the correlations among multipartite quantum states. If a system exhibits quantum entanglement, it necessarily possesses quantum coherence. Since quantum entanglement can be used to encode text strings and quantify inter-word correlations using entanglement entropy, can quantum coherence also quantify inter-word correlations?

Driven by the compatibility of quantum language models with complex-valued vectors, we investigate the relationship between quantum coherence and textual semantics in quantum physics to address the ABSA task. While considerable effort has been devoted to designing high-performance graph converters, there has been limited research on applying quantum-inspired theoretical methods to the ABSA task. Therefore, we propose a quantum-inspired attention-based semantic dependency fusion model (it will be referred to subsequently by the acronym QEDFM), which aims to construct superposition states and characterize and fuse textual semantics and utterance dependencies by introducing complex-valued embeddings. This approach seeks to model the diversity and complexity of textual inter-word subsystems and enhance the coding efficiency of textual features. To further improve contextual dependencies, we also introduce a Complex-Valued Quantum Cross-Attention Mechanism (QCA) that efficiently fuses dependencies, enabling the model to focus on those dependencies in utterances that are most relevant to aspect terms, thereby significantly reducing computational overhead.

Our contributions are as follows:

• We propose a quantum embedding module to build complex semantic systems and, for the first time, quantify inter-word relations in terms of quantum coherence.
• We propose a quantum cross-attention mechanism that emphasizes specific combinations of qubit or quantum states with dependencies, aiming to enhance the efficiency of feature fusion in text and its associated dependencies.
• Through numerous experiments on the ABSA task, we demonstrate the effectiveness of QEDFM. Additionally, visualization experiments for the quantum embedding module offer an intuitive understanding of this coding approach. The relative entropy of coherence experiments further enhance the model’s interpretability.

2. Related Work

In this section, we first introduce the classic Neural Network Language Model (NNLM) and state-of-the-art GNN methods used for ABSA tasks in recent years. Then, we describe the development of language models based on the quantum probability theory and quantum-inspired neural networks in recent times.

ABSA based on deep learning has attracted widespread attention, and various neural network-based models have been proposed, resulting in significant performance improvements [7,8,9]. Following this, due to the fact that different parts of a sentence contribute differently to the overall sentiment of the sentence, attention mechanisms have been widely used to obtain aspect-specific representations. The Attention-based Long Short-Term Memory network with Aspect Embedding (ATAE-LSTM) proposed by Wang et al. [10] is notably representative in this field. In addition to LSTM networks, recently, many methods for handling ABSA tasks have used pre-trained language models as their baseline for extension research. For example, the authors of [11] explored a novel post-training method on the pre-trained language model BERT, called bert-pt, to improve its fine-tuning performance in review reading comprehension (RRC). Another important research direction in the field of ABSA is the construction of explicit syntactic structure models for prediction. For example, Sun et al. [3] and Zhang et al. [2] employed GNNs [12] to model dependency trees in order to leverage syntactic information and word dependencies. Along this direction, various GNN-based methods have been proposed to explicitly utilize syntactic information. Wang et al. [13] proposed R-GAT, which constructs a new tree structure rooted at the target aspect based on the remodeling and pruning of the general dependency tree structure, and encodes and performs sentiment analysis through a relational graph attention network (GAT) [14]. The authors of [15] designed DGEDT, a dual-Transformer architecture to support mutual reinforcement between flat representation learning and dependency graph-based representation learning. Tian et al. [16] utilized a method for ABSA dependency types in the Type-aware Graph Convolutional Network (T-GCN), where they used a toolkit to perform dependency parsing of the text, constructed a graph with dependency-type labels, applied an attention mechanism to weigh the edges, and finally, integrated contextual information from GCN layers through a multi-layer combination. BERT4GCN [17] enhances GCN by utilizing the output of intermediate layers in BERT and positional information between words, thereby better encoding dependency graphs for downstream classification. SSEGCN [18] utilizes an aspect-aware attention mechanism combined with self-attention to learn aspect-related and global semantics. A syntactic mask matrix was constructed based on syntactic distance and integrated into the attention score matrix to combine syntactic and semantic information. Finally, a Graph Convolutional Network was used to enhance node representations for the ABSA task. AG-VSR [19] employs two representations, namely Attention-Assisted Graphical Representation and Variational Sentence Representation, for the final classification. It processes the attention-modified dependency tree through a GCN module and generates samples from a distribution learned by a class-conditional VAE encoder–decoder structure. Zhao et al. [20] proposed a multitask learning model that combines the tasks of Aspect Polarity Classification (APC) and Aspect Term Extraction (ATE). This model simultaneously utilizes a series of Relational Graph Attention Network (RGAT) processes to encode the reshaped and pruned dependency trees. Additionally, it applies Multi-Head Attention (MHA) to associate the dependency sequences with aspect extraction, enabling the model to focus on dependency sequences that are more closely related to these aspects. Jiang et al. [21] proposed a method that distinguishes between global and local aspects based on Semantic Relative Difference (SRD) during the process of transforming word vector representations using BERT. This method integrates a context focus mechanism and a speaker-aware attention mechanism for feature extraction. It generates context word representations through a Double Bidirectional Long Short-Term Memory network and finally integrates a GCN to perform aspect-based sentiment classification.

Quantum-inspired or quantum language models have demonstrated impressive performance across various tasks. Sordoni et al. [22] were the first to apply quantum-like probabilities to the field of information retrieval, realizing a new approach to language modeling by modeling individual terms and composite dependencies as projectors in vector spaces. This research has opened up a new research paradigm for applying quantum theory to natural language processing, leading to a surge in studies on quantum theory applications in natural language understanding and sentiment analysis. Wang et al. [4] proposed a complex-valued network called CNM, which first unifies different linguistic units within a single complex-valued vector space to construct hybrid embeddings for word sequences. The complex-valued network is then built with well-constrained complex-valued components for semantic matching. Li et al. [23] introduced the concept of density matrices into convolutional neural networks, capturing more semantic information through the encoding of density matrices. They achieved the expected results in sentiment analysis tasks. Recently, numerous studies have achieved integrations and breakthroughs in semantic sentiment classification by drawing connections between the characteristics of quantum states and human understanding of linguistic knowledge. Specifically, Gkoumas et al. [24] represented sentences as quantum superposition states of positive and negative sentiment judgments on a complex-valued Hilbert space with a positive operator-valued measure. They represented unimodal classifiers as mutually exclusive observables and established a multimodal decision fusion mechanism. Subsequently, research on complex-valued language models inspired by quantum principles emerged for the ABSA task. Zhao et al. [25] investigated the Hilbert space representation of ABSA models and established complex-valued versions of three real-valued baselines: a complex-valued LSTM model, an LSTM model based on complex-valued attention, and complex-valued BERT models. The study demonstrated that complex-valued embeddings can carry additional information beyond real-valued embeddings. Given the parallelism between language systems and entanglement phenomena in superposition states, a study by Yu et al. [6] proposed a sentence similarity calculation method based on quantum entanglement. The study verified that using quantum entanglement and dimensionality reduction in sentence embeddings can enhance model performance in terms of semantic relationships and syntactic structures, while reducing time costs. Concurrently, research based on quantum neural network structures that encode sentences from superposition states into entangled states [5] has also confirmed the richness and interpretability of entanglement theory in semantic feature encoding. Furthermore, a study by Zhao et al. [26] applied quantum entanglement to cross-lingual ABSA tasks. In this study, aspect sentiments were projected as quantum superposition states in a complex-valued Hilbert space, and entangled models specific to shared languages were established across different languages.

Given the lack of methods that introduce quantum coherence in quantum states to address the challenges and risks associated with the subtask of Aspect Sentiment Classification (ASC) within ABSA, and inspired by the concept of quantum coherence in quantum theory, we propose a quantum semantic dependency fusion model for ABSA tasks, which can be quantitatively characterized by quantum coherence theory. Quantum superposition enables a qubit to represent multiple classical states simultaneously, allowing for the representation of more information with fewer qubits compared to classical methods. Furthermore, by calculating the relative entropy of coherence, we can enhance the interpretability of the model. By combining complex-valued encoding with a quantum cross-attention mechanism to fuse sequential dependencies, we can optimize the richness of text feature representations while subtly integrating dependency relations into language modeling.

3. Materials and Methods

Since our work is based on quantum theory, thanks to the research of Khrennikov [27] on quantum-like framework investigation and Alodjants et al. [28] on quantum-inspired user cognitive modeling process, we will introduce the knowledge of quantum theory in this section of the medium. Following this, we elaborate on our proposed model for the ABSA task. The overall structure of the QEDFM is illustrated in Figure 1. QEDFM consists of four components: sequence preprocessing, an embedding module, a dependency fusion module, and sentiment classification.

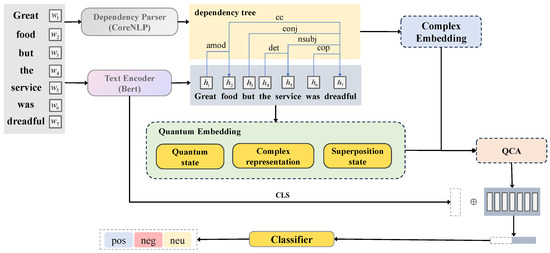
Figure 1. The structure of QEDFM.

3.1. Preliminaries on Quantum Theory

3.1.1. Quantum State

State vectors in quantum theory are defined on a Hilbert space H, which is a vector space with inner product operation, where the states of a quantum system are denoted as unit vectors [29,30]. We denote the complex unit vector $\overrightarrow{u}$ as the ket $|u⟩$, its conjugate transpose ${\overrightarrow{u}}^{†}$ is denoted as a bra $⟨u|$, and the inner and outer products of the two state vectors $|u⟩$ and $|v⟩$ are denoted as $⟨u|v⟩$ and $|u⟩⟨v|$.

A quantum state $|\psi ⟩$ is a complete description of a physical system and is a linear superposition of standard orthogonal bases in Hilbert space. The state of a system consisting of a single particle is called a pure state. The mathematical form of $|\psi ⟩$ is a complex-valued column vector. A pure state can also be expressed as a density matrix: $\rho =|\psi ⟩⟨\psi |$. When several pure states are mixed together in a classically probabilistic manner, we describe the system in terms of a mixed state. The density matrix can also represent a mixed state: $\rho ={\sum }_{i=1}^n{p}_i|{\psi }_i⟩⟨{\psi }_i|$, where $p_i$ denotes the probability distribution of each pure state, ${\sum }_{i=1}^n{p}_i=1$. Where the density matrix corresponding to the superposition state can be expressed as a weighted combination of the density matrices corresponding to the ground state. In this paper, a text sequence consists of a number of words, where each word can be viewed as a pure state, and this text sequence is a linear combination of these pure states.

Any quantum pure state can be described by a unit vector in H, which can be expanded over the ground state as

$$|q⟩=a_1|x_1⟩+\cdots +a_n|x_n⟩$$

(1)

where $\left\{\right|x_1⟩,|x_1⟩,\dots ,|x_n⟩\}$ are the standard orthogonal bases constituting the Hilbert space, The complex-valued probability amplitude is $\left\{a_i\right\}$ and satisfies ${\sum }_{i=1}^n{\left|a_i\right|}^2=1$. The set $\left\{{\left|a_i\right|}^2\right\}$ defines a classical discrete probability distribution; a quantum system can be in a superposition of different states at the same time, $|x_i⟩$, whose probability is given by ${\left|a_i\right|}^2$. If the quantum system is in Equation (1), then the system is physically in the $\left\{\right|x_1⟩,|x_1⟩,\dots ,|x_n⟩\}$ superposition state.

For any quantum state $\rho$, its state needs to satisfy $tr\left(\rho \right)=1$, ${\rho }^{†}=\rho$, and $\rho \ge 0$. In this paper, we focus on quantum pure states, so the inputs and outputs of the neural network module are complex-valued vectors representing pure states.

3.1.2. Quantum Evolution

In quantum mechanics, the Schrödinger equation describes how a system changes over time. It performs this by relating changes in the state of the system to the energy in the system, which is given by operators called Hamiltonian quantities. However, the Schrödinger equation is often difficult to solve, so the unitary transformation is applied to the Hamiltonian quantities to achieve a solution to the original equation [29]. The evolution is described by a unitary operator U, which is a bounded linear operator defined on a Hilbert space at the same time as a complex unitary matrix, satisfying $U{U}^{†}=I^2$, whose evolution is as follows:

$${\rho }^{\prime }=U\rho U^{†}$$

(2)

where as long as $\rho$ is a density matrix, then after unitary evolution, ${\rho }^{\prime }$ is also a density matrix. We consider this evolution process as a linear transformation process of the density matrix in this paper.

3.1.3. Quantum Coherence

Quantum coherence, as a pivotal physical resource, plays a crucial role in quantum information processing. In 2014, M.B. Plenio et al. [31] proposed a theoretical framework for quantifying quantum coherence. Within this framework, the quantification of quantum coherence necessitates first fixing a set of orthonormal bases $\left\{\right|i⟩\},i=1,\dots ,d$ in a d-dimensional Hilbert space. A quantum state is deemed incoherent if it can be expressed in the form of $\widehat{\delta }={\sum }_{i=1}^d{\delta }_i|i⟩⟨i|$; otherwise, it is considered a coherence state. In the theoretical framework of quantum coherence as a resource, there exist various measures for quantifying quantum coherence. This paper solely introduces two such measures: quantum relative entropy of coherence and l1-norm of coherence.

For quantum relative entropy $\mathcal{S}(\varrho \parallel \sigma )=tr[\varrho log\varrho ]-tr[\varrho log\sigma ]$, the induced measure can be denoted as ${\mathbb{C}}_r$. In addition to satisfying all the requirements for a coherence measure within the theoretical framework, ${\mathbb{C}}_r$ permits a closed-form solution, thus avoiding the need for minimization. Let $\delta ={\sum }_i{\delta }_i|i⟩⟨i|\in \mathcal{I}$, and for a given $\varrho ={\sum }_{i,j}{\varrho }_{i,j}|i⟩⟨j|$, denote ${\varrho }_{\mathrm{diag}}={\sum }_i{\varrho }_{i,i}|i⟩⟨i|$. Then, $\mathcal{S}(\varrho \parallel \delta )=\mathcal{S}\left({\varrho }_{\mathrm{diag}}\right)-\mathcal{S}\left(\varrho \right)+\mathcal{S}\left({\varrho }_{\mathrm{diag}}\parallel \delta \right)$, and hence,

$${\mathbb{C}}_r\left(\varrho \right)=\underset{\delta \in \mathcal{I}}{min}\mathcal{S}(\varrho ,\delta )=\mathcal{S}\left({\varrho }_{\mathrm{diag}}\right)-\mathcal{S}\left(\varrho \right)$$

(3)

Utilizing this formula, we can readily ascertain the maximum possible value of coherence for a given state. This holds true for any state $\varrho$ that satisfies the condition ${\mathbb{C}}_r\left(\varrho \right)\le S\left({\varrho }_{\mathrm{diag}}\right)\le log\left(d\right)$, where d is the dimensional Hilbert space, and it also provides the limit for the state of maximum coherence. This relative entropy measure has also been considered in the context of quantifying superposition.

For l1-norms, it serves as an intuitive measure of coherence that inherently relates to the off-diagonal elements of the considered quantum state. Therefore, it is desirable to quantify coherence through a functional that depends on these off-diagonal elements. $C_{l_1}\left(\varrho \right)={\sum }_{\begin{array}{c}i,j\\ i\ne j\end{array}}\left|{\varrho }_{i,j}\right|$ presents a widely adopted terminology for quantifier of coherence. If it satisfies all the requirements for a consistent measure within the theoretical framework of coherence, it would constitute another intuitive coherence monotone with an easy closed form. It would be a measure induced by the l1 matrix norm, ${\mathcal{D}}_{l_1}(\varrho ,\delta )={\parallel \varrho -\delta \parallel }_{l_1}={\sum }_{i,j}\left|{\varrho }_{i,j}-{\delta }_{i,j}\right|$. Thus, the l1 norm of coherence and the relative entropy of coherence constitute the most general monotonicity properties of coherence established in this paper.

3.1.4. Quantum Measurement

In quantum mechanics, the positive operator-valued measure [32] (POVM) removes a system state from uncertainty to a precise event by projecting a state to its certain corresponding basis state. The measurement process is described by an observable M:

$$M=\sum _{i=1}^n{\lambda }_i|m_i⟩⟨m_i|$$

(4)

where $\left\{\right|m_i⟩\}$ is the eigenstate of the measurement operator and the orthonormal basis in Hilbert space. $\left\{{\lambda }_i\right\}$ is the eigenvalue corresponding to the eigenstate. According to Born’s law [33], the probability of collapse of the pure state $|\psi ⟩$ to the ground state $|m_i⟩$ is calculated as follows:

$$P_i={\left|⟨m_i|\psi ⟩\right|}^2=tr\left(\rho \right|m_i⟩⟨m_i\left|\right)$$

(5)

where $\rho =|\psi ⟩⟨\psi |$. For a mixed state, the probability of collapsing to an eigenstate is the weighted sum of all pure state probability values. We use quantum measurements to compute the weights of utterance dependencies fused with textual features and identify the final sentiment.

3.2. Methodology

QEDFM consists of four components: sequence preprocessing, an embedding module, a dependency fusion module, and sentiment recognition. First, sentence dependency relations and sequential feature representations are extracted using various methods. Next, the sequential features are encoded into superposition states through the quantum embedding module, while the dependency relations are constructed into density matrices using complex-valued embeddings as input for the dependency fusion module. Subsequently, we employ a quantum cross-attention mechanism to treat the dependency relation features as an information source, allowing them to interact with the text sequence features. This approach facilitates bidirectional attention and information exchange between the dependency relation features and the text sequence features, thereby enhancing the model’s comprehension of sentence structure and semantics. Finally, we input the resulting aspect features into a classifier to recognize sentiments.

3.2.1. Sequence Preprocessing

For dependency parsing, we employ Stanford CoreNLP (https://stanfordnlp.github.io/CoreNLP, accessed on 15 December 2024) to construct the syntactic tree for each sequence. Through this method, we can obtain the corresponding density matrix, with element values representing the types of dependency relations. For the text encoder, we adopt the pre-trained BERT model [34] as the lexical encoder for computing sequential representations. The process is as follows:

$$W=embedding\left(S\right)$$

(6)

$$W^0,CLS=BERT\left(W\right)$$

(7)

where $W\in {\mathbb{R}}^{n\times d_w}$ denotes the $d_w$ dimensional word embedding matrix of the sentence S, and $CLS\in {\mathbb{R}}^d$ represents the representation of a special sequence used for global pooling, specifically the output of the BERT pooling layer.

3.2.2. Embedding Model

Complex-valued Embedding Module: The complex-valued embedding module is designed to construct the density matrix for sentence dependency relations, representing semantic dependency relations as pure states within a Hilbert space. This module embeds the dependency structure of sentences into a complex-valued Hilbert space through the form of complex tensors. In this module, we first map the structural information of the original dependency relations into real-part vectors u and imaginary-part vectors v through real-part embedding and imaginary-part embedding modules, respectively. Here, d represents the real-valued vector of the dependency relations. The formula is as follows:

$$u=Embeddin{g}_r\left(d\right)$$

(8)

$$v=Embeddin{g}_i\left(d\right)$$

(9)

Relying on the representation of complex numbers, these two vectors jointly constitute the complex-valued embedding vector w, with the calculation formula as follows:

$$w=u+i\ast v$$

(10)

where w represents the complex-valued embedding vector, u and v are the real and imaginary parts of the embedding representation of the dependency relation information, respectively, and i is the imaginary unit $(i=\sqrt{-1})$. This complex-valued density matrix not only provides a higher-dimensional embedding representation in terms of structural information but also lays the foundation for complex-valued operations in subsequent modules. Due to the fact that both coherence embedding and quantum cross-attention mechanisms are based on computations in the complex domain, the complex-valued density matrix can naturally support these operations in complex space, enabling deep interactions between dependency relations and quantum state encodings. The coupling between modules designed in this way can fully exploit the characteristics of complex-valued encodings, thereby enhancing the expressive power of model in modeling complex dependency relations and semantic information.

Quantum Embedding Module: In quantum mechanics, coherence refers to the existence of a definite phase relationship between quantum states, allowing the system to be in a superposition state. Coherence is one of the important characteristics distinguishing quantum systems from classical systems, enabling quantum states to be represented in complex-valued spaces through amplitude and phase. Therefore, we choose to simulate the fusion of multiple meanings between words by constructing superpositions among them within the sequence. In this paper, to satisfy the criteria for quantifying coherence, we fix a set of orthonormal bases $\left\{\left|e_1\right.⟩,\left|e_2\right.⟩,\dots ,\left|e_n\right.⟩\right\}$ in an n-dimensional Hilbert space $H_n$, which satisfy the orthonormality condition $⟨e_i\mid e_j⟩={\delta }_{ij},\forall i,j\in \{1,2,\dots ,n\}$, where ${\delta }_{ij}$ is the Kronecker delta function. The orthonormal bases we choose are the computational bases, denoted specifically as $\left|e_i\right.⟩={[0,\dots ,1,\dots ,0]}^T$, where the i-th position is 1 and the others are 0. We utilize the output $h_i=\left\{h_{i1},h_{i2},\cdots ,h_{in}\right\}$ from the last layer of BERT, where n denotes the embedding length and each $h_i$ represents the vector of a single word in the sequence. We map it onto the aforementioned fixed orthonormal basis to construct the quantum state $h_i=h_{i1}[1,0,\dots ,0]+h_{i2}[0,1,\dots ,0]+\dots +h_{in}[0,0,\dots ,1]$, where $h_{ij}$ represents the component of $h_i$ in the j-th dimension, and signifies the projection coefficient of $h_i$ onto the corresponding orthonormal basis. Taking the first word in the sequence as an example, it can be represented using Dirac notation as $\left|{\varphi }_1\right.⟩=h_{11}\left|e_1\right.⟩+h_{12}\left|e_2\right.⟩+\dots +h_{1n}\left|e_n\right.⟩$, where $|e_j⟩$ denotes the elements of the orthonormal basis, and $h_{1j}$ are the corresponding superposition coefficients satisfying the normalization condition ${\sum }_{j=1}^n{\left|h_{1j}\right|}^2=1$. Up to this point, we have been able to quantify the different degrees of semantic relatedness of different phrases or individual words in a sequence using relative entropy of coherence. Based on the calculation of coherence introduced in Section 3.1.3 on quantum coherence, we take the following sentence as an example: “great food but the service was dreadful!”. The entropy values of the phrases great food and service was dreadful are 3.0041 and 3.4688, which are significantly higher than those of other phrases. We constructed a mapping for the attention mask in the same manner and utilized it to create a complex-valued representation. Quantum states can be represented through density matrices, which describe the characteristics of the quantum state of the system. To convert the quantum state of each word into a density matrix, we perform a complex outer product, realizing the density matrix representation of the quantum state $|{\varphi }_i⟩$, which provides a probabilistic representation. The formula is as follows:

$${\rho }_i=\left|{\varphi }_i⟩⟨{\varphi }_i\right|$$

(11)

To further model the coherence and superposition properties between quantum states, we mix multiple quantum states through weighted combination and density matrix calculations, enabling information fusion among different words in the sequence and establishing indirect associations between words. This can be expressed in the following form:

$${\rho }_{mixed}=\sum _{i=1}^N{w}_i·{\rho }_i=\sum _{i=1}^N{w}_i·\left|{\varphi }_i⟩⟨{\varphi }_i\right|$$

(12)

where $w_i$ represents the weight assigned to the state of the i-th word, satisfying ${\sum }_{i=1}^n{w}_i=1$, and is computed from the hidden states O of BERT through a softmax function, i.e., $w_i=softmax\left(O\right)$. ${\rho }_i$ denotes the density matrix of the i-th word, and $|{\varphi }_i⟩$ represents the quantum state of the i-th word in the sentence. This global weighted summation indirectly simulates the interrelationships within the system, akin to the idea in quantum systems where the relationships between different particles are expressed through the superposition of multi-particle states. The quantum state $|{\varphi }_i⟩⟨{\varphi }_i|$ of each word influences the overall state ${\rho }_{mixed}$ of the sequence through the weights $w_i$. These weights perform a linear transformation on the density matrix through matrix multiplication, analogous to the operation of quantum gates on quantum states. Compared to the quantum circuits required for entanglement embedding, this approach significantly reduces computational complexity.

The mixing of quantum states reflects the contributions of various states to the overall features, thereby achieving a coherent representation among words. It determines how adjacent words interact or superpose with one another, shaping the relationships between words within the module and, to some extent, influencing their relative positions or degrees of association in the quantum state space. Ultimately, the superposition state is mapped back to classical information through projection measurement. In other words, the constructed density matrix is subjected to projection measurement to obtain a classical probability distribution, which is then utilized for subsequent model fusion and decision-making. Specifically, we use the constructed complex-valued measurement operator P to operate on the input density matrix $\rho$ to compute the probability distribution or outcome of the measurement. The measurement operator P consists of two parts, the real part $P_{real}$ and the imaginary part $P_{imag}$, and is formulated as follows:

$$P_{real}=K_{real}·K_{real}^T+K_{imag}·K_{imag}^T$$

(13)

$$P_{imag}=K_{imag}·K_{real}^T+K_{real}·K_{imag}^T$$

(14)

$$P=P_{real}+i·P_{imag}$$

(15)

where $K_{real}$ is the real part kernel, initially a unit matrix I, and $K_{imag}$ is the imaginary part kernel, initially a zero matrix. They are both complex-valued projection kernels used to define a subspace projection in a complex-valued space. The formula for the projection measure can be written as follows:

$${\rho }_{out}=tr\left(P{\rho }_{mixed}\right)$$

(16)

where $tr$ is the computational trace operation. To integrate the quantum representation with the classical output of BERT, we concatenate the original hidden states O, the density matrix representation ${\rho }_{\mathrm{mixed}}$, and the quantum measurement results ${\rho }_{\mathrm{out}}$ together to form the final feature representation:

$$\mathrm{F}=\left[O,{\rho }_{\mathrm{mixed}},{\rho }_{\mathrm{out}}\right]$$

(17)

This fused representation not only preserves BERT’s robust context modeling capabilities but also enhances the global expressive power and inherent structural information of the feature representation through quantum coherence.

3.2.3. Dependency Fusion Module

We use the quantum cross-attention mechanism to fuse the utterance sequence and dependency features, and the main process is shown in Figure 2. In the figure, ${\rho }_{\alpha }$ is the sequence feature representation after quantum embedding, and ${\rho }_{\beta }$ is the dependency feature after the complex-valued embedding modules are both fed into the three Q-linear layers, outputting K, V and Q, respectively, to achieve feature fusion through the cross-attention mechanism. Q-linear is analogous to the quantum unitary evolution of the linear layer to match the operations of the density matrix, as exemplified by ${\rho }_{\alpha }$ in Figure 2:

$$Q=U{\rho }_{\alpha }{U}^{†}$$

(18)

where U is a unitary matrix, and Q is a density matrix, while K and V of this set are obtained from ${\rho }_{\beta }$ by varying the unitary matrices in the same way. For pure state vectors, the attention score can be computed using the inner product, but since the input superposition state representation is in terms of density matrices, we introduced a linear transformation to compute the trace of the product of two density matrices according to Busemeyer [30]:

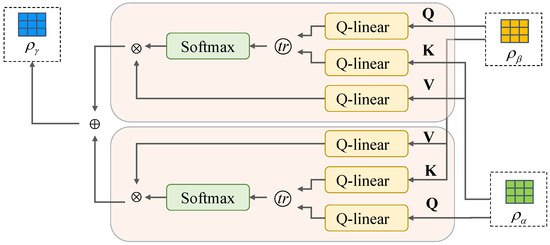
Figure 2. The structure of QCA.

$$\begin{array}{cc}\hfill tr\left({\rho }_{\alpha }{\rho }_{\beta }\right)& =tr\left(\sum _{i,j}{p}_i{p}_j|{\psi }_{\alpha ,i}⟩⟨{\psi }_{\alpha ,i}|{\psi }_{\beta ,j}⟩⟨{\psi }_{\beta ,j}|\right)\hfill \\ \hfill & =tr\left(\sum _{i,j}{p}_i{p}_j⟨{\psi }_{\alpha ,i}|{\psi }_{\beta ,j}⟩\left|{\psi }_{\alpha ,i}⟩⟨{\psi }_{\beta ,j}\right|\right)\hfill \\ \hfill & =\sum _{i,j}{p}_i{p}_j{⟨{\psi }_{\alpha ,i}|{\psi }_{\beta ,j}⟩}^2.\hfill \end{array}$$

(19)

Equation (19) proves that $tr\left({\rho }_{\alpha }{\rho }_{\beta }\right)$ is a weighted sum of inner products of pure states. In fact, this is a generalization of the inner product from vectors to density matrices, called the trace inner product [35,36]. Therefore, we compute the attention score between K and Q via the trace inner product, which is represented as

$$S=tr\left(K_{\beta }{Q}_{\alpha }\right)$$

(20)

$$\mu =Softmax\left(S\right)$$

(21)

$${\rho }_{\alpha \beta }=\mu V$$

(22)

where ${\rho }_{\alpha \beta }$ denotes the result of the operation with ${\rho }_{\alpha }$ as Q and ${\rho }_{\beta }$ as K. This is a one-way computation in the cross-attention mechanism. After that, the dependency features are used as Q and the utterance sequence features are used as K and V. The same operation is performed to obtain ${\rho }_{\beta \alpha }$. After performing the same operation, the results from both directions are combined to yield new features, which can be mathematically represented as

$$\begin{array}{cc}\hfill {\rho }_{\gamma }={\rho }_{\alpha \beta }+{\rho }_{\beta \alpha }& =Softmax\left(tr\left(K_{\beta }{Q}_{\alpha }\right)V_{\beta }\right)+Softmax\left(tr\left(K_{\alpha }{Q}_{\beta }\right)V_{\alpha }\right)\hfill \end{array}$$

(23)

where $Q_i$, $K_i$, $V_i$ denote the different feature sources as Q, K, V, ${\rho }_{\gamma }$ is the final density matrix.

3.2.4. Sentiment Classification

We use the output of QCA as the final word representation, and average pooling over all word representations from the same aspect to extract the aspect representation, formulated as

$$r={\displaystyle \frac{{\sum }_{j=1}^k{\rho }_j^{\gamma }}{k}}$$

(24)

where $r\in {\mathbb{R}}^d$ is an aspect representation, j is a word index in a word sequence, and k is a k-word aspect. Then, r is spliced with the semantic information CLS of the entire input sequence and fed into a classifier consisting of a linear function and softmax to produce a probability distribution about the polarity decision. Finally, the parameters are optimized based on cross-entropy loss.

3.3. Datasets

We conducted experiments on three publicly available ABSA benchmark datasets: Restaurant and Laptop from SemEval 2014 [37], which consist of reviews related to restaurants and laptops, respectively; and the Twitter dataset, which was constructed by Dong et al. [38], consisting of Twitter posts. Table 1 shows the statistics of the datasets.

Table 1. The dataset in our experiment. #Pos, #Neg, and #Neu denote the number of instances with positive, negative, and neutral moods, respectively.

	Train Data			Test Data
Domain	#Pos	#Neg	#Neu	#Pos	#Neg	#Neu
RESTAURANT	2159	800	632	730	195	196
LAPTOP	980	858	454	340	128	171
TWITTER	1567	1563	3127	174	174	346

This table summarizes the dataset used in our experiments.

4. Results

This section describes the comparison experiments, ablation experiments, and visualization experiments that we performed. The model was trained using the Adam optimizer with an initial learning rate of 0.001 and Xavier uniform initialization. The optimal hyperparameter settings were selected based on performance across multiple datasets during development. The number of epochs was set to 15, with a batch size of 16. For dropout regularization, we used 0.5 for input and feedforward layers, and 0.2 for attention modules. The BERT encoder was initialized with bert-base-uncased and fine-tuned with a learning rate of 2 × 10⁻⁵ and a dropout of 0.5, using a weight decay of 0.01. The source code is publicly available at Github (https://github.com/Drake8023/QEDFM, accessed on 15 May 2025).

4.1. Baselines

We compare QEDFM to a state-of-the-art ABSA baseline, where both use a pre-trained model (BERT) approach:

BERT [34] is an ordinary BERT model that makes predictions by feeding sentence–aspect pairs and using a representation of [CLS].

BERT-PT [11] post-trains BERT using an external domain-specific corpus to improve the performance of the model.

R-GAT-BERT [13] is R-GAT, which uses pre-trained BERT instead of BiLSTM as an encoder.

DGEDT-BERT [15] is the DGEDT model, which uses a pre-trained BERT instead of BiLSTM as an encoder.

BERT4GCN [17] enhances GCN using the output of the BERT middle layer and positional formation between words.

TGCN-BERT [16] distinguishes relation types by attention and learns features from multiple GCN layers using a collection of attention layers.

SSEGCN-BERT [18] acquires semantic information through attention and equips it with syntactic information with minimum tree distance.

AG-VSR-BERT [19] injects semantic information by correcting incorrect dependency connections through Attention-Assisted Graph Representation (A2GR) and Variable Sentence Representation (VSR).

C-BERT [25] constructs complex-valued word representations by treating real and imaginary contextual representations as linear functions of the dropout of the BERT output vector.

MHA+RGAT+BERT-ATE-APC [20] is a multitask learning model that integrates BERT and RGAT models for APC and ATE tasks, while associating dependency sequences with aspect extraction via MHA.

DCASAM [21] integrates BERT while using Context Dynamic Masking (CDM) and Talking Head Attention (THA) mechanisms to extract global and local contextual features, and finally captures structural information using a densely connected GCN.

4.2. Main Results

Table 2 presents the results of the experiments conducted on the Restaurant, Laptop, and Twitter datasets. The findings indicate that QEDFM consistently yields the best results in most cases.

Table 2. Comparison of models with various datasets. The best results are in bold, and the second-best results are underlined. ^† indicates that the baseline was rerun according to the open-source code and passed the significance statistic.

Models	Restaurant		Laptop		Twitter
	Acc.	F1	Acc.	F1	Acc.	F1
BERT †	85.97	80.09	79.91	76.00	75.92	75.18
BERT-PT	84.95	76.96	78.07	75.08	-	-
R-GAT+BERT	86.60	81.35	78.21	74.07	76.15	74.88
DGEDT+BERT	86.30	80.00	79.80	75.60	77.90	75.40
BERT4GCN	84.75	77.11	77.49	73.01	74.73	73.76
TGCN+BERT	86.16	79.95	80.88	77.03	76.45	75.25
SSEGCN+BERT †	86.15	79.96	79.75	76.38	77.70	76.36
AG-VSR+BERT	86.34	80.88	79.92	75.85	76.45	75.04
C-BERT	86.70	81.41	79.94	76.35	75.29	73.80
MHA+RGAT+BERT-ATE-APC †	86.88	81.16	80.56	77.00	76.59	74.67
DCASAM	86.70	81.19	80.56	77.00	76.88	75.25
QEDFM	87.31	81.88	80.85	78.35	77.40	76.45

In the Restaurant dataset, our QEDFM model outperforms the other ABSA baseline models in both accuracy (Acc.) and F1 score (F1) by margins of 0.53% to 0.71%. Although the Laptop and Twitter datasets do not achieve the highest results in terms of accuracy and F1 score, they remain competitive and reach the next best performance level. Several factors may contribute to this outcome, including the effectiveness of both DGEDT and TGCN models. These models leverage GNN to enhance aspectual representations by learning syntactic dependency trees or induced trees, which capture additional structural patterns for syntactic analysis, thereby improving performance. Additionally, the presence of certain special symbols in the comments within the dataset may introduce some noise, partially obscuring the semantic information.

We also tested our model for statistical significance by bootstrap resampling over 1000 iterations against the baseline model labeled by the dagger symbol in Table 2. For example, when comparing our model with SSEGCN, the 95% confidence interval for the difference in accuracy is [0.0861, 0.1297], with an average difference of 0.1079, indicating a statistically significant improvement. Similar results were observed on the Laptop and Twitter datasets. Overall, our approach of incorporating quantum embedding to represent the fusion of semantic features with dependency information demonstrates comparable superiority to classical modeling approaches for the current ABSA task.

4.3. Ablation Experiment

We performed ablation experiments to demonstrate the effectiveness of our quantum cross-attention mechanism with quantum coding. We made three sets of comparisons. In the QE-QA configuration, we focused attention solely on the utterance sequence features as Q and the dependency features as K and V, using the resulting feature matrix as input for subsequent classification. In the QE configuration, we directly superimposed the feature matrix obtained after quantum embedding with the dependencies derived from complex-valued embedding to ensure that the dependencies were preserved in comparison to the other methods. To demonstrate the effectiveness of our quantum coding, we also added a set without any (w/o any), using solely the output of the pre-trained model. The results are presented in Table 3. Initially, the comparison between QE and w/o any shows that our quantum embedding approach yields a significant improvement for the pre-trained model. The quantum self-attention mechanism, when applied on top of this, provides a slight enhancement in accuracy and F1 score due to the incorporation of dependency information. Furthermore, through the quantum cross-attention mechanism, the resultant accuracy is 0.54% to 0.95% higher compared to all other methods, while the F1 score improves by 0.09% to 1.57%, significantly enhancing the fusion effect of the dependent information. Overall, our quantum embedding approach alone considerably improves the results of the pre-trained model, and when combined with the attention mechanism, it effectively integrates the dependent information, highlighting the superiority of our quantum embedding and quantum cross-attention mechanism.

Table 3. Results of ablation experiments on the Restaurant dataset. The best results are in bold.

Models	Accuracy (Acc.)	F1 Score (F1)
QE-QCA	87.31	81.88
QE-QA	86.77	81.79
QE	86.59	81.54
w/o any	85.52	79.66

4.4. Case Study

We present several test cases in Table 4 to demonstrate the ability of QEDFM to differentiate between various aspects. These reviews were randomly selected from different datasets. The results indicate that QEDFM is more effective at determining the sentiment polarity of one or more aspects compared to the baselines. This improvement is attributed to the deep fusion of dependency features facilitated by the quantum cross-attention mechanism, which highlights the benefits of quantum-inspired modeling for syntactic and semantic context integration.

Table 4. A number of test cases were extracted from both datasets, where P stands for positive, N for negative, and O for neutral sentiment polarity. These examples illustrate predictions on a three-class aspect-based sentiment classification task.

Sentence	R-GAT	SSEGCN	QEDFM	True Label
Great food but the service was dreadful!	N-N	P-N	P-O	P-O
Can you buy any laptop that matches the quality of a MacBook?	P	O	P	P
Biggest complaint is Windows 8.	O	N	N	N
Try the rose roll (not on menu).	P-N	P-O	P-O	P-O

The bolded text indicates the aspect words in this sentence.

4.5. Post Hoc Interpretability

In quantum information theory, the quantum relative entropy $\mathcal{S}$ serves as a measure of the distinguishability between two quantum states. This paper provides a quantitative representation of the relationships between different words following quantum embedding by quantifying coherence based on relative entropy. The relative entropy of coherence is introduced in the quantum coherence Section 3.1.3, and its calculation formula can be expressed as follows:

$${\mathbb{C}}_r\left(\varrho \right)=\underset{\delta \in \mathcal{I}}{min}\mathcal{S}(\varrho ,\delta )=\mathcal{S}\left({\varrho }_{\mathrm{diag}}\right)-\mathcal{S}\left(\varrho \right)=-\sum _{x=1}^K{\lambda }_{x}log\left({\lambda }_x\right)+\sum _{y=1}^K{\lambda }_{y}log\left({\lambda }_y\right)$$

(25)

where ${\lambda }_x$ represents the states of the main diagonal elements only, ${\lambda }_y$ represents all states, and K is the minimum dimension of the subsystem.

Table 5 shows the most and least selected lexical phrase after we sorted the test data in both Laptop and Restaurant datasets by calculating their inter-word relative entropy of coherence after quantum embedding. Since the quantized concept establishes that the maximum coherence limit is $log\left(d\right)$, and given that the dimension of our density matrix is 100, the values falls within a range of 4. We consider values less than 2.5 to indicate low coherence, while values greater than 2.5 suggest high coherence. It can be observed that most word pairs exhibiting high coherence are fixed collocations or combinations of words that represent specific objects. For example, ask for and after all are abstract fixed collocations with high degrees of association, making them difficult to separate independently. Words like the thunder represent specific objects, and there is a clear modifier–referent relationship between the and thunder, which may indicate strong semantic coupling between them. Therefore, the density matrices of these phrases may exhibit more complex interactions, leading to higher coherence. These phrases play more important semantic roles in the context and are information-intensive, necessitating a more precise capture of their semantic associations to enhance the understanding capabilities of the model. Phrases with lower relative entropy, on the other hand, mostly serve as grammatical connecting structures, for example, to be or there was lack strong semantic connections and exhibit weaker dependencies between words. Words like is and a function more as grammatical auxiliaries. Therefore, they manifest as simple, basic syntactic functions or state descriptions with less information, making them more suitable as grammatical auxiliary structures with relatively straightforward roles. The model can appropriately simplify its processing of these phrases, resulting in correspondingly lower coherence.

Table 5. Semantic relative entropy of coherence in the two datasets.

Type	Word Combinations
Most relative in Laptop	(the, thunder), (the, process), (ease, of), (after, all), (the, mac)
Least relative in Laptop	(to, be), (there, are), (are, a), (it, is), (is, a)
Most relative in Restaurant	(not, only), (tells, us), (ask, for), (my, friend), (thick, fries)
Least relative in Restaurant	(it, was), (is, a), (there, was), (of, the), (has, a)

4.6. Visualization

We took a closer step to visualize the effect of model encoding. Figure 3a,b show the feature matrices after we extracted the quantum embedding in the model versus after only the pre-trained model, and visualized the inter-word correlations by plotting them using cosine similarity on the features of the text sequences after quantum encoding versus after only the pre-trained model, respectively. The corresponding sentence is “great food but the service was dreadful!” In terms of human language, the key to the expression of sentiment polarity in this sentence lies in the meaning after but, where the most important sentiment information of service is dreadful, which indicates that the subject of this sentence has a negative sentiment tendency, and we can see that after quantum embedding, our model learns a richer semantic information of the whole sentence, focusing on the difference between the words service and dreadful, and ignores great food, which interferes with the sentiment expression. On the other hand, the inter-word relationship without quantum embedding still has a lot of relevance in the first half of the sentence.

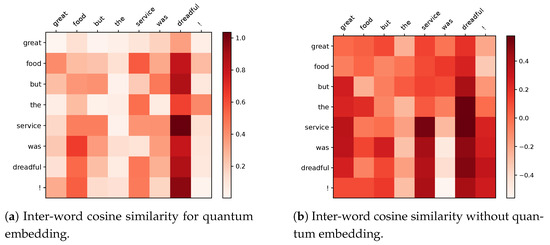
Figure 3. Comparison of inter-word cosine similarity with and without quantum embedding.

To further illustrate the advantages of quantum embedding in semantic representation, we constructed a kernel density plot of word pair distances to compare the performance of quantum embedding with that of a pre-trained model (BERT) in terms of the density matrix after processing sequences (see Figure 4). We observe that the word pair distances in quantum embedding are concentrated in shorter distance intervals, with density values in this region significantly higher than those of the pre-trained model. This indicates that superposition state encoding can more effectively capture semantically related word pairs, thereby enhancing semantic focus. In contrast, the word pair distance distribution produced by the pre-trained model is relatively uniform, suggesting that it possesses weaker semantic distinction capabilities for word pairs and is unable to effectively differentiate between semantically related and unrelated word pairs. The experimental results demonstrate that quantum embedding not only outperforms the pre-trained model in terms of density concentration but also exhibits stronger focusing and discrimination capabilities for semantically related word pairs, which holds significant application value in semantic understanding tasks.

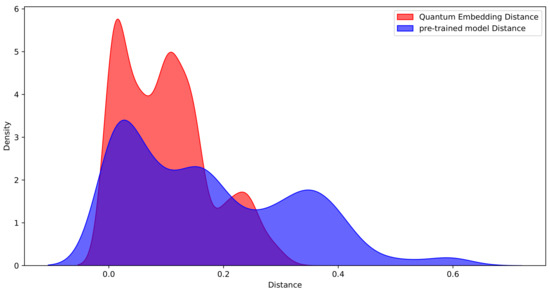
Figure 4. Kernel density map.

5. Conclusions and Discussion

In this paper, we analyze the advantages of quantum embedding in enhancing semantic understanding, as well as the challenges associated with model interpretability. To address these challenges, we propose a quantum embedding-based approach and present the Dependency Fusion Method for ABSA tasks. By introducing superposition states, we model the inherent uncertainty in human sentiment expressions, enabling the effective integration of sentence sequences that exhibit conflicting sentiment polarities. Furthermore, we propose a novel quantum cross-attention mechanism that leverages dependency relations as a guiding framework, thereby enabling the model to more accurately discern sentence sentiment polarity. Comprehensive experiments conducted on publicly available benchmark datasets validate the efficacy of our proposed method. In future research, we intend to integrate our cross-attention mechanism with graph convolution techniques to enhance the structured information fusion of dependency relations, aiming to achieve more sophisticated feature fusion within superposition state encoding.